ABC, 25 de Octubre de 2021
CIENCIA - El ABCdario de las matemáticas
Ernesto Estrada

El matemático y filósofo Frank P. Ramsey creó un teorema que estudia las condiciones que se han de cumplir para que en un conjunto dado aparezca un cierto tipo de orden

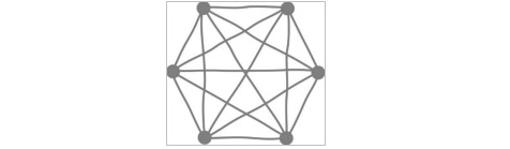
Hoy quiero comenzar esta sección proponiéndoles un pasatiempo para jugar entre dos personas. Solo necesitaremos un papel y dos lápices de colores. Con un lápiz normal dibujamos en el papel seis puntos conectados todos entre sí, como se ilustra en la Figura 1.

Figura 1

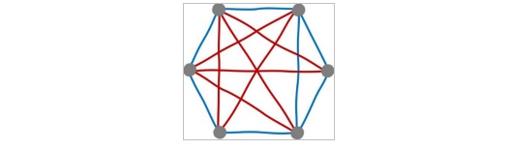
Cada jugador elegirá un color y ambos alternarán sus turnos. En cada turno el jugador correspondiente coloreará una de las líneas del gráfico con su color. Si una línea ya ha sido coloreada por un jugador, el otro no podrá volverla a colorear. Cada jugador evitará formar triángulos del mismo color y el juego terminará cuando un jugador se vea obligado a completar un triángulo de su color, en cuyo caso perderá el juego. En la Figura 2 hay un ejemplo en el que pierde el azul.

Figura 2

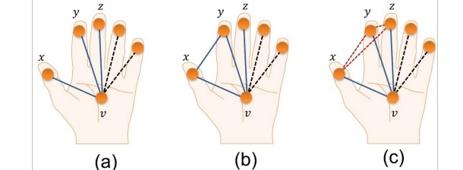
A diferencia de juegos como el de cruces y rayas, en este juego siempre habrá un ganador. Sí, os lo garantizo: siempre habrá un jugador obligado a completar un triángulo del mismo color. A ver, no es que me haya pasado todo el verano completando el juego con dos colores y me haya convencido a mí mismo de que siempre hay un ganador. En matemáticas, las cosas funcionan de otra manera: existe un teorema que demuestra que este es el caso. Y lo demostraremos aquí en un momento.

Para hacer las cosas más atractivas cambiemos las tornas y pongamos el siguiente escenario. Consideremos un grupo de seis personas de forma tal que entre cada par de ellos exista una relación. Ya sabemos que dichas relaciones podrían ser de amistad o de enemistad. Pues bien, nuestro teorema se puede formular de la siguiente manera:

Teorema: en cualquier grupo de seis personas mutuamente conectadas, habrá tres quienes serán mutuamente amigos, o tres que serán mutuamente enemigos.

Si consideramos que cada punto (vértice o nodo) de la Figura 1 representa a cada individuo y que las relaciones de amistad se representan con un color (digamos azul) y las de enemistad con el otro (digamos rojo), este teorema nos dice que siempre habrá un triangulo del mismo color y por tanto un ganador del juego que antes propusimos.

Veamos como demostrar el teorema. Solo necesitamos una de nuestras manos. En la palma de la mano dibujamos (imaginariamente) el punto que denominaremos v. El vértice v, como cualquier otro en la Figura 1, puede tener hasta 5 conexiones coloreadas. Por tanto, está claro que v puede estar unido a tres líneas del mismo color, ya sean rojas o azules. Pongamos nuestra atención solo en estas tres líneas del mismo color que se conectan a v, tal como se ilustra en el panel (a) de la Figura 3. Digamos que los individuos x, y, z son amigos de v. Si cualquier par de estos individuos x, y, z son amigos entre sí, entonces se habrá completado un triángulo de amistad junto a v, tal como se ilustra en la Figura 3 (b). Si tal par de amigos no existiese entre x, y, z, entonces es evidente que los tres individuos x, y, z son mutuamente enemigos y se completaría un triangulo de color rojo, como se ilustra en la Figura 3 (c). Con esto hemos demostrado que siempre existirá un triángulo azul o rojo, que siempre habrá una triada de amigos o de enemigos, y que siempre habrá un ganador en el juego.

Figura 3

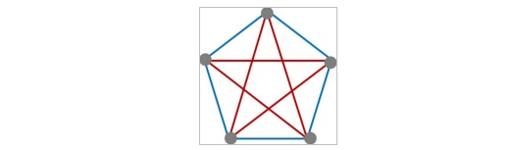
Si usásemos un número menor de vértices en la red inicial, por ejemplo 5 en lugar de 6, entonces podría haber un empate entre los dos jugadores, ya que no necesariamente tiene que existir un triángulo del mismo color (ver ejemplo en la Figura 4). O sea, que el mínimo número de personas mutuamente conectadas necesarias para que exista un triángulo de amistad o de enemistad es de seis.

Figura 4

Este teorema fue demostrado por el matemático, filósofo y economista inglés Frank P. Ramsey en 1930, el año de su muerte a los 27 años. En realidad, Ramsey demostró algo mas general y profundo. Para ello necesitamos un poco de terminología. Una red como la mostrada en la Figura 1 en que cada par de vértices están conectados se denomina una red completa. En el caso de la Figura 1 sería una red completa de 6 vértices y se representa por K6. Un triángulo sería una red completa de 3 vértices: K3. Por tanto, lo que hemos hecho antes es encontrar el número más pequeño r tal que exista: (i) una subred completa K3 cuyas aristas estén coloreadas en azul, o (ii) una subred completa K3 cuyas aristas estén coloreadas en rojo. Este número se denomina número de Ramsey y se expresa: R(3,3)=6. Ramsey demostró que el número R(n, m) siempre existe. Aquí consideraremos solo los casos cuando n=m, como el caso de los triángulos rojos o azules.

Veamos algunos ejemplos: R(4,4)=18, lo que significa que si quisiéramos jugar a completar cuartetos de vértices todos conectados entre si del mismo color, garantizando que no haya empates, tendríamos que hacerlo en una red completa de 18 vértices. Y ¿si quisiéramos completar quintetos de vértices del mismo color? Bueno, entonces solo podríamos decir que necesitaríamos una red completa de entre 43 y 49 vértices. O sea, que lo que sabemos es que 43≤R(5,5)≤49. Si aumentamos el tamaño del patrón que queremos completar estas cotas se hacen cada vez mas amplias, por ejemplo: 102≤R(6,6)≤165; 205≤R(7,7) ≤540;…; 798≤R(7,7)≤23,556.

Se cuenta que el matemático Pál Erdős comentó jocosamente que si una fuerza alienígena demandara de la humanidad el valor exacto de R(5,5) o en su defecto destruiría la Tierra, se podrían dedicar todos los super-ordenadores y a todos los matemáticos del mundo a resolver el problema e intentar encontrar dicho valor exacto. Pero, si en lugar de este valor los alienígenas preguntaran por R(6,6), entonces, habría que pensar no en hallar el número en cuestión sino en cómo destruir a los alienígenas.

Pensemos en alguien que no ha leído este artículo y que no conoce el teorema de Ramsey. Supongamos que esta persona es muy buen observador y se ha dado cuenta de que cada vez que asiste a una fiesta, cóctel o reunión, de cada seis personas mutuamente relacionadas siempre hay tres amigos o tres enemigos. Nuestro 'investigador' formula por tanto la hipótesis de que este 'fenómeno' es digno de estudiar. Así, alguien con interés en el tema, busca en las grandes bases de datos y con la ayuda de técnicas informáticas 'demuestra' que realmente la hipótesis es cierta. Nuestros hipotéticos investigadores han usado técnicas de Big Data y encontrado una correlación o patrón en los datos analizados. Pero sabemos que no hay nada especial en dicha observación. Las matemáticas demuestran que tal relación necesariamente existe por pura combinatoria sin que intervenga ninguna ley social o de otra naturaleza.

Pues bien, resulta que el Teorema de Ramsey y otro teorema del estilo publicado a principios del siglo XX por el matemático Bartel L. van der Warden imponen serios límites al uso 'indiscriminado' del Big Data. Van der Warden, al contrario que Ramsey que solo vivió 27 años, vivió 92 años. En 1927 demostró un teorema el cual garantiza que, una secuencia de longitud mayor que c, compuesta por c elementos distintos contiene una progresión geométrica de k apariciones del mismo elemento. Así tenemos el número de van der Waerden W(c, k) que será la longitud mínima de una secuencia de c elementos distintos conteniendo al menos k repeticiones en progresión geométrica del mismo elemento. Los elementos de estas secuencias pueden ser palabras, letras, números o colores. Por ejemplo, si tenemos solo dos elementos diferentes y tres repeticiones, entonces la longitud mínima de la secuencia es 9, o sea, W(2,3)=9. Pongamos por ejemplo la secuencia de votos que una persona emite a favor, (S), o en contra (N), de varias propuestas. Si el número de propuestas es menor que nueve, entonces no necesariamente tendrá que existir un patrón en las votaciones. Por ejemplo, en la secuencia

S N S N N S N S

no hay ningún patrón, ninguna regularidad. Pero intentemos añadir una nueva propuesta. Si el voto es en contra:

S N S N N S N S N

vemos que aparece un patrón en que los N están separados por un solo elemento. Si el voto es un S:

S N S N N S N S S

vemos que aparece un patrón en el que los S están separados por 2 elementos. Estos patrones no están causados por ninguna ley social o tendencia política, surgen como una necesidad combinatoria de la propia secuencia.

Los números de van der Waerden son más difíciles de obtener que los números de Ramsey. Los números W(2,4)=35, W(2,5)=178 se conocen desde los años 1970, pero W(2,6)=1,132 se obtuvo solo en 2008 y para los números superiores solo tenemos cotas. Por ejemplo, se sabe que W(2,7)>3,703,…,W(2,10)>103,474. Cuando el número de elementos distintos en la secuencia crece, los números de van der Waerden se convierten en verdaderos monstruos. Por ejemplo, con 6 elementos diferentes (digamos 6 colores diferentes) y 10 repeticiones, el número es mayor de 58 millardos: W(6,10)>58,292,388,322. Dicha cota se demostró solo en el año 2019 .

Las implicaciones que tanto el teorema de Ramsey como el Teorema de van der Waerden tienen sobre el uso de Big Data son enormes. Ellas fueron estudiadas por Giusepe Longo y Cristian Calude en un trabajo publicado en 2017 con el título (en Ingles): 'El diluvio de correlaciones falsas en Big Data'. En este trabajo los autores demuestran que las bases de datos muy grandes necesariamente contienen muchas correlaciones arbitrarias, puramente fortuitas. Las mismas son debidas al tamaño, no a la naturaleza, de los datos. Incluso, dichas correlaciones pueden aparecer en bases de datos generadas de forma totalmente aleatoria. Los autores concluyen que la mayoría de las correlaciones encontradas de esta forma son falsas. Esto no quiere decir que todas las correlaciones de las cuales se hayan extraído conclusiones con el uso de Big Data sean falsas, sino que, si tomamos todas las correlaciones posibles en una base de datos lo suficientemente grande, la mayoría de ellas serán puramente fortuitas. Estas correlaciones fortuitas son la consecuencia de las restricciones impuestas por los Teoremas de Ramsey y de van der Waerden, o como escribirían los matemáticos Ron Graham y Joel Spencer son debidas a que «el desorden completo es una imposibilidad. Cada gran conjunto de números, puntos u objetos contienen necesariamente un alto patrón de regularidad». Pero aquí los autores se referían a regularidad matemática, no de otra índole.

El trabajo de Longo y Calude venía a responder de forma científica a las fanfarrias que algunos daban al Big Data como la panacea que resolverá todos nuestros problemas. Por ejemplo, Chris Anderson, quien es periodista, escritor, físico y editor en jefe de la revista Wired, había publicado en 2008 en su revista el artículo titulado (en inglés): 'El fin de la teoría: el diluvio de datos convierte al método científico en obsoleto'. Allí Anderson expresaba que «con suficientes datos, los números hablan por ellos mismos». «La correlación reemplaza a la causalidad, y la ciencia puede avanzar incluso sin modelos coherentes, teorías unificadas» o que «La correlación es suficiente ... Podemos arrojar los números a los clústeres informáticos más grandes que el mundo haya visto y permitir que los algoritmos estadísticos encuentren patrones donde la ciencia no puede».

Pues bien, ignoremos a Ramsey y a van der Waerden, y sigamos a Anderson. A continuación, les doy algunas correlaciones ridículas que se pueden obtener a partir de grandes colecciones de datos. El lector puede obtener las suyas propias aquí. Para medir la significación estadística de una correlación se usa, entre otros parámetros, el coeficiente de correlación lineal, r². Este es un numero entre 0 y 1, con valores de 1 si los datos están perfectamente correlacionados y de cero si no están correlacionados en absoluto. Pues bien, podemos encontrar que: (i) «el gasto norteamericano en ciencia y tecnología correlaciona con el número de suicidios por ahorcamiento, estrangulación y asfixia» con un coeficiente de correlación lineal de r²=0.996; (ii) que «la tasa de divorcio en Maine correlaciona con el consumo per cápita de margarina» con r²=0.985; que «el consumo per cápita de queso mozarela correlaciona con el número de doctorados en ingeniería civil» con r²=0.919 y por último «que el número de doctorados concedidos en matemáticas correlaciona con la cantidad de uranio almacenado en la plantas nucleares norteamericanas» con r²=0.907. Todas estas correlaciones son muy significativas estadísticamente, pero sin ningún sentido.

Sin embargo, como bien definía el filósofo Leszek Kolakovski en su ley de la cornucopia infinita siempre habrá algunos a los que «nunca le escasearán argumentos para respaldar cualquier doctrina que se desee creer por las razones que sean». Lo que las matemáticas nos enseñan en este caso, y que los propulsores del Big Data como sustituto de la mente racional y analítica deberían escuchar, es que «demasiada información tiende a comportarse como muy poca información» como demuestra el trabajo de Longo y Calude, por lo que el método científico se puede enriquecer mediante la minería informática y el Big Data, pero nunca, nunca, podrá ser reemplazado por estos.

Ernesto Estrada es profesor de investigación del CSIC en el Instituto de Física Interdisciplinar y Sistemas Complejos (IFISC-CSIC-UIB), Campus Universitat de les Illes Balears, en Palma de Mallorca.

El ABCDARIO DE LAS MATEMÁTICAS es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME)