Conceptos de Matemáticas

Objetivo:
Los alumnos estudiarán la notación Phi y empezarán a trabajar con las aplicaciones de la Sección áurea en las matemáticas y la naturaleza.

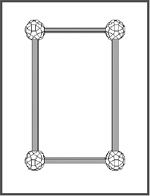
Requisitos previos
Conocimiento de los polígonos básicos (“Figuras geométricas”). Trabajo previo sobre números irracionales como pi.

Tiempo necesario
Una clase de 45-60 minutos.

Materiales
Uno o dos Kits Creador del Sistema Zome para 25-30 alumnos.
Una regla por equipo
Una calculadora por equipo.

Procedimiento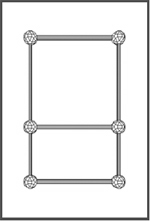

Divide la clase en grupos de 2-3 personas y reparte entre ellos las piezas del Sistema Zome, la regla y la calculadora. Pide a algunos de los alumnos que dibujen un rectángulo en la pizarra y midan su altura y anchura.  Calcula la relación entre el largo y el ancho del rectángulo. Compara cada resultado con 1,6 y explica que esa relación es conocida como la Sección de Oro, Proporción áurea o Divina proporción.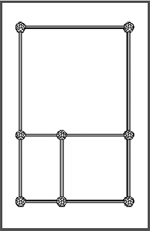

La primera tarea de los alumnos es construir un rectángulo con dos varillas pequeñas azules y dos varillas medianas azules. ¿Es un rectángulo corto y ancho o largo y delgado? ¿Habíais visto este rectángulo antes? Los dos lados del rectángulo guardan una razón especial llamada áurea, representada por φ (la letra griega phi). ¿Qué es una proporción? ¿Cómo describimos o medimos una proporción? Los lados guardan una relación 1: φ, donde el lado pequeño mide 1 unidad  y el lado largo φ unidades. ¿Cómo podemos encontrar φ? ¿Cuál es la mejor manera de medir este rectángulo? ¿Debemos incluir la anchura de los nodos en la medida?

Pide a los alumnos que calculen la relación entre los dos lados del rectángulo. Los representantes de algunos grupos pueden dar la respuesta al resto de la clase. ¿Todos los equipos obtienen el mismo resultado? ¿Qué estrategia han usado para calcular la proporción? Para encontrar la relación, los alumnos deberían haber divido las longitudes de los dos lados. Por ejemplo: (12,19 cm / 7,49 cm = 1,627 )

¿En qué unidad se mide φ? (Una relación no tiene unidades). El siguiente paso es añadir un cuadrado al rectángulo tal como se muestra en la figura. Mide el nuevo lado y escríbelo debajo. ¿Cuál es la relación? (Aproximadamente 19,68 cm / 12,19 cm = 1,614).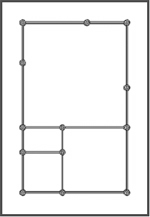

Anota ese dato. ¿Cuánto se aproxima a la proporción anterior? Esta proporción aproximada indica que el nuevo rectángulo es “similar” (misma forma y diferente tamaño) al original. Pide a los alumnos que repitan este proceso al menos dos veces más, añadiendo un cuadrado al lado más largo del rectángulo formado. Pueden crear una tabla para ir anotando los resultados. ¿Qué tiene de especial un rectángulo aúreo? ¿Cómo interactúan el rectángulo y el cuadrado? ¿Cuáles son las nuevas longitudes? (19,68; 31,87) ¿Cuál es la nueva relación (31,87/ 19,68 =1,619)? ¿Podemos continuar añadiendo cuadrados? ¿Cómo?

Reúne a la clase para que comenten sus resultados ¿Cómo podemos encontrar una proporción media de todas las relaciones  obtenidas?

El nombre de este cociente es phi, o φ. El valor real de phi es 1,6180339.... Como el número  pi, la constante usada en medidas de círculos y esferas, phi continúa infinitamente, y su patrón no se repite. Este tipo de número se llama irracional. Cada longitud que hemos medido ha sido mayor que la anterior 1,6180339... veces. Si nuestra primera longitud es 1 la segunda es phi = 1,618.

Phi aparece en numerosos lugares, normalmente como cociente entre dos longitudes. Por ejemplo, la mayoría de los templos de la Grecia Antigua, incluyendo el Partenón de Atenas, fueron construidos con forma rectangular y con exactamente la misma proporción que el rectángulo que los alumnos acaban de hacer.

Phi también aparece en muchos objetos de la naturaleza, incluyendo por ejemplo la mano del ser humano. La siguiente tarea es que los equipos calculen la relación entre los huesos de sus dedos. Usando la regla, deben medir la longitud de la primera sección del dedo (de la yema del dedo hasta la primera articulación, es decir, la primera falange) y anotarla en su cuaderno. Después deben medir hasta la segunda falange, la tercera… hasta llegar al metacarpo.

Haz cuatro columnas en la pizarra poniendo en la cabecera 1ª, 2ª, 3ª y 4ª sección. Cada alumno debe leer sus medidas. Calcula el promedio de cada columna. El cociente de la segunda sección entre la primera, la tercera entre la segunda y la cuarta entre la tercera, son todos aproximadamente phi.

Nuestro ombligo tiende a dividir nuestro cuerpo en la sección áurea, y nuestras cejas tienden a dividir en el mismo ratio. La razón phi se puede encontrar también en patrones de crecimiento en la naturaleza. El crecimiento de ciertas plantas tiende a estar en proporción áurea.

Como ampliación de la actividad puedes pedir a los alumnos que construyan una figura de su elección y hagan copias de ella guardando la proporción áurea.

Evaluación
Observa a los alumnos mientras trabajan y revisa sus cuadernos. Para alcanzar el objetivo de la lección los alumnos deben determinar las medidas de las figuras del sistema Zome, de los huesos de los dedos y calcular los cocientes tal como se ha descrito durante la lección.

Estándares del NCTM
Resolución de problemas matemáticos como método de investigación y aplicación (Estándar NCTM 1)
Las matemáticas como medio de comunicación (Estándar NCTM 2).
Conexiones matemáticas (Estándar NCTM 4)
El estudio de la geometría de dimensión 1, 2 y 3 en distintas situaciones (Estándar NCTM 12).

Posibilidades de ampliación
Más trabajo sobre patrones numéricos y la presencia de la sección áurea en la naturaleza y en el mundo construido por el hombre (“¿Qué es la simetría?”, “Simetría múltiple”, “Diviértete con Fibonacci” y “Números de Fibonacci y la Sección áurea”). Álgebra y trigonometría con la sección área (”Semejanza y la Sección áurea” y páginas 21-24 del Manual del Sistema Zome).