En este primer artículo del año vamos a recopilar material que puede ser interesante para el aficionado a las matemáticas y a la música (tenía que poner esa y en cursiva). Parte de ese material tiene un evidente sentido humorístico y otra parte es más serio.

Con frecuencia, cuando le preguntas a alguien cuál es la relación entre matemáticas y música te encuentras con que te canta una canción cuya letra es un enunciado matemático. Bueno, es cierto, hay una tradición de entender la relación entre las matemáticas y la música de esta manera. Aquí van unos cuantos vídeos al respecto (la mayor parte sacados de la divertida e instructiva página Division by Zero):

Este primer vídeo es una canción muy graciosa sobre los grupos finitos simples de orden 2:

Grupos finitos simples de orden 2.

En el siguiente vídeo tenemos una parodia de I will survive, de Gloria Gaynor, ahora transformada en I will derive:

I will derive

Ahora nos encontramos con el típico cantante de voz vaga, sin mucha proyección, un poco en plan canción protesta, narrando las dificultades que se encontraron los matemáticos con la irracionalidad del número pi. ¿Adivina el lector de quién tomó la música? Basta esperar al estribillo:

Mathematical Pi

Miramos a continuación al género del rap, donde también se encuentran canciones que glosan las bondades de las matemáticas:

Rhythm of Structure: The Math Graffiti Wall

En español y con mucha conciencia, Tote-King, un grupo de rap, enumera reflexiones, una tras otra:

Tote-King: Matemáticas.

Para acabar esta sección, no podíamos dejar sin mencionar el famoso teorema de Tales de Les Luthier:

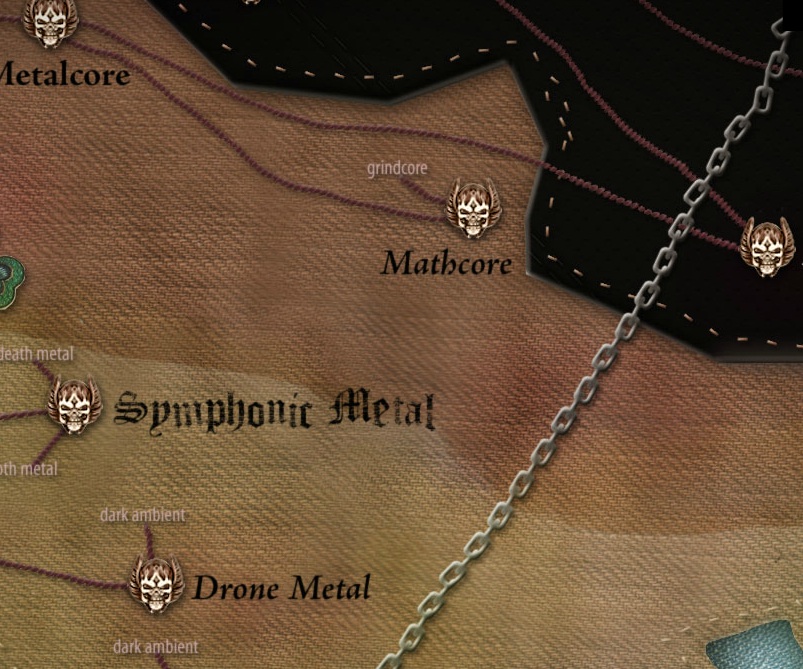
Les Luthier: El teorema de Tales.

Pero aún más sorpresas para el audaz lector: rock matemático. Sí, ha leído bien el amable lector. Se trata de una tendencia rock que usa compases irregulares -como 7/8, 11/8 y similares-, disonancias más atrevidas y preocupación por el uso de las texturas. Ciertamente, llamarlo rock matemático por el uso de esos compases es un poco exagerado, pero nada se puede hacer ya al respecto. El caso es que las percusiones de estos grupos son más interesantes que la de los grupos de rock clásicos, donde el uso de los compases binarios llega a resultar cansino. Para más información, véase la entrada de la Wikipedia Math Rock. Del rock matemático se pasó al metal matemático. Sí, ello es posible. Si el lector está interesado en adquirir una visión de conjunto de los géneros del metal, recomiendo que vaya a Map of Metal, página que los contiene todos, con información muy completa, tanto histórica como musical, y que permite escucharlos según se pasea uno por el mapa de los géneros. En la figura de abajo, hemos sacado un pantallazo de la parte del mathcore.

Detalle del mathcore del mapa del metal.

En el vídeo de abajo, tenemos un ejemplo de este metal matemático, del grupo The Dillinger Escape Plan, el tema 43% Burnt sacado en el album con el elocuente título Calculating Infinity (pincha en la imagen para ver el vídeo):

The Dillinger Escape Plan - 43% Burnt

Otro enfoque interesante, en la misma línea de cantar las matemáticas pero con propósitos didáctics, es la de Educational Rap, un sitio web que ofrece canciones rap para enseñar una gran variedad de materias, las duras matemáticas entre ellos. En el apartado de música, tienen un album con pistas que versan sobre gráficas de funciones, números negativos, fracciones, superficies, el sistema métrico decimal y otros temas.

Siguiendo este enfoque, la página Songs for Teaching tiene un amplio repertorio de canciones, muy bien compuestas y grabadas, para enseñar numerosos conceptos matemáticos, principalmente para educación primaria. Los conceptos van desde los números en educación infantil hasta media, moda y mediana que se ven en sexto de primaria. Las canciones forman parte del material pedagógico que ofrecen y por el cual hay que pagar. En español, quitando las canciones populares que incluyen números (la famosa Un elefante se balanceaba...), no he encontrado referencias que ofrezcan canciones en la línea de Songs for Teaching.

A veces, cuando un conocido se entera de que mi labor investigadora versa sobre las matemáticas y la música, me dicen cosas peregrinas, que me llevan a preguntarme qué idea tienen de ambas disciplinas. He oído cosas como:"están muy relacionadas, ¿no? Al principio de cada pieza hay una fracción", o también "en ambas materias se cuenta", o "¿qué es la música sino duración?, ¿y las matemáticas?: pues lo mismo. ¿no?". Huelga decir que las cejas se me fruncen de sorpresa. La relación entre las matemáticas y la música no se reduce al símil entre la disciplina métrica de la música y el rigor lógico de las matemáticas, o a que ambas inspiran belleza. Hay otros muchos aspectos, que pasan desapercibidos al observador ocasional, que unen a las matemáticas y a la música, como pueden ser las estructuras matemáticas que se encuentran en la música o el nivel de abstracción que comparten.

Para ahondar en esa relación y hacerlo de manera gozosa y relevante, vamos a recomendar al lector un libro. La mayor parte de los libros sobre matemáticas y música se quedan en la descripción física del sonido, en la afinación pitagórica y como mucho mencionan la sucesión de Fibonacci. Como digo, hay mucha más matemática detrás de la música. Una referencia inmejorable es el libro de David Benson Music: a Mathematical Offering.

Music: a Mathematical Offering, de David Benson.

Este libro creció a partir de unos apuntes de un curso que Benson empezó a impartir hace algunos años y se ha convertido ya en un clásico, por la exposición, clara y concisa, y por el material que cubre. Para que el lector aprecie el libro en su justa medida mostramos más abajo el índice (en inglés). Puede verse que aborda, sí, los clásicos fundamentos físicos, pero también cuestiones de forma (capítulo 9), de afinación incluyendo temperamentos modernos (capítulos 5 y 6), organología (capítulo 3), etc. No menos meritoria es la cantidad y la calidad de las referencias que se encuentra en el libro.

Y hasta aquí ha sido el artículo de este mes. Se pueden cantar las matemáticas y eso las relaciona con la música -al menos, en su práctica-, pero si lees el libro de Benson, entonces esa relación se hace más profunda y patente.

REFERENCIAS

• David Benson. Music: A mathematical offering. Existe una versión impresa publicada por Cambridge University Press en 2006. ISBN: 0521853877
• Division by Zero. Página web con puzzles, recursos académicos y tecnología aplicada a la enseñanza.
• Educational Rap. Página web con canciones rap para aprender diversos conceptos matemáticos.
• Música y matemáticas. Web creada bajo la dirección de Rafael Losada.
• Map of metal. Página web donde se muestran los géneros del metal.
• Wikipedia. Artículo Math Rock. Artículo consultado en diciembre de 2011.
• Songs for Teaching. Página con material para enseñar conceptos matemáticos a través de canciones.

Índice (versión en línea):

1. Waves and harmonics

1.1 What is sound?
1.2 The human ear
1.3 Limitations of the ear
1.4 Why sine waves?
1.5 Harmonic motion
1.6 Vibrating strings
1.7 Sine waves and frequency spectrum
1.8 Trigonometric identities and beats
1.9 Superposition
1.10 Damped harmonic motion
1.11 Resonance

2. Fourier theory

2.1 Introduction
2.2 Fourier coefficients
2.3 Even and odd functions
2.4 Conditions for convergence
2.5 The Gibbs phenomenon
2.6 Complex coefficients
2.7 Proof of Fejér's theorem
2.8 Bessel functions
2.9 Properties of Bessel functions
2.10 Bessel's equation and power series
2.11 Fourier series for FM synthesis and planetary motion
2.12 Pulse streams
2.13 The Fourier transform
2.14 Proof of the inversion formula
2.15 Spectrum
2.16 The Poisson summation formula
2.17 The Dirac delta function
2.18 Convolution
2.19 Cepstrum
2.20 The Hilbert transform and instantaneous frequency
2.21 Wavelets

3. A mathematician's guide to the orchestra

3.1 Introduction
3.2 The wave equation for strings
3.3 Initial conditions
3.4 The bowed string
3.5 Wind instruments
3.6 The drum
3.7 Eigenvalues of the Laplace operator
3.8 The horn
3.9 Xylophones and tubular bells
3.10 The mbira
3.11 The gong
3.12 The bell
3.13 Acoustics

4. Consonance and dissonance

4.1 Harmonics
4.2 Simple integer ratios
4.3 Historical explanations of consonance
4.4 Critical bandwidth
4.5 Complex tones
4.6 Artificial spectra
4.7 Combination tones
4.8 Musical paradoxes

5. Scales and temperaments: the fivefold way

5.1 Introduction
5.2 Pythagorean scale
5.3 The cycle of fifths
5.4 Cents
5.5 Just intonation
5.6 Major and minor
5.7 The dominant seventh
5.8 Commas and schismas
5.9 Eitz's notation
5.10 Examples of just scales
5.11 Classical harmony
5.12 Meantone scale
5.13 Irregular temparaments
5.14 Equal temperament
5.15 Historical remarks

6. More scales and temperaments

6.1 Harry Partch's 43 tone and other super just scales
6.2 Continued fractions
6.3 Fifty-three tone scale
6.4 Other equal tempered scales
6.5 Thirty-one tone scale
6.6 The scales of Wendy Carlos
6.7 The Bohlen-Pierce scale
6.8 Unison vectors and periodicity blocks
6.9 Septimal harmony

7. Digital music

7.1 Digital signals
7.2 Dithering
7.3 WAV and MP3 files
7.4 MIDI
7.5 Delta functions and sampling
7.6 Nyquist's theorem
7.7 The z-transform
7.8 Digital filters
7.9 The discrete Fourier transform
7.10 The fast Fourier transform

8. Synthesis

8.1 Introduction
8.2 Envelopes and LFOs
8.3 Additive synthesis
8.4 Physical modeling
8.5 The Karplus-Strong algorithm
8.6 Filter analysis for the Karplus-Strong algorithm
8.7 Amplitude and frequency modulation
8.8 The Yamaha DX7 and FM synthesis
8.9 Feedback, or self-modulation
8.10 CSound
8.11 FM synthesis using CSound
8.12 Simple FM instruments
8.13 Further techniques in CSound
8.14 Other methods of synthesis
8.15 The phase vocoder
8.16 Chebychev polynomials

9. Symmetry in music

9.1 Symmetries
9.2 The harp of the Nzakara
9.3 Sets and groups
9.4 Change ringing
9.5 Cayley's theorem
9.6 Clock arithmetic and octave equivalence
9.7 Generators
9.8 Tone rows
9.9 Cartesian products
9.10 Dihedral groups
9.11 Normal subgroups and quotients
9.12 Orbits and cosets
9.13 Burnside's lemma
9.14 Pitch class sets
9.15 Pólya's enumeration theorem
9.16 The Mathieu group M₁₂

Appendices

Appendix A: Answers to Almost All Exercices

Appendix B: Bessel functions

Appendix C: Complex numbers

Appendix D: Dictionary

Appendix E: Equal tempered scales

Appendix F: Frequency and MIDI chart

Appendix G: Getting stuff from the internet

Appendix I: Intervals

Appendix J: Just, equal and meantone scales compared

Appendix L: Logarithms

Appendix M: Music theory

Appendix O: Online papers

Appendix P: Partial derivatives

Appendix R: Recordings

Appendix W: The wave equation
Green's identities
Gauss' formula
Green's functions
Hilbert space
The Fredholm alternative
Solving Laplace's equation
Conservation of energy
Uniqueness of solutions
Eigenvalues are nonnegative and real
Orthogonality
Inverting the Laplace operator
Compact operators
The inverse of the Laplace operator is compact
Eigenvalue stripping
Solving the wave equation
Polyhedra and finite groups
An example

Bibliography

Index