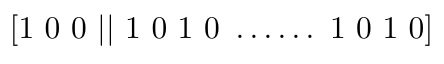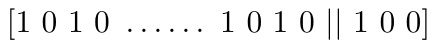Este mes el artículo de la sección está escrito al alimón con Ricardo Sanz y Tur, profesor de Pedagogía y Didáctica de la Música del Real Conservatorio Superior de Música de Madrid y el humilde responsable de esta columna. El artículo que ofrecemos al lector es un análisis de dos de las Seis danzas con ritmos búlgaros, de Béla Bartók, pertenecientes a sus conocidos cuadernos para piano Mikrokosmos. Presenta este análisis una feliz simbiosis, desarrollada con naturalidad, de conceptos musicales y matemáticos; así, se habla de compases de amalgama y métricas aksak, pero también de métricas euclídeas. Ilustra con bastante claridad cómo puede usar un músico las matemáticas, sin forzarlas, sin excederse, sino como la herramienta formidable que son, y con la voluntad de servicio debida al usuario. El artículo de este mes nos mueve a la una reflexión no por repetida menos cierta: Si los músicos supieran más ciencia..., si los científicos supieran más música..., ¡todos nos divertiríamos más y seríamos más sabios!

1. Análisis rítmico-métrico de «Six Dances in Bulgarian Rhythm (2)»

Todos los ejemplos de este artículo están tomados de Béla Bartók: Mikrokosmos. 153 Progressive Piano Pieces. Vol. 6. Londres: Boosey & Hawkes, 1987.

Figura 1: Béla Bartók: «Six Dances in Bulgarian Rhythm (2)». Compases 1-4

1.1. Compás de amalgama

En primer lugar, estamos ante un compás de amalgama. De acuerdo con Joaquín Zamacois, «se denominan de amalgama los compases que se forman por la reunión, en uno solo, de dos o más compases, cuyos tiempos son de igual unidad, pero distintos en número» (1). Por otro lado, así aparecen conceptuados los compases de amalgama en la Teoría de la música de la Sociedad Didáctico-Musical (S. D. M.) (2): «Compases de amalgama son aquellos que reúnen en uno, dos o más compases binarios, ternarios y cuaternarios, de subdivisión binaria o ternaria» (2). Fuera de nuestro país, hallamos la siguiente definición de «compases de amalgama» en el Diccionario Oxford de la música: «Designación de ciertos compases irregulares de cinco, siete o más tiempos, que son en realidad la unión de varios compases simples (de dos y tres tiempos en el de cinco, de tres y cuatro tiempos en el de siete). [...]» (3).

Nótese que hay ciertas discrepancias entre unas definiciones y otras (las definiciones no son verdaderas o falsas, sino útiles o inservibles). Para Scholes los compases de amalgama están formados por compases simples, es decir, de subdivisión binaria: compás binario, ternario y cuaternario de subdivisión binaria. Los ejemplos que aporta refuerzan esta perspectiva. En cambio, para la S. D. M. los compases pueden ser de subdivisión ternaria, esto es, compuestos (compases cuya figura representativa del valor de un tiempo es una figura con puntillo). No obstante, los casos que examina la S. D. M. son los tradicionales de 5/4, 5/8 y 7/4 (ninguno de subdivisión ternaria, y tampoco agrupación de compases simples y compuestos). Zamacois admite la amalgama o bien de compases simples (compás quinario compuesto de un compás binario y otro ternario o de un compás ternario y otro binario), o bien de compases compuestos (por ejemplo: 21/x = 12/x + 9/x o viceversa; 15/x= 6/x + 9/x o viceversa); pero no la mezcla de ambos tipos. Conforme a lo dicho, podemos inferir —con algunas reservas— que ninguna de las tres perspectivas teóricas admitiría como compás de amalgama la típicamente española hemiolia sucesiva (6/8 + 3/4), al tratarse de una yuxtaposición de compases de diferente denominador (en el primer compás la unidad de tiempo es de valor compuesto —negra con puntillo— y en el segundo la unidad de tiempo es de valor simple (negra sin puntillo). Por consiguiente, en aras de la coherencia, la hemiolia sucesiva debe analizarse como otra cosa, o bien, las explicaciones de los compases de amalgama han de ser revisadas.

Con todo, la amalgama de Bartók está constituida por compases simples de igual denominador (2/8 y 3/8) y mínimos métricos, por lo que no presenta problemas de adecuación a todas las definiciones anteriores.

Como se ha visto, el primero de los atributos de los compases de amalgama es que es una asociación o combinación de compases (en este caso, simples) de la que emerge un compás de amalgama (tal vez, un objeto unitario de superior nivel). Decimos tal vez porque, desde la perspectiva de la teoría sistémica, la amalgama puede analizarse de dos modos distintos: como mero encadenamiento o yuxtaposición de compases simples o como combinación de compases simples de la que emerge «una cosa radicalmente nueva, vale decir caracterizada por propiedades que sus componentes no poseen» (4).

Esto tiene su miga, porque si los compases de amalgama se conceptúan como mera asociación de compases simples, la naturaleza de estos no cambia, y la acentuación métrica sería F-D-F-D-F-D-D (F = acento métrico fuerte o pesado; D = acento métrico débil o ligero). Las barras de compás indican cuándo vuelve a repetirse la particular ordenación métrica, y nada más. La enunciación y nada más quiere decir que la barra de compás no implica necesariamente que el tiempo que la sigue deba ser un pulso métricamente más acentuado que otros de igual rango. Se distinguirían dos calidades acentuales, pues cada compás simple mantiene su acento métrico propio. En general, es lo que se hace cuando se palmean-zapatean los compases del flamenco.

Ahora bien, si los compases de amalgama se dilucidan como auténtica combinación, en uno solo, de compases de igual clase, emerge una realidad nueva, pues los compases simples precursores de la totalidad resultan modificados. En la renovada formulación métrica, el acento principal corresponde al ataque del compás. Y compás no hay más que uno: 7/8, por lo que solamente tenemos un acento fuerte: el primero. Los otros serían acentos secundarios (semifuertes) o tiempos débiles. La secuencia métrica quedaría así: F-D-SF-D-SF-D-D (F = acento métrico fuerte o pesado, principal; SF = acento métrico secundario, semifuerte; D = acento métrico débil o ligero). Ahora se distinguen tres calidades acentuales (F, SF y D), y de ahí el novedoso estado de cosas (la ensambladura de los componentes y la organización del compás resultante son distintas. Si antes el acento métricamente fuerte reaparecía cada dos o tres tiempos, ahora el ciclo de retorno de dicho acento se extiende a siete tiempos).

Aunque decimos que la realidad queda modificada en virtud de una u otra concepción, deseamos defendernos de la acusación de idealismo. La realidad queda modificada porque la música es un producto artístico-cultural (y, por ende, artificial) resultado de los bioprocesos cerebrales emergentes creativos o recreativos de los compositores e intérpretes operando en contextos sociales; véanse (17) y (18). Y para unos y otros, la teoría guía la composición o la interpretación.

La teoría sistémica (5) tiene poder explicativo para esclarecer por qué se componen, interpretan y perciben diferentemente la sucesión de 2 compases de 2/4 (F D | F D) y un 4/4 (F D SF D); el empalme de 2 compases de 3/8 (F D D | F D D) y un 6/8 (F D D SF D D). Se trata de objetos mensurales que manifiestan propiedades distintas. El nuevo compás emergente no es reductible a la mera concatenación de sus precursores.

Es discutible si Béla Bartók concibió la amalgama como mera yuxtaposición, agregación o adición de compases o como combinación sistémica de compases. Para saberlo con seguridad, habría que preguntárselo a él directamente. Pero hay muchos indicadores que hacen inclinarse la balanza hacia una u otra opinión. El compositor no expresa el compás como 7/8 utilizando divisorias de puntos para indicar la conformación de la amalgama, sino que lo representa como sucesión de sumandos (2 + 2 + 3). En el inicio de la obra sólo se distinguen dos «pesos» rítmico-armónicos, por así decir (y no tres): la mano izquierda con el intervalo armónico do-sol y la mano derecha con la nota sol (figura 1 arriba). En cuanto a la armonía, en la partitura no hay ninguna diferencia entre la primera célula (binaria), la segunda célula (también binaria) y la tercera célula (ternaria).

El análisis de otros fragmentos de la obra parece apuntar en la misma dirección. Por ejemplo, en los compases 37-39 el intervalo de la mano izquierda ya no es armónico (figura 2), sino que se despliega melódicamente, pero bate exactamente las mismas notas en ostinato: la b-do, la b-do, la b-do-do.

Figura 2: Béla Bartók: «Six Dances in Bulgarian Rhythm (2)», compases 37-39

De lo escrito no puede desprenderse distinta calidad acentual entre los tres 'las' bemoles de cada compás correspondientes a sendas células rítmicas binarias y ternarias. De hecho, no se observan diferencias de acentuación (ni dinámica, ni tónica, ni agógica...) entre ninguno de los nueve 'las' bemoles que aparecen en el fragmento escogido. Si tales diferencias se establecen en la interpretación (por ejemplo, cada tres 'las' bemoles), es como producto de la actividad constructiva del intérprete-pianista, que tal vez quiera resaltar levemente con ligeros apoyos el inicio de cada ciclo métrico. Algo, ciertamente, opinable.

Hay más partes de la obra en las que sucede otro tanto. En cada compás del siguiente fragmento (figura 3), ninguna disimilitud puede extraerse en cuanto a calidad acentual de los acordes compactos de la mano izquierda (todos están signados con subrayados-picados, tienen exactamente la misma duración y se repiten compás a compás con las mismas notas), o de ciertos diseños melódicos de la mano derecha (por ejemplo: do-re b do-re b do-re b-mi b; los tres 'dos' tienen idéntica acentuación dinámica, tónica y agógica).

Figura 3: Béla Bartók: «Six Dances in Bulgarian Rhythm. (2)», compases 46-49

Con arreglo a las pruebas y argumentos expuestos, nos inclinamos a pensar que la concepción bartokiana de la amalgama responde a la primera de las posibilidades apuntadas (asociación, yuxtaposición o encadenamiento de compases simples, conservando cada uno de ellos su acentuación métrica original). De este modo, la fórmula métrica que corresponde a dicha amalgama es F-D-F-D-F-D-D-F-D-F-D-F-D-D-F-D-F-D-F-D-D y así sucesivamente. Si la representamos utilizando el Time Unit Box System, TUBS: [x . x . x . .]. Desarrollándolo: [x . x . x . . x . x . x . . x . x . x . . x . x . x . .], &c. (en el sistema TUB, x = tiempo métricamente acentuado, o «fuerte» y . = tiempo débil).

Hay dos razones más por las que estimamos más plausible esta alternativa. La primera es que la composición de Mikrokosmos se extiende en el periodo de 1926 a 1939; la teoría general de sistemas, al menos en la formulación de Ludwig von Bertalanffy (5), es más tardía (data de mediados de siglo). Es bastante distinto estudiar los compases de amalgama como entidades integrales o como encadenamientos modulares de compases simples. Lo primero es propio de la teoría de sistemas; un enfoque que no estaba disponible en los años treinta del siglo XX. Por último, esta clase de rítmicas era muy novedosa en la época en que las escribió Bartók, hasta el punto de que fue el propio Béla Bartók quien presentó la noción de 'ritmo búlgaro' como un nuevo recurso para la composición en una conferencia radiofónica titulada «Lo que denominamos ritmo búlgaro» y pronunciada el 6 de abril de 1938, basándose en el trabajo de musicólogos búlgaros y su propio trabajo de campo, recogiendo ejemplos (6). Aun en la versión «asociacionista», la amalgama resultaba sumamente interesante para el periodo de tiempo al que nos referimos.

1.2. Métrica aksak auténtica

Este compás no solo es un compás (irregular) de amalgama, sino que además es una métrica aksak auténtica.

Basándose en sus características estructurales y númericas, Simha Arom ha propuesto una tipología del aksak (7). Arom denomina pseudo-aksaks a aquellos aksaks cuya suma de los valores que lo constituyen es par y, por tanto, divisibles por 2 o 4 y a veces también por 3 o 6. Hay un segundo tipo de aksaks que totalizan un número impar de valores fundamentales y que pueden reducirse a pulsaciones equidistantes, pero organizadas únicamente de forma ternaria. Estos son 'quasi-aksaks'. Por último, hay aksaks constituidos sobre números primos (5, 7, 11, 13) que sólo pueden ser divididos por ellos mismos (y por la unidad), que son los que Arom considera aksaks auténticos.

El aksak constituido sobre número primo más bajo es el aksak de 5 tiempos, organizado como 3 + 2 [x . . x .] o como 2 + 3 [x . x . .]. Para Arom, el aksak de 5 tiempos es el «aksak matricial», y es el que funda el principio de agrupamiento de células simples binarias y ternarias, si bien —como se ha anotado— este punto es más discutido. No obstante, el ejemplo analizado correspondiente a la «danza búlgara número 2» de Bartók tampoco presenta problemas en este sentido, porque está basada justamente en esos mínimos rítmico-métricos.

En resumen, es una métrica aksak auténtica porque 1) se basa en la combinación de células binariasy ternarias exclusivamente (8) y 2) la suma total de pulsos o tiempos constituye número primo: 7.

1.3. Métrica euclídea

Por añadidura, el compás elegido por Bartók para la composición de la obra corresponde a una métrica euclídea (9).

Las patrones métricos que presentan la propiedad de que sus acentos se hallan distribuidos lo más uniformemente posible y con la máxima regularidad a lo largo del ciclo métrico se denominan secuencias o métricas euclídeas. Este tipo de distribución crea tensión rítmica.

Existe una conexión interna o lógica entre el algoritmo de Bjorklund y las métricas euclídeas. La aplicación a la música del algoritmo de Bjorklund genera patrones métricos euclídeos.

He aquí el análisis de de por qué estamos ante una métrica euclídea. Las métricas euclídeas se formulan como E(k, n), donde k denota el número de pulsos acentuados y n el número total de pulsos de la secuencia, es decir, la longitud del ciclo métrico.

En el caso que analizamos, tenemos 7 pulsos (7 = 2 + 2 + 3) de los cuales 3 acentuados:

E(3, 7)
Aplicando paso a paso el algoritmo de Bjorklund (1 = tiempo métricamente acentuado; 0 = tiempo métricamente débil), obtenemos lo siguiente:

• 1.º paso. 7 secuencias de 1 pulso, tres acentuadas y cuatro no: [1] [1] [1] [0] [0] [0] [0].
• 2.º paso. 3 secuencias de 2 tiempos, restando un pulso no acentuado: [10] [10] [10] [0].
• 3.º paso. 1 secuencia de 3 tiempos y un resto de dos secuencias de dos tiempos cada una: [100] [10] [10].
• 4.º paso. 1 secuencia de 5 tiempos y un resto de 1 secuencia de 2 tiempos: [10010] [10].
• Secuencia final: [1001010] o, lo que es lo mismo, representándola con el TUBS: E(3,7) = [x . . x . x .]. Esta es la distribución de acentos más uniforme posible a lo largo del ciclo métrico.

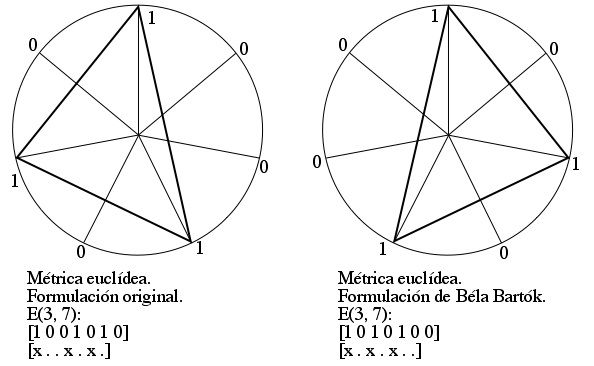
Bartók utiliza esa serie euclídea dándole la vuelta, al comenzarla en el cuarto tiempo (el primero de la primera célula binaria): [x . x . x . .]. Son dos ejemplos del mismo tipo métrico.

Es posible representar este ciclo métrico como un triángulo inscrito en un círculo. El primer tiempo está ubicado en la parte superior del círculo, y se lee en el sentido de las manecillas del reloj:

Figura 4: Béla Bartók: «Six Dances in Bulgarian Rhythm (2)». Representación icónica de la métrica euclídea.
A la izquierda la formulación original. A la derecha, la versión rotada empleada por Bartók, que es especular de la original.

2. Análisis rítmico-métrico de «Six Dances in Bulgarian Rhythm (5)»

Figura 5: Béla Bartók: «Six Dances in Bulgarian Rhythm (5)». Compases 1-3

Llevaremos a cabo un análisis similar con la «Danza en ritmo búlgaro núm. 5» de Béla Bartók. Como en el caso anterior, observamos un compás de amalgama. Es un compás de amalgama porque es un compás formado por la reunión, en uno solo, de cuatro compases que presentan distinto numerador, pero igual denominador.

El ciclo métrico se reinicia cada nueve tiempos de corchea. Por consiguiente, podría afirmarse que el compás unitario es de 9/8. Pero ocurre que el 9/8 es una métrica clásica; es un compás ternario de subdivisión ternaria (= compuesto): F-D-D-SF-D-D-SF-D-D. Indudablemente, ésa no es la fórmula métrica que busca Bartók. Por consiguiente, indica la constitución de la amalgama por medio de compases aditivos simples: 2 + 2 + 2 + 3.

Como la amalgama ya se ha expresado descompuesta al principio de la pieza, las líneas divisorias de puntos no son necesarias. Además, suena «umpa-umpa-umpa-úmpara», lo que también hace patente, de forma sonora, la organización rítmico-métrica de la obra; véase la figura 6.

El problema de si la amalgama es modular o sistémica admite en esta danza mayor discusión. Hay fragmentos que parecen sugerir mera asociación de compases (= ensambladura modular):

Figura 6: Béla Bartók: «Six Dances in Bulgarian Rhythm (5)». Compases 14-15

En cambio, hay otros compases, como los del principio o el ejemplo que se aporta más abajo en la figura 7 que, en virtud de sus diseños melódico-rítmicos, articulación, &c. insinúan una concepción más unitaria o integral del compás:

Figura 7: Béla Bartók: «Six Dances in Bulgarian Rhythm (5)». Compases 25-26

La métrica examinada no solo es un compás irregular de amalgama (compás aditivo), sino que además es una métrica quasi-aksak. Es quasi-aksak porque cumple la primera condición señalada en el análisis de la danza núm. 2 (se basa en la combinación de células binarias y ternarias exclusivamente), pero no cumple la segunda condición: la suma total de pulsos, aunque es número impar, no constituye número primo. No obstante, sí es una métrica euclídea. Tenemos 9 pulsos de los cuales 4 acentuados y 5 no:

E(4, 9)
Aplicando el algoritmo de Bjorklund:

• 1.º paso. 9 secuencias de un pulso, de las cuales 4 métricamente acentuadas y cinco no: [1] [1] [1] [1] [0] [0] [0] [0] [0].
• 2.º paso. Trasladando ceros, obtenemos cuatro secuencias de dos tiempos y nos resta un tiempo no acentuado: [10] [10] [10] [10] [0].
• 3.º paso. Procediendo de igual modo, estructuramos una secuencia de tres tiempos y tres secuencias de dos tiempos: [100] [10] [10] [10].
• 4.º paso. Ahora redistribuimos las secuencias de dos tiempos: [10010] [1010].
• Secuencia final: [100101010]. Representada utilizando el sistema TUB: [x . . x . x . x .]

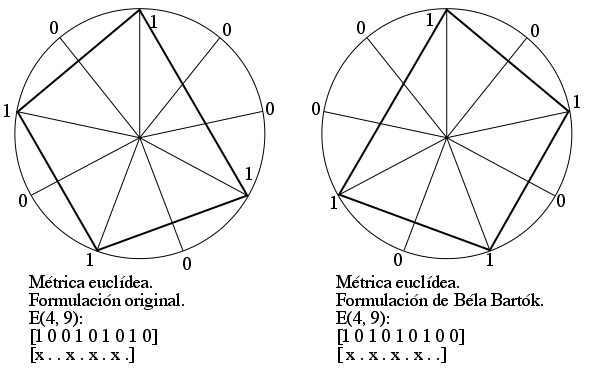
Bartók utiliza esa serie euclídea dándole la vuelta, al comenzarla en el cuarto tiempo (el primero de la primera célula binaria): [x . x . x . x . .]. Las dos secuencias son casos del mismo tipo métrico.

Figura 8: Béla Bartók: «Six Dances in Bulgarian Rhythm (5)». Representación icónica de la métrica euclídea.
A la izquierda la formulación original. A la derecha, la versión rotada empleada por Bartók. Ambas son casos particulares del mismo tipo métrico.

El nervio rítmico de la danza radica, en parte, en haber adoptado esta estructuración euclídea.

3. Propiedades comunes a las dos métricas

En las dos danzas analizadas las métricas que usa Bartók son E(3, 7) y E(4, 9). El número de acentos fuertes y el el número total de pulsos pueden parecer números tan buenos como otros cualesquiera. Sin embargo, tienen propiedades especiales. En general, si k es el número de acentos fuertes y n el de pulsos y se cumple la relación n=2*k+1, entonces aparece un tipo de patrón muy característico. En el caso de nuestro análisis, esta condición se cumple:7=3*2 +1 y 9=4*2 +1. ¿Cuál es esa relación? Si aplicamos el algoritmo de Bjorklund obtenemos el patrón:

Este patrón está formado por el grupo [1 0 0 ] seguido por la repetición k veces del grupo [1 0] (las dos rayas || se han puesto por claridad). Curiosamente, Bartók pone el grupo [1 0 0] al final y obtiene el patrón:

Este patrón métrico se puede interpretar desde un enfoque perceptual, en este caso de expectativa acentual, en la línea de la obra de Meyer Emotion and meaning in music (14) (o de autores posteriores que desarrollaron sus teorías, tales como Lerdahl y Jackendoff (15) o Narmour (16)). En efecto, la repetición del grupo [1 0] crea la expectativa de que la métrica entera va a consistir en esa distribución de acentos, pero en el último momento Bartók añade una parte débil más, la cual rompe dicha expectativa. Las distancias que aparecen en esta métrica son 2 y 3 ([1 0] y [1 0 0], respectivamente), y son el mínimo métrico binario y el mínimo métrico ternario. Por otra parte, si el número de pulsos es muy grande, entonces el número de repeticiones del grupo [1 0] es grande también y el efecto se pierde. Bartók elige unos patrones óptimos para el oído humano en términos de memoria musical. Si hubiese elegido E(5, 11) o E(6, 13) el efecto no habría sido tan eficaz.

Para saber más

Notación TUBS

La notación TUBS se conoce también como notación de caja. En Occidente fue inventada por Philip Harland, de la Universidad de California en Los Ángeles, en 1962. Sin embargo, en otras tradiciones musicales se conocía desde mucho antes. Por ejemplo, en el siglo XV era de uso común en la notación de la música en Corea; también se pueden encontrar ejemplos en la música árabe. La notación en caja se utiliza con frecuencia por los etnomusicólogos (10) para notar polirritmos africanos y de otras culturas. Los psicólogos de la música la emplean en sus experimentos de percepción del ritmo, donde tienen que dar instrucciones a sujetos que no conocen la notación occidental.

Ritmos euclídeos

Al principio, fue un problema matemático: dadas n cajas y k objetos, ¿cómo distribuir los objetos en las cajas de la manera más uniforme posible? ¿Qué significa de la manera más uniforme posible? Este problema fue abordado en diversos contextos de manera independiente: en música, con la teoría de escalas (11); en física, con las distribuciones de pulsos en intervalos fijos de tiempo (9-1); en informática gráfica, con el dibujo digital de líneas rectas (12). Para ver más ejemplos de este ubicuo problema, consúltense las referencias (9-2), (9-3) y (9-5). La conexión profunda que se dio con este problema es que el viejo algoritmo de Euclides, ese que se usaba para calcular con rapidez el máximo común divisor de dos números, servía, convenientemente modificado, para resolver el problema de una manera sencilla. En (9-4) se prueba que varios algoritmos existentes en la bibliografía para resolver el problema de distribuir objetos uniformemente son, en realidad, el mismo algoritmo y dan esencialmente las mismas soluciones.

En el caso que nos ocupa, las métricas, queremos distribuir acentos fuertes y débiles en un conjunto fijo de pulsos. Las métricas que han salido en el texto son E(3,7) y E(4, 9). En ambos casos el máximo común divisor del número de acentos fuertes y número total de pulsos es 1, con lo cual no salen patrones repetidos dentro de la métrica. He aquí unas cuantas propiedades que tienen las métricas euclídeas E(k, n) en general:

1. Están formadas por solo dos distancias, a saber, la parte entera del cociente n/k, y la parte entera del cociente n/k más 1. Por ejemplo, en el caso de E(3, 7), tenemos que la parte entera de 7/3=2,3333... es 2. Luego las distancias que pueden aparecer en E(3, 7) son 2 y 3. Y así es, E(3,7)=[x . x . . ], o escrito como sucesión de distancias, (2, 3).
2. Dado el ritmo E(k, n), si el máximo común divisor de k y n es d, entonces la métrica euclídea estará compuesta por la repetición d veces de un patrón P. Por ejemplo, la métrica E(8, 12) es [. x x . x x . x x . x x] , y vemos que es la repetición del patrón [. x x] 4 veces, exactamente el máximo común divisor de 12 y 8. El patrón que se repite es también euclídeo.
3. Las métricas euclídeas no cambian bajo rotaciones. Ello es porque la propiedad de regularidad, de máxima distribución uniforme, depende de las distancias entre las partes fuertes, y estas no cambian cuando se rota el ritmo. Para explorar las rotaciones de ritmos, véase (13).
4. La observación anterior trae la fascinante cuestión musicológica de por qué ciertas rotaciones de métricas (o ritmos) euclídeos son más frecuentes que otras. Aquí entra en juego el contexto cultural y el estilo en particular de que se trate.

Notas, referencias y bibliografía

(1) Joaquín Zamacois: Teoría de la Música. Dividida en cursos. Libro I. Barcelona: Labor, 1992, p. 126.

(2) Sociedad Didáctico-Musical: Teoría de la Música. Parte tercera. Madrid: Villena, 1958, p. 13.

(3) Percy A. Scholes: «Compases de amalgama», en Diccionario Oxford de la Música. Tomo I. Barcelona: Edhasa/Hermes/Sudamericana, 1984, p. 87.

(4) Mario Bunge: Emergencia y convergencia. Novedad cualitativa y unidad del conocimiento. Barcelona: Gedisa, 2003, p. 28.

(5) Ludwig von Bertalanffy: Teoría general de los sistemas. Fundamentos, desarrollo, aplicaciones. Madrid: Fondo de Cultura Económica, 1993. Véase especialmente el apartado «En torno a la historia de la teoría de los sistemas» de la introducción del libro, p. 9 y ss.

(6) Jérôme Cler: «Pour une théorie de l'aksak». Revue de Musicologie, vol. 80, núm. 2 (1994), 181-210, p. 182. Traducción nuestra.

(7) Simha Arom: « L'aksak. Principes et typologie» (en línea). Cahiers d'ethnomusicologie, núm. 17 (2004). Disponible en Internet: .. (consulta del 24 de octubre de 2012). Traducción nuestra.

(8) Aunque se reconoce que la combinación de células binarias y ternarias genera la mayor parte de las métricas aksak, últimamente se ha sugerido que, al menos teóricamente, combinaciones basadas en las razones 4:3 o 5:4 son posibles. Ibíd., pp. 195-196 y summary, al final (p. 210).

(9) Para el asunto de la métrica euclídea, pueden consultarse los siguientes artículos:

• (1) E. Bjorklund: «The Theory of Rep-Rate Pattern Generation in the SNS Timing System», SNS ASD Tech Note, SNS-NOTE-CNTRL núm. 99 (2003).
• (2) Godfried Toussaint: «The Euclidean Algorithm Generates Traditional Musical Rhythms». Montreal (Canadá): Universidad MCGill, 2005.
• (3) Perouz Taslakian: Musical Rhythms in the Euclidean Plane (tesis doctoral). Montreal (Canadá): Universidad McGill, 2008.
• (4) Erik Demaine y otros autores: «The distance geometry of music». Computational Geometry, vol. 42, núm. 5 (2009), 429–454.
• (5) Paco Gómez: «Si Euclides lo supiese..., se sentiría muy orgulloso. Patrones de regularidad máxima en Música, Geometría, Informática y otras disciplinas». Madrid: Universidad Politécnica. Escuela Universitaria de Informática, 2009.
• (6) Paco Gómez: «El algoritmo de Euclides como principio musical» (charla). Madrid: Universidad Politécnica.
• (7) Contrasteatro: Materritmo o el ritmo me mata. Espectáculo cómico-matemático-musical que explora los ritmos euclídeos.

(10) Laz E. N. Ekwueme. Concepts in African musical theory. Journal of Black Studies, 5(1):35–64, septiembre de 1974.

(11) J. Clough and J. Douthett. Maximally even sets. Journal of Music Theory, 35:93–173, 1991.

(12) Reinhard Klette and Azriel Rosenfeld. Digital straightness - a review. Discrete Applied Mathematics, 139:197–230, 2004.

(13) Paco Gómez. Rotaciones de ritmos. Columna de matemáticas y música de la revista Divulgamat. Junio de 2012.

(14) Leonard Meyer. Emotion and Meaning in Music. The University of Chicago Press. 1961.

(15) Lerdahl, Fred and Jackendoff, Ray. A Generative Theory of Tonal Music. MIT Press. 1983

(16) Narmour, E. The Analysis and Cognition of Melodic Complexity: The Implication-Realization Model. Chicago: University of Chicago Press. 1992.

(17) Mario Bunge: El problema mente-cerebro. Un enfoque psicobiológico. Madrid: Tecnos, 2002.

(18) Mario Bunge y Rubén Ardila: Filosofía de la Psicología. Barcelona: Ariel, 2002.