 129. Felicidad compartida, doble felicidad
129. Felicidad compartida, doble felicidad |
 |
 |
 |
| Escrito por Alfonso Jesús Población Sáez |
| Viernes 09 de Marzo de 2018 |
|
Quizá este conocido dicho sea el que mejor resuma el espíritu del cortometraje que hoy analizamos en torno a las Olimpiadas Matemáticas, con una visualización de la resolución de los problemas realmente atractiva.
Ficha Técnica: Ficha artística: Argumento (síntesis elaborada por el propio director del corto): William, un chico de 17 años, se presenta al examen de la Olimpiada Internacional de Matemáticas en Gran Bretaña. Le diagnosticaron el Síndrome de Asperger, y le encantan las matemáticas más que cualquier otra cosa, por lo que está convencido de que ganará una medalla. Espera que esto lo ayude a volver a conectar con otra estudiante que también se presenta, Sarah, con la que solía quedar para preparar ejercicios, salir a dar una vuelta, etc. Sin embargo, el peso de la responsabilidad y la incomprensión de por qué terminó esa amistad lo distraen de resolver las cuestiones. Comentario Tras la no muy lejana en el tiempo y excelente X+Y (ver reseña 107; también británica, por cierto), este cortometraje nos plantea muchas similitudes con aquella: adolescente con Asperger altamente capacitado para las matemáticas, la relación con su madre, su interés por una chica de su edad, etc. Por ello, y porque no es la primera película centrada en la IMO (International Mathematical Olympiad) (ver reseña 47) caben, por muy odiosas que sean, las comparaciones, o al menos, buscar similitudes y diferencias. Por empezar por lo menos conseguido, llama la atención la puesta en escena tan minimalista de un evento que mueve allí donde se celebra a cientos de personas (participantes, preparadores, profesores, familiares, etc.). Aquí es prácticamente una prueba de tres cuestiones realizada en un gimnasio, y sin nada alrededor más que un profesor vigilante, una madre preocupada por su hijo, y medio centenar de participantes. Es entendible, ya que estamos ante una producción de bajo presupuesto, y seguramente realizado como sucede en nuestro país con la mayor parte de los cortometrajes, a base de pedir favores a amigos, recaudar fondos para hacerlo, tener alguna subvención, y con el trabajo de actores y equipo de forma altruista. Es entendible. Sin embargo, hubiera sido mucho más ajustado a la realidad si se hubiera enmarcado en una competición para elegir a los miembros del equipo nacional, por ejemplo, o una prueba previa. Además, no puede tratarse de un evento internacional ya que en este caso la prueba es por equipos (seis miembros por equipo) y no una individual como aparece en el cortometraje. Seguramente el director ha querido mantener esa dimensión en escena para justificar la valía de la protagonista femenina, que posee una medalla de oro y otra de plata, al menos. Otro aspecto podría decirse no positivo, desde el punto de vista de las matemáticas, es que al final, da la impresión de que al chaval, en realidad las matemáticas le interesan más bien lo justo, y obtener medalla en la IMO mucho menos. Son sólo el instrumento para acercarse a la chica que le gusta. Una de las preocupaciones del director (sólo tiene en su haber dos cortos estrenados ambos en 2016) era tratar de presentar las matemáticas de una manera interesante y relacionada con la historia que se cuenta. Y desde luego, como puede verse en el apartado posterior sobre las matemáticas que aparecen, la presentación de los problemas (tomados de competiciones reales), los comentarios y pensamientos de William, el protagonista, y la resolución, están muy bien llevados. Pero la realidad es distinta. Al finalizar el tiempo para realizar la prueba, cruzan sus miradas, pero no se deciden a hablar. Es William quien finalmente, con la excusa de comentar qué tal le ha salido, cómo has hecho este o aquel problema, etc., comienza la conversación que la madre, súper comprensiva (quizá demasiado idílicas son siempre estas madres que nos plantean este tipo de películas en las que hay algún tipo de discapacidad en los personajes, en este caso el autismo; no digo que tengan que ser madres repelentes o maltratadoras, que también el cine nos las ha retratado en el otro extremo, pero sí un poco más “normales” en el sentido de con los defectos de cualquier persona, algo menos blandengue), anima a que continúe en un momento dado. Y al final, ¿qué? ¿solucionan también los asuntos de su relación? ¿Porque lo dejaron? Vedlo y disfrutadlo, en este enlace, que ya digo que, desde el punto de vista matemático, es estupendo. La mala noticia, espero que para los menos, es que está en inglés. Este cortometraje se produjo en la metfilm School de Londres y ganó un premio especial en el As Film Festival 2017 (Roma, Italia) y fue nominado para un Smart Screen Creative Award de la Metfilm London School en 2016.
Los problemas Problema 1: En el cuadrilátero convexo ABCD, las diagonales AC y BD son perpendiculares, y los lados opuestos AB y DC no son paralelos. Supongamos que el punto P, intersección de los bisectores perpendiculares de AB y DC, está dentro del cuadrilátero. Demostrar que ABCD es cíclico si, y sólo si, los triángulos ABP y CDP tienen áreas iguales.
Empecemos diciendo que un cuadrilátero es cíclico cuando sus vértices pasan por una misma circunferencia. Es lo mismo que cuadrilátero inscrito en una circunferencia. Esa circunferencia es obviamente la circunferencia circunscrita al cuadrilátero. Es simplemente otra terminología de algo que conocemos perfectamente. Sean H y K los puntos de intersección de las perpendiculares desde P a AC y BD, respectivamente. El problema consiste en probar que existe una circunferencia que pasa por los cuatro vértices del cuadrilátero, si, y sólo si, las áreas de los triángulos que sombreo en la imagen en verde, son iguales. Pongamos entonces que Área(ABP) = área(AJB) + área(BJP) – área (AJP) Área(CPD) = área(CPJ) + área(CJD) – área (DJP) El que área(ABP) fuera igual a área(CPD), equivaldría entonces a que área(AJB) + área(BJP) – área (AJP) = área(CPJ) + área(CJD) – área (DJP) [1] Por otro lado, los triángulos AJB y CJD son rectángulos, por lo que sus áreas serán, respectivamente, Además, área(BJP) + área (DJP) = área(PBD) = área(AJP) + área (CJP) = área(ACP) = ya que PBD y ACP son también rectángulos. Por tanto, la igualdad [1] nos lleva a que AJ × BJ – CJ × DJ + PB × PK – AC × PH = 0 [2] La imagen nos permite ver con facilidad que AJ = AH – HJ = AH – PK BJ = BK + KJ = BK + PH CJ = CH + HJ = CH + PK DJ = DK – JK = DK – PH Sustituyendo en [2], y simplificando, se concluye que AH × BK = CH × DK . O sea que, si las áreas de los triángulos indicados son iguales, se verifica esa condición.
AH × BK = CH × DK y por tanto, área(ABP) = área(CDP), tal y como se ha demostrado anteriormente. Recíprocamente, supongamos ahora que las áreas de esos triángulos son iguales. Entonces se tiene la igualdad anterior, AH × BK = CH × DK. Sabemos que PA = PB y PC = PD por construcción. Si demostramos que PA = PC, tendremos entonces que PA = PB = PC = PD = radio de la circunferencia. Razonemos por reducción al absurdo: supongamos que PA > PC. Entonces AH > CH, y por tanto PB > PD, y BK > DK. Con esos datos, AH × BK > CH × DK, llegando a una contradicción. Se razona análogamente en caso de que supongamos que PA < PC, por lo que PA = PC. Problema 2: Determinar todas las parejas de números enteros (x, y) tales que
1 + 2x + 22x+1 = y2 Problema propuesto por el norteamericano Zuming Feng, y apareció como cuarto problema de la 47ª IMO celebrada en Slovenia en julio de 2006. La solución, apenas vislumbrada en el folio que escribe el protagonista es correcta. Comienza del siguiente modo: escribimos la ecuación del siguiente modo: 2x (2x+1 +1) = (y + 1) (y – 1) Para x < –1, el primer miembro no proporciona valores enteros, por lo que para esos valores no hay soluciones. Si x = – 1, tendríamos que 1 = y2 – 1, es decir y2 = 2, que no tiene solución entera. Si x = 0, tendríamos que 3 = y2 – 1, es decir y2 = 4, que nos da como soluciones los pares (0, ±2). Para x > 0, y es impar, por tanto y = 2n +1. Reescribiendo la ecuación, tenemos que 2x (2x+1 +1) = (2n + 2) (2n) = 4n(n + 1) Simplificando, 2x–2 (2x+1 +1) = n(n + 1), con x > 2 (x = 2, nos llevaría a que 9 = n(n + 1), lo cual no es posible ya que ninguna descomposición en dos factores de 9 tiene esa forma). A partir de aquí, termina realizando algunas acotaciones. Me parece más sencillo terminar del siguiente modo: Obviamente, ni n = 2x–2, ni n + 1 = 2x–2 pueden darse (porque en cualquiera de los casos, el otro factor no cuadra ni con n+1, ni con n, respectivamente), por lo que es necesario que 2x+1 +1 se descomponga en factores (impares) r, s, tales que 2x–2 r = s ± 1 Entonces |r| < 8, porque en caso contrario 2x–2 |r| > 2x+1 +1. Por otro lado, 2x–2 r2 = sr ± r, y |r| = 3 es la única posibilidad factible. Entonces 2x–2 9 = (2x+1 +1) ± 3, de donde 2x–2 = 4, y de ahí x = 4 (y = ±23). Por tanto, las únicas soluciones enteras son (0, ±2) y (4, ±23). Problema 3: Cinco cilindros vacíos e idénticos de capacidad 1 decilitro se disponen en los vértices de un pentágono. Dos jugadores, A y B, efectúan una serie de rondas. Al principio de cada una, el jugador B toma medio decilitro de agua y lo vuelca arbitrariamente sobre los cinco cilindros. Entonces, el jugador A elige un par de cilindros adyacentes (que estén sobre el mismo lado del pentágono) y los vacía. Y comienza del mismo modo la siguiente ronda. El objetivo del jugador B es conseguir que alguno de los cilindros rebose, mientras que el del jugador A consiste en evitarlo. ¿Puede el jugador B alcanzar su objetivo?
Termino de redactar esto el 8 de marzo, día de la mujer trabajadora, y el corto es también un estupendo homenaje a las chicas que se dedican a las matemáticas, y un aliciente (espero) para fomentar la vocación matemática entre ellas: Sarah destaca claramente y ha ganado una medalla de oro y otra de plata. Recordad también que el día 14 es el PiDay. Así que marzo es un gran mes, a pesar de sus idus, que yo no me los creo (nací en marzo). Hasta el próximo mes. Esta dirección electrónica esta protegida contra spambots. Es necesario activar Javascript para visualizarla |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |







 Paradójicamente, es la que más matemáticas explicitas presenta (lo cual es un hecho reseñable, dado su reducido metraje) sin ser el tema prioritario del argumento, porque en realidad la película nos habla de la amistad (ya lo indica el lema publicitario que aparece en el cartel: Las matemáticas son complicadas. La amistad, no).
Paradójicamente, es la que más matemáticas explicitas presenta (lo cual es un hecho reseñable, dado su reducido metraje) sin ser el tema prioritario del argumento, porque en realidad la película nos habla de la amistad (ya lo indica el lema publicitario que aparece en el cartel: Las matemáticas son complicadas. La amistad, no). Pero lo que realmente me ha sorprendido de este corto (y llevo ya a cuestas muchas películas sobre matemáticas) es la maravillosa simulación en la resolución del primer problema, con una incorporación de CGI (Computer-generated Images.- Imágenes generadas por ordenador) realmente magistrales. Una gozada y una maravilla. Lo podemos ver en la imagen. William se pone a pensar en los problemas, se imagina solo en el gimnasio, y mientras lee el enunciado, aparecen frente a él representaciones gráficas enormes que se van construyendo a medida que él va pensando, como si en su mente tuviera un software geométrico que va generándose a medida que él avanza. Además, en el suelo, van apareciendo diferentes opciones, diferentes caminos por donde continuar resolviendo el ejercicio. A veces, su elección lo lleva a ninguna parte, y debe retroceder a una opción anterior para rectificar su decisión y continuar por otro lado. Pero no todo es tan sencillo. A veces se atasca, no sabe por dónde continuar, …. Y entonces aparece ella, su musa, su amiga Sarah (con la que ha dejado de salir por alguna razón, y ahora casi ni se dirigen la palabra en la realidad), con mayor experiencia e inteligencia matemática que le da indicaciones, no las soluciones, de por dónde proseguir. Enseña, no resuelve. Esto sucede en el tercer problema. Del segundo no se nos dan mayores explicaciones, pero vemos el folio con la resolución hecha por William. Y el primero, que se le resiste, logran resolverlo juntos, lo que los llena de emoción y alegría.
Pero lo que realmente me ha sorprendido de este corto (y llevo ya a cuestas muchas películas sobre matemáticas) es la maravillosa simulación en la resolución del primer problema, con una incorporación de CGI (Computer-generated Images.- Imágenes generadas por ordenador) realmente magistrales. Una gozada y una maravilla. Lo podemos ver en la imagen. William se pone a pensar en los problemas, se imagina solo en el gimnasio, y mientras lee el enunciado, aparecen frente a él representaciones gráficas enormes que se van construyendo a medida que él va pensando, como si en su mente tuviera un software geométrico que va generándose a medida que él avanza. Además, en el suelo, van apareciendo diferentes opciones, diferentes caminos por donde continuar resolviendo el ejercicio. A veces, su elección lo lleva a ninguna parte, y debe retroceder a una opción anterior para rectificar su decisión y continuar por otro lado. Pero no todo es tan sencillo. A veces se atasca, no sabe por dónde continuar, …. Y entonces aparece ella, su musa, su amiga Sarah (con la que ha dejado de salir por alguna razón, y ahora casi ni se dirigen la palabra en la realidad), con mayor experiencia e inteligencia matemática que le da indicaciones, no las soluciones, de por dónde proseguir. Enseña, no resuelve. Esto sucede en el tercer problema. Del segundo no se nos dan mayores explicaciones, pero vemos el folio con la resolución hecha por William. Y el primero, que se le resiste, logran resolverlo juntos, lo que los llena de emoción y alegría. Este problema fue propuesto por Charles Leytem, de Luxemburgo, y apareció como primer problema de la 39ª IMO celebrada en Taipei (Taiwan) en julio de 1998.
Este problema fue propuesto por Charles Leytem, de Luxemburgo, y apareció como primer problema de la 39ª IMO celebrada en Taipei (Taiwan) en julio de 1998. Por otro lado, bisector perpendicular es una línea perpendicular (90 grados) que corta por la mitad a un segmento. En la película, William “visualiza” la situación como aparece en la imagen. Percatémonos (lo dice en la película) que, al ser un cuadrilátero, las diagonales AC y BD son perpendiculares. Por tanto, aparecen marcados tres ángulos rectos, el de esas diagonales, y las perpendiculares de P a AB y de P a CD (los bisectores). A continuación, llama J al punto de intersección de las diagonales AC y BD. En este punto, vamos a hacer una demostración algo diferente de la que nos propone William, que, no obstante, se puede seguir con todo detalle en el corto.
Por otro lado, bisector perpendicular es una línea perpendicular (90 grados) que corta por la mitad a un segmento. En la película, William “visualiza” la situación como aparece en la imagen. Percatémonos (lo dice en la película) que, al ser un cuadrilátero, las diagonales AC y BD son perpendiculares. Por tanto, aparecen marcados tres ángulos rectos, el de esas diagonales, y las perpendiculares de P a AB y de P a CD (los bisectores). A continuación, llama J al punto de intersección de las diagonales AC y BD. En este punto, vamos a hacer una demostración algo diferente de la que nos propone William, que, no obstante, se puede seguir con todo detalle en el corto.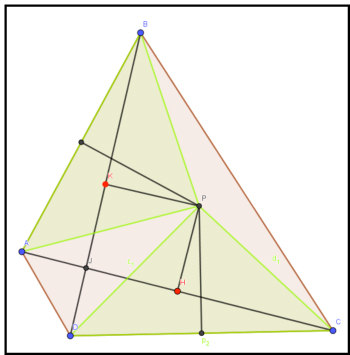 Trataremos de expresar las áreas de los triángulos buscados ABP y CDP en términos de otros triángulos para los que sepamos calcular el área fácilmente, que en este caso serán los triángulos rectángulos.
Trataremos de expresar las áreas de los triángulos buscados ABP y CDP en términos de otros triángulos para los que sepamos calcular el área fácilmente, que en este caso serán los triángulos rectángulos.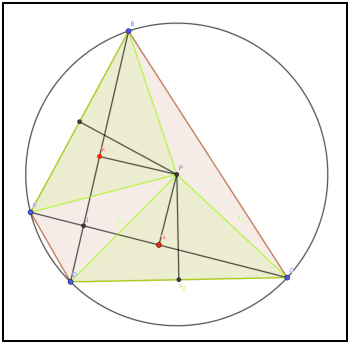 Pasemos a continuación a probar la condición necesaria y suficiente. Supongamos que el cuadrilátero ABCD es cíclico, tiene una circunferencia circunscrita. Entonces P debe ser el centro (obsérvese que PA = PD tal y como se han ido construyendo los triángulos anteriores) y AH = CH, BK = DK, con lo que al multiplicar ambas igualdades se tiene que
Pasemos a continuación a probar la condición necesaria y suficiente. Supongamos que el cuadrilátero ABCD es cíclico, tiene una circunferencia circunscrita. Entonces P debe ser el centro (obsérvese que PA = PD tal y como se han ido construyendo los triángulos anteriores) y AH = CH, BK = DK, con lo que al multiplicar ambas igualdades se tiene que No he encontrado que este curioso ejercicio de estrategia aparezca en ninguna IMO. William no ve claro la estrategia que debe seguir si fuera el jugador A (el que evita que rebosen los cilindros), así que su Sarah imaginaria le propone pasarse al lado contrario, que sea el jugador B. Así consigue hacerle ver lo que debe hacer para resolver la cuestión. No la detallo para no alargar en exceso esta reseña y que me tilden de pesado. En el corto aparece meridianamente explicado.
No he encontrado que este curioso ejercicio de estrategia aparezca en ninguna IMO. William no ve claro la estrategia que debe seguir si fuera el jugador A (el que evita que rebosen los cilindros), así que su Sarah imaginaria le propone pasarse al lado contrario, que sea el jugador B. Así consigue hacerle ver lo que debe hacer para resolver la cuestión. No la detallo para no alargar en exceso esta reseña y que me tilden de pesado. En el corto aparece meridianamente explicado.