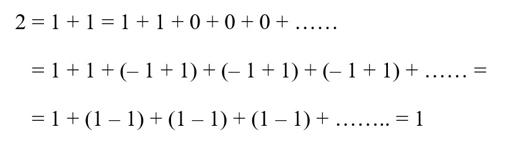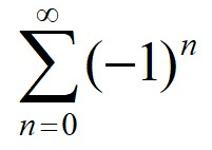ABC, 11 de Marzo de 2019
CIENCIA - El ABCdario de las matemáticas
Alfonso Jesús Población Sáez

Tras los múltiples razonamientos de los lectores al planteamiento de la semana pasada, el ABCdario de las Matemáticas retoma los secretos de esta operación básica

Fotolia

Realmente fueron sorprendentes las respuestas y razonamientos que los lectores han dado acerca de la cuestión de las sumas de la semana pasada. Reconozco que el tema del infinito no es elemental. De hecho, causó múltiples dilemas y contradicciones a matemáticos y expertos muy relevantes cuando se empezó a intentar trabajar, y les llevó bastante tiempo tratar de «domar al bicho». Por tanto, era difícil (salvo que lo escribiera alguien que haya realizado estudios de matemáticas superiores y de cierta especificidad), y no esperaba que se llegara a ninguna conclusión realmente correcta, pero tampoco esperaba que se argumentara tan «alegremente» a imagen y semejanza del caso finito, más aún cuando en la reseña se decía explícitamente que «las reglas y propiedades que rigen la suma de una cantidad finita de números no son las mismas cuando pasamos a una cantidad infinita». Un ejemplo más que he visto esta misma semana en una entrada en las redes sociales del profesor González Urbaneja, en el que se prueba que 2 = 1, lo cual como todo el mundo sabe es totalmente falso:

En este caso, leo con estupor respuestas como que en la penúltima igualdad se han «comido» un 1. No han entendido, con perdón, nada de lo que se ha hecho. Observemos con calma. Se han sumado en la segunda igualdad infinitos ceros, lo cual parece una simpleza. Pero no lo es, y no por el hecho de ser ceros, sino por el hecho de ser infinitos. Porque entonces, la siguiente «jugada» es describir esos ceros como (–1 + 1) (tampoco causa mucha extrañeza), pero después, ese segundo uno que el lector «cree» que se han comido, se coloca al lado del primer –1 del primer «paquete» de los paréntesis, y se reordenan esos «paquetes», poniéndolos ahora como (1 – 1). Y todos son cero. Y no sobra ni falta ninguno, porque como son infinitos, ¡no acaban nunca! No hay ningún error en ninguna operación. El problema está en añadir esos infinitos ceros, porque eso cambia radicalmente la naturaleza del objeto que estamos manejando.

Tampoco había ninguna operación mal hecha el otro día. No había divisiones por cero, como un lector sugería, por ninguna parte. Otros argumentaban en base a que estaba tratando de utilizar la propiedad conmutativa en restas (lo que como sabemos no se puede, porque la diferencia de números no es conmutativa, que quede claro: 3 – 2 no es lo mismo que 2 – 3). Pero es que en ningún momento se hacía eso, ni se mezclaban manzanas y peras tampoco por ninguna parte (aludiendo a manzanas para sumar y peras para restar, entiendo). ¿En qué momento se han cambiado el orden de los sumandos? Lo que se ha hecho es agrupar de otro modo las cantidades. ¡Pero son las mismas, y en el mismo orden! El problema está, lo repito, en que no sirve para estas sumas el tratamiento que se emplea en las sumas de una cantidad finita de sumandos.

Suma de series infinitas

Deseamos sumar una expresión como esta:

Lo primero que hay que hacer es, por analogía con las sumas de un número finito de sumandos (en lo sucesivo me referiré a esto como sumas finitas, que es un tostón escribir siempre «sumas de un número finito de sumandos»), ver cómo se comportan esas primeras sumas. Describimos entonces la siguiente secuencia de sumas:

A esta sucesión Sn así obtenida se le llama sucesión de sumas parciales (obvio el nombre, ¿no les parece?). ¿Y cómo se generaliza su comportamiento hasta infinitos sumandos? Por el paso al límite, es decir, se calcula:

Si su valor es un número real S, ese valor se toma como su suma, y se dice que la serie es convergente. Si es infinito, la serie es divergente; y si no existe el límite, se llama oscilante. A las series divergentes y oscilantes, las operaciones usuales y las propiedades asociativa y conmutativa no se pueden aplicar. Y eso es lo que pasa en los ejemplos que se pusieron la semana pasada: la primera era oscilante y la segunda divergente.

Vale, parece sencillo, pero no lo es, porque, en realidad casi nunca podemos encontrar una expresión concreta para Sn, así que, mal vamos a poder calcular el límite si ni siquiera podemos saber calcular esa suma (que es finita, por cierto, aunque con n sumandos). Entonces, ¿no se pueden sumar? Ya quisieran nuestros alumnos que eso fuera así, pero no. Hay resultados, proposiciones, teoremas, corolarios, criterios de convergencia, herramientas muy bonitas (a mí al menos me lo parecen) que nos permiten sumar y trabajar con series infinitas.

No les voy a dar la turra con una clase (eso que les he contado, se explica en los primeros cinco minutos del tema; háganse a la idea de que a este tema de series le dedicamos unas 20 horas, aproximadamente, ejercicios incluidos, claro). Pero si les voy a dejar caer el primer resultado (porque es muy fácil de demostrar, incluso de entender; pero no soplen, que no voy incluir tal demostración) que se llama condición necesaria de convergencia de una serie. Si una serie es convergente (o sea que suma un número real hemos quedado), entonces:

¡No se líen! Ese límite siempre podemos calcularlo, porque la sucesión an es conocida siempre, es la que me mandan sumar, la sucesión de los términos de la serie. Desafortunadamente, ese resultado es una condición necesaria, pero no suficiente. Y eso, ¿qué quiere decir? Muy sencillo: que si el límite no es cero, no converge, pero que si el límite es cero, no tenemos ni idea; a veces puede salir convergente, a veces, no. Hay que hacer un análisis del «enfermo» más exhaustivo (o sea, se necesitan más herramientas, más resultados). Pero con esa condición nos basta para explicar lo de las sumas del otro día. En la primera serie:

Claramente:

No existe (oscila entre – 1 y 1), mientras que en la segunda:

El valor de:

Por tanto, ninguna es convergente, y en ellas NO se pueden efectuar las manipulaciones algebraicas usuales.

Un último reto

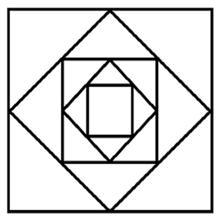
Para acabar, observen los cuadrados anidados de la imagen adjunta a la derecha. Se van construyendo a partir de los puntos medios de los lados de cada cuadrado. El primero, el más grande, tiene longitud de lado 1 cm. Si esta construcción continuara así hasta infinito, ¿serían capaces de calcular la suma de las áreas de esos infinitos cuadrados? ¿Y cuántos metros de madera necesitaríamos, si los lados fueran de ese material? Y al hilo de esto, ¿creen que existirá una longitud infinita que encierre un área finita? ¿Son capaces de imaginar una construcción plana que lo verifique? Hasta la próxima.

Alfonso J. Población Sáez es profesor de la Universidad de Valladolid y miembro de la Comisión de divulgación de la RSME.

El ABCDARIO DE LAS MATEMÁTICAS es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME)