1. Introducción

En el primer artículo de esta serie revisamos el concepto matemático de distancia y definimos formalmente la medida de similitud melódica; además, ilustramos estos conceptos con algunos ejemplos musicales. En este segundo artículo sobre la distancia matemática y la similitud melódica vamos a describir un buen número de medidas de similitud, las cuales agruparemos por familias dependiendo de su propósito y filosofía.

“El discurso musical progresa a través de múltiples transformaciones de su material musical”, decíamos en otra ocasión [Góm11]. En particular, en el ámbito melódico esa variación es fundamental. La trascendencia de la similitud melódica ha sido, y es, tal que numerosas disciplinas se han ocupado intensivamente de su estudio:

• En etnomusicología, por ejemplo, para entender la lógica musical, para evaluar los estilos y sus características, para conocer los criterios de improvisación. Véanse [BL51], [See66], [Hol10].
• En análisis musical, para construir modelos tanto teóricos como computacionales. Véanse [LJ83], [Mey73], [CIR98], [Typ07].
• En la resolución de conflictos de propiedad intelectual [Cro98].
• En tecnología musical, para aplicar los modelos obtenidos tras el correspondiente análisis. Véanse [MS90], [HSF98], [Pam06], [Hol10].
• En psicología de la música, para comprender mejor el hecho musical, para aportar conocimiento a un análisis integral de la música. Véanse [Sch99], [HE01], [MM01], [HE02], [HCR03].

Respecto a otro tema relacionado, la similitud rítmica, véanse las referencias citadas en el artículo [Góm11] de esta sección del mes de marzo de 2011.

2. Representación de melodías

Una melodía es un conjunto de notas que suenan en determinado orden y con determinadas duraciones. Esencialmente, una melodía es una combinación de alturas y ritmo. Las medidas de similitud se construyen a partir del siguiente proceso:

Figura 1: El proceso de construcción de una medida de similitud.

1. Obtención de la melodía. Esta puede venir descrita en formato audio, como un fichero de sonido de una grabación, o en formato simbólico, como un fichero midi o un fichero de partitura (Finale, Sibelius, etc.).
2. Representación de melodías abstractas. Según los propósitos perseguidos, la melodía se representa de varias formas. Estas representaciones que extraen ciertas características de las melodías reales se llaman representaciones abstractas. Varían en función del propósito final. Por ejemplo, en el análisis de cantes a palo seco en el flamenco, se ignora la duración de las notas, puesto que son cantes sin pulso regular y con mucho rubato.
3. Transformación de la melodía. La melodía abstracta sufre unas transformaciones que permiten el cálculo efectivo de la medida de similitud.
4. Diseño de la medida de similitud. Inicialmente, la mayor parte de las medidas se concentraron en un aspecto de las melodía, el cual medían con más o menos precisión. Poco a poco se han ido diseñando medidas que cuantifican varios aspectos de la melodía. El principal problema es cómo ponderar todos esos aspectos de manera coherente.

Es importante que la representación de las melodías cumpla las propiedades de invariancia que mencionamos en el primer artículo, esto es, invariancia por transposición de altura y tiempo más invariancia por cambio de tempo. Las melodías se suelen representar por una sucesión de pares (p_n,t_n), n = 1,…,N, donde p_n representa la altura y t_n las duraciones de cada nota. Esta representación obviamente no verifica las propiedades de invariancia. Se usan en su lugar dos representaciones diferentes, que sí respetan la invariancia:

• Para la altura se usa la representación por intervalo. En lugar de guardar las alturas absolutas, se anota el intervalo entre cada dos notas consecutivas I_n = p_n+1 - p_n.
• Para el ritmo se usa la representación IOI. Estas siglas vienen del inglés, inter-onset interval, o intervalo de duraciones relativas. Se calcula de manera similar al caso anterior, poniendo T_n = t_n+1 - t_n.

En el caso del ritmo también se usa otro método de representación, que consiste en expresar las duraciones en función de la duración mínima de la melodía. Esto no siempre es posible en todas las músicas, aunque sí en la mayor parte de la música occidental.

En las siguientes secciones del artículo describiremos las principales transformaciones melódicas que aparecen en las medidas de similitud.

3. Transformaciones de altura

3.1 Transformaciones de contorno

Este tipo de transformaciones se basa en el hecho de que la sucesión exacta de alturas en una melodía no es siempre lo más importante, sino la dirección melódica. Los puntos de giro de la melodía, los puntos en que cambia la dirección melódica, es un hecho que tiene relevancia en la percepción de la melodía. Si se representa la melodía como una línea poligonal, los puntos de giro se corresponden con los extremos relativos. La representación recibe el nombre de contorno melódico. En la figura de abajo tenemos de nuevo el tema principal de las variaciones K. 265 Ah, vous dirai-je, Maman. La línea poligonal que aparece sobre la melodía es el contorno melódico.

Para más información sobre los contornos melódicos véase el trabajo de Zhou y Kankanhalli [YK03].

3.2 Transformaciones borrosas

En muchas ocasiones la percepción de un estímulo no es totalmente nítida. Este tipo de transformaciones pretenden modelizar este hecho usando la lógica borrosa. La lógica borrosa usa un continuo de valores de verdad en el intervalo [0, 1]; consúltese [Hal03]. En este modelo los intervalos se acomodan en clases según la tabla siguiente:

Los intervalos se cuentan por semitonos en la tabla. Para ilustrar este concepto, consideremos la melodía abstracta dada por la sucesión {(p_i,t_i)}:

la cual está extraída de los primeros ocho compases del tema principal de las variaciones K. 265 Ah, vous dirai-je, Maman; véase la figura 2. De esta representación eliminamos el ritmo, la segunda componente, y calculamos los intervalos consecutivos:

Finalmente, calculamos la melodía borrosa (una vez que le aplicamos la clasificación por clases de la tabla 1):

3.3 Transformaciones usando la transformada de Fourier

La transformada discreta de Fourier proporciona una buena descripción general de la forma del contorno melódico, especialmente si hay células melódicas repetidas. Tiene también la ventaja de la invariancia. Por ejemplo, la transformada discreta es invariante por cambios de escala. Sin embargo, dado que la transformada discreta de Fourier está pensada para señales periódicas (infinitas), hay ciertos efectos indeseables, el llamado efecto frontera, que hay que tener en cuenta. Véase [Sch99], páginas 303 a 306, para una discusión sobre la transformada discreta de Fourier y sus ventajas e inconvenientes.

4. Transformaciones rítmicas

4.1 Gaussificación

La gaussificación de un ritmo consiste en representarlo como la combinación de lineal de distribuciones normales. Cada distribución normal tiene su media sobre cada nota del ritmo; las desviaciones son fijas e iguales para todas las normales. Si t_n, n = 1,…,N, es la sucesión de tiempos de la melodía, la gaussificación g(t) es

En la figura 3 tenemos un conocido ritmo, la clave son 3/2.

Si contamos el tiempo en semicorcheas de 0 a 15, las distribuciones normales en las notas ocurren en las posiciones 0, 3, 6, 10 y 12. Fijemos σ = 1 como desviación típica para todas esas distribuciones. Las medias de las normales serán las posiciones de las notas.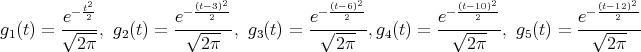

La figura 4 muestra el gráfico de estas 5 distribuciones normales.

La gaussificación del ritmo entero es la función g(t) = ∑⁵_i=1g _i(t)

4.2 Transformaciones borrosas

Al igual que las alturas, las duraciones también admiten un tratamiento vía la lógica borrosa. Las duraciones de una melodía se comparan con respecto a la duración d más frecuente en la melodía. Las clases de duraciones se obtienen tomando el cociente c entre el IOI T_n = t_n+1 -t_n y la duración d.

Esta clasificación no es la única posible y en la bibliografía se encuentran muchas más; véase la página 7 de [MF04].

5. Medidas simbólicas

Las medidas simbólicas consideran una melodía abstracta como una cadena de caracteres, esto es, como una sucesión finita de símbolos tomados de un alfabeto adecuado. Por ejemplo, la sucesión de alturas de una melodía se puede ver como una cadena de caracteres extraídos del alfabeto formado por el universo de frecuencias. El principal problema que aparece con las medidas simbólicas es que cuando las melodías tienen longitudes diferentes su manejo no es muy elegante y exigen modificaciones engorrosas. Las dos principales medidas simbólicas son la distancia de edición y los n-gramas.

5.1 Distancia de edición

El enfoque de la distancia de edición requiere la existencia de ciertas operaciones definidas en las cadenas. Dadas dos cadenas de caracteres, esas operaciones permiten transformar una cadena en la otra. Las operaciones más comunes son inserción, borrado y sustitución. La distancia de edición es el mínimo número de operaciones que hay que realizar para transformar una cadena en la otra. Cada operación tiene un coste asociado y la distancia final es la suma de los costes. Calcular el mínimo de operaciones se puede hacer usando algoritmos basados en programación dinámica. Véase Mongeau y Sankoff [MS90] para una descripción de este tipo de medidas.

Si d_e es una distancia de edición, entonces la expresión

es una medida de similitud, donde ∣c₁∣,∣c₂∣ son las longitudes respectivas de las cadenas.

Como ejemplo, consideremos las cadenas C₁ = {do, fa, sol, la} y C₂ = {re, sol, la, si}. Asociaremos a las operaciones de inserción, borrado y sustitución el mismo coste, que será de una unidad. La distancia de edición d_e(C₁,C₂) es 3. Esta distancia corresponde a hacer las siguientes transformaciones:

1. Sustitución de la nota do por re con coste 1: C₁ = {do, fa, sol, la}→{re, fa, sol, la}.
2. Borrado de la nota fa con coste 1: {re, fa, sol, la}→{re, sol, la}.
3. Inserción de la nota si con coste 1: {re, sol, la}→{re, sol, la, si} = C₂.

La medida de similitud es

5.2 n-gramas

La definición de n-grama no puede ser más simple: un n-grama es una cadena de longitud n. Para definir una medida de similitud con n-gramas se estudia la distribución de los n-gramas, para distintos valores de n, en la cadena dada. Por ejemplo, podemos definir la llamada medida del recuento de elementos distintos. Si a y b son dos cadenas, designemos por a_n el conjunto de los n-gramas distintos en a (se define b_n de manera similar). Entonces, la medida de recuento de distintos es

Existen otras medidas asociadas a los n-gramas, tales como la medida de Ukkonen o de la suma común; véase la página 10 de [MF04].

5.3 Conclusiones

En este segundo artículo hemos examinado el proceso de construcción de una medida de similitud melódica. Empezamos por estudiar las representaciones abstractas de melodías y continuamos con una revisión de las principales transformaciones de altura, rítmicas, así como las medidas simbólicas. En el próximo artículo estudiaremos medidas de similitud asociadas a las armonía y medidas vectoriales de similitud. Completaremos la serie sobre distancias y similitud melódica con la descripción de los experimentos que realizaron Müllensiefen y Frieler para establecer la medida de similitud en humanos.

Referencias