81. 110. (Noviembre 2020) Reseña del libro de Godfried Toussaint "The geometry of musical rhythm: what makes a “good” rhythm good?"

1. Introducción Este artículo es una reseña del libro de Godfried Toussaint The geometry of musical rhythm: what makes a “good” rhythm good? [Tou17a]. Godfried (en este artículo no lo llamaré Toussaint) fue mi director de tesis y amigo personal. Desgraciadamente, nos dejó en julio de 2019. Estaba dando una charla en una conferencia en Japón y cayó fulminado por causas todavía desconocidas pero que apuntan a un ataque al corazón. Figura 1: Godfried Toussaint Godfried era una persona apasionada de la vida en muchos aspectos. En los intelectuales y académicos, destaca su pasión por la geometría y la música. Empezó su carrera por la geometría, en particular la geometría computacional. Está considerado el padre de la Geometría Computacional. Estudió a fondo los aspectos teóricos de la geometría computacional así como sus aplicaciones a múltiples campos: reconocimiento de patrones (los algoritmos para encontrar los k vecinos más cercanos, análisis de agrupaciones), planificación de movimiento, visualización, teoría de nudos, configuraciones de articulados, los problemas de la galería de arte, triangulaciones, el problema del círculo vacío más grande, entre otros. Y fue productivo, como lo atestiguan sus cerca de 300 artículos en 50 años de carrera académica (su primer artículo data de 1969). Su otra gran pasión fue la música, en especial el ritmo y la percusión. Fue percusionista de música africana, afro-cubana y además tocaba la batería en un grupo de rock y pop formado por profesores de la universidad McGill (la universidad donde desarrolló su carrera) que tenía el significativo nombre de The Algorithmics. Godfried era un investigador de raza. Prefería con mucho inventar nuevos problemas, con perspectivas originales, que supusiese un cambio de perspectiva y metodología, antes que centrarse en problemas de investigación técnicos o de carácter demasiado concreto. Le gustaba pensar en abstracto, conectar varios campos con ideas insólitas; le gustaba ejercer la creatividad desde una cumbre de abstracción. Sin embargo, donde creo que Godfried brilló más fue en las relaciones personales. Godfried trataba bien a la gente con la que colaboraba. Les contagiaba la pasión que tenía por la geometría y la música, en general por la investigación y aun más por la vida misma. En los famosos talleres que organizaba en Barbados (asistí a diez de ellos) la risa pero también el trabajo duro eran constantes. Reconocía genuinamente el talento en otros, calmaba de forma magistral los atisbos de ego y sabía crear un ambiente de seguridad emocional que era altamente productivo y generaba un gran disfrute. 2. La reseña En la página de Amazon, encontramos las siguientes reseñas breves de varios especialistas en el campo del [Tou17b]. Por Marc Chemillier dice del libro: The late Godfried Toussaint studied the rhythms of the world like a gold panner, collecting with meticulousness and passion all the motifs that different cultures have given birth to. Thanks to his skill as a mathematician, he extracted fascinating properties from them. There is no doubt that this unique book will survive for a very long time. El eminente etnomusicólogo francés Simha Arom: Through the original use of distance geometry for analyzing musical rhythm and the visualization of rhythms as cyclic polygons, Godfried Tousssaint?s fascinating book will be extremely valuable to any researcher involved in in the field of rhythm. Y finalmente, los comentarios de Justin London: The new edition of The Geometry of Musical Rhythm takes us further along Godfried Toussaint?s journey through the world?s rhythms. There are new discussions of metric complexity, rhythm visualization, rhythmic performance, and the evolution of rhythmic patterns. Almost every chapter has been expanded and informed by the latest scholarship in music theory, music psychology, ethnomusicology, and music informatics. Specialists and lay readers alike will find this edition even more engaging and valuable than the first, giving us even more reasons to delight in what makes a “good” rhythm good. El libro está compuesto por 38 capítulos en los que el autor ofrece una descripción del ritmo desde sus predilecciones musicales y matemáticas; se trata además de un libro conceptual, donde no hay ejercicios ni está orientado a ser un libro de texto. Como dice el propio Godfried en los prolegómenos, “quería hacer un libro que fuera accesible a un público de músicos y gente del mundo universitaria, con diversas formaciones académicas y actividad musical, y a la vez con un nivel mínimo de prerrequisitos”. En su libro solo se examina música en formato simbólico. En el capítulo 1, titulado ¿qué es el ritmo?, pasa revista a diferentes definiciones dadas en el pasado y por diversos autores de este término. El concepto de ritmo adoptado por Godfried es simple y consiste en considerar una sucesión de k ataques distribuidos sobre un conjunto de n pulsos. Sigue, en el capítulo 2, con un distinción conceptual entre ritmo y pulso, y se adentra en cuestiones cognitivas para precisar tal distinción. Ya en el capítulo 3, se centra en un tipo de ritmo, los ritmos de clave u ostinatos, que será el grupo de ritmos que estudiará extensiva y profundamente en el resto del libro. Un ritmo de clave es un ritmo que se repite a lo largo de una pieza y que sirve como referente y estabilizador rítmico. Típicos ritmos de clave son los ritmos del son, la rumba, o la bossa-nova. En este capítulo encontramos una interesante historia del tresillo cubano (dos negras con puntillo seguidas de una negra en notación 2/2), la cual ilustra con alta erudición musical. Esta erudición musical es una de las características notables del libro de Godfried. En los capítulos 4 y 5 describe más a fondo los ritmos de clave, en especial su función rítmica, y además describe los instrumentos en los que se suelen tocar, esencialmente claves y campanas. En el capítulo 6, presenta la clave son, que en notación de caja es [×⋅ ⋅×⋅ ⋅×⋅ ⋅ ⋅×⋅ ×⋅ ⋅ ⋅ ]. En este punto encontramos una interesante discusión sobre por qué los ritmos más interesantes aparecen cuando k es menor que n∕2. También se discute algunos valores del número de pulsos en términos de su aparición en la práctica musical de diversas tradiciones. Termina este capítulo con un análisis matemático que justifica la particularidad rítmica de la clave son. En el capítulo 7 presenta los seis ritmos binarios objeto de estudio en buena parte del resto del libro. Son estos: Figura 2: Los seis ritmos de clave binarios Explica los orígenes de estos ritmos, su nomenclatura y su aparición en diversos contextos musicales. En los capítulos 8 y 9 presenta su método de visualización de los ritmos de clave a través de su representación geométrica en círculos. Figura 3: La geometría de los ritmos de clave Además, define varios conceptos que se usarán a lo largo del libro tales como contenido del intervalo, distancia entre notas (ataques), distancia geodésica, vector de intervalos, histogramas de distancias e histogramas de distancias adyacentes. También define los ritmos aksak (a partir del trabajo de Simha Arom [Aro91]). En el capítulo 10 se analizan los ritmos binarios y ternarios y se presentan las claves binarias de 5 y 7 notas más importantes, la clave fume-fume y el bembé (ritmos descritos con su terminología). Godfried hace una comparación entre ambos y estudia su contorno rítmico. El capítulo 11 es un capítulo aparte, pues realiza una comparación entre ritmo y alturas de sonido (escalas más bien). El capítulo 12 es una revisión de la obra de Rolando Pérez La binarización de los ritmos ternarios africanos en América Latina [PF86]. En esta obra Pérez propone una teoría de cómo los ritmos binarios que se oyen en América Latina provendrían de una binarización de ritmos ternarios de los esclavos africanos. Godfried hace un análisis de esta hipótesis con una perspectiva computacional y matemática. El capítulo 13 está dedicado a uno de los temas que más le gustaban en la teoría del ritmo: la síncopa. Examina y discute las varias definiciones de síncopa que encuentran en la literatura (como la de Jackendoff y Lerdahl [LJ83] o la de Keith [Kei91]). Gran parte de este capítulo es material de la tesis de maestría que dirigió a Eric Thul [Thu08]; véase también [Góm11]. En el capítulo 14 se zambulle en el fascinante mundo de las operaciones sobre ritmos, en particular, en los collares y las pulseras (necklaces y bracelets). Aplica toda esta teoría combinatoria al estudio de ritmos de clave y destila maneras de clasificar ritmos en base a si existe alguna operación que pase un ritmo a otro. Aquí es otro capítulo donde ilustra sus teorías con abundantes ejemplos de las tradiciones musicales más diversas. En el capítulo 15 estudia el índice de asimetría rítmica, propuesto inicialmente por Simha Arom, y lo aplica al análisis de la música de los pigmeos aka así como a los ritmos de clave seleccionados. Esta parte del libro es fuertemente algorítmica y se disfruta mucho la generación de ritmos en base a propiedades pre-establecidas. El capítulo 16 se especializa en el estudio de índice de contratiempo, que es una medida de complejidad rítmica con inspiración en la teoría de números. Y finalmente, en el capítulo 17 aborda el problema de la complejidad rítmica a través de conceptos tan potentes como puede ser la entropía. Los capítulos 18 a 22 están dedicados a los ritmos euclídeos o ritmos cuyas notas están distribuidas lo más regularmente posible. En el capítulo 18 argumenta muy elocuentemente porque la distancia geodésica en el círculo no es una buena medida de la dispersión de las notas en el ritmo. A continuación, propone la distancia intercordal como una medida de la regularidad de un ritmo y prueba que funciona. Figura 4: Distancias entre las notas de un ritmo En el capítulo 19 expone los aspectos algorítmicos de la generación de los ritmos euclídeos; en concreto, muestra de una manera muy instructiva la conexión entre el algoritmo de Euclides de cálculo del máximo común divisor y los ritmos euclídeos. Variando el número de notas y de pulsos, genera varios ritmos que aparecen en diversas músicas del mundo (el tresillo cubano, el bembé, la clave bossa-nova, ritmos de los pigmeos aka, entre otros). Los ritmos euclídeos o de regularidad máxima tienden a crear tensión rítmica, sobre todo si el número de notas y el número de pulsos son primos entre sí (no tienen divisores comunes salvo el 1). En este caso las notas “contradicen” las notas que se esperan a partir del número total de pulsos. Consideremos, por ejemplo, el ritmo [×⋅ ⋅×⋅ ⋅×⋅ ]. Tiene 8 pulsos y 3 notas y observamos que 3 y 8 son primos entre sí. Por ser 8 divisible por 2 y 4, las notas sobre múltiplos de 2 y 4 se perciben como estables. Sin embargo, este ritmo tiene notas en 0,3 y 7. Al tocar ese ritmo se percibe una superposición de un ritmo ternario, las tres notas del ritmo, sobre un ritmo binario, la estructura binaria de los pulsos. Todo ello, ciertamente, crea tensión rítmica. Demain y otros colegas, autores del trabajo The Distance Geometry of Music [DGM+05], investigaron la relación entre la distribución de regularidad máxima de patrones y otras disciplinas, con especial énfasis en el ritmo musical. ¿Cómo se transforma el cálculo del máximo común divisor en un método para generar patrones distribuidos con regularidad máxima? Ilustraremos el proceso con un ejemplo de ritmos. Supongamos que tenemos 17 pulsos y queremos distribuir de forma regular 7 notas en los 17 pulsos. Sigamos los pasos dados en la figura 5. Primero, alineamos el número de notas y el número de silencios (siete unos y diez ceros); véase la figura 5–paso (1). A continuación, formamos grupos de 7, los cuales corresponden a efectuar la división de 17 entre 7; obtenemos, pues, 7 grupos formados por [10] (en columnas en el paso (2) de la figura). Sobran tres ceros, lo cual indica que en el paso siguiente formaremos grupos de 3. Tras formar el primer grupo –véase el paso (3) de la figura– nos quedamos sin ceros. Continuamos agrupando de 3 en 3 tomando los grupos de la otra caja, en la que quedan 4 columnas (figura 5– paso (4)). Procedemos así que queden uno o cero grupos; de nuevo, esto es equivalente a efectuar la división de 7 entre 3. En nuestro caso, queda un solo grupo y hemos terminado (paso (5)). Finalmente, el ritmo se obtiene leyendo por columnas y de izquierda a derecha la agrupación obtenida (paso (6)). Figura 5: Generación de ritmos euclídeos. Aquí cada 1 representa una nota [×] y cada 0, un silencio [ ⋅ ]. El ritmo que hemos generado con nuestra notación se escribe entonces como [×⋅ ⋅×⋅×⋅ ⋅×⋅×⋅ ⋅×⋅×⋅ ] Los ritmos generados por este método se llaman ritmos euclídeos. El ritmo euclídeo de k notas y n pulsos se designa por E(k,n). Otra manera útil de designar un ritmo es mediante las duraciones de las notas en términos de pulsos. Así, por ejemplo, el ritmo de la sevillana [×⋅ ⋅×⋅ ⋅×⋅ ⋅×⋅ ⋅ ] se puede escribir como (3333), donde cada 3 indica que dura tres pulsos. El ritmo euclídeo que acabamos de obtener con esta notación se escribe E(7,17) = [×⋅ ⋅×⋅×⋅ ⋅×⋅×⋅ ⋅×⋅×⋅ ] = (3232322). Demain y sus coautores [DGM+05] probaron formalmente que este algoritmo proporciona, salvo rotaciones, la única manera de distribuir k objetos entre n del modo más regular posible. Aún más, había varios algoritmos propuestos de manera independiente y ellos probaron que, en realidad, eran todos equivalentes al viejo algoritmo de Euclides. Damos a continuación una pequeñísima muestra de ritmos euclídeos que se encuentran en las músicas tradicionales del mundo y que aparecen en el libro de Godfried. E(5,8) = [×⋅××⋅××⋅ ] = (21212) es el cinquillo cubano, así como el malfuf de Egipto, o el ritmo coreano para tambor mong P’yŏn. Si el ritmo se empieza a tocar desde la segunda nota aparece un popular ritmo típico de Oriente Próximo, así como el timini de Senegal. Si se empieza en la tercera nota tenemos el ritmo del tango. E(5,12) = [×⋅ ⋅×⋅×⋅ ⋅×⋅×⋅ ] = (32322) es un ritmo muy común en África central que tocan los pigmeos aka. Cuando se toca desde la segunda nota es, entre otros, la clave columbia de la música cubana y el ritmo de la danza chakacha de Kenya. E(5,16) =[×⋅ ⋅×⋅ ⋅×⋅ ⋅×⋅ ⋅×⋅ ⋅ ⋅ ] = (33334) es el ritmo de la bosa-nova de Brasil. Este ritmo se toca a partir de la tercera nota. Existen cerca de dos centenares de ritmos de músicas del mundo documentados que son generados por el algoritmo de Euclides. Para más información sobre ritmos euclídeos, recomendamos los artículos [GTT09b] y [GTT09a] El capítulo 20 trata de la aplicación de los ritmos euclídeos al cálculo de los años bisiestos. Proporciona una fascinante historia del problema de definir los años bisiestos y cómo se han resuelto en diversas culturas (desde la islámica a la cristiana). En el siguiente capítulo, el 21, se estudian los ritmos aproximadamente regulares, que son aquellos que difieren en un ritmo euclídeo por una nota; véase la figura de abajo. Figura 6: Ritmos aproximadamente regulares Para cerrar esta serie de capítulos sobre los ritmos euclídeos, Godfried estudia las conexiones entre estos ritmos y la cristalografía. El capítulo 23 está dedicado a los ritmos complementarios, esto es, a los ritmos obtenidos al intercambiar notas por silencios y viceversa. Estudia Godfried las propiedades que se conservan por la toma de complementarios y en particular analiza el teorema del hexacordo; véase [BBOG09]. El capítulo 24 es una conexión entre los ritmos y la radio astronomía que usa resultados del capítulo anterior. En el capítulo 25 se presentan los ritmos profundos, que son ritmos en que las distancias entre todas las notas ocurren de manera única. Si hacemos el histograma de un ritmo profundo, entonces es posible ordenar sus distancias de tal manera que el histograma sea creciente o decreciente estrictamente. La figura de abajo ilustra un ritmo profundo, en este caso, el bembé. Figura 7: Ritmos profundos El capítulo 26 versa sobre los ritmos cáscara. Dada una propiedad P de un ritmo (ser euclídeo, por ejemplo), se dice que es un ritmo cáscara con respecto a P si existe una sucesión de inserciones o borrados que mantiene la propiedad todo el tiempo. En el capítulo 27 Godfried estudia los ritmos fantasma, que son los ritmos resultantes de considerar como ritmos los silencios de un ritmo dado. En particular, discute las implicaciones cognitivas de estos ritmos. El capítulo 28 consiste en un examen de los cánones rítmicos y también de las simetrías axiales que se pueden encontrar en los ritmos. En el capítulo 29 el tema principal es los ritmos definidos por acentuación. Estos ritmos consisten en tocar todas las notas de los pulsos y acentuar unas cuantas de ellas, lo cual da lugar a un ritmo que destaca sobre la alfombra de pulsos. Este tipo de ritmos aparece, por ejemplo, en el flamenco. El capítulo 30 investiga varios tipos de simetría en los ritmos (simetría axial, palindrómica, etc.), ampliando así el capítulo 28. El capítulo 31 se adentra en los ritmos que tienen un número inusual de pulsos; se trata más bien de un examen musicológico de dichos ritmos más que un análisis matemático del mismo. En el capítulo 32 se discuten y analizan diversas representaciones de los ritmos, desde la notación de caja hasta las duraciones inter-notas. Ya en el capítulo 32 Godfried nos muestra uno de los temas más interesantes en la teoría del ritmo: la similitud rítmica. Examina diversas distancias de similitud, desde la distancia Hamming hasta la distancia de permutación dirigida (cuyo inventor fue él). En el capítulo 33 el autor se enfrenta a definir el concepto de regularidad e irregularidad para ritmos y cómo establecer una gradación entre ambos extremos. El capítulo 35 describe las aplicaciones de los árboles filogenéticos a la teoría del ritmo. Aquí expone buena parte de sus resultados [?] con esta técnica así como sus aplicaciones al análisis del flamenco. El capítulo 36 está consagrado al estudio combinatorio del ritmo. Finalmente, el capítulo 37 consiste en una defensa ardiente del ritmo de la clave son como el ritmo más popular y mejor construido (argumenta para ello su nivel de regularidad, su índice de asimetría, su índice de contratiempo, su complejidad métrica, entre otras). En el último capítulo del libro traza una historia y un recorrido musicológico de este ritmo. El libro cierra con un epílogo en que Godfried hace un resumen de su perspectiva e ideario sobre la teoría del ritmo y justifica una vez más la pertinencia del análisis matemático y computacional del ritmo.   Bibliografía [Aro91] Simha Arom. African Polyphony and Polyrhythm. Cambridge University Press, Cambridge, England, 1991. [BBOG09] B. Ballinger, F. Benbernou, N. Gomez, J. O’Rourke, and Toussaint G. The continuous hexachordal theorem. In E. Chew, A. Childs, and C-H. Chuan, editors, Mathematics and Computation in Music, pages 63–77. Springer, Berlin, 2009. [DGM+05] Erik Demaine, Francisco Gomez, Henk Meijer, David Rappaport, Perouz Taslakian, Godfried Toussaint, Terry Winograd, and David Wood. The distance geometry of deep rhythms and scales. In Proceedings of the 17h Canadian Conference on Computational Geometry, pages 160–163, University of Windsor, Windsor, Ontario, Canada, August 10-12, 2005. [GTT09a] F. Gómez, P. Talaskian, and G.T. Toussaint. Interlocking and euclidean rhythms. Journal of Mathematics and Music, 3(1):15–30, 2009. [GTT09b] F. Gómez, P. Talaskian, and G.T. Toussaint. Structural properties of euclidean rhythms. Journal of Mathematics and Music, 3(1):1–14, 2009. [Góm11] Paco Gómez. Medidas matemática de síncopa (I), 2011. [Kei91] Michael Keith. From Polychords to Pólya: Adventures in Musical Combinatorics. Vinculum Press, Princeton, 1991. [LJ83] F. Lerdahl and R. Jackendoff. A Generative Theory of Tonal Music. MIT Press, Cambridge, Massachussetts, 1983. [PF86] Rolando Antonio Pérez Fernández. La binarización de los ritmos ternarios africanos en América Latina. Casa de las Américas, Havana, 1986. [Thu08] Eric Thul. Measuring the complexity of musical rhythm. Master’s thesis, McGill University, Canada, 2008. [Tou17a] Godfried Toussaint. The geometry of musical rhythm: what makes a “good” rhythm good? CRC Press, Boca Raton, Florida, 2017. [Tou17b] Godfried Toussaint. The geometry of musical rhythm: what makes a “good” rhythm good?, 2017.

Lunes, 16 de Noviembre de 2020 | Imprimir | PDF |  Correo electrónico

82. 155. Nueva publicación matemático-cinéfila

En pleno confinamiento me llegó, por gentileza del autor, un nuevo libro dedicado a la relación entre las matemáticas y el cine. Teniendo en mente las próximas fechas navideñas, época de lecturas y regalos, echamos un vistazo al libro, y a lo que nos cuenta su autor, José María Sorando. Nuevamente con la editorial cordobesa Guadalmazán, José María Sorando, profesor jubilado de Secundaria nos propone un nuevo volumen, el tercero (aunque el autor tiene otro más sobre este tema con otra editorial; más abajo encontrareis las referencias de todos ellos), en el que continúa explorando las relaciones entre el cine y las matemáticas. Hagamos un pequeño recorrido por sus páginas antes de hablar con él. Tras una breve reflexión sobre la aparente dispar asociación para la persona de a pie entre estas dos disciplinas, cine y matemáticas, con la que otros autores y el propio Sorando suelen encabezar sus textos, encontramos una disposición en torno a siete elementos o momentos reconocibles en toda película: el espectador, los personajes, los escenarios, las imágenes, el título, el guion y el popular “The end”. Respecto al Espectador, se presentan ocho situaciones ante las que nos preguntaríamos al verlas durante la proyección si son ciertas, si tienen fundamento real, o son simples montajes. En la actualidad, gracias a las nuevas tecnologías, es mucho más económico y quedan más “realistas” muchas escenas. Pero hubo un tiempo en que la verosimilitud pasaba por la recreación real de secuencias con evidente riesgo para la integridad física del que las ejecutaba (en la imagen, Buster Keaton en One week (1920)). En muchos casos, los fundamentos para su realización se fundaban en su estudio físico o matemático. Ese tipo de escenas son las que integran este capítulo. Al final de cada capítulo, se incluye un espacio denominado Diálogos, que como su nombre indica, recopila conversaciones tal cual aparecen en algunas películas que guardan relación con las matemáticas. Asimismo, a lo largo de todo el texto, el autor nos permite esbozar alguna que otra sonrisa a partir de comentarios y/o razonamientos con cierta sorna y sarcasmo que provocan las situaciones que aparecen en las películas. De modo que no sólo aprenderemos a mirar las películas en clave matemática sino también pasaremos un buen rato. El capítulo dedicado a los Personajes se ha dividido en dos apartados generales. El primero para aquellos para los que las matemáticas no pasan de la aritmética elemental y el cálculo de porcentajes a lo sumo. Se citan algunos ejemplos en los que el cine ridiculiza y en cierto modo menosprecia las matemáticas. El siguiente apartado se dedica a los matemáticos profesionales, personificados mediante diferentes tópicos (locura; grandes calculistas; obsesivos, nunca desconectan de sus teoremas; poco seductores, torpes en las relaciones personales). Para cada caso, además de referencias a películas concretas, se reflexiona sobre cada una de estas caracterizaciones. En el capítulo sobre Escenarios, se considera la geometría del diseño del lugar, de objetos característicos, la composición de los planos utilizados por el director, y cómo estas elecciones buscan transmitir determinadas sensaciones. Así, la angulación extrema provoca desazón (expresionismo alemán, El gabinete del doctor Caligari, por ejemplo), o la rectitud frialdad, artificialidad, e incluso humor. Si hay una filmografía en la que predominan las rectas y la minimalidad esa es la japonesa, que evita distraer al espectador para que se centre en la personalidad y problemática de los personajes. El paralelismo de luces y sombras enmarca situaciones tensas (regímenes totalitarios, sugerencia de crímenes, etc.). También las curvas o las composiciones circulares pueden ser hábilmente elegidas para describir determinadas simbologías, o determinados cuerpos geométricos pueden ser indicativos de misterios, e incluso constituirse en personajes por encima de los humanos (como en 2001, una odisea en el espacio; en la foto el célebre obelisco, que no es un obelisco), o una maniática regularidad geométrica (con los elementos que estudiamos en las aulas: traslaciones, giros, simetrías, reflexiones, homotecias, etc.) puede transmitirnos situaciones inquietantes. Consideración aparte merecen los laberintos (símbolos desde la Antigüedad para representar múltiples ideas, además de su estética decorativa, que siempre queda bien en pantalla) para los que se describen dos de los muchos algoritmos existentes para salir de ellos (Tarry y Tremaux) gracias a la teoría de grafos. También el trabajo del artista Maurits C. Escher es incluido en este capítulo en relación a su aparición en películas, anuncios y series de animación. El capítulo siguiente está dedicado a las Imágenes, parte esencial de toda película, para las que las matemáticas son muy útiles, tanto en su formación (sobre todo en la actualidad con las técnicas digitales y los consabidos algoritmos que diseñan las CGI), como en la composición pautada de los planos escénicos. La composición en el cine es heredera de la de la pintura, más compleja, por el añadido del movimiento. El encuadre debe mucho a la geometría, teniendo el director de la película que elegir la perspectiva, las líneas que conforman la disposición de los elementos que desea enfatizar, y otros detalles. A este respecto existen varias técnicas muy utilizadas como la regla de los tercios, la búsqueda de simetrías, el control de los puntos de fuga, la creación de simetrías infinitas mediante la utilización de espejos, la simetría dinámica, la proporción aurea, la composición triangular o la regla de los impares. De todo ello, además de su explicación y justificación, se muestran bastantes ejemplos de películas concretas. En cuanto a los algoritmos se describen y comentan dos de ellos, los basados en fractales y el flocking. Los primeros permiten representar imágenes complejas a partir de estructuras sencillas que se repiten muchas veces. De un modo sencillo, pensando en el lector que no conozca nada sobre ellos, se describen escuetamente (el objetivo del libro no es entrar en detalles matemáticos; el que lo deseé puede ampliar en otros textos, de los que se da referencia, el asunto) algunas propiedades, así como el concepto de dimensión fractal y la autosemejanza. El flocking reproduce el comportamiento de bandadas de pájaros (y otras masas de animales), en las que la inteligencia colectiva permite que cada individuo conozca cómo debe comportarse para no colisionar con los cientos de compañeros de vuelo. El libro proporciona además enlaces a vídeos en los que se ejemplifican todos estos algoritmos. Este apartado finaliza con diferentes tipos de movimientos de cámara, como el travelling, el recurso del plano-contraplano y enumera las principales posiciones de la cámara respecto a lo que capta (cenital, picado, normal, contrapicado y nadir) que recorren de manera continua el intervalo [–p/2, p/2]. En la sección dedicada al Título, la más breve, se repasan algunos de los títulos de carácter matemático más representativos, algunos con cierto sentido, otros como simple llamada promocional. En cuanto al Guion, lo encontramos dividido en Estructura y Situaciones. Para la primera, encontramos varios epígrafes en los que volvemos a encontrar diferentes ejemplos. Entre éstos, la simetría argumental, las vidas paralelas, la convergencia, el guion circular, la autosemejanza, los ciclos sin fin, el ritmo del relato, el rechazo de Buñuel a la lógica (en donde el autor concluye acertadamente que, por mucho que se intente, negar la lógica nos lleva a una nueva pauta, un nuevo patrón, también lógico, lo que determina lo absurdo del propósito) y la simetría. El apartado dedicado a las situaciones, uno de los más extensos del texto, aparece dividido a su vez en tres: Historia de las matemáticas, Matemáticas Escolares y Matemáticas en cualquier ocasión. La historia de las matemáticas se recorre del siguiente modo (entre paréntesis, la película en la que se recrean esos momentos): la prehistoria, con los sistemas de numeración (El clan del oso cavernario), la escuela pitagórica (Donald en el país de las Matemáticas), Hipatia de Alejandría (Ágora), Gauss (Midiendo el mundo), Galois (a través del célebre cortometraje de Alexandre Astruc, recientemente subido a la red, lo que nos permite por fin descubrirlo después de años sin saber poco más que existía), Ramanujan (El hombre que conocía el infinito), Alan Turing (Enigma y Descifrando Enigma), John Nash (Una mente maravillosa), Andrew Wiles y el último teorema de Fermat (Los crímenes de Oxford), y problemas por resolver como la conjetura de Goldbach (La habitación de Fermat), las ecuaciones de Navier-Stokes (Un don excepcional) y P = NP (The Travelling Salesman). En cada caso con la descripción de las escenas más relevantes y la explicación del tema o noción matemática que se aborda en la película. De las Matemáticas Escolares se conocen también una abundante colección de escenas (muchas en el cine español) de las que se seleccionan algunas como introducción, para a continuación enmarcarlas dentro de las subsecciones Docentes, Estilos Didácticos, Superdotados (normalmente descritos como desdichados e inmersos en dramas, bien de tipo personal, bien como consecuencia de un entorno que no los entiende y tampoco se esfuerza en ello), En la pizarra (herramienta prácticamente imprescindible, sea la clásica o sea una digital, y por tanto presente en casi todas las películas sobre las matemáticas; el autor aprovecha para mostrarnos, a propósito de la resolución de una ecuación sencilla de primer grado, la poco didáctica manera que han tenido, y siguen teniendo muchos profesores, en su resolución, a base de recetas mecánicas que parecen pases mágicos. Obviamente, el cine también lo refleja de este modo), Demostraciones (comenta dos, en los filmes Adiós, muchachos y X + Y), El temido suspenso (tres ejemplos) y Teorema de Pitágoras, ... o algo así (cinco ejemplos). En cuanto a las Matemáticas en cualquier ocasión, aparece dividido en las subsecciones Tenemos un problema (normalmente en situaciones complicadas, al contrario de los alumnos cuyos problemas matemáticos son los de los libros de texto), Decisiones críticas (los algoritmos pueden controlar las situaciones, aunque el golpe de efecto cinematográfico prefiera dejar la decisión in extremis al héroe), Matemáticas Terapéuticas (en circunstancias muy tensas, las matemáticas pueden ayudarnos a relajarnos, a tranquilizarnos pensando en otra cosa). Y finalmente en The End, se hace una breve reflexión sobre la necesidad de afrontar todo en la vida desde diferentes puntos de vista, no sólo el inmediato o el primero que nos venga a la cabeza. La realidad, por muy simple que parezca, no lo es, y necesita cierto análisis. Esto nos lo enseñan también las matemáticas. Y aplicando esa máxima, quizá algunas cosas irían mucho mejor. Hay también un anexo con un listado de películas en las que el protagonista es un matemático, y una amplia bibliografía a la que acudir en caso de necesitar ampliar o consultar otras fuentes. De todo lo comentado, se deduce que estamos ante un libro de lectura asequible, entretenido, que uno puede leer en cualquier orden, y con el que descubrirá detalles de los que no se había percatado o parado a pensar, y con los que afrontar el visionado de las películas en lo sucesivo de una manera diferente. El autor José María Sorando es catedrático de Matemáticas de Educación Secundaria, en la actualidad ya jubilado de la docencia activa, pero dedicado a la difusión de su experiencia didáctica entre compañeros docentes y a la divulgación matemática entre todos los públicos. Su curriculum es muy extenso (a partir del enlace se accede a la mayor parte de sus actividades, publicaciones, conferencias, etc.), aunque la forma más certera de conocer su trabajo y personalidad es visitando su imprescindible página Matemáticas en tu mundo. Aun así, he querido charlar con él, sobre diferentes temas, además de sobre sus libros. He aquí, lo que nos contó: Sobre la docencia de las matemáticas 1.- Nos encontramos en unas circunstancias (Covid) distintas a las que siempre habíamos vivido. ¿Cómo se observa desde fuera (por tu jubilación) la situación docente? Me parece un tiempo muy complicado. La pasada primavera, de la noche a la mañana el profesorado tuvo que cambiar su sistema docente, cada cual como pudo, con muchísimo trabajo y voluntarismo. Se confiaba en que durante el verano las administraciones proveerían de medios y pautas para encarar el nuevo curso en el nuevo contexto, pero… ha habido de todo. En algunos casos, tan solo la proclama de que había que “empezar con normalidad”. Pero la normalidad ha cambiado radicalmente y era necesario haber dotado de medios y plantillas suficientes, cambiado la organización y los espacios escolares y, sobre todo, formar en el cambio metodológico necesario. 2.- Las matemáticas en particular, bajo mi punto de vista, son una asignatura en la que es esencial la presencialidad tanto para el alumno como para el profesor. La mitad del curso pasado tuvo que ser impartido bajo el confinamiento, y tal como están las cosas, puede que la situación se repita de nuevo. Desde tu perspectiva, ¿cómo se podría paliar, si es que se puede, la evidente pérdida de calidad en la enseñanza? ¿Qué opinión te merecen los vídeos grabados “enseñando” matemáticas, según ellos? ¿Crees que un alumno podría alcanzar el mismo nivel (o superior) en base a la docencia telemática? No creo que se pueda lograr esto último. En el aprendizaje de las matemáticas es imprescindible la interacción profesor-alumno que permite adaptar la enseñanza a la diversidad de grupos y de estudiantes. Un video grabado o una emisión en streaming se centra en la enseñanza magistral, igual para todos, pero no en el aprendizaje basado en preguntas, sugerencias o refuerzos en tiempo real. En esto último consiste el “arte de enseñar”, no en ser “bustos parlantes”. Por otra parte, la semipresencialidad se traduce en que cada grupo se convierte en dos, con un incremento del estrés docente. En este modelo se confía en que el alumno aprenderá solo en su casa haciendo tareas. En la enseñanza obligatoria, eso es ilusorio. Habrá mucha intervención paterna y mucha copia para salir del paso. Y por último, para bien y para mal, la enseñanza es un acto de comunicación marcado por el estilo personal del docente, lo cual requiere ser en vivo y en directo. Cuando esto no sea posible, habrá que recurrir a opciones creativas que siempre van a suponer un aumento de la dedicación del profesorado, que debiera ser compensado en los horarios. En mi experiencia (hace más de 4 años ya) el blog de aula permitió que la clase tuviera una prolongación en casa muy estimulante y viva, mediante las sugerencias del profesor y los comentarios de los alumnos. Seguro que ahora hay otras posibilidades que explorar y que, alejado de las aulas, desconozco; siempre, insisto, poniendo el foco en el aprendizaje. Sobre la divulgación de las matemáticas 3.- Tu dedicación a la divulgación de las matemáticas a trasladarlas y aplicarlas a situaciones cotidianas, ha sido, y sigue siendo, muy destacada. La magnífica página “Matemáticas en tu mundo” tiene detrás un trabajo impresionante, muchas horas dedicadas a ella. Actualmente, este tipo de recursos se ha multiplicado en nuestro país. ¿Consideras que todo ello redunda en una sociedad matemáticamente más preparada, o sólo acaba siendo de interés para los que les gustan de por sí? Hay un auge de la divulgación matemática que, aparte de tener un público fiel, se expande entre todo tipo de personas. Si las radios, los diarios y las editoriales le dan espacio es porque se escucha, se lee y se vende. En el fondo, ello es debido a la extendida necesidad de dar un sentido a las matemáticas, un saber que los ciudadanos encuentran en cada curso de su vida escolar, sin que muchas veces les haya llegado como una herencia cultural y una herramienta útil para comprender el mundo y tomar decisiones en sus vidas. Podríamos decir que gran parte de la población necesita “recuperar las Matemáticas”, como algo propio. Además, la actualidad las han traído a primera plana: con las reiteradas noticias sobre la alta demanda profesional de los matemáticos y, tristemente, con la interpretación de la avalancha de datos sobre la pandemia. La divulgación, más que aumentar la preparación matemática, vence prejuicios y falsos conceptos, cambiando su valoración. Es una tarea que debe comenzar en las aulas, para cimentar su aprendizaje en el interés y en el aprecio. Para ello hay dos sendas que explorar: la historia de las matemáticas y sus conexiones (sociales, tecnológicas, culturales, etc.). Personal y libro 4.- Por tus publicaciones, es claro que disfrutas enseñando y transmitiendo matemáticas, por supuesto, pero también la fotografía, el cine, los juegos de ingenio… ¿De dónde se sacan tiempo y ganas para seguir “en la brecha”? ¿Cuál es tu secreto? Todo empezó con mi experiencia docente. Pronto viví el fracaso como bienintencionado profesor del antiguo BUP que intentaba dar clases “de mucho nivel”. Los chicos de 15 años no podían ni querían buscar delta en función de épsilon… necesitaban otras matemáticas más atractivas para su edad, relacionadas con el mundo y con la historia; también, problemas estimulantes a su alcance, que pudieran vivir como juegos o retos intelectuales. Así que poco a poco empecé a recopilar recursos que años después, con la llegada de Internet, proliferaron y encontraron cauce en el sitio matematicasentumundo.es. Descubrí que eran de interés para otros compañeros y también para personas muy variadas en países de habla española. La web abrió paso a los libros, las conferencias y los programas de radio. Estar ahora jubilado no supone estar inactivo. Quería realizar alguna labor de utilidad social y, a tenor de la respuesta que recibo, seguir en la divulgación lo es. Divulgar es mi “voluntariado”. De ahí las ganas. El tiempo, como jubilado lo tengo más que nunca. El secreto, la perseverancia. Comencé la web en 2004 y la sigo actualizando a diario. 5.- Como aficionado al cine, aparte de las que contienen referencias matemáticas, ¿qué tipo de películas le gustan a José María Sorando?¿Director, actor preferido, género cinematográfico? Me gustan en especial las películas de dos directores bien diferentes. Stanley Kubrick, que en cada film tocó un género diferente (histórico, bélico, terror, etc.), transformándolo y logrando una obra maestra. Me fascina su perfeccionismo, repleto de estructuras, claves y simetrías que conducen a la belleza formal. Y también José Luis Cuerda, con su ternura y su humor ibérico y surrealista. En esa misma línea, los guiones de Rafael Azcona. Y declaro mi amor adolescente no superado por Jacqueline Bisset… 6.- Si tuvieras la posibilidad de escribir un guion para una película, ¿qué matemáticas incluirías? (puede ser un tema, una aplicación, un personaje, un género en el que crees que mejor caben las matemáticas, una historia, etc.). Creo que Evariste Galois ofrece elementos para una buena película, como icono del romanticismo en matemáticas: rebelde, incomprendido, muerto en plena juventud y genio transformador del álgebra. Hay un corto sobre él (Alexander Astruc, 1965) y referencias varias a lo largo de 3:19. Nada es casualidad (Dany Saadia, 2008), pero no se ha rodado la película que merece. En el corto se hace una aceptable descripción de la teoría de grupos, cuyo origen y sentido habría que esbozar. Y en el guion, además de la peripecia vital de Galois, también daría entrada de alguna manera (habría que discurrir cómo, para que no fuera muy forzada) a la presencia de los grupos de simetría en la cristalografía o en el arte nazarí y mudéjar. 7.- De vez en cuando, aparecen películas de interés con contenido matemático, pero suele ser de ciento en viento. Mientras, los que escribimos sobre las matemáticas y el cine, tenemos que dedicarnos a la arqueología cinematográfica para localizar nuevas referencias. ¿Crees que el tema ha dado de si lo que podía o puede seguir generando interés? Lo comento porque, ya sabes, para la gente más joven una película anterior a 2015, ya es “antigua” y sin interés. La década pasada ha sido fructífera en ese tipo de películas, pero parece que su frecuencia disminuye. Es un tema que interesa y seguirá avanzando, pero lentamente, lo cual concede un gran mérito a la labor que mes tras mes realizas en esta sección de Divulgamat. Sobre la “antigüedad” de las películas, es tarea de quienes nos dedicamos a esto descubrir a los nuevos lectores las obras de arte que se consiguieron en blanco y negro; e incluso en cine mudo. Pasa como con las matemáticas académicas. Si se hace bien, el entusiasmo se puede contagiar y conseguir nuevos “conversos”. 8.- Relacionada con la anterior, ¿estamos preparados los espectadores para “ver y entender” el cine? ¿No crees que tenemos un déficit importante de cultura visual, a pesar de estar todo el día consumiendo imágenes? Desde luego. Yo mismo al documentar “Matemáticas de cine”, he descubierto muchos aspectos no casuales presentes en películas que creía conocer. Técnicas de guion, encuadre o escenografía, por ejemplo, mediante las cuales se inducen en el espectador determinadas emociones o las opuestas. Son recursos también presentes en la publicidad o en los informativos, que condicionan nuestras opiniones, el consumo e incluso el voto. 9.- ¿En qué nuevos proyectos, si se pueden desvelar, anda metido José María Sorando? Ya tengo terminado un nuevo libro, a la espera de editorial. Trata sobre errores y engaños con matemáticas presentes en la vida pública y en los medios de comunicación; una feria de disparates entre el esperpento, el humor, la indignación y algo de didáctica. 10.- De este libro (y los demás publicados sobre este tema), ¿de qué parte o partes has quedado más satisfecho? De todo lo trabajado en ellos, ¿qué es lo que más te ha sorprendido, gustado? La mayor satisfacción es saber que las propuestas contenidas en “100 escenas de cine y televisión para la clase de Matemáticas” son aplicadas en las aulas por compañeros. También fue muy agradable el eco mediático que recibió “Aventuras matemáticas en el cine”. Y, tanto al escribir “Cine y matemáticas: resolviendo problemas” como “Matemáticas de cine”, como tantas veces me ocurrió al preparar las clases, he aprendido bastantes cosas nuevas. Ocurre siempre que exploras las relaciones de las matemáticas con otras parcelas del saber. Agradecemos enormemente a José María Sorando su amabilidad y excelente disposición a atender nuestras preguntas. Entre este libro que os presentamos y su nuevo proyecto, ha publicado otro (la verdad es que no para este hombre) en la colección Miradas Matemáticas en la editorial Catarata, en colaboración con la Federación Española de Sociedades de Profesores de Matemáticas (FESPM) y el Instituto de Ciencias Matemáticas (ICMAT) titulado La geometría de las ciudades, un magnífico complemento al anterior y un texto imprescindible para los aficionados a los paseos matemáticos por las ciudades, muy de moda en la actualidad gracias a aplicaciones como Math City Map, por ejemplo. Por otra parte, sobre los anteriores libros de cine de José María, podéis recordar las reseñas que les dedicamos en estos enlaces: Resolviendo problemas (reseña 116), Aventuras Matemáticas en el Cine (reseña 105), 100 Escenas de cine y televisión para la clase de Matemáticas (reseña 98). Alfonso Jesús Población Sáez

Martes, 03 de Noviembre de 2020 | Imprimir | PDF |  Correo electrónico

83. 187. (Noviembre 2020) Códigos de Reed-Solomon

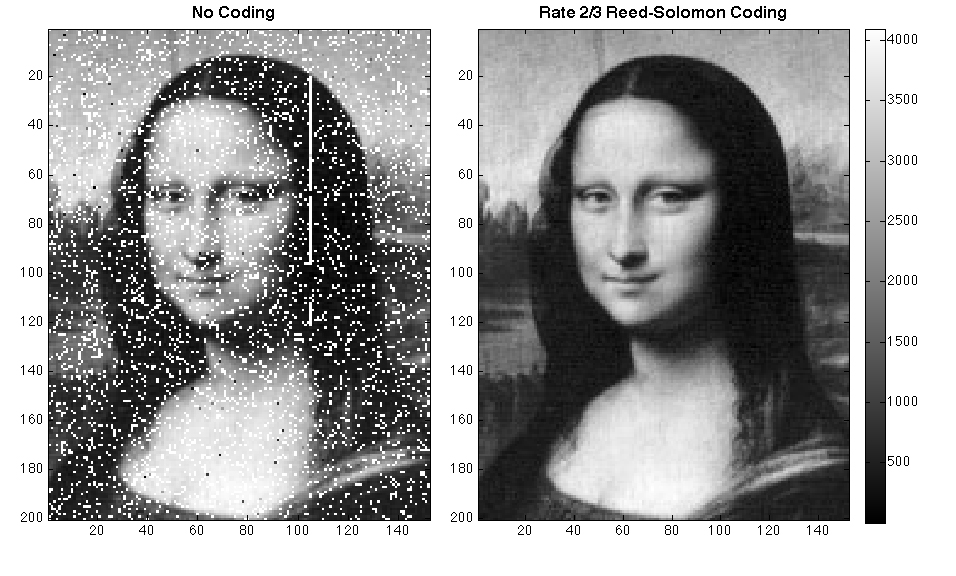
[Resultado de la corrección de errores en la imagen de la Mona Lisa mediante un código de Reed-Solomon, Wikipedia.] Dentro de la especialidad matemática llamada Teoría de Códigos son importantes las técnicas de corrección de errores, que se utilizan de forma cotidiana en multitud de dispositivos digitales. Estamos muy familiarizados con los códigos que detectan errores, como la letra del DNI, los billetes de la zona euro, los pitidos que escuchamos en la zona de cajas del supermercado al pasar los códigos de barras por el lector óptico, los mensajes de error del cajero (o del ordenador (o del móvil)) cuando tecleamos la clave equivocada, etc., pero, lamentablemente —o por suerte—, estos códigos no son capaces de adivinar el valor correcto, no corrigen el error. Aunque no seamos conscientes de ello, los que sí son capaces de corregir errores se utilizan en el proceso de almacenamiento de datos en dispositivos como CDs, DVDs, lápices de memoria, etc., para que podamos recuperar los datos que contienen a pesar de tener algunas zonas defectuosas o degradadas. Algunas de las técnicas sobre corrección de errores han sido objeto de varias aportaciones a la magia, aunque bajo la denominación de detección de mentiras lo que permite simular poderes adivinatorios por parte del artista. Ya se han desarrollado algunos ejemplos en este rincón: por ejemplo, los códigos de Hamming aparecieron en la transmisión telepática del número 80 (febrero de 2011), en el detector de mentiras del número 104 (abril de 2013) y en el juego del número 150 (junio de 2017); otros tipos de códigos aparecieron en el lápiz octal del número 128 (junio de 2015) o en el de adivinación que describimos en el número 163 (septiembre de 2018). También puedes encontrar información adicional sobre el uso de la magia en la teoría de códigos en el artículo «Códigos secretos y teoría de la información en la magia», publicado el año 2005 en el número 26 de la revista Sigma. 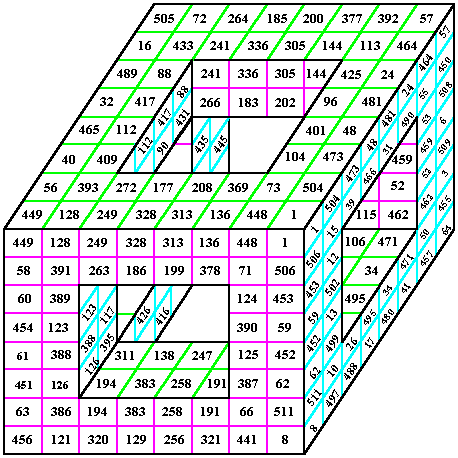Siempre con el ánimo de facilitar la comprensión de los códigos correctores de errores, muchos docentes e investigadores sugieren enfoques desenfadados para el desarrollo de estos temas y a veces podemos encontrar juegos de magia como los ya mencionados. En esta ocasión nos referiremos a dos trabajos de Todd Mateer, profesor de matemáticas en Howard Community College (Maryland, EEUU). El primero de ellos, titulado «A magic trick based on the Hamming code» se publicó en noviembre de 2013 en la revista Math Horizons y, como su título indica, aprovecha los códigos de Hamming para diseñar un juego de magia similar al que describimos en el ya citado detector de mentiras del número 104 (abril de 2013) pero que puede realizarse sin apoyo de un programa informático. El segundo trabajo es el titulado «A Reed-Solomon code magic trick» y se publicó en abril de 2014 en la revista Mathematics Magazine. En el artículo se describen las características principales de los códigos correctores de errores de Reed- Solomon (llamados así en honor de sus creadores, Irving Reeds y Gustave Solomon), las cuales se aplican en un juego de magia que vamos a versionar a continuación. Irving Reed y Gustave Solomon Para este juego se necesitan 16 cartas, de modo que busca una baraja y quédate con las cuatro figuras —incluyendo el as— de cada palo. Sólo usaremos la jota (J), dama (Q), rey (K) y as (A) de los palos de picas (P), corazones (C), tréboles (T) y rombos (R). Utilizaremos como motivo alegórico la rosa de los vientos que, como sabes, es un símbolo inventado por el teólogo mallorquín Ramon Llull en el que están marcados los rumbos en que se divide la circunferencia del horizonte, aunque aquí nos limitaremos a los cuatro puntos cardinales, norte, sur, este y oeste. Primera fase: Selecciona una de dichas cartas. Como verás, en las siguientes figuras se representan las rosas de los vientos en diferentes colores, azul y amarillo, y con las 16 cartas repartidas en los diferentes cuadrantes, cuatro de ellas apuntando al norte, cuatro al este, cuatro al sur y las otras cuatro al oeste. Busca la carta elegida en cada figura y anota el cuadrante en que se encuentra dicha carta. Ya puedo saber qué carta has elegido: se trata de la única carta que aparece repetida en los cuadrantes seleccionados. Para descubrirla fácilmente, gira cada círculo de modo que el cuadrante que contiene la carta elegida apunte hacia el norte. Por ejemplo, si has elegido la jota de picas (JP), verás que está situada al oeste en el círculo azul y al sur en el círculo amarillo. Si las giras como he indicado, las verás así: Se observa fácilmente que la JP es la única carta repetida entre las que están en el cuadrante superior. Segunda fase: Vamos a complicar un poco el proceso de adivinación de la carta elegida: vas a poder mentir una vez sobre la posición de la carta elegida. Como no será posible con las dos figuras anteriores, esta vez utilizaremos cuatro rosas de los vientos: además de la azul y amarilla, necesitaremos una roja y una verde, como las que aparecen a continuación. El proceso es el mismo de antes, así que debes elegir una carta entre las dieciséis seleccionadas y buscarla en cada uno de los cuatro círculos. A continuación, debes anotar las situaciones geográficas de la carta, pero puedes mentir en una de ellas, en la que quieras. Por ejemplo, supongamos que has apuntado: norte en la carta azul, oeste en la carta amarilla, norte en la carta roja y este en la carta verde. Pues bien, a pesar de la mentira, todavía puedo saber cuál es la carta elegida. En el caso del ejemplo propuesto, la carta elegida es el rey de corazones (KC) y la mentira se ha producido en el círculo azul. La respuesta es similar al caso anterior. Basta colocar los cuatro círculos de modo que todas las orientaciones correspondientes al cuadrante elegido señalen hacia arriba. La carta que aparezca repetida al menos tres veces será la elegida. Además, el círculo en el que no aparezca dicha carta señalando en la misma dirección será en el que se ha mentido. En el ejemplo propuesto, debemos disponer los cuatro círculos así: Se comprueba fácilmente que el rey de corazones (KC) aparece en el cuadrante superior de los círculos amarillo, rojo y verde, pero no en el círculo azul. Si interpretamos el resultado según la teoría de códigos, hemos podido detectar el error (círculo azul) y corregirlo (se trata de la KC y debemos girar ese círculo de modo que el sur señale hacia arriba). OBSERVACIONES FINALES: En la página Fun with RS Codes se ofrece una lista de actividades divertidas utilizando los códigos de Reed-Solomon. El artículo de Ricardo Teixeira titulado «Magical data restoration» y publicado en Math Horizons en febrero de 2017 contiene una nueva versión del juego de adivinación utilizando los códigos de Hamming. Pedro Alegría (Universidad del País Vasco - Euskal Herriko Unibertsitatea)

Lunes, 02 de Noviembre de 2020 | Imprimir | PDF |  Correo electrónico

84. 67. (Noviembre 2020) Fachadas con frescos matemáticos

(Alegoría de la Astronomía. Escuela Latina. Brugg) Las fachadas de muchos edificios históricos estaban cubiertas de pinturas y esgrafiados que junto a las esculturas o bajorrelieves daban cuenta de la solvencia, profesión o gustos del propietario. La conservación de los frescos es problemática y muchos han desaparecido si no fueron restaurados. Las escuelas  y las casas de nobles estudiosos  o burgueses ilustrados fueron proclives a adornar con alegorías matemáticas. Damos cuenta de algunos edificios de interés. Los más antiguos se corresponden con el auge cultural renacentista y dan testimonio del la penetración de las ideas difundidas por la imprenta y los grabados en amplias capas de la población. Fresco de la Geometría en Saluzzo Al sur de Turín, en la Saboya italiana, sobre una colina prealpina se alza  la bella ciudad medieval de Saluzzo. La parte alta conserva las majestuosas casas palaciegas, en especial la calle Salita al Castello. relojes solares, pinturas murales y pórticos dan idea del pasado esplendor. Junto al Museo Cívico, y el Palacio Comunal con Torreón, nos encontraremos el Palazzo delle Arti Liberali, edificio de finales del siglo XV mandado construir por el Marqués Ludovico II. Las cegadas arcadas restan algo de elegancia a la espléndida construcción. Todo el exterior se ha decorado en grisalla con deliciosos frescos de las Artes Liberales. En la parte superior se encuentra el trivium (gramática, retórica y dialéctica) y en la planta principal el quadrivium (aritmética, geometría, música y astronomía). La mejor conservada es la alegoría de la Gramática seguida por la Geometría y la Lógica. La bella alegoría femenina de la Geometría porta un gran compás en la mano derecha y un cuadrante en la izquierda. La filacteria con el nombre se puede leer claramente. (Alegoría de la Geometría. Palazzo delle Arti Liberali. Saluzzo) Las Artes Liberales en el Juego de Pelota de Praga En el foso Jelení příkop del Castillo de Praga hay un delicioso jardín y un soberbio edificio renacentista: La Sala del Juego de Pelota. La construcción, que fue ejecutada entre 1567 y 1569, se debe a los arquitectos Bonifác Wohlmuth y Oldřich Aostalis. La fachada principal del Juego de Pelota está decorada a lo largo de sus sesenta y ocho metros con espléndidos esgrafiados alegóricos: los cuatro elementos, las virtudes, las artes liberales y la teología. Como curiosidad, un añadido moderno de realismo socialista se ha conservado: el plan quinquenal y la hoz con el martillo. Las Alegorías de la Aritmética y la Geometría se encuentran a la derecha, en el segundo y tercer tramos. La Aritmética esta enseñando los números mientras la Geometría mide el globo terráqueo. (Alegoría de la Aritmética. Sala del juego de pelota. Praga) Siguiendo las prescripciones de Capella, los vestidos se decoran con motivos que hagan referencia al arte de cada dama. La Aritmética tiene un encintado con números donde se han olvidado del cinco. Pitágoras se representa en el libro. La escuela latina de Brugg El antiguo edificio de la Escuela Latina en Brugg tiene la fachada decorada con hermosos frescos que muestran ocho figuras alegóricas femeninas: representan las siete Artes Liberales y la Teología. Fueron pintados en 1640 por Rudolf Schwerter de Baden en tonos grises y ocres. Hay constancia de que la decoración ha sido restaurada en dos ocasiones, 1885 y por última vez en 1930. La Escuela se encuentra adosada transversalmente a la iglesia reformada, cuya parte más antigua data del siglo XIII. El edificio de tres plantas es de estilo barroco y su pared posterior formó parte de la fortificación. Los medallones bajo las ventanas están decorados con textos de la Biblia en alemán, latín, griego y hebreo. Brugg es una pequeña y apacible ciudad del norte de Suiza con apenas diez mil habitantes y cuyo origen se vincula a los Habsburgo. Las Escuelas Latinas venían a ser las escuelas secundarias, después Liceos o Gimnasios. En Alfeld reseñamos también otra escuela más modesta con las Artes Liberales. La Geometría se representa con escuadra y triángulo, la Aritmética operando con tablilla numérica, y la Astronomía con esfera armilar y ballestilla. Mitra geómetra en la Carrera del Darro de Granada El Paseo de los Tristes, bordeando el Darro, es un lugar obligado por sus vistas a la Alhambra, sus edificios renacentistas y el frescor del río cuando fluye. El Palacio de Mitra nos muestra sus pinturas murales de época. El Olimpo suele ser habitual en las representaciones de una cultura que quiere recuperar el esplendor grecorromano, pero en este caso a quien se rinde homenaje es a una deidad de origen iranio con gran seguimiento entre los militares romanos. Lamentablemente parte del fresco ha desaparecido y entre lo que se conserva destaca la vocación matemática de la deidad: una mano sujeta el compás como parte de un trabajo geométrico. Un triángulo y un cubo son las figuras, y a su lado parecen vislumbrarse unos números romanos. La inscripción DEO SOLI INVICTO MITHERE no deja lugar a dudas. La presencia de un joven puede deberse al contenido didáctico de la escena. El palacio tiene hoy uso hostelero. La capacidad del cristianismo para asimilar otros cultos nos ha conservado la tradición de la Navidad, fecha de nacimiento de Mitra, solsticio de invierno y regeneración solar, festividad que se extiende a la figura de Cristo. (Palacio de Mitra. Granada) Alegorías matemáticas en la Carrer d´Avinyó de Barcelona La Casa dels Quatre Rius es una antigua casa palaciega del siglo XVIII que se encuentra en el número 30 de la Carrer d´Avinhó, antiguo límite de la Barcino romana. Hoy se ha remodelado como instalación hotelera y ha visto restaurados sus interesantes esgrafiados de la fachada. El nombre de la casa se lo otorgan los cuatro grandes ríos de otros tantos continentes que han sido representados: Río de la Plata, Nilo, Ganges y Danubio. Lo que nos hace detenernos son los esgrafiados de la primera planta con erotes juguetones como alegorías de las artes y de las ciencias. La Geometría tiene un compás en la mano y la Astronomía con un globo y un compás en el suelo. El siglo de la Ilustración y de las Sociedades de Amigos del País ha dejado su presencia en las calles. (Alegorías de la Geometría y la Aritmética. Casa dels Quatre Rius. Barcelona) Toda la calle está cargada de referencias artísticas destacables: la domus romana con mosaicos y pinturas que fue hallada allí, los edificios modernistas y la rememoración de la picassiana Las señoritas de la calle de Avinyó. La Geometría en la Plaza Mayor de Graus La ciudad de Graus es una pequeña población del prepirineo de Huesca que destaca por el perfil singular del dominante santuario de la Virgen de la Peña. Merece la pena adentrarse en el interior de sus calles, palacios y, sobre todo, de su porticada Plaza Mayor. Varias casa de la plaza están decoradas con deliciosos frescos del siglo XIX. Merecen una parada la Casa del Barón con una alegoría de la Geometría y la Casa Heredia con un reloj solar declinante. (Alegoría de la Geometría. Casa del Barón. Graus) La Geometría va acompañada de dos erotes que refuerzan su iconografía; compás, escuadra, plomada y globo terrestre. La figura femenina tiene un papel en su mano izquierda cuyos rasgos no se distinguen: si fueran números se trataría de una alegoría de la Matemática. El reloj declinante muestra el alfa y omega de la temporalidad aunque los Pirineos nos den sensación de eternidad. Graus, además, recuerda y ensalza la figura de nuestro más famoso y perseverante regeneracionista, Joaquín Costa, que falleció en la población que le había dado sosiego tras tanta lucha por mejorar nuestra desventurada patria. Fachada Escher en Madrid (Fachada Escher. Madrid) La reconstruida fachada de la casa en la calle Conde Romanones, número 14, de Madrid, cercana al metro de Tirso de Molina, ha utilizado la Metamorfosis de Escher como modelo. Estamos ante un bello homenaje al pintor holandés que usó la perspectiva matemática, la geometría hiperbólica y los trampantojos para configurar una obra siempre interesante. Los mosaicos de la Alhambra dejaron una huella imborrable en Escher que decidió recrear en pleno siglo XX la representación del espacio en el plano. El breve recorrido por las fachadas matemáticas se puede completar con edificios modernistas como La copa de oro de Viena o la Maion Cauchie de Bruselas.

Domingo, 01 de Noviembre de 2020 | Imprimir | PDF |  Correo electrónico

85. 22. (Octubre 2020) Las esculturas geométrico-minimalistas de Robert Morris

1. Robert Morris, escultor minimalista y diseñador de laberintos Robert Morris (1931 – 2018) El escultor, pintor e ilustrador estadounidense Robert Morris, de Kansas City, estudió ingeniería en la Universidad de Kansas y filosofía en el Reed College. Se licenció en Historia del Arte en el Hunter College y perteneció al movimiento minimalista. En parte de su obra escultórica Morris introdujo objetos geométricos elementales tales como ortoedros, triángulos, «ángulos», anillos y cubos. Además, diseñó algunos laberintos univiariosi, uno de los cuales se encuentra en la Isla de las Esculturas (Pontevedra). En este artículo, para poner de manifiesto la presencia de la Geometría en las obras de arte,  presentamos algunas de sus «esculturas geométricas» minimalistas y un par de sus laberintos, considerados como «esculturas dinámicas». 2. Esculturas geométricas Floor Piece (Bench). 1964 Untitled (Corner Piece). 1964 Untitles (L-Beams). 1965 Untitled (Mirrored Cubes). 1965 – 1971 Untitled (Ring with Light). 1966 Voice (1974) 3. Laberintos Glass Labyrinth (Kansas City) Laberinto de Cristal (planta) Laberinto (Isla de las Esculturas. Pontevedra)   Referencias bibliográficas CASTRO FERNÁNDEZ, X. A. (2013). Robert Morris y el presente continuo en la imagen del laberinto de Pontevedra. QUINTANA. Revista de Estudos do Departamento de Historia da Arte, núm. 12, enero-diciembre, pp. 85-97. Universidade de Santiago de Compostela.   Referencias online https://www.wikiart.org/en/robert-morris/all-works#!#filterName:all-paintings-chronologically,resultType:masonry   NOTAS i Dentro del fascinante mundo de los laberintos, los más simples son los llamados univiarios. En ellos, una vez que se cruza la puerta de entrada, es preciso recorrer todo el circuito para llegar al centro. En otras palabras: en este tipo de dédalos no se ofrece la posibilidad de tomar caminos alternativos, no hay encrucijadas, y la puerta por la que se sale es la misma por la que se entra. En consecuencia, en estos recorridos es imposible perderse.  

Jueves, 29 de Octubre de 2020 | Imprimir | PDF |  Correo electrónico

86. 21. (Octubre 2020) Las espirales metálicas de Martín Chirino

1. Martín Chirino, hierro y espirales Martín Chirino (1925 – 2019) El escultor canario Martín Chirino López nació en Las Palmas de Gran Canaria. Estudió en la Escuela de Bellas Artes de San Fernando (Madrid) y fue cofundador, en 1957, del grupo «El Paso». La mayoría de las obras de Chirino, enmarcadas en el arte abstracto, son de hierro, se consagran a las espirales y se dedican al viento. Muchas de las espirales del artista palmense son transformaciones (deformaciones) de un objeto ideal y bidimensional, la espiral de Arquímedesi, en objetos reales 3D que «arrancan de la tierra, están firmemente posadas en el espacio y pugnan por elevarse hasta algún infinito». En las páginas siguientes ofrecemos al lector interesado en las Matemáticas y en el Arte una selección de las «espirales de Chirino». En dichas esculturas enrolladas se manifiesta de forma admirable la presencia de la Geometría en la escultura. 2. Esculturas enrolladas Parlamento de Canarias (Santa Cruz de Tenerife) Espiral del Viento (Las Palmas de Gran Canaria)   Referencias bibliográficas MEAVILLA SEGUÍ, V. (2007). Las matemáticas del arte. Inspiración ma( r)temática. Córdoba: Editorial Almuzara, S. L. VERA, F. (1970). Científicos griegos (dos volúmenes). Madrid: Aguilar, S. A. de Ediciones.   Referencias online http://www.fundacionmartinchirino.org/   NOTAS i Entre las curvas llamadas espirales, la más sencilla es la que describe una cuerda gruesa enrollada sobre sí misma. Entre los matemático se la conoce como espiral de Arquímedes dado que fue el sabio griego del siglo III a. C. el primero que realizó una profunda investigación matemática sobre dicha curva plana. La espiral de Arquímedes, en palabras del sabio de Siracusa, se define del modo siguiente: Si permaneciendo fijo uno de los extremos de una recta, esta gira en un plano con velocidad uniforme hasta volver a su posición inicial, y un punto, también con velocidad uniforme, recorre al mismo tiempo la recta que gira a partir del extremo fijo, este punto describirá en el plano una espiral. [Arquímedes. Sobre las espirales]

Jueves, 22 de Octubre de 2020 | Imprimir | PDF |  Correo electrónico

87. 20. (Octubre 2020) Los dígitos antropomorfos de ERTÉ

1. Romain de Tirtoff («Erté»): apunte biográfico Romain de Tirtoff Romain de Tirtoff («Erté») nació en San Petersburgo (1892) y falleció en París (1990). Fue ilustrador, diseñador, escenógrafo y pintor, perteneciente al movimiento art déco. Durante más de veinte años diseñó las portadas de la revista Harper’s Bazaar. En 1988, decoró una colección de ocho botellas, con sus envases correspondientes, para el afamado coñac Courvoisier. Matemáticamente hablando, son notables sus representaciones antropomórficas de los numerales indo-arábigos. 2. Los dígitos antropomorfos de Erté   Referencias online Erté https://es.wahooart.com/Art.nsf/Art_ES?Open&Query=Erté,Erté

Jueves, 15 de Octubre de 2020 | Imprimir | PDF |  Correo electrónico

88. 154. Cuando el profe de mates no es de fiar

Nos acercamos en esta ocasión a una película rodada para la televisión, difícilmente localizable al no haberse editado en España en ningún formato y con escasas referencias matemáticas. ¿Por qué la traemos a la sección entonces? Pasen y lean. Como el lector habitual de esta sección y el cinéfilo al que le gusten también las matemáticas saben, las películas en las que se menciona para algo esta disciplina se dividen entre las que quieren destacar algo o alguien relevante sobre el tema y por tanto incorporan escenas, diálogos y referencias suficientes (nunca tantas como a los que con ellas trabajamos nos gustaría, pero lo comercial siempre tiene la sartén por el mango), y las que simplemente traen a colación alguna anécdota, chascarrillo peyorativo, o frase más o menos ingeniosa para destacar lo que se tercie, bien desde un punto de vista de genialidad freakie, o bien como símbolo reconocible de nuestros recuerdos y padecimientos escolares. Y dentro de los estereotipos de los docentes, la cosa también suele ser maniquea (tipo científico despistado y en su mundo, o tipo hueso infame que no pasa una a nadie). Pero dentro de estos perfiles, casi siempre es un personaje de cierta integridad moral, quizá porque las matemáticas representan el paradigma de lo exacto, lo recto, lo lógico. Por eso me ha llamado la atención toparme con la presentación de un profesor bastante diferente a esas convenciones, lo que coloca la novela y este telefilme en un plano diferente: el real, porque seguro que, como en cualquier otra profesión, existen personalidades tan amorales y despreciables como el que aquí aparece. Y seguramente habrá aún peores, porque como indica la conocida sentencia, la realidad supera la ficción (y ampliamente, para nuestra desgracia). Antes de nada, los datos de siempre: Ficha Técnica: Título: Amy e Isabelle. Título Original: Amy & Isabelle. Nacionalidad: EE. UU., 2001. Dirección: Lloyd Kramer. Guion: Joyce Eliason y Lloyd Kramer, basado en la novela homónima de Elizabeth Strout. Fotografía: Eric Alan Edwards, en Color. Montaje: Scott Chestnut. Música: Ernest Troost. Producción: Oprah Winfrey y Doro Bachrach. Duración: 100 min. Telefilme emitido por la cadena ABC el 4 de marzo de 2001 simultáneamente en EE. UU. y Canadá. Ficha artística: Intérpretes: Elisabeth Shue  (Isabelle Goodrow), Hanna Hall (Amy Goodrow), Martin Donovan (Peter Robertson), Conchata Ferrell (Bev), Viola Davis (Dottie), Marylouise Burke (Arlene), Amy Wright (Rosie), Ann Dowd (Lenora), Stephi Lineburg (Stacy), James Rebhorn (Avery Clark), Matt Lutz (Paul Bellows), Aubrey Dollar (Karen Keane), Ashton Lunceford (Julie McGinn). Argumento: En 1971, en el pequeño pueblo de Shirley Falls, en Maine, la distante y solitaria secretaria Isabelle Goodrow cría sola a su hija adolescente Amy. Isabelle solo tiene dos amigas en su trabajo entre un montón de compañeras chismosas. La relación entre madre e hija es difícil y la comunicación mínima para convivir. Cuando su sobreprotegida hija Amy es seducida por su profesor de matemáticas Peter Robertson, el mundo de Isabelle se desmorona, sintiéndose humillada. Ambas pierden su confianza en la otra, dejándose de hablar, arruinando su relación. El vínculo se vuelve a atar cuando Isabelle revela a Amy asuntos del pasado que ella desconocía. La autora de la novela El éxito de Elizabeth Strout con su flamante premio Pulitzer por la novela Olive Kitteridge (y su no menos popular serie) han hecho que se recupere su primera novela, Amy e Isabelle, un claro precedente de la primera. Asimismo, el resto de sus obras, siete en total por el momento, la última aún no editada en castellano, han batido records de ventas. Como suele suceder en el noventa por ciento de los casos, la novela es más rica que la adaptación cinematográfica, que en este caso además es para la televisión, con las limitaciones presupuestarias que suele conllevar este tipo de productos. La novela va mostrando, de un modo muy medido e inteligente, los sentimientos de las dos protagonistas, siempre bajo una perspectiva íntima e intimista, sus deseos afectivos hacia el resto de personas que las rodean (incluyéndose ellas mismas) que, desgraciadamente, casi nunca logran. Eso les lleva a culparse a sí mismas, por no haber hecho las cosas bien. Esta conducta (que no deja de ser un recurso literario, o una trampa, si se quiere ser más crítico) hace que el lector inmediatamente se identifique con ellas, porque, también es notorio, la minuciosidad del tratamiento de las protagonistas femeninas, está mucho más diluido en los caracteres masculinos, en general bastante más primarios (insisto en la inteligencia de la autora: el número de potenciales lectores es bastante menor que el de lectoras, no hay más que consultar las estadísticas). En cualquier caso, me parece una autora recomendable. Las matemáticas del telefilme Aunque se ha emitido muchas veces por televisión (en La 2 en 2001 y 2004, y a través de la desaparecida plataforma Vía Digital, en 2002, fundamentalmente), no he podido acceder más que a la versión original, por lo que, en las siguientes descripciones, seguramente no utilice la misma traducción que la versión doblada en España. No obstante, tampoco son demasiadas las referencias. La llegada del profesor sustituto (en la imagen) al instituto de la aburrida localidad no pasa desapercibida, sobre todo para Amy. Su presentación en el aula es la siguiente: Profesor: Mi nombre es Peter Robertson. Estaré con vosotros el resto del año. La señorita Dayble ha sido hospitalizada con una fractura de cráneo. Ella estará bien, solo le llevará algún tiempo curarse. Ahora, antes de pasar al asunto de los números ... me gustaría saber un poco de vosotros. Alumna: ¿Saber qué? Profesor: Quienes sois. Dónde os veis dentro de 10 años. Alumno: A mí me gustaría lanzar para los Red Socks. Profesor: Fantástico. ¿Cómo es el efecto de tu bola? Porque si pudiéramos ralentizar una imagen de tu movimiento... Estoy insinuando algo. Euclides nos tiene mucho que decir aquí. Seguimiento de la pelota cuando cruza el plato ... podrías saber exactamente lo alta que debes poner la mano ... cuando sueltes la pelota. ¿No es asombroso? Profesor: ¿El siguiente? Amy: ¿Yo? Profesor: ¿Qué quieres ser? Amy: Maestra. Profesor: ¿En serio? Habría pensado en ... actriz o .... poeta, quizás. ¿Cómo te llamas? Amy: Amy. Profesor: ¿Amy qué? Amy: Amy Goodrow. Profesor: ¿De verdad quieres ser maestra? ¿O es lo que piensa tu padre que es lo apropiado? Tras esta presentación, los alumnos pronto comprobarán que no es de un carácter demasiado agradable. Es más, parece estar a disgusto en cada cosa que hace o dice, y ni los saluda por los pasillos del centro. En otra clase, hay un triángulo dibujado en el encerado. A Robertson le molesta cualquier ruido o cuchicheo de los alumnos, y pone expresión de fastidio: “Recordad: es un triángulo 30 – 60 – 90. Mirad a ver si podéis demostrarlo. Cuando lo terminéis, dejad los lápices.” Recordemos que la expresión 30 – 60 – 90 se refiere a los respectivos ángulos de un triángulo rectángulo (forzosamente debe ser rectángulo al tener un ángulo de 90º). Teniendo en cuenta las definiciones del seno y el coseno de un ángulo y los valores de los de 30º y 60º, se deduce fácilmente que los lados de un triángulo así tienen sus lados en la proporción  1:√3:2. Las medidas de los lados son por tanto x, x√3 y 2x. Es decir, en un triángulo 30 – 60 – 90, la longitud de la hipotenusa es dos veces la longitud del cateto menor, y la longitud del cateto mayor es veces la longitud del cateto más corto. Mediante el teorema de Pitágoras x2 + (x√3)2 = x2 + 3 x2 = 4 x2 = (2x)2 comprobamos que dicho triángulo es rectángulo. En otra clase, en una escena posterior, más sobre triángulos: Profesor: Tres simples líneas. ¿Podéis ver la belleza de esto? Si tuvieseis algo de sensibilidad, miraríais esto y lloraríais. Julie. Julie: Bien, B-C es cinco veces la raíz cuadrada de 3. Profesor: Mary Ann, como no te calles, te quedarás castigada después de la clase. Ahora, volviendo a lo que es A-B ... Amy a su compañera: ¿No crees que los deberes de ayer eran un montón de basura? Compañera: Yo creo que .... Profesor (enfadado): ¡Chicas, haced el favor de callaros! Amy: Al menos, no es la clase en casa con un Snoopy machacón. Profesor: Amy, una más y te quedas después de clase. Continua, Julie. Julie: Vale, 10 al cuadrado es 100, menos 75 son 25... ...así que A-B es 5. Profesor: Excelente. Muy bien, Julie. ¿Todo el mundo lo entiende? Amy: Es que los demás somos estúpidos. Profesor: De acuerdo, Amy. Te quedas tras la clase. ¿Dónde estamos? A-D era la raíz cuadrada de 3... Con los datos que se dicen, seguro que el lector puede deducir qué están calculando. Finalmente, en la siguiente escena, Robertson está solo en un aula con Amy. Está escribiendo (corrigiendo deberes se supone); ella mira sin hacer nada. Profesor: Empieza con tus deberes, si te parece. Amy: No quiero. Profesor: Amy... (se serena, y se acerca a ella).  Amy, ok. Amy: Conozco este poema de Edna St. Vincent Millay. Pensaba en él hoy durante toda la clase. El primer verso es “Sólo Euclides ha visto la Belleza desnuda”. Creo que es así. Profesor: “Que callen todos los que hablan de la Belleza” Amy: ¿Conoce ese poema? No puedo creer que lo conozca. ¿Conoce otros de Millay? Creo que he memorizado todos. Profesor: "El tiempo no da consuelo. Todos habéis mentido" Amy: "¿Quién me dijo que el tiempo me aliviaría de mi dolor?" Es evidente que conocen bien los poemas de la poetisa (o poeta; ambas acepciones son válidas) Edna St. Vincent Millay (1892 – 1950), la primera mujer en recibir el premio Pulitzer de poesía. Uno de sus trabajos más célebres es el soneto Sólo Euclides ha contemplado la belleza desnuda, publicado en 1923, para muchos una de las obras que mejor recogen la esencia de las matemáticas. En el telefilme sólo se citan los dos primeros versos; les adjunto el soneto original, y mi traducción al castellano (mi interpretación; disculpen los profesionales si “meto en algo la pata”. La describo desde la visión de un matemático, obviamente): Euclid alone has looked on Beauty bare. Let all who prate of Beauty hold their peace, And lay them prone upon the earth and cease To ponder on themselves, the while they stare At nothing, intricately drawn nowhere In shapes of shifting lineage; let geese Gabble and hiss, but heroes seek release From dusty bondage into luminous air. O blinding hour, O holy, terrible day, When first the shaft into his vision shone Of light anatomized! Euclid alone Has looked on Beauty bare. Fortunate they Who, though once only and then but far away, Have heard her massive sandal set on stone. “Mi” traducción: Sólo Euclides ha mirado la Belleza desnuda. Que callen todos los que hablan de la Belleza, Pongámosles boca abajo sobre la tierra y que paren de reflexionar sobre sí mismos, mientras miran a la nada, intrincadamente dibujada en ninguna parte bajo formas de cambiante descendencia; que dejen los gansos de parlotear y silbar, pero que busquen los héroes la liberación desde la servidumbre polvorienta hacia el luminoso aire. Oh hora cegadora, oh día santo y terrible, Cuando por primera vez el rayo en su visión brilló ¡De luz anatomizada! Sólo Euclides ha mirado la Belleza desnuda. Afortunados quienes, aunque una sola vez y luego muy lejanamente, hayan oído su poderosa sandalia sobre la piedra. Este poema fue publicado en la colección The Harp-Weaver, and Other Poems (El arpa tejedora y otros poemas), es un soneto escrito al inicio de la carrera de Millay. Toma como tema la belleza sagrada y deslumbrante de la forma pura, solo alcanzable para el matemático griego Euclides, que percibió una pureza que no ha sido igualada por el parloteo de las generaciones posteriores que han buscado imitaciones a esa belleza disfrazada de otras formas. Los dos cuartetos acaban con la orden de dejar a los gansos que balbuceen y silben (una alusión tanto al uso de los gansos como perros guardianes en la antigüedad como a aquellos que erróneamente gritan que dicen haber avistado la Belleza). Los dos tercetos se centran en la descripción de la luz cegadora y terrible que Euclides alcanzó cuando “miró la Belleza desnuda”, sugiriendo que los simples mortales son afortunados de no haber visto la Belleza completa, ya que no podrían haber soportado la intensidad cegadora de la visión de Euclides (utiliza la palabra "desnudo" con un doble significado: un adjetivo de personificación, y "puro", "sin adornos"). Los hombres tienen suerte si vislumbran en alguna ocasión el eco lejano del paso de la Belleza, a través de su huella, marcada en una roca lejana. Parece una composición simple y directa, aunque, según los críticos, es más complejo de lo que parece a primera vista, porque con la personificación de la belleza que describe la autora (ahora vestida, al menos con sandalias), desea reconocerse a sí misma como uno de esos mortales que siguieron a Euclides, y acepta, con ironía, sus propias limitaciones. Además, describe la visión de Euclides como de "luz anatomizada", no de Belleza en la forma tradicional femenina personificada. En fin, todos hemos leído alguna vez, interpretaciones de todo tipo de obras literarias y poemas. Posteriormente el profesor cita otro soneto de la misma autora, Time Does Not Bring Relief: You All Have Lied (El tiempo no da consuelo. Todos habéis mentido), que Amy continua sin problema. De hecho, describe bastante fielmente sus sentimientos en aquel caluroso verano de la América profunda. Este no le comento ya que nada tiene que ver con nuestras matemáticas, pero es fácilmente localizable en la Red. De este modo, Robertson, va ganándose su confianza (y la del espectador, ya que se muestra de principio como una persona sensible y atenta con ella), pero las cosas no son para nada lo que parecen…. Léanse la novela si no localizan la película si quieren saber cómo continua y termina. El telefilme Estrenado en los Estados Unidos y Canadá el 4 de marzo de 2001, la audiencia fue alta (19.4 millones de personas), si bien las críticas estuvieron divididas: para algunos es demasiado dependiente de la narración en off (comparto plenamente esa opinión), cae en un melodrama de desarrollo y conclusión predecible e inverosímil, sólo salvada por el aceptable trabajo de los actores. Hay que reconocer que no es fácil innovar en casi ningún campo, después de siglos de quehacer cultural. Pero hay veces que las cosas se “parecen demasiado” a otras. Desde el inicio, tanto novela como telefilme (más acusado en éste), me han parecido demasiado parecidos a la magnífica Matar a un ruiseñor, de Harper Lee, con unos pequeños retoques. Mismo ambiente opresor en un pueblo de la América profunda, sentimientos parecidos transportados a madre que cuida de adolescente, etc. Luego, el argumento toma su propio rumbo, demasiado maniqueo y estereotipado. Y como casi todos los telefilmes, la puesta en escena es claramente mejorable. No obstante, no es de los peores que he visto (las tardes de los sábados y domingos de algunas cadenas llevan años programando inmundicias).

Jueves, 08 de Octubre de 2020 | Imprimir | PDF |  Correo electrónico

89. 19. (Octubre 2020) Poliedros lewitianos

1. Sol LeWitt, minimalista y conceptual Sol LeWitt (1928 – 2007) El pintor y escultor norteamericano Solomon («Sol») LeWitt, nacido en una familia de inmigrantes judíos de Rusia, fue miembro de la escuela minimalista y pionero del arte conceptual. Se formó en la Universidad de Siracusa y participó en la Guerra de Corea. En muchas de sus obras intervienen como actores principales los cubos y las pirámides. En este artículo ofrecemos una muestra de sus pinturas protagonizadas por dichos poliedros. 2. Cubos Centered Cube within a Red Circle (1988) Double Cubes in Grays and Colors Superimpoded (1989) Mural con cubos isométricos (1994) Cube (1997) Distorted Cubes A y B (2001) Distorted Cubes C y D (2001) Distorted Cubes E (2001) Cubes in Colour on Colour (2003) 3. Pirámides Pyramid Red (1986) Pyramid Yellow (1986) Flat Top Pyramid with Color Superimposed (1988) Acuarela (sin título y sin año) Murales 4. Resumen brevísimo A lo largo de este modesto trabajo nos hemos limitado a constatar la presencia de determinados poliedros (cubos, pirámides y pirámides truncadas) en la obra pictórica de un gran artista minimalista norteamericano. Las imágenes que hemos utilizado para justificar este hecho se pueden usar con los alumnos de distintos niveles educativos para que se convenzan de que los antedichos cuerpos geométricos se suelen escapar de los libros de texto para producir bellas composiciones artísticas.   Referencias online http://www.lewittcollection.org/news/

Viernes, 09 de Octubre de 2020 | Imprimir | PDF |  Correo electrónico

90. 186. (Octubre 2020) Cubo mágico

[Imagen de John Hendricks extraída de la página www.magic-squares.net]. ¡Han pasado más de 16 (número cuadrado) años desde que nos asomamos a este rincón por primera vez y estamos empezando a redactar el artículo que corresponderá a la entrada 186 (número libre de cuadrados) de la saga! Allá por marzo de 2004 empezaba esta aventura escribiendo sobre el principio de paridad (o principio de los dobleces) aplicado a los cuadrados, figuras que han ido apareciendo regularmente durante este periodo (puedes repasar, por ejemplo, los artículos de agosto de 2004, septiembre de 2004, julio de 2007 y abril de 2008). Nunca hemos profundizado en el estudio de los cuadrados mágicos y tampoco lo haremos en esta ocasión pues no nos parece el lugar adecuado. Ahora bien, si quieres leer algo relacionado con el tema, en el artículo titulado "La magia de los cuadrados mágicos" —que apareció en 2009 en la revista SIGMA— encontrarás alguna información adicional. Esto no quiere decir que vayamos a desperdiciar cualquier ocasión de describir y comentar los juegos de magia que puedan crearse a partir de los cuadrados mágicos, siempre que estén basados en propiedades matemáticas y no solo en sutilezas y técnicas reservadas a la magia, en cuyo caso es aconsejable mantener el secreto con el que conseguir la sorpresa que toda representación de magia lleva emparejada. De hecho, esta vez iremos un poco más lejos: el juego que vamos a presentar está basado en ciertas propiedades mágicas de un cubo. Los cubos mágicos no son tan populares como los cuadrados mágicos, quizá por la dificultad de representarlos gráficamente. Tampoco tienen esa larga tradición que hace tan atractivos a los cuadrados mágicos, pues se dice que aparecen por primera vez en una carta de Pierre de Fermat a Marin Mersenne escrita en 1640, en la que incluía un cubo mágico de dimensiones 4 x 4 x 4 y suma constante igual a 130. Sin embargo, podemos encontrar algunos problemas interesantes y otros que están todavía sin resolver. La propia definición de cubo mágico ya presenta dificultades: lo normal es que sea constante la suma de los números de todas las filas y todas las columnas pero, ¿tiene que ser constante la suma de las diagonales de cada cara así como la de las diagonales que atraviesan el cubo? En la siguiente imagen (que aparece en WolframMathWorld) mostramos un ejemplo de la cantidad de líneas diagonales que se pueden considerar en un cubo. La idea que mostraremos a continuación es mucho más sencilla y el origen del juego más reciente: en 2019 se ha publicado la traducción (del alemán al inglés) del libro titulado "The math behind the magic", escrito por el matemático Ehrhard Behrends, a quien ya citamos en la anterior entrega de este rincón. El libro, como puedes imaginar, conjuga de forma precisa y didáctica distintos juegos de magia matemática y su fundamento teórico. Realiza un recorrido muy variado y completo sobre temas populares, como mezclas de cartas, propiedades de simetría, entretenimientos numéricos, decodificación de mensajes, etc., pero, sobre todo, plantea algunas generalizaciones que no son tan clásicas. Describe, cómo no, el juego del triángulo de colores sobre el que escribimos en la entrega anterior (septiembre de 2020) y extiende a tres dimensiones un juego clásico de predicción en un cuadrado a un resultado análogo sobre un cubo. Lo que sigue es la adaptación del juego que allí aparece y con el que celebramos, como ya hemos apuntado al principio, la edición 186 de este rincón. Observa el cubo de la figura, de tamaño 4 x 4 x 4, de modo que contiene 64 números. Para que puedan verse todos los números, hemos separado el cubo en sus cuatro capas horizontales: Si puedes, imprime la imagen para seguir fácilmente las indicaciones que te daré (si no, trata de seguir las instrucciones sobre la pantalla). Selecciona un número cualquiera entre todos ellos y rodéalo con un círculo (o anótalo en un papel) para no olvidarlo. Además, tacha todos los números que se encuentren en la misma fila y columna de su propia capa así como la fila y la columna correspondientes de las capas restantes. Por ejemplo, si has seleccionado el 48 de la tercera capa, rodearás con un círculo dicho número (o lo anotarás en un papel) y eliminarás del juego los números marcados en la siguiente figura: Selecciona un segundo número en otra de las capas, que no esté todavía tachado. De nuevo, rodéalo con un círculo y tacha todos los números en su misma fila y columna de su capa así como los de la fila y columna correspondientes en las demás capas. Realiza la misma operación dos veces más, de modo que habrás seleccionado de forma completamente libre (o casi) cuatro números, uno por cada capa horizontal del cubo. Por último, calcula la suma de estos cuatro números. ¿Entiendes ahora la insistencia de celebrar la entrada 186 del rincón matemágico? OBSERVACIONES FINALES: En el libro de Ehrhard Behrends encontrarás la explicación del juego y la forma de construir tu propio cubo con cualquier suma prefijada. La idea básica con cuadrados en lugar de cubos se explica en el artículo ya citado "La magia de los cuadrados mágicos" y su historia está descrita en el artículo "How to construct a forcing matrix" de Doug Dyment. En la página Magic Hyper Cube Generator se muestra un código java con el que generar diferentes hipercubos mágicos en varias dimensiones. En el caso de dimensión tres, no siempre es posible encontrar cubos mágicos perfectos (se puede disfrutar en la página de Walter Trump el apasionante desarrollo cronológico de los distintos descubrimientos realizados hasta la actualidad). En el artículo "An algorithm for making magic cubes", Marián Trenkler proporciona fórmulas simples para construir cubos mágicos. Pedro Alegría (Universidad del País Vasco - Euskal Herriko Unibertsitatea)

Jueves, 01 de Octubre de 2020 | Imprimir | PDF |  Correo electrónico