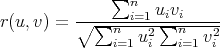101. 30. (Noviembre 2011) Medidas matemáticas de síncopa (II)

Este artículo es la segunda parte de la serie sobre medidas matemáticas de síncopa. Esta serie proviene del trabajo Mathematical measures of syncopation, presentado en el congreso BRIDGES: Mathematical Connections in Art, Music, and Science de 2005. Los autores son Andrew Melvin (Buckinghamshire Music Service, Inglaterra), David Rappaport (School of Computing, Queen's University), Godfried Toussaint (School of Computer Science, McGill University) y el autor de esta columna. 1. Medidas de síncopa Desde el punto de vista matemático, la música se ha formalizado y estudiado mucho, pero parece que han despertado más interés los fenómenos relacionados con la altura del sonido, tales como escalas, acordes y melodía  [17, 12, 16, 15, 2, 3, 9], que los relacionados con fenómenos rítmicos. Varios autores han puesto remedio a esta situación con el estudio de fascinantes cuestiones abiertas sobre el ritmo (véase, por ejemplo, [18, 13, 1, 12, 19, 6, 20, 21, 22, 23, 4]). Muy pocos autores, sin embargo, han abordado los muchos problemas que surgen alrededor de la síncopa (véase [11, 14, 8]). Por ejemplo, dados dos ritmos con la misma métrica, ¿cuál es más sincopado? ¿Existe una medida que pueda ordenar un conjunto de ritmos según su grado de síncopa? O ¿existe una medida matemática de síncopa que coincida con la medida humana de la síncopa? En [11], dentro del contexto de una teoría sobre el ritmo y la métrica, Johnson-Laird estudia la síncopa desde un punto de vista cualitativo, pero no describe una medida de síncopa para ritmos. La síncopa se ha estudiado en el contexto de los modelos de inducción de pulsos [8]. En el capítulo final de [12], Keith considera el problema de definir una medida matemática de síncopa y da una definición basada en combinatoria. Asimismo, en [23] se presenta una medida de preferencia para música africana del área subsahariana, la llamada medida de contratiempo, que se basa en teoría de grupos. La medida de contratiempo no solo parece ser una buena medida de preferencia, sino que también puede servir como medida de síncopa. El índice de asimetría rítmica [1, 5, 6] puede considerarse también como una aproximación a un medida de síncopa. Se basa en la partición de ritmos con ciertas propiedades. En este trabajo definimos una nueva medida de síncopa que no está basada ni en combinatoria ni en teoría de grupos, sino en el concepto de duración de distancia entre notas. En las siguientes secciones revisaremos medidas de síncopa definidas por otros autores e introduciremos la medida de la distancia ponderada de nota a parte. 1.1. Índice de asimetría rítmica Simha Arom [1] descubrió que los pigmeos aka usan ritmos que tienen lo que él llama la propiedad de asimetría rítmica [6, 5]. Un ritmo con un tramo temporal consistente en un número par de unidades de tiempo tiene la propiedad de asimetría rítmica si no hay dos notas que partan el ciclo (el tramo temporal entero) en dos subintervalos de igual longitud. Tal partición se llama un bipartición igual. Nótese que la propiedad de asimetría rítmica se define solo para tramos temporales de longitud par. Para tramos de longitud impar todos los ritmos tiene esa propiedad, lo que desprovee a la medida de todo interés. Aunque limitada, esta propiedad es un primer paso hacia una definición matemática de síncopa. Desafortunadamente, la capacidad de esta propiedad de discriminar ritmos según la síncopa es su mayor limitación. Considérese, por ejemplo, las diez ritmos de clave de campana de la música del África del Oeste y del Sur; estas claves están formadas por siete notas en un tramo temporal de doce unidades, con cinco intervalos de longitud dos y dos intervalos de longitud uno (véase [21] para más detalles). Los diez ritmos y sus vectores de intervalos son: Ritmo Vector de intervalos Partitura Soli (2 2 2 2 1 2 1) Tambú (2 2 2 1 2 2 1) Bembé (2 2 1 2 2 2 1) Bembé-2 (1 2 2 1 2 2 2) Yoruba (2 2 1 2 2 1 2) Tonada (2 1 2 1 2 2 2) Asaadua (2 2 2 1 2 1 2) Sorsonet (1 1 2 2 2 2 2) Bemba (2 1 2 2 2 1 2) Ashanti (2 1 2 2 1 2 2) Figura 1: Vector de intervalos para algunas claves africanas para campanas. Estos diez ritmos se obtienen a partir de rotaciones adecuadas de tres patrones canónicos (de nuevo, véase [21]) . Estos ritmos pertenecen a un conjunto más general de ritmos, que en total son veintiuno. La propiedad de asimetría no aparece en ninguno de ellos. Aún más, entre los diez ritmos usados aquí, algunos son más sincopados que otros, pero la propiedad de asimetría rítmica no capta esa diferencia. Toussaint [21] propuso una generalización de esta propiedad que tenía más capacidad de discriminación. Originalmente, Simha Arom [1] definió la propiedad de asimetría rítmica de una manera estrictamente dicotómica, blanco o negro, todo o nada, esto es, el ritmo o tiene la propiedad o no la tiene. Este concepto se puede generalizar a una variable que tome más valores y que mida la cantidad de asimetría rítmica que un ritmo posee. Esta variable de asimetría rítmica se define como el número de biparticiones iguales que admite un ritmo. Cuantas menos biparticiones un ritmo admita, más asimetría rítmica tendrá. 1.2. La medida de contratiempo Consideremos en primer lugar los ritmos definidos sobre un tramo temporal de 12 unidades de tiempo. Un intervalo de 12 unidades se puede dividir de manera exacta, sin resto, por cuatro números mayores estrictamente que 1 y menores que 12. Estos números son 6, 4, 3 y 2. Dividir el círculo de 12 unidades por estos números da lugar a un segmento, un triángulo, un cuadrado y un hexágono, respectivamente. Normalmente, la música africana incorpora un tambor u otro instrumento de percusión que toca al menos una porción de estos patrones. A veces la música se acompaña con ritmos de palmas que usan alguno de estos patrones. Por ejemplo, la musica funeral neporo del noroeste de Ghana emplea el triángulo, el cuadrado y el hexágono en sus ritmos de palmas [24]. En cualquier caso, el ritmo tiene un pulso que podemos asociar con la posición “cero” en el ciclo. En la música polirrítmica estos cuatro subpatrones forman los posibles patrones métricos. Dos de estos patrones, el segmento y el cuadrado, son binarios y dos, el triángulo y el hexágono, ternarios. Por tanto, las notas que se tocan en otras posiciones están en posiciones de contratiempo en un sentido fuertemente polirrítmico. Hay cuatro posiciones que no aparecen en ninguno de estos cuatro patrones. Esas posiciones son 1, 5, 7 y 11. Las notas en esas posiciones se llamarán notas a contratiempo. Un ritmo que contenga al menos una nota en una de esas posiciones se dirá que tiene la propiedad del contratiempo. La medida de contratiempo es el número de notas a contratiempo que contiene. Estas notas a contratiempo (1, 5, 7, y 11) tienen una interpretación en términos de teoría de grupos. Las 12 posiciones para las 12 posibles notas forman un grupo cíclico de orden 12 designado por C12. Los valores de las posiciones de las notas a contratiempo corresponden a los tamaños de los intervalos que tienen la propiedad de que, si se recorre el ciclo empezando en “cero” en sentido horario en saltos de tamaño igual al tamaño de uno de estos intervalos, entonces en algún momento se vuelve al punto de inicio tras haber visitado todas las 12 posiciones. Recíprocamente, si las longitudes de los saltos se toman del conjunto complementario , entonces el punto de inicio se alcanzará sin haber visitado las 12 posiciones del ciclo. Por esta razón, los elementos 1, 5, 7 y 11 se llaman generadores del grupo C12. Los números que indican la posición de las notas a contratiempo en el ciclo también tienen una interpretación desde el punto de vista de la teoría de números. Consideremos un tramo temporal de n unidades. Las posiciones de las notas a contratiempo se conocen como coprimos1 de n (véase [7]) . Los coprimos de n son los enteros positivos menores que n que son primos relativos con n. Dos números son primos relativos si el único divisor que tienen en común es 1. La función indicatriz de Euler2, designada por φ(n), es el número de coprimos de n, y es por tanto el valor máximo que la medida de contratiempo puede tomar para un ritmo con un tramo temporal de n unidades. Volviendo a los diez ritmos de campanas de África del Oeste en 12/8 que introdujimos antes, la medida de contratiempo no solo discrimina mejor que el índice de asimetría rítmica en términos de síncopa, sino que muestra que un valor más alto de la medida de contratiempo tiene una correlación más alta con la aceptación popular del ritmo. El ritmo del bembé es el patrón que se usa más frecuentemente. Entre estos diez ritmos, el valor más alto para la medida de contratiempo es 3 y solo el bembé alcanza dicho valor. Ya que cada grupo cíclico Cn tiene un conjunto de generadores, la medida de contratiempo descrita se puede generalizar a ritmos definidos sobre tramos temporales de n unidades, donde n puede tomar otros valores distintos a 12. Aunque la medida funciona mejor con valores pares de n, tiene alguna aplicabilidad para valores impares de n. Por otra parte, si n es un número primo p, entonces todos los números entre 1 y p - 1 son coprimos con p. En tal caso la medida es infructuosa, ya que todas las posiciones entre 1 y p - 1 serían notas a contratiempo bajo la presente definición de contratiempo. 1.3. La medida de Keith En [12] Keith examina varios fenómenos de naturaleza rítmica y lleva a cabo un análisis matemático de ellos. Como ejemplo ilustrativo, Keith aborda el problema de medir el grado de síncopa de un ritmo dado. Su definición se apoya en la distinción de tres eventos: retardo, cuando una nota empieza en parte fuerte3 y termina fuera de ella; anticipación, cuando la nota empieza fuera de parte y termina sobre parte; y síncopa, que se concibe como una combinación de los dos eventos previos (véase la figura 2; de izquierda a derecha: retardo, anticipación y síncopa). Figura 2: Retardo, anticipación y síncopa. De manera algo arbitraria, Keith asigna valores de 1 al retardo, de 2 a la anticipación y de 3 a la síncopa. Esta asignación parece, por lo menos, subjetiva y el propio Keith reconoce que “el problema de decidir la “fuerza” rítmica relativa del retardo, la anticipación y la síncopa es un interesante problema filosófico”. La medida de Keith se limita a métricas compuesta de n pulsos, donde n es una potencia de 2. Vamos a dar su definición detallada con el fin de entender esta limitación. Su idea principal es que, dadoa un evento musical (una nota), para saber si está en parte fuerte o no hay que compararla con una plantilla métrica, que indica las partes fuertes y débiles según el tamaño (duraciones) del evento. Por ejemplo, si la potencia de 2 es 3, entonces habrá 23 = 8 corcheas y las plantillas de partes fuertes y débiles se ilustra en la tabla abajo (F es para la parte fuerte y D para la débil). F D D D D D D D F D D D F D D D F D F D F D F D F F F F F F F F Figura 3: Diferentes niveles métricos en la definición de síncopa de Keith. Un evento de tamaño 8 se compara con la primera plantilla (léase de arriba abajo). Los eventos de tamaño entre 4 y 7 se comparan con la segunda plantilla; los que van de 2 a 3, con la tercera plantilla; y finalmente, las corcheas, de tamaño 1, con la última plantilla, que solo está formada por partes fuertes. Podemos representar un ritmo de n notas por una sucesión circular (s0,s1,…,sn-1). Usaremos también la sucesión de intervalos entre notas (δ0,δ1,…,δn-1), donde δi = si+1 - si, para 0 ≤ i < n. El número δn es igual a L - sn-1, siendo L la longitud del ritmo completo. La localización de las partes fuertes es una función de la longitud del intervalo entre notas consecutivas. Una hipótesis implícita es que la métrica es siempre binaria y que las partes fuertes ocurren en algún múltiplo de una potencia de dos. Para cualquier nota dada si, la partes fuertes adyacentes se pueden describir como j2k y (j + 1)2k, donde k es el entero tal que 2k ≤ δi < 2k+1, y j es el entero tal que j2k ≤ si < (j + 1)2k. Ahora expresamos este método más precisamente mediante un algoritmo (figura 4). Figura 4: Algoritmo para la medida de síncopa de Keith. Hagamos un ejemplo que ilustre cómo se calcula la medida de síncopa de Keith para el ritmo de la bossa-nova; véase la figura 5. La bossa-nova tiene la sucesión de notas (0,3,6,10,13,16) y la sucesión de intervalos entre notas (3,3,4,3,3). Nótese que la sucesión que damos para la bossa-nova tiene una nota de más para enfatizar el carácter circular de la sucesión. La siguiente tabla muestra los cálculos para obtener 9, el valor de la medida de síncopa, que está dado por la suma de los pesos wi. 0 1 2 3 4 5 si 0 3 6 10 13 16 δi 3 3 4 3 3 wi 1 2 3 1 2 j × p 0 × 2 2 × 2 1 × 4 5 × 2 6 × 2 Figura 5: Anotación de los cálculos de la medida de síncopa de Keith para el ritmo de la bossa-nova. 1.4. La medida ponderada de nota a parte En la definición de nuestra medida centramos nuestra atención en los ataques de las notas entre partes fuertes en lugar de la estructura métrica, como hace Keith, o en el número de generadores de Cn, como ocurre en el caso de la medida de contratiempo. Nuestra definición se basa en el concepto de distancia y es más flexible en cuanto que nos permite cuantificar el nivel de síncopa de un amplio abanico de ritmos. Por ejemplo, consideremos los ritmos que se muestran en la figura 6; ni la medida de Keith ni la medida de contratiempo son adecuadas para medir ritmos de esta complejidad. Figura 6: Ritmos que no pueden medirse con la medida de contratiempo o con la medida de Keith. Sin embargo, con la medida ponderada de nota a parte sí es posible medirlo; de hecho, tiene valor igual a 41∕8. Otro ejemplo más radical se puede encontrar en la obra Aïs, de Iannis Xenakis (figura 7). Figura 7: Ritmos complejos de medir en la obra Aïs, de Iannis Xenakis. La distancia ponderada de nota a parte (a partir de ahora DPNP) se define como sigue. En primer lugar, supondremos que cada nota termina donde empieza la siguiente. Sean pi,pi+1 dos partes fuertes de la métrica. Sea sj una nota que empieza después o sobre la parte fuerte pi pero antes de la parte fuerte pi+1; primero definimos T(sj) = mín, donde d es la distancia entre notas en términos de duraciones. Aquí la distancia entre dos partes fuertes se toma como la unidad, y, por tanto, la distancia d es siempre una fracción. Por ejemplo, las negras en un compás de 4/4 son partes fuertes, y, si las notas de la figura 8 se refieren a la parte fuerte más cercana: Figura 8: Síncopa medida con la DPNP measure. entonces, las distancias respectivas T(sj) son ,,,,,. En la medida de síncopa de Keith la parte fuerte más cercana a una nota estaba implícita. Para permitir una mayor variedad de ritmo la medida DPNP exige especificar cuales son las partes fuertes. En el ejemplo anterior las partes fuertes están dadas por el compás. Así, en el ejemplo de la figura 6 las partes fuertes se encuentran a intervalos de negra. La medida DPNP está especialmente diseñada para entradas en notación estándar, ya que las partes fuertes se deducen del compás. La medida DPNP D(sj) de una nota sj se define entonces como sigue: 0, si sj = pi; , si la nota sj ≠ pi termina antes o en pi+1; , si la nota sj ≠ pi termina después de pi+1 pero antes de o en pi+2; y , si la nota sj ≠ pi termina después de pi+2. Sea n el número de notas de un ritmo. Entonces la medida DPNP de un ritmo es la suma D(sj), para todas las notas sj, dividida por n. La tabla de la figura 11 proporciona una lista de los valores DPNP para varios ritmos. Usaremos la notación que introdujimos antes para representar un ritmo como una sucesión circular, junto con una sucesión de intervalos entre notas y las partes fuertes dadas por el compás para escribir el algoritmo de la medida DPNP. Consideremos una nota si. Esta nota puede empezar en una parte fuerte pj o puede caer entre dos partes fuertes consecutivas. Definimos di como Ahora asignamos un peso wi a una nota si como sigue: si si = pj entonces wi ← 0 si pj < si < si+1 ≤ pj+1 entonces wi ← 1∕di si pj < si < pj+1 < si+1 < pj+2 entonces wi ← 2∕di si pj < si < pj+1 < pj+2 ≤ si+1 entonces wi ← 1∕di Nótese que asignamos el mayor valor de síncopa a una nota si en el caso en que si y si+1 caigan entre dos partes fuertes consecutivas. Detallamos a continuación el algoritmo para calcular la medida DPNP. Figura 9: Algoritmo para la medida DPNP. En la figura 10 hemos registrado los cálculos para determinar la medida DPNP para el ritmo de la bossa-nova. Nótese que el compás implica que las partes fuertes son las blancas. Esto se traduce en un vector de partes fuertes igual a (0,4,8,12,16). 0 1 2 3 4 5 si 0 3 6 10 13 16 di 0 1/4 1/2 1/2 1/4 wi 0 2 × 4 2 × 2 2 × 2 1 × 4 Figura 10: Anotación de los cálculos de la medida DPNP para el ritmo de bossa-nova. Nótese que si n no se introduce en la definición de DPNP, entonces la medida crece según lo hace el número de notas del ritmo. Eso daría como resultado una medida incorrecta. En la tabla 11 hay una columna que muestra la suma de las distancias D(x). Se puede apreciar cómo se comporta tal suma en términos de n y la influencia del número de notas en la medida. Rhythm Musical Scores ∑ xD(x) DPNP Hesitation 2 1/2 Anticipation 2 1/2 Syncopation 6 6∕5 = 1.2 Triplet 6 6/6=1 Quintuplet 15 15/8=1.875 Bembé 21 21/7=3 Son 14 14/5=2.8 Bossa-Nova 20 20/5=4 Irregular Rhythm 35 35/7=5 Figura 11: Ejemplos de la medida DPNP. Los pesos que aparecen en la definición de la medida merecen una explicación. Es razonable dar un peso a una nota que se toca fuera de una parte fuerte. Nuestra medida da menos peso cuando la nota aparece entre dos partes fuertes consecutivas y, según se aproxima la nota a la siguiente parte fuerte, gana más peso. Sin embargo, hay una gran diferencia si la nota cruza una parte fuerte o sencillamente termina antes o en la siguiente parte fuerte. En el primer caso hay una sensación de síncopa más fuerte que en el segundo. Por tanto, recibe más peso con el fin de reflejar este hecho musical. Se puede ver que, según una nota x se aproxima a una parte fuerte, su distancia T(x) decrece, y en consecuencia, su medida de síncopa D(x) crece. Parece que si T(x) tiende a cero, entonces D(x) tiende a infinito. Sin embargo, debe establecerse un límite inferior de manera que si una nota x está a cierta distancia de una parte fuerte su distancia se toma como cero. Considérese el ejemplo de la figura 12. Ritmo DPNP Measure Rhythm DPNP Measure 2 8 4 0 Figura 12: Límite inferior para la medida WNBD. En este ejemplo, excepto en el último ritmo, la medida de síncopa de cada ritmo crece ya que la nota se aproxima a la nota blanca. El último ritmo tiene distancia cero porque la segunda nota es de adorno. La cuestión de cómo elegir ese límite inferior a partir del cual se considera una nota como de adorno es difícil. Es razonable suponer que dependa de la velocidad a la que se toquen los ritmos (con tempi rápido el límite debería ser inferior que en tempi lentos). Para ritmos que comparten una unidad mínima de duración, la medida DPNP funciona bastante bien, ya que el tempo no es importante para comparar los ritmos. 2. Conclusiones En este artículo hemos definido las principales medidas de síncopa. En el próximo compararemos las medidas entre sí midiendo varios conjuntos de ritmos, tanto binarios como ternarios. Analizaremos también la robustez de las medidas en términos de sus pesos.   Notas: 1 Totatives se llaman en inglés. 2 En inglés, totient function. 3 La terminología española es parte fuerte para lo que en inglés llaman strong beat o sencillamente beat; a veces el término pulse se usa como equivalente a parte fuerte. Bibliografía [1] Arom, S.; African Polyphony and Polyrhythm, Cambridge University Press, England, 1991. [2] Assayag, G.; Fiechtinger, H-G.; Rodrigues, J. F. (editors); Mathematics and Music, Springer-Verlag, 2002. [3] Benson, D.; Mathematics and Music. Book published on the web. See the site http://www.math.uga.edu/∽ djb/html/math-music.html [4] Díaz-Báñez, J. M.; Farigu, G.; Gómez, F.; Rappaport, D.; G. T. Toussaint; El Compás Flamenco: A Phylogenetic Analysis, Proceedings of BRIDGES: Mathematical Connections in Art, Music, and Science, Winfield, Kansas, 61-70, July, 2004. [5] Chemillier, M.; Ethnomusicology, ethnomathematics. The logic underlying orally transmitted artistic practices, in G. Assayag, H. G. Feichtinger and J. F. Rodrigues, editors of Mathematics and Music, pp. 161-183, Springer-Verlag, 2002. [6] Chemillier, M. and Truchet, C.; Computation of words satisfying the ‘rhythmic oddity property’ (after Simha Arom’s work), Information Processing Letters, 86:255-261, 2003. [7] Conway, J. H. and Guy, R. K.; Euler’s Totient Numbers, The Book of Numbers, pp. 154–156, New York, 1996. [8] Desain, P. and Honing, H. (1994). Advanced issues in beat induction modeling: syncopation, tempo and timing, Proceedings of the 1994 International Computer Music Conference,San Francisco, 92-94. , 1995. [9] Fauvel, J.; Flood, R.; Wilson; R. (editors); Music and Mathematics: From Pythagoras to Fractals, Oxford University Press, Oxford, 2003. [10] Fubini, E.; History of Music Aesthetics, Macmillan Press, London, 1991. [11] Johnson-Laird, P.N.; Rhythm and Meter: a Theory at the Computational Level, Psychomusicology, 10:88-106, 1991. [12] Keith, M.; From Polychords to Pólya: Adventures in Music Combinatorics, Vinculum Press, Princeton, 1991. [13] Lerdahl, F. and Jackendoff, R.; A Generative Theory of Tonal Music, MIT Press, Cambridge, Massachussetts, 1985. [14] Longuet-Higgins, H.C. and Lee, C.S.; The rhythmic interpretation of monophonic music, Music Perception, 1:424-441, 1984. [15] McCartin, B.; Prelude to Musical Geometry, Coll. Math. Jour, 29:354-370, 1998. [16] Maidín, O.; A geometrical algorithm for melodic distance, Computing in Musicology, 11:65-72, 1998. [17] Pierce, J.; The Science of Musical Sound, Scientific American Books, Freeman, 1983. [18] Pressing, J.; Cognitive Isomorphisms between Pitch and Rhythm in World Musics: West Africa, the Balkans and Western Tonalities, Studies in Music, 17:38-61, 1983. [19] Temperley, D.; The Cognition of Basic Musical Structures, The MIT Press, Massachussetts, 2001. [20] Toussaint, G. T.; A Mathematical Analysis of African, Brazilian, and Cuban Clave Rhythms, Proceedings of BRIDGES: Mathematical Connections in Art, Music and Science, pp. 157-168, Towson University, Towson, MD, 2002. [21] Toussaint, G. T.; Classification and Phylogenetic Analysis of African Ternary Rhythm Timelines, Proceedings of BRIDGES: Mathematical Connections in Art, Music and Science, pp. 25-36, Universidad de Granada, Granada, 2003. [22] Toussaint, G. T.; A Comparison of Rhythmic Similarity Measures. Proc. 5th International Conference on Music Information Retrieval, pp. 242-245, Universitat Pompeu y Fabra, Barcelona, 2004. [23] Toussaint, G. T.; A Mathematical Measure of Preference in African Rhythm. In Abstracts of Papers Presented to the American Mathematical Society, volumen 25, pp. 248, Phoenix, Arizona, January, 2004. American Mathematical Society. [24] Wiggins, T.; Techniques of variation and concepts of musical understanding in Northern Ghana, British Journal of Ethnomusicology, 7:117–142, 1998.

Miércoles, 02 de Noviembre de 2011 | Imprimir | PDF |  Correo electrónico

102. 29. (Octubre 2011) Medidas matemáticas de síncopa (I)

Los tres siguientes artículos de esta sección provienen del trabajo Mathematical measures of syncopation, presentado en el congreso BRIDGES: Mathematical Connections in Art, Music, and Science de 2005. Los autores son Andrew Melvin (Buckinghamshire Music Service, Inglaterra), David Rappaport (School of Computing, Queen's University), Godfried Toussaint (School of Computer Science, McGill University) y el autor de esta columna. 1. Introducción La música es emoción y tiene el poder de crear complejos mundos de sentimientos psicológicos. Psicólogos, críticos, musicólogos, compositores, intérpretes y oyentes en general se han interrogado sobre la importante cuestión de cómo la música hace aflorar las emociones, esto es, cuáles son los procesos específicos por los cuales el material sonoro se transforma en emoción. En las últimas décadas investigadores de varias disciplinas han mostrado un creciente interés por esta cuestión así como otras no menos fascinantes, a saber, el problema del significado en la música (significado designativo versus significado no referencial), el papel del aprendizaje en la experiencia musical, la descripción de los cambios propiciados por la música, por nombrar solo unos cuantos ejemplos (véase [7, 2, 4, 5]). Los psicólogos de la música han descubierto que la emoción causada por la música puede tener sus orígenes en un proceso de creación y relajación de tensión [7, 8, 3]. Este proceso comprende los estímulos mismos, las expectativas que la música genera en los oyentes (que indudablemente están determinadas por su familiaridad con el estilo musical en cuestión y la experiencia adquirida en el pasado, entre otros factores), y, finalmente, la tensión creada entre esas expectativas y su resolución final en la pieza musical. La presencia de la tensión/resolución ocurre a todos los niveles del fenómeno musical. Se puede encontrar en la melodía, la armonía y en los elementos rítmicos así como en el timbre y la forma musical. Normalmente, la tensión está equilibrada entre todos estos elementos musicales. Este trabajo se centra en los mecanismos rítmicos que crean tensión en una pieza musical. En particular, nos interesa la síncopa, uno de los mecanismos más sorprendentes y transgresores para producir tensión rítmica. La síncopa es fácil de percibir pero difícil de definir con acierto, pues sus manifestaciones con numerosas y de distinta naturaleza. En la siguiente sección, definiremos formalmente la síncopa dentro un marco abstracto. En la siguiente entrega de esta serie abordaremos el problema de formalizar matemáticamente la síncopa; revisaremos trabajos previos e introduciremos nuestra medida de síncopa, la llamada distancia ponderada de nota a parte. En la tercera entrega se probará la bondad de esta medida con varios ritmos (básicamente ritmos de clave) tomados de diversas tradiciones musicales. 2. Definición de síncopa El fidedigno Harvard Dictionary of Music [9] contiene la siguiente definición de síncopa, la cual creemos que captura su esencia: “Síncopa: una contradicción momentánea de la métrica o pulso predominante”. Otras definiciones, similares a esta en términos de perspicacia, se pueden encontrar en [10] y [6]. Ese mismo diccionario detalla aún más la definición y añade que “la síncopa se puede crear por los los valores de las notas mismos o por la acentuación, la articulación, el contorno melódico o el cambio armónico en el contexto por otro lado de una sucesión de notas no sincopadas”. Esto clarifica dos extremos sutiles, a saber: primero, para que exista una contradicción tiene que haber un patrón de regularidad con el que contrastar; segundo, esa contradicción se puede revelar a través de varios elementos musicales, no sola y puramente de elementos rítmicos. Más aún, la síncopa puede materializarse bien por un cambio del carácter principal de la métrica o como una contradicción entre las notas en parte fuerte y débil contra otras partes de la textura musical cuyo contexto métrico está fijo. El primer tipo de síncopa, el cambio de métrica, puede producirse a través de una transformación de tiempo binario a ternario (hemiola) u otras de similar clase. Este recurso rítmico se usó mucho en las progresiones cadenciales de compositores hasta el Barroco inclusive; también se encuentra con frecuencia en la música de Beethoven. En la figura 1 tenemos una reducción del Concerto Grosso no 4, compases de 97 a 99, de Haendel. En este ejemplo se aprecia un agrupamiento ternario en las voces superiores contra un agrupamiento binario en las voces inferiores. Esto crea un tensión entre dos métricas en conflicto, cuya resolución se alcanza en el la menor final. Figura 1: Hemiola como una forma de síncopa. El mismo recurso se puede apreciar en la sonata opus 53, no 1, compases 82-86, de Beethoven, en un pasaje en que la hemiola aparece en un nivel submétrico, en este caso, un tresillo de semicorcheas contra dos semicorcheas en un compás de 2/4; véase la figura 2. Figura 2: Una hemiola en un nivel submétrico. El otro tipo de síncopa implica ataques de notas entre partes fuertes en lugar de sobre ellas como forma principal de contradicción. Como se dijo arriba, tiene que haber un contexto métrico fijo, un patrón fijo de partes fuertes y débiles encima del cual la síncopa destaca. Estos complejos recursos rítmicos que usaron los compositores del periodo barroco y clásico tienen su evolución lógica en periodos anteriores de la música occidentales, retrocediendo hasta las primeras formas de notación rítmica precisa en la Edad Media. Según la música coral religiosa se fue desarrollando a partir de la monodia del canto gregoriano hasta llegar a varias voces cantando simultánea e independientemente, los compositores sintieron la necesidad de sincronizar esas voces usando una pulsación métrica fija y unas relaciones temporales entre las voces precisas. Esto dio lugar a conceptos como hoquetus. El hoquetus consiste en una única línea melódica que es compartida por dos voces, una que va a tiempo y otra a contratiempo: Figura 3: Ejemplo tomado de la música mediaval. Aunque el ritmo resultante en su conjunto quizás no se considere como sincopado, la particularidad de la voz superior, que siempre cae en mitad de dos partes fuertes, sí dota de un carácter sincopado a la melodía y le impregna de su peculiar vitalidad rítmica. Este recurso también se puede observar en la música del Barroco y en concreto en la música de Bach: Figura 4: Invención no 1, compases 1-4, de Bach. Se puede apreciar que, aunque el efecto de la síncopa está presente, el efecto final es de equilibrio entre las notas a tiempo y a contratiempo, lo cual es un reflejo de las preocupaciones compositivas de Bach con respecto a la creación de una visión equilibrada y ordenada del universo. Otra característica del concepto de contratiempo es que no necesariamente tiene que producirse a la mitad exacta de dos partes fuertes consecutivas, como ocurría en los ejemplos anteriores. Beethoven ponía las notas a contratiempo a tres cuartos de distancia, más cerca de la siguiente parte fuerte que de la parte fuerte de la propia nota. Este recurso se conoce como anticipación, y en el ejemplo de abajo (figura 5) produce un efecto como dislocado, algo jazzístico, que se puede considerar incluso humorístico: Figura 5: La sonata para piano sonata opus 31, no 1, de Beethoven. Esta ubicación dislocada de la nota a contratiempo produce un efecto de desequilibrio que dota al pasaje de un sentido del drama y de la tensión característicos de Beethoven. Aquí se puede ver al compositor explotando y estirando las nociones de a tiempo y a contratiempo para producir un agudo sentido de síncopa e impredictibilidad rítmica. Sin embargo, esa experimentación rítmica se puede considerar tímida comparada con las técnicas revolucionarias usadas por el compositor ruso Igor Stravinsky en su ballet de 1912 La consagración de la primavera, por ejemplo, en los Augurios de la primavera (la danza de las jóvenes). Aunque se puede ver un ritmo constante de 2/4 con un patrón constante de corcheas, el patrón de acentos (de volumen) cambian sin cesar y de modo impredecible. En la música clásica de las generaciones anteriores la línea melódica era esencial. En este ejemplo, la línea melódica se reduce a una sola nota y las síncopas acaparan toda la atención. Los patrones de acentos de las corcheas se producen según la secuencia (10,2,6,3,4,5,3); véase la figura 6, que muestra los 8 primeros compases de esa sección en una reducción para piano. Stravinsky afirmaba que La consagración de la primavera fue un producto de su intuición y que la pieza se le presento a él en un sueño. En efecto, a pesar de que se ha analizado la obra extensamente, no hay pruebas contundentes de que haya un sistema racional detrás de esta música. Figura 6: Síncopas en La consagración de la primavera. No obstante, el patrón de acentos nos sugiera ciertas observaciones. Primero, incluso aunque las posiciones cambien sin cesar, el número total de partes en el ciclo se encuentra con mucha frecuencia en la música clásica: 32. En un vals de Johann Strauss, por ejemplo, una frase musical puede durar 32 partes o una sección puede durar en total 32 compases. Sin embargo, en un vals se esperaría que una sección de 32 se dividiese en dos mitades iguales de 16, mientras que el ejemplo de Stravinsky no tiene semejante división. Al contrario, el resultado es dos partes de 17 y 15, y la propensión natural de los compositores a subdividir en 16, 8, 4 y 2 partes (o compases) se reemplaza por una sucesión irregular de 7 números, de los cuales solo dos son divisores de 32. Por esta razón, algunos teóricos encuentran más adecuado analizar esta y otras obras de Stravinsky tomando una unidad mínima de duración y descomponer el resto de las notas en términos de esa unidad a diferencia del enfoque de tomar un número más grande de partes (que forman el compás o la frase) y subdividirlas; esta última manera de proceder es característica de la composición clásica de periodos anteriores. El concepto de trabajar desde la unidad más pequeña se llama ritmo aditivo, mientras que el de las métricas divisibles regulares se llama ritmo divisivo. La propensión a crear estructuras rítmicas irregulares se extendió entre los compositores de principios del siglo XX, incluido el compositor húngaro Bela Bartok, cuya pieza para piano Síncopa es un laberinto de distorsiones y giros rítmicos, silencios inesperados y patrones interrumpidos que, como en el ejemplo de Stravinsky, tienen prioridad sobre las preocupaciones melódicas. Para un análisis en profundidad de esa pieza, véase  [11]. En modo alguno fue Stravinsky el primer músico en usar ritmos aditivos en música. En las tradiciones de música folklórica del mundo esta manera de crear ritmos existía hacía mucho, como en las canciones folklóricas de Rusia, Bulgaria y en la música de los pigmeos aka de África Central, cuya música ha sido investigada en profundidad por Simha Arom [1]. La música de percusión de los pigmeos aka, como la de la samba brasileña, por ejemplo, consiste en una malla de patrones rítmicos cíclicos que forman una urdimbre con varios hilos individuales. Sin embargo, como en el siguiente ejemplo (figura 7), se puede ver que incluso un solo hilo tiene una estructura rítmica interna muy compleja: Figura 7: Música de los pigmeos aka. Los pigmeos aka no tienen tradición de música escrita y este ejemplo se ha transcrito a notación occidental. La música se acomoda fácilmente a 4 compases en 6/8, dando un total de 24 corcheas. Sin embargo, inspeccionando el agrupamiento interno de las corcheas, vemos que las 24 corcheas no se dividen en partes iguales -más bien se obtiene una sucesión irregular como sigue: 3,3,3,2,3,3,3,3,2-. En términos de notación, el ejemplo se configura con un alto grado de síncopa, aunque, en verdad, puede ser confuso representar esta música con la notación occidental con su sistema de partes fuertes y débiles, sistema que no está presente en la tradición musical de los pigmeos aka. Es posible representar el mismo ritmo tomando compases irregulares como los que Stravinsky usó para sus estructuras rítmicas aditivas: Figura 8: Música de los pigmeos aka transcrita con una métrica diferente. Una vez más, a partir de este agrupamiento podemos ver que el ciclo no está dividido en partes iguales (12+12), sino en dos partes no iguales de 11 y 13. Este principio de un ciclo rítmico consistente en dos partes no iguales se encuentra en mucha de la música aka, lo cual da como resultado un forma única de tensión rítmica de gran complejidad. La cuestión de si Stravinsky y los ejemplos de la música aka son síncopas se hace más compleja de contestar debido a la naturaleza aditiva de los ritmos. Ya que los ritmos divisivos crean nociones predecibles de las partes a tiempo y a contratiempo, la música se puede percibir como yendo a tiempo (no sincopada) o a contratiempo (sincopada). Sin embargo, dado que en los ejemplos de Stravinsky y la música de los pigmeos aka esas relaciones binarias de estar a tiempo o a contratiempo no existen, ese patrón de partes no existe para el oyente y así en lugar de escuchar partes a tiempo o a contratiempo percibirá el ritmo en el sentido aditivo de agrupar unidades mínimas de duración para crear notas de mayor duración. En este sentido se podría mantener que la síncopa es en su naturaleza más una característica de los ritmos divisivos que de los aditivos. Otro tipo de música del siglo XX que hace un uso explícito de la síncopa es el jazz. Aquí la música en la mayoría de los casos se basa en un pulso firme dado por la percusión y el bajista contra el cual el resto de los músicos reaccionan tocando a contratiempo. Estos es característico del swing de Duke Ellington, cuya famosa composición It Don’t Mean a Thing (if it Ain’t Got that Swing) sobresale por esta particularidad. El swing en jazz consiste en una nota a contratiempo que se mueve ligeramente un poco más allá de la mitad justa hacia la siguiente parte fuerte (la distancia precisa es difícil de medir, lo cual da lugar a la máxima de que el swing se siente y no se puede medir). En la notación musical esta nota a contratiempo se representa bien por una nota a mitad de parte o a tres cuartos de parte, aunque hablando estrictamente es inexacto. Como la notación occidental no puede representar con precisión el swing, la palabra se pone arriba de la partitura para que el músico traduzca las aproximaciones de la notación al lenguaje del jazz. Según fueron surgiendo los distintos estilos del jazz, los compositores de jazz progresivo llevaron al límite las fronteras de la irregularidad rítmica como antes había hecho Stravinsky con la música clásica. Sin embargo, normalmente incluso estos compositores se mantuvieron dentro del marco de frases de 12 o 16 compases. Este marco proporciona al oyente una plantilla con la que medir la síncopa, no importa cuán complejos sean los ritmos internos. Como un buen ejemplo de esto se puede pensar en la pieza de Thelonious Monk Evidence. Más recientemente, el compositor de música contemporánea Brian Ferneyhough, quien compuso Carceri d’Invenzione, llevo el nivel de síncopa a tal extremo que pervirtió su misma naturaleza. Es indudable de que el nivel de síncopa es muy alto en esta pieza (figura 9). De hecho, diríamos que, sin la partitura, sería imposible decir dónde están las partes fuertes. Figura 9: Música de Ferneyhough. Como apuntábamos al principio de este trabajo, la síncopa puede ser compleja y numerosas sus manifestaciones, como hemos visto en esta breve revisión de ejemplos musicales. Por tanto, un intento de medir la síncopa siempre implica ciertos riesgos. En este artículo nos restringiremos al segundo tipo de síncopa, esto es, la contradicción entre partes fuertes y débiles con respecto a un contexto métrico fijo. Bibliografía [1] Arom, S.; African Polyphony and Polyrhythm, Cambridge University Press, Inglaterra, 1991. [2] Cooper, G. and Meyer, L.B. ; The Rhythmic Structure of Music, University of Chicago Press, Chicago, 1963. [3] Deutsch, D.; The Psychology of Music, Academic Press, 1998. [4] Fubini, E.; History of Music Aesthetics, Macmillan Press, Londres, 1991. [5] Juslin, P.N. and Sloboda, J.A. ; Music and Emotion: Theory and Research, Oxford University Press, Oxford, 2001. [6] Kennedy, M. (editor); The Oxford Dictionary of Music, Oxford University Press, Oxford, 1998. [7] Meyer, L. B.; Emotion and Meaning in Music, Chicago University Press, Chicago, 1956. [8] Peretz, I. and Zatorre, R. J.; The Cognitive Neuroscience of Music, Oxford University Press, Oxford, 2003. [9] Randel, D. (editor); The Harvard Dictionary of Music, Harvard University Press, 1986. [10] Randel, D. (editor); The New Grove Dictionary of Music and Musicians, Akal, 1986. [11] Roeder, J.; Rhythmic Process and Form in Bartók’s Syncopation, artículo no publicado. Véase http://theory.music.ubc.ca/roeder.html

Viernes, 07 de Octubre de 2011 | Imprimir | PDF |  Correo electrónico

103. 28. (Septiembre 2011) La liga de compositores de música automática

1. Introducción Hace algún tiempo cayó en mis manos un disco de La liga de compositores de música automática, cuya portada se puede ver en la imagen de la izquierda. Fueron los pioneros de la música algorítmica, en particular, de la música generada por ordenadores que se comunican entre sí y reaccionan ante la música de otros ordenadores (en inglés es conocida por network computer music). No cabe duda de que los presupuestos estéticos que fundamentan la música algorítmica difieren notablemente de otras corrientes musicales y, por ello, merece la pena analizarlos, más aún si tenemos en cuenta la vigencia de la música electrónica tanto en la música culta como en la música popular. Tras la canícula, especialmente severa este año, en este mes de septiembre de carácter fugaz, analizaremos la obra de La liga de compositores de música automática. Al calor de ese análisis, reflexionaremos sobre la relación entre la música y la algorítmica. Pocas veces me he encontrado con unas notas tan completas, bien documentadas y sinceras en un CD de música. En muchos casos las notas consisten en un relleno más o menos sucinto de unas pocas páginas, a veces refritos de una enciclopedia o una obra de referencia, pero en general nada especialmente original. Aquí, en cambio, nos encontramos con notas escritas por Tim Perkins y John Bischoff, nada menos que dos miembros de La liga, en las que nos presentan un estudio completo de la obra, los protagonistas y el contexto histórico, escrito con sinceridad y apasionamiento. Es aún más raro contar con el testimonio de los compositores en las mismas notas del CD. Dada la calidad de las notas, he decidido traducirlas y dejar que ellas sean la base de mis reflexiones finales. Pido perdón desde ahora mismo por los posibles errores de traducción. 2. Notas del CD La liga de los compositores de música automática (1978-1983) Notas escritas por Tim Perkins y John Bischoff. Agosto de 2007 La liga de los compositores de música automática fue una banda/colectivo de experimentadores de música electrónica muy activos en el área de la bahía de San Francisco entre 1977 y 1983. Considerados por muchos como los primeros músicos en incorporar los nuevos microordenadores disponibles entonces en la ejecución musical en vivo, La liga creó redes de ordenadores que interactuaban entre sí y con otros dispositivos electrónicos, con especial empeño en la gestación de "inteligencias artificiales musicales" nuevas y sorprendentes. Concebimos las redes de ordenadores como un gran instrumento interactivo compuesto por máquinas programadas independientemente que hacían música automática, la cual se podía calificar de ruidosa, difícil de escuchar, con frecuencia impredecible y ocasionalmente bella. Contexto cultural: California del norte en los 70 El trabajo de La liga formó parte de la singular atmósfera cultural del área de la bahía de San Francisco en los 70 y 80, una mescolanza de ideologías comunales, cultura radical, innovación tecnológica, efervescencia intelectual y una actitud pragmática que ha sido el sello característico de la vida californiana desde los días de los primeros pioneros. Flotaba en el aire de entonces una sensación de nuevas posibilidades así como el sentimiento de la necesidad de construir la cultura desde el suelo hacia arriba. En concreto, para la música esto significaba redefinir todo tal y como se había hecho hasta ahora, desde los instrumentos y los sistemas de afinación hasta las formas musicales, los locales para los conciertos y las relaciones sociales entre intérpretes y público. Aunque todavía no era conocido por ese nombre, Silicon Valley bullía de actividad; el anuncio casi diario de nuevos circuitos integrados hacían posible el nacimiento de una nueva subcultura, y aficionados y entusiastas de la informática , muchos relacionados marginalmente con las industrias tecnológicas, o bien directamente de fuera de ellas, estaban creando la revolución del microordenador. En la bahía de San Francisco el acceso a las nuevas tecnologías digitales y a la gente que las desarrollaba fue quizás el más expedito en el mundo. En esos emocionantes primeros días muchos informáticos se centraban menos en las riquezas potenciales que se derivaban de la tecnología que en su potencial revolucionario -esto es, en el sueño de una nueva sociedad construida sobre los cimientos de la inteligencia artificial y del acceso a la información libre y abierto. A partir de la tradición americana de música experimental, representada por los californianos John Cage (1912-1992), Henry Cowel (1897-1965), Harry Partch (1901-1974) y Lou Harrison (1917-2003), se instaló una sensación de lejanía estética respecto a Europa, demasiado distante, y de que nuestra cultura musical podía nutrirse perfectamente de cualquier tradición del mundo -musical y de cualquier otra clase- como fuente de inspiración e influencia. Estos compositores formaron también la base de una tradición de construcción de instrumentos asentada en la costa oeste, que incluía desde el Rhythmicon (1930) de Cowell, una máquina para explorar relaciones rítmicas de alta complejidad, pasando por las orquestas de latas y tambores de freno dirigidas por Harrison y Cage, hasta los instrumentos caseros de afinación microtonal de Partch. En la mescolanza cultural de la época había también una viva tradición de música improvisada de carácter ruidoso. Dicha tradición, que vivía sin respaldo comercial e institucional y que la practicaban músicos provenientes de las sesiones de improvisación hippies, el free jazz, la música clásica o el punk rock, encarnaba una sensibilidad de exuberancia, disonancia, ritmo libre y composición en colaboración. No menos importantes fueron las corrientes intelectuales de la época. Una floreciente corriente de pensamiento más o menos científico sobre la naturaleza de los sistemas complejos y su comportamiento proclamó con fuerza que un nuevo nivel de entendimiento de la física, la biología y la cultura estaba a la vuelta de la esquina. Cibernética (Norbert Wiener), teoría de los sistemas complejos (Prigogine), algoritmos genéticos (John Holland), sinergética (Buckminster Fuller), teoría de las catástrofes (Rene Theom), redes neuronales (McCollough), teoría del caos (Crutchfield y sus colaboradores), ecología cultural (Bateson), eran temas cuyos autores respaldaban la creencia del momento de que los fenómenos complejos pueden entenderse analizando las interacciones dinámicas de componentes relativamente simples conectados entre sí. (El salto que hay desde afirmar que podemos analizar los procesos complejos, aquellos capaces de emular la vida, en términos de componentes simples en mutua interacción hasta imaginar que podemos crear comportamientos complejos, también capaces de emular la vida, conectando componentes simples -y hacerlo dentro de un contexto musical- no parece demasiado arriesgado.) Finalmente, el hecho de que había una falta de oportunidades reales en la costa oeste para conseguir apoyo y publicidad para la música culta hizo que los compositores de la zona de la bahía de San Francisco abrazaran con más facilidad las estéticas experimentales. Ya que el público interesado era escaso y las oportunidades para una carrera seria infructuosas, ¿por qué no gastar los esfuerzos de uno explorando el potencial de fantásticas ideas en lugar de preocuparse de aplicaciones prácticas de esas ideas dentro de los tradicionales dominios musicales? ¿Por qué no extender las ideas experimentales sobre composición comunal, música algorítmica y comportamiento en red a las nuevas tecnologías electrónicas? ¿Por qué no arriesgarse a crear música que puede que no tenga éxito alguno en su misión de ser inteligible? Center for Contemporary Music and League Beginnings El Center for Contemporary Music (CCM) en Mills College en Oakland proporcionó un centro de reunión único para el encuentro de todas estas corrientes culturales. En esa época la universidad albergaba la sede del CCM , pero este tenía su identidad propia y única, y ofrecía estudios para los músicos de fuera de la comunidad universitaria. Allí había una oportunidad para que experimentadores de la universidad, improvisadores, entusiastas de la electrónica, músicos de rock y otras variedades de heterodoxos se encontraran y crearan algo nuevo. En la mitad de los años 70 el ambiente en Mills College estaba fuertemente enraizado en una tradición de experimentalismo y los músicos estaban absortos fabricando circuitos caseros para su uso en los conciertos en vivo de música electrónica; de hecho, el diseño y construcción de los circuitos específicos se veía como una parte inseparable del proceso compositivo. Para muchos compositores una nueva pieza significaba diseñar nuevos circuitos: como una partitura gráfica, un esquema de un circuito determinaba la actividad musical de una pieza. La idea de usar el sistema electrónico mismo como un actor musical, en oposición a su consideración como una mera herramienta, había empezado ya con compositores como David Tudor (1926-1996) y Gordon Mumma (n. en 1935). Por ejemplo, en el trabajo de Tudor Untitled (1972), el compositor interconectaba una mesa llena de cajas pequeñas, la mayor parte de fabricación casera, que contenía circuitos analógicos: amplificadores, atenuadores, filtros, desfasadores. El comportamiento autónomo de estos circuitos -solo con los ajustes ocasionales y menores del intérprete- definían el carácter de la música. A partir de Tudor -quien estuvo en Mills como compositor visitante durante este periodo- surgió una poderosa noción que pronto fue aceptada allí: el trabajo principal de un intérprete/compositor de música durante el concierto era la de escuchar antes que determinar y crear cada sonido que se produce durante la ejecución. Su estilo de música exige de nosotros, ya desempeñemos el papel de compositor, intérprete o público, que escuchemos una representación sonora del comportamiento de una sistema autónomo. El interés de la obra no reside en ninguna otra cosa que en percibir y disfrutar el comportamiento complejo del sistema. A mitad de los 70 los primeros ordenadores personales se lanzaron al mercado de consumo. Estas máquinas, llamadas microordenadores porque su tamaño era pequeño comparado con los grandes servidores de la universidad y la industria, ahora podían comprarse por 250 dólares. Su disponibilidad marcó la primera vez en la historia que personas corrientes y molientes podían poseer y programar ordenadores fuera de las grandes instituciones. Para los compositores de esta comunidad fue un verdadero hito: había un componente radicalmente más flexible y potente que tenían que incorporar rápidamente a los equipo electrónicos con que trabajaban hasta entonces. Horton y La orquesta de silicio El compositor que comprendió el potencial de los microordenadores más claramente fue Jim Horton (1944-1998). Horton fue un músico pionero de la música electrónica y un intelectual radical; fue además quien en primer lugar compró una de las nuevas máquinas: una KIM-1 en 1976. El incontenible entusiasmo de Horton por la KIM pronto contagió al resto de la comunidad. En poco tiempo muchos compraron máquinas KIM y empezaron a estudiar de modo autodidacta cómo programarlas en lenguaje máquina 6502. Las máquinas eran bastante primitivas; los programas se metían directamente en la memoria de un kilobyte del KIM a través de un teclado hexadecimal, y se grababan en una cinta de audio (de cassette), y esto da una idea de cuán rudimentaria era la forma de trabajo. Había un fuerte sentimiento de comunidad entre los compositores que estaban aprendiendo a programar estos minúsculos ordenadores, un espíritu compartido que fue particularmente útil cuando había que adentrarse en los esotéricos, intrincados y a veces engorrosos modos de operaciones del KIM. Horton improvisaba con la flauta y el sintetizador analógico. Anteriormente había trabajado construyendo sistemas de sintetizadores analógicos con cierta interactividad; a veces conectaba su sintetizador con los de sus amigos para construir el sistema más grande y complejo posible, el cual dejaba que tocase durante ocho horas en conciertos que duraban la noche entera. Rich Gold (1950-2003), uno de los fundadores de La liga recuerda: "Jim Horton fue un genio... brillante, agudo, lleno de complicidad, un artista tocado por la pobreza que vivía en un apartamento cutre, lleno de libros, que olía a tabaco Buggler. Sufría dolores atroces a causa de una artritis paralizante, y fue de ese dolor del que pienso que finalmente murió. Lo conocí porque fue uno de los primeros compradores del sintetizador Serge (había ahorrado dinero de las prestaciones sociales quedándose sin comer). Fue la primera persona en hacer música seria con el KIM-1 y también la fuerza motriz que empujaba a La liga de los compositores de música automática." Tim Perkins: "Conocer a Jim Horton fue inmediatamente una experiencia liberadora para mí. Horton aparecía en un concierto con una maraña de cables sueltos y componentes electrónicos metidos en una cómoda que usaba circunstancialmente para transportar su equipo. Con mi cabeza llena de dudas, pues mis conocimientos sobre circuitos eran escasos y estaban mal asimilados, asombraba ver a alguien sencillamente yendo al fondo de la cuestión, retorciendo cables pelados, conectando todo con todo, y trabajando la música de manera conceptualmente profunda, con una motivación fortísima, y todo ello sin esperar a que el equipo adecuado apareciera. Vivía en una pobreza que nunca le pareció una limitación, y trabajó con cualesquiera medios que estuviesen a su alcance." En 1977 fue Horton quien introdujo la idea de una banda formada por una red de microordenadores. John Bischoff: "Unos cuantos de nosotros se reunían regularmente para escuchar la música que estábamos creando; alguna música estaba hecha con nuestros KIM y otra con circuitos analógicos en conjunción con otros instrumentos. Recuerdo una discusión una tarde en la que Horton hablaba con excitación sobre la posibilidad de construir una "orquesta de silicio" -una orquesta de microordenadores unidos por una matriz interactiva. El concepto me sonaba alucinante e imposible en aquel tiempo." Más tarde en ese año, Horton y Gold colaboraron en una pieza en la cual unían sus KIM por primera vez en una actuación en Mills College. Gold interactuaba con un programa de inteligencia artificial de su propia creación mientras Horton ejecutaba una precursora pieza algorítmica basada en la teoría armónica del matemático del siglo XVIII Leonhard Euler. A principios de 1978 Horton y Bischoff desarrollaron una pieza a dúo para dos KIM donde los tonos que sonaban ocasionalmente en la máquina de Bischoff provocaban en la máquina de Horton una transposición de la actividad melódica acorde a la nota "principal" de Bischoff. En la primavera de 1978, Horton, Bischoff y Gold actuaron como un trío en red en el Blind Lemon, un espacio gestionado por artistas en Berkley. Al trío pronto se unió David Behrman (nacido en 1937), quien se había mudado al oeste para desempeñar el puesto de co-director del CCM en Mills. (Gold y Bischoff fueron estudiantes en Mills; Horton nunca estudió allí oficialmente.) Behrman fue quien proporcionó una de las técnicas clave para darle forma al trabajo de La liga en los siguientes años. Anteriormente Behrman había compuesto piezas en que los circuitos electrónicos "escuchaban" la música que tocaban los intérpretes en vivo y acompañaban o remarcaban determinadas combinaciones de alturas (On the Other Ocean, de 1977). Muchos de las posteriores configuraciones en las interconexiones entre máquinas seguirían este principio, el de que máquinas detectaban y enfatizaban una combinación armónica producida por uno o más de los restante intérpretes. Fue este cuarteto el que primero actuó bajo el nombre de La liga de los compositores de música automática en noviembre de 1978. El nombre del nuevo grupo era en parte una referencia a la histórica Liga de compositores creada por Aaron Copland y otros en los años 20. Se buscaba también transmitir el predominio de la inteligencia artificial en las actividades de La liga, ya que empezaban a ver la mitad del grupo como "humano" (los compositores) y la otra mitad como "artificial" (las máquinas). Como se afirmaba en los programas de aquellos conciertos "La liga es una organización que busca inventar nuevos miembros a través de sus proyectos... SE SIMULAN Y SE PONEN AL DESCUBIERTO VALORES MUSICALES". Antes de acabar 1980 Gold y Behrman habían dejado ya el grupo para dedicarse a otros proyectos, y entonces el compositor Tim Perkins se unió al grupo. Tim tenía una licenciatura en vídeo por la California College of Arts and Crafts en Oakland. Era un activo intérprete de gamelán, un entusiasta de la entonación justa, además de haber recogido docenas de sistemas de afinación de todo el mundo y haber creado instrumentos con que tocarlos. El trío continúo con esta nueva incorporación, dando conciertos regularmente en el área de la bahía de San Francisco durante los siguientes cuatro años. Siguiendo las prácticas musicales habituales en el área de la bahía, muchas sesiones se celebraban en colaboración con otros músicos acústicos y electrónicos de la zona, incluyendo el artisto de vídeo Donald Day, el trombonista Ron Heglin y los músicos electrónicos Brian Reinbolt y Kenneth Atchley. Bischoff: "Cada dos domingos, después de comer, empleábamos unas cuantas horas en configurar nuestra red de ordenadores en el Finnish Hall en Berkley, y los dejamos sonar, haciendo pequeños ajustes aquí y allá, durante un par de horas. El público podía ir y venir a su gusto, hacer preguntar, o sencillamente sentarse y escuchar. Esto era una especie de evento comunitario, pues otros compositores aparecían por allí y tocaban o compartían circuitos electrónicos que habían diseñado y construido. Un interés por construir instrumentos electrónicos de todo tipo parecía flotar "en el ambiente". Los eventos del Finnish Hall constituían una escena típica en Berkley, ya que los paisajes sonoros generados por los ordenadores se mezclaban con los sonidos de los grupos de danzas folclóricas que ensayaban en el piso de arriba, y también con las reuniones del partido comunista, que se celebraban en la habitación de detrás en el venerable y viejo edificio." La estética de La liga y sus métodos de trabajo Es quizás confuso para los oídos modernos incluso llamar a estos primeros microordenadores que estábamos usando "ordenadores" en algún sentido. Con menos capacidad de procesamiento que una cafetera o un ratón del siglo XXI, comparten muy poquito con los ordenadores de hoy en día, y los programas que escribían los miembros de La liga no eran nada comparados con la vasta infraestructura de software que conforma la actual producción musical profesional. El uso del ordenador en la producción musical en el siglo XXI tiene sus descendientes principalmente en la práctica y la estética de la música por ordenador de los años 70 y 80. Mundos musicales enteros, consistentes en crear sonidos y simulaciones de sonidos reales, se manipulaban y reproducían dentro del ordenador. El énfasis se pone en el control, la perfección y en la domesticación de la complejidad. El enfoque de La liga no podía ser más alejado de la tradición de música por ordenador sobre cinta de aquella época. Como Perkins escribió por aquel entonces: "Veo la estética que influye este trabajo quizás como una reacción a las otras tendencias en música por ordenador: en lugar de intentar lograr un control absoluto sobre cada aspecto de la música, buscamos más sorpresa a través de la respuesta viva e impredecible de estos sistemas, y esperamos generar una respuesta activa a esa sorpresa en la ejecución musical. Y en lugar de intentar eliminar al ejecutante humano imperfecto, tratamos de usar las herramientas electrónicas disponibles para mejorar el aspecto social de la composición musical." Para nosotros, la música nunca estuvo "en el ordenador". Los microordenadores fueron siempre solo componentes con un comportamiento particularmente interesante que incorporar en nuestras redes, las cuales incluían otros circuitos electrónicos así como seres humanos. El núcleo de nuestro trabajo consistía en bricolaje o ensamblaje físico, esencialmente una práctica de escultura musical. Aunque a veces los microordenadores se usaban como dispositivos de audio, generalmente se empleaban como dispositivos de control sobre unidades de producción de sonido, bien analógicas o digitales. (No tenían suficiente capacidad de procesamiento como para crear otra cosa que no fuera sonidos digitales caracterizados por el ruido y la aspereza, los cuales se usaban a veces para crear buenos efectos viscerales, pero que tenían limitaciones materiales.) Sentíamos que nuestro trabajo era más afín al de nuestro mentores y amigos que construían gamelanes (Lou Harrison y Bill Colvig) o instrumentos mecánicos o electro-mecánicos (Tom Nunn y Chris Brown), o bien a los músicos que incorporaban juguetes musicales electrónicos a los que habían modificados los circuitos, que a la música por ordenador que se presentaba en los circuitos institucionales de música contemporánea. Siempre había una sensación de que la música salía de la situación material, de la idiosincrasia individual de los intérpretes y de sus arreglos anárquicos y ad hoc. La música era siempre en directo, sin ninguna secuencia planeada de antemano. Cada estación de un intérprete tocaba su propia composición, tenía su propia unidad de producción de sonido y recibía y enviaba información desde otras estaciones. El significado de esta información podía cambiar completamente de una estación a otra: una indicación de altura de sonido de un intérprete podía ser un control de ritmo en otro intérprete, por ejemplo. Ninguna estación tenía funciones ejecutivas o algo parecido a una partitura de director. Cualquier forma musical que emergía lo hacía de manera muy misteriosa, a partir de las interacciones y la influencia mutua de las diferentes estaciones. Una típica sesión de La liga consistía en configurar los ordenadores en una habitación y conectarlos entre sí tras mucho esfuerzo. Con los cables por todos sitios y con los ordenadores conectados en red ya libres de errores de programación, tras varias horas finalmente se iniciaba el sistema y empezaba la sesión musical. Los poníamos a funcionar, los afinábamos y escuchábamos muy atentamente cómo interactuaban entre sí las máquinas. Cuando nuevas formas de musicalidad aparecían, tomábamos notas de los parámetros de configuración de los programas individuales con la esperanza de reconstruir esos parámetros en un concierto y que diesen resultados similares. La forma estructural de nuestros conciertos era esencialmente una serie de parámetros acordada antes, donde los detalles momento a momento, claro es, siempre quedaban en un interactivo estado de cambio continuo. [Nota: Se puede ver un ensayo del grupo en un raro vídeo que se encuentra en Youtube.] Conclusión Para 1983 la artritis reumatoide de Horton lo había paralizado en grado sumo y hacer conciertos se había vuelto complicado. Las actividades de La liga se fueron ralentizando hasta que se interrumpieron y a finales de ese año el grupo se disolvió. Durante todos los años de actividades de La liga había aspiraciones grandiosas y utópicas, así como una juvenil sensación de que estábamos en el umbral de una nueva consciencia hombre-máquina, una fase completamente nueva de la cultura humana. Concebíamos el grupo no como una banda de músicos con miembros fijos, sino como la vanguardia de un nuevo estilo, una nueva práctica social, una nueva manera de hacer música: quizás un cibernético y revolucionario primo del jazz. Cuando muchos compositores en nuestra comunidad y fuera de ella empezaron a trabajar en vivo con ordenadores pensamos que esta práctica se extendería finalmente fuera de nuestro círculo. Bob Gonsalves, un compositor y estudiante del Mills College a finales de los 70 que escribía en EAR, una revista local sobre música experimental, expresó muy bien el sueño de la época: "Un silencio cae sobre el público cuando los músicos suben al escenario. Los intérpretes toman sus instrumentos y los conectan en las líneas de datos, 8 por 8, hasta que todos los controles indican que están listos. El Robomaster afina el Master Oscillator, todos los circuitos están en sincronía, las memorias de escrituras están habilitadas, las luces se apagan... ¿Te suena familiar? Si es así, ¡estás viviendo en el futuro, tío!" Tras la desaparición de La liga, nosotros (Perkis y Bischoff) continuamos el trabajo; intentamos normalizar el lioso y complicado proceso de interconectar los sistemas construyendo una interfaz estándar para los sistemas de ordenadores que llamamos el concentrador (the hub). La intención en ese momento fue hacer más fácil la implicación de otros intérpretes en este tipo de práctica musical; y de nuevo no teníamos en mente crear un grupo con un número fijo de intérpretes, sino promocionar el desarrollo de esta nueva práctica musical y que otros intérpretes se uniesen. Sin embargo, este trabajo condujo a la formación de un nuevo grupo, llamado The Hub, al cual se unieron Chris Brown, Scot Gresham-Lancaster, Phil Stone y Mark Trayle, grupo que ha trabajado de modo intermitente durante los últimos 20 años. Solo recientemente la noción de una práctica general de música por ordenadores conectados en red ha adquirido cierta aceptación (véase la bibliografía). Aunque el espíritu revolucionario de aquellos primeros días se ha atemperado y nuestros objetivos se han hecho más modestos, a veces es bonito soñar que la visión medio irónica de Jim Horton se ha hecho realidad: "Cuando los programas se ejecutan autónomamente, ligeramente más allá de mi comprensión, interpretando música que probablemente no se me habría ocurrido, música producida por mis propios dispositivos, me gusta imaginar que somos los precursores de una edificante inteligencia artificial (IA) musical, algo extraña, del siglo XXI. ¡Oh, cuánto espero y deseo que la cibercultura contemporánea conduzca a un utópico mundo de Bondad, bello y compasivo!" 3. Reflexiones En lo que sigue haremos unas breves reflexiones a partir de las notas del CD traducidas más arriba. En La liga confluyen varios factores que explican su génesis y su estética. Son herederos de la tradición anclada en una fascinación por la tecnología. Esta no es nueva y se remonta a principios de siglo con el futurismo de Marinetti. Cuando Marinetti afirma, muy provocadoramente, que "Un automóvil de carreras es más hermoso que la Victoria de Samotracia" está renunciando a la belleza según el canon clásico y en este sentido es equivalente a la afirmación de La liga de que su música es "ruidosa, difícil de escuchar, con frecuencia impredecible y ocasionalmente bella". Pero desde la época de Marinetti la ciencia y la tecnología han avanzado de modo impensable, desde la física cuántica o la lógica probabilista hasta la inteligencia artificial o los fractales. La Segunda Escuela de Viena entona el réquiem por los principios musicales que rigieron el periodo de la práctica comúny en la estética de La liga, por su parte, ignoran la forma musical en el sentido clásico, las reglas de armonía o contrapuntoy ciertas convenciones melódicas. La liga trasciende todo esto, como hicieron antes otros, y propone un cambio radical: el público va a un concierto a escuchar una "representación sonora de un sistema autónomo", una sonificación. No importa la cantidad de disonancias, y si estas se resuelven; no importa el sentido de propincuidad tan necesario en la música melódica; no importa la función de la armonía; no importa la forma musical con sus repeticiones, con sus codas y con sus reexposiciones; lo que importa es el seguimiento de ese comportamiento musical, que básicamente se expresa a través de la textura, de un acusado sentido de lo impredecible y de la exposición de pequeñas células melódicas, a modo de estrellas fugaces. Desde un punto de vista social La liga pone un fuerte acento en la composición en colaboración y en la repercusión de la obra en la comunidad. En las notas de CD Perkins y Bishcoff nos explican en detalle el contexto histórico y social. Por un lado, está el ambiente liberal reinante en la bahía de San Francisco, consecuencia de la posguerra de Vietnam, pero también de la nueva efervescencia tecnológica de la costa oeste. Por otro lado, está la reacción estética hacia el modernismo según lo encarna Boulez y Xenakis, pero también hay un rechazo de los presupuestos estéticos del minimalismo según lo encarna Reich. La liga comparte con Xenakis su fascinación por la ciencia, pero las consecuencias musicales son muy diferentes. Xenakis busca emular procesos físicos y matemáticos con su música, como por ejemplo en su obra Pithoprakta. Sin embargo, la música de La liga es el proceso físico mismo producido por los dispositivos de audio y sus interconexiones; son máquinas musicales que comunican entre sí y el público tiene la misión de escuchar los resultados de esa comunicación. De la estética minimalista La liga rechaza el ansia de eliminar al "intérprete humano imperfecto" de que habla Reich en sus obras para cinta. La liga tiene una idiosincrasia social muy pronunciada y antes que rechazar al intérprete lo sustituye por máquinas que colaboran entre sí. Hay más énfasis en la composición que en la interpretación. La interpretación la llevan a cabo las máquinas, pero estas máquinas llevan las ideas de los compositores escritas en sus líneas de código. La parte social de la composición consiste en la interacción entre esas máquinas. Otra característica de la música de La liga fue la de explorar nuevos instrumentos y afinaciones, hecho que concuerda con la importancia que dan a la textura. La tecnología que surgía poderosa en esa zona, la futura Silicon Valley, fue asimismo de importancia, en especial, la inteligencia artificial. Esta disciplina estaba en un estado incipiente, pero sus partidarios prometían niveles de comprensión y resultados que lamentablemente no han llegado. Ciertamente, la inteligencia artificial ha avanzado mucho, pero no ha dado el salto conceptual que soñaban los miembros de La liga. Incluso hoy en día muchos de los objetivos que se marcaron los pioneros de esta disciplina aparecen como inalcanzables a medio plazo. En el campo de la música hace falta construir modelos muy complejos, basados en principios psicológicos, en conocimientos musicológicos, con fuerte componente computacional. No es válida la premisa simple de que "los fenómenos complejos pueden entenderse analizando las interacciones dinámicas de componentes relativamente simples conectados entre sí". Sin embargo, parte del encanto de la música de La liga puede encontrarse en esta inocencia. 4. Bibliografía Bischoff, J., Gold, R. and Horton, J. 1985. Microcomputer Network Music (Cambridge, MA: Foundations of Computer Music, editor: Curtis Roads, MIT Press). Bischoff, J. 1991. Software as Sculpture: Building Music from the Ground Up (Oxford: Leonardo Music Journal Vol.1 No. 1, Pergamon Press). Brown, C. and Bischoff, J. 2005. Computer Network Music Bands: A History of the League of Automatic Music Composers and The Hub (Cambridge, MA: At A Distance: Precursors to Art and Activism on the Internet, pp. 372-390, MIT Press). http://crossfade.walkerart.org/brownbischoff/ Collins, N., McLean, A., Rohrhuber, J. and Ward, A. 2003. Live Coding in Laptop Performance (Organised Sound 8 (3):pp. 321-330, Cambridge University Press). Kahn, D. 2004. A Musical Technography of John Bischoff (Cambridge, MA: Leonardo Music Journal Vol. 14, pp. 74-79, MIT Press). Perkis, T. 1996. Bringing Digital Music to Life. 1996. ( Cambridge, MA: Computer Music Journal 20:3, MIT Press). Perkis, T. 2003. Complexity and Emergence in the Experimental Music Tradition (Amsterdam: Art and Complexity, editor: J. Casti, Elsevier). 5. Discografía Lovely Little Records, John Bischoff, with the League. Lovely Music Ltd. EP 101-06 (1980) The Hub: Computer Network Music, Artifact Recordings ART1002 (1989) Artificial Horizon, Tim Perkis and John Bischoff, Artifact Recordings CD ART1003 (1990) Wreckin' Ball, The Hub, Artifact Recordings CD ART1008 (1994) Simulated Winds and Cries, Jim Horton, Artifact Recordings CD ART1013 (1996) On the Other Ocean, David Behrman, Lovely Music CD 1041 (1996) The Glass Hand, John Bischoff, Artifact Recordings CD ART1014 (1996) Fuzzybunny, Tim Perkis, Chris Brown, Scot Gresham-Lancaster, Sonore (2000) Motive, Tim Perkis, Praemedia CD praecd002 (2002) Luminous Axis, Wadada Leo Smith, with Bischoff, Perkis et al. Tzadik CD 7083 (2002) Aperture, John Bischoff, 23Five Inc. CD 006 (2003) Boundary Layer, the Hub, upcoming release Tzadik (2008)

Miércoles, 07 de Septiembre de 2011 | Imprimir | PDF |  Correo electrónico

104. 27. (Julio 2011) Distancia y similitud musical - III

1. Introducción Este es el último artículo de la serie sobre el concepto matemático de distancia y similitud melódica. En el primer artículo revisamos las principales propiedades de la distancia como objeto matemático e hicimos una lista de los numerosos campos en que se usa este fructífero concepto. En ese mismo artículo introdujimos el concepto de similitud melódica y lo ilustramos con las famosas variaciones de Mozart K. 265 sobre el tema popular Ah, vous dirai-je, Maman. En el segundo artículo entramos en detalles más técnicos. En primer lugar, definimos las representaciones abstractas de las melodías y, en segundo lugar, cómo se aplican ciertas transformaciones a esas representaciones de las cuales sale la medida de similitud. Transformaciones las hay de muy diversa naturaleza y en el segundo artículo examinamos las siguientes entre las más relevantes: las transformaciones de altura, las transformaciones rítmicas y las medidas simbólicas. Por razones de longitud, dejamos para este artículo las transformaciones basadas en medidas sobre vectores y las medidas armónicas. Por último, en este artículo describiremos los experimentos de Müllensiefen y Frieler [MF04] para la validación perceptual de esas medidas. La gran dificultad de diseñar una medida que refleje fielmente la medida de similitud humana es precisamente tener datos de referencia -lo que inglés se llama ground truth-. No sabemos si una medida es buena o no porque no tenemos los verdaderos valores de la similitud melódica en humanos. Müllensiefen y Frieler suplieron esa deficiencia a través de sus experimentos. Con los resultados obtenidos pudieron comparar las distintas medidas de similitud que hay en la bibliografía y, finalmente, concluir cuál es la que más se acerca a la medida de similitud humana. 2. Medidas sobre vectores En esta sección definiremos una de las medidas sobre vectores más habituales: la correlación. No debe confundirse una medida sobre vectores con una medida vectorial; este último concepto pertenece al campo de la teoría de la medida. Dados dos vectores, u, v, de ℜn, queremos definir una medida que cumpla las propiedades de medida de similitud enunciadas en el primer artículo de esta serie. En nuestro contexto es habitual tomar vectores producidos por las transformaciones descritas en el artículo anterior de esta serie (las transformaciones de altura y ritmo más las medidas simbólicas) y, aplicando una medida sobre los vectores, obtener a su vez una medida de similitud. La forma más común de llevar a cabo esto es la correlación. La correlación mide el grado de dependencia entre dos vectores y aquí se usa para relacionar el grado de similitud melódica con esa dependencia. Dados dos vectores de n dimensiones, u = (u1,…,un) y v = (v1,…,vn), definimos la correlación como: Nótese que r(u,v) ∈ [-1, 1] y que, por tanto, no cumple los requisitos para ser medida de similitud (ser una función no negativa). Para solucionar esta situación se puede redefinir r(u,v) estableciendo que todos los valores negativos se asignen al 0. No en todos los contextos esta es la opción más adecuada, pero para nuestros propósitos basta. Sin embargo, esta medida tampoco cumple las propiedades de invariancia respecto a la transposición por altura, duración y cambio de tempo. De nuevo, se puede adaptar la medida r(u,v) para que lo cumpla. Por ejemplo, la invariancia respecto a la altura se consigue restando la altura media de la melodía. De manera similar se puede conseguir la invariancia respecto a la duración. Otro punto delicado es el de la longitud de los vectores. La correlación solo está definida para vectores de igual dimensión. En la práctica, en la inmensa mayoría de los casos las melodías no tienen la misma longitud. De nuevo, hay varias maneras de solucionar este escollo. Supongamos que m1 y m2 son dos soluciones con longitudes respectivas ∣m1∣≥∣m2∣. Una solución muy usada es considerar todas las melodías consecutivas de m1 que tienen longitud ∣m2∣ y calcular la correlación de esas dos la melodías. La medida de similitud se toma como el máximo de entre las ∣m1∣-∣m2∣ + 1 medidas parciales de correlación. En el trabajo de Müllensiefen y Frieler usaron la correlación entre todas las transformaciones de altura, rítmicas y medidas simbólicas que se han descrito en los artículos de esta serie y otras más. 3. Medidas armónicas Krumhansl y Kessler ([Kru90] y [KK82]) llevaron a cabo experimentos con sujetos para establecer con precisión una jerarquía entre los grados de la escala. Fijada una tonalidad base y un modo, dedujeron de los resultados de sus experimentos la importancia de cada grado de la escala temperada con respecto a la tonalidad base. Obtuvieron dos tablas, que se muestran abajo, con dos vectores de tonalidades, uno por cada modo. El vector TM es para el modo mayor y Tm para el modo menor. TM 6,33 2,23 3,48 2,33 4,38 4,09 2,52 5,19 2,39 3,66 2,29 2,88 Tm 6,33 2,68 3,52 5,38 2.60 3,53 2,54 4,75 3,98 2,69 3,34 3,17 Tabla 1: Los vectores de tonalidad de Krumhansl. Obsérvese que en el modo mayor los grados más relevantes de mayor a menor son la tónica, la dominante, la subdominante y la mediante (el tercer grado) y luego el resto de los tonos. En el modo menor, la clasificación empieza por la tónica, y sigue por la mediante, la dominante, la superdominante y después el resto de los grados. Posteriormente, Toiviainen y Krumhansl generalizaron este modelo para explicar los cambios de tonalidad que se producen a lo largo de una pieza; véase [TK03]. Volvamos una vez más al ejemplo de las variaciones K. 265 de Mozart. En la figura 1 tenemos los cinco primeros compases. Figura 1: El proceso de construcción de una medida de similitud. Calculamos su medida tonal m usando los pesos de los vectores TM (el tema está en modo mayor): m =  6,33 ⋅ 2 + 5,19 ⋅ 2 + 3, 66 ⋅ 2 + 5,19 ⋅ 2 + 4,09 ⋅ = 102, 32 Hay varias maneras de calcular medidas de similitud basadas en la tonalidad. Una de ellas -bastante adaptada a la música occidental- es la de calcular para cada compás la tonalidad de mayor valor. Para una pieza dada eso da una cadena de tonalidades. El modo de comparar dos piezas dadas es a través de la distancia de edición aplicada a las cadenas de tonalidad. También se pueden diseñar medidas de similitud basadas en la correlación de medidas de tonalidad. Consulte el lector interesado la sección 8.2.7 de [MF04]. 4. La validación perceptual Para estudiar la peliaguda cuestión de la validación perceptual Müllensiefen y Frieler llevaron a cabo varios experimentos, los cuales describimos a continuación. A partir de esos experimentos determinaron qué combinación de distancias/medidas y con qué pesos se aproximaban mejor a la percepción humana de la similitud melódica. 4.1. Los experimentos Müllensiefen y Frieler impusieron dos condiciones necesarias para seleccionar a los sujetos de sus experimentos: Su evaluación de la similitud debía ser consistente en el tiempo. Tenía que reconocer melodías idénticas con un alto valor de similitud (recuérdese que estamos trabajando en el espacio de las melodías módulo la transposición de alturas, duración y cambio de tempo). Tras unos cuantos experimentos preliminares, decidieron eliminar a aquellos sujetos sin formación musical. Su evaluación de la similitud era demasiado inestable en el tiempo o inconsistente con respecto a melodías muy similares. Estos sujetos muestran una tendencia a evaluar en función de factores que no son estrictamente musicales, a veces tan alejados de la música como la posición de una pieza dada en el orden de presentación o la duración del experimento. Müllensiefen y Frieler escogieron 82 estudiantes de la Universidad de Hamburgo; tras las pruebas previas para determinar su consistencia musical solo quedaron 23. Estas pruebas se llevaron a lo largo de varias semanas. Los 23 sujetos eran estudiantes de musicología con una media de 12 años de práctica instrumental. Creo que la dificultad en encontrar sujetos válidos para los experimentos da una idea de lo complejo que es el problema de evaluar la similitud melódica. Respecto al material de los experimentos, los autores prepararon 14 melodías tomadas de un corpus de melodías de música popular occidental. Por ejemplo, tomaron As long as you love me, de los Back Street Boys, o From Me to You, de los Beatles. Las melodías se escogieron acorde a los siguientes criterios: Cada melodía debía tener entre al menos tres frases diferentes, descontando repeticiones. Cada melodía debía tener al menos dos motivos distintos. No debían ser conocidas por los sujetos. Debían ser de carácter popular. Una vez construido el corpus, se procedió a variar las melodías. En la figura 2 tenemos un ejemplo del corpus; se trata de Wonderland, del grupo Passion Fruit. Se puede comprobar cómo hay dos motivos en la partitura. Figura 2: Melodía original: Wonderland, del grupo Passion Fruit. En la figura 3 se ve una de las variaciones de esta pieza. Se puede apreciar cómo se han eliminado las síncopas entre los compases 1 y 2 y 3 y 4 (pero se han introducido otras en diferentes sitios); además, en el comienzo de la segunda semifrase se ha cambiado la nota fa por la nota la, lo cual cambia la dirección del movimiento melódico. La bajada por grados conjuntos del compás 7 se ha cambiado por una bordadura. En el final del fragmento, la bajada melódica de si bemol a fa se ha sustituido por una subida de la bemol a do. Los círculos muestran dónde tienen lugar esos cambios. Figura 3: Variación de la melodía Wonderland, del grupo Passion Fruit. Estos son los tipos de cambio que introdujeron los autores para variar el corpus. De las 14 melodías originales extrajeron 84 variaciones. Los tipos de error los diseñaron acorde a la bibliografía sobre memoria de errores para melodías (véase [MB02], [Pau02]). Los cinco tipos de errores que definieron para los experimentos fueron: errores rítmicos, errores en las alturas, errores de altura que cambian el contorno melódico, errores en el orden de las frases musicales y errores de modulación. Los experimentos que realizaron Müllensiefen y Frieler, como decimos, son complejos. Los detalles son bastante técnicos y detallarlos aquí haría este artículo farragoso; no obstante, el lector interesado los puede encontrar en el artículo de estos autores [MF04]. 4.2. Resultados Una vez que se concluyeron los experimentos, se tenía un conjunto de medidas de similitud entre todas las melodías dadas por los sujetos. Estas medidas se compararon una a una con cerca de 30 medidas algorítmicas (la mayor parte se han descrito en esta serie de artículos). La forma de comparar ambos conjuntos de medidas, los dados por los sujetos y los algorítmicos, fue por medio de la correlación. Como dijimos anteriormente, la combinación lineal de medidas de similitud da asimismo una medida de similitud. La correlación arrojó como mejor distancia de similitud la siguiente combinación: σ =  3,355 ⋅ DEPST  + 2,852 ⋅ NGC donde DEPST es la distancia de edición ponderada sin transformación y NGC es la distancia n-gramas con la medida del recuento de distintos. Los datos técnicos son estos: r = 0, 911, R2 = 0, 83, R2 corregido = 0, 826. Sin contemplar combinaciones entre ellas, las mejores medidas fueron la medida qbh de Fraunhofer, la distancia DEPST, la distancia NGC, correlación armónica con distancia de edición y distancia de edición sobre ritmos con borrosidad. 5. Conclusiones En esta serie de artículos hemos revisado el concepto de distancia matemática en sí misma (en el primer artículo), y en conexión con un problema musical, el de la similitud melódica. En el artículo segundo examinamos una serie de transformaciones que conducían a la definición de distancias algorítmico-matemáticas de similitud melódica. En este último artículo hemos revisado el trabajo que hicieron Müllensiefen y Frieler para validar perceptualmente las medidas/distancias de similitud. Su estudio dio lugar a una combinación de medidas, una de edición y otra de n-gramas, como la medida que mejor aproxima la medida perceptual obtenida en sus experimentos. Bibliografía [KK82] C. L. Krumhansl and E. J. Kessler. Tracing the dynamic changes in perceived tonal organization in a spatial representation of musical keys. Psychological Review, 89:334–368, 1982. [Kru90] C. L. Krumhansl. Cognitive Foundations of Musical Pitch. Oxford University Press, New York, 1990. [MB02] C. Meek and W. Birmingham. Johnny can’t sing: A comprehensive error model for sung music queries. In International Symposium on Music Information Retrieval, pages 124–132, 2002. [MF04] D. Mullensiefen and K. Frieler. Cognitive adequacy in the measurement of melodic similarity: Algorithmic vs. human judgments. Computing in Musicology, 13:147–176, 2004. [Pau02] S. Pauws. Cuby hum: A fully operational query-by-humming system. In International Symposium on Music Information Retrieval, pages 187–196, 2002. [TK03] P. Toiviainen and C. L. Krumhansl. Measuring and modeling real-time responses to music: the dynamics of tonality induction. Perception, 32(6):741–766, 2003.

Martes, 05 de Julio de 2011 | Imprimir | PDF |  Correo electrónico

105. 24. (Abril 2011) Flamenco: elementos para la transcripción. Del cante y de la guitarra

De nuevo tenemos un artículo del etnomusicólogo. Esta vez se nos presenta el problema de la transcripción en el cante y la guitarra y cómo medir la distancia entre dos líneas melódicas. El artículo toca cuestiones musicales que tienen trasfondo matemático y que como apasionados de ambos campos disfrutamos con profundo deleite. Recordemos que Philippe Donnier es doctor en Etnomusicología por la Universidad París X e ingeniero superior por la École Supérieure de Physique et Chimie de Paris (ESPCI). Lleva dedicado al estudio del flamenco desde hace más de 30 años, aparte, claro está, de su actividad como músico flamenco. Es un placer tenerlo una vez más entre nosotros. Francisco Gómez Martín Flamenco: elementos para la transcripción Del cante y de la guitarra Philippe Donnier, doctor en etnomusicología Introducción La cultura musical clásica sigue siendo la referencia para la transcripción de cualquier tipo de música. La educación musical impartida en los conservatorios trata casi exclusivamente de músicas cuya estructura rítmica esta construida a partir de una pulsación isométrica organizada en periodos rítmicos más o menos sencillos. La desaparición completa de la transmisión oral en los ámbitos clásicos hace imperativa la necesidad de poder "leer" música sin referente auditivo previo. Esta lectura es factible únicamente cuando las relaciones entre valores temporales sucesivos son fracciones simples. Una evaluación rigurosa del tiempo es posible sólo cuando se puede recurrir a una marca consciente o inconsciente de pulsaciones de referencia. Estudios psicológicos han demostrado que, en ausencia de toda marca de referencia, la capacidad humana para evaluar las duraciones es pésima (Mc.Adams/Bigand 1994: 76-121). En el marco de la cultura clásica, no hay lectura posible en ausencia de pulso consciente o inconsciente. Estas observaciones suponen aparentemente unas consecuencias dramáticas para el etnomusicólogo. Fuera de las músicas de carácter métrico, no hay transcripción posible. Según esta conclusión, tampoco hubiera sido posible ningún sistema de escritura de los múltiples lenguajes humanos. ¿Cómo se puede resolver esta contradicción aparente? ¿A qué maestro se le ocurriría intentar enseñar a leer y escribir a un niño que no sepa previamente entender y hablar perfectamente su propio idioma? El dominio completo que tenemos de nuestro lenguaje nos hace pensar que leemos realmente lo que hay escrito. En realidad, es pura ilusión. Cada conjunto de signos que percibimos, y que hemos tardado largos años en aprender y memorizar, desencadena el recuerdo y la activación de la versiones orales de las palabras correspondientes. Según el contexto, el origen geográfico, la cultura... y el estado de ánimo de cada uno, el mismo texto será interpretado de múltiples maneras, todas conformes con el sistema fonológico y el contenido semántico propio del idioma hablado, si los lectores son nativos o pertinentemente aculturados. La pobreza expresiva de los lectores sintéticos disponibles en los ordenadores actuales es una demostración de los límites de cualquier sistema de escritura utilizado sin posibilidad de recurrir a una amplia cultura previa y a una sensibilidad al contexto. Por tanto, no existe ningún dominio de la escritura ni de la lectura sin un aprendizaje previo de la lengua correspondiente. El mismo conjunto de signos /papá/ (sistema único de fonemas) puede corresponder a dos emisiones vocales totalmente diferentes si el padre a cual se refiere se encuentra al lado del niño [papá] o en el cerro de enfrente [papaaaaaaa] (infinidad de variantes fonéticas). La semántica exige que el segundo [pa] sea algo más largo que el primero (relación de orden), la proporción entre las duraciones respectiva depende de la expresión que se le quiera dar. El ritmo del lenguaje hablado no radica en un sistema de proporciones fijas entre duraciones sucesivas sino en relaciones de orden (más o menos largo) mucho más flexibles. Podríamos hacer el mismo análisis para lo que se refiere a las inflexiones melódicas. Los sistemas de escritura tienen muy pocos recursos para regular la gestión expresiva y esta última es el fruto de una larga experiencia y de los parámetros emocionales y expresivos de cada uno. La cultura clásica ha olvidado los orígenes orales de la escritura hasta tal punto que se enseña a menudo a escribir y a leer música antes de saber practicarla. Tal sistema puede funcionar únicamente si se ponen vallas a los márgenes expresivos. La pulsación puede cambiar de velocidad, pero nunca de forma caótica; en tal caso, dejaría de ser una pulsación perceptible. Sólo estas limitaciones consentidas autorizan una lectura y una escritura en la casi ausencia de referentes orales previos. Muchas músicas de tradición oral siguen un sistema de pulsaciones regulares y son susceptibles de ser transcritas por medio de la notación clásica. La estructura temporal de otras muchas recuerdan el lenguaje hablado. En este último caso, no se puede pretender transcribirlas con el sistema clásico. Las numerosas transcripciones de concienzudos folkloristas están aquí para demostrar el resultado desastroso de cualquier interpretación realizada a partir de estas partituras en ausencia de todo referente oral previo. ¿Quiere decir por tanto que no hay transcripción posible? Si pretendemos utilizar estas transcripciones como se utilizan las clásicas, por supuesto que no. El empeño de los folkloristas proviene de una ceguera total delante de las culturas de tradición oral. Aunque parezca una perogrullada decirlo, no se puede pretender hacer un estudio pertinente y/o querer transmitir algo de las culturas orales haciendo la economía de cualquier proceso oral. Sugerencias para representaciones gráficas del cante flamenco Si la referencia a los sistemas de escritura de los lenguajes hablados nos han permitido una reflexión crítica en cuanto a una utilización a ciegas del sistema clásico, tampoco tenemos que caer en la trampa de querer adaptar el sistema fonémico al lenguaje musical. Tenemos que adoptar una definición más amplia de lo que puede ser sistemas de escritura pertinentes y utilizables. Cualquier representación gráfica de un fragmento de música x dirigida a un utilizador especifico que permita a este utilizador reconocer el fragmento x será considerado pertinente. Esta exigencia restringida a la identificación sin necesidad de interpretación corresponde a una transcripción con fines descriptivos. Descartamos aquí todo fin prescriptivo, siendo contradictorio con la esencia misma de toda tradición oral. Si se puede admitir la elaboración de materiales escritos que hacen más fácil el análisis y el entendimiento de una música oral, pretender enseñar músicas de tradición oral por medio de documentos escritos sería totalmente contradictorio. Aceptada esta definición, podemos adoptar varios niveles de escritura en función de la meta perseguida y del utilizador a quien se dirige la transcripción. Tomaremos como ejemplo la primera frase de un cante por Malagueña conocido como "de La Trini" Nivel 1 Los programas de sonidos actuales permiten obtener representaciones de la frecuencia en función del tiempo. Estos sonogramas proporcionan una información detallada sobre toda las inflexiones de voz y la constitución armónica de la voz analizada (fig.1). Fig. 1: Sonagrama En el fichero FOSFORITO (fichero Director comprimido), que se puede descargar pinchando en el enlace, se tiene una animación de la figura de arriba. Para una mejor comprensión de cómo se puede extraer información a partir de los sonogramas, en el fichero CAITA (fichero Director comprimido), hay otra animación, esta vez de La Caita, en la que se aísla el segundo armónico. Nivel 2 Se seleccionan varias interpretaciones del mismo cante, el criterio de identidad debiendo ser el de uno o varios aficionados competentes. Partiendo de los sonagramas, se realizan transcripciones gráficas proporcionales al tiempo real de cada interpretación (fig.2). Fig. 2: Transcripciones de nivel 2 El flujo continuo de la voz ha sido sustituido por una serie discontinua de "notas" más o menos largas. La comparación de las cuatro versiones pone en evidencia varias características: - Al unir todas las notas y al descartar algunos movimientos de un grado ascendente o descendente, aparecen trayectorias melódicas idénticas si despreciamos el parámetro tiempo (fig.3). Fig. 3: Trayectorias melódicas - El número de notas en cada segmento de la trayectoria es variable de una interpretación a la otra. - La duración de cada segmento melódico es también muy variable. - La cuatro versiones están identificadas como Malagueña "de La Trini". Estas observaciones nos llevan a concluir que la trayectoria melódica es el único rasgo que permite la identificación, siendo los valores de tiempo bastante arbitrarios. Un estudio más fino muestra que existe una cierta relación de orden entre la duraciones de cada segmento melódico (Donnier 1996:262-264). Nivel 3 En el lenguaje hablado, la variabilidad de las duraciones de cada sílaba y el conocimiento oral de complejas leyes de la elocución han llevado a unos sistemas de escritura que prescinden completamente o parcialmente (lenguas acentuadas como el castellano) de indicaciones de duración. Lo mismo proponemos para la transcripción del cante flamenco. Nuestra experiencia personal a lo largo de numerosos seminarios de iniciación al conocimiento del cante flamenco confirman la ausencia de pulsación claramente perceptible y la dificultad consiguiente para evaluar las duraciones respectivas de cada nota. Al ser muy difícil cambiar el significado de los signos utilizados en la escritura clásica, hemos ideado un sistema original partiendo de las escrituras neumáticas usadas para transcribir el canto gregoriano. Para la escritura de los neumas, nos hemos guiado por el estudio paleográfico realizado por Don Eugene Cardine (Cardine 1970), teniendo en cuenta en cuenta varios parámetros: - establecer una diferencia gráfica clara entre partes silábicas y partes melismáticas, - conservar la posibilidad de marcar los contrastes de duración más destacados, - evitar la creación de signos nuevos cuando signos existentes ofrecen unas soluciones satisfactorias, - conservar la precisión melódica del pentagrama clásico. Notas silábicas Adoptamos neumas parecidos a los que se utilizan en la notación gregoriana moderna, conservamos tres valores de tiempo. Grupos de notas melismáticas Para establecer un contraste claro entre segmentos silábicos y segmentos melismáticos, hemos adoptado signo inspirados de la escritura neumática antigua. El uso de puntos en el pentagrama permite simplificar la escritura tradicional. Para señalar una nota sensiblemente más larga dentro de un grupo neumático, se utiliza una marca (episema). Cuando es posible, escribimos los neumas melismáticos en rojo, lo que ofrece un contraste mayor y un atractivo estético indudable (fig.4). Figura 4: Ejemplo de transcripción neumática de una soleá de Alcalá cantada por Manuel Torre. El uso de este sistema presenta varias ventajas: - La labor de transcripción es mucho más rápida que con el sistema convencional, al ahorrar las dudas constantes sobre la elección de un supuesto compás y sobre la duración respectiva de cada nota. - La transcripciones se resisten a todo intento de repentización, evitando así cualquier interpretación folklorizada. - La lectura es mucho más asequible a los no músicos o malos lectores (que representan una mayoría dentro del público interesado por las músicas tradicionales). Hemos podido comprobar este hecho tanto a lo largo de numerosos seminarios de formación como en los medios aficionados al flamenco. - El trazo continuo de los grupos neumáticos se asemeja a la realidad de un flujo melismático horizontal mientras que la escritura clásica presenta notas sueltas relacionadas por plicas verticales que rompen la continuidad melódica. Aunque no se tenga cultura previa, se puede seguir perfectamente la transcripción mientras se escucha la versión correspondiente. Una vez adquirida la cultura, la escritura neumática da la información suficiente para reconocer el cante. Suponiendo que un cantaor se haya iniciado a este sistema, pudiera interpretar el cante libremente sin las trabas que supone una precisión rítmica fuera de lugar en el caso del cante flamenco. Nivel 4 El nivel 3 tiene todavía un carácter "fonético". Las inflexiones melódicas visiblea en el nivel 1 y la precisión de las duraciones presentes todavía en el nivel 2 han desaparecido pero todas las "notas" de la versión transcrita están representadas. Muchas notas son variantes personales o estéticas que tienden a enturbiar la percepción de la estructura común a todas las versiones, armazón que cumple una función semántica al permitir la identificación del cante interpretado. Para que aparezcan los elementos comunes a todas la versiones de un mismo cante, hay que practicar nuevas reducciones en la representación. Llegaremos así a un nivel "fonémico", el único que permite un entendimiento claro del sistema de oposiciones entre formas melódicas consideradas como distintas en la cultura autóctona. Un análisis de tipo fonémico supone que todos los ejemplares reales que forman una clase de equivalencia según los criterios autóctonos están representado por un conjunto de caracteres o rasgos idénticos. El número de rasgos seleccionados tiene que ser suficiente para diferenciar (oponer) todas las clases de equivalencia del corpus elegido. La realización de transcripciones sinópticas pone en evidencia los elementos comunes a distintas versiones de un mismo cante. Después de haber comparado de cinco a diez versiones de más de cuarenta formas melódicas distintas (Donnier 1996:250-526), aparecen unas cuantas características comunes a la mayoría de los cantes flamencos: - La mayoría de los movimientos melódicos se realizan por grado conjunto. - Existe un núcleo melódico estable común a todas las versiones. Este núcleo esta constituido por pequeños elementos que llamamos genes melódicos. Estos genes aparecen siempre en el mismo orden pero pueden estar separados por segmentos específicos propios de cada cantaor (parte de cuales pueden ser comunes a todo una escuela cantaora). Esta estructura permite un verdadero estudio genético del cante. Los genes estables comunes a todas la versiones definirían los distintos genotipos flamencos, cada cantaor siendo definido por su propio fenotipo. Ciertas versiones mutantes han resistido la prueba del tiempo, enriqueciendo así el material genético flamenco. Existe también la posibilidad de cruces entre cante, fuertemente rechazados por la tendencia eugenésica de los flamencólogos oficiales. Las modernas técnicas electrónicas de clonación permiten la reproducción ad infinitum del material tradicional, eliminando así toda posibilidad de evolución. Elementos rebeldes han recurrido a la exogamia, contrayendo uniones prohibidas con hijos de la bossa nova, del rock o del jazz, poniendo así fin a la gran época añorada de un supuesto flamenco puro... El fin analítico perseguido en este último nivel es poner en evidencia de manera rapidamente perceptible las oposiciones entre los diferentes formas melódicas. Para conseguir este resultado, seguiremos un proceso de reducción en varias etapas. Etapa1 Extracción del esqueleto melódico constituido por la serie de los genes concatenados. Para obtener representaciones sintéticas que permiten comparar rapidamente varias formas melódicas, hemos adoptado un representación geométrica. Se adapta el pentagrama clásico representando los doce semitonos de la escala temperada (fig.5), la línea que corresponde a la tónica del modo usado se resalta en rojo o en gris (tono de Mi en modo de Mi o modo flamenco1, como lo llamaremos de ahora en adelante, en el ejemplo de la figura 5). Fig. 5: Representación geométrica A toda subida o bajada por grados conjuntos dentro del modo corresponden triángulos con pendiente a 45 grados. Los saltos por grados disjuntos aparecen con triángulos de pendiente acentuada. La alteraciones accidentales provocan irregularidades en la trayectoria melódica, se ponen en evidencia con triángulos finos. La figura 6 muestra el proceso de extracción del patrón melódico común a siete versiones de una Soleá conocida como "de La Serneta". Fig. 6: Transcripciones sinópticas de siete versiones de la Solé de La Serneta. La primera transformación consiste en cambiar la escritura clásica por la representación triangular (fig. 7a). Las notas repetidas aparecen como un círculo (una repetición) o como óvalo (varias repeticiones). Etapa 2 Se suprimen las notas repetidas (fig. 7b) Etapa 3 Se suprimen las repeticiones de movimientos de un grado (fig. 7c) Etapa 4 Se suprimen los movimientos de ida y vuelta de un grado (fig.7d). Se elige la etapa de reducción que se adapta mejor al nivel de precisión descriptiva deseado. Fig. 7: Etapas de reducción del patrón melódico de la Soleá de La Serneta Estudio comparativo de distintos tipos melódicos de un mismo palo El repertorio del cante flamenco esta subdividido en palos, todos los tipos melódicos de un mismo palo tienen en común el mismo toque de guitarra. Cada toque esta definido por un tipo de ciclo rítmico o compás y por el tono en el cual se toca. La noción de tono en la guitarra flamenca difiere de la noción clásica. Un tono flamenco engloba el modo (mayor, menor o flamenco) asociado al conjunto de posturas digitales. La altura absoluta no es pertinente pues la cadencia andaluza que acaba en un acorde de La mayor tocada sin cejilla (Rem, Do7, Sib, La en altura absoluto) y el mismo conjunto de posturas (conjunto de posiciones digitales) tocado con la cejilla colocada al quinto traste (Solm, Fa7, Mib, Re en altura absoluta) definirían en ambos casos el tono por medio porque "suenan igual" salvando la diferencia de altura. La cadencia andaluza acabada en acorde de Mi mayor (Lam, Sol, Fa, Mi en altura absoluta) transportada con la cejilla al quinto traste se transforma en Rem, Do, Sib, La en altura aboluta. No obstante "suena igual" (en altura relativa) que la cadencia Lam, Sol, Fa, Mi, al tener el mismo sistema de digitación y, por tanto, las misma inversiones para cada acorde de la serie. Este segundo sistema de digitación define el tono por arriba. Así, al mismo compás de Seguiriya corresponden tres toques según el modo y el tono flamenco elegido: - toque de Seguiriya en modo flamenco interpretado en tono por medio, - toque de Serrana en modo andaluz por arriba, - toque de Cabal en modo mayor de Mi (posición de referencia sin cejilla). Una vez definido el toque de Seguiriya o de Solá, una gran variedad de tipos melódicos "por Seguiriya" o "por Soleá" se amoldan a un mismo tipo de acompañamiento bastante estereotipado. Cada tipo melódico se identifica por un nombre específico que recuerda el origen geográfico o el supuesto creador (Soleá de La Serneta; de Triana; de Juaniquin..., Seguiriya de Los Puertos, de Cagancho, de Manuel Molina ...). Bajo unas apariencias de organizacián anárquica y gran libertad interpretativa, el cante flamenco y su acompañamiento a la guitarra están sujeto a unas patrones rítmico-melódicos muy estructurados. Una escucha pertinente del flamenco supone la identificación del toque y del tipo melódico del cante interpretado. Todo aficionado que se precie reconoce cada toque y un sinfín de variantes melódica, cruces e influencias interpretativas. Los esquemas reducidos que proponemos pueden ser de una gran ayuda para quien pretende acercarse rapidamente a la cultura flamenca. Fig. 8: Patrones melódicos reducidos de cinco tipos melódicos de cante por Soleá En el fichero LA SERNETA (fichero Director comprimido) se encuentra una animación que ayuda a entender los cinco tipos melódicos de esta soleá. La figura 8 permite la comparación de los patrones melódicos reducidos de cinco tipos melódicos por Soleá. Relaciones cante/guitarra A la hora de describir un fenómeno, muchos problemas surgen por no haber elegido el nivel de precisión adecuado. En astronomía, no es pertinente tener en cuenta la existencia de montañas y mares en la tierra. Los procesos químicos están interesados únicamente por las capas electrónicas externas y el estudio de la mecánica física no tiene en cuenta la estructura química de los móviles estudiados. Para entender algo del funcionamiento del cante flamenco, hay tener una visión bastante lejana de las formas melódicas. Un análisis "microscópico" o demasiado "fonético" hace perder de vista la grande organizaciones que rigen el desarrollo del cante y de su acompañamiento. No tenemos aquí espacio para entrar en muchos detalles descriptivos, pero unos esquemas simples permitirán al lector hacerse una idea del tipo de mecanismo que rige las interpretaciones flamencas. Para simplificar la descripción, nos atendremos a los cante dichos "a compás" que van acompañados por ciclos rítmicos periódicos. Para los cantes dichos "libres" la guitarra se limita a marcar los fines de cada frase por una cadencia melódica sin compás definido. Cada compás puede representarse por un rectángulo con zonas contrastadas, el contraste corresponde a variaciones de la textura sonora (rasgueos, golpes en la tapa, arpegios, acentos marcados etc.) y/o de estructura armónica. Una vez definida la forma melódica del cante, se puede prescindir del pentagrama, los que interesa ahora siendo la relaciones temporales entre cante y guitarra. El patrón melódico reducido de cada frase pone en evidencia notas características comunes a todas las versiones estudiadas. Todos los ciclos de acompañamientos son iguales (12 en el caso de la Soleá), una vez reducidos bajo forma de esquema rectangulares. En cuanto al cante, todas las versiones tienen un patrón melódico común pero la realización material de este patrón puede deformarse y desplazarse a lo largo de los compases de guitarra de una versión a la otra. La figura 9 muestra el grado de libertad del cante al comparar siete versiones de una Soleá de La Serneta. Fig. 9: Elasticidad del cante En el fichero RELACIONES CANTE/GUITARRA (fichero Director comprimido) se encuentra una animación que ayuda a entender los cinco tipos melódicos de esta soleá. Este análisis desvela una característica tan original como interesante: el cante es de naturaleza no acompasada y se desarrolla en el tiempo como una entidad deformable con un cierto grado de elasticidad. No obstante, la guitarra crea una suerte de "campo magnético-musical". Notas características del patrón melódico parecen como atraídas por zonas correspondientes del compás de guitarra (fig.10). Fig. 10: Acumulación de las notas de principio y fin sobre ciertas zonas del compás de guitarra. El fenómeno es muy parecido a lo que ocurre con las trayectorias electrónicas. Al medir posiciones sucesivas de un mismo electrón en relación con el núcleo del átomo, parecen disfrutar de una gran libertad. Sólo después de millones de mediciones, aparece una "nube" o orbital constituida por el conjunto de todas las posiciones sucesivas. Esta orbital define una porción de espacio que "atrae" al electrón y representaba el conjunto de las posiciones más probables, aunque en cada momento, el electrón puede, sólo aparentemente, situarse donde "le apetezca". Podemos traducir este último párrafo en términos de cante flamenco: Las posiciones sucesivas del patrón melódico parece disfrutar de una gran libertad. Después de haber medido muchas versiones, aparecen zonas del compás de guitarra a la proximidad de cuales se acumulan notas características del patrón melódico del cante. Estas zonas definen puntos del compás que "atraen" a las notas correspondientes y representan sus posiciones respectivas más probables. Estas notas pueden, sólo aparentemente, situarse donde "le apetezca". Como en toda metáfora, existen diferencias notables. El compás de guitarra disfruta de una cierta elasticidad, mayor o menor según los toques. Esto permite al guitarrista aminorar ciertos desfases extremos. En caso de gran deformación del cante, se puede añadir un ciclo de compás. Nuestra experiencia del acompañamiento confirma los resultados de este análisis formal. El cantaor tiene evidentemente un esquema melódico guía a partir del cual desarrolla cada versión. La inercia de la voz y el impulso emocional de la interpretación actúan como una fuerza centrífuga que tiende a provocar un desfase entre el cante en relación con el compás de guitarra. A su vez el compás de guitarra actúa como un conjunto de zonas magnéticas que atraen a ciertas zonas del cante. Este sistema dinámico puede funcionar de múltiples maneras según las características de cada interprete. La realización de un compás muy contrastado aumenta el magnetismo y permite atraer al cantaor aficionado cuya fuerza centrifuga es demasiado fuerte. En cuanto al cantaor profesional, el magnetismo de su cante es lo suficientemente fuerte parea no necesitar de un compás exageradamente contrastado para centrar correctamente su cante. A mi parecer, el tan misterioso Duende aparece surge cuando se establece un tenso equilibrio entre fuerza centrífuga del cantaor y magnetismo centrípeto del guitarrista. Esto sin contar con los efectos relativista que conllevan una deformación del espacio temporal cuando la energía musical alcanza grandes niveles de densidad... Conclusión Después de este breve y evidentemente incompleto análisis, destacaremos los puntos que nos parecen más importante en cuanto a sus consecuencias sobre posibles aplicaciones a otras músicas. Un sistema semiológico dado se puede aplicar únicamente a la realidad para cual se ha forjado. Aplicar el sistema clásico a cualquier música tradicional expone a muchos errores. Todo sistema de escritura es una mera huella de una realidad viva, única referencia tangible y pertinente. No existen transcripciones objetivas, sino transcripciones realizadas con un objetivo claramente definido. A cada objetivo corresponde uno o varios tipos de representación. Dentro de los objetivos, se tiene que tener en cuenta el tipo los conocimientos culturales y técnicos del público, al cual van dirigidas las transcripciones. El manejo pertinente de transcripciones de músicas de tradición oral no se puede imaginar sin aculturación previa. Esta aculturación puede ir desde simples ejemplos musicales cortos acompañando las transcripciones hasta la adquisición de un conocimiento y/o práctica experta de la tradición estudiada. En este último caso, la escritura sirve para activar esquemas o variaciones de esquemas ya conocidos. De poco sirven las transcripciones de bajo nivel de tipo fonético para la comprensión de un sistema musical, constituyen sólo un primer paso. Esta comprensión supone la elaboración de representaciones de alto nivel basada en análisis paradigmáticos y en la puesta en evidencia de los mecanismos de construcción y de interpretación de la música estudiada. La aparición de las reciente técnicas multi-media pueden ofrecer un nuevo puente entre la oralidad y la cultura escrita. La potencialidades de estos medios queda todavía por descubrir y suponen un reto para la jóvenes generaciones de etnomusicólogos. Nota 1 Hay que distinguir escalas y modo. Todo modo se genera a partir de una sistema escalar de referencia pero los tratamientos de la misma escala de Mi en músicas árabe, sefardí, gregoriana o andaluza son sensiblemente diferentes. Un modo se define tanto por el sistema escalar generador como por las formas características de organizarlo. Hablaremos pues de modo flamenco. Bibliografía AROM, S. 1985. Polyphonies et polyrythmies instrumentales d'Afrique centrale. Paris: SELAF CARDINE, E.. 1970. 'Sémiologie grégorienne'. Etudes Grégoriennes. Abbaye Saint Pierre de Solesmes, Sablé sur Sarthe,Tome XI. CHAULLEY, J. 1967.La musique et le signe. Lausanne. Editions Rencontre. DONNIER, Ph. 1996. Flamenco, structures temporelles et processus d'improvisation. Tesis doctoral Université Paris X. Nanterre. FRAISSE, P. 1974.La psychologie du rythme. Paris: PUF. McADAMS, S., E. BIGAN. 1994. Penser les sons, psychologie cognitive de l'audition. Paris: PUF.

Miércoles, 13 de Abril de 2011 | Imprimir | PDF |  Correo electrónico

106. 26. (Junio 2011) Distancia y similitud musical - II

1. Introducción En el primer artículo de esta serie revisamos el concepto matemático de distancia y definimos formalmente la medida de similitud melódica; además, ilustramos estos conceptos con algunos ejemplos musicales. En este segundo artículo sobre la distancia matemática y la similitud melódica vamos a describir un buen número de medidas de similitud, las cuales agruparemos por familias dependiendo de su propósito y filosofía. “El discurso musical progresa a través de múltiples transformaciones de su material musical”, decíamos en otra ocasión [Góm11]. En particular, en el ámbito melódico esa variación es fundamental. La trascendencia de la similitud melódica ha sido, y es, tal que numerosas disciplinas se han ocupado intensivamente de su estudio: En etnomusicología, por ejemplo, para entender la lógica musical, para evaluar los estilos y sus características, para conocer los criterios de improvisación. Véanse [BL51], [See66], [Hol10]. En análisis musical, para construir modelos tanto teóricos como computacionales. Véanse [LJ83], [Mey73], [CIR98], [Typ07]. En la resolución de conflictos de propiedad intelectual [Cro98]. En tecnología musical, para aplicar los modelos obtenidos tras el correspondiente análisis. Véanse [MS90], [HSF98], [Pam06], [Hol10]. En psicología de la música, para comprender mejor el hecho musical, para aportar conocimiento a un análisis integral de la música. Véanse [Sch99], [HE01], [MM01], [HE02], [HCR03]. Respecto a otro tema relacionado, la similitud rítmica, véanse las referencias citadas en el artículo [Góm11] de esta sección del mes de marzo de 2011. 2. Representación de melodías Una melodía es un conjunto de notas que suenan en determinado orden y con determinadas duraciones. Esencialmente, una melodía es una combinación de alturas y ritmo. Las medidas de similitud se construyen a partir del siguiente proceso: Figura 1: El proceso de construcción de una medida de similitud. Obtención de la melodía. Esta puede venir descrita en formato audio, como un fichero de sonido de una grabación, o en formato simbólico, como un fichero midi o un fichero de partitura (Finale, Sibelius, etc.). Representación de melodías abstractas. Según los propósitos perseguidos, la melodía se representa de varias formas. Estas representaciones que extraen ciertas características de las melodías reales se llaman representaciones abstractas. Varían en función del propósito final. Por ejemplo, en el análisis de cantes a palo seco en el flamenco, se ignora la duración de las notas, puesto que son cantes sin pulso regular y con mucho rubato. Transformación de la melodía. La melodía abstracta sufre unas transformaciones que permiten el cálculo efectivo de la medida de similitud. Diseño de la medida de similitud. Inicialmente, la mayor parte de las medidas se concentraron en un aspecto de las melodía, el cual medían con más o menos precisión. Poco a poco se han ido diseñando medidas que cuantifican varios aspectos de la melodía. El principal problema es cómo ponderar todos esos aspectos de manera coherente. Es importante que la representación de las melodías cumpla las propiedades de invariancia que mencionamos en el primer artículo, esto es, invariancia por transposición de altura y tiempo más invariancia por cambio de tempo. Las melodías se suelen representar por una sucesión de pares (pn,tn), n = 1,…,N, donde pn representa la altura y tn las duraciones de cada nota. Esta representación obviamente no verifica las propiedades de invariancia. Se usan en su lugar dos representaciones diferentes, que sí respetan la invariancia: Para la altura se usa la representación por intervalo. En lugar de guardar las alturas absolutas, se anota el intervalo entre cada dos notas consecutivas In = pn+1 - pn. Para el ritmo se usa la representación IOI. Estas siglas vienen del inglés, inter-onset interval, o intervalo de duraciones relativas. Se calcula de manera similar al caso anterior, poniendo Tn = tn+1 - tn. En el caso del ritmo también se usa otro método de representación, que consiste en expresar las duraciones en función de la duración mínima de la melodía. Esto no siempre es posible en todas las músicas, aunque sí en la mayor parte de la música occidental. En las siguientes secciones del artículo describiremos las principales transformaciones melódicas que aparecen en las medidas de similitud. 3. Transformaciones de altura 3.1 Transformaciones de contorno Este tipo de transformaciones se basa en el hecho de que la sucesión exacta de alturas en una melodía no es siempre lo más importante, sino la dirección melódica. Los puntos de giro de la melodía, los puntos en que cambia la dirección melódica, es un hecho que tiene relevancia en la percepción de la melodía. Si se representa la melodía como una línea poligonal, los puntos de giro se corresponden con los extremos relativos. La representación recibe el nombre de contorno melódico. En la figura de abajo tenemos de nuevo el tema principal de las variaciones K. 265 Ah, vous dirai-je, Maman. La línea poligonal que aparece sobre la melodía es el contorno melódico. Figura 2: El contorno melódico. Para más información sobre los contornos melódicos véase el trabajo de Zhou y Kankanhalli [YK03]. 3.2 Transformaciones borrosas En muchas ocasiones la percepción de un estímulo no es totalmente nítida. Este tipo de transformaciones pretenden modelizar este hecho usando la lógica borrosa. La lógica borrosa usa un continuo de valores de verdad en el intervalo [0, 1]; consúltese [Hal03]. En este modelo los intervalos se acomodan en clases según la tabla siguiente: Clase Intervalos Nombre -4 < -7 Salto descendente grande -3 -7,-6,-5 Salto descendente -2 -4,-3 Paso descendente grande -1 -2,-1 Paso descendente 0 0 Unísono 1 1, 2 Paso ascendente 2 3, 4 Paso ascendente grande 3 5, 6, 7 Salto ascendente 4 > 7 Salto ascendente grande Tabla 1: Clasificación de los intervalos usando lógica borrosa. Los intervalos se cuentan por semitonos en la tabla. Para ilustrar este concepto, consideremos la melodía abstracta dada por la sucesión : la cual está extraída de los primeros ocho compases del tema principal de las variaciones K. 265 Ah, vous dirai-je, Maman; véase la figura 2. De esta representación eliminamos el ritmo, la segunda componente, y calculamos los intervalos consecutivos: Finalmente, calculamos la melodía borrosa (una vez que le aplicamos la clasificación por clases de la tabla 1): 3.3 Transformaciones usando la transformada de Fourier La transformada discreta de Fourier proporciona una buena descripción general de la forma del contorno melódico, especialmente si hay células melódicas repetidas. Tiene también la ventaja de la invariancia. Por ejemplo, la transformada discreta es invariante por cambios de escala. Sin embargo, dado que la transformada discreta de Fourier está pensada para señales periódicas (infinitas), hay ciertos efectos indeseables, el llamado efecto frontera, que hay que tener en cuenta. Véase [Sch99], páginas 303 a 306, para una discusión sobre la transformada discreta de Fourier y sus ventajas e inconvenientes. 4. Transformaciones rítmicas 4.1 Gaussificación La gaussificación de un ritmo consiste en representarlo como la combinación de lineal de distribuciones normales. Cada distribución normal tiene su media sobre cada nota del ritmo; las desviaciones son fijas e iguales para todas las normales. Si tn, n = 1,…,N, es la sucesión de tiempos de la melodía, la gaussificación g(t) es En la figura 3 tenemos un conocido ritmo, la clave son 3/2. Figura 3: El ritmo de la clave son. Si contamos el tiempo en semicorcheas de 0 a 15, las distribuciones normales en las notas ocurren en las posiciones 0, 3, 6, 10 y 12. Fijemos σ = 1 como desviación típica para todas esas distribuciones. Las medias de las normales serán las posiciones de las notas. La figura 4 muestra el gráfico de estas 5 distribuciones normales. Figura 4: Gaussificación de un ritmo. La gaussificación del ritmo entero es la función g(t) = ∑5i=1g i(t) 4.2 Transformaciones borrosas Al igual que las alturas, las duraciones también admiten un tratamiento vía la lógica borrosa. Las duraciones de una melodía se comparan con respecto a la duración d más frecuente en la melodía. Las clases de duraciones se obtienen tomando el cociente c entre el IOI Tn = tn+1 -tn y la duración d. Clase Cociente c Nombre 4 c > 3, 3 duración muy larga 3 1, 8 < c ≤ 3, 3 duración larga 2 0, 9 < c ≤ 1, 8 duración normal 1 0, 45 < c ≤ 0, 9 duración corta 0 c ≤ 0, 45 duración muy corta Tabla 2: Clasificación de las duraciones usando lógica borrosa. Esta clasificación no es la única posible y en la bibliografía se encuentran muchas más; véase la página 7 de [MF04]. 5. Medidas simbólicas Las medidas simbólicas consideran una melodía abstracta como una cadena de caracteres, esto es, como una sucesión finita de símbolos tomados de un alfabeto adecuado. Por ejemplo, la sucesión de alturas de una melodía se puede ver como una cadena de caracteres extraídos del alfabeto formado por el universo de frecuencias. El principal problema que aparece con las medidas simbólicas es que cuando las melodías tienen longitudes diferentes su manejo no es muy elegante y exigen modificaciones engorrosas. Las dos principales medidas simbólicas son la distancia de edición y los n-gramas. 5.1 Distancia de edición El enfoque de la distancia de edición requiere la existencia de ciertas operaciones definidas en las cadenas. Dadas dos cadenas de caracteres, esas operaciones permiten transformar una cadena en la otra. Las operaciones más comunes son inserción, borrado y sustitución. La distancia de edición es el mínimo número de operaciones que hay que realizar para transformar una cadena en la otra. Cada operación tiene un coste asociado y la distancia final es la suma de los costes. Calcular el mínimo de operaciones se puede hacer usando algoritmos basados en programación dinámica. Véase Mongeau y Sankoff [MS90] para una descripción de este tipo de medidas. Si de es una distancia de edición, entonces la expresión es una medida de similitud, donde ∣c1∣,∣c2∣ son las longitudes respectivas de las cadenas. Como ejemplo, consideremos las cadenas C1 = y C2 = . Asociaremos a las operaciones de inserción, borrado y sustitución el mismo coste, que será de una unidad. La distancia de edición de(C1,C2) es 3. Esta distancia corresponde a hacer las siguientes transformaciones: Sustitución de la nota do por re con coste 1: C1 = →. Borrado de la nota fa con coste 1: →. Inserción de la nota si con coste 1: → = C2. La medida de similitud es 5.2 n-gramas La definición de n-grama no puede ser más simple: un n-grama es una cadena de longitud n. Para definir una medida de similitud con n-gramas se estudia la distribución de los n-gramas, para distintos valores de n, en la cadena dada. Por ejemplo, podemos definir la llamada medida del recuento de elementos distintos. Si a y b son dos cadenas, designemos por an el conjunto de los n-gramas distintos en a (se define bn de manera similar). Entonces, la medida de recuento de distintos es Existen otras medidas asociadas a los n-gramas, tales como la medida de Ukkonen o de la suma común; véase la página 10 de [MF04]. 5.3 Conclusiones En este segundo artículo hemos examinado el proceso de construcción de una medida de similitud melódica. Empezamos por estudiar las representaciones abstractas de melodías y continuamos con una revisión de las principales transformaciones de altura, rítmicas, así como las medidas simbólicas. En el próximo artículo estudiaremos medidas de similitud asociadas a las armonía y medidas vectoriales de similitud. Completaremos la serie sobre distancias y similitud melódica con la descripción de los experimentos que realizaron Müllensiefen y Frieler para establecer la medida de similitud en humanos. Referencias [BL51] Béla Bartók and Albert Lord. Serbo-Croatian Folk Songs: Texts and Transcriptions of SeventyFive Folk Songs from the Milman Parry Collection and a Morphology of Serbo-Croatian Folk Melodies. Columbia University Press, 1951. [CIR98] T. Crawford, C.S. Iliopoulos, and R. Raman. String matching techniques for musical similarity and melodic recognition. melodic comparison: Concepts, procedures, and applications. Computing in Musicology, 1(11):73–100, 1998. [Cro98] Charles Cronin. Concepts of Melodic Similarity in Music-Copyright Infringement Suits. Computing in Musicology (ed. Walter B. Hewlett and Eleanor Selfridge- Field). MIT Press, Cambridge, 1998. [Góm11] P. Gómez. Similitud rítmica en el flamenco. Divulgamat, Marzo 2011. [Hal03] Joseph Y. Halpern. Reasoning about uncertainty. The MIT Press, Cambridge, 2003. [HCR03] Ulrike Hahn, Nick Chater, and Lucy B. Richardson. Similarity as transformation. Cognition, 87:1–32, 2003. [HE01] Ludger Hofmann-Engl. Towards a cognitive model of melodic similarity. In Proceedings of ISMIR Conference, Bloomintong, Indiana, 2001. [HE02] Ludger Hofmann-Engl. Rhythmic similarity: A theoretical and empirical approach. In C. Stevens, D. Burnham, G. McPherson, E. Schubert, and J. Renwick, editors, Proceedings of the Seventh International Conference on Music Perception and Cognition, pages 564–567, Sidney, Australia, 2002. [Hol10] A. Holzapfel. Similarity methods for computational ethnomusicology. PhD thesis, Computer Science Deparment. University of Crete, 2010. [HSF98] W. B. Hewlett and E. Selfridge-Field, editors. Melodic Similarity: Concepts, Procedures, and Applications. The MIT Press, 1998. [LJ83] F. Lerdahl and R. Jackendoff. A Generative Theory of Tonal Music. MIT Press, Cambridge, Massachussetts, 1983. [Mey73] Leonard Meyer. Explaining Music: Essays and Explorations. University of Chicago Press, Chicago, 1973. [MF04] D. Mullensiefen and K. Frieler. Cognitive adequacy in the measurement of melodic similarity: Algorithmic vs. human judgments. Computing in Musicology, 13:147–176, 2004. [MM01] Stephen McAdams and Daniel Matzkin. Similarity, invariance, and musical variation. Annals of the New York Academy of Sciences, 930:62–76, 2001. [MS90] M. Mongeau and D. Sankoff. Comparison of musical sequences. Computers and the Humanities, 24:161–175, 1990. [Pam06] Elias Pampalk. Computational Models of Music Similarity and their Application in Music Information Retrieval. PhD thesis, Fakultät für Informatik, Technischen Universität Wien, 2006. [Sch99] Mark Schmuckler. Testing models of melodic contour similarity. Music Perception, 16:109–150, 1999. [See66] Charles Seeger. Versions and Variants of the Tunes of “Barbara Allen”. Selected Reports in Ethnomusicology, 1(1), 1966. [Typ07] Rainer Typke. Music Retrieval based on Melodic Similarity. PhD thesis, Utrecht University, Netherlands, February 2007. [YK03] Z. Yongwei and M. Kankanhalli. Melody alignment and similarity metric for content-based music retrieval. In Proceedings of SPIE-IS&T Electronic Imaging, pages 112–121, SPIE, December 7-9 2003.

Viernes, 24 de Junio de 2011 | Imprimir | PDF |  Correo electrónico

107. 25. (Mayo 2011) Distancia y similitud musical - I

1. El concepto matemático de distancia Uno de los conceptos fundamentales con que enseguida nos topamos en matemáticas es el de distancia. La distancia matemática no es más que la abstracción del concepto de cercanía y su cuantificación. Ambas, abstracción y cuantificación, son necesarias para objetivar muchos fenómenos que se encuentran en la práctica matemática. Inicialmente, la distancia se refería al término físico de medir una magnitud física. Pero pronto los matemáticos la aplicaron a otros muchos dominios fuera de la física. En este artículo vamos a examinar el concepto de distancia en el campo de la música, en particular, en el campo de la similitud melódica. Veremos que la formalización del concepto de distancia de similitud melódica implica dificultades que hay que tratar con sumo cuidado, siendo la validación perceptual probablemente la de más envergadura. La generalización de la distancia física en matemáticas recibe el nombre de métrica, especialmente en geometría. Nosotros usaremos ambos términos como sinónimos. Dado un conjunto A, que puede ser lo abstracto y arbitrario que se quiera, una métrica es una aplicación d : A × A → [0,∞), que verifica las siguientes propiedades: Positividad de la métrica: d(x,y) ≥ 0, para todo par x,y ∈ A d(x,y) = 0 si y solo si x = y. Simetría: d(x,y) = d(y,x). Desigualdad triangular: d(x,z) ≤ d(x,y) + d(y,z). En la sencilla y juguetona recta real ℜ, la distancia entre dos números se reduce al conocido valor absoluto: d(x, y) = ∣x - y∣ donde x,y ∈ ℜ. En ℜ2, la distancia es la longitud del segmento que une dos vectores v1 = (x1,y1), v2 = ( x2,y2): Bien conocido es que está fórmula proviene del teorema de Pitágoras y que la distancia d(v1,v2) es la hipotenusa del triángulo rectángulo formado por los puntos (x1,y1), (x2,y1) y (x2,y2). La generalización de la distancia al pomposo y vertical espacio ℜn, de n dimensiones, de esas que no podemos ver, solo colegir, es: donde v1 = (x1,…,xn), v2 = (y1,…,yn). En estos espacios de altas dimensiones se suele hablar de distancia euclídea. Pero la fórmula anterior es solo una de las muchas maneras de definir distancias en ℜn. Tenemos las siguientes: La distancia L1: d(v1,v2) = ∑ni=1∣xi - yi∣. En general, la distancia Lp: d(v1,v2) = (∑ni=1∣xi - yi∣p)1∕p. La llamada norma infinito L∞: d(v1,v2) = limp→∞(∑ni=1∣xi - yi∣p)1∕p = max(∣x1 - y1∣,∣x2 - y2∣,...,∣xn - yn∣). La distancia en el espacio euclídeo es la longitud de la trayectoria más corta y este hecho se puede usar para generalizar el concepto de distancia a otros espacios más complicados, como es una esfera, donde la distancia se da por trayectorias geodésicas. En ese caso la distancia se calcula a través de fórmulas de longitud de arco. El concepto de distancia se generaliza a espacios geométricos no euclídeos a través de dichas fórmulas. Dado que la distancia proviene de un concepto tan general como el de cercanía, aparece en muchísimos más áreas de las matemáticas que la geometría, por más que esta área sea vasta. Tan ubicuo es el concepto de distancia que hay un libro de título Dictionary of distance [DD06], Diccionario de distancias, donde los autores hacen un recorrido por las áreas de la matemática en que la distancia tiene un papel relevante. Lo recomendamos vivamente al lector interesado. Así que como muestra de la ubicuidad e importancia vamos a enumerar a modo de telegrama, de fogonazo conceptual, de repaso ufano, las áreas en que aparece la distancia defendiendo sus fueros. DISTANCIAS Y MÉTRICAS Espacios topológicos, m-métricas, distancias topológicas, Métricas en conjuntos arbitrarios NORMAS Distancias geodésicas, geometría proyectiva y geometría afín, métricas riemannianas Teoría de la información Métricas en superficies, métricas intrínsecas, distancias en nudos, distancias en cuerpos convexos Métricas en grupos, métricas en relaciones binarias, métricas en mallas Distancias en cadenas, distancias en permutaciones Métricas en polinomios, métricas en matrices, métricas en espacios funcionales, métricas en operadores lineales Distancias entre variables aleatorias, distancias entre distribuciones Distancias en grafos ponderados, distancias en árboles, distancias entre códigos Distancias de SIMILITUD, distancias de correlación Distancias entre planificaciones de movimiento, distancias entre autómatas Distancias MOEA Métricas digitales Distancias de Voronoi, distancias entre imágenes, distancias entre sonidos, distancias entre redes Distancias entre genes, distancias entre proteínas Distancias en Química, distancias en Geofísica, distancias en Astronomía O más gráficamente: Figura 1: El concepto de distancia en diversas áreas de las matemáticas. 2. Distancias en la música Después de observar cuán flexible y ubicuo es el concepto de distancia, nos preguntamos cómo aparece en la música. En general, todo lo que se refiera a distancias perceptuales se sale de la intuición. Abajo tenemos tres sonidos, llamémosles S1, S2 y S3. Pongamos que la frecuencia de S1 son x hercios. Hacemos saber al lector que las frecuencias de S2 y S3 son, respectivamente, 2x y 3x. Tenga ahora el lector la amabilidad de pinchar sucesivamente en los sonidos de la figura de más abajo (súbase el volumen si es necesario). S1 S2 S3 Figura 2: Tres sonidos diferentes. ¿Le ha parecido al lector que había más distancia entre S1 y S2 que entre S2 y S3? ¿Quizás ha sido al revés? ¿O aún mejor no hay diferencia entre los dos saltos? Al fin y al cabo la diferencia en frecuencia entre cada par es constante. El lector -acaso un poco confundido- dirá que el salto entre S1 y S2 le ha parecido mayor que entre S2 y S3. Y, en efecto, así es. Nuestro oído, acorde con la famosa ley de Weber-Fechner, percibe la relación entre un estímulo y su percepción siguiendo una función logarítmica. Esto explica que el salto de S1 a S2, de proporción 2 : 1, se perciba como mayor que el de S2 a S3, de proporción 3 : 2, que es menor. El problema de la similitud musical -y de la obtención de una distancia- es de los más complejos e importantes. Como Pampal [PFW05] describe con acierto “desgraciadamente, el problema de la similitud melódica es muy complejo, multidimensional, fuertemente dependiente del contexto y de muy mala definición”. La similitud musical es un fenómeno que comprende tres niveles diferentes: el físico, el musical y el psicosocial. En el físico se estudian conceptos de acústica, relacionados con los aspectos físicos del sonido, tal como frecuencia fundamental, armónicos, energía, espectros, duraciones, etc. En el musical, se analizan variables como intervalos (como frecuencias percibidas), ritmos, métrica, armonía, conducción de voces, forma musical, fraseo, etc. Por último, en el nivel sociocultural se examinan variables como la emoción, la motricidad, el carácter, así como aspectos socioculturales. Un modelo de similitud melódica que aspire a ser fiel a la similitud humana ha de tener en cuenta estos tres niveles fenoménicos. Aucouturier y Pachet [AF04] advierten de que hay una limitación intrínseca si solo se modeliza la similitud con variables pertenecientes a uno solo de esos niveles; es necesario tener en cuenta todos. Estos autores hacen estas observaciones porque en el pasado se construyeron muchos modelos basados en la pura descripción física del sonido y, a pesar de su creciente complejidad, no conseguían los resultados esperados. Recientemente, se han empezado a incluir variables de los niveles musical y psicosocial. En esta serie de artículos no vamos a estudiar la similitud musical sino solamente la similitud melódica, que es un problema más pequeño pero no necesariamente más fácil. Perseguimos diseñar una distancia matemática de similitud melódica que refleje lo más fielmente posible la distancia de similitud melódica que tenemos los humanos. Veamos cómo. 3. Similitud melódica Empezaremos por definir formalmente lo que es una medida de similitud melódica, término que como veremos difiere ligeramente del de distancia de similitud melódica. Seguiremos en parte la exposición de Müllensiefen y Frieler [MF04]. Una medida de similitud melódica se define como una aplicación σ : M → [0, 1], donde M es el espacio de melodías, con las siguientes propiedades matemáticas: σ(m1,m1) = 1. La similitud de una melodía consigo misma toma el valor 1. σ(m1,m2) = 1 si y solo si m1 = m2. De hecho, ese valor no se alcanza en ninguna otra situación. σ(m1,m2) = σ(m2,m1). Propiedad de simetría. Sin embargo, dado que estamos en presencia de un fenómeno musical, la anterior definición no es del todo satisfactoria. Por ejemplo, dos melodías transpuestas se oyen claramente como la misma. Acorde a la definición anterior, tendría medida positiva, lo cual contradice la intuición musical. Definimos en M, el espacio de melodías, una relación de equivalencia: m1 está relacionada con m2 si y solo si m2 es una transposición por altura, por tiempo o por un cambio de tempo (velocidad) de m1. Transposición por altura quiere decir que las alturas de las notas de m1 y m2 difieren en una constante; transposición por tiempo significa que dos melodías iguales tocadas en instantes diferentes se consideran iguales; cambio de tempo significa que una melodía tocada a diferente tempo se considera la misma que tocada a su tempo original (esto último es dentro de unos límites razonables, pues se sabe que el tempo puede afectar a la percepción melódica). El espacio de las medidas de similitud es convexo. Dado un conjunto de medidas σ1,…,σn, y un conjunto de pesos ω1,…,ωn tal que ∑ni=1ωi = 1, la función es una medida de similitud. Una distancia de similitud cumple las propiedades enunciadas en la sección 1 al principio del artículo. Es bastante frecuente trabajar con distancias que cuentan el número de diferencias entre dos melodías en lugar de las similitudes, que puede ser más abstracto. Estas distancias se llaman de disimilitud. A partir de una distancia de disimilitud d se puede definir una medida de similitud σd sobre cualquier espacio finito de melodías como sigue: σd(m1,m2) = 1 - d(m1,m2)/δ donde δ = max. Se puede comprobar que si d cumple las propiedades de invariancia musical, entonces σd es una medida de similitud. Para que el lector sea consciente de la dificultad del problema de la similitud melódica, considérese las conocidas variaciones de Mozart K. 265 sobre el tema popular Ah, vous dirai-je, Maman. La melodía es diáfana, compuesta por intervalos simples y con una estructura sencilla, una subida y una bajada en la primera y dos bajadas en la segunda frase. En la figura 3 se puede ver la partitura; si se pincha en la partitura suena el tema completo, con la mano izquierda. Figura 3: El tema principal de las variaciones K. 265 de Mozart. La primera variación consiste en una versión ornamentada en corcheas del tema principal. Ahora las subidas y bajadas, casi todas por grados conjuntos, se multiplican y el oyente se da cuenta de esa fragmentación de la dirección melódica. También aparecen pequeñas dominantes secundarias que sugieren refuerzos de los grados V y VI (sol y la). En la figura 4 tenemos la partitura (de nuevo pinchando en la figura se puede oír la variación): Figura 4: La primera variación del K. 265 de Mozart. Por último consideremos la variación V, que consiste en cambios de figuración rítmica. Mozart pasa de las dos negras del tema a la figura negra, silencio de corchea y corchea. Más tarde esta figura a un puro contratiempo. Desde el punto de vista de las alturas, aparecen más intervalos cromáticos. Se puede ver la partitura en la figura 5. Figura 5: La quinta variación del K. 265 de Mozart. En el siguiente vídeo se puede ver una interpretación de las variaciones completas. En el minuto 2:05 está la quinta variación. Las preguntas son las siguientes: ¿Cuál de las dos variaciones, la I o la V, es más similar al tema principal? ¿Cómo se cuantifica tal diferencia? ¿En que variables se fundamenta la respuesta, cualquiera que sea el resultado? ¿Cómo obtener un modelo de similitud melódica que sea fiel a la medida humana de similtud? 4. Conclusiones Concluimos aquí este primer artículo sobre la distancias matemáticas y la similitud melódica. Primero, hemos repasado algunos conceptos matemáticos de distancia. Después hemos expuesto cómo se define en música la distancia de similitud melódica. En el siguiente artículo glosaremos las distancias más importantes y explicaremos cuál es la razón de ser de cada una. En el tercer y último artículo abordaremos la peliaguda cuestión de la validación perceptual de todas esas distancias. Bibliografía [AF04] J.-J. Aucouturier and Pachet F. Improving timbre similarity: How high is the sky? Journal of Negative Results in Speech and Audio Sciences, 1(1), 2004. [DD06] E. Deza and M. Deza. Dictionary of Distances. Elsevier Science, 2006. [MF04] D. Mullensiefen and K. Frieler. Cognitive adequacy in the measurement of melodic similarity: Algorithmic vs. human judgments. Computing in Musicology, 13:147–176, 2004. [PFW05] Elias Pampalk, Arthur Flexer, and Gerhard Widmer. Improvements of audio-based music similarity and genre classificaton. In ISMIR’05, pages 628–633, 2005.

Sábado, 21 de Mayo de 2011 | Imprimir | PDF |  Correo electrónico

108. 23. (Marzo 2011) Similitud rítmica en el flamenco

1. Introducción El discurso musical progresa a través de múltiples transformaciones de su material musical. Estas transformaciones ocurren en el ámbito melódico, rítmico, armónico, tímbrico, en la conducción de voces y en la estructura formal. Cómo varíe el material musical, acorde a qué reglas gramaticales, es propio e idiomático de cada estilo y época. Además, la percepción y evaluación de las transformaciones del material musical por parte del oyente dependerán intrínsecamente del concepto de similitud musical. Dada su importancia, este concepto se ha examinado con profundidad y aún hoy sigue siendo objeto de investigación intensa. La similitud musical se ha estudiado por varias disciplinas: en etnomusicología [BL51], [See66]; en análisis musical [LJ83], [Mey73]; en la resolución de conflictos de propiedad intelectual [Cro98]; en tecnología musical [MS90]; en psicología de la música [Sch99], [HE01], [MM01], [HE02], [HCR03]. Sin embargo, es un problema difícil de abordar, bien escurridizo, pues la percepción de la similitud musical es subjetiva y cambia fácilmente con el contexto. La similitud melódica y armónica se ha estudiado con más detalle que la rítmica, aunque esta situación ha empezado a cambiar recientemente. En este artículo vamos a examinar medidas de similitud rítmica en la música flamenca. Varios autores han estudiado cómo medir la complejidad rítmica. En general, las medidas explotan diversas propiedades del fenómeno rítmico. Por ejemplo, ciertas medidas asignan pesos según la jerarquía métrica, como la de Longuet-Higgins y Lee [LHC84], la complejidad métrica de Toussaint [Tou02] o el índice de contratiempo [Tou03]; otras medidas adjudican pesos a ciertos eventos musicales, tales como la medida de Keith [Kei91], de carácter combinatorio, o la medida WNBD (weighted note-to-beat distance) [GMRT05], basada en la distancia de las notas a las partes fuertes de la métrica. Para un estudio completo de estas medidas, véase Gómez et al. [GTT07]. Sin embargo, la crítica que se hace a todas estas medidas es la falta de validación perceptual, esto es, la falta de experimentos rigurosos que prueben que las medidas evalúan correctamente la similitud perceptual. El objetivo al diseñar una medida de estas características es obtener una medida que se corresponda con la percepción humana de la similitud musical, al menos bajo determinadas condiciones. Con frecuencia, las medidas se construyen en base a ciertas hipótesis o a ciertas propiedades de los ritmos, pero posteriormente no se comprueba la validez perceptual de la medida. Gómez y sus colegas en [GTT07] comprobaron la validez de 10 medidas de síncopa distintas a partir de los datos experimentales de Shmulevich y Povel [SP98]. Ese trabajo puso de manifiesto que algunas medidas tenían una validez perceptual muy pobre. Otro trabajo a destacar es el de Guastavino y sus colegas [GGT+09], en el que analizan dos distancias de similitud rítmica, presentadas en [DBFG+04], y realizan experimentos con sujetos para estudiar la correlación entre los resultados predichos por las medidas y los obtenidos por los sujetos. En el artículo de este mes examinamos las ideas y resultados expuestos en el trabajo de Guastavino y sus colegas. 2. Similitud rítmica 2.1. El ritmo flamenco El flamenco es una música que surgió a finales del siglo XVIII en Andalucía y que está formada por una mezcla de varias influencias, tales como la propia música folclórica de Andalucía, junto con la música gitana, árabe, bizantina, incluso la música judía. La mezcla de estas influencias, destiladas por el alambique del tiempo y la práctica musical, produjeron una música altamente estilizada y compleja, con características muy peculiares. Entre las características más llamativas del flamenco se encuentra su acompañamiento con palmas. Las palmas pueden ser fuertes o sordas y en flamenco sirven como elemento métrico, como patrón de referencia temporal e incluso actúan como voz independiente, con su propia personalidad rítmica. Aquí trataremos los patrones rítmicos que sirven como referencia temporal. En música algunos autores los llaman claves [Uri96], [Ort95]. Una clave se define como un patrón rítmico que se repite durante la pieza y cuyas funciones principales son la estabilización rítmica y la organización del fraseo musical (no confundir clave con referente de densidad). Los estilos flamencos, atendiendo a su compás, se clasifican en binarios, ternarios, alternos e irregulares [Fer04]. Cada estilo en el flamenco tiene una clave asociada. Los estilos binarios usan como clave un mismo patrón rítmico, [. x x x], donde [.] representa una palma sorda y [x] una palma fuerte; no obstante, a veces se toca como la palma sorda como silencia y la palma fuerte como palma normal. Los patrones ternarios son 5 y abarcan muchos más estilos, y son el objeto de nuestro estudio. En la figura de abajo tenemos las claves asociadas a los ritmos ternarios representados con la notación de y [. ] y [x]. Figura 1: Las claves ternarias del flamenco. Claves ternarias. Pínchese en cada patrón rítmico para escuchar una versión de MIDI. FANDANGO: SOLEÁ: BULERÍA: SEGUIRIYA: GUAJIRA: Quede claro el hecho de que es posible que la clave no se toque en una interpretación determinada de una pieza. Eso no obsta para que los músicos flamencos tengan la clave en la cabeza y la organización musical se rija por ella. Es igualmente posible oír versiones muy ornamentadas de la clave. Una misma clave sirve para varios estilos y, por tanto, los nombres que aparecen en la figura están elegidos según la nomenclatura de Gamboa [Gam02]. Por ejemplo, el patrón del fandango se usa para las sevillanas; el de la soleá para las bulerías bulerías o alegrías; el de la bulería para las bulería por soleá; el de la seguiriya para las serranas o saetas; y, finalmente, el de la guajira para las peteneras. Para ilustrar el fenómeno de la clave, vamos a escuchar la guajira Hermosísima cubana en la interpretación de Pepe de Lucía en la película Flamenco. Ciertamente aquí no se oye a un palmero tocar el ritmo [x . . x . . x . x . x. ], pero está presente en toda la pieza. Es claro a partir de la introducción lenta y lírica de la pieza, en el minuto 0:27, y muy evidente a partir del minuto 1:00. 2.2. Distancias de similitud rítmica Las dos medidas de similitud rítmica que estudiaron Guastavino y sus colegas fueron la distancia cronotónica y la distancia de permutación dirigida. La primera fue propuesta por Gustafson [Gus88] para medir la distancia rítmica entre segmentos de habla. La segunda fue propuesta por Díaz-Báñez y sus colegas en [DBFG+04]. La distancia cronotónica representa el ataque de las notas y su duración a la vez. Para ello, usa una especie de histograma en que en el eje x se representan los ataques y en el eje y la duración de las notas. En la figura 2 se muestra las representaciones cronotónicas (también llamadas TEDAS) de las claves ternarias. Figura 2: La representación cronotónica de las claves ternarias del flamenco. La distancia cronotónica se calucla midiendo el área que queda entre dos ritmos superpuestos entre sí. La zona rayada de la última gráfica de la figura 3 representa la distancia entre el patrón del fandango y el de la bulería. Figura 3: La distancia cronotónica entre el fandango y la seguiriya (tomado de [DBFG+04]). La distancia de permutación dirigida se basa en contar el número mínimo de operaciones para transformar un ritmo dado en otro. Es una generalización de la distancia de Hamming. Esas operaciones se limitan a intercambios de notas o silencios entre posiciones adyacentes y tienen las siguientes restricciones: Ambos ritmos han de tener el mismo número de pulsos. En nuestro caso todos tienen 12 pulsos. Se convierte el ritmo de más notas, R1, al de menos notas, R2. Cada nota de R1 tiene que moverse a una nota de R2. Cada nota de R2 ha de recibir al menos una nota de R1. Las notas no pueden cruzar el final del ritmo y aparecer por el principio. En la figura 4 se muestra la distancia de permutación dirigida entre el fandango y la seguiriya; se pueden apreciar los movimientos de las notas de la seguiriya para transformarse en el fandango. El número de movimientos es mínimo. Figura 4: La distancia de permutación dirigida entre el fandango y la seguiriya (tomado de [DBFG+04]). En las tablas 2.2 y 2.2 tenemos las matrices de disimilitud para ambas distancias. Las matrices se llaman de disimilitud porque las distancias reflejan cuán lejos está un ritmo de otro. Soleá Bulería Guajira Seguiriya Fandango Soleá 0 Bulería 6 0 Guajira 4 8 0 Seguiriya 8 12 8 0 Fandango 10 14 6 6 0 Tabla 1: Matriz de disimilitud para la distancia cronotónica. Soleá Bulería Guajira Seguiriya Fandango Soleá 0 Bulería 1 0 Guajira 7 8 0 Seguiriya 11 12 4 0 Fandango 7 8 2 4 0 Tabla 2: Matriz de disimilitud para la distancia cronotónica. 2.3. Grafos filogenéticos El conjunto de distancias de las matrices es difícil de visualizar y aún menos los posibles agrupamientos que puedan esconder los datos. Desde hace mucho tiempo los bioinformáticos usan una herramienta tremendamente útil para este propósito: los árboles filogenéticos. Técnicamente, deberían llamarse grafos filogenéticos, puesto que pueden salir grafos generales, pero por razones históricas se ha mantenido el nombre así. Estos grafos se construyen de tal manera que la distancia entre dos nodos corresponde tan exactamente como es posible a la distancia dada en la matriz. Hay un índice de ajuste asociado al grafo filogenético que indica la bondad del ajuste del grafo a la matriz de distancias. El algoritmo que construye el grafo es iterativo. En principio, el algoritmo intenta ajustar la matriz a un árbol; si ello no es posible, introduce un número mínimo de nodos para realizar el ajuste. El programa que usaron Díaz-Báñez y Guastavino fue SplitsTree, creado por Hudson y Bryant [HB06]. En las figuras 5 y 6 se exponen los árboles correspondientes a ambas distancias. Nótese que el índice de ajuste es muy alto para cada distancia, 99,2% y 100%, respectivamente. Esto asegura que el grafo refleja fielmente la distancia.   Figura 5: Árbol filogénetico para la distancia cronotónica (tomado de [GGT+09]).   Figura 6: Grafo filogénetico para la distancia de permutación dirigida (tomado de [GGT+09]). De la figura 5 se sigue que el grafo de la distancia cronotónica sugiere tres grupos: uno formado por el fandango y la seguiriya; un segundo, por la soleá y la bulería. Para la distancia de permutación dirigida el agrupamiento sugerido es ligeramente distinto: un primer grupo lo componen la soleá y la bulería; otro central, la guajira y el fandango; por último, está la seguiriya en un grupo aislado. 3. La validación perceptual 3.1. Los experimentos Guastavino y sus colegas comprobaron la validez perceptual de las dos distancias en cuestión a través de una serie de experimentos. Sospechaban que la formación musical influía en la percepción, de modo que diseñaron tres experimentos: el primero fue para sujetos sin conocimientos de flamenco ni formación musical reglada; el segundo para músicos con formación clásica; y el tercero para músicos de flamenco. Por brevedad solo describiremos el primer experimento. El lector interesado puede consultar los detalles en [GGT+09]. En el experimento participaron 12 sujetos, con media de edad 25 y desviación típica 4. El experimento se diseñó para que los sujetos se concentrasen en la duración de las notas, puesto que las distancias matemáticas fueron diseñadas con esa intención. Por ello, el estímulo del experimento consistió en sonidos de palmas generados vía MIDI con el programa Finale. Los ritmos se generaron en tres diferentes tempi (es sabido que el tempo influye en la percepción musical); dichos tempi fueron 50, 70 y 90 negras por minuto, respectivamente. Se programó una aplicación para que los sujetos introdujesen los índices de disimilitud. El experimento tuvo lugar en una habitación acústicamente aislada. Los ritmos, como es habitual en estos experimentos, se presentaron en orden aleatorio. Se pedía a los sujetos que evaluasen la disimilitud entre todas las parejas de patrones rítmicos. Pinchando en la lista de ritmos se pueden oír los estímulos correspondientes al tempo de 70; a los sujetos solo se les presentaba cada ritmo una sola vez, pero ellos podían todas las veces que quisiesen. Estímulos: FANDANGO: SOLEÁ: BULERÍA: SEGUIRIYA: GUAJIRA: Asimismo, se llevó a cabo un análisis de varianza y se encontró que no había diferencias significativas con respecto al tempo. Cada sujeto proporcionó una matriz de disimilitud. Se sumaron todas las matrices y se obtuvo una matriz global de disimilitud. El árbol correspondiente a dicha matriz se puede observar a continuación; compárese con las figuras 5 y 6.   Figura 7: Grafo filogénetico de la distancia perceptual (tomado de [GGT+09]). Ignórese el nodo marcado como "ancestral" en la figura 7, pues es un ritmo extra que se añadió para comprobar cierta hipótesis que sale fuera del alcance de este artículo. Para hallar la correlación entre las matrices de disimilitud se usó el test de Mantel. 3.2. El test de Mantel Como es conocido, hay muchas técnicas para estudiar agrupamiento: técnicas jerárquicas y no jerárquicas, escalamiento multidimensional, análisis de correspondencia, etc. Estas técnicas generan agrupamientos de los datos de entrada, pero no permiten una adecuada comparación entre dos agrupamientos dados. En nuestro estudio obtuvimos dos matrices de disimilitud y elegimos como método de agrupamiento los árboles filogenéticos, muy usados en Bioinformática. Tienen ciertas ventajas sobre otros métodos de agrupamiento y entre ellas se cuenta la facilidad de visualización. Sin embargo, el problema aquí es cómo comparar dos matrices, o equivalentemente cómo comparar dos matrices de disimilitud. Hacer la correlación directa entre las matrices sería incorrecto matemáticamente. Las distancias de las matrices claramente no son independientes, ya que cambiar una distancia afectaría a n-1 distancias. Por tanto, no podemos evaluar la relación entre las dos matrices simplemente evaluando su coeficiente de correlación entre los dos conjuntos de distancias y examinando si es estadísticamente significativa. El test de Mantel resuelve este problema realizando varios test sobre permutaciones de las matrices. El procedimiento del test de Mantel se describe brevemente a continuación (véase [Wik11] y sus referencias): Procedimiento: El procedimiento consiste en un test de permutación. Se calcula la correlación entre los dos conjuntos de [(n(n-1))/2] de distancias. Dicha correlación es a la vez la medida de correlación y el estadístico sobre el que se basa el test. En principio, cualquier coeficiente de correlación se puede usar, pero es muy frecuente tomar el coeficiente de correlación de Pearson. Contraste de hipótesis: Al contrario del procedimiento habitual con el coeficiente de correlación, para evaluar cualquier desviación de la correlación nula, las filas y columnas de la matriz se someten a permutaciones aleatorias varias veces, y se calcula el coeficiente de correlación cada vez. La significación de la correlación observada es la proporción de dichas permutaciones que conducen a un coeficiente de correlación alto. La hipótesis nula: el razonamiento es que si la hipótesis nula de que no hay relación entre las matrices es cierta, entonces permutar las filas y las columnas de la matriz debería producir con igual probabilidad un menor o mayor coeficiente. Además de superar el problema de la dependencia estadística de los elementos de las dos matrices, usar los test de permutación elimina la necesidad de hacer hipótesis sobre la distribución estadística de los elementos de las matrices. 3.3. Resultados El test de Mantel para determinar la correlación entre las matrices de las distancias matemáticas y las distancias perceptuales arrojó los siguientes resultados: Correlación entre las medidas perceptuales y la distancia de permutación dirigida: r=0'76 y p=0'03. Correlación entre las medidas perceptuales y la distancia cronotónica: r=0'66 y p=0'017. Se puede ver que la correlación es más alta para la distancia de permutación dirigida que para la distancia cronotónica, si bien en ambos casos es alta. También se puede observar que las medidas perceptuales se acercan más a la distancia de permutación dirigida que a la distancia cronotónica, tanto en términos de agrupamiento como del ritmo más diferente. 4. Conclusiones Como dijimos al principio del artículo, el trabajo de Guastavino y colaboradores tiene la virtud de comprobar la validez perceptual de las distancias matemáticas. Los resultados del experimento corroboran su validez. No obstante, los resultados son limitados, pues el número de patrones rítmicos es muy pequeño. En mi (humilde) opinión, y a pesar de ser coautor de los dos artículos, creo que la distancia de permutación dirigida no refleja la distancia perceptual del ritmo. He aquí un ejemplo que ilustra mi objeción. Consideremos los dos ritmos siguientes: R1 = [x . . x . . x . . . x . x . . . ] (la clave son). R2 = [x . . x . . x . . . x . . x . . ] (la clave bossa-nova). Su distancia de permutación dirigida es 1; basta mover la quinta nota de la clave son un pulso hacia delante para obtener la clave bossa-nova. Sin embargo, perceptualmente son muy diferentes. El primer ritmo, la clave son, tiene una clara estructura de pregunta/respuesta; pínchese en el ritmo para comprobarlo. Mientras que el segundo, la clave bossa-nova no tiene esa estructura, sino otra más compleja. La clave bossa-nova está formada por cuatro notas de duración tres pulsos y una nota de duración cuatro pulsos. Esta composición hace que tras oírse unas cuantas veces, a causa del principio de continuación, la clave se perciba como un único tren de pulsos regulares de duración tres pulsos acabado por uno de cuatro; pínchese en el ritmo para comprobarlo. Con este ejemplo vemos que dos ritmos a distancia 1, la mínima distancia que puede dar la distancia de permutación dirigida, pueden ser perceptualmente muy diferentes. CLAVE SON: CLAVE BOSSA-NOVA:   Bibliografía [BL51] Béla Bartók and Albert Lord. Serbo-Croatian Folk Songs: Texts and Transcriptions of SeventyFive Folk Songs from the Milman Parry Collection and a Morphology of Serbo-Croatian Folk Melodies. Columbia University Press, 1951. [Cro98] Charles Cronin. Concepts of Melodic Similarity in Music-Copyright Infringement Suits. Computing in Musicology (ed. Walter B. Hewlett and Eleanor Selfridge- Field). MIT Press, Cambridge, 1998. [DBFG+04] Miguel Díaz-Bañez, Giovanna Farigu, Francisco Gómez, David Rappaport, and Godfried T. Toussaint. El compás flamenco: a phylogenetic analysis. In Proceedings of BRIDGES: Mathematical Connections in Art, Music and Science, pages 61-70, Southwestern College, Winfield, Kansas, July 30 - August 1 2004. [Fer04] Lola Fernández. Teoría musical del flamenco. Acordes Concert, Madrid, 2004. [Gam02] José Manuel Gamboa. Cante por Cante: Discolibro Didactico de Flamenco. New Atlantis Music, Alia Discos, Madrid, 2002. [GGT+09] Catherine Guastavino, Paco Gómez, Godfried Toussaint, Fabrice Marandola, and Emilia Gómez. Measuring similarity between flamenco rhythmic patterns. Journal of New Music Research, 38(2):174-176, 2009. [GMRT05] Francisco Gómez, Andrew Melvin, David Rapapport, and Godfried Toussaint. Mathematical measures of syncopation. In Proceedings of BRIDGES: Mathematical Connections in Art, Music and Science, pages 73-84, Banff, Alberta, July 31 - August 3 2005. [GTT07] Francisco Gómez, Eric Thul, and Godfried Toussaint. An experimental comparison of formal measures of rhythmic syncopation. In Proceedings of the International Computer Music Conference, pages 101-104, Copenhagen, Denmark, August 2007. [Gus88] Kjell Gustafson. The graphical representation of rhythm. In (PROPH) Progress Reports from Oxford Phonetics, volume 3, pages 6-26, University of Oxford, 1988. [HB06] Daniel H Huson and David Bryant. Application of phylogenetic networks in evolutionary studies. Mol Biol Evol, 23(2):254-267, 2006. [HCR03] Ulrike Hahn, Nick Chater, and Lucy B. Richardson. Similarity as transformation. Cognition, 87:1-32, 2003. [HE01] Ludger Hofmann-Engl. Towards a cognitive model of melodic similarity. In Proceedings of ISMIR Conference, Bloomintong, Indiana, 2001. [HE02] Ludger Hofmann-Engl. Rhythmic similarity: A theoretical and empirical approach. In C. Stevens, D. Burnham, G. McPherson, E. Schubert, and J. Renwick, editors, Proceedings of the Seventh International Conference on Music Perception and Cognition, pages 564-567, Sidney, Australia, 2002. [Kei91] Michael Keith. From Polychords to P\' olya: Adventures in Musical Combinatorics. Vinculum Press, Princeton, 1991. [LHC84] H.C. Longuet-Higgins and C.S. The rhythmic interpretation of monophonic music. Music Perception, 1:424-441, 1984. [LJ83] F. Lerdahl and R. Jackendoff. A Generative Theory of Tonal Music. MIT Press, Cambridge, Massachussetts, 1983. [Mey73] Leonard Meyer. Explaining Music: Essays and Explorations. University of Chicago Press, Chicago, 1973. [MM01] Stephen McAdams and Daniel Matzkin. Similarity, invariance, and musical variation. Annals of the New York Academy of Sciences, 930:62-76, 2001. [MS90] M. Mongeau and D. Sankoff. Comparison of musical sequences. Computers and the Humanities, 24:161-175, 1990. [Ort95] Fernando Ortiz. La Clave. Editorial Letras Cubanas, La Habana, Cuba, 1995. [Sch99] Mark Schmuckler. Testing models of melodic contour similarity. Music Perception, 16:109-150, 1999. [See66] Charles Seeger. Versions and Variants of the Tunes of "Barbara Allen". Selected Reports in Ethnomusicology, 1(1), 1966. [SP98] I. Shmulevich and D. Povel. Rhythm complexity measures for music pattern recognition. In Proceedings of the IEEE Workshop on Multimedia Signal Processing, Redondo Beach, California, December 7-9 1998. [Tou02] Godfried T. Toussaint. A mathematical analysis of African, Brazilian, and Cuban clave rhythms. In Proceedings of BRIDGES: Mathematical Connections in Art, Music and Science, pages 157-168, Towson University, Towson, MD, July 27-29 2002. [Tou03] Godfried T. Toussaint. Classification and phylogenetic analysis of African ternary rhythm timelines. In Proceedings of BRIDGES: Mathematical Connections in Art, Music and Science, pages 25-36, Granada, Spain, July 23-27 2003. [Uri96] Ed Uribe. The Essence of Afro-Cuban Persussion and Drum Set. Warner Brothers Publications, Miami, Florida, 1996. [Wik11] Wikipedia. Mantel test. http://en.wikipedia.org/wiki/Mantel_test, accedido en febrero de 2011.

Jueves, 10 de Marzo de 2011 | Imprimir | PDF |  Correo electrónico

109. 22. (Febrero 2011) Claves para El Duende y el Reloj

Presentar a quien se admira es un raro placer del que hoy disfruto con total desinhibición. Hoy tenemos a Philippe Donnier entre nosotros, esto es, tenemos a un músico y científico, pues es doctor en Etnomusicología por la Universidad París X e ingeniero superior por la École Supérieure de Physique et Chimie de Paris (ESPCI); pero también a un bohemio genuino, profundo amante del flamenco, que lo aprendió en las cuevas del Sacromonte, que se curtió en los tablaos más exigentes; tenemos ante nosotros a todo un personaje por carácter y bonhomía,  por rigor intelectual y pasión musical. Lo traigo aquí porque hace un tiempo escribió un delicioso cuento llamado El duende y el reloj. En él explora y explica la rítmica flamenca a la vez que trata temas como el tiempo y su carácter relativo,  o propone un viaje iniciático al estilo de Alicia en el país de las maravillas o El principito. Pronto le ofrecieron adaptarlo a la escena y así el 7 de julio de 2010 se estrenaba la obra en el Gran Teatro de Córdoba. La compañía de Javier Latorre tuvo el honor, con música original de Gabriel Expósito y Juan Requena. El duende y el reloj es una obra que contiene claves musicales mucho más sutiles que las proporcionadas por una lectura somera. En este artículo, cuyos resultados ya fueron presentados en sociedad en el Concurso Nacional de Arte Flamenco de Córdoba de 2010,  Philippe Donnier desentraña esas claves. Parte de esas claves pueden entenderse, sin duda, en relación a las matemáticas, y es por ello que este artículo en esta en esta sección. Sin embargo, no espere el lector un artículo al uso, sino provocación, sentido del humor, erudición y autenticidad. En suma, Philippe Donnier en estado puro. Francisco Gómez Martín Claves para El Duende y el Reloj Philippe Donnier, doctor en etnomusicología Nacimiento de un cuento El cuento original nació de un proyecto educativo de “2006 Año del Flamenco” dirigido a alumnos y profesores de música de escuelas de enseñanza primaria de Córdoba. Escribí la primera versión (unas noventa páginas) como texto de referencia del curso de tres meses que iba a contar con la colaboración de alumnos del Conservatorio Superior y de la Escuela de Danza. A pesar del apoyo de todas las instituciones implicadas, el proyecto fue rechazado por la Delegación de Educación y Ciencia por razones todavía enigmáticas. El pobre Duende se quedó durmiendo un año, hasta que la editorial cordobesa Puntoreklamo[1] tuvo el buen gusto de proponerme la edición de la primera parte[2]. Mientras tanto, se me ocurrió enseñar las cuatro primeras páginas del manuscrito a Javier Latorre. Se entusiasmó inmediatamente y me pidió una adaptación escenográfica para representarla con su compañía. Después de dos intentos fallidos, se estrenó el 7 de julio 2010 en el Gran Teatro de Córdoba. El propósito de este artículo es desarrollar los análisis teóricos más originales que han sido claves para el desarrollo de la obra. A modo de prolegómeno, me parece útil presentar unos cuantos conceptos básicos relacionados con las ciencias humanas. Paradigmas y etnocentrismo. Según el epistemólogo Thomas S. Kuhn 1922-1996)[3], los modelos paradigmáticos que proporcionan los preconceptos a partir de los cuales se forman las diferentes teorías de nivel inferior son tan metafísicos como científicos (y tan conscientes como inconscientes). A lo largo de la historia (eje diacrónico) los cambios de paradigma, de naturaleza revolucionaria, han sido a menudo traumáticos. En el campo de las ciencias humanas la postura etnocéntrica es también de tipo paradigmático pero el cambio no se hace en el tiempo sino en el espacio[4], el nuevo paradigma es el de un “otro” contemporáneo (plano sincrónico), hay tanto paradigmas como culturas. Para evitar desarrollos teóricos bastará con unos cuantos ejemplos: - “lo que hace más fácil el español es que las cosas se dicen como son y no como vosotros, los extranjeros, que le cambiáis el nombre a todo”, me decía un viejo andaluz. - “¡Que mal educados son los andaluces, nunca dan las gracias!”, dirá un francés al no concebir que, en el ámbito familiar, dar las gracias cada vez que te sirven agua o te pasan el pan es de bien educado en Francia pero de pesao en Andalucía. - “El compás de Seguiriya es un 6/8;3/4[5] que los flamencos cuentan al revés con acentos irregulares”, considerará un músico clásico. Dentro de la postura etnocentrista, Mi cultura es LA cultura, Mi código de buena educación es LA buena educación, Mi moral es LA moral. El lingüista americano Kenneth L. Pike (1912–2000)[6] introdujo la oposición entre descripción ética[7] y descripción émica, cogiendo de la lingüística las sílabas finales de los términos fonética y fonémica. Las descripciones fonéticas pertenecen al campo de la acústica (sonido producido) y al de la fisiología (punto de articulación y tipo de emisión de voz que permite describir el mecanismo de formación de los sonidos hablados), son de carácter objetivo y universal. Al contrario, una descripción fonémica explica el sistema lingüístico de una cultura en particular y se entiende desde la cultura estudiada. Así en etnología, una descripción ética es teóricamente del orden de la descripción objetiva, independiente de la cultura estudiada, de tipo etnográfico (aunque corra siempre el peligro de caer en un etnocentrismo paradigmático). Al contrario, una descripción émica se tiene que realizar desde la subjetividad de la cultura estudiada, es de tipo etnológico; exige del investigador aceptar el relativismo cultural e intentar, cueste lo que cueste, establecer una relación de empatía con la cultura estudiada para poner en evidencia los rasgos pertinentes de los objetos estudiados, adentrándose en su sistema de valores a priori diferente del suyo. En realidad, las dos posturas son algo utópicas pero tienen que servir de referencia ideal o de brújula para cada investigador. Al ser el flamenco una música de tradición oral y para hacer la lectura asequible al más amplio público, intentaré usar lo menos posible la escritura musical clásica, creada desde y para la música étnica de la burguesía occidental[8]. Queda por tanto bien claro que el flamenco es “otra música” cuyos rasgos pertinentes son a priori ajenos al mundo clásico, aunque se aproveche a posteriori todos los elementos de la teoría clásica compatibles con un análisis émico (desde la cultura flamenca) del corpus estudiado[9]. Para evitar cualquier confusión, me referiré siempre en este artículo al flamenco reconocido por la mayoría de los investigadores actuales como “clásico”, el que podemos disfrutar en las mejores antologías publicadas entre los años 50 y los 80, las más representativas siendo las dos publicadas por Hispavox[10]. Creación del tiempo y ciclos métricos básicos de 2 a 6 tiempos En el cuento, el tiempo nace de la nada por acción de una pluma que roza la nariz de un Duende etéreo con el corazón parado. El Big Bang desencadenado por un improbable efecto mariposa evoca el carácter casual y aparentemente repentino del acto creador. El horrible crack de carraca que marca la única hora del reloj despierta los primeros latidos del corazón, la emoción del Duende se manifiesta por una lágrima. Es esta lágrima que da finalmente vida al Duende de carne y huesos que aparece en el escenario en su esencia desnuda[11]. El sentir flamenco, como cualquier emoción estética andaluza, pasa a menudo por el dolor[12]. El reloj, medidor del tiempo físico ni siente ni piensa, solamente funciona, mientras no esté sometido a los ruidos “parásitos” del grupo de guiris que interfieren con su regularidad; figura el carácter dictatorial del pulso metronómico mecánico. En cuanto al Duende, este tiempo unario eternamente repetido le aburre rápidamente. Necesita contrastes que le sirvan de referencias en el fluir del tiempo. A punto llega el cojo con su pata de palo (C) o Dalí con su bastón (T)[13] para marcar un contraste binario: - ni más flojo ni más fuerte, solamente diferente, comenta el Duende, que descansa después de haber descubierto el 2 y sueña un baile de Zambra (T, C), muy en boga en los tiempos de Sabicas, que da vida así al ciclo binario. Investigando, el Duende encuentra solito el ciclo ternario que cuenta 1-2-3 explicitando además “con el acento en el 3”. Verdiales (C) y jaleos soñados (T) se construyen sobre esta referencia métrica. Los flamencos no suelen contar los verdiales pero usan para enseñar este ritmo con las castañuelas la serie onomatopéyica siguiente: riá riá pi ta 1 2 3 Según la teoría clásica, esto dejaría suponer una percepción “anacrúsica” que, por sistema, coloca el tiempo fuerte al principio del compás:  . No obstante, como vimos antes, a priori no tenemos porque por qué adoptar esta nomenclatura. Esperaremos adentrarnos más profundamente en el sistema rítmico flamenco antes de tomar una decisión. Para llegar a 4, nuestro Duende aritmético naïf piensa que basta con sumar 2+2. Craso error pues las estructuras rítmicas, que se rigen por las leyes de las funciones periódicas, vuelven a tomar el mismo valor al cabo de cada ciclo. Aparece el filósofo y matemático Descartes quién, socarrón, le comunica desde el cielo que, en la aritmética de los ciclos[14], 2+2=2. El Duende encuentra la solución cambiando la suma anterior por 1+3, esta manera de analizar los ciclos rítmicos no se basa en una supuesta acentuación periódica sino en agrupaciones perceptivas[15], consecuencias de contrastes entre texturas o formas sonoras distintas. / palma palma palma pie / / / 1 2 3 4 Un baile por tango (C) o un sueño por farruca (T) dan vida al ciclo métrico cuaternario. En cuanto al 5, el Duende lo rechaza por impar y primo. ¡Allá el! En el País Vasco, se canta y se baila el zortzico sobre ciclos de cinco tiempos (C). Al llegar al 6, el Duende cae otra vez en la trampa periódica 3+3=6 pero una mirada irónica de Descartes le hace recapacitar y propone el ciclo 3+2+1, coherente con la asimetría de palmas y toques por Huelva y sevillanas, compás enigmático desde la teoría clásica. La marca ternaria del pie induce a transcribir los fandangos de Huelva encajándolos en compás de 3/4, dejando así sin diferenciar las estructuras básicas del verdial y de Huelva (sevillanas en C y T). ¿Por qué Huelva y verdiales tienen aires tan distintos? El espacio unidimensional de los compases clásicos no permite esclarecer este enigma. En realidad la particularidad de Huelva radica en un ritmo multidimensional inducido por el ritmo del cante. Cuando un músico no flamenco escucha el conocido fandango “Alosnoo – , Con tu reejas - de acerooo...”, marca instintivamente con el pie ciclos binarios sobre las sílabas destacadas en negritas[16]. Para acompañar un cante por Huelva, guitarristas populares habrán utilizado el toque de verdial (cuya textura sonora tiene una periodicidad ternaria como hemos visto más arriba). Esta superposición de dos referencias métricas distintas ha engendrado una estructura rítmica multidimensional. Los ciclos ternarios de los rasgueos de guitarra “contaminados” por los acentos binarios del cante han generado ciclos de 6 tiempos. Un experimento formal permite comprobar esta teoría. Para evitar toda subjetividad de parte del guitarrista, gravamos el sonido MIDI de la transcripción de un compás de verdial tocado en bucle. Con un programa de sonido subimos la intensidad de las percusiones impares sobre un ciclo de 6 pulsos (2 ciclos de verdial) Cuando presento este ciclo sintético asimétrico en congresos, conferencias y seminarios, los aficionados flamencos suelen reconocer el “aire” de Huelva. El gráfico siguiente describe Huelva como ritmo bidimensional en un espacio intensidad x textura x tiempo[17] La estructura armónica de los fandangos de Huelva confirma la ambigüedad binaria/ternaria de este toque. Si generalizamos este análisis, podemos establecer la ley siguiente: cuando una serie sonora tiene n dimensiones, el periodo del conjunto es el mínimo común múltiplo de los n periodos correspondientes a cada dimensión. Las dimensiones musicales pueden ser muy variadas: percusión, melodía, armonía, timbre, etcétera. En todos estos casos, no tiene porque por qué haber ningún acento que defina los motivos periódicos, basta con contrastes de sonido o distancias temporales, de ahí la reflexión del Duende cuando descubre el ciclo binario: - Ni más flojo, ni más fuerte, solamente diferente. La acentuación binaria (real o virtual) superpuesta a la textura ternaria lleva a una segmentación perceptiva asimétrica con desaparición o debilitación importante del tiempo 6 del motivo rítmico:[18] Aunque el pie marque ciclos de tres tiempos, las palmas básicas por Huelva y por sevillanas son también asimétricas y generan un motivo cíclico de 6 tiempos, confirmando así nuestro análisis. Al analizar las falsetas por Huelva a la luz de los contrastes de texturas o de movimientos melódicos en lugar de buscar hipotéticos acentos, se descubren estructuras atípicas que no cuadran en absoluto con el compás de 3/4. Las tres fórmulas más frecuentes son: [3+2+1] [3 x 2] [1      2      3      |1      2      |1      ]          [1      2      |1      2      |1      2      ] tipo [3+2+1] (esquemas de referencia) tipo [3 X 2] (Niño Ricardo) Sistema de improvisación En la época clásica, el guitarrista flamenco no solía improvisar como lo hacen los músicos de jazz, creando melodía nueva en cada actuación sobre una “rueda” rítmico-armónica fija propia de una melodía “estándar”. En la guitarra flamenca “clásica”, se improvisa concatenando módulos prefabricados que son de dos tipos: - Módulos que combinan rasgueos y percusiones en compases[19] rítmicos o secciones libres[20] sobre acordes de la tonalidad respetando los usos del toque elegido. - Falsetas que son pequeñas obras melódicas autónomas desarrolladas dentro de los cánones de cada toque. Los dos tipos de módulos alternan libremente en función de las circunstancias (cante, baile o sólo) y de la inspiración. Cada guitarrista tiene un amplio repertorio de falsetas propias o imitadas de otro que tiene que elegir y encajar en el ciclo rítmico del toque correspondiente. La célula rítmica mínima por Huelva es de 6 tiempos y las ruedas armónicas del cante son de 12. El compás de Huelva de referencia costa por tanto de 12 tiempos. Siguiendo la norma que adoptamos en “El Duende tiene que ser matemático”[21], indicaremos los tiempos del compás de referencia en cifras romanas y los tiempos de los “sub-periodos” o “módulos” en cifras árabes. Los módulos básicos que sirven para construir tanto secuencias de compases como falsetas son de 6 tiempos. Hay tres clases rítmicas básicas que describimos en el esquema siguiente: a, b1 y b2. Los cambios de grises señalan las fronteras entre grupos perceptivos. Representamos ahora el esquema de improvisación con motivos de tipo [3+2+1]: Cuando el guitarrista está en stand by, toca de forma casi automática compases (ciclo percusivo-armónicos) variados de 12 tiempos. Cuando quiere “entrar” una falseta como suelen decir los guitarristas, Huelva permite 3 tipos de entradas[22]: al I, al XI o al X. Lo más frecuente por Huelva es “entrar al XI”. El guitarrista se descuelga de la rueda del compás olvidándose de ella. Se atiene ahora a la estructura propia de la falseta con ciclos de 6 de tipo a o b1, el número de módulos de 6 tiempos puede ser par o impar, si el último ciclo acaba en acorde de tónica[23], se considera que acaba en el tiempo X del compás de referencia o en el tiempo IV si acaba en acorde de dominante[24]. El esquema anterior describe el primer caso: al entrar, la falseta ha robado los tiempos XI y XII (riá mh) del ciclo principal que tiene que devolver tocando (riá mh)[25] antes de reengancharse al tiempo I del compás de referencia. Se pueden encadenar también módulos de varios tipos y multiplicar así las combinaciones. La transcripción de un toque de Huelva en el aburrido e impertinente[26] 3/4 da poca información sobre los mecanismos de producción de la música viva, es una labor de carácter ético, (externa al sistema flamenco). El camino hacia una descripción émica consiste en adentrarse en los procesos cognitivos propios de los músicos flamencos “nativos”. El esquema anterior describe mecanismos de improvisación que ponen en evidencia la composición de tipo modular. El hecho de que el pie (rayas rojas) coincida con el 1 o con el 3 del grupo /123/ del módulo [123/12/1] demuestra que no marca ningún acento sino que tiene la función de las rayas rojas del papel cuadriculado: referencia espacial o referencial en el sentido matemático de la palabra. El análisis del toque por bulerías confirma esta función pues los guitarristas flamencos son capaces de tocar motivos ternarios con pie binario y a la inversa. Además estos mecanismos típicamente “bricoleur”[27] liberan al guitarrista de cualquier angustia, permitiéndole salir siempre de cualquier apuro. Si falla la memoria (o los dedos), se puede reenganchar cualquier motivo rítmico de compás o de otra falseta, con la única condición de no perder la rueda de referencia (números romanos). El Cheri, cantaor de la familia Plantón que lleva el tablao “La Bulería”[28] en Córdoba, me soltó un día esta genialidad: “Un fallo no es tal hasta que tú lo reconozcas”, reflejo de una filosofía musical basada en tal dominio del tiempo que puede gestionarlo con total libertad. Un silencio de 6 tiempos seguido de un acorde fuerte transmuta un fallo en golpe de genio... Por estas razones considero tan peligroso para la formación de verdaderos flamencos el aprendizaje de la guitarra flamenca basado en el estudio de obras de concierto, a menudo descifradas más que leídas. El guitarrista tiene que aprender a concatenar compases y falsetas al azar y a salto de mata para adquirir la soltura y los mecanismos propios del flamenco, imprescindibles para el acompañamiento del cante y del baile, base de la cultura flamenca. Además no tiene porque imitar nada al pie de la letra sino “recortar a su medida” cualquier falseta de otro para tocarla con total dominio. El 7 La aparición de un indio desgranando un “Talá”[29] onomatopéyico es un guiño a las otras músicas del mundo y permite además introducir las onomatopeyas como medio muy eficaz en la educación rítmica. Las percusiones indias, unas de las más complejas del mundo, han alcanzado un alto nivel de sofisticación gracias a su sistema onomatopéyico totalmente formalizado. A cada tipo de percusión sobre el tabla corresponde una onomatopeya. Los bailaores flamencos utilizan constantemente onomatopeyas para describir y memorizar los pasos[30]. La diferencia con la percusiones indias es que no hay formalización sistemática de la correspondencia pasos>onomatopeyas. Tenemos allí un campo virgen para la investigación pedagógica. El 8 con cierre del compás de tango al 7 tiene poco interés teórico y como El Duende rechaza el 9, el 10 y el 11 con bromitas, saltaremos directamente al 12. El 12 Como lo comentaba ya en el Duende tiene que ser matemático, el 12 es interesante al ser múltiplo de 1, 3, 4 y 6, lo que permite una gran variedad de combinaciones. El Duende no encuentra solución y los sarcasmos de Descartes y de Dalí le desesperan. Acaba “jugándoselo a los dados”, forma de sugerir la intervención del azar en la creación artística. Al tirar 3 + 3 no sale del ciclo de 3 pero la tirada siguiente de 2 lleva de pronto a un ciclo de 8 y las dos siguientes de 2 al anhelado ciclo de 12. Con gran alegría, todo el grupo “rapea” el compás del toque por soleá acentuando el último tiempo de cada grupo perceptivo. Cuando la aventura del 12 parece concluir felizmente, aparece Leonardo, evocación del espíritu renacentista cuyo máximo representante ha sido Leonardo da Vinci (1452-1519), artista, científico, ingeniero, inventor, anatomista, escultor, arquitecto, urbanista, botánico, músico, poeta, filósofo y escritor. Representa también la oposición entre la cultura clásica y la cultura oral tradicional e intuitiva del Duende. Justo cuando se acerca al tablao, dentro del cual el grupo sigue contando a voces el compás  (desde fuera se oye unas voces indescifrables), se abre la puerta coincidiendo por casualidad con el primer grupo 1-2[31]. Leonardo percibe pues la serie propia del toque por seguiriya. Leonardo y el Duende se enfrentan, cada uno encerrado en su percepción hasta que el Duende hambriento reclame un bocadillo de jamón. Al oír la voces del Duende jamónjamónjamón, Leonardo encuentra la solución: jamón – monja / soleá – seguiriya Demuestra su teoría haciendo bailar al grupo los dos compases desfasados: Tanto Duende como Leonardo abren su mente a la percepción del otro. Melodía y armonía Principio de la secunda parte: Leonardo escribe frenéticamente, concentrado en su libreta. Recuerda al antropólogo Castaneda (1925-1998) que quería también escribirlo todo durante sus encuentros con el chaman Don Juan[32]. La estructura lineal de lo escrito compite con dificultad con la versatilidad de la creación tradicional. El Duende se mofa irónicamente de Leonardo por tener tan poca memoria. Las largas sesiones de ensayos me han confirmado con creces observaciones anteriores: memoria asombrosa de bailaores y guitarristas, capacidad de extraer esquemas rítmicos complejos de falsetas de guitarra para traducirlos al instante en pasos de baile, memoria estructural del cantaor que llega pocos días antes del estreno y memoriza entradas, salidas y letras de los diferentes estilos de cante que sostienen las coreografías. Javier y su compañía me han hecho pasar momentos mágicos a lo largo de largas sesiones de ensayo. Que estas reflexiones sirvan de homenaje a todos los artistas que han concurrido al éxito del estreno, especialmente al cuerpo de baile cuya total dedicación ha sido de máxima calidad. Durante toda la primera parte del espectáculo dedicada a la construcción de los ciclos de percusión, los artistas van vestido de blanco y negro. Se visten de color únicamente durante los sueños. Al principio de la segunda parte, el Duende se queja de la tristeza del mundo real, comparado con el de sus sueños, más alegre y bonito. Leonardo le comenta que sueña en color, melodía y armonía siendo los colores de la música. Los contrastes de colores ofrecen interesantes recursos escénicos como metáfora de los cambios de modos musicales. Se suceden así pares modalmente contrastados flamenco/mayor: soleá/alegrías, seguiriya/cabal o con cambio de fase VIII/XII: cabal/guajira. Los cambios de un palo al otro por variación de un solo parámetro demuestran que el flamenco, lejos de ser un arte anárquico fruto de una inspiración misteriosa, está fundamentado en un sistema musical complejo y fuertemente estructurado. Burla, burla, Bulería Lo de burla[33] se refiere aquí a la versatilidad del compás de Bulerías. Tenemos que considerar el compás de referencia resumido en los esquemas de palmas del ejemplo siguiente como una mera fuente de módulos rítmicos muy variados haciendo del toque por bulerías un sofisticado juego combinatorio. Hemos analizado ya los juegos modulares con el compás de Huelva, el toque por bulerías lleva estos juegos hasta la máxima complejidad. La guitarra y el baile con los contrastes de rasgueos o de redobles de taconeo aumentan la variedad de módulos que se entremezclan en una aparente anarquía perfectamente controlada. El baile del “ornitorrinco flamenco” ilustra con jocosos juegos rítmicos esta complejidad. Desgraciadamente, el copiar y pegar ha invadido los estudios de grabación y se están reduciendo a menudo las palmas a un solo esquema comodín: Relatividad del tiempo En las últimas escenas, la aparición de Einstein y Dalí permite analizar la elasticidad del tiempo musical[34]. El signo calderón encima de una nota (), no suele plantear ningún problema teórico al músico clásico, le han enseñado que si una negra está afectada por un calderón, su duración es algo más larga (el algo depende del estilo, del profesor, del alumno y del momento). ¿Cómo una negra, unidad de tiempo musical, puede ser más larga que otra? Si es más larga será una blanca o una redonda pero en absoluto una negra. Es como afirmar que hay centímetros más largos que otros. Pues eso fue precisamente lo que afirmó Eisntein en su teoría de la relatividad. En el paradigma newtoniano (física clásica), los metros son iguales en todo el universo así como los segundos. La revolución relativista[35] afirma lo contrario: el espacio y el tiempo se deforman en función de la del campo energético en el cual se encuentran inmersos. En la obra, la marioneta de Einstein afirma: - en un planeta más gordo, los segundos duran más que en un planeta chico. Al ser la energía E equivalente a la materia (cuya cantidad se mide por su masa M), esto es valido también cuando uno está inmerso en un campo electromagnético. Esta equivalencia está expresada en la famosa fórmula E = MC2 [36]. Einstein afirma también que la única forma de medir el tiempo es tomar como referencia cualquier fenómeno físico que se reproduce periódicamente y de forma natural. Es el caso del péndulo del reloj que pasa regularmente por las mismas posiciones: un segundo es el lapso de tiempo que separa una posición dada del péndulo de la siguiente vuelta a la misma posición. Cuando el tiempo se dilata, es el sustrato, el soporte del tiempo que se dilata. Pintemos cuadrículas de tablero de ajedrez en un globo con un caballo en la posición B 7. Cuando inflamos el globo, las cuadriculas se dilatan también y podemos decir que el caballo ha cambiado de sitio (las distancias han crecido) pero no ha cambiado de posición (el caballo sigue situado en B7). Una hormiga plana pegada al globo no apreciará ninguna diferencia, al dilatarse a la misma vez que el globo. Por tanto es la vuelta de lo idéntico el único recurso que tenemos para situarnos en el espacio (cuadrículas para las distancias y péndulo para el tiempo). En el mundo real necesitamos referencias para situarnos en el tiempo: los relojes públicos dan los cuartos y las horas con campanadas distintas. El amanecer y el anochecer son también momentos señalados e identificables en el fluir continuo del tiempo. Todas estas observaciones demuestran que no hay quién mida el tiempo sin observar la vuelta regular de fenómenos idénticos a sí mismos. ¿Y qué tendrá que ver esto con la música? Mucho, muchísimo pues la música se dibuja en el tiempo. El acento de los compases clásicos no es otra cosa que la vuelta regular de un acontecimiento idéntico a sí mismo. El metrónomo impone la duración de un segundo musical (negra) invariable. Se puede tocar una obra de forma mecánica inmerso en un tiempo newtoniano indeformable. Si apartamos las músicas de discoteca y las militares, toda música debería interpretase[37] dentro de un espacio relativista de tiempo deformable. El calderón señala un estiramiento del substrato temporal (el tempo), es la batuta del director o el pie del intérprete y no el metrónomo que marcan la duración del segundo musical. La negra sigue valiendo lo mismo: una ida y vuelta del pie o el movimiento correspondiente de la batuta. Aceptaremos la regla general siguiente: el tiempo se dilata (los segundos musicales duran más, las negras son más largas, la música se hace más lenta) cuando el campo energético crece. En la física, la energía se presenta bajo varias apariencias: materia, campos electromagnéticos, campos de fuerza nucleares etcétera. En la música tenemos varios productores de campos energéticos: unos internos al “texto” musical escrito (cadencia armónica importante en finales de frases, influencia del contenido emocional de unas letras, punto álgido de una melodía...) y otro externos (estado emocional del intérprete y del público, relación entre ambos...). Cuando el texto está escrito, no es demasiado problemático atribuir una duración a cada nota pues el mismo compositor ha tomado de antemano la decisión de medir su música de la forma que nos señala la partitura. Normalmente se dan indicaciones de dilatación o contracción de tiempo a lo largo de la partitura (valores metronómicos: 100 negras al minuto, calderones, ritardandos y otros accelerandos). Queda al intérprete ejecutar estas indicaciones de la forma más adecuada al contexto energético del texto y del contexto. El problema es muy distinto cuando se trata de percibir el tempo de una música no escrita de estructura temporal flexible. Recordemos que la evaluación del tiempo es posible únicamente gracias a la observación de acontecimientos idénticos que marcan los periodos. En la física relativista, es la materia / energía que crea el tiempo pero sigue siendo la vuelta de idénticos que permite medirlo. Imaginemos el planeta del Principito atravesando campos energéticos variables, su reloj marca segundos variables pero como él está sometido a los mismos efectos, evalúa correctamente el tiempo. Para un observador lejano, el reloj del Principito se ha vuelto loco al no tener regularidad alguna. Algo similar le pasa al musicólogo lejano: mide la música del otro con su propio reloj y no entiende el tiempo del otro que le parece desestructurado, al no conocer las formas musicales “autóctonas”, no reconoce los idénticos[38] que vuelven regularmente y marcan los ciclos periódicos, generadores de tiempos musicales. La única forma de entenderlo es acercarse hasta adentrarse en la planeta cultural ajeno. El caso del toque por seguiriya es emblemático: es uno de los toques flamenco que soporta las interpretaciones “rubato” más flexibles del repertorio dicho “a compás”[39]. Cualquier aficionado será capaz de marcar o percibir los tiempos I   II   III IV   V al escuchar la serie siguiente de formas sonoras. Además, la percepción del tiempo no consiste solamente en detectar pertinentemente la vuelta de los segundos, consiste también identificar el origen o el referencial de los ciclos temporales. Los flamencos perciben motivos periódicos iniciados en el primer chak (tiempo I del ciclo), la mayoría de los clásicos lo inician en el último a del trrriaaaaaa para poder así encajar el compás en el único compás de amalgama que conocen: el de 6/4;3/8. Estas últimas observaciones ponen seriamente en duda la supuesta universalidad del lenguaje musical, uno de los muchos tópicos propagados por un romanticismo populista propio de los medios de comunicación. Cuántos conciertos de violinistas famosos con virtuosos del sitar tienen más valor mediático que profundidad musical. Una música ajena a mi cultura me puede gustar y puedo disfrutar con ella pero no puedo pretender escuchar y captar de forma pertinente los detalles de una estética y de una gramática musical que ignoro. No se puede tocar rubato por seguiriya sin dominar a fondo la gramática y la semántica musical que la caracterizan. La notación musical clásica asociada a un toque metronómico permite un acceso universal a este toque pero ¿a costa de qué? Como ilustración de las clases de Einstein y Leonardo sobre relatividades, Dalí baila por fandango natural (rubato) pintando sus famosos relojes blandos que chorrean como quesos camembert (según el mismo Dalí), símbolos del tiempo flexible. El reloj clásico deja el mando para convertirse a la relatividad, dejando el papel de jefe para adoptar el de notario del tiempo creado por el artista, más humilde pero más vivo (C). Desgraciadamente, al final de la obra (T) gana el reloj clásico. Por necesidades tecnológicas de las grabaciones en estudio, el uso de la “claqueta” prohibe todo rubato a la seguiriya. A pesar de todos los pesares que puedo sentir, como guionista, al ver algo transformado este niño que he parido, no puedo acabar este artículo sin manifestar todo mi agradecimiento a Javier, a los artistas y a todo el equipo técnico por haber trabajado tanto y con tanto entusiasmo para dar vida a mi sueño.   Notas: [1] Ahora Editorial el páramo [2] Philippe Donnier, El Duende y El Reloj, ilustraciones de Francisco Naharro,, Córdoba, el páramo, 2ª ed. 2010. [3] Thomas S. Kuhn, La estructura de las revoluciones científicas, 1962. [4] Espacio geográfico o sociológico, puede haber tanta distancia cultural entre un Conservatorio y una peña flamenca como entre España e India. [5] La primera vez que pregunté a un flamenco que me explique el compás de seguiriya, me dijo: tiene cinco tiempos y se cuenta I  II  III  IV  V. Después de haberlo pensado un poco añadió, pero con dos tiempos algo más largos. [6] Kenneth L. Pike, Language in relation to a unified theory of structure of human behaviour, 2nd ed.: Mouton, The Hague, 1967 [7] No confundir con la ética en el sentido de moral. [8] Así denomino últimamente la música clásica de modo voluntariamente provocativo para dejar bien sentado que, dentro del conjunto de las músicas del mundo, es una música entre otras muchas. [9] Para que no haya confusión, me referiré siempre en este artículo al flamenco reconocido por la mayoría de los investigadores actuales como “clásico”, el que podemos disfrutar en las mejores antologías publicadas desde los años 50 hasta los 80 (Antología de Hispavox [10] Tomás Andrade de Silva, Antología del cante flamenco. HISPAVOX, 1958. José Blas Vegas, Magna Antología del Cante Flamenco, HISPAVOX, 1982. [11] El Duende va vestido con una malla color carne. [12] En mi primera estancia en Granada, un restaurador de cuadro se paró delante de una pintura y me dijo profundamente afectado: “este cuadro me duele”. Desde mi paradigma cultural, sencillamente no entendí lo que me quería decir. [13] Por necesidades escénicas o de coreografía, existen algunas diferencias entre el cuento escrito y la versión teatral. De ahora en adelante, notaremos (C) para el cuento y (T) para la versión teatral. [14] Aritmética “modular”. [15] Ver G. Cooper y L. Meyer, Estructura rítmica de la música, IDEAS BOOKS, Barcelona, 2000 y F. Lerdahl y R. Jackendoff, Teoría generativa de la música tonal, Akal, Madrid, 2003. [16] Hipólito Rossy se refiere a los ritmos superpuestos del cante y de la guitarra en las sevillanas sin llegar a analizar las incidencias estructurales en el compás de guitarra, ver Teoría del cante jondo, CREDSA, Barcelona, 1966, pag. 126. [17] Se atribuye de manera arbitraria un número a cada textura: golpe = 1 y rasgueo = 2). [18] Usamos el “mh” como onomatopeya representativa del silencio. [19] En el sentido de secuencias  percusivo-armónicas específicas de cada toque (estilo guitarrístico). [20] Toques libres como malagueñas o granaínas [21] Philippe Donnier, El Duende tiene que ser matemático, Virgilio Márquez, Córdoba, 1987. [22] Siempre habrá contraejemplos pero describimos aquí los casos mas comunes. [23] La en el tono flamenco por medio. [24] Aquí Sib. [25] La identificación de los tiempos del ciclo de referencia con texturas sonoras (y con la digitación correspondiente) permite al guitarrista no contar pues, a reconocer una forma, sabe a donde est á. Del mismo modo a nadie se le ocurre contar le números de los portales de su calle para volver a su casa porque la conoce y la reconoce. El contar lleva a un cierto autismo musical, substituyendo la numerología al sentido y al sentir musical. [26] En el sentido literal de sin pertinencia. [27] Ver técnicas del ingénieur et du bricoleur in Claude Lévi-Strauss, La pensée sauvage, Plon, Paris 1962, p. 26. [28] Donde toqué la guitarra durante ocho años. [29] Ciclo de percusión. [30] Angel Muñoz, premio nacional de baile en Córdoba, me decía hace años: si no me canto los pasos, soy incapaz de bailar. Durante los ensayos del Duende, Javier Latorre daba cada día un festival de onomatopeyas. [31] Esto me ocurrió en un curso de baile, cuando, al abrir la puerta al VIII de un ciclo por soleá, percibí un compás por seguiriya. [32] Carlos Castaneda,. The Teachings of Don Juan: A Yaqui Way of Knowledge, Washington Square Press Publication, 1968 [33] Etimología supuesta por algún flamencólogo por el carácter jocoso de este palo. [34] Ver la relatividad del tempo musical en: Philippe Donnier, Flamenco: structures temporelles et processus d’improvisation, thèse de doctorat, Université Paris X, Nanterre, 1996. [35] Cuyas consecuencias no están todavía asumidas por gran parte de la población. [36] E: energía, M: masa de materia transformada en energía, C: velocidad de la luz. [37] Desgraciadamente, las necesidades de limpieza de grabación, y los costes de la hora de estudio imponen grabaciones en pistas independientes que obligan al uso generalizado de la claqueta (marca sonora metronómica). [38] Idéntico no quiere decir igual, se refiere a una función musical idéntica del mismo modo que la mil y una maneras diferentes de pronunciar la ch (variantes fonéticas) tienen la misma función fonémica dentro de la cadena lingüística. [39] Reconocidos como periódicos por los aficionados al flamenco. A finales de los 80, hice escuchar a musicólogos del seminario de etnomusicología del Museo de Hombre de Paris grabaciones de toques por seguiriya muy flexibles. Todos atribuyeron a esta música un carácter no métrico, o libre como dicen los flamencos.

Viernes, 04 de Febrero de 2011 | Imprimir | PDF |  Correo electrónico

110. 21. (Enero 2011) De feraces relaciones

Matemáticas y música, dos Soles hermanos, con luz propia que inunda impetuosamente ventanales y descubre al ojo despreocupado partículas de polvo en suspensión, insospechadas, juguetonas, testigos de una vida secreta que desconocíamos. Cada Sol descubre con su luz el confín recóndito rebelde, la escurridiza terra ignota en el mapamundi del saber. Pero las luces de estos formidables Soles no iluminan mundos disgregados, lejanos, ajenos; iluminan un solo mundo: éste, el nuestro, el poblado por seres con sentidos y mente. Y es en este mundo ígneo donde se funde la luz de los dos Soles, como el limo fértil, como el vientre preñado, como el fragante presagio de una tormenta. La luz entreverada de los dos Soles bruñe los sentidos y afila las mientes. Ahora el ojo, antaño despreocupado, aprecia de los objetos circundantes los delicados detalles que se desperezan con el calor de ese fulgor, con el amor encerrado en una caja de plata que se cuece en volcanes que vomitan lava de diamante. Esa lava tornasola la bóveda del cielo con dientes de león que rugen en caída libre sobre el mar curvado de las pestañas del ojo, ahora sí, atento. Las matemáticas son la abstracción como voluntad, la profundidad intelectual infinita, la belleza rebelde de la conexión cierta e inesperada. Llegamos a ellas por el músculo de la razón, por el nervio de la curiosidad insaciable, por el hambre de belleza estructural, por el hambre estructural de belleza, por la bella hambre de estructura. Las matemáticas nos poseen, nos desfloran como una amante urgida, nos corroen como un feroz mal de Ébola, nos consumen como una pasión no correspondida. Las matemáticas son las mariposas bordadas en el abanico de fondo rojo bermellón que en un giro de cabeza imprevisto vimos aleatar con coquetería y, solo en ese momento y no en otro, los reflejos iridiscentes levantaron la tapa de los sesos de la vida, y solo en ese momento y no en otro, vimos girar su mecanismo, frenético y misterioso. Para cuando parpadeamos y sacudimos la cabeza incrédulos, quizás aún confiados en que la tapa seguiría abierta, solo vimos las mariposas hiératicas, glaciales, casi desafiantes, en el mar rojo bermellón del abanico. Un problemas de matemáticas es el acantilado anfractuoso bañado por la espuma de nuestros penosos intentos de solución, ablución, absolución (que nos tortura, de la mácula de nuestra torpeza, del desdoro de nuestra flaqueza). Cuando el Sol de la perseverancia ha lucido lo suficiente, cuando el firme viento de la inteligencia sopla con la necesaria humildad, cuando la sal marina abrasa su tez cuarteada, entonces el acantilado nos muestra sus recovecos secretos, sus fallas por las que hender la lanza rugiente del entendimiento, sus pasadizos conducentes al centro de sus entrañas majestuosas. Un problema de matemáticas es un duende de gorro rojo líquen que se ríe a carcajada limpia mientras trenza y destrenza los nervios del demiurgo arrebolado que sube la montaña de su esfuerzo con arrojo. El duende salta, siempre riéndose, por un entramado de andamios, el gran castillo de la abstracción. Se cuela por los huecos cuando intentas atraparlo de frente; no, no es así como se le caza, has de subir más alto que él, ocultarte del Sol del mediodía para que tu sombra no te delate, no hacer ruido alguno e ir limpio de prejuicios. Solo así podrás acercarte al duende. Encarámate a los pisos más altos con las lianas de la lógica, con la fuerza de la creatividad, con la astucia de un depredador, con la humildad de un pordiosero. Y entonces abalánzate sobre él y rápido como un rayo arráncale de las entrañas el secreto. La música, ama poderosa y tranquila compañera, siempre nos escucha con sabiduría, es cómplice discreta, entinta las vacías viñetas de nuestra vida, nos da un sentido de lo único y lo colectivo. La música es comunicación y comunión, clausura y aprehensión de uno mismo. ¿Qué comunica la música? Estructuras de sonido, superposiciones de fenómenos canoros, patrones repetidos de modo sutil pero reconocible, baile de tensiones y equilibrios, malabares de expectativas perceptuales. Pero sobre todo es comunicación de emociones y de su sabia templanza. La música pone a vibrar nuestro ser en su frecuencia natural llamando al arquero del viento, quien pone en cada flecha una emoción que viajará hasta el propileo de la aurora. Allí, una vez cruzado el umbral, estallará la emoción en mil pedazos que teñirán cada objeto del universo de una tinta que no es otra cosa que su propia esencia. Las emociones mantienen unidas las de otro modo partículas centrífugas de la realidad. La música es el alimento de toda emoción. Una nota, una lágrima. Un acorde, una euforia. Un ritmo, un consuelo. Una tesitura, una sonrisa. Una frase, una memoria vívida. Una canción, toda una tesitura vital, toda una vida. Por ello, porque en música y matemáticas hay emoción, las dos celebran continuas orgías de amantes de furor uterino al amanecer de cualquier día teñido de púrpura candor. Llaman a sus hieródulas, que salen de los gineceos cubiertas de sencillas túnicas, y se aproximan al amplio claro del bosque de las Unciones. Contemplamos signos de integral lascivos que son acariciados por corcheas complacientes; letras griegas liban montes de Venus de todo tipo de cromáticas alteraciones; conjuntos de todo pelaje, de naturales a complejos, lamen la piel brillante, esplendorosa de frecuencias fundamentales, de duraciones, de compases de amalgama, ante la presencia divertida de la madre armonía. Lenguas jugosas, rosa carnoso, se buscan y saborean las salivas recíprocas; lenguas jugosas, rosa carnoso, dan mil vueltas en espiral sobre pezones expectantes, triunfantes, aquiescentes, incandescentes. Se funden abstracción y emoción en un magma cósmico y vitelino. Se oyen, como consecuencia de esta orgía salvaje entre matemáticas y música, sonidos telúricos, aullidos omnipotentes, alaridos de fecundidad. Así es la relación entre las matemáticas y la música: feraz.

Martes, 11 de Enero de 2011 | Imprimir | PDF |  Correo electrónico