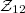111. 20. (Diciembre 2010) Las matemáticas en la música de Xenakis III

1. Introducción Xenakis fue una persona polifacética, con una gran capacidad analítica y sintética, así como una desbordante creatividad. No solo fue un compositor excepcional en cuanto que introdujo principios matemáticos en la composición musical, dando lugar así a una de las síntesis más fascinantes de la música contemporánea, sino que siempre tuvo una gran preocupación por las cuestiones teóricas, bien en el análisis musical bien en la invención de nuevos principios compositivos. Este es el último artículo de una serie de tres dedicado a Xenakis justo antes del décimo aniversario de su muerte acaecida en febrero de 2001. En este artículo, más que analizar un principio matemático que Xenakis transformó en una principio compositivo, examinaremos algunas ideas suyas que inciden más en su faceta de teórico de la música. Xenakis usó las matemáticas también como una herramienta de análisis musical, especialmente para la música del siglo XX que más radicalmente se apartaba de la tradición tonal, armónica y métrica. Siguiendo la naturaleza universal, sistematizadora, unificadora, abstracta y al tiempo analítica de las matemáticas, Xenakis estudiaba fenómenos musicales bajo la lupa de esa asombrosa disciplina. Husmeaba estructuras comunes a varios objetos musicales, reconocía qué peculiaridades se podían identificar entre los fenómenos musicales y los matemáticos, fijaba qué operaciones eran relevantes entre ellos y, finalmente, soldaba pródigamente las piezas para erigir su edificio conceptual. Cierto es que con frecuencia sus teorías no están descritas con todo detalle, pero ello no es signo de negligencia o de falta de profundidad intelectual. Xenakis seguramente dejaba esa labor para que otros teóricos de la música la completaran, pues siempre tenía la tensión de la composición sobre sí. La teoría de cribas, expuesta en su libro Formalized Music [Xen01] entre otros escritos, se ocupa de la teoría de escalas desde un punto de vista bastante general. Aquí la palabra criba puede usarse en el sentido de la criba de Eratóstenes, el procedimiento para calcular los primos tachando múltiplos sucesivos o bien en un sentido más general, como técnicas de teoría de números para contar o estimar el tamaño de conjuntos de números [Mol09] [Har07]. Xenakis usa la palabra en un sentido más bien arcaizante y, como veremos, tiene más que ver con el primer sentido, con la idea de saltar de múltiplo en múltiplo de un número dado. En el fondo las matemáticas que usa son la aritmética modular y la teoría de conjuntos. El empeño que acometió Xenakis fue el de construir una teoría de escalas que comprendiese las escalas de más de 12 notas, esto es, escalas definidas en divisiones no iguales de la octava. En la siguiente sección recordaremos algunos conceptos de la teoría de escalas. En la tercera sección expondremos los principios básicos de la teoría de cribas de Xenakis aplicada a la teoría de escalas. En la cuarta sección examinaremos algunas consecuencias de esa aplicación. 2.  Escalas musicales El primer fenómeno musical al que querríamos referirnos es el de la llamada equivalencia perceptual de la octava. El hecho de que dos tonos que están separados por una octava se perciban como equivalente perceptualmente está bastante aceptado (véase [Deu98] y sus referencias para una explicación general y [DB84] para detalles más técnicos). Dos tonos están separados por una octava si la proporción entre la frecuencia del más agudo y el más grave es 2:1. Esta equivalencia está implícita en la construcción de escalas que se encuentran en muchas tradiciones musicales, y no solo en la occidental. Como ejemplo, tenemos abajo una melodía, el comienzo de la Pequeña serenata nocturna de Mozart. Si se pincha en la imagen, se oye la melodía: Figura 1: Comienzo de la Pequeña serenata nocturna KV 525, de Mozart. Si la trasladamos la melodía una octava arriba (pínchese en la imagen para oír la nueva melodía): Figura 2: La misma melodía pero tocada una octava arriba. Nos parece mucho más similar que si la oímos, por ejemplo, una cuarta aumentada más arriba (pínchese en la imagen): Figura 3: La misma melodía ahora tocada una cuarta aumentada más arriba. 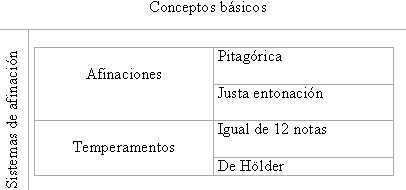Para construir una escala la octava se subdivide en un número fijo de notas y se elige un subconjunto de estas notas como la escala. La elección de las notas en que se divide la octava se llama afinación. A veces una afinación se ajusta por motivos musicales, fundamentalmente para eliminar disonancias en las modulaciones, y entonces a ese ajuste se le llama temperamento. Tras un proceso largo y no exento de dificultades [Gol92], en la música occidental se adoptó la subdivisión de la octava en 12 partes iguales, llamada temperamento igual. Cada parte de la subdivisión se llama un semitono y un tono está formado por dos semitonos. Las escalas más importantes en la música occidental son la escala mayor y la escala menor natural. La escala mayor, si la recitamos desde un do, se compone de las notas . Figura 4: La escala mayor. Si nombramos las notas de esta escala mediante el número de semitonos que componen cada nota, entonces tendríamos el conjunto , donde el 0 corresponde a la nota do. La escala menor enunciada a partir de do es y descrita numéricamente es . Figura 5: La escala menor natural. Hay dos variantes importantes de la escala menor natural, llamadas escala menor melódica y menor armónica, aparecen en las dos primersa líneas de la tabla 1. En esa misma tabla podemos observar otras escalas con distintos intervalos y número de notas. Por ejemplo, la escala que se compone de todas las notas posibles dentro de la octava se llama cromática y su descripción numérica es . La escala que salta por tonos enteros, y que Debussy popularizó, se escribe como . La escala octotónica, de ocho notas, que se forma alternando un tono y un semitono. Con este esquema de alternación salen dos escalas y (escalas octotónica I y II, respectivamente, en la tabla 1). Stravinsky usó este tipo de escala en su obra La consagración de la primavera. Otras escalas muy frecuente en muchas y diversas tradiciones musicales son las pentatónicas, esto es, las formadas por cinco notas. En la tabla de abajo mostramos la pentatónica mayor () y la pentatónica menor (). Tabla 1: Distintas escalas musicales basadas en la subdivisión de la octava en 12 partes. Hay que advertir aquí que las escalas que se muestran en la tabla 1 aparecen en otras muchas tradiciones musicales con diferentes nombres. Hemos elegido un nombre únicamente por facilidad de referencia. Una escala dada se puede nombrar cíclicamente a partir de una nota suya cualquiera y da lugar así a otra escala. Las reordenaciones de una escala se llaman modos. Por ejemplo, la escala mayor , cuando se enuncia a partir de la sexta nota (un la o el semitono 9), resulta la escala ; esta escala llevada al do inicial de nuevo, restándole 9 semitonos, da la escala menor natural . Así que la escala menor natural es un modo de la escala mayor. Véase [Har01] para una buena introducción a la teoría musical y en particular a los modos. En otras tradiciones musicales la octava no se divide en 12 partes iguales, sino que ésta sufre divisiones más finas. El sistema tonal árabe moderno usa una subdivisión de la octava en 24 partes iguales. En otras palabras, la unidad tonal básica es el cuarto de tono. En la música clásica del sur de la India, la música carnática, usan una subdivisión en 22 partes. En la música del gamelán de Java también se usan afinaciones con más de 12 partes por octava y además estas partes no son de igual tamaño. Los temperamentos anteriores al temperamento igual tenían asimismo intervalos menores que el semitono (la afinación justa o el temperamento mesotónico; véase [Gol92]). En la Grecia clásica también se encuentran afinaciones con subdivisiones muy finas de la octava. Aristóxenes propone una afinación con 72 subdivisiones de la octava. 3. Teoría de cribas Como dijimos en la introducción, Xenakis usó la aritmética modular para dar una teoría general de la construcción de escalas bajo divisiones iguales de la octava. Superaba así el temperamento igual de 12 subdivisiones. Consideró escalas que se podían construir con cualquier unidad: semitonos temperados (1/12 de octava), segmentos de Aristóxenes (doceavos de un tono), cuartos de tono, tonos enteros, segundas, terceras, cuartas y quintas. Por completitud en la exposición, repasaremos brevemente algunos conceptos básicos de la aritmética modular. Sea n un entero al que llamaremos módulo. Dados dos enteros x e y, se dice que x es congruente con y módulo n si x-y es divisible por n. La relación de congruencia es una relación de equivalencia, esto es, es reflexiva, simétrica y transitiva (es muy fácil de probar). Como tal relación de equivalencia tiene un conjunto cociente. Fijado un módulo n y dado un entero x, su clase de equivalencia está formada por el conjunto: Las clases de equivalencia identifican aquellos elementos separados por un múltiplo entero del módulo y sirven para trabajar con operaciones cíclicas. El conjunto de clases de equivalencia módulo n se designa por . Fijado un módulo n y un entero a, una criba elemental es una aplicación afín discreta en , dada por: Por ejemplo, si n=12, el caso del temperamento igual, entonces 20 = , donde los números entre llaves han de interpretarse como clases de equivalencia. Si escogemos un número que es primo relativo con 12, por conocidas propiedades de la aritmética modular, obtenemos el conjunto entero . Tomemos, a=2 y x=5, por ejemplo: Una criba compuesta es un conjunto de clases que se obtiene tomando uniones e intersecciones finitas y complementarios de cribas elementales. Si seguimos en el universo de los doce semitonos iguales y tomamos las siguientes cribas elementales: entonces podemos generar cribas compuestas como sigue: La escala cromática, la que comprende todos los semitonos de la octava, se expresa como la criba elemental 10. La escala de tonos enteros se escribe como 20. ¿Cómo se escribiría la escala mayor? Esta escala no se puede escribir como una criba elemental, pues sus notas no están dispuestas regularmente en la octava. La escala mayor se expresa como la siguiente criba compuesta: Comprobemos que es así. Por un lado tenemos: Haciendo la unión de las intersecciones resultantes sale la escala mayor . Anteriormente, afirmamos que la escala menor es un modo de la escala mayor. Basta enunciar la escala mayor a partir de la nota la para obtener la escala menor. La correspondiente criba compuesta para esa escala es: Dejamos al lector los cálculos, que son directos y fáciles. ¿Hay alguna relación entre la criba de una escala mayor y cualquiera de sus modos? Sí, y no es muy difícil darse cuenta de que es un juego de índices y módulos. Si queremos generar la criba del modo de una escala mayor a k semitonos de distancia, ésta es: Los índices de las cribas elementales generadas por las terceras menores aumentan módulo 3, mientras que las cribas de las cuartas lo hacen módulo 4. Si consideramos una subdivisión de la octava en cuartos de tono, entonces la criba asociada con la escala mayor es: donde k=0,1,..., 23 se toman módulo 3 u 8, según el caso. Las cribas de Xenakis pueden describir de manera relativamente concisa escalas de distintos temperamentos iguales, como la división de Aristóxenes e incluso escalas mixtas, como la bizantina, que mezcla tetracordos cromáticos y diatónicos (véase [Xen01], páginas 197 y siguientes). 4. Conclusiones Esperamos que con estos pequeños ejemplos haber ilustrado las ideas teóricas de Xenakis. La idea de las cribas resultó atractiva a varios teóricos y analistas de la música, los cuales incluso la llevaron incluso más lejos. En particular, ha encontrado fervientes partidarios en el análisis transformacional de David Lewin. Thomas Noll y sus coautores [NAA06] aplican la teoría de cribas al análisis del estudio para piano opus 63, número 5, de Scriabin. El análisis es exitoso pues ese estudio de Scriabin usa escalas de tonos enteros y octotónicos, que se describen con facilidad con cribas. Varios autores importantes han dedicado artículos a la teoría de cribas, bien desde un punto de vista filosófico o desde un punto de vista puramente analítico. Jones [Jon01] sistematiza las cribas y formaliza ciertos aspectos algorítmicos de la formulación inicial de Xenakis. Exarchos [Exa07] aborda la generalización de las cribas a otros paramétros musicales. Harley, en su libro Xenakis: His Life in Music, dedica un capítulo a las cribas y sus implicaciones musicales en la obra de Xenakis. Como no podía ser de otro modo, Xenakis empleó las cribas en sus composiciones musicales. Una de las primeras obras en que las probó fue Nomos Alpha, para violonchelo solo. Aparte de las cribas usa otras ideas matemáticas, como grupos de simetrías y lógica proposicional. Para un análisis exhaustivo y clarificador, véase el excelente artículo de Jan Vriend [Vri81]. En el vídeo de más abajo se puede oír esta pieza por el excelente percusionista Steve Schick. 5. Para saber más Se recomienda al lector interesado en la teoría de escalas el libro de Sloniminsky [Slo75]. Este autor estudia la construcción de escalas a partir de la subdivisión des una octava a once octavas; también hace un examen exhaustivo de otros criterios de construcción de escalas. También recomendamos el libro de Yamaguchi [Yam06]. Para profundizar en el apasionante tema de las afinaciones y temperamentos, véase el libro de Javier Goldaraz [Gol92] y las referencias en él contenidas. La escala mayor tiene una interesante estructura. Se escribe como , y se observa que tiene una primera parte que va por tonos enteros, del do al mi, después hay un semitono, y de nuevo progresa por tonos. Pressing [Pre83] interpretó esta secuencia en el dominio del ritmo y halló que corresponde a un ritmo de clave, escrito en notación de caja como [x . x . x x . x . x . x], llamado el ritmo estándar por los musicológos, tan frecuente e importante es. Pressing lo ve como el análogo rítmico a nuestra escala mayor. Referencias [DB84] Diana Deutsch and Richard Boulanger. Octave equivalence and the immediate recall of pitch sequences. Music Perception, 2(1):41-53, 1984. [Deu98] Diana Deutsch. The Psychology of Music. Academic Press, second edition edition, 1998. [Exa07] Dimitri Exarchos. Injecting periodicities: Sieves as timbres. In Proceedings SMC'07, 4th Sound and Music Computing Conference, 2007. [Gol92] Javier Goldaraz. Afinacion y temperamento en la musica occidental. Alianza, 1992. [Har01] Jonathan Harnum. Basic Music Theory: How to Read, Write, and Understand Written Music. Questions Ink. Publishing, 2001. [Har07] Glyn Harmann. Prime-Detecting Sieves. (London Mathematical Society Monographs). Princeton University Press, 2007. [Jon01] Eva Jones. Residue-class sets in the music of iannis xenakis: an analitical algorithm and a general intervalic expression. Perspectives of New Music, 39(2):229-261, 2001. [Mol09] Richard Mollin. Advanced Number Theory with Applications. Chapman and Hall/CRC, 2009. [NAA06] Thomas Noll, Moreno Andreatta, and Carlos Agon. Computer-aided transformational analysis with tone sieves. In SMC 06, 2006. [Pre83] Jeff Pressing. Cognitive isomorphisms between pitch and rhythm in world musics: West Africa, the Balkans and Western tonality. Studies in Music, 17:38-61, 1983. [Slo75] Nicolas Slonimsky. Thesaurus Of Scales And Melodic Patterns. Music Sales America, 1975. [Vri81] Jan Vriend. Nomos Alpha for violoncello solo (xenakis 1966) analysis and comments. Journal of New Music Research, 10:15-82, 1981. [Xen01] Iannis Xenakis. Formalized Music: Thought and Mathematics in Composition. Number 6 in Harmonologia. Pendragon Press, Hillsdale, NY, 2001. [Yam06] Masaya Yamaguchi. The Complete Thesaurus of Musical Scales. Masaya Music, 2006.

Jueves, 09 de Diciembre de 2010 | Imprimir | PDF |  Correo electrónico

112. 19. (Noviembre 2010) Las matemáticas en la música de Xenakis II

Estrategias musicales 1. El conflicto En esencia, la música es conflicto. El discurso musical progresa a través de la dialéctica entre sus partes. En cualquier pieza de música se observan episodios de tensión combinados con otros de equilibrio. Esa dialéctica generadora del conflicto aparece en varios niveles musicales: en la melodía, en la armonía, en el ritmo, en la conducción de las voces, en la instrumentación y, por supuesto, en la forma. En distintas épocas los estilos musicales predominantes han marcado preferencias sobre la forma de usar el conflicto como motor de la música. Sabemos, por ejemplo, que los conceptos de disonancia y consonancia han ido ensanchándose a lo largo de la historia de la música. En el Barroco un acorde de séptima de dominante, considerado disonante, tenía que resolverse; eso no es tan evidente en la música de principios del siglo XX, donde se aceptan esos acordes con total naturalidad, y aún menos en el jazz. Analicemos la presencia del conflicto con un breve ejemplo tomado de la Pequeña serenata nocturna KV 525, de Mozart. El primer movimiento de esta serenata tiene forma sonata con dos temas que contrastan entre sí. El pasaje que examinamos en la figura 1 en una reducción para piano es el paso del primer tema, en sol mayor, al segundo tema, en re mayor. Figura 1: Pasaje de la Pequeña serenata nocturna KV 525, de Mozart Para dar interés musical a ese paso entre los dos temas, Mozart introduce varios elementos de tensión: Dinámica (volumen). Obsérvensen los compases 1 y 2, en que hay un sforzando (cambio súbito de volumen), un sf seguido de un piano (p). Al final de compás 3 hay una escala ascendente que tocan los violines en vibrato; esta escala comienza un crescendo (aumento progresivo de volumen) que culmina en el re final del compás 5 tocado en forte (fuerte). Armonía. En los tres primeros compases hay un pedal de tónica. Un pedal es una nota o armonía que se mantiene fija mientras se producen otros cambios armónicos. En este caso es la nota sol sobre la que se alternan los acordes de sol mayor y re mayor. En los compases 3 y 4 aparece la cadencia IV-VII6-I para afirma la tonalidad de sol, con el acorde de séptima de dominante incompleto. En el compás 4 se produce la secuencia de acordes V-I en sol, que, sin embargo, es reinterpretada como la secuencia I-V en la nueva tonalidad de re mayor. Esta técnica de cambio de tonalidad (llamada modulación en el lenguaje musical) se llama del acorde pivote y consiste en usar acordes comunes a dos tonalidades para modular. Al entrar en la nueva tonalidad Mozart usa de nuevo la cadencia IV-VII6-I (compases 4 y 5) y un pedal de tónica V7/I (compases 5 y 6). En los compases 8 y 9 se oye la secuencia II56-V56 del V-V, que no es sino una afirmación del quinto grado de re (el la) por medio de dominantes secundarias. La secuencia desemboca en una cadencia rota con un pedal de dominante. En los compases 1 y 2 el ritmo es relativamente sencillo, con las notas sobre las partes fuertes de la métrica. En los compases 5 y 6 el ritmo se agita más al aparecer combinaciones de negras y corcheas ambas con puntillo. Finalmente, en los compases 7 y 8 las voces superiores hacen una síncopa (contradicción momentánea de la métrica establecida), que es además un pedal de la nueva tónica. En el compás 8 Mozart añade sutilmente un mi, que forma un intervalo disonante de segunda mayor con el re del pedal, y que sirve de apoyo a la progresión II56-V56 del V. En el compás 9 la síncopa se resuelve así como la disonancia y la melodía vuelve a una figuración de corcheas sobre las partes fuertes. Con este pequeño ejemplo se ve cómo opera el conflicto en varios niveles musicales. Las ideas musicales del compositor se plasman en la partitura, de la cual director e instrumentistas extraen la información necesaria para mostrar la música y sus conflictos internos. Xenakis reflexionó sobre el conflicto interno en la música, sobre todo a finales de los 50 y a principios de los 60. También reparó en que durante la ejecución de la obra musical emerge otro tipo de conflicto: el de la propia ejecución. En efecto, existe también una dialéctica entre partitura e intérprete. En ambos tipos de conflicto -indagaba Xenakis- no hay margen para la improvisación. Por un lado, el compositor ha fijado, hasta donde le permite la notación musical, sus ideas musicales, reveladas a través de la dialéctica de los elementos musicales; y éstos, por otro lado, determinan el conflicto partitura versus interpretación. En todo caso, es siempre un conflicto interno. Xenakis llamó a la música caracterizada por estos conflictos internos música autónoma. Incluso en la música estocástica, aunque goce de más margen de maniobra, las tensiones siguen confinadas a la partitura. Xenakis quería superar la música autónoma y experimentar con música que no solo poseyera ese carácter interno. Introduce, pues, el concepto de conflicto externo [Xen01], página 111): "Sería interesante y probablemente fructífero imaginar otra clase de discurso musical, el cual introdujese el concepto de conflicto exterior entre, por ejemplo, dos orquestas o instrumentistas contrarios". Su formación matemática y su creatividad musical le señalaron el camino una vez más. Imaginó la superación de la premisa del conflicto interno vía la teoría de juegos. En teoría de juegos tenemos dos jugadores que juegan por turnos y que siguen ciertas estrategias para ganar el juego. Xenakis pensó en dos orquestas compitiendo entre sí en un juego finito de suma cero. Cada orquesta dispondría de ciertas tácticas sonoras y los directores de las orquestas jugarían en función de lo que escuchan. En la siguiente sección explicamos algunos conceptos sencillos de teoría de juegos que nos ayudarán a entender la música de Xenakis que analizamos en el artículo de hoy. 2. Teoría de juegos La Teoría de Juegos es una disciplina matemática de pleno derecho (clasificación AMS: 90D). Su objetivo es el estudio de la estrategia para ganar en juegos modelizados matemáticamente. Esta definición, si bien general, se adapta con versatilidad a varios y dispares campos de aplicación. Con particular éxito, la teoría de juegos se ha usado en Economía para estudiar desde la competitividad en el mercado hasta la distribución de la riqueza. Podemos encontrar aplicaciones de la teoría de juegos en la Biología (problemas de equilibrio ecológico), en el diseño de acciones militares, en Sociología o en Ciencias Políticas (sistemas de votación), en Filosofía (para estudiar el concepto de convención) y, por supuesto, en Informática. Aquí nos contentaremos con introducir unas cuantas definiciones básicas para entender las ideas musicales de Xenakis. Para profundizar más en este fascinante tema se remite al lector a [Pet08] y a sus referencias bibliográficas. Empezaremos con un ejemplo. Dos equipos de exploradores, llamémosles A y B, tienen que someterse a una prueba. El equipo A tiene que ir desde el campamento este al campamento oeste y para ello tienen dos rutas disponibles, por el norte que se tarda 2 días, y por el sur que se tarda 3 días. El equipo A sale primero y unas horas más tarde, el equipo B, cuya misión es rastrear y dar alcance al equipo A. El equipo B desconoce qué ruta tomará el equipo A. Si el equipo B toma la ruta equivocada, puede regresar al campamento este y desde allí tomar la otra ruta. Ese error, no obstante, le cuesta al equipo B un día de retraso en la persecución del equipo A. La prueba se puede modelizar como un juego de dos personas, los equipos A y B, que compiten entre sí. La siguiente matriz modeliza matemáticamente el juego (figura 2): Figura 2: Matriz de un juego. La matriz se interpreta como sigue: Las elecciones de la ruta del equipo B se leen por filas. Las elecciones de la ruta del equipo A se leen por columnas. Las elecciones que hace cada equipo son independientes entre sí y se hacen simultáneamente. Los números de la matriz se leen como el pago que el equipo A hace al equipo B. Esta es una convención habitual en teoría de juegos. ¿Cuál es la estrategia ganadora para este juego? Si el equipo A elige la ruta norte, tendrá 1 o 2 días de persecución; en cambio, yendo por el sur dicho número de días sube a 2 o 3. En cuanto al equipo B, si elige la ruta por el norte siempre dispondrá de 2 días de persecución independientemente de la elección del equipo A. Por tanto, ambos equipos eligen la ruta norte. El lector quizás se haya dado cuenta de que la combinación norte-norte es máxima en su columna (2 1) y mínima en la fila (2 2). Una posición en la matriz para la que ocurre esto se llama punto de silla (equilibrio de Nash). También se observa que en el punto de silla el equipo B maximiza el pago mínimo recibido y el equipo A minimiza el pago máximo entregado. Este tipo de juegos se llama juego de suma cero porque la cantidad que recibe un jugador es igual a la que pierde el otro jugador para cualquier estrategia. 3. La Teoría de Juegos en la música de Xenakis Las obras más emblemáticas en las que Xenakis usó la teoría de juegos son Duel(1959) y Stratégie (1962). Analizaremos esta última para ilustrar la materialización de las ideas de Xenakis. Stratégie (1962) es una obra para dos orquestas, cada una con su propio director. Las orquestas se colocan una enfrenta de la otra, con los directores dándose la espalda. Los directores disponen de seis construcciones sonoras, como las llama Xenakis, de naturaleza estocástica (véase el artículo anterior de esta serie), numeradas del I al VI. Estas construcciones estocásticas se calcularon con la ayuda de un ordenador IBM 7090. Las construcciones sonoras son las partes constitutivas de las tácticas del juego, que son las siguientes: I.- Instrumentos de viento (madera y metal).II.- Instrumentos de percusión.III.- Toques con la mano en la caja de resonancia de los instrumentos de cuerda.IV.- Efectos puntillistas con los instrumentos de cuerda.V.- Glissandi con los instrumentos de cuerda.VI.- Armonías continuas tocadas por los instrumentos de cuerda A cada director se le permite ejecutar dos o tres tácticas simultáneamente, pero Xenakis determina la compatibilidad entre ellas en la siguiente tabla: En total, hay 19 tácticas: 6 tácticas formadas por una única construcción sonora (I a VI), 9 formadas por dos construcciones (VII a XV) y 4 formadas por tres construcciones (XVI a XIX). Por tanto, en cada turno los directores pueden tocar una de las 192=361 posibles combinaciones de tácticas. La pieza Stratégie se concibe como la ejecución de un juego finito de suma cero para dos personas. Las reglas son las siguientes: Elección de las tácticas. Aunque Xenakis ofrece varios sistemas para elegir las tácticas (véase la página 23 de [Xen01]), aquí describiremos solo uno de ellos, el sistema de elección arbitraria. Consiste en que cada director elige su táctica en función de su propio gusto musical y de la táctica que ha elegido el otro director. Matriz del juego. Hay una matriz que contiene los pagos para cada posible táctica. Esta matriz está delante de los directores durante la ejecución de la pieza. En la figura 3 tenemos dicha matriz (la matriz está tomada del libro de Xenakis [Xen01], página 128). Figura 3: Matriz del juego de la obra Stratégie. Los símbolos que aparecen a los lados de la matriz son iconos para ayudar al director a reconocer las cualidades sonoras de cada táctica. Xenakis introdujo dos matrices auxiliares para simplificar la lectura de la matriz principal durante la ejecución de la pieza. Duración de los turnos. Los turnos tendrán una duración mínima de 10 segundos. No habrá duración máxima. Duración del juego. Los directores acordarán jugar un número fijo de turnos. Obtención de los puntos. De nuevo, Xenakis ofrece varias posibilidades. Una de ellas es tener un árbitro que cuente los puntos obtenidos en cada turno. Lectura de las tácticas. Las orquestas tocan las tácticas de manera cíclica hasta que reciban la señal de parar por parte del director. El director puede empezar una táctica en ciertos puntos que se encuentran marcados en la partitura con letras. El director indica el número de táctica y la letra con unas tarjetas que muestra a la orquesta. Resultado. Al cabo de los turnos establecidos se termina la pieza y se hace el recuento de los puntos de cada director. Gana quien más puntos haya obtenido. En la figura 4 vemos un gráfico de Xenakis durante la concepción de Xenakis. Figura 4: Disposición de la orquesta en Stratégie ([Xen01]). Para terminar gozosamente esta sección, dejamos aquí dos vídeos con la música de Stratégie: Parte 1. Parte 2. 4. Conclusiones Xenakis transcendió el concepto de conflicto interno forzando a que el conflicto alcanzara al director de orquesta. Tomó dos orquestas y las puso a competir musicalmente sobre la base de un juego finito de suma cero para dos personas. Así, Xenakis expande los fundamentos matemáticos de la música en todas sus dimensiones: alturas y escalas, ritmo, timbre, forma y en esta ocasión también la naturaleza de la propia dialéctica musical. Al contrario de la mayoría de los músicos, Xenakis estaba al tanto de los nuevos avances en ciencia y tecnología. Este conocimiento alimentaba su imaginación y sus teorías musicales. 5. Para saber más El capítulo 2 del libro de Curtis Roads [Roa04] es un análisis del concepto de microsonido. Examina la obra de varios compositores que han usado este concepto, entre ellos, Xenakis. Ton de Leeuw analiza en su libro Music of the Twentieth Century: a Study of its Elements and Structure [dL06] la música del siglo XX desde un punto de vista estructural e incluye a Xenakis en dicho análisis. El libro de Dutta [Dut99], profesor del MIT, es un texto clásico que explica la teoría de juegos para estudiantes de ciencias económicas. Para una referencia de teoría de juegos desde un punto de vista algorítmico pero todavía abstracto, véase [NRÉTV10]. Para ver una cronología de la teoría de juegos, que se remonta a los babilonios y que en nuestros días cuenta con premios Nobel, véase la página web de Paul Walker [Wal10]. La página Les amis de Xenakis [Xen10] contiene información completa sobre su vida, su obra, así como la posibilidad de escuchar fragmentos de su obra. Bibliografía [dL06] Ton de Leeuw. Music of the Twentieth Century. Amsterdam University Press, 2006. [Dut99] Prajit K. Dutta. Strategies and games: theory and practice. The MIT Press, 1999. [NRÉTV10] Noam Nisan, Tim Roughgarden, Éva Tardos, and Vijay Vaziraini. Algorithmic game theory. http://www.cambridge.org/journals/nisan/downloads/Nisan_Non-printable.pdf Accedido en octubre de 2010. [Pet08] Hans Peters. Game Theory. Springer, 2008. [Roa04] Curtis Roads. Microsound. The MIT Press, 2004. [Wal10] Paul Walker. A chronology of game theory. http://www.econ.canterbury.ac.nz/personal_pages/paul_walker/gt/hist.htm Accedido en octubre de 2010. [Xen01] Iannis Xenakis. Formalized Music: Thought and Mathematics in Composition. Number 6 in Harmonologia. Pendragon Press, Hillsdale, NY, 2001. [Xen10] Xenakis.org. Les amis de Xenakis. http://www.iannis-xenakis.org/ Accedido en 2010.

Miércoles, 03 de Noviembre de 2010 | Imprimir | PDF |  Correo electrónico

113. 18. (Octubre 2010) Las matemáticas en la música de Xenakis I

1. Introducción Recién acabada la carrera de Matemáticas y con ocho años de estudio de piano tuve la gran suerte de conocer a Andrew Melvin, a la sazón miembro del grupo de música contemporánea Secuencia. Andrew Melvin fue mi profesor de piano y composición durante un tiempo. Al poco de conocernos -yo creo que cuando estuvo seguro de mi sensibilidad musical- me mostró la música de Iannis Xenakis. Su música me fascinó desde el primer momento, me cayó como un chorro de luz corpórea y sin darme tiempo a reaccionar me llevo a hermosos mundos de emociones. Muchos días a última hora de la tarde, aún sin tener clase con él, iba a buscarlo con unos bocadillos, nuestra humilde cena, y nos quedábamos escuchando a Xenakis, sin mediar palabra, absortos en nuestro misticismo musical, solo sonriéndonos mutuamente al terminar alguna pieza. Escuchábamos con fruición sus primeras obras (Metastasis, Pithoprakta, Achorripsis), la música estocástica (la serie de los ST), las obras para solista (Mika, Evryali), las obras con percusión (Pleiades, Aïs, los dos Idmen), todo lo que caía en nuestras manos. En aquel tiempo yo no era consciente de la importancia conceptual de Xenakis como habilitador de la formalización matemática en la composición musical. Estaba sencillamente deslumbrado por su estética, tan original y revolucionaria. La música de Xenakis, obviamente, superaba el tonalismo, pero también la música de la segunda escuela de Viena (el atonalismo y el dodecafonismo) y también constituía una reacción reflexiva y genuina contra el indeterminismo de Cage. Su música, al contrario que otras músicas modernas, siempre me emocionaba. Años más tarde leí Formalized Music [Xen01] (figura 1) y adquirí consciencia de la importancia teórica de la obra de Xenakis. La gran cantidad de libros, artículos y conferencias que nos dejó revelan su preocupación por aclarar su pensamiento musical. Figura 1: Portada del libro Formalized Music: Thought and Mathematics in Music. 2. Breve biografía de Xenakis Xenakis nació en 1922 en Rumania, aunque su familia era griega. Su madre era pianista y es la que le introduce en la música desde temprana edad. La madre de Xenakis muere cuando él tiene cinco años de edad, hecho que le traumatiza -"su muerte me dejó profundamente asustado", diría años más tarde. A la edad de 10 años Xenakis vuelve a Grecia y su padre lo envía a un internado. Allí estudia filosofía, literatura europea, matemáticas, ciencias y música. Xenakis canta en un coro de música polifónica del Renacimiento y de música litúrgica bizantina. Por esa época empieza a estudiar piano. Mientras, estalla la Segunda Guerra Mundial y las tropas italianas, y más tarde las alemanas, invaden Grecia. Esto fuerza a Xenakis a interrumpir sus estudios de ingeniería que hace poco ha empezado. Se une a la resistencia de izquierdas, unión que le cuesta la cárcel en varias ocasiones. En 1944 una bomba de mortero lo alcanza y lo pone al borde de la muerte. La explosión le provoca la pérdida de un ojo y le desfigura la parte izquierda del rostro. En 1946 acaba sus estudios de ingeniería. A causa de su activismo político tiene que pasar a la clandestinidad. Su padre arregla los papeles para que pueda emigrar y en 1947 llega a París. En aquella época Xenakis siente un profundo desencanto hacia la política y las instituciones sociales en general. Siente que su vida debe cambiar de rumbo. Poco después de su llegada a París entra a trabajar como ingeniero en el estudio del famoso arquitecto Le Corbusier. En esa etapa Xenakis participa en varios proyectos importantes tales como el convento de La Tourette o el Pabellón Philips de la Exposición Universal de Bruselas (1956). Le Corbusier y Xenakis comparten un gusto por los sistemas de proporciones. Xenakis no deja en ningún momento su carrera musical. Empieza a estudiar con Honegger y Milhaud, pero los ejercicios de armonía y contrapunto que le proponen no satisface sus necesidades musicales y pronto deja sus clases. A sugerencia de Le Corbusier se presenta ante Messian para que le dé clases de composición. Messian lo anima a que aplique sus ideas matemáticas a la composición musical. Xenakis adquiere un buen conocimiento de los modos de Messian, no solo en la altura, sino también en la duración, la dinámica y la articulación. El contacto con Messian le hace consciente del poder de la abstracción en la composición. En aquellos convulsos años 50 hay una gran polémica sobre la aceptación o rechazo del serialismo. Xenakis rechaza tanto el serialismo europeo como el indeterminismo americano y, como Messian, toma un camino diferente. A partir de finales de los años 50 Xenakis empieza a aplicar sistemáticamente las matemáticas en la composición a través de una formalización de los parámetros y procesos musicales. En su obra podemos encontrar obras cuyos principios compositivos se basan en la teoría de probabilidades, en las cadenas de Markov, en la teoría de juegos, en principios geométricos y en otras ramas de las matemáticas. En 1953 se casa con la periodista y escritora Françoise Xenakis, con quien tiene una hija, Mâkhi. Más tarde, Xenakis entra en contacto con los fundadores de la música concreta, Pierre Schaeffer y Pierre Henry. También colabora con Edgar Varèse. En 1963 publica la primera versión de Formalized Music (en francés), que luego amplía, reescribe en inglés y revisa en sucesivas ediciones (1971, 1990, con posteriores reediciones). Xenakis es también un pionero de la música electrónica. Funda un laboratorio, el CEMAMu, en que estudia la aplicación de la informática a la música. A principios de los años Xenakis es una figura reconocida de la música contemporánea del siglo XX. Tiene una carrera exitosa como compositor, pedagogo y teórico de la música que dura hasta 1997, año en que su salud le impide componer. Muere en 2001 tras una larga enfermedad. 3. Matematización de los parámetros musicales Las primeras frases del capítulo de su libro Formalized Music [Xen01] son en sí mismas una declaración de principios: "El arte, y por encima de todo la música, tienen una función fundamental, y ésta es la de catalizar la sublimación que tiene lugar a través de cualquier medio de expresión". Xenakis fue, ante todo, un verdadero artista. En el análisis de su obra se ve que la decisión artística, la voluntad de expresividad a ultranza, está por encima de las consideraciones matemáticas y sus posibles constricciones. Las matemáticas, con proporcionar una nueva manera de concebir la composición, siempre estuvieron para Xenakis al servicio del concepto artístico. Xenakis se sentía ajeno tanto a la estética del serialismo, con su música sobreestructurada, aperiódica, compleja, así como del postserialismo encarnado por Cage, con su música basada en la indeterminación y el azar. De los serialistas rechazaba Xenakis su extraordinaria complejidad y arguía: "La polifonía lineal se destruye a sí misma a causa de su propia complejidad; lo que se oye no es en realidad más que una masa de notas en diversos registros. Su enorme complejidad impide al oyente seguir el entramado de las líneas, y tiene como efecto macroscópico una dispersión irracional y fortuita de sonidos a lo largo de toda la extensión del espectro. Hay, por tanto, una contradicción entre el sistema polifónico lineal y el resultado percibido, que es de una superficie o masa. Esta contradicción inherente a la polifonía desaparece cuando la independencia del sonido es total". Xenakis llama polifonía lineal al contrapunto serialista. Aunque consta de varias voces, todas han de percibirse como un todo, como una única voz; y de ahí, el adjetivo lineal. Aquí aparece uno de los principios más importantes en la música de Xenakis, el cual le permite superar la susodicha contradicción: la independencia total del sonido. Respecto al indeterminismo, Xenakis objeta la falta de un principio causal en la concepción musical. Si las alturas de una pieza se eligen en base a las imperfecciones de un papel (como es el caso de Music for piano, de Cage, por ejemplo), Xenakis duda seriamente de que esa elección transmita algún tipo de significado estético-musical al oyente. Sobre este problema del indeterminismo el crítico Pousseur [Pou66] ya había señalado que "donde se usan las más abstractas construcciones, uno tiene la impresión de encontrarse ante la presencia de las consecuencias de sonidos tocados libre y aleatoriamente". La respuesta de Xenakis a los problemas estéticos de ambas tendencias proviene de las matemáticas. Por un lado, el sonido ha de tener total independencia y, por otro lado, la música ha de poseer un significado global, derivado éste de la acumulación de los efectos individuales de las partes. Xenakis identificó estas dos condiciones con el enunciado de la ley de los grandes números de Bernouilli (véase [RS00]). Para otras versiones más generales del teorema así como para su demostración, véase [RS00] y sus referencias. El significado musical resultante está aquí representado por la media μ común a todas las variables independientes. Es el significado global, macroscópico, que surge de las causas independientes. Xenakis emprendería un camino de exploración de esas ideas matemáticas en la composición musical. La primera obra en que puso en práctica estas ideas fue Metastasis (1953-54), donde formalizó ciertos parámetros musicales de modo matemático, sobre todo usando geometría y matemática discreta. Fue aún más lejos en otra obra posterior, Pithoprakta (1955-56), donde, siguiendo con su razonamiento, se inspiró en la mecánica estadística para su composición, en particular, en la teoría cinética de los gases de Boltzmann [MF71]. Esta teoría se basa también en la ley de los grandes números. Boltzmann explica el efecto macroscópico de la presión como el efecto de los choques de las moléculas, choques que son independientes, cada uno de ellos de efecto muy pequeño y que ocurren en número muy alto. Xenakis propone en Pithoprakta una representación sonora (una sonificación [vaaat10]) de ese fenómeno. 4. Formalización matemática de los parámetros musicales Xenakis, como hemos dicho, usó una amplia gama de técnicas matemáticas para formalizar la música. Las que exponemos en esta sección pertenecen a su llamada música estocástica, que debe su nombre al hecho de que la formalización descansa en la teoría de probabilidades. Para su música estocástica Xenakis formalizó los siguientes parámetros musicales: la duración de las notas, la densidad de la nube de alturas, la velocidad del glissando, las dinámicas y la instrumentación. Duración de las notas. Xenakis usó la distribución exponencial para determinar la longitud de las notas. La función de densidad es: f(x) = δ · e-δx (1) donde δ es la densidad (en lo que sigue usaremos la notación del propio Xenakis). Como se sabe la esperanza o media de esta distribución es E(X) = 1/δ,de modo que la densidad es la inversa de la duración media de la nota. Una densidad alta produce notas cortas y en cambio una densidad baja, notas largas. En la figura 2 se muestra la gráfica de la función de densidad con los parámetros δ = 1y δ = 2. Figura 2: Función de densidad que rige la duración de las notas. La probabilidad P de que la duración de una nota esté entre dos valores l1, l2 está dado por: Densidad de la nube de notas. Este parámetro está gobernado por otros dos a su vez, la densidad y la altura. La densidad se refiere propiamente al número de notas que suenan en un determinado intervalo de tiempo. La densidad de la nube sigue una distribución de Poisson. Para la composición se establecerá una densidad media de notas μ0 > 0. La función de masa queda como sigue: (2) La distribución de Poisson es la versión discreta de la distribución exponencial como se puede apreciar en la figura 3 (aparecen dos curvas con valores k=2 y k=5). Figura 3: Función de masa que rige la densidad de la nube de notas. En cuanto a las alturas de la nube, se empieza por una altura generada aleatoriamente también y a partir de ella se generan sucesivamente los intervalos aleatorios con la siguiente función de densidad: (3) donde a es el máximo intervalo especificado por el compositor. Para decidir la dirección del intervalo se usa una variable discreta de dos valores (intervalo ascendente o descendente), cada uno con probabilidad 1/2. En la figura 4 tenemos la gráfica de Θ(γ) con los valores γ = 5 y γ = 10. Se observa que los intervalos tienden a ser pequeños, aunque no tanto como los generados por la distribución exponencial. El papel del parámetro a es limitar los intervalos poco habituales o que resulten imposibles de tocar en el instrumento. Figura 4: Función de densidad que rige la altura de las notas. Velocidad del glissando. El glissando es el paso de una nota a otra de manera continua. En la orquesta solo lo pueden ejecutar los instrumentos de cuerda y el trombón de vara. Ya que Xenakis quería recrear ciertos fenómenos físicos de carácter continuo, necesitaba formalizar este parámetro también. Para ello, utilizó la distribución normal de función de densidad: (4) donde b es un parámetro que Xenakis, inspirándose en la teoría cinética de gases, llamó la temperatura resultante (aggregate temperature); véase la figura 5 (las dos gráficas corresponden a los valores b=5 y b=10). Figura 5: Función de densidad que rige la velocidad del glissando. Las dinámicas. Xenakis divide el rango dinámico en cuatro zonas, representadas por ppp, p, f y ff, que corresponden respectivamente a muy suave, suave, fuerte y muy fuerte. Suele usar sucesiones de tamaño 3, de modo que hay 64 posibles (43=64). Sin embargo, descarta algunas por motivos musicales y el número total se reduce a 44. Las dinámicas se obtienen mediante una distribución uniforme discreta de probabilidad (cada sucesión 1/44). La instrumentación. En primer lugar, se separan los instrumentos que poseen un timbre similar. A continuación, según distribución lineal, se determina un porcentaje para cada clase de instrumentos. Este porcentaje marca la proporción de notas totales de la composición que el grupo instrumental tocará. 5. Pithokrapta En Pithokrapta Xenakis explora las relaciones entre la ley de los grandes números (el sentido global) y la teoría cinética de los gases de Boltzmann (la independencia total del sonido). Para esta obra Xenakis imagina un gas ideal a temperatura constante e identifica las moléculas y sus choques con una orquesta de cuerda. Veamos los compases 53 a 60, uno de los pasajes donde son más evidentes las intenciones del compositor. Para las velocidades de las moléculas Xenakis usa la distribución normal similar a la ecuación (4): donde a es aquí la temperatura del gas y v la velocidad de las moléculas. Para este pasaje la velocidad de cada molécula se traduce en un glissando tocado en pizzicato (pulsando la cuerda, sin el arco). La pendiente de cada glissando es proporcional a la velocidad de cada partícula. Estos sucesos sonoros, los glissandi, representan la distribución molecular del gas. Xenakis fija 58 intervalos distintos para las velocidades y usando la distribución normal genera 1.148 velocidades distintas de moléculas de un gas a temperatura constante. Como la orquesta no dispone de un número tan alto de voces, Xenakis redujo el número de voces independientes a 46. Cada una de estas voces toca una media de 25 notas en los 18,5 segundos que dura este pasaje. La manera de trabajar de Xenakis era muy meticulosa, como correspondía a su formación científica. Para esta obra, dibujó en papel milimetrado los glissandi. El eje de abscisas representa el tiempo. Cada marca son 26 MM del metrónomo Mälzel (0,433 segundos por marca). El eje de ordenadas representa la altura del sonido. El intervalo entre dos marcas consecutivas es de medio tono. Xenakis dividió el eje de ordenadas en 15 rangos de una tercer mayor (cuatro semitonos) cada uno. A cada tesitura (rango) se le asignó un cierto número de instrumentistas. En la figura 6 tenemos la gráfica que dibujó Xenakis para este pasaje. Figura 6: Grafo de Pithoprakta (imagen tomada de [Zog10]). En la realidad los choques de las moléculas del gas no son simultáneos. Xenakis refuerza la idea del caos imponiendo divisiones métricas con números de partes que son primos relativos entre sí. Así, por ejemplo, encontramos quintillos, tresillos, negras, pero también subdivisiones de 15 o de 20. La figura 7 muestra la escritura en notación musical convencional del mismo pasaje. Figura 7: Partitura final de Pithoprakta. En la figura 8 se puede apreciar con más detalle los glissandi así como las articulaciones métricas tan peculiares de esta obra. Figura 8: Detalle de Pithoprakta. Resumiendo, en este pasaje tenemos las siguientes características ([Xen01], página 15): Las duraciones de las notas no varían. Las alturas varían de acuerdo a sus distribuciones de probabilidad. La densidad de sonidos se mantiene constante en todo momento. La dinámica es constante e igual a ff (muy fuerte). El timbre es constante; solo hay instrumentos de cuerda. Las velocidades determinan una "temperatura" sujeta a fluctuaciones locales y que sigue una distribución normal. Por último, dejo aquí un vídeo con la música de Pithoprakta. 6. Conclusiones Tal y como había hecho Heisenberg con la mecánica cuántica, Xenakis introduce la probabilidad en el mundo de la composición musical. A pesar de la aparente excesiva formalización del proceso compositivo, Xenakis dota a su obra de expresividad. La influencia que ejerció en los compositores de las generaciones posteriores fue formidable, no solo por el gran salto conceptual que había dado con su música, sino también por su ejemplo incansable de creatividad. 7. Para saber más Edward Childs disecciona la obra Achorripsis en su artículo [Chi02], que también se basa en teoría de las probabilidades. Tako Oda tiene un artículo en que compara las teorías estéticas de Xenakis y Cage. Se llama Iannis Xenakis and John Cage:Two Sides of a Tossed Coin y se puede encontrar en [Oda10]. Para un estudio músico-matemático de las últimas obras de Xenakis, véase la tesis de Ronald Squibbs [Squ96]. Robert Strizich [Str10] en un interesante artículo analiza el papel de la textura en varios compositores de la posguerra, incluyendo Xenakis. La textura fue uno de los aspectos que más investigó y experimentó Xenakis. Sin duda, está considerado como un gran inventor de texturas. Recordemos la incorporación de la percusión africana a la orquesta sinfónica, por poner un ejemplo. La página Les amis de Xenakis [Xen10] contiene información completa sobre su vida, su obra, así como la posibilidad de escuchar fragmentos de su obra. Para profundizar más en la estética de las primeras obras de Xenakis, véase el artículo de Markos Zografos [Zog10]. Referencias [Chi02] Edward Childs. Achorripsis: a Sonification of Probability Distributions. In International Conference on Auditory Display, Kyoto, julio 2002. [MF71] A. Marcelo and E. Finn. Física III. Fundamentos cuánticos y estadísticos. Addison Wesley, 1971. [Oda10] Tako Oda. Iannis xenakis and john cage: Two sides of a tossed coin. http://people.mills.edu/toda/chance/frames.html, accedido en septiembre de 2010. [Pou66] Henry Pousseur. The question of order in the new music. Perspectives in New Music, 1:93-111, 1966. [RS00] V. K. Rohatgi and E. Saleh. An Introduction to Probability and Statistics. Wiley-Interscience, 2000. [Squ96] Ronald Squibbs. An Analytical Approach to the Music of Iannis Xenakis: Studies of Recent Works. Yale University. PhD thesis, Universidad de Yale, New Haven, Connecticut, 1996. [Str10] Robert Strizich. Texture in post-world war ii music. http://www.ex-tempore.org/strizich91/strizich.htm, accedido en septiembre de 2010. [vaaat10] Varios autores asociados a International Community for Auditory Display. Sonification report: Status of the field and research agenda. http://www.icad.org/websiteV2.0/References/nsf.html, accedido en septiembre de 2010. [Xen01] Iannis Xenakis. Formalized Music: Thought and Mathematics in Composition. Number 6 in Harmonologia. Pendragon Press, Hillsdale, NY, 2001. [Xen10] Xenakis.org. Les amis de xenakis. http://www.iannis-xenakis.org/, accedido en septiembre de 2010. [Zog10] Markos Zografos. Iannis xenakis: the aesthetics of his early works. http://www.furious.com/perfect/xenakis.html, accedido en septiembre de 2010.

Martes, 05 de Octubre de 2010 | Imprimir | PDF |  Correo electrónico

114. 17. (Septiembre 2010) Conjuntos de área máxima y la armonía

Es un gran placer para mí presentar un artículo de David Rapapport (fotografía de la izquierda), geométra interesado en la música y músico interesado en la geometría. Su artículo que presentamos en esta sección, Conjuntos de área máxima y la armonía, es una exploración deliciosa de la armonía a través de conjuntos de área máxima inscritos en un círculo. El autor caracteriza escalas fundamentales en la improvisación en la música del jazz. Francisco Gómez Martín BIOGRAFÍA: David Rapapport es profesor en la School of Computing y Vicedecano en la School of Graduate Studies en Queen's University, en Canadá. Obtuvo un grado en Matemáticas por la Universidad de Concordia y un tesis de maestría y de doctorado por la Universidad de McGill, ambas en Canadá. Su investigación se centra en geometría discreta y computacional con especial énfasis en algoritmos y optimización. También está interesado en las conexiones entre matemáticas y música. ARTÍCULO: 1. Introducción La Geometría y la Música están relacionadas entre sí de varias maneras. La notación musical usa la forma y el espacio para transmitir la información sobre la altura y la duración. Los guitarristas visualizan las estructuras armónicas, así escalas, arpegios y acordes, como formas geométricas en el traste. Los orígenes de nuestro sistema musical de siete notas extraídas de un conjunto de doce alturas se puede describir en términos de cuerdas vibrantes de varias longitudes. Dimitri Tymocko, en un reciente artículo suyo [17], ha usado la geometría para analizar la conducción de voces en música. La Combinatoria es otra rama de las Matemáticas que se utiliza en el análisis de la música. Inevitablemente, la visión combinatoria se apoya en una imagen, esto es, en una representación geométrica. Considérese un círculo con doce puntos equidistantes distribuidos en su circunferencia. Los doce puntos representan las doce alturas del universo cromático dado por el temperamento igual. De estos doce puntos elegimos un subconjunto de al menos cinco puntos, porque musicalmente se llama una escala a un subconjunto de cinco o más alturas. Algunos de estos conjuntos, o escalas, son elementos esenciales de la armonía occidental. En los ejemplos que se muestran en la figura 1 un subconjunto de puntos se conecta en orden para construir un polígono convexo. Consideraremos polígonos distintos salvo rotaciones. Esto equivale a considerar que los distintos modos musicales provenientes de una misma escala no son escalas distintas. Ya que hay 12 puntos equiespaciados sobre la circunferencia, es razonable llamar a estos diagramas diagramas de reloj. La representación de las notas de una escala por un polígono aparece en un artículo publicado en 1937 por E. Krenek [8], de modo que algunas veces estos diagramas se llaman diagramas de Krenek, como por ejemplo en el artículo de McCartin [10]. Sin embargo, en una recensión de Nolan [11], Heinrich Vincent ya usaba esta misma representación en un artículo suyo publicado en 1862 [18]. El uso de los diagramas de reloj es omnipresente en la teoría matemática de la música. Cuando se considera la escala diatónica usual, se observa que las notas están distribuidas lo más regularmente posible entre las doce notas cromáticas. La distancia entre dos notas puede medirse como el número de notas de la escala entre ellas, o bien como el número total de notas cromáticas entre ellas. De este modo, distinguimos entre la distancia de la escala y la distancia cromática de un par de notas. Clough and Douthett [1] definen un conjunto de regularidad máxima cuando la distancia cromática entre un par de notas difiere de su distancia de escala en una unidad como máximo. Los conjuntos de regularidad máxima (conjuntos RM de aquí en adelante) son únicos (salvo rotaciones) como se prueba en [1] y también en [4]. Los conjuntos RM incluyen algunas de las escalas más ampliamente usadas en la música occidental, a saber, la escala diatónica, la escala pentatónica anhemitónica común, la escala de tonos enteros de seis notas y la escala octotónica (véase la figura 1). Figura 1. Los subconjuntos en a) y b) representan dos modos de la escala diatónica, el jónico y el eólico, también conocidos como modo mayor y modo menor natural, respectivamente. Para nuestros propósitos estas dos escalas se consideran equivalentes. El diagrama de la parte c) representa la escala menor melódica ascendente y ésta es distinta de las de a) y b). Cuando los conjuntos RM se representan por un diagrama de reloj, entonces esos puntos son subconjuntos que maximizan de modo único la suma de las distancias entre puntos [2-4]. Fejes Tóth [14] describe un caso continuo similar al considerado aquí. En ese artículo se prueba que un conjunto finito de N puntos que maximizan la suma de las distancia entre puntos se encuentra en los vértices de un polígono regular convexo de N lados. Dicho de otro modo, los puntos están distribuidos tan regularmente como sea posible sobre la circunferencia del círculo. En su libro sobre armonía el músico Levine [9] describe cuatro escalas fundamentales que son útiles para la improvisación en jazz. Estas cuatro escalas son la escala mayor de siete notas, la escala menor melódica de siete notas, la escala simétrica de tonos enteros de seis notas y la escala octotónica. En la terminología jazzística el término "menor melódica" se refiere a la escala ascendente melódica menor y aquí seguiremos esa convención. Tres de estas escalas son de máxima regularidad, siendo la excepción la escala menor melódica, que no lo es. Así, dados los pares (12, 8), (12, 6) y (12, 7) podemos preguntarnos si hay una caracterización matemática que describa exactamente las cuatro escalas fundamentales de Levine. En estas notas llegamos a una caracterización llamada los conjuntos complementarios de área máxima. Este artículo está organizado como sigue. En la siguiente sección entablaremos una discusión matemática sobre una clase de subconjuntos de K elementos tomados entre N posibles. Esta caracterización es a la vez combinatoria y geométrica. Empezaremos por describir los llamados conjuntos de área máxima, de los cuales probaremos algunas propiedades suyas. Los conjuntos de área máxima son interesantes por derecho propio, pero no satisfacen las condiciones mencionadas anteriormente, ya que esta caracterización, como veremos, incluye subconjuntos de (12, 8) y (12, 7) que no son de las cuatro escalas fundamentales. En la sección 3 definiremos y analizaremos entonces los conjuntos complementarios de área máxima y mostraremos que esa caracterización sí satisface las condiciones impuestas antes. El artículo acaba con una sección de conclusiones. 2. Conjuntos de área máxima Un concepto erróneo bastante común es el de pensar que el prefijo di- en la palabra diatónico se refiere al número dos, queriendo significar que la característica es que hay dos tipos de intervalos en el conjunto diatónico habitual. Sin embargo, la verdad es que el prefijo dia- se refiere a la distancia desde la tónica [12]. No obstante, esta definición nos proporciona el trampolín ideal desde el cual lanzar una exploración de las escalas que satisfacen esta propiedad, esto es, colecciones de subconjuntos de siete alturas tomadas de entre las doce del universo cromático de modo que el espacio entre alturas consecutivas es o bien un tono o un semitono. Resultan tres escalas distintas. Usando diagramas de reloj podemos ver las tres escalas en la figura 2 más abajo. En (a) podemos reconocer la escala diatónica estándar; (b) representa la escala menor melódica; y en (c) tenemos la escala simétrica de tonos enteros más una nota, escala que también se llama escala mayor napolitana. No es difícil comprobar que los polígonos que representan cada escala tienen todos la misma área y que esa área se maximiza para cualquier elección de siete puntos sobre doce. Así pues, llamaremos a estas escalas escalas de área máxima, o más generalmente subconjuntos de área máxima (lo abreviaremos como conjuntos AM). Figura 2. Diagramas de reloj de las tres escalas AM. La estructura de los intervalos de esta escala es a) la escala diatónica; b) la escala menor melódica ascendente; c) la escala mayor napolitana. Generalizamos esta noción a cualquier colección de K alturas seleccionadas de entre un universo cromático de N alturas. Será más conveniente definir los subconjuntos en términos de particiones de números enteros. Una partición entera de un número natural N es una forma de escribir N como una suma no ordenada de numeros naturales. En [7] Keith señala la conexión entre las particiones de enteros y las escalas musicales. Definición. Un conjunto de K alturas tomadas de entre un universo cromático de N alturas numeradas de 1,...,N es un conjunto AM si satisface las siguientes dos condiciones: Hay una partición entera de N que usa exactamente K sumandos enteros positivos, esto es, . Los sumandos difieren como máximo en 1, esto es, , para todo i, j. La siguiente proposición proporciona fundamento matemático para construir y analizar los conjuntos AM. Proposición 1. Dados dos enteros N, K con K <N, existen dos únicos enteros u y m tales que N=mu+(K-m)(u+1). Obsérvese que para N, K, u, m, definidos así, tenemos una partición entera con , para i=1,...,m y , para i=m+1,...,K. Aquí se sobreentiende que i=m+1,...,K es el conjunto vacío en el caso en que m=K, esto es, cuando K divide a N. Demostración: Sean los siguientes números: Nótese que si K divide a N, entonces v=u; en otro caso, v=u+1. Para el caso en que v=u, tenemos que N=Ku. Considerando ahora el caso en que v=u+1, tenemos la igualdad (N-Ku)v+(Kv-N)u=N(v-u)=N. Por lo tanto, m=Kv-N=K(u+1)-N. Ya que u determina m, basta mostrar que u es el único valor que satisface las condiciones requeridas. Cuando K divide a N, la unicidad se sigue del algoritmo de la división [6]. Cuando K no divide a N, examinamos los casos en que se usa un número mayor o menor que el valor de u. Sea, pues, w un entero mayor que . Esto implica, sin embargo, que Kw >N, lo cual lleva a una contradicción y w no puede ser mayor que u. Un argumento simétrico similar al anterior muestra que tomar w < lleva a una contradicción. Por tanto, queda demostrado que u es único, y esto completa la demostración. QED. Recuérdese que en los conjuntos MR según fueron definidos por Clough y Douthett [2, 3] cuando la distancia cromática entre dos pares denotas difieren como máximo en una unidad de la distancia de escala. Esto lleva inmediatamente a la proposición siguiente. Proposición 2. Si un conjunto es MR, entonces también es un conjunto AM. Como se ilustró en el ejemplo de la figura 2, aunque para cualquier N, K, hay dos valores únicos de u y m, uno puede obtener más de una escala con intervalos u y u+1 sencillamente reordenando las posiciones de dichos intervalos. Dados los números (N, K, u, m), podemos enumerar las distintas escalas (salvo rotaciones) que son escalas AM. Este valor depende solo de K y m, y es el número de collares (necklaces) binarios de longitud K usando dos tipos de cuentas, m cuentas blancas y K-m cuentas negras. En general, un collar p-ario se define como la clase de equivalencia de cadenas p-arias bajo rotaciones; véase [13]. Los distintos collares se pueden enumerar en tiempo constante por collar usando un algoritmo de Sawada y Ruskey [13]. Volvemos ahora a la cuestión del área de los polígonos que representan a las escalas. Haciendo referencia a la figura 3, es claro que el área del heptágono se obtiene sumando las áreas de los triángulos. Suponiendo que el heptágono que representa estas escalas está circunscrito a un círculo de radio la unidad, una fórmula que da el área del polígono es: . Figura 3. Uno puede obtener el área de un heptágono sumando las áreas de los triángulos en la partición en triángulos que sugiere la figura. El area del triángulo a, b, c está dado por sen . El perímetro del polígono inscrito es también una función de los ángulos centrales. Por ejemplo, la longitud de la arista bc es . En general, el área de los polígonos se puede obtener sumando el área de los triángulos que forman la partición del polígono. Para nuestros propósitos es más conveniente tomar la partición del polígono con triángulos que comparten un vértice común en el centro del círculo que circunscribe y cuyos lados son los radios. De ahora en adelante nos referiremos a esta partición como la partición en triángulos del polígono. La suma de las áreas de cualquier representación poligonal (N, K, u, m) está dada por la fórmula: Nótese que el área es una función que depende solo de los valores de los ángulos de los triángulos del centro del círculo. Llamaremos a estos ángulos ángulos centrales. Afirmamos que todos esos heptágonos maximizan el área. Es fácil verlo en el ejemplo dado. Probaremos el resultado para el caso general en el siguiente lema. Además, probaremos que estos polígonos maximizan también el perímetro. El hecho de que el perímetro se maximice queda claro cuando uno se percata de que el perímetro es también una función de los ángulos centrales. La fórmula para el perímetro de una representación poligonal (N, K , u, m) está dada por la fórmula: Lema 1. Dada (N, K , u, m), la representación poligonal de estos conjuntos AM tiene área máxima y perímetro máximo. Prueba: Considérese un polígono X de K lados que no es una representación de un conjunto AM. Entonces, hay dos triángulos en la partición triangular de X con ángulos centrales y y tales que la diferencia . Supongamos que, por ejemplo, . Si ponemos , tenemos la fórmula (1): Ya que el orden de los triángulos no tiene efecto en el cálculo del área o del perímetro del polígono, podemos reordenarlos de manera que esos dos triángulos estén adyacentes. Podemos escribir la suma del área de esos dos triángulos como . Si tomamos la primera derivada del área con respecto a , esto es, , e igualamos a cero, vemos que el valor es el valor máximo. La derivada es positiva para todos los valores . Sean y . Por la ecuación (1), vemos que . Por tanto, la suma de la nueva área es mayor y X no puede tener área máxima. Para el perímetro usamos un argumento similar. La suma de las aristas del polígono está dada por la ecuación , y su primera derivada es . Vemos de nuevo que la suma se maximiza para , y su derivada es positiva . De nuevo, ponemos y . Por la ecuación 1, vemos que y X no puede tener perímetro máximo. QED. 3. Conjuntos complementarios de área máxima Las cuatro escalas que distingue Levine en su libro [9] en el capítulo Acordes/Escalas en su libro sobre armonía en el jazz son la escala de tonos enteros simétrica, la escala mayor, la escala menor melódica y la escala octotónica. Definimos una clase de escalas, las escalas complementarias de área máxima de manera que las escalas dadas por (12, 6), (12, 7) y (12,8) corresponden idénticamente a las escalas dadas por Levine. Definición: Un conjunto de K alturas tomadas de un universo cromático de N alturas numeradas de 1 a N es un conjunto complementario de área máxima (conjunto CAM) si cumple las siguientes propiedades: El conjunto es AM. Las N-K notas del conjunto complementario forman un conjunto AM también. Probamos en su momento que los conjuntos RM son también AM. Los conjuntos RM son también CAM porque el complemento de un conjunto RM es también un conjunto RM; véase [1]. Así pues, las escalas CAM constituyen una clase estrictamente mayor que la de las escalas RM. Hay una única escala, la escala simétrica de tono enteros (12, 6), que es un conjunto AM, como muestra la figura 4. Claramente esta escala es autocomplementaria y es, por tanto, un conjunto CAM. De los tres conjuntos AM dados por (12, 7), dos tienen complementarios que son conjuntos AM. Estas escalas (12, 5) AM se muestran en la figura 4. Figura 4. Los conjuntos de área máxima de cinco y seis notas. Hay diez conjuntos (12, 8) AM, como se describe en la página 31 de [7]; los reproducimos en la figura 5. Figura 5. Los diez conjuntos de área máxima con ocho notas. Hay solo uno de estos conjuntos cuyo complementario es también un conjunto AM. En la figura 6 mostramos este conjunto y su complementario de cuatro notas. Figura 6. La única escala complementaria de área máxima de ocho notas (una escala disminuida) con su complementario (el acorde de séptima disminuida). Así pues, hemos sido capaces de captura una propiedad matemática que caracteriza las cuatro escalas fundamentales de Levine. 4. Conclusiones Hemos probado que una partición entera particular de N en K partes conduce a los polígonos de área máxima cuando éstos se representan con un diagrama de reloj. Estos conjuntos llamados de área máxima son fáciles de calcular computacionalmente. Sin embargo, una clasificación que parece más interesante usa los conjuntos complementarios de área máxima. Hemos demostrado que los conjuntos complementarios de área máxima para (12, 6), (12, 7) y (12,8) contienen las cuatro escalas fundamentales definidas por Levine en su libro sobre improvisación en jazz. Estas escalas fundamentales no agotan en modo alguno el gran número de escalas que los músicos de jazz usan regularmente. En un capítulo aparte Levine discute las escalas pentatónicas y el papel que desempeñan en la improvisación jazzística. Con mucho la escala pentatónica más importante es la anhemitónica, que ya sabemos que es una escala CAM. Hay una colección más de escalas pentatónicas que son CAM, las cuales se muestran en la figura 4 b). Esta escala se puede llamar escala pentatónica dominante, ya que contiene un acorde de dominante; sin embargo, esta escala parece algo desconocida y Levine no la menciona en absoluto en su libro. Si consideramos el análogo rítmico de los diagramas de reloj, esto es, los puntos seleccionados representan ataques, entonces los conjuntos CAM de cinco elementos representan los patrones rítmicos de palmas que se usan en la soleá, la bulería y el fandango [5]. Bibliografía 1. J. Clough and J. Douthett: Maximally even sets. Journal of Music Theory, 35, (1991) 93–173. 2. J. Clough and G. Myerson: Musical scales and the generalized circle of fifths. American Mathematical Monthly 93:9 (1985) 695–701. 3. J. Clough and G. Myerson: Variety and multiplicity in diatonic systems. Journal of Music Theory 29 (1985) 249–270. 4. Erik D. Demaine, Francisco Gómez-Martin, Henk Meijer, David Rappaport, Perouz Taslakian, Godfried T. Toussaint, Terry Winograd, and David R. Wood: The distance geometry of music. submitted to Computational Geometry: Theory and Applications, (2006). 5. Miguel Díaz-Bañez, Giovanna Farigu, Francisco Gómez, David Rappaport, and Godfried T. Toussaint: El compás flamenco: a phylogenetic analysis. Proceedings of BRIDGES: Mathematical Connections in Art, Music and Science, Winfield, Kansas (2004) 61–70. 6. Ralph Grimaldi: Discrete and Combinatorial Mathematics: An Applied Introduction. Addison Wesley (1998). 7. Michael Keith: From Polychords to Polya: Adventures in Musical Combinatorics. Vinculum Press, Princeton (1991). 8. E. Krenek: Über Neue Musik. chapter Musik und mathematik. Verlag der Ringbuchhandlung, Vienna (1937) 71–89. 9. Mark Levine: The Jazz Theory Book. Sher Music Co. (1995). 10. Brian J. McCartin: Prelude to musical geometry. The College Mathematics Journal, 29:5 (1998) 354–370. 11. Catherine Nolan: Combinatorial space in nineteenth- and early twentieth-century music. Music Theory Spectrum, 25:2 (2003) 205–241. 12. D. Randel (editor): The Harvard Dictionary of Music. Harvard University Press (1986). 13. J. Sawada and F. Ruskey: An efficient algorithm for generating necklaces with fixed density SIAM Journal on Computing 29:2 (1999) 671–684. 14. L. Fejes T´oth: On the sum of distances determined by a pointset. Acta. Math. Acad. Sci. Hungar. 7:3 (1956) 97–101. 15. Godfried T. Toussaint: A mathematical analysis of African, Brazilian and Cuban clave rhythms. Proceedings of BRIDGES: Mathematical Connections in Art, Music and Science, Towson, Maryland (2002) 157–168. 16. Godfried T. Toussaint: Classification and phylogenetic analysis of African ternary rhythm timelines. Proceedings of BRIDGES: Mathematical Connections in Art, Music and Science, Granada, Spain (2003) 25–36. 17. Dmitri Tymoczko: The Geometry of Musical Chords. Science 313 (2006) 72–74. 18. Heinrich Vincent: Die Einheit in der Tonwelt. Verlag von Heinrich Matthes, Leipzig (1862).

Viernes, 10 de Septiembre de 2010 | Imprimir | PDF |  Correo electrónico

115. 16. (Julio 2010) El teorema del hexacordo III

1. Introducción En este último artículo sobre el teorema del hexacordo veremos una demostración basada en la transformada de Fourier y conoceremos un poco de la historia y personalidad de David Lewin, uno de los primeros autores en usarla en el contexto musical. La demostración será un poco más complicada que la de Juan Iglesias [Igl81] o que la del teorema continuo del hexacordo [BBOG09], pero merece la pena por la conexión con ese hermoso y fecundo objeto matemático que es la transformada de Fourier. Pero empecemos por el hombre. David Lewin (1933-2003) fue un músico y matemático que impulsó el análisis formal de la música por medio de las matemáticas. Neoyorquino de nacimiento, empezó a tocar el piano desde muy niño, aunque su interés por las ciencias, en particular por las matemáticas, le llevó a estudiar matemáticas en la Universidad de Harvard. En 1954 terminaría la licenciatura en Matemáticas. Nunca había abandonado la música y después de terminar la carrera Lewin estudió composición con músicos de la talla de Roger Sessions, Edward Cone o el influyente Milton Babbitt. Tras esta etapa, orientó su carrera hacia la música y empezó a enseñar composición y teoría de la música en varias universidades: Harvard, Berkeley, la universidad estatal de Nueva York en Stony Brook, Yale. Llegó a ser el presidente de la Society for Music Theory norteamericana. Recibió a lo largo de su vida varios doctorados honoris causae. Aunque más conocido por sus teorías sobre el análisis musical, fue también un compositor prolífico y experimentador. Por ejemplo, fue el primer músico en componer una pieza musical totalmente generada por ordenador (véase [Coh01]). Ello ocurrió en los laboratorios Bell en 1961. La obra más influyente de Lewin es su libro Generalized Musical Intervals and Transformations [Lew87], publicada en 1987. En ella Lewin sienta las bases de lo que poco más tarde recibiría el nombre de teoría de transformaciones (transformational theory, en inglés). Lewin concibe la música como la transformación continua del material musical y su idea es modelizar matemáticamente tanto el material musical, el "conjunto S de objetos musicales" (capítulo 7), como las transformaciones musicales en sí, las cuales se ven como funciones matemáticas sobre S. Principalmente, Lewin se sirvió de la teoría de grupos para modelizar dichas funciones. Por ejemplo, la escala cromática de 12 semitonos la concibe como el grupo cíclico . Esta modelización recoge el hecho perceptual de que una misma nota colocada en distintas octavas en ciertos contextos se percibe como una única nota. Sus modelos se aplicaron a diversos parámetros musicales aparte de a la altura del sonido, incluyendo el ritmo, la métrica y el timbre así como a la música tonal y atonal. Aplicadas a la música tonal, las teorías de Lewin se han considerado como parte de un análisis neoschenkeriano [CG06] que ha prolongado las teorías clásicas del análisis musical; aplicadas a la música atonal, se han visto como un nuevo modo de análisis más flexible y versátil, capaz de explicar las nuevas relaciones musicales provenientes de la música contemporánea. El enfoque de Lewin es, sin duda, muy abstracto y frecuentemente se citan sus métodos de análisis en términos de idealismo abstracto. Para una lista completa de las publicaciones, véase la página de Wikipedia sobre David Lewin [Wik10]. En su artículo Re: Intervallic Relations between Two Collections of Notes [Lew59], de 1959, Lewin investiga cómo reconstruir conjuntos de notas a partir de ciertas propiedades. Lewin, demasiado avanzado para su tiempo, piensa que no será entendido demasiado bien y en el mismo artículo declara que: "The mathematical reasoning by which I arrived at this result is not communicable to a reader who does not have considerable mathematical training. For those who have such a training, I append a sketch of the proof." ["El razonamiento matemático por el cual llegué a este resultado no es comunicable a un lector que no posea un considerable instrucción matemática. Para aquellos que la tengan agrego un bosquejo de la prueba."] La prueba apenas está bosquejada, pero claramente menciona la transformada de Fourier y la convolución. En la sección siguiente seguiremos su rastro y completaremos la formalización de Lewin en términos de la transformada de Fourier. Para una exposición profunda del tema, recomendamos al lector el excelente artículo de Amiot [Ami07]. 2. La transformada de Fourier Empezaremos por unas sencillas definiciones a modo de recordatorio. Dado un conjunto cualquiera X, llamaremos 1X a su función característica: Dadas las aplicaciones que nos interesan aquí, las musicales, consideraremos la transformada de Fourier sobre el grupo cíclico . Dado un subconjunto de , la transformada (discreta) de A, designada por , es una función compleja definida por La transformada de Fourier se puede pensar como un operador, esto es, una aplicación que transforma unas funciones en otras. En ese caso, designamos solo por la transformada y escribimos . Como es bien sabido, la transformada es un operador lineal; véase [Kam08] para más información. En el mencionado artículo [Lew59], Lewin introduce la llamada función de intervalo , donde . Su definición es como sigue: donde |·| indica el cardinal de un conjunto. Como ya vimos en el artículo pasado, El teorema del hexacordo - II, el teorema del tono común nos dice que: donde . Esta última fórmula no es sino la convolución de las funciones 1A y 1B. Luego, podemos escribir: Una vez provistos de las definiciones necesarias, examinamos la primera propiedad que nos permitirá probar el teorema del hexacordo. PROPIEDAD 1 (P1): Si , entonces . Cuando , entonces . Demostración: Si , tenemos: El caso en que , cada término del sumatorio es 1 y el resultado se prueba inmediatamente. A continuación usamos la propiedad P1 para ver qué relación existe entre las transformadas de Fourier de y . PROPIEDAD 2 (P2): Sea con y . Entonces, se cumple la igualdad: Demostración: En el sumatorio podemos separar los términos que viene del conjunto de aquellos que vienen de . De esta igualdad se deduce que , como queríamos. Ahora examinamos la relación que existe entre las transformadas de Fourier de y . PROPIEDAD 3 (P3): Sea con y . Entonces, se cumple la igualdad: Demostración: De nuevo es un argumento sencillo sobre los términos del sumatorio. Se sigue, pues, que , cuando . Si combinamos esta ecuación con la propiedad P2, , tenemos el resultado buscado, . Para el caso en que , la igualdad es cierta solo cuando . La prueba se deja como divertimento para el lector. A continuación consideramos el módulo de , , que es una función que asocia a cada el número . Usaremos la notación del valor absoluto para indicar el módulo; no debe confundirse con el cardinal de un conjunto. Recordamos, por último, que la transformada de Fourier tiene inversa: 3. El teorema del hexacordo Diremos que dos conjuntos cumplen la relación de Lewin si para todo . La relación de Lewin se conserva bajo la aplicación de movimientos rígidos (giros y simetrías), pero el recíproco no es cierto; véase [Ami07] para una prueba de este hecho. El contenido interválico, definido formalmente, es una función Si calculamos la transformada de Fourier de CI(A), obtenemos: Teorema del hexacordo. Sea con n par y . Entonces . Demostración. He aquí la demostración de dos líneas. Línea 1: . Línea 2: implica que como consecuencia de la aplicación de la inversa de la transformada de Fourier. 4. Para saber más Aparte de sus teorías matemáticas para modelizar la música, Lewin se ocupó del problema del texto y la música. Escribió varios artículos sobre esta cuestión. Véase, por ejemplo, [Lew92], donde analiza los aspectos estructurales de la música que pueden servir como base de la interpretación dramática. En el artículo de Amiot [Ami07] se analizan extensa y profundamente la relación de la transformada de Fourier. Gran parte de ese trabajo está dedicado al fascinante tema de los conjuntos de máxima regularidad (a los que se dedicará una serie en esta sección en un futuro muy próximo). Bibliografía [Ami07] Emmanuel Amiot. David Lewin and maximally even sets. Journal of Mathematics and Music, 1(3):157-172, 2007. [BBOG09] B. Ballinger, F. Benbernou, N. Gomez, J. O'Rourke, and Toussaint G. The continuous hexachordal theorem. In E. Chew, A. Childs, and C-H. Chuan, editors, Mathematics and Computation in Music, páginas 63-77. Springer, Berlin, 2009. [CG06] Allen Cadwallader and David Gagne. Analysis of Tonal Music: A Schenkerian Approach. Oxford University Press, USA, 2006. [Coh01] Richard Cohn. Lewin, David. Macmillan Publishers, London, 2001. The New Grove Dictionary of Music and Musicians, second edition, edited by Stanley Sadie and John Tyrrell. [Igl81] Juan E. Iglesias. On Patterson's cyclotomic sets and how to count them. Zeitschrift für Kristallographie, 156:187-196, 1981. [Kam08] David W. Kammler. A First Course in Fourier Analysis. Cambridge University Press, 2008. [Lew59] David Lewin. Re: Intervallic relations betwen two collections of notes. Journal of Music Theory, 3(2):298-301, noviembre 1959. [Lew87] David Lewin. Generalized Musical Intervals and Transformations. Yale University Press, 1987. [Lew92] David Lewin. Musical Analysis as Stage Direction. Cambridge University Press, 1992. In Music and Text: Critical Inquiries, editor. S.P. Scher. [Wik10] Wikipedia. David Lewin. http://en.wikipedia.org/wiki/David_Lewin, 2010.

Viernes, 09 de Julio de 2010 | Imprimir | PDF |  Correo electrónico

116. 15. (Junio 2010) El teorema del hexacordo II

1. La versión continua del teorema del hexacordo Seguimos (en presente) con el teorema del hexacordo, ahora en su versión continua. En el artículo anterior conocimos el interés de Schoenberg por los hexacordos, vimos cómo los saboreó, cómo los deglutió, cómo intuyó sus propiedades; pero, aunque quiso, no pudo dar con el resultado apetecido. Después aprendimos qué es el contenido interválico y qué movimientos lo dejan invariantes. Seguimos (en pasado) con el teorema del hexacordo, enunciándolo con precisión, y continuamos (¿También éste? ¡Qué oficio! Sí, claro, en pasado) la historia de su demostración. Una historia llena de intentos fallidos, desconocimientos mutuos, refinamientos sucesivos y, por fin, demostraciones epigramáticas, certeras como puñales, breves como haikús. Dimos la demostración de Iglesias, por elegante y corta. Consistía, si recordáis, en un juego de recuento entre puntos blancos y negros. Y ahí el mes pasado nos quedamos. El presente mes presentamos una generalización del teorema del hexacordo al caso continuo, demostración incluida. Es corta y profunda, pues une dos mundos, el discreto y el continuo. 1.1. Ritmos y pesos Para generalizar el teorema del hexacordo necesitamos un cambio de enfoque, que provoque choque y que apoque el enroque mental tendencial. Pasaremos de acordes y escalas a ritmos de modo inmisericorde. Pero ¿qué es un ritmo? Tomemos el círculo y pongamos n puntos equiespaciados en él, a los que llamaremos pulsos. En cada pulso elegimos si ponemos una nota o un silencio. Solo se pueden poner notas o silencios en los pulsos, pero no entre dos pulsos consecutivos. Un ritmo es una sucesión de notas y silencios puestos sobre un conjunto de n pulsos. En música los pulsos no suenan, no se tocan; la división del tiempo sencillamente está en la mente del intérprete, como referencia temporal. En la figura 1 tenemos el ritmo [x . . x . . x . . x . .] definido sobre 12 pulsos, donde la x representa un sonido y el punto un silencio. Figura 1: Un ritmo y su representación geométrica. Este ritmo, interpretado como un acorde, sería el acorde disminuido de do (do - mi bemol - fa sostenido - la), que es el acorde que divide la octava en cuatro partes iguales. Este ritmo consiste en la división de una unidad de tiempo, dada por la longitud del círculo, en cuatro partes iguales. Se ve la equivalencia entre el enfoque de acordes y el enfoque rítmico. Seguimos (en presente a partir de aquí): sea R un ritmo; asignamos a cada nota del ritmo un peso y a cada silencio un peso . Formamos el vector de pesos del ritmo R, . Llamaremos a la suma el peso W(R) del ritmo, cuyo valor no es otro que el número de notas de R. El complementario de un ritmo R tiene como pesos . Estamos lanzados: consideremos el histograma HR del ritmo R. Dicho histograma nos informa, educadamente, para cada distancia , del número de veces que ocurre sin más que mirar a la altura de sus cajitas. El histograma HR determina, pues, una función de la distancias; llamemos HR(d) a esa función de d. Enunciamos de nuevo el teorema del hexacordo acorde a la nueva terminología: Teorema 1 Sea R un ritmo sobre un conjunto de n pulsos, donde n es par. Si W(R) = n/2, entonces R y son homométricos, esto es, para todo d, . Antes de seguir daremos un teorema, conocido en teoría de la música como el teorema del tono común [Joh03], y que servirá de base para la generalización en ciernes. Por completitud, incluimos una prueba sencilla del teorema; para una prueba más compleja, basada en teoría de grupos, consúltese [JK03]. Teorema 2 [Teorema del tono común] , donde los índices se interpretan módulo n. Demostración. Si en las posiciones i e i+d hay notas, entonces y se cuenta, en efecto, la ocurrencia de la distancia d. Si en alguna de esas posiciones hay un silencio, el producto es 0. Por tanto, la suma cuenta 1 por cada aparición de la distancia d en el ritmo R. Queda por ver que cada par de puntos a distancia d solo contribuya una vez a la suma, excepto en el caso del diámetro que contribuye dos veces. Si el par (i, i+d) contribuye dos veces a la suma es porque la distancia de i a i+d es la misma que de i a i-d. Entonces, se tiene que: i+d = i-d mod n Al ser distancia geodésica, y, por tanto, 2d. Estamos en el caso del diámetro con toda seguridad. Como ejemplo, cojamos el ritmo sobre 16 pulsos dado por , esto es, hay notas en las posiciones 0, 3, 6, 10 y 12 y silencios en el resto. Su peso es . Para , la función da lugar al histograma de la figura de abajo. Figura 2: La función histograma HR(d). 1.2. La generalización al caso continuo La generalización se produce en dos sentidos. Primero, pasaremos del círculo de n pulsos a un círculo continuo. Se puede tomar, sin pérdida de generalidad, como el círculo unidad. Segundo, los pesos discretos son ahora funciones reales f(x), con . Aquí la variable x indica un punto del círculo medido desde las 12 del mediodía; f(x) indica su peso. El peso de un ritmo R se define como la integral . Las definiciones en el caso continuo son análogas al caso discreto. El complementario tiene peso y HR(d) es una función sobre el intervalo . Como definición de HR(d) tomamos la versión continua del teorema del tono común: Ilustremos con un ejemplo este salto del caso discreto al continuo. Consideremos el ritmo continuo R dado por la función . Su función histograma es donde . La gráfica de f(x) y su histograma se muestran en la figura 3. Figura 3: La función f(x) y la función histograma HR(d). 1.3. La demostración en el caso continuo Teorema 3 Si R es un ritmo integrable y , entonces para toda distancia , se tiene que . Demostración. Empecemos por fijar d. De la definición del histograma tenemos que: Aplicando la definición de ritmo complementario obtenemos: Multiplying out los términos queda: Efectuando el producto dentro de la integral da: La primera integral da 1. Dado que , la segunda integral también vale 1/2. La tercera integral también da 1/2; el área de f(x) y f(x+d) es la misma, ya que f(x) es una función periódica en [0,1]. Finalmente, llegamos a: Esto prueba que para todo d. 1.4. De vuelta al teorema discreto Afirmábamos antes que el teorema continuo del hexacordo recién probado es una generalización del teorema original, discreto, sin duda. Se deduce que este teorema es un caso particular de la versión continua. Así es. Para verlo basta tomar un ritmo discreto y transformarlo en una función integrable f(x) en [0, 1] como sigue: donde es la función característica del intervalo , esto es, la función que vale 1 si y 0 en caso contrario. Se puede probar que la función histograma asociada a f(x) es proporcional a la función histograma asociada al ritmo . En efecto, en la versión continua usamos el círculo unidad mientras que en la versión discreta tenemos n pulsos. Entonces, en la versión discreta la función histograma se transforma en la siguiente función en la versión continua: Esta igualdad prueba que el histograma discreto es proporcional al histograma continuo. De aquí se desprende que si el teorema del hexacordo es cierto en el caso continuo, también lo es en el caso discreto. 2. Para saber más Completamos brevemente en esta última sección algunos puntos que se quedaron en el tintero. Volvemos ahora a la cuestión de por qué se cuenta el diámetro dos veces en el contenido interválico. En primer lugar, por comodidad. Si no se cuenta el diámetro de esta manera, la fórmula que aparece en el teorema del tono común hay que reescribirla de una manera farragosa. Los resultados no cambian si se cuenta solo una vez el diámetro, pero su descripción es menos concisa. También se puede justificar esta convención estudiando el comportamiento de cuando . La fórmula que aparece en el teorema del tono común, , es, en realidad, una función de autocorrelación discreta. Varias demostraciones del teorema del hexacordo han surgido del campo de la teoría de funciones gracias a la relación que proporciona esa fórmula. Véanse [JK03] y [Ami07] para más información. La generalización que hemos mostrado aquí sirve también para probar otros resultados más generales que el teorema del hexacordo. Por ejemplo, el primer teorema de Patterson, que establece que, si dos ritmos tienen el mismo número de notas y son homométricos, entonces sus complementarios también son homométricos. Véase [BBOG09] para los detalles de esta demostración usando la versión continua del teorema del hexacordo. References [Ami07] Emmanuel Amiot. David Lewin and maximally even sets. Journal of Mathematics and Music, 1(3):157-172, 2007. [BBOG09] B. Ballinger, F. Benbernou, N. Gomez, J. O'Rourke, and Toussaint G. The continuous hexachordal theorem. In E. Chew, A. Childs, and C-H. Chuan, editors, Mathematics and Computation in Music, pages 63-77. Springer, Berlin, 2009. [JK03] Philippe Jaming and Mihalis Kolountzakis. Reconstruction of functions from their triple correlations. New York Journal of Mathematics, 9:149-164, 2003. [Joh03] Timothy Johnson. Foundations of Diatonic Theory. Key College Publishing, 2003.

Martes, 01 de Junio de 2010 | Imprimir | PDF |  Correo electrónico

117. 7. (Mayo 2008) Melodías Desmoduladas

En busca de las moléculas musicales Los músicos, musicólogos y matemáticos fueron paulatinamente percibiendo que detrás de cualquier composición musical existe un orden analizable, ya sea sencillo o complejo, no sólo en la obra como conjunto sino también en sus partes moleculares. La búsqueda de un sistema “universal” de análisis de ese orden sigue vigente. En el siglo XX destaca un método que permite, en cierta medida, la clasificación y comparación de “moléculas musicales”, que puede aplicarse tanto a composiciones renacentistas como a modernas. Este método, denominado Teoría Musical de Conjuntos, nos sumerge de nuevo en la combinatoria y en la aritmética modular. Erik Satie (1866–1925) Parece encontrarse suficientemente documentado que ya a finales del siglo XIX compositores como Satie, utilizaban métodos sistemáticos de composición. No por ello, curiosamente, son menos emotivas sus -generalmente breves- piezas. También se puede generar (recuérdese el juego combinatorio de Mozart) música al azar. Si las notas son completamente aleatorias se consigue un pobre resultado ("música blanca"). Pero si se dictan unas normas (unos patrones), los resultados mejoran. La atonalidad A finales del siglo XIX se comenzó a cuestionar la base tonal de la música occidental. Hasta entonces, las notas que conformaban una composición formaban una red de órbitas alrededor de un centro gravitatorio que las cohesionaba. Por ejemplo, una obra compuesta en la tonalidad de Si bemol mayor desarrolla esa estructura tonal. Cuando escuchamos una obra compuesta bajo el sistema tonal, es decir, prácticamente cualquiera entre los siglos XV y XIX, podemos intuir –antes de oírlas- muchas de las notas siguientes a las que escuchamos, especialmente las que cierran las frases melódicas. Esto es consecuencia de la estructura tonal. Nuestro oído espera constantemente un regreso a las cercanías del tono o tonos que sirven de centros gravitatorios, de los cuales el fundamental es la tónica. A principios del siglo XX los compositores buscan una estructura que evite la presencia de esos centros tonales, de forma que el oyente no pueda anticiparse en ningún momento a la frase musical antes de terminar de oírla. Esta nueva estructura se conoce como atonalidad. Los adelantados El uso extremo del cromatismo, es decir, el empleo del semitono más que del tono como base de la composición, reduce considerablemente la percepción de tonalidad. Este recurso ya fue usado por Wagner y Debussy en algunas partes de sus obras. Richard Wagner (1813–1883) Claude Debussy (1862–1918) Otros compositores, como Charles Ives, también lograron reducir, e incluso hacer desaparecer, la influencia de los atractores tonales mediante diversas técnicas. El musicólogo y matemático Graeser fue el primer teórico de la música que aplicó sistemáticamente "grupos de simetrías" al análisis musical. Wolfgang Graeser (1906–1928) La Segunda (?) Escuela de Viena Sin embargo, fue Schönberg el primer compositor en aplicar conscientemente órbitas completas de "grupos de simetrías" a la composición musical. La técnica dodecafónica de Schönberg (hacia 1920) es la primera aplicación sistemática de un método algorítmico de composición. En su obra Pierrot Lunaire, también aparece un fragmento palíndromo. Arnold Schönberg (1874–1951) Este método o sistema de composición, conocido como serialismo dodecafónico, se basa en asignar el mismo protagonismo a cada uno de los 12 semitonos que componen la octava, independientemente de su altura. Es decir, todas las notas del mismo nombre, como Re bemol, se consideran equivalentes e igualmente importantes. Anton Webern (1883–1945) Alban Berg (1885–1935) La repercusión de este sistema en la música del siglo XX fue enorme. A Schönberg, junto con sus discípulos en Viena, Anton Webern y Alban Berg, se les concedió el nombre colectivo de La Segunda Escuela de Viena, aludiendo, por contraste, al grupo de influyentes compositores (Haydn, Mozart, Beethoven y Schubert) vinculados desde antiguo a esa ciudad, que formarían parte de una supuesta Primera Escuela de Viena que en realidad nunca existió. Descentralización La ruptura con la tonalidad coincide, históricamente, con la aparición del cubismo. Perspectiva monocéntrica Visión policéntrica De la perspectiva monocéntrica se pasa a la visión policéntrica, en donde un objeto aparece desde múltiples puntos de vista. Cada punto del espacio tiene iguales posibilidades de ser centro. Igual ocurre con los semitonos en la dodecafonía: todos juegan el mismo papel. Percepción Junto con la ruptura de la tonalidad, surge una pregunta: ¿somos capaces de aceptar una música sin tono central y sin las usuales pautas (los acordes y sus transformaciones isométricas)? En la imagen se observan las simetrías tonales en el análisis de una obra musical tonal. En el sistema dodecafónico, las clásicas transformaciones isométricas son ahora reemplazadas por permutaciones simétricas módulo 12. Es decir, para ver las simetrías e inversiones es necesario, previamente, reducir módulo 12. Veamos un ejemplo. En la parte inferior de la imagen siguiente, aparece una melodía atonal. Su gráfica parece caótica, desmodulada. Sin embargo, una vez realizada la reducción módulo 12, es decir, trasladando todas las notas del mismo nombre a la misma octava, las simetrías vuelven a aparecer, como muestra la parte superior de la imagen. De esta forma, la simetría estática del sistema tonal clásico es sustituida por una simetría dinámica basada en permutaciones de un sistema secuencial (serial). Paul Hindemith (1895–1963) Hindemith ejemplifica cómo las simetrías mantienen su papel principal en su Ludus tonalis, creando un postludio que coincide con el preludio tras un giro de 180 grados. La Teoría Musical de Conjuntos de Hanson y Forte Esta teoría, iniciada por Hanson para el análisis de la música tonal y posteriormente desarrollada por Forte para el análisis de la música atonal, contempla la definición de conjuntos de notas susceptibles de organizar la música en torno a ellos y sus distintas manipulaciones. Howard Hanson (1896–1981) Allen Forte (1926–) El análisis de las clases de estos conjuntos es el resultado de los esfuerzos de los teóricos de la música por revelar los sistemas que compositores como Schönberg y sus seguidores usaron para organizar el contenido tonal en sus trabajos. De la misma forma que los vectores y matrices permiten calcular resultados de movimientos en el plano, los vectores y matrices de Forte permiten calcular resultados de movimientos melódicos o armónicos. Hay que tener presente que los conjuntos y sus clases, que veremos a continuación, determinan únicamente el contenido tonal; los compositores continúan libres de modificar cualquier otro aspecto musical de acuerdo con sus deseos artísticos. Calculadora musical Para la mejor comprensión de los términos empleados, nos serviremos de una calculadora... musical. Se trata de un applet de Java, basado en el original realizado en 1997 por Jay Tomlin, muy útil para ensayar y comprobar los distintos procedimientos que iremos detallando. Para abrir la calculadora, basta pulsar en la siguiente imagen. Para elegir las notas, o desactivarlas, se pulsa sobre los números del disco (parte inferior izquierda). En el caso de que algún elemento gráfico deje de visualizarse, deberemos pulsar el botón Repintar. En cualquier momento se puede pulsar directamente sobre el teclado para oír el sonido de la nota correspondiente. Los conjuntos tonales Un conjunto tonal es simplemente una colección desordenada de entre 12 notas. Las doce únicas notas del teclado (en una octava) son numeradas de 0 a 11, empezando por Do. Por ejemplo, el conjunto tonal de las notas Do, Mi, Sol se puede escribir como (0,4,7). Número Nombre Intervalo (desde Do) 0 Do Unísono 1 Do sostenido 2ª menor 2 Re 2ª mayor 3 Re sostenido 3ª menor 4 Mi 3ª mayor 5 Fa 4ª justa 6 Fa sostenido 4ª aumentada o 5ª disminuida 7 Sol 5ª justa 8 Sol sostenido 6ª menor 9 La 6ª mayor 10 La sostenido 7ª menor 11 Si 7ª mayor 12 (= 0 mod12) Do 8ª Los compositores tratan estos conjuntos con diversos grados de libertad cuando aplican el método a su música atonal. El conjunto (0,1,6) se hizo tan popular entre Schönberg y sus discípulos que ha sido bautizado como El tricorde vienés. Calculadora. Ejercicio 1 Cuando la calculadora se inicia, el conjunto (0,1,6) es el que aparece por defecto. Para introducir un nuevo conjunto, se puede elegir entre: A. Pulsar el botón Escala, seleccionar un conjunto predefinido y pulsar OK. B. Escribir sobre el campo "Conjunto tonal" y presionar la tecla Intro. C. Introducir el conjunto directamente sobre el disco numérico, con el ratón. Cuando se escriba un conjunto (opción B) hay que asegurarse de que los números quedan separados por comas. Cualquier número superior a 11 se reducirá automáticamente a su equivalente módulo 12. Los espacios en blanco serán ignorados. La elección quedará señalada automáticamente sobre el disco de números y sobre el teclado del piano. Para oír el conjunto tonal, basta pulsar el botón Toca que aparece bajo el teclado. Se puede elegir entre escuchar las notas una a una (melodía) o simultáneamente (acorde). En el primer caso, se respetará el orden del conjunto. También se puede usar el botón Rotar para cambiar este orden. Inversiones Una melodía es invertida cambiando el sentido de los intervalos. Si el original es una tercera menor, la inversión devolverá una sexta mayor. En la Teoría de Conjuntos, cualquier nota puede ser invertida por sustracción de 12 (la inversión de 1 es 11, la de 2 es 10, etc.; las notas 0 y 6 son inversas de sí mismas). Observando el disco de números, se aprecia que la inversión de un conjunto produce su imagen reflejada en un espejo. El eje de inversión es la recta que une 0 y 6, así que veremos la inversión como si el original sufriese una reflexión horizontal. Calculadora. Ejercicio 2 Para invertir el conjunto en la calculadora, se pulsa el botón Invertir. Observemos en el disco de números que el conjunto queda reflejado respecto al original. También podemos obtener el complementario de un conjunto pulsando sobre el botón del mismo nombre, que cambia el conjunto por uno nuevo en donde figuran todas las notas que no pertenecían al conjunto original. Intervalos mínimos Los conjuntos pueden ponerse en intervalo mínimo, que es la forma de ordenar las notas del conjunto de manera que sea la más “compacta”. Esto significa que el mayor de los intervalos entre dos notas consecutivas pase a ser el que separa la primera y última nota. Si observamos el disco de números, el intervalo mínimo representará el recorrido más corto que recorra todas las notas. El conjunto (2,9,10), por ejemplo, no está escrito como intervalo mínimo porque el intervalo entre 2 y 9 es mayor que el intervalo entre 9 y 10 o entre 10 y 2. Para poner el conjunto (2,9,10) como intervalo mínimo, deberemos escribirlo como (9,10,2). Así, el intervalo más grande quedará "fuera". Si no existe ningún intervalo mayor que el resto, entonces el intervalo mínimo es la representación del conjunto en la que los intervalos más pequeños queden al principio del conjunto y los mayores al final, o dicho de otra forma, “más compactado a la izquierda”. Por ejemplo, el intervalo mínimo de (0,4,5,8) es (4,5,8,0). Calculadora. Ejercicio 3 La calculadora encuentra automáticamente el intervalo mínimo de cada conjunto, como podemos comprobar ensayando con distintos conjuntos. Formas básicas o clases de conjuntos Si obtenemos el intervalo mínimo de un conjunto y el intervalo mínimo de su inversión, entonces su forma básica es el conjunto más "compacto" de los dos anteriores, trasladado al 0. Por ejemplo, consideremos el conjunto (7,8,2,5), que llamaremos A: El intervalo mínimo de A es (2,5,7,8). La inversión de A es (5,4,10,7). El intervalo mínimo de la inversión de A es (4,5,7,10). Como (4,5,7,10) está más compactado a la izquierda que (2,5,7,8), elegimos (4,5,7,10) y lo trasladamos para que comience en 0. Obtenemos (0,1,3,6) que es la forma básica. Las representaciones en forma básica también son nombradas como clases de conjuntos. Por ejemplo, los conjuntos tonales (1,2,7), (8,2,3), y (0,11,6) pertenecen a la misma clase de conjuntos (0,1,6). Aplicación de las formas básicas La forma básica es una abstracción de las clases de conjuntos que nos ofrece una única imagen de esa colección particular de notas. Si dos conjuntos tienen la misma forma básica podemos asegurar que sonarán parecidos uno al otro. Los conjuntos con la misma forma básica contienen el mismo número de notas y la misma colección de intervalos entre ellas, así que existe una cierta equivalencia auditiva, de la misma forma que todos los acordes mayores son auditivamente equivalentes en la música tonal. Calculadora. Ejercicio 4 La calculadora encuentra automáticamente la forma básica de cada conjunto. Números de Forte Forte catalogó cada forma básica de conjuntos de 3 a 9 elementos y las ordenó de acuerdo a su contenido de intervalos. Asignó a cada forma básica un código, como "5-35". En este código, el primer número es un índice que indica el número de notas del conjunto, y el segundo número fue asignado por Forte. Los conjuntos complementarios tienen el mismo número de catálogo en el sistema de clasificación de Forte (por ejemplo, el complementario de 5-35 es 7-35). Aquí puedes ver una breve lista de algunos números de Forte populares: Forma Básica Número de Forte Tricordio vienés (0,1,6) 3-5 Tríadas mayor y menor (0,3,7) 3-11 Escalas mayor y menor (0,1,3,5,6,8,10) 7-35 Escala octatónica (0,1,3,4,6,7,9,10) 8-28 Calculadora. Ejercicio 5 La calculadora encuentra automáticamente el número de Forte de cada conjunto. Para ver una lista completa de los números de Forte, pulsemos el botón Escala y elijamos "Números de Forte" como criterio para seleccionar un conjunto predefinido. Vectores de clases de intervalos Los intervalos que son inversos uno del otro están en la misma clase de intervalo. (Los intervalos 1 y 11 están en la clase 1; 2 y 10 en la clase 2; 3 y 9 en la clase 3, y así sucesivamente.) Sólo hay 6 clases diferentes de intervalos, desde el 1 al 6. Así, el intervalo entre las notas 2 y 9 es 7 y pertenece a la clase de intervalos 5. Observa que los intervalos no tienen relación con las notas, sino con la distancia entre ellas. El vector de clase de intervalo es una disposición ordenada de 6 números <i1,i2,i3,i4,i5,i6> correspondientes al número de apariciones de cada clase de intervalo encontradas en un conjunto tonal. Por ejemplo, consideremos el conjunto (2,3,9). Aparece una vez la clase de intervalo 1 (entre 2 y 3), una vez la clase de intervalo 6 (entre 3 y 9) y una vez la clase de intervalo 5 (entre 2 y 9). Así, el vector de clase de intervalo correspondiente a (2,3,9) es <1,0,0,0,1,1>. Aplicación de los vectores de clases de intervalos El vector de clase de intervalo ofrece un resumen del contenido interválico de un conjunto y, por ello, una fiable indicación sobre su sonido. Calculadora. Ejercicio 6 La calculadora encuentra automáticamente el vector de clase de intervalo de un conjunto. T(n) y T(n)I La notación T(n) indica otro conjunto cuyas notas han sido trasladadas n semitonos respecto al original. Por ejemplo, si el conjunto original es (1,2,7), entonces T(3) deberá ser (4,5,10). La notación T(n)I significa lo mismo, pero con respecto a la inversión del original. Calculadora. Ejercicio 7 La calculadora encuentra automáticamente T(n) y T(n)I. Para cambiar el valor de n se utiliza la barra vertical a la izquierda de los campos T(n) y T(n)I. Para trasladar el propio conjunto se utiliza el botón < y el botón >. Matrices Cada matriz normal se genera como diferencia (T-matriz) o suma (I-matriz) de un conjunto consigo mismo, elemento a elemento. Por ejemplo, la matriz normal (I-matriz) generada por el conjunto (2,3,9) es: 2 3 9 2 4 5 11 3 5 6 0 9 11 0 6 Aplicación de las matrices Se puede usar una matriz para determinar si existe o no una inversión de sí mismo, y si es así, dónde. Por “inversión en sí mismo” se entiende la propiedad inherente a algunos conjuntos por la cual existe algún número n tal que T(n)I devuelve el mismo conjunto original. Para un conjunto con x notas, si existe un número n que aparece exactamente x veces en la matriz, entonces T(n)I contendrá las mismas notas que el conjunto original. Tomemos, por ejemplo, el conjunto (0,1,2,5,9): 0 1 2 5 9 0 0 1 2 5 9 1 1 2 3 6 10 2 2 3 4 7 11 5 5 6 7 10 2 9 9 10 11 2 6 Como (0,1,2,5,9) tiene 5 elementos, buscaremos algún número en el interior de la matriz que aparezca 5 veces. En este caso, sólo aparece uno de estos números: el 2. Esto significa que T(2)I nos devuelve el conjunto original: T(2)I de (0,1,2,5,9) es (2,1,0,9,5). Los compositores y teóricos llaman a esta propiedad combinabilidad. Calculadora. Ejercicio 8 Para generar la matriz de un conjunto, se pulsa el botón Matrices. Aparecerán nuevos botones que permitirán elegir entre la forma normal de la matriz, o invertir previamente el conjunto original. Sugerencia: Si un conjunto es combinable, ensayemos a pulsar el botón Rotar las veces suficientes para que un mismo número aparezca en la diagonal secundaria (arriba derecha - abajo izquierda) de la matriz. En el ejemplo anterior, si pulsamos Rotar cuatro veces, esa diagonal aparece cubierta por el número 2. 9 0 1 2 5 9 6 9 10 11 2 0 9 0 1 2 5 1 10 1 2 3 6 2 11 2 3 4 7 5 2 5 6 7 10

Jueves, 01 de Mayo de 2008 | Imprimir | PDF |  Correo electrónico

118. 5. (Enero 2008) Combinatoria Musical

Un desastre de piano Una buena interpretación de una composición, incluso a cargo de una sola voz o de un solo instrumento, suele envolver sutiles matices, ligeras modificaciones en la duración, timbre, volumen o forma de atacar cada nota. Pero, en aras de una mayor claridad expositiva, concedámonos la libertad de simplificar al máximo, a pesar del rigor que indudablemente perderemos con ello, y pasar por alto estas sutilezas. Supongamos, pues, que contamos con un piano en un estado realmente lamentable. Las cuerdas están afinadas, pero sólo funcionan las 24 teclas centrales, entre teclas blancas y negras (dos octavas). Los pedales tampoco funcionan y, para colmo, cada nota suena exactamente igual independientemente de la fuerza o duración que empleemos en pulsar cada tecla. Abreviando, tenemos un instrumento que al teclearlo sólo puede dar 24 sonidos distintos. Por supuesto, la mayoría de los intérpretes rechazarían ejecutar una pieza musical con un instrumento así, incluso aunque la pieza fuera una simple melodía para la que bastasen las 24 notas con que contamos. Ahora bien, al margen de la calidad de la interpretación, estos mismos intérpretes admitirían ser capaces de tocar un sinfín de melodías lo suficientemente conocidas o populares para que el auditorio las reconociera de inmediato. Letras y notas Asociemos ahora a cada una de las teclas del maltrecho piano una letra, distinta en cada caso, de nuestro alfabeto, reservando el espacio en blanco para el silencio. Disponemos con ello de un simple sistema de transcripción melódica. Así, una melodía puede comenzar “KKLEK LNEK TLE...” Por último, supongamos que las frases melódicas que el paciente auditorio es capaz de reconocer corresponden con las frases con significado y sentido en nuestra lengua. Evidentemente, este es un paso audaz que requiere un especial consentimiento. La distribución de las notas y los silencios en una composición se encuentra lejos de parecerse a la distribución de letras y espacios en una frase. Mas, sea, consintamos generosamente, a pesar del manifiesto abuso. Atendamos ahora al público. Ante el comienzo anteriormente expuesto, el auditorio permanece impávido (tal vez confuso, tal vez horrorizado: ¿LNEK?), mientras que ante la melodía “LA LUZ AZUL ROZA...” sonríe y bate palmas. El teorema de los infinitos monos Si aporreamos el desastrado piano al azar, es casi seguro que el auditorio no reconocerá nada de lo que toquemos, pues difícilmente surgirán palabras inteligibles y mucho menos frases con sentido. Nos encontramos ante el “teorema de los infinitos monos” del matemático francés Émile Borel (1871-1956): letras escogidas al azar difícilmente podrán componer una obra literaria ya escrita. En nuestra versión, notas aleatorias difícilmente compondrán una melodía conocida. La composición Como vemos, el azar puro, incluso limitando las infinitas posibilidades reales a sólo 24 sonidos atómicos, es bastante ingobernable como proceso de creación musical. El azar en la creación artística semeja un fuerte condimento en una receta culinaria: puede darle el toque, pero no es la base. Se ha empleado el uso calculado y dirigido de alguna distribución de probabilidad como un componente en la creación de obras musicales, pero esa es otra historia (de la que hablaremos en otra ocasión). La composición, es decir, la planificación de todos los elementos que constituyen la obra, no sólo otorga consistencia y unidad a la misma sino que además facilita el reconocimiento tanto de la obra completa como de cada una de sus partes. Limitando el azar La libertad de tocar cualquier tecla del lamentable piano conduce, como hemos visto, a un resultado caótico. Limitemos pues los grados de libertad. Primero, no se podrá elegir cualquier letra (nota) sino sólo palabras (grupos de notas) de la lengua española (reconocibles). Esta limitación es muy fuerte, pues el número de palabras existentes es ridículo frente al número de variaciones posibles de letras aleatorias. No obstante, muchas melodías carecerán todavía de sentido: “PERRO LA LLOVER SIN...” Segundo, las palabras (grupos de notas) se clasificarán y ordenarán previamente, de forma que, por ejemplo, a un artículo le sucederá un sustantivo, a este un adjetivo, a este un verbo... facilitando así la conexión entre ellas para formar una frase con sentido. En música, esta clasificación se puede establecer atendiendo especialmente a la primera y última nota del grupo, fundamentales para marcar la tonalidad y enlazar un grupo de notas con el siguiente. Tercero (y decisivo), las palabras no pueden ser cualesquiera, sino que deben elegirse en cada caso una en una lista cerrada de posibilidades. Esto evita faltas de concordancia (como “LA PERRO”). Por ejemplo, la primera palabra sólo puede ser EL, UN, ALGÚN, OTRO, ESTE, ESE, AQUEL u otra similar. Permutaciones En 1974 Ernö Rubik inventa un rompecabezas que años más tarde se convierte en tal éxito de ventas a escala mundial que no necesita más presentación: su famoso cubo. El número de piezas es reducido, sólo 26, pero el número de diseños posibles es enorme: más de 43 trillones, un número de 20 cifras. No es la primera vez que un puzzle se populariza a esta escala. Un siglo antes, una humilde cajita con 15 piezas obsesionó a europeos y americanos. Inventada por un cartero de Canastota (NY), Noyes Chapman, fue no obstante el creador de acertijos Sam Loyd quien la popularizó ofreciendo una recompensa de 1.000 dólares -de la época (1880)- a quien fuese capaz de resolverlo a partir de una posición inicial... de distinta paridad, es decir, irresoluble. (En la posición inicial de Loyd, los números 14 y 15 aparecían permutados.) El número total de posibles permutaciones -a partir de una dada- es de más de medio billón (y otro tanto para las posiciones con distinta paridad). Pulsa aquí para ver una versión interactiva. Las recompensas continúan hoy siendo un buen reclamo publicitario. Actualmente, se ofrece un premio de dos millones de dólares a la primera persona que consiga resolver, durante este año 2008, un puzzle de 256 piezas comercializado como Eternity II. Al contrario que en el caso anterior, la existencia de solución está garantizada (incluso hay más de una, aunque muy pocas), pero el número posible de disposiciones de las piezas es inimaginable... ¡Tiene unas 600 cifras! En los casos expuestos vemos que la clave del atractivo, premios aparte, consiste en el gran contraste entre el escaso número de piezas fácilmente manipulables y el gran número de configuraciones posibles. Juego de dados musical En 1787, Mozart compone Musikalisches Würfelspiel (Juego de dados musical), una pieza que tiene la particularidad de que... ¡cada vez que se interpreta nadie la había escuchado antes, ni siquiera el propio Mozart! La obra consiste en 176 compases numerados, de los cuales todos se dedicarán a un minueto de 16 compases y 96 de ellos a un trío también de 16 compases. Complementa la obra una serie de instrucciones para la elección de los compases. Antes de interpretar la obra... ¡hay que crear la partitura! Para ello, se deben arrojar dos dados. La suma de los puntos obtenidos, entre 2 y 12, indicará el número del primer compás del minueto según la siguiente tabla. Se vuelven a arrojar los dados, y la puntuación indicará ahora el número del segundo compás. Sucesivamente, se completarán los 16 compases que constituyen el minueto. Minueto 1º 2º 3º 4º 5º 6º 7º 8º 9º 10º 11º 12º 13º 14º 15º 16º 96 22 141 41 105 122 11 30 70 121 26 9 112 49 109 14 32 6 128 63 146 46 134 81 117 39 126 56 174 18 116 83 69 95 158 13 153 55 110 24 66 139 15 132 73 58 145 79 40 17 113 85 161 2 159 100 90 176 7 34 67 160 52 170 148 74 163 45 80 97 36 107 25 143 64 125 76 136 1 93 104 157 27 167 154 68 118 91 138 71 150 29 101 162 23 151 152 60 171 53 99 133 21 127 16 155 57 175 43 168 89 172 119 84 114 50 140 86 169 94 120 88 48 166 51 115 72 111 98 142 42 156 75 129 62 123 65 77 19 82 137 38 149 8 3 87 165 61 135 47 147 33 102 4 31 164 144 59 173 78 54 130 10 103 28 37 106 5 35 20 108 92 12 124 44 131 Las casillas azules muestran, como ejemplo, un posible resultado de arrojar los dos dados 16 veces. En el primer lanzamiento se obtuvo una suma 2, en el segundo una suma 8, etc. Los compases correspondientes que se deben interpretar son los numerados como 96, 60, etc. Mozart no dispuso los compases al azar, sino mediante reglas estrictas que limitan el azar suavizando el paso de unos a otros, a la vez que rigen los intervalos armónicos y la tonalidad. Por ejemplo, los compases de la primera y última columna muestran el mismo tono fundamental, y entre ambos abundan los intervalos de quinta y cuarta, lo que favorece la armonía global según los gustos de la época. Una vez concluida la partitura del minueto, creamos la partitura del trío. El método es el mismo, salvo que ahora se arroja un solo dado al aire. La tabla correspondiente es la siguiente: Trío 1º 2º 3º 4º 5º 6º 7º 8º 9º 10º 11º 12º 13º 14º 15º 16º 72 6 59 25 81 41 89 13 36 5 46 79 30 95 19 66 56 82 42 74 14 7 26 71 76 20 64 84 8 35 47 88 75 39 54 1 65 43 15 80 9 34 93 48 69 58 90 21 40 73 16 68 29 55 2 61 22 67 49 77 57 87 33 10 83 3 28 53 37 17 44 70 63 85 32 96 12 23 50 91 18 45 62 38 4 27 52 94 11 92 24 86 51 60 78 31 La partitura resultante en nuestro ejemplo se puede ver y oír aquí. Cada uno de los 176 compases, por separado, lo puedes oír aquí. Probabilidad Observemos que mientras que todos los compases del trío tienen la misma probabilidad de aparecer en la partitura, no sucede igual con los compases del minueto. Al arrojar dos dados, la distribución de probabilidad de la puntuación, es decir, la serie de probabilidades de obtener cada suma, no es uniforme, pues sólo hay una forma de obtener suma 2 (1+1), mientras que existen 6 modos distintos de obtener suma 7 (1+6, 2+5, 3+4, 4+3, 5+2 y 6+1). La siguiente tabla nos muestra la probabilidad de cada puntuación al arrojar dos dados: Suma 2 3 4 5 6 7 8 9 10 11 12 Prob. 1/36 2/36 3/36 4/36 5/36 6/36 5/36 4/36 3/36 2/36 1/36 Esto significa que los compases que aparecen asociados a una de las sumas aparecerán, de media, en 2 de cada 3 compases (cuantos más minuetos generemos, más nos acercaremos a esta media). Contando posibilidades Calculemos cuántos minuetos y tríos distintos podemos formar. Para agilizar el cálculo, obviaremos que alguno de los 176 compases que integran Musikalisches Würfelspiel se repite, a pesar de tener distinta numeración. Esto reduce un poco el resultado que obtendremos, pero no significativamente. Para cada minueto, existen 11 elecciones posibles del primer compás. Por cada una de ellas, otras 11 para el segundo, y así sucesivamente. Habrá por tanto 1116 minuetos posibles, casi 46 mil billones, aunque no todos con la misma probabilidad, como hemos visto. Tenemos, de igual manera, 616 tríos posibles, casi 3 billones, todos ellos equiprobables. Conjuntamente, la obra minueto y trío alcanza 6616 posibilidades, un número de 30 cifras. Si cada habitante del planeta, unos 6 mil millones, interpreta una posibilidad distinta cada cinco minutos, hasta agotarlas todas, tardaríamos más de 200 billones de años (aunque es casi seguro que ni el sistema solar ni nuestra galaxia continuasen existiendo para entonces). Ahora bien, no es lo mismo agotar todas las posibilidades que estimar qué número de interpretaciones se deben haber realizado para que sea más probable que improbable que se produzca alguna repetición. Es decir, estimar cuándo una partitura generada según las reglas del juego ya no es un estreno, sino una reposición. ¿Cómo estimar este número? El problema del cumpleaños Este problema, famoso por su poco intuitiva solución, tiene un enunciado muy similar al que acabamos de exponer. Pregunta cuál es el mínimo número de personas necesarias para que entre ellas sea más probable que improbable que haya dos con la misma onomástica (no se consideran los años bisiestos). La sorprendente respuesta es 23. [Nota: Si usted no está familiarizado con este problema, debe prestar atención a que no se pretende la coincidencia de algún cumpleaños de las personas del grupo con otro concreto (el de usted, por ejemplo), sino de cualquiera de ellos con cualquier otro. La variante “¿cuántas personas como mínimo debe haber  para que sea más probable que improbable que alguna tenga mi onomástica?” ofrece una solución mucho más abultada: 253 personas.] Para alcanzar esa solución, denotemos por n el número de posibles cumpleaños, 365. Si hay x personas, cada una con n posibilidades, el número total de posibilidades es nx. Por otra parte, la primera persona puede tener cualquier cumpleaños. Para que no coincida la segunda, esta debe cumplir años en uno de los n - 1 días restantes. La tercera, en alguno de los n – 2 que quedan, y así sucesivamente. Por lo tanto, la probabilidad de que en x personas no coincida ningún cumpleaños es: La probabilidad buscada, de que exista alguna coincidencia, será por tanto: Con n = 365, basta una calculadora y un poco de paciencia para comprobar que para x = 22 esta probabilidad no alcanza 0.5, pero para x = 23 personas, ya la supera ligeramente. Sin embargo, en vez de la calculadora usaremos algo más potente como es el programa Derive: Conectando problemas Veamos ahora por qué es casi imposible repetir una partitura ya interpretada. Para poder aplicar el método anterior al Juego de dados musical, primero tenemos que solventar la dificultad presentada por la falta de uniformidad de la distribución de probabilidad que rige la generación de los minuetos. ¿Cuál es la probabilidad de que un compás de un minueto coincida con el mismo compás en otro? Para que se produzca esta coincidencia, debe ser igual la puntuación obtenida con los dados en ambos casos. Para que esto suceda con dos puntuaciones “2”, se debe obtener puntuación 2 en uno (probabilidad 2/36) e, independientemente, en el otro (misma probabilidad). La probabilidad de que ambos sucesos ocurran a la vez será por tanto (2/36)2. De la misma forma, la probabilidad de que coincidan dos puntuaciones “3” será (3/36)2, y sucesivamente, hasta la coincidencia de dos puntuaciones “12” con probabilidad, igual a la primera, de (2/36)2. Sumando todas estas fracciones, obtenemos la probabilidad de coincidencia de dos compases en la misma posición: 1/9. Para que coincida un minueto con otro, todos sus 16 compases deben coincidir uno por uno. Por lo tanto, la probabilidad de tal coincidencia es 1/916. Por otra parte, la probabilidad de que coincidan dos tríos era 1/616. Conjuntamente, tenemos que la probabilidad de una repetición exacta de una obra concreta es 1/5416. Ya podemos aplicar el mismo sistema usado en el problema del cumpleaños, sólo que ahora el año no tiene 365 días, sino 5416: Desafortunadamente, la expresión anterior se muestra ahora intratable, dado lo elevado de los números implicados. Si intentamos resolver con Derive la ecuación resultante de igualarla a 0.5, como hemos hecho antes, no obtendremos resultados (de hecho, para resolver la ecuación para n = 365 Derive ya necesitó 70 segundos en el ordenador que empleamos). Habrá que buscar alguna forma de simplificarla primero. La fórmula de Stirling Esta fórmula permite aproximar muy bien los grandes factoriales (cuanto más grandes, mejor es la aproximación, y en nuestro caso los factoriales son realmente grandes): Aplicándola a nuestra probabilidad y reduciendo, obtenemos: La ecuación correspondiente, igualando a 0.5, continúa resultando impracticable para Derive. Pero ahora tenemos exponenciales en vez de factoriales, lo que nos permite aplicar logaritmos y obtener por fin la ecuación: (n – x + 0.5)(L(n) – L(n−x)) – x + L(2) = 0 Su solución la encuentra Derive al instante: Un número de 17 cifras. Retomando el ejemplo del planeta, si cada terrícola genera e interpreta una obra cada cinco minutos, siguiendo las reglas de Mozart, es de esperar que al cabo de unos 78 años se produzca alguna repetición. Claro que si sólo es un (infatigable) habitante el encargado de la tarea, deberíamos esperar que la coincidencia se produzca en un plazo seis mil millones de veces mayor. Webs En las siguientes direcciones de Internet podemos oír y generar automáticamente una partitura según las reglas de Mozart. En el primero, además, podemos guardar una copia: http://sunsite.univie.ac.at/Mozart/dice/ http://web.ard.de/radio/mozart/wuerfelspil/wuerfelspiel.swf

Martes, 01 de Enero de 2008 | Imprimir | PDF |  Correo electrónico

119. 1. (2004-2005) Afinación

1. Introducción 2. Afinaciones y Temperamentos 3. Conceptos básicos 4. Sistemas de afinación 4.1. Afinación pitagórica 4.2. Justa entonación 4.3. Temperamentos cíclicos regulares 5. Bibliografía 1. Introducción Para estudiar un sonido hay, al menos, tres cualidades que debemos tener en cuenta: La intensidad que es la medida de lo fuertes o débiles que son los sonidos. Por extraño que parezca es difícilmente apreciable por el oído si no están en el mismo tono. El tono determina la altura de un sonido, es decir lo grave o agudo que es. El timbre es la cualidad que nos permite distinguir sonidos idénticos emitidos por instrumentos distintos. En esta sección, como vamos a estudiar la afinación, sólo estamos interesados en el tono, y por tanto vamos a identificar cada sonido con la frecuencia que nos da el tono. Los archivos sonoros, salvo que se advierta de lo contrario, están generados con el programa MATHEMATICA® Como muestra intuitiva de la importancia que tiene en la música la “forma de afinar”, a continuación analizamos dos fragmentos en los que se puede observar y escuchar dos tipos de música de estilos muy diferentes. Sin embargo, obviando las grandes diferencias técnicas (la primera es una grabación del año 2002 hecha en Estambul y la segunda una grabación del año 1929 extraída de un disco de pizarra), ambos fragmentos comparten muchas características fundamentales. La primera es obra de un compositor contemporáneo turco y la segunda de una interpretación de de “cançò d’estil” de Paterna -Valencia. En ellas, aunque se desconozca su origen, y con independencia de la cultura musical de cada uno, cualquiera puede apreciar que se trata de música popular. Las razones que nos permiten situarlas dentro de la música folclórica son, básicamente las siguientes: 1. Los ritmos, tipo instrumentación, etc. no son los de la música sinfónica 2. Aparecen notas diferentes a las que se escuchan en otros tipos de música En estos momentos, a nosotros nos interesa especialmente el segundo aspecto: Se utilizan muchas más notas que en la música occidental sinfónica. ¿Significa esto que hemos escuchado notas que están desafinadas?. Sin duda, la respuesta es no. Lo que ocurre es que no están afinadas en el sistema temperado al que está habituado nuestro oído. Analicemos más detenidamente los dos primeros compases del primer pentagrama: 2. Afinaciones y Temperamentos Si los interpretamos en el sistema temperado de 12 notas (el más extendido en la música occidental actual) y en el sistema de afinación pitagórico comprobamos que hay diferencias claramente perceptibles: Escuchemos, por ejemplo, la cuarta nota (Si b) en cada uno de los sistemas y luego juntas para apreciar la diferencia El objetivo de esta sección es entender situaciones como ésta e intentar responder con argumentos matemáticos a preguntas como las siguientes: ¿Qué es afinar? ¿Ha sido siempre así? ¿Por qué en la música occidental se utilizan 7 o 12 notas por octava y no otras cantidades? ¿Se puede afinar una orquesta sinfónica? ¿Cuál es el papel de las matemáticas en la afinación? El esquema que seguiremos será el siguiente: A lo largo de la Historia han aparecido centenares de afinaciones de las que sólo se siguen utilizando alrededor de media docena. La razón por la que trataremos estas cuatro formas de afinar es que éstas son las cuatro afinaciones que conviven en la orquesta clásica actual. 3. Conceptos básicos Una afinación o un sistema de afinación es el conjunto de los sonidos que utiliza la Música. En el conjunto de las frecuencias de todos los sonidos, R+ tenemos que elegir aquellos que sirven para hacer música y descartar el resto. Los sonidos admitidos por el sistema de afinación se denominarán sonidos afinados o notas musicales. Según sea la naturaleza de los números elegidos se tiene dos tipos de sistemas de afinación: las afinaciones y los temperamentos. En las primeras todos los números son racionales mientras que en los temperamentos algunos (o todos) son irracionales. Ahora bien, a pesar de que esta clasificación cada día se usa más en los tratados de música lo cierto es que tanto histórica como conceptualmente los temperamentos han surgido como aproximaciones a las afinaciones sin que, normalmente, se tuviese en cuenta el tipo de números utilizados. Una vez introducido, aunque sea grosso modo, el concepto de afinación, cabe preguntarse si éste puede ser todavía un tema de interés para alguien que no se dedique al estudio de la Historia. La aparición esporádica de artículos en revistas de física o matemáticas tratando temas de música podrían dar una contestación a esta pregunta. Sin embargo, las necesidades de músicos y musicólogos proporcionan un respuesta mucho más convincente. Éstos han establecido dos campos de actuación: • la búsqueda de nuevas afinaciones que aumenten las posibilidades en la creación musical • la recuperación de la fidelidad a partituras antiguas. En este último sentido, M. Bernal asegura que "uno de los principales problemas que se presentan en la praxis de la música antigua para tecla es el de la elección del temperamento adecuado" Revista de Musicología, 22 (1999) Entendiendo por adecuado aquel temperamento para el que fue concebida. De hecho, incluso la expresión "buen temperamento", empleada al menos a partir de la obra Clave bien temperado (Das wohltemperierte Klavier I, 1721) de J. S. Bach, resulta imprecisa. Como aclara J. J. Goldáraz buen temperamento no designa una única forma de afinar y continúa siendo un tema de discusión conocer si se trataba realmente del sistema de afinación de 12 notas por octava o se tratataba de otro temperamento de los que en la época se utilizaban en Alemania. La octava En todos los sistemas de afinación aparece el concepto de octava. Un sonido de frecuencia f1 se dice que es una octava más grave que otro f2 si f2 = 2·f1. Hasta tal punto es intuitiva esta idea, que se usa de forma natural aunque no se tenga formación musical. Piénsese, por ejemplo, cuando cantan juntos un hombre y una mujer. El hombre suele cantar una octava más grave y sin embargo cualquiera reconoce que están interpretando las mismas notas. A partir del concepto de octava, lo que se hace es partir el intervalo de frecuencias audibles por octavas: … [f, 2f], [2f, 4f], [4f, 8f], … e identifican las notas que están a diferente octava. Es decir, hablaremos de un Do sin importarnos la octava en la que se encuentra. Por tanto, es mucho más cómodo suponer que las notas están en el intervalo [1,2]. Afinar es elegir una cantidad finita de puntos del intervalo [1, 2] Siete notas Al menos desde el primer milenio antes de Cristo, los caldeos relacionaron muy estrechamente la música con la astrología y las matemáticas. De hecho, el destino de los hombres y la armonía del Universo se explicaba usando especulaciones matemáticas a las que atribuían multitud de propiedades. Parece ser que esto dio lugar a que numerosos fenómenos cósmicos fuesen representados por la comparación entre las longitudes de cuerdas tirantes. De este modo aparecieron cuatro relaciones asociadas con las cuatro estaciones del año que, por su importancia, tomaron nombres propios: 1/1 unísono 3/2 quinta 4/3 cuarta 2/1 octava Entre los números cuyas propiedades eran especialmente útiles en la predicción de sucesos destacaban el 4 y el 7. De hecho, probablemente la antigua escala caldea era de siete notas. En occidente, a partir de los caldeos y sobre todo de los pitagóricos (siglo VI. a. C.) se ha considerado que las notas fundamentales eran 7 y que el resto eran alteraciones de estas notas. A las alteraciones se les llama sostenidos ( # ) si aumentan la frecuencia y bemoles ( b ) si la disminuyen. Pero no precisaremos más en la definición de las alteraciones porque, como se verá más adelante, dependiendo del sistema de afinación significarán una cosa u otra. Tonos y semitonos Se trata de intervalos que en la práctica se emplean más que los dados anteriormente. Dadas dos notas f1, f2 se tienen las siguientes relaciones: Tono ( T ): Decimos que f2 es un tono más alta que f1 si se puede obtener a partir de f1 subiendo dos quintas y bajando una octava. Semitono cromático ( Sc ): Decimos que f2 es un semitono cromático más alta que f1 si se puede obtener a partir de f1 subiendo siete quintas y bajando cuatro octavas. Semitono diatónico ( Sd ) Decimos que f2 es un semitono diatónico más alta que f1 si se puede obtener a partir de f1 subiendo cinco quintas y bajando dos octavas. Hay sistemas de afinación en los que aparecen varios tipos de quinta, por tanto la distancia de tonos y semitonos dependerá del sistema. Algunas de estas afinaciones verifican: T=Sc+Sd e incluso se da Sc=Sd. Sin embargo, en general, no tienen por qué darse estas condiciones. 4.1. Afinación pitagórica Es muy probable que Pitágoras de Samos (580 –500 a. de C.), tras un largo periodo de estudio en las escuelas mesopotámicas, llevase las teorías de la música y los principios de la afinación a Grecia. Tal y como hacían los caldeos, estableció que el sonido musical producido por una cuerda vibrante varía en razón inversa a su longitud, esto es: "cuanto más corta sea la cuerda, más aguda será la nota producida". Además, estableció cuatro intervalos, o relaciones entre las longitudes de las cuerdas que producían las únicas consonancias admitidas: Para producir todos los sonidos afinados (notas musicales) sólo se dispone de estos cuatro intervalos y sus combinaciones. Expresado de forma axiomática, el sistema de afinación pitagórico se obtiene de la forma siguiente: P1. La música se basa en 7 notas. P2. La longitud de las cuerdas puede ser multiplicada o dividida por 3 cualquier número de veces. P3. La longitud de las cuerdas puede ser multiplicada o dividida por 2 cualquier número de veces. En lugar de manejar la longitud de las cuerdas estudiaremos las frecuencias producidas por éstas. El axioma P2 sube quintas cuando se multiplica por 3 y las baja cuando se divide y el axioma P3 sube o baja octavas cuando se multiplica o divide por 2. El sistema de afinación que se obtiene con los axiomas anteriores es relativo porque dada una cuerda L de cualquier longitud, aplicando P1, P2 y P3 se obtienen notas que suenan afinadas con la producida por L. Para que este sistema de afinación sea absoluto, y por tanto aplicable, necesitamos imponer que una nota, a la que denominaremos nota patrón o diapasón, forme parte de las notas afinadas: Notas afinadas: Consideramos una frecuencia patrón f0. Dado un sonido f diremos que está afinado en el sistema pitagórico si existen n y m números enteros de manera que: 3n 2m f0 = f Ya estamos en condiciones de obtener de forma práctica las notas de la afinación pitagórica. Todas las notas de la afinación pitagórica se obtienen aumentado o disminuyendo quintas, es decir, dada una frecuencia f multiplicamos o dividimos por 3/2 cualquier número de veces. Ahora bien, como hemos dicho que una afinación consiste en elegir puntos de [1,2], debemos dividir o multiplicar por una potencia de 2 adecuada de manera que el factor que multiplica a f esté en el intervalo [1,2]. Ejemplo Supongamos que el sonido f lo subimos dos quintas. La nota que se obtendría es: Para llevar esta nota a la misma octava que f (hacer que el factor que multiplica a f esté en el intervalo [1,2] debemos dividir por 2. Es decir que la nueva nota afinada será: Método para obtener las notas 1.- Asociamos cada una de las notas con un número, es decir 0 = Do, 1 = Re, 2 = Mi, 3 = Fa, 4 = Sol, 5 = La, 6 = Si 2.- Escribimos tablas de 7 columnas y 4 filas: 0 1 2 3 4 5 6 0 1 2 3 4 5 6 0 1 2 3 4 5 6 0 1 2 3 4 5 6 En la primera fila marcamos la nota central (3) 0 1 2 3 4 5 6 0 1 2 3 4 5 6 0 1 2 3 4 5 6 0 1 2 3 4 5 6 A partir de la nota 3 marcamos las notas que se obtienen contando 5 casillas (OJO porque la casilla de partida también se cuenta) 0 1 2 3 4 5 6 0 1 2 3 4 5 6 0 1 2 3 4 5 6 0 1 2 3 4 5 6 Cada vez que hemos marcado una casilla nueva hemos aumentado una quinta, y repitiendo el proceso siete veces obtenemos las notas naturales en el orden siguiente: Fa – Do – Sol – Re - La - Mi - Si Para obtener más notas ampliamos el número de matrices o tablas. Con ellas aparecerán, en un sentido, las notas con un sostenido, con dos, etc y en el sentido contrario las notas con 1 bemol, 2 bemoles, etc. Cada vez que vamos de una nota marcada a otra bajando en la tabla multiplicamos por 3/2 tantas veces como notas marcadas haya. Y en el sentido contrario lo que haremos es dividir por 3/2 . Ejemplo: A partir de un Do (natural), ¿cómo se obtiene un Fa# y un Mib? a) Desde el Do (natural) al Fa# hay que subir 6 quintas (hemos contado 6 casillas de las que hemos marcado previamente) por tanto se obtiene de la forma siguiente: Para que el Do (natural) y el Fa# estén en la misma octava debemos dividir por una potencia de 2 , en concreto 2 3, es decir: b) Desde el Do (natural) al Mib hay que bajar 3 quintas (hemos contado 3 casillas de las que hemos marcado previamente) por tanto se obtiene de la forma siguiente: Para que el Do (natural) y el Mib estén en la misma octava debemos multiplicar por una potencia de 2 , en concreto 2 2, es decir : Las fracciones para obtener las notas más frecuentes son las siguientes: Para el sistema pitagórico, por ejemplo un Lab y un Sol# son dos notas diferentes:   ¿Cuántas notas deben aparecer dentro de una octava? Con el método que hemos descrito podríamos generar una cantidad infinita de notas dentro de una misma octava, por tanto debemos añadir algún criterio que permita detenernos cuando se tiene una cantidad razonable de ellas. Sería lógico pensar que un buen momento para parar es cuando empiecen a repetirse los sonidos. Sin embargo, como se puede demostrar que esto no va a ocurrir nunca, deberemos conformarnos con aceptar como iguales sonidos que sean “muy parecidos”. En la gráfica siguiente hemos representado las 70 primeras notas de la afinación pitagórica. En el eje de abcisas se representa el orden en el que aparecen y en el de ordenadas la fracción con la que se obtiene. Por ejemplo, la primera nota es el punto (0,1). Cuando obtengamos una nota cuya ordenada esté muy próxima al 1 nos detendremos. La primera vez que nos acercamos al sonido inicial es cuando tenemos 12 notas, y ésta es la razón por la que la inmensa mayoría de la música que se escucha en la actualidad está hecha para el Temperamento Igual de 12 notas del que más tarde hablaremos. Si queremos mayor precisión necesitamos 53 notas, y si continuásemos 665 notas, etc., pero sin duda estas cantidades resultarían poco prácticas. Como se ve, el hecho de fijar 7, 12 u otro número de notas por octava no es una cuestión trivial y depende de la precisión que se exija en el parecido con la nota de partida. De hecho, esta elección no siempre se ha hecho con éxito. Por ejemplo, Robert Smith, en Harmonics, or the Philosophy of Musical Sounds (1749), propone 21 divisiones por octava para el temperamento de 5/18 de coma zarliniana y, como se apreciaría más tarde desde el punto de vista práctico, esto no tenía sentido. 4.2. Justa entonación Con el nombre de afinación justa o de los físicos se conocen varios sistemas de afinación que añaden el intervalo 5/4 a la afinación pitagórica para representar la tercera. La forma de incorporarlo es ajustando algunas notas de la afinación pitagórica, por tanto deben considerarse correcciones a la afinación pitagórica. En la afinación pitagórica, la tercera no se considera un intervalo consonante, sino que aparece subiendo cuatro quintas. Tercera pitagórica Tercera justa Do->Mi Do->Mi Oyéndolas juntas se percibe bien la diferencia: De todos los intentos por incorporar el intervalo de tercera a la afinación pitagórica, el que se utiliza en la práctica es el de Aristóxeno-Zarlino. No obstante, a continuación citamos otras propuestas bastante conocidas. Modificaciones de Arquitas Arquitas de Tarento (430-360 a.C.) es un discípulo de Pitágoras que dedicó gran parte de su investigación a la afinación. Advirtió que los intervalos pitagóricos 2/1, 3/2 y 4/3 son de la forma Teniendo en cuenta esto, propuso dividir la cuarta en tres intervalos que verifiquen esta relación, para lo cual propuso añadir tres nuevas proporciones: Así aparecen los valores siguientes: entre los que, por primera vez, se tiene el intervalo de tercera 5/4 que había estado prohibido por los primeros pitagóricos. Modificaciones de Tolomeo Claudio Tolomeo (100-170) parte de los conceptos pitagóricos de afinación y en su obra Harmónicos expone una teoría matemática de los sonidos en las que aparecen dos tipos de escala una fija, tética, y una móvil, dinámica. A pesar de que su sistema de afinación es más complejo que los dos anteriores, en él siempre aparece el intervalo de tercera. Como ocurría con los pitagóricos, los sonidos que consideran afinados están relacionados con su modelo del Universo. Modificaciones de Zarlino y Delezenne Gioseffo Zarlino (1517-1590) justificó los acordes con razones matemáticas que resultaron totalmente premonitorias de los armónicos. Estableció que había una afinidad entre los sonidos cuyas frecuencias son proporcionales a 1, 2, 3, 4, 5, 6 y comprobó que éstos eran emitidos por cuerdas de longitudes Delezenne (1776-1866) modificó la afinación de Zarlino y de hecho en la actualidad es habitual que en la afinación justa se mezclen notas de Zarlino con las de Delezenne. Ha habido otras muchas más propuestas, como la de Johannes Kepler (1571-1630) que, a pesar de resultar muy ingeniosas, no han supuesto aportaciones considerables a la consolidación de la Justa Entonación. Afinación de Aristóxeno-Zarlino Arsitóxeno de Tarento (360-300 a.C.) es un discípulo de Aristóteles que estudió con profundidad las doctrinas pitagóricas. Rechaza asociar las consonancias naturales de quinta, cuarta y tercera con relaciones numéricas y sostiene que basta con el oído para conseguir la afinación. A pesar de que históricamente no se introdujo como se expondrá a continuación, una forma sencilla de presentar la afinación de Aristóxeno-Zarlino es la siguiente: Consideramos una aproximación de la quinta pitagórica (3/2) dada por A partir de aquí (y en todos los tratados de música), como conviene distinguir entre ambos intervalos, se les da nombres diferentes. La quinta dada por 3/2 se llama quinta natural y la quinta dada por 40/27 se llama quinta sintónica. Una vez fijada esta aproximación, la afinación de Aristógeno-Zarlino es una afinación hecha por quintas naturales (como la de Pitágoras) pero en la que algunas de ellas han sido sustituidas por quintas sintónicas. En la tabla siguiente marcamos sólo las sintónicas y entenderemos que el resto son naturales: Teniendo en cuenta estas correcciones a la afinación pitagórica, las notas más frecuentes se obtendrían con las siguientes fracciones: A pesar de la diferencia entre las fracciones que aparecen en la afinación pitagórica y la de Aristóxeno-Zarlino, podéis comprobar que el resultado es parecido: Escala Pitagórica Escala Justa Entonación En la afinación de Aristóxeno-Zarlino, al aparecer dos tipos de quinta, aparecen dos tipos de tono: Tono grande: 9/8 Ejemplo: Do-Re Tono pequeño: 10/9 Ejemplo: Re-Mi y tres tipos de semitono: Semitono diatónico grande: 27/25 Ejemplo:Do-Reb Semitono diatónico pequeño: 16/15 Ejemplo:Mi-Fa Setinono cromático: 25/24 Ejemplo: Do-Do# Sin duda, esta circunstancia dificulta enormemente el uso de la justa entonación en la música polifónica. Comentario Desde un punto de vista meramente aritmético podemos decir que el sistema pitagórico sólo maneja sonidos que se pueden obtener mediante potencias de 2 y de 3 a partir de una frecuencia dada f0. La justa entonación añade al sistema pitagórico las potencias del 5. Vista esta secuencia lógica, la pregunta es evidente: ¿por qué no seguir con las potencias de 7 y de 9, etc.? Las razones para detenernos en el 5 son de diversa índole. En primer lugar hay razones estéticas: el intervalo de séptima convive con dificultad con los intervalos de la afinación de Zarlino. Por otro lado, cada vez que se añaden nuevas frecuencias se están incrementando los inconvenientes de los sistemas de afinación. Sirva como resumen de estos razonamientos el fragmento de la carta, fechada el de 3 de mayo de 1760, que Leonhard Euler (1077-1783) escribió a Federica Carlota Ludovica von Brandenburg Schwedt, princesa de Anhalt Dessau (1745 – 1808), para instruirla sobre temas de música (Euler, 1990): Carta VII: De los doce tonos del clavecín: “Mi intención era presentar a Vuestra Alteza el verdadero origen de los sonidos empleados en la música, casi totalmente desconocido para los músicos; pues no es la Teoría lo que los ha conducido al conocimiento de los tonos, lo deben más bien a la fuerza oculta de la verdadera Armonía, actuando tan eficazmente en sus oídos que, por así decirlo, los forzó a recibir los tonos actualmente en uso, aunque no estén suficientemente decididos sobre su justa determinación. Ahora bien, los principios de la Armonía se reducen en último término a números, [...] el número 2 produce sólo octavas [...]. Después el número 3 produce los tonos que difieren de los anteriores en una quinta. Pero introduzcamos también el número 5 y veamos cuál sería el tono que produce 5 vibraciones, mientras que el F no hace más que una. [...] los músicos lo indican con la letra , [...] es llamado una tercera mayor y produce una consonancia muy agradable, estando contenido en una proporción de números bastante pequeña, 4 y 5. [...] (Así ) tendréis las teclas principales del clavecín que según los antiguos, constituye la escala llamada diatónica que deriva del número 2, del número 3 repetido tres veces y del número 5. No admitiendo más que estos tonos, se está en condiciones de componer muy bellas melodías, cuya belleza se fundamenta únicamente en la simplicidad de los números que producen estos tonos. [...] Si se quisiera también introducir el número 7, el número de tonos de una octava sería mayor, y se llevaría toda la música a un grado más alto. Pero aquí la Matemática abandona la armonía a la Música.” 3 de mayo de 1760 Ventajas e inconvenientes de las afinaciones Ventajas En las afinaciones, como los sonidos afinados se obtienen con números racionales, los intervalos que aparecen son naturales, es decir, que las notas musicales se corresponden con armónicos de la serie natural. Por ejemplo, en el sistema pitagórico están afinados todos los armónicos que son múltiplos de 2 y de 3, mientras que en el sistema de Zarlino, están afinados los múltiplos de 2, de 3 y de 5. Dicho de otro modo, el primer armónico que no está afinado en el sistema de Pitagóras es el quinto, mientras que en el sistema de Zarlino es el séptimo. Inconvenientes Para determinar el número de notas por octava hemos supuesto que dos notas son iguales cuando en realidad son muy parecidas. Esto hace que al sonar dos o más instrumentos diferentes simultáneamente las afinaciones resulten poco prácticas. Veámoslo en el siguiente ejemplo. Ejemplo: Un cantante tiene dificultades para interpretar los tonos graves y prefiere que se suba toda la música una quinta. A esto se le llama transposición. Transposición: Consiste en subir (o bajar) una nota o un conjunto de ellas un intervalo p/q. Para ello basta con multiplicar (o dividir) las frecuencias de las notas por p/q. Si los instrumentos afinaban en el sistema pitagórico con 12 notas: Mib Sib Fa Do Sol Re La Mi Si Fa# Do# Sol# cuando en la partitura aparece un Sol# , al subir una quinta el efecto será Sol#·(3/2) = (38/212)·(3/2) = 39/213 = Re# Sin embargo, esta nota no aparece entre las 12 que hemos seleccionado. La más parecida es Mib = 25 / 33 Así, cuando se interpreta Mib en lugar de Re# el error que se está cometiendo es el que ya habíamos escuchado cuando distinguíamos entre Lab y Sol# : 4.3. Temperamentos cíclicos regulares Los temperamentos cíclicos surgen en la práctica para evitar, entre otros, los problemas que acabamos de analizar. Lo que se hace es disminuir las quintas “templar” de manera que se repita la primera nota, pero claro está, de manera que el resultado sea aceptable. A continuación analizaremos los dos temperamentos más utilizados en nuestros días: El temperamento igual de 12 notas, que es un temperamento regular e igual y el temperamento de Holder, que es un temperamento regular mesotónico. Matemáticamente, la forma de obtener los temperementos cíclicos es muy sencilla. Si queremos obtener un temperamento cíclico de n notas dividimos el intervalo [1, 2] en n subintervalos iguales. Para obtener el extremo inferior del 2º subintervalo multiplicamos por x el extremo inferior del 1º, para obtener el del 3º multiplicamos el del 2º, es decir x2 por el 1, y así sucesivamente hasta obtener el último que sería xn por 1, etc. Con este proceso lo que aseguramos es que si multiplicamos el 1 por x n veces debemos obtener el 2, es decir xn x 1 = 2 => x = Por tanto, las notas afinadas en un temperamento cíclico de n notas serán: Temperamento igual de 12 notas Divide la octava en 12 semitonos iguales. Fue el español Bartolomé Ramos de Pareja (1440 - 1491) quien lo sistematizó en 1482, cuando ejercía como profesor de Música en la Universidad de Salamanca y en Bolonia. En su tratado Música Práctica (1482) se encuentran teorías renovadoras y maneras de calcular diferentes clases de intervalos. Este sistema, que tardó mucho tiempo en imponerse, lo consagró J. S. Bach (1685 - 1750) en su obra El Clave Bien Temperado donde realiza 48 Preludios y fugas (en dos libros) en todas las tonalidades. A pesar de su pobreza, debida a que elimina algunas notas naturales que vienen dadas por la escala de armónicos, el temperamento igual de 12 notas es el sistema más empleado por sus ventajas teóricas y prácticas. Por propia construcción, la distribución de semitonos en el sistema temperado de 12 notas resulta totalmente uniforme: Temperamento de Holder William Holder (1614-1697) utiliza un procedimiento mediante el cual divide la octava en 53 partes, notas o comas, de esta forma un tono contiene 9 comas, el semitono cromático 5 y el diatónico 4. El sistema utilizado por Holder no es más que una adaptación del sistema Pitagórico y, de hecho, cuando se compara ambos sistemas dan resultados prácticamente iguales. En el temperamento de Holder, si nos quedamos con las notas más habituales, 7 notas naturales, 5 notas con sostenido y 5 notas con un bemol, la distribución que se obtiene es prácticamente la misma que en la afinación pitagórica: Ventajas y desventajas de los temperamentos El Temperamento de 12 notas Ventajas Como hemos señalado, en este temperamento cada una de las doce partes es un semitono temperado. Todos los semitonos son iguales, por tanto, las notas enarmónicas coinciden, así La#=Sib, Mi#=Fa, etc. Obviamente, en este sistema sólo existe un tipo de tono y de quinta, lo que le proporciona grandes ventajas: a) Puede modularse libremente a cualquier tonalidad sin que existan intervalos impracticables. b) El número de notas resulta muy apropiado para la práctica musical. Inconvenientes a) No existen intervalos justos. Al obtener los intervalos mediante números irracionales, éstos no se corresponden exactamente con la serie armónica de ninguna nota. b) Aunque las quintas son bastante buenas, las terceras mayores están muy desviadas. Según J. J. Goldáraz (Goldáraz, 1992) la desafinación de las terceras, junto con la igualdad de los semitonos “que empobrecían la expresividad musical, fue lo que hizo que se retrasase su aplicación general al menos dos siglos a partir de las primeras formulaciones del siglo XVI”. Sin embargo, en la actualidad, estamos tan acostumbrados a este temperamento que el intervalo justo de tercera nos suele parecer excesivamente apagado. En cualquier caso, surge un orden de prioridades a la hora de valorar las propiedades de los temperamentos. En términos generales, es perferible la perfección en las quintas que en las terceras (Lattard, 1988; Goldáraz, 1992). El Temperamento de Holder Desde el trabajo del profesor Robert Dussaut, Explicación de las comas en los distintos sistemas acústicos (Chailley, Challan, 1965), el sistema de Holder se ha considerado como un sistema de afinación idóneo para trabajar con la afinación pitagórica. Ventajas Las ventajas de este sistema de afinación aparecen en los estudios teóricos. Las diferencias con el sistema pitagórico son inapreciables, sin embargo el hecho de dividir la octava en 53 comas-holder iguales hace que sea mucho más fácil de manejar. Inconvenientes En cuanto a los inconvenientes, posee los de cualquier temperamento: los intervalos que aparecen no se corresponden exactamente con los sonidos de la serie armónica. Pero sin duda, el mayor inconveniente práctico de este sistema es que 53 notas por octava resulta un número excesivamente grande. Como muestra de las diferencias entre los sistemas que hemos analizado, podemos observar las frecuencias de las notas más habituales en los cuatro sistemas de afinación: NOTA: Para elaborar esta tabla se ha fijado el diapasón, La4 , a 440 Hz. 5. Bibliografía J. Agulló (Editor), Acústica musical. Ed. Prensa Científica S. A., Barcelona, 1989. P. Bailache, Travaux en histoire de l'acoustique musicale, http://baihache.humana.univ-nantes.fr/thmusique/ A. Baker, A concise introduction to the theory of numbers. Ed. Cambridge University Press, 1984. M. Bernal Ripoll, El temperamento de Nassarre: Estudio Matemático. Revista de Musicología, 22, pp. 157-174, Madrid, 1999. W. F. Bynum et al., Diccionario de historia de la ciencia. Ed. Herder, Barcelona, 1986. A. Calvo-Manzano Ruiz, Acústica físico-musical. Ed. Real Musical, Madrid, 1993. J. Chailley, H. Challan, Teoría completa de la Música. Ed. Alphonse Leduc, Paris, 1965. L. Euler, Cartas a una princesa de Alemania sobre diversos temas de Física y Filosofía, Ed. Universidad de Zaragoza, Zaragoza, 1990. G. Fernández de la Gándara, M. Lorente, Acústica Musical. Ed. Instituto Complutense de Ciencias Musicales, Madrid, 1998. J. Girbau, Les matemàtiques i les escales musicals. Butlletí de la secció de matemàtiques de la Societat Catalana de Ciències, 18, pp. 3-25, Barcelona, 1985. J. J. Goldáraz Gaínza, Afinación y temperamento en la música occidental. Ed. Alianza Editorial, Madrid, 1992. R. W. Hall, K. Josíc, The Mathematics of Musical Instruments. The American Mathematical Monthly, 108, pp. 347-357, Washintong, 2001. J. Halusca, Equal Temperament and Pythagorean Tuning: a geometrical interpretation in the plane. Fuzzy Sets and Systems, 114, pp. 261-269, Amsterdam, 2000. The Harvard Dictionary of Music. Harvard University Press, 1986. J. Lattard, Gammes et tempéraments musicaux. Ed. Masson, Paris, 1988. V. Liern, Taller de Música y Matemáticas. Primer Congreso Iberoamericano de Educación Matemática, Sevilla, 1990. V. Liern, Aristógeno versus Pitágoras: dos criterios matemáticos para la afinación musical. XIXth International Congress of History of Science, Zaragoza, 1993. V. Liern, La música y sus materiales: una ayuda para la clase de Matemáticas. Suma, 14, pp. 60-64, Granada, 1994. V. Liern, Métodos numéricos en música. Epsilon, 30, pp. 51-60, Sevilla, 1994. V. Liern, Algoritmos matemáticos y afinación musical. Educación Matemática, 6, pp. 45-55, México, D.F., 1994. V. Liern, Fuzzy tuning systems: the mathematics of musicians. Fuzzy Sets and Systems, 150, 35-52, Holanda, 2005. J. L. Monzo, The measurement of Aristoxenus's Divisions of the Tetrachord. http://tonalsoft.com/monzo/aristoxenus/318tet.htm U. Michels, Atlas de Música 1 y 2. Ed. Alianza Editorial, Madrid, 1994. J. Neubauer, The Emancipation of Music from Language. Departure from Mimesis in Eighteenth-Century Aesthetics. Ed. Yale University Press, 1986. R. Osserman, Rational and Irrational: Music and Mathematics en "Essays in Humanistic Mathematics" publicado por Mathematical Association of America pp. 53-59, 1993. J. Piles Estellés, Intervalos y gamas. Ed. Piles, Valencia, 1982. A. Robertson y D. Stevens, Historia general de la Música (vol. I). Ed. Alpuerto, Madrid, 1989. D. Schell, Optimality in musical melodies and harmonics progressions: The travelling musician, European Journal of Operational Resarch, 140, pp. 354-372, Amsterdam, 2002. M. Serres, Historia de las ciencias. Ed. Cátedra, Madrid, 1989. I. Stewart, Matemáticas de la escala musical. Investigación y Ciencia, Barcelona, 1996. R. Taton, Historia general de las Ciencias (vol. I). Destino S.A., Barcelona, 1985. F. Vera, Historia de la Ciencia. Ed. Iberia, Barcelona, 1937.

Jueves, 01 de Enero de 2004 | Imprimir | PDF |  Correo electrónico

120. 14. (Mayo 2010) El teorema del hexacordo I

1. Introducción Dejadme que os hable del teorema del hexacordo, que no es incordio. Hexacordo significa seis notas, una tras otra. Lo inventó Guido d'Arezzo, para solfear, con salero y aderezo. Mucho más tarde, cuando el tonalismo arde, Schoenberg estudia los hexacordos. Como sabéis, Schoenberg es furioso practicante del dodecafonismo, sistema que basa la composición musical en la elección de una seria serie de 12 notas distintas, alrededor de la cual gira toda la elaboración formal del material musical. Por ejemplo, la seria, digo serie, de abajo aparece al comienzo de su ópera La escalera de Jacob, tocada en ostinato por los violonchelos. Figura 1: Serie dodecáfonica perteneciente a La escalera de Jacob. Schoengerg dividía la serie en dos hexacordos y se afanaba por encontrar en ellos alguna brillante propiedad, con talante y gravedad. Una que le llamaba la atención, le regañaba, era el contenido interválico. Schoenberg contaba, algunas veces incluso cantaba, todos los intervalos entre las notas de un hexacordo. Estaba calculando su contenido interválico. Se asombraba al comprobar que los contenidos interválicos de los dos hexacordos de una serie coincidían. Estaba, en esencia, en presencia del teorema del hexacordo. Lo usó de manera intuitiva, sin duda fruitiva y quizás algo plausiva (Babbit [Bab87] dixit). Schoenberg se planteaba un erotema (no teman; de eros, nada): "¿Habrá teorema del hexacordo? Acorde a mí, sí (de mi a si, sin acento: una quinta)" -se decía el compositor. Pero no sabía cómo establecerlo. Veamos qué es el teorema del hexacordo con ayuda de la geometría. Una nota de una serie dodecafónica puede representar una nota de cualquier octava; en la figura 1 las notas de la serie se escribieron en el ámbito de una octava. Las notas de la serie son en realidad clases de alturas. Las 12 notas representaremos como puntos en un círculo; las sentaremos equiespaciadas, donde la distancia entre dos puntos es un semitono. La figura 2 muestra el hexacordo de más arriba. Figura 2: Representación geométrica de un conjunto de notas. El contenido interválico, como decimos, lo forman todos los intervalos entre los puntos del hexacordo. El intervalo entre dos notas está dado por el camino más corto en el círculo (distancia geodésica). En la figura vemos la filatura de segmentos urdidos de nota a nota. Denota, anota (perdón por el tuteo): el primer hexacordo, a la izquierda; el segundo, en el centro; a la derecha, el histograma común. Figura 3: Dos hexacordos complementarios y sus contenidos interválicos. Es importante avisar aquí que las notas separadas por un diámetro, el llamado tritono o diabolus in musica, cuentan como 2. Más adelante, en la segunda parte de esta serie, se verá el porqué y la utilidad de esta convención. El contenido interválico depende solo de la distancia entre los puntos del círculo. Así, los movimientos rígidos preservarán el contenido interválico. Esos movimientos son los giros, las simetrías respecto a un diámetro y las simetrías seguidas por giros. Pongamos un ejemplo; consideremos el conjunto A=. Si lo giramos 4 posiciones obtenemos T4(A)=. Si le aplicamos una simetría S respecto al diámetro que pasa por 0, resulta el conjunto S(A)=. Por último, la composición de ambas operaciones da S(T4(A))=. Bea se la figura (chica lista). Figura 4: Transformaciones de notas mediante movimientos rígidos. Hablemos con congruidad de congruencia: dos conjuntos de puntos se dicen congruentes si uno se obtiene del otro mediante movimientos rígidos. Hablemos con congruidad de contenido interválico: dos conjuntos de puntos se dicen homométricos si ambos tienen el mismo contenido interválico. La pregunta natural, obligada, casi ahogada, gutural, es: ¿existen, por ventura, conjuntos no congruentes que poseen el mismo contenido interválico? La respuesta es sí, yes, oui. Por ejemplo, A= y B=. Véase la figura de Bea (la hizo ella). Figura 5: Dos acordes homométricos pero no congruentes. Ahora es hora de describir, reescribir, circunscribir, lo anterior a términos musicales. Un acorde o una escala se puede concebir como un subconjunto de puntos en el círculo. Un giro corresponde a una transposición de un acorde o una escala. La menta hable mente, transposición en música no significa lo mismo que en teoría de grupos1, y eso a veces causa confusión. Aquí usaremos ese término en el sentido mus y cal. Las transposiciones de un acorde se corresponden con las permutaciones circulares del conjunto de puntos asociado. Figura 6: Transposición de un acorde. Los giros de un conjunto de puntos se corresponden con un cambio de fundamental en el acorde. Figura 7: Cambio de fundamental de un acorde vía transposición. Las simetrías seguidas de giros dan cuenta de diversos cambios de acordes. Permiten, por ejemplo, cambiar de modo. En la figura 8 se ve un cambio de do mayor a do menor. Figura 8: Cambio del modo de un acorde vía la simetría. O también pasar de un acorde de séptima de dominante a un acorde séptima de sensible: Figura 9: Transposición de un acorde. En música los conjuntos homométricos se llaman isómeros o también se dice que tienen la propiedad Z [For77]. 2. El teorema del hexacordo y su demostración Sin pérdida de tiempo, sin dilación, con apuro y premura, con urgencia y diligencia, con... ¡No te alargues más! ¡Enuncia el teorema ya! Me digo entonces: ¡Basta! (No tengo tiempo ni para las comillas). Helo aquí al vuelo: dos hexacordos complementarios son siempre homométricos. ¿Cómo? ¿Olvidé decir qué son los hexacordos complementarios? Tanta prisa no puede ser buena: son aquellos que no tienen notas comunes y cuya unión dan las 12 notas del círculo. Aunque enunciado aquí para 12 notas, en el contexto musical, el aserto es cierto para cualquier número de puntos. Es el teorema del hexacordo uno de esos resultados que flota en el ambiente de toda una época. Muchos lo intuían y solo unos pocos perseguían su demostración, pero ésta se escurría como pez plateado, como diente de león, como sombra furtiva. La demostración mariposeaba, risueña, burlona, coqueta casi, retando a su cazador. Ocurrió también que en varios campos se conocía el resultado, pero los protagonistas no se cultivaban entre sí ni recogían cosechas ajenas. En Teoría de la Música la primera demostración se debe a Lewin en 1959 [Lew59]. Lewin publicó un artículo que contenía una semilla, un germen, de demostración. Un año más tarde, en un nuevo artículo [Lew60] la germina, la gratina, la refina, la afina, con fino La Ína. Más tarde, en 1974, Regener [Reg74] descubrió una demostración simple que explota propiedades combinatorias de los intervalos. Desde entonces se han publicado otras demostraciones, unas más simples y otras más bien de complejidad enrevesada. Mazzola [Maz03] y Jedrzejewski [Jed06] tienen demostraciones cortas construidas sobre monumentales moles de granito matemático. Amiot [Ami07] publicó una demostración elegante, corta y defatigante, basada en la transformada del cabo fourrier Fourier. Blau [Bla99] en 1999 presentó una demostración muy elemental y perspicaz; estudió una pequeña propiedad, hizo un par de observaciones agudas, de piccolo, y dedujo el teorema sin despeinarse. Los teóricos de la música ignoraban por completo que en Cristalografía el teorema del hexacordo ya era conocido. En Cristalografía aparece el problema de determinar un conjunto de puntos a partir de sus distancias. En un principio, los cristalógrafos pensaron que podían recuperar las posiciones del conjunto de puntos a partir de sus distancias. Su gozo en un pozo; sus esperanzas, vanas; en fin, sollozo y escorrozo. Pronto dieron ejemplos de conjuntos de puntos distintos que tenían el mismo conjunto de distancias. A estos conjuntos los llamaron ciclotómicos. Retomemos la historia del teorema del hexacordo. Curiosa y ambagiosa situación: Patterson, un cristalógrafo, enunció el teorema, anunció una demostración [Pat44] (en 1944), renunció a publicarla. ¿Por qué? No se sabe. Nadie denunció la falta de la prueba. Solo en 1975 Buerger aportó y reportó una demostración sólida y pulida, nada dadá, nada gagá. Su demostración, no obstante ser triunfante por correcta, era pesante por circunspecta: usaba álgebra muy teórica, una demostración poco intuitiva. ¡Pero con Iglesias hemos topado! Sí, porque Iglesias, Juan Iglesias [Igl81], cristalógrafo, en 1981 dio una demostración simple y muy elegante, usando mera inducción; la reproducimos más adelante. Una demostración muy geométrica es la proporcionada por Senechal [Sen08]. Probablemente, Ballinger y sus coautores [BBOG09] han dado la demostración más sencilla y corta hasta el momento, demostración que generaliza el teorema del hexacordo al caso continuo (¿acordes continuos?). Más adelante, damos la demostración. El teorema del hexacordo se ha generalizado en varias direcciones, entre ellas, estudiando ritmos de diferentes cardinalidades; véanse las referencias  [Lew76], [Lew87], [Igl81], [Mor90], [Sod95] y [AG00]. 3. La demostración de Juan Iglesias Iglesias probó el teorema del hexacordo con una demostración sencilla, de blanco elegante, con blanco guante. Iglesias consideró un círculo con N puntos equiespaciados y puso sobre el círculo dos conjuntos, complementarios entre sí, uno con n puntos negros y el otro con b puntos blancos. Se dijo: "Observemos todas las distancias entre los dos conjuntos. Hum... las hay de tres tipos claramente: entre puntos negros, las llamaré distancias n-n; entre puntos blancos, serán las b-b; y entre puntos de distinto color, las n-b". Iglesias ve entonces una relación entre esas distancias. "Fijo una distancia d primero" -musita inspiradamente-; "pongamos que d ocurre ann veces entre puntos negros, abb veces entre puntos negros y anb veces entre puntos de distinto color". Continúa así: "Entonces podría escribir la siguiente relación, bella, ella: Iglesias llevó a cabo un pequeño análisis de casos que le condujo a la demostración de esa relación. "¿Qué pasa si cambio un punto negro por un punto blanco?" -se preguntó, juguetón, creativo, curioso- "¿Cómo cambia la relación anterior? ¿Cómo variarán las cantidades ann, abb y anb?" Así. Cada punto negro tiene solo otros dos puntos, del color que sea, a distancia d exactamente. Con estos puntos tres casos despuntan: Los dos puntos a distancia d son blancos: Figura 10: Caso 1 de la demostración de Iglesias. El número de distancias entre puntos blancos aumenta en 2 y el de distancias negro-blanco disminuye en 2. Los dos puntos a distancia d tienen distinto color: Figura 11: Caso 2 de la demostración de Iglesias. El número de distancias entre puntos blancos aumenta en 1 y el de distancias negras disminuye en 1. Los dos puntos a distancia d son negros: Figura 12: Caso 3 de la demostración de Iglesias. El número de distancias entre puntos negros disminuye en 2 y el de distancias negro-blanco aumenta en 2. "Si la relación es cierta para un conjunto de n puntos negro y su complementario, con b puntos blancos, ¿qué pasa con la relación (1) cuando se cambia un punto negro?" -se preguntó finalmente Iglesias. Nada cambia: Para el caso (1): Para el caso (2): Para el caso (3): ¿Cómo se prueba el teorema del hexacordo a partir de las relaciones que descubrió Juan Iglesias? En un abrir y cerrar de ojos, en un plis plas, en un suspiro. Sea N par el número total de puntos en el círculo. En el caso del teorema del hexacordo los conjuntos tienen N/2 puntos cada uno, es decir, n=b=N/2. Luego: y así ann = abb. Nótese que esta igualdad, cuando se interpreta en la música, señala precisamente que el contenido interválico es idéntico. ¿Qué más decir? Bella y elegante demostración. Iglesias: amén. 4. Para saber más Completamos brevemente en esta última sección algunos puntos que se quedaron en el tintero. En el análisis de la música atonal, en especial en la dodecafónica, se usa frecuentemente las clases de alturas. Dos notas se dicen equivalentes si están en una misma octava. Esta relación es de equivalencia. Las clases de alturas son las clases de equivalencia dadas por esa relación. El conjunto de las clases de alturas tiene la misma estructura que Z12. Como ejemplo del uso de los hexacordos en Schoenberg, veamos los compases iniciales de La escalera de Jacob (figura 13). Figura 13: Los hexacordos de La escalera de Jacob. La obra comienza con los violonchelos exponiendo el primer hexacordo, [1, 2, 5, 4, 8. 7], en ostinato. Una a una van entrando las notas del hexacordo complementario, [0, 3, 11, 10, 6, 9], en un largo arpegio, hasta que se logra un acorde de 6 notas con un amplio registro. Después de esta exposición los instrumentos entran en un contrapunto (no se muestra ya en la figura) con diferentes órdenes de las notas del primer hexacordo. Desde el punto de vista perceptual, es natural preguntarse si tras la escucha de un hexacordo o un ritmo se puede captar con precisión el contenido interválico y si dicha percepción constituye un factor musical relevante. Varios autores han llevado a cabo experimentos con sujetos para determinar si las estructuras de teoría de conjuntos usadas en la música atonal tienen correlato perceptual. Bruner [Bru84] descubrió en sus experimentos que los juicios de similitud entre acordes, presentados de varias maneras, no se correspondían con las propiedades de los sonidos como conjuntos, sino con otras tales como consonancia, número de notas en común o relaciones armónicas. Gibson realizó varios experimentos para investigar esta cuestión. En [Gib86] Gibson quiso probar las relaciones de similitud expuestas por Forte [For77] en su libro The Structure of Atonal Music. De 39 sujetos, solo 3 calificaron la similitud entre acordes siguiendo las teorías de Forte. En [Gib88] Gibson explora la relevancia perceptual de las clases de alturas y en [Gib93], la de los hexacordos complementarios concretamente. En ambos experimentos el porcentaje de sujetos que juzgaron la similitud entre acordes según las teorías de Forte fue similar al dado por el puro azar. A pesar de lo dicho más arriba sobre la relevancia perceptual de ciertos conceptos matemáticos, las matemáticas constituyen una gran herramienta de análisis, sobre todo de la música contemporánea atonal. Un ejemplo de ello es el libro Foundations of Diatonic Theory, de Johnson [Joh03]. Es un libro para músicos, parte de un proyecto llamado Mathematics Across the Curriculum, que explica muchos conceptos de teoría de la música con conceptos de matemáticas introducidos con total pertinencia. Bibliografía [AG00] T. A. Althuis and F. Göbel. Z-related pairs in microtonal systems. Memorandum 1524, University of Twente, The Netherlands, April 2000. [Ami07] Emmanuel Amiot. David Lewin and maximally even sets. Journal of Mathematics and Music, 1(3):157-172, 2007. [Bab87] Milton Babbitt. Milton Babbitt: Words About Music. The Wisconsin University Press, Madison, WI, 1987. Edited by Joseph Nathan Straus and Stephen Dembski. [BBOG09] B. Ballinger, F. Benbernou, N. Gomez, J. O'Rourke, and Toussaint G. The continuous hexachordal theorem. In E. Chew, A. Childs, and C-H. Chuan, editors, Mathematics and Computation in Music, pages 63-77. Springer, Berlin, 2009. [Bla99] Steven K. Blau. The hexachordal theorem: A mathematical look at interval relations in twelve-tone composition. Mathematics Magazine, 72(4):310-313, October 1999. [Bru84] C.L. Bruner. The perception of contemporary pitch structures. Music Perception, 2(1):25-39, 1984. [For77] Allen Forte. The Structure of Atonal Music. The Yale University Press, Madison, WI, 1977. [Gib86] D.B. Gibson. The aural perception of nontraditional chords in selected theoretical relationships: A computer-generated experiment. Journal of Research in Music Education, 34(1):5-23, 1986. [Gib88] D.B. Gibson. The aural perception of similarity in nontraditional chords related by octave equivalence. Journal of Research in Music Education, 36(1):5-17, 1988. [Gib93] D.B. Gibson. The effects of pitch and pitch-class content on the aural perception of dissimilarity in complementary hexachords. Psychomusicology, 12(1):58-72, 1993. [Igl81] Juan E. Iglesias. On Patterson's cyclotomic sets and how to count them. Zeitschrift für Kristallographie, 156:187-196, 1981. [Jed06] Golan Jedrzejewski. Mathematical Theory of Music. Editions Delatour France, 2006. [JK03] Philippe Jaming and Mihalis Kolountzakis. Reconstruction of functions from their triple correlations. New York Journal of Mathematics, 9:149-164, 2003. [Joh03] Timothy Johnson. Foundations of Diatonic Theory. Key College Publishing, 2003. [Lew59] David Lewin. Intervallic relations betwen two collections of notes. Journal of Music Theory, 3(2):298-301, November 1959. [Lew60] David Lewin. The intervallic content of a collection of notes, intervallic relations between a collection of notes and its complement: An application to schoenberg's hexachordal pieces. Journal of Music Theory, 4(1):98-101, April 1960. [Lew76] David Lewin. On the interval content of invertible hexachords. Journal of Music Theory, 20(2):185-188, Autumn 1976. [Lew87] David Lewin. Generalized Musical Intervals and Transformations. Yale University Press, 1987. [Maz03] Guerino Mazzola. The Topos of Music. Birkhäuser Basel, 2003. [Mor90] Robert D. Morris. Pitch-class complementation and its generalizations. Journal of Music Theory, 34(2):175-245, Autumn 1990. [Pat44] A. Lindo Patterson. Ambiguities in the x-ray analysis of crystal structures. Physical Review, 64(5-6):195-201, March 1944. [Reg74] Eric Regener. On Allen Forte's theory of chords. Perspectives of New Music, 13(1):191-212, Autumn-Winter 1974. [Sen08] Marjorie Senechal. A point set puzzle revisited. European Journal of Combinatorics, 29(1):1933-1944, 2008. [Sod95] Stephen Soderberg. Z-related sets as dual inversions. Journal of Music Theory, 39(1):77-100, Spring 1995. Notas a pie de página: 1 Una transposición en teoría de grupos es una biyección entre grupos finitos que deja todos los elementos fijos salvo dos.

Miércoles, 05 de Mayo de 2010 | Imprimir | PDF |  Correo electrónico