Febrero 2006: Rompecabezas del Teorema de Pitágoras (publicado en la revista SUMA, número 43, 2003)
Febrero 2006: Rompecabezas del Teorema de Pitágoras (publicado en la revista SUMA, número 43, 2003) |
 |
 |
 |
| Escrito por Grupo Alquerque | ||||||||||
| Miércoles 01 de Febrero de 2006 | ||||||||||
|
INTRODUCCIÓN Sin duda, el matemático más conocido en nuestro tiempo por las personas que no tienen una relación corriente con las matemáticas es Pitágoras (aunque algún alcalde de ciudad importante piense que no haya hecho mucho por ella). Quizás de su vida se conozca poco, no se sepa en qué época vivió, cuáles fueron sus estudios, pero lo que es indudable es que todo el mundo conoce el teorema que lleva su nombre, e incluso personas que perdieron hace mucho tiempo su relación con la escuela son capaces de repetir su enunciado.
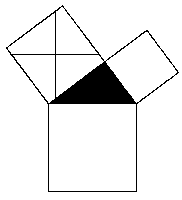
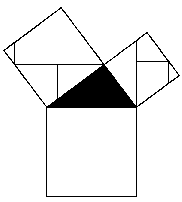
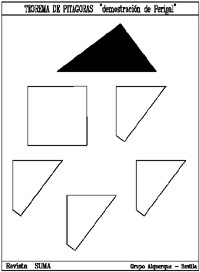
Aparte de las comprobaciones numéricas y demostraciones algebraicas, existe una gran variedad de demostraciones geométricas, que pueden aprovecharse para montar juegos de rompecabezas. El Teorema de Pitágoras era conocido antes que él por babilonios, hindúes, chinos o egipcios (al menos para ciertos triángulos rectángulos) y ha recibido a lo largo de la historia nombres muy significativos. Por ejemplo los hindúes lo llamaban el Teorema de la Silla de la Esposa. En la Edad Media se conocía como Teorema Maestro de la Matemática pues todo aquel que deseaba acceder a la categoría de maestro en matemáticas debía presentar una demostración propia (de ahí la gran cantidad de demostraciones geométricas existentes). En el siglo XVIII se conocía como el Teorema del Puente de los Burros, pues el que superaba ese Teorema entraba en el mundo del conocimiento matemático. Hoy en día se calcula que pueden existir cerca de 1.000 demostraciones, hechas no sólo por matemáticos, sino también por personajes tan diferentes como filósofos, monjes, políticos... PUZZLES DE PITÁGORAS Los siguientes juegos se basan en este conocido teorema. La forma de presentarlos es como un puzzle en el que partiendo de un triángulo rectángulo y al montar las piezas se puede formar por un lado el cuadrado sobre la hipotenusa, y con las mismas piezas se construyen por otro los cuadrados sobre los catetos. Estos rompecabezas se pueden usar en primaria como simples juegos para trabajar equivalencias de superficies, y en secundaria como complemento a las comprobaciones numéricas y demostraciones algebraicas. Tal vez la disección más conocida es la atribuida a Henry Perigal (1801-1898), corredor de bolsa londinense y astrónomo, y que se encuentra grabada en piedra en la lápida de su tumba en Essex. En ella se divide en cuatro partes el cuadrado construido sobre el cateto mayor a partir de su centro (que se puede hallar por intersección de las diagonales), trazando posteriormente por él una paralela y una perpendicular a la hipotenusa del triángulo.
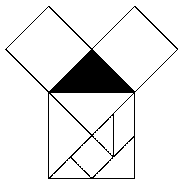
Otra demostración fácil de realizar utiliza las siete piezas del Tangram Chino. En este caso el triángulo sobre el que se trabaja no es un triángulo rectángulo cualquiera sino rectángulo e isósceles, y coincide con uno de los triángulos mayores del tangram.
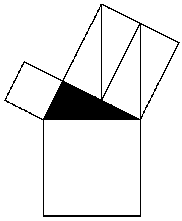
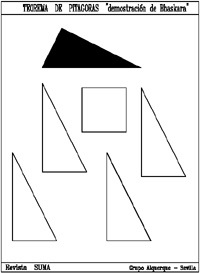
Posiblemente el puzzle más simple en su construcción se basa en la demostración realizada por el matemático y astrónomo hindú Bhaskara Akaria (1114-1185), autor del libro Lilavati dedicado a problemas aritméticos, geométricos y combinatorios. En él uno de los catetos ha de ser doble que el otro.
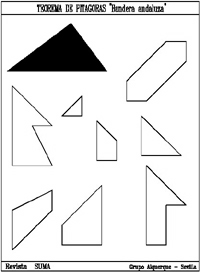
Hace unos años la Junta de Andalucía presentó la siguiente división como divulgación de la bandera de nuestra comunidad, ya que si el cuadrado sobre el cateto grande se dibuja de verde y el del pequeño de blanco, al montar el cuadrado sobre la hipotenusa aparece en diagonal la bandera de la comunidad andaluza (verde-blanco-verde).
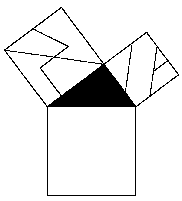
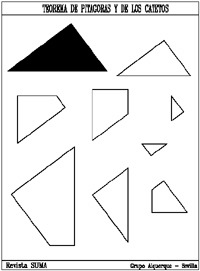
Por último presentamos otra demostración mediante rompecabezas del Teorema de Pitágoras que puede ser utilizada para demostrar asimismo el Teorema de los Catetos ya que el cuadrado sobre la hipotenusa queda dividido en dos rectángulos cuyas áreas son respectivamente el producto de la hipotenusa por la proyección de cada cateto sobre ella.
A continuación se acompañan las piezas necesarias para montar cada uno de los puzzles comentados (salvo el tangram chino) que pueden ser copiadas en cartulina y recortadas para jugar.
|
||||||||||
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |