Arquímedes y la medida del círculo
Arquímedes y la medida del círculo |
 |
 |
 |
|
ABC, 11 de Enero de 2021 El matemático Urtzi Buijs y la ingeniera Miriam González explican cómo el genio tuvo un conocimiento preciso del número pi y su relación con esta medida
El número π siempre ha estado ahí, desde que el mundo es mundo, en todos los círculos y esferas de la naturaleza. Pero, ¿cuándo advirtió la humanidad su presencia? ¿Tuvo un descubridor? Es fácil imaginar que el inventor de la rueda repararía en que cuando esta giraba una vuelta completa la longitud que recorría era poco más más del triple de su diámetro. Egipcios y babilonios intuyeron este número e intentaron aproximarlo. Pero el primer matemático que tuvo un conocimiento preciso de la existencia del número π fue Arquímedes de Siracusa (287 a. C - 212 a. C). Arquímedes está considerado uno de los grandes matemáticos de todos los tiempos. Su vida y obra son una leyenda: inventó la catapulta, la polea compuesta, los espejos cóncavos y el tornillo sin fin que lleva su nombre. Utilizó con astucia la ley de la palanca, descubrió el principio fundamental de la hidrostática, el área y volumen de la esfera... ¡Y se anticipó casi 2.000 años al cálculo integral! (Spoiler: si sigues leyendo tendrás una muestra de esto último) . Este genial matemático murió durante el sitio de Siracusa, asesinado por un soldado romano que había recibido la orden de no hacerle ningún daño. La leyenda cuenta que Arquímedes estaba tan abstraído en sus cálculos que no obedeció cuando el soldado le requirió que lo acompañara. Esa misma leyenda es la que afirma que sus últimas palabras fueron: «Noli turbare circulos meos» (no molestes a mis círculos).
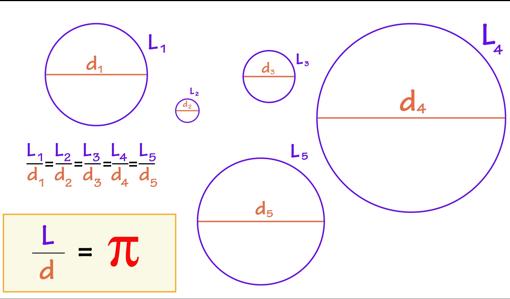
Lo que no forma parte de la leyenda es la inscripción de su tumba. Arquímedes pensaba que su mayor descubrimiento era el ingenioso cálculo del volumen de la esfera, como dos tercios del volumen del cilindro circunscrito a ella y pidió a sus familiares que grabarán esa figura en su lápida junto con la siguiente frase: La razón del exceso que hubiese entre el sólido continente y el contenido. Más de un siglo después, Cicerón comienza su carrera como cuestor en Lilibea (Sicilia). En Roma había tenido noticias de la inscripción de la tumba de Arquímedes y les pregunta a los siracusanos por su paradero, estos le responden que lo desconocen y que probablemente ni exista la tumba, ni nunca haya existido ese tal Arquímedes. Cicerón busca la tumba, la encuentra y le rinde honores, y este es para muchos autores la mayor aportación de Roma a las matemáticas, dado el desinterés extremo de los romanos por las mismas. Unos siglos después la tumba desapareció nuevamente, y hoy en día se desconoce su ubicación, aunque algunos afirman que se encuentra en el hall de un hotel de Siracusa. Pero volvamos al descubrimiento del número π. Arquímedes no usó esa letra para referirse a ese número (no empezó a usarse el símbolo π hasta principios del siglo XVIII), lo que descubrió es que, para todos los círculos, ya sean grandes o pequeños, el cociente de la longitud de su perímetro y la longitud de su diámetro es constante. Esta constante universal de los círculos bien merece un nombre, y en efecto, estamos hablando de… ¡El número π!
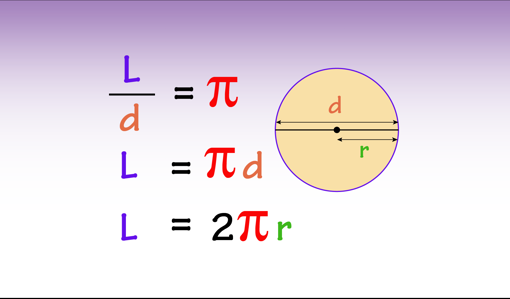
La anterior definición del número π como cociente es equivalente a la conocida fórmula para la longitud del perímetro del círculo. En efecto, dado que el radio es justamente el doble del diámetro, despejando la longitud L de la definición de π obtenemos que el perímetro del círculo es L=2 π r.
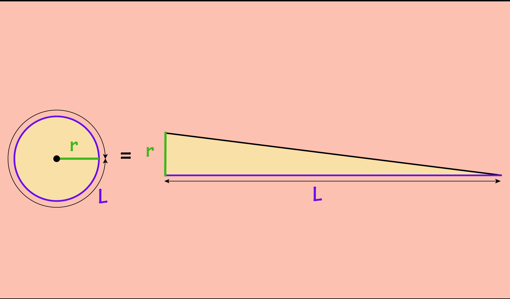
Arquímedes siguió adelante hasta encontrar una fórmula para el área de un círculo. Este resultado es la PROPOSICIÓN 1 de su tratado «Sobre la medida del círculo» y lo enunció del siguiente modo: Todo círculo es equivalente a un triángulo rectángulo, uno de cuyos catetos es igual al radio y el otro al perímetro del círculo.
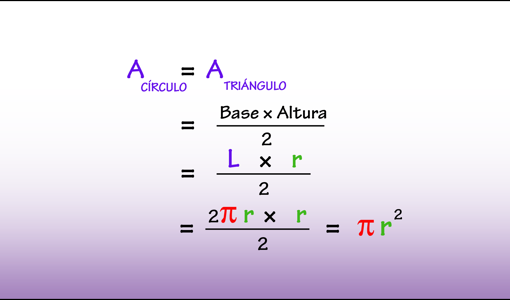
De esta Proposición podemos deducir fácilmente una fórmula explícita para el área del círculo:
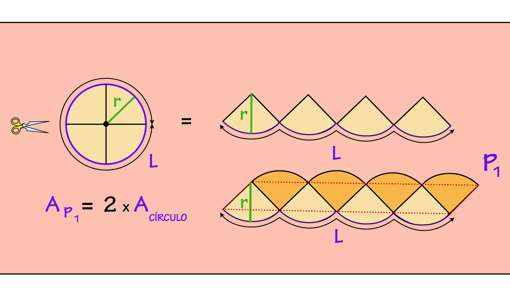
Esta es la fórmula que todos conocemos a día de hoy. ¿Pero sabéis cómo se le pudo ocurrir tan brillante idea? Si cortamos el círculo en cuatro porciones iguales. La figura resultante tendrá la misma área que el círculo original. Si la duplicamos obtendremos una figura P1 cuya área duplica la del círculo.
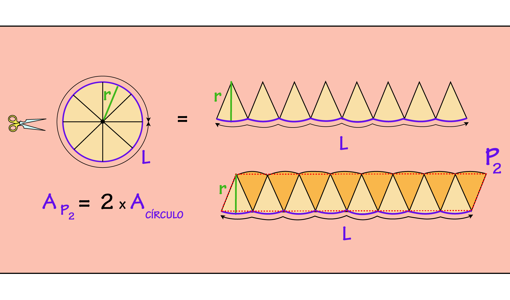
La figura P1 nos recuerda ligeramente a un paralelogramo cuya área si sabemos calcular (base x altura). Podemos hacer la misma operación dividiendo el círculo en 8 partes esta vez. De este modo obtenemos una nueva figura que sigue teniendo el doble de área que el círculo original, pero de forma que cada vez se parece más a un paralelogramo.
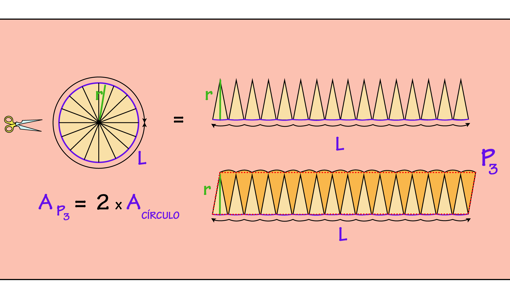
Si dividimos cada vez en más porciones el círculo 16, 32, 64, 128… vemos que la figura resultante Pn se parece cada vez más a un paralelogramo.
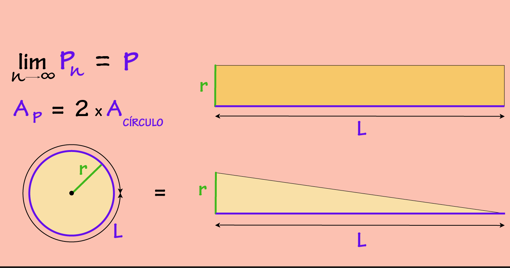
En el límite la figura resultante sigue teniendo la misma área que el círculo y al duplicarla obtenemos un rectángulo de base L y altura r.
Por tanto, el área del círculo coincide con la de un triángulo rectángulo de base L y altura r. Esto bien se merece un ¡EUREKA!
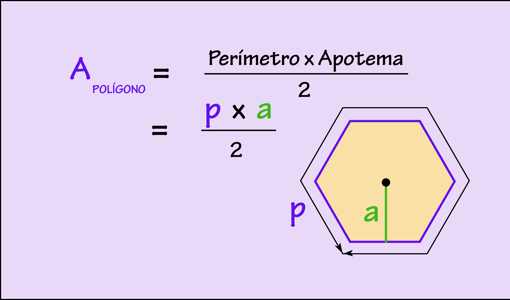
Estas fórmulas dependen de la constante π. Pero, ¿cuál es el valor de este número? Pues, si no conocemos su valor de poco nos sirven las fórmulas. El genio de Siracusa también dio respuesta a esta pregunta en uno de sus resultados más notables. En la PROPOSICIÓN 3 de su tratado sobre la Medida de Círculo, Arquímedes acota el valor de π. Para entender su método recordemos primero la fórmula del área de un polígono regular. El área de un polígono regular es la mitad del producto del perímetro por la apotema.
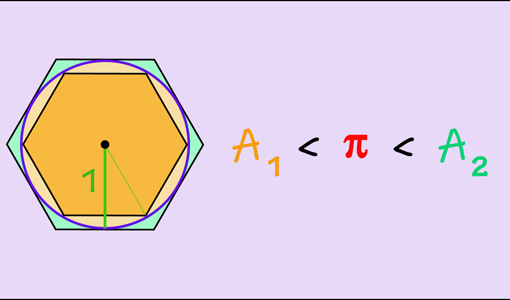
La idea de Arquímedes consistía en partir de un círculo de radio 1, cuya área es A = π, y considerar un polígono inscrito en la circunferencia y otro circunscrito. Si denotamos por A1 el área del polígono inscrito y por A2 el área del polígono circunscrito, tenemos que A1 < π < A2.
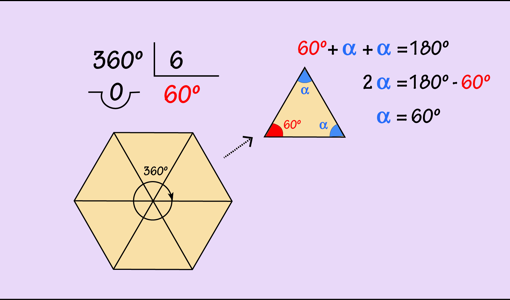
Y dado que conocemos la fórmula para el área del polígono regular, podemos acotar el valor de π. Vamos a ilustrar el método de Arquímedes con el hexágono. El hexágono está formado por 6 triángulos equiláteros como podemos comprobar.
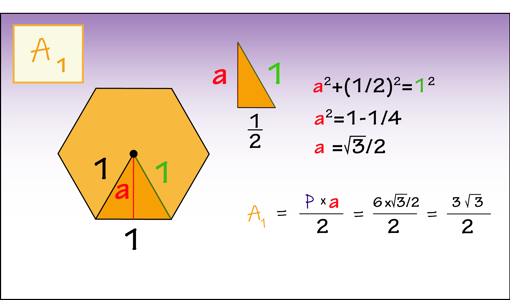
El hexágono inscrito tiene lado de medida 1. Por tanto, su perímetro p es 6. Para calcular la apotema consideramos el triángulo rectángulo del que conocemos la hipotenusa 1 y un cateto 1/2. Aplicando el Teorema de Pitágoras obtenemos: Por tanto, el área del hexágono inscrito es la mitad de 3 veces raíz de 3:
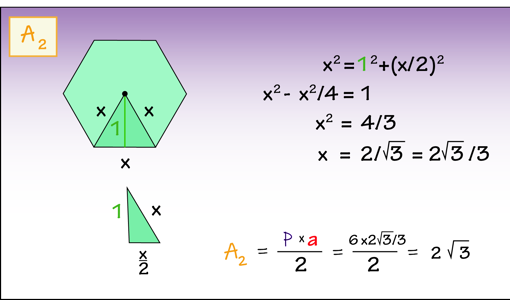
El hexágono circunscrito tiene lado desconocido y apotema de medida 1. De nuevo por el Teorema de Pitágoras se tendría que este lado desconocido es 2 veces raíz de 3 entre 3. Luego el área del hexágono circunscrito es el doble de raíz de 3:
Teniendo en cuenta que 2’598 es menor que 3 por raíz de 3 entre 2 y que 2 veces raíz de 3 es menor que 3,4642, llegamos a la conclusión de que el número π se encuentra comprendido entre estos valores: 2,598 < π < 3,4642. La anterior aproximación no resulta muy precisa, pero Arquímedes no se quedó ahí. Hizo cálculos similares a los vistos para los polígonos regulares de 12, 24, 48 y 96 lados, llegando a la asombrosamente precisa acotación: 3,1412989 < π < 3,1428265 Y esto se merece un ¡No me pises los círculos!
Como despedida os dejamos un enlace en el que podéis consultar los elementos de este artículo en formato vídeo ¡Hasta luego! Urtzi Buijs es Profesor Titular del área de Geometría y Topología en la Universidad de Málaga. Miriam González es Desarrolladora de Software en la Universidad de Málaga. Ambos son fundadores del canal de Youtube Archimedes Tube. El ABCDARIO DE LAS MATEMÁTICAS es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME) |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |