 Pitágoras (Siglo VI a.C.)
Pitágoras (Siglo VI a.C.) |
 |
 |
 |
| Escrito por Pedro Miguel González Urbaneja (IES Sant Josep de Calassanç, Barcelona) | |||||||||||||||||||||||||||||||||
Pitágoras, entre la historia y la leyenda
Además de su decisiva contribución al acervo matemático griego, Pitágoras es el principal responsable –a través de la práctica de la demostración– del nacimiento en Grecia de la Matemática racional como ciencia especulativa y deductiva. Como filósofo del número, para Pitágoras y los pitagóricos, Filosofía, Ciencia, Matemáticas y Religión son aspectos indisociables que se integran en una apasionada actividad intelectual presidida por un misticismo de carácter aritmético–geométrico. Al acuñar para la posteridad, en el lenguaje del saber, los términos Filosofía («amor a la sabiduría») y Matemáticas («lo que se conoce», «lo que se aprende»), Pitágoras es uno de los artífices del milagro griego como principal instaurador de la tradición filosófica y matemática en occidente, contribuyendo su legado de forma incuestionable a establecer una íntima y duradera relación entre Matemática, Ciencia y Filosofía. Entre la historia y la ficción, la extraordinaria figura de Pitágoras ha sido muy controvertida, estando inmersa en un halo misterioso que envuelve a leyendas y tradiciones sobre el personaje. Se ha llegado incluso a dudar de su existencia. El mismo Aristóteles que vivió tan sólo doscientos años después de Pitágoras, es muy cauto y no se compromete, a pesar de la tradición, con atribuciones personales a Pitágoras de doctrina matemática, musical o cosmológica alguna y prefiere hablar de los pitagóricos más que de Pitágoras, a quien, mencionando sólo en dos ocasiones, parece poner en entredicho su existencia real. Estas suposiciones son desmentidas por algunos documentados testimonios de Heráclito y Herodoto. Actualmente la investigación histórica parece haber dejado fuera de toda duda la historicidad de Pitágoras, pero de todas formas la figura histórica de Pitágoras ha sido muy edulcorada por parte de quienes más que biógrafos son hagiógrafos, sobre todo Diógenes Laercio y Porfirio, del siglo III d.C. y Jámblico, del siglo IV. Lástima que la obra de Aristóteles Sobre los Pitagóricos se haya perdido, aunque es plausible que en ella se hallara más doctrina pitagórica que biografía del maestro. Durante mucho tiempo hubo un gran escepticismo sobre la verosimilitud de las biografías de Pitágoras, atribuyéndoles más novela que historia, ante el estilo laudatorio sobre las peripecias científicas y las enseñanzas religiosas del sumo pontífice del Pitagorismo. Actualmente, la investigación y la crítica histórica de algunos eruditos han separado la ganga fantástica de la mena histórica y sobre todo tras la reciente publicación de la obra de B.L. Van der Waerden Die Pythagoreer (Zurich, 1979), se tiende a dar más credibilidad a los biógrafos aludidos considerando que ellos pudieron tal vez disponer de documentos próximos a los tiempos del Pitagorismo. Pitágoras nació en la isla de Samos. Tras una exquisita formación intelectual bajo la dirección de los filósofos Ferecides y Hermodomas, es probable –y así lo asegura Jámblico– que visitara a Tales en Mileto y aprendiera directamente de él –lo que por proximidad cronológica y geográfica habría sido posible–. Avido de ampliar conocimientos, al haber agotado las fuentes del saber griego de la época, con un alma helénica, inquieta y viajera, y aconsejado por la experiencia personal de Tales, Pitágoras habría estado en Egipto y Mesopotamia, donde los sacerdotes y escribas le debieron inculcar no sólo de la ciencia exotérica, como a Tales, sino también de la ciencia esotérica que impregnaría toda su elaboración científica y la transmisión de la misma a sus discípulos. Es posible incluso que en sus peregrinaciones Pitágoras llegara hasta la India donde habría asimilado tanto conocimientos matemáticos y astronómicos como mucho bagaje religioso, en particular las doctrinas sobre la reencarnación y la transmigración de las almas, que sería un lugar común en la Comunidad Pitagórica. Incluso se le atribuyen viajes por el Mediterráneo desde Fenicia hasta las Columnas de Hércules y de aquí a las Galias y a las Islas Británicas para aprender de los druidas. El saber milenario de egipcios, fenicios, judíos, árabes, caldeos, persas, indios y druidas habría conformado, según tradiciones legendarias, la extraordinaria sabiduría de Pitágoras. Al regreso de sus viajes, Pitágoras sesienteimbuido de una función casi mesiánica de transmisión de la verdad y el conocimiento y empieza a exponer doctrina matemática, filosófica y religiosa, primero en Samos y después en Crotona, colonia dórica de la Magna Grecia, situada en la costa sudeste de Italia, donde funda una comunidad de carácter científico y religioso. La leyenda persigue a Pitágoras hasta el umbral de su muerte que se ha descrito con todo tipo deversiones más o menos peregrinas, algunas incluso de tipo violento en relación con las frecuentes hostilidades entre Crotona y Sibaris. Según lo más fiable parece ser que murió en Metaponto, hacia el año 500 a.C. Pitágoras: Filosofía, Religión, Ciencia y Matemáticas Nicómaco de Gerasa (en Introducción a la Aritmética), Diógenes Laercio (en Vida de los filósofos más ilustres ) y Jámblico (en Vida pitagórica), entre otros, atribuyen a Pitágoras los términos Filosofía y Filósofo, como el amor y el amante de la Sabiduría, respectivamente. Pitágoras fue el primero en utilizar el término Cosmos para describir el orden y la armonía inherentes a un universo regido por unas leyes cognoscibles e inteligibles por el hombre a través del número que es el principio elemental, «la esencia de todas las cosas», componente esencial de la armonía matemática que debe guiar, con finalidad religiosa, toda investigación sobre el universo. Pitágoras alcanzaría esta iluminación, tras sus viajes, a través de su propia reflexión sobre la sabiduría milenaria de los pueblos de Oriente Próximo. De los egipcios aprendería que las formas de las figuras geométricas se ajustan a números y proporciones y de Mesopotamia que los movimientos de los astros están regidos por leyes numéricas. De su propia experimentación, Pitágoras deduce que la armonía musical también está regida por el número. De estos tres hechos, tras una audaz extrapolación, Pitágoras estableció que «el número es la esencia del universo» y que «el número es la raíz y fuente de la naturaleza eterna». Bajo estos presupuestos vitales e intelectuales, Pitágoras funda una comunidad en la que los aspectos científicos y religiosos están íntimamente asociados de forma mística. Se trata de una secta animada por el culto ritual que recuerda a los adoradores de Orfeo, donde las armonías y misterios de la Matemática y de la Filosofía eran partes esenciales y cuya influencia no tardó en hacerse sentir en toda la Magna Grecia e incluso en Roma. El principal objeto de las doctrinas pitagóricas era la purificación del alma o catarsis mediante la permanente prosecución de estudios filosóficos, matemáticos y cosmológicos, emprendidos como factores de sublimación espiritual para la dirección de la existencia, merced a la identificación intelectual –filosófica– con la gran idea divina ordenadora del universo: el número, que integra y confiere unidad a todo un sistema de pensamiento filosófico, científico y religioso. Las propias palabras Filosofía y Matemática parece que fueron acuñadas por el propio Pitágoras para describir sus actividades intelectuales, como elementos de elevación moral hacia la salvación. Los pitagóricos perseguían penetrar en el secreto de la armonía de los números, ya que desvelado éste creían poder comprender la armonía del universo. Soñaban con poder captar la esencia del universo bajo la forma de números enteros, imaginándose estar tras las huellas del misterio último de las cosas. Los pitagóricos vinculaban íntimamente Mística, Religión y Ciencia; Geometría, Música, y Cosmología; Aritmología, Metafísica y Filosofía; cuerpo, alma y espíritu en una armoniosa síntesis. Quizá resida en esa capacidad unificadora del Pitagorismo entre lo científico-racional y lo místico-religioso su radicación profunda en la matriz de la Cultura Griega y por ende en su heredera, nuestra llamada Cultura Occidental. Pero más allá de la Filosofía, la Mística y la Religión, Pitágoras y los pitagóricos aportaron un ingente caudal de conocimientos matemáticos. Proclo escribe Sobre Pitágoras en su celebre Comentario al Libro I de Los Elementos de Euclides: «Pitágoras transformó la doctrina filosófica que trata de la geometríaen enseñanza liberal, examinó desde lo alto sus principios, investigó los teoremas de un modo inmaterial e intelectual y descubrió la dificultad de los números irracionales y la construcción de las figuras cósmicas [poliedros].» Según Proclo, Pitágoras marca un hito en la Historia de la Matemática, al transformar la Geometría en saber puramente teórico e investigar los teoremas de forma abstracta, es decir, de manera discursiva e intelectual, trascendiendo el empirismo y situándose en el umbral de la Matemática racional como artífice supremo del «milagro griego en Matemáticas», en cuyo ámbito la idea y la necesidad de la demostración es uno de los componentes capitales del patrimonio pitagórico, fundamento de la instrucción liberal que proclama Proclo respecto de Pitágoras, al indicarnos que este sabio fue el primero en someter la Matemática a la exigencia de la rigurosa deducción lógica, que generación tras generación, se hizo cada vez más imperiosa. La evidencia sensible reiterada por la empírica percepción sensorial que va forjando prescripciones útiles se manifiesta, para Pitágoras, insuficiente en el plano de las necesidades racionales, lo que obliga a trascender lo que hasta entonces era la práctica empírica sobre los casos particulares desarrollando métodos deductivos para demostrar de forma general. Cierto que en muchas ocasiones una comprobación geométrico-empírica de carácter inductivo puede satisfacer el espíritu y producir resultados visualmente palmarios, como ocurre en la inmensa parafernalia de fórmulas aritméticas que los propios pitagóricos obtienen con el atomismo numérico-geométrico de los números poligonales; pero hay problemas transcendentales de la Matemática, sobre todo aquellos en los que subyace la presencia del infinito, en los que sólo una rigurosa demostración, como acto intelectual puro, más allá de la intuición sensible, puede ser satisfactorio; por ejemplo, el estudio de la inconmensurabilidad del lado y la diagonal de un cuadrado o un pentágono, que no es comprobable empíricamente y que tal vez fue la primera demostración verdaderamente matemática realizada por los pitagóricos. He aquí pues, en la demostración, la contribución fundamental del Pitagorismo a la Matemática, valorado siempre muy por encima de sus magníficas contribuciones particulares en ámbitos concretos de esta ciencia, siendo considerada, además, la demostración, como elemento esencial en el tránsito del mito al logos que tiene lugar en la cultura griega. La demostración va mucho más allá de la mera persuasión de la Retórica en la que los griegos eran grandes maestros, pues, es posible con persuasión argüir lo falso contra lo verdadero (de ahí los reproches de Sócrates hacia los sofistas). La demostración convence por la ilación argumental incontrovertible que alcanza algo legítimo mientras no se pongan en entredicho las leyes de la lógica. Por eso a partir de Pitágoras la Matemática es universalmente considerada como un manantial primario de verdad objetiva.
Textos de Bertrand Russell sobre Pitágoras
B.Russell. Historia de la Filosofía Occidental. Austral, Madrid, 1995, vol.1.
SIMBOLISMO DE LOS ATRIBUTOS MATEMÁTICOS EN LA COMUNIDAD PITAGÓRICA
La Arcadia pitagórica, una atmósfera mística impregnada de música y simbología matemática, donde la comunidad pitagórica desarrollaba la pasión por el conocimiento mediante especulaciones filosóficas y matemáticas como base moral para la consecución de la armonía interior y con el entorno, de acuerdo con el orden natural de las cosas que emana de Dios, supremo ordenador cósmico a través del maravilloso poder de la armonía matemática y musical, metáforas del orden universal. El Dodecaedro como quintaesencia de la Cosmogonía pitagórica, la sagrada Tetractys como fuente y raíz de la naturaleza eterna, el triángulo rectángulo depositario de la inconmensurabilidad, el Pentagrama místico símbolo de identificación de los pitagóricos y de la salud, son los talismanes de la actividad intelectual del «modo de vida pitagórico», en el que la música –cuya armonía es de naturaleza matemática– ejerce una influencia definitiva en el equilibrio emocional. La comunidad pitagórica, de carácter científico y religioso, se basaba en un ideario común fundamentado en todo un cuerpo de doctrina sobre el hombre, el alma, la sociedad, el cosmos, etc., que conducía necesariamente al estudio, a la reflexión filosófica y a la especulación matemática y cosmológica, actividades en las que el adquisición del conocimiento participaba más del carácter de una iniciación religiosa que de una mera instrucción o investigación, es decir, religión y ciencia son aspectos íntimamente vinculados en un tipo de vida llamado pitagórico (Platón, República, 600b) y la actividad científica es una consecuencia de la doctrina, no el móvil inicial como sería en la Academia platónica, en el Liceo de Aristóteles o en el Museo de Alejandría. Pitágoras organizó en su comunidad dos tipos distintos de enseñanza, que darían lugar según Jámblico (Vida Pitagórica, XVIII.80–87) a dos tipos de miembros en la primitiva comunidad pitagórica: los Matemáticos («conocedores»), jóvenes especialmente dotados para el pensamiento abstracto y el conocimiento científico y los Acusmáticos («auditores»), hombres más simples, pero igualmente sensibles, que reconocían la verdad de forma intuitiva a través de dogmas, creencias, sentencias orales indemostrables y sin fundamento, principios morales y aforismos. La diferenciación entre los dos grupos de pitagóricos que se corresponde con las dos tendencias, la racional y la religiosa –que convergían en el propio Pitágoras, pero no así en todos los pitagóricos–, tendría una decisiva incidencia sobre la ulterior evolución de la hermandad. Los Acusmáticos eran devotos religiosos que se encargaron de velar por la pureza del «modo de vidapitagórico», las esencias originales y la fidelidad a la primigenia doctrina pitagórica, mientras que los matemáticos –no comprometidos solamente con el cultivo de las matemáticas, sino con la totalidad del conocimiento o gnosis– se consideraban continuadores del espíritu especulativo de Pitágoras y de su natural evolución y magnificación del acervo científico y matemático. El misticismo aritmético‑geométrico pitagórico. Los números místicos Los pitagóricos basaron su filosofía y su modo de vida en el culto a los números llevándolo hasta el paroxismo. Para los pitagóricos todo era una encarnación del número. La fuente primaria más cualificada sobre la Filosofía pitagórica es, sin duda alguna, el capítulo V del libro I de la Metafísica de Aristóteles –que tiene por título «Los pitagóricos y su doctrina de los números»–, donde se lleva a cabo una exposición general del Pitagorismo que empieza con estas palabras (Metafísica, 985b, 986a):
Este texto de Aristóteles resume el núcleo de la metafísica pitagórica. El entusiasmo ante el descubrimiento pitagórico de la base numérica de los intervalos musicales –los intervalos básicos de la música griega podían representarse mediante las razones 1/2, 3/2 y 4/3– encendió un chispazo de inspirada intuición hacia una fórmula de aplicación universal: «si los números son la clave de los sonidos musicales, ¿no serán también la clave de toda la naturaleza?». Los pitagóricos vivieron imbuidos de un efervescente entusiasmo místico hacia los números, hasta el punto de que Filolao (el pitagórico favorito de Aristóteles) llegó a afirmar:
Cuando los pitagóricos decían, como médula de su metafísica, que todos los objetos estaban compuestos de números, que «los números son la esencia del universo», o que el número es el arjé, el principio elemental –como para otros filósofos presocráticos era el agua, el aire, la tierra, el fuego– lo entenderían en sentido literal, porque los números eran para ellos como los átomos para Demócrito, pero átomos con magnitud y extensión. Para los pitagóricos el gran sistema del mundo reposa sobre ciertas bases de las que el ser, la forma y la acción de todas las cosas, tanto las particulares como las generales, son una consecuencia natural de la consideración de los números. Quien conoce sus propiedades y sus mutuas relaciones, conoce las leyes merced a las cuales la naturaleza existe. Los números determinan el nexo de unión de todas las cosas y la mecánica del universo entero, son la base del espíritu y el único medio por el cual se manifiesta la realidad. Según el neoplatónico Porfirio:
Además, la Geometría permitía someter a los números a operaciones metafísicas de gran significado simbólico. A esta doctrina pitagórica se la llama, a veces, misticismo numérico, como queriendo indicar la atribución a los números, no sólo de un carácter sagrado, sino también de una realidad sustancial descriptiva tanto de los aspectos cualitativos como de los aspectos físicos de las cosas. Los pitagóricos denominaron Década a los diez primeros números y en la consideración de sus propiedades místicas y cabalísticas y de sus virtudes mágicas desarrollaron, más allá de la Aritmética, un cierto misticismo numérico, una Aritmología (la palabra número deriva del término griego «Aritmo») al establecer que cada número poseía sus propios atributos especiales que le dotaban de ciertas propiedades vitales. Con base en Filolao, Platón –en algunos de sus Diálogos– Aristóteles –en su Metafísica–, Alejandro de Afrodisias (comentador de Aristóteles), Teón, Porfirio, Jámblico, Sexto Empírico y Nicómaco de Gerasa resumimos estos atributos de acuerdo con la tabla sintética siguiente:
El Número 1 o mónada representa el principio activo frente a la diada que es el principio pasivo. Es la verdadera esencia de todas las cosas, el principio y fundamento de cuanto existe. Símbolo del buen principio (el Dios único, expresado en latín por Solus, de donde deriva la palabra Sol). Símbolo de la razón suprema, asociada al concepto de Dios, inteligente e increado, supremo paradigma del Bien y la Belleza. Símbolo del Sumo Poder, Creador y Conservador. Generador de todos los números y de todas las dimensiones. Espacio aritmético entre los números enteros y los fraccionarios. Símbolo de inmutabilidad aritmética (1·1=1, 1/1=1, 11=1). Para Filolao «el uno es el Padre de los Seres, Padre y Demiurgo del mundo, artífice de la permanencia de las cosas.» El Número 2 o díada, es el símbolo de la diversidad, de la opinión, de la contraposición, y en particular de la expresión de los contrastes de la naturaleza y de la mayoría de las cosas que afectan al ser humano en forma de dualidad (noche y día, luz y oscuridad, humedad y sequedad, calor y frío, salud y enfermedad, dulce y amargo, bueno y malo, grande y pequeño, belleza y fealdad, etc.).
Es la llamada «lista pitagórica de los contrarios», de sorprendente similitud con la doctrina del Yin-Yang de la filosofía china, que indicaría que todos los fenómenos se originarían por la interacción de dos fuerzas cósmicas o principios antagónicos. El Número 5 tenía un gran simbolismo para los pitagóricos, como conjunción de los principios masculino y femenino y por tanto símbolo del matrimonio (2+3=5); también de lo par y lo impar; como número esférico o circular porque sus potencias termina en cinco; como menor número cuyo cuadrado es suma de cuadrados (52=32+42, representación aritmética del triángulo divino), en relación con el Teorema de Pitágoras. Además, cinco son los sólidos poliedros regulares (tetraedro, octaedro, cubo, dodecaedro e icosaedro), conocidos más tarde por el nombre de Cuerpos Platónicos al ser tomados por Platón de los pitagóricos.
Una de las curiosas propiedades del Pentagrama, que imponía respeto a los pitagóricos era su «unicursalidad»: «la estrella pentagonal puede ser trazada por el movimiento de un punto sin pasar dos veces por el mismo lado». Una segunda propiedad profundamente aritmológica en su esencia inspiraba a los pitagóricos un entusiasmo místico, relacionando el pentagrama con la palabra salud (ugieia = higieia, de donde deriva higiene). Aunquela palabra ugieia tiene seis letras, a veces se producía una contracción que hacía desaparecer la primera i (como atestiguan algunas inscripciones), quedando entonces con cinco letras ugeia, que se situaban sobre cada uno de los vértices del Pentagrama, que de esta forma se convertía en el anagrama supremo de la salud.
El Número 10 es el de mayor carga simbólica y el más sagrado de todos los números. Puesto que los cuatro primeros números contienen el secreto de la escala musical, su suma (1+2+3+4=10), el número diez, la década, puede «parecer que abarca», como dice Aristóteles, «la naturaleza toda del número», sería en sí «algo perfecto», y representa el número del universo, la suma de todas las posibles dimensiones geométricas. Para Filolao la Década era «grande, todopoderosa y generadora de todo, comienzo y guía tanto de la vida divina como de la terrestre» y para Sexto Empírico «la razón de la composición de todas las cosas.»
La Cosmología pitagórica La veneración hacia el número diez tiene para los pitagóricos una implicación cosmológica transcendental en su doctrina acerca de la configuración del universo, al ser la inspiradora del primer sistema astronómico no geocéntrico. Según Aristóteles (Metafísica, 986a):
Aristóteles desarrolla estas ideas más ampliamente en su obra Del Cielo (293a):
Ocho cuerpos celestes: la tierra, la luna, el sol y los cinco planetas conocidos (Mercurio, Venus, Marte, Júpiter y Saturno), giran en órbitas circulares concéntricas en torno al fuego central –«Trono de Zeus»–, situado en el centro del universo. Con la Esfera de las estrellas fijas se llega al valor nueve. Como falta uno para alcanzar el valor diez de la Tetractys, emblema sagrado de los pitagóricos, se añade al sistema –«de modo que toda su teoría fuera coherente»–, como dice Aristóteles, la antitierra, situada en la órbita más interior, en equilibrio con la tierra, alineada con ésta y con el fuego central y con el mismo período de revolución diaria que ella. El sol no era el centro del universo, ni era el creador de su propio calor, sino que era una especie de cristal reflector que recogía la luz y el calor del fuego central, en torno al cual giraba con un período de un año. Las estrellas fijas permanecían estacionarias, mientras que la tierra mantenía, durante su movimiento, el mismo hemisferio deshabitado hacia el fuego central de modo que sus habitantes no podían ver jamás ni el fuego central ni la anti-tierra. Al desplazar a la tierra del centro del universo, la cosmología pitagórica supone un heroico salto de imaginación científica. No se trata de una mera fantasía arbitraria. De hecho el sistema proporcionaba una explicación plausible de los eclipses. No es exactamente una anticipación de la teoría heliocéntrica, pero algunos estudiosos de la Historia de la Cosmología lo consideran de rango superior en importancia a la identificación del fuego central con el sol. La teoría pitagórica es de una gran originalidad. Para Tales y otros filósofos presocráticos como Anaxímenes, Heráclito, Parménides y Empédocles la tierra estaba ciertamente en reposo en el centro del universo esférico y más tarde Eudoxo y por supuesto Aristóteles volvieron a situar con firmeza la tierra en el centro, del que no se movería hasta los primeros balbuceos heliocéntricos de Aristarco. Para pensadores como G. Bruno el giro copernicano no sería una novedad sino la restauración de la antigua Cosmología pitagórica. Así pues, como en otros muchos aspectos del pensamiento pitagórico, carácter místico y religioso, no le resta valor científico. Clasificación y denominación pitagóricas de los números Según Isidoro de Sevilla (Etimologías, III.2): «Pitágoras fue el primero que escribió sobre la ciencia del número», es decir, a Pitágoras se debe la primera depuración filosófica o teórica de la Aritmética –la liberación de la Ciencia del Número de la práctica de artesanos y mercaderes que constituían la llamada Logística–. Sobre ello escribe Aristóxeno:
Los pitagóricos realizaron diversas clasificaciones y acuñaron numerosos nombres para los diversos tipos de números. Pero debido a su proceder místico, muchas de sus definiciones son bastante abstrusas de forma que conviene a veces recurrir a los preliminares del Libro VII de Los Elementos de Euclides, donde se recogen gran parte de ellas, en el lenguaje inteligible y riguroso característico del gran compilador de la Matemática griega elemental. Veamos los nombres y definiciones de algunos números: Números pares e impares: definiciones 6 y 7 de Euclides VII.
Los números pares e impares se subdividen en cuatro clases: (Definiciones VII.8 a VII.10):
«Es divisor de» (Euclides D.VII.3). «Es múltiplo de» (Euclides D.VII.5). Números primos (Euclides D.VII.11) y compuestos (Euclides D.VII.13). Números lineales, planos y sólidos:
Números perfectos, deficientes y abundantes. Números amigos.
Los números perfectos y los números amigos han causado siempre una gran fascinación, por eso la búsqueda de números perfectos y amigos ha desplegado un derroche de tinta matemática desde los primeros tiempos pitagóricos hasta nuestros días, en los que se aplican potentes instrumentos de computación. Los primeros pitagóricos sólo conocían los números perfectos 6 y 8. Euclides define el número perfecto en D.VII.22. A los números amigos, literalmente habría que llamarlos números enamorados. Los pitagóricos sólo conocieron el par 220, 284:
Jámblico atribuye el descubrimiento de los números amigos al propio Pitágoras, embelleciendo el relato del mismo con la siguiente anécdota: «Siendo preguntado Pitágoras –¿qué es un amigo?, contestó –Alter ego. Por analogía aplicó el término amigos a dos números cuya suma de partes alícuotas es igual al otro». La Música pitagórica y la Teoría de las medias Según Nicómaco, Gaudencio, Porfirio, Diógenes Laercio, Teón de Esmirna, Jámblico, Boecio y otros pitagóricos, Pitágoras estudió, quizá por primera vez en la historia, las primeras leyes cuantitativas de la Acústica, al determinar el fundamento matemático de la armonía musical con la realización de la primera experiencia científica que consigna la historia, mediante la construcción de un instrumento, el monocordio (Jámblico, XXXVI.119; Diógenes Laercio, VIII.12),con el propósito de interrogar a la naturaleza y obligarla a responder a una cuestión concreta: ¿cuál es la relación precisa, si es que existe, entre la armonía musical y los números? Pitágoras descubre que las cuerdas que daban el tono, la cuarta, la quinta y la octava, tenían longitudes proporcionales a 12, 9, 8 y 6. Y puesto que las razones entre los números 12, 9, 8 y 6 son iguales a las que hay entre 1, 3/4, 2/3 y 1/2, que son las más sencillas que se pueden formar con los números de la sagrada Tetractys, 1, 2, 3 y 4, Pitágoras dedujo que ésta es «la fuente y raíz de la Naturaleza eterna» como dicen los Versos Dorados. Como en tantos aspectos pitagóricos los números de la Tetractys eran la piedra angular de la armonía musical. Mediante una mística extrapolación, la Tetractys sería la fuente del conocimiento de las raíces de la armonía del Cosmos divino, alcanzable a través del número.Si en el número está la clave del tono musical, en él residirá también la clave de toda la naturaleza y en ultima instancia aparecía la matriz de la filosofía pitagórica: «el número es la esencia de todas las cosas». Con este feliz descubrimiento Pitágoras instaura algo nuevo en la Historia del Pensamiento: el método experimental y la expresión en fórmulas matemáticas de las leyes de la naturaleza. La teoría musical de Pitágoras tiene que ver también con la Teoría de las medias de raíz pitagórica. Así lo señala el pitagórico Arquitas: «En música hay tres medias: la media aritmética, la media geométrica y la subcontraria, llamada también armónica». Dados dos números a y b, se definen las medias aritmética, m, armónica, h, y geométrica, g, de la forma:
La Armonía de las Esferas La doctrina pitagórica de la Armonía de las Esferas es la quintaesencia de la belleza en la explicación pitagórica del Cosmos divino armonizado de forma fascinante por la concordancia de las proporciones aritméticas y musicales, que extrapoladas al universo entero determinarían que los cuerpos celestes debían emitir en sus movimientos unos tonos musicales armoniosos cuya combinación producía una maravillosa melodía permanente: «La Música de las Esferas». Tal vez Pitágoras se remontaría a la Mitología puesto que en el himno de Ares, Homero se dirige a los planetas como si fueran un coro de voces divinas. Además, conocemos la afición de los pitagóricos a los ritos de Orfeo vinculados al poder del número y de la música. De modo que Pitágoras racionalizaría el sistema y la daría un valor místico y científico. Según relata Jámblico (Vida Pitagórica XV.65, pp.52–53):
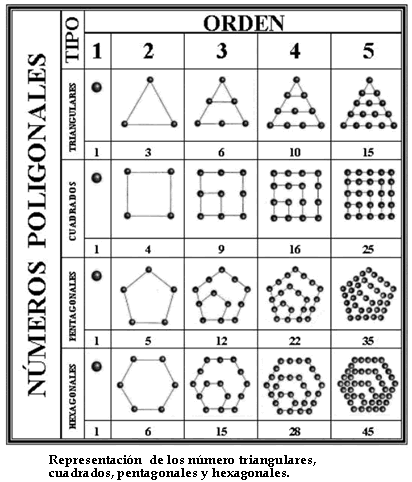
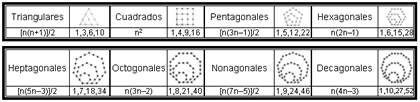
La música cósmica se produce porque los cuerpos celestes, al ser de tamaño tan grande y moverse a velocidades gigantescas, emitían a través deléter un conjunto de sonidos de la misma manera que los cuerpos terrenales producen vibraciones cuando se mueven en el aire, como por ejemplo las velas de un barco cuando suenan con la brisa. Pero los hombres no pueden escuchar la melodía del barco cósmico porque han crecido acostumbrados a ella, lo mismo que el herrero se ha acostumbrado al ruido de sus martillos. Además, los cuerpos celestes que giran sin tregua en sus órbitas circulares, producen permanentemente armonías, de modo que al no haber intervalos de silencio no se puede apreciar la música cósmica. Es decir, el sonido armonioso de las esferas nos es congénito, pero no lo podemos oír ya que el sonido y el silencio se perciben por mutuo contraste. En realidad la música de los hombres no es más que un eco de la Música de las Esferas, pero su instinto innatoque hace que su alma resuene con la música, le proporciona un indicio de la naturaleza de las armonías matemáticas que se hallan en su fuente cósmica. El sonido emitido por cada esfera corresponde a un tono diferente de la escala musical, dependiendo de los radios de sus órbitas como los tonos musicales emitidos por la cuerdas dependen de su longitud. La vida en la Tierra se ve afectada por la Música de las Esferas porque ésta gobierna los ciclos temporales de las estaciones, los ciclos biológicos y todos los ritmos de la naturaleza. He aquí en breve síntesis la doctrina pitagórica de la Armonía de las Esferas, desarrollada de forma clara y crítica por Aristóteles en su obra Del Cielo (290 b y siguientes.) La doctrina de la Armonía de las Esferas prendió en la imaginación de escritores de las generaciones posteriores, variando los detalles según la evolución de las teorías sobre el movimiento planetario. Platón, Plinio, Ptolomeo, Cicerón, Plotino, Jámblico, San Agustín, Boecio, Filón, Casiodoro, San Isidoro, Shakespeare y otros muchos, aluden a ella frecuentemente. Pero quizá sea en la Oda a Salinas de Fray Luis de León donde la mística pitagórica alcanza la más bella descripción poética de la Música de las Esferas. La idea pitagórica de la Música de las Esferas no deja de ser una especulación fantástica que hoy «nos suena a música celestial», pero tanto Kepler como Newton le escribieron pentagrama y Einstein fugas y límites. Kepler basó en ella su inspiración en la búsqueda de la armonía del movimiento planetario, y en efecto, una ferviente combinación de mística pitagórica y meticulosa experimentación permitió a Kepler encontrar sus famosas Leyes. Como es natural la doctrina de la Armonía de las Esferas ha tenido su influencia sobre la música sinfónica, de modo que la crítica musical ha querido ver reminiscencias pitagóricas en algunas composiciones como La Creaciónde Haydn, Así habló Zaratustra de R.Strauss y La Consagración de la Primavera de Stravinski. Modernamente también Vangelis parece haberse inspirado en laMúsica de las Esferas para la realización de algunas de sus composiciones, sobre todo en los de la serie televisiva Cosmos de C.Sagan. Los números poligonales Los pitagóricos solían representar los números mediante puntos en un pergamino o piedrecillas en la arena y los clasificaban según las formas poligonales de estas distribuciones de puntos, es decir, asociaban los números a figuras geométricas obtenidas por la disposición regular de puntos, cuya suma determina el número representado. Así obtenían los diversos tipos de números poligonales o figurados:
Los números poligonales aparecieron en los albores de la Escuela Pitagórica como un elemento esencial de su misticismo numérico: «no sólo las cosas son en esencia números sino que los números son concebidos como cosas», de modo que las expresiones «números triangulares» o «números cuadrados» no son meras metáforas sino que esos números son, efectivamente, ante el espíritu y ante los ojos, triángulos y cuadrados.
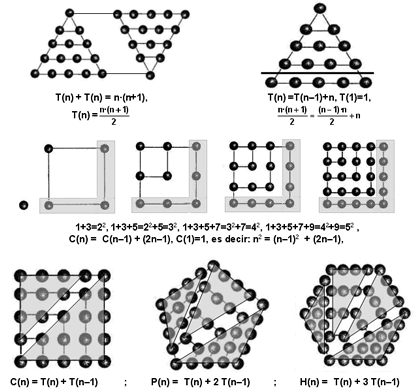
La asociación del número con la imagen geométrica permitió a los pitagóricos la representación visual de los números combinando las dos esencias con que tiene que ver la Matemática: el número y la forma, confiriendo a los números propiedades y relaciones entre ellos que son completamente independientes de todo simbolismo introducido para representarlos, otorgándoles de este modo un carácter universal e inmutable. La consideración de los números poligonales y su representación geométrico-visual permitía, por una parte, constatar que ciertos números tienen características diferentes que otros a tenor de las diferentes configuraciones geométricas a que dan lugar, y por otra, el descubrimiento de forma geométrico-empírica, casi corpórea, de importantes propiedades de los números y la obtención de interesantes relaciones entre ellos. La polifiguración numérica llevaba a extender conceptos de la Aritmética como generalización de la experiencia práctica, desarrollando un atomismo numérico bellamente ilustrado en una geometría de números figurados. Éstos, que son las primeras y las más simples estructuras de la Geometría numérica están en el corazón de las Matemáticas y constituyen la matriz del desarrollo ulterior de la Teoría de Números. A partir de las distribuciones geométricas de puntos que hicieron los pitagóricos con los números poligonales, aparecían, como evidencia empírico–visual, numerosas propiedades de los números enteros, al considerar la relación entre órdenes consecutivos de números de un determinado tipo y relaciones entre números poligonales de tipos diferentes. Así por ejemplo, si llamamos T(n), C(n), P(n), H(n) al n-ésimo número triangular, cuadrado, pentagonal y hexagonal, respectivamente, los siguientes esquemas gráficos nos proporcionan importantes propiedades aritméticas de los números enteros:
Los números poligonales han sido uno de los tópicos más atractivos de la Historia de la Aritmética tratado por matemáticos de la talla de Nicómaco, Diofanto, Mersenne, Euler, Gauss, Lagrange, Legendre y Cauchy. Forman parte de las raíces históricas de la Teoría de Números, apareciendo en numerosos ámbitos como por ejemplo en el Triángulo de Pascal. Juegan un importante papel en el Análisis combinatorio, intervienen en el Binomio de Newton y en el Cálculo de Probabilidades y fueron ampliamente utilizados por Fermat, Pascal, Wallis y Roberval para la obtención de sus resultados sobre cuadraturas. En la actualidad el estudio de los números poligonales ha alcanzado un valor práctico en una incipiente aplicación criptográfica a la seguridad en las comunicaciones, de modo que, como en otros muchos otros aspectos, Pitágoras se sitúa en el umbral del pensamiento matemático.
La expresión de los diez primeros números poligonales
El Teorema llamado de Pitágoras Una tradición muy persistente con base documental en Vitrubio, Plutarco, Diógenes Laercio, Ateneo y Proclo, atribuye el Teorema de Pitágoras al propio Pitágoras. Pero los descubrimientos arqueológicos de los restos de las culturas de Mesopotamia, Egipto, India y China, han revelado que estas civilizaciones conocían aspectos del Teorema de Pitágoras muchos siglos antes que este sabio. Las referencias prehelénicas al Teorema no contienen, sin embargo, pruebas del mismo, mientras que es generalizada la creencia de que fue Pitágoras el primero en proporcionarnos una demostración lógica del Teorema, lo que hará justo que éste haya pasado a la historia con su nombre. Diógenes Laercio en su Vida de filósofosrecoge (Pitágoras VIII.7) una referencia de un tal Apolodoro «El Calculador» sobre Pitágoras, en la que asegura que este filósofo sacrificó una hecatombe (cien bueyes), habiendo hallado que en un triángulo rectángulo «la potestad de la línea hipotenusa es igual a la potestad de las dos que lo componen». Continua diciendo que Apolodoro compuso un epigrama en verso: «Pitágoras hallada / aquella nobilísima figura / bueyes mató por ello en sacrificio». Estas anécdotas son, sin duda, ficticias, porque contradicen la filosofía pitagórica sobre la transmigración de las almas, pero han contribuido a magnificar la leyenda que envuelve a Pitágoras, y además determinaron que en la Edad Media al Teorema de Pitágoras se le llamara «Inventum hecatombe dignum».
Sea ABC un triángulo rectángulo, con el ángulo recto en A, y sea AD perpendicular al lado BC. Según Euclides VI.8 los triángulos DBA y DAC son ambos semejantes con el triángulo ABC y semejantes entre sí. Prueba 1. De la semejanza de los triángulos ABC, DBA y DAC resulta: BA/BD = BC/BA , AC/CD = BC/AC (Euclides VI.4). De aquí se hayan las expresiones del llamado «Teorema del cateto»: BA2 = BD·BC , AC2 = CD·BC, que al sumarlas, se obtiene: BA² + AC² = (BD+CD)·BC = BC·BC = BC², es decir: BA2 + AC2 = BC2. En esta demostración del Teorema de Pitágoras –basada en el Teorema del cateto–, se descompone, de forma implícita, el cuadrado sobre la hipotenusa, BCIK,en dos rectángulos, BDJK y DCIJ, cada uno de ellos con el mismo área que cada uno de los cuadrados construidos sobre los catetos –el rectángulo BDJK de área como el cuadrado ABEF sobre el cateto AB –ya que BA2 =BD·BK, y el rectángulo DCIJ de área como el cuadrado ACHG sobre el cateto AC –ya que AC2 = CD·CI–. Debemos observar que la figura exhibida forma parte de la figura que utiliza Euclides en su demostración del Teorema de Pitágoras en la Proposición I.47 de Los Elementos de Euclides, y además, puntualizar que variantes de esta prueba se encuentran en el hindú Bhaskara, en Leonardo de Pisa (Fibonacci)y en Wallis. Prueba 2. De la semejanza de los triángulos ABC, DBA y DAC resulta, según Euclides VI.19 («la razón entre las áreas de los triángulos semejantes será igual al cuadrado de la razón de semejanza»): DBA/AB² = DAC/AC² = ABC/BC². Pero de las propiedades de la suma de proporciones (Euclides 5.12) resulta: ABC/BC2 = DBA/AB2;= DAC/AC2;= (DBA+DAC) / (AB2+AC2) = ABC / (AB2+AC2) por tanto se tiene: AB2+AC2 = BC2. Como vemos, estas pruebas del Teorema de Pitágoras mantienen su plena vigencia en los libros de texto de matemáticas escolares elementales. Quizá ningún teorema de la amplia Matemática haya recibido tantas demostraciones diversas como el Teorema de Pitágoras. De todas ellas la más famosa es sin duda la realizada por Euclides en la Proposición I.47 de Los Elementos. En la Edad Media esta Proposición se la consideraba la base de toda sólida formación matemática. En algunos centros docentes además de exigir, para obtener el grado de maestro, un profundo conocimiento del Teorema, se obligaba a exhibir una nueva y original demostración del mismo, por eso el Teorema de Pitágoras alcanzó la honrosa designación de «Magister matheseos». Este hecho y la gran significación del teorema explica la razón de las innumerables demostraciones que los matemáticos y no matemáticos de todas las épocas y personajes tan diversos como filósofos, monjes, políticos, juristas, ingenieros y artistas, han encontrado del más famoso Teorema de la Geometría. El Teorema de Pitágoras aparece por doquier en la Matemática. Es la base de multitud de teoremas geométricos, de la trigonometría y de la Geometría analítica. La ecuación pitagórica x2+y2=z2 es la ecuación de la circunferencia, la base de la fórmula cos2a+sen2a=1 y el origen del Análisis indeterminado de Diofanto y Fermat. También pudo ser el germen del dramático alumbramiento de la inconmensurabilidad en la Escuela pitagórica. La aparición del Teorema de Pitágoras en el horizonte histórico cultural pero también en el horizonte escolar señala el primer salto intelectual entre los confines de la especulación empírica y los dominios del razonamiento deductivo. Así pues, estamos ante un auténtico paradigma para la Matemática y sobre todo para la Educación matemática. Por esto y por su universalidad el Teorema de Pitágoras pertenece al imaginario cultural de casi todos los pueblos. La Divina Proporción y el Pentagrama pitagórico Uno de los tópicos pitagóricos más fascinantes y que más influencia ha tenido sobre el Arte, la Mística, la Biología e incluso la Magia ha sido la Sección Áurea o Divina Proporción.Euclides introduce la noción en la Definición VI.3 de Los Elementos:
Importantes especulaciones filosóficas, teológicas, naturales y estéticas han surgido en torno a la Divina Proporción desde que la humanidad empieza a reflexionar sobre las formas geométricas que conforman el mundo, siendo el Pitagorismo quien comienza a dar consistencia racional a toda esta doctrina. Puede decirse que donde haya una especial intensificación de la belleza y la armonía de las formas, ahí se encontrará la Divina Proporción, por ejemplo en muchos aspectos de la naturaleza, de donde muchos artistas extraerán su inspiración. La Divina Proporción, sobre todo en forma de rectángulo áureo (con las dos dimensiones en proporción áurea), constituye uno de los métodos canónicos de composición para obras de arte más utilizados por toda clase de artistas a lo largo de toda la Historia del Arte interviniendo, además, en el canon ideal de la belleza humana, en particular en las dimensiones del rostro y de la mano. Buena parte de la Geometría pitagórica en relación con la sección áurea, tuvo que ver con el pentágono regular. Ya se comentó que la figura de la estrella de cinco puntas que se forma al trazar las cinco diagonales de un pentágono llamada Pentagrama místico era una especie de símbolo de identificación de la Escuela Pitagórica; por eso los pitagóricos estudiaron exhaustivamente la construcción y propiedades del pentagrama. El pentagrama místico de Pitágoras fue un diagrama simbólico esencial del esoterismo geométrico de los pitagóricos que trasmitido desde la antigüedad hasta el siglo XVIII forma parte de dos tradiciones culturales importantes: los trazados de los arquitectos y las estrellas pentagonales del simbolismo mágico europeo, corrientes subterráneas que emergen a la luz a través de la obra de Luca Pacioli LaDivina Proporción, que con finalidad teológica racionaliza los arcanos del misticismo geométrico pitagórico, exhumando una ciencia geométrica en cuyas fuente beberán Alberti, Durero y otros muchos artistas del Renacimiento.
El descubrimiento de las magnitudes inconmensurables La grandeza sublime del Teorema de Pitágoras y la mágica belleza del Pentagrama místico pitagórico fueron dos caballos de Troya para la Geometría griega, porque llevaban en su interior el germen de la profunda crisis de la secta pitagórica donde aparecieron. Los Pitagóricos, que, como filósofos presocráticos, habían considerado como núcleo dogmático de su Filosofía que «los números son la esencia del universo», encuentran que las consecuencias de su Teorema atentan contra los fundamentos de su doctrina, que les había llevado a establecer un paralelismo entre el concepto numérico y la representación geométrica. En efecto, el cuadrado que es una de las figuras geométricas más simples, proporciona un terrible ente geométrico, la diagonal, que no es conmensurable con el lado. Lo mismo sucede entre la diagonal y el lado del pentágono. La creencia de que los números podían medirlo todo era una ilusión. Así quedaba eliminada de la Geometría la posibilidad de medir siempre con exactitud. Se había descubierto la magnitud inconmensurable, lo irracional –no expresable mediante razones–, «el alogon», que provocaría una crisis sin precedentes en la Historia de la Matemática. La sacudida que la aparición del nuevo ente provocó en la Matemática griega puede calibrarse por la leyenda apocalíptica que relata un viejo escolio (atribuido a Proclo) del Libro X de Los Elementos de Euclides:
En el mismo tono apocalíptico escribe Jámblico (Vida Pitagórica. XXXIV, 246–247, p.141):
Las circunstancias concretas del primer reconocimiento de inconmensurables son tan desconocidas como la fecha en que tuvo lugar. Aunque Proclo –en sus Comentarios–, lo atribuye al propio Pitágoras cuando escribe que este filósofo «descubrióla dificultad de los números irracionales» suele admitirse que fue hacia el 480 a.C. por Hipasos de Metaponto. El descubrimiento pudo tener lugar al intentar reiteradamente de forma empírica encontrar una unidad que permitiera medir, de manera exacta, simultáneamente la diagonal y el lado del cuadrado o bien la diagonal y el lado de un pentágono regular. El descubrimiento de la inconmensurabilidad marca un hito en la Historia de la Geometría, porque no es algo empírico, sino puramente teórico. Con el descubrimiento de los inconmensurables quedaban afectadas y debían ser reconstruidas todas las pruebas pitagóricas de los teoremas en los que haya que comparar razones de magnitudes geométricas. Se explica, pues, el consiguiente secretismo de los pitagóricos sobre la cuestión irracional y la leyenda del castigo por su divulgación. Leyendas y conjeturas aparte, se comprende que el descubrimiento de las magnitudes inconmensurables produjera un escándalo lógico en todo el ámbito pitagórico, ya que exigía una revisión a fondo de los fundamentos de su Matemática y su Filosofía, pero fue no sólo la cuna de la Geometría griega sino uno de los componentes esenciales del milagro griego en Matemáticas. La tempestad provocada por el descubrimiento pitagórico de los irracionales precipitó la primera crisis de fundamentos en la Historia de la Matemática, propiciando «el horror al infinito», que caracteriza casi toda la Matemática griega posterior. Como reacción al lenguaje ingenuo de los pitagóricos, mezcla de brillantes ideas matemáticas, actitudes místicas y aforismos religiosos, se impondrá el severo rigor de Los Elementos de Euclides. Pero el desarrollo de La Geometría al margen de la Aritmética, la ausencia de un Álgebra simbólica y la conversión de toda la Matemática en Geometría, con un estilo sintético de exposición que oculta la vía heurística del descubrimiento, fue el efecto más inmediato. La Cosmogonía poliédrica pitagórica Diversos historiadores de las Matemáticas admiten que las antiguas civilizaciones egipcias y babilónicas tenían conocimiento del cubo, tetraedro y octaedro y que este saber se trasmitiría a Grecia a través de los viajes de Tales y Pitágoras. Proclo en sus Comentarios al Libro I de los Elementos de Euclides atribuye a Pitágoras la construcciónde «las figuras cósmicas», nombre relacionado con su uso en la elaboración de una cosmogonía pitagórica que asociaría los cuatro elementos primarios –fuego, tierra, aire y agua–, con los cuatro sólidos– tetraedro, cubo, octaedro e icosaedro–, respectivamente, mientras el dodecaedro como símbolo general del universo se relacionaba de forma mística con el Cosmos, representación del universo armónico ordenado por el número. Aecio (basándose en Teofrastro) atribuye a Pitágoras la cosmogonía descrita con estas palabras (W.K.C.Guthrie. Historia de la Filosofía griega. Vol.1. Gredos, Madrid,1999, p.256):
También Filolao y en parte Simplicio aseguran lo mismo, mientras que algunos escoliastas del Libro XIII de Los Elementos de Euclides aseguran que los cinco cuerpos platónicos no tuvieron su origen en Platón, sino que el cubo, la pirámide [el tetraedro] y el dodecaedro derivaban de los pitagóricos y las otras dos formas de Teeteto. Los pitagóricos estaban fascinados por los sólidos regulares, sobre todo por el dodecaedro, debido a la presencia del emblemático pentágono en sus caras, generador al trazar las diagonales de la estrella pentagonal, llamada Pentagrama místico, que era el símbolo de identificación de los miembros de la secta pitagórica y responsable, junto con el Teorema de Pitágoras, de la aparición de la inconmensurabilidad. La construcción del dodecaedro era un secreto guardado celosamente, hasta el punto de que se fue fraguando una leyenda sobre el terrible fin de quien osó divulgar sus misterios, relatada entre otros autores por Jámblico (Vida Pitagórica, XVIII.88, p.97):
Y también, más adelante (en Vida Pitagórica, XXXIV, 247, p.141), Jámblico escribe:
Este texto recuerda la descripción apocalíptica de muchos escritores acerca de la maldición que cayó sobre Hipasos de Metaponto por haber revelado la aparición de lo inconmensurable. La analogía entre ambas leyendas avalaría la tesis de que el advenimiento de la inconmensurabilidad habría tenido lugar a través del pentágono de las caras del dodecaedro. Aunque lo aseguren las fuentes mencionadas, la crítica histórica considera improbable que Pitágoras hubiera planteado la cosmogonía descrita, ya que, por una parte, fue Empédocles de Agrigento el primero que distinguió explícitamente los cuatro elementos primarios –fuego, tierra, aire y agua–, y por otra, según mencionan diversas fuentes, los primeros pitagóricos habrían reconocido sólo el tetraedro, el cubo y el dodecaedro, atribuyéndose el octaedro y el icosaedro al brillante matemático de la Academia, Teeteto, que realizó importantes aportaciones sobre los inconmensurables y que fue honrado por su amigo Platón con el nombre de uno de sus Diálogos (142a–210d).
El Quadrivium Pitagórico Mediante lo que se considera la primera aplicación histórica de la Matemática a la descripción de las leyes de la naturaleza, Pitágoras encuentra el fundamento matemático de la consonancia musical. ¿Quién podría imaginar que el espacio, el número y el sonido se combinaban en una correlación armoniosa? La Aritmética y la Geometría entraban en una comunión divina con la armonía musical que es patrimonio de la Estética y en ultima instancia aparecía la matriz de la Filosofía pitagórica: «el número es la esencia de todas las cosas». Si en el número está la clave del tono musical en él residirá también la clave de toda la naturaleza. Así pues, la Aritmética y la Geometría se vinculan con la Música, que de esta forma se convierte en una rama de las Matemáticas. Para Pitágoras la congruencia de lasconsideraciones científicas sobre los números, las figuras y las notas musicales, es decir, la concordancia de las proporciones aritméticas, geométricas y musicales, y su extrapolación al Cosmos, determina que los astros emiten en sus movimientos unos tonos musicales armoniosos cuya combinación producía una maravillosa melodía perpetua: «La Música de las Esferas». El misticismo aritmético de la Década también había llevado a Pitágoras al establecimiento del primer sistema cosmológico no geocéntrico. Ambos elementos pitagóricos, la Música de las Esferas y su Cosmología incluyen también a la Astronomía en el ámbito matemático, el cual quedaasí completado en lo que con posterioridad –a partir de Boecio que acuñaría el término en su obra aritmética– se llamó las cuatro Artes del Quadrivium pitagórico –Aritmética, Geometría, Música y Astronomía–, que junto con las tres Artes del Trivium –Gramática, Retórica y Dialéctica– constituyen las Siete Artes liberales del curriculum medieva.
El legado de Pitágoras. Herencia y vigencia del Pitagorismo La pervivencia de la estela pitagórica a lo largo de los siglos es uno de los fenómenos culturales más interesantes de la Historia del Pensamiento. Con Pitágoras nace por primera vez en la historia la confianza ilimitada en nuestra capacidad para explorar este universo, entendiendo por tal todo lo que el ser humano, que es razón y sentidos, puede percibir, incluyendo el universo interior. Por tanto podríamos calificar de pitagórica la fe que ha presidido la tarea humana de ir haciendo comprensible para el hombre el Cosmos global (macrocosmos y microcosmos) y que ha inspirado toda la actividad científica durante los últimos 2500 años. La comunidad pitagórica de índole religiosa, científica y filosófica alumbró el llamado Pitagorismo, uno de los movimientos intelectuales más influyentes y persistentes en la Historia de la Cultura. A partir de rudimentos órficos,la concepción pitagórica del Cosmosamalgama elementos filosóficos, racionales y matemáticos con poéticos, religiosos y místicos, buscando la comunión con lo divino en la contemplación racional del universo, alcanzando una síntesis sumamente atractiva no sólo para sus coetáneos sino para muchas corrientes de inspiración pitagórica durante muchos siglos. Pitágoras alcanza una armoniosa síntesis entre la mística del espíritu religioso oriental –del que se impregna en sus viajes a Oriente– y la científica visión del universo, desarrollando un potente movimiento cultural que llegó a ser mucho más que una Escuela de Pensamiento, un auténtico estilo de vida: «el modo de vida pitagórico», del que habla Platón en La República (Libro X, 600b). De la Filosofía pitagórica arrancan dos sistemas de pensamiento muy diferentes. Los aspectos más abstractos y lógicos fueron adoptados por Parménides, y muy contaminados de misticismo, constituyen la base del idealismo platónico. En sentido opuesto, el atomismo numérico-geométrico pitagórico (por ejemplo, los números poligonales), recogido por Leucipo, adoptará un contenido materialista en el atomismo de Demócrito. La mayor parte de la doctrina del Timeo –que Platón no pone en labios de Sócrates sino de un pitagórico natural de Lócride, ciudad próxima a Crotona–, y en particular la cosmogonía poliédrica de Platón es pitagórica. De hecho la filosofía platónica tendió a ser interpretada como Pitagorismo por sus contemporáneos y sucesores. Así sucedió ya no sólo con la cosmogonía del Timeo, sino también con la concepción platónica del almay la Teoría de las Ideas, por citar algunos de los aspectos más sobresalientes de la Filosofía de Platón. El propio Aristóteles, que fue miembro de la Academia Platónica durante veinte años, escribe refiriéndose a Platón (Metafísica, I.6, 987b): «Su Filosofía sigue, en la mayoría de las cosas, la de los pitagóricos.» También B. Russell se expresa de forma parecida (Historia de la Filosofía Occidental. v.I.p.75): «[...] lo que aparece como Platonismo [en muchos Diálogos de Platón] resulta después de analizarlo, esencialmente Pitagorismo». La famosa inscripción que se encontraba en el umbral de la entrada de la Academia Platónica «No entre nadie ignorante en Geometría» es de indudable origen pitagórico, como actitud reverencial del gran filósofo ateniense hacia las Matemáticas. Podemos, por tanto, asegurar la decisiva influencia de la Filosofía pitagórica sobre Platón, quien con su incomparable profundidad filosófica y su inefable sensibilidad estética, fue el prominente vehículo de transmisión de gran parte del pensamiento pitagórico a la posteridad, en particular a la ciencia alejandrina y a la primitiva iglesia cristiana, ambas empañadas de Platonismo. La desaparición de la Escuela pitagórica produjo una cierta diáspora hacia la región griega del Ática que compondría el germen de la futura Academia Platónica, pero la tradición pitagórica no se interrumpió en tierras italianas, sobresaliendo sobre todo las figuras de Filolao que sistematizó y difundió la doctrina pitagórica y Arquitas de Tarento (en cuyas fuentes directas bebería Platón). El propio Cicerón asegura que «el verbo de Pitágoras no ha dejado de resonar en Roma», y es más que «en Roma nadie era considerado instruido si no era pitagórico» (Tusculanas, I.1, XVI). La influencia pitagórica continúa en la Roma imperial; citemos a Séneca y Moderato de Cádiz (por aludir a dos figuras de raíces hispánicas), a San Agustín (que en su aplicación de la doctrina de los números lleva el misticismo pitagórico hasta el paroxismo), a los reconocidos pitagóricos Nicómaco de Gerasa (de quien Proclo decía que era una reencarnación del mismo Pitágoras) y Teon de Esmirna, a los célebres biógrafos de Pitágoras, Porfirio y Jámblico, al propio Proclo y a toda una pléyade de pitagóricos menores cuya doctrina, en amalgama bastarda con aspectos de la joven Iglesia de Cristo, hará aparecer la Gnosis pitagórica con Simón el Mago, que en el curso de los siglos evolucionará, a través de corrientes subterráneas de la cultura que tienen que ver con sus propios orígenes órficos, hacia las tendencias de Filosofía Hermética que llegan hasta Agrippa de Nettesheim, Paracelso, Goethe, y alcanzan a las logias actuales. La Edad Media también sufrió la influencia del Pitagorismo. Por ejemplo, la doctrina de la Armonía de las Esferas encuentra en el Medioevo su más gloriosa expresión en la arquitectura de la grandes abadías y catedrales conscientemente diseñadas según las proporciones de la armonía aritmética, geométrica y musical, metáfora del orden universal. Además, las cofradías de constructores y artesanos medievales trasmitieron de generación en generación un ritual iniciático en el que la Geometría pitagórica desempeñó un papel preponderante, interviniendo en la construcción de las grandes catedrales góticas donde hayamos toda una enciclopedia gráfica en los trazados de rosetones en los que el místico símbolo pitagórico del Pentagrama irradia luminosa magnificencia a través de los vitrales. En el Renacimiento la figura de Pitágoras tiene gran incidencia sobre el pensamiento de Nicolas de Cusa, de Jerónimo Cardano y sobre todo de Giordano Bruno, quien llegaa escribir: «[...] quedé muy sorprendido al conocer las doctrinas pitagóricas». Pero la mayor influencia del pensamiento filosófico y matemático pitagórico tiene lugar en la Filosofía de la Estética, de modo que todas las cuestiones tratadas –el concepto de Cosmos como universo ordenado a través de la armonía matemática y musical, el fundamento aritmético de la armonía musical, la Teoría de las Medias y Proporciones, la Música de las Esferas, el Quadrivium pitagórico, la Divina Proporción y los Poliedros regulares, son tópicos pitagóricos de gran incidencia en la Historia del Arte. La fuente primigenia de la armonía y la proporción en el Arte del Renacimiento se remonta a las concepciones matemáticas del pensamiento pitagórico, que al descubrir las sorprendentes relaciones proporcionales de la consonancia musical creyó haber alcanzado la verdad absoluta de la estructura armónica del universo, tomándolas como principio generador en el macrocosmos y en el microcosmos del orden y la armonía, basados en los números. Estas ideas, reveladas por Pitágoras y plasmadas en el Timeo por Platón, han sido de trascendental importancia en la Historia de la Cultura, en general, pero sobre todo en el Arte, que al intentar dar expresión a ese orden se apoya en la verdad irrebatible de los números y las relaciones espaciales, que parecen revelar esa armonía preestablecida, ya que para muchos artistas la armonía espacial será el eco visible y el espejo de la armonía cósmica pitagórica, de ahí que para los teóricos y artistas del Renacimiento la armonía como esencia y fuente de la belleza, se concibe como la perfecta relación entre el todo y las partes y de éstas entre sí, en términos de proporciones y razones matemáticas. La concreción práctica de las concepciones pitagóricas sobre la armonía en la configuración de las proporciones artísticas en el Renacimiento se resume en la aplicación de dos tipos canónicos de proporciones: las conmensurables relativas a las consonancias musicales y las inconmensurables vinculadas a la Divina Proporción. Ambas derivan de la tradición pitagórica. Sirva como frase emblemática la plasmada por L. B. Alberti en De re Aedificatoria (1450-1485):
Pitágoras es uno de los artífices de la revolución científica de la Filosofía jónica por haber encontrado, de forma empírica, el fundamento aritmético de la armonía musicalmediante la primera experiencia científica de la que hay constancia histórica, de modo que Pitágoras probablemente fue quien primero estudió las más antiguas leyes cuantitativas de la Física, siendo el primer sabio convencido de que los fenómenos de la naturaleza podrían entenderse y explicarse por medio de la Matemática. Las investigaciones de Pitágoras sobre la música constituyen las primeras leyes matemáticas completamente generales aplicadas a desvelar los misterios de la naturaleza, el primer intento en la tradición occidental de reducir las leyes de la física a relaciones matemáticas, el primer paso hacia la matematización de la experiencia humana. En la Astronomía le cabe a Pitágoras el gran mérito de haber establecido el primer sistema cosmológico no geocéntrico. Aunque no se trata de un sistema propiamente heliocéntrico tuvo una gran influencia en la revolución copernicana. El espíritu pitagórico pleno de pasión mística por el conocimiento reaparece en momentos históricos en los que la evolución del pensamiento científico realiza un viraje esencial. Tal es el caso de Kepler que, convencido de que la armonía matemática pitagórica debía haber presidido la labor del creador, aplica la mística de la Cosmogonía pitagórica y de la Música de las Esferas, para alumbrar sus famosas leyes planetarias.
Para muchos pensadores Pitágoras es el fundador de la Filosofía y de la Matemática europeas. Así lo expresa literalmente el filósofo y matemático A.N.Whitehead en su obra Science in the Modern World de 1925. De hecho fue Pitágoras, como se ha dicho, quien acuñó para siempre, los términos Filosofía y Matemáticas. Pitágoras es el iniciador del método deductivo en Matemáticas que hace de esta disciplina una ciencia racional independiente del empirismo. Pitágoras planta la semilla del razonamiento geométrico que germinará con sus sucesores pitagóricos, florecerá en la Academia Platónica y fructificará con Euclides. Fue, pues, Pitágoras quien inició «el milagro griego» de realizar la organización racional de la Matemática, añadiendo el elemento de estructura lógica a la Geometría. Es decir, el mérito de Pitágoras, más allá de la magnificación inconmensurable del acervo matemático –buena parte del contenido de Los Elementos de Euclides es de procedencia pitagórica–, fue la propia instauración de la Matemática como ciencia racional a través de la idea y la práctica de la demostración. Según B.Russell (Historia de la Filosofía Occidental, vol.1, p.67):
La demostración es, pues, la aportación esencial de Pitágoras a la Matemática. Con Pitágoras, además, el talento griego para la generalización, para la extracción de la ley universal a partir de los casos concretos –en sentido aristotélico: la «forma» a partir de la «materia»–, había empezado ya a causar su efecto. Por eso Pitágoras marca también un hito en la Historia de la Matemática. A partir de Pitágoras la Matemática es universalmente considerada como un manantial inagotable de verdad objetiva, la ciencia por excelencia, «la reina de las Ciencias» que diría Gauss. Para los pitagóricos la Matemática era la ciencia tipo paradigma del conocimiento; todo su sistema tiende al matematismo que impregna la ciencia de hoy. Y más que la Matemática en general, la ciencia de los números: la Aritmética. La suprema máxima pitagórica que resume su Metafísica «el número es la esencia de todas las cosas» es un antecedente de la célebre frase de Galileo en Il Saggiatore resumida en la forma: «El libro de la naturaleza está escrito en lenguaje matemático.» Actualmente el aforismo pitagórico, más allá de su sentido alegórico, es una auténtica realidad; y ello por varias razones. Hoy muchas disciplinas científicas, incluso dentro del ámbito social, están fuertemente matematizadas. Es más, la propia Matemática, tras las penosas crisis de fundamentos de siglos pasados, ha encontrado sus cimientos lógicos en un proceso de aritmetización progresiva, que permite completar la cita de Gauss: «[...] y la Aritmética es la reina de la Matemática», dando pleno significado a la célebre frase de Kronecker: «Dios creo los números naturales y todo lo demás es obra del hombre», que debemos interpretar como un mayestático pronunciamiento pitagórico, que prepararía la celebre frase de B. Russell publicada en La Nation (27-10-1924):
Más aún, hoy, a través del proceso informático de digitalización, puede llegar a ser un número –sucesiones de ceros y unos– buena parte de la creación del intelecto humano desde una argumentación discursiva hasta una composición musical o una pintura en un lienzo y gracias a tal estructura magnética ser trasmitido, de forma casi instantánea, por vía telemática, a cualquier lugar del orbe terráqueo. Así que Pitágoras, el filósofo del número está de plena actualidad. También en el terreno de la Educación Pitágoras es un pionero ya que el Quadrivium pitagórico –Aritmética, Geometría, Música y Astronomía– sancionado por Platón en La República, se convierte en la médula de una instrucción liberal dominando gran parte del pensamiento pedagógico casi hasta nuestros días. Si a propósito del Teorema de Pitágoras habíamos dicho que «este teorema pertenece al imaginario cultural de casi todos los pueblos», a estas alturas podemos extrapolar la expresión para afirmar categóricamente que la propia figura de Pitágoras pertenece al imaginario cultural de casi todos los pueblos. Pitágoras no sólo es el instaurador de la tradición filosófica, científica y matemática en Occidente sino que su proyección ulterior en la Historia de la Ciencia, de la Matemática, de la Filosofía y del Pensamiento y la Cultura en general, es inmarcesible e imperecedera. No es extraño que el gran filósofo y matemático B.Russell comience el capítulo dedicado a Pitágoras de su Historia de la Filosofía Occidental, con esta palabras (vol.I, p.65): «Pitágoras es intelectualmente uno de los hombres más importantes que han existido y que mayor influencia ha ejercido en la Historia del Pensamiento.»
La extensa e intensa actividad intelectual de Pitágoras y su Escuela ha dejado un legado que está en la raíz de la Filosofía, la Ciencia, la Matemática, la Cosmología, la Música, ..., y ha tenido influencia decisiva en el Arte, la Educación, la Literatura, la Religión, la Mística, la Ecología, e incluso en la Magia y el Esoterismo. Para Pitágoras Filosofía, Ciencia, Matemáticas, Cosmología y Religión, son aspectos indisociables que conforman un estilo de vida: «el modo de vida pitagórico», imbuido por un entusiasmo místico que promueve una pasión por el conocimiento mediante la especulación filosófica y matemática como parámetros esenciales cotidianos de la existencia.
El Pitagorismo, tamizado por la Filosofía platónica, está en la base de la fundamentación filosófica e ideológica del Cristianismo. En Pitágoras encontramos el primer antecedente histórico del sincretismo cultural Oriente-Occidente, del pacifismo,del feminismo,del socialismo, del vegetarianismo, del ecologismo y de otros muchos «ismos» y tendencias que hoy son lugares corriente en nuestra cultura. Pitágoras es «el filósofo del número» artífice máximo del «milagro griego». Su figura histórica crea «las raíces de la Filosofía y de la Matemática», por eso su entidad intelectual es tan inconmensurable, que debemos situarla en «el umbral del pensamiento occidental», como «cuna del saber y del conocimiento» Pitágoras y los pitagóricos aportaron un ingente caudal de conocimientos matemáticos que fluíanen el ambiente místico y filosófico de la Escuela Pitagórica:
Pero lo más importante del legado pitagórico matemático es la propia instauración la Matemática como ciencia racional a través de la práctica de la demostración.
BIBLIOGRAFÍA
Ediciones de Los Elementos de Euclides
Bibliografía de Historia de la Ciencia y de la Matemática
Bibliografía de Historia de la Filosofía y Filosofía de la Ciencia y de la Matemática
|
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |






 Este escrito está dedicado con admiración a la figura humana y científica del Profesor Miguel de Guzmán, apasionado estudioso de Pitágoras y el Pitagorismo.
Este escrito está dedicado con admiración a la figura humana y científica del Profesor Miguel de Guzmán, apasionado estudioso de Pitágoras y el Pitagorismo.


 Aristóteles resume esta dualidad en la Metafísica (986a): «Otros pitagóricos admiten diez principios coordinados entre sí en este orden [cuadro adjunto]».
Aristóteles resume esta dualidad en la Metafísica (986a): «Otros pitagóricos admiten diez principios coordinados entre sí en este orden [cuadro adjunto]».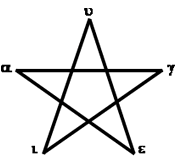 El número 5 corresponde al Pentagrama místico pitagórico, Pentalfa, o estrella de cinco puntas –obtenida al trazar las diagonales de un pentágono regular o prolongando sus lados– emblema de la salud y símbolo de identificación de los pitagóricos como miembros de una comunidad. El Pentagrama místico fue uno de los tópicos geométricos más importantes de la Escuela Pitagórica por sus bellísimas propiedades geométricas de las que nace su simbolismo místico. Esta figura geométrica pudo estar en la base del más importante hallazgo científico de los pitagóricos –el descubrimiento de las magnitudes inconmensurables–, una de las causas de la profunda crisis que arruinó a la cofradía pitagórica.
El número 5 corresponde al Pentagrama místico pitagórico, Pentalfa, o estrella de cinco puntas –obtenida al trazar las diagonales de un pentágono regular o prolongando sus lados– emblema de la salud y símbolo de identificación de los pitagóricos como miembros de una comunidad. El Pentagrama místico fue uno de los tópicos geométricos más importantes de la Escuela Pitagórica por sus bellísimas propiedades geométricas de las que nace su simbolismo místico. Esta figura geométrica pudo estar en la base del más importante hallazgo científico de los pitagóricos –el descubrimiento de las magnitudes inconmensurables–, una de las causas de la profunda crisis que arruinó a la cofradía pitagórica.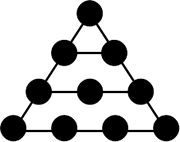 El número diez, cuya veneración, no es tributaria, paradójicamente, de la anatomía de la mano del hombre, es la quintaesencia del misticismo pitagórico. Los pitagóricos lo representaban mediante 10 puntos, piedrecillas o alfas dispuestos bajo la forma de un triángulo equilátero. A este anagrama, representación visual y geométrica del hecho de que 10=1+2+3+4, le llamaron la Tetractys de la Década. Tenía, para ellos tanta significación esotérica como el Pentagrama místico, y su importancia simbólica deriva de que por él juraban en sus ceremonias más solemnes, sobre todo en el rito iniciático de incorporación a la comunidad: «¡lo juro por Aquel que ha dado a nuestro alma la Tetractys, fuente y raíz de la Naturaleza eterna!» (Versos Dorados, 47) juramento referente al secreto sobre el contenido de la enseñanza pitagórica (Porfirio, Vida de Pitágoras, 20).
El número diez, cuya veneración, no es tributaria, paradójicamente, de la anatomía de la mano del hombre, es la quintaesencia del misticismo pitagórico. Los pitagóricos lo representaban mediante 10 puntos, piedrecillas o alfas dispuestos bajo la forma de un triángulo equilátero. A este anagrama, representación visual y geométrica del hecho de que 10=1+2+3+4, le llamaron la Tetractys de la Década. Tenía, para ellos tanta significación esotérica como el Pentagrama místico, y su importancia simbólica deriva de que por él juraban en sus ceremonias más solemnes, sobre todo en el rito iniciático de incorporación a la comunidad: «¡lo juro por Aquel que ha dado a nuestro alma la Tetractys, fuente y raíz de la Naturaleza eterna!» (Versos Dorados, 47) juramento referente al secreto sobre el contenido de la enseñanza pitagórica (Porfirio, Vida de Pitágoras, 20).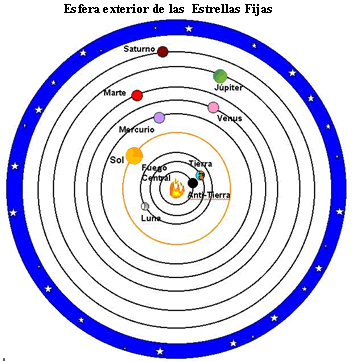

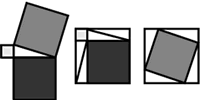 La tradición ha establecido que Pitágoras habría dado una prueba empírica del Teorema con base en las figuras adjuntas.
La tradición ha establecido que Pitágoras habría dado una prueba empírica del Teorema con base en las figuras adjuntas.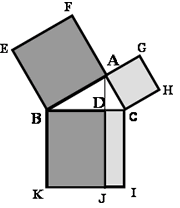 Muchos historiadores admiten que la demostración de Pitágoras se basaría en su propia Teoría de las Proporciones –imperfecta por aplicarse sólo a cantidades conmensurables–, de modo que la prueba de Pitágoras podría haber sido alguna de las dos siguientes :
Muchos historiadores admiten que la demostración de Pitágoras se basaría en su propia Teoría de las Proporciones –imperfecta por aplicarse sólo a cantidades conmensurables–, de modo que la prueba de Pitágoras podría haber sido alguna de las dos siguientes :
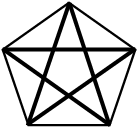 El Pentagrama místico pitagórico se obtiene a partir de tres triángulos isósceles iguales que tienen los ángulos iguales dobles del ángulo desigual. Este tipo de triángulo –llamado áureo porque los lados iguales están en proporción áurea con el lado menor– se construye en la Proposición 10 del Libro IV de Los Elementos de Euclides, cuyo contenido es de raíz pitagórica en su mayor parte. En la siguiente Proposición, la IV.11, se construye efectivamente el Pentagrama a base de inscribir en un círculo un pentágono regular y trazar las diagonales, las cuales de forma sorprendente se cortan determinando segmentos que están en proporción áurea siendo el segmento mayor igual al lado del pentágono (Euclides XIII.8).
El Pentagrama místico pitagórico se obtiene a partir de tres triángulos isósceles iguales que tienen los ángulos iguales dobles del ángulo desigual. Este tipo de triángulo –llamado áureo porque los lados iguales están en proporción áurea con el lado menor– se construye en la Proposición 10 del Libro IV de Los Elementos de Euclides, cuyo contenido es de raíz pitagórica en su mayor parte. En la siguiente Proposición, la IV.11, se construye efectivamente el Pentagrama a base de inscribir en un círculo un pentágono regular y trazar las diagonales, las cuales de forma sorprendente se cortan determinando segmentos que están en proporción áurea siendo el segmento mayor igual al lado del pentágono (Euclides XIII.8).




