|
En la enseñanza matemática correspondiente a los niveles no universitarios, especialmente en Secundaria, el Azar y la Probabilidad representa, sin lugar a dudas, la hermana pobre. Los temas de ese bloque, estratégicamente colocados siempre al final de los libros de texto, son obviados con frecuencia por compañeros que no suelen sentirse a gusto en esa parte de la matemática. Dado que los temarios son muy amplios, en cuanto nos encontramos con algún tropiezo que nos ralentice la marcha de la asignatura, quien sale perjudicada es la probabilidad. Muchos profesores que se llevan las manos a la cabeza si sus alumnos no saben resolver inecuaciones en Secundaria, no tienen ningún reparo en no explicar nunca el bloque de probabilidad, a pesar de que la Estadística y el Azar están entre las partes de la matemática más utilizadas en la vida cotidiana que nos rodea.
Muchos profesores, especialmente el Grupo Cero de Valencia, han estudiado y desarrollado juegos que sirven para introducir de una forma lúdica esta parte. Algunos de ellos los repasaremos en esta sección.
Dentro de la clasificación que realiza la profesora Ana García Azcarate en juegos preinstrucionales, coinstrucionales y postinstrucionales, la mayoría de los juegos de probabilidad pueden incluirse en el primer grupo, es decir no se necesita haber impartido ningún contenido probabilístico para poder comenzar a utilizarlos. Son juegos en los que el alumno puede comprobar fácilmente que aunque en un fenómeno probabilístico antes de realizar el experimento no pueda saberse a ciencia cierta qué va a salir, la actividad aleatoria se rige por unas reglas que es posible conocer.
La carrera de caballos.
Este juego es quizás el más conocido pues aparece en muchos libros de texto utilizando todo tipo de elementos: caballos, motos, caracoles, etc. Aunque la versión más conocida utiliza la suma de dados, existe otra versión donde se trabaja con la diferencia que también veremos aquí. Esas dos modalidades suelen utilizar tableros distintos, uno con dorsales del 1 al 12 para la suma y del 0 al 6 para la diferencia, sin embargo nosotros preferimos utilizar un solo tablero ampliado.
(1) Carrera con la suma.
Material: Dos dados cúbicos, una ficha (de colores distintos) para cada alumno y un tablero como el del Anexo I.
Forma de jugar:
- Cada jugador elige un caballo y coloca su ficha en el redondel con el número correspondiente. No pueden haber dos jugadores con el mismo caballo. Si no se ponen de acuerdo se lanzan primero los dos dados y eligen según la puntuación que hayan sacado.
- Por turno, cada jugador lanza los dos dados y suma los números que salen. El caballo cuyo dorsal coincide con esa suma avanza una casilla (aunque no sea el del jugador que ha lanzado los dados).
- Gana la partida el jugador cuyo caballo llega primero a la meta.
(2) Carrera con resta.
Es igual en todo a la anterior con la salvedad de que en el apartado b) se realiza la diferencia entre los valores que han salido en los dados y avanza el caballo con el dorsal que corresponde a esa resta.
Aspectos educativos:
- Nosotros preferimos utilizar un solo tablero para los dos juegos ya que de esa forma dejamos abierta la posibilidad de que algún alumno, sin pararse a pensar, elija un dorsal no válido, lo que descubre cuando comienza a jugar.
- El número de jugadores puede variar, aunque es aconsejable que no sea superior a seis, sobre todo en la segunda opción pues si no algún jugador debe elegir un caballo que no se moverá.
- Si juegan tres o cuatro jugadores en la versión de la suma, se encontrarán que muchas veces sale un valor de la suma correspondiente a un caballo que no ha elegido nadie, por lo que bastantes tiradas no servirán para que avance ninguno de los caballos seleccionados. Una forma de solucionar lo anterior es que en ese caso cada jugador elija dos caballos distintos, con lo cual al participar seis u ocho caballos la partida es más dinámica.
- Es interesante que los alumnos vayan anotando los valores que van saliendo en las tiradas (aunque no haya ningún caballo que avance) para que al final tengan recogido estadísticamente todo lo que ha salido, y de esa manera puedan ver claramente qué sumas tienen más posibilidad de salir.
- Muchas veces a los alumnos les gusta seguir jugando aunque ya haya ganado uno de ellos, para ver en qué orden van llegando sus caballos. Como todos van lanzando los dados, ninguno se aburre (aunque haya llegado su caballo) por lo que se les puede dejar que terminen la partida cuando todos hayan llegado.
- Si se juegan varias partidas, antes de comenzar cada una de ellas, deben elegir de nuevo los caballos. En estos casos (en que ya han visto los valores que más salen) es conveniente que lancen los dados para seleccionar el orden en que van a hacer la elección pues si no suele haber piques entre quien elige uno u otro caballo.
- El orden en que presentamos este juego en clase es primero utilizar la suma; cuando ya han jugado varias veces entonces se plantea el de la diferencia. Una vez acabado los dos lo más importante es hacer el estudio matemático de porqué un caballo u otro avanza más rápido. Este análisis es fácil de hacer por los alumnos pues sólo tienen que construir dos tablas de valores con los posibles resultados, tanto para la suma como para la resta.
|
+
|
1
|
2
|
3
|
4
|
5
|
6
|
|
-
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
1
|
0
|
1
|
2
|
3
|
4
|
5
|
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
2
|
1
|
0
|
1
|
2
|
3
|
4
|
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
3
|
2
|
1
|
0
|
1
|
2
|
3
|
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
4
|
3
|
2
|
1
|
0
|
1
|
2
|
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
5
|
4
|
3
|
2
|
1
|
0
|
1
|
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
6
|
5
|
4
|
3
|
2
|
1
|
0
|
- Al hacer el estudio anterior se puede observar que el 7 tiene ventaja (se puede aprovechar para hacer ver la razón por la que en las películas de casinos, quienes lanzan los dados siempre quieren un 7) en el caso de la suma. Sin embargo los resultados previstos teóricamente se pueden ver alterados por el azar. Por ello cuando se lanzan los dados, en algunos grupos puede ser que gane el caballo con dorsal 6 u 8 o incluso más alejados del 7. Lo mismo ocurre con el 1 en la diferencia, aunque en este caso al haber dos puntos de diferencia entre ese valor y el siguiente (que es el 2), es más raro que no gane el caballo de dorsal 1.
El asalto al castillo.
Este juego está pensado para grupos de entre tres y seis jugadores.
Material: Una moneda, dos fichas por cada jugador (de colores distintos para los jugadores) y un tablero como el del Anexo II.
Forma de jugar:
- Se sortea el orden para escoger casilla y cada jugador coloca una de sus fichas en una de las casillas superiores (no pueden haber dos fichas en una casilla) que se mantendrá fija y su otra ficha en la casilla inferior que es la de salida (donde se acumularán una ficha por jugador) que será la que se vaya moviendo a lo largo de la partida.
- Cada jugador, por turno, lanza la moneda y avanza su ficha al nivel superior. Si le sale cara coloca la ficha en la casilla superior izquierda, si sale cruz en la derecha.
- Se repite el proceso hasta que las fichas llegan a la última fila de casillas. Si la ficha de un jugador acaba en la casilla que había elegido previamente (y que había señalado con su otra ficha) se anota un punto. Si cae en otra casilla distinta no se anota nada.
- Se repite el juego diez veces y gana la partida el jugador que al final tenga mayor puntuación.
Aspectos educativos:
- Las partidas son muy rápidas de realizar (sobre todo con tres o cuatro jugadores) por eso hemos indicado que se repita el juego diez veces. Este número es indicativo. Si se quiere puede reducirse y jugar varias partidas. En este último caso, antes de cada partida, los jugadores deben elegir de nuevo la casilla a la que esperan llegar.
- Si se observa bien el tablero y la dinámica del juego, puede verse que estamos jugando en una máquina de Galton aunque visualmente esté invertida.
- Para estudiar la casilla que tiene ventaja elegir, se puede hacer un estudio del número de caminos que llega a cada casilla. Si se hace sistemáticamente comenzando por el principio nos aparecerá sin dificultad el Triángulo de Tartaglia, por lo que el número de caminos que llegan al final son 1, 5, 10, 10, 5 y 1 respectivamente. Como cada camino tiene una probabilidad de (1/2)5, es fácil hallar la probabilidad de conseguir acertar.
- En este juego, a diferencia del anterior, hay dos elecciones que tienen la mayor probabilidad de acertar, por eso no hay un ganador claro. Si se elige la casilla 3, hay la misma probabilidad de que la ficha acabe en la 4, con lo que no obtendremos ningún punto. Lo que se ve evidente es que mientras más nos alejemos del centro menos posibilidades hay de acertar, aunque como en cualquier experimento aleatorio, el azar nos puede dar sorpresas en casos puntuales.
- Como en el juego anterior, es interesante que los alumnos vayan anotando las casillas en las que van terminando las fichas, independientemente de si se han conseguido puntos o no, de tal manera que igual que la Máquina de Galton, al final se vea dónde se acumulan las terminaciones de las fichas.
Bibliografía.
- GRUPO CERO (Valencia) (1995): Matemáticas para la Educación Secundaria. 3 vol. M.E.C. y Edelvives. Madrid.
- MARTÍNEZ, P.; BAENA, J. y GUERRERO, S. (1994): Estadística. Octaedro, Barcelona.

Anexo 1: Tablero de la carrera de caballos |
|
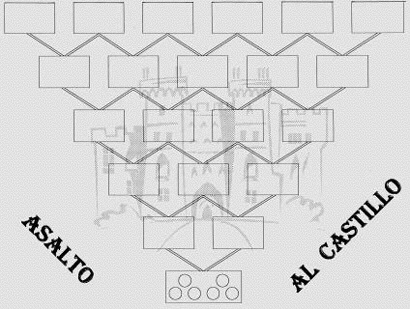
Anexo 2: Tablero del asalto al castillo
|
Tableros en PDF 
|
 Julio 2007: La carrera de caballos (publicado en la revista SUMA, número 51, 2006)
Julio 2007: La carrera de caballos (publicado en la revista SUMA, número 51, 2006)











