4. Las matemáticas de los fluidos

Los modelos matemáticos de los fluidos son algunos de los objetos matemáticos más complejos y relevantes sobre los que aún no se dispone una comprensión completa. Son muchos los factores que hacen que esto sea así. Uno de ellos es el hecho de que las soluciones desarrollen choques o discontinuidades, del mismo modo que las olas marinas se rompen al llegar al litoral. Esto hace que los métodos matemáticos habituales, basados en la intuición y técnicas desarrolladas en el ámbito de las superficies y funciones regulares, y que conducen a los gradientes de los funcionales que hemos de emplear en la implementación de los métodos de descenso, no puedan ser utilizados sin una revisión a fondo de los mismos. ¹⁰

Los choques o singularidades en Mecánica de Fluidos son un tema clásico y sin duda uno de los más importantes para la teoría actual de EDP. Por otra parte, las ondas de choque son de hecho uno de los fenómenos más relevantes en muy diversos ámbitos de la Mecánica (detonaciones, terremotos, fracturas, etc.) y, como vamos a ver, influyen de manera decisiva en los diseños aeronáuticos.

Desde un punto de vista matemático, sin ir más lejos, la unicidad y regularidad de las soluciones de las ecuaciones de Navier-Stokes en tres dimensiones espaciales constituye uno de los problemas del milenio de la Fundación Clay.¹¹ El modelo más sencillo en el que este tipo de fenómenos queda de manifiesto es la ecuación de Burgers uni-dimensional. En su versión viscosa, las ecuaciones correspondientes son¹²

con un parámetro de viscosidad ν > 0 dependiente del fluido en cuestión, y sus soluciones son regulares. Sin embargo en ausencia de viscosidad, es decir ν = 0, obtenemos el modelo

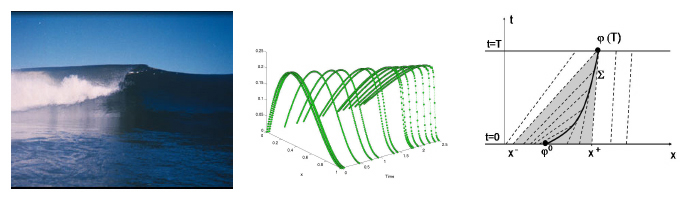
que se asemeja a las ecuaciones de Euler de los fluidos perfectos en tres dimensiones espaciales. Sus soluciones desarrollan discontinuidades, también denominadas choques, de igual modo que las olas del mar, con perfiles suaves en alta mar, se rompen al llegar a la costa, tal y como se ilustra en la Figura 4. Esto es así pues las soluciones toman valores constantes a lo largo de las trayectorias que describen las denominadas curvas características que son las que trazan las propias partículas del fluido en movimiento. Al colisionar dos partículas las soluciones se encuentran ante el conflicto de tomar dos valores distintos, generando una discontinuidad, del mismo modo que el tubo de una ola, antes de romperse, se enrolla sobre sí mismo en una configuración aparentemente imposible.

Figura 4: Izquierda: Imagen de una ola que en su lado izquierdo ya se ha roto y que en el otro está a punto de hacerlo. Centro: Evolución de un frente solución de la ecuación de Burgers sin viscosidad que, de izquierda a derecha, se observa como desarrolla un choque. Derecha: Rectas características que colisionan describiendo una curva sobre la que se propaga un choque.

Tal y como hemos señalado, uno de los elementos clave en el desarrollo de la metodología que acabamos de presentar, es la utilización de esquemas numéricos eficaces para la aproximación de las soluciones puesto que éstas rara vez pueden ser obtenidas de forma explícita.

En el marco de la ecuación de Burgers, en ausencia de viscosidad, los esquemas más habituales son de la forma,

(4.1)

donde, , siendo g el flujo numérico¹³ que ha de satisfacer la relación de consistencia g(u, u) = u²/2. Esta condición de consistencia garantiza que el esquema numérico es, efectivamente, una aproximación de la ecuación de fluidos en consideración, en este caso la ecuación de Burgers.

Se trata de esquemas en diferencias finitas de tres puntos que proporcionan, a través del valor de la función discreta , una aproximación de la solución u en los puntos (jΔx, nΔt), donde Δx y Δt son los pasos del mallado en la dirección espacial x y temporal t, respectivamente. Tal y como hemos mencionado anteriormente e ilustrado en la Figura 3, en la práctica, los mallados considerados han de ser irregulares para adaptarse a la compleja geometría de las aeronaves, aunque el análisis numérico muchas veces se restringe en una primera etapa, a los mallados cartesianos regulares (gráfica de la derecha de la Figura 3) en los que la bondad de los esquemas de discretización empleados puede verificarse con mayor facilidad.

Existen muchos esquemas numéricos que satisfacen estas condiciones de consistencia (Lax-Friedrichs, Engquist-Osher, Godunov, Roe, etc.) y se distinguen, en particular, por tener una eficacia muy distinta cuando se trata de aproximar soluciones que presentan choques.

Frecuentemente, los esquemas más eficaces, como el de Godunov y Roe, no son diferenciables, al involucrar una función de flujo g que no lo es,¹⁴ lo cual impide la aplicación de los métodos de descenso basados en el gradiente del funcional, tal y como los hemos presentado. En efecto, la posible presencia de discontinuidades o choques en las soluciones hace que los esquemas tengan que ser sensibles al direccionamiento del flujo e incluso a su amplitud. Esto hace que todo buen esquema haya de incorporar limitadores, términos que se activan sólo en determinadas circunstancias en función del valor de ciertos sensores que miden, en particular, la inminencia de los posibles choques. De este modo los esquemas dejan de ser suaves en el paso de un nodo a otro y el formalismo de linealización anterior deja de ser válido. Este problema es inevitable pues los esquemas suaves, para capturar los choques de las soluciones, necesitan unos mallados tan finos que en la práctica suponen un coste computacional excesivo y no pueden ser utilizados.

Esto conduce a un difícil dilema: Necesitamos esquemas que resuelvan bien los posibles choques que se presentan en el fluido, pero esto nos obliga a utilizar esquemas numéricos que no son diferenciables, lo cual dificulta considerablemente el empleo de los métodos de descenso.

Se trata éste de un tema de gran importancia, que se acrecienta en problemas más complejos derivados de las aplicaciones a la aeronáutica que describimos y que son objeto aún de investigaciones exhaustivas.

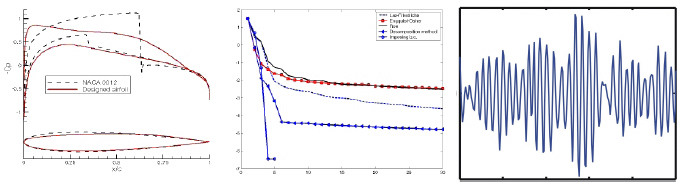
Figura 5: Izquierda: Evolución del coeficiente de presiones C_p a lo largo de la superficie del ala, al pasar de la geometría inicial (en negro) a la nueva (en rojo) tras un proceso de optimización. Centro: Rendimiento de los diversos métodos de descenso aplicados a la ecuación de Burgers mediante diferentes esquemas de discretización y diferenciando, sobre todo, el tratamiento de los choques. Derecha: Inestabilidades numéricas.

5. Inestabilidades

Una vez de haber desarrollado el programa matemático expuesto y el algoritmo de descenso en alguno de los lenguajes de programación más avanzados, pondremos el programa en marcha en el ordenador (normalmente un superordenador o granja de ordenadores para simulaciones de características realistas) a la espera de obtener un diseño algo mejor que el que teníamos anteriormente, tal y como se ilustra a la izquierda de la Figura 5. En la tabla comparativa del centro de dicha gráfica mostramos experimentos numéricos realizados en la ecuación de Burgers sin viscosidad en presencia de choques. Constatamos cómo los diferentes métodos empleados, que se diferencian esencialmente en el esquema numérico utilizado para discretizar la ecuación y el modo en que se tiene en cuenta la presencia de choques en la solución, evolucionan en función del número de iteraciones del algoritmo gradiente. Algunos de ellos descienden de manera muy lenta lo cual, en la práctica, supone la no convergencia del método pues en las aplicaciones reales, el número de iteraciones que se puede realizar, debido a su gran coste computacional, es muy pequeño. El algoritmo que presenta un mejor rendimiento, llegando en cuatro iteraciones a un valor mucho menor de lo que los demás métodos son capaces de alcanzar en 30, ha sido diseñado en el seno del proyecto DOMINO.

Pero no hay que excluir que nos encontremos, de manera inesperada y contrariamente a nuestras expectativas, con resultados un tanto desconcertantes. En efecto, es frecuente que cuando, al cabo de un gran número de iteraciones y de haber consumido el tiempo computacional disponible, paramos un algoritmo, observar un resultado fuertemente oscilante como el ilustrado en la derecha de la Figura 5 que resulta a todas luces inutilizable puesto que una deformación de este tipo de la forma de un vehículo es irrealizable y contraria al propio sentido común. Estamos frente a una falsa solución, espúrea, producida por el método numérico, un fantasma numérico, y no la que corresponde al problema real original planteado. Es una situación producida por la acumulación de errores numéricos que en los que en cada paso del complejo proceso de optimización vamos incurriendo y que acaban corrompiendo completamente los resultados numéricos finales. Es una manifestación de haber violado la condición de estabilidad que, junto con la de consistencia antes mencionada, según el Teorema de Peter Lax (Premio Abel 2005), garantiza la convergencia de un método numérico. Esta inestabilidad es la que produce este tipo de resultado altamente oscilante, de alta frecuencia y gran amplitud.

Es por eso que los algoritmos iterativos de tipo gradiente que hemos descrito han de ser suplementados con frecuencia con técnicas de filtrado y/ o regularización de las altas frecuencias espúreas, lo cual se realiza con frecuencia mediante la utilización de varios mallados simultáneos, del mismo modo que las obras de arte necesitan de un acabado o pulido final antes de considerarse terminadas.

6. Conclusiones: Algunos retos

En este artículo hemos descrito los ingredientes principales de los métodos matemáticos de Diseño óptimo de formas, centrándonos en la aeronáutica. Como hemos visto, son muy diversos los elementos que intervienen en el desarrollo de una metodolgía global y sistemática y en la que las Matemáticas juegan un papel central, en coordinación con otras disciplinas y muy en particular con la Computación. El programa que hemos descrito está fuertemente inspirado en las ideas de algunos de los clásicos como Euler y Newton, pero utiliza los desarrollos más actuales y avanzados de muy diversos ámbitos de las Matemáticas. Hemos mencionado las dificultades que surgen en su implementación y algunos problemas abiertos a los que esto conduce, que son de profundo calado matemático. En esta última sección realizamos un breve resumen de las principales problemas abiertos que se plantean en éste área, no sin antes recordar que la metodología descrita tiene un carácter universal por su amplio e importante espectro de aplicaciones al que aludíamos al inicio de este artículo, más allá de los propios de la aeronáutica.

Entre los problemas más relevantes que quedan por resolver en este campo cabe mencionar:

• Regularidad y unicidad de las soluciones de las ecuaciones de los fluidos en tres dimensiones espaciales.
• Desarrollo de métodos de identificación de choques y singularidades, lo cuál requerirá el empleo y desarrollo de técnicas propias del tratamiento de imágenes y de la geometría computacional.
• Análisis de la sensibilidad de los funcionales de coste habituales con respecto a las singularidades del fluido.
• Métodos eficaces para resolver numéricamente las ecuaciones adjuntas que, aunque tengan un aspecto semejante a los modelos clásicos de la Mecánica de Fluidos, poseen soluciones con características muy distintas a las ecuaciones de estado que no son fáciles de capturar.
• Desarrollo de nuevos métodos de minimización, que transciendan los métodos gradiente habituales, puesto que estos últimos permiten mejorar los diseños ya existentes pero no dar con otros más innovadores.
• Desarrollo de métodos de filtrado y regularización de las oscilaciones espúreas que funcionen de manera sistemática y de modo que el calibrado de los parámetros relevantes pueda automatizarse.

Todos estos problemas técnicos se enmarcan en un esfuerzo colectivo, que necesita un abordaje multidisciplinar, y que tiene como objetivo último el desarrollo de métodos computacionales integrados en los que los procesos de simulación del fluido y la optimización se realicen en paralelo, proporcionando herramientas de diseño que puedan ser usados de manera intuitiva, creativa, versátil y en tiempo real en entornos avanzados de diseño, dotados de las más modernas tecnologías, en particular, de realidad virtual.

Notas:

¹ Entendemos por ello que, con la capacidad de cálculo de los ordenadores actuales, el tiempo necesario para realizar el cálculo es tan largo que, en la práctica, éste resulta irrealizable o simplemente exige más tiempo del que disponemos. Es también frecuente que, cuando las simulaciones numéricas se prolongan excesivamente, las inestabilidades que introduce el propio algoritmo computacional acaben corrompiendo los resultados y los hagan finalmente inservibles.

² La terminología “coste” en este contexto se utiliza en el sentido que, en muchas aplicaciones, el funcional J representa en efecto el coste económico que supone una determinada configuración. Minimizar el “coste”, tal y como nos proponemos aquí, es pues un objetivo natural desde un punto de vista de la rentabilidad económica.

³ Se trata en la práctica de un vector de tres componentes que proporciona la velocidad (rapidez escalar y direccionamiento) de la partícula de aire que ocupa el lugar x en el exterior de la región Ω ocupada por la aeronave, en el instante t.

⁴ Desafortunadamente hay una cierta ambigüedad en la terminología que se emplea para denominar las figuras que presentan la forma que se indica en a izquierda de la Figura 2. En efecto, mientras que en la literatura matemática avanzada éstas se denominan “convexas”, tal y como lo hacemos aquí, en cursos elementales de Matemáticas se denominan “cóncavas”.

⁵ En este caso, en ausencia de convexidad, es fácil imaginar cómo la canica se perdería en una dinámica ininterrumpida sobre la superficie con esta geometría compleja, por efecto de la gravedad, sin nunca llegar a un punto de mínimo.

⁶ En este punto y en lo sucesivo abusamos de la notación. Para dar un sentido riguroso a estas fórmulas deberíamos considerar el funcional definido en un espacio de Hilbert, definir la distancia entre dominios, sus deformaciones a través de campos que apunten en la dirección normal, etc. Se dispone una teoría matemática consistente que arranca en los trabajos de J. Hadamard y que permite dar rigor a todo lo que aquí describimos.

⁷ De manera más rigurosa la regla de avance que permite obtener el nuevo dominio Ω_k+1 a partir del anterior Ω_k es Ω_k+1 = Ω_k − ρ∇J(Ω_k), k ≥ 0, siendo ∇J(Ω_k) el gradiente del funcional J, en la configuración Ω_k que representa la dirección de máxima pendiente sobre la gráfica del funcional J.

⁸ En esta ecuación b(Ω) representa los datos del problema, el operador A(Ω) el modo en que el sistema responde ante estos datos, y u(Ω), el estado en consideración, es precisamente la respuesta del sistema. Formalmente la solución u(Ω) puede simplemente obtenerse por la fórmula u(Ω) = A(Ω)⁻¹(b(Ω)). En la práctica esto no es sin embargo fácil de hacer. Dar sentido a esta inversión del operador A(Ω) es, de hecho, en algunos casos, un verdadero reto intelectual aún pendiente de realizar.

⁹ Con el objeto de ilustrar el método adjunto, consideremos, para simplificar la presentación, un funcional de la forma

en el que B es un operador simétrico. Entonces la variación del funcional J es δJ(Ω) = < Bu, δu >, donde du es la variación del estado. Para evitar el cálculo de du que, para cada parámetro de diseño, nos obliga a la resolución de un sistema semejante al de las propias ecuaciones de estado, introducimos el estado adjunto p que satisface A*(Ω)p = Bu. Aquí, mediante A(Ω)* denotamos el operador adjunto de A(Ω) que se caracteriza por la propiedad de que < A(Ω)*v, w > = < v, A(Ω)w >. Vemos entonces que

< Bu, du > = < A*(Ω)p, δu > = < p, A(Ω)δu > = < p, δb − δAu >,

y, por lo tanto, δJ puede ser calculado tomando productos escalares del estado adjunto p con cantidades que sólo dependen del estado ya conocido u y de las variaciones de los coeficientes del sistema, pero sin necesidad de recalcular δu. El método adjunto permite por tanto realizar cada paso de la iteración del método gradiente resolviendo dos sistemas: la ecuación de estado para el cálculo de u, y la de estado adjunto, para el cálculo de p.

¹⁰ En efecto, del mismo modo que la derivada de una función discontinua como la función H de Heaviside (H = 0, x < 0; H = 1, x > 0) tiene como derivada la delta de Dirac  δ₀ (medida singular que concentra una masa unidad en un sólo punto, x = 0), al linealizar una EDP en torno a una solución que presenta discontinuidades, se producen términos singulares soportados en el lugar geométrico de los choques.

¹¹ Lo cual corresponde a justificar la inversión el operador A(Ω) al que antes aludíamos para obtener la expresión u(Ω) = (A(Ω))⁻¹(b(Ω)) para los fluidos tridimensionales.

¹² En este caso utilizamos la notación u en lugar de u con el objeto de subrayar que se trata de una función escalar que representa, por ejemplo, la altura de una ola en un canal unidimensional.

¹³ El flujo numérico tiene como objeto simular en el modelo computacional la cantidad de fluido que entra y sale por los extremos del intervalo [x_j , x_j+1], siendo x_j = jΔ x los nodos del mallado espacial.

¹⁴ Lo mismo que ocurre con la función valor absoluto |x| = x, si x ≥ 0 y |x| = −x, si x ≤ 0, que no es diferenciable en el punto x = 0 en el que la gráfica de la función presenta dos pendientes distintas ±1, a ambos lados.

"Las Matemáticas del diseño aeronáutico: avances y retos": Financiado por los proyectos MTM2005-00714, DOMINO CIT-370200-2005-10 del programa PROFIT, el Proyecto Ingenio Mathematica (i-Math) del Programa CONSOLIDER INGENIO 2010 del MEC y el proyecto SIMUMAT de la CM. Este trabajo ha sido redactado durante la visita de su autor al Isaac Newton Institute de Cambridge en el marco del programa “Highly Oscillatory Problems”. El autor agradece a Eduardo Artamendi (Departamento de Arquitectura de la UPV/EHU) por su revisión del manuscrito y valiosas sugerencias.