 43. SOLUCIÓN CONCURSO DEL VERANO DE 2009
43. SOLUCIÓN CONCURSO DEL VERANO DE 2009 |
 |
 |
 |
| Escrito por Alfonso J. Población Sáez |
| Lunes 14 de Septiembre de 2009 |
|
Poco a poco nos vamos adentrando en la rutina de un nuevo curso escolar (que no tiene porqué ser vista como algo peyorativo, para eso, entre otras opciones, estamos nosotros aquí). Mientras esperamos impacientes el estreno de Ágora, para abrir boca, veamos cómo han ido las tareas del verano. Recordemos que teníamos cuestiones (de cine y de matemáticas) y fotografías relacionadas de algún modo con esas cuestiones, que también teníamos que explicar. Seguimos el orden en que se presentaron. Foto 1.- Veíamos una montaña nevada que poco nos dice de momento. Por su aspecto da la impresión de estar en la cordillera del Himalaya, aunque de momento es una mera conjetura. Cuestiones 1ª y 2ª.- Probablemente sean las más difíciles de resolver de todas las que se proponen (hay que empezar jugando fuerte). Sin embargo la introducción que se hace da la pista. Se comentaba que en diferentes lugares del mundo van apareciendo fotografías o fragmentos de películas que se consideraban perdidos para siempre (recientemente ha pasado con Metrópolis, con la que nos ocupa, y con otras muchas). Habitualmente esos materiales se encuentran ocultos en almacenes, trasteros, sótanos, lugares nada aptos para la conservación de unos elementos tan perecederos. Por eso, cuando se trata de verlos, aparecen con rayas, partes descoloridas o completamente desaparecidas, etc. (en adelante a este tipo de “impurezas” la denominaremos como se las conoce científicamente: ruido de la imagen), y con las técnicas actuales hay que tratar de restaurarlos. Para ello se emplean procedimientos de realce de imagen, basadas en operaciones matemáticas que mecánicamente se realizan a través del ordenador (implementadas en software; uno de los programas comerciales más conocidos popularmente es Photoshop, aunque hay muchos, y otros que el técnico restaurador se programa él mismo con lo que quiera conseguir). Según el ruido que se tenga, se aplican unos métodos u otros. Así se puede desear reducir el ruido de fondo, eliminando la textura que tenga dicho fondo resaltando los objetos que estén presentes. En otras ocasiones se quiere ajustar la intensidad y/o el contraste. En la actualidad, se trabaja con imágenes digitales. Esto significa que una imagen no es más que un conjunto (una matriz) de números que guardan la información de cada píxel de la imagen (color, intensidad, contraste, etc.). Y sobre los números se pueden efectuar todas las operaciones que se deseen. Una de las operaciones más empleadas en el tratamiento de imágenes es el paso de un filtro. Hay diferentes tipos (de paso bajo, de paso alto, de mediana, adaptativos, etc.) dependiendo de lo que se quiera conseguir. Aunque pueda parecer complicado, lo que se hace es muy sencillo: a cada píxel se le cambia su valor haciendo una operación sencilla (suma, resta, mediana, varianza, etc.) de acuerdo con los valores de los píxeles de alrededor. A veces se toman sólo los píxeles a izquierda, derecha, arriba, abajo y los de las diagonales (esto se llama utilizar una máscara 3x3) cada uno afectado por un valor adecuado (un peso); en otras ocasiones se toman máscaras 5x5, 7x7, etc., siempre con valores impares. Y eso se ejecuta sobre cada píxel de la imagen. El resultado es una nueva imagen, la imagen filtrada. En la actualidad se siguen estudiando nuevos tipos de filtros, tratando de mejorar más estas técnicas. Algunas de ellas utilizan ideas de la Física, como el que nos ocupa. Se parte de la idea de la difusión de los gases. Este proceso se describe mediante una ecuación diferencial de la forma
donde I(x) es la función de intensidad de la imagen, x es un vector que almacena la posición de cada píxel de la imagen, t es el tiempo, I(x, t) es por tanto la evolución de la imagen con el tiempo, c(x, t) es una función llamada coeficiente de difusión, y esos símbolos tan extraños div y ∇ son unos operadores matemáticos llamados divergencia y gradiente, respectivamente. Los procesos en los que c(x, t) es constante se llaman procesos isotrópicos y en caso contrario, anisotrópicos. La fórmula que aparece en la cuestión es un tipo particular de difusión anisotrópica.
Aparecen en la I subíndices i, j y superíndices t. Eso se llama una discretización de la fórmula que no es más que tomar un conjunto finito (aunque grande; todo lo hace el ordenador así que ese valor puede ser enorme) de valores en la imagen, y para cada uno se aplica la ecuación. Es un tipo concreto de filtro llamado SRAD (Speckle Reducing Anisotropic Diffusion) que yo he castellanizado como DARS (Difusión Anisotrópica de Reducción del Speckle). El Speckle no tiene una traducción exacta al castellano. Es un tipo de ruido que afecta a las imágenes, sobre todo a aquellas captadas mediante ultrasonidos, utilizadas habitualmente en medicina para hacer radiografías. Estas técnicas por tanto se utilizan sobre todo en imágenes médicas, más que en la de restauración de fotografías o de películas. Entre las respuestas recibidas, también ha surgido la de Digital Adaptative Recording System y Digital Analog Re-mastering System, que no dudo que existan pero que no tiene relación con la fórmula de la ecuación del calor de la primera cuestión. Seguro que pensáis que me he pasado tres pueblos pero con las facilidades de internet hay que liar un poco las cosas. Además sólo son veinte puntillos de nada. Foto 2.- Claramente es Paris Hilton. ¿Qué tendrá que ver con el tema que nos ocupa? ¿Tendrá la película lugar en París? ¿Estará protagonizada por George Sanders o Zsa Zsa Gabor, antepasados cinematográficos de la Hilton? Sigamos leyendo…. Cuestión 3ª.- Primera cuestión matemática. El cine comenzó en mil ochocientos noventa y tantos, así que el año de estreno sólo puede ser 189x, 19yz o 200t (donde x, y, z, t son dígitos desconocidos). Se dice que “la suma de los dígitos del año del estreno de la película (y curiosamente también la suma de los dígitos del año del estreno de un remake posterior) es el número del siglo al que esa fecha corresponde”. Si fuera la primera opción, 1 + 8 + 9 + x = 19, con lo que x = 1, pero en ese año el cine aún no existía, o sea que descartado. Tampoco 2 + t = 21 es factible, así que será 1 + 9 + y + z = 20, con lo que y + z = 10. Es decir que nos restringimos a los años 1919, 1991, 1928, 1982, 1937, 1973, 1946, 1964 o 1955. Por otra parte, “la diferencia entre ambas fechas (se refiere a la película y su remake) es un cuadrado perfecto, y alguna de ellas es un número primo”. No tenemos más que probar con dichas cantidades. Sin embargo, cuando calculamos las diferencias entre todas esas cantidades, nos damos cuenta de que hay trece posibilidades, que afectan a todos ellos, por lo que a priori no podemos descartar ninguno. Ahora bien se dice que al menos uno de los dos años que nos interesan es un número primo. Sólo el 1973 es primo, con lo que las posibilidades se reducen a tres: 1973 - 1937 = 36, 1982 - 1973 = 9, 1973 - 1964 = 9. Si hacemos caso al comentario de que la película principal que buscamos es de “hace mucho, mucho tiempo”, en las citadas la fecha más antigua es 1937, con lo que las fechas deberían ser 1937 y el remake de 1973. Pero lo confirmaremos o refutaremos más adelante,…. A continuación se dan muchos datos sobre la película: el argumento, que ganó dos Oscars@, que su remake es una de las peores películas de la historia, se detallan algunos párrafos de la novela, aparece una nueva foto (la 3ª) de una idílica montaña y el nombre en chino del desfiladero que atraviesan, y un problema.
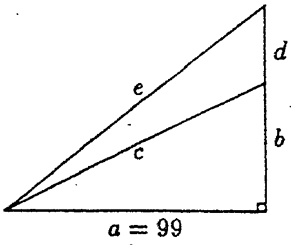
992 + (b + d)2 = e2 = (99 + b - d)2 = 992 + 2 × 99 (b - d) + (b - d)2 Sin demasiadas dificultades, desarrollando los binomios, simplificando y despejando d, se obtiene:
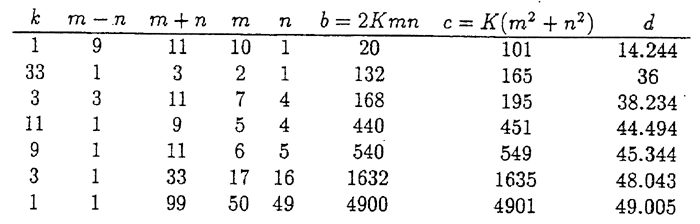
Se trataría ahora de encontrar valores enteros de b y d (y por supuesto de c y e). Por seguir un procedimiento diferente del puro tanteo o de que el ordenador lo encuentre, podemos acudir al resultado más conocido sobre ternas pitagóricas (que además se localiza fácilmente a través de los socorridos Google o Yahoo): Cada terna pitagórica puede construirse a partir de dos números enteros positivos m y n primos relativos, de distinta paridad, con m > n de la siguiente forma: (2Kmn , K(m2 – n2), K(m2 + n2)), con K número entero. Pequeño apunte notacional: lo de m y n primos relativos se suele describir como (m, n) = 1 (o mcd(m, n) = 1) y lo de distinta paridad, como m ≡ n + 1 mod 2, que es lo mismo, pero mucho más conciso, preciso y económico respecto a la cantidad de caracteres utilizados. Como 99 es un número impar, no puede obviamente ser de la forma 2Kmn, ni K(m2 + n2), con lo que tratamos de escribirlo como K(m – n) (m + n). Encontramos únicamente las siete posibilidades que aparecen en la siguiente tabla:
La última columna, los valores de d, se han calculado a partir de la fracción obtenida anteriormente. El único valor entero se consigue para d = 36 y b = 132. Comprobad que se verifican todas las condiciones del enunciado. Así pues la respuesta a la cuarta cuestión es b = 132 Brahms. Cuestión 5ª.- Es obvio que el monje no ha resuelto el problema que plantea (probablemente solo se ha aprendido los datos, como sucede con algunos guías reales), sino no hablaría de trigonometría (si se intenta resolver el problema metiendo en danza razones trigonométricas, no se llega a ninguna parte). Foto 4ª.- La única foto de las que aparecen que realmente es de la película (de la primera versión).
D = mcd(A, B) (A / mcd(A, B) + B / mcd(A, B) - 1 ) = A + B - mcd(A, B). En la cuestión 7, como 819 = 9 x 7 x 13, 1001 = 7 x 11 x 13, el mcd(819, 1001) = 7 x 13 = 91. Es decir, se tienen 91 rectángulos de tamaño 9 x 11. De la expresión anterior se sigue que el número de cuadrados que corta la diagonal es D = 819 + 1001 - 91 = 1729 (respuesta a la cuestión 7). Para saber por cuantos vértices de los cuadrados pasa la diagonal (cuestión 6), basta darse cuenta de que cada uno de los 91 rectángulos 9 x 11 proporciona un punto por el que pasa la diagonal. Si descartamos el último que coincide con el vértice del rectángulo grande, nos quedan 90 cuadrados. Foto 5ª.- Probablemente esta es la foto CLAVE., o al menos una de las clave, porque es muy conocida. Es la foto promocional e icono de la película Adios Mr. Chips (Goodbye Mr. Chips, Sam Word, Reino Unido, 1939). La novela y el personaje en los que se basa, Mr. Chips, un profesor de universidad, fueron concebidos por el escritor James Hilton, un autor muy popular en su tiempo, hoy prácticamente olvidado. Además de las novelas relativas a Mr. Chips, escribió Horizontes Perdidos, llevada varias veces a la pantalla, dos de las cuales, 1937 y 1973, son las películas que estamos buscando. Cuestión 8ª.- Una vez descubierta la película (o el libro), es fácil ir atando cabos. En este caso el hecho de que el avión que inicialmente debía llevarlos a Shanghai los traslade a Sangri-La, no es casual. Sondra, una de las habitantes de Sangri-La, había propuesto a Conway como la persona idónea para suceder al padre Perrault, enfermo desde hace tiempo. Por eso fue “secuestrado”. Foto 6ª.- Vemos una imagen de una luna azul. Se trata de un fenómeno en el que se puede apreciar una segunda Luna llena durante un mismo mes del calendario, teniendo lugar cada dos años y medio aproximadamente. El fenómeno Blue Moon cobró popularidad de manera casual, debido a que en el mes de enero y marzo de 1999 sucedieron dos veces respectivamente. Los medios de comunicación reseñaron ampliamente éste acontecimiento, poco conocido hasta entonces. El mes de febrero de dicho año no se produjo ninguna luna llena. Cuatro años de cada siglo, se observan dos “lunas azules” en un mismo año. La primera siempre se produce en enero y la segunda, por lo general, en marzo. Se observará una el día 31 de diciembre de 2009 (el primer plenilunio de ese mes será el día 2 de diciembre). Pero la relación con nuestro concurso es que el idílico monasterio del que habla la novela, Shangri-La, se localiza en el valle de la Luna Azul.
Cuestión 9ª.- Existen 166 hexacubos diferentes con los que se pueden construir complicadas estructuras que generan a su vez interesantes problemas matemáticos. Aunque los 8 tetracubos también han motivado diversas cuestiones, es a partir de los 29 pentacubos donde surgen la mayor parte de los tos artículos y trabajos más populares. Cuestión 10º.- El hexacubo en cuestión es el que muestra la imagen adjunta enviada por uno de nuestros participantes, en la que se ve perfectamente cómo este hexacubo es idéntico a su imagen especular. También es claro que no tiene ningún plano de simetría.
Cuestión 11ª.- La canción The world is a circle, aparece en la banda Sonora del remake Lost Horizon (1973) dirigida por Charles Jarrott con un reparto estelar entre los que aparecen Peter Finch, John Gielgud, Liv Ullmann, Charles Boyer, Michael York, entre otros. Fue compuesta por el famoso compositor Burt Bacharach. Cuestión 12ª.- Figura 1.- Sea E un punto sobre AB de modo que el triángulo ∆EBD sea equilátero. La imagen adjunta fue enviada por uno de los concursantes. Su razonamiento concluye así:
Aplicando razones trigonométricas obtenemos que:
Despejando:
Y racionalizando: CD = EA = OA√3. Figura 2.- Sea E la otra intersección de AB con el círculo y sea F un punto sobre BD tal que EF⊥BD. En ese caso, EF = EB/2 = AB. Como ∠EBD = 30º, entonces ∠EOD = 60º y ED = EO = OB. Entonces DF = OA = CB, y de ahí CD = BF = EF√3 = AB√3. Foto 7ª.- Se trata de una imagen de una de las protagonistas de la serie Lost (Perdidos), Evangeline Lilly (Kate). La relación con nuestras películas enigma es únicamente el adjetivo Perdidos, que en inglés también coincide con el de las películas en cuestión. Bueno, también en la isla en la que están tiene algo que ver con Shangri-La por aquello de la sanación de enfermedades terminales. Cuestión 13ª.- En el primer trayecto en el que se va de puerta en puerta, se abren todas. Está claro que si en los restantes 99 trayectos, una puerta es visitada un número impar de veces, entonces quedará al final cerrada y su morador no será seleccionado. Por el contrario, las puertas visitadas un número par de veces quedarán finalmente abiertas. Por ejemplo, la puerta 7, sólo es visitada una vez: en la séptima ronda. Quedará pues finalmente cerrada, como cualquier otra que sea un número primo. La número 10, es visitada en la ronda 2ª, en la 5ª y en la 10ª (cerrar-abrir-cerrar), y queda finalmente cerrada. Debemos por tanto fijarnos en los divisores de cada número de puerta. Los únicos números entre 1 y 100 que tienen un número par de divisores (exceptuando el 1 y contando el propio número) son los cuadrados perfectos, esto es, 1, 4, 9, 16, 25, 36, 49, 64, 81 y 100, cuyos monjes son los finalmente elegidos para el desfile. Foto 8ª.- Uno de los momentos impactantes del remake de 1973: al salir de Shangri-La, se recupera la edad verdadera, con lo que la enamorada de Michael York, Olivia Hussey (María) queda reducida a cenizas ipso-facto. Cuestión 14ª.- Aunque ya lo hemos venido comentando, volvemos a recordarlo: Horizontes Perdidos (Lost Horizons, Frank Capra, EE. UU., 1937), y Horizontes Perdidos (Lost Horizon, Charles Jarrott, EE. UU., 1973). Cuestión 15ª.- A lo largo del texto ya se han comentado todas las fotos. Sólo la imagen 4ª, de la película de 1937, y la 8ª, del remake de 1973, son auténticas. Cuestión 16ª.- Aunque las películas mantiene el espiritu de la novela, hay bastantes diferencias. Citemos algunas indicadas por los concursantes:
Cuestión 17ª.- Shangri-La fue el primer nombre de la sede de descanso presidencial estadounidense en Camp David. Se lo puso su primer ilustre hospedado, el presidente Franklin Delano Roosevelt en 1942. En 1953 Dwight David Eisenhower la renombró como Camp David, en recuerdo de su nieto.
Los concursantes que habéis participado en el concurso me habéis dejado realmente sorprendido por vuestro altísimo nivel, no en datos sobre la novela y las películas que eso más o menos con paciencia se localiza en internet, sino en vuestras resoluciones de los problemas matemáticos. Recibid pues desde DivulgaMAT nuestra más sincera enhorabuena. Tras el recuento paciente de la puntuación de cada cuestión, el podium ganador ha quedado del siguiente modo: 1º.- Miguel Herraiz Hidalgo.- 130 puntos.
2º.- Emilio Diaz Rodríguez .- 120 puntos.
3º.- Elías Villalonga Fernández.- 103 puntos.
|
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |






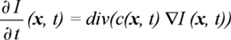
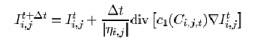
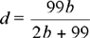
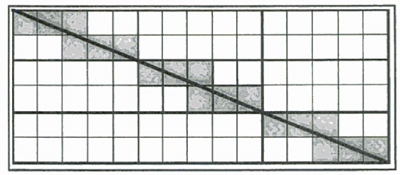
 Si contamos además los vértices inicial y final del rectángulo completo tendremos que la respuesta es 92 cuadrados.
Si contamos además los vértices inicial y final del rectángulo completo tendremos que la respuesta es 92 cuadrados. Entre las cuestiones octava y novena, se dice que el apellido del protagonista recuerda a un matemático. El personaje principal es Robert Conway. En efecto hay al menos un matemático que se apellida así: John Horton Conway (nacido en Liverpool, Gran Bretaña, el 26 de diciembre de, curiosamente, 1937). Ha trabajado en multitud de áreas matemáticas, entre ellas, en la teoría de conjuntos, teoría de nudos, teoría de números, teoría de juegos y códigos. También ha dedicado parte de su trabajo a la matemática recreativa: creador en 1970 del juego de la vida, el juego del drago, el Phutball y ha realizado análisis detallados de otros muchos juegos y problemas, como el cubo Soma. Martin Gardner ha difundido sus trabajos ampliamente en libros y artículos. Actualmente es profesor de matemáticas en la Universidad de Princeton.
Entre las cuestiones octava y novena, se dice que el apellido del protagonista recuerda a un matemático. El personaje principal es Robert Conway. En efecto hay al menos un matemático que se apellida así: John Horton Conway (nacido en Liverpool, Gran Bretaña, el 26 de diciembre de, curiosamente, 1937). Ha trabajado en multitud de áreas matemáticas, entre ellas, en la teoría de conjuntos, teoría de nudos, teoría de números, teoría de juegos y códigos. También ha dedicado parte de su trabajo a la matemática recreativa: creador en 1970 del juego de la vida, el juego del drago, el Phutball y ha realizado análisis detallados de otros muchos juegos y problemas, como el cubo Soma. Martin Gardner ha difundido sus trabajos ampliamente en libros y artículos. Actualmente es profesor de matemáticas en la Universidad de Princeton.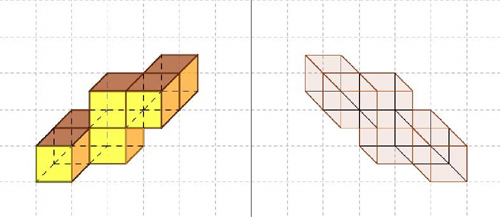
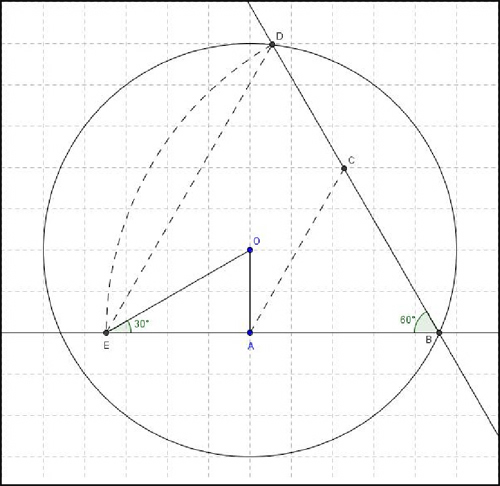 El punto O, por ser el centro de la circunferencia que pasa por B y D, pertenece a la mediatriz del lado DB. Dado que el triángulo ∆EBD es equilátero, la mediatriz coincide con la bisectriz, y por tanto el ángulo ∠OEA = 30º.
El punto O, por ser el centro de la circunferencia que pasa por B y D, pertenece a la mediatriz del lado DB. Dado que el triángulo ∆EBD es equilátero, la mediatriz coincide con la bisectriz, y por tanto el ángulo ∠OEA = 30º.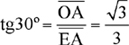
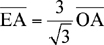
 Cuestión 18ª.-
Cuestión 18ª.-