9. Demostrando

9.1. Pruebas y demostraciones

¿Existe la duda en matemáticas? ¿Es posible darse por satisfecho con una serie de hipótesis cuando éstas se verifican en un 99%?

Las demostraciones constituyen la base de la actividad de los matemáticos y, de hecho, es lo que verdaderamente distingue a la suya de otras actividades.

Las primeras demostraciones eran sencillas, estaban escritas en unas pocas líneas y podía comprenderlas todo aquél que tuviera estudios medios.

Hoy en día, existen demostraciones que ocupan cientos de páginas, para las que hay que hacer uso de ordenadores y de las que sólo pueden emitir un dictamen un reducido grupo de especialistas.

La complejidad del mundo plantea cada vez más preguntas a los matemáticos, que para responderlas deben enunciar conjeturas y demostrar a continuación lo adecuado de las mismas.

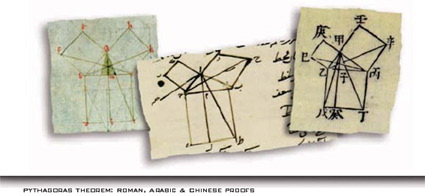
9.2. De Pitágoras a Wiles

¿Cómo demostrar hipótesis que parecen verdaderas? ¿Existen números enteros tales que x² + y² = z²? ¿O tales que xⁿ + yⁿ = zⁿ, cuando n es un entero mayor que 2?

Los griegos fueron los primeros que trataron de resolver estos problemas. Así, Pitágoras dio su nombre al teorema sobre “el cuadrado de la hipotenusa...” del que Euclides formuló la demostración más antigua que se conoce.

Más tarde, Fermat afirmó que este resultado no se podía generalizar. ¡Y Wiles demostró esta conjetura en 1994! Para ello, se sirvió de los últimos trabajos de investigación realizados en áreas muy diversas de las matemáticas.

En general, los matemáticos se esfuerzan en llamar nuestra atención sobre los grandes problemas aún por resolver.

• Pitágoras (siglo VI a. C.)
• Euclides (siglo III a. C.)
• Pierre de Fermat (1601-1665)
• Andrew Wiles (Cambridge, 1953)

9.3. Verdadero... y sin embargo indemostrable

¿Podemos siempre probar una cosa de la que sabemos su veracidad?

En 1931, en un genuino golpe de teatro, Kurt Gödel dio una respuesta negativa a esta pregunta con su famoso teorema de la “incompletitud”.

Gödel demostró que las nociones de verdad y de demostrabilidad no son coincidentes, al descubrir una fórmula sobre números enteros que es verdadera, pero de la que sin embargo no es posible ofrecer una demostración en términos de aritmética elemental.

Para mayor sorpresa de todos, Gödel mostró también, en el mismo espíritu, que en el ámbito de la aritmética no es posible ni refutar ni probar que jamás vaya a llegarse a una contradicción.

La aritmética elemental es además indecidible. Esto implica, por ejemplo, que resulta imposible crear un programa informático capaz de comprobar si una determinada fórmula sobre números enteros es o no verdadera.

• Kurt Gödel (1906-1978)