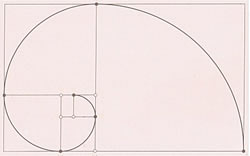
"La espiral es un círculo espiritualizado. En la forma espiral, el círculo, desenrollado, devanado, ha dejado de ser vicioso... La vuelta sigue a la vuelta, y toda síntesis es la tesis de la nueva serie..."
Vladimir Nabokov

La espiral:

La espiral es sin duda la curva más emblemática en la historia de la humanidad. Desde la más remota antigüedad la encontramos en los motivos decorativos de casi todas las culturas.

Sus especiales características la convierten en la curva del crecimiento en la naturaleza. Pero el concepto de espiral ha transcendido los fenómenos naturales para adentrarse también en las actividades sociales.

¿Quién no ha oído o leído en múltiples lugares y ocasiones expresiones del tipo "aprendizaje en espiral" o formación en espiral". Son expresiones que a todos nos sugieren algo similar: acumulación creciente de conocimientos manteniendo la base y la forma inicial.

Como en la Naturaleza, la idea de formación en espiral nos evoca la forma más natural de crecer en nuestro desarrollo.

Una de estas enigmáticas curvas, quizás la más popular, es una curva con mucha historia detrás: la espiral de Durero.

Durante muchos siglos esta curva ha estado asociada con el crecimiento natural de los seres vivos y desde un punto de vista estético con la idea de armonía.

De alguna manera, la espiral de Durero será al mismo tiempo nuestra inspiración y nuestra meta en esta excursión por el fantástico mundo de las espirales.

	1. El Mundo de las Espirales
	2. Espirales en la Naturaleza
	·	2.1. En el Mundo Vegetal
	·	2.2. Fibonacci
	·	2.3. En el Reino Animal
	3. Espirales en Matemáticas
	·	3.1. Espiral de Arquímedes
	·	3.2. Espiral Logarítmica
	·	3.3. Espiral de Durero
	4. Libros y vídeos