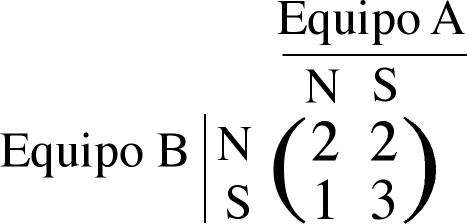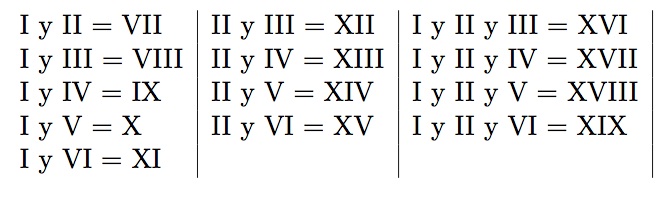Estrategias musicales

1. El conflicto

En esencia, la música es conflicto. El discurso musical progresa a través de la dialéctica entre sus partes. En cualquier pieza de música se observan episodios de tensión combinados con otros de equilibrio. Esa dialéctica generadora del conflicto aparece en varios niveles musicales: en la melodía, en la armonía, en el ritmo, en la conducción de las voces, en la instrumentación y, por supuesto, en la forma. En distintas épocas los estilos musicales predominantes han marcado preferencias sobre la forma de usar el conflicto como motor de la música. Sabemos, por ejemplo, que los conceptos de disonancia y consonancia han ido ensanchándose a lo largo de la historia de la música. En el Barroco un acorde de séptima de dominante, considerado disonante, tenía que resolverse; eso no es tan evidente en la música de principios del siglo XX, donde se aceptan esos acordes con total naturalidad, y aún menos en el jazz. Analicemos la presencia del conflicto con un breve ejemplo tomado de la Pequeña serenata nocturna KV 525, de Mozart. El primer movimiento de esta serenata tiene forma sonata con dos temas que contrastan entre sí. El pasaje que examinamos en la figura 1 en una reducción para piano es el paso del primer tema, en sol mayor, al segundo tema, en re mayor.

Figura 1: Pasaje de la Pequeña serenata nocturna KV 525, de Mozart

Para dar interés musical a ese paso entre los dos temas, Mozart introduce varios elementos de tensión:

• Dinámica (volumen). Obsérvensen los compases 1 y 2, en que hay un sforzando (cambio súbito de volumen), un sf seguido de un piano (p). Al final de compás 3 hay una escala ascendente que tocan los violines en vibrato; esta escala comienza un crescendo (aumento progresivo de volumen) que culmina en el re final del compás 5 tocado en forte (fuerte).
  
  
• Armonía. En los tres primeros compases hay un pedal de tónica. Un pedal es una nota o armonía que se mantiene fija mientras se producen otros cambios armónicos. En este caso es la nota sol sobre la que se alternan los acordes de sol mayor y re mayor. En los compases 3 y 4 aparece la cadencia IV-VII⁶-I para afirma la tonalidad de sol, con el acorde de séptima de dominante incompleto. En el compás 4 se produce la secuencia de acordes V-I en sol, que, sin embargo, es reinterpretada como la secuencia I-V en la nueva tonalidad de re mayor. Esta técnica de cambio de tonalidad (llamada modulación en el lenguaje musical) se llama del acorde pivote y consiste en usar acordes comunes a dos tonalidades para modular. Al entrar en la nueva tonalidad Mozart usa de nuevo la cadencia IV-VII⁶-I (compases 4 y 5) y un pedal de tónica V⁷/I (compases 5 y 6). En los compases 8 y 9 se oye la secuencia II₅⁶-V₅⁶ del V-V, que no es sino una afirmación del quinto grado de re (el la) por medio de dominantes secundarias. La secuencia desemboca en una cadencia rota con un pedal de dominante.
  
  
• En los compases 1 y 2 el ritmo es relativamente sencillo, con las notas sobre las partes fuertes de la métrica. En los compases 5 y 6 el ritmo se agita más al aparecer combinaciones de negras y corcheas ambas con puntillo. Finalmente, en los compases 7 y 8 las voces superiores hacen una síncopa (contradicción momentánea de la métrica establecida), que es además un pedal de la nueva tónica. En el compás 8 Mozart añade sutilmente un mi, que forma un intervalo disonante de segunda mayor con el re del pedal, y que sirve de apoyo a la progresión II₅⁶-V₅⁶ del V. En el compás 9 la síncopa se resuelve así como la disonancia y la melodía vuelve a una figuración de corcheas sobre las partes fuertes.

Con este pequeño ejemplo se ve cómo opera el conflicto en varios niveles musicales. Las ideas musicales del compositor se plasman en la partitura, de la cual director e instrumentistas extraen la información necesaria para mostrar la música y sus conflictos internos. Xenakis reflexionó sobre el conflicto interno en la música, sobre todo a finales de los 50 y a principios de los 60. También reparó en que durante la ejecución de la obra musical emerge otro tipo de conflicto: el de la propia ejecución. En efecto, existe también una dialéctica entre partitura e intérprete. En ambos tipos de conflicto -indagaba Xenakis- no hay margen para la improvisación. Por un lado, el compositor ha fijado, hasta donde le permite la notación musical, sus ideas musicales, reveladas a través de la dialéctica de los elementos musicales; y éstos, por otro lado, determinan el conflicto partitura versus interpretación. En todo caso, es siempre un conflicto interno. Xenakis llamó a la música caracterizada por estos conflictos internos música autónoma. Incluso en la música estocástica, aunque goce de más margen de maniobra, las tensiones siguen confinadas a la partitura. Xenakis quería superar la música autónoma y experimentar con música que no solo poseyera ese carácter interno. Introduce, pues, el concepto de conflicto externo [Xen01], página 111):

"Sería interesante y probablemente fructífero imaginar otra clase de discurso musical, el cual introdujese el concepto de conflicto exterior entre, por ejemplo, dos orquestas o instrumentistas contrarios".

Su formación matemática y su creatividad musical le señalaron el camino una vez más. Imaginó la superación de la premisa del conflicto interno vía la teoría de juegos. En teoría de juegos tenemos dos jugadores que juegan por turnos y que siguen ciertas estrategias para ganar el juego. Xenakis pensó en dos orquestas compitiendo entre sí en un juego finito de suma cero. Cada orquesta dispondría de ciertas tácticas sonoras y los directores de las orquestas jugarían en función de lo que escuchan. En la siguiente sección explicamos algunos conceptos sencillos de teoría de juegos que nos ayudarán a entender la música de Xenakis que analizamos en el artículo de hoy.

2. Teoría de juegos

La Teoría de Juegos es una disciplina matemática de pleno derecho (clasificación AMS: 90D). Su objetivo es el estudio de la estrategia para ganar en juegos modelizados matemáticamente. Esta definición, si bien general, se adapta con versatilidad a varios y dispares campos de aplicación. Con particular éxito, la teoría de juegos se ha usado en Economía para estudiar desde la competitividad en el mercado hasta la distribución de la riqueza. Podemos encontrar aplicaciones de la teoría de juegos en la Biología (problemas de equilibrio ecológico), en el diseño de acciones militares, en Sociología o en Ciencias Políticas (sistemas de votación), en Filosofía (para estudiar el concepto de convención) y, por supuesto, en Informática. Aquí nos contentaremos con introducir unas cuantas definiciones básicas para entender las ideas musicales de Xenakis. Para profundizar más en este fascinante tema se remite al lector a [Pet08] y a sus referencias bibliográficas. Empezaremos con un ejemplo. Dos equipos de exploradores, llamémosles A y B, tienen que someterse a una prueba. El equipo A tiene que ir desde el campamento este al campamento oeste y para ello tienen dos rutas disponibles, por el norte que se tarda 2 días, y por el sur que se tarda 3 días. El equipo A sale primero y unas horas más tarde, el equipo B, cuya misión es rastrear y dar alcance al equipo A. El equipo B desconoce qué ruta tomará el equipo A. Si el equipo B toma la ruta equivocada, puede regresar al campamento este y desde allí tomar la otra ruta. Ese error, no obstante, le cuesta al equipo B un día de retraso en la persecución del equipo A. La prueba se puede modelizar como un juego de dos personas, los equipos A y B, que compiten entre sí. La siguiente matriz modeliza matemáticamente el juego (figura 2):

Figura 2: Matriz de un juego.

La matriz se interpreta como sigue:

• Las elecciones de la ruta del equipo B se leen por filas.
  
  
• Las elecciones de la ruta del equipo A se leen por columnas.
  
  
• Las elecciones que hace cada equipo son independientes entre sí y se hacen simultáneamente.
  
  
• Los números de la matriz se leen como el pago que el equipo A hace al equipo B. Esta es una convención habitual en teoría de juegos.

¿Cuál es la estrategia ganadora para este juego? Si el equipo A elige la ruta norte, tendrá 1 o 2 días de persecución; en cambio, yendo por el sur dicho número de días sube a 2 o 3. En cuanto al equipo B, si elige la ruta por el norte siempre dispondrá de 2 días de persecución independientemente de la elección del equipo A. Por tanto, ambos equipos eligen la ruta norte. El lector quizás se haya dado cuenta de que la combinación norte-norte es máxima en su columna (2 1) y mínima en la fila (2 2). Una posición en la matriz para la que ocurre esto se llama punto de silla (equilibrio de Nash). También se observa que en el punto de silla el equipo B maximiza el pago mínimo recibido y el equipo A minimiza el pago máximo entregado. Este tipo de juegos se llama juego de suma cero porque la cantidad que recibe un jugador es igual a la que pierde el otro jugador para cualquier estrategia.

3. La Teoría de Juegos en la música de Xenakis

Las obras más emblemáticas en las que Xenakis usó la teoría de juegos son Duel(1959) y Stratégie (1962). Analizaremos esta última para ilustrar la materialización de las ideas de Xenakis. Stratégie (1962) es una obra para dos orquestas, cada una con su propio director. Las orquestas se colocan una enfrenta de la otra, con los directores dándose la espalda. Los directores disponen de seis construcciones sonoras, como las llama Xenakis, de naturaleza estocástica (véase el artículo anterior de esta serie), numeradas del I al VI. Estas construcciones estocásticas se calcularon con la ayuda de un ordenador IBM 7090. Las construcciones sonoras son las partes constitutivas de las tácticas del juego, que son las siguientes:

I.- Instrumentos de viento (madera y metal).

II.- Instrumentos de percusión.

III.- Toques con la mano en la caja de resonancia de los instrumentos de cuerda.

IV.- Efectos puntillistas con los instrumentos de cuerda.

V.- Glissandi con los instrumentos de cuerda.

VI.- Armonías continuas tocadas por los instrumentos de cuerda

A cada director se le permite ejecutar dos o tres tácticas simultáneamente, pero Xenakis determina la compatibilidad entre ellas en la siguiente tabla:

En total, hay 19 tácticas: 6 tácticas formadas por una única construcción sonora (I a VI), 9 formadas por dos construcciones (VII a XV) y 4 formadas por tres construcciones (XVI a XIX). Por tanto, en cada turno los directores pueden tocar una de las 19²=361 posibles combinaciones de tácticas.

La pieza Stratégie se concibe como la ejecución de un juego finito de suma cero para dos personas. Las reglas son las siguientes:

1. Elección de las tácticas. Aunque Xenakis ofrece varios sistemas para elegir las tácticas (véase la página 23 de [Xen01]), aquí describiremos solo uno de ellos, el sistema de elección arbitraria. Consiste en que cada director elige su táctica en función de su propio gusto musical y de la táctica que ha elegido el otro director.
   
   
2. Matriz del juego. Hay una matriz que contiene los pagos para cada posible táctica. Esta matriz está delante de los directores durante la ejecución de la pieza. En la figura 3 tenemos dicha matriz (la matriz está tomada del libro de Xenakis [Xen01], página 128).

   
   
   Figura 3: Matriz del juego de la obra Stratégie.

   Los símbolos que aparecen a los lados de la matriz son iconos para ayudar al director a reconocer las cualidades sonoras de cada táctica. Xenakis introdujo dos matrices auxiliares para simplificar la lectura de la matriz principal durante la ejecución de la pieza.
   
   
3. Duración de los turnos. Los turnos tendrán una duración mínima de 10 segundos. No habrá duración máxima.
   
   
4. Duración del juego. Los directores acordarán jugar un número fijo de turnos.
   
   
5. Obtención de los puntos. De nuevo, Xenakis ofrece varias posibilidades. Una de ellas es tener un árbitro que cuente los puntos obtenidos en cada turno.
   
   
6. Lectura de las tácticas. Las orquestas tocan las tácticas de manera cíclica hasta que reciban la señal de parar por parte del director. El director puede empezar una táctica en ciertos puntos que se encuentran marcados en la partitura con letras. El director indica el número de táctica y la letra con unas tarjetas que muestra a la orquesta.
   
   
7. Resultado. Al cabo de los turnos establecidos se termina la pieza y se hace el recuento de los puntos de cada director. Gana quien más puntos haya obtenido.
   
   

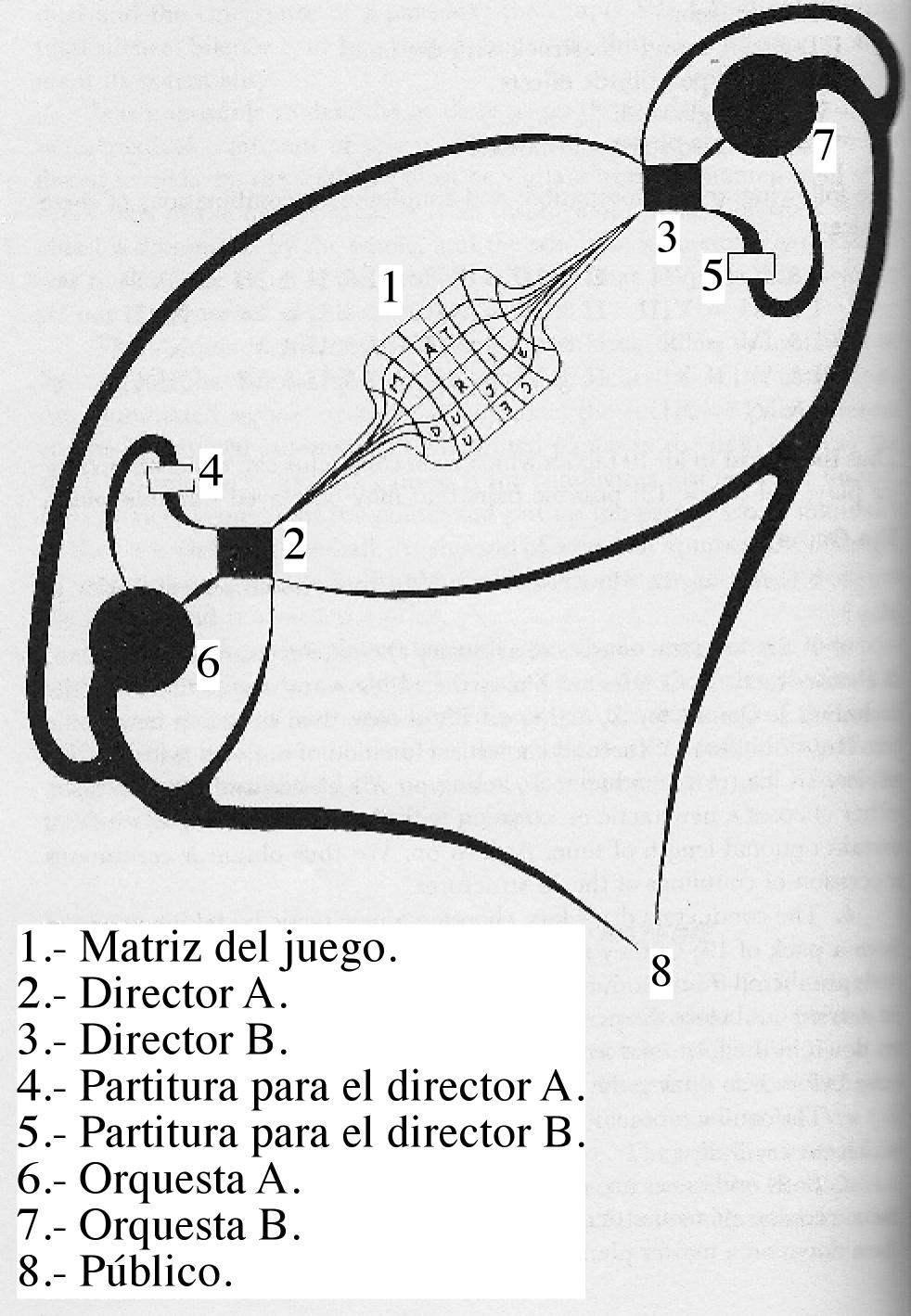
En la figura 4 vemos un gráfico de Xenakis durante la concepción de Xenakis.

Figura 4: Disposición de la orquesta en Stratégie ([Xen01]).

Para terminar gozosamente esta sección, dejamos aquí dos vídeos con la música de Stratégie:

Parte 1.

Parte 2.

4. Conclusiones

Xenakis transcendió el concepto de conflicto interno forzando a que el conflicto alcanzara al director de orquesta. Tomó dos orquestas y las puso a competir musicalmente sobre la base de un juego finito de suma cero para dos personas. Así, Xenakis expande los fundamentos matemáticos de la música en todas sus dimensiones: alturas y escalas, ritmo, timbre, forma y en esta ocasión también la naturaleza de la propia dialéctica musical. Al contrario de la mayoría de los músicos, Xenakis estaba al tanto de los nuevos avances en ciencia y tecnología. Este conocimiento alimentaba su imaginación y sus teorías musicales.

5. Para saber más

1. El capítulo 2 del libro de Curtis Roads [Roa04] es un análisis del concepto de microsonido. Examina la obra de varios compositores que han usado este concepto, entre ellos, Xenakis.
   
   
2. Ton de Leeuw analiza en su libro Music of the Twentieth Century: a Study of its Elements and Structure [dL06] la música del siglo XX desde un punto de vista estructural e incluye a Xenakis en dicho análisis.
   
   
3. El libro de Dutta [Dut99], profesor del MIT, es un texto clásico que explica la teoría de juegos para estudiantes de ciencias económicas.
   
   
4. Para una referencia de teoría de juegos desde un punto de vista algorítmico pero todavía abstracto, véase [NRÉTV10].
   
   
5. Para ver una cronología de la teoría de juegos, que se remonta a los babilonios y que en nuestros días cuenta con premios Nobel, véase la página web de Paul Walker [Wal10].
   
   
6. La página Les amis de Xenakis [Xen10] contiene información completa sobre su vida, su obra, así como la posibilidad de escuchar fragmentos de su obra.
   
   

Bibliografía

[dL06]

Ton de Leeuw. Music of the Twentieth Century. Amsterdam University Press, 2006.

[Dut99]

Prajit K. Dutta. Strategies and games: theory and practice. The MIT Press, 1999.

[NRÉTV10]

Noam Nisan, Tim Roughgarden, Éva Tardos, and Vijay Vaziraini. Algorithmic game theory. http://www.cambridge.org/journals/nisan/downloads/Nisan_Non-printable.pdf Accedido en octubre de 2010.

[Pet08]

Hans Peters. Game Theory. Springer, 2008.

[Roa04]

Curtis Roads. Microsound. The MIT Press, 2004.

[Wal10]

Paul Walker. A chronology of game theory. http://www.econ.canterbury.ac.nz/personal_pages/paul_walker/gt/hist.htm Accedido en octubre de 2010.

[Xen01]

Iannis Xenakis. Formalized Music: Thought and Mathematics in Composition. Number 6 in Harmonologia. Pendragon Press, Hillsdale, NY, 2001.

[Xen10]

Xenakis.org. Les amis de Xenakis. http://www.iannis-xenakis.org/ Accedido en 2010.