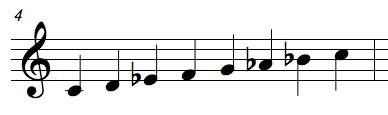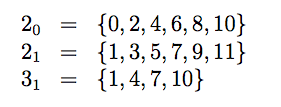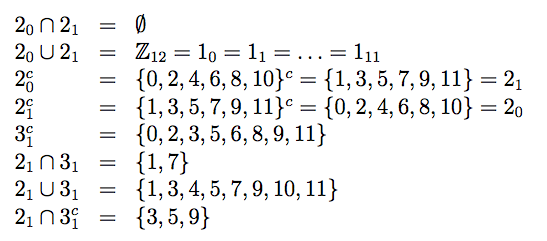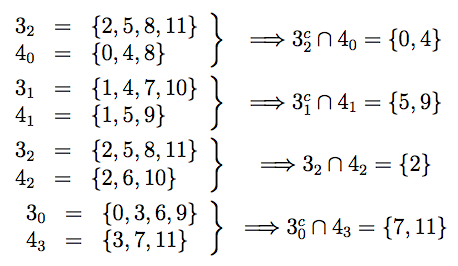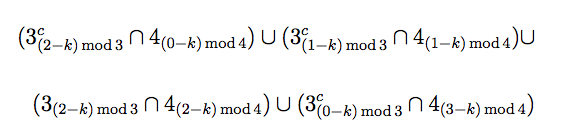1. Introducción

Xenakis fue una persona polifacética, con una gran capacidad analítica y sintética, así como una desbordante creatividad. No solo fue un compositor excepcional en cuanto que introdujo principios matemáticos en la composición musical, dando lugar así a una de las síntesis más fascinantes de la música contemporánea, sino que siempre tuvo una gran preocupación por las cuestiones teóricas, bien en el análisis musical bien en la invención de nuevos principios compositivos. Este es el último artículo de una serie de tres dedicado a Xenakis justo antes del décimo aniversario de su muerte acaecida en febrero de 2001. En este artículo, más que analizar un principio matemático que Xenakis transformó en una principio compositivo, examinaremos algunas ideas suyas que inciden más en su faceta de teórico de la música. Xenakis usó las matemáticas también como una herramienta de análisis musical, especialmente para la música del siglo XX que más radicalmente se apartaba de la tradición tonal, armónica y métrica. Siguiendo la naturaleza universal, sistematizadora, unificadora, abstracta y al tiempo analítica de las matemáticas, Xenakis estudiaba fenómenos musicales bajo la lupa de esa asombrosa disciplina. Husmeaba estructuras comunes a varios objetos musicales, reconocía qué peculiaridades se podían identificar entre los fenómenos musicales y los matemáticos, fijaba qué operaciones eran relevantes entre ellos y, finalmente, soldaba pródigamente las piezas para erigir su edificio conceptual. Cierto es que con frecuencia sus teorías no están descritas con todo detalle, pero ello no es signo de negligencia o de falta de profundidad intelectual. Xenakis seguramente dejaba esa labor para que otros teóricos de la música la completaran, pues siempre tenía la tensión de la composición sobre sí. La teoría de cribas, expuesta en su libro Formalized Music [Xen01] entre otros escritos, se ocupa de la teoría de escalas desde un punto de vista bastante general. Aquí la palabra criba puede usarse en el sentido de la criba de Eratóstenes, el procedimiento para calcular los primos tachando múltiplos sucesivos o bien en un sentido más general, como técnicas de teoría de números para contar o estimar el tamaño de conjuntos de números [Mol09] [Har07]. Xenakis usa la palabra en un sentido más bien arcaizante y, como veremos, tiene más que ver con el primer sentido, con la idea de saltar de múltiplo en múltiplo de un número dado. En el fondo las matemáticas que usa son la aritmética modular y la teoría de conjuntos. El empeño que acometió Xenakis fue el de construir una teoría de escalas que comprendiese las escalas de más de 12 notas, esto es, escalas definidas en divisiones no iguales de la octava. En la siguiente sección recordaremos algunos conceptos de la teoría de escalas. En la tercera sección expondremos los principios básicos de la teoría de cribas de Xenakis aplicada a la teoría de escalas. En la cuarta sección examinaremos algunas consecuencias de esa aplicación.

2.  Escalas musicales

El primer fenómeno musical al que querríamos referirnos es el de la llamada equivalencia perceptual de la octava. El hecho de que dos tonos que están separados por una octava se perciban como equivalente perceptualmente está bastante aceptado (véase [Deu98] y sus referencias para una explicación general y [DB84] para detalles más técnicos). Dos tonos están separados por una octava si la proporción entre la frecuencia del más agudo y el más grave es 2:1. Esta equivalencia está implícita en la construcción de escalas que se encuentran en muchas tradiciones musicales, y no solo en la occidental. Como ejemplo, tenemos abajo una melodía, el comienzo de la Pequeña serenata nocturna de Mozart. Si se pincha en la imagen, se oye la melodía:

Figura 1: Comienzo de la Pequeña serenata nocturna KV 525, de Mozart.

Si la trasladamos la melodía una octava arriba (pínchese en la imagen para oír la nueva melodía):

Figura 2: La misma melodía pero tocada una octava arriba.

Nos parece mucho más similar que si la oímos, por ejemplo, una cuarta aumentada más arriba (pínchese en la imagen):

Figura 3: La misma melodía ahora tocada una cuarta aumentada más arriba.

Para construir una escala la octava se subdivide en un número fijo de notas y se elige un subconjunto de estas notas como la escala. La elección de las notas en que se divide la octava se llama afinación. A veces una afinación se ajusta por motivos musicales, fundamentalmente para eliminar disonancias en las modulaciones, y entonces a ese ajuste se le llama temperamento. Tras un proceso largo y no exento de dificultades [Gol92], en la música occidental se adoptó la subdivisión de la octava en 12 partes iguales, llamada temperamento igual. Cada parte de la subdivisión se llama un semitono y un tono está formado por dos semitonos. Las escalas más importantes en la música occidental son la escala mayor y la escala menor natural. La escala mayor, si la recitamos desde un do, se compone de las notas {do, re, mi, fa, sol, la, si}.

Figura 4: La escala mayor.

Si nombramos las notas de esta escala mediante el número de semitonos que componen cada nota, entonces tendríamos el conjunto {0, 2, 4, 5, 7, 9, 11}, donde el 0 corresponde a la nota do. La escala menor enunciada a partir de do es {do, re, mi♭, fa, sol, la♭, si♭, } y descrita numéricamente es {0, 2, 3, 5, 7, 8, 10}.

Figura 5: La escala menor natural.

Hay dos variantes importantes de la escala menor natural, llamadas escala menor melódica y menor armónica, aparecen en las dos primersa líneas de la tabla 1. En esa misma tabla podemos observar otras escalas con distintos intervalos y número de notas. Por ejemplo, la escala que se compone de todas las notas posibles dentro de la octava se llama cromática y su descripción numérica es {0, 1, 2, 3, 4, 5, 6, 7, , 8, 9, 10, 11}. La escala que salta por tonos enteros, y que Debussy popularizó, se escribe como {0, 2, 4, 6, 8, 10}. La escala octotónica, de ocho notas, que se forma alternando un tono y un semitono. Con este esquema de alternación salen dos escalas {0, 2, 3, 5, 6, 8, 9, 11} y {0, 1, 3, 4, 6, 7, 9, 10} (escalas octotónica I y II, respectivamente, en la tabla 1). Stravinsky usó este tipo de escala en su obra La consagración de la primavera. Otras escalas muy frecuente en muchas y diversas tradiciones musicales son las pentatónicas, esto es, las formadas por cinco notas. En la tabla de abajo mostramos la pentatónica mayor ({0, 2, 4, 7, 9}) y la pentatónica menor ({0, 3, 5, 7, 10}).

Tabla 1: Distintas escalas musicales basadas en la subdivisión de la octava en 12 partes.

Hay que advertir aquí que las escalas que se muestran en la tabla 1 aparecen en otras muchas tradiciones musicales con diferentes nombres. Hemos elegido un nombre únicamente por facilidad de referencia. Una escala dada se puede nombrar cíclicamente a partir de una nota suya cualquiera y da lugar así a otra escala. Las reordenaciones de una escala se llaman modos. Por ejemplo, la escala mayor {0, 2, 4, 5, 7, 9, 11}, cuando se enuncia a partir de la sexta nota (un la o el semitono 9), resulta la escala {9, 11, 12, 14, 16, 17, 19}; esta escala llevada al do inicial de nuevo, restándole 9 semitonos, da la escala menor natural {0, 2, 3, 5, 7, 8, 10}. Así que la escala menor natural es un modo de la escala mayor. Véase [Har01] para una buena introducción a la teoría musical y en particular a los modos. En otras tradiciones musicales la octava no se divide en 12 partes iguales, sino que ésta sufre divisiones más finas. El sistema tonal árabe moderno usa una subdivisión de la octava en 24 partes iguales. En otras palabras, la unidad tonal básica es el cuarto de tono. En la música clásica del sur de la India, la música carnática, usan una subdivisión en 22 partes. En la música del gamelán de Java también se usan afinaciones con más de 12 partes por octava y además estas partes no son de igual tamaño. Los temperamentos anteriores al temperamento igual tenían asimismo intervalos menores que el semitono (la afinación justa o el temperamento mesotónico; véase [Gol92]). En la Grecia clásica también se encuentran afinaciones con subdivisiones muy finas de la octava. Aristóxenes propone una afinación con 72 subdivisiones de la octava.

3. Teoría de cribas

Como dijimos en la introducción, Xenakis usó la aritmética modular para dar una teoría general de la construcción de escalas bajo divisiones iguales de la octava. Superaba así el temperamento igual de 12 subdivisiones. Consideró escalas que se podían construir con cualquier unidad: semitonos temperados (1/12 de octava), segmentos de Aristóxenes (doceavos de un tono), cuartos de tono, tonos enteros, segundas, terceras, cuartas y quintas. Por completitud en la exposición, repasaremos brevemente algunos conceptos básicos de la aritmética modular. Sea n un entero al que llamaremos módulo. Dados dos enteros x e y, se dice que x es congruente con y módulo n si x-y es divisible por n. La relación de congruencia es una relación de equivalencia, esto es, es reflexiva, simétrica y transitiva (es muy fácil de probar). Como tal relación de equivalencia tiene un conjunto cociente. Fijado un módulo n y dado un entero x, su clase de equivalencia está formada por el conjunto:

Las clases de equivalencia identifican aquellos elementos separados por un múltiplo entero del módulo y sirven para trabajar con operaciones cíclicas. El conjunto de clases de equivalencia módulo n se designa por . Fijado un módulo n y un entero a, una criba elemental es una aplicación afín discreta en , dada por:

Por ejemplo, si n=12, el caso del temperamento igual, entonces 2₀ = {0, 2, 4, 6, 8, 10}, donde los números entre llaves han de interpretarse como clases de equivalencia. Si escogemos un número que es primo relativo con 12, por conocidas propiedades de la aritmética modular, obtenemos el conjunto entero . Tomemos, a=2 y x=5, por ejemplo:

Una criba compuesta es un conjunto de clases que se obtiene tomando uniones e intersecciones finitas y complementarios de cribas elementales. Si seguimos en el universo de los doce semitonos iguales y tomamos las siguientes cribas elementales:

entonces podemos generar cribas compuestas como sigue:

La escala cromática, la que comprende todos los semitonos de la octava, se expresa como la criba elemental 1₀. La escala de tonos enteros se escribe como 2₀. ¿Cómo se escribiría la escala mayor? Esta escala no se puede escribir como una criba elemental, pues sus notas no están dispuestas regularmente en la octava. La escala mayor se expresa como la siguiente criba compuesta:

Comprobemos que es así. Por un lado tenemos:

Haciendo la unión de las intersecciones resultantes sale la escala mayor {0, 2, 4, 5, 7, 9, 11}. Anteriormente, afirmamos que la escala menor es un modo de la escala mayor. Basta enunciar la escala mayor a partir de la nota la para obtener la escala menor. La correspondiente criba compuesta para esa escala es:

Dejamos al lector los cálculos, que son directos y fáciles. ¿Hay alguna relación entre la criba de una escala mayor y cualquiera de sus modos? Sí, y no es muy difícil darse cuenta de que es un juego de índices y módulos. Si queremos generar la criba del modo de una escala mayor a k semitonos de distancia, ésta es:

Los índices de las cribas elementales generadas por las terceras menores aumentan módulo 3, mientras que las cribas de las cuartas lo hacen módulo 4. Si consideramos una subdivisión de la octava en cuartos de tono, entonces la criba asociada con la escala mayor es:

donde k=0,1,..., 23 se toman módulo 3 u 8, según el caso. Las cribas de Xenakis pueden describir de manera relativamente concisa escalas de distintos temperamentos iguales, como la división de Aristóxenes e incluso escalas mixtas, como la bizantina, que mezcla tetracordos cromáticos y diatónicos (véase [Xen01], páginas 197 y siguientes).

4. Conclusiones

Esperamos que con estos pequeños ejemplos haber ilustrado las ideas teóricas de Xenakis. La idea de las cribas resultó atractiva a varios teóricos y analistas de la música, los cuales incluso la llevaron incluso más lejos. En particular, ha encontrado fervientes partidarios en el análisis transformacional de David Lewin. Thomas Noll y sus coautores [NAA06] aplican la teoría de cribas al análisis del estudio para piano opus 63, número 5, de Scriabin. El análisis es exitoso pues ese estudio de Scriabin usa escalas de tonos enteros y octotónicos, que se describen con facilidad con cribas. Varios autores importantes han dedicado artículos a la teoría de cribas, bien desde un punto de vista filosófico o desde un punto de vista puramente analítico. Jones [Jon01] sistematiza las cribas y formaliza ciertos aspectos algorítmicos de la formulación inicial de Xenakis. Exarchos [Exa07] aborda la generalización de las cribas a otros paramétros musicales. Harley, en su libro Xenakis: His Life in Music, dedica un capítulo a las cribas y sus implicaciones musicales en la obra de Xenakis.

Como no podía ser de otro modo, Xenakis empleó las cribas en sus composiciones musicales. Una de las primeras obras en que las probó fue Nomos Alpha, para violonchelo solo. Aparte de las cribas usa otras ideas matemáticas, como grupos de simetrías y lógica proposicional. Para un análisis exhaustivo y clarificador, véase el excelente artículo de Jan Vriend [Vri81]. En el vídeo de más abajo se puede oír esta pieza por el excelente percusionista Steve Schick.

5. Para saber más

Referencias

[DB84]

Diana Deutsch and Richard Boulanger. Octave equivalence and the immediate recall of pitch sequences. Music Perception, 2(1):41-53, 1984.

[Deu98]

Diana Deutsch. The Psychology of Music. Academic Press, second edition edition, 1998.

[Exa07]

Dimitri Exarchos. Injecting periodicities: Sieves as timbres. In Proceedings SMC'07, 4th Sound and Music Computing Conference, 2007.

[Gol92]

Javier Goldaraz. Afinacion y temperamento en la musica occidental. Alianza, 1992.

[Har01]

Jonathan Harnum. Basic Music Theory: How to Read, Write, and Understand Written Music. Questions Ink. Publishing, 2001.

[Har07]

Glyn Harmann. Prime-Detecting Sieves. (London Mathematical Society Monographs). Princeton University Press, 2007.

[Jon01]

Eva Jones. Residue-class sets in the music of iannis xenakis: an analitical algorithm and a general intervalic expression. Perspectives of New Music, 39(2):229-261, 2001.

[Mol09]

Richard Mollin. Advanced Number Theory with Applications. Chapman and Hall/CRC, 2009.

[NAA06]

Thomas Noll, Moreno Andreatta, and Carlos Agon. Computer-aided transformational analysis with tone sieves. In SMC 06, 2006.

[Pre83]

Jeff Pressing. Cognitive isomorphisms between pitch and rhythm in world musics: West Africa, the Balkans and Western tonality. Studies in Music, 17:38-61, 1983.

[Slo75]

Nicolas Slonimsky. Thesaurus Of Scales And Melodic Patterns. Music Sales America, 1975.

[Vri81]

Jan Vriend. Nomos Alpha for violoncello solo (xenakis 1966) analysis and comments. Journal of New Music Research, 10:15-82, 1981.

[Xen01]

Iannis Xenakis. Formalized Music: Thought and Mathematics in Composition. Number 6 in Harmonologia. Pendragon Press, Hillsdale, NY, 2001.

[Yam06]

Masaya Yamaguchi. The Complete Thesaurus of Musical Scales. Masaya Music, 2006.