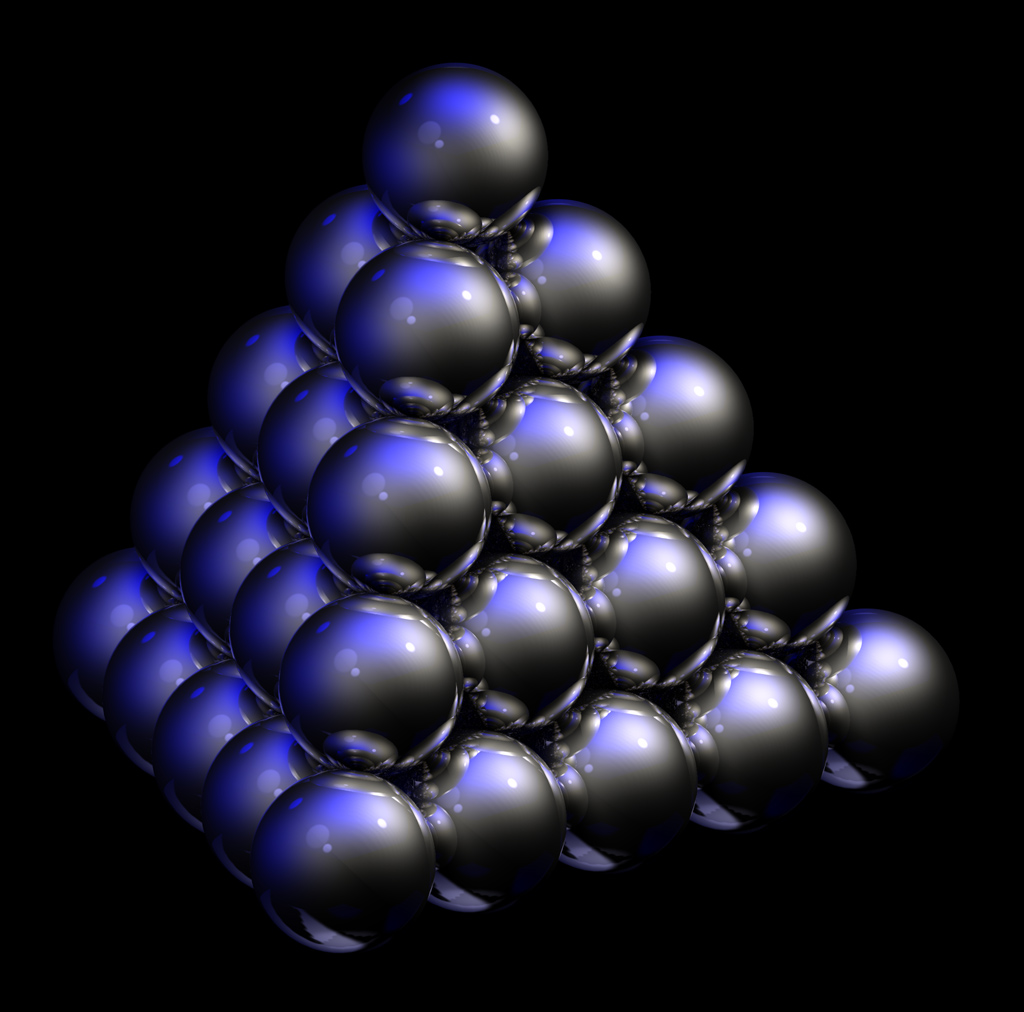
Alguna información más sobre E8:

Daremos solo algunos datos básicos, sin entrar en la teoría de grupos de Lie, ni la aplicaciones importantes que tiene el grupo de Lie asociado, E8, en una propuesta para la teoría del todo en Física matemática.

El politopo E8 vive en el espacio 8-dimensional R⁸.  La figura que hemos construido con hilos es una proyección sobre el llamado plano de Coxeter, un plano en el que se ven los 240 vértices y se aprecia una simetría rotacional de orden 30.

Los 240 vértices son, por un lado, de la forma (±1, ±1, 0, 0, 0, 0, 0, 0) y todas sus permutaciones, en total ,  y por otro lado, de la forma  (±1/2, ±1/2, ±1/2, ±1/2, ±1/2, ±1/2, ±1/2, ±1/2) con un número par de coordenadas negativas, lo que da 2⁸/2 = 128.

Cada vértice está unido a los otros 56 más cercanos, situados a distancia √2, lo que da 56 x 240/2 = 6720 aristas. En la proyección sobre el plano de Coxeter, muchas de estas aristas se solapan con otras. Por ejemplo, podéis observar que de cada vértice de la corona exterior salen 28 aristas. En breve colgaremos un programa de Mathematica para dibujarlas.

Todos los vértices viven en la esfera 7-dimensional de radio √2, definida por la ecuación

x₁² + x₂² + x₃² + x₄² + x₅² + x₆² + x₇² + x₈² = 2

Si en cada uno de los 240 vértices centramos otra esfera 7-dimensional de radio √2/2 obtenemos una configuración que da la solución al llamado “kissing number” en dimensión 8:  Es decir, 240  es el mayor número de esferas que podemos colocar “besando” o siendo tangente a una central.  Por otro lado, el retículo que genera esta configuración en R⁸ proporciona también el empaquetamiento (o apilamiento) más denso de esferas.

Apilamiento más denso de 2-esferas. Fuente: wikipedia

Algunos enlaces y referencias:

• “Regular polytopes” by H.S.M. Coxeter (1973).
• Más sobre el  politopo E8, en wikipedia.
• Sobre el grupo de Lie excepcional E8, en wikipedia.
• Sobre planos de Coxeter en la página de  John Stembridge.
• Cien años de E8, por Jaume Aguadé. Aquí explica, entre otras muchas cosas, como usar el retículo de E8 para enviar información empaquetada de forma eficiente, a través de un modem, por ejemplo. Podéis leer también el artículo ampliado en catalán.
• Sobre empaquetamiento de esferas, en wikipedia.
• Atlas de grupos de Lie y sus representaciones

Para más información: http://topologia.wordpress.com/2010/10/10/e8-con-hilo-tensado/