Septiembre 2011: Hilorama de E8
Septiembre 2011: Hilorama de E8 |
 |
 |
 |
| Viernes 23 de Septiembre de 2011 | |||||||
Nuestro más sincero agradecimiento a los autores de esta exposición por permitirnos incluirla dentro de las exposiciones virtuales de DivulgaMAT y que todos podamos disfrutar de su contenido. Fue Peter McMullen quien hacia 1960 dibujó a mano esta maravillosa representación del politopo de Gosset 4_21 (descrito en 1900). Se le nombra a menudo también como politopo E8 por tener como vértices el sistema de raices del grupo de Lie excepcional E8. Más recientemente, John Stembridge dió la primera imagen por ordenador, de donde nos hemos inspirado para reproducirlo aquí con hilos de colores. Este politopo vive en un espacio de 8 dimensiones. Su 1-esqueleto consta de 240 vértices y 6720 aristas, aunque no todas se ven en la figura plana pues se solapan unas con otras (al final del artículo damos más detalles). Para visualizar este tipo de objetos multidimensionales se suele estudiar sus proyecciones planas. La que aquí mostramos es sin duda una de la más bellas pues se ven todos los vértices. Se distribuyen en 8 coronas concéntricas de 30 vértices cada una, donde los vértices de cada corona están conectados entre sí por lineas rectas, excepto los diametralmente opuestos. Nuestra construcción con hilos: A continuación ilustramos una a una las 8 fases de su construcción con hilos de colores. Bajo la imagen de cada foto encontraréis una combinación de 14 números, donde cada número del 1 al 8 indica un color distinto. La combinación nos indica el color de las aristas que concurren en un vértice al conectarse con el resto de vértices de su corona, cuando las recorremos en sentido de las agujas del reloj (o al revés). Observar que basta indicar los 14 primeros, pues el de la posición 15 no tiene arista (es el opuesto), y del 16 al 29 se repite la combinación al revés, por simetría. Así, por ejemplo, en la fase 5, uniremos los vértices en las posiciones en las que aparezca el color 5, que son la 2, 5, 7, 9, 11, 12 y 14 posición. Saber esto facilita mucho el trabajo, por si alguien se anima a repetirlo. Se puede tardar unas 10 horas sin pausa, aunque la verdad es que merece la pena pararse y contemplar cada una de las fases. Alguna información más sobre E8: Daremos solo algunos datos básicos, sin entrar en la teoría de grupos de Lie, ni la aplicaciones importantes que tiene el grupo de Lie asociado, E8, en una propuesta para la teoría del todo en Física matemática. El politopo E8 vive en el espacio 8-dimensional R8. La figura que hemos construido con hilos es una proyección sobre el llamado plano de Coxeter, un plano en el que se ven los 240 vértices y se aprecia una simetría rotacional de orden 30. Los 240 vértices son, por un lado, de la forma (±1, ±1, 0, 0, 0, 0, 0, 0) y todas sus permutaciones, en total Cada vértice está unido a los otros 56 más cercanos, situados a distancia √2, lo que da 56 x 240/2 = 6720 aristas. En la proyección sobre el plano de Coxeter, muchas de estas aristas se solapan con otras. Por ejemplo, podéis observar que de cada vértice de la corona exterior salen 28 aristas. En breve colgaremos un programa de Mathematica para dibujarlas. Todos los vértices viven en la esfera 7-dimensional de radio √2, definida por la ecuación x12 + x22 + x32 + x42 + x52 + x62 + x72 + x82 = 2 Si en cada uno de los 240 vértices centramos otra esfera 7-dimensional de radio √2/2 obtenemos una configuración que da la solución al llamado “kissing number” en dimensión 8: Es decir, 240 es el mayor número de esferas que podemos colocar “besando” o siendo tangente a una central. Por otro lado, el retículo que genera esta configuración en R8 proporciona también el empaquetamiento (o apilamiento) más denso de esferas.
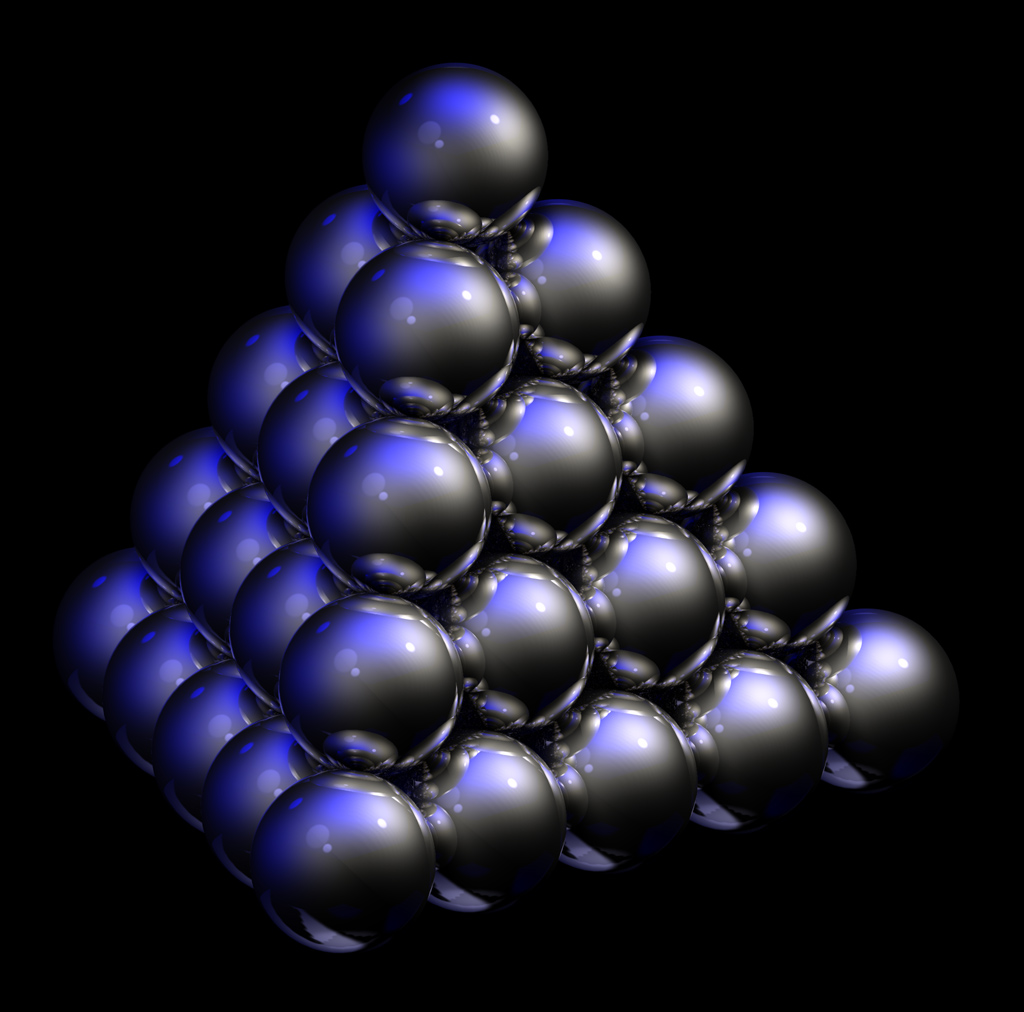
Apilamiento más denso de 2-esferas. Fuente: wikipedia Algunos enlaces y referencias:
Para más información: http://topologia.wordpress.com/2010/10/10/e8-con-hilo-tensado/ |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |