El teorema chino de los restos

Dos números enteros a y b son congruentes respecto de otro entero m si su diferencia es múltiplo de m (o si dan idéntico resto al ser divididos entre m). Esto se escribe así: a ≡ b (mod m). El menor número congruente con a respecto de m se llama el resto de a en relación a m, y es justamente el resto de dividir a por m. Las congruencias mantienen las operaciones aritméticas, de modo que si a ≡ b (mod m) y c ≡ d (mod m), entonces a + c ≡ b + d (mod m) y ac ≡ bd (mod m). La idea de número congruente no fue claramente definida hasta el  siglo XVIII, pero fue utilizado desde mucho antes. Supongamos ahora que tenemos dos series de números enteros a₁, a₂,..., a_n y m₁, m₂,..., m_n, y que queremos encontrar un número x para el cual se cumpla lo siguiente:

x ≡ a₁ (mod m₁)
x ≡ a₂ (mod m₂)
...................
x ≡ a_n (mod m_n)

El llamado teorema chino de los restos, afirma que la condición necesaria y suficiente para que el número buscado exista consiste en que a_i ≡ a_j (mod m_ij), siempre que i ≠ j, y siendo m_ij el máximo común divisor de m_i y m_j.

En el Brama Sputa Siddhanta se encuentra el siguiente problema que es un caso particular del teorema chino:

Tenemos una cesta de huevos. Si los cogemos de dos en dos, sobra uno, si de tres en tres, sobran dos, si de cuatro en cuatro, sobran tres, si de cinco en cinco, sobran cuatro, si de seis en seis, sobran cinco, y si los cogemos de siete en siete, no sobra ninguno. ¿Cuál es el mínimo número de huevos que puede haber en la cesta?

Si x es el número de huevos, tenemos la siguiente colección de ecuaciones:

El problema se resuelve aplicando sucesivamente el método de Aryabhata, y se llega de este modo a la solución más pequeña posible, que es 119. En el lenguaje de los números congruentes, el problema puede  ahora ser formulado de esta manera:

Es fácil comprobar que cumple las hipótesis del teorema chino. Así que, antes de resolverlo, ya se sabe que tiene solución.

La ecuación de Pell

Entre los problemas indeterminados que aparecen en la obra de Brahmagupta ocupa un importante lugar la ecuación que la posteridad llamaría ecuación de Pell:

x² - Dy² = 1

Si D = d², no hay soluciones (salvo x = 1 e y = 0): si D = d², resultaría que (x + dy)(x - dy) = 1, y esto es imposible. Pero si D no es un cuadrado, hay infinitas. Y es fácil encontrar las más sencillas por tanteo. Brahmagupta dio con un camino para, a partir de dos soluciones, fabricar una tercera. Este método (que en sánscrito se denomina samasa) es el siguiente: si los pares de números (α,β) y (χ,δ) son soluciones, también lo es el par de números calculados de la siguiente manera:

σ = αχ + βδD
ω = αδ + βχ

Que esto es así es algo de muy simple comprobación. Sea, por ejemplo, la ecuación:

x² - 8y² = 1

Fácilmente se llega a la solución (3,1). Compuesta consigo misma, tenemos otra solución (17,6), y componiendo las dos, una tercera (99,35). Y así sucesivamente.

Triángulos racionales

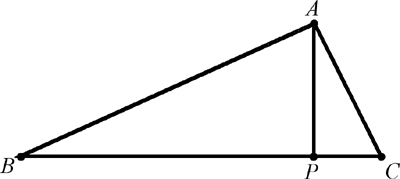
Un triángulos cuyos lados y cuya superficie son números racionales (y en consecuencia también sus alturas) se llama triángulo racional. Brahmagupta tiene la siguiente aportación sobre triángulos racionales. Si los lados de un triángulo son:

entonces es racional, resultado de yuxtaponer dos triángulos rectángulos con un cateto común de longitud p (ver la figura que aparece a continuación): AP = p, AC = b, AB = c, PB = c - r y PC = b - q.

El cuadrilátero cíclico

Por tres puntos no alineados siempre pasa una circunferencia. Por cuatro puntos no siempre sucede así. Por esta razón no todo cuadrilátero tiene una circunferencia circunscrita. Los que sí la tienen se llaman cíclicos. Sobre ellos descubrió  Brahmagupta un hermoso teorema que pasamos a describir.

Llamamos fórmula de Herón a la expresión del área de un triángulo en función de sus lados. Si éstos son a, b y c, y  p = (a+b+c)/2 es el semiperímetro, la superficie es:

Esta fórmula ha sido muy utilizada por agrimensores y topógrafos, porque no necesita buscar la altura del triángulo, cosa que en terreno abierto no siempre es fácil. Brahmagupta encontró una fórmula que amplía la de Herón a cuadriláteros cíclicos. Si a, b, c y d son los lados del cuadrilátero y p es el semiperímetro, la superficie es:

Si d = 0 sale la fórmula de Herón. Pero ignoramos (los textos sánscritos son muy oscuros) si Brahmagupta sabía que su teorema no era válido para cualquier cuadrilátero.