 Febrero 2013: Geometría flexible con Polifieltros 3D - 11. Fractales
Febrero 2013: Geometría flexible con Polifieltros 3D - 11. Fractales |
 |
 |
 |
| Escrito por José Luis Rodríguez Blancas (Universidad de Almería) |
| Miércoles 06 de Febrero de 2013 |
|
Página 13 de 13
11. FRACTALES El niño o niña podrá construir el famoso triángulo de Sierpinski, doblando simplemente pestañas en el siguiente modelo de fieltro que presentamos aquí, o 3 de ellos de diferentes colores para realizar una iteración más.  El cosido de velcro en los bordes, permite formar también la 2a iteración del tetraedro de Sierpinski, así como la 3a iteración combinando 4 de copias de distintos colores. Sobra decir que este modelo puede hacerse para la primera iteración o para iteraciones superiores.  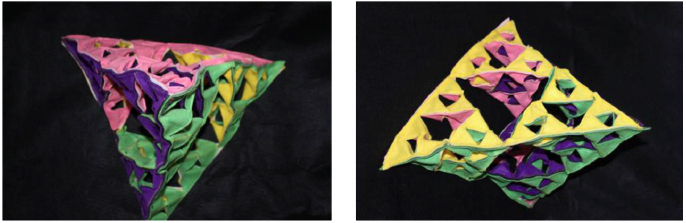 La esponja de Menger es mucho más complicada de elaborar con fieltro. De momento hemos obtenido la primera iteración.  Este modelo está formado tan solo por dos piezas, tal y como se muestra en la última imagen, el cubo exterior donde se han abierto "ventanas" en el centro de cada cara, y la cruceta interior modelada por una tira rectangular con entrantes y salientes. Podéis ver cómo se desmonta poco a poco en el video "stop motion" http://youtu.be/oQevUDo91FQ.
|
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |






