 Febrero 2013: Geometría flexible con Polifieltros 3D - 4. Deltaedros
Febrero 2013: Geometría flexible con Polifieltros 3D - 4. Deltaedros |
 |
 |
 |
| Escrito por José Luis Rodríguez Blancas (Universidad de Almería) |
| Miércoles 06 de Febrero de 2013 |
|
Página 6 de 13
4. DELTAEDROS El juego contiene también piezas separadas que el niño/a debe unir para montar figuras más complejas. Los deltaedros, por ejemplo, son poliedros que están formados por triángulos equiláteros. Con triángulos de fieltro se pueden construir infinitos deltaedros de colores. El modelaje de superficies con triángulos y otras tantas figuras que veremos en el apartado 10 es un aliciente para el niño o niña que desarrollará su aptitud diseñadora. Pueden formarse también con rombos (unión de dos triángulos equiláteros). En la primera imagen vemos un tetraedro, un icosaedro y un octaedro formado por rombos de colores. Pero estos son solamente ejemplos, podemos formar también los 8 deltaedros convexos, y por supuesto, deltaedros no convexos como el octaedro estrellado.  También otras figuras libres como estas espirales.  En fin, como se puede apreciar, las posibilidades son infinitas, y más si las combinamos con otros polígonos. Las tres fotos siguientes muestran, por ejemplo, dos maneras equivalentes de formar la tercera estelación del icosaedro: la primera con hexágonos rojos y rombos naranjas, y otra con rombos lilas y naranjas. La flexibilidad del material nos permite meter y sacar las puntas del poliedro fácilmente, algo difícil de realizar con las correspondientes figuras de papel u otros juegos de construcción similares. 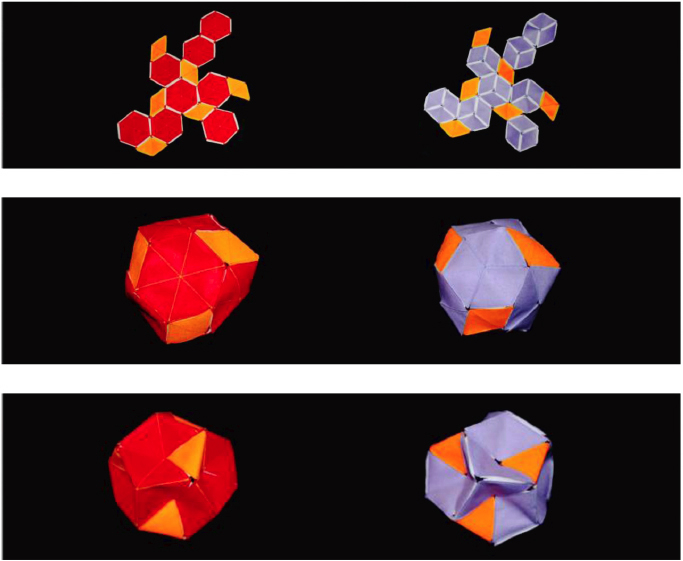 |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |






