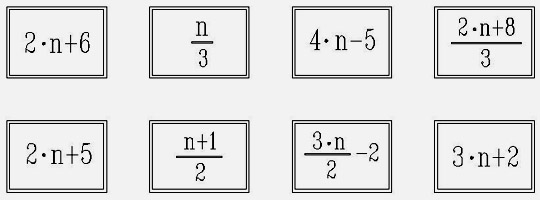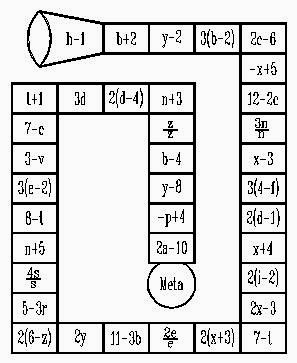
1. INTRODUCCIÓN.

La entrega de este número vamos a dedicarla a juegos de Álgebra.

Ya sabemos que el Álgebra es la parte más abstracta y, muchas veces, árida de las matemáticas. Es difícil hacer entender al alumnado su importancia en muchos procesos resolutivos y trabajar en clase con verdaderas aplicaciones cotidianas y no meramente unas seudo-matemáticas aplicadas a nuestro alrededor.

Por ello en este bloque solemos trabajar en clase con juegos que resultan mucho más atractivos que meras colecciones de ecuaciones y expresiones algebraicas planteadas en tediosos boletines de ejercicios. Desde hace muchos años hemos aplicado en clase actividades lúdicas de todo tipo: dominós, puzzles, juegos de tableros y fichas, pasatiempos, etc. Para ello nos hemos aprovechado del excelente trabajo desarrollado por los grupos Azarquiel de Madrid y Cero de Valencia, que en sus publicaciones tienen multitud de juegos que abarcan casi la totalidad del Álgebra que se trabaja en Educación Secundaria.

Ya en el número 36 de SUMA publicamos en esta sección un juego algebraico con el título “Sopa Polinómica” en el que se trabajaba la descomposición de polinomios. Desde esa lejana fecha de 2001 (¡como pasa el tiempo!) no habíamos vuelto a tocar esta parte de las matemáticas, por lo que ya iba siendo hora.

Como las posibilidades son tan grandes y hay tanta variedad, nos vamos a centrar en un aspecto muy concreto dejando abierta la posibilidad más adelante, si la sección y el cuerpo aguantan, de volver a tocar otros aspectos algebraicos igual de atractivos.

En esta ocasión vamos a trabajar con juegos que se basan en la sustitución de números en expresiones algebraicas, es decir, en hallar el valor numérico de distintas expresiones según los valores que nos salgan en los dados que utilizaremos. Aunque son juegos indicados para Secundaria, como su dinámica se basa en sustituir en una expresión y hacer operaciones básicas, también pueden ser utilizados en Primaria, profundizando en ellos tanto como se quiera.

2. JUEGO DE SUSTITUCIÓN.

En este juego pueden participar varios jugadores. Sólo se necesita una ficha de color distinto por jugador, un dado cúbico y un tablero como el de la figura 1.

Reglas del juego:

1. Los jugadores colocan sus fichas en la casilla embudo de salida.
2. Por turno, los jugadores lanzan el dado y sustituyen la letra de la expresión algebraica que aparece en la casilla en que se encuentran en ese momento por el valor del dado. Realizan la operación y el resultado es el número de casillas que deben avanzar o retroceder en el tablero.
3. Gana el primer jugador en llegar a la meta.

Respecto al último punto hay varias formas de afrontar la llegada a la meta. Lo más usual es considerar dos posibilidades.

• a) Sobrepasar la meta. En este caso si obtenemos un número que sobrepasa el número de casillas que quedan para la meta se considera que el jugador gana ya que atraviesa la meta.
• b) Llegar y rebotar. En este caso, más complicado que el anterior, solo se gana con la cantidad justa de casillas, lo que sobre se cuenta hacia atrás. Es decir, si estamos a tres casillas de la meta y nos sale un 5, contamos tres lugares hasta la meta y los dos restantes valores se cuentan hacia atrás en el tablero.

Lo interesante de esta actividad es aprovechar las expresiones del tablero para hacer un estudio exhaustivo de las posibilidades. Por ejemplo, podemos observar fácilmente que en varias de las casillas cercanas a la meta siempre se retrocede, independientemente de lo que se saque en los dados.

Es también curioso jugar sin dado, es decir, cada jugador decide en cada momento que número del 1 al 6 sustituir en la casilla en que se encuentra. De esta manera deja de ser un juego basado en el azar y comienza a ser un juego de estrategia, pues hay que investigar en qué casillas nos interesa caer y qué valor podemos sustituir para avanzar o retroceder lo mínimo posible.

En esta línea, si consideramos que es necesario sacar el valor exacto de casillas, podemos hacer un estudio de qué casillas son las que nos permiten ganar. Sería seguir el procedimiento de considerar el problema resuelto y comenzar hacia atrás. De esa manera podemos ver que la única posibilidad de llegar a la meta de forma redonda es sacar un 2 en la casilla –p+4. Para llegar ahí solo hay la posibilidad de sacar un 6 en la casilla b-4. Pero para llegar a esa casilla hay ya varias posibilidades.

3. DEMOS VALORES A N.

Ahora nos encontramos con un juego para dos jugadores. Necesitamos como material dos dados cúbicos, un tablero de juego como el de la figura 2, ocho fichas para cada jugador y un juego de ocho tarjetas como las de la figura 3, también por jugador.

Reglas del juego:

1. Cada jugador, en su turno, lanza los dos dados, suma los valores obtenidos y elige una tarjeta.
2. Si al sustituir el valor en la tarjeta el resultado es una casilla libre del tablero, coloca una de sus fichas en la casilla y descarta la tarjeta que ha utilizado.
3. Si al sustituir el valor en la tarjeta, la casilla con ese resultado ya está ocupada, o ese número no pertenece al tablero, el jugador pierde el turno, pero conserva la tarjeta que ha probado.
4. Gana el primer jugador que consigue colocar sus ocho fichas sobre el tablero.

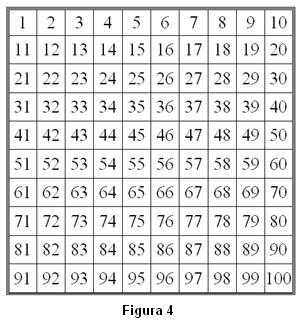
Nuestra experiencia es que es muy difícil conseguir acabar colocando las ocho fichas, por lo que lo usual es que, pasado un tiempo prudencial, se acabe el juego ganando quien ha colocado más fichas.

El motivo por el que casi nunca es posible acabar el juego es porque es muy fácil acabar ocupando las casillas que son resultado de varias tarjetas y al final quedan tarjetas con las que ya no es posible conseguir ninguno de los números sin asignar ficha.

Por eso, el siguiente paso del juego consiste en estudiar qué valores podemos utilizar en las distintas tarjetas. Ya que, por ejemplo, en la tarjeta 4n – 5 sólo se pueden utilizar valores menores que 7, pues en caso contrario el número que se obtiene está fuera del rango del tablero. En la tarjeta  sólo podemos utilizar los valores 2, 5, 8, y 11. Y así podemos analizar todas las demás.

Después del estudio el juego pasa a ser de estrategia pues ya hay que decidir, según los valores que van saliendo, qué tarjetas debemos utilizar para que no se nos queden colgadas las que son más difíciles de sustituir.

Este juego lo hemos adaptado de uno tomado de los materiales del Grupo Cero de Valencia (aunque no tenemos claro si la autoría es suya o del grupo Azarquiel, lo sentimos), reduciendo el tablero y modificando las expresiones de las tarjetas. En sus publicaciones es posible encontrar la otra versión

4. LO TUYO Y LO MIO.

Durante la primera década del siglo XXI, un grupo de profesores de Sevilla formamos, primero, un grupo de trabajo que después terminó en Proyecto de Innovación, sobre “La atención a la diversidad en el aula de matemáticas”. En dicho proyecto, aprobado y financiado por la Junta de Andalucía, trabajamos con muchos juegos y, en concreto, con el que vamos a presentar ahora que adaptamos para nuestra investigación. Recibe el nombre de “Lo tuyo y lo mío” y aparece en el libro del grupo Azarquiel. Veamos primero el juego.

Necesitamos un tablero con los números del 1 al 100 como el de la figura 4, dos dados cúbicos, 10 fichas de distinto color por jugador y una colección de tarjetas como las que aparecen en el anexo 1.

Reglas de juego:

1. Sale quien menor puntuación saque en la primera tirada.
2. El primer jugador tira los dados y el número obtenido se denominará “Lo tuyo”. El siguiente jugador toma una tarjeta del mazo, con el número obtenido por los dados (lo tuyo), calcula el número que corresponderá a “Lo mío” utilizando la frase de la tarjeta y colocará una de sus fichas sobre el tablero en el número que coincide con “lo mío”.
3. Si el número obtenido no está en el tablero, el jugador pierde turno. Si la casilla ya está ocupada, el jugador pierde turno. Si el jugador contrario observa que la operación ha sido incorrecta, se anula la tirada y pasa turno.
4. El jugador que ha utilizado la tarjeta la devuelve al final del mazo, coge los dados y los tira para dar un número al siguiente jugador, prosiguiendo el juego de la misma forma.
5. Gana, quien consiga colocar todas sus fichas sobre el tablero.

Veamos un ejemplo:

Un jugador tira los dados y obtiene 7. El siguiente jugador saca una tarjeta del montón que dice:

“¡Vaya! Lo tuyo es sólo la cuarta parte de lo mío”.

Lee la tarjeta y razona, dirigiéndose al jugador que ha tirado los dados:

“Si LO TUYO ha sido 7, LO MÍO será cuatro veces lo tuyo, es decir, 28"

El juego consta de 30 tarjetas, numeradas del 1 al 30. El único objetivo de esa numeración es seleccionar el grado de dificultad que queremos darle al juego. De esa manera podemos escoger las tarjetas teniendo en cuenta la siguiente distribución:

• Nivel básico: tarjetas de la 1 a la 15.
• Nivel medio: tarjetas de la 1 a la 20.
• Nivel alto: las 30 tarjetas.

Lo importante es comprobar que los alumnos aplican correctamente la frase al valor que se le entrega. Nosotros, después del juego trabajamos la simbolización, de esa manera, una vez acabado el juego, los alumnos deben escribir la expresión algebraica que corresponde a las tarjetas que han utilizado, considerando que Lo tuyo lo representamos por x y Lo mío por y. Posteriormente hacemos una puesta en común para ver qué expresión algebraica ha puesto cada alumno para una determinada tarjeta y de esa manera detectar los errores típicos de traducción del lenguaje natural al lenguaje algebraico.

Bibliografía:

• Azarquiel, Grupo (1993): Ideas y actividades para enseñar Álgebra. Colección Matemáticas: cultura y aprendizaje, nº 33. Síntesis, Madrid.
• Cero, Grupo (1995): Matemáticas para la Secundaria Obligatoria. Tres volúmenes. MEC y Edelvives.