Noviembre 2019: Más juegos de lápiz y papel II
Noviembre 2019: Más juegos de lápiz y papel II |
 |
 |
 |
| Escrito por José Muñoz Santonja | ||||||||||||||||
| Viernes 15 de Noviembre de 2019 | ||||||||||||||||
|
1. Recordemos. En la primera parte de esta entrega de juegos de lápiz y papel, hablamos de una serie de juegos que han formado parte de nuestra infancia y juventud. Juegos, en ocasiones muy conocidos, que tienen la característica de utilizar unos materiales muy asequibles y que se pueden jugar en cualquier momento y lugar. Para nosotros, como profesores, tienen además el interés de poder estudiar las estrategias que llevan a buscar la solución mejor. Unas estrategias que son similares a las que se utilizan en la resolución de problemas, y que nos permiten aprender y practicar esos heurísticos que después aplicaremos en los problemas matemáticos. En la anterior entrega presentamos juegos que, en algunas ocasiones, eran bastante antiguos, algunos de ellos incluso pueden remontarse al siglo XIX. En esta parte vamos a ver una serie de juegos de creación más reciente. Como veremos existe un gran número de matemáticos que han creado nuevos juegos de lápiz y papel con estudios y estrategias muy interesantes, entre ellos podemos citar a Eric Solomon o John Conway, de los que hablaremos en las siguientes líneas. 2. Brotes. El juego titulado Sprout puede traducirse por brotes o coles, aunque también se conoce en español como Plantón o puntos y líneas. Martín Gardner le da el nombre de “drago” debido al árbol del mismo nombre. Fue creado en 1967 por el profesor, de la Universidad de Cambridge, John Horton Conway, más conocido por ser el creador, entre otros, de “El juego de la vida”, junto al estudiante Michael S. Paterson de la misma universidad. Este juego se considera un juego básicamente topológico. Es un juego pensado para dos jugadores, aunque si hay más de tres es conveniente que se jueguen varias partidas y en cada una de ellas empiece un jugador distinto. Se comienza dibujando una serie de puntos en un papel y cada jugador, en su turno, debe trazar una línea que comience en uno de los puntos y termine en otro, que puede ser el mismo punto. Una vez dibujada la línea, el jugador debe dibujar un punto dentro de la línea que no coincida con ningún otro punto ya dibujado. Los jugadores siguen dibujando líneas con únicamente dos restricciones:
El juego termina cuando un jugador no puede dibujar una nueva línea con las condiciones impuestas. Gana el último jugador que ha dibujado una línea. Existe también una versión llamada Misère en la que gana el primer jugador que no puede dibujar una línea. Veamos una partida partiendo de dos puntos.
Como vemos en esta partida ha ganado el segundo jugador, pues el primero, al que le toca mover, no puede unir los dos únicos puntos que tienen aún algún grado de libertad sin cruzar otra línea ya existente. En el estudio que realiza Martin Gardner, supone que cada punto tiene inicialmente tres vidas, o tres grados de libertad, cuando un punto tiene tres líneas que parten o confluyen en él, ha perdido sus vidas, luego está muerto. En cada movimiento, se pierden dos vidas al trazar las líneas, una del punto inicial y otra del final y se añade una nueva vida, correspondiente al punto nuevo que se coloca, que ya tiene dos líneas que confluyen en él, pues básicamente ese punto divide a la línea en dos. Por tanto, en cada partida se pierde como mínimo una vida. Pueden ser más si se quedan puntos bloqueados como hemos visto en el ejemplo de partida. Si partimos de n puntos, inicialmente hay 3n vidas y por tanto ninguna puede durar más de 3n – 1 movimientos (pensemos que si queda un único punto para dibujar es imposible seguir). También es posible deducir que cualquier partida puede durar como mínimo 2n movimientos. Al estudiar los primeros casos podemos encontrarnos con las siguientes opciones. Si partimos de un solo punto, el juego es trivial pues sólo es posible hacer dos movimientos y gana el segundo jugador. Si partimos de dos puntos, es fácil comprobar que gana el segundo jugador y que puede forzar ganar en cuatro movimientos, como se ha visto en el ejemplo. Basta estudiar todos los movimientos de comienzo del primer jugador, que sólo hay tres posibles, salvo simetrías, y estudiar como continuar en cada caso.
El propio Conway demostró que con tres puntos el primer jugador puede ganar siempre. Un estudiante de matemáticas de Cambridge, Denis Mollison, demostró que el primer jugador tiene las de ganar con cuatro y cinco puntos, mientras que con seis gana el segundo. Las partidas más usuales se comienzan con tres puntos. Lógicamente, mientras más puntos se coloquen al principio, más tiempo se tarda en acabar y más complicada es la estrategia para llegar al final. El doctor en matemáticas por la Universidad de Southampton, Eric Solomon, diseñador de juegos y programador de software, ha realizado el siguiente estudio. Cada línea que se dibuja, que en realidad son dos líneas por el punto que se coloca en medio, produce sobre la zona de juegos o bien una nueva región, zona encerrada por una línea, o bien une dos partes separadas, considerando como parte a todo elemento (línea o punto) independiente de otro. Con esas características, se cumple la siguiente regla de Euler: “el número de regiones más el de puntos es igual a la suma del número de partes más el de líneas”. Si nos fijamos en la última jugada de la partida anterior, tenemos una sola parte, ya que está todo conectado, tres regiones, 6 puntos y 8 líneas (recordemos que una línea se considera desde un punto hasta el más próximo, luego en cada jugada un jugador traza dos líneas). Por tanto, 3 + 6 = 1 + 8. Más adelante, Conway realizó una versión que llamó Brussels Sprouts (Coles de Bruselas) cuya variación es que en lugar de puntos se dibujan cruces, y las líneas parten de uno cualquier de los extremos de las cruces. En la línea se dibuja un nuevo trazo como se ve en el dibujo.
En esta versión, de cada trazo de la cruz, que se prolonga para conectarlo con otro trazo, sólo puede salir una línea, por lo que ese brazo de la cruz queda invalidado al dibujar una línea. Conway demostró que, partiendo con n cruces, el juego siempre termina después de 5n – 2 movimientos. Si el número de cruces es impar gana el primer jugador, y el segundo con un número par de cruces. 3. Colorear mapas. Veamos ahora un bloque de juegos que se basan en colorear unos determinados mapas. 3.1. El juego de los colores.Este juego aparece en el libro de Luis Ferrero y no he conseguido encontrar más información de la que allí aparece, pero me ha parecido interesante incluirlo. Se basa en el conocido Teorema de los cuatro colores, un resultado típico en la topología Según este teorema, un mapa plano que tiene regiones continuas puede ser coloreado utilizando únicamente cuatro colores, de forma que cada región adyacente tenga distinto color. Se considera región adyacente a la que tiene un poco de frontera común entre las regiones, no se incluye si el contacto se reduce a un solo punto. Para este juego se dispone de cinco colores y está indicado para dos jugadores, aunque se puede jugar también con tres o cuatro. En el caso de ser más de dos jugadores y jugar varias partidas, es conveniente que en cada partida, los jugadores cambien el orden en que están situados. La forma de jugar es la siguiente: El primer jugador dibuja una región cualquiera, y a partir de ese momento, cada jugador en su turno, debe colorear la región que ha dibujado el contrario, con la condición de no poder utilizar un color que se repita en algunas de las regiones adjuntas ya coloreadas. Una vez coloreada la región del oponente, el jugador, aún en su turno, debe añadir una nueva región a las ya existentes. Entonces pasa el turno al siguiente jugador. Pierde el jugador que utilice el quinto color en la región que debe colorear. Veamos el comienzo de una partida con dos jugadores. Suponemos que la jugada del primer jugador ha sido dibujar el recinto que ha coloreado el segundo jugador.
Se observa, en las dos últimas jugadas, que al abarcar las tres regiones, se obliga a utilizar un cuarto color, pero al encerrar una de las regiones, ese color, en nuestro caso el verde, se puede utilizar para la nueva región sin problemas. Hay una versión que a veces he utilizado y consiste en entregar sólo cuatro colores y un mapa ya dibujado. El primer jugador dibuja una región de un color y, a partir de él, cada jugador debe colorear una región adyacente, al menos a una de las regiones ya coloreadas. Pierde el jugador que debe utilizar el cuarto color. 3.2. Otros juegos con menos colores.Hay toda una colección de juegos basados en el objetivo de colorear mapas, la mayoría de ellos basados en el Teorema de los cuatro colores. Este tipo de juegos se estudian en la “Teoría combinatoria de juegos”. Básicamente se basan en colorear regiones con varios colores, de forma que las regiones que tienen frontera común no lleven el mismo color, aunque hay versiones en que se pide lo contrario. En algunos de estos juegos se aplica una regla vinculante según la cual, cada región que se colorea debe ser vecina de la región coloreada en la jugada anterior. En general, gana el jugador que colorea la última región posible, aunque también se puede jugar al modo contrario, es decir, la versión misère en la que pierde el último que puede colorear. Hay incluso variantes en la que se cuentan las regiones coloreadas con un determinado color, si es que se rellenan todas las posibles según los colores de los jugadores, independientemente del turno que les corresponda. El número de colores puede cambiar según el método de juego. El experto en juegos David L. Silverman, creador entre otros del juego Senderos, que presentamos en el artículo de SUMA de 2002, hace una clasificación de juegos en su libro “Your move: Logic, Math and Word Puzzles for Enthusiasts” de 1976 según el número de colores. Todos ellos se juegan sobre un mapa ya dibujado previamente y son juegos consideramos imparciales, es decir, los dos jugadores tienen las mismas posibilidades de juego en todo momento.
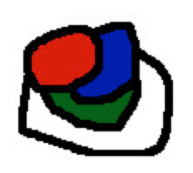
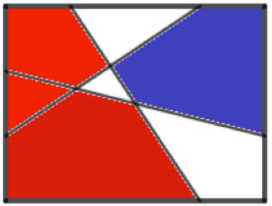
Silverman también presenta un juego llamado Contact en la que se utiliza un solo color por jugador y se aplica la opción vinculante, es decir, cada región que se colorea debe tener contacto con la región coloreada en la versión anterior. En su libro “Sobre números y juegos” de 1991, John Conway presenta y estudia las dos siguientes versiones de juegos que son considerados partidistas, pues en el desarrollo del juego hay diferentes movimientos disponibles para uno y otro jugador: 3.2.1. COL. Conway atribuye este juego a su colega Colin Vout. Sería una versión simple en la que cada jugador dispone de un color diferente y hay que colorear regiones con la condición de que las regiones no tengan frontera común con otra del mismo color. En la siguiente imagen tenemos una partida terminada en la que el color rojo, que fue el que comenzó la partida, es el que gana.
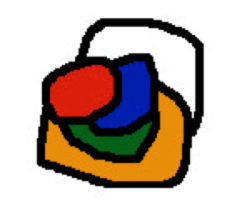
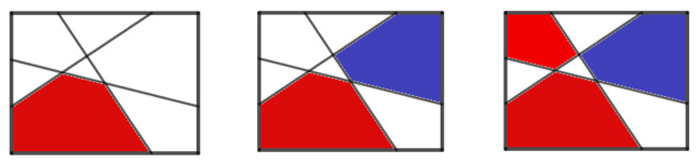
3.2.2. SNORT. Atribuido al colega de Conway, Simon Norton. En ella cada jugador tiene un color y se van coloreando regiones con la restricción de que no puede haber dos regiones contiguas con colores diferentes. En las siguientes imágenes puede verse una partida de Snort.
Después de la tercera jugada, el jugador azul no puede mover, queda bloqueado, aunque el jugador rojo aún tiene una jugada posible.
4. Agresión.
Vamos a presentar un juego que, aunque sigue la tónica de los juegos del apartado anterior, se sale un poco del perfil que hemos visto hasta el momento. Básicamente, este juego es de estrategia, más concretamente de lo que se conoce como wargame, es decir, juegos de guerra, y que está inspirado en el conocido juego de batallas llamado Risk. Aunque, como veremos, algunos especialistas hablan de su interés como juego aritmético para Primaria. Ya hemos hablado antes del matemático Eric Solomon, un importante creador británico de juegos. En 1973 publicó un libro con el título de “19 juegos con papel y lápiz” en el que presentaba varios juegos inventados por él, entre ellos éste que llamó simplemente aggression. Es un juego para dos jugadores, cada uno de ellos juega con un lápiz de distinto color. El juego se compone de tres fases diferentes, en cada una de ellas comienza siempre el mismo jugador que en esa partida es el primero.
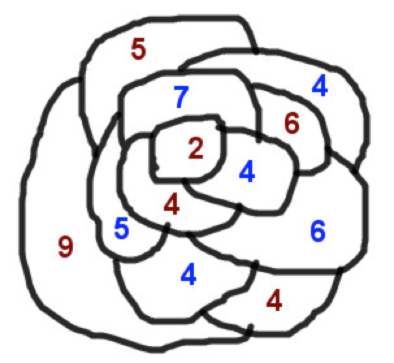
El número de regiones y de unidades de combate varían según se decidan al comienzo de la partida. Solomon propone unas 20 regiones y unas 100 unidades de combate. Lo ideal es comenzar con menos regiones y menos unidades. Veamos un ejemplo. En la siguiente imagen vemos un mapa en el que aparecen 12 regiones donde hay repartidas 30 unidades de cada uno de los jugadores. Se puede considerar que cada jugador sólo puede poner unidades de combate en las regiones que él ha dibujado, o permitir colocarlas en cualquier sitio. He considerado esta segunda opción, por eso no se distinguen colores en el dibujo del mapa.
Como hemos indicado en las instrucciones, es posible atacar desde una sola región o desde varias del mismo jugador, en las imágenes siguientes vemos los dos casos.
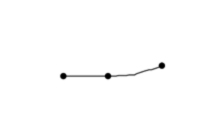
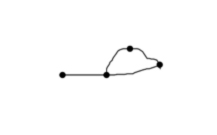
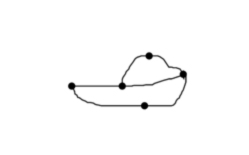
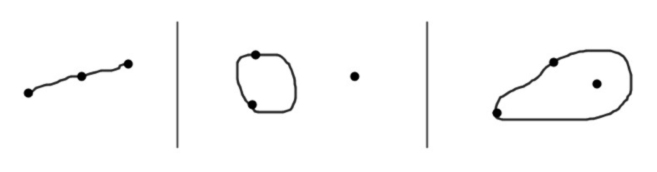
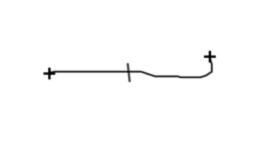
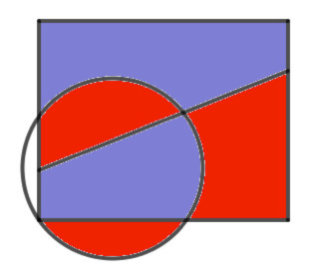
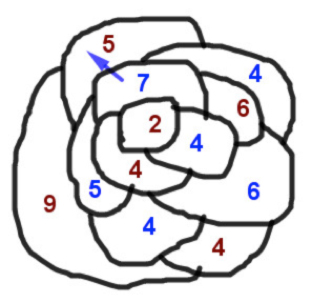
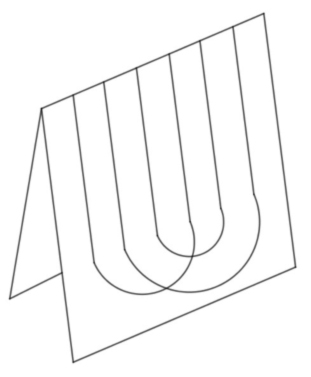
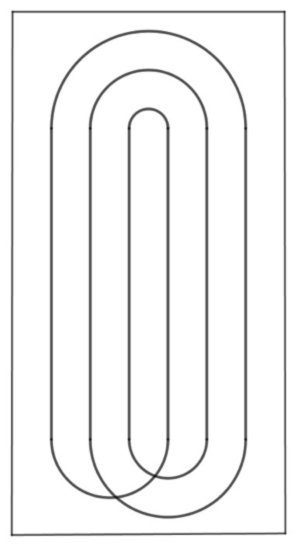
Es fácil encontrar información sobre este juego en la web. En particular quiero hacer referencia al sitio MathPickle, una página apoyada por el Instituto Americano de Matemáticas. Contiene muchos recursos gratuitos para utilizar en clase. Se pueden encontrar puzles y juegos adaptados a niveles educativos diversos. En esa página, su creador Gordon Hamilton, ha adaptado el juego anterior llamándolo Un poco de agresión, para que no parezca tan violento, y lo plantea para trabajar sumas y restas de números enteros. Comienza con propuestas para trabajar del 1 al 10 y después para trabajar del 1 al 100. En los juegos se propone que, en lugar de crear el mapa los propios jugadores, se utilicen mapas reales. Hamilton propone varios en sus escritos, uno de ellos por cierto el de la península ibérica, donde combaten franceses contra ingleses durante la Guerra de Sucesión del siglo XVIII. En la siguiente dirección se puede encontrar la explicación de cómo realizar el juego. http://mathpickle.com/project/a-little-bit-of-aggression/ Existe también un pdf, aunque en inglés, en el que se describe paso por paso la realización de una partida y otro en el que hay muchos mapas con indicaciones de cuantas unidades de combate utilizar en cada caso. Las direcciones son: http://mathpickle.com/wp-content/uploads/2016/01/TpT-A-little-bit-of-aggression-2016.pdf 5. El juego de las hojas de hierba. Para terminar, me gustaría incluir un juego diferente, ya que aunque se puede jugar igual que los anteriores, con lápiz y papel, no es propiamente un juego de estrategia sino más bien un juego aleatorio, pues en su resultado interviene el azar. Se dibujan seis líneas verticales paralelas en una hoja. Se dobla la hoja por la mitad y uno de los jugadores, sin que el contrario lo vea, une esas seis líneas en parejas mediante tres arcos. Posteriormente, tapando lo dibujado, el otro jugador une las seis líneas de la parte contraria. Se despliega el papel. Si se ha conseguido un lazo continuo cerrado y único, gana el segundo jugador, en caso contrario gana el primero. Veamos una partida posible.
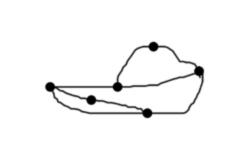
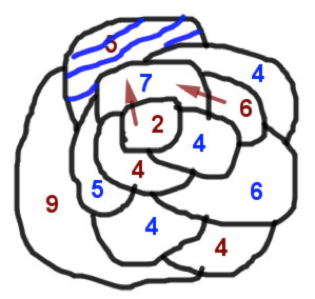
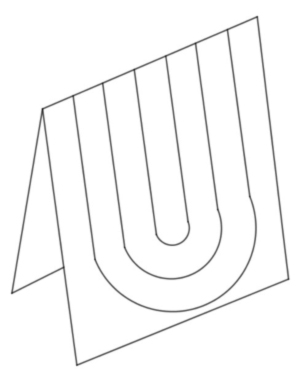
Al abrir la hoja se puede ver la unión completa. En este caso se observa que ha ganado el segundo jugador, pues ha conseguido cerrar un círculo completo, es decir, no hay lazos independientes unidos.
Sin más que ver la partida, se puede observar que en el ganar o perder influye poderosamente el azar, ya que el segundo jugador no sabe cómo ha unido sus extremos el primer jugador. Lo interesante es estudiar quién de los dos jugadores tiene mayor probabilidad en ganar en esta partida. En su libro Comunicación extraterrestre, Martin Gardner nos habla de la historia de las muchachas casaderas rusas, que utilizaban un método similar para saber si el futuro les deparaba un buen matrimonio, historia en la que se basa este juego. También hace el estudio probabilístico según el cual, el segundo jugador tiene una probabilidad algo superior al del primer jugador. 6. ¡Llegó la hora de jugar! Como comentábamos al principio de la entrega anterior, existen una gran variedad de juegos de lápiz y papel que son relativamente recientes y que son interesantes para investigar las estrategias que permiten tener más posibilidades de ganar. En los libros de la bibliografía quedan aún muchos más para trabajar conceptos muy diversos. En internet existen multitud de páginas con alguna entrada en que se recogen juegos de lápiz y papel, y en muchos de ellos se puede jugar directamente a esos juegos. Yo no conozco ninguna página en español especializada en estos juegos, pero si existe una página imprescindible en inglés llamada Pencil And Paper Games (www.papg.com) en la que se explican muchos juegos y en varios casos es posible jugar en línea. En concreto los juegos de brotes, col, snort, agresión, toros y vacas y puntos y cajas se tratan en la página, aunque solo se pueden jugar los dos últimos. Varios de estos juegos se presentaron en la primera parte del artículo. Ya solo me queda invitarles a disfrutar con recursos tan fáciles de conseguir, hoy en día, como un lápiz y un papel. 7. Referencias. FERRERO, L. (1991): El juego y la matemática. La Muralla, Madrid. GARDNER, M. (1980): Carnaval matemático. Alianza Editorial, Madrid. GARDNER, M. (1987): Comunicación extraterrestre y otros pasatiempos matemáticos. Catedra, Madrid. Colección Teorema. GRUPO ALQUERQUE (2002): “Juegos de lápiz y papel”. SUMA nº 40, pp. 123-124. SOLOMON, E. (2008): 19 juegos con papel y lápiz. RBA Editores, Barcelona.
|
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |