Al-Hacen (~965-1039) |
 |
 |
 |
| Escrito por Ricardo Moreno (Universidad Complutense de Madrid) | ||||
Página 1 de 2
La proposición 4 del libro II propone el siguiente problema: partimos en dos trozos una esfera de radio R mediante un plano que la corta a una distancia de R - x del centro, como se puede ver en la figura 1:
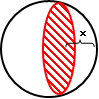 Figura 1
Los volúmenes de cada uno de los trozos son respectivamente:
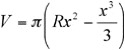 y  Se trata de calcular x de manera que la relación entre ambos sea un número decidido de antemano. Es fácil comprobar que x ha de ser raíz de la ecuación siguiente:
 En la obra citada no se dice como encontrar la solución, pero según Eutocio (un comentarista bizantino de comienzos del siglo VI), Arquímedes logró resolverla geométricamente cortando secciones cónicas. En el siglo IX al-Mahani (matemático de la escuela de Bagdad) intentó sin éxito hacerlo algebraicamente. Alhacén dio con una solución, siguiendo un camino parecido al trazado por Arquímedes, ayudándose de una parábola y una hipérbola.
En un libro titulado Tesoros de la óptica plantea Alhacén un problema (que todavía en el siglo XVII despertó el interés de matemáticos como Huygens y Barrow) que conduce a una ecuación de grado cuatro. También la resolvió mediante intersecciones de secciones cónicas. Consiste en localizar sobre un espejo circular el punto en el que se ha de reflejar un rayo salido de un punto A para que incida en un punto B (ver figura 2). Sea éste el punto M. 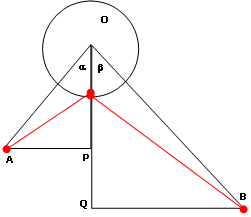 Figura 2
Si r es el radio del espejo, a = AO, b = BO, α el ángulo AOM y β el ángulo BOM, tenemos lo siguiente: MP = a cosα - r, MQ = b cosβ - r, AP = a senα, BQ = a senβ
Ahora bien, sabemos por las leyes de la reflexión que los triángulos rectángulos AMP y BMQ tienen un ángulo igual, en consecuencia son semejantes. Entonces:
 Como el ángulo α + β = AOB es conocido, lo mismo que a, b y r, la última igualdad conduce a una ecuación de grado cuatro.
|
Abu Ali al-Hasan ibn al Hasan ibn al-Haytam, más conocido en occidente como Alhacén, vivió aproximadamente entre los años 965 y 1039 y formó parte del grupo de científicos del Cairo, aunque nació en Basra, Persia (la actual Irak). Fue uno de los primeros matemáticos árabes que abordó con éxito ecuaciones de grado superior al segundo, al resolver geométricamente una de tercero que, más de mil doscientos años antes, había planteado Arquímedes en su obra Sobre la esfera y el cilindro.
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |