 Pitágoras (Siglo VI a.C.) - Página 6
Pitágoras (Siglo VI a.C.) - Página 6 |
 |
 |
 |
| Escrito por Pedro Miguel González Urbaneja (IES Sant Josep de Calassanç, Barcelona) | ||||||||||||||
Página 6 de 10
El Teorema llamado de Pitágoras Una tradición muy persistente con base documental en Vitrubio, Plutarco, Diógenes Laercio, Ateneo y Proclo, atribuye el Teorema de Pitágoras al propio Pitágoras. Pero los descubrimientos arqueológicos de los restos de las culturas de Mesopotamia, Egipto, India y China, han revelado que estas civilizaciones conocían aspectos del Teorema de Pitágoras muchos siglos antes que este sabio. Las referencias prehelénicas al Teorema no contienen, sin embargo, pruebas del mismo, mientras que es generalizada la creencia de que fue Pitágoras el primero en proporcionarnos una demostración lógica del Teorema, lo que hará justo que éste haya pasado a la historia con su nombre. Diógenes Laercio en su Vida de filósofosrecoge (Pitágoras VIII.7) una referencia de un tal Apolodoro «El Calculador» sobre Pitágoras, en la que asegura que este filósofo sacrificó una hecatombe (cien bueyes), habiendo hallado que en un triángulo rectángulo «la potestad de la línea hipotenusa es igual a la potestad de las dos que lo componen». Continua diciendo que Apolodoro compuso un epigrama en verso: «Pitágoras hallada / aquella nobilísima figura / bueyes mató por ello en sacrificio». Estas anécdotas son, sin duda, ficticias, porque contradicen la filosofía pitagórica sobre la transmigración de las almas, pero han contribuido a magnificar la leyenda que envuelve a Pitágoras, y además determinaron que en la Edad Media al Teorema de Pitágoras se le llamara «Inventum hecatombe dignum».
Sea ABC un triángulo rectángulo, con el ángulo recto en A, y sea AD perpendicular al lado BC. Según Euclides VI.8 los triángulos DBA y DAC son ambos semejantes con el triángulo ABC y semejantes entre sí. Prueba 1. De la semejanza de los triángulos ABC, DBA y DAC resulta: BA/BD = BC/BA , AC/CD = BC/AC (Euclides VI.4). De aquí se hayan las expresiones del llamado «Teorema del cateto»: BA2 = BD·BC , AC2 = CD·BC, que al sumarlas, se obtiene: BA² + AC² = (BD+CD)·BC = BC·BC = BC², es decir: BA2 + AC2 = BC2. En esta demostración del Teorema de Pitágoras –basada en el Teorema del cateto–, se descompone, de forma implícita, el cuadrado sobre la hipotenusa, BCIK,en dos rectángulos, BDJK y DCIJ, cada uno de ellos con el mismo área que cada uno de los cuadrados construidos sobre los catetos –el rectángulo BDJK de área como el cuadrado ABEF sobre el cateto AB –ya que BA2 =BD·BK, y el rectángulo DCIJ de área como el cuadrado ACHG sobre el cateto AC –ya que AC2 = CD·CI–. Debemos observar que la figura exhibida forma parte de la figura que utiliza Euclides en su demostración del Teorema de Pitágoras en la Proposición I.47 de Los Elementos de Euclides, y además, puntualizar que variantes de esta prueba se encuentran en el hindú Bhaskara, en Leonardo de Pisa (Fibonacci)y en Wallis. Prueba 2. De la semejanza de los triángulos ABC, DBA y DAC resulta, según Euclides VI.19 («la razón entre las áreas de los triángulos semejantes será igual al cuadrado de la razón de semejanza»): DBA/AB² = DAC/AC² = ABC/BC². Pero de las propiedades de la suma de proporciones (Euclides 5.12) resulta: ABC/BC2 = DBA/AB2;= DAC/AC2;= (DBA+DAC) / (AB2+AC2) = ABC / (AB2+AC2) por tanto se tiene: AB2+AC2 = BC2. Como vemos, estas pruebas del Teorema de Pitágoras mantienen su plena vigencia en los libros de texto de matemáticas escolares elementales. Quizá ningún teorema de la amplia Matemática haya recibido tantas demostraciones diversas como el Teorema de Pitágoras. De todas ellas la más famosa es sin duda la realizada por Euclides en la Proposición I.47 de Los Elementos. En la Edad Media esta Proposición se la consideraba la base de toda sólida formación matemática. En algunos centros docentes además de exigir, para obtener el grado de maestro, un profundo conocimiento del Teorema, se obligaba a exhibir una nueva y original demostración del mismo, por eso el Teorema de Pitágoras alcanzó la honrosa designación de «Magister matheseos». Este hecho y la gran significación del teorema explica la razón de las innumerables demostraciones que los matemáticos y no matemáticos de todas las épocas y personajes tan diversos como filósofos, monjes, políticos, juristas, ingenieros y artistas, han encontrado del más famoso Teorema de la Geometría. El Teorema de Pitágoras aparece por doquier en la Matemática. Es la base de multitud de teoremas geométricos, de la trigonometría y de la Geometría analítica. La ecuación pitagórica x2+y2=z2 es la ecuación de la circunferencia, la base de la fórmula cos2a+sen2a=1 y el origen del Análisis indeterminado de Diofanto y Fermat. También pudo ser el germen del dramático alumbramiento de la inconmensurabilidad en la Escuela pitagórica. La aparición del Teorema de Pitágoras en el horizonte histórico cultural pero también en el horizonte escolar señala el primer salto intelectual entre los confines de la especulación empírica y los dominios del razonamiento deductivo. Así pues, estamos ante un auténtico paradigma para la Matemática y sobre todo para la Educación matemática. Por esto y por su universalidad el Teorema de Pitágoras pertenece al imaginario cultural de casi todos los pueblos. La Divina Proporción y el Pentagrama pitagórico Uno de los tópicos pitagóricos más fascinantes y que más influencia ha tenido sobre el Arte, la Mística, la Biología e incluso la Magia ha sido la Sección Áurea o Divina Proporción.Euclides introduce la noción en la Definición VI.3 de Los Elementos:
Importantes especulaciones filosóficas, teológicas, naturales y estéticas han surgido en torno a la Divina Proporción desde que la humanidad empieza a reflexionar sobre las formas geométricas que conforman el mundo, siendo el Pitagorismo quien comienza a dar consistencia racional a toda esta doctrina. Puede decirse que donde haya una especial intensificación de la belleza y la armonía de las formas, ahí se encontrará la Divina Proporción, por ejemplo en muchos aspectos de la naturaleza, de donde muchos artistas extraerán su inspiración. La Divina Proporción, sobre todo en forma de rectángulo áureo (con las dos dimensiones en proporción áurea), constituye uno de los métodos canónicos de composición para obras de arte más utilizados por toda clase de artistas a lo largo de toda la Historia del Arte interviniendo, además, en el canon ideal de la belleza humana, en particular en las dimensiones del rostro y de la mano. Buena parte de la Geometría pitagórica en relación con la sección áurea, tuvo que ver con el pentágono regular. Ya se comentó que la figura de la estrella de cinco puntas que se forma al trazar las cinco diagonales de un pentágono llamada Pentagrama místico era una especie de símbolo de identificación de la Escuela Pitagórica; por eso los pitagóricos estudiaron exhaustivamente la construcción y propiedades del pentagrama. El pentagrama místico de Pitágoras fue un diagrama simbólico esencial del esoterismo geométrico de los pitagóricos que trasmitido desde la antigüedad hasta el siglo XVIII forma parte de dos tradiciones culturales importantes: los trazados de los arquitectos y las estrellas pentagonales del simbolismo mágico europeo, corrientes subterráneas que emergen a la luz a través de la obra de Luca Pacioli LaDivina Proporción, que con finalidad teológica racionaliza los arcanos del misticismo geométrico pitagórico, exhumando una ciencia geométrica en cuyas fuente beberán Alberti, Durero y otros muchos artistas del Renacimiento.
|
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |






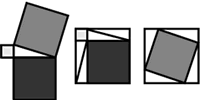 La tradición ha establecido que Pitágoras habría dado una prueba empírica del Teorema con base en las figuras adjuntas.
La tradición ha establecido que Pitágoras habría dado una prueba empírica del Teorema con base en las figuras adjuntas.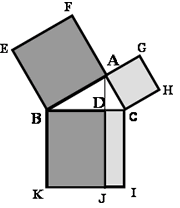 Muchos historiadores admiten que la demostración de Pitágoras se basaría en su propia Teoría de las Proporciones –imperfecta por aplicarse sólo a cantidades conmensurables–, de modo que la prueba de Pitágoras podría haber sido alguna de las dos siguientes :
Muchos historiadores admiten que la demostración de Pitágoras se basaría en su propia Teoría de las Proporciones –imperfecta por aplicarse sólo a cantidades conmensurables–, de modo que la prueba de Pitágoras podría haber sido alguna de las dos siguientes :
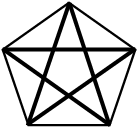 El Pentagrama místico pitagórico se obtiene a partir de tres triángulos isósceles iguales que tienen los ángulos iguales dobles del ángulo desigual. Este tipo de triángulo –llamado áureo porque los lados iguales están en proporción áurea con el lado menor– se construye en la Proposición 10 del Libro IV de Los Elementos de Euclides, cuyo contenido es de raíz pitagórica en su mayor parte. En la siguiente Proposición, la IV.11, se construye efectivamente el Pentagrama a base de inscribir en un círculo un pentágono regular y trazar las diagonales, las cuales de forma sorprendente se cortan determinando segmentos que están en proporción áurea siendo el segmento mayor igual al lado del pentágono (Euclides XIII.8).
El Pentagrama místico pitagórico se obtiene a partir de tres triángulos isósceles iguales que tienen los ángulos iguales dobles del ángulo desigual. Este tipo de triángulo –llamado áureo porque los lados iguales están en proporción áurea con el lado menor– se construye en la Proposición 10 del Libro IV de Los Elementos de Euclides, cuyo contenido es de raíz pitagórica en su mayor parte. En la siguiente Proposición, la IV.11, se construye efectivamente el Pentagrama a base de inscribir en un círculo un pentágono regular y trazar las diagonales, las cuales de forma sorprendente se cortan determinando segmentos que están en proporción áurea siendo el segmento mayor igual al lado del pentágono (Euclides XIII.8).
