La órbita de Ceres

Desde que en 1781 Herschel descubriera el planeta Urano, una fiebre por descubrir el esquivo planeta que los astrónomos Titius y Bode habían situado entre Marte y Júpiter.
El siglo XIX no puede empezar con mejores augurios en esta desesperada búsqueda. Exactamente la noche del primer día de enero de 1801, Giuseppe Piazzi, un clérigo de Palermo y astrónomo aficionado observa por primera vez lo que él piensa, como Herschel unos años antes, que es un nuevo cometa, un objeto de magnitud 8. Durante cuarenta y dos días, hasta la noche del 11 de febrero realiza el seguimiento del nuevo objeto en su viaje por el fondo de estrellas. Pero una inoportuna gripe le mantiene alejado del telescopio las noches siguientes. Cuando se reincorpora a la observación el astro ha dejado de ser visible durante la noche. Sencillamente ha desaparecido ocultado por el Sol. El corto periodo de observaciones no le permite fijar la órbita del “cometa” y predecir dónde volvería a aparecer en el cielo nocturno. Sus datos abarcaban sólo un arco de 9 grados de la órbita.
Cuando los datos de sus observaciones se divulgan un hecho parece claro, la distancia heliocéntrica del objeto lo sitúa entre Marte y Júpiter. En el mes de junio de ese mismo año el astrónomo alemán Franz von Zach utilizando los datos de Piazzi realiza un estudio previo de la órbita, sin ningún éxito.
Como el supuesto “cometa” no aparece por ninguna parte del firmamento, Zach envía los datos a un joven matemático de 24 años afincado en Gottingen, cuya fama se empieza extender por toda Alemania para que realice su propia estimación de la órbita. Se trata de Johann Friedrich Carl Gauss.

La posición del astro que se deducen de los cálculos de Gauss es muy diferente de todas las demás. Las predicciones de Zach y de otros astrónomos profesionales resultaron erróneas. No así las del joven Gauss, que puso en el intento además de su enorme capacidad de cálculo una de las herramientas matemáticas más fructífera para el cálculo de órbitas planetarias como se demostrará a lo largo del siglo: la ley de mínimos cuadrados, descubierta por Gauss unos seis años antes y que mantuvo sin publicar hasta 1809.

En diciembre, Zach decide por fin probar con las predicciones de Gauss y muy cerca de donde los cálculos teóricos de éste situaban el deseado objeto aparece un pequeño punto brillante; es la noche del 7 de diciembre. Las observaciones se prolongan todas las noches de diciembre, al menos todas en las que las condiciones meteorológicas lo permiten y por fin, el 1 de enero de 1802, Orbels en Bremen puede afirmar con toda certeza que el objeto observado encaja a la perfección con los datos de las observaciones de Piazzi de hace un año y con la órbita prevista teóricamente por Gauss. El pretendido cometa de Piazzi era en realidad un nuevo planeta que será observado por los astrónomos más prestigiosos a lo largo de los próximos meses en toda Europa: el 3 de febrero Maskelyne confirma su avistamiento en Grenwich, y unos días más tarde el propio Bode en Berlín y Méchain en París. Pero en el lugar del planeta perdido entre Marte y Júpiter no había uno, sino un rosario de pequeños planetas, los asteroides.

Gracias a Ceres, al final del primer año del nuevo siglo, Gauss es además de uno de los matemáticos más notables, el astrónomo más popular de Europa.

En marzo de 1802 Olbers descubre Pallas y plantea a Gauss la fijación de su órbita. El método de los mínimos cuadrados vuelve a manifestar su potencia... Orbels le propone la dirección del nuevo observatorio de Gottingën, aún por construir. En noviembre el joven Gauss, que cuenta con 25 años es nombrado miembro de la Real Sociedad de Ciencias de Gottingën. Tres meses más tarde rechazará una oferta para instalarse en San Petersburgo como miembro de la Academia de Ciencias.

La década triunfal. 1800-1810

La primera década del siglo XIX es la década triunfal del joven matemático. En 1805 se casa con Johanna Ostoff con la que tendrá tres hijos: Joseph, Minna y Louis. Al año siguiente, poco después del nacimiento de su primer hijo, participará con el coronel francés Epailly en la triangulación de Brunswick, lo que dará origen a su interés por la geodesia.

En 1807 es nombrado profesor en Gottingën y director de su observatorio astronómico que por los avatares políticos, la ocupación napoleónica de gran parte de los estados germánicos, no se terminará hasta 1816.

Durante estos años prepara la que será la obra cumbre de la astronomía teórica durante más de medio siglo, la Theoria motus corporum coelestium in sectionibus conicis solem ambientium (Teoría del movimiento de los cuerpos celestes que giran alrededor del Sol siguiendo secciones cónicas)., publicada en 1809, una obra en dos volúmenes, el primero trata de las ecuaciones diferenciales, las secciones cónicas y las órbitas elípticas, en el segundo Gauss explica su método de mínimos cuadrados para la determinación de la órbita de un planeta. Aunque conocido y aplicado por Gauss desde 1796, la publicación de Legendre de un método similar en 1806 alimentó una agria polémica entre ambos sobre la paternidad del mismo.

Gauss es el padre de la moderna teoría de errores. Descubrió que la función de distribución de los errores es: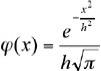

, la célebre campana de Gauss.

En la memoria presentada a la Real Sociedad de Gottingen el 15 de febrero de 1821, titulada Método de Mínimos Cuadrados. Teoría de la combinación de las observaciones, Gauss desarrolla de forma completa y general sus ideas ya esbozadas en 1809 en Theoría motus corporum coelestium...

Pero 1809 también será un año negro para Gauss; en octubre muere esposa al mes de dar a luz a su tercer hijo Louis, que morirá a los tres meses.

Un año más tarde y tras rechazar una oferta de Humbolt para ocupar una plaza en la universidad de Berlín, Gauss contrae nuevo matrimonio con Minna Waldeck, amiga de Johanna, con la que tendrá dos hijos varones Eugen y Wilhelm y una hija Therèse.

1810 -1830. Astronomía, Geodesia y Matemáticas.

Desde 1810 hasta 1830 la mente de Gauss se ocupa de sus tareas como director del astronómico que se inaugurará en 1816 y que le obligará a realizar uno de los pocos viajes conocidos de Gauss para adquirir material científico para el mismo, pero no abandona sus investigaciones matemáticas.
Investiga sobre series infinitas y sobre la serie hipergeométrica, sobre aproximación de integrales y sobre estimadores estadísticos.

En 1816 confiará en carta a su ex -alumno Schumacher (profesor de Astronomía en Copenhague) sus ideas sobre la geometría no euclídea que llevaba desarrollando desde hacía 20 años.

En 1818 el ministro Arnswaldt encarga a Gauss la triangulación y medición de Hannover. Es una práctica muy habitual sobre todo tras la medición del meridiano realizada por los franceses e impuesta por las necesidades militares – toda Europa está en guerra - de una cartografía precisa. Durante casi 8 años, hasta 1825, Gauss dedicará sus esfuerzos a una práctica rutinaria y agotadora, al alcance de cualquier calculista mediano: efectúa mediciones durante el día y realiza los cálculos durante la noche, que le apartarán de actividades mucho más productivas en el ámbito de las matemáticas. Podemos afirmar que durante casi 20 años el genial Gauss perdió gran parte de su tiempo en tediosos cálculos astronómicos y geodésicos. Pero fruto de esta tarea nacerán más de 70 escritos sobre Geodesia,  la aplicación del método de mínimos cuadrados a medidas terrestres, el invento del heliotropo, un mecanismo ingenioso gracias al cual pueden ser transmitidas instantáneamente señales por medio de la luz del sol reflejada, y su interés por la geometría de superficies.

La triangulación de Hannover se reinició en 1828, duró hasta 1844, y en ella participó su hijo Joseph, oficial del ejército.

Geometría diferencial: 1827. Disquisitiones circa generales superficies curvas

Esta obra, fruto de las ideas sobre la geometría de superficies nacidas de sus observaciones geodésicas constituye la contribución definitiva de Gauss a la geometría diferencial.
Gauss concibe la superficie “no como el límite de un sólido, sino como un sólido flexible e inextensible, una de cuyas dimensiones está obligada a desvanecer”.

Pero su gran aportación va a ser no estudiar la superficie desde un punto de vista global sino desde un punto de vista local, en el entorno de un punto. Esto le va a permitir despreciar las potencias de grado superior a dos en el cálculo de las distancias.
En esta obra está Gauss aborda tres grandes problemas: la medida de la curvatura, la representación conforme y la aplicabilidad de superficies.

Gauss define la curvatura total de una porción de superficie encerrada dentro de una curva C de la siguiente manera: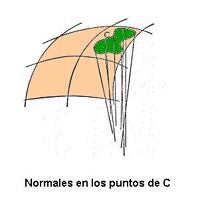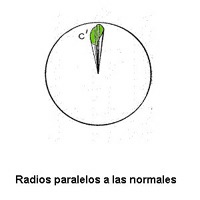

La normal a una superficie en un punto dado es la recta que pasa por el punto y que es perpendicular al plano tangente a la superficie en el punto. En cada punto de C existe una normal a la superficie. Si trazamos todas las normales en los puntos de C tendremos un haz de rectas.

En una esfera de radio unidad trazamos las paralelas a las rectas normales a C que pasen por el centro de la esfera.

Este haz de rectas corta a la superficie esférica determinando una curva C'. El área encerrada de la superficie esférica encerrada por esta curva C' se denomina curvatura total de la porción de superficie limitada por C.

La curvatura total en un punto interior de C es el límite de la razón entre el área de C' y el área de C cuando la superficie C tiende al punto.

Cada normal en un punto de una superficie genera un haz de planos que lo tienen como eje. Cada uno de esos planos corta a la superficie en curvas planas dentro de ellos. Cada una de esas curvas en el punto de apoyo de la normal tiene una curvatura dada. Entonces dado un punto de una superficie habrá un conjunto de curvaturas planas. Se sabe que hay una máxima y una mínima. La curvatura gaussiana que es el producto de la curvatura máxima por la curvatura mínima, las curvaturas principales introducidas por Euler.

En su estudio de superficies Gauss utiliza de forma magistral la representación paramétrica introducida por Euler, realizando una visión intrínseca de la superficie como una variedad bidimensional, las coordenadas (x, y, z) de un punto vienen dadas por tres ecuaciones dependiendo de dos parámetros: x=x(u,v); y=y(u,v);  z=z(u,v).

Demuestra que si dos superficies son isométricas (aplicable la una sobre la otra) la curvatura total en dos puntos correspondientes es la misma. (theorema egregium). Una conclusión inmediata es que para mover sin distorsión una parte de una superficie sobre otra parte de la misma superficie es necesario que la superficie tenga curvatura constante. Así una parte de una esfera puede ser desplazada sin distorsión sobre otra, pero esto no ocurrirá con un paraboloide.
Trata también el problema de determinar las geodésicas (el equivalente a las rectas en el plano) de una superficie.

En un artículo publicado en 1827 demuestra que la curvatura total de un triángulo cuyos lados son geodésicas y los ángulos α₁, α₂ y α₃ viene dada por ∫∫KdA = α₁+α₂+α₃-π, donde K es la curvatura variable en los puntos del triángulo.

En esta obra se pone definitivamente de manifiesto una observación interesante: la superficie puede ser un espacio en sí misma y las líneas rectas son las geodésicas siendo su geometría, una geometría no euclídea.

Los números complejos

Desde 1799 Gauss dominaba la idea de una representación bidimensional de los complejos, de hecho los utilizó en su tesis doctoral aunque no de forma explícita. Y en 1811, tiene completamente acabada no sólo la representación de los complejos como puntos de un plano bidimensional, sino también la idea de integración de funciones complejas, el teorema integral y el desarrollo en serie de potencias de funciones analíticas. Buena prueba de ello es la carta que dirige a Bessel este año, comentando un ensayo de éste sobre la integral logarítmica ∫, en la que podemos leer:

¿Qué debemos entender por ∫φ(x)·dx para x=a+bi?
Evidentemente si se quiere partir de conceptos claros es necesario admitir que x, partiendo del valor para el cual la integral debe ser cero, mediante incrementos infinitesimales (cada uno de la forma a + bi) pasa a x = a + bi y entonces se suman todos los φ(x)·dx.

Así el sentido de la integral queda completamente establecido. Pero el paso se puede dar de infinitas maneras: así como la totalidad de las magnitudes reales se pueden imaginar en forma de una recta infinita, también la totalidad de todas las magnitudes reales e imaginarias se puede en imaginar mediante un plano infinito, cada uno de cuyos puntos de abscisa a y ordenada b representará la magnitud a+bi. El paso continuo de un valor de x a otro a+bi se representa entonces mediante una línea, posiblemente de infinitas maneras.
Afirmo ahora que la integral ∫φ(x)·dx para dos caminos distintos siempre conserva un mismo valor si dentro de la parte del plano comprendida entre las dos líneas representantes del cambio, φ(x) no se hace infinita.
Este maravilloso teorema, cuya demostración no es difícil la daré en otro momento. El teorema está vinculado con otras verdades magníficas relacionadas con el desarrollo en series”

Gauss, como 150 años antes hiciera Fermat con su famoso último teorema, nos amenaza con la publicación de una demostración, que él ya parece tener, de un resultado que será demostrado por Cauchy  en 1825 y que hoy se conoce como teorema de la integral compleja de Cauchy.

Habrá que esperar hasta 1831, para que Gauss, en una extensión de la teoría de los restos bicuadráticos a los números complejos, haga su presentación definitiva y su representación geométrica ante la sociedad matemática, propiciando gracias a su reconocida autoridad su aceptación definitiva. En esta obra introduce la noción de enteros complejos sobre los que generalizará resultados obtenidos para enteros reales.

Gauss y la geometría no euclídea.

La preocupación de Gauss por el problema de las paralelas, el quinto postulado de Euclides, data de 1796, de su estancia en Gottingën. Su profesor Kastnër disponía de una biblioteca de varios miles de volúmenes sobre este tema y seguro que contagió su inquietud a dos jóvenes inquietos como Gauss y Bolyai.
A partir de 1813 hasta 1831 elabora su geometría no euclídea. En 1813 escribe a Schumacher: “En la teoría de las líneas paralelas, nosotros, no nos encontramos más allá de Euclides. Esta es la parte de la matemática, que más tarde o más temprano debe adquirir una fisonomía absolutamente distinta”. Gauss
encuentra numerosos resultados pero no se atreve a publicarlos. En 1829 en carta a Bessel le comunica: “Pasará tiempo antes de que yo elabore para conocimiento público mis extensas investigaciones, y quizás esto no llegue a ocurrir durante mi vida, pues temo el griterío de los beocios (das geschrei der böotier), si alguna vez me propusiera exponer mi criterio”.

No es de extrañar que cuando Gauss recibe en 1831 el anexo de Johann Bolyai, hijo de su viejo compañero, La ciencia absoluta del espacio, exponiendo sus ideas sobre una geometría no euclídea, Gauss responda a Wolgang: “Si empiezo diciendo que no puedo alabar semejante trabajo te sentirás desconcertado, pero no puedo hacer otra cosa, porque alabarlo sería alabarme a mí mismo, pues todo el contenido del escrito, el camino seguido por tu hijo y los resultados a los que ha llegado coinciden casi completamente con mis meditaciones, parte de las cuales han tenido lugar desde hace 30 o 35 años”.

Sin embargo Gauss consideró públicamente a Janos Bolyai y a Lobachevski, cuando conoció los escritos de éste en 1841, como genios de primera magnitud; de hecho y a propuesta de Gauss Lobachevski fue nombrado miembro de la Academia de Gottingën en 1842.
Hoy nadie discute que la paternidad de la primera geometría no euclídea es una gloria compartida por Gauss, Bolyai y Lobachevski.

El magnetismo terrestre

1831 será un año clave en la vida de Gauss. Si un año antes su hijo Eugen emigra a Estados Unidos al parecer por desavenencias familiares, este año muere Minna la segunda esposa de Gauss. Desde entonces será su hija Therèse la que se encargará de los asuntos domésticos.  Pero a finales de ese año llega a Gottingën Wilhelm Weber, para ocupar la plaza de profesor de Física. A partir de este momento un decaído Gauss va a encontrar otra vez en la ciencia la solución de sus males familiares.

En estrecha colaboración con Weber Gauss desarrollará una intensa labor en el estudio del magnetismo terrestre. Acoge con entusiasmo la propuesta de Alexander von Humbodlt de crear una red de observatorios magnéticos que cubran toda la superficie terrestre. En la década de los 30 publica varias obras sobre el tema: Intensitas vis magneticae terrestris ad mensuram absolutam revocata (1832), que trata teorías actuales sobre magnetismo terrestre, anticipando las ideas de Poisson, la medida absoluta de la fuerza magnética y una definición empírica del magnetismo terrestre,  Allgemeine Theorie Erdmagnetismus (1839), en la que demuestra que solo puede haber dos polos y sienta las bases para determinar la intensidad de la componente horizontal de la fuerza magnética junto con el ángulo de inclinación. Se ayuda de la ecuación de Laplace y especifica la ubicación del polo sur magnético. Ambos construyen el primer telégrafo electromagnético que conseguía transmitir hasta nueve letras por minuto a una distancia de 500 pies, la que se paraba el Observatorio Astronómico de la Facultad de Física.

Junto a Weber es autor del primer atlas geomagnético terrestre y de más de 40 obras sobre mediciones magnéticas de la Sociedad de Magnetismo, fundada por ellos, y de nuevas herramientas para medir el campo magnético. Sin embargo, un hecho va a truncar esta fructífera colaboración, Weber, junto a otros 6 profesores, es despedido de su cargo por negarse a jurar fidelidad al nuevo rey Ernesto Augusto von Cumberland, que había derogado la constitución de 1833. Gauss, de carácter conservador, no movería un dedo a pesar de su influencia para detener el despido, a pesar de que entre los 7 de Gottingën estaban su propio yerno y su inseparable colaborador.

Tras la marcha definitiva de Weber de Gottingën la producción científica de Gauss disminuye de forma rotunda. Trabaja en sus observaciones astronómicas, en dióptrica, en la teoría del potencial, en geodesia pero todas son obras menores.

Los últimos años

En 1849, con motivo del cincuentenario de su doctorado impartirá su famosa conferencia en la que presentará su cuarta demostración del Teorema Fundamental del Álgebra, una variación de la presentada en su tesis, incorporando ya de manera abierta los coeficientes complejos. Jacobi y Dirichlet serán testigos excepcionales. El reconocimiento de Gauss es general en Alemania y en toda Europa.

Continuará con sus observaciones astronómicas hasta 1851, contando entre sus alumnos en estos años a Dedekind y Cantor. Y en junio de 1854, será el presidente del tribunal de la prueba para la habilitación de Riemann como profesor de matemáticas. En ella, Riemann a petición del tribunal leerá su famosa exposición, Sobre las hipótesis en que se fundamenta  la geometría, que sin duda impactó al anciano Gauss por lo que suponía de reconocimiento de las geometrías no  euclídeas.

Curioso ante el progreso tecnológico visitará unos días más tarde las obras del ferrocarril Hannover – Gottingen, excursión en la que casi pierde la vida al sufrir un grave accidente el coche de caballos en que viajaba. De cualquier manera, el corazón del anciano Gauss, aquejado de hidropesía, está dando sus últimos latidos. Y dejará de latir de forma irremediable en la madrugada del 23 de febrero de 1855 mientras dormía plácidamente. Tenía 77 años, 10 meses y 22 días y sobre sus hombros la obra matemática más grandiosa en la historia de Humanidad. Sin duda, como muy bien reflejaba la inscripción de la  moneda acuñada en su honor por el rey Jorge V de Hannover, Gauss era “el Príncipe de los Matemáticos”.

Como decía su amigo Sartorius von Waltershausen, "Gauss fue sencillo y sin afectación desde su juventud hasta el día de su muerte. Un pequeño estudio, una mesita de trabajo con un tapete verde, un pupitre pintado de blanco, un estrecho sofá, y, después de cumplir los 70 años, un sillón, una lámpara con pantalla, una alcoba fresca, alimentos sencillos, una bata y un gorro de terciopelo eran todas sus necesidades".