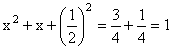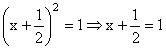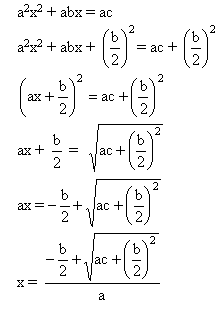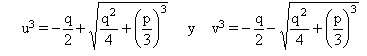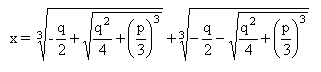1. Algunos datos biográficos y científicos

2.1. La ecuación cuadrática

La resolución de la ecuación de segundo grado se remonta a los comienzos de la matemática en general y a los del álgebra en particular. A modo de ejemplo, sirvan los siguientes testimonios históricos en los que sepone de manifiesto la habilidad de los matemáticos de otros tiempos y, además, y se detectan algunos de los tres estilos (retórico, sincopado y simbólico) que aparecen en el desarrollo y evolución del simbolismo algebraico.

2.1.1. La resolución de la ecuación de segundo grado en Babilonia

La tablilla cuneiforme BM13901 contiene abundante material relativo a la resolución de ecuaciones de segundo grado con una incógnita.

En el siguiente texto se pueden apreciarlos conocimientos que sobre el particular tenían los matemáticos babilonios allá por el año 2000 a. C.

BM13901 / Problema 1	Traducción al simbolismo algebraico moderno
He sumado el área y el lado de un cuadrado [y he obtenido]: 3/ 4
Escribe 1, el coeficiente [del lado del cuadrado]. Divídelo en dos partes iguales. Multiplica 1/ 2 por 1/ 2: 1/ 4. Añade 1/ 4 a 3/ 4: 1.
Esto es el cuadrado de 1.
Quita 1/ 2 de 1. El lado del cuadrado es 1/2.

2.1.2. La ecuación de segundo grado en la India

Para resolver la ecuación x² – 10x = –9, el matemático indio Brahmagupta (ca. 628 d. C.) propuso el siguiente procedimiento:

Multiplica el número absoluto, –9, por el [coeficiente del] cuadrado, 1; el resultado es –9.

Añádelo al cuadrado de la mitad [del coeficiente del] término medio, 25, y resulta 16; cuya raíz cuadrada, 4, menos la mitad del [coeficiente de la] incógnita, –5, es 9; y dividido por el [coeficiente del] cuadrado, 1, da como resultado el valor de la incógnita, 9.La “regla de Brahmagupta”, aplicada a la ecuación ax² + bx = c, se puede traducir del modo siguiente:

2.1.3. La resolución de la ecuación cuadrática en Arabia

El matemático árabe Mohamed ibn Musa al-Khowarizmi (s. IX) utilizó la siguiente estrategiapara resolver la ecuación x² + 10x = 39.

Debes tomar la mitad del número de las raíces, que es 5, y multiplicarlo por sí mismo y obtienes 25 al que le sumas el número 39, con el resultado 64. Tomas la raíz cuadrada de este número, que es 8, y le restas la mitad de las raíces, 5, y obtienes 3, que es el valor buscado.

2.1.4. La ecuación de segundo grado en el Renacimiento

Juan Pérez de Moya (ca. 1512 – 1596), en su Aritmética Práctica y Especulativa (1562), resolvió en versión sincopada el siguiente problema cuadrático:

Dame vn numero que juntandole 5 y por otra parte quitandole 2 y multiplicando la suma por la resta, monte 98. Pon que el numero demandado es 1.co. [= x] si le juntares 5.n. [= 5] será 1.co. p.5.n. [= x + 5]. Si le quitas 2 quedará 1.co.m.2. [= x – 2] multiplicando 1.co.p.5.n. que es la suma, por 1.co.m.2.que es la resta, (...) monta 1.ce.p.3.co.m.10.n. [= x² + 3x – 10] lo qual igualarâs a 98.n. [= 98] que quisieras que vinieran desta manera 1.ce.p.3.co.m.10.n. ig. a 98.n. [x² + 3x – 10 = 98]. Passa los 10.n. que vienen menos en la vna parte de la balança a la otra (...) y quedará la igualacion desta manera 1.ce.p.3.co. ig.a 108.n. [x² + 3x = 108]. Sigue la regla partiendo llanamente los 3 y los 108 que es lo que viene con los menores caracteres, por 1 que viene con el ce. [= x²] que en este exemplo es el mayor, y vendrà a los quocientes lo mismo: despues saca la mitad del quociente del mediano, que es 3, y serâ vno y medio, quadra vno y medio, y seràn dos y vn quarto [= 9/4], juntalo con 108 que es el quociente del menor carácter, y montará 110 y vn quarto saca la r. Serà diez y medio , quita desto la otra mitad del quociente del mediano, que es vno y medio, y quedaran nueue . Estos nueue es el valor de vna cosa [= incógnita] y respuesta de la demanda.

2.1.5. A modo de resumen

A la vista de los resultados obtenidos en los ejemplos anteriores se observa que las raíces de la ecuación de segundo grado con una incógnita se pueden obtener por una fórmula en la que los coeficientes de la ecuación están ligados únicamente por las operaciones de adición, sustracción, multiplicación, división y radicación. Dicho en otras palabras: la ecuación cuadrática es resoluble por radicales.

2.2. La ecuación cúbica

2.2.1. Tercetos de tercer grado

Los acontecimientos que tuvieron lugar en torno al problema de la resolución de la ecuación de tercer grado configuran uno de los episodios más apasionantes de la historia del álgebra.

En 1539,Nicolò Fontana “Tartaglia” (ca. 1499 – 1557) comunicó a Girolamo Cardano (1501 – 1576), mediante unos tercetos, las reglas que permitían resolver tres tipos de ecuaciones de tercer grado [x³ + px = q ; x³ = px + q; x³ + q = px, (p, q >0)].

He aquí la traducción e interpretación matemática de los tres tercetos en los que el “tartamudo de Brescia”describe la regla para calcular la única raíz positiva de la ecuación x³ + px = q.

Cardano, como muestra de agradecimiento, se comprometió a no revelarlas hasta que Tartaglia las hiciese públicas. No obstante, ante la tardanza de dicha publicación, Cardano las dio a conocer en su Ars Magna (1545).

Este hecho provocó que, al año siguiente, Nicolò Fontana publicase algunos comentarios despectivos sobre Girolamo que originaron una polémica nada edificante entre Tartaglia y Ludovico Ferrari (1522 – 1565), otro de los grandes matemáticos italianos del Renacimiento.

En las líneas siguientes, utilizando el simbolismo moderno y mediante un proceso similar al de Tartaglia-Cardano, presentamos la fórmula que permite resolver la ecuación de tercer grado por radicales.

Es un hecho bien conocido que cualquier ecuación general de tercer grado se puede transformar, mediante los cambios pertinentes, en otra sin término de segundo grado y cuyo primer coeficiente es 1. En consecuencia, basta con estudiar las ecuaciones del tipo:.

x³ + px + q = 0 [1]

A partir de la identidad (u + v)³ = u³ + v³ + 3uv (u + v) se puede escribir la siguiente relación:

(u + v)³ – 3uv(u + v) – (u³ + v³) = 0 [2]

Comparando [1] y [2], se tiene que:

x = u + v
3uv = – p
u³ + v³ = – q

A partir de las dos últimas igualdades no resulta difícil obtener que:

De donde, por extracción de la raíz cúbica, se obtienen tres valores para u y tres valores para v, a partir de los cuales se generan nueve parejas (u, v). De ellas sólo tres verifican las restricciones 3uv = – p y u³ + v³ = – q.

Con esto, las tres raíces de la ecuación [1] vienen dadas por:

Si, < 0 estamos en presencia del “caso irreducible” cuyas soluciones reales se deben calcular haciendo intervenir números complejos.

2.3. La ecuación cuártica

Se debe a Ludovico Ferrari, discípulo de Cardano, la resolución por radicales de la ecuación de cuarto grado.

En esencia, el procedimiento de Ferrari se puede resumir, utilizando el simbolismo algebraico moderno, en los siguientes términos:

Sea la cuártica

Entonces:

En esta situación, para un valor arbitrario y se tiene que

[3]

Recordando que la condición necesaria y suficiente para que el polinomio de segundo grado ax² + bx + c sea cuadrado perfecto es que b² – 4ac = 0, resulta que para que el segundo miembro de [3] sea un cuadrado perfecto deberá cumplirse que:

[4]

La ecuación [4], de tercer grado en y, puede resolverse por radicales. Esto permite escribir los dos miembros de [3] como cuadrados perfectos y, por extracción de la raíz cuadrada en sus dos miembros, determinar las soluciones de la ecuación cuártica propuesta. En otras palabras: la ecuación de cuarto grado con una incógnita es resoluble por radicales.

Acabamos de ver que, desde el siglo XVI, se sabía que las ecuaciones polinómicas de grado inferior a cinco eran resolubles por radicales.

¿Podía afirmarselo mismo de las ecuaciones de grado superior?

Esta cuestión mantuvo ocupado a Paolo Ruffini durante buena parte de su vida.

En su Teoria generale delle equazioni, in cui si dimostra impossibile la soluzione algebraica delle equazioni generali di grado superiore al quarto, publicada en 1799, presentó una demostración sobre la imposibilidad de resolver por radicales las ecuaciones de grado superior al cuarto. Dicha demostración fue revisada en las versiones de 1803, 1808 y 1813.En la introducción de su memoria puede leerse:

La resolución algebraica de las ecuaciones generales de grado mayor que el cuarto es siempre imposible. (...) presentar la prueba de ello es la razón principal para publicar este volumen. El inmortal Lagrange, con sus reflexiones sublimes, ha proporcionado las bases de mi demostración.

La demostración de Ruffini no fue concluyente, dado que se apoyaba en una hipótesis incompleta, ni fue bien recibida por la mayoría de sus contemporáneos (algunos de ellos ni la entendieron) y sucesores.

Joseph Louis Lagrange (1736 – 1813) no contestó a las cartas de Ruffini en las que le solicitaba su opinión acerca de su memoria.

Giovanni Francisco Malfatti (1731 – 1807), en su Dubbii proposti al socio Paolo Ruffini sulla sua dimostrazione della imposibilita di risolvere le equazioni superiori al quarto grado, manifestó sus dudas acerca de la irresolubilidad de la quíntica.Adrien Marie Legendre (1752 – 1833) y Lazare Carnot (1753 – 1823) también se expresaron en similares términos.

Ruffni: Teoria Generale delle equazioni

Por su parte, Niels Henrik Abel (1802–1829) al que se debe la demostración definitiva de la irresolubilidad, refiriéndose a la prueba de Ruffini se despachaba así:

El primero, si no me equivoco, el único antes de mi que ha intentado demostrar la imposibilidad de la resolución algebraica de las ecuaciones generales, es el geómetra Ruffini; pero su memoria es tan complicada que es difícil juzgar la veracidad de su razonamiento. Me parece que su razonamiento nosiempre es satisfactorio.

El único matemático de prestigio que apoyó a Ruffini fue Augustin-Louis Cauchy (1789 – 1857) que, en una carta remitida en 1821, le decía:

(...) a mi juicio, su memoria prueba completamente la imposibilidad de resolver algebraicamente ecuaciones de grado superior al cuarto.

Lo que resulta sorprendente y extraño es que nadie descubriese el error cometido y se lo comunicase al interesado.

En su demostración Ruffini se apoyó en algunos resultados de Lagrange sobre grupos de permutaciones pero también utilizó conceptos, procedimientos y teoremas originales de Teoría de Grupos (véase el cuadro adjunto). Consideró funciones racionales de las raíces de la ecuación general de grado n y estudió el conjunto de las p permutaciones que las dejan invariables.

RESULTADOS DE LAGRANGE Toda función racional no simétrica de n variables admite un grupo de sustituciones cuyo orden es divisor de n! Si una función Ψ de n variables admite un grupo de p sustituciones, entonces el número de funciones distintas obtenidas al aplicarle todas las sustituciones posibles es n!/p = i [= índice del grupo]. Los valores i de una función racional de x1, x2, . . . , xn son las raíces de una ecuación de grado i (resolvente de Lagrange): cuyos coeficientes son funciones simétricas de x1, x2, . . . , xn. APORTACIONES ORIGINALES DE RUFFINI Conceptos: orden de un elemento, conjugación, grupo primitivo, grupo imprimitivo. Procedimientos: descomposición de una permutación en ciclos Teoremas: El orden de una permutación es el mínimo común múltiplo de las longitudes de los ciclos disjuntos en que puede factorizarse. Todo elemento de S5 de orden 5 es un 5-ciclo. Si G es un subgrupo de S5 y su orden es divisible por 5, entonces G tiene algún elemento de orden 5. S5 no tiene subgrupos de índices 3, 4 y 8.