La mayor parte del álgebra de Simone Stevino Brugense se desarrolla en L’Arithmetique, texto escrito en francés y publicado en 1585, que contiene además un apéndice (La Pratique d’Arithmetique), Les Tables d’Interest (versión francesa de Tafelen van Interest, midtsgaders de constructie der selver), La Disme (traducción al francés de  De Thiende), los cuatro primeros libros de álgebra de Diofanto y un tratado de magnitudes inconmensurables con la explicación del décimo de Euclides.

En  L’Arithmetique, Stevin consideró tres tipos de “números”:

1) Los aritméticos, que eran los números abstractos.
2) Los geométricos, asociados a segmentos rectilíneos, cuadrados, cubos y bloques rectangulares, que nosotros denotaríamos por a, a², a³,. . ., a^1/2, a^1/3,etc.
3) Los algebraicos, combinaciones lineales de números geométricos.

En su intento de establecer analogías entre la geometría (números geométricos) y la aritmética (números aritméticos), el álgebra (teoría de ecuaciones) de Stevin consistió en la aplicación de la regla de tres a los números algebraicos. Por tanto, el álgebra de Stevinius forma parte de su aritmética general.

Stevin introdujo algunas simplificaciones en la notación algebraica. Así, usó el signo + para la adición y el símbolo – para la sustracción, la letra M para la multiplicación y la letra D para la división; sin embargo, no dispuso de un símbolo especial para la igualdad. Para la raíz cuadrada y la raíz cúbica también utilizó caracteres especiales, parecidos a los actuales.

En su teoría de ecuaciones, para representar las sucesivas potencias de la incógnita, Stevin adoptó un simbolismo similar al del matemático boloñés Rafael Bombelli. No hizo uso de los números complejos (introducidos por el autor italiano) pero si de los negativos. En el tratamiento de las ecuaciones de tercer y cuarto grado con una incógnita se inspiró en los trabajos de Girolamo Cardano (1501 – 1576) y  Ludovico Ferrari (1522 – 1565).

En el Appendice Algebraique (1594), opúsculo de seis páginas publicado en Leiden, Stevin (mediante las cúbicas x³ = 300x + 33915024  y  x³ = 300x + 33900000) presentó un método general para el cálculo aproximado de las soluciones reales de una ecuación de cualquier grado.

Stevin y el cálculo infinitesimal

El libro segundo del tratado de Estática De Beghinselen der Weeghconst (1586), se dedica al cálculo de centros de gravedad. En él, Stevin sustituye el método indirecto de exhausción (utilizado por Arquímedes y otros insignes matemáticos griegos) por un método directo que representa un gran paso hacia el concepto matemático de límite.

El método de exhausción Cuando Arquímedes quería demostrar que una cierta magnitud Q, por ejemplo el volumen de un segmento parabólico, era igual a A, probaba que las hipótesis Q < A y Q > A eran absurdas y, por tanto, Q = A era la única opción posible. El método de Stevin Si la diferencia entre dos magnitudes B y A se puede hacer menor que cualquier cantidad arbitrariamente pequeña, entonces B = A.

El procedimiento de Stevin se puede ejemplificar en la demostración de la proposición siguiente: El centro de gravedad de un triángulo pertenece a su mediana.

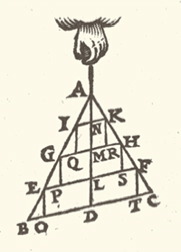Sea ABC un triángulo cualquiera y AD el segmento que une el vértice A con el punto medio del lado BC.

Dibújense los segmentos EF, GH e IK paralelos a BC y que cortan a AD en los puntos L, M y N respectivamente. Dibújense los segmentos EO, GP, IQ, KR, HS y FT paralelos a AD.

Dado que EF es paralelo a BC , y EO y FT lo son a LD, el cuadrilátero EFTO es un paralelogramo en el que EL es igual a LF y también a OD y DT. Entonces, en virtud de la primera proposición de este libro (el centro geométrico de cualquier figura plana también es su centro de gravedad), el centro de gravedad de EFTO está en DL. Por la misma razón, el centro de gravedad del paralelogramo GHSP está en LM y el de IKRQ en MN.

Por tanto, el centro de gravedad de la figura IKRHSFTOEPGQ, formada por los antedichos cuadriláteros, estará en el segmento ND o AD. Ahora bien, del mismo modo que se han inscrito tres cuadriláteros en el triángulo, también se puede inscribir un número infinito de ellos y el centro de gravedad de la figura inscrita estará en el segmento AD. Además, cuantos más cuadriláteros se inscriban, la diferencia entre el triángulo ABC y la figura compuesta por ellos se podrá hacer menor que cualquier figura plana por pequeña que sea. Si los “pesos” de los triángulos ABD y ACD no fuesen iguales, entonces tendrían una diferencia fija. Pero no puede haber una tal diferencia dado que cada uno de dichos triángulos difiere de la suma de los paralelogramos inscritos en él (que en ambos triángulos son iguales) en una figura plana tan pequeña como se quiera. En consecuencia, los “pesos” de ABD y ACD son iguales y, por tanto, el centro de gravedad del triángulo ABC está en la mediana AD.

En las líneas precedente hemos presentado las aportaciones más significativas de Simon Stevin al campo de las Matemáticas. Sin embargo, la actividad científica del sabio de Brujas no se redujo solamente a esta parcela del saber.

Se pueden encontrar contribuciones originales de Stevinius, que se mueven en la frontera de lo teórico y lo práctico, en terrenos tan diversos como Mecánica, Hidrostática, Astronomía, Geografía, Navegación, Tecnología, Arquitectura militar, Arquitectura civil, Música, Política y Lógica.

Si a esto se añade su obsesión por divulgar los conocimientos científicos a todos los estratos sociales, no resulta descabellado afirmar que Simone Stevinio fue uno de los científicos más notables del siglo XVI.