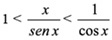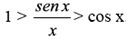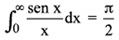37. La chica matemática (2)
37. La chica matemática (2) |
 |
 |
 |
| Escrito por Alfonso J. Población Sáez |
| Jueves 01 de Enero de 2009 |
|
Un nuevo año suele ser un buen momento para proponerse nuevas metas, gracias a la recarga de energías que proporciona el turrón y al cargo de conciencia de no haber hecho nada en vacaciones. Nosotros, algo más modestos, nos conformamos de momento con seguir con la tarea iniciada y terminar lo que estaba pendiente. Retomamos así a Math Girl, la chica matemática, heroína concebida motivar a los alumnos USAmericanos en conceptos teóricamente difíciles de asimilar (para ellos). El segundo capítulo de la trilogía puede verse en versión original en http://es.youtube.com/watch?v=Ceui-CIQZe4. Basa su argumento en el límite
Tras los títulos aparece un rótulo que reza: Población de Calculópolis:
Math Girl se encuentra tomando un refresco en una mesa de la terraza del Café Cauchy. Su amigo Pat pasa por allí. Math Girl: ¡Hola Pat! ¿Dónde vas? Comentarios y Discusión Al igual que sucediera en el primer episodio, se nos facilita el número de habitantes de Calculópolis, observando que ha aumentado considerablemente (55000 millones frente a los escasos 42 del capítulo previo). Respecto a matemáticos ilustres, se mencionan aparte del citado, a Cauchy (dando nombre a un Café), y Newton y Leibniz, (designados como los creadores del Cálculo; quizá sea mucho decir, sin restarles mérito alguno por supuesto, pero el propio Newton reconoce la labor de sus predecesores en este asunto en la famosa frase que todos recordaréis. Lo digo porque tratándose de un cartoon didáctico, la afirmación no resulta demasiado rigurosa). Obviamente se invoca a éstos puesto que el asunto a resolver se enmarca tradicionalmente dentro de esta rama de las Matemáticas. Un nuevo personaje aparece en este episodio: el malvado Cero Factorial (0!). Ciertamente a cualquier estudiante o persona que se acerque a las matemáticas, le choca el convenio 0! = 1 conocida la definición del factorial. Recordemos que el factorial de un número natural n es el número que resulta de multiplicar n por todos los números naturales menores que él (esto es, n! = n(n–1)(n–2) …. 3 · 2 · 1). Su utilización es imprescindible en combinatoria y probabilidades. ¿La razón? El factorial de n expresa el número de formas distintas en que pueden colocarse n objetos (recuérdese también que esto es calcular el número de permutaciones que pueden realizarse con esos objetos). Pero, ¿por qué 0! = 1? De lo dicho, no parece que tenga mucho sentido plantear el factorial de cero, puesto que no hay ningún número natural menor que cero (según qué autores el cero no se considera natural, sino entero; a mí siempre me definieron al uno como el primer natural, y así lo considero y explico, ya que, a mi entender y valga la redundancia es lo más “natural”). Muchas expresiones en las que aparecen los factoriales se definen de manera recurrente, es decir, teniendo en cuenta los valores previos. Por ejemplo, n! = n (n–1)! Al ir a calcular 1! nos aparece 0! (salvo que tomemos la expresión para n > 1). Si no convenimos que 0! = 1, no obtenemos el 1! Y sin este tampoco podemos calcular 2!, etc., etc. Por tanto parece razonable utilizar ese convenio que pone en marcha todo el proceso. Esto se entiende perfectamente cuando queremos introducir estas fórmulas en un lenguaje de programación. Martin Gardner, dedica el cuarto capítulo de su Mathematical Magic Show (Festival Mágico-matemático, en castellano, editado por Alianza Editorial) a comentar algunas curiosidades factoriales. De allí os propongo la siguiente cuestión que me ha resultado llamativa: Platón, en el Libro V de sus Leyes, propone que 7! (= 5040) es el número ideal de habitantes de una población, ya que ese número admite 60 divisores diferentes, cantidad interesante desde el punto de vista de posibles repartos, divisiones, etc. Sin embargo no es el número de cuatro cifras con mayor número de divisores. ¿Cuál sería ese número? ¿Y con cinco cifras? La forma razonable que se me ocurre para dar respuesta a estas cuestiones pasa por hacer un pequeño programita que nos de la respuesta, pero si a alguien se le ocurre otro modo menos pedestre, que nos lo cuente. Otra expresión curiosa y útil con los factoriales es la conocida como fórmula de Stirling (en honor al matemático escocés James Stirling, 1692 – 1770, aunque al parecer fue Abraham de Moivre el primero en publicarla, en 1730, en su forma casi definitiva, con demostración incluida. Stirling publica algunos meses después una mejora de la fórmula con un desarrollo asintótico con cinco términos. De Moivre y Stirling eran buenos amigos, y conocer las contribuciones exactas de cada uno no es fácil.):
Mucho cuidado con el símbolo de aproximación que probablemente más de uno meterá la pata. Las dos expresiones que aparecen separados por ese símbolo son valores que tienden a infinito cuando n tiende a infinito. Esa aproximación simplemente indica que ambos infinitos son equivalentes, es decir que
lo cual es extremadamente útil en el cálculo de algunos límites en los que interviene el factorial. Pero ese comportamiento similar “cuando n es lo suficientemente grande” como se indica en muchos sitios, no implica que aproxime como desearíamos el factorial de un número concreto. La fórmula de Stirling también se escribe como ln n! ~ n ln n – n (es fácil ver que es la misma expresión que la mostrada arriba tras tomar exponenciales) El factorial de n puede generalizarse a cualquier número real positivo mediante la Función Gamma
La notación Γ fue ideada por Adrien-Marie Legendre (1752 – 1833). La función Gamma aparece en funciones de distribución de probabilidad, por lo que es bastante usada tanto en probabilidad y estadística como en combinatoria. Entre sus propiedades citaremos que verifica la ecuación funcional Γ(n+1) = n Γ(n) (obsérvese que esta propiedad es precisamente la que define el factorial para valores naturales) y que está estrechamente relacionada con otra función esencial del Análisis Matemático, la función zeta de Riemann, ζ(s):
A la derecha podéis ver el aspecto que presenta la función gamma en el plano complejo. Por otro lado, el sabotaje que ha preparado Cero Factorial en la montaña rusa es la supresión del valor en t = 0 de la función
Cuando se trabaja o estudia en cursos universitarios, uno ya está habituado a considerar como infinitésimos equivalentes el sen x y x en un entorno de x = 0. Quizá sea pertinente recordar cómo se llega a dicha equivalencia utilizando únicamente argumentos trigonométricos: Consideremos la circunferencia de radio unidad (en la gráfica OM = OA = 1). Sea x el ángulo MOB, donde 0 < x < π/2. En la gráfica se observa que Calculemos estos datos Área triángulo MOA = ½ OA · MB = ½ sen x. sen x < x < tan x. Si dividimos por sen x la desigualdad, se tiene que
Tomando inversos,
Dichas desigualdades se han obtenido para x > 0. Cambiando x por (–x), y teniendo en cuenta la paridad del seno y el coseno (es decir, que sen (–x) = – sen x, cos (–x) = cos x), se concluye que las desigualdades anteriores también son ciertas para x < 0. (Pregunta: ¿Por qué era necesario comprobar esto?). Tomando límites cuando x tiende a cero en dichas desigualdades, se concluye que el límite buscado es 1. Por lo tanto, la discontinuidad es evitable, y se soluciona el problema de la montaña rusa, volviendo a definir correctamente f(0). Uno puede pensar que Cero Factorial anda un tanto escaso de recursos, pero preparar una discontinuidad de otro tipo en la función le llevaría más trabajo (tendría que romperla, y eso se notaría antes de poner en marcha la atracción). De todos modos parece una situación un poco siniestra para ser mostrada como recurso didáctico, ¿no os parece? Los pobres niños sólo se han pirado una clase un día. En fin, no afinemos más que podemos llegar a peores conclusiones aún. Finalmente, MathGirl emplea un artilugio que he traducido por “mecanismo epsilon-delta” (epsilon delta device en la versión original) para aplicar la definición de límite. Recordemos que esta definición indica que “ Para cada ε>0, existe un δ>0 tal que si 0 < |t| < δ, entonces |sen t / t – 1| < ε ” En el episodio ni siquiera tienen que encontrar el δ que hace falta en función de un ε dado para verificar la condición de límite. Simplemente si t < 1.0024, entonces |sen 1.0024 / 1.0024 – 1| < 0.15. Vamos, que una simple calculadora también lo haría. Ya veremos si en otros capítulos tiene alguna otra característica más relevante. Aprovechando la inclusión de esta función en el argumento del dibujo animado, y dado que teóricamente está orientado a alumnos universitarios, se me ocurre que podrían haberle sacado un poco más de partido, planteando por ejemplo alguna historia relacionada con la integral impropia
obteniendo ese valor (hay que pasar a argumentos de integración de Lebesgue), o probar que no es de Lebesgue, etc. La integral de Lebesgue (Henri Lebesgue (1875 – 1941) es una extensión de la clásica integral de Riemann, que permite integrar funciones más generales, y hacerlo en mayor variedad de conjuntos que los intervalos cerrados y acotados [a, b] de la recta real (en conjuntos medibles; aquí entronca con la teoría de la medida, aunque esta integral puede estudiarse perfectamente sin salirse del terreno del Análisis clásico). En la integral de Lebesgue se verifican más resultados de convergencia que en la integral de Riemann. El más importante es seguramente el teorema de la convergencia dominada de Lebesgue que no se cumple en integrales de Riemann. En fin, otra vez, será.
|
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |






 Episodio 2.- La discontinuidad de Cero Factorial (Zero!’s Dis-Continuity, 2006). (Duración: 5:14).
Episodio 2.- La discontinuidad de Cero Factorial (Zero!’s Dis-Continuity, 2006). (Duración: 5:14).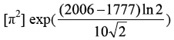
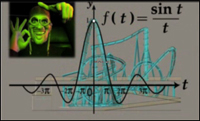 Zero!: Apartaré a los chicos del poder y gobernaré yo mismo en Calculópolis con mi invención malvada más reciente, la montaña rusa sent/t. El genio total que hará que los gemelos no puedan resistir la vuelta estremecedora. ¡Idiotas! Deberían haber estado más tiempo en clase. Parece (la montaña rusa) bonita y suficientemente suave como le gusta a la gente de Calculopolis. Pero, ¡sorpresa, sorpresa! Hay un agujero en su parte superior. No saben que la división por cero no está permitida. ¡Ah, Ah, Ah! Aprenden la lección cuando se hunden en su destino.
Zero!: Apartaré a los chicos del poder y gobernaré yo mismo en Calculópolis con mi invención malvada más reciente, la montaña rusa sent/t. El genio total que hará que los gemelos no puedan resistir la vuelta estremecedora. ¡Idiotas! Deberían haber estado más tiempo en clase. Parece (la montaña rusa) bonita y suficientemente suave como le gusta a la gente de Calculopolis. Pero, ¡sorpresa, sorpresa! Hay un agujero en su parte superior. No saben que la división por cero no está permitida. ¡Ah, Ah, Ah! Aprenden la lección cuando se hunden en su destino.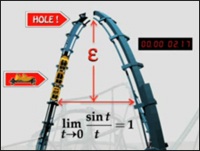 Math Girl: Tengo un plan. ¡Taparemos el agujero! Como el limite de sent/t cuando t tiende a cero es igual a 1, se trata de una discontinuidad evitable.
Math Girl: Tengo un plan. ¡Taparemos el agujero! Como el limite de sent/t cuando t tiende a cero es igual a 1, se trata de una discontinuidad evitable. En realidad lo único que parece pretenderse (se me ocurre a mí, no lo he visto escrito en ninguna parte) es incluir números o fechas de unas características concretas. En este caso aparecen el número trascendente π, el 10 (base de nuestro sistema de numeración), las funciones exponencial, logarítmica (ln 2), raíz cuadrada y potencial cuadrática, el irracional √2, el año de producción del episodio (2006), el año de nacimiento de Gauss (1777; a este matemático alude BigMath en su primer comentario), y además del 2 el número primo 229 (2006 – 1777). No se me ocurre otra explicación acerca de esta cantidad.
En realidad lo único que parece pretenderse (se me ocurre a mí, no lo he visto escrito en ninguna parte) es incluir números o fechas de unas características concretas. En este caso aparecen el número trascendente π, el 10 (base de nuestro sistema de numeración), las funciones exponencial, logarítmica (ln 2), raíz cuadrada y potencial cuadrática, el irracional √2, el año de producción del episodio (2006), el año de nacimiento de Gauss (1777; a este matemático alude BigMath en su primer comentario), y además del 2 el número primo 229 (2006 – 1777). No se me ocurre otra explicación acerca de esta cantidad.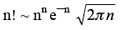
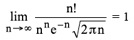
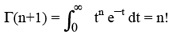
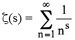 , para s > 1, es dicha función zeta.
, para s > 1, es dicha función zeta.
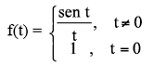
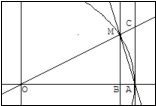 Área triángulo MOA < área sector MOA < área triángulo COA
Área triángulo MOA < área sector MOA < área triángulo COA