79. LAS ESFERAS

Sobre una plataforma horizontal hay situada una semiesfera de radio 10 metros apoyada sobre su base, y 6 esferas iguales de radio R, cada una tangente a la semiesfera, a la plataforma, y a otras dos esferas.

Encuentra el valor de R.

De acuerdo a las condiciones del enunciado realizamos un pequeño esquema con los siguientes dibujos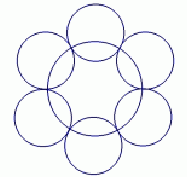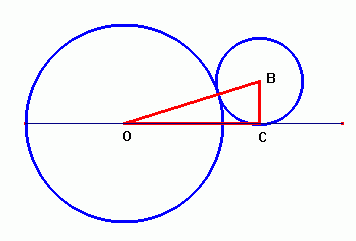

Aplicando el teorema de Pitágoras tenemos que :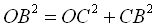

Llamando r al radio de la circunferencia pequeña, y x al valor del segmento OC podemos escribir que :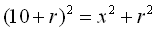

De donde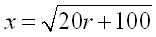

Si desechemos las pequeñas esferas y nos quedamos sólo con los puntos de tangencia con el plano de la mesa. Como todos los puntos tangenciales consecutivos y equidistan unos de otros, el polígono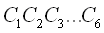

es un hexágono regular. Si miramos la figura desde arriba tenemos la siguiente representación:

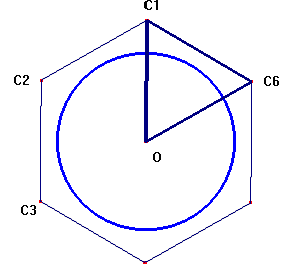Razonando con cualquiera de los triángulos representados en la figura y teniendo en cuenta que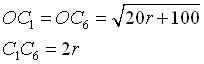

Y además al ser triángulos equiláteros, se verifica que: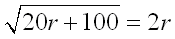

Resolviendo esta ecuación irracional e interpretando las raíces llegamos a la solución, dándonos por solución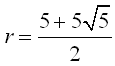

Volver