La Comisión de Divulgación de la Real Sociedad Matemática Española (DivulgaMAT) quiere agradecer a Javier Barrallo, así como al colectivo "The Frontier between Art and Science", que hayan cedido esta exposición a la R.S.M.E.

Esta exposición puede solicitarse para su exhibición a través de DivulgaMAT:

Esta dirección electrónica esta protegida contra spambots. Es necesario activar Javascript para visualizarla

INTRODUCCIÓN

Esta exposición se compone de una colección de imágenes generadas mediante ordenador por un grupo de artistas y/o científicos especializados en la representación de fórmulas matemáticas de manera poco usual.

La expresión matemática y los parámetros empleados confieren a cada imagen un colorido y una estética única e irrepetible. Al igual que un pintor o escultor transmite a su obra su personalidad y sensibilidad mediante su técnica, los autores de esta exposición se expresan a través de fórmulas y algoritmos, modificándolos progresivamente hasta conseguir el objetivo deseado, en la frontera entre el Arte y las Matemáticas.

La generación de cada cuadro, si se contempla como una imagen sintética producida por ordenador, puede parecer algo frío y mecánico pero detrás de cada cuadro hay cientos de horas de trabajo en las fórmulas, algoritmos y parámetros que crean la imagen. Si se analiza cada figura cuidadosamente se podrá apreciar las emociones de su autor en cada forma y cada color. Y es que las Matemáticas también pueden expresar sensibilidades.

The Frontier between Art and Science

El grupo “The Frontier between Art and Science” se reunió por primera vez en Septiembre de 1997. Su primera exposición conjunta tuvo lugar en la prestigiosa Galería RioCentro, en Río de Janeiro. A esta exposición le han seguido numerosas actividades individuales y colectivas en diferentes países del mundo, como Alemania, Argentina, Austria, Brasil, España, Francia, Japón o Yugoslavia.

Sus miembros son Linda Allison (EE.UU.), Domenick Annuzzi (EE.UU.), Javier Barrallo (España), Michael Field (EE.UU.), Sylvie Gallet (Francia), Earl Hinrichs (EE.UU.), Damien Jones (EE.UU.), Klaus-Peter Kubik (Alemania), Daniel Kuzmenka (Ucrania-EE.UU.), Mario Markus (Chile-Alemania)), Kerry Mitchell (EE.UU.), Samuel Monnier (Suiza), Luke Plant (Inglaterra), Janet Preslar (EE.UU.), Iñigo Quilez (España), Frederik Slijkerman (Holanda), Mark Townsend (Australia) y Sharon Webb (EE.UU.)

Este es un grupo muy heterogéneo: sus miembros proceden de diferentes países. Algunos autores trabajan en famosos centros científicos y universitarios, mientras que otros son simples aficionados a la programación o a las Matemáticas.

En su condición fronteriza, de mestizaje artístico y científico, su único objetivo es la búsqueda del reconocimiento por parte de ambas comunidades, la científica y la artística, a través de actividades como esta exposición.

Un poco de historia matemática

A finales del siglo XIX y principios del XX un grupo de matemáticos encabezados por Peano, Hilbert, Cesaro, Koch y Sierpinski, entre otros, formulaban una nueva familia de curvas, de inquietantes propiedades matemáticas, que escapaban a cualquier clasificación realizada hasta el momento.

A diferencia de la Geometría utilizada hasta entonces (formada por rectángulos, circunferencias, triángulos, elipses, etc.) esta nueva Geometría describe sinuosas curvas, espirales y filamentos que se envuelven sobre sí mismos formando elaboradas figuras cuyos detalles se pierden en el infinito.

En 1977, el científico franco polaco Benoit Mandelbrot consigue dibujar con ayuda del ordenador la primera figura de esta nueva Geometría, que posteriormente bautizaría como Geometría Fractal. En 1980, la publicación de su libro "The Fractal Geometry of Nature" populariza la Geometría Fractal siendo el origen de imágenes como las que se presentan en esta colección.

En realidad podemos entender la Geometría Fractal como la Geometría de la Naturaleza, del Caos y del Orden, con formas y secuencias imprevisibles localmente pero a la vez ordenadas en su conjunto, en contraposición a la clásica Geometría Euclídea que representa los objetos creados por el hombre.

Mª Francisca Blanco

Catálogo de Obras:

Angels in Green Thai Tower The Coral Reef Eyes of the Beh... Faeries Petrified Bilbao La Luz de la Lu... Volcano Blue Columns Hell Fire Avalanche Evening over Sa... Alien Blood Banded Clouds Fractal Pi Spade Shattered Wheel of Time Weathered Max Planck Inst... Ascension Big Bang The Sea Oscillations Polygon 1 Supernova Cubist Joie de Coeur Taupensky Then I saw a ne... Genesis Jewelry The Joy of Life The Mysterious ... Gateway KEDAJA

ARTÍCULO: ARTE FRACTAL. Las matemáticas más hermosas

Autor: Javier Barrallo (E.T.S. Arquitectura, Universidad del País Vasco). Este artículo ha sido publicado en la revista SIGMA, número 26, 2005.

¿Qué son los fractales?

Esta pregunta tan simple no puede ser respondida sin una respuesta larga y compleja. En realidad, tendríamos que explicar el concepto de dimensión de Hausdorff-Besicovitch para comprender que existen conjuntos fuera del ámbito de la Geometría Euclidea, cuya dimensión no tiene porqué ceñirse al conjunto de los números enteros, y allí es donde encontraríamos a los conjuntos fractales.

Este tipo de definición no ayuda mucho, pues requiere un alto grado de jerga matemática que muy poca gente puede llegar a comprender. Podemos definir un fractal de forma mucho más fácil e intuitiva como un conjunto, objeto o forma (elija usted el concepto que le resulte más sencillo) el cual al ser observado en una pequeña porción mantiene un aspecto similar (aunque no necesariamente idéntico) al que presenta al ser observado de forma completa.

Tomemos por ejemplo una montaña de naturaleza rocosa. Desde la distancia el perfil escarpado de la montaña será muy parecido al de sus rocas. A su vez las pequeñas rocas tienen una geometría muy similar a las grandes rocas y por tanto a la montaña en su conjunto. El mismo ejemplo puede aplicarse a una coliflor, que parece estar a su vez compuesta de pequeñas coliflores, a una nube, cuyos fragmentos parecen mostrar la misma estructura que la nube en su globalidad o de un árbol cuyo ramaje parece repetirse a menor escala cada vez que las ramas se bifurcan.
Esta propiedad, denominada autosemejanza, es la que define de modo práctico los fractales y que debe ser empleada en su enseñanza cuando no exista un alto grado de especialización matemática.

Fractales y ordenadores

Todos los que hemos trabajado con Sistemas Dinámicos, la rama de la Matemática en la que se encuadran las imágenes fractales somos conscientes de que la representación de un conjunto fractal requiere del empleo de la informática. Una pequeña imagen, por ejemplo de 640x480 píxeles, contiene 307.200 puntos que deben ser calculados. Cada uno de estos puntos puede requerir ser calculado por la fórmula que determina el fractal unas 1.000 veces. Esto implica que la fórmula ha de ser calculada más de 300 millones de veces. Y esto sólo para una imagen de pequeñas dimensiones. Algunas de las imágenes de gran formato que he elaborado para exposiciones han requerido más de un billón de cálculos y, consecuentemente, varios días de cálculo.

Para calcular una imagen a partir de una fórmula se sigue el método conocido como iteración. Este proceso consiste en calcular una fórmula repetidas veces a partir de un valor inicial. En el caso de los fractales este valor inicial estará relacionado con cada punto del plano o del espacio que necesitemos calcular y vendrá dado en función de su posición geométrica. Una vez calculada la fórmula por primera vez, tomamos el valor resultante y volvemos a introducirlo en la fórmula. El nuevo resultado se vuelve a calcular y así sucesivamente. Esto es lo que se conoce como iteración.

Si se continúa este proceso, basta con observar que ocurre y asignar un color en función de los resultados. En algunas ocasiones los números parecen “explotar” en la fórmula y avanzan rápidamente hacia el infinito, en otros casos convergen hacia un valor finito y otras veces se estabilizan en ciclos que se repiten con una periodicidad dada. Pues bien, basta colorear cada punto en función del comportamiento mostrado durante la iteración. Un punto cuyo valor asociado tiende hacia infinito será coloreado con una determinada paleta de color, generalmente con diferentes tonalidades en función de la rapidez con la que diverge. Un punto que converge hacia un valor finito con mayor o menor velocidad será coloreado de la misma forma y, en la mayoría de los casos, con una paleta de color diferente.

Sin embargo lo más interesante no es el proceso de iteración en sí mismo, sino las formulas y las regiones del plano o el espacio sobre las que aplicamos este proceso. En algunas ocasiones, y esto es lo que hace fascinante la exploración fractal, el comportamiento de dos puntos muy próximos es radicalmente opuesto (por ejemplo uno diverge hacia infinito y otro converge hacia un valor dado). Visualmente los colores pueden variar drásticamente formando espirales, arborescencias y otras complicadas formas. Las regiones del plano en las que se da este cambio abrupto de color son las que definen la forma del fractal.

Sin embargo, para los exploradores fractales, el proceso no ha hecho sino empezar. Al aumentar una región del conjunto fractal aparecen ante nuestros ojos nuevos diseños, que se tornan diferentes al continuar sumergiéndonos dentro del conjunto. Un único conjunto fractal, como el famoso Conjunto de Mandelbrot, nos permite explorarlo ilimitadamente obteniendo siempre giros y cambios inesperados pese a mantener un aspecto familiar durante toda la exploración –recordar el concepto de similitud que caracteriza a los fractales.

Con los ordenadores y programas actuales es muy fácil aumentar un fractal y tener prácticamente la certeza de que nunca nadie ha estado allí antes, pues la enorme rapidez con la que nos sumergimos en la imagen nos permite disponer con sólo unas pocas pulsaciones del ratón de una extensión para explorar mayor que nuestro sistema solar.

The Joy of Life. Esta imagen, obra de Mark Townsend muestra claramente las nuevas tendencias seguidas por el Arte Fractal: algoritmos de color, transformaciones, texturas y efectos de iluminación se combinan hasta obtener el efecto deseado, muy lejos de las primeras imágenes fractales.

Si, es bonito. Pero ¿Es realmente Arte?

Las imágenes fractales están basadas en matemáticas, calculadas mediante algoritmos matemáticas, coloreadas empleando procedimientos matemáticos, pero no están determinadas por las matemáticas.

Casi todas las expresiones del Arte dependen del las herramientas empleadas en su creación y ejecución: pinceles y brochas, cámaras fotográficas, instrumentos musicales, martillo y cincel, etc. son imprescindibles en la creación artística de su correspondiente disciplina. De la misma manera, el ordenador sólo debe considerarse como una herramienta en del proceso de creación de una imagen fractal.

Podríamos incluso decir que el ordenador es un mero instrumento, necesario para organizar las ecuaciones, parámetros, algoritmos y transformaciones empleados para sintetizar el Arte Fractal. Pero jamás un ordenador podría ser responsable de una obra de arte sin el respaldo de una mente humana que supervise la toma de decisiones en cada fase del proceso.

La matemática por si misma no es capaz de combinar los elementos necesarios para crear una imagen fractal de relevancia, pero aunque por azar lo fuera, no tendría potencial para evaluar su valor artístico. Veamos el siguiente ejemplo: una imagen de 800 x 600 puntos contiene 480.000 píxeles o puntos de pantalla que pueden combinarse en una imagen de 10^3467865 formas diferentes, esto es, un 10 seguido de más de tres millones de ceros. Un ordenador no posee la capacidad de seleccionar imágenes de entre esta inmensa colección y determinar las que son bellas o no lo son. En contraposición, el cerebro humano es excepcionalmente rápido y poderoso reconociendo patrones geométricos y es capaz de determinar el valor estético de las imágenes que percibe. No en vano discernir la belleza es una característica netamente humana que aún no ha podido ser trasladada satisfactoriamente al ámbito de los sistemas expertos.

La polémica sobre la catalogación de las imágenes fractales como Arte o como mera representación gráfica tiene su origen durante la creación de las primeras obras entre los años 1980 y 1995. La simplicidad de los algoritmos (la mayoría de los autores sólo utilizaban uno: el denominado algoritmo de tiempo de escape), la sencillez de las primeras paletas de 16 y 256 colores además de las limitaciones técnicas en los ordenadores de la época hicieron muy poco creíbles las imágenes fractales como obras de Arte.

Personalmente siempre me opuse a la consideración de Arte para estas primeras imágenes fractales, extremadamente elementales y con una mínima elaboración más allá de los cálculos meramente técnicos.

A estas consideraciones hay que añadir que cada obra fractal es puramente digital y puede reproducirse sin pérdida de calidad ilimitadamente. Sólo existe un Guernica de Picasso, un David de Miguel Ángel, pero pueden coexistir un número ilimitado de copias de cualquier obra maestra fractal sin poder discernir cual de entre todas es la original. En este aspecto, el Arte Fractal guarda similitudes con la Fotografía, una disciplina cuyo reconocimiento como Arte también se vio rodeada de escepticismo en sus inicios.

Cubist, de Janet Parke. La llegada de una nueva generación de programadores y artistas impulsó la exploración de formas artísticas aparentemente antagónicas a la Geometría Fractal, como en este caso el Cubismo Abstracto

Sin embargo, desde la llegada de una nueva generación de programadores, creadores y artistas fractales todo parece haber cambiado. Las obras son radicalmente diferentes entre sí. Cada autor imprime un sello personal en su obra, que alcanza cotas de complejidad y elaboración inimaginables hace sólo una década.

Es paradójico que algunos de los mejores artistas fractales, creadores de obras de gran belleza, apenas pueden explicar la matemática que emplean en sus obras. Otros más innovadores se dedican sin embargo a la experimentación y creación de nuevas formas y efectos sin ninguna ambición artística en sus creaciones.

Este es uno de los aspectos más fantásticos de los programas fractales de última generación: el hecho de que aunque estos programas se basen en complejos algoritmos matemáticos, la simplicidad de sus interfaces permiten utilizarlos sin llegar a entender totalmente la matemática que subyace. Las fórmulas y algoritmos pueden intercambiarse mediante menús, el color y los parámetros se modifican en intuitivas ventanas y la región del plano a representar se manipula con cómodos movimientos de ratón.

Una nueva generación de creadores fractales

Al ser las ecuaciones fractales el elemento matemático más obvio, el principal objetivo para los primeros programadores fue la creación y experimentación con nuevas fórmulas, introduciendo rápidamente centenares de nuevos tipos fractales. Durante los años posteriores la mayor parte de la energía creativa se dedicó a elegir cuidadosamente parámetros para refinar el color, la forma y el encuadre. El progresivo incremento en la calidad de los resultados y la respuesta entusiasta por parte de la comunidad científica introdujeron de forma pionera el concepto de Arte Fractal.

Sin embargo, ya en 1995 prácticamente se había agotado la posibilidad de crear nuevos tipos fractales de especial relevancia. La imaginería fractal era incapaz de sorprender con imágenes novedosas y, sobre todo, la capacidad de expresión artística estaba muy limitada al recurrirse reiteradamente a las formas espirales y filamentos típicos de las primeras imágenes fractales.

La mayor innovación se produce entonces no al buscar nuevas ecuaciones fractales, ya prácticamente agotadas, sino al crear nuevas formas de colorear las ecuaciones ya existentes. Es la creación de los algoritmos de color el elemento clave y fundamental en el desarrollo de lo que hoy denominamos Arte Fractal.

La idea consiste en diseñar algoritmos que permitan colorear una misma fórmula de diferentes modos. No se calculan nuevos valores, simplemente se buscan nuevas formas de transformar en colores los resultados obtenidos. Ante una biblioteca de fórmulas fractales extenuada, se abre entonces un mundo de algoritmos de color que permiten reinterpretar estas fórmulas creando figuras increíbles nunca vistas anteriormente y, ante todo, se dota al programador de una fantástica libertad para elaborar sus cuadros.

A medida que estos nuevos algoritmos de coloreado se hacen más complejos, los artistas y programadores regresan a las ecuaciones fractales más simples, ya que la flexibilidad de estos nuevos algoritmos de color, cada vez más sofisticados, proporcionan en sí mismos mayor versatilidad y posibilidad de expresión artística personal.

Imágenes de la exposición The Frontier between Art and Science.

En 1995 la exposición de Arte Fractal por parte del grupo The Frontier between Art and Science en la prestigiosa Galería RioCentro en Río de Janeiro presenta una exposición rompedora con el pasado, basada en los nuevos algoritmos de color. Esta exposición conmociona la forma de diseñar imágenes fractales y se consolida como la más importante jamás realizada en su género, con exhibiciones en España, Francia, Japón, Austria, Yugoslavia, Alemania, Argentina, Brasil y Bélgica. La muestra contiene obras de gran formato realizadas por Linda Allison (EE.UU.), Domenick Annuzzi (EE.UU.), Javier Barrallo (España), Michael Field (EE.UU.), Sylvie Gallet (Francia), Earl Hinrichs (EE.UU.), Damien Jones (EE.UU.), Klaus-Peter Kubik (Alemania), Daniel Kuzmenka (Ucrania), Mario Markus (Chile), Kerry Mitchell (EE.UU.), Samuel Monnier (Suiza), Luke Plant (Inglaterra), Janet Parke (EE.UU.), Iñigo Quilez (España), Frederik Slijkerman (Holanda), Mark Townsend (Australia) y Sharon Webb (EE.UU.)

Muchas veces me pregunto como evolucionará el Arte Fractal en la próxima década. La sofisticación en los últimos años ha sido tan increíble que incluso las obras que se presentan en este artículo parecen ya antiguas tan sólo un par de años después de haber sido creadas. Sin duda la tendencia futura ensalzará las obras que logren el equilibrio de tres características intrínsecamente humanas: creatividad, expresividad e inteligencia y que constituirán la base del Arte Fractal de la próxima generación.

Los Algoritmos de Color

Cada fórmula fractal produce por iteración una secuencia de valores de variable compleja z₀, z₁, z₂, z₃,...z_n para cada punto computado. Las imágenes fractales se crean generando una de estas secuencias para cada píxel que aparece en la imagen. Posteriormente, el algoritmo de color es el encargado de interpretar la secuencia numérica para producir un color final.

Ejemplo de una paleta de color utilizando curvas Spline como elemento interpolador del espacio RGB (Red Green Blue), cuyos ejes se corresponden con los colores Rojo, Verde y Azul.

Típicamente, el algoritmo de color produce un único valor para cada píxel. Dado que el color es interpretado en los ordenadores como un espacio tridimensional RGB (Red Green Blue - Rojo Verde Azul), este valor unidimensional debe ser expandido para poder producir un color. El método más común es la creación de una paleta, una secuencia de valores de color 3D, definidos por un línea (denominada gradiente) que recorre el espacio tridimensional.

La selección del gradiente es una de las decisiones artísticas más críticas al crear una imagen fractal. Un gradiente de color puede enfatizar partes de la imagen u ocultar otras. En casos extremos, dos imágenes fractales con los mismos parámetros pero diferentes esquemas de color pueden parecer completamente diferentes.

Podemos efectuar una primera división entre los algoritmos de color: los que producen valores discretos y los que producen valores continuos. Los valores discretos muestran saltos o bandas en la transición el color. Hasta hace unos años esto no era importante, ya que las tarjetas gráficas de 8 bits producían, en cualquier caso, un escalonado en la imagen. Sin embargo la llegada masiva de las tarjetas gráficas de 24 bits hizo que los algoritmos continuos cobraran una especial preponderancia, ya que permiten interpolar un color cualquiera del gradiente con la precisión deseada.

La creciente importancia de los algoritmos de color en las imágenes fractales ha dado lugar a centenares de nuevos tipos, de entre los que podemos destacar los que se detallan a continuación.

Algoritmo de tiempo de escape

El algoritmo de tiempo de escape es, probablemente, el algoritmo de color más antiguo y para muchos programas fractales la única opción disponible. Su simplicidad lo convierte en el favorito de los que se inician en la programación fractal, sin embargo, desde el punto de vista artístico se considera menos importante, dado que produce valores discretos y se ha visto ampliamente superado por los algoritmos de color continuos.

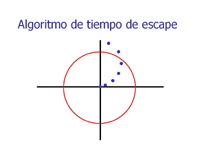
Este algoritmo está basado en el número de iteraciones necesario para determinar si la secuencia iterada por el sistema dinámico tiende a infinito o no. Puede demostrarse estrictamente que cuando la órbita de cualquier valor z₀, z₁, z₂, z₃,...z_n excede una región frontera R siempre diverge hacia el infinito. La forma y el tamaño mínimo de la región R son diferentes para cada fórmula fractal, por supuesto. La secuencia iterada es interrumpida tan pronto como z_n rebasa la región frontera R, entonces el valor de coloreado para el algoritmo de tiempo de escape es simplemente la longitud de la secuencia, esto es n.

Tradicionalmente, R se define como un círculo, centrado en el origen y con radio 2. Este valor se debe a que en el conjunto de Mandelbrot puede ser probado que tan pronto como |z|>2 la iteración diverge. Y aunque matemáticamente R debe definirse como un círculo de radio 2 para probar la divergencia de forma precisa, esto no ha impedido a algunos artistas experimentar con diferentes radios.

Ejemplo de un algoritmo de color discreto (izquierda) y continuo (derecha). En la actualidad prácticamente todos los algoritmos son continuos, pues evitan las desagradables bandas de la imagen izquierda y proporcionan la suavidad característica de la imagen derecha.

Algoritmo de Estimación de distancias

El algoritmo de tiempo de escape puede ser considerado como una medida no Euclidea de la distancia de un punto cualquiera z₀ a la frontera del conjunto. El uso de un valor discreto (el número de iteraciones es siempre un entero) produce una apariencia de bandas similar al de un mapa topográfico.

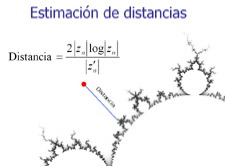
El uso creativo de los gradientes puede en algún caso sacar provecho de este efecto (también denominado “rayado de tigre”) pero la mayoría de los artistas ha desarrollado algoritmos que ocultan este efecto. Claramente, el objetivo final es desarrollar funciones continuas para medir estas distancias. Aunque los algoritmos empleados no proporcionan una distancia Euclídea exacta, si que proporcionan una aproximación aceptable utilizando valores continuos.

Algoritmo de ángulo de escape

Los algoritmos descritos anteriormente consideraban la magnitud del valor complejo z y la cuenta de iteraciones. Si consideramos la magnitud z como una parte de las coordenadas polares de z_n, entonces parece lógico considerar también la otra parte -el ángulo de z- como elemento para colorear. La familia de algoritmos de ángulo de escape cubre todos aquellos algoritmos basados en el estudio del ángulo de z_n.

El primer algoritmo sería la descomposición binaria. En este algoritmo, los valores de z_n que toman ángulos por encima del eje real (0-180º) toman un determinado color, mientras que los que toman valores por debajo del eje real (180-360º) toman otro diferente.

Variaciones del esquema de la descomposición binaria pueden incrementar el número de divisiones del plano Por ejemplo, una descomposición cuaternaria podría asignar un color diferente a los ángulos de zn correspondientes a cada cuadrante. El incremento del número de divisiones del plano incrementa, lógicamente, el número de colores a emplear.

Otro aspecto de la secuencia z₀, z₁, z₂, z₃,...z_n que puede ser medido es la curvatura entre iteraciones consecutivas. Una estimación rápida puede hacerse utilizando los dos últimos puntos de la iteración. Otras variantes permiten utilizar el radio de la circunferencia que pasa por los valores de las tres últimas iteraciones o el área del triángulo formado por tres iteraciones. Estas últimas variantes recogen no sólo la curvatura de las iteraciones, sino también la distancia entre ellas.

Algoritmo de captura de órbitas

Constituye sin duda la más versátil familia de algoritmos de color, dada la gran versatilidad que muestra para la expresión artística. La idea básica consiste en elegir una región del plano complejo (denotada por T) y estudiar la relación entre los valores de z_n y T. T es definido usualmente como una forma (generalmente de cálculo simple como un punto, línea, rectángulo o círculo) y una distancia de tolerancia. Cualquier iteración dentro de la distancia de tolerancia se considera “capturada”.

The Coral Reef (El Arrecife de Coral), de Linda Allison. Pocos cuadros han representado como éste el potencial del algoritmo de captura de órbitas. La introducción de diversas formas geométricas a modo de “trampas” para capturar las iteraciones permite a su autora representar mediante formas fractales un arrecife de coral entre las corrientes marinas.

Las implementaciones primitivas del algoritmo de captura de órbitas simplemente buscaban cualquier z_n que cayera dentro de la región T, también denominada “trampa” (en inglés orbit trap). Cuando se producía esta circunstancia la iteración se finalizaba y se coloreaba el píxel de acuerdo a la distancia al centro de la región T. De ahí el término “trampa”; una vez que la órbita cae en T, ésta es “atrapada” y la iteración finalizada.

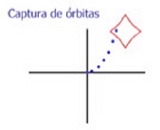
Existen muchas variantes para este método. En primer lugar, la forma de la región T puede variar y transformarse en figuras más complejas como elípses, astroides, hipérbolas, curvas trigonométricas o polares como espirales o cardioides. Más lejos aún, estas trampas puedes distorsionarse o rotarse, incluso incrementalmente con cada iteración.

Otro tipo de variantes trata la relación entre las distancias de cada valor z_n respecto a T. La implementación clásica, mencionada anteriormente, se detenía cuando un valor z_n caía dentro de la distancia de tolerancia T. Pero otras variantes pueden utilizar el último valor z_n en caer en la trampa, o el más cercano, o el más lejano, etc. E incluso métodos más exóticos pueden combinar varias de estas distancias simultáneamente, hasta el punto de hacer casi imposible predecir que tipo de resultados se obtendrán.

Algoritmo de los enteros Gaussianos

Un entero Gaussiano es un número complejo cuyo componente real e imaginario son ambos enteros. El algoritmo calcula la distancia de cada z_n al entero Gaussiano más cercano, y entonces lo colorea basándose en la menor distancia obtenida en la iteración.

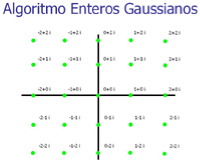
Conceptualmente, este método es similar a una captura de órbitas, donde la trampa T (definida como un punto) se repite a lo largo del plano complejo en una malla regular coincidente con los enteros Gaussianos. Percibido de esta manera, es claro que esta técnica puede ser extendida a cualquier otra forma T, con diferentes espaciados, e incluso mayas no rectangulares, como las radiales o las triangulares.

Big Bang, de Kerry Mitchell. Los infinitos atractores del algoritmo de Enteros Gaussiano crean está sorprendente imagen a caballo entre la psicodelia de los años 70 y la fotografía de una galaxia lejana.

Algoritmo de atractores finitos

No todas las secuencias iteradas z₀, z₁, z₂, z₃,...z_n tienden hacia infinito. Las órbitas que no tienden hacia infinito a menudo convergen en un solo punto o en un ciclo periódico. Aunque la mayoría de las técnicas descritas anteriormente pueden aplicarse a estas secuencias convergentes, requieren ciertas modificaciones.

El método más sencillo consiste en buscar un cambio decreciente en z. Así, cuando z_n converge hacia un punto fijo, la expresión |z_n-z_n-1| tiende hacia cero. Una vez que esta diferencia rebasa una tolerancia establecida, consideramos que el punto ha convergido suficientemente hacia el punto atractor y lo coloreamos (puede ser de acuerdo al número de iteraciones o cualquier otro algoritmo visto anteriormente).

Algoritmo de efecto tridimensional

Aunque las imágenes fractales son creadas típicamente con un aspecto bidimensional, es posible crear una imagen con un aspecto tridimensional utilizando algunos efectos de programación. Esencialmente, éste método consiste en calcular varios puntos adyacentes siguiendo la supuesta trayectoria de un rayo de luz. Una vez calculados, se genera una “altura” para cada punto y se define un plano tangente a la superficie y un vector normal a la misma que determina de forma realista la cantidad de luz y sombra que debe administrarse a cada punto.

Si se utilizan otros esquemas de color diferente al RGB, por ejemplo el HSL (Hue, Saturation, Luminace – Tonalidad, Saturación, Luminosidad) basta cambiar la luminosidad para producir sombras en la imagen de forma muy sencilla. En caso contrario bastan unas simples operaciones matemáticas.

Algoritmo de movimiento Browniano

El movimiento Browniano, ese movimiento pseudo caótico que se produce en las partículas de polvo suspendidas en el aire o en el agua turbia, ha sido transportado al campo de los fractales con gran éxito. Gracias a este movimiento se consiguen tramas y texturas de gran realismo que son profusamente utilizadas como fondo de las imágenes o como textura para los motivos en primer plano.

Casi todos los fractales de nueva generación utilizan de alguna variante de este algoritmo que permite dotar a las imágenes de un aspecto más cálido y orgánico. Como curiosidad puede señalarse que las texturas fractales generadas mediante este procedimiento han sido trasladas profusamente al cine y al mundo de los videojuegos para producir imágenes realistas.

Weathered (Maduro), de Daniel Kuzmenka. El uso de los algoritmos de movimiento Browniano contribuye a la creación de texturas cálidas y realistas.

Fractales multicapa

Hoy en día la técnica más relevante de creación artística consiste en combinar varios de los algoritmos aquí descritos en capas que se superponen como si fueran transparencias a través de la luz de un proyector. Al resultado lo denominamos fractales multicapa, y constituye la vanguardia del arte fractal, con unas posibilidades de combinación prácticamente inagotables. De hecho podríamos considerar cada combinación de algoritmos multicapa como un nuevo algoritmo. La posibilidad de combinar distintos algoritmos de color e incluso diferentes fórmulas o regiones del plano en una única imagen permite una libertad de composición y expresión artística impensable antes de desarrollar esta técnica.

A estas posibilidades hay que añadir las que se derivan de la combinación de capas. Aunque intuitivamente al superponer varias capas transparentes ante la luz se produce un único resultado, no hay que olvidar que las capas de las que hablamos son imágenes digitales compuestas por colores con estructura vectorial (RGB – Rojo Verde Azul) y por tanto con infinidad de combinaciones numéricas posibles: adición, sustracción, producto, media aritmética, desviación típica, módulo, ángulo y una largísima lista de posibles operaciones con resultados siempre sorprendentes.

=

Volcano, de Javier Barrallo. Las figuras superiores muestran las tres capas de las que se compone la imagen. La primera resalta la elevación introduciendo luces y sombras, la segunda establece la base de color y la tercera produce las texturas de fuego y humo.

Taupenski, de Janet Parke. Esta imagen fractal constituye un prodigio de elegancia y sencillez utilizando una paleta de color en blanco y negro teñida de ligeros tonos sepia. Para muchos expertos constituye la mejor imagen fractal jamás diseñada y, al igual que la mayoría de las presentadas en este artículo, ha sido creada mediante el programa Ultrafractal.

Para comenzar a explorar

Sin duda alguna el software más completo que existe en la actualidad es Ultrafractal, programado por Frederik Slijkerman, cuyo diseño ha contado con la colaboración de casi todos los miembros del grupo The Frontier between Art and Science. Pese a la complejidad de sus funciones más avanzadas, permite explorar los fractales más famosos, como el Conjunto de Mandelbrot, sin ninguna dificultad. Puede descargarse una versión de demostración de este programa en:

www.ultrafractal.com

En cuanto a otros recursos en la World Wide Web, la página Fractalus, regentada por Damien Jones es el punto de partida ideal, conteniendo suficiente material para saciar la curiosidad de cualquier amante de las imágenes fractales. Su dirección es:

www.fractalus.com

Spade (Pica), de Damien Jones. Una exuberante imagen en la que se percibe la composición sobre diferentes capas de los motivos (azul, blanco y marrón) que la componen.