1. Introducción

Este artículo es la segunda entrega de la serie Enseñanza de música vía las matemáticas, en la vamos a seguir con el análisis del excelente libro de Timothy Johnson [Joh03] Foundations of diatonic theory (Fundamentos de teoría diatónica), libro que adopta un enfoque matemático de la enseñanza de la teoría diatónica. En la primera entrega revisamos los siguientes conceptos: los diagramas circulares para representar la octava; la subdivisión de dichos diagramas en 12 partes, una por semitono; el problema de la distribución de máxima regularidad de puntos en círculos; diagramas complementarios; distribuciones de máxima regularidad para 2, 3, 4, 5, 6, 7 y 8 puntos; y, finalmente, las correspondencias de esas distribuciones con conceptos musicales (intervalos, triadas, acordes de séptima y escalas).

2. La definición de máxima regularidad

La definición de distribución de regularidad máxima, aunque intuitiva, no es fácil de formalizar. Johson (página 14) empieza considerando una definición geométrica, bastante intuitiva, no del todo práctica, pero que sirve a su propósito de ilustrar cómo funcionan las distribuciones de regularidad máxima. Se trata del algoritmo del vecino más cercano (véase [Góm12] y [DGM+09]). Esta definición fue analizada en la columna anterior (véase la figura 2 de ese artículo).

Al final del capítulo 1 (página 26 y siguientes) Johson presenta una definición más rigurosa si bien algo farragosa. En esta columna vamos a estudiar la definición de Johnson y luego daremos otra, más sencilla, basada en el algoritmo de Euclides. En el libro se empieza por definir dos conceptos básicos, la distancia de semitonos y las distancias de puntos; allí se llaman c distances y d distances, respectivamente. Dada una configuración de puntos sobre un diagrama circular, la distancia de semitonos entre dos puntos mide el número de saltos entre semitonos consecutivos que hay que dar para ir del punto de partida al punto final en sentido horario. La distancia de puntos, análogamente, mide la distancia entre dos puntos como el número de saltos entre puntos consecutivos que hay que recorrer para ir del punto de partida al punto final en sentido horario (las cursivas en estas definiciones no son casuales). La figura 1, extraída del libro, ilustra esta definición; la distancia de semitonos se designa por c y la de puntos por d, y nosotros seguiremos la misma notación.

Figura 1: Distancias de semitonos y distancias de puntos.

Obsérvese que dados dos puntos en el diagrama su distancia se mide de dos maneras distintas, con la distancia d y la distancia c, las cuales no tienen por qué coincidir. En la figura 1, si partimos de las 12 del mediodía y consideramos los dos primeros puntos tenemos d=1 y c=3. Obviamente, la distancia c entre dos puntos es mayor o igual que la distancia d.

La definición de distribución de máxima regularidad de Johnson reza como sigue:

1. Para cada par de puntos en el diagrama circular, calcúlense la distancia c y la distancia d.
2. Considérese para cada valor de la distancia d todos los valores de las distancias c asociadas a ella.
3. Si para toda distancia d, las correspondiente distancias están formadas por un único valor o por dos valores consecutivos, entonces la distribución es de máxima regularidad.

En realidad, esta definición supone la comprobación exhaustiva de la propiedad enunciada en el punto 3). Johson construye para ello las llamadas tablas de intervalos. Vamos a ver un ejemplo sencillo para entender cómo aplicar esta definición; véase la figura 2. Hay un diagrama circular con 4 puntos, A, B, C y D. De las distancias d hay 3 posibles, que toman valores 1, 2, y 3. Para cada valor, las distancias c asociadas son, respectivamente, 3, 6 y 9. Como han dado valores únicos, la definición se verifica y esta distribución es de máxima regularidad.

Figura 2: Cálculo de tablas de intervalos.

Intuitivamente, se veía claramente que esta distribución era de máxima regularidad, más aún si tenemos en cuenta que el número de puntos, 4, es un divisor de 12, el número de subdivisiones del círculo.

Veamos una distribución no regular. Por ejemplo, si en el diagrama anterior movemos el punto D una posición hacia arriba, habremos destruido la propiedad de máxima regularidad. Veamos cómo falla la definición.

Figura 3: un ejemplo de distribución no regular.

Simplemente calculando las distancias asociadas a pares de puntos adyacentes, AB, BC, CD y DA, vemos enseguida que la definición no se cumple, pues las distancias c asociadas son 2, 3, 4, que no están formadas por dos valores consecutivos (aquí hay tres valores consecutivos). La definición falla en realidad con todos los valores de la distancia d. En general, basta con que falle en un caso para que no la distribución no sea de regularidad máxima.

Para acabar esta sección, tomemos un ejemplo un poco más complejo con cinco notas, como el de abajo.

Figura 4: Máxima regularidad de un diagrama de 5 puntos.

3. Distribuciones euclídeas

El contenido de esta sección no aparece en el libro de Johnson. La añadimos para una mejor comprensión de la propiedad de máxima regularidad. La definición que propone Johson es, como hemos visto, larga de comprobar y poco intuitiva. Nosotros vamos a dar una definición equivalente basada en el algoritmo de Euclides para el cálculo del máximo común divisor. Vamos a recordar al lector cómo funciona este bello algoritmo.

3.1 El algoritmo de Euclides

El máximo común divisor de dos números es el mayor divisor común que tengan. El máximo común divisor (mcd) siempre existe pues 1 divide a cualquier número. Por ejemplo, el mcd de 12 y 16 es 4. Típicamente, se enseña a calcular el mcd obteniendo los factores primos de los dos números. Así, por ejemplo, si queremos calcular el mcd de 1089 y 924, averiguamos su descomposición en factores primos:

1089=3² •11² y 924=2•3•7•11

A partir de esa descomposición, basta tomar los factores comunes con menor exponente; en el caso de este ejemplo 3 y 11. El mcd(1089, 924) sera, pues, igual a 3•11=33. Sin embargo, obtener el mcd calculando los factores primos es largo y tedioso. La forma elegante y rápida de calcular el máximo común divisor es usando el algoritmo de Euclides. Este matemático griego, que vivió alrededor del año 300 antes de Cristo, se percató de una propiedad que permite calcular el máximo común divisor con suma rapidez. Supongamos que queremos hallar el máximo común divisor de a y b. Escribimos la ecuación de la división entera:

donde q es el cociente y r es el resto. Como es bien sabido, el resto tiene la propiedad de que 0 ≤ r < b. Si d es un divisor de a y b, también lo será de b y r En efecto:

Entonces, el máximo común divisor de a y b es el mismo que el de b y r. El proceso se puede repetir todas las veces que haga falta. En cada paso el resto que obtenemos es menor estrictamente que el anterior, de modo que finalmente encontraremos un resto nulo. El máximo común divisor será el último resto no nulo que encontremos en esta serie de divisiones sucesivas. Aquí tenemos el ejemplo de más arriba ahora calculado con el algoritmo de Euclides.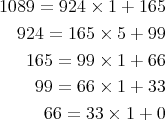

El último resto no nulo es 33, que es el máximo común divisor que habíamos encontrado antes.

3.2 Distribuciones regulares vía el algoritmo de Euclides

Para empezar, vamos a introducir una notación que nos permitirá describir distribuciones en la octava de una manera más rápida. El diagrama de la figura 4 se puede escribir como [x . x . . x . x . . x .], donde una x representa un punto en el círculo y un . una posición no ocupada por un punto. Esta notación se llama notación de caja.

Empezamos, pues, por fijar un círculo -una octava- dividido en 12 partes iguales o semitonos. Si queremos distribuir 4 puntos en el círculo de la manera más regular posible, entonces basta con usar la división. Tendremos que dividir 12 por 3.

y la distribución resultante sería [x . . x . . x . . x . .]. Ahora aparece una nueva propiedad. Cuando efectuamos la división de 12 por 3, obtenemos 4 grupos. Esto ha sido equivalente a asignar un punto a cada grupo de 3 semitonos y exactamente en la misma posición, en este caso, en la primera. ¿Cómo asignamos las notas a los pulsos a través de una división? El procedimiento es el siguiente: primero ponemos las notas (la parte (1)-A de la figura), que ahora y por simplicidad designaremos con unos, tantas como tengamos; segundo, rellenamos con los ceros necesarios hasta completar el número de semitonos (la parte (1)-B de la figura); tercero, efectuamos la agrupación como sabemos (paso (2) de la figura); y cuarto, leemos la distribución resultante (paso (3) de la figura). La distribución resultante se lee por columnas de arriba abajo y de izquierda a derecha.

Se ve claramente cómo la división ejecutada como formación de grupos ha dado lugar a una distribución correcta de los puntos en los semitonos de la octava.

Si queremos distribuir 6 puntos, entonces tenemos que dividir 12 por 2:

y la distribución resultante sería [x . x . x . x . x . x .] Volviendo a hacer nuestro juego de divisiones y agrupaciones, tenemos:

Si queremos distribuir 8 puntos, entonces tenemos que dividir 12 por... ¿cuánto?

Estrictamente hablando no se puede hacer. No hay número entero x tal que  = 8. La solución está en generalizar el concepto de división de tal manera que todavía sirva a nuestros propósitos, tanto matemáticos como musicales. Esta generalización es el principio de regularidad, que es el principio en que se apoya Johnson en su libro. Lo enunciamos como sigue:

Ante el enunciado de ese principio, surgen varias preguntas: ¿Qué significa “de la manera más regular posible”? ¿Cómo se obtiene esa distribución de puntos? ¿Es único? Vamos a contestar a estas preguntas con un ejemplo; más tarde daremos las definiciones formales necesarias.

¿Es la distribución [x x x x x x x x . . . . ] de máxima regularidad? Es evidente que no, que tiene todas los puntos apelotonados al principio y ninguno al final. Tendríamos que mover puntos para hacerlo más regular. Pero ¿cómo? Hay dos observaciones que nos van a ayudar y que ya habían aparecido en el libro de Johnson:

1. En una distribución de regularidad máxima solo puede haber dos distancias.
2. Además, esas dos distancias tienen que ser c y c + 1.

Llamaremos sucesión de distancias a las distancias entre puntos consecutivos según se obtienen leyendo la distribución de izquierda a derecha; por ejemplo, la sucesión de distancias de la distribución [x . . x x . x . . . ] es (3, 1, 2, 4). Recordemos que estamos tratando con diagramas circulares y que las distribuciones se leen de manera circular. Esto significa que se cuenta la distancia entre la última nota y la primera; de ahí el 4 en la sucesión de distancias anterior.

Si la condición (1) no se cumple y hay tres distancias c₁,c₂ y c₃, con c₁ < c₂ < c₃, se pueden cambiar las notas a distancias c₁ y c₃ para que sean más regular. Por ejemplo, la distribución [x x . . x . ], que tiene como sucesión de distancias consecutivas a (1, 3, 2), se puede convertir en [x . x . x .], con distancias (2, 2, 2), que es una distribución más regular. Si solo hay dos distancias, pero c₁ < c₂ + 1, por el argumento anterior, se puede conseguir una distribución más regular cambiando un punto. La distribución [x . x . . .], por ejemplo, tiene sucesión de distancias (2, 4), y se puede hacer más regular moviendo el segundo punto para transformarlo en [x . . x . .], con distancias (3, 3).

Volviendo a la distribución que nos ocupa, [x x x x x x x x . . . . ] movemos sus puntos para intentar obtener una escala de regularidad máxima. He aquí los frutos de nuestros intentos: [ x x x x x . x . x . x .] Esta distribución cumple las dos propiedades (1) y (2) enunciadas arriba, pero no es de regularidad máxima. Esto significa que las dos propiedades de arriba son condiciones necesarias pero no suficientes para construir una distribución de regularidad máxima. Por ello, en la definición de Johnson se exige que se comprueben todos los valores de las distancias d.

Si escribimos las distancias entre puntos consecutivos de esta distribución tenemos la siguiente sucesión:

(1, 1, 1, 1, 2, 2, 2, 2)

Es intuitivamente claro que una sucesión de distancias (1, 2, 1, 2, 1, 2, 1, 2) daría una distribución de mayor regularidad: [x x . x x . x x . x x .]. Y este es la distribución de regularidad máxima que buscábamos. En este punto se hace evidente que una distribución de regularidad máxima no es única. Podíamos haber tomado una rotación de esta distribución, por ejemplo, [. x x . x x . x x . x x]. Una curiosidad: ¿cuál es el máximo común divisor de 12 y 8? Cuatro, que es el número de veces que se repite el patrón [ . x x] en la escala anterior. Esto, por supuesto, no es un hecho fortuito. Veamos qué hay detrás.

Se puede ejecutar el algoritmo de Euclides pensándolo también como la formación de grupos. Haremos divisiones sucesivas moviendo ceros y unos, como hicimos anteriormente. Cojamos como ejemplo, el máximo común divisor de 12 y 8. Ponemos 8 unos seguidos de 4 ceros, como abajo.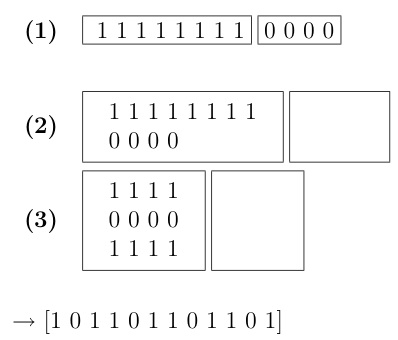

En este caso el número de columnas final es el máximo común divisor. De modo que simulando el algoritmo de Euclides con divisiones en formación de grupos, llegaremos a distribuciones regulares. Fijémonos que en los unos están distribuidos regularmente.

Y por último, si queremos distribuir 7 puntos, entonces tengo que dividir 12 por... ¿cuánto? Pues tampoco se puede

pero volvemos a aplicar el principio de regularidad otra vez, y la distribución resultante (salvo rotaciones) sería [ x . x . x x . x . x . x]. Si hacemos las divisiones (formaciones de grupos), tenemos: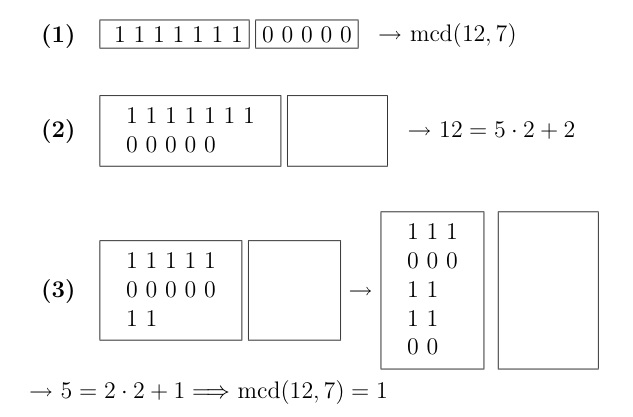

La distribución resultante, una vez leídas las columnas, es:

que no es la distribución que hemos mostrado antes. La razón es que la rotación de una distribución de regularidad máxima no altera esta condición.

Las distribuciones producidas con el principio de regularidad se llaman distribuciones euclídeas. El principio de regularidad se ha revelado como una generalización de la división.

4. Comprobación de la definición de máxima regularidad

Llegado a este punto, vamos a comprobar cómo verificar la definición de máxima regularidad vía el algoritmo de Euclides es más corto y elegante que vía el procedimiento de Johnson. En la figura 4 teníamos el diagrama siguiente:

Figura 5: Un diagrama con cinco puntos.

Este diagrama escrito en notación de caja es [x . x . . x . x . . x .], cuya sucesión de distancias consecutivas es (2 3 2 3 2). Tenemos 12 posiciones (semitonos) para distribuir 5 puntos. Aplicando el algoritmo de Euclides tenemos: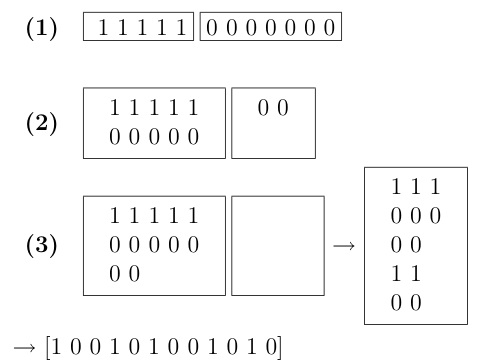

El resultado que obtenemos, leyendo por columnas el último bloque, es [x . . x . x . . x . x .], o escrito como sucesión de distancias consecutivas (3 2 3 2 2). Esta sucesión es una rotación de (2 3 2 3 2) y, por tanto, es de máxima regularidad.

En la columna del mes que viene relacionaremos todo lo visto hasta aquí con conceptos musicales. Estudiaremos qué intervalos, triadas, acordes de séptima y escalas aparecen asociados a las distribuciones de máxima regularidad. Esto dará cuenta de la segunda mitad del libro de Timothy Johnson al que estamos dedicando esta serie.

Bibliografía

• [DGM+09] Demaine, E., Gómez, F., Meijer, H., Rappaport, D., Taslakian, P., Toussaint, G. T., Winograd, T. and Wood, D. R. The Distance Geometry of Music. Computational Geometry: Theory and Application, 42, págs. 429-454, 2009.
• [Góm12] Gómez, F. Enseñanza de música vía las matemáticas - I Columna de la sección Matemáticas y música de la web Divulgamat.
• [Joh03] Timothy A. Johnson. Foundations of diatonic theory. Key College Publishing. Ithaca, New York. 2003.