- (**) Los pitagóricos consideraban que "los números son
el principio, la sustancia y la causa de todas las cosas"
(Aristóteles) y, que por tanto, todas las cosas que pueden ser
conocidas tienen un número. En efecto, podemos definir la medida
de una magnitud, respecto de otra tomada como unidad, como el
número por el cual es necesario multiplicar la unidad para obtener
la magnitud dada. Sin embargo, el propio teorema de Pitágoras nos muestra
la imposibilidad de medir siempre con exactitud: la hipotenusa
de un triángulo rectángulo cuyos catetos miden la unidad no es
conmensurable con el lado, es irracional (no expresable mediante
razón).
La demostración de la "irracionalidad" de 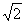 ha sido -como el teorema de Pitágoras- realizada
en infinidad de ocasiones. Por ejemplo, Hardy (1981, pp. 95-96)
la presenta del siguiente modo: ha sido -como el teorema de Pitágoras- realizada
en infinidad de ocasiones. Por ejemplo, Hardy (1981, pp. 95-96)
la presenta del siguiente modo:
Que es irracional quiere decir que no puede expresarse como una
fracción irreducible 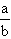 de números enteros: de números enteros:
Procedamos por reducción al absurdo, supongamos
que 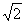 puede expresarse de esta forma puede expresarse de esta forma
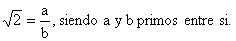
Elevando al cuadrado
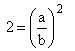 , ,
y,
por tanto,
a2 = 2·b2
de esta ultima igualdad se deduce que a2 es par (múltiplo
de 2) y, por tanto, a es par (el cuadrado de un número impar es siempre
impar), es decir:
a
= 2·c
Sustituyendo
en la igualdad anterior tenemos:
2·b2
= a2 = (2·c)2 = 4·c2
simplificando:
b2 = 2·c2
luego b2 es par y, por la misma razón que antes, b también
es par.
En definitiva, a y b son números pares y, por tanto, tienen como divisor
común el 2, lo cual contradice la hipótesis inicial de que a y b
son primos entre si.
En consecuencia, la hipótesis inicial es falsa y
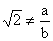
donde 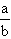 es una fracción
irreducible. es una fracción
irreducible.
Haciendo uso de este modelo, demuestra que 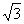 es
también irracional. es
también irracional.
-
(**) A pesar de lo que acabamos
de señalar
existen triángulos rectángulos ABC cuyos lados a, b, c son números
naturales no nulos (3, 4 y 5, por ejemplo). En este
caso se dice que
ABC es un triángulo pitagórico y que los números
a, b, c forman una terna pitagórica. ¿Podrías citar algún triángulo pitagórico?
Comprueba que si m es un número entero impar, los números
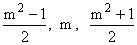
forman una terna pitagórica.
- (**) El matemático hindú Bhaskara (1114-1185)
propuso los siguientes ejercicios:
(El bambú roto) Si un bambú de 32 codos
de altura se rompe por el viento de tal manera que su extremo superior
se apoya en el suelo a una distancia de 16 codos de su base, ¿a qué altura del suelo se ha producido la caida?
- (**) (El pavo real y la culebra) Un
pavo real se encuentra posado en el extremo de un poste
vertical en cuya base hay un agujero de culebra; observando la culebra
a una distancia
del pie del poste igual a tres veces su altura, el
pavo real se lanza sobre ella en línea recta mientras la culebra intenta ganar su agujero.
Si el pavo real captura a la culebra cuando ambos han recorrido exactamente
la misma distancia, ¿a cuántos codos de distancia del agujero se
produjo la captura?
|
|
| En cualquiera de los
siguientes trabajos podemos encontrar una buena colección de
demostraciones del teorema de Pitágoras,
asequibles para los alumnos de secundaria:
- Gacetilla matemática (http://www.arrakis.es/~mcj/teorema.htm)
- GONZÁLEZ URBANEJA, P. M. (2001) Pitágoras. El filósofo del número. "La matemática en sus personajes, nº 9".
Madrid, Nivola.
- MEAVILLA SEGUÍ, V. (2001) Aspectos históricos de las matemáticas
elementales. Zaragoza, Prensa Universitaria de Zaragoza.
- La demostración de que
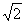 es un número irracional puede encontrase en infinidad de trabajos.
es un número irracional puede encontrase en infinidad de trabajos.
En
particular en:
- HARDY, G. H. (1981) Autojustificación de un matemático. Barcelona,
Ariel. (En 1999 Nivola publicó una nueva edición de esta obra, prologada
por Miguel de Guzmán).
- ALMODÓVAR,
J. A. el al. (1999) Órbita 2000 Matemáticas 2º.
Madrid, Santillana.
Para conocer la obra de Euclides podemos consultar:
- DOU, A. (1970) Fundamentos de la matemática. 2ª ed. Barcelona,
Labor.
- EUCLIDES (1991) Elementos. Libros I-IV. Madrid, Editorial
Gredos. (Introducción de L. Vegas, traducción y notas de M. L. Puertas Castaños).
- LEVI, B. (2000) Leyendo a Euclides. Buenos Aires, Libros Zorzal.
(Prólogo de Mario Bunge).
|
|