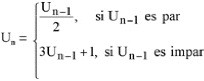19. Seguimos Perdidos
19. Seguimos Perdidos |
 |
 |
 |
| Escrito por Alfonso J. Población Sáez | ||||||||||||||||||||
| Lunes 01 de Enero de 2007 | ||||||||||||||||||||
|
El presente mes están programados cinco episodios de Numb3rs que incluyen mucha información matemática (que por cuestiones de espacio no está descrita totalmente). El lector que no pueda ver la serie no se encontrará, sin embargo, perdido ya que se procura que todo el mundo pueda seguir estas reseñas. A propósito de Perdidos, seguimos respondiendo enigmas….
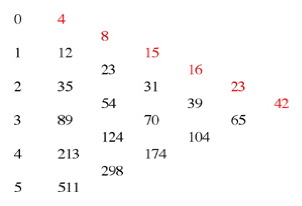
Nadie por el momento me ha enviado la prueba de que dado P(x), polinomio interpolador de esos números, P(n)∈Ζ, para cada n∈Ζ. Os dejaremos pensarlo otro mes más. P(x) = Hay otro polinomio que se cita en la Red sobre estos números, el llamado polinomio de Shaw-Basho (le bautizo como SB(x)), que alguien propuso (ni Shaw ni Basho, al parecer, existen), SB(x) = que verifica que al sustituir x por 0, 1, 2, 3, etc. devuelve 4, 12, 35, 89, 213, 511, 1194, 2622, …, respectivamente. En la página http://www.dougshaw.com/lost/ se indica que lo curioso de esta sucesión es que al ir haciendo sucesivas diferencias entre esos números, se van obteniendo los siguientes resultados: 1ª Sucesión: 4, 12, 35, 89, 213, 511, 1194, 2622, 5346, 10150, 18093, ... Obsérvese que los primeros términos de las sucesivas sucesiones (en rojo) son los famosos números. Nada que decir, ya que el polinomio se ha construido precisamente para que cumpla esa condición (ver abajo). Luego se afirma, como si fuera algo increíble, que la sucesión se autodestruye. Desde luego, ¡se ve cada cosa por ahí escrita¡. La página pertenece al parecer a un profesor, doctor en Matemáticas en la Universidad de Iowa. Pues bien, señores míos (me voy a tomar la molestia de mandar al autor de la página un e-mail a ver si se pone a estudiar algo de Cálculo Numérico), para CUALQUIER conjunto de valores numéricos que verifique un cierto polinomio de grado menor o igual que N, TODAS sus diferencias divididas de grado mayor o igual que N+1 se anulan. Aquí no son exactamente diferencias divididas, pero funcionan igual. Si se quiere obtener un tal polinomio, basta con construir una tabla del siguiente modo:
Necesitamos para ello disponer de las imágenes de los nodos (los nodos son los valores de la primera columna, 0, 1, 2, 3, 4, 5), y calcular el polinomio interpolador. Para el que sepa cómo se construye el polinomio interpolador mediante diferencias divididas, una tabla similar a ésta, quizá piense que ya podríamos construir el polinomio así: L(x) = 4 + 8 (x − 0) + 15 x(x − 1) + 16 x(x − 1) (x − 2) +23 x(x − 1) (x − 2)(x − 3) + 42 x(x −1) (x − 2)(x −3) (x − 4) = 42 x5 − 397 x4 + 1348 x3 − 1880 x2 + 895 x + 4 Pero si calcula las sucesiones de diferencias descritas con anterioridad, verá que no se cumplen. ¿Por qué? Porque la forma anterior de componer el polinomio interpolador está basado en diferencias divididas (para calcular la tercera columna se restan los valores consecutivos de la columna anterior pero hay que dividirlos por 2, para la cuarta hay que dividirlos por 3, etc. la diferencia entre los nodos). Lo que buscamos nosotros es ligeramente distinto: queremos que los valores de TODAS las columnas sean los valores de rojo, pero sin dividir por ningún valor. Es decir queremos una tabla en diferencias SIN DIVIDIR. Entonces vamos calculando, desde el final al principio los valores de los asteriscos, hasta que tengamos las imágenes de cada nodo (es decir, la segunda columna completa). Es sencillo, sólo hay que sumar. (42 + 23 = 65, etc.). Se tiene entonces la tabla
Véase que por columnas son justamente los valores de las sucesiones que aparecen arriba. Bien, se calcula entonces el polinomio interpolador que pasa por los puntos (0,4), (1, 12), (2, 35), (3, 89), (4, 213) y (5, 511), y se obtiene obviamente el polinomio ÚNICO SB(x), el polinomio de Shaw-Basho cuya obtención no tiene nada de misteriosa, ni tiene ninguna propiedad especial que no tenga cualquier otro polinomio así construido. Los números estos se han elegido completamente al azar. Sin embargo algunos seguidores de la serie, parece que por no tener una ocupación mejor, se empeñan en cientos de blogs en buscarles tres pies al gato. En 1959 el neuropsicólogo Klaus Conrad (1905−1961) definió la apofenia como la experiencia (esto es un eufemismo; debería decir el trastorno) consistente en ver patrones, conexiones o ambos en sucesos aleatorios o datos sin sentido alguno. Conrad describió originalmente este fenómeno en relación con la distorsión de la realidad presente en la psicosis, pero se utiliza en un sentido más amplio para describir esta tendencia en individuos sanos sin que esto implique necesariamente la presencia de enfermedades neurológicas o mentales (espero que este último sea el caso de los lectores de estas páginas). La apofenia se usa a menudo como explicación de afirmaciones paranormales o religiosas. Otros estudios describen la apofenia como un vínculo entre la psicosis y la creatividad. ¿A qué viene este apunte? Pues porque les voy a deleitar con las casualidades que más me han llamado la atención sobre estos números, para que observen cómo hila de fino el personal y para advertirles que estas cosas no deben tenerlas más que como curiosidades.
2.- Tomando las diferencias entre pares consecutivos de los números y sumándolas, se obtiene la diferencia entre el último y el penúltimo número (que como se ve en el fotograma de la lotería de uno de los protagonistas, está separado del resto, es el número complementario): (8 − 4) + (15 − 8) + (16 −15) + (23 −16) = (42 − 23) 3.- Una combinación lineal de cinco de los números genera el sexto. Además siempre son tres sumas y dos diferencias de factor unidad:
4.- La suma de los números (108; recordemos, cada 108 minutos los sufridos supervivientes deben introducir los números en un ordenador), su producto (7418880) y su media aritmética (18) tienen como suma de dígitos el valor 9. Normal, ocurre para cualquier múltiplo de 9, y esos tres valores son múltiplos todos de 9 (véase, por otro lado, la descomposición de los números en factores primos). 5.- En la mitología budista e hindú, el número 108 es muy importante. Observan 108 pecados en el Ser Humano, por lo que en las celebraciones de Año Nuevo, tañen una campana 108 veces. Además se dice que los dioses hindúes tienen 108 nombres.
Y muchas más peregrinas coincidencias y apariciones (véase el número de placa policial de Catwoman en la imagen) ….. Viendo toda la parafernalia generada por unas simples cifras que nos pueden dar pie hasta para explicar cómo se calcula un polinomio interpolador, por favor, señores guionistas, introduzcan más cosillas de este tipo en sus producciones, aunque si fuera posible, que nos dieran más juego, algo así como lo que sucede en NUMB3RS, de la que ya me ocupo. Coincide que este mes el día 1 de Enero es lunes, es decir que hay capítulo nuevo de Numb3rs. Entenderéis (espero) los cientos de seguidores de estas humildes reseñas que esta vez no esté colgada de la red a tiempo, aunque se procurará que esté lo antes posible. No os preocupéis, que se re-emiten varios días.
Muy apropiada la emisión de este capítulo en periodo navideño en el que tradicionalmente jugamos alguna que otra partida a las cartas. Y un buen episodio para aprender algunas cosas sobre casas de juego y probabilidades que ojalá hagan recapacitar a más de uno sobre un conocido dicho: La Banca nunca pierde. En el episodio se juega al Blackjack. Comencemos describiendo las reglas de este juego, muy similar a nuestras Siete y Media. Usualmente se juega entre dos personas, el que juega y el croupier (puede En el blackjack el jugador (no la banca) tiene más opciones: ♣ Doblar su apuesta (título del capítulo, double down): si las dos primeras cartas del jugador suman 9, 10 u 11, puede doblar su apuesta. En este caso, le será servida una sola carta. ♣ Separar parejas (Splitting Pairs): Si las dos primeras cartas del jugador son del mismo valor, podrá separarlas depositando una apuesta igual a la inicial y jugando dos manos independientes. Puede separar tantas manos como cartas del mismo valor le sean servidas. Si separa un par de ases, sólo podrá recibir una carta para cada as, y si una de estas cartas fuese un 10 o una figura, su puntuación será de 21, pero no de Blackjack. Es bastante arriesgado separar dos reyes puesto que tienes ya una buena puntuación (20). Es lo que hace Alex Chernov en este episodio. ♣ Seguro (Insurance): Si la primera carta del croupier es un as, los jugadores pueden asegurar sus apuestas contra el posible Blackjack de la banca, depositando una suma igual, como máximo, a la mitad de la apuesta. Si el croupier logra el blackjack, pagará al jugador el seguro a razón de 2 a 1; si no lo consigue, el jugador perderá su apuesta de seguro.
Las reglas del blackjack varían ligeramente entre los diferentes casinos del mundo. Esto es consecuencia directa del descubrimiento por parte de jugadores de mentalidad matemática durante los años sesenta (entre ellos el célebre profesor Edward O. Thorp), de que en el blackjack no sólo era posible jugar en igualdad de condiciones que la Banca, sino también con mayor ventaja. Con ayuda de los ordenadores se ha estudiado cual sería la jugada óptima para cada una de las distintas situaciones que se puede dar en el blackjack. Por ejemplo, la mayor parte de los jugadores de blackjack sabe que la peor carta que pueden recibir es un 5, ya que ofrece posibilidades muy pobres de cara a hacer un buen juego y con frecuencia conduce al «fiambre», lo cual, evidentemente, favorece a la banca. Después del 5 y por orden de importancia, las peores cartas son 4, 3, 2 y 6. No es sorprendente, por tanto, que los gerentes de los casinos efectuaran modificaciones en las reglas del juego que les favorecieran. Para aquéllos que dominan la complejidad del juego y se dedican lo suficiente a aplicar los descubrimientos de los expertos, el blackjack puede representar una profesión de la que poder vivir, aunque en realidad pocos lo hacen, ya que cuando un casino descubre a un profesional, con toda seguridad, le impiden jugar. Recuérdese por ejemplo el caso de la familia Pelayo y sus ganancias en la ruleta. La página http://www.bjmath.com/bjmath/toc.htm contiene gran cantidad de artículos matemáticos (para seguir algunos es necesario conocer bastante a fondo ciertos temas de estadística e investigación operativa) aplicados a este juego. A menos que se tenga una súper memoria y uno sea capaz de hacer cálculos con mucha rapidez, es muy difícil saber si se tiene ventaja sobre el croupier. Todos los sistemas se basan en recordar las cartas que han salido, aunque en ningún caso se puede saber con certeza cuando se va a ganar. Los tres estudiantes del capítulo han analizado sin embargo otra faceta del juego. Los casinos suelen utilizar un barajador automático para mezclar las cartas. Estos artilugios utilizan un algoritmo para simular aleatoriedad, pero los informáticos y los matemáticos saben que cualquier máquina (ordenadores incluidos) nunca genera números aleatorios, sino seudo-aleatorios. Por definición un número seudo-aleatorio es un número generado por un proceso algorítmico o una fórmula. A pesar de no mostrar ningún patrón o regularidad aparente desde un punto de vista estadístico, al generarse por un procedimiento determinista, las mismas condiciones iniciales producen siempre el mismo resultado. En cambio un número aleatorio como su propio nombre indica no debe estar sujeto a ningún proceso, sólo a variables al azar. Los seres humanos vivimos en un medio aleatorio y nuestro comportamiento lo es también. No podemos conocer de antemano el momento en que se fundirá una bombilla, o cuando empieza o deja de llover, la cantidad de palabras que decimos en una hora, incluso la longitud de nuestra vida, Todo lo que nos sucede depende de muchísimos factores. A cada instante, con cada paso que se da y con cada decisión que se toma (incluso las inconscientes reflejas), se opta por una de entre infinitas posibilidades. Para cualquier inicio de día existen incontables posibles finales. Por eso para generar números aleatorios se emplean procedimientos tomados de la Naturaleza (que nos garantiza entropía máxima); los más usuales, el ruido eléctrico generado por la agitación y movimiento de los electrones o la desintegración de elementos radiactivos. La generación de números aleatorios es importante en diversas áreas, especialmente en todo lo referido a la criptografía (que como venimos indicando en estos artículos es indispensable para garantizar la seguridad en las comunicaciones, en las trasferencias bancarias, el uso de tarjetas de crédito, etc.). El número de posibilidades de colocar un mazo de 52 cartas es de 52! (un número del orden de 8 x 1067) y en teoría cada una de esas posiciones de las cartas tiene la misma probabilidad. La magnitud del número anterior hace prácticamente imposible la posibilidad de que dos mazos seleccionados aleatoriamente tengan, o hayan tenido jamás la misma distribución de sus naipes. Sin embargo si que es posible hacer predicciones de tipo probabilística en un mazo que no esté barajado de una forma puramente aleatoria. Los protagonistas del capítulo al parecer han logrado determinar, a partir de datos experimentales, generar una simulación del algoritmo que tiene implementado el barajador. El mago y matemático Persi Diaconis es un experto en el barajado de cartas de forma teórica y práctica (es también profesor de Estadística, ¡como no!, en la Universidad de Stanford). En un estudio de años ha concluido que se necesitan al menos cinco barajamientos “perfectos” para empezar a hablar de aleatoriedad y más de siete para garantizarla. Y eso barajando correctamente, porque si la técnica no es correcta se necesitan muchos más. De formas de barajar las cartas saben mucho los magos e ilusionistas. Existen muchas formas (para ellos son técnicas) de barajar. El barajado perfecto anteriormente citado (lo hemos visto en las películas muchas veces) consiste en dividir la baraja en dos mitades e ir hojeándolas con los pulgares para que se vayan intercalando las cartas de ambas mitades. Si en lugar de eso, cortamos la baraja a la mitad y colocamos la parte inferior sobre la superior, sería necesario hacer 2500 veces esa operación para lograr el mismo grado de aleatoriedad que la de las 7 veces del modo “perfecto”. Este modo de barajar se llama en inglés “Riffle” del cual no sé si hay una traducción al castellano. En este enlace podéis haceros una idea de la gran variedad de formas distintas de barajado que podemos realizar. Finalmente, en el capítulo Charlie y Amita citan las series temporales como herramienta de apoyo en la reconstrucción del juego y el intercambio de dinero que los jóvenes realizaron antes del asesinato de uno de ellos, y así tratar de reproducir cuales fueron los pasos que siguieron el, o los, asesinos. Brevemente, se define una serie temporal (también llamada histórica, cronológica o de tiempo) como un conjunto de datos correspondientes a un determinado fenómeno, ordenados respecto al tiempo. Por ejemplo, las ventas de una empresa en los últimos cinco años, o la cantidad de lluvia caída al día en el último trimestre. Aunque entre más dentro del campo de la computación, en el episodio también se muestra la identificación de personas a partir de dos fotografías tomadas en diferentes épocas (en el capítulo, una foto de un carné de conducir y una foto escolar). Hoy en día hay software muy potente que realiza este tipo de pruebas (lo hemos visto en muchas películas). Sin embargo no todo es tan “bonito” como suele presentarse, hay bastantes limitaciones. Por ejemplo, las fotos deben haberse tomado en unas condiciones determinadas de luz, con una buena resolución y a ser posible en una postura similar. Quizá en otro momento, expliquemos este asunto con un poco más de detalle.
Don y su equipo localizan un laboratorio oculto en los sótanos de un viejo motel en el que se están llevando a cabo transplantes ilegales de órganos. Encuentran restos de sangre y un bloque de hielo en un rincón. Cuando Charlie observa el charco formado por el hielo, pide las fotografías que ha tomado el FBI para tratar de estimar, a partir del ritmo de deshielo del bloque, del tamaño del charco (superficie que abarca) y suponiendo que la temperatura del lugar se mantiene constante, el momento en el que el lugar fue utilizado por última vez. Se trata de una cuestión elemental de razones de cambio (derivadas) relacionadas. En la discusión para resolver el asunto, Charlie y Amita exponen también algunas de las propiedades del agua sobre diferentes superficies. Hablan de conceptos físicos como la adhesión (atracción molecular a las superficies), la cohesión (atracción de las moléculas entre sí) y la tensión superficial. En un fluido cada molécula interacciona con las que le rodean. El radio de acción de las fuerzas moleculares es relativamente pequeño, abarca a las moléculas vecinas más cercanas. Como todo sistema tiende a adoptar espontáneamente el estado de energía potencial más baja, los líquidos tienen tendencia a presentar al exterior la superficie más pequeña posible. Otro tema que se plantea es el de tratar de identificar los posibles destinos de la ambulancia que transporta los órganos a partir de rutas no determinadas. Para ello, el matemático expone que se puede utilizar un modelo oculto de Markov que permita disminuir el amplio número de posibilidades que se les presentan. Este tipo de modelos permiten caracterizar procesos estocásticos para los que no se cuenta con demasiadas observaciones. La idea consiste, a grandes rasgos, en modelizar un proceso doble, para el que se supone que los datos observados son producto de hacer pasar el proceso real (el que está oculto) a través de un medio cuyo resultado sea el proceso que sí es observable. Viene a ser como una caja negra en la que la secuencia de símbolos de salida generados con respecto, por ejemplo, al tiempo, es visible, pero la secuencia de estados por los que se ha pasado es desconocida. Algunas de las aplicaciones en las que se utilizan estos modelos es la de determinar cambios meteorológicos, reconocimiento automático de la voz, clasificación de los estados del sueño, configuración de procedimientos para segmentar eficazmente las direcciones postales de interés para una empresa, etc. Estos métodos se desarrollaron a partir de la década de los cincuenta del siglo pasado, y deben su nombre al matemático Andrei Markov (1856 – 1922), uno de cuyos trabajos consistió precisamente en ilustrar gráficamente la probabilidad de un suceso que afectara a probabilidades futuras, información almacenada en una matriz a partir de la cual se establecen los diferentes cálculos. Finalmente, tras analizar los recorridos de la ambulancia, Charlie aventura, a partir de diferentes medidas de distancias, que es probable que los lugares que buscan se encuentren en los focos de una elipse. En este capítulo se hace referencia al apellido de Amita, Ramanujan,
Desde los Pitagóricos sabemos de las relaciones entre la música y las matemáticas. La diferente longitud de cuerdas tensas o distintos diámetros de tubos producen notas musicales diferentes. Por ejemplo, si la longitud de una cuerda es doble que la de otra, la más corta produce un sonido una octava más alto que el más largo. Este es el intervalo que separa un Do del Do de la escala siguiente. Las notas de la escala no guardan igual espacio entre sí. La distancia mayor entre una nota y otra se llama tono, y la distancia menor se llama semitono. La escala más conocida y utilizada es la formada normalmente por siete notas, Do, Re, Mi, Fa, Sol, La Si, aunque las hay también de seis u ocho. Si a esas notas le añadimos el siguiente Do, obtenemos la escala diatónica.
La proporción de mayor interés es la de 3/2. Si una cuerda tiene una longitud de 3 unidades y otra de 2, la más corta proporciona la distancia exacta entre Do y Sol. Otras proporciones son la de 4/3, una cuarta perfecta (distancia de Do a Fa), o 81/64, una tercera mayor (distancia de Do a Mi). Sabemos que los sonidos se producen mediante una sencilla vibración. El número de vibraciones por unidad de tiempo se denomina frecuencia. Si dos cuerdas o tubos tienen longitudes o diámetros, respectivamente, proporcionales, entonces las frecuencias que producen están en una proporción inversa, es decir, a menor longitud, mayor frecuencia. Si un Do tiene una frecuencia de 256, entonces el Sol correspondiente tiene una frecuencia de 256 por 3/2, es decir, 384. Una quinta (una proporción de 3/2) puede utilizarse para obtener todas las notas de la escala que utilicemos. Tomemos un Do y saltemos por quintas, obtendremos Do – Sol – Re – La – Mi – Si – Fa# – Do# llegando a Do#, en el llamado “ciclo de quintas”. Si reordenamos las cinco primeras notas de la forma Do, Re, Mi, Sol, La, se obtiene la escala pentatónica mayor. Estas escalas son las más simples de todas y probablemente las más utilizadas en estilos como el blues, el heavy metal y el rock. (la escala de Blues contiene una nota adicional, la llamada nota de blues (blue note), que se sitúa entre la cuarta y la quinta). Ocurre que hay bastantes problemas para crear todas las notas de la escala usual a partir del ciclo de quintas, ya que no volvemos exactamente al Do en el que empezamos (ver la sucesión anterior) y algunas de las notas intermedias que deberían estar a una quinta, no lo están. Esto creó muchos problemas con diferentes instrumentos a lo largo de la historia. A principios del s. XVIII se solucionó con una correcta afinación de los instrumentos. La idea es, básicamente, dividir la proporción 2 a 1 (la octava) en 12 partes iguales, 12 porque hay 12 semitonos en una octava: Do, Do#, Re, Re#, Mi, Fa, Fa#, Sol, Sol#, La, La#, Si (después de Si vuelve a Do). La proporción de las frecuencias entre notas sucesivas en la escala cromática (la de 12 tonos) es la misma. Esto equivale a que el producto de las 12 proporciones debe ser igual a la de 2/1 de la octava, es decir, numéricamente, 2. Luego cada proporción es la raíz doceava de 2, 21/12 (1.059463094). Para ir de Do a Sol, un espacio de siete semitonos, hay que multiplicar la frecuencia de Do por 21/12 siete veces, es decir 27/12 (aproximadamente 1.4983, muy próximo a 3/2 = 1.5, aunque no exacto). Charlie habla en este capítulo una flauta pentatónica (ver foto).
Estas flautas son ideales para explorar la escala pentatónica. (Él se construye otro tipo de flauta, sin agujeros para los dedos, que sigue la escala armónica y cuyos sonidos se producen únicamente soplando a diferentes longitudes). Charlie explica que para poder construir una flauta pentatónica (es decir, para situar los agujeros correctamente) es necesario aproximar un número irracional (el explicado anteriormente) por un número racional. Esto se logra matemáticamente mediante los desarrollos en fracciones continuas. Esta presentación musical puede ser por tanto una buena introducción para esos alumnos de secundaria tan poco receptivos, y de paso quizá aprendan también que sus canciones favoritas existen porque las matemáticas lo han querido. Vayamos a otro asunto. Está extendida entre la gente la idea de que todos los números tienen una distribución uniforme y aleatoria, y que todos son igualmente probables. Basándose en este supuesto, una de las técnicas que utilizan los investigadores (y en este episodio Charlie) para descubrir si ciertos datos han sido falsificados, es acudir a la Ley de Benford, también conocida como ley del primer dígito: en un conjunto de datos numéricos que provengan del “mundo real”, la probabilidad de que el primer dígito en esos datos sea un 1 es mayor que la de que sea un 2, ésta a su vez mayor que la de que sea un 3, y así sucesivamente. Este hecho fue estudiado en 1881 por el astrónomo Simon Newcomb al darse cuenta de que las páginas iniciales de su libro de logaritmos estaban más desgastadas por el uso que las restantes. En 1938, el físico Frank Benford retomó la idea. Durante seis años, analizó cerca de 20000 datos de los más variopintos lugares (constantes científicas, resultados del mercado de valores, profundidades de lagos, números aparecidos en la prensa, etc.). Cuando sus investigaciones corroboraron sus hipótesis, desarrolló el enunciado anterior, junto con la expresión p(d) = log (1 + 1/d), una estimación de la probabilidad de que el dígito d aparezca el primero en un conjunto de datos cualquiera. De esta expresión se obtendría la siguiente tabla
Como vemos, según esta ley, el 1 es más de seis veces más probable de liderar un número que el 9, una diferencia considerable. Hay algunas restricciones a la hora de utilizar esta ley: no se debe aplicar a conjuntos de números prefijados (tales como números de la seguridad social o listas telefónicas), ni a números con una distribución uniforme de dígitos (números de lotería) o a conjuntos de números que presenten valores máximos o mínimos. El trabajo de Benford presupone que los datos puedan seguir una progresión geométrica (por ejemplo, un crecimiento exponencial), por lo que dos ejemplos típicos de aplicación pueden ser el crecimiento de la población o la información financiera. No obstante, en otros tipos de datos como tasas de mortalidad o los números de Fibonacci, la ley de Benford también parece cumplirse. En el siguiente enlace de la revista Matematicalia, podéis ampliar esta información en un magnífico artículo.
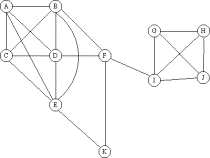
Como sucedía en el capítulo 2.13, Bandas Callejeras, Charlie utiliza análisis social de redes. En este caso examina las relaciones entre miembros de grupos organizados que protestaban durante los años sesenta y setenta contra la guerra de Vietnam (en este episodio es contra la Guerra en Irak). Organizar tantos datos es posible hoy día gracias a la potencia de los ordenadores que tenemos. Veamos un ejemplo. El grafo siguiente representa los contactos entre diferentes personas por teléfono o correo electrónico al menos una vez por semana en un periodo de un año.
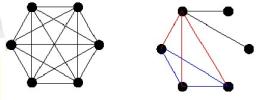
Este tipo de diagramas son generados automáticamente por un programa informático que ha manejado miles de llamadas telefónicas. Con un diagrama como éste podemos, entre otras cosas, medir el grado de cada nodo (el número de contactos que una persona ha tenido con las demás). En el ejemplo, B, D y E tienen grado 5, mientras que K sólo tiene grado 2. Asimismo puede observarse claramente que F tiene un papel destacado ya que conecta dos bloques diferentes. Si la red anterior representara una organización en la que los segmentos fueran las diferentes líneas de mando y que K fuera el jefe, observaríamos que éste depende en gran medida de F. En la práctica el software de este tipo puede manejar una enorme cantidad de datos e individuos pudiendo presentar distintas clases de conexiones, algunas totalmente insospechadas a simple vista. Como vemos, los grafos pueden ayudarnos a interpretar y analizar toda esa información. Relacionados con ellos están los números de Ramsey, que surgen al responder a cuestiones como la siguiente: en cualquier reunión de 6 personas, ¿cuál es el mínimo número de ellas que no se conocen entre sí? ¿Y el mínimo número de ellas que se conocen? La respuesta es que o bien 3 de ellas se conocen o bien 3 de ellas no se conocen. ¿Por qué? Observemos los grafos siguientes:
De todas las posibles conexiones entre todas las personas (dibujo de la izquierda), se puede dibujar como mínimo o un triángulo rojo (personas que se conocen) o uno azul (personas que no se conocen). El teorema de Ramsey establece que para cualquier par de enteros positivos m y n, siempre existe un número de Ramsey R(m, n), aunque no existe una fórmula que nos proporcione tales números (números que son enormes a partir de cierto valor). En el caso del ejercicio anterior R(3, 3) = 6, es decir, 6 es el mínimo número de personas que debe haber en una reunión para que o bien 3 se conozcan o bien 3 no se conozcan. Estos números fueron introducidos por Frank Plumpton Ramsey (1903 – 1930) y han interesado a muchos matemáticos, entre ellos, el célebre Paul Erdös. Los números de Ramsey no sólo se aplican a reuniones de personas, sino también a otros asuntos como determinar el número mínimo de puntos necesario para construir un polígono convexo. Existen aún muchas incógnitas sobre estos números, así que el que quiera pasar a la posteridad, aquí tiene un tema al que dedicarse. En una de las pizarras de Charlie aparece la conjetura de Collatz (también conocida como conjetura 3n+1), un problema en el que Charlie trabaja en sus ratos libres. Para formar una sucesión de Collatz, se parte de un número natural cualquiera. Si es par, se divide por 2; si es impar se multiplica por 3 y se le suma 1. Se repite el proceso varias veces, y siempre se acaba en el bucle 1, 4, 2, sea cual sea el valor inicial. Esta conjetura, no demostrada aún rigurosamente, fue propuesta por Lothar Collatz en 1937. Más formalmente, el proceso es el siguiente:
Existen diversos grupos de computación que se dedican a comprobar la conjetura para números cada vez más grandes. A fecha de 12 de Diciembre de 2006, se había comprobado hasta el valor 12 x 258. En este enlace, podéis leer más sobre esta cuestión y actualizar datos. Como ocurría con el último teorema de Fermat o la conjetura de Goldbach es una evidencia intuitiva fuerte a favor de la veracidad del resultado, aunque matemáticamente no demuestra absolutamente nada. Es un ejemplo de sucesión definida recursivamente (para calcular algunos términos se necesitan uno o más de los anteriores). La famosa sucesión de Fibonacci (Fn = Fn−1 + Fn−2 , para n>2, con F1 = F2 = 1) es otro ejemplo de sucesión de este tipo. Otro ejemplo es el de los llamados números felices: aquellos en los que al elevar sus dígitos al cuadrado y sumarles, al cabo de un número finito de pasos, obtenemos el número 1. Por ejemplo, el número 19 es un número feliz porque
Los números que no verifican esta condición se les llama infelices o tristes. Un entretenimiento para nuestros alumnos: ¿será el 2007 un año feliz?
Para probar los poderes del vidente, los agentes le muestran 25 naipes tapados y le piden que prediga el color de cada carta. Como el porcentaje de fallo es del 50%, si fuera de verdad vidente es esperable que acierte en algo más de la mitad de los naipes. Larry apunta: “la probabilidad de acertarlos todos es la misma que la de fallarlos todos”. Los videntes afirman poseer lo que se ha dado en llamar percepción extrasensorial (ESP, en inglés), un poder a partir del cual pueden conocer, visualizar o percibir, según los casos, situaciones que escapan a los sentidos de una persona normal. Se puede dejar un mínimo margen de confianza, pero lo que es realmente constatable es que desde hace décadas, la CSICOP (organización norteamericana que estudia científicamente hechos paranormales) realiza tests a cientos de personas que afirman tener ESP y por ahora nadie ha pasado ninguna de esas pruebas. El ex mago James Randi (el que descubrió el truco de los dobleces de cucharas de Uri Géller) ofrece UN MILLÓN DE DÓLARES a quien pueda demostrar y realizar repetidamente algún acto de este tipo y que él mismo sea incapaz de repetir. Hasta ahora nadie ha ganado el premio, así que anímense señores tarotistas, brujos y sanadores que hay por ahí, que la fortuna les espera sin necesidad de engañar a nadie. Por otro lado, Charlie emplea la ecuación de Fokker-Planck (se trata de una ecuación en derivadas parciales de segundo orden, cuya descripción supera los contenidos esperables de una sección como ésta; el lector interesado puede buscarla no obstante en Google y allí localizará cientos de artículos detallados) para predecir el flujo de inmigrantes ilegales. Esta ecuación fue originalmente desarrollada para estudiar el movimiento browniano, es decir, el aparentemente aleatorio movimiento de una partícula nanoscópica que se halla en un medio fluido (por ejemplo polen en una gota de agua). Recibe su nombre en honor a Robert Brown que lo describe en 1827. La descripción matemática del fenómeno fue elaborada por Albert Einstein y constituye el primero de sus artículos del "año mirabilis" 1905. La teoría de Einstein demostraba la teoría atómica, todavía en disputa a principios del siglo XX, e iniciaba el campo de la física estadística. Posteriormente Norbert Wiener y Paul Levy elaboraron el modelo que describe una partícula que en cada instante se desplaza de manera independiente de su pasado: es como si la partícula “olvidara” de donde viene y decidiese continuamente y mediante un procedimiento al azar hacia adonde ir. En definitiva, que este movimiento, a pesar de ser continuo, cambia en todo punto de dirección y de velocidad. Tiene trayectoria continua, pero no tiene tangente en ningún punto. Un refinamiento de los cálculos de Einstein fue realizado por el físico Paul Langevin que diferenció dentro del movimiento browniano una fuerza externa (gravedad, magnetismo u otras fuerzas deterministas), una fuerza viscosa (causada por el rozamiento entre moléculas) y un “ruido” aleatorio (imprevisible). La ecuación de Langevin describe, estadísticamente, la fuerza total sobre una partícula. Este modelo se ajusta mejor al análisis que hace Charlie: la fuerza externa es la atracción que los inmigrantes sienten hacia las ofertas de empleo y casa ofrecidas por ranchos y granjeros; la fuerza viscosa (negativa) es el control policial ejercido en los puestos fronterizos; y el “ruido” aleatorio viene determinado por la confusión de los inmigrantes sobre las decisiones a tomar. Los valores numéricos que Charlie asigna a cada una de estas fuerzas no aparecen justificados, son apreciaciones suyas. Este esquema no parece demasiado realista, pero ciertamente los guionistas también deben explayarse de vez en cuando… |
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |






 Entiéndase bien el título de este mes. No es que hayamos perdido el rumbo, es que estamos visionando los capítulos de esta serie desde la primera temporada, rastreando afanosamente si hay alguna clave que ayude a resolver la génesis de la misteriosa sucesión que determina (según el argumento de la serie) el destino de la Humanidad (ecuación de Valenzetti la han llamado). Por cierto, que en el fondo no hay sucesión que valga, por lo que no se entiende ese afán por saber el siguiente término. Son seis números sin más.
Entiéndase bien el título de este mes. No es que hayamos perdido el rumbo, es que estamos visionando los capítulos de esta serie desde la primera temporada, rastreando afanosamente si hay alguna clave que ayude a resolver la génesis de la misteriosa sucesión que determina (según el argumento de la serie) el destino de la Humanidad (ecuación de Valenzetti la han llamado). Por cierto, que en el fondo no hay sucesión que valga, por lo que no se entiende ese afán por saber el siguiente término. Son seis números sin más.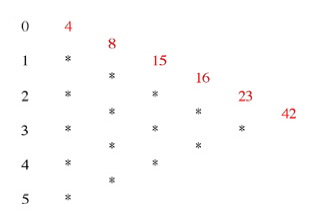
 1.- Si sumamos cualquiera de los seis números de tres en tres, el resultado es siempre un múltiplo de 3. (¿Y qué? Esto se logra de infinitas maneras)
1.- Si sumamos cualquiera de los seis números de tres en tres, el resultado es siempre un múltiplo de 3. (¿Y qué? Esto se logra de infinitas maneras) 6.- Esos dorsales de los Yankees de béisbol están retirados en memoria de los grandes jugadores que los llevaron: 4.- Lou Gehrig (recuerden la peli de Gary Cooper, El orgullo de los Yankees), 8.- Yogi Berra y Hill Dickney, 15.- Thurman Munson (que murió en un accidente de avión, precisamente), 16.- Whitey Ford, 23.- Don Mattingly, 42.-Mariano Rivera. Sabiendo lo pesados que se ponen los norteamericanos con este deporte, no diría yo que no fuera ésta la causa más plausible de elección de estos números.
6.- Esos dorsales de los Yankees de béisbol están retirados en memoria de los grandes jugadores que los llevaron: 4.- Lou Gehrig (recuerden la peli de Gary Cooper, El orgullo de los Yankees), 8.- Yogi Berra y Hill Dickney, 15.- Thurman Munson (que murió en un accidente de avión, precisamente), 16.- Whitey Ford, 23.- Don Mattingly, 42.-Mariano Rivera. Sabiendo lo pesados que se ponen los norteamericanos con este deporte, no diría yo que no fuera ésta la causa más plausible de elección de estos números. haber hasta 7 jugadores; no obstante el resto sólo pueden apostar sobre la mano del que juega, siempre que éste lo permita, y sin poder dar consejos ni instrucciones a los demás. En la imagen, mesa típica del juego). A cada jugador se le dan dos cartas, una se muestra sobre la mesa; la otra sólo la ve el jugador. Se pueden pedir más cartas, pero sólo una puede estar oculta. Gana el jugador que tiene el valor más cercano a 21 sin pasarse. Los ases pueden valer 1 u 11 (a discreción del jugador; si decide que valga 1 o si no aparecen ases, se denomina “mano fuerte”; si elige 11, es una “mano floja”); dieces, jotas, reinas y reyes valen 10, y el resto de cartas toman su valor facial. El término “blackjack” hace referencia a conseguir 21 con sólo dos cartas. Se trata de un juego tipo chemin de fer (esta expresión significa ferrocarril). Se originó en los casinos franceses en torno al 1700 y ha derivado en un conjunto de variantes que incluyen el Baccarat, Vingt-Et-Un (conocido como el 21 en Norteamérica y como Pontoon en Australia). Como ya hemos dicho, en nuestro país la variante más popular de este tipo son las Siete y Media.
haber hasta 7 jugadores; no obstante el resto sólo pueden apostar sobre la mano del que juega, siempre que éste lo permita, y sin poder dar consejos ni instrucciones a los demás. En la imagen, mesa típica del juego). A cada jugador se le dan dos cartas, una se muestra sobre la mesa; la otra sólo la ve el jugador. Se pueden pedir más cartas, pero sólo una puede estar oculta. Gana el jugador que tiene el valor más cercano a 21 sin pasarse. Los ases pueden valer 1 u 11 (a discreción del jugador; si decide que valga 1 o si no aparecen ases, se denomina “mano fuerte”; si elige 11, es una “mano floja”); dieces, jotas, reinas y reyes valen 10, y el resto de cartas toman su valor facial. El término “blackjack” hace referencia a conseguir 21 con sólo dos cartas. Se trata de un juego tipo chemin de fer (esta expresión significa ferrocarril). Se originó en los casinos franceses en torno al 1700 y ha derivado en un conjunto de variantes que incluyen el Baccarat, Vingt-Et-Un (conocido como el 21 en Norteamérica y como Pontoon en Australia). Como ya hemos dicho, en nuestro país la variante más popular de este tipo son las Siete y Media. que como todos sabemos, corresponde al mejor matemático indio de todos los tiempos, Srinivasa Ramanujan (1887 – 1920). La familia de Amita es de procedencia Tamil (una de las culturas e idiomas más extendidos de la India), natural de Chennai, una de las mayores ciudades costeras de la India, con unos 7 millones de habitantes, antes conocida (antes de 1996) como Madrás. Srinivasa Ramanujan también provenía de la cultura Tamil, aunque era natural de un pequeño pueblo llamado Kumbakonam, y como es sabido fue un genio autodidacta. Sobre su vida podéis encontrar abundante información en la red.
que como todos sabemos, corresponde al mejor matemático indio de todos los tiempos, Srinivasa Ramanujan (1887 – 1920). La familia de Amita es de procedencia Tamil (una de las culturas e idiomas más extendidos de la India), natural de Chennai, una de las mayores ciudades costeras de la India, con unos 7 millones de habitantes, antes conocida (antes de 1996) como Madrás. Srinivasa Ramanujan también provenía de la cultura Tamil, aunque era natural de un pequeño pueblo llamado Kumbakonam, y como es sabido fue un genio autodidacta. Sobre su vida podéis encontrar abundante información en la red.