Lobachevski no intentó probar el quinto postulado como teorema, sino que estudió las consecuencias que tenía, respecto a la geometría, el hecho de que no se cumpliera necesariamente el quinto postulado. Una de sus obras principales, en la que se muestra este nuevo espíritu geométrico, es: Geometría (1823). Dicho libro fue severamente criticado por el académico ruso N. I. Fuss (1755-1826). En honor a la verdad, su Geometría resultó muy atrevida para su época, y posiblemente el académico Fuss no comprendió el trasfondo de un planteamiento tan novedoso y rupturista. La propia disposición de los distintos capítulos llama poderosamente la atención.

Los cinco primeros capítulos de su libro se construyen sin utilizar en ningún momento el quinto postulado de Euclides. Por tanto estaba elaborando una Geometría Absoluta (aquella que no depende del quinto postulado, sino únicamente de los cuatro primeros postulados). Desde el punto de vista histórico, este hecho es fundamental, ya que es la primera persona que trata de manera autónoma la Geometría Absoluta.

Posiblemente influido por la filosofía expresada por D’Alembert (1717-1783), se inclina por un tratamiento desde el punto de vista "métrico". El libro se compone de 13 capítulos, diez de ellos están dedicados a la medida de diferentes elementos geométricos (líneas, ángulos, poliedros, triángulos, prismas, etc.). Los  tres  últimos capítulos los dedica a la teoría de las perpendiculares, de las paralelas y a la igualdad de los triángulos.

El aspecto métrico es clave en su trabajo, Lobachevski se da cuenta que la medida de ángulos y de los segmentos no depende del quinto postulado, mientras que la medida de las áreas depende directamente del famoso quinto postulado. Por esta razón, el aspecto de cálculo de áreas de diversas figuras no es abordada hasta bien avanzado el libro.

En el tratamiento que realiza de la teoría de las paralelas ya se pueden reconocer breves trazos de sus ulteriores  trabajos. En efecto, en el trabajo presentado,  Lobachevski intentó demostrar el postulado de las paralelas a la inversa de la manera que  fue enunciado por Playfair.

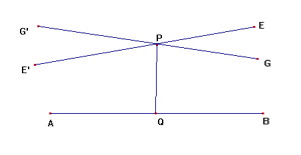
Esto es, supuso que por un punto P no situado en la recta  AB pasan,  en el plano, más de una recta  no secante con AB, tal como muestra el dibujo.

En todo caso el texto no llegó a publicarse hasta varios años más tarde. Sin duda, el libro de Lobachevski fue la semilla de sus investigaciones geométricas posteriores.

A pesar de las severísimas críticas  recibidas, siguió trabajando y profundizando en la teoría de las paralelas. Tres años más tarde, el 11 de Febrero de 1826, en una reunión de la Facultad Físico-Matemática, Lobachevski presentó un informe de cara a conocer la opinión de sus colegas profesores, respecto a sus investigaciones geométricas. Dicho informe llevaba "Expositiòn succinte des principies de la gèometrie avec une dèmonstration rigoureuse du thèoréme des parallèles" (1826) ( Exposición sucinta de los principios de la geometría, con una demostración rigurosa del teorema de las paralelas),en él se  recogía buena parte de sus  revolucionarias ideas. Para valorar el informe se reunió una comisión de tres profesores de la Universidad. A pesar de que dichos docentes no estaban al corriente de las cuestiones relativas a la Geometría , adoptaron la decisión de valorar negativamente la publicación del trabajo de Lobachevski. Nuevamente Lobachevski fue vilipendiado. Si bien el trabajo no se editó, sí estamos en condiciones de hablar de su contenido, ya que tres años más tarde, el mismo Lobachevski publicó en la revista “El mensajero de Kazán“ (una revista educativa, de carácter general, que se publicaba en la Universidad de Kazán), una memoria titulada “Acerca de los principios de geometría” (1829). Esta  memoria  es compleja y difícil de leer, pero podemos señalar tres partes diferenciadas: La primera se centra en el estudio de la llamada Geometría Absoluta, en realidad es un resumen su "Geometría" presentada el año 1823 y que tan mal acogida tuvo. La segunda parte expone el contenido de su  “Exposition succinte.....”. A lo largo de muchas páginas se dedica a estudiar  y obtener el ángulo de paralelismo, que él llama π(x).

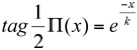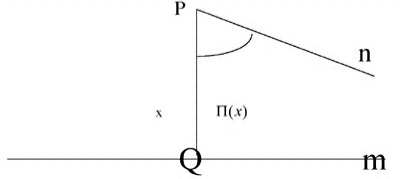El dibujo nos indica que la recta  n es  paralela a m pasando por el punto P. Siendo π(x) el ángulo que forman dichas rectas paralelas en el punto P, dónde x expresa la distancia del punto P a Q. Al igual que los estudios realizados por Lambert, Taurinus, Gauss y tantos otros, aparece en la fórmula del ángulo el valor K. ¿qué significa K?.

Lobachevski  dice :

“teóricamente K puede tener cualquier valor, cada uno de los valores de la constante K le corresponde una geometría imaginaria .........no hay una sola geometría imaginaria; existe un número infinito de variedades correspondientes a los diversos valores de la constante K. Entre ellas, la vieja geometría euclidiana corresponde al caso límite (cuando K tiende a infinito).

La última parte del libro está dedicada  a la medida de longitudes, áreas y volúmenes. El estudio se hace mediante procesos de integración. Además muchos de los cálculos los realiza por varios procedimientos para verificar que las operaciones coinciden. Este hecho le reafirmaba en su convicción de que la geometría que estaba edificando era correcta desde un punto de vista lógico. En 1832 (recordemos que Lobachevski era rector de la Universidad) el Consejo de la Universidad de Kazán, pidió a la Academia de Ciencias de San Petersburgo, un informe "Acerca de los principios de geometría”. La Academia encargó el trabajo al académico M. V. Ostrogradski, que después de estudiarlo hizo la siguiente crítica verbal:

"... después de haber estudiado una obra del rector Lobachevski, tengo que observar que: la obra está redactada con tan poco cuidado, que una gran parte es ininteligible. Por eso estimo que dicha obra de Lobachevski no merece la menor atención de la Academia."

A Lobachevski le debió molestar enormemente la crítica tan ofensiva del académico ruso. Por lo que nuevamente hizo un gran esfuerzo por explicarse mejor. Con esta intención publica una memoria titulada “Geometría imaginaria” (1835), continuando el año siguiente con  “Aplicación de la geometría imaginaria a algunas integrales” (1836). En realidad estas memorias, publicadas en Memorias de la Universidad de Kazán, no aportaban nada nuevo  a sus trabajos anteriores, pero al disponer de más espacio Lobachevski  explica mejor los procesos  y sus cálculos son más entendibles. La obstinación de Lobachevski le llevó a redactar una y otra vez sus trabajos desde diferentes ópticas, él era consciente que sus escritos no eran sencillos de leer: su concisión, la originalidad de sus planteamientos, las consecuencias derivadas de su teoría y  el escribir en contra del pensamiento geométrico establecido( defendido por el filósofo alemán I. Kant) le llevó a escribir un tratado crucial: “Geomeytrish e Untersuchungen zur theorie der parallellinien” (1840) (Investigaciones geométricas de la teoría de las paralelas).

Por medio de este pequeño librito, escrito en alemán, la comunidad matemática toma contacto con las revolucionarias ideas geométricas de Lobachevski. Este librito  debió impresionar a Gauss, ya que en noviembre de 1842 propuso la candidatura de Lobachevski, como "uno de los excelentes matemáticos del Estado Ruso", para que  fuera  nombrado miembro de la Sociedad Científica de Göttingen, que ya entonces tenía el rango de Academia. Sin duda este reconocimiento por parte del mejor matemático vivo, es la consagración de sus teorías geométricas. Actualmente este reconocimiento es compartido con el matemático húngaro J. Bolyai, que de manera independiente, también  trabajó en  la creación de la geometría hiperbólica.

El trabajo de Lobachevski en temas no relacionados directamente con la geometría es muy sugestivo. Su pasión por las matemáticas le llevó a interesarse por  otras muchas partes de las matemáticas. Exponemos aquí un listado, de algunos trabajos no geométricos, publicados entre los años 1823 y 1852: “Acerca de la convergencia de las series trigonométricas” (1834), “Sur la probabilité des resultats moyens, tirés des observations répétées” (1842), “Acerca de los valores de algunas integrales definidas” (1852). Pero sin duda la obra, no geométrica, más importante, tanto por su contenido como por su extensión, fue su tratado de Álgebra (1834). Dicho manual  es muy original y constituyó  una obra de matemáticas notable, de hecho Lobachevski era conocido en su época por el contenido de este libro y no por su investigaciones geométricas. Para finalizar diremos que un año antes de su muerte se  celebraba el cincuentenario de la fundación de la Universidad de Kazán, por ese motivo invitaron a Lobachevski a escribir un artículo sobre sus investigaciones geométricas. A pesar de estar enfermo e impedido visualmente, aún tuvo ánimos para escribir su última obra titulada “Pangeometría”, aparecida en las “Memorias de la Universidad de Kazán” el año 1855 (en ruso).