1. 201. (Febrero 2022) Bibliografía y referencias (segunda parte)

Esta es la segunda y última parte de las referencias utilizadas en la preparación y elaboración de los artículos que han aparecido en este rincón. Estoy seguro de que muchas de estas referencias contienen información adicional que te servirá de inspiración para profundizar en el amplio mundo de la magia matemática. Matem102 Michael Kleber, The Best Card Trick, Mathematical Intelligencer, vol. 24 (2002). Michael Jørgensen, The 5-card trick. En "Numericana" (2004). Wallace Lee, Math Miracles (1950). [Matem110] Colm Mulcahy, All you need is cards. En “Puzzlers’ tribute: a feast for the mind” (editado por David Wolfe y Tom Rodgers), AK Peters (2002). Shai Simonson y Tara Holm, Using a card trick to teach Discrete Mathematics, PRIMUS, vol. 13 (2003). Matem103 Karl Fulves, Charles Jordan's best card tricks, Dover (1992). [Matem134] Jean Hugard, Encyclopedia of card tricks (1937). Phil Goldstein, Zen Poker. En "Thequal" (1984). Matem104 Pedro Alegría, Códigos secretos y teoría de la información en la magia, SIGMA 26 (2005). [Matem187] Matem105 Jim Steinmeyer, Impuzzibilities, Hahne (2002). [Matem195] Matem106 Banachek, Ring of truth. En "Banachek's Psi Series, vol. 2". Matem107 Persi Diaconis y Ronald Graham, Magical Mathematics, the mathematical ideas that animate great magic tricks, Princeton (2011). [Matem125]-[Matem146]-[Matem150]-[Matem180] Martin Gardner, Mathematics, Magic and Mystery, Courier (1956). [Matem132]-[Matem190] Martin Gardner, 6th Book of Mathematical Diversions, Chicago (1984). [Matem191] Fernando Blasco, Matemagia, Temas de Hoy (2007). Matem108 Pedro Alegría y Juan Carlos Ruiz de Arcaute, La matemagia desvelada, SIGMA 21 (2002). Matem109 John Ratey, El cerebro: manual de instrucciones, Mondadori (2003). Matem110 Royal Heath, Mathemagic (1953). Arthur Benjamin y Michael Shermer, Secrets of mental math, Three Rivers (2006). [Matem111] Matem111 Arthur Benjamin y Michael Shermer, Mathemagic: how to look like a genius without really trying, Lowell House (1993). Jakow Trachtenberg, The Trachtenberg speed system of basic mathematics, Praeger (1982). Harry Lorayne y Jerry Lucas, The Memory Book: The Classic Guide to Improving Your Memory at Work, at School, and at Play, Random House (1996). Matem112 Matt Sheppeck, Dice trick. En "Math Puzzle". Matem114 Alfred Brousseau, Fibonacci magic cards, The Fibonacci Quarterly, vol. 10 (1972). Matem115 Colm Mulcahy, Mathematical Card Magic: fifty-two new effects, CRC Press (2013). [Matem192] Matem117 Brian Brushwood, Scam School: your guide to scoring free drinks, doing magic and becoming the life of the party, Skyhorse (2013). [Matem119] Ian Stewart, Cups and downs, The College Mathematics Journal, vol. 43 (2012). Matem118 Erik Demaine, Recreational Computing, American Scientist, n. 98 (2010). Martin Gardner, The rotating table. En "Fractal Music, Hypercards and More" (1992). Matem120 José Muñoz, Cartomagia del 1 al 9, Números, vol. 82 (2013). Pedro Alegría, Magia por principios, Publidisa (2008). [Matem122]-[Matem150] Peter Winkler, Mathematical Puzzles: A Connoisseur's Collection, AK Peters (2003). Colm Mulcahy, Better Poker Hands Guaranteed. En "Card Colm" (2006). Matem121 JokerGil Magia, Clasificación de Ilusionismo (2013). Javier Tejerina, 19 relatos fantásticos de magia bizarra, Magos Artesanos (2014). Matem122 S. Brent Morris, Magic tricks, card shuffling and dynamic computer memories, MAA (1998). Pedro Alegría, Entre la matemática y la magia: la leyenda de Josefo y la mezcla australiana, Eureka 9 (2012). [Matem127]-[Matem158] Matem123 Phil Goldstein, Armchair bowler, Apocalypse (1978). Shigeo Futagwa, Numeral -oh-gee, Apocalypse (1979). Fernando Blasco, El universo matemágico de Martin Gardner, Temas 77 (2014). Matem124 Karl Fulves, Self-working number magic, Dover (1983). Matem125 Anónimo, The Whole Art and Mystery of Modern Gaming Fully Expos'd and Detected, Londres (1726). Richard Vollmer, The very best of Dai Vernon, Magix (1978). [Matem192] Matem126 Karl Fulves, My best self-working card trick, Dover (2001). Matem127 Gaspard Monge, Réflexions sur un tour de cartes, París (1773). Peter Duffie, Mind Blasters! (2008). Matem128 Alex Elmsley, The mathematics of the weave shuffle, The Pentagram (1957). Jean Hugard y Fred Braue, Expert card technique, George Starke (1944). Stephen Minch, The Collected Works of Alex Elmsley I & II, L&L (1991 & 1994). [Matem193] Matem129 Armando Martínez, Los grupos de permutación. En "Matemáticas de la simetría" (2011). Matem130 Werner Miller, Ear Marked, Shane (2006). Matem131 Chris Wardle, Math tricks & number magic, Lulu (2016). Matem132 Bob Hummer, Mathematical 3 Card Monte, Frank Werner (1951). [Matem176] Jack Yates, Minds in close-up, Goodliffe (1954). Karl Fulves, Big book of magic tricks, Dover (1977). Paul Curry, Paul Curry Presents (1974). Matem133 Leonhard Euler, Solutio problematis ad geometriam situs pertinentis (1741). Teo Paoletti, Leonard Euler's solution to the Konigsberg problem. En "Math DL". Luca Pacioli, De viribus quantitatis (1494). [Matem143] Marta Macho, ¿Qué es la Topología?, SIGMA (2002). Martin Gardner, The Second Scientific American Book of Mathematical Puzzles and Diversions, Chicago (1987). Michael Close, Complete Workers (2005). Jean-Pierre Petit, El Topologicón. En "Saber sin fronteras" (2005). Matem134 Horatio Galasso, Giochi di carte bellissimi di regola e di memoria, Venecia (1593). [Matem192] Claude-Gaspard Bachet, Problèmes plaisans et delectables qui se font par les nombres, Lyon (1612). Joseph Diez Gergonne, Récréations mathématiques. Recherches sur un tour de cartes, Annales de Mathématiques pures et appliquées, IV (1814). Jon Racherbaumer, 7-7-7, the 21 card trick, Spade and Archer (2007). Philippe Billot y Pierre Guedin, Prestidigitation, mille et une sources, Groupe CCEE (2011). Jacques Ozanam, Récréations mathématiques et physiques, París (1694). Matem135 Maria Lando, Card Tricks. En "The Math Mom" (2010). Edmé-Gilles Guyot, Nouvelles récréations physiques et mathématiques, París (1769). [Matem136]- [Matem149] Roy Quintero, El truco de las 21 cartas a través de permutaciones, EDUCERE (2006). Ethan Bolker, Gergonne's card trick, positional notation and radix sort, Mathematics Magazine 83 (2010). Carlos Vinuesa, Matemagia básica, La Gaceta de la RSME 14 (2010). H2G2, Why the 21 card trick works (2001). Matem136 William Hooper, Rational Recreations, Londres (1774). [Matem149] Albert Ross Eckler, A card trick mnemonic revisited, Word Ways 27 (1994). Tom Sellers, Magical Pleasantries (1931). Matem137 Professor Hoffmann, Modern Magic, David McKay (1876). [Matem155] Walter Rouse Ball, Mathematical Recreations and Essays, McMillan (1905). Philip Davis, Mathematics and Hocus Pocus, SIAM News (2003). Matem138 Jean Leurechon, Récréation mathématique, Pont-A-Mousson (1626). William Oughtred, Mathematicall Recreations, Londres (1653). Justin Highan, A brief analysis of the 21 card trick and related effects (2001-2006). Adi Shamir, Ronald Rivest y Leonard Adleman, Mental Poker. En "The Mathematical Gardner" (1981). Matem139 Gene Finnell, Free cut principle (1967). John Hamilton, Eyes of the Gods, The Pallbearer's Review (1970). Matem140 Pedro Alegría, Santiago Fernández, Raúl Ibáñez y Goyo Lekuona, Juegos didácticos, BBKmáticas. Henry Dudeney, The Canterbury Puzzles, Nelson (1907). Matem142 Temple Patton, Card tricks anyone can do, Castle (1968). Matem143 Fernando Blasco, Mathematical magic and society, Mathknow (2009). Girolamo Cardano, De subtilitate rerum (1550). Vanni Bossi, Magic and Card Tricks in Luca Paciolo’s De Viribus Quantitatis. En "A Lifetime of Puzzles", AK Peters (2008). Dario Bressanini y Silvia Toniato, I giochi matematici di fra' Luca Pacioli, Dedalo (2011). Vanni Bossi, Antonietta Mira y Francesco Arlati, Mate-magica, I giochi di prestigio di Luca Pacioli, Aboca (2012). Tiago Hirth, Luca Pacioli and his 1500 book De viribus quantitatis, Universidad de Lisboa (2015). Matem144 Xuxo Ruiz, Educando con magia, Narcea (2013). Juan Sebastián Barrero, Portal Magia Matemática. Manuel Maldonado, La magia como recurso educativo en el aula de matemáticas de 1º de ESO, TFM UNIR (2013). Nerea Casas, Metodología para enseñar probabilidad y estadística mediante juegos de magia en matemáticas de 3º de ESO, TFM UNIR (2014). María Teresa Pérez, Miguel Ángel Mirás, Carmen Quinteiro y Pedro Alegría, Competencias transversales a través de la magia, Educación Editora (2016). Matem145 Harlan Tarbell, Tarbell course in magic, Tannen (1927). Glenn Gravatt y Jean Hugard, Encyclopedia of card tricks, Robbins (1937). Stephen Minch, The Vernon Chronicles 2, L&L (1988). Matem146 John Scarne, Scarne on card tricks, Crown (1950). Matem147 Imanol Ituiño, Engaños a orejas vistas (2016). Michael Lugo, A card trick from Diaconis and Graham. En "God plays dice" (2012). Matem148 Marta Macho, El chocolate infinito. En "ZTFNews" (2013). Martin Gardner, Los acertijos de Sam Loyd, RBA (2011). Anónimo, The magician's own book, Nueva York (1857). David Richeson, The famous trick donkeys. En "Division by Zero" (2009). Richard Worth y Jordan Collver, A certain symmetry (2015). Matem149 Greg Frederickson, Dissections: plane and fancy, Cambridge (1997). Pedro Alegría, Geometría recortable, SIGMA 28 (2006). Jean Jacquelin, Pastiches, paradoxes, sophismes, absurdités et autres bizareries (2011). Greg Ross, Corner Market. En "Futility Closet" (2014). John Sharp, Fraudulent dissection puzzles, Mathematics in School 31 (2002). Matem150 Karl Fulves, Bob Hummer's collected secrets, Dover (1980). [Matem165]-[Matem176]-[Matem190] Bob Hummer, Face up face down mysteries, Frank Werner (1942). Colm Mulcahy, Many Fold Synergies. En "Card Colm" (2006). John Bannon, Dear Mr. Fantasy (2004). Matem152 Peter Prevos, The Möbius strip in magic (2018). Terri Rogers, Secrets, Martin Breese (1986). Ralph Fox, A quick trip through knot theory. En "Topology of 3-manifolds", Prentice-Hall (1962). Matem153 Alexander Dewdney, The magic machine: handbook of computer sorcery, Freeman (1990). Jim Bumgardner, The art of computer deception. Alexander Dewdney, Digital prestidigitation: the fine art of magic and illusion by computer, Scientific American 255 (1986). Mariano Tomatis, L'algoritmo telepatico di Nikola Tesla, Mesmer (2016). Howard Williams y Peter McOwan, Magic in the machine: a computer magician's assistant, Frontiers in Psychology 17 (2014). Matem154 Louis Kauffman, The mathematics of Charles Sanders Peirce, Cybernetics and Human Knowing 8 (2001). Charles Peirce, Some amazing mazes, The Monist 18 (1908). Alex Elmsley, Pierce Arrow. En "The Collected Works of Alex Elmsley I", L&L (1991). Kurt Eisemann, Number-theoretical analysis and extensions of "The most complicated and fantastic trick ever invented", American Mathematical Monthly 91 (1984). Matem157 Stewart James, Anagramatic Facsimile, TOPS 18 (1953). Thomas A. Waters, Signse. En "Mind, Myth and Magick", Hermetic Press (1993). Peter Turner, Star Sign Divination. En "Mentalism Masterclass Series 9" (2016). The Jerx, Transgresive Anagrams (2016). Patrick Schlagel, Mnemosign (2006). Matem158 Aldo Colombini, Jackula. En "Impromptu card magic", Mamma mia (2003). Karl Fulves, Capture by ritual. En "Vampire Chronicles" (1997). Geoffrey Mott-Smith, Mathematical puzzles for beginners and enthusiast, Dover (1954). Matem159 Karl Fulves, Self-working handkerchief magic, Dover (1988). Karl Fulves, And a packet of cards (1989). Karl Fulves, Letter of intent. En "Deceptive Practices" (1992). Matem160 Raúl Ibáñez, El siete: un número muy popular. En "Matemoción" (2016). L. Vosburg Lyons, Mentrix, Ibidem 5 (1956). Matem161 L. Vosburg Lyons, Heavenly Sevens, Ibidem 7 (1956). Matem162 L. Vosburg Lyons, Dizzy Discs, The Phoenix 55 (1944). Matem163 Leo Boudreau, Lie to me (2009). Jeremiah Farrell, Cubist magic. En "Puzzlers' tribute: a feast for the mind", AK Peters (2001). Matem164 Tomas Blomberg, The Konami Code. En "Blomberg Laboratories", Vanishing (2014). Nelo Maestre, Matemáticas del Caribe. En "Divermates". Four Suits, Konami at the dinner table (2007). The Jerx, Variations on the Konami Code (2015). Matem165 Martin Gardner, The Last Recreations, Springer (1997). Matem166 Leo Boudreau, A number divination. En "The magic café" (2004). Matem167 Stephen Minch, Mind Novas, Micky Hades (1980). Milbourne Christopher, ESP, Seers & Psychics: what the occult really is, Thomas Crowell (1970). George Hansen, The trickster and the paranormal, Xlibris (2001). Ricardo Marré,  Magia con cartas ESP, Marré (2013). Matem168 Royal V. Heath, ESP miracle, The Sphinx (1938). Theodore Annemann, Yggdrasil, The Jinx (1938). James G. Thompson jr., Moonlight madness, The Jinx (1941). Doug Dyment, Stimulacra (2007). Matem169 Javier Serrano, Análisis matemático de algunos juegos de magia (2006). Matem170 Martin Gardner, Some recreations involving the binary number system. En "New mathematical diversions" (1966). Carlos Vinuesa, Matemagia básica, La Gaceta de la RSME (2011). Martin Gardner, Logic Machines and Diagrams, McGraw-Hill (1958). Matem171 Nicolas Chuquet, Triparty en la science des nombres, Roma (1484). Franka Bueckler, Guessing the numbers, Mathematics in Europe (2016). Matem172 George Pólya, Mathematics and plausible reasoning, Princeton (1954). Franka Brueckler, Inductive Magic. En "Mathematics in Europe" (2016). Matem173 Martin Gardner, Flexagons, Scientific American 195 (1956). Harapan Ong, Principia, Vanishing Inc (2018). Anthony Conrad y Daniel Hartline, Flexagons, RIAS (1962). David Mitchell, The magic of flexagons, Tarquin (1999). Pedro Alegría, Las sin cuenta caras de un papel. En "Gardner para principiantes", SM y RSME (2014). Matem174 Howard Adams, Mirakastak. En "Mathcasts Aspellonu", H&R (2003). Matem175 József Kovács, Cardopia (2013). Matem176 Pierre Boc e Yves Meret, Inv3rsion (2017). Gabriel Werlen, The green neck system, Marchand des trucs (2017). Matem177 Michael Bennett, La posada. En "Didáctica Mágica" (2017). Werner Miller, Lure. En "Enigmaths 1" (2009). William Tappe, Types of Math Numbers. En "Math Goodies". Matem178 Francisco González, Matemagia: descubre la magia de las matemáticas (2019). Matem179 Arthur Benjamin, The magic of math, Basic Books (2015). Raúl Ibáñez, Los secretos de la multiplicación, Catarata (2019). Matem180 Simon Singh, Los Simpson y las matemáticas, Ariel (2013). Martin Gardner, Undiluted Hocus-Pocus, Princeton (2013). Martin Gardner, The Collosal Book of Mathematics, Norton (2001). Martin Gardner, Matemagia, Páginas (2019). Karl Fulves, Octet (1981). Colm Mulcahy, Quantitative Reasoning in Small Groups. En "Card Colm" (2006). Matem181 William Lane, Willane's Wizardry, ARCAS (1947). Milbourne Christopher, Tricky Road Sign. En "Hugard's Magic Monthly" (1951). Steve Beam, Upside down. En "The Trapdoor" (1983). Matem182 George Sands, Lucky 13. En "The Pallbearers Review" (1975). Lewis Jones, Lucky, Lucky, Lucky. En "Semi-Automatic Card Tricks 5" (2004). Matem183 Larry Barnowsky, Magica Analytica (2014). Nelo Maestre, La mágica fórmula de Euler. En "Divermates" (2015). Matem185 Colm Mulcahy, All or Nothing Trickle Treat. En "Card Colm" (2012). Gary Antonick, Triangle Mysteries. En "Wordplay" (2013). Yutaka Nishiyama, The three-color triangle problem, International Journal of Pure and Applied Mathematics 85 (2013). Erhard Behrends y Steve Humble, Triangle Mysteries, The Mathematical Intelligencer 35 (2013). Erhard Behrends, Pyramid Mysteries, The Mathematical Intelligencer 36 (2014). Matem186 Pedro Alegría, La magia de los cuadrados mágicos, SIGMA 34 (2009). Erhard Behrends, The math behind the magic, AMS (2019). Doug Dyment, How to construct a forcing matrix. En "Deceptionary". Marián Trenkel, An algorithm for making magic cubes, The PIME Journal 12 (2005). Matem187 Todd Mateer, A magic trick based on the Hamming code, Math Horizons 21 (2013). Todd Mateer, A Reed-Solomon Code Magic Trick, Mathematics Magazine 87 (2014). Ricardo Teixeira, Magical data restoration, Math Horizons 24 (2017). Matem188 Steve Butler, Persi Diaconis y Ron Graham, The mathematics of the flip and horseshoe shuffles, The American Mathematical Monthly 123 (2016). Steve Butler, A card trick inspired by perfect shuffling. En "Gathering for Gardner 13 (2018). Jeremy Rayner, Flipping perfect shuffles, Metagrobologist Magazine 1 (2014). Matem189 Stewart James, Murder by Suggestion, New Pentagram 12 (1980). Allan Slaight, The Essential Stewart James, Magicana (2007). Shane Causer, Automata: beyond self-working magic (2005). Matem190 David Eppstein, Twenty proofs of Euler's formula. En "The Geometry Junkyard". Alexander Bogomonly, Pythagorean Theorem. En "Cut-the-knot". Bob Hummer, Three Pets, Frank Werner (1945). Joe Turner, Dice, dice, baby. En "Celebration of Mind" (2020). Karl Fulves, Self-working table magic, Dover (1981). George Kaplan, El arte de la magia, Páginas (1998). Matem191 Charles Trigg, Geometry of Paper Folding II: tetrahedral models, School Sci. and Math. 54 (1954). Charles Trigg, Collapsible modelsw of the regular octahedron, The Mathematics Teacher 65 (1972). Martin Gardner, The second book of mathematical puzzles and diversions, Simon and Schuster (1961). Nelo Maestre, Octaedro I Ching. En "Divermates". Matem192 Timothy Weeks, Mathematical Explorations of Card Tricks, Senior Honors Project 73 (2015). Morgan Mitchell y Jay Cummings, When and how to use math based card tricks in the classroom, McNair Scholars Journal (2017). Kevin Elder, David Deviney, Ronald McKinnon y John Dyer, Using illusions in the classroom: principles, best practices and measurement, AABRI (2012). Pablo Nagata, La pasión de un cartómago aficionado (2014). Ramón Riobóo, La magia pensada, Páginas (2002). Ramón Riobóo, Más magia pensada, Páginas (2010). Enric Ramiro y Pilar Gandía, 100 jocs automàtics de matemàgia, Cossetània (2021). Stephen Minch, The Vernon Chronicles, L&L (1988). Matem193 Charles Seife, Impressions of Conway, The Sciences (1994). Alexander Kraus, Sum total, Ibidem 12 (1957). Arthur McTier, Card Concepts, Davenport (2000). Julian Havil, Impossible?, Princeton (2011). Matem194 Fernando Blasco, Un conejo matemático en la chistera, Síntesis (2016). Edward Marlo, Automatic Placement, The New Phoenix 329 (1955). Matem195 Jim Steinmeyer, Hiding the elephan: how magicians invented the impossible and learned to disappear, Arrow Books (2005). Kuniyasu Fujiwara, Automatic Aces, Genii 63 (2000). Martin Gardner, Paradox Papers, The Pallbearers Review 6 (1971). Henry Dudeney, Modern Puzzles and how to solve them, Pearson (1926). Nick Trost, Quadraplex. "En Subtle Card Creations" (2001). John Bannon, Degrees of Freedom. En "Dear Mr. Fantasy" (2004). Matem196 Persi Diaconis y Ron Graham, The magic of Charles Sanders Peirce. En "The Mathematics of Various Entertaining Subjects 3", Princeton (2019). [Matem197] Matem198 José María Sorando, Polígonos estrellados. En "Matemáticas en tu mundo". Ludovic Simonet, Les secrets du pentacle, Hypercube 46-47 (2003). George Sands, Prime Choice, The Chronicles 8 (1978). Matem199 Martin Gardner, Fractal Music, Hypercards and More ..., Freeman (1992). Tom Frame, The Hypercard Project (2006). Jack Botermans, Paper Capers, Henry Holt (1986). Erik Demaine, Martin Demaine, Tomoko Taniguchi y Ryuhei Uehara, Impossible Folding Font. En "Bridges Conference" (2019). VVAA, The world of wonders (1882). Will Goldston, Simple Conjuring Tricks That Anyone Can Perform, Pearson (1913). Peter Prevos, The Jastrow Illusion in Magic (2016). Augustin Charpentier, Analyse experimentale: De quelques elements de la sensation de poids (1891). David Murray, Robert Ellis y Christina Bandomir, Charpentier (1891) on the size-weight illusion, Perception & Psychophysics 61 (1999). Hasta aquí hemos llegado. Mi agradecimiento a quienes me han animado durante todo este periodo y mi enhorabuena a quienes me han seguido hasta el final. Por lo menos, hasta este final.   Pedro Alegría (Universidad del País Vasco - Euskal Herriko Unibertsitatea)

Martes, 01 de Febrero de 2022 | Imprimir | PDF |  Correo electrónico

2. 200. (Enero 2022) Bibliografía y referencias

Llegamos simultáneamente al año 2022 y al número 200 de este serial mágico-matemático. Esto significa que debemos respetar religiosamente dos tradiciones. En primer lugar, ¿podemos destacar algunas características del número 2022? Lo más visible es que, aunque no es primo, sólo tiene tres factores primos, 2, 3 y 337. ¡Ah!, pero 337 es un primo del tipo 4k+1, así que es un número pitagórico y su cuadrado es la suma de dos números cuadrados: 3372 = 1752 + 2882. Multiplicando por 6, resulta que 20222 = 10502 + 17282. Tal como apuntamos en el número 178 de este rincón (enero de 2020), hemos llegado por tercer año consecutivo a un número infeliz (y nos quedan tres más). Como contrapartida, es un número admirable, pues se puede expresar como suma de sus divisores propios, teniendo uno de ellos signo negativo: 2022 = 1 + 2 + 3 - 6 + 337 + 674 + 1011. Por ser el número 2022 múltiplo de la suma de sus cifras, recibe el nombre de número de Harshad. Para no salirse de la norma, también puede obtenerse mediante operaciones aritméticas con las nueve cifras significativas, en orden. Por ejemplo, así: 2022 = 1 x 2 x 3 + 4 x (-5 + 6) x 7 x 8 x 9. ¡Me ha salido una operación palindrómica! 9 x 8 x 7 x (6 - 5) x 4 + 3 x 2 x 1 = 2022. Por otra parte, como si de un voluminoso tratado con esta cifra redonda de capítulos se tratara, merece rematarse con una lista pormenorizada de los libros, artículos, enlaces de internet, etc., utilizados a lo largo del trabajo. He elegido como patrón el orden cronológico de aparición de los artículos, eliminando algunos enlaces que ya no son accesibles y aquellas referencias que la frágil memoria de este corresponsal impiden ser rescatadas. Sólo indicaré los enlaces en los que se puede acceder al contenido completo del correspondiente artículo o libro. Dada la cantidad de material recopilado en este rincón durante todo este periodo de tiempo, vamos a dividirlo en dos partes, dejando para el próximo mes la relación bibliográfica correspondiente a la segunda centena de artículos. Matem1 Henry Dudeney, Modern Puzzles (1926). Matem2 Ken Beale, The Pallbearers Review, v. 9, n. 3 (1974). Matem3 Claude-Gaspar Bachet de Méziriac, Problèmes Plaisants et Délectables qui se font par les nombres, (1612). [Matem90]-[Matem93] Matem4 Juan Tamariz y Gema Navarro, Por arte de Verbimagia, Producciones mágicas Tamariz (2005). [Matem87] Matem8 Theodore DeLand, Mysterious Match Trick, Goldston Magic Monthly (1915). Matem10 Banachek, Think a month, Magick Magazine. Matem18 Royal V. Heath, Mathemagic, Simon & Schuster (1933). Matem25 Sam Loyd, Cyclopedia of 5000 puzzles, tricks and conundrums, Pinnacle Books (1914). Matem29 Martin Gardner, Los mágicos números del Dr. Matrix, Prometheus Books (1985). Matem36 Ennio Peres, Giochi matematici, Editori Riuniti (1986). Matem38 William Jefferys, What is the day of the week, given any date? John Conway, Tomorrow is the day after Doomsday, Eureka (1973). Matem40 Gary Fabjance, Interactive Magic Tricks. Matem41 Dean Clark y Dilip Datta, Arithmetic Matrices and the Amazing Nine-Card Monte, The College Mathematics Journal (1993). Matem43 Stewart James, Stewart James in Print: The first fifty years, Jogestja (1989). Werner Miller, Ear Marked, Shane (2006). Matem45 Martin Gardner, The paradox of the nontransitive dice and the elusive principle of indifference, Scientific American 223 (1970). Matem46 Martin Gardner, Checker jumping, Sichermann dice, and Kruskal's card trick, Scientific American 238 (1978). Matem47 Nicolas Chuquet, Triparty en la science des nombres (1484). Matem48 Luca Pacioli, De viribus quantitatis (1496). Matem50 Martin Gardner, Mathematics, Magic and Mystery (1956). Elwyn Berlekamp y Tom Rodgers (eds.), The Mathemagician and Pied Puzzler: a collection in tribute to Martin Gardner, AK Peters (1999). Henry Perigal, On Geometric Dissections and Transformations, Messenger of Mathematics (1875). Matem52 Jesús García Gual, Juegos basados en sistemas de numeración, Estalmat (2010). Matem54 Rafael Losada, Cómo descubrir la moneda falsa sin desesperarse, Suma 33 (2000). Matem55 Walter Rouse Ball y Harold Coxeter, Mathematical Recreations and Essays, Dover (1987). [Matem93] Matem58 Blaise Pascal, Traité du triangle arithmetique (1653). Matem59 Jeremiah Farrell, Cubist Magic. En Puzzlers' tribute (editado por David Wolfe y Tom Rodgers), AK Peters (2002). Matem60 Jon Racherbaumer, The Artful Dodges of Eddie Fields, Tannen (1968). Mulawa Dreaming web. Matem64 Ian Stewart, El laberinto mágico, Crítica (2011). Matem65 José Muñoz, Ernesto, el aprendiz de matemago, Nivola (2010). José Chamoso y William Rawson, A vueltas con los números, Nivola (2003). Matem68 Colm Mulcahy, Low Down Triple Dealing, Card Colm (2004). Matem69 Volker Tanger, Euro note serial number check. Matem71 Colm Mulcahy, Quantitative Reasoning in Small Groups, Card Colm (2006). Matem72 Roberto Giobbi, The magic memories, 07. Matem73 Gérard Michon, Ternary Cards (2009). Matem76 Jim Steinmeyer, Impuzzibilities, Hahne (2002). [Matem83]-[Matem92] George Sands, Lucky 13, Pallbearers Review (1975). Matem77 Martin Gardner, Hexaflexagons and other mathematical diversions, Simon and Schuster (1959). Matem78 Paul Curzon y Peter McOwan, Mathemagic: the magic of computer science. [Matem80] Matem81 Walter Penney, Penney-Ante, Journal of Recreational Mathematics 2 (1969). Yutaka Nishiyama y Steve Humble, Winning odds, Plus Magazine (2010). Martin Gardner, On the paradoxical situations that arise from nontransitive relations, Scientific American 231 (1974). Matem84 Martin Gardner, Riddles of the sphinx, AMS (1987). [Matem86] Matem88 Kuniyasu Fujiwara, Automatic Ace Triumph, Genii Magazine 63 (2000). Matem89 Kjartan Poskitt, Prime Numbers, Murderous Maths. Thérèse Eveilleau, La balada de los pares y de los impares, Mathematiques Magiques. Matem91 John Scarne, Scarne on card tricks, Crown Publishers (1950). Matem92 Boris Kordemsky, Moscow Puzzles (1956). Brian Daniel, The Bermuda Square, Magic Magazine (2010). Brian Daniel, Teach by Magic (2010). Gianni Sarcone, The 13th magic crystal skull, Archimedes' Laboratory. Matem93 Juan Mieg, El brujo en sociedad, Madrid (1839). Jacques Ozanam, Récréations mathématiques et physiques, París (1694). Martin Gardner, Mathematical Circus, New York (1979). Matem94 Charles Jordan, Thirty card mysteries (1919). Colm Mulcahy, What's black and red and red all over?, Card Colm (2008). Persi Diaconis y Ronald Graham, Magical Mathematics, Princeton (2011). [Matem99] Matem95 Karl Fulves, My best self-working card tricks, Dover (2001). Matem96 Dominique Souder, Maths et Magiques, SOS Education (2015). Matem98 Yakov Perelman, Aritmética Recreativa, Leningrado (1938). Matem99 Leonardo Pisano, Liber Abaci (1202). Pedro Alegría, Sucesiones de recurrencia en la matemática recreativa, Revista Eureka (2009). Martin Gardner, Fibonacci Fantasy, Apocalypse (1978). Arthur McTier, Card Concepts, Davenport (2000). Colm Mulcahy, Gibonacci Bracelets, Card Colm (2007).   Pedro Alegría (Universidad del País Vasco - Euskal Herriko Unibertsitatea)

Lunes, 10 de Enero de 2022 | Imprimir | PDF |  Correo electrónico

3. 199. (Diciembre 2021) Ilusiones mágicas

Llevamos más de 17 años dando muestras mensuales de la estrecha relación que existe entre la magia y la matemática. Después de este recorrido tan extenso, es posible que hayas tenido la impresión de que toda la magia es matemática o de que toda la matemática es mágica pero, a poco que conozcas algo más de cualquiera de estas dos disciplinas, concluirás que hay vida más allá de ambas. Digo esto porque hoy quiero dedicar nuestra reunión mensual en este rincón a explorar algunas relaciones de la magia con otras ciencias, concretamente con las ciencias cognitivas. Esto tampoco nos aleja de las matemáticas porque el estudio de la lógica del cerebro y la lógica de la razón están lógicamente relacionados, por pura lógica. Así que voy a realizar un pequeño recorrido por algunos juegos más o menos clásicos en los que el razonamiento lógico choca contra la percepción sensorial. 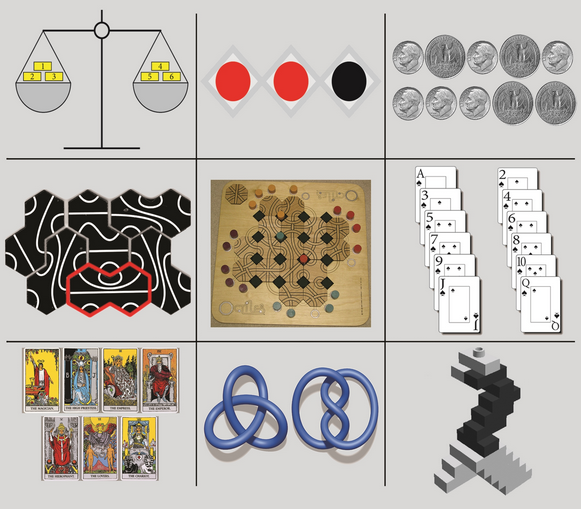(1) LA HIPERCARTA El primer ejemplo es el que aparece en la imagen que encabeza el artículo: ¿crees que es posible que esta figura se haya construido con una sola carta sin haberla roto completamente? Parece imposible que la sección vertical corresponda exactamente con los dos huecos contrapuestos que se han formado en la parte horizontal. Pues, contrariamente a la razón, es posible y muy fácil de realizar. El acertado nombre comercial de esta ilusión es "hipercarta" debido a que, aparentemente, se debe viajar a la cuarta dimensión para conseguir que los dos huecos se conviertan en un solo trozo. Se desconoce el origen de esta ilusión pero, en el capítulo 8 del libro Fractal Music, Hypercards and More ... (Freeeman, 1992), Martin Gardner señala que la construcción de este modelo fue propuesta como examen de ingreso para la escuela de arquitectura en la Universidad de Leningrado (la actual San Petersburgo). En ese mismo capítulo, Gardner explica el método para construir la hipercarta y desvela algunas ideas elaboradas por varios magos para convertir esta ilusión en juego de magia. Un estudio riguroso y completo, realizado por Tom Frame, culminó con el libro titulado The Hypercard Project (2006), donde se pueden encontrar diferentes variaciones y muchas sorpresas. A modo de ejemplo, van estas dos figuras: la imagen de la izquierda consiste en una banda de Möbius con aspecto de hipercarta, ideada por Paul Merva y Alexis Gilliand y la imagen de la derecha (¿te animas a construirla?) es una sorprendente construcción realizada por Jack Botermans, especialista en puzles y problemas de ingenio, como aparece en su libro Paper Capers (1986). Aunque la propia ilusión ya produce en sí misma una sorpresa mágica, una estupenda adaptación como juego de magia la ofreció el mago californiano Daryl Easton (fallecido en 2017 bajo extrañas circunstancias) con el juego Hyper-Bent-Elation. Una última sugerencia: no dejes de consultar el artículo "Impossible Folding Font", firmado por Erik Demaine, Martin Demaine, Tomoko Taniguchi y Ryuhei Uehara, que fue presentado para la edición de 2019 de las Conferencias Bridges, en las que se exploran las conexiones de las matemáticas con el arte, la música, la arquitectura y la cultura. En ese trabajo crean todo un alfabeto con figuras «imposibles» como las que vemos en las imágenes de aquí abajo. (2) EL BOOMERANG El segundo ejemplo que quiero mostrar recibe el nombre de «ilusión del boomerang». Consiste en dos láminas o tiras de cartón u otro material con forma de rectángulo curvado, como se ve en estas dos imágenes. Si nos fijamos en la imagen de la izquierda, parece evidente que la pieza A es de menor tamaño que la pieza B. Ahora bien, si intercambiamos las posiciones de las dos piezas, resulta que la pieza B tiene ahora menor tamaño que la pieza A, como se puede apreciar en la imagen de la derecha. La realidad es que ambas plantillas son exactamente iguales. Sólo la posición relativa entre ellas y la forma curvada de su construcción produce la sensación de que una de ellas es mayor que la otra (al alinearse las dos piezas por los lados cortos de su izquierda, la figura superior queda desplazada hacia la izquierda de forma inapreciable por el subconsciente). En este videoclip de la página Mighty Optical Illusions se muestran las distintas posiciones relativas de las piezas y la ilusión óptica que hace variar nuestra sensación sobre su tamaño relativo. Se dice por ahí que esta ilusión óptica fue ideada por el psicólogo estadounidense —de origen polaco — Joseph Jastrow en 1892, razón por la cual se conoce popularmente como "ilusión de Jastrow". Sin embargo, aparece impresa —¿por primera vez?— en la enciclopedia "The world of wonders: a record of things wonderful in nature, science, and art", publicada alrededor del año 1882, bajo el título Wonderful optical delusion, como se muestra en la imagen de la izquierda. Esta misma ilusión fue publicada por el psicólogo alemán Felix Müller-Lyer para la revista Archiv fur Anatomie und Physiologie en 1889 junto a una selección de ilusiones similares (que se muestran en la imagen central) y por Wilhelm Wundt unos años más tarde. El estudio de la forma que deben tener las figuras para maximizar la ilusión fue estudiado por otro psicólogo, el japonés Shogu Imai en 1960. Aquí intervinieron las matemáticas pues la conclusión de Imai fue que los bordes curvos de las láminas debían tener forma de arcos de circunferencia, que la razón entre los radios debía ser 3/5 y el ángulo central ideal debía medir 80 grados. No pasó mucho tiempo para que la ilusión se convirtiera en un juego de magia. La referencia más temprana que se conoce corresponde al libro de Will Goldston titulado Simple Conjuring Tricks That Anyone Can Perform y publicado en 1913. Un completo y documentado estudio sobre esta ilusión ha sido escrito recientemente por Peter Prevos (quien se autodefine como ingeniero civil y científico social con incursiones esporádicas a la magia teatral) bajo el título The Jastrow Illusion in Magic, publicado en 2016. Él mismo escribió en 2017 una breve reseña del folleto en el artículo titulado "The science of the boomerang illusion", publicado en el número 8 de la revista Journal of Magic Research (de la que hablaremos más adelante). Muchas y variadas versiones de la ilusión del boomerang se han desarrollado como juegos de magia. Una de mis preferidas se debe al ingenio de Terri Rogers (ya citada en este rincón en el número 152 de septiembre de 2017), con el juego titulado Top of the bill, donde van cambiando de tamaño los carteles con los nombres de Stan Laurel y Oliver Hardy, los famosos "el gordo y el flaco". Otro enfoque interesante es el juego comercializado en 2006 por Chuck Leach bajo el título Boomerang Card Across; éste consiste en un sorprendente viaje de una carta pensada desde un paquete de cartas hacia otro con la ayuda de la ilusión del boomerang. Las imágenes sin palabras que muestro aquí abajo corresponden a otras versiones ingeniosas del juego. También puedes ver un video donde el mago japonés Mizoguchi realiza el juego titulado Arch Illusion y, si quieres adquirir un modelo barato, el matemago reinounidense Andrew Jeffrey comercializa la ilusión que titula la mariposa creciente. (3) UNO ES MAYOR QUE TRES La tercera y última ilusión paradójica que quiero comentar ya no se trata de un efecto óptico ni visual sino táctil. Antes de entrar en detalles, quiero que la experimentes personalmente para lo cual basta que sigas las instrucciones que leerás a continuación. Necesitarás tres barajas de cartas, aunque lo importante no son las cartas sino sus estuches de cartón. En su defecto, valen tres cajas iguales de dimensiones similares a las de los estuches de cartas, como las cajas grandes de cerillas. Vacía dos de las tres cajas y deja la tercera llena (puede ser con las propias cartas o con muchas monedas o llena de granos de arroz o de tornillos). Cuanto mayor sea su peso, más sorprendente será el efecto. Coloca las tres cajas apiladas, una sobre otra, pero dejando la más pesada encima de las otras dos. Agarra las tres cajas desde arriba con una mano, colocando el dedo pulgar en la parte interior y el resto de los dedos en la parte exterior y levanta todo el conjunto. Toma nota mental de su peso. Deja todo el conjunto sobre la mesa y agarra ahora solamente la caja superior. Levanta la caja y observa su peso. Por arte de magia, resulta que esta única caja pesa más que la suma de las tres. ¿Menos es más? Si no crees lo que has sentido, repite el experimento todas las veces que quieras, incluso empezando por levantar primero el paquete superior y después los tres juntos. ¡Increíble pero cierto! Si te ha parecido interesante el experimento, puedes construir tus propias cajas con el diseño que ha realizado Mark Fuller, el cual está disponible en el portal www.thingiverse.com, y que puedes reproducir con una impresora 3D. Si te parece más cómodo, puedes adquirir el juego en la tienda online Grand Illusions o una versión con ingredientes adicionales y material de gran calidad en Vanishing Magic. Este juego me lo enseñó Fernando Blasco (citado ya en este rincón en varias ocasiones) quien, a su vez, lo conoció en una de las famosas reuniones Gathering for Gardner, que se celebran cada dos años en Atlanta (capital del estado norteamericano de Georgia) reuniendo todo tipo de personas que comparten con Martin Gardner tres de sus grandes pasiones, la magia, las matemáticas y los juegos de ingenio. El efecto está basado en la conocida por los psicólogos como ilusión peso/tamaño de Charpentier, por haber sido el oftalmólogo francés Augustin Charpentier el primero en realizar el experimento y mostrar la ilusión creada en el artículo titulado "Analyse experimentale: De quelques elements de la sensation de poids" y publicado en 1891 (se puede leer un resumen de dicho artículo, así como otros aspectos históricos de la ilusión, en el trabajo de 1999 titulado "Charpentier (1891) on the size-weight illusion", firmado por David Murray, Robert Ellis y Christina Bandomir). El experimento inicial consistía en disponer de varios objetos, todos del mismo peso pero de distintas formas y tamaños, y estimar su peso levantándolos individualmente. La conclusión que se obtenía era que el objeto más pequeño parecía que fuera el más pesado. El fenómeno sigue suscitando debates entre los especialistas ya que no queda completamente resuelta la causa que origina esta ilusión. Intervienen aspectos físicos —como la diferencia de tamaño—, aspectos fisiológicos —como la dificultad de agarrar el objeto más grande o que la mano ejerce más presión sobre la parte superior del objeto que es la más pesada— o aspectos psicológicos —como la idea preconcebida de que más grande equivale a más pesado—, aunque es posible que la respuesta esté en la suma de todos ellos. Muchos artículos científicos se han publicado en relación con esta ilusión y es fácil encontrarlos gracias a la existencia de buscadores virtuales tan eficientes como veloces. Sólo citaré el artículo titulado "The size-weight illusion", al que puedes acceder desde el portal Science is Fun, mantenido por Bassam Shakhashiri, profesor de Química de la Universidad de Wisconsin-Madison, y que presidió en 2012 la American Chemical Society. La revista electrónica The Journal of Magic Research, disponible bajo registro en el portal Ask Alexander (la mayor biblioteca virtual sobre magia del mundo), está dedicada a promocionar la investigación científica en la magia; su lema es: "cuando mides cualquier cosa y lo expresas con números, entonces ya sabes algo sobre ella". En la revista se pueden encontrar artículos que relacionan la magia con las matemáticas, la neurociencia, psicología, biología, física, química y otras disciplinas científicas. Pues bien, en el número 5 de dicha revista (que apareció en febrero de 2014), Gerry Hayes escribe el artículo titulado "Can you fool yourself?" en el que cita este juego a partir de la descripción dada por Ian Rowland en la revista Magic Circular, que es el órgano de difusión del longevo y selecto club londinense «Magic Circle». Hayes pide a los lectores de la revista que se pronuncien sobre el fenómeno y propongan respuestas a las causas que lo originan. En el siguiente número de la revista podemos encontrar un par de contribuciones de magos que comentan sus propios métodos para realizar el juego, sin profundizar en la posible explicación. Independientemente de las causas que originan esta ilusión, puede presentarse ante el público como juego de magia, bien para demostrar los poderes de sugestión que tiene el mago, bien para hacer creer que existen fuerzas ocultas que se ejercen por la voluntad del mago, o mediante cualquier explicación pseudocientífica que se te ocurra. La buena noticia es que nadie descubrirá el truco porque ... ¡no hay truco! Para saber más Como podrás imaginar, hay muchos otros ejemplos que se podrían proponer en la línea de los citados aquí. Para no extenderme demasiado en el tema, terminaré indicando algunos enlaces en los que puedes empezar a navegar si te interesa el tema de la psicología en la magia. La ilusión del vaso de tubo era uno de los juegos favoritos de Martin Gardner (como puedes comprobar en la imagen) y está descrito en uno de los artículos de la revista digital Computer Science for Fun, de la Universidad Queen Mary de Londres. En el portal Psychology of magic, del grupo formado por investigadores de las Universidad McGill y British Columbia, aparecen publicados algunos resultados de investigación realizados con el objetivo de entender cómo la magia actúa sobre nuestra mente. El artículo de Susan Krauss (Universidad de Massachusetts Amherst), titulado 5 amazing psychology magic tricks (2012), enseña cinco juegos de magia como ejemplos de demostraciones científicas que pueden ser utilizados en institutos o escuelas de psicología. Diversos trabajos del mago y psicólogo Richard Wiseman, como los libros "Magic in Theory", "Blink and you'll miss it" o "Magic and wellbeing", abundan en el tema de la relación entre la magia y la psicología. Han sido (y son) muy populares en la red sus ilusiones ópticas y otros efectos mágicos, que se pueden disfrutar en el canal de YouTube titulado Quirkology. Pedro Alegría (Universidad del País Vasco - Euskal Herriko Unibertsitatea)

Jueves, 02 de Diciembre de 2021 | Imprimir | PDF |  Correo electrónico

4. 198. (Noviembre 2021) Primos estrellados

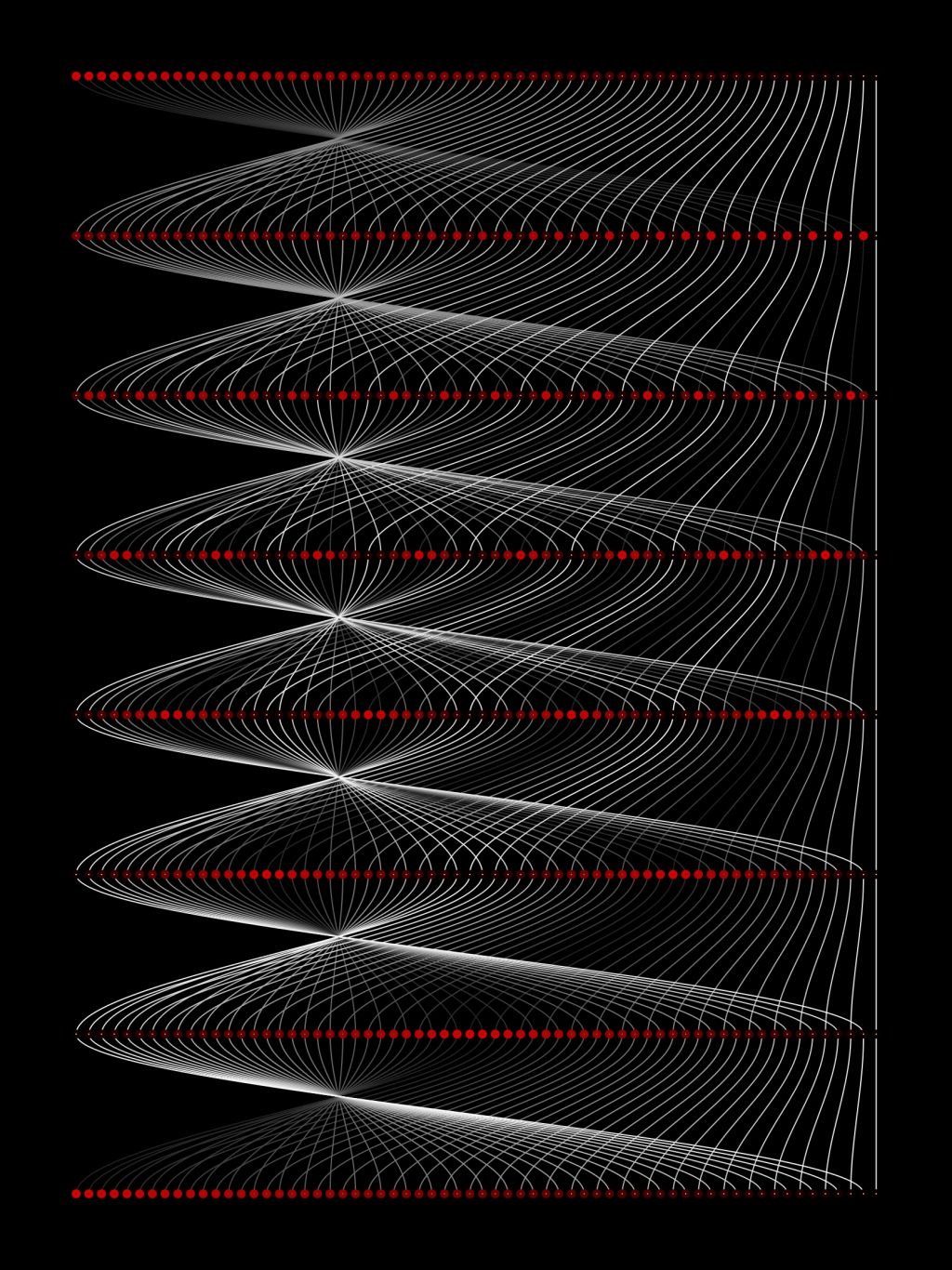
Seguro que ya sabes lo que pasa cuando se dibujan 5 puntos equidistantes sobre una circunferencia y se une, empezando por uno de ellos, cada uno de los puntos con el siguiente, hasta volver al punto de partida. Cierto, se obtiene un pentágono regular. También sabrás que este procedimiento es completamente general: si se dibuja cualquier otra cantidad de puntos —digamos n— equidistantes sobre una circunferencia, al unir puntos consecutivos hasta volver al punto de partida se obtiene un polígono regular de n lados. En la siguiente figura se muestran los casos del pentágono y el heptágono regulares. Creo que no es difícil tampoco adivinar lo que ocurre cuando se unen los vértices del pentágono anterior no de forma consecutiva sino saltando un punto cada vez. Haz la prueba, numera los cinco puntos (por ejemplo, en el sentido de las agujas del reloj), traza un segmento uniendo el 1 con el 3 (saltando el 2), luego el 3 con el 5 (saltando el 4), luego el 5 con el 2 (saltando el 1), éste con el 4 y, por último, el 4 con el 1. Efectivamente, conseguirás la famosa estrella de cinco puntas o pentagrama, que fue símbolo de la escuela pitagórica y que oculta numerosas sorpresas matemáticas. Ahora bien, a diferencia del proceso de construcción de los polígonos regulares, si el número de puntos no es cinco, no se puede asegurar que la figura obtenida sea una estrella. Por ejemplo, con seis puntos, empieza trazando un segmento uniendo el 1 con el 3, luego el 3 con el 5 y el 5 con el 1; no hay forma de pasar por los puntos numerados con el 2, 4 ni 6. Ahora bien, si se empieza uniendo el punto 2 con el 4, el 4 con el 6 y el 6 con el 2, se consigue un segundo triángulo que, junto con el anterior, forman también una estrella, símbolo que la religíón judía conoce como sello de Salomón o estrella de David. La estrella pentagonal es un ejemplo de polígono estrellado (figura que se obtiene al unir de forma alterna, ya sea de dos en dos, de tres en tres, etc., los vértices de un polígono regular) y la estrella hexagonal es un ejemplo de falso polígono estrellado (figura que se obtiene superponiendo varios polígonos girados entre sí). En la figura se muestran las estrellas poligonales de cinco, seis, siete y ocho vértices, entre las cuales hay dos que son falsos polígonos estrellados. La pregunta que te surge ahora es: ¿cuántos lados debe tener un polígono para que se pueda dibujar una estrella poligonal y cuántas estrellas poligonales se pueden construir sobre un mismo polígono? La clave para dar con la respuesta es que, al unir los vértices, no se vuelva al punto de partida hasta que se hayan recorrido todos. Matemáticamente, esto significa que el número de lados y el salto entre vértice y vértice sean números primos entre sí. Por esta razón, sólo hay una estrella pentagonal pues 5 y 2 son primos entre sí (claro, también lo son 5 y 3 pero la figura resultante al saltar de dos en dos que de tres en tres es la misma) y no hay ninguna estrella hexagonal (vale, 6 y 5 son primos entre sí pero no sale ninguna estrella saltando de cinco en cinco pues es lo mismo que saltar de uno en uno, pero en sentido contrario). Como no quiero profundizar en estas interesantes y entretenidas cuestiones, citaré un par de referencias por si quieres aprender un poco más: el apartado "Polígonos estrellados" del blog Matemáticas en tu mundo de José María Sorando, ilustrado con gran variedad de originales fotografías, y el trabajo de Inmaculada Fernández Benito titulado "Polígonos estrellados, estrellas y formas estrelladas", presentado en la sexta reunión nacional de Estalmat (marzo de 2009). Te estarás preguntando qué relación tiene esta extensa introducción con el juego de magia que estás esperando. Para prolongar un poco más el misterio, hagamos primero el juego y, si nos queda tiempo (a mí) y paciencia (a ti), daremos las pertinentes justificaciones. Prepara siete cartas, del as al siete de cualquier palo y ordénalas de menor a mayor formando un paquete (el as es el que quedará a la vista, si las cartas están cara arriba). Quedará algo así como esta figura: Cierra la extensión de cartas y, manteniendo el paquete con las cartas cara abajo, reparte dos montones sobre la mesa, dejando alternativamente una carta en el montón de la izquierda y una carta en el montón de la derecha. Recoge los dos montones colocando uno de ellos sobre el otro. Ahora puedes cortar y completar el corte para no saber cuál es la posición de las cartas. Muy bien, gira cara arriba la carta superior y déjala nuevamente como carta superior. ¿Es el siete? Lo sabía. ¡Ah!, que no es el siete (lástima, habría sido la predicción perfecta). Pasa entonces de arriba abajo del paquete tantas cartas como indique dicho número (el as corresponde al uno, claro). Por ejemplo, si es un tres, pasa tres cartas de arriba abajo del paquete (el tres seguirá estando cara arriba pero las demás quedarán cara abajo). Gira ahora cara arriba la nueva carta superior y repite el proceso indicado en el paso anterior con este nuevo número. En este momento habrá dos cartas cara arriba y cinco cartas cara abajo. Vuelve a repetir el mismo proceso anterior hasta encontrar que la nueva carta superior ya está cara arriba. Podría apostar a que, en este momento, sólo queda una carta cara abajo. Además, sé incluso de qué carta se trata: ahora sí es el siete. Como podrás apreciar, el juego tiene un aire similar a los de tipo combinatorio que citamos en el número 193 (mayo de 2021) de este rincón, y seguro que sería muy del gusto del genio mágico John Conway. Para comprender el fundamento de este juego, debemos detenernos en el efecto que producen los dos pasos clave del proceso: el reparto inicial de los dos montones y la secuencia numérica de las cartas que se van girando. Con el primer reparto se han separado las cartas pares de las impares. El hecho de cortar el paquete puede alterar la posición de las cartas pero no el orden cíclico (si pensamos que las cartas están colocadas en los vértices de un heptágono regular, veremos las cartas pares de menor a mayor seguidas de las cartas impares, también de menor a mayor). En este momento, independientemente del valor de la primera carta, sólo hay una posible secuencia de cartas que se van girando cara arriba: 1 - 3 - 2 - 6 - 4 - 5. Hay que entender de nuevo que esta secuencia es cíclica, es decir, si la carta superior es, por ejemplo, el 5, la secuencia de cartas giradas es 5 - 1 - 3 - 2 - 6 - 4. Así pues, se recorren todas las cartas excepto el siete de modo que la predicción es infalible. Esto conduce inexorablemente a plantearse la siguiente pregunta: ¿el juego se puede realizar con cualquier cantidad de cartas? La respuesta inmediata es ¡NO! Haz la prueba con seis cartas. Recuerda el proceso: ordénalas de menor a mayor, reparte dos montones, reúnelos, corta y gira la carta superior: si es un seis, se acaba el juego. Si no, pasa de arriba abajo tantas cartas como indique su valor, repite el proceso. Verás que aparece una cara cara arriba antes de girar todas. El juego no funciona. ¿Y con cinco cartas? Ahora sí, la secuencia de cartas giradas es 1 - 3 - 4 - 2 (o cualquier reordenación cíclica de ésta). ¡Vaya!, resulta que con cinco y siete vértices se podía construir un polígono estrellado pero con seis no. ¿Tendrá algo que ver? Sigamos investigando, pero antes quiero citar el artículo donde se detallan las ideas fundamentales que he rescatado aquí: se trata del titulado "Les secrets du pentacle", escrito por Ludovic Simonet en el número 46-47 (año 2003) de la revista Hyper Cube, cuya portada se muestra en la imagen. En dicho artículo, el autor atribuye al mago George Sands (1920-2006), el mismo que inventó-descubrió-ideó-creó el principio del número primo que protagonizó el número 76 (octubre de 2010) de este rincón, el origen del método de adivinación descrito. Misteriosamente, los números primos también van a aparecer aquí. Este es el enfoque desarrollado por Ludovic Simonet (y quizá también por George Sands (ver comentarios finales)): Dibuja un número impar arbitrario de puntos equidistantes en una circunferencia, digamos 2n + 1; Escribe el número 1 junto a uno cualquiera de los puntos; Saltando n puntos en el sentido de las agujas del reloj, escribe el número 2 en el punto al que has llegado; Repite el paso anterior y escribe el número 3 en el nuevo punto al que has llegado; Sigue recorriendo los puntos marcados como se ha indicado y escribiendo números de forma consecutiva; Por último, traza un segmento uniendo el punto 1 con el 2, luego el 2 con el 3, el 3 con el 4 y así hasta volver al punto de partida. ¡Acabas de construir un polígono estrellado de 2n + 1 puntas! Has recorrido todos los puntos sin repetir ninguno de ellos debido a que los números 2n + 1 y n son primos entre sí, sea cual sea el valor de n (¿sabrías demostrar esta propiedad?). Además, si recorres los vértices de la estrella en el sentido de las agujas del reloj, aparecen los números impares, en orden creciente, y, a continuación, los números pares, también en orden creciente (precisamente, como se debían colocar para realizar el juego anterior). Esto significa que podíamos plantear el juego utilizando una estrella con los vértices numerados de esta forma en lugar de cartas, tachando los números a los que se llega después del recorrido por la estrella. El único punto que no quedará tachado sería siempre el número 2n + 1. En la figura puedes ver la disposición de los números y la forma de las estrellas con siete y nueve puntas. ¡Última sorpresa! Sería un poco aburrido que el juego se pudiera realizar con cualquier estrella que tenga un número impar de vértices. Ya hemos visto que funciona con 5 y 7 vértices pero no sale con 9, 11, 13 ni 15. Sí funciona con 17 (número que utiliza Ludovic Simonet en su artículo), con 19, 29, 31 y 43. ¿Cuál es el siguiente? ¿Sólo vale con algunos números primos? Como yo no sé las respuestas, planteo estas cuestiones a mi amigo Juan Carlos Ruiz de Arcaute —mago, matemático e informático, entre otras habilidades— y, como resultado de sus indagaciones, me devuelve la lista de los primeros valores, resumida en esta tabla: Pues sí, son todos primos, que podríamos bautizar como "primos estrellados" si no fuera porque ya estaban bautizados previamente (con otro nombre): se trata de la sucesión catalogada como A019334 en la "Enciclopedia de Sucesiones de Números Enteros", fundada en 1964 por el inagotable matemático Neil Sloane. Resulta que se trata de la sucesión de números primos con raíz primitiva 3, lo cual conduce a nuevas e inquietantes preguntas, como por ejemplo: ¿qué tienen que ver estos números con el proceso de conteo que se lleva a cabo en el juego descrito? Comentarios finales Un precursor del juego que aquí hemos mostrado es el titulado "Prime choice", ideado por George Sands y publicado por Karl Fulves en el número 8 de la revista The Chronicles (1978). En primer lugar nos hace aprender la frase mnemotécnica "A furry kitten fights seven to try at joinning six queens" (algo así como "Un gatito peludo pelea contra siete para tratar de unirse a seis reinas") como regla para recordar el orden As-4-K-10-5-7-2-3-8-J-9-6-Q. Por ejemplo, "furry" recuerda a "four", "fight" a "five", etc. Ahora basta tener preparadas trece cartas con esa ordenación, dar a elegir una carta del resto de la baraja, sustituirla por la K en la preparación anterior y dejar las trece cartas en las manos de tu asistente. Esta persona corta el paquete, completa el corte y gira cara arriba la carta superior. Ya sabes el resto: si es la carta elegida, perfecto; si no, pasa de arriba abajo tantas cartas como indica el valor de la carta girada (el as cuenta como 1, la J como 11 y la Q como 12), repite el proceso hasta que sólo quede una carta cara arriba. Será la elegida. Pedro Alegría (Universidad del País Vasco - Euskal Herriko Unibertsitatea)

Martes, 02 de Noviembre de 2021 | Imprimir | PDF |  Correo electrónico

5. 197. (Octubre 2021) La magia de Charles Peirce

[Visualización artística de siete "mezclas lecheras" de Roger Antonsen.] Como apéndice al artículo publicado el mes pasado en este rincón (dedicado al principio disléxico) sobre la revisión de las contribuciones a la magia matemática de Charles Peirce realizada por Persi Diaconis y Ron Graham en el artículo "The magic of Charles Sanders Peirce", quiero referirme a la última parte de este artículo, que contiene un descubrimiento reciente y un juego que oculta algunas sorpresas matemáticas. Diaconis y Graham desvelan parte del contenido de una carta que envió Charles Peirce a su amigo y mentor —así como también aficionado a los juegos de magia con cartas— Chauncey Wright el 2 de septiembre de 1865, carta que se encontró recientemente entre los papeles de éste, los cuales están recopilados por la Sociedad Filosófica Americana (y cuya reproducción puedes leer en este enlace). En dicha misiva y después de compartir algunas ideas sobre filosofía, Peirce explica a su colega un nuevo principio matemático relacionado con ciertas mezclas de cartas. Para comprenderlo, propongo que hagamos juntos una versión simplificada del juego con las cartas en la mano. Busca una baraja y sigue leyendo: Selecciona las cartas del as al cinco de los cuatro palos y ordénalas formando un paquete como el de esta figura (el orden de los palos es irrelevante, sólo es importante que todos los palos estén ordenados de la misma forma): Manteniendo las cartas con las caras hacia abajo, realiza una mezcla lechera —también llamada mezcla Klondike— TRES VECES. Si no recuerdas cómo se hace esta mezcla, puedes repasar el número 122 de este rincón, correspondiente a diciembre de 2014. De nuevo con las cartas cara abajo en la mano, cuenta las cuatro primeras, invirtiendo su orden, mientras las pasas de una mano a la otra. Cuenta las cuatro siguientes cartas, sin invertirlas, y las pasas a la otra mano debajo de las cuatro primeras. Repite esta doble mezcla, contar las cuatro cartas superiores invirtiendo su orden y pasarlas sobre las de la otra mano y contar las siguientes cuatro cartas sin invertir su orden y pasarlas bajo las de la otra mano, continuando el mismo proceso hasta que hayas pasado todas las cartas de una mano a la otra. Por último, gira cara arriba el paquete de cartas y reparte sobre la mesa cuatro montones. Observarás que las cartas han vuelto a colocarse en el orden inicial. La secuencia que consiste en pasar grupos de cuatro cartas de una mano a otra, uno de ellos arriba y el otro abajo, es una generalización de la mezcla Monge, que también hemos descrito en este rincón (por ejemplo, en el número 127 de mayo de 2015). En la mezcla Monge original, sólo se pasan las cartas de una en una pero nadie se había planteado antes (que sepamos) el reparto por bloques de cartas. Lo interesante y sorprendente del juego que acabamos de describir es que se puede hacer con cualquier cantidad de cartas que sea múltiplo de cuatro, no necesariamente con cuatro conjuntos de cinco cartas. Pero, además, el número de mezclas lecheras siempre será tres, independientemente del número de cartas con las que se haga el juego. Ya se conocen muchas propiedades de las permutaciones obtenidas al realizar una mezcla Monge (por ejemplo, que después de 12 mezclas, una baraja de 52 cartas recupera su orden inicial) pero —que yo sepa— no se han estudiado, aparte de lo que ocurre en este juego de Peirce, las propiedades de la mezcla Monge generalizada. En la postdata de la carta que Diaconis y Graham analizan en su artículo, Charles Peirce regala a Chauncey Wright un par de juegos relacionados con el anterior, el segundo de ellos adornado con una historia de encuentros y desencuentros. Incluye además las fórmulas y los cálculos realizados para conseguir el resultado deseado. Puedes leer todos los detalles en el citado artículo. Para terminar, quiero compartir mi sorpresa al descubrir que Charles Sanders Peirce sigue entre nosotros, de modo que, si quieres conocer sus pensamientos, sus ideas filosóficas y lógicas y demás aspectos de su vida y obra, puedes seguirle en su perfil de Facebook (aunque, para disimular, haya puesto como foto de portada una recreación de la imagen de Karl Marx). Pedro Alegría (Universidad del País Vasco - Euskal Herriko Unibertsitatea)

Lunes, 04 de Octubre de 2021 | Imprimir | PDF |  Correo electrónico

6. 196. (Septiembre 2021) El pricnipio deslíxico

La colección de libros The Mathematics of Various Entertaining Subjects (que va ya por su tercer volumen), editados por Jennifer Beineke y Jason Rosenhouse y publicados por Princeton University Press en 2015, 2017 y 2019, recoge las aportaciones de destacados especialistas en el área de la matemática recreativa dictadas en las conferencias MOVES (acrónimo de Mathematics Of Various Entertaining Subjects), organizadas cada dos años por el Museo Nacional de Matemáticas (MoMath) en Nueva York. En el prólogo del tercer volumen de la colección —cuyo subtítulo es precisamente "The magic of mathematics" (en la figura adjunta se muestra un fragmento de la portada)—, el medallista Fields Manjul Bhargava reflexiona sobre el concepto de matemática recreativa y el papel de cohesión que esta disciplina protagoniza para establecer las diferencias y similitudes entre matemática pura y matemática aplicada. Destaca también el gran éxito logrado por Martin Gardner al poner de manifiesto el poder de la matemática recreativa como fuente de inspiración de matemáticos y no matemáticos en su objetivo final de disfrutar de las matemáticas. Justifica con estas palabras la iniciativa de las citadas conferencias MOVES: Debe quedar claro que —con la creciente importancia del enfoque educativo conocido como STEM (acrónimo de Science, Technology, Engineering and Mathematics) para el avance de la sociedad y la humanidad— la matemática recreativa, además de ser divertida, también puede desempeñar un papel fundamental para alentar a la juventud a dedicarse a las matemáticas y campos relacionados. Es con este último objetivo en mente que la conferencia MOVES fue creada en 2013. MOVES reúne a maestros, estudiantes, aficionados y profesionales de todo el mundo para celebrar y compartir ideas y avances en matemática recreativa. En los últimos años, cada conferencia de MOVES ha tenido un tema. En 2017, el tema de MOVES fue "La magia de las matemáticas". Fue un gran placer participar en MOVES 2017 y un verdadero honor ser uno de sus dos oradores principales junto con mi maestro y gran amigo, Persi Diaconis. En el capítulo 12 del libro encontramos el artículo firmado por Persi Diaconis y Ron Graham titulado "The magic of Charles Sanders Peirce" (artículo que también puede encontrarse entre los papeles del recientemente fallecido Ron Graham). En dicho artículo tratan de desentrañar los secretos que ocultan los sofisticados juegos de magia que Charles Peirce publicó en 1908 y 1909 para la revista The Monist bajo el título común "Some amazing mazes". Casi simultáneamente a la conferencia de Diaconis y Graham, ya recogimos en este rincón (en el número 154 de noviembre de 2017) algunos intentos anteriores de comprender el fundamento matemático de la magia de Charles Peirce por parte de ilustres magos como Tom Ranson y Alex Elmsley pero profundizaremos un poco más recogiendo algunas ideas desarrolladas en este nuevo artículo. El artículo es muy extenso y prolijo así que nos limitaremos a describir un original principio contenido en los trabajos de Peirce y aclarado  por Diaconis y Graham, bautizado por estos como "principio disléxico". Lo ilustraremos con un ejemplo para el que necesitarás doce tarjetas o papeles rectangulares. En seis de ellos escribirás las seis primeras letras del alfabeto y en los otros seis escribirás los seis primeros números naturales. Coloca sobre la mesa las tarjetas formando dos filas, donde la fila superior contiene las seis letras, por orden alfabético, y la fila inferior contiene los seis números, en orden creciente. Te quedará algo como esta figura: Elige libremente cualquier tarjeta de la fila superior y cualquier tarjeta de la fila inferior. Luego intercambia sus posiciones; habrá un número en la fila superior y una letra en la fila inferior, pero no puedo saber dónde está cada símbolo. Repite esta misma operación con los otros cinco pares de letras y números. En cada paso elegirás una letra de la fila superior y un número de la fila inferior e intercambiarás sus posiciones. Evidentemente, cada vez la elección será menos libre porque habrá menos letras en la fila superior. Al final del proceso tendrás nuevamente dos filas de tarjetas pero ahora la fila superior tendrá sólo números y la fila inferior tendrá sólo letras. Lo más importante es que nadie puede saber el orden en que han quedado los símbolos en ambas filas. Si quieres sorprenderte a ti mismo, gira caras abajo las tarjetas de la fila inferior. Quedará algo parecido a esta figura (aunque el orden de los números será el que tú has elegido): Voy a tratar de adivinar qué posición ocupa la letra A. Para ello, sólo necesito saber cuál es el primer número de la fila superior. Si es un 1, la letra A será la primera carta de la fila inferior; si es un 2, será la segunda; si es un 3, será la tercera y así sucesivamente. En la imagen anterior, la letra A ocuparía la segunda posición de su fila. Seguro que sabrás encontrar también las posiciones de las demás letras. Por ejemplo, para saber dónde está la letra D, busca el valor de la cuarta carta de la fila superior; dicho valor indicará la posición del cuatro en la fila inferior. En nuestro ejemplo, como la cuarta carta es el 1, la letra D será la primera carta de la fila. Con un poco de reflexión, se comprende fácilmente el fundamento del juego: como sólo se intercambian las tarjetas por parejas, la posición de una de ellas determina el valor de la otra. Esto significa que no importa el número de tarjetas que tiene cada fila, el juego se puede realizar con cualquier cantidad de tarjetas. Además, se puede ocultar un poco el secreto si las tarjetas no se colocan inicialmente en el orden natural: para ello debes ser capaz de llevar la cuenta mental de las posiciones iniciales de cada tarjeta. Incluso, se puede jugar con otro tipo de tarjetas, dos palabras con las mismas letras pero con diferente significado (por ejemplo, ANCESTRO/CARTONES, BOLERAS/ARBOLES, ARSENICO/ESCARNIO, o cualesquiera que puedas descubrir en páginas generadoras de anagramas), dos conjuntos de cartas, digamos rojas y negras, como el juego original de Peirce o la versión de Diaconis y Graham, etc. Más interesante todavía es el resultado matemático del proceso seguido en el juego: resulta que las dos permutaciones obtenidas en las filas de tarjetas son inversas. No vamos a desarrollar aquí la teoría de grupos finitos que contiene el estudio de las permutaciones pero, si tienes ganas, el artículo de Diaconis y Graham detalla un poco más esta analogía. Aprovechando esta propiedad, se comprueba fácilmente que el juego también se puede realizar a partir de dos permutaciones inversas cualesquiera. En resumidas cuentas, los juegos de magia de Charles Peirce podían ser poco prácticos pero los principios matemáticos involucrados fueron muy originales y complejos y todavía no se ha desvelado todo su potencial. El propio Martin Gardner lo evaluaba con estas palabras: No puedo recomendarlo para quien quiera entretener a los amigos a menos que tengan pasión por la teoría de números, pero es excelente para un profesor que quiera motivar el interés de los estudiantes hacia la aritmética de congruencias. Pedro Alegría (Universidad del País Vasco - Euskal Herriko Unibertsitatea)

Lunes, 06 de Septiembre de 2021 | Imprimir | PDF |  Correo electrónico

7. 195. (Julio 2021) La magia de los dobleces

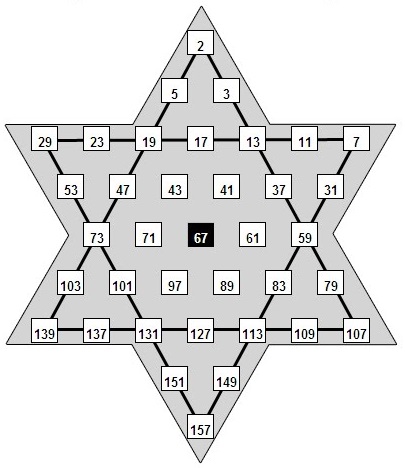
¿Quién recuerda el primer artículo que apareció en esta sección? Pues hoy ha tocado el turno de retomar el tema que allí se trató (en el improbable caso de que lo hayas olvidado, puedes repasarlo de nuevo). Diferentes aspectos relacionados con la paridad de los elementos de una matriz o de una cuadrícula —ya esté formada por símbolos, números o cartas— han sido utilizados de forma regular por los aficionados a la magia matemática. Es una tarea muy sencilla identificar las posiciones pares e impares en una fila pero no lo es tanto cuando hay varias filas y columnas involucradas. En matemáticas, para determinar si un determinado elemento de una matriz ocupa una posición par o impar se deben tener en cuenta cuál es la fila y la columna que ocupa: la suma de ambos valores es la que define la paridad de dicho elemento. Algunas propiedades elementales, pero no demasiado conocidas o convenientemente disimuladas, sobre el cambio de paridad de los elementos de la matriz cuando se intercambian algunas filas o columnas han permitido crear diversos juegos de magia matemática, como los incluidos en aquel primer artículo y los que citaremos a continuación. Pero, antes de eso, hablaremos de una personalidad muy destacada en el universo mágico. Jim Steinmeyer, gran erudito, historiador de la magia (no hay que perderse su libro "Hiding the elephant: how magicians invented the impossible and learned to disappear") e imaginativo creador de ilusiones y efectos teatrales que han catapultado a la fama a personajes como Doug Henning, David Copperfield y otros, ha escrito (y sigue escribiendo) una colección de folletos dedicados a juegos de magia automática, muchos de ellos basados en propiedades matemáticas sencillas, con una denominación común: Impuzzibilities. Esta serie, cuyo primer número se publicó en 2002, ha tenido una continuidad muy notable gracias a la versatilidad de los juegos que se incluyen: Further Impuzzibilities (2006), Subsequent Impuzzibilities (2010), Ensuing Impuzzibilities (2013), Treacherous Impuzzibilities (2014), Devilish Impuzzibilities (2015), Unexpected Impuzzibilities (2017), Curious Impuzzibilities (2020) y Virtual Impuzzibilities (2020), por el momento. Toda la colección y el resto de su producción se puede adquirir a través de la editorial Hahne Books. Por cierto, ya hemos descrito algunos juegos de su primer libro en este rincón (por ejemplo, en el número 76 de octubre de 2010, en el número 83 de mayo de 2011, en el número 92 de marzo de 2012 o en el número 105 de mayo de 2013), lo que demuestra la estrecha relación de la magia y las matemáticas en toda la colección. En el cuarto folleto de la colección, titulado "Ensuing impuzzibilities", el autor describe un juego que el mago japonés Kuniyasu Fujiwara (especialista en el desarrollo de la relación entre la magia y el origami) publicó por primera vez en el volumen 63 (mayo de 2000) de la revista Genii: the Conjurors' Magazine bajo el título Automatic Aces, basado en el principio de los dobleces pero bien disimulado durante su desarrollo. Por ser un juego automático, se puede realizar a distancia siguiendo la lista de instrucciones siguiente: Busca los cuatro ases de la baraja y colócalos en una fila sobre la mesa, caras hacia arriba. Coloca tres cartas sobre cada as, todas ellas con las caras hacia abajo. Reúne los dos montones de la izquierda, mezcla el paquete de ocho cartas para perder los ases y deja sobre la mesa el nuevo montón. Realiza la misma operación con los dos montones de la derecha pero gira todo el paquete antes de dejarlo sobre la mesa. Recoge la carta superior del paquete de la izquierda, coloca sobre ella la carta superior del paquete de la derecha, coloca sobre ambas la carta superior del paquete de la izquierda y así sucesivamente, para volver a juntar todas las cartas en un solo montón. Reparte las cuatro primeras cartas sobre la mesa formando una fila, reparte las cuatro siguientes sobre las anteriores, una a una, y así sucesivamente hasta que hayas repartido cuatro manos de cuatro cartas. Coloca las cuatro cartas del montón de la izquierda sobre el montón que está a su derecha pero girando el paquete como si fuera un libro (los bordes laterales actúan como una bisagra); realiza la misma operación con este nuevo montón y luego sobre el último, siempre girando todas las cartas como si fueran páginas de un libro. Extiende todas las cartas: solo los ases están en un sentido, destacando así del resto. El hecho de recoger las cartas plegando cada montón sobre el siguiente es el que permite recuperar los ases en sentido contrario al resto de las cartas. El principio matemático que explica este resultado se conoce como "principio de los dobleces" (basado a su vez en el principio de paridad), planteado por primera vez en el juego de magia que Martin Gardner publicó con el título de "Paradox Papers" en la revista The Pallbearers Review, en julio de 1971, y que reproducimos en estas imágenes. No vamos a detallar el origen de este principio, que se remonta al menos al problema de determinar el número posible de dobleces que pueden realizarse en una tira de sellos, como planteó Henry Dudeney —considerado el mayor creador de rompecabezas británico por la calidad y cantidad de sus creaciones— en el libro de 1926 "Modern Puzzles and how to solve them" (disponible online en el portal Bodleian Libraries de la Universidad de Oxford) y republicado posteriormente en el libro "536 Puzzles and Curious Problems", editado por Martin Gardner en 1967. Al estudiar el problema, el propio Martin Gardner lo convirtió en el citado juego de magia, y posteriormente lo incluyó en la extensa recopilación "Martin Gardner Presents", publicado en 1993, y traducido por la editorial Páginas en 2019 en forma de trilogía: Matemagia, Cartomagia y Magia de Cerca. A lo largo del tiempo, muchas mentes brillantes de la magia han elaborado ingeniosas adaptaciones y novedosas variantes basadas en el principio de los dobleces. Sólo destacaré dos de ellas: Quadraplex, de Nick Trost (descrito en el volumen 3 de su libro "Subtle Card Creations", 2011) y Degrees of Freedom, de John Bannon (de su libro "Dear Mr. Fantasy", 2004). Bueno, una más: en el libro "The Violet Book of Mentalism", Phil Goldstein publicó el juego titulado Kirigami donde aplica el mismo principio utilizando letras en lugar de cartas o números. Pedro Alegría (Universidad del País Vasco - Euskal Herriko Unibertsitatea)

Jueves, 01 de Julio de 2021 | Imprimir | PDF |  Correo electrónico

8. 194. (Junio 2021) Conejos matemáticos

A simple vista, no parece que los conejos sean una especie animal que se caracterice por sus dotes matemáticas sino, más bien, por su capacidad reproductiva. Sin embargo, quien conoce algo de historia de las matemáticas relaciona rápidamente las palabras "conejos" y "matemáticas". No repetiré la historia del problema sobre la velocidad de reproducción de una familia de conejos, particulamente prolífica y longeva, que propuso Leonardo Pisano —popularmente conocido como Fibonacci— en su libro "Liber abaci" de 1202, porque es muy fácil encontrar abundante información sobre la misma, simplemente tecleando "origen de la sucesión de Fibonacci" en tu buscador favorito. En las imágenes adjuntas se muestran las traducciones al italiano y al inglés del problema original de los conejos de Fibonacci, realizadas por Luciano Ancora y Laurence Sigler, respectivamente. Después de tantos siglos, el término "conejo matemático" ha vuelto a la vida: en la prehistoria de los programas informáticos infantiles apareció un interesante y divertido juego con el que practicar las operaciones matemáticas básicas de una manera entretenida y dinámica. Dicho programa se llamaba (o se llama) «El conejo matemático», juego de ordenador desarrollado en 1986 por "The Learning Company" y dirigido a niños de 4 a 7 años de edad. Pertenecía a la colección "Aprender Jugando" de la serie "Conejo Lector" y poseía cuatro actividades diferentes, destinadas a practicar la numeración y operaciones de sumas y restas con números menores de 100. En la pantalla aparecía un circo con un conejo matemático que ejercía de anfitrión, guiando a los invitados por las distintas actividades, ofreciendo ayuda, indicando los errores cometidos y acumulando premios con los aciertos. Tenía cuatro diferentes entornos de trabajo: Cuenta con Calíope, Show de la cuerda floja, Show de la foca y Atrapa el globo. No sé si este programa fue la inspiración para el título del libro que escribió el matemático y mago Fernando Blasco "Un conejo matemático en la chistera" (2016, Editorial Síntesis) para la colección Descubrir la Ciencia, más tarde reeditado bajo el título "Como por arte de magia" (El País, 2019), esta vez dentro de la colección Grandes ideas de las matemáticas. Como es un excelente libro que trata sobre el tema estrella de este rincón, no será difícil encontrar entre sus páginas material interesante de magia matemática que puedas aprovechar, bien para disfrute propio, bien para entretener a tus allegados, bien como complemento a tu actividad didáctica. Entre la gran cantidad y variedad de juegos que se detallan en el libro, vamos a detenernos un poco en uno con cartas, de apariencia sencilla pero de gran recorrido en el mundo de la magia matemática, y que lleva por título "Una cuestión de orden". Busca una baraja, no importa que esté incompleta, y mézclala concienzudamente. Vas a elegir primero un número de forma libre y aleatoria: retira un pequeño paquete de cartas y cuéntalas. Aparta de momento estas cartas pero recuerda su número. Ahora elegirás una carta: reparte cartas, una a una y caras hacia abajo, desde la parte superior del paquete restante formando un montón sobre la mesa, mientras las cuentas. Cuando llegues al número que habías recordado, gira la carta que aparece en ese momento, fíjate en su valor y recuérdala, será la carta elegida. Sigue repartiendo cartas como antes hasta que hayas formado un paquete de quince cartas sobre la mesa. Muy bien, recoge las cartas de la mesa y colócalas, de nuevo caras hacia abajo, sobre las cartas de la mano. Por último, recoge las cartas del principio (con las que elegiste el número) y colócalas sobre el resto. En este momento, tu carta está perdida en la baraja. Sin embargo, creo que podré encontrarla. Reparte sobre la mesa tres filas de cinco cartas cada una, caras hacia arriba. Veo que no está tu carta entre ellas. Gira la siguiente: ¿es tu carta? El principio matemático en el que se basa este truco es una pequeña variación del llamado "principio de colocación automática", atribuido al legendario mago Edward Marlo (1913-1991), quien lo aplicó en un juego publicado en la revista The New Phoenix en agosto de 1955, aunque tiene sus raíces en juegos que se remontan a finales del siglo XVIII. Se comprende que la carta elegida puede aparecer en cualquier lugar determinado previamente por el mago, incluso en la posición que el propio espectador elija. En el ejemplo anterior, la carta elegida apareció en la posición 16 porque el número de cartas repartidas era 15. Si se reparten X cartas y se recogen las cartas como se indica en la descripción del juego, la carta elegida ocupará la posición X + 1. Hay muchas variantes y refinamientos de este principio pero, como son objeto de estudio entre los magos profesionales, van un poco más allá del cometido divulgativo que pretende ofrecer este rincón. Seguro que, si tienes interés, encontrarás información adicional al revisar en tu hemeroteca mágica. Pedro Alegría (Universidad del País Vasco - Euskal Herriko Unibertsitatea)

Miércoles, 02 de Junio de 2021 | Imprimir | PDF |  Correo electrónico

9. 193. (Mayo 2021) Combinatoria con cartas

La especialidad matemática llamada Combinatoria (que ya se ha asomado a este rincón en el número 159 de abril de 2018) tiene como punto de partida el desarrollo de técnicas eficientes para contar el número de elementos de un conjunto. Esto es fácil de hacer con los dedos si los conjuntos son pequeños pero muchos problemas interesantes, tanto de matemática "recreativa" como de matemática "seria", tratan con conjuntos muy grandes y no tan fáciles de identificar. Un par de ejemplos, uno fácil y uno difícil: ¿cuántos números menores de un millón son capicúas?; ¿cúantos números menores de un millón se pueden descomponer como suma de números consecutivos? Si eres asiduo a este rincón, ya sabrás que se pueden plantear muchos problemas de Combinatoria con una simple baraja de cartas, desde los clásicos ¿cuántas posibles ordenaciones pueden presentarse en una baraja? o ¿cuántas ordenaciones de una baraja hacen que los colores de las cartas estén alternados?, hasta los más elaborados, algunos de los cuales veremos a continuación. Por cierto, la imagen que encabeza el artículo corresponde a una solución de otro problema clásico ya que muestra una posible disposición de las 16 figuras de una baraja (incluyendo los ases) en forma de cuadrado greco-latino: no hay dos cartas del mismo palo ni del mismo valor en ninguna fila, ninguna columna y ninguna diagonal. ¿Cuántas posibles soluciones tiene este problema? En el artículo titulado "Impressions of Conway" (publicado en la revista The Sciences en 1994), el matemático y periodista científico Charles Seife observa que el famoso matemático (fallecido en 2020) John Horton Conway disfrutaba realizando ante sus allegados el siguiente juego (en cuya traducción he tenido que introducir algunas modificaciones obvias): John saca una baraja de su estuche y va pasando cartas de arriba abajo, una a una, mientras deletrea la palabra A-S (una carta por cada letra). Gira la siguiente carta y resulta que es un as. Deletrea a continuación la palabra D-O-S pasando nuevamente una carta de arriba abajo por cada letra. Al girar la siguiente carta, se trata de un dos. Entrega la baraja a su colega y le pregunta: ¿quieres probar? El colega deletrea la palabra T-R-E-S pero, al girar la siguiente carta, es un comodín. ¡No!, exclama John. Le arrebata la baraja y deletrea T-R-E-S y gira la siguiente carta: es un tres. Vuelve a pasar la baraja a su interlocutor y este deletrea la palabra C-U-A-T-R-O. De nuevo, la siguiente carta es un comodín. El juego continúa de la misma forma, la víctima siempre vuelve un comodín y John siempre vuelve la carta correcta. Por último, John recoge todas las cartas, las ordena adecuadamente y las guarda en el estuche, preparadas para el siguiente voluntario inocente. Seguro que no necesitas mi ayuda para descubrir el orden inicial de las cartas con las que conseguir este efecto. Por si acaso, te doy aquí una posible solución y algunas variantes. Parece que Alexander Kraus es el autor de este otro deletreo numérico, bastante impactante si se realiza con suficiente destreza: Busca una baraja y ordena todas las cartas como se indica en las figuras: ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀ Gira la primera carta y déjala sobre la mesa: As de Picas. Gira la siguiente y déjala sobre la mesa: Dos de Picas. Como es un dos, pasa una carta de arriba abajo y gira la siguiente, dejándola sobre la mesa: Tres de Picas. Como es un 3, pasa dos cartas de arriba abajo y gira la siguiente, dejándola sobre la mesa: Cuatro de Picas. Como es un 4, pasa tres cartas de arriba abajo y gira la siguiente, dejándola sobre la mesa: Cinco de Picas. Repite la misma operación, pasando tantas cartas de arriba abajo como el valor de la última carta girada, excepto la última, que se gira y se deja sobre la mesa. Así irán apareciendo todas las cartas, en orden, de los palos de picas, corazones y rombos. Por último, gira todas las cartas de la mano y aparecen en orden todas las cartas del palo de tréboles. Ya que citamos a Alexander Kraus, comentaremos el juego titulado «Sum total» que publicó como problema en el número 12 de la revista de magia Ibidem, en diciembre de 1957 (excelente añada), y cuya solución publicó en el número 13 de la misma revista, en marzo de 1958. El juego está basado en un principio matemático, conocido posteriormente con el nombre —cómo no— de principio de Kraus. Ordena la baraja como en el juego anterior. Ahora realiza la siguiente secuencia de movimientos: Corta para dejar el 3P como carta superior. Deja sobre la mesa, cara arriba, la primera carta. Deja en un segundo montón, contando cara abajo y una por una, tantas cartas como el valor de la última carta cara arriba (el as vale 1, la J vale 11, la Q vale 12 y la K vale 13). Como se trataba de un tres, reparte tres cartas en un montón. Gira cara arriba la carta superior de dicho montón. Repite la operación formando un tercer montón que tiene tantas cartas como el valor de la última carta cara arriba y gira la última carta de ese montón. Al terminar de repartir todas las cartas, suma los valores de las cartas que están cara arriba. El resultado es 52, igual al número de cartas de la baraja. El mismo resultado se obtiene si se empieza colocando como carta superior el 4P, 5P, …, 10P. La razón es que dichas cartas forman un ciclo al ser las únicas que se giran cara arriba durante el proceso descrito. En su artículo, Alexander Kraus demuestra que la ordenación propuesta tiene la propiedad de que, si se empieza el proceso con cualquier otra carta, en algún momento se alcanza una de las cartas del ciclo, de modo que, a partir de entonces, ya no se sale del ciclo. Comentarios finales Se puede probar que cualquier permutación de las 52 cartas debe contener algún ciclo: al empezar por cualquier carta y recorrer toda la baraja, si se termina en la primera carta, esta ya forma un ciclo; si no, esta carta no pertenece al ciclo. Al seguir la cuenta, se llegará a una carta por segunda vez. Esta ya pertenece al ciclo y, a partir de ella, ya no se sale del mismo. El ciclo más pequeño es el formado por los cuatro reyes, espaciados cada trece cartas, cuya suma es, evidentemente, igual a 52. Un método sencillo de conseguir un ciclo —como observó Tom Ransom en el mismo número 13 de «Ibidem»— es tener ordenadas en la parte inferior de la baraja trece cartas con valores ordenados del as al rey, siendo el as la carta inferior. Así cualquier recorrido llegará a una de estas cartas con la que se termina el ciclo. De hecho, con esta preparación, no importa el número de cartas que tiene el paquete pues la suma de los valores de las cartas giradas será igual al número de cartas de dicho paquete. Es posible que un ciclo tenga que recorrer la baraja más de una vez; en este caso, la suma de sus valores es igual a 52 multiplicado por el número de veces que se recorra la baraja. Es fácil destruir este ciclo eliminando una de sus cartas. En este caso, la suma final será 51. Una cuestión no resuelta es: ¿existe algún ciclo con el que se utilizan todas las cartas? Si fuera así, debe recorrer la baraja siete veces debido a que 7 x 52 = 364, que es la suma de todas las cartas. Un par de efectos que utilizan el principio de Kraus están ideados por el mago e informático Alex Elmsley (publicado en el segundo volumen de «The Collected Works of Alex Elmsley» de Stephen Minch en 1994) y por el banquero Arthur McTier (descrito en el libro «Card Concepts», publicado en 2000). En los años 70, el principio de Kraus se convirtió en el principio de Kruskal cuando el físico Martin Kruskal lo modificó ligeramente para convertirlo en un método de adivinación de una carta después de un proceso sugerido por la idea de Kraus, un camino pseudoaleatorio que converge a un lugar concreto de la baraja. De este modo, un tema de Combinatoria se convirtió en una cuestión relacionada con la Teoría de Probabilidades. El capítulo 12 del libro «Impossible?» de Julian Havil desarrolla la teoría de probabilidades necesaria para analizar el principio de Kruskal. En este rincón también rendimos cuentas a este principio, en el número 46, allá por enero de 2008. El Dr. Maths, seudónimo de Steve Humble (inventor del juego «Triangle Mysteries» que describimos en el número 185 de septiembre de 2020), realizó una actuación en Alchemist Cafe de Dublin (2010), donde presentó un juego basado en el principio de Kruskal, involucrando a varios espectadores. El video con esta entretenida presentación puede verse en YouTube. Pedro Alegría (Universidad del País Vasco - Euskal Herriko Unibertsitatea)

Martes, 04 de Mayo de 2021 | Imprimir | PDF |  Correo electrónico

10. 192. (Abril 2021) Magia en el aula

Al amparo de este rincón, en muchas ocasiones hemos destacado las propiedades didácticas de los juegos de magia matemática. También hemos querido señalar aquellos autores que han publicado material pedagógico con el que potenciar la enseñanza de las matemáticas a través de la magia (como, por ejemplo, en el número 179 de febrero de 2020 y en el número 144 de diciembre de 2016). Parece que esta tendencia es imparable y ya es constante el flujo de información relacionada con este tema y la gran diversidad de enfoques que los profesionales de la educación están desarrollando para aprovechar las bondades de la magia en la didáctica de las matemáticas. Esta vez quiero comentar dos de los últimos trabajos que he encontrado y me han parecido interesantes. El primero de ellos se titula "Mathematical Explorations of Card Tricks", su autor es Timothy Weeks de la Universidad John Carroll en Ohio (EEUU) y se ha publicado en el número 73 de Senior Honors Projects en la primavera de 2015. En la introducción, el autor recoge una famosa sentencia de Martin Gardner: «La magia matemática combina el aspecto académico de las matemáticas con el valor de entretenimiento de la magia». A lo largo de su trabajo, el autor recorre algunos juegos basados en ciertas propiedades combinatorias en las que se basa un determinado reparto de las cartas de una baraja, así como aplicaciones del principio del palomar o de la teoría de códigos correctores de errores. Los juegos seleccionados son adaptaciones de otros contenidos en el libro "Mathematical Card Magic", escrito por Colm Mulcahy y publicado por CRC Press el año 2013 pero proporciona las demostraciones matemáticas de los resultados obtenidos. El segundo artículo que quiero citar es el trabajo de Morgan Mitchell y Jay Cummings (aquí en la foto) titulado "When and how to use math based card tricks in the classroom", publicado en McNair Scholars Journal el año 2017. Con el fin de mejorar la percepción de los estudiantes sobre su propia habilidad en la comprensión de las matemáticas, su respuesta emocional hacia los retos que plantean y la ansiedad que produce su propia inseguridad, los autores desarrollan una colección de juegos de magia con cartas así como las explicaciones matemáticas en las que se apoyan. Pretenden así ofrecer a los educadores algunas herramientas con las que "reenganchar" a los estudiantes y mostrarles los aspectos lúdicos a la vez que formativos de la magia matemática. En este trabajo se cita el estudio titulado "Using Illusions in the Classroom: Principles, Best Practices, and Measurement" de Kevin Elder, David Deviney, Ronald MacKinnon y John Dyer (2012), quienes apuntaron cuatro principios básicos sobre el uso de la magia en el aula: No dejar que la ilusión sobrepase a la lección. Practicar antes de ejecutar. Nunca repetir un truco ante la misma audiencia. No explicar el truco porque no dejaría apreciar la ilusión y el misterio. No entraré a discutir la idoneidad de estas reglas básicas así que pasaré directamente a comentar algún juego de los que allí se proponen. Algunas versiones de la mayoría de los juegos que se incluyen en los dos artículos anteriores están tratados en este rincón así que he optado por mostrar algunas variantes del primer juego que enseñan Morgan Mitchell y Jay Cummings en su trabajo, que es básicamente el que apareció sin explicación en el número 7 nada menos que en julio de 2004. En el libro «The very best of Dai Vernon», de Richard Vollmer (escrito en francés), aparece esta versión titulada "Las cartas calculadoras". A grandes rasgos, este es el juego: Busca una baraja, comprueba que está completa (tiene las 52 cartas) y mézclala. Recoge la baraja con las caras hacia ti y reparte sobre la mesa, caras hacia abajo, varios montones de cartas, de la siguiente forma: Pasa de una mano a otra la carta superior y mira su valor. Pasa a continuación tantas cartas como hace falta para llegar a 13, una encima de otra formando un montón. Por ejemplo, si la carta superior es un 6, pasa a la otra mano siete cartas más; si es una dama, pasa una carta más (la dama cuenta como 12); si es un as, pasa 12 cartas más. La forma más sencilla es contar de una en una las cartas mientras las vas pasando de una mano a otra, empezando por el número de la primera carta y terminando en 13. Deja el montón así formado sobre la mesa, caras hacia abajo. Una vez que haya sobre la mesa unos seis o siete montones, selecciona tres de ellos. Retira los montones eliminados añadiéndolos al resto de cartas que te quedan en la mano. De los tres montones seleccionados, gira cara arriba la carta superior de dos de ellos. Suma sus valores y reparte, del paquete que tienes en la mano, tantas cartas como el valor de dicha suma. Reparte luego diez cartas más, porque me da la gana, y cuenta el número de cartas que quedan sin repartir. Dicho valor coincidirá con el de la carta superior del tercer montón que quedaba. Como indican los autores del trabajo citado, es una buena tarea para el estudiante hacer las operaciones necesarias con el fin de averiguar el funcionamiento del truco. Veamos: si las cartas superiores de los tres montones elegidos tienen valores desconocidos X, Y y Z, dichos montones contienen 14 - X, 14 - Y y 14 - Z cartas, respectivamente. En la mano tienes entonces 52 - (14 - X) - (14 - Y) - (14 - Z) = 10 + X + Y + Z cartas. Supongamos que el montón elegido es que tiene el valor X como carta superior. Al girar las cartas superiores de los otros dos montones, aparecerán los valores Y y Z. Se retiran entonces Y + Z cartas y, por último 10 cartas. Evidentemente, quedan únicamente X cartas. Otra versión, algo diferente, es la siguiente: Busca una baraja francesa (también completa) y selecciona nueve cartas. Deja el resto sobre la mesa. Elige una de esas nueve cartas, dejando las demás en un montón caras abajo sobre la mesa. Después de mirar y recordar la carta elegida, déjala sobre el montón de las ocho cartas no elegidas. Coloca el resto de la baraja sobre este montón. Recoge de nuevo la baraja completa y reparte la carta superior sobre la mesa, girándola cara arriba, diciendo "diez". Sobre ella reparte la segunda diciendo "nueve", y así sucesivamente hasta que aparezca una carta cuyo valor coincida con el número nombrado en ese momento. Esas cartas formarán el primer montón. Si has repartido la décima carta diciendo "uno" y no ha habido ninguna coincidencia, reparte una carta más cara abajo tapando dicho montón. En cualquiera de los casos, repite el mismo procedimiento tres veces más hasta que haya sobre la mesa cuatro montones. Suma entonces los valores de las cartas superiores de cada montón (si están cara arriba) y, con las cartas que tienes todavía en la mano, reparte tantas cartas como indica dicha suma. La última carta repartida será la que habías elegido inicialmente. Vayamos con la justificación del juego. Observemos en primer lugar que la carta elegida está en la posición 44 de la baraja (tiene sólo 8 cartas bajo ella). Al repartir cuatro montones, si no ha habido ninguna coincidencia, cada montón tiene 11 cartas, lo que hace un total de 44. La última carta es precisamente la elegida. Si el montón i-ésimo tiene ni cartas, el valor de la carta superior es 11 - ni. En total se han repartido n1 + n2 + n3 + n4 cartas. Al sumar los valores de las cartas superiores, se reparten 11 - n1 + 11 - n2 + 11 - n3 + 11 - n4 cartas, precisamente las que faltan para llegar a 44 cartas. Por cierto, si el paquete no está completo, basta restar de 9 el número de cartas que faltan para que funcione el juego. El mismo principio permite diversas adaptaciones como la siguiente (que es una variante del juego "Afinidades" publicado en el segundo volumen de "The Vernon Chronicles" por Stephen Minch). Busca una baraja completa (de 52 cartas) y mézclala. Teniendo las cartas con las caras hacia arriba, forma sobre la mesa varios montones de cartas, de la siguiente forma: pela la primera carta y fíjate en su valor (en lo sucesivo, las figuras cuentan como 10); empieza una cuenta mental con el valor de dicha carta; sigue pelando cartas, formando un paquete en la otra mano (dejando cada carta sobre la anterior), y siguiendo la cuenta mental, hasta que hayas pasado tantas cartas como sea necesario para llegar a doce. Un ejemplo: si la carta de cara es un siete, pásala a la otra mano empezando la cuenta por siete; al pasar la siguiente carta, cuenta "ocho"; pasa otra más contando "nueve"; otra más a la cuenta de "diez", una más a la cuenta de "once" y la última para llegar a "doce". Deja sobre la mesa, con las caras hacia abajo, el montón de cartas que has formado. Repite el proceso hasta dejar en la mesa un grupo de más de seis montones. No hace falta utilizar todas las cartas pero sí la mayoría de ellas. Selecciona cuatro montones volviendo cara arriba la carta superior de cada montón elegido. Retira los montones no elegidos y forma un paquete con todos ellos y con las cartas no utilizadas anteriormente. Recuerda que los valores de las cartas vueltas son completamente aleatorios ya que has mezclado la baraja y has elegido esos montones y no otros. Suma los valores de dichas cartas (recuerda que las figuras valen 10) y comprueba que las cartas tienen la habilidad de adelantarse a los acontecimientos. Resulta que la suma de los valores de las cuatro cartas elegidas coincide con el número de cartas que forman el paquete desechado. Comentarios finales: El principio utilizado en estos juegos es el llamado «principio del complemento a 13» o, por su nombre en inglés «10, 9, 8, ... Count», pero también podría llamarse el del complemento a doce o a cualquier otro número. Su origen es desconocido aunque apareció publicado el año 1593 en el libro "Giochi di carte bellissimi di regola e di memoria" de Horatio Galasso (en la imagen), tan antiguo que se puede disfrutar digitalizado en el Archivo de Internet (en este caso, se aplica el principio del complemento a 15, con una baraja de 48 cartas). En el libro "La pasión de un cartómago aficionado" de Pablo Nagata se detalla el gran recorrido y desarrollo que ha tenido esta simple propiedad matemática a lo largo de la historia de la magia. Este principio y otros similares han dado lugar a sucesivos refinamientos e ingeniosas adaptaciones. Quiero destacar las aportadas en los maravillosos libros "La magia pensada" y "Más magia pensada" del maestro Ramón Riobóo, cuya reciente pérdida seguimos lamentando. ¡Que tengas buen viaje, Ramón! Aunque ya sabemos que las casualidades no existen, cuando estaba a punto de dejar terminada esta reseña, la editorial Cossetània me hizo llegar un nuevo libro dedicado a las aplicaciones didácticas de la magia matemática. Se trata del titulado "100 jocs automàtics de matemàgia" escrito por Enric Ramiro y Pilar Gandía, que han dedicado toda su carrrera a la docencia. Como su título indica, recoge de manera estructurada una gran selección de juegos que podrán ser utilizados en el aula como material complementario a todos los niveles de educación básica. Seguro que un docente encontrará más de un juego con el que salir de la rutina diaria y motivar a sus estudiantes para interesarse en las matemáticas. Pedro Alegría (Universidad del País Vasco - Euskal Herriko Unibertsitatea)

Martes, 06 de Abril de 2021 | Imprimir | PDF |  Correo electrónico