1. 130. (Enero 2023) Grafos Parsimónicos para una Selección de Escalas Heptatónicas y Pentatónicas (2/2)

1. Introducción El presente artículo fue presentado en junio de este año 2022 en la Conferencia Internacional de Matemáticas y Computación en Música, celebrada en Atlanta (GA, USA). Para facilitar su difusión entre un conjunto de lectores lo más amplio posible se ha simplificado en cierta medida su parte más teórica, pero se han mantenido en su totalidad los resultados obtenidos. En todo caso, el artículo completo puede consultarse en la referencia indicada al final de este artículo (Nuño 2022a). La primera parte de este trabajo se ha dedicado a la selección de ocho tipos de escalas heptatónicas, al análisis de sus características armónicas y a la obtención de un grafo parsimónico, denominado 7-Cíclope, que relaciona dichas escalas mediante transformaciones monosemitonales. A continuación, se llevará a cabo un proceso análogo para las escalas pentatónicas y se estudiará la relación acústica existente entre las escalas heptatónicas y pentatónicas consideradas aquí. Finalmente, se incluye un ejemplo de análisis musical con escalas heptatónicas. En caso de duda sobre alguno de los conceptos utilizados aquí, se recomienda consultar los artículos de Nuño (2020, 2021a y 2021d), anteriormente publicados en esta misma página Web. Al igual que se hizo en la primera parte de este estudio, emplearemos la notación inglesa para las notas musicales (C=Do, D=Re, E=Mi, F=Fa, G=Sol, A=La y B=Si). 2. Escalas Pentatónicas En esta sección se va a realizar la selección, análisis armónico y desarrollo de un grafo parsimónico para escalas pentatónicas, mediante un proceso totalmente análogo al seguido para las heptatónicas. 2.1. Selección de las Escalas Pentatónicas Para mantener un completo paralelismo con las escalas heptatónicas previamente seleccionadas, tomaremos ahora como escalas pentatónicas las complementarias de aquellas. La Tabla 5 muestra estos tipos de escalas con sus nombres de Forte extendidos, los símbolos para representarlas, sus estructuras interválicas y sus vectores de clases de intervalos. Los símbolos de la forma “m…P” y “7…P” representan, respectivamente, variantes de las escalas pentatónica menor (mP) y pentatónica “dominante” (7P), cuyas estructuras interválicas son 32232 y 22332. Nótese que la escala “mP” es un modo de la escala pentatónica mayor (MP). Tabla 5. Tipos de Escalas Pentatónicas considerados aquí. Escala Pentatónica Símbolo Estructura Interválica Vector de Clases de Intervalos 5-22 5-30a 5-30b 5-32a 5-32b 5-33 5-34 5-35 mΔ♯4P mΔP Δ♯5P m♯4P 7♯9P 7♯5P 7P MP 33141 32241 42231 33132 31332 22422 22332 22323 202321 121321 121321 113221 113221 040402 032221 032140 Estos ocho tipos de escalas también pueden obtenerse de forma análoga a como se obtuvieron las escalas heptatónicas combinando las cuatro notas alteradas más cercanas a la tonalidad de partida. Sin embargo, dado que las escalas pentatónicas no definen tonalidades, hablaremos ahora de notas modificadas en lugar de alteradas. Así, si partimos de la escala de C pentatónica mayor, debemos determinar, en primer lugar, cuáles de sus notas, modificadas en un semitono, dan lugar a otras escalas pentatónicas mayores. Un sencillo análisis nos revela que hay únicamente dos posibilidades: elevar E a F, obteniendo FMP, o bien rebajar C a B, obteniendo GMP. Y, a continuación, repetimos este proceso para hallar las siguientes escalas pentatónicas más cercanas a ellas, obteniendo así la Tabla 6, que es análoga a la Tabla 3 de la primera parte de este estudio, pero para las escalas pentatónicas. Podemos comprobar que, efectivamente, obtenemos los mismos ocho tipos de escalas de la Tabla 5. Tabla 6. Escalas Pentatónicas obtenidas a partir de CMP combinando dos notas modificadas. Notas Modificadas - E → F A → B♭ E → F, A → B♭ - C → B G → F♯ C → B, G → F♯ CMP GMP D7P DMP FMP G7P D7♯9P Bm♯4P C7P Em♯4P D7♯5P BmΔP B♭MP G7♯9P F♯Δ♯5P BmΔ♯4P Las características armónicas de estas escalas se muestran en la Tabla 7, utilizando para ello los vectores de tipos de tricordos y de tetracordos. Esta tabla es análoga a la Tabla 4 de la primera parte de este estudio, pero para las escalas pentatónicas, y en ambas se han aplicado los mismos criterios. Tabla 7. Vectores de Tipos de Tricordos y de Tetracordos para las Escalas Pentatónicas. Escala Vector de Tipos de Tricordos Vector de Tipos de Tetracordos 5-22 000111111-0000001111 000000000010-000000000000000011110-0000000000 5-30a 000100110-1011110101 000000000000-000000000001001000100-0010100000 5-30b 000011001-1101110011 000000000000-000000000000110000010-0100100000 5-32a 000110010-0110101210 000000000000-000000000001000101000-0000001100 5-32b 000110001-0111001120 000000000000-000000000000100110000-0000001010 5-33 000000000-3003300001 000000000000-000000000000000000000-2000210000 5-34 000000000-2111111110 000000000000-000000000000000000000-1110000110 5-35 000000000-1220030110 000000000000-000000000000000000000-0112001000 2.2. 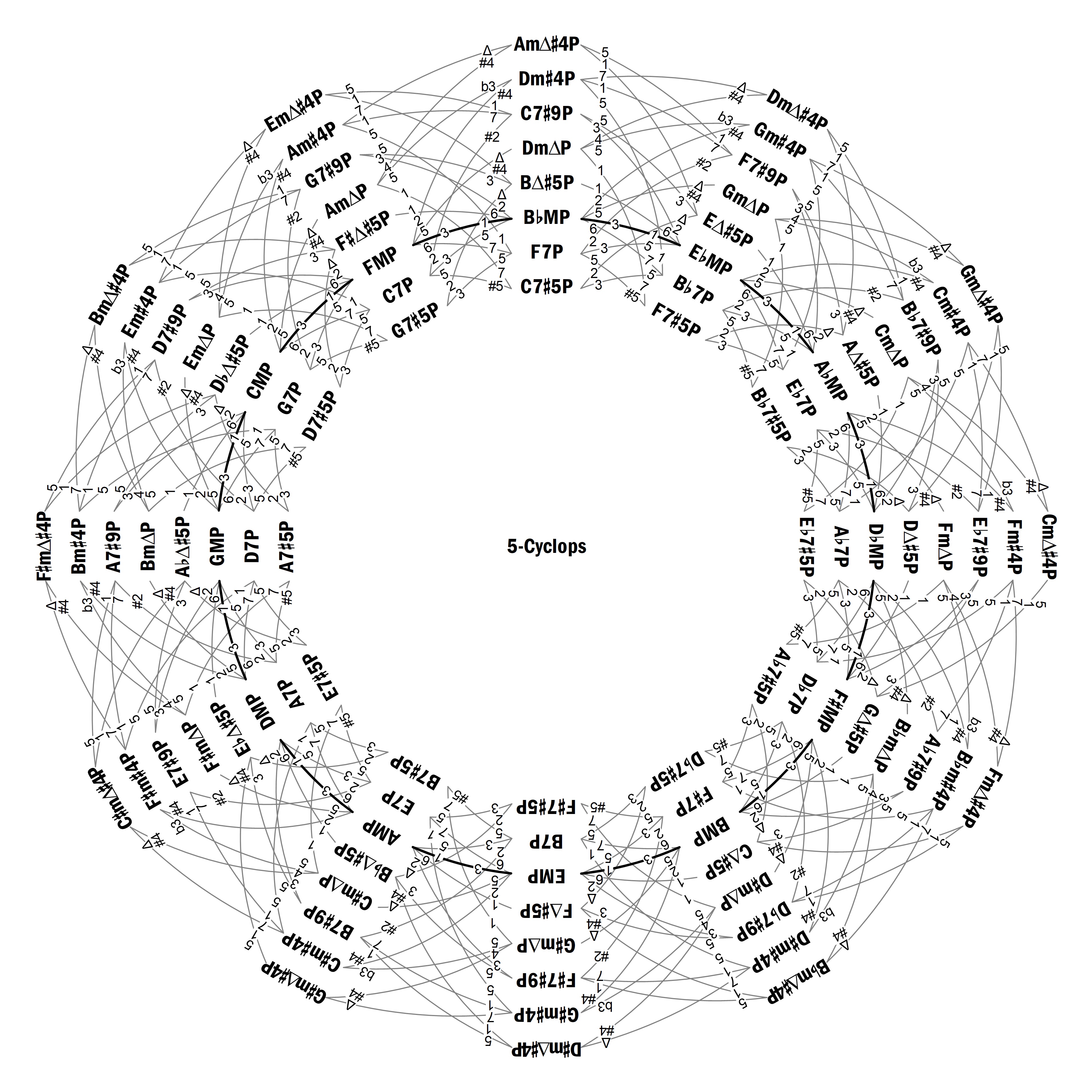Grafo Parsimónico para las Escalas Pentatónicas Seleccionadas La Figura 2 es un grafo cíclico circular que he denominado 5-Cíclope, que muestra todas las escalas pentatónicas de los tipos incluidos en la Tabla 5, conectadas mediante transformaciones monosemitonales. Dado que, si dos escalas están relacionadas mediante una transformación monosemitonal, también lo estarán sus complementarias, resulta que esta figura es completamente análoga a la Figura 1, y en ambas se han aplicado los mismos criterios. Puesto que los números 5 y 12 también son coprimos, en cada zona tenemos justamente una escala de cada tipo. Nótese que las escalas pentatónicas mayores son las únicas que pueden transformarse en otras de su mismo tipo, a la vez que los enlaces entre ellas forman ahora el ciclo de cuartas, que es la única circunferencia posible en este grafo (la línea gruesa). Fig. 2. El 5-Cíclope, con los tipos de escalas pentatónicas considerados en la Tabla 5. 2.3. Relación entre las Escalas Heptatónicas y Pentatónicas Seleccionadas Aparte de la relación de complementariedad que tenemos entre las escalas heptatónicas y pentatónicas consideradas aquí, existen entre ellas unas relaciones acústicas muy interesantes que pueden observarse mediante el vector de tipos de pentacordos, que es otra generalización del vector de tipos de intervalos. Este nuevo vector indica cuántos pentacordos (o escalas pentatónicas) de cada tipo contiene una escala dada. La Tabla 8 muestra este vector para las escalas heptatónicas incluidas en la Tabla 2 de la primera parte de este estudio, más el par 7-31a/7-31b considerado por Žabka (2014). En dicho vector, cada dígito corresponde a un tipo de escala pentatónica en el orden establecido por Nuño (2021c o, en español, 2020 y 2021a). Se han representado en negrita los dígitos correspondientes a las escalas pentatónicas consideradas aquí. Así, de izquierda a derecha, el primer dígito en negrita corresponde a la escala 5-22 y los últimos nueve dígitos (que están después de un espacio en blanco) corresponden a las escalas 5-30a, 5-30b, 5-31a, 5-31b, 5-32a, 5-32b, 5-33, 5-34 y 5-35. Tabla 8. Vector de Tipos de Pentacordos para diversas Escalas Heptatónicas. Escala Vector de Tipos de Pentacordos 7-22 0000000001100-000000000000001111111110011112-00000000001100 000011000 7-30a 0000000000100-010001000010001000001010011100-00110001110100 200010110 7-30b 0000000001000-001000100001001000010100011010-00110010111000 020001110 7-31a 0000000000000-000210000000000120000002100000-00002100002100 003021000 7-31b 0000000000000-000120000000000210000001200000-00001200001200 000312000 7-32a 0000000000000-000100000100000010100110001101-10001011010011 102110000 7-32b 0000000000000-000010000100000100100110010011-01000111100011 011201000 7-33 0000000000000-111000000011001000000000000000-00110011001100 110000610 7-34 0000000000000-000110000000000000100000000000-11111111001111 110000121 7-35 0000000000000-000000000100000000000000011000-22111100220011 000000013 Como podemos ver en la tabla, la escala 7-35 contiene tres escalas del tipo 5-35. Este es, además, el máximo número de escalas 5-35 contenidas en cualquiera de las diferentes escalas heptatónicas (no solo las incluidas en la tabla), ya que en el resto de los casos este número no es superior a dos. Así mismo, las escalas 7-34, 7-33 y 7-22 contienen, respectivamente, el máximo número de escalas 5-34, 5-33 y 5-22, que son 2, 6 y 2 (el resto de las escalas heptatónicas no contienen más de una en cada caso). En cuanto a los pares de escalas formados por un tipo a y un tipo b, debemos tener en cuenta que la complementaria de un tipo a es un tipo b y viceversa (Nuño 2021c o, en español, 2020 y 2021a). Entonces, las escalas 7-30a y 7-30b contienen, respectivamente, el máximo número de escalas 5-30a y 5-30b (es decir, las inversas de sus complementarias), que es dos (el resto de las escalas heptatónicas no contienen más de una), mientras que no contienen ninguna de sus correspondientes escalas complementarias. Así mismo, las escalas 7-31a y 7-31b contienen, respectivamente, el máximo número de escalas 5-31a y 5-31b, que es tres (el resto de las escalas heptatónicas no contienen más de dos) y tampoco contienen a sus correspondientes escalas complementarias. Pero, en cuanto al contenido en escalas 5-32a y 5-32b, resulta que son las escalas heptatónicas 7-31a y 7-31b las que contienen, respectivamente, el máximo número de ellas, que es dos (el resto de las escalas heptatónicas no contienen más de una). Por su parte, las escalas 7-32a y 7-32b contienen, respectivamente, una escala 5-32a y una 5-32b (de nuevo, las inversas de sus complementarias) y no contienen a sus correspondientes escalas complementarias. Por tanto, en todos estos casos existe, en mayor o menor medida, una clara relación acústica entre cada tipo de escala heptatónica y la inversa de su complementaria (que es pentatónica). 3. Ejemplo de Análisis Musical Žabka (2014) incluye en su artículo el análisis de un pasaje cromático muy interesante: la Fantasía en C menor, K. 475, de Mozart, compases 1–25. Para ello, determina cuáles son las escalas heptatónicas utilizadas en cada caso, aunque algunas de ellas aparecen de forma incompleta. 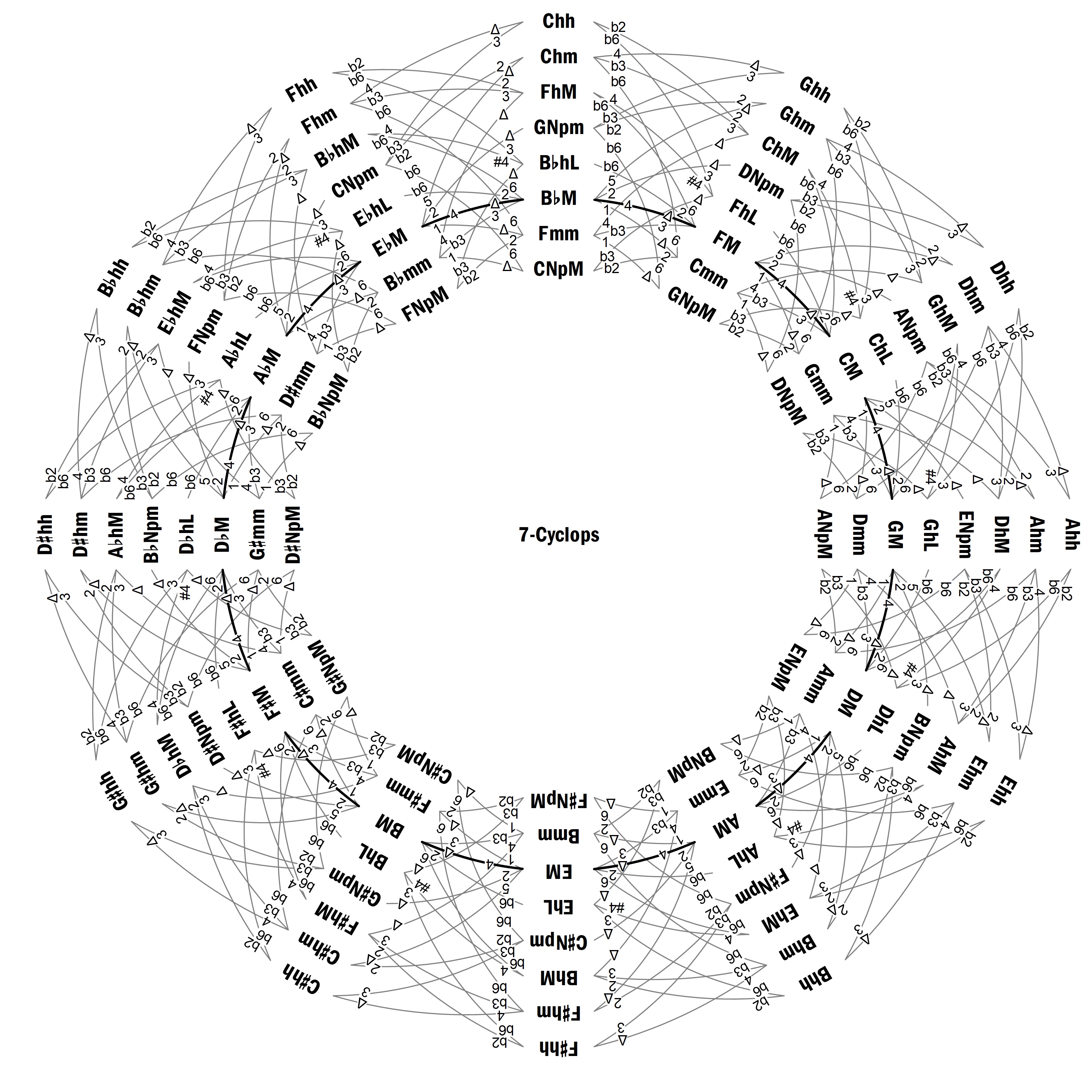Con la nomenclatura usada en el presente artículo, estas escalas son: Ghh  %  FhM  %  D♭M  E♭mm  FNpm  B♭hm  B♭Npm  BM  %  G♯Npm D♭hL  F♯Npm  C♭hL  BhM  Bhm  GM  %  %  F♯Npm–F♯hh  F♯hM  %  %  % donde cada escala o cada pareja de escalas unidas por un guión dura un compás y el símbolo “%” significa repetir el compás anterior. Las representaciones de este pasaje realizadas por Žabka (2014) presentan algunas complicaciones y pueden compararse con la que se muestra en la Figura 3 en el 7-Cíclope, el cual contiene todas las escalas requeridas, y donde la primera de ellas se ha indicado con una línea doble. Aunque la composición está en C menor, Mozart no incluye ninguna alteración en la armadura; y, como se aprecia en la Figura 3, no se utiliza ninguna de las escalas Chm, Cmm o C menor natural (E♭M). No obstante, la escala inicial, Ghh, contiene el acorde de C menor, cuyo arpegio se ejecuta empezando justamente por la nota C (cuarto modo de Ghh). A partir de ahí, las escalas se mueven en el diagrama en sentido antihorario, es decir, en la dirección de los bemoles (con algunos movimientos hacia delante y hacia atrás), hasta llegar a GM, cuya tónica (en el bajo) es la dominante de C. Sin embargo, la resolución no se hace sobre una escala de C menor, sino sobre varias escalas de tónica F♯, que está a un intervalo de tritono de C, y los últimos cuatro compases están basados, de hecho, en el acorde de F♯ mayor. Fig. 3. Mozart, Fantasía en C menor, K. 475, compases 1–25. Análisis con el 7-Cíclope. 4. Conclusiones e Información Adicional Como conclusiones del artículo completo, podemos decir que, siguiendo unos criterios puramente musicales, se han seleccionado ocho tipos de escalas heptatónicas y sus complementarias pentatónicas. Sus características armónicas se han analizado mediante los vectores de clases de intervalos, de tipos de tricordos y de tipos de tetracordos. Además, se han desarrollado dos nuevos grafos parsimónicos, denominados 7-Cíclope y 5-Cíclope, que relacionan cada uno de estos tipos de escalas mediante transformaciones monosemitonales. En estos grafos destacan, respectivamente, los ciclos de quintas y de cuartas, que son las únicas circunferencias posibles que conectan escalas del mismo tipo en esta clase de grafos (aparte de los casos triviales de escalas de una u once notas). Por otra parte, se ha encontrado una relación acústica entre cada escala heptatónica y la inversa de su complementaria, utilizando para ello el vector de tipos de pentacordos. Finalmente, se ha incluido un ejemplo de aplicación al análisis musical de una obra bastante compleja, por lo que toda esta información se estima que puede ser de interés tanto para teóricos como para compositores. Los lectores interesados en los tipos de vectores utilizados aquí, tanto para el caso del sistema de afinación temperado de doce notas como para otros sistemas más generales, pueden encontrar información adicional en Nuño (2022b). En ese artículo se presenta un riguroso estudio considerando la división de la octava en un número arbitrario de notas n y se incluyen diferentes teoremas que proporcionan una visión global y un conocimiento detallado de estos tipos de vectores.   Referencias Balzano, G. 1980. “The Group-Theoretic Description of 12-Fold and Microtonal Pitch Systems”. Computer Music Journal 4 (4), 66–84. Cohn, R. 1996. “Maximally Smooth Cycles, Hexatonic Systems, and the Analysis of Late-Romantic Triadic Progressions”. Music Analysis 15 (1), 9–40. Cohn, R. 2012. Audacious Euphony: Chromatic Harmony and the Triad’s Second Nature. New York: Oxford University Press. Douthett, J., Steinbach, P. 1998. “Parsimonious Graphs: A Study in Parsimony, Contextual Transformations, and Modes of Limited Transposition”. Journal of Music Theory 42 (2), 241–263. Forte, A. 1973. The Structure of Atonal Music. New Haven: Yale University Press. Hook, J. 2011. “Spelled Heptachords”. En: Agon, C., et al. (eds.) Mathematics and Computation in Music 2011, pp. 84–97. Heidelberg: Springer. Nuño, L. 2020. “La Tabla Periódica Musical (1/2).” DIVULGAMAT, Centro virtual de divulgación de las matemáticas, RSME: Real Sociedad Matemática Española, No. 111. Diciembre 2020. https://www.divulgamat.net/index.php?option=com_content&view=article&id=18500&directory=67 Nuño, L. 2021a. “La Tabla Periódica Musical (2/2).” DIVULGAMAT, Centro virtual de divulgación de las matemáticas, RSME: Real Sociedad Matemática Española, No. 112. Enero 2021. https://www.divulgamat.net/index.php?option=com_content&view=article&id=18516&directory=67 Nuño, L. 2021b. Parsimonious Graphs for the Most Common Trichords and Tetrachords. Journal of Mathematics and Music 15(2), 125–139 (2021). Nuño, L. 2021c. A Detailed List and a Periodic Table of Set Classes. Journal of Mathematics and Music 15(3), 267–287. Nuño, L. 2021d. “Grafos Parsimónicos para los Tricordos y Tetracordos más Comunes.” DIVULGAMAT, Centro virtual de divulgación de las matemáticas, RSME: Real Sociedad Matemática Española, No. 119. Octubre 2021. https://divulgamat.net/index.php?option=com_content&view=article&id=18666&directory=67 Nuño, L. 2022a. “Parsimonious Graphs for Selected Heptatonic and Pentatonic Scales”. En: Montiel, M., Agustín-Aquino, O.A., Gómez, F., Kastine, J., Lluis-Puebla, E., Milam, B. (eds) Mathematics and Computation in Music. MCM 2022. Lecture Notes in Computer Science, vol 13267. Springer, Cham. https://doi.org/10.1007/978-3-031-07015-0_3 Nuño, L. 2022b. “Type and Class Vectors and Matrices in ℤn. Application to ℤ6, ℤ7 and ℤ12.” Journal of Mathematics and Music. https://www.tandfonline.com/doi/full/10.1080/17459737.2022.2120214 Piston, W. 1988. Harmony. 5th edn. New York: W. W. Norton and Co. Popley, H. A. 1921. The Music of India. London: Oxford University Press. Ring, I. 2022 (15 marzo). The Exciting Universe of Music Theory, https://ianring.com/musictheory/scales/ Schönberg, A. 1983: Theory of Harmony. 3rd edn. Berkeley, Calif.: University of California Press. Tymoczko, D. 2011. A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice. New York: Oxford University Press. Žabka, M. 2014. “Dancing with the Scales: Subchromatic Generated Tone Systems”. Journal of Music Theory 58 (2), 179–233.

Domingo, 01 de Enero de 2023 | Imprimir | PDF |  Correo electrónico

2. 129. (Diciembre 2022) Grafos Parsimónicos para una Selección de Escalas Heptatónicas y Pentatónicas (1/2)

Tenemos otra vez más el placer de contar como autor invitado a Luis Nuño, que ya ha escrito en esta columna anteriormente. Luis Nuño es catedrático de universidad en la Universidad Politécnica de Valencia y autor de la Rueda Armónica. Es un gran investigador de la teoría matemática y computacional de la música así como un divulgador de la misma. Ha publicado varios artículos de investigación en la prestigiosa revista Journal of Mathematics and Music. Siguiendo con su trabajo de grafos parsimónicos, esta vez estudia dichos grafos sobre escalas heptatónicas y pentatónicas. Este trabajo que trae a Divulgamat consta de dos partes; la segunda la veremos en enero. De nuevo, estamos ante un artículo iluminador y profundo. Espero que los lectores de esta columna lo disfruten tanto como lo he hecho al leerlo. Paco Gómez Martín 1. Introducción El presente artículo fue presentado en junio de este año 2022 en la Conferencia Internacional de Matemáticas y Computación en Música, celebrada en Atlanta (GA, USA). Para facilitar su difusión entre un conjunto de lectores lo más amplio posible se ha simplificado en cierta medida su parte más teórica, pero se han mantenido en su totalidad los resultados obtenidos. En todo caso, el artículo completo puede consultarse en la referencia indicada al final de este artículo (Nuño 2022a). La escala mayor es la base de la música occidental. Por ello, aunque pueda parecer superfluo, conviene revisar algunas de sus principales características. Se trata de un conjunto de siete notas que guardan entre sí una gran afinidad acústica, de manera que es muy “completo y versátil”. Así, muchas canciones populares – y no tan populares – están compuestas en una tonalidad mayor. Nuestra notación musical, basada en el pentagrama y las armaduras, es idónea para escribir música en las tonalidades mayores. El piano, considerado el “instrumento rey”, está perfectamente adaptado para tocar en la tonalidad de Do mayor. Los nombres de las notas son siete – en lugar de doce –, precisamente las de la escala de Do mayor. El término octava (derivado de “ocho”) indica su extensión (repitiendo la tónica al final), mientras que los términos tono y semitono describen los intervalos entre dos de sus notas sucesivas. Así mismo, la calificación de los intervalos (justo, mayor, menor, etc.) se establece tomando como referencia una escala mayor. En resumen, la escala mayor es fundamental en teoría de la música y composición. Además, a partir de la escala mayor pueden obtenerse directamente otros tipos de escalas. Por ejemplo, tomando cualquiera de sus notas como como tónica, obtenemos siete modos, de los cuales el eólico constituye la escala menor, que es también característica de la música occidental. En este caso, sus grados sexto y séptimo pueden ser naturales o alterados (elevados un semitono), lo que da lugar a las escalas menores natural, melódica y armónica. Por otra parte, la escala complementaria de una escala mayor (es decir, la formada por el resto de las doce notas) es una escala pentatónica mayor. En general, las escalas pentatónicas – y no solo la pentatónica mayor – han sido utilizadas por diferentes culturas desde la antigüedad. Aunque son predominantes en los países del este (China, Japón, India, Java, etc.), también se han empleado en diferentes estilos occidentales, tanto en la música clásica como en la escocesa, andina, jazz, etc. Este estudio está basado en el sistema de afinación temperado de doce notas, utilizándose como nomenclatura los nombres de Forte y las clases de conjuntos (Forte 1973), que aquí llamaremos clases de escalas. De entre ellas, las no inversionalmente simétricas se dividen en dos tipos de escalas relacionados entre sí por inversión, llamados a y b, de acuerdo con Nuño (2021c o, en español, 2020 y 2021a). Con respecto a las escalas mayor y pentatónica mayor podemos decir que son las escalas de siete y cinco notas, respectivamente, que tienen sus notas más uniformemente espaciadas. Y, además, poseen una propiedad exclusiva: aparte de los casos triviales de las escalas de una u once notas, son las únicas que pueden transformarse en otras de su mismo tipo mediante una transformación monosemitonal (es decir, cambiando una sola nota y solo un semitono, que puede ser ascendente o descendente). Por ejemplo, subiendo en la escala de Do mayor la nota Fa un semitono obtenemos la escala de Sol mayor. Esta propiedad, para el caso de las escalas mayores, da lugar al orden de los sostenidos y los bemoles, así como al ciclo de quintas (Balzano 1980, Cohn 1996), que es fundamental en la teoría de la modulación, es decir, el cambio de una tonalidad a otra. En este sentido, dada una tonalidad, las más “cercanas” a ella son las que tienen un sostenido o un bemol de más o de menos en su armadura (Schönberg 1983, Piston 1988). Esto también es aplicable a las tonalidades menores, ya que sus armaduras son las mismas que las de sus relativas mayores. El concepto de transformación parsimónica es algo más general, ya que, en este caso, son una o más notas las que cambian en uno o dos semitonos (en la práctica, no más de dos semitonos en total), mientras el resto permanecen fijas (Douthett y Steinbach 1998). A este respecto, el Tonnetz es una primera representación de este tipo de transformaciones para las tríadas mayores y menores, mientras que Douthett y Steinbach (1998) presentan otros grafos más complejos e interesantes. En el s. XIX, diversos compositores hacen un uso extensivo de este tipo de transformaciones, varias de cuyas obras son analizadas por Cohn (2012). Por su parte, Tymoczko (2011) sigue un planteamiento distinto, representando los conjuntos de notas en unos espacios particulares denominados orbifolds. En cambio, Nuño (2021b o, en español, 2021d) desarrolla unos grafos cíclicos circulares, llamados Cíclopes, que relacionan los tricordos y tetracordos “más comunes”, mediante los cuales se puede analizar de forma práctica un buen número de dichos tipos de obras. En este artículo se presentan dos nuevos grafos similares a ellos para relacionar diferentes escalas heptatónicas y pentatónicas. En cada caso, se han seleccionado ocho tipos de escalas siguiendo unos criterios puramente musicales. Además, muestran de forma gráfica un resultado anteriormente mencionado: el ciclo de quintas para las escalas mayores, que es complementado con el ciclo de cuartas para las escalas pentatónicas mayores, los cuales corresponden a las únicas circunferencias posibles que conectan escalas del mismo tipo en estas clases de grafos (Balzano 1980, Cohn 1996). Este trabajo consta de dos partes, la primera de las cuales se dedica a las escalas heptatónicas y la segunda a las pentatónicas, en la cual se estudiará también la relación acústica existente entre ambas y se incluye, además, un ejemplo de análisis musical con escalas heptatónicas. En caso de duda sobre alguno de los conceptos utilizados aquí, se recomienda consultar los artículos de Nuño (2020, 2021a y 2021d), anteriormente publicados en esta misma página Web. 2. Selección de las Escalas Heptatónicas La música tonal está basada en las escalas mayor, menor melódica y menor armónica (Schönberg 1983, Piston 1988), cuyos nombres de Forte “extendidos” son 7-35, 7-34 y 7-32a, respectivamente. Para completar esta serie numérica podemos considerar también las escalas 7-32b (mayor armónica) y 7-33 (napolitana mayor, según la nomenclatura de Ring 2022). Estas son, además, las escalas heptatónicas cuyas notas están más uniformemente espaciadas, sobre todo la escala mayor (7-35). Para obtener otras escalas heptatónicas a partir de ellas podemos, simplemente, descomponerlas en tetracordos (entendidos ahora como grupos de cuatro notas consecutivas) y combinar dos de ellos. Este es el procedimiento utilizado, por ejemplo, en la música tradicional de India para obtener las escalas heptatónicas denominadas “Melakarta ragas” (Popley 1921). Otra opción es partir de una escala mayor y elevar o rebajar una o más notas un semitono, tal como se hace con la escala menor natural para obtener las escalas menores armónica y melódica. En este caso, lo lógico es tomar las notas alteradas de las tonalidades más cercanas a la considerada. A continuación, usaremos ambos procedimientos para obtener un número “razonable” de escalas heptatónicas que nos permitan obtener unos grafos de complejidad aceptable y que pueden ser de interés para teóricos y compositores. Por otra parte, en adelante emplearemos la notación inglesa para las notas musicales (C=Do, D=Re, E=Mi, F=Fa, G=Sol, A=La y B=Si). 2.1. Combinaciones de dos Tetracordos Consideremos la escala de C mayor. Podemos ver que está compuesta por los tetracordos C – D – E – F y G – A – B – C, donde el primero de ellos comienza por la nota C y el segundo por G. En ambos casos, sus “estructuras interválicas”, en semitonos, son iguales: 221, siendo el intervalo entre los dos tetracordos de 2 semitonos. Por tanto, podemos escribir la estructura interválica de la escala completa como 221 2 221 y al tetracordo 221 lo llamaremos “mayor”. Si empezamos esa misma escala por las notas D o A, las primeras cuatro notas formarán un tetracordo de la forma 212, que llamaremos “menor”. Si, en cambio, empezamos por las notas E o B, resulta un tetracordo del tipo 122, que llamaremos “frigio”. Y, por último, si empezamos por la nota F, obtenemos un tetracordo del tipo 222, que llamaremos “lidio”. Así, podemos obtener diferentes escalas heptatónicas combinando dos cualesquiera de estos cuatro tetracordos. Pero, para obtener las escalas armónicas, tanto mayores como menores, necesitamos otro tipo de tetracordo: el 131, que llamaremos “armónico”. La Tabla 1 muestra las 25 posibles combinaciones de dos de estos cinco tipos de tetracordos. Se indican también las estructuras interválicas de las escalas resultantes, así como los nombres y símbolos usados para representarlas. Los nombres menos comunes se han tomado de Ring (2022) y se ha utilizado el mismo nombre para todos los modos de una misma escala. Además, en todos los casos, el intervalo entre los dos tetracordos se ha elegido de manera que la primera y la última nota de cada escala sea la misma. Es decir, que la suma de todos los semitonos en cada escala sea igual a 12. Tabla 1. Tipos de escalas heptatónicas obtenidas combinando dos de los cinco tetracordos considerados aquí, junto con sus correspondientes estructuras interválicas. Los símbolos utilizados para representar las escalas son: M: mayor, mm: menor melódica, hm: menor armónica, hM: mayor armónica, NpM: napolitana mayor, Npm: napolitana menor, hL: lidia armónica, hh: doble armónica o húngara y WT: escala de tonos. 1º ↓ \ 2º → mayor menor frigio lidio armónico mayor 221 2 221 M 221 2 212 M 221 2 122 mm 221 1 222 NpM 221 2 131 hM menor 212 2 221 mm 212 2 212 M 212 2 122 M 212 1 222 mm 212 2 131 hm frigio 122 2 221 NpM 122 2 212 mm 122 2 122 M 122 1 222 M 122 2 131 Npm lidio 222 1 221 M 222 1 212 mm 222 1 122 NpM 222 222 WT 222 1 131 hL armónico 131 2 221 hL 131 2 212 hM 131 2 122 hm 131 1 222 Npm 131 2 131 hh Como podemos ver, la combinación de dos tetracordos lidios da lugar a la escala de tonos (WT), que solo tiene seis notas, por lo que no la incluiremos en este estudio. El resto de las combinaciones dan lugar a ocho tipos diferentes de escalas, entre las que se encuentran las cinco mencionadas al principio de la Sección 2, siendo, además, un número adecuado (ni muy grande ni muy pequeño) para desarrollar los grafos parsimónicos deseados. La Tabla 2 muestra estos tipos de escalas con sus nombres de Forte extendidos, los símbolos para representarlas y sus estructuras interválicas. La última columna es el vector de clases de intervalos, que consta de seis dígitos que indican correlativamente cuántos intervalos de cada clase (de 1 a 6 semitonos) contiene la escala considerada. Así, por ejemplo, este vector indica que la escala mayor (7-35) contiene “2” intervalos de 1 semitono, “5” intervalos de 2 semitonos, “4” intervalos de 3 semitonos, “3” intervalos de 4 semitonos, “6” intervalos de 5 semitonos y “1” intervalo de 6 semitonos. Tabla 2. Tipos de Escalas Heptatónicas considerados aquí. Escala Heptatónica Símbolo Estructura Interválica Vector de Clases de Intervalos 7-22 hh 1312131 424542 7-30a Npm 1222131 343542 7-30b hL 2221131 343542 7-32a hm 2122131 335442 7-32b hM 2212131 335442 7-33 NpM 1222221 262623 7-34 mm 2122221 254442 7-35 M 2212221 254361 2.2. Combinaciones de las Notas Alteradas pertenecientes a las Tonalidades más Cercanas Consideremos de nuevo la escala de C mayor. Sus dos tonalidades más cercanas, siguiendo tanto el orden de los sostenidos como el de los bemoles, dan lugar a las notas alteradas F♯, C♯, B♭ y E♭. Así, partiendo de la escala de C mayor y utilizando estas cuatro notas, bien naturales o alteradas, resultan 16 combinaciones, las cuales se muestran en la Tabla 3, junto con las escalas resultantes. Como puede verse, obtenemos los mismos ocho tipos de escalas heptatónicas que con el procedimiento anterior. Además, de acuerdo con el studio de Hook (2011), estas son justamente las escalas que tienen un “span” menor o igual que 10. Por todo ello, estos serán los tipos de escalas heptatónicas que consideraremos en este estudio y cuyas principales características están recogidas en la Tabla 2. Tabla 3. Escalas Heptatónicas obtenidas a partir de CM combinando dos notas alteradas. Notas Alteradas - F → F♯ C → C♯ F → F♯, C → C♯ - CM GM Dmm DM B → B♭ FM Gmm Dhm DhM E → E♭ Cmm GhM DNpM GhL B → B♭, E → E♭ B♭ M Ghm DNpm Dhh 2.3. Características Armónicas de las Escalas Heptatónicas Seleccionadas Para analizar las características armónicas de las escalas heptatónicas seleccionadas podemos utilizar dos generalizaciones del vector de clases de intervalos: el vector de tipos de tricordos y el vector de tipos de tetracordos, los cuales indican, respectivamente, cuántos tricordos y tetracordos de cada tipo contiene la escala considerada. La Tabla 4 muestra estos vectores para las escalas seleccionadas, donde cada uno de sus dígitos corresponde a un tipo de acorde en el orden establecido por Nuño (2021c o, en español, 2020 y 2021a). Así, por ejemplo, los primeros dígitos del vector de tipos de tricordos, de derecha a izquierda, corresponden a las tríadas aumentada, mayor, menor y disminuida. Y los primeros dígitos del vector de tipos de tetracordos, también de derecha a izquierda, corresponden al acorde de séptima disminuida, acorde de séptima de dominante, acorde semidisminuido (o de séptima de sensible) y acorde menor con séptima menor. Los dígitos en negrita corresponden a los tricordos y tetracordos “más comunes”, según el artículo de Nuño (2021b o, en español, 2021d). Tabla 4. Vectores de Tipos de Tricordos y de Tetracordos para las Escalas Heptatónicas. Escala Vector de Tipos de Tricordos Vector de Tipos de Tetracordos 7-22 111333322-0112212331 000111110220-000110011111111222222-0000011110 7-30a 111212321-3123321321 010001110110-011010011112012101202-2120211110 7-30b 111123212-3213321231 001010110110-011100011110221110022-2210211110 7-32a 022222221-1221224321 000100000110-111212112011011112211-0011101211 7-32b 022222212-1222124231 000100000110-111121221100111121121-0101101121 7-33 111111111-6116611112 011000110000-011110000111111000110-6110630110 7-34 022111111-3333332221 000100000000-211111111111111000110-2222211220 7-35 022002211-3441151330 000000000010-222001122110011000002-1334003110 3. Grafo Parsimónico para las Escalas Heptatónicas Seleccionadas La Figura 1 es un grafo cíclico circular que he denominado 7-Cíclope, que muestra todas las escalas heptatónicas de los tipos considerados en la Tabla 2, conectadas mediante transformaciones monosemitonales. Así, se pasa de una escala a otra adyacente cambiando una nota un semitono, el cual puede ser ascendente, si giramos en sentido horario, o descendente, si lo hacemos en sentido antihorario. Los números que hay en los extremos de las líneas que conectan las escalas indican las notas inicial y final referidas a las tónicas de estas escalas, donde 1 a 6 representan intervalos justos o mayores, que pueden alterarse mediante ♯ o ♭, mientras que las séptimas mayores y menores se representan mediante Δ y 7, respectivamente. Haciendo una analogía con la carátula de un reloj, cada acorde se ha colocado en una “zona”, que viene definida por “la suma de sus notas”, módulo 12 (Cohn 2012, p. 102). Así, por ejemplo, la escala CM = (C, D, E, F, G, A, B) está en la zona 0 + 2 + 4 + 5 + 7 + 9 + 11 = 2 (mod 12) y, análogamente, la escala B♭ M = (B♭ , C, D, E♭, F, G, A) está en la zona 0. De esta manera, si se sube o baja un semitono una nota de una escala, pasamos a la siguiente zona girando en sentido horario o antihorario, respectivamente. Y las escalas relacionadas por movimiento puramente contrario, como CM y Dhm = (D, E, F, G, A, B♭ , C♯) están en la misma zona (en este caso, 2). Puesto que los números 7 y 12 son coprimos, en cada zona tenemos justamente una escala de cada tipo. Nótese que las escalas mayores son las únicas que pueden transformarse en otras de su mismo tipo, a la vez que los enlaces entre ellas forman el ciclo de quintas, que es la única circunferencia posible en este grafo (la línea gruesa). Fig. 1. El 7-Cíclope, con los tipos de escalas heptatónicas considerados en la Tabla 2. En cuanto a otros diagramas similares, tenemos el desarrollado por Tymoczko (2011, p. 136), el cual incluye las escalas mayores (que llama diatónicas), las menores melódicas (que llama acústicas y cuya tónica es la cuarta justa de la correspondiente escala menor melódica), las menores y mayores armónicas, más otras tres escalas no heptatónicas y con simetría transposicional: la escala de tonos (6-35), la hexatónica (6-20, también llamada aumentada) y la octatónica (8-28, también llamada disminuida semitono/tono), cuyas estructuras interválicas son, respectivamente, 222222, 131313 y 12121212. En este caso, para colocar adecuadamente todas estas escalas se utilizan 36 posiciones angulares que, lógicamente, no pueden coincidir con las zonas consideradas aquí, a la vez que no se indican las notas que cambian de una escala a otra. Así mismo, algunas de estas escalas están repetidas varias veces dentro del diagrama. Otro trabajo relevante es el publicado por Žabka (2014), que está basado en lo que denomina “series de transición comática”, y que incluye, además de las escalas de la Tabla 2, el par 7-31a/7-31b y las escalas de tonos con una nota enarmónica adicional. Estas escalas las distribuye en tres diagramas diferentes, por lo que no se muestran las conexiones existentes entre algunas de ellas, a la vez que tampoco se indican las notas que cambian de una escala a otra. Por otra parte, la nomenclatura utilizada para algunas de estas escalas es distinta de la empleada aquí. 4. Conclusiones Siguiendo unos criterios puramente musicales se han seleccionado ocho tipos de escalas heptatónicas. Sus características armónicas se han analizado mediante los vectores de clases de intervalos, de tipos de tricordos y de tipos de tetracordos. Además, se ha desarrollado un nuevo grafo parsimónico, denominado 7-Cíclope, que relaciona todas esas escalas mediante transformaciones monosemitonales. En este grafo destaca claramente el ciclo de quintas, que es la única circunferencia posible que conecta escalas del mismo tipo en este grafo. En la segunda parte de este trabajo se llevará a cabo un proceso análogo para las escalas pentatónicas y se estudiará la relación acústica existente entre las escalas heptatónicas y pentatónicas consideradas aquí. Además, se incluirá un ejemplo de análisis musical con escalas heptatónicas. Finalmente, para los lectores interesados en un estudio más general de los vectores empleados en este estudio, se recomienda el artículo de Nuño (2022b), recientemente publicado.   Referencias Balzano, G. 1980. “The Group-Theoretic Description of 12-Fold and Microtonal Pitch Systems”. Computer Music Journal 4 (4), 66–84. Cohn, R. 1996. “Maximally Smooth Cycles, Hexatonic Systems, and the Analysis of Late-Romantic Triadic Progressions”. Music Analysis 15 (1), 9–40. Cohn, R. 2012. Audacious Euphony: Chromatic Harmony and the Triad’s Second Nature. New York: Oxford University Press. Douthett, J., Steinbach, P. 1998. “Parsimonious Graphs: A Study in Parsimony, Contextual Transformations, and Modes of Limited Transposition”. Journal of Music Theory 42 (2), 241–263. Forte, A. 1973. The Structure of Atonal Music. New Haven: Yale University Press. Hook, J. 2011. “Spelled Heptachords”. En: Agon, C., et al. (eds.) Mathematics and Computation in Music 2011, pp. 84–97. Heidelberg: Springer. Nuño, L. 2020. “La Tabla Periódica Musical (1/2).” DIVULGAMAT, Centro virtual de divulgación de las matemáticas, RSME: Real Sociedad Matemática Española, No. 111. Diciembre 2020. https://www.divulgamat.net/index.php?option=com_content&view=article&id=18500&directory=67 Nuño, L. 2021a. “La Tabla Periódica Musical (2/2).” DIVULGAMAT, Centro virtual de divulgación de las matemáticas, RSME: Real Sociedad Matemática Española, No. 112. Enero 2021. https://www.divulgamat.net/index.php?option=com_content&view=article&id=18516&directory=67 Nuño, L. 2021b. Parsimonious Graphs for the Most Common Trichords and Tetrachords. Journal of Mathematics and Music 15(2), 125–139 (2021). Nuño, L. 2021c. A Detailed List and a Periodic Table of Set Classes. Journal of Mathematics and Music 15(3), 267–287. Nuño, L. 2021d. “Grafos Parsimónicos para los Tricordos y Tetracordos más Comunes.” DIVULGAMAT, Centro virtual de divulgación de las matemáticas, RSME: Real Sociedad Matemática Española, No. 119. Octubre 2021. https://divulgamat.net/index.php?option=com_content&view=article&id=18666&directory=67 Nuño, L. 2022a. “Parsimonious Graphs for Selected Heptatonic and Pentatonic Scales”. En: Montiel, M., Agustín-Aquino, O.A., Gómez, F., Kastine, J., Lluis-Puebla, E., Milam, B. (eds) Mathematics and Computation in Music. MCM 2022. Lecture Notes in Computer Science, vol 13267. Springer, Cham. https://doi.org/10.1007/978-3-031-07015-0_3 Nuño, L. 2022b. “Type and Class Vectors and Matrices in ℤn. Application to ℤ6, ℤ7 and ℤ12.” Journal of Mathematics and Music. https://www.tandfonline.com/doi/full/10.1080/17459737.2022.2120214 Piston, W. 1988. Harmony. 5th edn. New York: W. W. Norton and Co. Popley, H. A. 1921. The Music of India. London: Oxford University Press. Ring, I. 2022 (15 marzo). The Exciting Universe of Music Theory, https://ianring.com/musictheory/scales/ Schönberg, A. 1983: Theory of Harmony. 3rd edn. Berkeley, Calif.: University of California Press. Tymoczko, D. 2011. A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice. New York: Oxford University Press. Žabka, M. 2014. “Dancing with the Scales: Subchromatic Generated Tone Systems”. Journal of Music Theory 58 (2), 179–233.

Lunes, 12 de Diciembre de 2022 | Imprimir | PDF |  Correo electrónico

3. Enero 2023: Jugar al golf con calculadora

1. Ese “peligroso” artilugio: la calculadora. En la enseñanza de la matemática no existe una herramienta que cree mayor controversia y puntos de vista enfrentados e irreconciliables que el uso de la calculadora. No deja de ser curioso que hay profesores de matemáticas que, aunque no los utilicen, aceptan que otros compañeros puedan utilizar ordenadores u otros medios como los audiovisuales, pero están totalmente en contra de la utilización de las calculadoras en el aula. Y eso a pesar de que las recomendaciones para su uso como material didáctico no es algo nuevo. “No hay duda de que las calculadoras son, ahora, la herramienta natural para realizar las operaciones aritméticas. Por esta razón, aprender a usar una calculadora – y usarla con sensatez – debe formar parte del aprendizaje de la aritmética. Cualquier intento de evitar su uso sería tonto y provocaría solamente el alejamiento de los alumnos de las matemáticas escolares.” La frase anterior está sacada del informe “Las matemáticas en Primaria y Secundaria en la década de los 90”, un seminario internacional organizado por la International Commission on Mathematicasl Instruction en Kuwait en 1986. Se podrían poner referencias más contundentes como las de los estándares del National Council Of Teachers of Mathematics o las referencias que aparecen en los curricula del Ministerio de Educación, pero creemos que es una buena muestra de que la calculadora debería formar parte de los utensilios corrientes de nuestras aulas. Especialmente porque nadie realiza cálculos a mano fuera del ámbito escolar. Podríamos pensar que cualquier profesor que insistiera en sus clases que la mejor forma de enviar un mensaje a un amigo es escribirle una carta o un telegrama debería revisarse sus neuronas, pero nos parece normal imponer las obligaciones de los algoritmos de lápiz y papel, muy denostados por varios didactas. El profesorado que está en contra de su utilización suele aducir que el uso habitual de la calculadora llevará aparejado que los alumnos no aprendan los algoritmos básicos de operaciones con lo que no podrán enfrentarse a situaciones problemáticas. Pero los estudios hechos hace decenas de años demuestra que este argumento es falso. No solamente no hay ningún estudio que demuestre que los alumnos que manejan calculadoras están peor preparados para las matemáticas, sino que se ha demostrado que los alumnos que investigan con esa herramienta están mejor preparados para afrontar la resolución de problemas. Mi experiencia es que los profesores que muestran su disconformidad con el uso de esta herramienta es simplemente por desconocimiento de sus posibilidades, algo que suele ser evidente si se asiste a cualquier reunión de coordinación de las pruebas de la EBAU, en donde se pone de manifiesto el amplio desconocimiento de las posibilidades de las calculadoras. Ya que lo primero que hay que tener presente es que el uso de las calculadoras debe cambiar la metodología de la clase, y el tipo de pruebas que el alumnado debe realizar. “Así pues, consideramos que los tribunales de examen deben diseñar sus programas y exámenes partiendo del supuesto de que todos los examinandos tendrán la posibilidad de utilizar una calculadora en 1985”. La frase anterior está extraída del informe de una comisión británica, que a finales de la década de los años 70 del pasado siglo estudió las matemáticas que en ese momento se impartía en el ámbito no universitario, y propuso una serie de recomendaciones para la enseñanza en las siguientes décadas. Por el nombre de su presidente este documento se conoce como el Informe Cockcroft[i]. La principal ventaja de las calculadoras es que los alumnos pueden comenzar a realizar investigaciones años antes de ver algunos conceptos que requieren una precisión de cálculo que lleva tiempo conseguir. Además, los juegos que tienen la calculadora como elemento auxiliar suelen estar pensados para desarrollar el cálculo mental y el razonamiento lógico previamente a la utilización de la calculadora. Es decir, el cálculo con la herramienta sólo se hace una vez se ha decidido qué operación es la adecuada para resolver la situación en la que nos encontramos. Ejemplos de estos juegos ya se propusieron[ii] en la sección de juegos inmersa en la revista SUMA de la FESPM y hoy vamos a ver otro enfoque más interesante, la simulación del juego de golf con la ayuda de la calculadora. 2. La puntuación en el golf. Aunque es una actividad de todos conocidas, bien por ser aficionados o por haberla visto en alguna película, la forma de puntuar puede ser diferente. Hay páginas donde se pueden encontrar hasta 18 formas distintas de puntuar[iii]. Como vamos a simular una partida es conveniente que tengamos en cuenta algunos conceptos que van a aparecer en las reglas. En el golf, los hoyos se clasifican según una medida llamada par, se considera el par como el número de golpes que hay que dar a la bola para llegar al agujero correspondiente. En el golf de verdad esa cantidad depende de la distancia a la que esté el hoyo, pero en nuestro juego es una estimación de la cantidad de cálculos que hay que hacer para resolver el problema propuesto. Si se realizan menos o más golpes, se indican que son bajo o sobre par lo que tiene una terminología correspondiente que no nos aporta nada a nuestro juego. En general, ganará quien tenga menos golpes acumulados al final de la partida. 3. El juego del golf con calculadora. Este es un juego de estimación. Es decir, el jugador debe suponer cuál será el valor que resuelva el problema propuesto y una vez que lo haya indicado realizará el cálculo con la calculadora. Por ello, la máquina de calcular sólo será una herramienta para realizar un cálculo mecánico y repetitivo, y no aportará nada a la resolución del problema, si el jugador es incapaz de estimar el valor a probar. Lo recalco ya que la estimación es un aspecto que no se suele trabajar en las clases de matemáticas, y sin embargo es una situación con la que nos vamos a encontrar a menudo en nuestra vida cotidiana. Este juego aparece en mucha documentación sobre calculadoras, pero como no se suele indicar claramente de dónde se ha extraído, es difícil saber a ciencia cierta quien es el autor original del juego. Yo he utilizado principalmente los libros de Brian Bolt, en concreto el de “Más actividades matemáticas” que como su versión original es de 1985, debe ser de los primeros en citar el juego. Vamos con el juego en sí. Es un juego en el que pueden jugar de dos a cuatro jugadores e incluso se puede jugar en gran grupo. Cada jugador necesita papel y lápiz para hacer los cálculos y una calculadora. Se dispone de una serie de tarjetas como las siguientes: En el libro citado de Bolt sólo aparecen alguna de las tarjetas. El conjunto completo está tomado de otro libro de Bolt del que tengo versión portuguesa. La forma del juego es muy simple. Se barajan las tarjetas y se colocan boca abajo sobre la mesa. Se levanta una tarjeta y se muestra. Todos los jugadores van proponiendo valores que estiman que cumplirán las desigualdades y entonces realizan la operación con la calculadora. Si no consiguen el resultado, prueban con otro valor hasta dar con el resultado. En todos los casos antes de utilizar la calculadora hay que estimar el tiro. Al final se anota el número de intentos que ha necesitado para conseguir el hoyo, es decir, para resolver el problema. Veamos un ejemplo. Ha salido la tarjeta correspondiente al hoyo h y se realizan los siguientes intentos: h (h-10)/(h+10) 100 0,818… 150 0,875 190 0,9 200 0,904… El jugador ha necesitado cuatro tiros para lograr el hoyo. Los jugadores van anotando todos los golpes que necesitan en todo el recorrido y al final gana el que haya necesitado menos golpes para conseguir todos los hoyos. En algunas versiones a la cantidad de golpes que se ha necesitado para conseguirlo se le resta el número del par, con lo que se obtendrá un número negativo si se han necesitado menos golpes o uno positivo si se han necesitado más. Se suman todos y de nuevo gana quien tiene un valor más pequeño dentro de los posibles negativos. En otras referencias donde se encuentra este juego se pueden ver tarjetas variadas, pero además, una vez visto el objetivo, cada profesor puede crear sus tarjetas según la operación que se quiera repasar. También se puede ampliar o reducir el recorrido de la partida. En mi opinión, para atraer la atención hacia el juego, es conveniente comenzar con tarjetas más simples, en las que se necesite menos golpes para lograr hoyo, de forma que se aprenda la dinámica del juego antes de comenzar con otras tarjetas más complicada. Por ejemplo, las siguientes: 4. Mejorar el hándicap. En el golf, y en otros deportes, existe lo que se llama hándicap. En éste caso es el número de golpes que necesita un jugador para realizar un recorrido completo. Algo que suele interesarle al alumnado es mejorar su hándicap. Es decir, una vez que se ha realizado el juego se les propone que intenten, ya que tienen práctica, pasar de nuevo el circuito y hacerlo en menos golpes. Para ello se les vuelve a proponer el juego pero cambiando en las tarjetas los números que limitan el valor a buscar, dejando la misma operación. De esta forme puede haber alumnos que no ganen, pero que mejoren su hándicap respecto a la partida anterior, lo que suele ser gratificante para esos alumnos.   5. Referencias. Bolt, Brian (1988): Más actividades matemáticas. Labor, Barcelona. Bolt, Brian (1996): Puzzles de matemática. Terramar, Lisboa.   Notas: [i] Se puede descargar pdf gratuito desde la página del Ministerio de Educación. https://sede.educacion.gob.es/publiventa/las-matematicas-si-cuentan-informe-cockcroft/pedagogia/1129 [ii] Se puede consultar en esta sección de juegos de divulgamat en la dirección http://www.divulgamat.net/index.php?option=com_content&view=article&id=10118&directory=67 [iii] Por ejemplo en https://www.golfsitges.com/modalidades-de-juego

Domingo, 01 de Enero de 2023 | Imprimir | PDF |  Correo electrónico

4. Desafíos matemáticos en El País

Cuarenta desafíos matemáticos propuestos por la Real Sociedad Matemática Española, con ocasión de su Centenario en 2011, que aparecieron semanalmente en la portada de la edición digital del diario El País. Además se encuentran disponibles los desafíos extraordinarios de Navidad, los desafíos matemáticos electorales y los desafíos matemáticos del verano de 2014. ARTÍCULOS: Un problema de ciudades y carreteras Solución al primer desafío Una hormiga amenazada Solución al segundo desafío Un cuadrado mágico de productos Solución al tercer desafío Un reloj de dos colores Solución al cuarto desafío Un PAÍS de palillos Solución al quinto desafío Una cuestión de sombreros Solución al sexto desafío Un piano gigantesco Solución al séptimo desafío Un cubo de suma cero Solución al octavo desafío Una enorme potencia de 2 Solución al noveno desafío Cómo rellenar con piezas un tablero Solución al décimo desafío Pesando tornillos Solución al undécimo desafío Una exhibición de coches de carrera Solución al duodécimo desafío Una camiseta bordad en zigzag Solución al decimotercer desafío Partículas en colisión Solución al decimocuarto desafío Una cuestión de unos y ceros Solución al decimoquinto desafío Una molécula de siete átomos Solución al decimosexto desafío Una mesa y un mantel Solución al decimoséptimo desafío De un lado para otro Solución al decimoctavo desafío Cuadrados que suman grandes cifras Solución al decimonoveno desafío ¡Todo el mundo a su silla! Solución al vigésimo desafío Un sistema de riego eficiente Solución al vigésimo primer desafío Un cuadrado mágico especial Solución al vigésimo segundo desafío Doce vértices y ¿seis distancias distintas? Solución al vigésimo tercer desafío Cómo tapar una mesa Solución al vigésimo cuarto desafío Dos alfombras triangulares Solución al vigésimo quinto desafío Construyendo superficies Solución al vigésimo sexto desafío Cómo elegir un equipo goleador Solución al vigésimo séptimo desafío Un problema de grandes números Solución al vigésimo octavo desafío Una paradoja electoral Solución al vigésimo noveno desafío Apuesta arriesgada Solución al trigésimo desafío Números elegantes Solución al trigésimo primer desafío Partículas en movimiento Solución al trigésimo segundo desafío Una azarosa taba Solución al trigésimo tercer desafío Dos gusanitos y una golondrina voraz Solución al trigésimo cuarto desafío Un rectángulo de cuadrados Solución al trigésimo quinto desafío Unas medias enteras Solución al trigésimo sexto desafío Un vecindario emprendedor Solución al trigésimo séptimo desafío Rock and roll en la plaza del pueblo Solución al trigésimo octavo desafío Dos segmentos iguales y en ángulo recto Solución al trigésimo noveno desafío Un mensaje cifrado de despedida ¡Hasta siempre! (solución al cuadragésimo desafío) DESAFÍOS EXTRAORDINARIOS DE NAVIDAD: Navidad 2012: Números bonitos, números feos Solución al desafío extraordinario de Navidad 2012 Navidad 2013: Un número curioso Solución al desafío extraordinario de Navidad 2013 Navidad 2014: Superstición... y probabilidad Solución al desafío extraordinario de Navidad 2014 Navidad 2015: Un maniático de las terminaciones Solución al desafío extraordinario de Navidad 2015 Navidad 2016: Un megabillete de lotería Solución al desafío extraordinario de Navidad 2016 Navidad 2017: Un éxito del 10% Solución al desafío extraordinario de Navidad 2017 Navidad 2018: Un sorteo galáctico Solución al desafío extraordinario de Navidad 2018 Navidad 2019: Un reintegro de otro planeta Solución al desafío extraordinario de Navidad 2019 Navidad 2020: Un décimo rayado Solución al desafío extraordinario de Navidad 2020 Navidad 2021: Una suerte que se comparte Solución al desafío extraordinario de Navidad 2021 Navidad 2022: ¿Se queda su décimo o me lo cambia? LOS DESAFÍOS MATEMÁTICOS ELECTORALES: El malévolo gobernador que manejaba las circunscripciones (11/04/2019) Solución: Así amañana los distritos el gobernador Jugando a ser Victor D'Hondt (17/04/2019) Solución al desafío: Y D'Hondt repartió los escaños ¿Puede ser una pésima idea ir en coalición? (09/05/2019) Solución: Cuando ir en coalición es una mala idea ¿Quién me ha robado mi escaño? (05/11/2019) Solución al desafío: Se resuelve el misterio del escaño robado LOS DESAFÍOS MATEMÁTICOS DEL VERANO (2014): 1. Número a la parrilla Solución al primer desafío del verano 2. El desafío de Dido de Tiro Solución al segundo desafío del verano 3. Un torneo de verano Solución al tercer desafío del verano 4. Billar a muchas bandas Solución al cuarto desafío del verano 5. Una carita feliz Solución al quinto desafío del verano

Sábado, 21 de Diciembre de 2019 | Imprimir | PDF |  Correo electrónico

5. Desafíos matemáticos en El País

Cuarenta desafíos matemáticos propuestos por la Real Sociedad Matemática Española, con ocasión de su Centenario en 2011, que aparecieron semanalmente en la portada de la edición digital del diario El País. Además se encuentran disponibles los desafíos extraordinarios de Navidad, los desafíos matemáticos electorales y los desafíos matemáticos del verano de 2014. ARTÍCULOS: Un problema de ciudades y carreteras Solución al primer desafío Una hormiga amenazada Solución al segundo desafío Un cuadrado mágico de productos Solución al tercer desafío Un reloj de dos colores Solución al cuarto desafío Un PAÍS de palillos Solución al quinto desafío Una cuestión de sombreros Solución al sexto desafío Un piano gigantesco Solución al séptimo desafío Un cubo de suma cero Solución al octavo desafío Una enorme potencia de 2 Solución al noveno desafío Cómo rellenar con piezas un tablero Solución al décimo desafío Pesando tornillos Solución al undécimo desafío Una exhibición de coches de carrera Solución al duodécimo desafío Una camiseta bordad en zigzag Solución al decimotercer desafío Partículas en colisión Solución al decimocuarto desafío Una cuestión de unos y ceros Solución al decimoquinto desafío Una molécula de siete átomos Solución al decimosexto desafío Una mesa y un mantel Solución al decimoséptimo desafío De un lado para otro Solución al decimoctavo desafío Cuadrados que suman grandes cifras Solución al decimonoveno desafío ¡Todo el mundo a su silla! Solución al vigésimo desafío Un sistema de riego eficiente Solución al vigésimo primer desafío Un cuadrado mágico especial Solución al vigésimo segundo desafío Doce vértices y ¿seis distancias distintas? Solución al vigésimo tercer desafío Cómo tapar una mesa Solución al vigésimo cuarto desafío Dos alfombras triangulares Solución al vigésimo quinto desafío Construyendo superficies Solución al vigésimo sexto desafío Cómo elegir un equipo goleador Solución al vigésimo séptimo desafío Un problema de grandes números Solución al vigésimo octavo desafío Una paradoja electoral Solución al vigésimo noveno desafío Apuesta arriesgada Solución al trigésimo desafío Números elegantes Solución al trigésimo primer desafío Partículas en movimiento Solución al trigésimo segundo desafío Una azarosa taba Solución al trigésimo tercer desafío Dos gusanitos y una golondrina voraz Solución al trigésimo cuarto desafío Un rectángulo de cuadrados Solución al trigésimo quinto desafío Unas medias enteras Solución al trigésimo sexto desafío Un vecindario emprendedor Solución al trigésimo séptimo desafío Rock and roll en la plaza del pueblo Solución al trigésimo octavo desafío Dos segmentos iguales y en ángulo recto Solución al trigésimo noveno desafío Un mensaje cifrado de despedida ¡Hasta siempre! (solución al cuadragésimo desafío) DESAFÍOS EXTRAORDINARIOS DE NAVIDAD: Navidad 2012: Números bonitos, números feos Solución al desafío extraordinario de Navidad 2012 Navidad 2013: Un número curioso Solución al desafío extraordinario de Navidad 2013 Navidad 2014: Superstición... y probabilidad Solución al desafío extraordinario de Navidad 2014 Navidad 2015: Un maniático de las terminaciones Solución al desafío extraordinario de Navidad 2015 Navidad 2016: Un megabillete de lotería Solución al desafío extraordinario de Navidad 2016 Navidad 2017: Un éxito del 10% Solución al desafío extraordinario de Navidad 2017 Navidad 2018: Un sorteo galáctico Solución al desafío extraordinario de Navidad 2018 Navidad 2019: Un reintegro de otro planeta Solución al desafío extraordinario de Navidad 2019 Navidad 2020: Un décimo rayado Solución al desafío extraordinario de Navidad 2020 Navidad 2021: Una suerte que se comparte Solución al desafío extraordinario de Navidad 2021 Navidad 2022: ¿Se queda su décimo o me lo cambia? LOS DESAFÍOS MATEMÁTICOS ELECTORALES: El malévolo gobernador que manejaba las circunscripciones (11/04/2019) Solución: Así amañana los distritos el gobernador Jugando a ser Victor D'Hondt (17/04/2019) Solución al desafío: Y D'Hondt repartió los escaños ¿Puede ser una pésima idea ir en coalición? (09/05/2019) Solución: Cuando ir en coalición es una mala idea ¿Quién me ha robado mi escaño? (05/11/2019) Solución al desafío: Se resuelve el misterio del escaño robado LOS DESAFÍOS MATEMÁTICOS DEL VERANO (2014): 1. Número a la parrilla Solución al primer desafío del verano 2. El desafío de Dido de Tiro Solución al segundo desafío del verano 3. Un torneo de verano Solución al tercer desafío del verano 4. Billar a muchas bandas Solución al cuarto desafío del verano 5. Una carita feliz Solución al quinto desafío del verano

Sábado, 21 de Diciembre de 2019 | Imprimir | PDF |  Correo electrónico

6. Raíz de 5

Las Matemáticas más hipotenusas, con Santi García. Este es el primer programa de Matemáticas en la radio de ámbito nacional, todos los lunes a las 15:30 (todos los sábados a las 12:37 hasta el 29 de septiembre de 2018). Un programa semanal de Matemáticas en Radio 5, con todos sus lados, ecuaciones y ondas transformadas para entender desde lo concreto a lo abstracto. Un programa presentado por Santi García Cremades, matemático, divulgador y profesor de la UMH, con las secciones "Latidos de Historia", con Antonio Pérez Sanz; "Están en todas partes", con Javier Santaolalla; y algunas incógnitas más. Deja de utilizar los catetos, y escucha las matemáticas más hipotenusas, en RAÍZ DE 5. ¿Cuál es la mejor forma de jugar a la Lotería de Navidad? - 19/12/22 Homenaje a Sarkovkii y a la teoría del caos - 12/12/22 Curvas matemáticas que hacen que los puentes no se caigan - 05/12/22 ¿Qué hay detrás de la Inteligencia Artificial? - 28/11/22 Estadísticas en el "Mundial de la vergüenza" - 21/11/22 Una historia de guisantes matemáticos - 14/11/22 El matemático que nos metió en el país de las Maravillas - 07/11/22 Ciencia y miedo en el Parque Warner - 31/10/22 La ciencia ficción que inspira a la ciencia, con H.G. Wells - 24/10/22 ¿Qué es exactamente el Big Data? Con Juanjo Milla - 17/10/22 El 7% de los españoles tiene problemas de ansiedad - 10/10/22 Fotogrametría submarina, una técnica matemática - 03/10/22 '¿Cómo funciona la investigación científica? - 26/09/22 ¿Cómo sobrevivir a la incertidumbre?', con Anabel Forte - 19/09/22 Tu profesor de matemáticas quiere que tú triunfes - 12/09/22 La educación es el arma más poderosa del mundo - 05/09/22 Nuestro pensamiento es bayesiano - 18/07/22 El orgullo de las matemáticas - 11/07/22 Enseñamos y aprendemos matemáticas en Valencia - 04/07/22 ¿Por dónde pasa el futuro de la energía? - 27/06/22 Síndrome de Dravet, los números de una enfermedad - 20/06/22 La historia se repite: polémica con la EvAU de matemáticas - 13/06/22 La ciencia y los números de Rafa Nadal - 06/06/22 ¿Tenía el Real Madrid probabilidades de ganar la Champions? - 30/05/22 La gran familia de la bioestadística - 23/05/22 ¿Se vota correctamente en Eurovisión? - 16/05/22 Pitágoras y los Fitipaldis - 09/05/22 ¿De qué trabaja un matemático? - 02/05/22 Canarias se llena de triángulos - 25/04/22 Las simetrías de la Primavera - 18/04/22 ¿Por qué Semana Santa empieza cada año en fechas diferentes? - 11/04/22 La agricultura que nos hizo descubrir las matemáticas - 04/04/22 Cine y matemáticas: en el móvil, TV, cine o Youtube - 28/03/22 Un tebeo de Maryam Mirzakhani - 21/03/22 ¿Cómo celebras las matemáticas? - 14/03/22 ¿Qué es el efecto tijera? - 07/03/22 Matemáticas contra la guerra - 28/02/22 Sesgos everywhere - 21/02/22 Agnesi y otros errores científicos de la historia - 14/02/22 Futuro de niñas y mujeres en carreras ingeniería y software - 07/02/22 Las estadísticas del Benidorm Fest, ¿ha habido justicia? - 31/01/22 ¿Eres discreto o continuo? - 24/01/22 Martin Gardner, el padre de los juegos matemáticos - 17/01/22 Bioinformática, el futuro de la ciencia - 10/01/22 Propósitos matemáticos de 2022 - 03/01/22 Lo más hipotenuso de 2021 - 27/12/21 COVID y Lotería de Navidad - 20/12/21 Cinco cosas sobre las vacunas y el COVID - 13/12/21 Las matemáticas que miden el mundo y el universo - 06/12/21 Mucho por hacer en la política científica - 29/11/21 María Andresa Casamayor, una figura que ya no es oculta - 22/11/21 ¿Qué podemos aprender del tiempo? - 15/11/21 ¿Está todo escrito en nuestros genes? - 08/11/21 Cómo predecir y prevenir la violencia de género - 01/11/21 Un torneo matemático silenciado - 25/10/21 ¿De qué trabaja un matemático? - 18/10/21 Los premios matemáticos, 'Fields' y 'Abel' - 11/10/21 Las matemáticas de los volcanes - 04/10/21 ¿Qué es el famoso coeficiente R^2? - 27/09/21 La Alhambra matemática - 20/09/21 ¿Qué es hacer una regresión lineal? - 13/09/21 Empieza la 6ª Temporada. Matemáticas socioemocionales - 06/09/21 ENEM 2021, la fiesta de las matemáticas - 26/07/21 Problema del viajero y paradoja de Simpson - 19/07/21 Los museos de ciencia - 12/07/21 Otra pandemia: el cáncer - 28/06/21 StatWars: el imperio de los datos - 21/06/21 Alfonso Gracia Saz, nos ha dejado un genio - 14/06/21 ¿Cómo es la prueba de Matemáticas en Selectividad (EvAU, EBAU, PAU)? - 07/06/21 Midiendo el mundo y el aprendizaje bayesiano - 31/05/21 Leo Costa, la Olimpiada Matemática y el tamaño muestral - 24/05/21 Estalmat y la mejor fotografía matemática' - 17/05/21 Maria Gaetana Agnesi, la mal llamada 'bruja' - 10/05/21 Estadísticas en las elecciones, variantes y vacunas - 03/05/21 Vida y obra de Mary Somerville - 26/04/21 Nuestros libros de ciencia y de matemáticas - 19/04/21 El (bajo) riesgo de la vacuna AstraZeneca - 12/04/21 Buscando talentos matemáticos - 05/04/21 Las matemáticas de la Luna - 29/03/21 Música y matemáticas, algoritmos y números - 22/03/21 Pilares matemáticos: arquitectura, poesía y exposición del mes de las matemáticas - 15/03/21 El mes de las matemáticas con A - 08/03/21 Poesía y matemáticas, una relación unívoca - 01/03/21 La vida de Marie Curie con la mirada de Rosa Montero - 22/02/21 ¿Cómo se hace la Encuesta General de Medios? - 15/02/21 No more matildas: Especial 11F - 08/02/21 Moda matemática y la chi-cuadrado - 01/02/21 ¿Qué es la estadística bayesiana? - 25/01/21 La vida de Émile Borel, la resistencia matemática - 18/01/21 Vacunas y estadísticas, con Alfredo Corell - 11/01/21 Libros de ciencia y la ciencia de los libros - 04/01/21 Lo mejor de la ciencia de 2020 - 28/12/20 Apostar o no apostar, esa es la cuestión - 21/12/20 Hablemos de contaminación lumínica - 14/12/20 Gauss, el Príncipe de las Matemáticas - 07/12/20 300 años soñando con Andresa Casamayor - 30/11/20 ¿Qué es la Investigación Operativa? - 23/11/20 Premio Global Teacher Awards, Bárbara de Aymerich y la ciencia para niños - 16/11/20 ¿Tenemos la vacuna definitiva? (con David Quinto) - 09/11/20 El Libro Blanco de las Matemáticas - 02/11/20 Euclides, el best seller de las Matemáticas - 26/10/20 Datos significativos, con Kiko Llaneras - 19/10/20 Inteligencia artificial y ética: una combinación necesaria - 12/10/20 Docentes de matemáticas y estadística, con Marta Cuenca - 05/10/20 Ojos que miran pero no ven: de la discapacidad a las matemáticas - 28/09/20 El diseño de experimentos, con Picanúmeros - 21/09/20 Las fases de las vacunas, con Ignacio Crespo - 14/09/20 'Educar no es enseñar a saber, sino a hacer' - 07/09/20 Estrenamos 5ª Temporada: Corazones matemáticos y estadística - 31/08/20 ¿Qué hace la prueba PCR? Con Dario García (BiotecX) - 24/08/20 Vuelta al cole y retos de la ciencia actual - 17/08/20 Matemáticas contra la pandemia - 10/08/20 La máquina del tiempo de la ciencia - 04/08/20 Segunda ola y las huelgas MIR - 27/07/20 EBAU y las matemáticas, con Pedro Daniel Pajares - 20/07/20 Historias extraordinarias de Matemáticas - 13/07/20 Nuevo atentado contra las matemáticas - 29/06/20 Álex Tenas, Jarabe de Palo y un eterno Pau - 22/06/20 Instrumentos de medida, con Javier Santaolalla y Espiciencia - 15/06/20 Diario de una científica: Tests COVID-19, ¿qué sensibilidad tienen? - 08/06/20 JJ Priego: Comienza una nueva era en el espacio, con Space X - 01/06/20 Anabel Forte y Patricia Contreras - 25/05/20 Xavier Ros-Oton, el 'Pau Gasol' de las Matemáticas - 18/05/20 COVID-19: día 72. Adolfo García-Sastre - 11/05/20 COVID-19: día 65. El partido de nuestra vida - 04/05/20 COVID-19: día 58. Rocío Benavente, de Maldita Ciencia - 27/04/20 COVID-19: día 51. David Quinto y Daniel Orts - 20/04/20 COVID-19: día 44. Dilemas de cuarentena - 13/04/20 COVID-19: día 37 - 06/04/20 Modelos matemáticos sobre el coronavirus, con Javier Álvarez Liébana - 30/03/20 José Manuel López Nicolás: el Messi de la Divulgación Científica - 16/03/20 Blaise Pascal: una especie de Sheldon Cooper del siglo XVII - 09/03/20 Centro de Visión por Computador: una imagen vale más que mil palabras - 02/03/20 Rompiendo las redes: desde Instagram a Spiderman, con Sara Fructuoso - 24/02/20 ¿Cómo entiende la música una Inteligencia Articial? Con DotCSV - 17/02/20 El test que mide la brecha de género en el cine - 10/02/20 Los jóvenes investigadores de las Matemáticas - 03/02/20 Estalmat y los juegos matemáticos - 27/01/20 Sophie Germain: una autodidacta contra su tiempo - 20/01/20 Los 'solfamidas' matemáticos: la Tesis, los chistes y Paco de Lucía - 13/01/20 Los propósitos de año nuevo de los números Pi y Tau - 06/01/20 El año de Mendeléyev, la química (y las Matemáticas) están en todas partes - 30/12/19 ¿Cómo vieron el 2019 Blader Runner e Isaac Asimov? - 23/12/19 Los números del cambio climático y el Mar Menor - 16/12/19 Los '5' teoremas con los nombres más curiosos de las Matemáticas - 09/12/19 René Descartes, el cráneo que lo cambió todo - 02/12/19 El infinito, desde los números hasta los conjuntos de Cantor - 25/11/19 Innovar en el aula: visitamos SIMO 2019 - 18/11/19 Cuentos científicos y homenaje a Margarita Salas - 11/11/19 La revolución cuántica en la computación - 04/11/19 Elecciones, sorteos e injusticias matemáticas - 28/10/19 El jamón de York no existe, con Marian García - 21/10/19 Los Premios a la Investigación Matemática, con Paco Marcellán - 07/10/19 Las matemáticas pueden hacer universos paralelos - 30/09/19 Mitos matemáticos y la grafía de los números - 23/09/19 Un teorema que vale tres millones de dólares y la importancia de los números - 16/09/19 La suma de las partes es más que el todo - 09/09/19 Ciclos hamiltonianos y nunca es tarde para aprender -02/09/19 Eventos que cambian el mundo, del ICIAM al ENEM -29/07/19 Matemáticas y extinciones masivas de la Tierra -15/07/19 Matemáticas y amor: ecuación de Backus y parada óptima - 08/07/19 Matemáticas, cocina y tecnologías cuánticas - 01/07/19 Rompiendo estereotipos, aplicando metaheurísticas - 24/06/19 ¿Cuál es tu número favorito? - 17/06/19 Complejidad de un problema y el "polémico" examen de la PAU - 10/06/19 Falacias formales, informales y paradoja de Simpson - 03/06/19 La cinta de Moebius, la música y los patrones armonicos, con Claim - 27/05/19 Desde Rafael Nadal al Pint of Science, pasando por el Imaginary - 20/05/19 Programa 101: en directo con el grupo Claim - 13/05/19 ESPECIAL 100 PROGRAMAS: ¿de donde venimos? - 06/05/19 Fermat, la historia de un teorema que cambió nuestro mundo - 29/04/19 Analizamos la Ley d'Hondt y sus alternativas - 22/04/19 Powehi: el primer agujero negro de la historia visto por la ciencia - 15/04/19 Matemáticas y cambio climático - 08/04/19 ¿Por qué están de moda las Matemáticas? #25añosRadio5 - 01/04/19 Un pequeño paso para el hombre y para la humanidad, con Eugenio Manuel Fernández - 25/03/19 Matemáticas y marketing digital, con Fernando Maciá - 18/03/19 Debate matemático: ¿eres más de Pi o de Tau? - 11/03/19 Las matemáticas más frikis: desde los Power Rangers a ¿Dónde está Wally? - 25/02/19 ¿Cómo suenan los números? - 18/02/19 Día de la Mujer y la Niña en las Matemáticas. #11F - 11/02/19 La naturaleza programa en paralelo, con José María Cecilia - 04/02/19 Sesgos en ciencia y en educación - 28/01/19 2006, el año dorado de la matemática española, con Manuel de León - 21/01/19 El refranero español y las Matemáticas - 14/01/19 2019 es un año especial, matemáticamente hablando - 07/01/19 Libros matemáticos para 2019 y un Calendario Científico Solidario - 31/12/18 Navidad matemática: detalles fractales, fiesta de San Alberto, elige tu aventura - 24/12/18 Matemáticas y ajedrez - 17/12/18 Modelos, algoritmos, Voronoi: Matemáticas que salvan vidas - 10/12/18 Del mito a la ciencia, con Daniel Torregrosa - 03/12/18 Que no te engañen con ofertas. Las matemáticas te hacen libre - 26/11/18 Cristalografía y la Alhambra - 19/11/18 Ciencia en el Parlamento, matemáticas y Napoleón - 12/11/18 Matemáticas y Medicina, el mundo de la salud y los datos - 05/11/18 Matemáticas por tierra, mar y aire. Evento MATRIX, blog Gaussianos y estadísticas H20 - 29/10/18 Teorema de Tales - 22/10/18 La paradoja del cumpleaños, aplicada - 15/10/18 Premios matemáticos: desde el Big Data hasta la computación cuántica - 08/10/18 La Hipótesis de Riemann - 01/10/18 DNI, Dinosaurios y cambio de horario - 29/09/18 Las matemáticas en China - 22/09/18 Regla de Barrow y canción a las integrales - 15/09/18 'Somos escutoides', una nueva figura geométrica made in Spain revoluciona la biomedicina - 08/09/18 Matemáticas Directo, entrevistas en la calle imaginaria de los grandes matemáticos de la historia - 01/09/18 ¿Viajar o quedarse en casa? - 28/07/18 Matemáticas y Cine, referencias de película - 21/07/18 Matemáticas y fútbol: La geometría del Mundial de Rusia - 14/07/18 Matemáticas y comics: con Salva Espín (Marvel) - 07/07/18 Las matematicas que están dentro de tu móvil - 30/06/18 Red DiMa: Amor por lo nuestro - 23/06/18 La división y Euclides - 16/06/18 Quién enseña a los profesores. Oposiciones e innovación - 09/06/18 La vida y obra de Maryam Mirzakhani - 02/06/18 Salir de la Tierra es posible - 26/05/18 La unión matemática hace la fuerza - 19/05/18 Arquímedes de Siracusa: Desde Eureka hasta el punto de apoyo - 05/05/18 El maravilloso mundo de los algoritmos - 28/04/18 Los tres problemas clasicos - 21/04/18 Especial 50 programas de Raíz de 5 - 14/04/18 El calendario y las matemáticas - 31/03/18 El infinito, hasta Cantor y más allá - 24/03/18 John Nash, el equilibrio y el dilema del prisionero - 17/03/18 Matemáticas, frambuesas, amor y música con Ruth Lorenzo - 10/03/18 Axiomas de Peano y la construcción de los números naturales - 03/03/18 Matemáticas en la II Guerra Mundial - 24/02/18 Grupos, anillos y álgebra no conmutativa o asociativa, con Mercedes Siles - 17/02/18 Especial 11F: Día de la Mujer y la Niña en la Ciencia - 10/02/18 Los número irracionales - 03/02/18 La cuesta de enero, las derivadas y el último alquimista - 27/01/18 Los juegos de mesa y las matemáticas - 20/01/18 Arte, literatura y matemáticas - 13/01/18 Los Números Perfectos - 30/12/17 La lotería de navidad y la memoria de las bolas - 23/12/17 Teoría de grafos, desde Facebook hasta el Clash Royale - 16/12/17 El rock'n roll es actitud y las matematicas también - 09/12/17 El mundo de la tecnología y la teoría de la información - 02/12/17 Los misterios de un cono - 25/11/17 Los premios Ignobel y las matemáticas - 18/11/17 Los límites en matemáticas y los límites del humor (con Dani Gove) - 11/11/17 Los instrumentos musicales y sus matemáticas - 04/11/17 Divulgar matemáticas, un reto una pasión - 28/10/17 Lista de listos, los mejores matemáticos españoles de la historia - 14/10/17 Premios para jóvenes matematicas españolas - 07/10/17 El número Phi: áureo, divino, y ¿sobrevalorado? - 30/09/17 La aleatoriedad, lo "random", lo impredecible - 23/09/17 Los problemas abiertos en matemáticas - 16/09/17 ¿Cómo contamos? Sistema de posicionamiento número y el poder del cero - 09/09/17 Volvemos y empezamos por el uno, con mucho Woodstock y con continuidad - 02/09/17 Música, armonía y números. Las estadísticas de la música del verano - 29/07/17 El teorema de la bola peluda, tormentas, mapas y energía limpia - 22/07/17 Juegos matematicos y azar - 15/07/17 El GPS del pulmón. Posicionamiento en los bronquios y en el espacio - 08/07/17 Los 4 elementos desde Platón a Apolinio. Juego de tronos y matemáticas - 01/07/17 Las matemáticas al poder. Rectores y políticos matematicos - 24/06/17 Duelo matemático por el cálculo: Newton vs Leibniz - 17/06/17 Educación Matemática. ¿Cómo han sido nuestros maestros? - 10/06/17 La Normalidad de Gauss y el Teorema Central del Límite. Todo es normal - 03/06/17 MC Escher, entre el arte, la magia y la geometría - 27/05/17 Los números primos: los átomos de la aritmética - 20/05/17 Alan Turing, guerra e Inteligencia Artificial - 13/05/17 Los puentes, los arcos y las curvas catenarias - 06/05/17 La Teoría del Caos, Lorenz y el Efecto Mariposa -29/04/17 Leonardo DaVinci, las matemáticas y los nuevos genios del siglo XXI - 22/04/17 Aritmética del reloj y la Semana Santa - 15/04/17 Olimpiadas y retos matemáticos - 08/04/17 Triángulos, desde las estrellas a Pitágoras - 01/04/17 Sistema binario, transistores y la hegemonía de los ceros y unos - 25/03/17 Dia de Pi, los rios, la física cuántica y su aproximación - 18/03/17

Lunes, 19 de Diciembre de 2022 | Imprimir | PDF |  Correo electrónico

7. Raíz de 5

Las Matemáticas más hipotenusas, con Santi García. Este es el primer programa de Matemáticas en la radio de ámbito nacional, todos los lunes a las 15:30 (todos los sábados a las 12:37 hasta el 29 de septiembre de 2018). Un programa semanal de Matemáticas en Radio 5, con todos sus lados, ecuaciones y ondas transformadas para entender desde lo concreto a lo abstracto. Un programa presentado por Santi García Cremades, matemático, divulgador y profesor de la UMH, con las secciones "Latidos de Historia", con Antonio Pérez Sanz; "Están en todas partes", con Javier Santaolalla; y algunas incógnitas más. Deja de utilizar los catetos, y escucha las matemáticas más hipotenusas, en RAÍZ DE 5. ¿Cuál es la mejor forma de jugar a la Lotería de Navidad? - 19/12/22 Homenaje a Sarkovkii y a la teoría del caos - 12/12/22 Curvas matemáticas que hacen que los puentes no se caigan - 05/12/22 ¿Qué hay detrás de la Inteligencia Artificial? - 28/11/22 Estadísticas en el "Mundial de la vergüenza" - 21/11/22 Una historia de guisantes matemáticos - 14/11/22 El matemático que nos metió en el país de las Maravillas - 07/11/22 Ciencia y miedo en el Parque Warner - 31/10/22 La ciencia ficción que inspira a la ciencia, con H.G. Wells - 24/10/22 ¿Qué es exactamente el Big Data? Con Juanjo Milla - 17/10/22 El 7% de los españoles tiene problemas de ansiedad - 10/10/22 Fotogrametría submarina, una técnica matemática - 03/10/22 '¿Cómo funciona la investigación científica? - 26/09/22 ¿Cómo sobrevivir a la incertidumbre?', con Anabel Forte - 19/09/22 Tu profesor de matemáticas quiere que tú triunfes - 12/09/22 La educación es el arma más poderosa del mundo - 05/09/22 Nuestro pensamiento es bayesiano - 18/07/22 El orgullo de las matemáticas - 11/07/22 Enseñamos y aprendemos matemáticas en Valencia - 04/07/22 ¿Por dónde pasa el futuro de la energía? - 27/06/22 Síndrome de Dravet, los números de una enfermedad - 20/06/22 La historia se repite: polémica con la EvAU de matemáticas - 13/06/22 La ciencia y los números de Rafa Nadal - 06/06/22 ¿Tenía el Real Madrid probabilidades de ganar la Champions? - 30/05/22 La gran familia de la bioestadística - 23/05/22 ¿Se vota correctamente en Eurovisión? - 16/05/22 Pitágoras y los Fitipaldis - 09/05/22 ¿De qué trabaja un matemático? - 02/05/22 Canarias se llena de triángulos - 25/04/22 Las simetrías de la Primavera - 18/04/22 ¿Por qué Semana Santa empieza cada año en fechas diferentes? - 11/04/22 La agricultura que nos hizo descubrir las matemáticas - 04/04/22 Cine y matemáticas: en el móvil, TV, cine o Youtube - 28/03/22 Un tebeo de Maryam Mirzakhani - 21/03/22 ¿Cómo celebras las matemáticas? - 14/03/22 ¿Qué es el efecto tijera? - 07/03/22 Matemáticas contra la guerra - 28/02/22 Sesgos everywhere - 21/02/22 Agnesi y otros errores científicos de la historia - 14/02/22 Futuro de niñas y mujeres en carreras ingeniería y software - 07/02/22 Las estadísticas del Benidorm Fest, ¿ha habido justicia? - 31/01/22 ¿Eres discreto o continuo? - 24/01/22 Martin Gardner, el padre de los juegos matemáticos - 17/01/22 Bioinformática, el futuro de la ciencia - 10/01/22 Propósitos matemáticos de 2022 - 03/01/22 Lo más hipotenuso de 2021 - 27/12/21 COVID y Lotería de Navidad - 20/12/21 Cinco cosas sobre las vacunas y el COVID - 13/12/21 Las matemáticas que miden el mundo y el universo - 06/12/21 Mucho por hacer en la política científica - 29/11/21 María Andresa Casamayor, una figura que ya no es oculta - 22/11/21 ¿Qué podemos aprender del tiempo? - 15/11/21 ¿Está todo escrito en nuestros genes? - 08/11/21 Cómo predecir y prevenir la violencia de género - 01/11/21 Un torneo matemático silenciado - 25/10/21 ¿De qué trabaja un matemático? - 18/10/21 Los premios matemáticos, 'Fields' y 'Abel' - 11/10/21 Las matemáticas de los volcanes - 04/10/21 ¿Qué es el famoso coeficiente R^2? - 27/09/21 La Alhambra matemática - 20/09/21 ¿Qué es hacer una regresión lineal? - 13/09/21 Empieza la 6ª Temporada. Matemáticas socioemocionales - 06/09/21 ENEM 2021, la fiesta de las matemáticas - 26/07/21 Problema del viajero y paradoja de Simpson - 19/07/21 Los museos de ciencia - 12/07/21 Otra pandemia: el cáncer - 28/06/21 StatWars: el imperio de los datos - 21/06/21 Alfonso Gracia Saz, nos ha dejado un genio - 14/06/21 ¿Cómo es la prueba de Matemáticas en Selectividad (EvAU, EBAU, PAU)? - 07/06/21 Midiendo el mundo y el aprendizaje bayesiano - 31/05/21 Leo Costa, la Olimpiada Matemática y el tamaño muestral - 24/05/21 Estalmat y la mejor fotografía matemática' - 17/05/21 Maria Gaetana Agnesi, la mal llamada 'bruja' - 10/05/21 Estadísticas en las elecciones, variantes y vacunas - 03/05/21 Vida y obra de Mary Somerville - 26/04/21 Nuestros libros de ciencia y de matemáticas - 19/04/21 El (bajo) riesgo de la vacuna AstraZeneca - 12/04/21 Buscando talentos matemáticos - 05/04/21 Las matemáticas de la Luna - 29/03/21 Música y matemáticas, algoritmos y números - 22/03/21 Pilares matemáticos: arquitectura, poesía y exposición del mes de las matemáticas - 15/03/21 El mes de las matemáticas con A - 08/03/21 Poesía y matemáticas, una relación unívoca - 01/03/21 La vida de Marie Curie con la mirada de Rosa Montero - 22/02/21 ¿Cómo se hace la Encuesta General de Medios? - 15/02/21 No more matildas: Especial 11F - 08/02/21 Moda matemática y la chi-cuadrado - 01/02/21 ¿Qué es la estadística bayesiana? - 25/01/21 La vida de Émile Borel, la resistencia matemática - 18/01/21 Vacunas y estadísticas, con Alfredo Corell - 11/01/21 Libros de ciencia y la ciencia de los libros - 04/01/21 Lo mejor de la ciencia de 2020 - 28/12/20 Apostar o no apostar, esa es la cuestión - 21/12/20 Hablemos de contaminación lumínica - 14/12/20 Gauss, el Príncipe de las Matemáticas - 07/12/20 300 años soñando con Andresa Casamayor - 30/11/20 ¿Qué es la Investigación Operativa? - 23/11/20 Premio Global Teacher Awards, Bárbara de Aymerich y la ciencia para niños - 16/11/20 ¿Tenemos la vacuna definitiva? (con David Quinto) - 09/11/20 El Libro Blanco de las Matemáticas - 02/11/20 Euclides, el best seller de las Matemáticas - 26/10/20 Datos significativos, con Kiko Llaneras - 19/10/20 Inteligencia artificial y ética: una combinación necesaria - 12/10/20 Docentes de matemáticas y estadística, con Marta Cuenca - 05/10/20 Ojos que miran pero no ven: de la discapacidad a las matemáticas - 28/09/20 El diseño de experimentos, con Picanúmeros - 21/09/20 Las fases de las vacunas, con Ignacio Crespo - 14/09/20 'Educar no es enseñar a saber, sino a hacer' - 07/09/20 Estrenamos 5ª Temporada: Corazones matemáticos y estadística - 31/08/20 ¿Qué hace la prueba PCR? Con Dario García (BiotecX) - 24/08/20 Vuelta al cole y retos de la ciencia actual - 17/08/20 Matemáticas contra la pandemia - 10/08/20 La máquina del tiempo de la ciencia - 04/08/20 Segunda ola y las huelgas MIR - 27/07/20 EBAU y las matemáticas, con Pedro Daniel Pajares - 20/07/20 Historias extraordinarias de Matemáticas - 13/07/20 Nuevo atentado contra las matemáticas - 29/06/20 Álex Tenas, Jarabe de Palo y un eterno Pau - 22/06/20 Instrumentos de medida, con Javier Santaolalla y Espiciencia - 15/06/20 Diario de una científica: Tests COVID-19, ¿qué sensibilidad tienen? - 08/06/20 JJ Priego: Comienza una nueva era en el espacio, con Space X - 01/06/20 Anabel Forte y Patricia Contreras - 25/05/20 Xavier Ros-Oton, el 'Pau Gasol' de las Matemáticas - 18/05/20 COVID-19: día 72. Adolfo García-Sastre - 11/05/20 COVID-19: día 65. El partido de nuestra vida - 04/05/20 COVID-19: día 58. Rocío Benavente, de Maldita Ciencia - 27/04/20 COVID-19: día 51. David Quinto y Daniel Orts - 20/04/20 COVID-19: día 44. Dilemas de cuarentena - 13/04/20 COVID-19: día 37 - 06/04/20 Modelos matemáticos sobre el coronavirus, con Javier Álvarez Liébana - 30/03/20 José Manuel López Nicolás: el Messi de la Divulgación Científica - 16/03/20 Blaise Pascal: una especie de Sheldon Cooper del siglo XVII - 09/03/20 Centro de Visión por Computador: una imagen vale más que mil palabras - 02/03/20 Rompiendo las redes: desde Instagram a Spiderman, con Sara Fructuoso - 24/02/20 ¿Cómo entiende la música una Inteligencia Articial? Con DotCSV - 17/02/20 El test que mide la brecha de género en el cine - 10/02/20 Los jóvenes investigadores de las Matemáticas - 03/02/20 Estalmat y los juegos matemáticos - 27/01/20 Sophie Germain: una autodidacta contra su tiempo - 20/01/20 Los 'solfamidas' matemáticos: la Tesis, los chistes y Paco de Lucía - 13/01/20 Los propósitos de año nuevo de los números Pi y Tau - 06/01/20 El año de Mendeléyev, la química (y las Matemáticas) están en todas partes - 30/12/19 ¿Cómo vieron el 2019 Blader Runner e Isaac Asimov? - 23/12/19 Los números del cambio climático y el Mar Menor - 16/12/19 Los '5' teoremas con los nombres más curiosos de las Matemáticas - 09/12/19 René Descartes, el cráneo que lo cambió todo - 02/12/19 El infinito, desde los números hasta los conjuntos de Cantor - 25/11/19 Innovar en el aula: visitamos SIMO 2019 - 18/11/19 Cuentos científicos y homenaje a Margarita Salas - 11/11/19 La revolución cuántica en la computación - 04/11/19 Elecciones, sorteos e injusticias matemáticas - 28/10/19 El jamón de York no existe, con Marian García - 21/10/19 Los Premios a la Investigación Matemática, con Paco Marcellán - 07/10/19 Las matemáticas pueden hacer universos paralelos - 30/09/19 Mitos matemáticos y la grafía de los números - 23/09/19 Un teorema que vale tres millones de dólares y la importancia de los números - 16/09/19 La suma de las partes es más que el todo - 09/09/19 Ciclos hamiltonianos y nunca es tarde para aprender -02/09/19 Eventos que cambian el mundo, del ICIAM al ENEM -29/07/19 Matemáticas y extinciones masivas de la Tierra -15/07/19 Matemáticas y amor: ecuación de Backus y parada óptima - 08/07/19 Matemáticas, cocina y tecnologías cuánticas - 01/07/19 Rompiendo estereotipos, aplicando metaheurísticas - 24/06/19 ¿Cuál es tu número favorito? - 17/06/19 Complejidad de un problema y el "polémico" examen de la PAU - 10/06/19 Falacias formales, informales y paradoja de Simpson - 03/06/19 La cinta de Moebius, la música y los patrones armonicos, con Claim - 27/05/19 Desde Rafael Nadal al Pint of Science, pasando por el Imaginary - 20/05/19 Programa 101: en directo con el grupo Claim - 13/05/19 ESPECIAL 100 PROGRAMAS: ¿de donde venimos? - 06/05/19 Fermat, la historia de un teorema que cambió nuestro mundo - 29/04/19 Analizamos la Ley d'Hondt y sus alternativas - 22/04/19 Powehi: el primer agujero negro de la historia visto por la ciencia - 15/04/19 Matemáticas y cambio climático - 08/04/19 ¿Por qué están de moda las Matemáticas? #25añosRadio5 - 01/04/19 Un pequeño paso para el hombre y para la humanidad, con Eugenio Manuel Fernández - 25/03/19 Matemáticas y marketing digital, con Fernando Maciá - 18/03/19 Debate matemático: ¿eres más de Pi o de Tau? - 11/03/19 Las matemáticas más frikis: desde los Power Rangers a ¿Dónde está Wally? - 25/02/19 ¿Cómo suenan los números? - 18/02/19 Día de la Mujer y la Niña en las Matemáticas. #11F - 11/02/19 La naturaleza programa en paralelo, con José María Cecilia - 04/02/19 Sesgos en ciencia y en educación - 28/01/19 2006, el año dorado de la matemática española, con Manuel de León - 21/01/19 El refranero español y las Matemáticas - 14/01/19 2019 es un año especial, matemáticamente hablando - 07/01/19 Libros matemáticos para 2019 y un Calendario Científico Solidario - 31/12/18 Navidad matemática: detalles fractales, fiesta de San Alberto, elige tu aventura - 24/12/18 Matemáticas y ajedrez - 17/12/18 Modelos, algoritmos, Voronoi: Matemáticas que salvan vidas - 10/12/18 Del mito a la ciencia, con Daniel Torregrosa - 03/12/18 Que no te engañen con ofertas. Las matemáticas te hacen libre - 26/11/18 Cristalografía y la Alhambra - 19/11/18 Ciencia en el Parlamento, matemáticas y Napoleón - 12/11/18 Matemáticas y Medicina, el mundo de la salud y los datos - 05/11/18 Matemáticas por tierra, mar y aire. Evento MATRIX, blog Gaussianos y estadísticas H20 - 29/10/18 Teorema de Tales - 22/10/18 La paradoja del cumpleaños, aplicada - 15/10/18 Premios matemáticos: desde el Big Data hasta la computación cuántica - 08/10/18 La Hipótesis de Riemann - 01/10/18 DNI, Dinosaurios y cambio de horario - 29/09/18 Las matemáticas en China - 22/09/18 Regla de Barrow y canción a las integrales - 15/09/18 'Somos escutoides', una nueva figura geométrica made in Spain revoluciona la biomedicina - 08/09/18 Matemáticas Directo, entrevistas en la calle imaginaria de los grandes matemáticos de la historia - 01/09/18 ¿Viajar o quedarse en casa? - 28/07/18 Matemáticas y Cine, referencias de película - 21/07/18 Matemáticas y fútbol: La geometría del Mundial de Rusia - 14/07/18 Matemáticas y comics: con Salva Espín (Marvel) - 07/07/18 Las matematicas que están dentro de tu móvil - 30/06/18 Red DiMa: Amor por lo nuestro - 23/06/18 La división y Euclides - 16/06/18 Quién enseña a los profesores. Oposiciones e innovación - 09/06/18 La vida y obra de Maryam Mirzakhani - 02/06/18 Salir de la Tierra es posible - 26/05/18 La unión matemática hace la fuerza - 19/05/18 Arquímedes de Siracusa: Desde Eureka hasta el punto de apoyo - 05/05/18 El maravilloso mundo de los algoritmos - 28/04/18 Los tres problemas clasicos - 21/04/18 Especial 50 programas de Raíz de 5 - 14/04/18 El calendario y las matemáticas - 31/03/18 El infinito, hasta Cantor y más allá - 24/03/18 John Nash, el equilibrio y el dilema del prisionero - 17/03/18 Matemáticas, frambuesas, amor y música con Ruth Lorenzo - 10/03/18 Axiomas de Peano y la construcción de los números naturales - 03/03/18 Matemáticas en la II Guerra Mundial - 24/02/18 Grupos, anillos y álgebra no conmutativa o asociativa, con Mercedes Siles - 17/02/18 Especial 11F: Día de la Mujer y la Niña en la Ciencia - 10/02/18 Los número irracionales - 03/02/18 La cuesta de enero, las derivadas y el último alquimista - 27/01/18 Los juegos de mesa y las matemáticas - 20/01/18 Arte, literatura y matemáticas - 13/01/18 Los Números Perfectos - 30/12/17 La lotería de navidad y la memoria de las bolas - 23/12/17 Teoría de grafos, desde Facebook hasta el Clash Royale - 16/12/17 El rock'n roll es actitud y las matematicas también - 09/12/17 El mundo de la tecnología y la teoría de la información - 02/12/17 Los misterios de un cono - 25/11/17 Los premios Ignobel y las matemáticas - 18/11/17 Los límites en matemáticas y los límites del humor (con Dani Gove) - 11/11/17 Los instrumentos musicales y sus matemáticas - 04/11/17 Divulgar matemáticas, un reto una pasión - 28/10/17 Lista de listos, los mejores matemáticos españoles de la historia - 14/10/17 Premios para jóvenes matematicas españolas - 07/10/17 El número Phi: áureo, divino, y ¿sobrevalorado? - 30/09/17 La aleatoriedad, lo "random", lo impredecible - 23/09/17 Los problemas abiertos en matemáticas - 16/09/17 ¿Cómo contamos? Sistema de posicionamiento número y el poder del cero - 09/09/17 Volvemos y empezamos por el uno, con mucho Woodstock y con continuidad - 02/09/17 Música, armonía y números. Las estadísticas de la música del verano - 29/07/17 El teorema de la bola peluda, tormentas, mapas y energía limpia - 22/07/17 Juegos matematicos y azar - 15/07/17 El GPS del pulmón. Posicionamiento en los bronquios y en el espacio - 08/07/17 Los 4 elementos desde Platón a Apolinio. Juego de tronos y matemáticas - 01/07/17 Las matemáticas al poder. Rectores y políticos matematicos - 24/06/17 Duelo matemático por el cálculo: Newton vs Leibniz - 17/06/17 Educación Matemática. ¿Cómo han sido nuestros maestros? - 10/06/17 La Normalidad de Gauss y el Teorema Central del Límite. Todo es normal - 03/06/17 MC Escher, entre el arte, la magia y la geometría - 27/05/17 Los números primos: los átomos de la aritmética - 20/05/17 Alan Turing, guerra e Inteligencia Artificial - 13/05/17 Los puentes, los arcos y las curvas catenarias - 06/05/17 La Teoría del Caos, Lorenz y el Efecto Mariposa -29/04/17 Leonardo DaVinci, las matemáticas y los nuevos genios del siglo XXI - 22/04/17 Aritmética del reloj y la Semana Santa - 15/04/17 Olimpiadas y retos matemáticos - 08/04/17 Triángulos, desde las estrellas a Pitágoras - 01/04/17 Sistema binario, transistores y la hegemonía de los ceros y unos - 25/03/17 Dia de Pi, los rios, la física cuántica y su aproximación - 18/03/17

Lunes, 19 de Diciembre de 2022 | Imprimir | PDF |  Correo electrónico

8. El «cubli», un cubo que sabe ‘caminar’

El «cubli» es un cubo que es capaz de mantenerse sobre uno de sus vértices sin ninguna ayuda externa. Las ruedas de reacción montadas sobre sus tres caras giran a altas velocidades angulares y luego frenan bruscamente, haciendo que el «cubli» salte. Cuando el «cubli» casi ha alcanzado la posición deseada –se mantiene sobre una arista–, se aplican torques controlados para conseguir el equilibrio sobre un vértice. Además del equilibrio, los torques también se pueden usar para lograr una caída controlada: se puede obligar al  «cubli» a caer en cualquier dirección. Combinando estas tres capacidades –salto, equilibrio y caída controlada– el «cubli» es capaz de ‘caminar’. Más información: Gajamohan Mohanarajah and Raffaello D’Andrea, Building cubes that can jump up and balance, Institute for Dynamic Systems and Control, ETH Zurich (Suiza) Cubli – A cube that can jump up, balance, and walk across your desk, Robohub Visto en Neatorama Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Miércoles, 21 de Diciembre de 2022 | Imprimir | PDF |  Correo electrónico

9. El gigante Gulliver

El historietista e ilustrador  –y también profesor de la Facultad de Bellas Artes de Valencia– Vicent Josep Llobell Bisbal, Sento, cumple hoy años. De sus muchas obras os traigo ésta: Parque Gulliver, Jardín del Turia, Valencia (Google Earth) ¿No distingues bien? Mira más de cerca… Parque Gulliver, Jardín del Turia, Valencia (Google Earth) … un poquito más cerca aún: Parque Gulliver, Jardín del Turia, Valencia (Google Earth) Estas imágenes pertenecen al Parque Gulliver, que se encuentra en el Jardín del Turia en Valencia. http://www.sento.es/images/gulliver/gulliver.html La principal atracción de este parque es una escultura monumental de Gulliver –el personaje de la novela de Jonathan Swift–, de 70 metros, que representa el  momento en el que Gulliver acaba de llegar a Liliput y ha sido inmovilizado por sus habitantes… Rampas, toboganes y escaleras permiten acceder a la estatua y divertirse… como auténticos liliputienses alrededor del gigante Gulliver. http://www.sento.es/images/gulliver/gulliver.html El Ayuntamiento de Valencia encargó en 1990 este proyecto al arquitecto Rafael Rivera y al artista fallero Manolo Martín, a partir de  un diseño de Sento. Los liliputienses miden 6 pulgadas –15 cm– frente a los 6 pies –180 cm– de Gulliver: es decir, el protagonista de la novela de Swift mide 12 veces más que un liliputiense. Gulliver explica cómo le transportan desde la playa hasta la ciudad: Quinientos carpinteros e ingenieros se pusieron inmediatamente a la obra para disponer la mayor de las máquinas hasta entonces construida. Consistía en un tablero levantado tres pulgadas del suelo, de unos siete pies de largo y cuatro de ancho, y que se movía sobre veintidós ruedas. Los gritos que oí eran ocasionados por la llegada de esta máquina, que, según parece, emprendió la marcha cuatro horas después de haber pisado yo tierra. La colocaron paralela a mí; pero la principal dificultad era alzarme y colocarme en este vehículo. Ochenta vigas, de un pie de alto cada una, fueron erigidas para este fin, y cuerdas muy fuertes, del grueso de bramantes, fueron sujetas con garfios a numerosas fajas con que los trabajadores me habían rodeado el cuello, las manos, el cuerpo y las piernas. Novecientos hombres de los más robustos tiraron de estas cuerdas por medio de poleas fijadas en las vigas, y así, en menos de tres horas, fui levantado, puesto sobre la máquina y en ella atado fuertemente. Todo esto me lo contaron, porque mientras se hizo esta operación yacía yo en profundo sueño, debido a la fuerza de aquel medicamento soporífero echado en el vino. ¿El cálculo de Swift es correcto? ¿Bastarán 900 liliputienses para transportar a Gulliver? Sigamos leyendo un poco más: El lector puede tener el gusto de observar que en la última de las normas necesarias para recobrar la libertad, el Emperador estipula que se me conceda una cantidad de comida y bebida suficiente para mantener a 1.728 liliputienses. Algún tiempo después, habiendo preguntado a un amigo de la Corte cómo se las arreglaron para fijar una cifra tan concreta, me dijo que los matemáticos de su Majestad, tras medir la altura de mi cuerpo usando un cuadrante y descubrir que era más grande que el suyo en la proporción de doce a uno, concluyeron por la semejanza de sus cuerpos que el mío debía contener, al menos, 1.728 de los suyos y consecuentemente requeriría tanto alimento como se necesitaba para mantener el mismo número de liliputienses. Con esto puede el lector hacerse una idea del ingenio de aquella gente, así como de la prudente y escrupulosa administración de soberano tan grande. Swift habla de 900 liliputienses –aproximadamente, la mitad de 1.728–, con lo que cada uno de ellos debería desplazar el equivalente a dos veces él mismo: esto es perfectamente posible para liliputienses fuertes y ayudados –como se dice en el texto– por un sistema de cuerdas y poleas. ¡Un perfecto cálculo de proporciones! Nota: Ver también Una infalible manera de aprender matemáticas Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Jueves, 08 de Diciembre de 2022 | Imprimir | PDF |  Correo electrónico

10. Jan Łukasiewicz y la notación polaca

El matemático, lógico y filósofo Jan Łukasiewicz (1878-1956) nació un 21 de diciembre. Su trabajo se centró en la lógica, pensando innovar en la tradicional lógica proposicional, el principio de no contradicción y el principio del tercero excluido. Trabajó en lógica polivalente –incluyendo su propio cálculo de tres valores de verdad–, la primera lógica de cálculo no clásica. También se dedicó a otras áreas de la filosofía, aproximándose a los aspectos humanos de la creación de la teoría científica con ideas similares a las de Karl Popper. En 1920, Łukasiewicz inventó la llamada notación polaca para la lógica proposicional: en ella los conectivos lógicos son prefijados en vez de infijados –como ocurre en la notación usual–, y tiene importancia teórica para las ciencias de la computación. Para explicar esta notación, tomemos, por ejemplo, la expresión 5 * (12+4). La notación prefijada retoma la estructura de esta frase y la traduce en: (* 5 (+ 12 4)); el operador se sitúa delante de los operandos, en vez de estar situado entre los dos. También se puede usar la notación postfijada o polaca inversa, en la que el operador se sitúa tras los operandos: 5 12 4 + *. La ventaja es que no se precisa de paréntesis ni del signo de igualdad. Las calculadoras  Hewlett-Packard usan la notación polaca inversa, económica en número de entradas, pero que requiere un esfuerzo adicional para la interpretación del resultado. El principio de la mínima acción –que aquí se transforma en el principio del mínimo esfuerzo– hace que estas calculadoras sean finalmente poco usadas. Más información: Alfredo Deaño, Jan Łukasiewicz, Estudios de lógica y filosofía; Universidad Arcis Blog à Maths Jan Łukasiewicz, Elementos de lógica matemática, Państwowe Wydawnictwo Naukowe, 1963 Jan Łukasiewicz, La silogística de Aristóteles desde el punto de vista de la lógica formal moderna, Tecnos, 1977 Artículo publicado en el blog de la Facultad de Ciencia y Tecnología (ZTF-FCT) de la Universidad del País Vasco ztfnews.wordpress.com.

Miércoles, 21 de Diciembre de 2022 | Imprimir | PDF |  Correo electrónico