1. 130. (Enero 2023) Grafos Parsimónicos para una Selección de Escalas Heptatónicas y Pentatónicas (2/2)

1. Introducción El presente artículo fue presentado en junio de este año 2022 en la Conferencia Internacional de Matemáticas y Computación en Música, celebrada en Atlanta (GA, USA). Para facilitar su difusión entre un conjunto de lectores lo más amplio posible se ha simplificado en cierta medida su parte más teórica, pero se han mantenido en su totalidad los resultados obtenidos. En todo caso, el artículo completo puede consultarse en la referencia indicada al final de este artículo (Nuño 2022a). La primera parte de este trabajo se ha dedicado a la selección de ocho tipos de escalas heptatónicas, al análisis de sus características armónicas y a la obtención de un grafo parsimónico, denominado 7-Cíclope, que relaciona dichas escalas mediante transformaciones monosemitonales. A continuación, se llevará a cabo un proceso análogo para las escalas pentatónicas y se estudiará la relación acústica existente entre las escalas heptatónicas y pentatónicas consideradas aquí. Finalmente, se incluye un ejemplo de análisis musical con escalas heptatónicas. En caso de duda sobre alguno de los conceptos utilizados aquí, se recomienda consultar los artículos de Nuño (2020, 2021a y 2021d), anteriormente publicados en esta misma página Web. Al igual que se hizo en la primera parte de este estudio, emplearemos la notación inglesa para las notas musicales (C=Do, D=Re, E=Mi, F=Fa, G=Sol, A=La y B=Si). 2. Escalas Pentatónicas En esta sección se va a realizar la selección, análisis armónico y desarrollo de un grafo parsimónico para escalas pentatónicas, mediante un proceso totalmente análogo al seguido para las heptatónicas. 2.1. Selección de las Escalas Pentatónicas Para mantener un completo paralelismo con las escalas heptatónicas previamente seleccionadas, tomaremos ahora como escalas pentatónicas las complementarias de aquellas. La Tabla 5 muestra estos tipos de escalas con sus nombres de Forte extendidos, los símbolos para representarlas, sus estructuras interválicas y sus vectores de clases de intervalos. Los símbolos de la forma “m…P” y “7…P” representan, respectivamente, variantes de las escalas pentatónica menor (mP) y pentatónica “dominante” (7P), cuyas estructuras interválicas son 32232 y 22332. Nótese que la escala “mP” es un modo de la escala pentatónica mayor (MP). Tabla 5. Tipos de Escalas Pentatónicas considerados aquí. Escala Pentatónica Símbolo Estructura Interválica Vector de Clases de Intervalos 5-22 5-30a 5-30b 5-32a 5-32b 5-33 5-34 5-35 mΔ♯4P mΔP Δ♯5P m♯4P 7♯9P 7♯5P 7P MP 33141 32241 42231 33132 31332 22422 22332 22323 202321 121321 121321 113221 113221 040402 032221 032140 Estos ocho tipos de escalas también pueden obtenerse de forma análoga a como se obtuvieron las escalas heptatónicas combinando las cuatro notas alteradas más cercanas a la tonalidad de partida. Sin embargo, dado que las escalas pentatónicas no definen tonalidades, hablaremos ahora de notas modificadas en lugar de alteradas. Así, si partimos de la escala de C pentatónica mayor, debemos determinar, en primer lugar, cuáles de sus notas, modificadas en un semitono, dan lugar a otras escalas pentatónicas mayores. Un sencillo análisis nos revela que hay únicamente dos posibilidades: elevar E a F, obteniendo FMP, o bien rebajar C a B, obteniendo GMP. Y, a continuación, repetimos este proceso para hallar las siguientes escalas pentatónicas más cercanas a ellas, obteniendo así la Tabla 6, que es análoga a la Tabla 3 de la primera parte de este estudio, pero para las escalas pentatónicas. Podemos comprobar que, efectivamente, obtenemos los mismos ocho tipos de escalas de la Tabla 5. Tabla 6. Escalas Pentatónicas obtenidas a partir de CMP combinando dos notas modificadas. Notas Modificadas - E → F A → B♭ E → F, A → B♭ - C → B G → F♯ C → B, G → F♯ CMP GMP D7P DMP FMP G7P D7♯9P Bm♯4P C7P Em♯4P D7♯5P BmΔP B♭MP G7♯9P F♯Δ♯5P BmΔ♯4P Las características armónicas de estas escalas se muestran en la Tabla 7, utilizando para ello los vectores de tipos de tricordos y de tetracordos. Esta tabla es análoga a la Tabla 4 de la primera parte de este estudio, pero para las escalas pentatónicas, y en ambas se han aplicado los mismos criterios. Tabla 7. Vectores de Tipos de Tricordos y de Tetracordos para las Escalas Pentatónicas. Escala Vector de Tipos de Tricordos Vector de Tipos de Tetracordos 5-22 000111111-0000001111 000000000010-000000000000000011110-0000000000 5-30a 000100110-1011110101 000000000000-000000000001001000100-0010100000 5-30b 000011001-1101110011 000000000000-000000000000110000010-0100100000 5-32a 000110010-0110101210 000000000000-000000000001000101000-0000001100 5-32b 000110001-0111001120 000000000000-000000000000100110000-0000001010 5-33 000000000-3003300001 000000000000-000000000000000000000-2000210000 5-34 000000000-2111111110 000000000000-000000000000000000000-1110000110 5-35 000000000-1220030110 000000000000-000000000000000000000-0112001000 2.2. 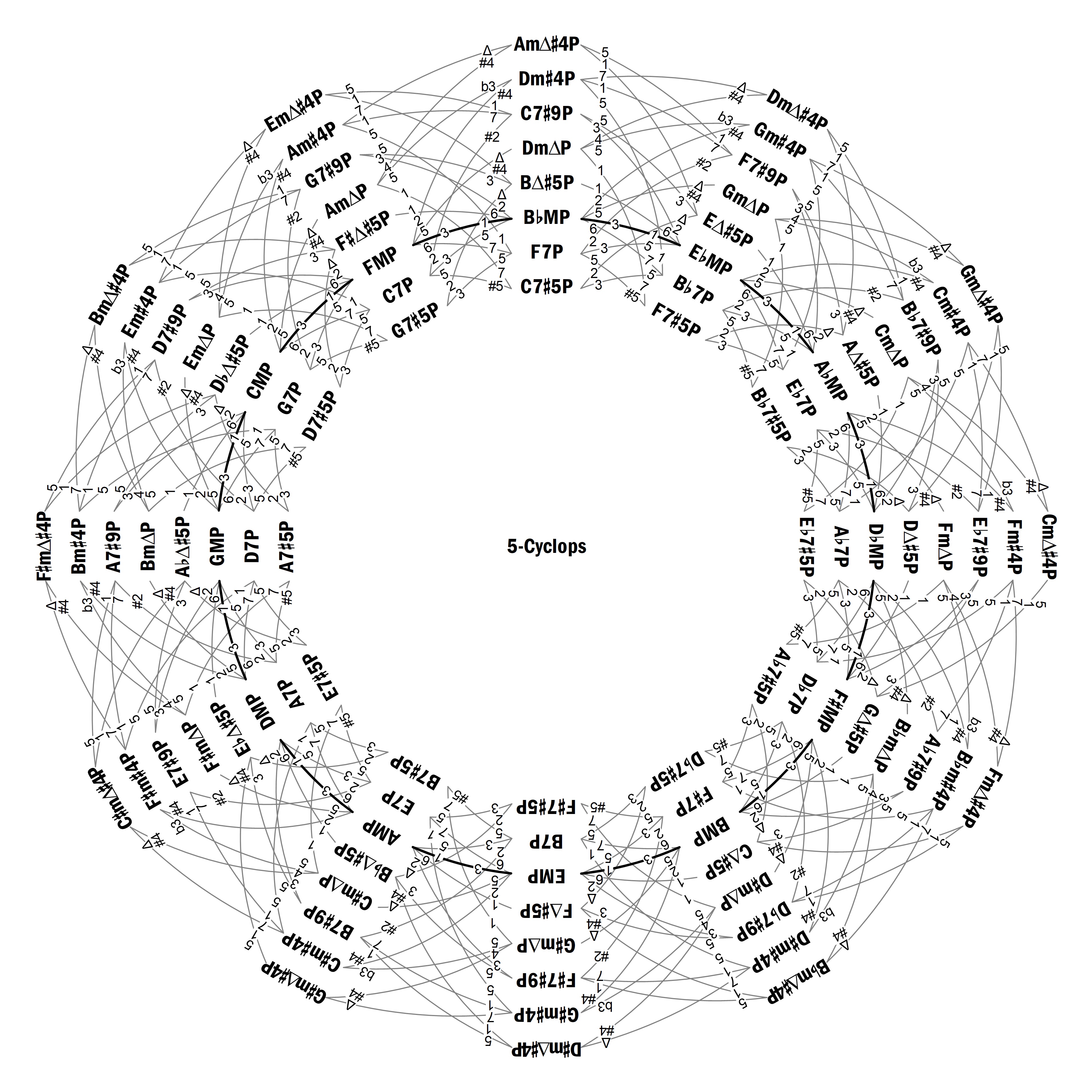Grafo Parsimónico para las Escalas Pentatónicas Seleccionadas La Figura 2 es un grafo cíclico circular que he denominado 5-Cíclope, que muestra todas las escalas pentatónicas de los tipos incluidos en la Tabla 5, conectadas mediante transformaciones monosemitonales. Dado que, si dos escalas están relacionadas mediante una transformación monosemitonal, también lo estarán sus complementarias, resulta que esta figura es completamente análoga a la Figura 1, y en ambas se han aplicado los mismos criterios. Puesto que los números 5 y 12 también son coprimos, en cada zona tenemos justamente una escala de cada tipo. Nótese que las escalas pentatónicas mayores son las únicas que pueden transformarse en otras de su mismo tipo, a la vez que los enlaces entre ellas forman ahora el ciclo de cuartas, que es la única circunferencia posible en este grafo (la línea gruesa). Fig. 2. El 5-Cíclope, con los tipos de escalas pentatónicas considerados en la Tabla 5. 2.3. Relación entre las Escalas Heptatónicas y Pentatónicas Seleccionadas Aparte de la relación de complementariedad que tenemos entre las escalas heptatónicas y pentatónicas consideradas aquí, existen entre ellas unas relaciones acústicas muy interesantes que pueden observarse mediante el vector de tipos de pentacordos, que es otra generalización del vector de tipos de intervalos. Este nuevo vector indica cuántos pentacordos (o escalas pentatónicas) de cada tipo contiene una escala dada. La Tabla 8 muestra este vector para las escalas heptatónicas incluidas en la Tabla 2 de la primera parte de este estudio, más el par 7-31a/7-31b considerado por Žabka (2014). En dicho vector, cada dígito corresponde a un tipo de escala pentatónica en el orden establecido por Nuño (2021c o, en español, 2020 y 2021a). Se han representado en negrita los dígitos correspondientes a las escalas pentatónicas consideradas aquí. Así, de izquierda a derecha, el primer dígito en negrita corresponde a la escala 5-22 y los últimos nueve dígitos (que están después de un espacio en blanco) corresponden a las escalas 5-30a, 5-30b, 5-31a, 5-31b, 5-32a, 5-32b, 5-33, 5-34 y 5-35. Tabla 8. Vector de Tipos de Pentacordos para diversas Escalas Heptatónicas. Escala Vector de Tipos de Pentacordos 7-22 0000000001100-000000000000001111111110011112-00000000001100 000011000 7-30a 0000000000100-010001000010001000001010011100-00110001110100 200010110 7-30b 0000000001000-001000100001001000010100011010-00110010111000 020001110 7-31a 0000000000000-000210000000000120000002100000-00002100002100 003021000 7-31b 0000000000000-000120000000000210000001200000-00001200001200 000312000 7-32a 0000000000000-000100000100000010100110001101-10001011010011 102110000 7-32b 0000000000000-000010000100000100100110010011-01000111100011 011201000 7-33 0000000000000-111000000011001000000000000000-00110011001100 110000610 7-34 0000000000000-000110000000000000100000000000-11111111001111 110000121 7-35 0000000000000-000000000100000000000000011000-22111100220011 000000013 Como podemos ver en la tabla, la escala 7-35 contiene tres escalas del tipo 5-35. Este es, además, el máximo número de escalas 5-35 contenidas en cualquiera de las diferentes escalas heptatónicas (no solo las incluidas en la tabla), ya que en el resto de los casos este número no es superior a dos. Así mismo, las escalas 7-34, 7-33 y 7-22 contienen, respectivamente, el máximo número de escalas 5-34, 5-33 y 5-22, que son 2, 6 y 2 (el resto de las escalas heptatónicas no contienen más de una en cada caso). En cuanto a los pares de escalas formados por un tipo a y un tipo b, debemos tener en cuenta que la complementaria de un tipo a es un tipo b y viceversa (Nuño 2021c o, en español, 2020 y 2021a). Entonces, las escalas 7-30a y 7-30b contienen, respectivamente, el máximo número de escalas 5-30a y 5-30b (es decir, las inversas de sus complementarias), que es dos (el resto de las escalas heptatónicas no contienen más de una), mientras que no contienen ninguna de sus correspondientes escalas complementarias. Así mismo, las escalas 7-31a y 7-31b contienen, respectivamente, el máximo número de escalas 5-31a y 5-31b, que es tres (el resto de las escalas heptatónicas no contienen más de dos) y tampoco contienen a sus correspondientes escalas complementarias. Pero, en cuanto al contenido en escalas 5-32a y 5-32b, resulta que son las escalas heptatónicas 7-31a y 7-31b las que contienen, respectivamente, el máximo número de ellas, que es dos (el resto de las escalas heptatónicas no contienen más de una). Por su parte, las escalas 7-32a y 7-32b contienen, respectivamente, una escala 5-32a y una 5-32b (de nuevo, las inversas de sus complementarias) y no contienen a sus correspondientes escalas complementarias. Por tanto, en todos estos casos existe, en mayor o menor medida, una clara relación acústica entre cada tipo de escala heptatónica y la inversa de su complementaria (que es pentatónica). 3. Ejemplo de Análisis Musical Žabka (2014) incluye en su artículo el análisis de un pasaje cromático muy interesante: la Fantasía en C menor, K. 475, de Mozart, compases 1–25. Para ello, determina cuáles son las escalas heptatónicas utilizadas en cada caso, aunque algunas de ellas aparecen de forma incompleta. Con la nomenclatura usada en el presente artículo, estas escalas son: Ghh  %  FhM  %  D♭M  E♭mm  FNpm  B♭hm  B♭Npm  BM  %  G♯Npm D♭hL  F♯Npm  C♭hL  BhM  Bhm  GM  %  %  F♯Npm–F♯hh  F♯hM  %  %  % donde cada escala o cada pareja de escalas unidas por un guión dura un compás y el símbolo “%” significa repetir el compás anterior. Las representaciones de este pasaje realizadas por Žabka (2014) presentan algunas complicaciones y pueden compararse con la que se muestra en la Figura 3 en el 7-Cíclope, el cual contiene todas las escalas requeridas, y donde la primera de ellas se ha indicado con una línea doble. Aunque la composición está en C menor, Mozart no incluye ninguna alteración en la armadura; y, como se aprecia en la Figura 3, no se utiliza ninguna de las escalas Chm, Cmm o C menor natural (E♭M). No obstante, la escala inicial, Ghh, contiene el acorde de C menor, cuyo arpegio se ejecuta empezando justamente por la nota C (cuarto modo de Ghh). A partir de ahí, las escalas se mueven en el diagrama en sentido antihorario, es decir, en la dirección de los bemoles (con algunos movimientos hacia delante y hacia atrás), hasta llegar a GM, cuya tónica (en el bajo) es la dominante de C. Sin embargo, la resolución no se hace sobre una escala de C menor, sino sobre varias escalas de tónica F♯, que está a un intervalo de tritono de C, y los últimos cuatro compases están basados, de hecho, en el acorde de F♯ mayor. Fig. 3. Mozart, Fantasía en C menor, K. 475, compases 1–25. Análisis con el 7-Cíclope. 4. Conclusiones e Información Adicional Como conclusiones del artículo completo, podemos decir que, siguiendo unos criterios puramente musicales, se han seleccionado ocho tipos de escalas heptatónicas y sus complementarias pentatónicas. Sus características armónicas se han analizado mediante los vectores de clases de intervalos, de tipos de tricordos y de tipos de tetracordos. Además, se han desarrollado dos nuevos grafos parsimónicos, denominados 7-Cíclope y 5-Cíclope, que relacionan cada uno de estos tipos de escalas mediante transformaciones monosemitonales. En estos grafos destacan, respectivamente, los ciclos de quintas y de cuartas, que son las únicas circunferencias posibles que conectan escalas del mismo tipo en esta clase de grafos (aparte de los casos triviales de escalas de una u once notas). Por otra parte, se ha encontrado una relación acústica entre cada escala heptatónica y la inversa de su complementaria, utilizando para ello el vector de tipos de pentacordos. Finalmente, se ha incluido un ejemplo de aplicación al análisis musical de una obra bastante compleja, por lo que toda esta información se estima que puede ser de interés tanto para teóricos como para compositores. Los lectores interesados en los tipos de vectores utilizados aquí, tanto para el caso del sistema de afinación temperado de doce notas como para otros sistemas más generales, pueden encontrar información adicional en Nuño (2022b). En ese artículo se presenta un riguroso estudio considerando la división de la octava en un número arbitrario de notas n y se incluyen diferentes teoremas que proporcionan una visión global y un conocimiento detallado de estos tipos de vectores.   Referencias Balzano, G. 1980. “The Group-Theoretic Description of 12-Fold and Microtonal Pitch Systems”. Computer Music Journal 4 (4), 66–84. Cohn, R. 1996. “Maximally Smooth Cycles, Hexatonic Systems, and the Analysis of Late-Romantic Triadic Progressions”. Music Analysis 15 (1), 9–40. Cohn, R. 2012. Audacious Euphony: Chromatic Harmony and the Triad’s Second Nature. New York: Oxford University Press. Douthett, J., Steinbach, P. 1998. “Parsimonious Graphs: A Study in Parsimony, Contextual Transformations, and Modes of Limited Transposition”. Journal of Music Theory 42 (2), 241–263. Forte, A. 1973. The Structure of Atonal Music. New Haven: Yale University Press. Hook, J. 2011. “Spelled Heptachords”. En: Agon, C., et al. (eds.) Mathematics and Computation in Music 2011, pp. 84–97. Heidelberg: Springer. Nuño, L. 2020. “La Tabla Periódica Musical (1/2).” DIVULGAMAT, Centro virtual de divulgación de las matemáticas, RSME: Real Sociedad Matemática Española, No. 111. Diciembre 2020. https://www.divulgamat.net/index.php?option=com_content&view=article&id=18500&directory=67 Nuño, L. 2021a. “La Tabla Periódica Musical (2/2).” DIVULGAMAT, Centro virtual de divulgación de las matemáticas, RSME: Real Sociedad Matemática Española, No. 112. Enero 2021. https://www.divulgamat.net/index.php?option=com_content&view=article&id=18516&directory=67 Nuño, L. 2021b. Parsimonious Graphs for the Most Common Trichords and Tetrachords. Journal of Mathematics and Music 15(2), 125–139 (2021). Nuño, L. 2021c. A Detailed List and a Periodic Table of Set Classes. Journal of Mathematics and Music 15(3), 267–287. Nuño, L. 2021d. “Grafos Parsimónicos para los Tricordos y Tetracordos más Comunes.” DIVULGAMAT, Centro virtual de divulgación de las matemáticas, RSME: Real Sociedad Matemática Española, No. 119. Octubre 2021. https://divulgamat.net/index.php?option=com_content&view=article&id=18666&directory=67 Nuño, L. 2022a. “Parsimonious Graphs for Selected Heptatonic and Pentatonic Scales”. En: Montiel, M., Agustín-Aquino, O.A., Gómez, F., Kastine, J., Lluis-Puebla, E., Milam, B. (eds) Mathematics and Computation in Music. MCM 2022. Lecture Notes in Computer Science, vol 13267. Springer, Cham. https://doi.org/10.1007/978-3-031-07015-0_3 Nuño, L. 2022b. “Type and Class Vectors and Matrices in ℤn. Application to ℤ6, ℤ7 and ℤ12.” Journal of Mathematics and Music. https://www.tandfonline.com/doi/full/10.1080/17459737.2022.2120214 Piston, W. 1988. Harmony. 5th edn. New York: W. W. Norton and Co. Popley, H. A. 1921. The Music of India. London: Oxford University Press. Ring, I. 2022 (15 marzo). The Exciting Universe of Music Theory, https://ianring.com/musictheory/scales/ Schönberg, A. 1983: Theory of Harmony. 3rd edn. Berkeley, Calif.: University of California Press. Tymoczko, D. 2011. A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice. New York: Oxford University Press. Žabka, M. 2014. “Dancing with the Scales: Subchromatic Generated Tone Systems”. Journal of Music Theory 58 (2), 179–233.

Domingo, 01 de Enero de 2023 | Imprimir | PDF |  Correo electrónico

2. 129. (Diciembre 2022) Grafos Parsimónicos para una Selección de Escalas Heptatónicas y Pentatónicas (1/2)

Tenemos otra vez más el placer de contar como autor invitado a Luis Nuño, que ya ha escrito en esta columna anteriormente. Luis Nuño es catedrático de universidad en la Universidad Politécnica de Valencia y autor de la Rueda Armónica. Es un gran investigador de la teoría matemática y computacional de la música así como un divulgador de la misma. Ha publicado varios artículos de investigación en la prestigiosa revista Journal of Mathematics and Music. Siguiendo con su trabajo de grafos parsimónicos, esta vez estudia dichos grafos sobre escalas heptatónicas y pentatónicas. Este trabajo que trae a Divulgamat consta de dos partes; la segunda la veremos en enero. De nuevo, estamos ante un artículo iluminador y profundo. Espero que los lectores de esta columna lo disfruten tanto como lo he hecho al leerlo. Paco Gómez Martín 1. Introducción El presente artículo fue presentado en junio de este año 2022 en la Conferencia Internacional de Matemáticas y Computación en Música, celebrada en Atlanta (GA, USA). Para facilitar su difusión entre un conjunto de lectores lo más amplio posible se ha simplificado en cierta medida su parte más teórica, pero se han mantenido en su totalidad los resultados obtenidos. En todo caso, el artículo completo puede consultarse en la referencia indicada al final de este artículo (Nuño 2022a). La escala mayor es la base de la música occidental. Por ello, aunque pueda parecer superfluo, conviene revisar algunas de sus principales características. Se trata de un conjunto de siete notas que guardan entre sí una gran afinidad acústica, de manera que es muy “completo y versátil”. Así, muchas canciones populares – y no tan populares – están compuestas en una tonalidad mayor. Nuestra notación musical, basada en el pentagrama y las armaduras, es idónea para escribir música en las tonalidades mayores. El piano, considerado el “instrumento rey”, está perfectamente adaptado para tocar en la tonalidad de Do mayor. Los nombres de las notas son siete – en lugar de doce –, precisamente las de la escala de Do mayor. El término octava (derivado de “ocho”) indica su extensión (repitiendo la tónica al final), mientras que los términos tono y semitono describen los intervalos entre dos de sus notas sucesivas. Así mismo, la calificación de los intervalos (justo, mayor, menor, etc.) se establece tomando como referencia una escala mayor. En resumen, la escala mayor es fundamental en teoría de la música y composición. Además, a partir de la escala mayor pueden obtenerse directamente otros tipos de escalas. Por ejemplo, tomando cualquiera de sus notas como como tónica, obtenemos siete modos, de los cuales el eólico constituye la escala menor, que es también característica de la música occidental. En este caso, sus grados sexto y séptimo pueden ser naturales o alterados (elevados un semitono), lo que da lugar a las escalas menores natural, melódica y armónica. Por otra parte, la escala complementaria de una escala mayor (es decir, la formada por el resto de las doce notas) es una escala pentatónica mayor. En general, las escalas pentatónicas – y no solo la pentatónica mayor – han sido utilizadas por diferentes culturas desde la antigüedad. Aunque son predominantes en los países del este (China, Japón, India, Java, etc.), también se han empleado en diferentes estilos occidentales, tanto en la música clásica como en la escocesa, andina, jazz, etc. Este estudio está basado en el sistema de afinación temperado de doce notas, utilizándose como nomenclatura los nombres de Forte y las clases de conjuntos (Forte 1973), que aquí llamaremos clases de escalas. De entre ellas, las no inversionalmente simétricas se dividen en dos tipos de escalas relacionados entre sí por inversión, llamados a y b, de acuerdo con Nuño (2021c o, en español, 2020 y 2021a). Con respecto a las escalas mayor y pentatónica mayor podemos decir que son las escalas de siete y cinco notas, respectivamente, que tienen sus notas más uniformemente espaciadas. Y, además, poseen una propiedad exclusiva: aparte de los casos triviales de las escalas de una u once notas, son las únicas que pueden transformarse en otras de su mismo tipo mediante una transformación monosemitonal (es decir, cambiando una sola nota y solo un semitono, que puede ser ascendente o descendente). Por ejemplo, subiendo en la escala de Do mayor la nota Fa un semitono obtenemos la escala de Sol mayor. Esta propiedad, para el caso de las escalas mayores, da lugar al orden de los sostenidos y los bemoles, así como al ciclo de quintas (Balzano 1980, Cohn 1996), que es fundamental en la teoría de la modulación, es decir, el cambio de una tonalidad a otra. En este sentido, dada una tonalidad, las más “cercanas” a ella son las que tienen un sostenido o un bemol de más o de menos en su armadura (Schönberg 1983, Piston 1988). Esto también es aplicable a las tonalidades menores, ya que sus armaduras son las mismas que las de sus relativas mayores. El concepto de transformación parsimónica es algo más general, ya que, en este caso, son una o más notas las que cambian en uno o dos semitonos (en la práctica, no más de dos semitonos en total), mientras el resto permanecen fijas (Douthett y Steinbach 1998). A este respecto, el Tonnetz es una primera representación de este tipo de transformaciones para las tríadas mayores y menores, mientras que Douthett y Steinbach (1998) presentan otros grafos más complejos e interesantes. En el s. XIX, diversos compositores hacen un uso extensivo de este tipo de transformaciones, varias de cuyas obras son analizadas por Cohn (2012). Por su parte, Tymoczko (2011) sigue un planteamiento distinto, representando los conjuntos de notas en unos espacios particulares denominados orbifolds. En cambio, Nuño (2021b o, en español, 2021d) desarrolla unos grafos cíclicos circulares, llamados Cíclopes, que relacionan los tricordos y tetracordos “más comunes”, mediante los cuales se puede analizar de forma práctica un buen número de dichos tipos de obras. En este artículo se presentan dos nuevos grafos similares a ellos para relacionar diferentes escalas heptatónicas y pentatónicas. En cada caso, se han seleccionado ocho tipos de escalas siguiendo unos criterios puramente musicales. Además, muestran de forma gráfica un resultado anteriormente mencionado: el ciclo de quintas para las escalas mayores, que es complementado con el ciclo de cuartas para las escalas pentatónicas mayores, los cuales corresponden a las únicas circunferencias posibles que conectan escalas del mismo tipo en estas clases de grafos (Balzano 1980, Cohn 1996). Este trabajo consta de dos partes, la primera de las cuales se dedica a las escalas heptatónicas y la segunda a las pentatónicas, en la cual se estudiará también la relación acústica existente entre ambas y se incluye, además, un ejemplo de análisis musical con escalas heptatónicas. En caso de duda sobre alguno de los conceptos utilizados aquí, se recomienda consultar los artículos de Nuño (2020, 2021a y 2021d), anteriormente publicados en esta misma página Web. 2. Selección de las Escalas Heptatónicas La música tonal está basada en las escalas mayor, menor melódica y menor armónica (Schönberg 1983, Piston 1988), cuyos nombres de Forte “extendidos” son 7-35, 7-34 y 7-32a, respectivamente. Para completar esta serie numérica podemos considerar también las escalas 7-32b (mayor armónica) y 7-33 (napolitana mayor, según la nomenclatura de Ring 2022). Estas son, además, las escalas heptatónicas cuyas notas están más uniformemente espaciadas, sobre todo la escala mayor (7-35). Para obtener otras escalas heptatónicas a partir de ellas podemos, simplemente, descomponerlas en tetracordos (entendidos ahora como grupos de cuatro notas consecutivas) y combinar dos de ellos. Este es el procedimiento utilizado, por ejemplo, en la música tradicional de India para obtener las escalas heptatónicas denominadas “Melakarta ragas” (Popley 1921). Otra opción es partir de una escala mayor y elevar o rebajar una o más notas un semitono, tal como se hace con la escala menor natural para obtener las escalas menores armónica y melódica. En este caso, lo lógico es tomar las notas alteradas de las tonalidades más cercanas a la considerada. A continuación, usaremos ambos procedimientos para obtener un número “razonable” de escalas heptatónicas que nos permitan obtener unos grafos de complejidad aceptable y que pueden ser de interés para teóricos y compositores. Por otra parte, en adelante emplearemos la notación inglesa para las notas musicales (C=Do, D=Re, E=Mi, F=Fa, G=Sol, A=La y B=Si). 2.1. Combinaciones de dos Tetracordos Consideremos la escala de C mayor. Podemos ver que está compuesta por los tetracordos C – D – E – F y G – A – B – C, donde el primero de ellos comienza por la nota C y el segundo por G. En ambos casos, sus “estructuras interválicas”, en semitonos, son iguales: 221, siendo el intervalo entre los dos tetracordos de 2 semitonos. Por tanto, podemos escribir la estructura interválica de la escala completa como 221 2 221 y al tetracordo 221 lo llamaremos “mayor”. Si empezamos esa misma escala por las notas D o A, las primeras cuatro notas formarán un tetracordo de la forma 212, que llamaremos “menor”. Si, en cambio, empezamos por las notas E o B, resulta un tetracordo del tipo 122, que llamaremos “frigio”. Y, por último, si empezamos por la nota F, obtenemos un tetracordo del tipo 222, que llamaremos “lidio”. Así, podemos obtener diferentes escalas heptatónicas combinando dos cualesquiera de estos cuatro tetracordos. Pero, para obtener las escalas armónicas, tanto mayores como menores, necesitamos otro tipo de tetracordo: el 131, que llamaremos “armónico”. La Tabla 1 muestra las 25 posibles combinaciones de dos de estos cinco tipos de tetracordos. Se indican también las estructuras interválicas de las escalas resultantes, así como los nombres y símbolos usados para representarlas. Los nombres menos comunes se han tomado de Ring (2022) y se ha utilizado el mismo nombre para todos los modos de una misma escala. Además, en todos los casos, el intervalo entre los dos tetracordos se ha elegido de manera que la primera y la última nota de cada escala sea la misma. Es decir, que la suma de todos los semitonos en cada escala sea igual a 12. Tabla 1. Tipos de escalas heptatónicas obtenidas combinando dos de los cinco tetracordos considerados aquí, junto con sus correspondientes estructuras interválicas. Los símbolos utilizados para representar las escalas son: M: mayor, mm: menor melódica, hm: menor armónica, hM: mayor armónica, NpM: napolitana mayor, Npm: napolitana menor, hL: lidia armónica, hh: doble armónica o húngara y WT: escala de tonos. 1º ↓ \ 2º → mayor menor frigio lidio armónico mayor 221 2 221 M 221 2 212 M 221 2 122 mm 221 1 222 NpM 221 2 131 hM menor 212 2 221 mm 212 2 212 M 212 2 122 M 212 1 222 mm 212 2 131 hm frigio 122 2 221 NpM 122 2 212 mm 122 2 122 M 122 1 222 M 122 2 131 Npm lidio 222 1 221 M 222 1 212 mm 222 1 122 NpM 222 222 WT 222 1 131 hL armónico 131 2 221 hL 131 2 212 hM 131 2 122 hm 131 1 222 Npm 131 2 131 hh Como podemos ver, la combinación de dos tetracordos lidios da lugar a la escala de tonos (WT), que solo tiene seis notas, por lo que no la incluiremos en este estudio. El resto de las combinaciones dan lugar a ocho tipos diferentes de escalas, entre las que se encuentran las cinco mencionadas al principio de la Sección 2, siendo, además, un número adecuado (ni muy grande ni muy pequeño) para desarrollar los grafos parsimónicos deseados. La Tabla 2 muestra estos tipos de escalas con sus nombres de Forte extendidos, los símbolos para representarlas y sus estructuras interválicas. La última columna es el vector de clases de intervalos, que consta de seis dígitos que indican correlativamente cuántos intervalos de cada clase (de 1 a 6 semitonos) contiene la escala considerada. Así, por ejemplo, este vector indica que la escala mayor (7-35) contiene “2” intervalos de 1 semitono, “5” intervalos de 2 semitonos, “4” intervalos de 3 semitonos, “3” intervalos de 4 semitonos, “6” intervalos de 5 semitonos y “1” intervalo de 6 semitonos. Tabla 2. Tipos de Escalas Heptatónicas considerados aquí. Escala Heptatónica Símbolo Estructura Interválica Vector de Clases de Intervalos 7-22 hh 1312131 424542 7-30a Npm 1222131 343542 7-30b hL 2221131 343542 7-32a hm 2122131 335442 7-32b hM 2212131 335442 7-33 NpM 1222221 262623 7-34 mm 2122221 254442 7-35 M 2212221 254361 2.2. Combinaciones de las Notas Alteradas pertenecientes a las Tonalidades más Cercanas Consideremos de nuevo la escala de C mayor. Sus dos tonalidades más cercanas, siguiendo tanto el orden de los sostenidos como el de los bemoles, dan lugar a las notas alteradas F♯, C♯, B♭ y E♭. Así, partiendo de la escala de C mayor y utilizando estas cuatro notas, bien naturales o alteradas, resultan 16 combinaciones, las cuales se muestran en la Tabla 3, junto con las escalas resultantes. Como puede verse, obtenemos los mismos ocho tipos de escalas heptatónicas que con el procedimiento anterior. Además, de acuerdo con el studio de Hook (2011), estas son justamente las escalas que tienen un “span” menor o igual que 10. Por todo ello, estos serán los tipos de escalas heptatónicas que consideraremos en este estudio y cuyas principales características están recogidas en la Tabla 2. Tabla 3. Escalas Heptatónicas obtenidas a partir de CM combinando dos notas alteradas. Notas Alteradas - F → F♯ C → C♯ F → F♯, C → C♯ - CM GM Dmm DM B → B♭ FM Gmm Dhm DhM E → E♭ Cmm GhM DNpM GhL B → B♭, E → E♭ B♭ M Ghm DNpm Dhh 2.3. Características Armónicas de las Escalas Heptatónicas Seleccionadas Para analizar las características armónicas de las escalas heptatónicas seleccionadas podemos utilizar dos generalizaciones del vector de clases de intervalos: el vector de tipos de tricordos y el vector de tipos de tetracordos, los cuales indican, respectivamente, cuántos tricordos y tetracordos de cada tipo contiene la escala considerada. La Tabla 4 muestra estos vectores para las escalas seleccionadas, donde cada uno de sus dígitos corresponde a un tipo de acorde en el orden establecido por Nuño (2021c o, en español, 2020 y 2021a). Así, por ejemplo, los primeros dígitos del vector de tipos de tricordos, de derecha a izquierda, corresponden a las tríadas aumentada, mayor, menor y disminuida. Y los primeros dígitos del vector de tipos de tetracordos, también de derecha a izquierda, corresponden al acorde de séptima disminuida, acorde de séptima de dominante, acorde semidisminuido (o de séptima de sensible) y acorde menor con séptima menor. Los dígitos en negrita corresponden a los tricordos y tetracordos “más comunes”, según el artículo de Nuño (2021b o, en español, 2021d). Tabla 4. Vectores de Tipos de Tricordos y de Tetracordos para las Escalas Heptatónicas. Escala Vector de Tipos de Tricordos Vector de Tipos de Tetracordos 7-22 111333322-0112212331 000111110220-000110011111111222222-0000011110 7-30a 111212321-3123321321 010001110110-011010011112012101202-2120211110 7-30b 111123212-3213321231 001010110110-011100011110221110022-2210211110 7-32a 022222221-1221224321 000100000110-111212112011011112211-0011101211 7-32b 022222212-1222124231 000100000110-111121221100111121121-0101101121 7-33 111111111-6116611112 011000110000-011110000111111000110-6110630110 7-34 022111111-3333332221 000100000000-211111111111111000110-2222211220 7-35 022002211-3441151330 000000000010-222001122110011000002-1334003110 3. 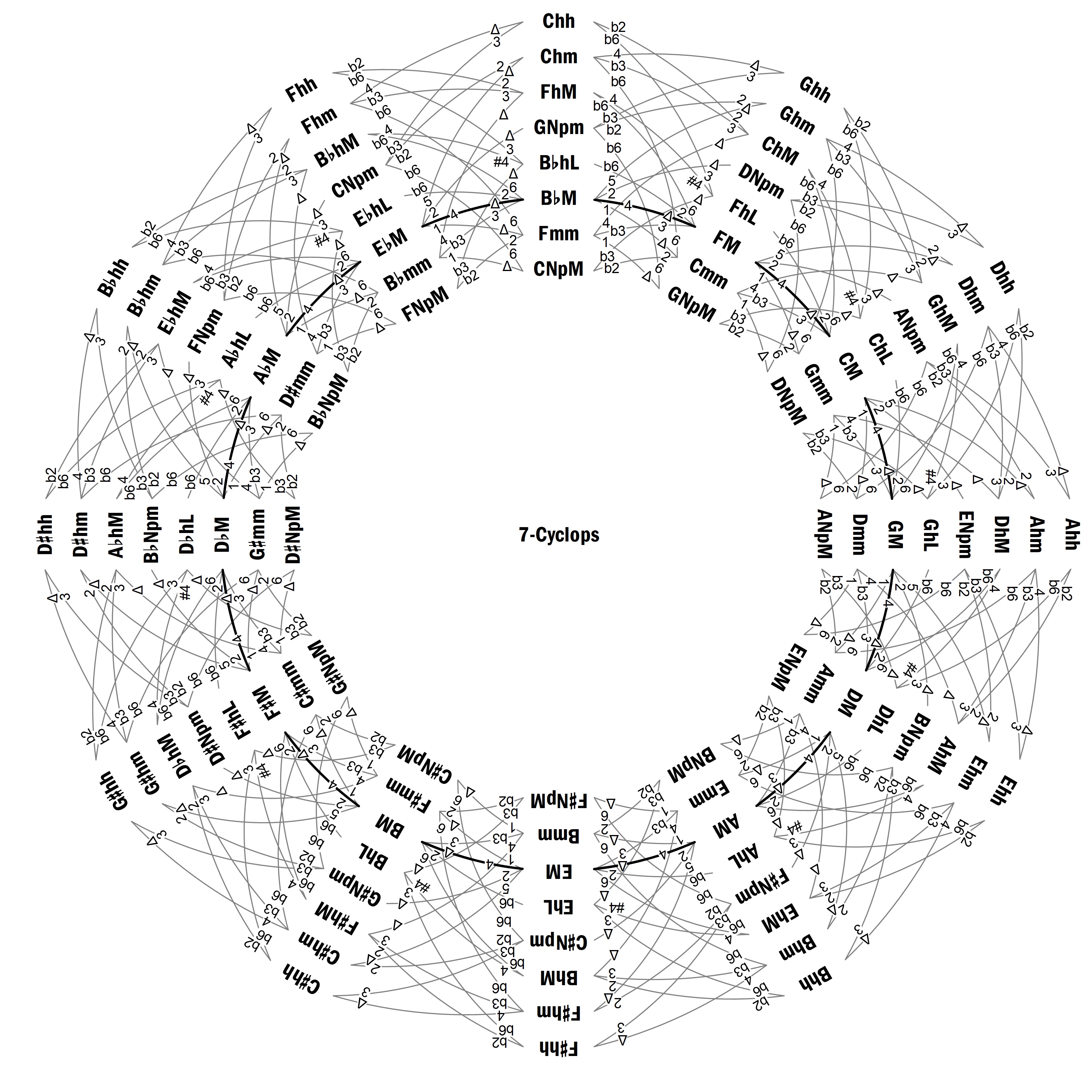Grafo Parsimónico para las Escalas Heptatónicas Seleccionadas La Figura 1 es un grafo cíclico circular que he denominado 7-Cíclope, que muestra todas las escalas heptatónicas de los tipos considerados en la Tabla 2, conectadas mediante transformaciones monosemitonales. Así, se pasa de una escala a otra adyacente cambiando una nota un semitono, el cual puede ser ascendente, si giramos en sentido horario, o descendente, si lo hacemos en sentido antihorario. Los números que hay en los extremos de las líneas que conectan las escalas indican las notas inicial y final referidas a las tónicas de estas escalas, donde 1 a 6 representan intervalos justos o mayores, que pueden alterarse mediante ♯ o ♭, mientras que las séptimas mayores y menores se representan mediante Δ y 7, respectivamente. Haciendo una analogía con la carátula de un reloj, cada acorde se ha colocado en una “zona”, que viene definida por “la suma de sus notas”, módulo 12 (Cohn 2012, p. 102). Así, por ejemplo, la escala CM = (C, D, E, F, G, A, B) está en la zona 0 + 2 + 4 + 5 + 7 + 9 + 11 = 2 (mod 12) y, análogamente, la escala B♭ M = (B♭ , C, D, E♭, F, G, A) está en la zona 0. De esta manera, si se sube o baja un semitono una nota de una escala, pasamos a la siguiente zona girando en sentido horario o antihorario, respectivamente. Y las escalas relacionadas por movimiento puramente contrario, como CM y Dhm = (D, E, F, G, A, B♭ , C♯) están en la misma zona (en este caso, 2). Puesto que los números 7 y 12 son coprimos, en cada zona tenemos justamente una escala de cada tipo. Nótese que las escalas mayores son las únicas que pueden transformarse en otras de su mismo tipo, a la vez que los enlaces entre ellas forman el ciclo de quintas, que es la única circunferencia posible en este grafo (la línea gruesa). Fig. 1. El 7-Cíclope, con los tipos de escalas heptatónicas considerados en la Tabla 2. En cuanto a otros diagramas similares, tenemos el desarrollado por Tymoczko (2011, p. 136), el cual incluye las escalas mayores (que llama diatónicas), las menores melódicas (que llama acústicas y cuya tónica es la cuarta justa de la correspondiente escala menor melódica), las menores y mayores armónicas, más otras tres escalas no heptatónicas y con simetría transposicional: la escala de tonos (6-35), la hexatónica (6-20, también llamada aumentada) y la octatónica (8-28, también llamada disminuida semitono/tono), cuyas estructuras interválicas son, respectivamente, 222222, 131313 y 12121212. En este caso, para colocar adecuadamente todas estas escalas se utilizan 36 posiciones angulares que, lógicamente, no pueden coincidir con las zonas consideradas aquí, a la vez que no se indican las notas que cambian de una escala a otra. Así mismo, algunas de estas escalas están repetidas varias veces dentro del diagrama. Otro trabajo relevante es el publicado por Žabka (2014), que está basado en lo que denomina “series de transición comática”, y que incluye, además de las escalas de la Tabla 2, el par 7-31a/7-31b y las escalas de tonos con una nota enarmónica adicional. Estas escalas las distribuye en tres diagramas diferentes, por lo que no se muestran las conexiones existentes entre algunas de ellas, a la vez que tampoco se indican las notas que cambian de una escala a otra. Por otra parte, la nomenclatura utilizada para algunas de estas escalas es distinta de la empleada aquí. 4. Conclusiones Siguiendo unos criterios puramente musicales se han seleccionado ocho tipos de escalas heptatónicas. Sus características armónicas se han analizado mediante los vectores de clases de intervalos, de tipos de tricordos y de tipos de tetracordos. Además, se ha desarrollado un nuevo grafo parsimónico, denominado 7-Cíclope, que relaciona todas esas escalas mediante transformaciones monosemitonales. En este grafo destaca claramente el ciclo de quintas, que es la única circunferencia posible que conecta escalas del mismo tipo en este grafo. En la segunda parte de este trabajo se llevará a cabo un proceso análogo para las escalas pentatónicas y se estudiará la relación acústica existente entre las escalas heptatónicas y pentatónicas consideradas aquí. Además, se incluirá un ejemplo de análisis musical con escalas heptatónicas. Finalmente, para los lectores interesados en un estudio más general de los vectores empleados en este estudio, se recomienda el artículo de Nuño (2022b), recientemente publicado.   Referencias Balzano, G. 1980. “The Group-Theoretic Description of 12-Fold and Microtonal Pitch Systems”. Computer Music Journal 4 (4), 66–84. Cohn, R. 1996. “Maximally Smooth Cycles, Hexatonic Systems, and the Analysis of Late-Romantic Triadic Progressions”. Music Analysis 15 (1), 9–40. Cohn, R. 2012. Audacious Euphony: Chromatic Harmony and the Triad’s Second Nature. New York: Oxford University Press. Douthett, J., Steinbach, P. 1998. “Parsimonious Graphs: A Study in Parsimony, Contextual Transformations, and Modes of Limited Transposition”. Journal of Music Theory 42 (2), 241–263. Forte, A. 1973. The Structure of Atonal Music. New Haven: Yale University Press. Hook, J. 2011. “Spelled Heptachords”. En: Agon, C., et al. (eds.) Mathematics and Computation in Music 2011, pp. 84–97. Heidelberg: Springer. Nuño, L. 2020. “La Tabla Periódica Musical (1/2).” DIVULGAMAT, Centro virtual de divulgación de las matemáticas, RSME: Real Sociedad Matemática Española, No. 111. Diciembre 2020. https://www.divulgamat.net/index.php?option=com_content&view=article&id=18500&directory=67 Nuño, L. 2021a. “La Tabla Periódica Musical (2/2).” DIVULGAMAT, Centro virtual de divulgación de las matemáticas, RSME: Real Sociedad Matemática Española, No. 112. Enero 2021. https://www.divulgamat.net/index.php?option=com_content&view=article&id=18516&directory=67 Nuño, L. 2021b. Parsimonious Graphs for the Most Common Trichords and Tetrachords. Journal of Mathematics and Music 15(2), 125–139 (2021). Nuño, L. 2021c. A Detailed List and a Periodic Table of Set Classes. Journal of Mathematics and Music 15(3), 267–287. Nuño, L. 2021d. “Grafos Parsimónicos para los Tricordos y Tetracordos más Comunes.” DIVULGAMAT, Centro virtual de divulgación de las matemáticas, RSME: Real Sociedad Matemática Española, No. 119. Octubre 2021. https://divulgamat.net/index.php?option=com_content&view=article&id=18666&directory=67 Nuño, L. 2022a. “Parsimonious Graphs for Selected Heptatonic and Pentatonic Scales”. En: Montiel, M., Agustín-Aquino, O.A., Gómez, F., Kastine, J., Lluis-Puebla, E., Milam, B. (eds) Mathematics and Computation in Music. MCM 2022. Lecture Notes in Computer Science, vol 13267. Springer, Cham. https://doi.org/10.1007/978-3-031-07015-0_3 Nuño, L. 2022b. “Type and Class Vectors and Matrices in ℤn. Application to ℤ6, ℤ7 and ℤ12.” Journal of Mathematics and Music. https://www.tandfonline.com/doi/full/10.1080/17459737.2022.2120214 Piston, W. 1988. Harmony. 5th edn. New York: W. W. Norton and Co. Popley, H. A. 1921. The Music of India. London: Oxford University Press. Ring, I. 2022 (15 marzo). The Exciting Universe of Music Theory, https://ianring.com/musictheory/scales/ Schönberg, A. 1983: Theory of Harmony. 3rd edn. Berkeley, Calif.: University of California Press. Tymoczko, D. 2011. A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice. New York: Oxford University Press. Žabka, M. 2014. “Dancing with the Scales: Subchromatic Generated Tone Systems”. Journal of Music Theory 58 (2), 179–233.

Lunes, 12 de Diciembre de 2022 | Imprimir | PDF |  Correo electrónico

3. 176. El drama personal de X

Un nuevo y reciente cortometraje con aspectos matemáticos como telón de fondo. Aunque pudiera parecer dirigido a público infantil, es probable que los adultos encuentren algún que otro “zasca” sobre la sociedad que han construido. Ficha Técnica: Título Original: Finding X. Nacionalidad: Australia, 2022. Dirección: Benjamin Zaugg. Guion: Toby Hendy. Música: Cassie To. Asesor Científico: Petr Lebedev. Asesor Literario: Dan Simpson. Producción: Toby Hendy y Cedric Scheerlinck. Duración: 11 min. Ficha artística: Intérpretes: Voz de Toby Hendy Argumento En el mundo de los números, la vida estaba claramente definida, las cosas bastante bien organizadas; todo el mundo conocía su valor numérico. Un día, sin embargo, todos los patrones se desbocaron al nacer x, a partir de una ecuación demasiado difícil de analizar. Según fue creciendo, x fue descubriendo como todos lo rechazaban, al no saber dónde encuadrarlo. Hasta que un día, harto de desprecios, decide ir a la busqueda de su identidad. Breve Comentario Encontrando a x es un simpático cortometraje, plagado de referencias matemáticas elementales (anímese el lector a localizarlas todas, que hay más de las que parecen tras un primer visionado), con mensaje (no solo matemático sino también humano, aplicable a todos los que por alguna razón se hayan sentido distintos o desplazados de su entorno social en alguna ocasión). En esta ocasión no voy a describir el argumento al pie de la letra, para que sea una sorpresa lo que podéis encontrar. Toby Hendy, el alma mater de este corto, tiene una destacada carrera con un montón de méritos. Se graduó en matemáticas y física por la Universidad de Canterbury (Nueva Zelanda), logrando una beca de astronomía Aurora que le permitió pasar largas temporadas entre semestres en el Observatorio de la Universidad de Monte John en Tekapo, además de diferentes estancias en la Universidad de California en Los Angeles (concretamente en el laboratorio de Propulsión a Chorro de la NASA), en el Observatorio Macdonald de Texas, en la Universidad de Columbia Británica, en el Observatorio NRC (National Research Council) Victoria en Canadá y en el telescopio CHFT (siglas de Canada, Francia, Hawái) en Hawaii. Posteriormente se doctoró en la Universidad Nacional de Australia, en Canberra, con un tesis titulada “Examen de la respuesta mecánica de la Arabidopsis thaliana usando nanoindentación y modelado de elementos finitos”, con una calificación ciertamente sobresaliente (93 puntos de 100 posibles). Paralelamente, participó en el certamen Famelab de divulgación científica de su país quedando en un digno segundo lugar. Esto la animó a comenzar una segunda carrera como Youtuber científica. En la actualidad tiene un canal propio con más de 100000 suscriptores, y ha dejado un poco de lado la parte academica formal para dedicarse de lleno a la comunicación con un montón de trabajos y experiencias positivas (colaboración con Vsauce3, Physics Girl, Cody'sLab, Andrew Dotson, Flammable Maths, Up and Atom, Knowing Better, RiverTechJess y Science Petr). Ha realizado videos sobre exámenes difíciles de todo el mundo, explicando conceptos matemáticos sobre una pizarra junto a otros de historia de la ciencia. Volviendo al corto, aunque la realización parezca muy sencilla, se han empleado diferentes técnicas en su elaboración. Entre ellas, se han hecho cientos de fotografias, así como la inclusión de elementos de stop-motion y de animación digital. El cortometraje puede verse integramentte (y subtitulado en español; ojo con alguna palabra, como cuadratura por cuadratics, que se refiere a las ecuaciones de segundo grado, no a la cuadratura, o línea de números en vez de recta real) en este enlace.  La página principal del mismo es https://findingxfilm.com/, donde se puede ampliar la información sobre la autora y sobre todo disfrutar con otro trabajos, como el que describe la trayectoria profesional de Terence Tao, realmente interesante (éste no está traducido). Os dejo un par de imágenes del corto, en el que seguro localizareis algunos elementos matemáticos curiosos. Disfrutad del corto, y sobre todo pensad en su conclusión, sobre el verdadero significado de las matemáticas. ¡¡Felices Navidades para todos!!

Miércoles, 07 de Diciembre de 2022 | Imprimir | PDF |  Correo electrónico

4. 88. (Diciembre 2022) La eclosión moderna de la medida

(Girolamo Mazzola. Pitágoras. Palacio Farnesio. Piacenza) Tú lo has dispuesto todo con medida, número y peso. Biblia. Libro de la sabiduría. Los filósofos pitagóricos.. supusieron que las cosas existentes son números Aristóteles. Metafísica. Est modus in rebus [Hay medida en todas las cosas] Horacio. Sátiras. La sociedad medieval estaba regida por la tradición y la costumbre. El naciente capitalismo procede racionalmente. Se calcula y se mide, introduce la contabilidad y usa maquinas. Edgar Zilsel Medir, contar y pesar son actividades humanas desde tiempos inmemoriales, pero en los inicios de la modernidad occidental se convierten en la característica de la época. Los historiadores hacen de la cuantificación una de las expresiones de los inicios de la revolución científica. The Measure of Reality (1998) de Alfred W. Crosby, The Sociological Roots of Science (1942) de Edgar Zilsel o In Measure, Number and Weight (1994) de Jens Hoyrup son algunos de los testimonios los estudios actuales. Los artistas del Renacimiento y el Barroco fueron conscientes de que estaba emergiendo una mentalidad que hacía de la medida una de sus señas de identidad. Repasemos algunas pinturas y grabados que lo ponen de manifiesto. “Los medidores” de Hendrick van Balen El History of Science Museum de Oxford, abigarrado de instrumentos matemáticos, ha incorporado a su colección una pintura que en sí misma contiene todo un programa iconográfico con algunas razones para la enseñanza de la matemática. Hendrick van Balen el Joven (Amberes, 1623–1661) fue un pintor historicista que aprendió el arte de su padre y que colaboró con otra gran saga flamenca, la de los Breughel. El Museo de Oxford tuvo el acierto de adquirir Los medidores, un interesantísimo cuadro atribuido a Van Balen. (Hendrick van Balen. Los medidores. Oxford) No son hombres de ciencia, son trabajadores artesanos, hombres y mujeres, los que realizan la actividad de medir y calcular como una necesidad para ser buenos en su trabajo: una modista mide su tela, un carpintero dibuja su obra con todo tipo de instrumentos, unos cargadores al fondo pesan en una balanza, unos vinateros miden líquidos,… Mientras se desarrolla tanta actividad, un niño aprende apaciblemente geometría consciente de su importancia: todo lo que le rodea lo requiere. Pocas veces encontramos algo que de forma tan explicita nos da cuenta de la matematización del trabajo. La pintura de Van Balen reproduce un grabado anterior, obra de Frans Floris. (Frans Floris. Los medidores) Con medida, número y peso en El Escorial La espectacular Biblioteca del Monasterio de El Escorial reproduce las siete Artes Liberales en sus bóvedas y en los laterales muestra ejemplos de sus aplicaciones. El fresco de Salomón y la Reina de Saba de Bartolomeo Carducci reproduce en hebreo el “con medida, número y peso” bíblico. (Bartolomeo Carducci .  Salomón y la Reina. San Lorenzo de El Escorial) Los números, la balanza y la regla sobre la mesa. Las vasijas con medidas precisas ilustran la importancia determinante de la Aritmética en la vida cotidiana. Resulta curioso que dos reyes se comuniquen con la lengua de los signos matemáticos. Los escultores medidores de Lugo La sillería del coro de a Catedral de Santa María en Lugo tiene una hermosa muestra de la importancia de la medición en los nuevos tiempos. La modernidad se caracteriza tanto por el paso de un mundo estático a otro dinámico como por la hegemonía de lo cuantitativo frente a lo cualitativo. (Francisco de Moure.  Escultores medidores. Catedral de Lugo) Los artistas matemáticos se reivindican y lo reflejan en sus obras con toda rotundidad. Es el caso del escultor gallego Francisco de Moure (1595 – 1636), que siguiendo el estilo de Juan de Juni y Alonso Berruguete, expone una gran lección de geometría en un dosel de sitial del coro inferior (último en la esquina izquierda). Dos escultores atienden las explicaciones de otro que está ¡midiendo un pie!, mientras un cuarto talla un crucifijo y el quinto utiliza un compás para medir una calavera. La filacteria trata de dar un mensaje religioso a lo que es orgullo profesional: entre los santos hay sitio para el artista que modela. Si Santa Teresa opinaba que Dios podía estar ente los pucheros, Moure lo encuentra en el taller del ebanista que no descuida los detalles. Pitágoras y Euclides en el Palacio Farnesio de Piacenza El Museo Cívico de Piacenza utiliza el Palazzo Farnese, parte de la fortaleza de los Visconti,  para mostrar su rica pinacoteca, el museo de carruajes, las esculturas y el archivo. Girolamo Mazzola Bedoli (1500-1569) es el pintor de Parma que decoró las dos planchas que formando un díptico cierran el órgano de una familia noble de la ciudad y donde fueron representados Euclides y Pitágoras. Pitágoras aparece muy a menudo como creador de la música. Los martillos crean el sonido mientras que la balanza y el compás ponen medida para hacerlo armonioso. El Museo del Prado archiva un dibujo de Bedoli representando a Pitágoras que contiene similares elementos iconográficos: martillo con yunque, una romana y una cítara al fondo. La música era aritmética aplicada. (Girolamo Mazzola. Pitágoras. Museo del Prado) De proprietatibus rerum Bartholomaeus Anglicus (1203 – 1272) fue el autor medieval de una exitosa enciclopedia: De proprietatibus rerum. Se conservan muchos manuscritos bellamente iluminados ; reproducimos una ilustración del siglo XIV que muestra como la medida y el número son esenciales. Un monarca se dedica a a música, un tendero a pesar y medir, y un escolar usa la escuiadra. (Bartholomaeus Anglicus  De proprietatibus rerum) Los medidores del Palacio Zwinger Los electores y las cortes imperiales alemanas, como ocurría  con los príncipes renacentistas italianos y  anteriormente con los reinos de taifas andalusíes, también competían por el arte y la ciencia. Los museos del Palacio Zwinger de Dresde son muestras espectaculares de cómo belleza y matemáticas van unidas. El Salón Matemático Físico exhibe los objetos de mayor tamaño, los demás están repartidos formando una unidad con el mobiliario y el arte. Durante el recorrido palaciego iremos encontrando lujosos instrumentos de cálculo como los compases de proporción, las calculadoras mecánicas y hasta cifradoras de mensajes secretos. Seleccionamos un lujoso cuadrante de agrimensor y arquitectura por estar ribeteado por multitud de detalles en miniatura de las aplicaciones del instrumento. ¡Todo hay que medirlo! (Cuadrante. Palacio Zwinger Drede) La Templanza y la Medida La Templanza es la más matemática entre las Virtudes y muchas veces va acompañada de un compás como símbolo. Un grabado de Pieter Brueghel el Viejo (1525 - 1569) va más allá y reproduce todo un mundo de personajes que se afanan en medir y calcular por doquier. Los astrónomos miden el cielo; sus alcances, los artilleros; los comerciantes, su contabilidad; sus obras, los artistas; los geógrafos, las distancias;... (Pieter Brueghel el Viejo. La Templanza. 1560)

Jueves, 01 de Diciembre de 2022 | Imprimir | PDF |  Correo electrónico

5. 175. Los Oscars® de las matemáticas (y II)

Las matemáticas han motivado procedimientos que, una vez implementados informáticamente, han generado potentes herramientas gráficas que han posibilitado la creación de animaciones espectaculares, logrando no sólo el favor del público. Los premios no se han hecho esperar. En la reseña pasada recordamos que PIXAR fue el primer estudio en realizar una película íntegramente con CGI (Computer Generated Images), Toy Story (Toy Story, John Lasseter, EE. UU., 1995). Partiendo de unos guiones gráficos elaborados por dibujantes al estilo clásico, posteriormente se digitalizaron con el software Avid Media Composer. En promedio se emplearon tres horas para concretar cada una de las 1560 tomas que constituyen la edición definitiva del largometraje, para las que se utilizaron 400 modelos matemáticos que tuvieron que instalarse en cada ordenador. Esta comenzó con el diseño tridimensional de los personajes con el programa informático Modeling Environment (Menv, en siglas). Cada toma era trabajada eventualmente por ocho equipos diferentes. El diseño de cada personaje se realizaba creando una escultura a escala en arcilla, que era digitalizada después mediante el software adecuado (como Polhemus 3 Space Digitizer, por ejemplo, que facilita su manejo tridimensional). Posteriormente, se diseñaron y configuraron los controles de articulación y movimiento de los personajes, a partir de las grabaciones de voz de los actores del reparto. El vaquero Woody resultó ser el más complejo, empleándose 723 controles de movimiento, de los que 212 eran exclusivamente para su rostro y 58 adicionales para su boca. Para sincronizar las voces de los actores con las bocas de los personajes, y que casaran con las expresiones faciales los animadores emplearon una semana. La fase siguiente, el sombreado, utilizó los programas Amazon, Adobe Photoshop y Unwrap, este último desarrollado por los ingenieros de Pixar, mientras que los efectos de iluminación se produjeron de forma similar a un filme con imágenes reales. Finalmente se realizó la renderización y edición con ayuda de software de RenderMan, Avid Technology y Sun, respectivamente. En total, se invirtieron 800000 horas por máquina para producir la película, y un promedio de 2 a 15 horas para renderizar cada toma. El metraje final se envió a Skywalker Sound, en donde se mezclaron los efectos de sonido con la banda sonora. En opinión de su director, John Lasseter, “En la animación computarizada, es fácil lograr que las cosas se muevan, pero es el trabajo minucioso el que hace que parezca real. Cada hoja de césped tuvo que ser creada desde cero. Además, todo ese universo debe parecer realista, y para ello, las puertas tiene que aparecer con golpes y el suelo ha de verse desgastado.”​ Estas nuevas técnicas de animación no han sustituido otras más tradicionales (se siguen produciendo películas al modo tradicional, otras con plastilina y stop motion, etc.), pero sí han captado la atención de los estudios de animación, al punto de que raro es aquel que no los utiliza en alguna de sus producciones. La segunda película, según los historiadores, íntegramente realizada mediante CGI fue HormigaZ (AntZ, Eric Darnell y Tim Johnson, EE. UU., 1998), producida por otro estudio diferente, DreamWorks Animation. Tras el éxito de Toy Story, nadie se quería quedar atrás, y DreamWorks contrató a la empresa Pacific Data Images (PDI) en Palo Alto, California, para tratar al menos de emular a Pixar. Dos fueron los retos no llevados a cabo nunca anteriormente que se plantearon para su película: recrear una escena con más de 10.000 caracteres animados individualmente en varias escenas de multitudes, y simular las propiedades del agua (crear un agua digital, en una inundación). Los fluidos y los gases, debido a su impredecible movimiento y evolución, son difíciles de reproducir verosímilmente en un ordenador. Hasta ese momento, el rodaje en el cine de escenas catastróficas que involucran los elementos de la Naturaleza (inundaciones, vadeo de ríos, salto de cascadas, naufragios, incendios, personas abrasándose, huracanes, etc.), siempre se había realizado mediante el diseño y la construcción de maquetas en las que se recreaba la situación, a veces a escala diferente (que posteriormente se magnificaba o reducía, dependiendo de la situación), a veces a escala real. En cualquier caso, el coste de producción de estas simulaciones era alto (y el riesgo a los accidentes), y en determinados casos (los primeros mencionados, sobre todo) el truco puede notarse en la visualización, lo que perjudica notablemente el resultado final (recuérdense películas como Superman (Richard Donner, EE. UU., 1978), o la pobre impresión que transmiten los hoy artesanos efectos animatrónicos de Ray Harryhausen). Gracias a la informática, y al software desarrollado (detrás del que están ineludiblemente las matemáticas) se han mejorado enormemente los efectos especiales. El segundo de los retos mencionados (la simulación de una inundación) se consiguió recurriendo a las ecuaciones de Navier-Stokes, formuladas independientemente por Claude-Louis Navier en 1822 y George Gabriel Stokes en 1842. Estas ecuaciones modelizan el movimiento de los fluidos incompresibles (aquellos cuya densidad permanece constante con el tiempo y se oponen a la compresión, es decir, ni la masa ni el volumen pueden modificarse; aunque todos los fluidos son compresibles en mayor o menor medida, para simplificar las ecuaciones, se suele considerar que todos los líquidos son incompresibles). Estas ecuaciones se obtienen aplicando los principios de conservación de la mecánica y la termodinámica a un volumen fluido, resultando un conjunto de ecuaciones en derivadas parciales no lineales (ver imagen). Estas ecuaciones gobiernan la atmósfera terrestre, las corrientes oceánicas, el flujo alrededor de vehículos, aeronaves o proyectiles y, en general, cualquier fenómeno en el que se involucren fluidos. El problema es que no se conoce una solución general para este conjunto de ecuaciones (ni siquiera una débil), y salvo para ciertos tipos de flujo y situaciones muy concretas no es posible hallar una solución analítica. Por ello en muchas ocasiones hay que recurrir al análisis numérico para determinar una solución aproximada, o sencillamente como realizó Nick Foster, ingeniero de software de AntZ, obviar algunos de los sumandos que aparecen en el sistema de ecuaciones ya que el espectador no va a percibir la diferencia visualmente. No es exactamente agua, pero se le parece mucho. Obviamente esta simplificación no puede hacerse al azar, ya que las características básicas del fluido deben ponerse de manifiesto. En el caso del agua, uno de los elementos visuales clave que debe permanecer es el de la rotación, o como se conoce en términos de la mecánica de fluidos, la vorticidad. Esta magnitud trata precisamente de cuantificar el grado de rotación de un fluido. En una corriente, bien sea de un líquido o de un gas, la vorticidad aparece siempre que el vector velocidad no sea constante a lo largo del recorrido, tanto por cambios en su módulo como en la dirección que sigue. Matemáticamente para modelizar ese giro dentro de un campo vectorial, se utiliza un operador clásico: el rotacional. El rotacional suele manejarse como el producto vectorial del gradiente por el campo (en el caso de fluidos, la vorticidad se designa por tanto por la expresión , donde es el campo vectorial que designa el movimiento). La ecuación que permite estudiar las variaciones de la vorticidad se obtiene aplicando el rotacional en las ecuaciones de Navier-Stokes. Todas estas consideraciones y conceptos físico-matemáticos, en absoluto elementales, fueron utilizadas en el ordenador para diseñar la inundación de AntZ. El resultado es realmente creíble: lo que vemos parece agua. Y gracias a ello, Nick Foster logró el Oscar® en 1998 (gala 78 delos premios) en la categoría de premios científicos y técnicos. PDI/DreamWorks cuenta con una plantilla de 15 programadores que dan soporte a aproximadamente 200 animadores gráficos. Lo habitual es que los programadores utilicen software comercial en su trabajo; DreamWorks en cambio usa herramientas escritas y desarrolladas por sus propios programadores, para modelar, deformar modelos, renderizar, deformar personajes, y todo tipo de efectos especiales. Y para efectuar cálculo matemático complejos recurren a Maple, según explica Shawn Neely, director senior de I+D de PDI/DreamWorks Neely. Entre las necesidades constantes de los animadores gráficos se encuentra el proceso de sombreado de los objetos que aparecen en la película. Cuando uno hace un dibujo, sabe perfectamente el nivel de sombra que debe dar a la imagen, y si no queda a su gusto, lo modifica manualmente. Sin embargo, hacerlo con el ordenador requiere de muchos cálculos, de muchas pruebas hasta decidir que el resultado es el deseado, que es realista. Esas pruebas (y esos cálculos, por tanto) no pueden hacerse a mano, porque son una cantidad muy grande, además de los posibles errores que una persona puede cometer. Un programa de cálculo de cierta potencia, como Maple en el caso de DreamWorks, es necesario. Shawn Neely lo explicaba mediante un ejemplo concreto: Por ejemplo, ahora estoy trabajando en un renderizador de volumen para un nuevo proyecto, en este caso, técnicas para proporcionar algo que parezca niebla. Los modelos tradicionales dan como resultado una salida que es simple y uniforme: obtienes niebla que aumenta en densidad a medida que la cámara se va alejando. Deseábamos algo que produjera efectos más sutiles: mechones, texturas, el tipo de detalle que diferencia lo extraordinario de lo ordinario. Queríamos hacer una integración directa y eficiente de estos efectos, de modo que tomamos un rayo en el espacio y calculamos la densidad de la niebla en función de los puntos extremos. Usé Maple para ayudarme a resolver algunos de estos problemas, y también resolví algunos casos límite relacionados con la aplicación”. Otro de los usos de Maple es “para generar expresiones en una forma que podemos compilar rápidamente en código C, y luego usamos nuestros propios programas para hacer la visualización". Por otra parte, según Neely, una de las cosas que ha consolidado el uso de Maple por parte de PDI/DreamWorks a largo plazo es el compromiso de Maplesoft con Linux en PC: “Hemos estado usando máquinas SGI que ejecutan Irix, por lo que nuestro desarrollo está basado en Unix", dice. "Nos gustaría seguir así; y como nuestra ruta de migración actual es incorporar más PC, Maple bajo Linux en PC tiene sentido. Otros paquetes no están disponibles o sólo están disponibles bajo Windows". La implementación de las matemáticas ha facilitado que el rodaje actual de este tipo de escenas sea más rápido, más eficiente (no hace falta ser un excelente y paciente dibujante), más económico, y con una imagen final más nítida y realista. No sólo en películas de animación. Muchos de los efectos de las películas de superhéroes de la factoría Marvel han incorporado este tipo de herramientas con unos resultados espectaculares (de hecho, uno de los méritos de los actores que participan en estas películas es mostrar naturalidad ante objetos y situaciones que no existen, que se han añadido en la sala de montaje, cuando en la mayor parte de los casos en todo el rodaje no han salido de una habitación). Desde aquellos años, otras películas han logrado el Oscar® u otros galardones, gracias al software y las ideas generadas por las matemáticas. Un último botón como nueva muestra: el cortometraje animado Bunny (Chris Wedge, EE. UU., 1998) también lo obtuvo en 1999. En este caso, lo produjo Blue Sky Studios, tercera compañía norteamericana destacada en animación en 3D. En este enlace puede visualizarse.

Miércoles, 09 de Noviembre de 2022 | Imprimir | PDF |  Correo electrónico

6. 87. (Noviembre 2022) Iconografía masónica y matemáticas

(Colgante de ex-venerable. Salamanca) Los orígenes míticos de la Masonería la sitúan entre los constructores del Templo de Jerusalén, de forma que la escuadra y el compás son su emblema característico. La realidad histórica no nos aleja tanto en el tiempo: la francmasonería parece más vinculada a miembros de la Royal Society inglesa, en los inicios de la revolución científica y asociada al cambio de mentalidad que tiene sus frutos en la Ilustración. La simbología geométrica alcanza su máxima expresión en la representación del Teorema de Pitágoras en su versión euclídea, según la figura que acompaña a la proposición 47 del libro 1 de Los elementos. La masonería hace uso de la iconografía geométrica por ser hija del racionalismo que iba a definir su época de esplendor. Plomada, regla, o escuadra son presentadas como emblema de la rectitud de sus acciones y sus objetivos. Presentamos algunas muestras de la vinculación matemática en unos pocos lugares, empezando por el gran templo masónico londinense, paseando por el Cementerio Civil de Madrid o caminando por las calles de Burdeos. El templo pitagórico del Freemasson´s Hall en Londres La iconografía del teorema de Pitágoras según la demostración de Euclides tiende a desaparecer en las imágenes modernas. Una de las pervivencias de la tradición euclídea se encuentra en la simbología masónica. Inglaterra como cuna de la masonería -lugar con gran arraigo y organización- tiene abiertas las puertas de un soberbio edificio Art Decó: el Freemason´s Hall en Great. Queen Street. La construcción actual sustituyó a la logia anterior para rendir homenaje a los fallecidos en los combates durante la primera guerra mundial. Se realizan visitas guiadas a la sala de reuniones, museo, biblioteca, pasillos de iniciación y el gran templo. La escuadra y compás forman parte de toda la decoración desde las lámparas a las vidrieras. Nos detenemos por su interés en los coloristas mosaicos de la bóveda del Gran Templo: en un lado Salomón e Hiran con compás y al otro Euclides y Pitágoras con la ilustración del teorema entre ellos. En muchas iglesias hay representaciones de Euclides y Pitágoras, normalmente acompañando a la Alegoría de la Geometría y la Aritmética o la Música, pero nunca en un lugar tan destacado como en la logia londinense. (Mosaico de Euclides y Pitágoras. Freemasson´s Hall de Londres) Masonería y matemáticas en Salamanca Al depositarse en Salamanca el archivo de la mal llamada “Guerra Civil”, también se ha reproducido una tétrica logia y se dispone la creación de un museo de la disuelta y cruelmente reprimida masonería. Los orígenes míticos de la masonería se sitúan en el templo de Salomón, el rey sabio que ya se reproduce repetidamente en el Monasterio de San Lorenzo de El Escorial. Entre sus fundadores se encuentran matemáticos, por ello no debe extrañarnos que el elemento central del frontispicio de la primera edición (1723) del libro de las “Constituciones masónicas” de Anderson sea el Teorema de Pitágoras. La clásica imagen del triángulo rectángulo con los tres cuadrados de sus lados. (Constituciones masónicas. Museo de la logia de París) El famoso teorema del triángulo rectángulo es el símbolo usado para el ex-venerable masónico. Por ello su medallón reproduce la figura de las proposiciones 47 y 48 con las que se cierra el libro I de los “Elementos” de Euclides. El museo salmantino conserva tres medallones pitagóricos. La unidad entre la filantropía, la teosofía y la matemática se presenta de múltiples formas. Museo masónico en la Logia de París Le musée de la franc-maçonnerie se localiza en un edificio moderno en la Rue Cadet, 16, sede del Gran Oriente de Francia. Las instalaciones no tienen el encanto del Freemasons’ Hall de Londres con su espectacular templo, en cambio, la gran sala de exposición está repleta de objetos y documentos de interés. Incluso el recuerdo del efímero y vilipendiado rey masón José Bonaparte. La masonería está ligada desde los orígenes a la matemática; Euclides y Pitágoras son modelos a seguir. Los símbolos geométricos están siempre presentes. Encabezamos con un mandil con estrella nonágona, compás con arco y triángulo inscrito en circunferencia. (Mandil ceremonial. Museo de la logia de París) El museo contiene gran cantidad de vajillas, cristalerías, relojes, insignias y otros objetos personales. El compás y la escuadra aparecen por doquier: la rectitud geométrica era una forma de vivir. Entre los iniciados se encuentran algunos personajes españoles asentados en París como el cubista Juan Gris. (Insignias masónicas. Museo de la logia de París) Imaginería masónica matemática en las calles de Burdeos La masonería fue muy importante en Burdeos durante su etapa de esplendor del siglo XVIII. La masonería como institución muy emparentada en sus inicios con la Royal Society de Londres -y el mundo de las nuevas ciencias matemáticas- como hemos visto hace gran uso iconográfico de los instrumentos geométricos y del Teorema de Pitágoras. La extensión de la masonería se hace principalmente a través de las ciudades comerciales. El mercantilismo necesita el amparo ético y solidario de personas con los mismos intereses. Filantropía y hermandad van de la mano con las necesidades del comercio. No debe sorprendernos que sean Cádiz en España y Burdeos en Francia dos grandes centros de los caballeros francmasones. (Mascarón masónico. Burdeos) Un aliciente más para pasear por Burdeos es encontrar bajorrelieves en piedra o madera en las fachadas de sus casas. Así, en la Rue Fernand Philippart encontramos el mascarón masónico del compás y la escuadra, en la Rue Tanesse otro compás, al igual que en la Galería Comercial, o los globos del Banco Curtois al lado del Gran Teatro. Geometría masónica en el cementerio civil de Madrid El Cementerio Civil de Madrid quizá sea el rincón más romántico y nostálgico de la ciudad. La otra historia de España late entre sus muros, la de los heterodoxos, hebreos, protestantes, ateos, republicanos, anarquistas, socialistas y comunistas. Mujeres y hombres, cuyos restos sólo tenían cabida en ese lugar. (Tumba masónica. Cementerio civil de Madrid) Un breve recorrido es suficiente para sentir el más profundo sobrecogimiento.  La tumba de Nicolás Salmerón, uno de los presidentes de la primera republica, nos recuerda que dimitió por no firmar una sentencia de muerte. En el Civil podemos encontrar el símbolo del infinito, las estrellas de seis puntas y otros dibujos geométricos, pero concentraremos nuestra mirada -por su abundancia e interés- en los bajorrelieves masónicos. La escuadra, la plomada y el compás acompañan a los masones en su vida y en su muerte: les recuerdan que deben ser constructivos y rectos. La geometría masónica en la loza de Nevers Nevers, en la cabecera del aristocrático río Loira, fue un gran centro de producción cerámica de loza. El Museo Municipal Frédéric Blandin recogía una buena representación de su producción. El palacete que ocupa el museo ha sido remodelado tras un incendio y reconvertido en Museo Nacional de la Cerámica. Entre las miles de piezas expuestas nos quedamos con unas botellas poliédricas y  con los platos masónicos de finales del siglo XIX, elaborados en pleno sueño de liberación redentora de la humanidad. (Plato masónico. Museo de Nevers) El compás, la escuadra, o la recta plomada, son los símbolos del albañil utópico constructor de un nuevo orden más justo. Uno de los platos parece la conmemoración del centenario de la gran revolución de 1789, recogiendo el levantamiento de 1848 y la Comuna de 1870. Marianne con su gorro frigio, y con escuadra y compás, sigue marcando el camino hacia una sociedad de iguales. (Jarra masónica. Museo de Nevers) La cervecería Trindade de Lisboa Una parada obligada en Lisboa debe ser para disfrutar con los azulejos del siglo XIX de la Cervejeria Trindade en el Chiado, el Barrio Alto. Aunque suele estar atestada hay que pasar a su salón para admirar la decoración cerámica. Tampoco debe dejar de verse la azulejería de fachada que se extiende a la calle lateral bajando a la Baixa. Suele asociarse todo el programa iconográfico a la masonería. Hemos escogido como ilustración dos murales masónicos de la Trindade que suelen pasearse por exposiciones temporales por ser los más expresivos. (Panel de azulejos. Lisboa) El compás de San José y Santa Bárbara de Xàtiva El paseo a pie desde el centro de la ciudad de Xátiva hasta su castillo está jalonado de interesantes paradas. La iglesia donde se acumulan más detalles resaltables, tanto técnicos como matemáticos,  es la ermita de San José y Santa Bárbara, reconstruida en el siglo XVIII. Las tumbas de piedra, taracea marmórea y de cerámica son dignas de contemplar. La que no nos podemos perder es la lápida central con su gran compás. Medir la rectitud de las obras que cada uno ha hecho forma parte de la iconografía religiosa tradicional, cuando aparece el compás se tiende a buscar relaciones con la masonería. Quizá no sea una conjetura muy desacertada,  pues los símbolos matemático-arquitectónicos en el templo son insistentes, como la puerta de la sacristía o su lavamanos de mármol de una pieza. La simbología dominante hace gran referencia al gremio de los carpinteros, colectivo vinculado a la ermita. (Lápida en San José y Santa Bárbara. Xàtiva)

Miércoles, 02 de Noviembre de 2022 | Imprimir | PDF |  Correo electrónico

7. 128. (Octubre 2022) Retos musicales y matemáticos

1. Introducción En el artículo de este otoñal octubre vamos a proponer al lector una serie de retos matemático-musicales, que están dirigidos principalmente a alumnos de los últimos cursos de primaria y a los de secundaria. Los encontré por pura casualidad en la excelente página web Get the math [DL22] producida por la organización sin ánimo de lucro Next Generation Learning Challenges [Aut22]. Los retos están diseñados por Manny Domínguez and Luis López, que forman el duo DobleFlo (véase su trabajo en Spotify en https://soundcloud.com/dobleflo). En el vídeo que aparece en la página de presentación, Luis López habla de cómo las matemáticas lo empujaron a seguir una carrera musical en hip-hop y achaca tal hecho a la figura del profesor durante sus años de instituto. En su caso, el profesor de matemáticas y el de música era la misma persona (¡hecho bastante inusual!). No cabe duda de que López estuvo en contacto con una persona que supo aunar ambas disciplinas y transmitirlas con la suficiente pasión como para que alguien quisiese seguir el camino de la música (pero con matemáticas). Ese es el verdadero papel de la divulgación. Figura 1: Get the math in the music En ese mismo vídeo, a partir del minuto 3:55 se presenta el primer reto matemático-musical. El reto se le presenta a un grupo de alumnos de instituto y consiste en sincronizar el tempo de dos pistas musicales. Hay varias ideas interesantes que aparecen en el reto. Primero, ha de haber una medida común del tempo para ambas pistas. Una vez fijada, hay que hacer los ajustes necesarios para sincronizar las pistas. El reto se puede encontrar aquí (está en inglés): https://www.thirteen.org/get-the-math/interactives/get-the-math-in-music-take-the-challenge/21/. En esta página se puede meter las soluciones a través de varias pantallas. En la página https://www.thirteen.org/get-the-math/video/get-the-math-in-music-see-how-the-teams-solved-the-challenge/22/ aparece la solución dada por los alumnos, solución que luego es probada en el estudio con DobleFlo. Tras el vídeo de la solución, DobleFlo propone al lector otros retos similares donde hay que mezclar correctamente tres extractos musicales (cada extracto comprende una muestra instrumental y una base rítmica). Esos retos se encuentran en https://www.thirteen.org/get-the-math/interactives/get-the-math-in-music-try-other-music-challenges/23/; véase la figura siguiente. Figura 2: Retos matemático-musicales En otra sección de la página Get the math, encontramos una sección interesante, Math in Special Effects, presentada y escrita por Jeremy Chernick, quien trabaja para la compañía J&M Special Effects. Chernick aparece en un vídeo hablando de su trabajo y su experiencia con las matemáticas durante su vida; el vídeo está en https://www.thirteen.org/get-the-math/video/math-in-special-effects-introduction/243/. Durante el primer minuto, Chernick se queja de lo mal que se le daba aprender matemáticas en la escuela y el instituto. Menciona de hecho un defecto de aprendizaje que le dificulta memorizar hechos, en particular, hechos que presentan nexos lógicos entre sí. También menciona que la enseñanza de las matemáticas que tuvo fue altamente memorística y con poco razonamiento. ¿Cómo es tal cosa posible? ¿Cómo puede algo tan creativo y conceptual enseñarse de una manera memorística e irracional (siento que no hay otra palabra más adecuada aquí)? Más adelante en el vídeo, Chernick afirma que ya no tiene miedo a las matemáticas porque ahora las ve como una herramienta para solucionar los problemas que le surgen en el diseño de efectos especiales. En este vídeo, este diseñador de efectos especiales plantea un reto matemático (ahora ya no musical) que está relacionado con la iluminación de una toma de vídeo. En el reto se investiga la relación entre distancia e iluminación de un sujeto en una toma. El reto está aquí: https://www.thirteen.org/get-the-math/interactives/math-in-special-effects-take-the-challenge/242/. Figura 3: Retos matemático-musicales   Bibliografía [Aut22] Varios Autores. Next Generation Learning. https://www.nextgenlearning.org/, consultado en septiembre de 2022. [DL22] Manny Domínguez and Luis López. Math in music. https://www.thirteen.org/get-the-math/video/get-the-math-in-music-introduction/20/, consultado en septiembre de 2022.

Viernes, 14 de Octubre de 2022 | Imprimir | PDF |  Correo electrónico

8. 174. Los Oscars® de las matemáticas (I)

Repasamos en esta reseña y en la del próximo mes, ejemplos, ambos en películas de animación, en los que las matemáticas han sido las responsables de merecer y conseguir el más preciado de los galardones del mundo cinematográfico: el Oscar® de Hollywood. Si preguntáramos, a modo de curiosidad, a personas elegidas al azar, qué le sugiere la palabra PIXAR, seguramente sólo acertarían a decirnos algo coherente algunos aficionados al cine, padres de niños menores de diez años y algún amante de los dibujos animados, menor de cuarenta años, probablemente. Sonsacando lo más aprovechable, nos dirían que se trata de un estudio cinematográfico de animación por ordenador subsidiario de Walt Disney Studios y propiedad de The Walt Disney Company, con sede en Emeryville, California, Estados Unidos. Seguramente también nos dirían que fueron los que sacaron las películas Disney de la ñoñería con que los sucesivos responsables de la empresa fueron encorsetándolas, tras la muerte de su fundador (ñoñería en algunos aspectos, como los insufribles números musicales, porque en otros no se cortaban un pelo si tenían que mostrar los más bajos instintos; en definitiva, la doble moral yanki de la que ya se ha hablado muchas veces). Lo cierto es que la aparición de estos estudios de animación, con técnicas distintas a las clásicas (No se le puede negar a Walt Disney sus innovaciones y avances en animación; invirtió mucho tiempo y dinero en su mejora, lo que no hicieron los herederos de su emporio) y argumentos más atractivos, revolucionaron este tipo de películas, además de atraer no sólo a públicos infantiles. Una de sus señas de identidad fue el diseño realista de personajes y fenómenos naturales por ordenador. Y para lograrlo necesitaron muchas matemáticas y muy novedosas. Así lo indican los responsables de efectos visuales en las numerosas charlas y conferencias que han impartido por todo el mundo. Pero no solo montando un par de presentaciones llamativas y epatantes, sino poniendo por delante artículos serios de investigación que además coloca la empresa a disposición libre de todo aquel que quiera acercarse a ellos en su página web. Si echáis un vistazo a alguno de ellos, como curiosidad simplemente, comprobareis que no los puede leer cualquiera, sino que hay matemáticas muy avanzadas detrás de ellos. Cuesta, al menos para el que esto escribe, tratar de explicar de manera sencilla lo que hay detrás de muchos de ellos. Lo intentaré con un par de conceptos que han desarrollado, simplificando mucho las cosas. Paralelamente, describiré la trayectoria del científico que logró con su primer trabajo para PIXAR la preciada estatuilla con un cortometraje: Tony DeRose. Tony DeRose es actualmente científico sénior y director del grupo de investigación de Pixar Animation Studios. Se licenció en Física en la Universidad de California, Davis, y se doctoró en Informática de la Universidad de California, Berkeley. Entre 1986 a 1995, DeRose fue profesor de informática e ingeniería en la Universidad de Washington, y trabajando en un grupo de investigación centrado en la representación de superficies y otros problemas geométricos motivados por gráficos por ordenador. En varias entrevistas y en las charlas que imparte, remarca que siempre le fascinó la parte aplicada de las matemáticas. Desde niño le apasionaba la capacidad de cálculo de las matemáticas, lo que podía saber y averiguar sin necesidad de medir físicamente las magnitudes o esperar a que se produjeran los experimentos. Al acabar sus estudios universitarios e iniciar los de posgrado comenta que se le presentaban dos opciones: tratar de mejorar 400 años de físicos brillantes, o quedarse esencialmente en la planta baja de los gráficos por ordenador, ya que prácticamente no se sabía nada del tema en aquel momento. Eligió esta segunda opción, trasladándose a Berkeley, incorporándose al equipo de Brian Barsky, que estaba trabajando en representaciones de superficies, splines, y cosas de ese estilo. Ahí fue donde encontró la belleza de hacer matemáticas constructivas, y los gráficos por ordenador fueron una forma de hacerlas visuales, tangibles. En aquel momento, muy cerca, literalmente en frente a su puesto de trabajo, George Lucas había contratado a Edwin Catmull para iniciar The Graphics Group, la división computacional de Lucasfilm que tras ser adquirido en 1986 por el co-fundador de Apple Computer, Steve Jobs, pasó a ser Pixar Animation Studios. Catmull se había graduado en la Universidad de Utah, doctorándose posteriormente en Ciencias de la Computación. Creó en 1972 el primer dibujo en animación 3D, una recreación de su propia mano izquierda. Quedó tan realista que fue aprovechada para la película Mundo futuro (Futureworld, Richard T. Heffron, EE. UU., 1976) (la secuela de la célebre Almas de metal (Westworld, Michael Crichton, EE. UU., 1973)). Catmull formaría parte del comité asesor en la tesis doctoral de DeRose. Catmull ha ganado cuatro Premios de la Academia por sus proezas técnicas y ha colaborado en crear algunos de los principales softwares de imágenes generadas por computadora en los que confían los animadores en la actualidad. Diez años después, ya siendo profesor en la Universidad de Washington, Ed Catmull propone a DeRose trabajar más estrechamente en gráficos después del enorme éxito obtenido por la película Toy Story (Toy Story, John Lasseter, EE. UU., 1995), primera producción en la historia de la animación totalmente realizada con CGI (Computer Generated Images). Catmull fue el diseñador del software de renderización de imágenes de la película, además de productor. Además del público y la crítica, técnicos y especialistas de todo tipo valoraron muy positivamente muchos aspectos de Toy Story. La historia enganchó al público, los personajes de juguete eran creíbles, convincentes, pero observaron que, cada vez que aparecía un ser humano en la pantalla, la cosa no cuadraba tan bien; de hecho, se apreciaban discordancias. Decidieron que uno de los objetivos en futuros trabajos debería ser mejorar la presencia de personas, tanto gráfica como argumentalmente. Y aquí es donde entró DeRose junto a un completo equipo de informáticos, ingenieros y matemáticos. Matemáticas pioneras En sus conferencias divulgativas, DeRose suele remarcar la importancia de las matemáticas en la concepción de este tipo de películas. "No debería sorprender en absoluto que las matemáticas desempeñen un papel relevante", comenta. “Las imágenes resultantes son todas digitales. Tres números definen cada píxel, uno para la cantidad de rojo, verde y azul. Todo lo que tenemos básicamente son números que representan posiciones de geometría y valores de grados de libertad, por lo que tiene que haber un gran cálculo en el camino". Hablemos de tres ideas, utilizadas en otros tantos apartados de animación de gráficos. La iluminación global de una escena implica simular cómo la luz rebota en un entorno: "Matemáticamente, dados dos puntos cualesquiera, pongamos y, z, es necesario calcular cuánta luz viaja desde y hacia z. Uno de los instrumentos utilizados para modelizar esta situación es la función de distribución de reflectancia bidireccional, fr (wi, wr) (BRDF, siglas en inglés). Fue definida hacia 1965 por el físico Fred Nicodemus, del siguiente modo fr (wi, wr) = En la imagen, tenemos sobre un punto situado en una superficie opaca, tres direcciones: wi indica la luz entrante desde la fuente de luz, wr es la luz reflejada y apunta hacia la cámara (o al espectador, en general) que recoge la luz percibida, y n indica la superficie normal. La función está definida como el cociente entre la variación de la radiancia L (potencia por unidad de ángulo sólido en la dirección de un rayo por unidad de área proyectada perpendicular al rayo) y la variación de la irradiancia E (potencia por unidad de superficie). Ese cálculo de la cantidad de luz entre dos puntos, hay que hacerlo para cada par de puntos en el entorno, que, al ser un espacio continuo, se convierte en una integral: la denominada ecuación de renderizado. En el enlace se accede a un artículo sobre esta ecuación de James T. Kajiya de 1986 en el que la aplica en la computación gráfica. Se trata de una ecuación integral que describe la cantidad total de luz emitida desde un punto a lo largo de una dirección de visualización particular, dada una función para la luz entrante y una función de distribución de reflectancia bidireccional. Básicamente, la luz saliente de cada punto es la suma de la luz emitida y la luz reflejada. Ésta última, la luz reflejada, es la suma de todas las direcciones de la luz entrante multiplicada por la reflexión superficial y el coseno del ángulo incidente. Lo que los ordenadores hacen es aproximar esa la ecuación integral mediante un conjunto de ecuaciones lineales. Hay una ecuación para cada punto de cada objeto que aparece en cada secuencia. De media, entre un millón y diez millones de puntos por cada cuadro de película. Estimen el número de ecuaciones total. Existen diferentes técnicas de representación realista para resolver este tipo de ecuaciones. Resolver la ecuación de renderizado para cualquier escena dada es el principal desafío en el renderizado realista. Un enfoque para hacerlo se basa en métodos de elementos finitos. Otro enfoque diferente utiliza los métodos Monte Carlo, dando lugar a muchos algoritmos diferentes. Por otra parte, aunque la ecuación de renderizado es muy general, no es capaz de contemplar todos los aspectos del reflejo de la luz. Entre sus limitaciones se encuentran los efectos no lineales, el efecto Doppler, la polarización, la fosforescencia, las interferencias, entre otras. Subdivisión de superficies Otro aspecto presente en la animación de gráficos por ordenador es la representación de superficies tridimensionales complejas de manera eficiente en un ordenador, preservando en la medida de lo posible la ilusión de suavidad. El modo más extendido ha sido la utilización de NURBS (B-splines racionales no uniformes). Pero un gran inconveniente de utilizar NURBS es el requisito de que las redes de control (el conjunto de puntos de control) tenga que ser una cuadrícula rectangular regular. Esa elección limita mucho el tipo de objetos que pueden representarse porque no existen procedimientos de refinado local de la superficie, dando lugar a abombamientos u otros defectos del dibujo final. Una alternativa es la técnica de las superficies de subdivisión, definidas como límite de un proceso de refinamiento infinito. Este método mejora muchas de las deficiencias de los NURBS. Por ejemplo, las imágenes que se muestran a continuación, a partir de una malla de control inicial, se pasa a un proceso de refinamiento mediante iteraciones. Las imágenes muestran el resultado con una etapa, dos y la final con un refinamiento infinito, respectivamente. Las superficies de subdivisión son fáciles de implementar, pueden modelar superficies de tipo topológico arbitrario y, como se ha indicado, la continuidad de la superficie se puede controlar localmente. Aunque las superficies de subdivisión se conocen desde hace quince años, su uso se ha visto obstaculizado por la falta de una forma cerrada: se definen solo como límite de un procedimiento infinito. La técnica de subdivisión de superficies se utilizó por primera vez en animación para crear el personaje de Geri en el cortometraje El juego de Geri (Geri's Game, Jan Pinkava, EE. UU., 1997), que le valió a Tony DeRose un Oscarâ de la Academia a los efectos visuales. En el enlace pueden contemplar el cortometraje al completo. Observen el realismo de los cambios de expresión del rostro del personaje. Como explica el propio DeRose, se trata de un proceso similar al control de los movimientos mediante cuerdas en las marionetas, sólo que aquí las cuerdas son digitales. Las cuerdas digitales sirven como controles de la animación, que permiten a los animadores definir todos los movimientos de los personajes, desde doblar un codo hasta levantar una ceja. En una marioneta física tenemos media docena, una docena de cuerdas a lo sumo; aquí se pueden controlar hasta 700, lo que da unos grados de libertad de movimientos impresionante. Imagínense una marioneta controlada por 700 cuerdas. Con eso es con lo que se trabaja gracias al ordenador y las matemáticas. Coordenadas armónicas Un tercer aspecto novedoso en las técnicas de animación mediante ordenador es la creación y el control de las deformaciones de volumen utilizadas para articular personajes. Para ello, los ingenieros de Pixar han recurrido a las coordenadas armónicas. Las coordenadas armónicas son una generalización de las coordenadas baricéntricas que se pueden extender a cualquier dimensión; describen cómo se mueven los puntos interiores dentro de polígonos en el plano o poliedros en el espacio. Las coordenadas baricéntricas son ternas de números (t1, t2, t3) que responden a masas situadas en los vértices de un triángulo de referencia. En la imagen tenemos las coordenadas baricéntricas (0.41, 0.3, 0.29). Una característica es que la suma de esos tres valores es la unidad, y que esas masas determinan entonces un punto P, que es el baricentro geométrico de las tres masas (de ahí su nombre). Las coordenadas baricéntricas fueron descubiertas por Möebius en 1827, y tiene muchas aplicaciones que el lector interesado puede consultar en cualquier texto de geometría afín. Sobre las coordenadas armónicas y su utilización en el modelo gráfico por ordenador puede verse este video de apenas seis minutos de duración (en inglés). Gracias a este tipo de coordenadas, los animadores reducen considerablemente el tiempo y el esfuerzo que dedican a mover los objetos. Una visita a Pixar in a box En un loable intento por promocionar las materias STEM relacionadas con el trabajo de los estudios Pixar, han incorporado a su página web, con la colaboración de un centro educativo, unas unidades básicas (con vídeos explicativos, ejercicios, animaciones, etc.) que explican lo que se necesita en la realización de una película. A esta sección la han llamado Pixar in a box. Entre el material desarrollado hay algunas unidades de matemáticas, muy elementales (es una sección dirigida a un público más bien joven), pero no triviales (el cálculo de curvas de Bézier, por ejemplo, muy útil en la animación por ordenador, no puede decirse que sea evidente).

Jueves, 13 de Octubre de 2022 | Imprimir | PDF |  Correo electrónico

9. 86. (Octubre 2022) Alegorías de la Perspectiva

(La Perspectiva y Especularia de Euclides. Madrid, 1585) El renacimiento medieval europeo del siglo XIII y la revalorización de la matemática deben mucho al redescubrimiento de la óptica geométrica. El conocimiento de la óptica de Euclides por Robert Grosseteste, y la de Alhacén por Roger Bacon, John Pecham y Witelo prepararon el camino que nos condujo hasta Galileo, Kepler, Descartes y Newton. La matemática se fue construyendo sobre técnicas aplicadas desde la antigüedad. La agrimensura, la construcción, la canalización, la contabilidad o el calendario van desde las primeras civilizaciones sentando las bases de una ciencia abstracta cada vez más compleja.  Hay dos disciplinas que empiezan a destacar hasta el punto de hacerse parte de la matemática: la Astronomía y la Perspectiva (nombre antiguo de la Óptica). El mismo Aristóteles ya incluyó la Perspectiva como matemática aplicada. A Euclides no solo se deben los XIII libros de Los Elementos también conservamos de su mano un tratado sistemático titulado en castellano Perspectiva y Especularia (1585), traducido por Pedro Ambrosio Ondériz de la Academia de Matemáticas creada por Juan de Herrera en Madrid al amparo de Felipe II. A la sistematización de la óptica geométrica de Euclides siguen en Alejandría la formalización del principio del camino mínimo por Herón  y los estudios de Ptolomeo con espejos curvos (catóptrica) y de la refracción (dióptrica). La ciencia árabe superó el nivel griego con el descubrimiento de la hoy llamada ley de Snell de la refracción por Ibn Sahl y sobre todo con la deslumbrante Perspectiva de Alhacen, el Arquímedes árabe. El renacimiento de los estudios matemáticos de Oxford en el siglo XIII se deben a la Perspectiva. Algo parecido ocurre con el arte del Renacimiento italiano, se redescubre la Perspectiva a hombros de Euclides. Así un Leonardo podía decir no lea mis escritos quien no sea matemático. La Perspectiva se va convirtiendo durante el siglo XVII en Óptica aupándose en gigantes como Kepler, Descartes, Huygens y Newton. La importancia es tal que nueva ciencia amplia los límites de lo observado: el telescopio e Galileo y la Micrographia.de Hooke extienden el mundo en varios ordenes de magnitud. Los artistas no solo usaron la Perspectiva, también la representaron. Pasamos a ver algunas muestras de alegorías. La Perspectiva en el Mausoleo de Sixto IV Como Papa renacentista, Sixto IV tiene esculpidas en bronce las artes liberales en su panteón funerario. Antonio Pallaiolo fue el ejecutor de esta soberbia obra, que fue terminada en 1493. Las imágenes hablan por si mismas del esplendor de la tumba. Cisneros encargo algo parecido, y un precedente se encuentra en la tumba de Roberto de Anjou en Nápoles. La Capilla Sixtina debe su nombre a Sixto IV. Para ver la tumba hay que localizar el Museo del Tesoro de San Pedro, cuya entrada está en el lateral izquierdo de la basílica. (Alegoría de la Perspectiva. Mausoleo de Sixto IV. Vaticano) La Perspectiva usa un circulo graduado con una alidada, similar a los astrolabios marinos, y que servia para medir ángulos. El libro es un elemento que también caracteriza la alegoría. Gnomónica catóptrica y Perspectiva en el Palazzo Spada de Roma Una curiosa aplicación de la catóptrica, teoría de la reflexión de la luz en un espejo, nos la ofrecen los espectaculares relojes solares astronómicos “de techo”, de los que se han conservado tres soberbios ejemplares en funcionamiento, dos en Roma y uno en Grenoble. Los dos romanos son obra del padre Emmanuel Maignan de la orden de los Mínimos: uno se localiza en el convento de la Trinitá dei Monti (parte superior de la escalinata de la Plaza de España) y otro en la Galería del Palazzo Spada. La luz reflejada en un pequeño espejo horizontal tiene la ventaja de verse en los techos interiores de los pórticos lo que facilita mucho la lectura. Se considera que el primer constructor de un reloj solar catóptrico fue Copérnico en el castillo de Olsztyn, recientemente restaurado, y se extendieron con el diseñado para el Palacio de los Papas en Avignon por el jesuita Atanasius Kircher, hoy desaparecido. Las alegorías de la Geometría, la Aritmética y la Astronomía colaborando con la Perspectiva expresan muy bien como la construcción de un reloj especular requiere el uso de las cuatro disciplinas. El arte termina de darle belleza a la representación. En el lomo del libro se lee Witellionis, el autor de la Perspectiva que divulga la de Alhacen. (Alegorías de la Perspectiva, la Geometría, la Astronomía y la Aritmética. Palazzo Spada. Roma) La alegoría de la Perspectiva en la Villa del Príncipe en Génova El palacio de Andrea Doria, la Villa del Príncipe, es uno de los mejores ejemplos de la concepción renacentista de los saberes, de cuando las disciplinas recogen distintas tradiciones y toman nombres que hoy nos resultan chocantes. La sala que cuenta la historia de Aracne, la mítica tejedora de las Metamorfosis de Ovidio, tiene incrustadas doce artes, tres por lado, en lugar de las siete de Marciano Capella. Las alegorías femeninas de la Astronomía, la Aritmética y la Geometría están en el mismo lado en ese orden. La Astronomía porta una esfera sólida, la Geometría lleva un compás en una mano y una estrella hexagonal en la otra y la Aritmética sujeta una tablilla con operaciones y un triángulo. La decoración del palacio fue encargada a los pintores il Beccafumi, il Pordenone o Girolamo da Treviso, todos del siglo XVI. Las otras artes matemáticas que se representan son la Estereografía y la Perspectiva, ambas emparentadas y fundamentales para la pintura. Lo que resulta más llamativo es la presencia de la Mágica: la Magia Natural es nuestra Física. El estado de conservación de los frescos no es bueno. (Alegorías de la Estereografía y la Perspectiva. Villa del Príncipe. Génova) La Perspectiva según Wentzel Jamnitzer El orfebre geómetra Jamnitzer escribió Perspectiva corporum regularium (1568) y en su portada diseñó un esquema de lo que iba a ser su placa mortuoria. Un marco de espejo en plata que se exhibe en Nueva York reproduce fielmente la portada pero el diseño en fundición de la lápida es algo diferente. En ambas la alegoría de la Geometría y la Aritmética se encuentra en la parte superior mientras la Arquitectura y la Perspectiva ocupan la inferior. La Perspectiva observa a través de un circulo con alidada extendida y su otra mano reposa sobre un globo celeste. En el Germanisches Nacional Museum se expone la placa original pero es más agradable ver la copia en su lugar original, en el cementerio histórico de San Juan (Johannisfriedhof) (Alegorías de la Perspectiva, la Geometría, la Arquitectura  y la Aritmética. Núremberg) La Perspectiva en la Iconología de Ripa y en los grabados La extensión de las artes decorativas y la imprenta dieron lugar a tratados de iconología siendo el más célebre el de Cesare Ripa (1560-1622). Artistas y artesanos encuentran en los tratados o en grabados sus fuentes de inspiración. (Perspectiva. Iconología Cesare Ripa) Los accesorios para la Perspectiva de Ripa son la escuadra, el compás, la plomada y el espejo sujetos con la mano derecha y los libros con la izquierda. Un colgante con un ojo completa la alegoría femenina. Los grabados de Étienne Delaune (1518-1595) nos muestran a la alegoría mirando por una barra de nivel (el catalejo no se había inventado) mientras en la otra mano sujeta un compás y una vara de medir. (Perspectiva. 1572. Étienne Dalaune) De la Perspectiva a la Óptica en Alcora La Reial Fàbrica de Pisa i Porcellana que fundó el ilustrado Conde de Aranda en l´Alcora tuvo una larga aunque azarosa existencia entre 1727 y 1944. Una época brillante fue la de sus inicios, cuando fueron contratados artistas y ceramistas franceses para la fabricación de productos de alta calidad. La nueva monarquía borbónica trajo consigo los gustos versallescos que la nobleza terminó adoptando. En 1666 se funda la Academia de Ciencias francesa y un año después se construye el Observatorio Astronómico de París. La pintura y la imprenta dan cuenta de que la revolución científica es imparable: la realeza y la aristocracia no pueden permanecer al margen. Así, en la producción de l´Alcora nos encontramos con  imágenes de los acontecimientos que se están produciendo en la ciencia y la industria. (Alegoría de la Óptica. 1740. Museu de l´Alcora) El Museu de Ceràmica de l´Alcora exhibe en depósito una salvilla que representa alegóricamente a la Óptica y que reproduce un grabado francés de Corneille y Simonneau (1740) que proviene de Bernard Picart. Al fondo aparece el Observatorio de París todavía en obras. La salvilla forma parte de una serie de reproducciones de los avances científicos de los dan testimonio incluso las mesas de los nobles ilustrados españoles. Es destacable ya la presencia del telescopio o el catalejo. La Perspectiva de Bayeu en el Palacio de El Pardo El fresco de Francisco Bayeu (1734 –1795) en el Palacio de El Pardo es posterior a la salvilla de cerámica pero el pintor utiliza la iconología tradicional, nada de telescopio, un espejo, escuadra, plomada, y compás. Los libros son los tratados de Ptolomeo y Witelo. El pintor de Corte de Carlos III reproduce modelos que ignoran la revolución científica moderna: se queda en la ciencia antigua y medieval.

Lunes, 03 de Octubre de 2022 | Imprimir | PDF |  Correo electrónico

10. 173. SOLUCIONES DEL XVIII CONCURSO DEL VERANO 2022

CUESTIONES MATEMÁTICAS M – 1.- Existen diferentes estrategias para resolver laberintos de este tipo. Entre todos los concursantes ha habido varias (grafos, ensayo-error, backtracking, etc.). Utilicemos la más difundida a nivel elemental para abordar los laberintos regulares: comenzar desde el final e ir determinando el trayecto desde el inicio (backtracking). Para cada casilla, analizamos desde cuál de alrededor podemos llegar a parar allí. Previamente vamos a definir un sistema de notación y localización. Podríamos utilizar coordenadas después de fijar un origen, pero creo que es más sencillo e inmediato en este caso considerar el cuadro completo como una matriz 5x5 de elementos aij, siendo el primer subíndice, la i, la fila, y el segundo, la j, la columna. De este modo el elemento a11, primera fila primera columna, corresponde al +2. El punto de inicio sería el elemento a53 = +1. Dicho esto, situémonos en la casilla final, a33 = 0. De las casillas que la rodean sólo es válida aquella que tenga un 1, ya que solo podremos alcanzarla después de dar un único paso. Por tanto a ella sólo se puede llegar desde a23 = –1. Y estando en a23, la pregunta es la misma: ¿cómo llegamos allí, desde arriba, abajo, izquierda o derecha? - Desde arriba: imposible, ya que la casilla tiene un 4 (demasiado grande) - Desde abajo: imposible, ya que los pasos a dar son 1 (demasiado pequeño) o 3 (demasiado grande) - Desde la izquierda: imposible, ya que los pasos a dar son en ambos 3 (demasiado grandes). - Desde la derecha: ¡hay un candidato!, a25 = –2, porque al saltar dos casillas a la izquierda desde allí, terminamos en a23. De este modo vamos razonando con esa misma lógica. Si hay más de una posibilidad, podemos hacer dos cosas: o elegir una, o mirar todas ellas. Eligiendo sólo una, resolvemos el laberinto sin tener en cuenta el signo (modalidad sencilla); si examinamos todas, en alguna seguro que aparece la solución de la modalidad experto (teniendo en cuenta el signo y llegar a suma cero). Aunque no se imponían más condiciones, algún participante ha tratado después de dar una solución a cada modalidad, imponerse otros retos, como encontrar soluciones que visiten todas las casillas, o dar recorridos lo más cortos posibles. Agradeciendo y admirando sus iniciativas, la puntuación ha sido la misma para todos: 5 puntos para cada uno de los recorridos válidos, independientemente de su tenacidad, que no obstante elogiamos (y tendremos en cuenta en caso de empate). Exponemos soluciones de cada modalidad (hay más): Recorrido modalidad sencilla (visitando todas las casillas, encontrada por Alejandro Apezteguia Torres): a53 → a52 → a32 → a43 → a55 → a35 → a25 → a14 → a15 → a34 → a54 → a44 → a24 → a45 → a23 → a22 → a12 → a21 → a13 → a11 → a31 → a41 → a42 → a51 → a33 La más corta modalidad sencilla (con dos recorridos simétricos): a53 → a43 → a33 Recorrido modalidad experto: En la que recorre todas las casillas expuesta arriba, la suma es +2. Eliminando una única casilla, la a42 = +2, se tiene suma cero (también de Alejandro): a53 → a52 → a32 → a43 → a55 → a35 → a25 → a14 → a15 → a34 → a54 → a44 → a24 → a45 → a23 → a22 → a12 → a21 → a13 → a11 → a31 → a41 → a51 → a33 El más corto, en sólo seis pasos (de Celso de Frutos): a53 (+1) → a52 (–2) → a41 (–3) → a44 (+2) → a35 (+3) → a23 (–1) → a33 La mejor solución con suma 0 que yo tenía era en 14 pasos: a53 (+1) → a52 (–2) → a32 (–2) → a43 (–2) → a54 (–3) → a51 (+4) → a11 (+2) → a31 (+1) → a41 (–3)  → a44 (+2) → a42 (+2) → a22 (+3) → a25 (–2) → a23 (–1) → a33 M – 2 Si denotamos por an la distancia recorrida por la bola en el segundo n-ésimo, del enunciado se tiene que an = 2/3 an-1, para n ≥ 2  y  a1 = 10 Esas condiciones nos llevan, sin más que ir calculando los términos, a que an = 10 (2/3)n-1, una progresión geométrica, cuya suma se calcula como S = 10 = 30. Por tanto, la bola se detiene a los 30 cm. de haber iniciado su andadura. M – 3 i.- El número 3.816.547.290 tiene la propiedad de que el número formado por los primeros n dígitos es divisible por n, para n = 1, 2, 3, …10. Si los movimientos se llevan a cabo en este orden, entonces el juego puede terminar en empate. ii.- El primer jugador (en este caso Andrew) tiene una estrategia ganadora. Obsérvese que, según las condiciones, Milo debe jugar un dígito par en cada uno de sus movimientos. Por tanto, el objetivo de Andrew es “gastar” tantos números pares como sea posible. Por ejemplo, Andrew puede poner un 6 para empezar. En ese caso, hay tres posibilidades a considerar para el segundo movimiento: (1) Si Milo juega un 4 o un 2, entonces Andrew utiliza el otro en tercer lugar. Milo debe a continuación jugar un número par porque su número ahora tiene que ser divisible por 4, así que, si  utiliza el 8, entonces Andrew pone el 0 y Milo pierde porque en el sexto movimiento, tendría que jugar un número par y no queda ninguno. Si Milo jugara un 0, entonces Andrew pone el 5 y Milo también pierde porque ahora debe jugar un número par en el sexto movimiento, y el único que queda es un 8, pero ni 642.058 ni 624.058 son divisibles por 6. (2) Si Milo juega un 0, entonces Andrew usa el 9. Milo debe entonces jugar el 2 para hacer que el número de cuatro dígitos sea divisible por 4. Entonces Andrew coloca el 5. Milo debe emplear el 8 para hacer que su número sea divisible por 6. Y Andrew puede contrarrestar con el 3, ya que 6.092.583 es ​​divisible por 7. El único número par que Milo puede utilizar ahora es el 4, pero 60.925.834 no es divisible por 8, por lo que pierde. (3) Si Milo juega el 8, entonces Andrew pone el 4. La única opción de Milo es entonces el 0. Entonces Andrew echa mano del 5. Y la única opción de Milo sería el 2, pero 684052 no es divisible por 6, por lo que pierde. Téngase en cuenta que esto cubre todos los casos porque Milo debe jugar un dígito par en el segundo movimiento. Por lo tanto, Andrew siempre puede forzar una victoria. Otra estrategia ganadora: Andrew comienza con el 4. Luego, Milo debe colocar un número par. Si responde con un 2 o un 8, entonces el siguiente movimiento de Andrew es un 0. Si la respuesta de Milo fuera un 0 o un 6, entonces el siguiente movimiento de Andrew es un 2. En el caso de que se haya escrito el número 480, Milo no puede encontrar un dígito para hacer un número de cuatro dígitos divisible por 4, por lo que inmediatamente pierde. En los otros tres casos, hay al menos un dígito que Milo puede elegir para permanecer en el juego. Por lo tanto, después de cuatro movimientos, si el juego durara tanto tiempo, uno de los siguientes números estarán en la mesa: 4028, 4208, 4620 o 4628. Entonces Andrew pondría el 5, y en cada uno de esos cuatro casos, será imposible para Milo hacer un movimiento para que el nuevo número de seis dígitos sea divisible por 6, ya que todos los dígitos que necesita se han utilizado. Por lo tanto, si Andrew sigue esta estrategia, puede siempre forzar una victoria. iii.- Aunque describirlo con detalle nos llevaría mucho espacio, en efecto este juego es más justo ya que el segundo jugador no está tan restringido por los movimientos del primero. Hay cuatro números que pueden colocarse en cualquier momento (1, 2, 5, 0) para cualquiera de los jugadores (salvo que el primer jugador no puede empezar con el 0). Además, si los dos últimos números que quedan por poner son el 9 y el 0, ambos pueden colocarse en cualquier orden con finalización exitosa y empate entre los jugadores. Además, hay un movimiento garantizado: colocar el 6 inmediatamente después de haber puesto el 3, ya para ser divisible entre 6, el número lo ha de ser entre 2 (lo es pues 6 es par) y entre 3 (también lo es pues estaríamos sumando un 6, que es un múltiplo de 3 a otro número que ya era múltiplo de 3). No parece haber estrategia ganadora para ninguno. Alejandro Azpeteguia indica una estrategia “empatadora” para cualquier jugador. Eso convierte este juego en más justo, pero sin interés, si ambos conocen dicha estrategia, obviamente. Debo indicar que esta cuestión fue inventada y por tanto abierta, siendo su orden de complejidad bastante alto por el número enorme de posibilidades (como pasa con estas cosas). Celebro que la mayor parte de los participantes sin embargo, hayan pensado en ella deportivamente, y hayan llegado a mi misma conclusión. M – 4 Es claro que las velocidades de las agujas de las horas y del minutero son diferentes. La primera tarda 12 horas en recorrer toda la esfera, por lo que su velocidad (espacio/tiempo) es La aguja del minutero sin embargo recorre toda la esfera (o sea el espacio 2πt) en una sola hora, por lo que su velocidad es asimismo 2πt. Queremos saber cuándo están ambas agujas formando 90º (un ángulo recto; en radianes π/2) y eso sucede un número impar de veces (porque en un número par la diferencia es π). Por tanto, deseamos conocer los valores de t para los que 2πt - = (2n + 1) Simplificando nos queda que  t = (2n + 1) Dando valores a n, se comprueba que para n = 22, obtenemos un valor que supera 12 (concretamente, 135/11 ≈ 12.272727…), por lo que en una vuelta completa de la aguja de los minutos (12 horas) hay 22 veces en las que se forma un ángulo recto. Al cabo del día, por tanto, que era la pregunta, hay 44 veces en las que las agujas forman un ángulo recto. Calculamos esos 22 valores de una vuelta completa para n entre 0 y 21: Para obtener a qué horas corresponden exactamente, basta con tomar la parte entera como la hora, e ir multiplicando la parte decimal por 60 para saber los minutos (y por 3600 si quisiéramos los segundos. Por ejemplo, = 0.272727… 0.272727 x 60 = 16.363636…. 0.363636 x 60 = 21.818181… Luego serían las 0 horas 16 minutos 21 segundos. Haciendo lo mismo con las demás, tenemos que todas las horas en las que las manecillas forman un ángulo recto son: 1.- 0 horas 16 minutos 21 segundos (00:16:21) 2.- 0 horas 49 minutos 5 segundos (00:49:05) 3.- 01:21:49 4.- 01:54:32 5.- 02:27:16 6.- 03:00:00 7.- 03:32:43 8.- 04:05:27 9.- 04:38:10 10.- 05:10:54 11.- 05:43:38 12.- 06:16:21 13.- 06:49:05 14.- 07:21:49 15.- 07:54:32 16.- 08:27:16 17.- 09:00:00 18.- 09:32:43 19.- 10:05:27 20.- 10:38:10 21.- 11:10:54 22.- 11:43:38 Obsérvese la simetría existente en los minutos y los segundos antes y después de las 6 horas (la mitad del recorrido de la aguja de las horas). Se han señalado en rojo las dos posibilidades existentes entre las 7 y las 8 tal y como se pedía en el enunciado. M – 5 Supongamos que tenemos N cuadrados de cada tipo embaldosando un cuadrado de lado S (en cm2). Entonces, S2 = N × 1 + N × 4 = 5N El S más pequeño que satisface esta ecuación es 5, lo que implica N = 5. Sin embargo, no hay una disposición posible de los mosaicos que satisfaga esto, como se puede ver en la figura, ya que cualquier ficha 2 x 2 colocada en el cuadrado, taparía alguno de los cuadrados coloreados en gris. Por tanto, no se pueden poner fichas 2 x 2 en un cuadrado 5 x 5. El siguiente S posible que satisface la ecuación es 10, lo que implica N = 20. Un posible mosaico se muestra a la derecha. Por tanto, el cuadrado más pequeño que se puede formar con números iguales de cada tipo de baldosas tiene una longitud de lado de 10 cm. M – 6 Si contamos el número de triángulos pequeños de que está compuesto el hexágono, comprobamos que son 96. Sea el área de cada uno de esos triángulos igual a 1. Llamaremos s al lado de cada pequeño triángulo equilátero. Entonces = 1 (no hay más que calcular la altura de cada triángulo equilátero mediante el teorema de Pitágoras, s √3/2, y después utilizar la expresión del área del triángulo). Sea d la longitud del lado de la esmeralda (triángulo equilátero de color verde), cuya superficie queremos calcular. En la imagen se ha representado un triángulo de color rojo, de lados d, 5s y 2s, con un ángulo de 120º opuesto a d. Por el teorema del coseno obtenemos que d2 = (2s)2 + (5s)2 - 2 (2s)(5s) cos 120º = 4s2 + 25s2 + 10s2 = 39s2. Entonces el área de la esmeralda (triángulo equilátero verde) es = 39 M – 7 A primera vista, parece que el segundo lanzamiento es irrelevante: como nuestra habilidad es constante, el segundo lanzamiento no influye de ninguna manera en el tercer lanzamiento. Además, da la impresión de que esta pregunta solo puede responderse en términos de la distancia desde el centro al lugar donde cayó el primer lanzamiento. Si denotamos esa distancia por d, y suponemos que el área del tablero de dardos es 1, la probabilidad de que el tercer lanzamiento sea más lejano que el primero aparentemente sería el área del anillo, dada por 1− π d2. Pero esta aproximación se puede mejorar. Sin embargo, podemos razonar de otro modo. Llamemos di a la distancia del i-ésimo lanzamiento al centro. Los posibles resultados, asumiendo que el segundo lanzamiento es más lejano que el primero, son: d3 < d1 < d2 d1 < d3 < d2 d1 < d2 < d3 Y los que satisfacen la pregunta que se hace son sólo los dos últimos, de modo que la probabilidad buscada sería 2/3. Otro modo de razonar, más “elaborado”. Sean f1(r), f2(r), f3(r) las funciones de densidad de probabilidad de la distancia desde el centro de los tres dardos, respectivamente, y F1(r), F2(r), F3(r) sus funciones de distribución acumulativa. (Estos, por supuesto, serán iguales porque suponemos que los dardos son idénticos, están por tanto idénticamente distribuidos). f1(r) = f2(r) = f3(r) = 2r/R2 F1(r) = F2(r) = F3(r) = r2/R2   p(d1 < d2) = M – 8 El primer jugador tiene una estrategia ganadora. Su primer movimiento es colocar una moneda en el centro de la mesa. A partir de ahí, lo único que debe hacer es ir poniendo monedas en una posición simétrica respecto al centro a las que ponga el segundo jugador. Este argumento sirve igualmente para cualquier mesa que tenga simetría central, obviamente. M – 9 La solución al crucigrama se muestra al final de la página. Está compuesto por 84 palabras. Quien haya resuelto al menos 42 tiene 5 puntos. Hasta 52, 6 puntos; Hasta 62, 7 puntos; Hasta 72, 8 puntos; Hasta 80, 9 puntos; y entre 81 y 84, 10 puntos. M – 10 Aunque lo suyo sería que se pudieran obtener las fechas de ambas películas únicamente con los datos del enunciado, lo cierto es que debe utilizarse información de apartados anteriores; incluso les habrá sucedido a muchos participantes que ya conocieran de qué películas se trataba antes de afrontar esta cuestión, con lo que simplemente les servirá para confirmar sus sospechas. No obstante, veamos que podemos inferir exclusivamente del enunciado de esta cuestión. Sólo se ha valorado con 10 puntos (o una cantidad proporcional) aquellas respuestas con algún razonamiento matemático que ayude a determinar el año. Quienes simplemente hayan puesto el año, sin mayor explicación, la puntuación que se ha dado ha sido 4. Desde luego, el dato más objetivo es el de que el año actual es el 2022. Veamos en que columna estaría colocado. De acuerdo con la disposición en columnas de los números son claras las congruencias dispuestas al pie de cada columna Como 2022 ≡ 6 mod 8, se halla en la columna E. Además, nos dicen que el año de la segunda versión es dentro del siglo XXI (por tanto del 2001 en adelante), que comparte la misma columna que la diferencia entre el año actual con ese año, y que además es un múltiplo de cinco. Eso nos lleva a los años Año:               2017               2012               2007               2002 Diferencia          5                    10                   15                   20 Sólo se encuentran en la misma columna de la tabla 2017 y 5 (columna D) y 2007 y 15 (columna D). Sea la que sea, están en la columna D, por lo que el año de la primera versión, y la diferencia entre 2022 y ese año, no se encuentran en las columnas D ni E (porque dicen que están en columnas diferentes todas salvo la del año del remake y la de diferencia de ésta con el año actual). Entre las imágenes de la película, vemos al guitarrista troglodita con una guitarra eléctrica. Este instrumento data de 1920, pero el modelo de la estatua es como poco de mediados de los años sesenta del siglo pasado, pongamos de 1965 (¡¡gran año!!) en adelante. Otra de las imágenes, la del retrato, corresponde a la actriz Joanne Woodward (véase pregunta C – 7), que nació en 1930, si bien su primer trabajo en el cine es en 1955 (en televisión comenzó en 1952). En el retrato, no obstante, tiene un aspecto que desde luego es posterior a ese 1965 que hemos fijado como extremo del intervalo donde asignar el año de la primera versión. Y es claramente inferior a 1980 si observamos alguna foto de la actriz en ese año, como la de la imagen de la derecha del telefilme La caja oscura (The Shadow Box, Paul Newman, EE. UU., 1980). Eso nos deja como posibles años únicamente 1968, 1969, 1970, 1971, 1972, 1976, 1977, 1978, 1979 y 1980 (ninguno en columnas D o E). Sin embargo, como la diferencia de años con el actual debe ser un múltiplo de 5, en realidad sólo quedan 1972 y 1977 (con 50 y 45 años de diferencia, respectivamente). Pero 45 ≡ 5 mod 8, lo que sitúa este valor en la columna D, por lo que no sirve. La película se estrena por tanto en 1972 (que estaría en la columna C), hace 50 años (columna A). M – 11 Buscando películas rodadas aquel año (1972) que hayan tenido una nueva versión, llegamos con poco esfuerzo a La huella (Sleuth, Joseph L. Mankiewicz, Reino Unido, 1972) y La huella (Sleuth, Kenneth Branagh, EE. UU., 2007). CUESTIONES CULTURALES Algunas tienen pregunta múltiple. Cuando he utilizado alguna baremación para repartir la puntuación, lo indico en color azul oscuro. C – 1 La solución aparece en la imagen adjunta. C – 2 Se pedían tres laberintos reales, y se indicaba que se valorarían aspectos como estar cercano al de la película, estar en España y antigüedad. Lo ideal por tanto es poner uno de cada. Pero quien haya dado tres que cumplan todo a la vez, también es correcto. Los participantes han recopilado un montón de laberintos, con imágenes sugestivas de cada uno. No voy a enumerarlos todos, sino que voy a indicar, uno de cada una de las características pedidas. Más cercano al lugar de rodaje: Laberinto de Longleat Hedge Maze, en Warminster,  Inglaterra. Los exteriores y la casa de la película son visitables y se llama Athelhampton House, construida en 1485, en Dorset, Inglaterra. En España (pongo varios): Jardines del Palacio Real de La Granja de San Ildefondo (Segovia, sobre 1730), El Capricho (Madrid, 1784), Laberinto de Horta (Barcelona, 1808); Laberinto de Villapresente (Cantabria, 2007), Más antiguo: Il Labirinto, Villa Pisani, Venecia (Italia, 1720). Esta página puede resultaros curiosa: https://www.elle.com/es/living/viajes/news/g795538/los-10-laberintos-mas-impresionantes-del-mundo/ C – 3 Es tal la cantidad de objetos que aparecen en la película que hacer una lista de todos los juegos es complicado. Con dar media docena de ellos, he considerado la cuestión resuelta. Los que yo he visto son: laberinto, ajedrez, senet, puzzle, billar, ruleta, diana y dardos, crucigrama, croquet, backgammon, adivinanzas, ... Casi todos los concursantes han incluido también los juguetes que aparecen. Estrictamente no son juegos, pero también se han dado por válidos (son juegos para Andrew Wyke). C – 4 La estatua del guitarrista troglodita aparece en la discoteca de la película Play It Cool! (Michael Winner, Reino Unido, 1962), también aparece en una escena de discoteca en Band of Thieves (Peter Bezencenet, Reino Unido, 1962); en el bar de Rudi en el episodio 6 de la primera temporada de la serie de televisión británica The Human Jungle (1963) titulado A Friend of the Sergeant Major emitido el 4 de mayo de 1963; y en la nuestra, en el laberinto de la casa de Laurence Olivier en La huella (Sleuth, Joseph L. Mankiewicz, Reino Unido, 1972). En la primera de esas películas, se pretendía lanzar un emulo de Elvis Presley en el Reino Unido, el cantante Billy Fury (1940 – 1983). Allí tuvo cierto éxito (igualó el récord de 24 éxitos de los Beatles en la década de 1960, y estuvo 332 semanas en las listas de éxitos del Reino Unido; sólo fue superado por los Beatles, Cliff Richard y Elvis Presley), pero nunca alcanzó un número uno. En España no es demasiado conocido, y esa película nunca se ha estrenado. La actualidad a que se aludía en el enunciado de la cuestión es el reciente estreno de la película Elvis (Baz Luhrmann, EE. UU., 2022). C – 5.- Se comenta que el padre de Milo Tindle (Michael Caine) fue relojero. Además, hacia el final del primer acto, Andrew Wyke (Laurence Olivier) atormenta a Milo con el tiempo que le queda de vida, lo que reproducirá en el tercer acto Milo con él, con el tiempo que le queda para encontrar unos objetos que lo incriminan antes de que llegue la policía. Aparecen también relojes en las muñecas de los protagonistas (marcando su estilo la diferencia de clase social), y por supuesto el reloj de péndulo de la escalera en el que se esconde una de las pruebas incriminatorias, además de ser enfocado numerosas veces a lo largo de la película. C – 6.- Andrew Wyke es escritor de novelas de crímenes y detectives. El busto sobre la repisa de la chimenea de la imagen corresponde al premio Edgar Allan Poe que ganó el autor de la obra teatral, Anthony Shaffer, precisamente por esta obra, Sleuth. Pero lo hizo en 1971, que no se corresponde con ese 1946 de la imagen. El director de la película, Joseph L. Mankiewicz también ganó un Edgar Allan Poe por Operación Cicerón (Five Fingers, EE. UU.,1952). Otros detectives literarios mencionados o referenciados en la película son Lord Peter Whimsey (de la escritora británica Dorothy Leigh Sayers; de hecho, el detective al que Wyke alude en la película como su creación, St. John Lord Merridew, es claramente un homenaje Whimsey, que utiliza monóculos en sus pesquisas); el detective Nero Wolfe (del escritor norteamericano Rex Stout; es un gran amante de las orquídeas, referencia que aparece también en la película); por supuesto Sherlock Holmes (del británico Arthur Conan Doyle; destaca por su inteligencia, su hábil uso de la observación y el razonamiento deductivo, y conocemos muchas de sus aficiones que aparecen de algún u otro modo en la película: es muy habilidoso disfrazándose, fuma en pipa, le gustan las galletas, toca el violín con maestría (un Stradivarius, a menudo a horas poco adecuadas), es un experto apicultor, excelente boxeador, tiene un gran conocimiento científico, en especial en química, y, cuando se aburre por falta de los retos intelectuales que suponen sus casos, consume cocaína en una solución al siete por ciento. Además, viste una gorra típica de las cacerías que también está en la película); el padre Brown (creado por el novelista inglés G. K. Chesterton, es el contrapunto a Sherlock Holmes, ya que resuelve sus casos por intuición y conocimiento de la naturaleza humana más que de la ciencia; su característico sombrero de pala también está presente en la película). Y por supuesto encontramos entre las fotografías de la pared a Agatha Christie, creadora de Hercules Poirot y la Srta. Marple. Y finalmente, se menciona o referencia un par de veces al malvado Fu Manchú, creado por el escritor Sax Rohmer, cuyos malvados planes siempre son desbaratados por Sir Denis Nayland Smith, junto a su acompañante, el doctor Petrie. Indicar el oficio del protagonista: 5 puntos. Los otros cinco autores y sus creaciones: 5 puntos (uno por cabeza). C – 7.- Es un retrato de la actriz norteamericana Joanne Woodward, que interpreta sin aparecer físicamente a la esposa de Andrew y amante de Milo, Marguerite Wyke. Joanne fue una de las actrices que hicieron una prueba para encarnar a Cleopatra en la película homónima de J. L. Mankiewicz (junto a Joan Collins y otras actrices), antes de que finalmente se lo adjudicaran a Elizabeth Taylor. Es la única relación que he encontrado acerca de la utilización de esta actriz para esta película. Además del retrato, aparece en una fotografía junto a Laurence Olivier en otro trabajo que hicieron juntos, justamente la foto a la que Andrew hace un agujero con su revólver. Sobre la presencia del retrato de Joanne Woodward, algunos participantes indican otras posibilidades: ganó el Óscar a la mejor actriz en 1957 por Las tres caras de Eva. En esa película interpreta un personaje que posee personalidad múltiple (hasta 3 diferentes), muy en la línea de engaños y falsos personajes de La huella. Recordemos además que Mankiewicz fue el director de Eva al desnudo. Además siendo niña, acudió a la premiere de Lo que el viento se llevó (1939) en Atlanta, y logró sentarse en el regazo de Laurence Olivier (quien tenía entonces 32 años), que era entonces el compañero sentimental de Vivien Leigh. Otro concursante nos dice que en la biografía del director Mankiewicz, Pictures Will Talk,  se indica que esta presencia no es sino una broma (una más de la película) entre él y sus amigos Joanne Woodward y Paul Newman (ya saben, pareja en la vida real). Se proponen cuatro cuestiones: 2.5 por cada una resuelta. C – 8 En los títulos de crédito aparecen los nombres de seis actores, pero la película sólo tiene dos. Los otros no existen (el del detective, Alec Cawthorne, es casi un anagrama de "O Michael Caine": se invierte la "W" en Cawthorne para obtener la "M" en Michael, y se separan las líneas horizontales y verticales en la letra "T" para obtener las dos "I" necesarias). En 1993, Mankiewicz afirmó en una entrevista que los cuatro restantes eran nombres reales de parientes de su esposa, aunque Eve Channing es claramente una mezcla entre Eve Harrington y Margo Channing, nombres de dos de las protagonistas de Eva al desnudo. Los concursantes han aportado un buen número de películas con uno o dos personajes solamente. En algunas, aunque el peso de toda la película sea sólo de uno o dos, si aparecen más personas, aunque sean de fondo, no se han considerado. He aquí una selección:: Locke (Locke, Steven Knight, Reino Unido/EE. UU., 2013). Un único actor, Tom Hardy, y voces de otros. La Venus de las pieles (La Vénus à la fourrure, Roman Polanski, Francia, 2013). Dos actores solamente, Mathieu Amalric y Emmanuelle Seigner. Gravity (Gravity, Alfonso Cuarón, Reino Unido/EE. UU., 2013). Sólo Sandra Bullock y George Clooney, con voces de otros. Buried (Rodrigo Cortés, España, 2010). Un único actor, Ryan Reynolds, y voces de otros. Vida/perra (Javier Aguirre, España, 1982). Una única actriz, Esperanza Roy Give 'em Hell, Harry! (Steve Binder y Peter H. Hunt, EE. UU., 1975), con James Whitmore como único actor. Infierno en el Pacífico (Hell in the Pacific, John Boorman, EE. UU., 1968). Sólo dos actores, Lee Marvin y Toshirô Mifune. C – 9 Nos referiremos a la primera versión como v1, y a la segunda como v2. Diferencias: 1.- En v1 Milo es propietario de una cadena de salones de belleza, mientras que en v2 es un joven escritor en paro. 2.- En v1 hay diálogos cargados de ironía y sutilidad mientras que en v2 hablan a gritos, insultando y diciendo palabrotas. 3.- En v1 el interior de la casa está decorada con numerosos muñecos, juegos, objetos singulares, muy recargada, mientras que en v2 es todo minimalista y con muchos aparatos tecnológicos. 4.- La duración del metraje de v2 es sensiblemente inferior a la de v1 (50 minutos menos). 5.- En v1 el autor de la obra de teatro, Anthony Shaffer, es quien hace el guion, mientras que en v2, lo hace Harold Pinter, premio nobel de literatura. 6.- En la escena inicial de v1, Milo aparca su coche en solitario, mientras que en v2 lo aparca junto al de Andrew, pudiéndose así apreciar la diferencia de tamaños entre estos, indicador claro del nivel económico de cada uno. 7.- La realización cinematográfica de v1 es más clásica, mientras que en v2 hay una amplia gama de planos. 8.- En v2, las alusiones a la homosexualidad son mucho más explícitas que en v1. 9.- En v1 aparecen en los títulos de crédito actores inexistentes, mientras que en v2 aparecen personajes que no están en los títulos de crédito (salen por televisión). 10.- El sentido del juego y el desenlace son diferentes. 11.- Milo es invitado a la casa en v1, mientras que en v2 aparece por su cuenta. 12.- El carácter de Milo en v1 es respetuoso inicialmente e incluso con cierto complejo de inferioridad, mientras que en v2 es muy agresivo y muy seguro de si mismo. Andrew en v2 es también más perverso. Semejanzas 1.- Michael Caine protagoniza ambas, aunque con diferentes papeles: en la v1 es Milo Tindle, mientras que en la v2 es Andrew Wyke. C – 10 En la versión original de la película en inglés, Andrew indica a Milo (minuto 41, aproximadamente), “If you'll be good enough to follow me, Miss Rebecca”. En la versión española dice “Si es usted tan amable de seguirme, mi querido amigo”. Además en la versión original, Laurence Olivier imita la forma de hablar de la señorita Danvers, personaje de Rebeca (Rebecca, Alfred Hitchcock, EE. UU., 1940), en la que Olivier encarna al marido de la difunta Rebeca. Es claramente, como sucede en toda la película, un nuevo guiño al espectador. En cuanto al actor que rechazó interpretar a Milo (algún concursante ha pensado que la pregunta era sobre Rebeca) fue Alan Bates, que tras los primeros ensayos manifestó que el papel no estaba a su altura. Albert Finney fue descartado previamente por ser un poco regordete. Michael Caine fue la tercera opción. C – 11 Me alegra que la película haya gustado a todos los participantes (menos el remake, que tiene sus virtudes, pero claramente muy por debajo de la original). No es una película sencilla de ver para el público actual, en el que tanto diálogo (junto a las reflexiones que conlleva) puede resultarles agotador (a eso se ha mal acostumbrado a la gente: lo vemos diariamente en entrevistas o debates, en las que enseguida se corta al orador; por supuesto eso conlleva un deficiente estudio de nada. El síndrome Twitter, lo podemos llamar). PUNTUACIONES FINALES Como cada año, el nivel mostrado por todos los participantes ha sido más que sobresaliente. Las diferencias son mínimas y normalmente por cuestiones de detalle. Recordemos que la puntuación máxima que se podía obtener en esta ocasión era de 220 puntos (110 las cuestiones matemáticas, en rojo; y 110 las de tipo cultural, en azul). Así ha quedado al final: 1.- Alejandro Apezteguia Torres  212 (107 + 105) 2.- Francisco Pi Martínez   205 (101 + 104) 3.- Equipo formado por Engracia, María y Javier   205 (96 + 109) 4.- Paz Jiménez Seral     177 (97 + 80) 5.- Celso de Frutos de Nicolás   175 (96 + 79) 6.- Alba Diez Mariño    153 (51 + 102) En el caso del segundo y tercer puesto, he terminado por ponerlos en ese orden primando las preguntas de tipo matemático. Aunque leer y valorar todos los documentos recibidos lleva un tiempo no despreciable, debo agradecer a los participantes su excelente trabajo del que no dejo de aprender cada año (hay razonamientos y resoluciones realmente magníficas), y me he divertido enormemente con sus comentarios tanto sobre las cuestiones matemáticas como las culturales y de cine. Y celebro especialmente que haya habido tantas mujeres como hombres involucradas en el concurso. Ojalá sea la tendencia futura en todo. Espero que todos hayan pasado de verdad un buen rato. En breve recibiréis un mail, algunos para pediros una dirección postal a la que enviaros un pequeño obsequio de DivulgaMAT (ignoro a fecha de hoy el número de obsequios de los que dispone la organización), y a todos para detallaros las puntuaciones de cada cuestión, una vez hayáis leído las soluciones. ¡¡Enhorabuena a todos!!

Jueves, 08 de Septiembre de 2022 | Imprimir | PDF |  Correo electrónico