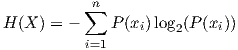101. 185. (Septiembre 2020) Pascal en Technicolor

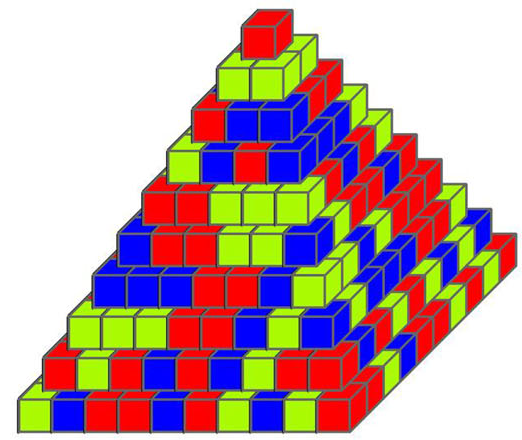
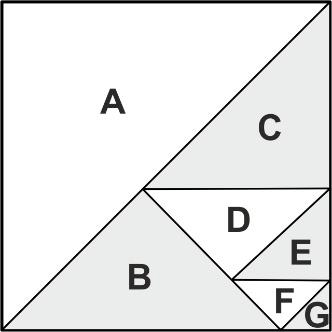
[Imagen extraída del artículo Pyramid Mysteries de Ehrhard Behrends.] Comenzábamos el número anterior de nuestro rincón (julio de 2020) destacando que el triángulo de Pascal oculta muchas propiedades que podemos convertir en juegos de magia. Allí desarrollamos dos juegos que aprovechaban las características especiales del triángulo cuando se escriben sus elementos en base nueve o base diez. Terminábamos dicho artículo proponiendo una versión basada en propiedades de la aritmética binaria. Como se puede suponer, es posible diseñar versiones del juego para cualquier sistema de numeración pues las características se mantienen y el secreto es el mismo en todos ellos. El problema es que no resulta natural en un juego de magia pedir la construcción de un triángulo donde los números utilizados no sean mayores que cierta cantidad, salvo que exista una justificación adecuada. En algunos casos, resulta bastante sencillo plantear alguna excusa; por ejemplo, se puede disimular el uso de la aritmética binaria utilizando los colores de las cartas de una baraja, rojo y negro, si establecemos, por ejemplo, la correspondencia “rojo = 0”, “negro = 1”. De este modo, como la tabla de sumar en la aritmética binaria es simplemente 0 + 0 = 1 + 1 = 0 y 0 + 1 = 1 + 0 = 1, podríamos plantear el siguiente juego, para el que necesitarás solamente una baraja (y una mesa despejada). Coloca sobre la mesa, y formando una fila, un conjunto de cartas, con las caras hacia arriba. Supongamos, por ejemplo, que las cartas colocadas son las siguientes: Construye una segunda fila sobre la anterior, siguiendo estas reglas relativas a dos cartas consecutivas: Sobre dos cartas del mismo color, coloca una carta roja (por aquello de que 0 + 0 = 1 + 1 = 0). Sobre dos cartas de distinto color, coloca una carta negra (representando las sumas 1 + 0 = 0 + 1 = 1). Siguiendo nuestro ejemplo, como las dos primeras cartas son de distinto color, sobre ellas se colocaría una carta negra; como la segunda y tercera cartas son del mismo color, sobre ellas se colocaría una carta roja. Al repetir este proceso con todas las parejas de cartas consecutivas, llegaríamos a una segunda fila que tendría esta pinta: Sigue formando filas de cartas sobre las anteriores obedeciendo las mismas reglas anteriores. Al final llegarás a una fila formada por una sola carta, que podrá ser roja o negra. Pues bien, una simple inspección de la primera fila proporciona información suficiente para saber el color de la última carta colocada. Ahora viene la inevitable cuestión: ¿cómo deducir rápidamente cuál será el color de la última carta? La respuesta se basa nuevamente en interpretar el triángulo de Pascal escrito en el sistema binario y realizar la correspondencia que habíamos establecido entre los colores y los números. Hay que tener en cuenta que la operación puede ser más o menos inmediata según el número inicial de cartas. Por esta razón, es conveniente que el número de cartas que se colocan en la primera fila se corresponda a una fila del triángulo de Pascal que sea fácilmente identificable. Veamos los casos más simples a la vista de este triángulo, donde el color rojo corresponde al cero y el color azul al uno: Si el número inicial de cartas es una potencia de dos (2, 4, 8, 16, etc.), la fila correspondiente del triángulo de Pascal sólo contiene unos. Por tanto, el mago debe contar el número de cartas negras (o rojas) que hay en la primera fila formada por el espectador. Si hay un número par, la carta final será roja; si hay un número impar, la carta final será negra. Este es precisamente el caso que hemos puesto como ejemplo, donde colocamos ocho cartas en la primera fila; como cuatro de ellas son negras, la carta que ocupará la última fila será roja. Si el número inicial de cartas es una unidad mayor de una potencia de dos (3, 5, 9, 17, etc.), la fila que le corresponde en el triángulo de Pascal sólo contiene ceros, salvo los dos unos en los extremos. Basta fijarse en los colores de las cartas en los extremos: si son del mismo color, la carta final será roja; si son de distinto color, la carta final será negra. Si el número inicial de cartas es una unidad menor que una potencia de dos (3, 7, 15, 31, etc.), la fila que le corresponde en el triángulo de Pascal contiene unos y ceros de forma alternada. Así pues, el mago debe contar el número de cartas negras que ocupan los lugares impares. Como en el primer caso, si hay un número par, la carta final será roja; si hay un número impar, la carta final será negra. Así pues, un poco de psicología barata ayudaría en las demás situaciones: si el número de cartas que coloca el espectador no corresponde a uno de estos tres casos, el mago podría pedirle que añadiera algunas cartas más para «complicar» la adivinación. En caso necesario, el mago podría incluso completar él mismo las primeras filas como «ejemplo» de lo que pretende que haga el espectador hasta llegar a un número de cartas donde el cálculo sea sencillo. A pesar del innegable interés didáctico del juego, no parece muy mágico intentar adivinar un color entre dos posibles, pues la probabilidad de acertar es del 50%. De hecho, el objetivo principal de esta entrega es el de presentar una versión más divertida y sorprendente: el caso de la aritmética en base tres. La idea básica es similar a la anterior pero, como no hay cartas de tres colores en las barajas (aunque Colm Mulcahy propone usar tres palos de la baraja o bien distinguir entre cartas rojas, negras o de dorso), lo realizaremos con cartulinas de colores. Para ello, sería interesante disponer de un surtido de tarjetas o cartulinas de tres colores. En condiciones normales, bastará con 25 rojas, 25 azules y 25 verdes. Para una versión simiplificada en papel, necesitarás tener a mano tres rotuladores, uno rojo, uno verde y uno azul. En cualquier caso, para comprender el desarrollo del juego, deberás seguir estas indicaciones: Coloca diez de las cartulinas en una fila, con los colores al azar. En esta imagen mostramos un ejemplo (por el momento, los números no son importantes): Sobre esta fila, coloca otra fila de nueve cartulinas, siguiendo estas reglas: Si dos cartulinas consecutivas son del mismo color, coloca sobre ellas otra del mismo color que ambas. Si dos cartulinas consecutivas son de distinto color, coloca sobre ellas una cartulina del color diferente a ambas. Según el ejemplo anterior, las dos primeras filas serían como las de esta imagen (las dos primeras son rojas, de modo que la fila superior empieza en rojo; la segunda es roja y tercera es verde, de modo que sobre ellas irá una azul; la tercera es verde y la cuarta es azul, con lo que sobre ellas irá una roja; y así sucesivamente): Continúa formando filas con las cartulinas de colores siguiendo las mismas reglas establecidas en el punto anterior hasta llegar a una fila con una sola cartulina. Siguiendo con el ejemplo, el triángulo completo sería el que termina en una cartulina verde como se ilustra a continuación: Sí, has adivinado: una vez colocada la primera fila de cartulinas, puedo saber el color de la cartulina que ocupará el vértice superior del triángulo. La solución es sorprendentemente simple: basta aplicar las reglas anteriores a la primera y última cartulinas de la primera fila. En el ejemplo con el que hemos ilustrado el proceso, como estos colores son rojo y azul, la cartulina que ocupará la última fila deberá ser verde. Por cierto, ¿te has percatado de que las mismas reglas se aplican a los triángulos sombreados que tienen cuatro cartulinas en cada lado? ¿Y que esas mismas propiedades se mantienen al girar 120 grados cualquiera de esos triángulos? Te habrás preguntado también qué interpretación tienen los números asociados a cada color. La respuesta es que las dos reglas de formación del triángulo a partir de los colores corresponden a unas operaciones aritméticas con sus números. Estas operaciones pueden sintetizarse en la siguiente tabla (mostramos las dos versiones, la de colores y la de números): A R V A A V R R V R A V R A V 0 1 2 0 0 2 1 1 2 1 0 2 1 0 2 Como se puede comprobar, no se trata de la suma habitual, ni siquiera en base tres, pero sí conserva las propiedades algebraicas básicas: es conmutativa y asociativa. Esto significa que este juego ya no está basado en el triángulo de Pascal y hay que buscar la solución mediante otros argumentos. Es posible que estas pistas te sugieran la justificación del funcionamiento del juego. Por si acaso, en este enlace propongo mi versión, que no requiere conocimientos matemáticos. OBSERVACIONES FINALES: Los dos juegos que hemos descrito tienen un gran recorrido histórico que me gustaría compartir. Sobre el triángulo de Pascal binario, hace unos años recibí un mensaje de Ricardo Ramírez, músico y seguidor de este rincón. En su comunicación describía este juego sugerido por un problema que le propuso su profesor de Análisis Matemático, el recordado Miguel de Guzmán, precisamente el problema que planteábamos en este rincón al final de la entrega 58 de febrero de 2009. Copio y pego el último párrafo de aquel artículo: Por último, un problema: Escribe una sucesión de ceros y unos. Debajo de cada par consecutivo escribe un cero si los dos números son iguales, y un uno si son distintos. Repite el proceso hasta que te quede un único dígito en la sucesión. ¿Puedes predecir cuál va a ser el dígito final? Si conoces la respuesta, puedes realizar un juego de magia simulando los unos con cartas cara arriba y los ceros con cartas cara abajo (o viceversa). Pues bien, al proceso eliminatorio que parte de una fila de cartas, rojas y negras, y construye sucesivamente filas de cartas hasta llegar a una fila con una sola carta a partir de las reglas ya explicadas en el juego, Ricardo dio el nombre de «cuenta Stendhal» (nombre sugerido por el famoso título "Rojo y negro" de la novela de Stendhal y supongo que también por la belleza y sorpresa final del proceso asociadas al famoso síndrome). Él había estudiado y deducido el resultado final de la cuenta para cualquier cantidad inicial de cartas (hasta 52), incluso diseñó una completa y elaborada rutina con varios juegos de cartas en los que se utilizaba esta y otras cuentas con cartas. Comparto su opinión de que estas ideas pueden ser muy apropiadas para ayudar en la comprensión y motivar el estudio de los números combinatorios y sus aplicaciones. La historia detrás del juego de los tres colores también es interesante y productiva (puedes encontrar los detalles en el artículo del 13 de mayo de 2013 del blog Wordplay escrito por Gary Antonick y titulado Triangle Mysteries). Descubrimos que el inventor del juego es Steve Humble -más conocido por su pseudónimo DrMaths-, profesor en el Departamento de Educación de la Universidad de Newcastle y prolífico autor de material didáctico para la educación primaria. Tras compartir el juego con Ehrhard Behrends, profesor en el Departamento de Matemáticas e Informática de la Universidad Libre de Berlín y autor de un interesante libro de magia y matemáticas, ambos publicaron los resultados y sus generalizaciones en el volumen 35 (año 2013) de la revista The Mathematical Intelligencer. Allí aparece la siguiente foto en la que se ve a Steve Humble supervisando el juego ante un grupo de escolares: Posteriormente, Yutaka Nishiyama, profesor de matemáticas en la Universidad de Economía de Osaka, trató el mismo juego en el artículo The three-color triangle problem (en el que se cuela una errata al considerar que operación correspondiente a las reglas de formación de los colores tiene estructura de grupo abeliano). En su artículo relaciona el problema y su solución con el triángulo de Sierpinski, estructura fractal que aparece en la representación binaria del triángulo de Pascal. En este enlace de Youtube, Nishiyama publica una versión animada del proceso. Es fácil encontrar en internet otras adaptaciones y estudios sobre este interesante juego. Muchas preguntas surgen al querer comprender en profundidad el fundamento del juego de los colores. Me limitaré a plantear tres de ellas: ¿Qué pasa si modificamos las reglas de formación del triángulo de colores? Lo más natural -matemáticamente hablando- sería que, al simbolizar cada color con un número, digamos como antes 0 = azul, 1 = rojo, 2 = verde, aplicáramos la aritmética usual, es decir, azul + azul = azul, rojo + rojo = verde, verde + verde = rojo, azul + rojo = rojo, azul + verde = verde, rojo + verde = azul. Esta situación corresponde precisamente al comportamiento del triángulo de Pascal en base tres, de modo que el número de filas necesarias para que las cartulinas de los extremos sean las únicas que proporcionan la solución será la que contenga todo ceros (salvo los dos unos de los extremos). Observando la imagen adjunta, llegamos a la misma conclusión: si se empieza con una fila formada por 3n + 1 cartulinas, la suma de los valores correspondientes a los colores de las esquinas da como resultado el valor correspondiente al color de la última cartulina colocada. ¿Qué podemos decir si utilizamos cartulinas de cuatro colores y aplicamos alguna regla adecuada? Dejo la cuestión en el aire. 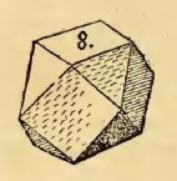¿Se pueden obtener propiedades similares para juegos en más dimensiones? Pues sí, el propio Ehrhard Behrends se permitió el lujo de proporcionar nuevas versiones de este juego en espacios de tres o más dimensiones. En lugar de empezar con filas de colores, se puede empezar con cuadrados o triángulos y construir pirámides con reglas similares a las utilizadas en el plano de modo que el color de la cúspide de la pirámide se puede deducir solamente a partir de algunos colores de la base. Los detalles de su trabajo están publicados bajo el título “Pyramid Mysteries” en la revista Mathematical Intelligencer, volumen 36, número 3 (2014), artículo en el que aparece la imagen que encabeza este artículo. Pedro Alegría (Universidad del País Vasco - Euskal Herriko Unibertsitatea)

Jueves, 03 de Septiembre de 2020 | Imprimir | PDF |  Correo electrónico

102. 65. (Septiembre 2020) Matemáticas en los órganos

(Alegoría de la Música, 1580. Jan Soens. Museo Cívico de Piacenza) La Música formó parte de la Matemática durante muchos siglos. Desde que Pitágoras (o su escuela) relacionó la escala musical con fracciones simples, la Música fue considerada como Aritmética aplicada. La figura de Pitágoras es representada muchas veces como acompañante de la alegoría de la Música y no con la Aritmética, como en el portal de la Catedral de Chartres o en la Biblioteca del Monasterio de San Lorenzo de El Escorial. Cuando el imperio romano occidental se desmoronaba, algunos pensadores reflejaron la cultura de ese mundo en descomposición, uno de ellos fue Marciano Capella, quien en un latín semibárbaro, en prosa y verso, escribe Las nupcias de Filología y Mercurio. Las siete disciplinas, que constituirían el trivium y el quadrivium, tomaron desde entonces forma alegórica de mujer, y sus cultivadores las acompañarán en un festivo cortejo. Teofrasto, Aristóxeno y Pitágoras son los sabios vinculados a la dama Armonía según Capella. Pero la Música no solo estará vinculada a la Aritmética, también se relaciona con la Astronomía. La música mundana no es sino reflejo de la música de las esferas, de los astros. Las siete estrellas errantes de la antigüedad (Luna, Venus, Mercurio, Sol, Marte, Júpiter y Saturno) nos proporcional las siete notas de la escala musical. Quizá la expresión más acabada de la música de las esferas se encuentra en El sueño de Escipión de Marco Tulio Cicerón del siglo I a.C, uno de los tratados fundamentales de la cultura grecorromana: ¿Qué es esta música tan encantadora y tan dulce que llega a mis oídos? Es –me contestó- aquella que está compuesta por intervalos desiguales que, con todo, se caracterizan por tener una proporción racional; la produce el impulso y el movimiento de las esferas,… No debe sorprendernos que en la decoración de los órganos tanto de palacios como de iglesias aparezcan personajes y alegorías matemáticas. Exponemos algunas de ellas. Alegorías matemático-musicales del Museo Cívico en Piacenza El Museo Cívico de Piacenza, ubicado en el Palazzo Farnese, exhibe en su pinacoteca dos espectaculares dípticos que se usaron como puertas de órganos en palacios de Parma. Presentamos en primer lugar el espléndido díptico pintado por Jan Soens il Fiamingo (1547 – 1611). Se trata de dos alegorías relacionadas con la música según la concepción renacentista: la propia Música y la Astronomía. Al igual que se hablaba del hombre como microcosmos frente al macrocosmos, se consideraban dos tipos de música: la mundana que deleita nuestros oídos y la música de las esferas expresión de la armonía del cosmos. Las siete notas y los siete planetas están en concordancia. (Alegoría de la Astronomía, 1580. Jan Soens. Museo Cívico de Piacenza) La correlación de la música de las estrellas y la instrumental encuentra en las liras de la Oda a Salinas de Fray Luís de León su más deliciosa expresión castellana (cuarta estrofa): Traspasa el aire todo hasta llegar a la más alta esfera, y oye allí otro modo de no perecedera música, que es la fuente y la primera. La Astronomía mira el cielo representado al modo ptolomeico de la época y calcula con un compás. A sus pies un cuadrante y una esfera armilar. (Alegorías de la Astronomía y la Música, 1580. Jan Soens. Museo Cívico de Piacenza) La Música también mide y muestra su vinculación pitagórica con la Aritmética. Pocas veces la armonía matemática del cosmos se ha expuesto tan brillantemente como en este díptico que cerraba un órgano palaciego de 1580. Pitágoras y Euclides en el Palacio Farnesio de Piacenza La pinacoteca del Museo Cívico de Piacenza tiene una segunda puerta que vincula la música y las matemáticas. Girolamo Mazzola Bedoli (1500-1569) es el pintor de Parma que decoró las dos planchas que formando un díptico cierran el órgano de una familia noble de la ciudad y donde fueron representados Euclides y Pitágoras. (Pitágoras y Euclides, 1545. Girolamo Mazzola. Museo Cívico de Piacenza) Pitágoras aparece muy a menudo como creador de la música. Los martillos crean el sonido mientras que la balanza y el compás ponen medida para hacerlo armonioso. Euclides como padre de la geometría y de las proporciones aritméticas completa con su compás el potente conjunto. El dinamismo de los personajes es ya plenamente manierista. El Museo del Prado archiva un dibujo de Bedoli representando a Pitágoras que contiene similares elementos iconográficos: martillo con yunque, una romana y una cítara al fondo. La música era aritmética aplicada. (Pitágoras, 1545. Detalle. Girolamo Mazzola. Museo Cívico de Piacenza) Órgano de las Artes Liberales en Bristow Al norte de Alemania, en la paradisíaca orilla noroeste del lago Malchin, se encuentra la minúscula aldea de Bristow, que hoy forma parte del municipio de Schorssow. El mariscal y administrador del distrito Werner Hahn fundó allí en 1597 tanto la  bonita iglesia como el túmulo funerario. Su hijo Hans Hahn (1558-1633) se encargó de ampliarla magníficamente al estilo renacentista. El altar, el púlpito y el órgano son testigos. La tribuna y soporte en madera del órgano data de 1601 y fue decorado con representaciones alegóricas de las siete artes liberales: Dialéctica, Retórica, Música, Aritmética y Astronomía al frente, y la Geométrica y la Gramática a ambos lados. (Órgano de las Artes Liberales en Bristow, 1601) La Aritmética con tablilla, la Geometría, coronada y con compás, y la Astronomía alada recuerdan mucho a las alegorías de Marten de Vos. El tallista se tomó algunas libertades para encajarlas en su lugar. Las tallas del órgano son menos coloristas que las del púlpito y el altar, pero no tienen porqué ser acordes con las originales tras cuatro siglos. La iglesia de Bristrow es una buena muestra de la extensión de la cultura renacentista por lugares remotos. (Alegoría de la Aritmética. Órgano de las Artes Liberales. Bristow, 1601) Los “mirones” de la Catedral de Viena La Catedral de San Esteban de Viena admite múltiples relatos donde no pueden faltar los matemáticos o numerológicos: proporciones, medidas, relojes o representaciones. Entre todos los posibles nos quedamos en primer lugar con el geómetra mirón, los dos autorretratos del escultor y arquitecto renacentista moravo Anton Pilgram (1460-1516). La mirada que penetra, que va más allá, es la base donde se apoya la razón. ¿Lo veis? es lo que solemos decir a nuestros alumnos en lugar de ¿lo comprendéis? Los vieneses empezaron a llamar mirón a la figura que debajo del púlpito abría una ventana sin soltar su compás: un observador atento de la realidad que le rodea. (Anton Pilgram. Catedral de Viena) Durante mucho tiempo se atribuyó a Pilgram la autoría del púlpito gótico pero hoy se considera anterior. Lo que sí se debe al arquitecto es el gran píe del viejo órgano. Se considera que Pilgram se autorretrató en la base misma de apoyo de dicho píe con los atributos del geómetra, escuadra y compás, y del bonete universitario. La reproducción del bellísimo púlpito es de la misma figura que hay en el órgano. Antón Pilgram mirándolo todo y dispuesto a medirlo y calcularlo. (Pie del viejo órgano. Catedral de Viena)

Miércoles, 02 de Septiembre de 2020 | Imprimir | PDF |  Correo electrónico

103. 108. (Agosto 2020) Música y entropía - II

1. Modelos musicales Esta es la segunda entrega de la serie Música y entropía. En el primer artículo [Góm20] examinamos de manera general el concepto de entropía y su relación con la música y el análisis musical. Describimos allí el origen moderno de ese interés —el trabajo de Meyer [Mey56]— así como ideas recientes de la aplicación de la entropía al análisis musical. Consideramos tanto el potencial analítico de la entropía como sus limitaciones. En este artículo vamos a examinar la entropía en el contexto más general de los modelos musicales; en particular, vamos a hacer una recensión del artículo Minimum description length modeling of musical structure [Mav08]. Este artículo contiene una profunda reflexión sobre los modelos musicales, la complejidad de estos (aquí es donde entra la entropía), una propuesta de modelo, los modelos de descripción mínima, y una aplicación de estos al canto litúrgico griego. 1.1. Modelos El artículo de Mavromatis abre con una frase contundente: ”el problema de la selección de los modelos es de suma importancia en todos los estudios empíricos”. La primera pregunta que surge aquí es: ¿qué es un modelo? El concepto de modelo aparece al final de un camino de conceptos previos que empiezan con el concepto mismo de fenómeno. Un fenómeno es cualquier suceso que puede ser observado. Por observable entendemos sucesos que pueden ser percibidos por los sentidos. Los fenómenos se pueden clasificar de muchos modos, pero hay dos grandes categorías: los fenómenos cuantificables y los fenómenos no cuantificables. Los primeros admiten una descripción numérica y los segundos, no. En el caso de la entropía, los modelos musicales van a ser con frecuencia cuantificables, esto es, se van a construir en base a los aspectos cuantificables de la música tales como la frecuencia de las notas, su altura, la duración, los grados de la escala, entre otros. Los modelos cuantificables suelen ser modelos matemáticos y computacionales. Un modelo matemático consta de los siguientes componentes: (1) Una entrada, normalmente un conjunto de números, vectores u otras estructuras numéricas; (2) Un conjunto de variables independientes, que están asociadas con la descripción conceptual del fenómeno bajo estudio. Con frecuencia, se relacionan con las causas del fenómeno en cuestión; (3) Un conjunto de parámetros, los cuales sirven para refinar y ajustar el modelo; (4) Un conjunto de variables dependientes, que representan el efecto observado en el fenómeno; (5) Un conjunto de relaciones, que conectan las variables independientes y las variables dependientes. Estas relaciones se suelen dar en forma de funciones, aplicaciones, transformaciones u operadores; (6) Una salida son el resultado de una observación particular. 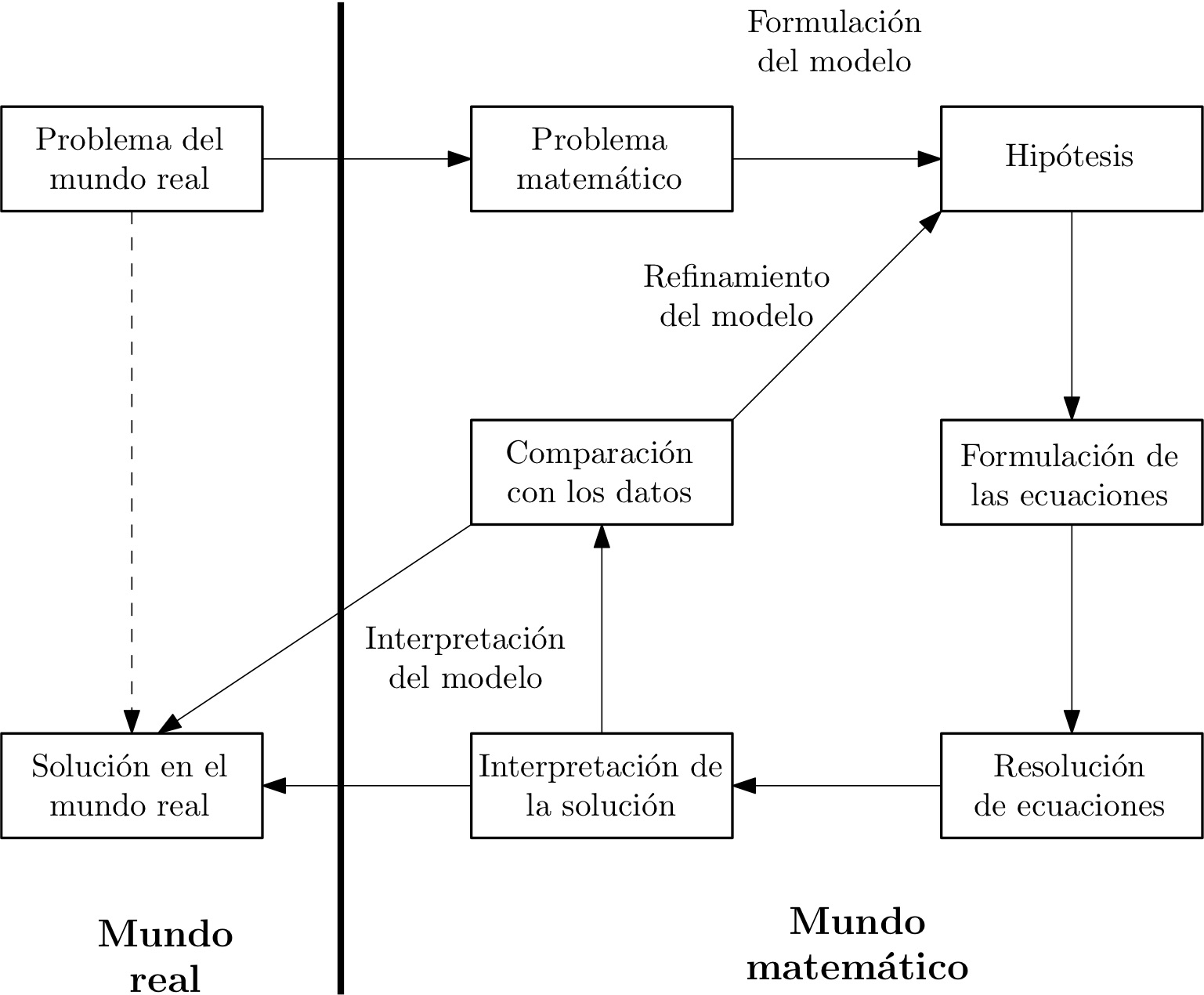Sin embargo, como dijimos arriba, el modelo matemático es parte de un proceso más general llamado modelización matemática. Los bloques constituyentes de una modelización matemática son: (1) Formulación del problema. Se escoge un fenómeno de interés y se identifica un problema relativo a él. La formulación del problema también recibe el nombre de pregunta de investigación. (2) Sistematización. Mediante un proceso de abstracción se seleccionan aquellos objetos y relaciones del fenómeno que son relevantes para el problema en cuestión. Este proceso se llama abstracción. (3) Creación del modelo matemático. Los objetos y relaciones del apartado anterior se traducen a su vez en objetos y relaciones en el mundo y lenguajes matemáticos. En la creación del modelo matemático se tiene en cuenta el principio de parsimonia. Este establece que un buen modelo minimiza su complejidad y maximiza su poder explicatorio y predictivo. En otras palabras, siempre es preferible la explicación científica más simple que concuerde con la realidad. Este principio se conoce también con el nombre de principio de la navaja de Occam. (4) Resolución del problema matemático. Uso de métodos matemáticos para resolver los problemas derivados de la modelización del fenómeno. (5) Interpretación de los resultados y conclusiones en el contexto del fenómeno y del problema planteado. (6) Evaluación de la validez del modelo por comparación con el comportamiento del fenómeno o bien con la teoría previamente consolidada acerca del mismo. Es de particular importancia la validación del modelo en cuanto a su capacidad de predicción. Para más información sobre modelos, consultése el artículo de la Wikipedia Conceptual model [Wik20]. La figura de abajo resume la discusión anterior. Figura 1: Modelización matemática 1.2. Evaluación de modelos Normalmente, la calidad o bondad de un modelo se evalúa en función de cuán precisas son sus explicaciones y predicciones hechas a partir de los datos observados. Mavromatis da un paso conceptual hacia delante y propone evaluar la calidad de un modelo en base la capacidad explicativa y predictiva del modelo y además en base a la propia complejidad del modelo (a igual capacidad explicativa y predictiva, son más preferibles los modelos simples a los modelos complejos simplemente por pura aplicación del principio de parsimonia). La manera en que Mavromatis evalúa la complejidad de los modelos tomando prestadas ideas de la teoría de la información. En un modelo musical, la estructura musical está caracterizada por variables simbólicas que representan diversos aspectos de la música tales como la altura de sonido, duración, dinámica, armonía, etc. Un modelo trata de identificar esas variables y su aparición. Esto da lugar a su vez a lo que Mavromatis llama restricciones sintácticas, las cuales dependen del estilo musical. Los valores que toman las variables del modelo se presentan en forma de regularidades estadísticas, las cuales dan lugar a patrones de comportamiento musical. Un campo fecundo de investigación musical es la detección de esos patrones. Volviendo al concepto de parsimonia, perseguiremos que nuestro modelo sea tan simple como sea posible y al mismo tiempo tenga una buena capacidad explicativa y predictiva. Un buen ajuste entre un modelo y los datos se llama bondad del ajuste. En la figura de abajo tenemos un ejemplo sencillo. Supongamos que en nuestro fenómeno observamos una variable dependiente y, representada en el eje Oy, como función de una variable independiente x, representada en el eje Ox. Los puntos negros son las observaciones; se trata de pares de puntos (x1,y1),…,(xn,yn), suponiendo n observaciones. La siguiente pregunta es qué tipo de relación hay entre las variables x e y (en nuestro ejemplo ambas son numéricas). Un modelo muy simple es el modelo lineal, que supone que hay una relación lineal del tipo y = ax + b (una recta), donde a,b son parámetros a determinar en función de los datos observados. La recta de color azul es la recta que mejor explica los datos, mientras que la recta roja arroja un peor modelo. La bondad del modelo es un valor que en la figura aparece como SSE; el mejor modelo es el que tiene este valor lo más bajo posible. Este valor mide los errores cometidos por el modelo al aproximar los datos y en la figura está dado por las distancias verticales de los puntos a la recta. La figura 3 muestra las tres situaciones. Figura 2: Bondad del ajuste en modelos Es posible construir modelos que se ajusten muy muy bien a los datos demasiado bien, reflejando idiosincrasias insignificantes, a base de añadir variables extra. Esto se llama sobreajuste. Esto ocurre cuando el modelo no acierta con el nivel adecuado de abstracción. Produce modelos excesivamente complejos. Lo contrario se llama subajuste: el modelo es pobre y se pierde características importantes del fenómeno. En la figura 3 (a) tenemos un caso de subajuste. El conjunto de datos, que claramente sugiere una forma curva, es aproximado por una recta. En la figura 3 (b) vemos una curva que pasa por todos los puntos observado y el ajuste es perfecto (comete error cero), pero este modelo requiere un alto número de variables independientes que no son parte esencial del modelo. Por último, la figura 3 (c) muestra un modelo más razonable, con pocas variables independientes y con un error de ajuste razonable. Figura 3: Subajuste y sobreajuste (figura tomada de [Mav08]) 2. Modelos de longitud de descripción mínima El modelo propuesto por Mavromatis en su trabajo es un modelo de longitud de descripción mínima (LDM, de aquí en adelante). Este modelo es de tipo inductivo, esto es, se construye a partir de la observación de datos asociados al fenómeno bajo estudio. El modelo LDM no solo evalúa el ajuste de los datos, como los modelos clásicos, sino también evalúa la propia complejidad del modelo. Cualquier regularidad detectada en los datos se puede usar para comprimir ese conjunto de datos. Comprimir aquí significa codificar los datos observados de una manera más corta que si los datos se dejan sin comprimir. Cuantas más regularidades se observen en los datos, más se podrán comprimir estos. Por ejemplo, si los datos se pueden codificar a partir de símbolos del alfabeto A = , la cadena C1 = aaaa se puede comprimir como a4, pero la cadena C2 = aabb se puede comprimir como a2b2, cuya compresión es más larga que a4. En este caso, la codificación de C1 tiene longitud 2 (dos símbolos para a2) y la de C2 tiene 4. El LDM mide la bondad de un modelo por la capacidad de comprimir los datos en base a sus regularidades y por la capacidad de comprimirse a sí mismo. Un modelo LDM está constituido por varias piezas. Primero, hay un conjunto de datos D, típicamente obtenidos de la observación del fenómeno. En nuestro caso, consistirán en piezas musicales extraídas de algún corpus musical. A continuación, un modelo M que modeliza el fenómeno, en particular, los datos D. Después, una función de una codificación C, que transforma los datos en un cadena de caracteres tomados de un alfabeto (puede ser un conjunto de números, los bits 1 y 0, caracteres alfanuméricos, etc.). A continuación, una función LC que mide la longitud del código C. Por último, una función de descripción, que está dada por donde C1,C2 son esquemas de codificación, el primero del modelo M y el segundo de los datos. La expresión D∣M significa la codificación de D según el modelo M. Las codificaciones tienen que tener la propiedad de ser únicas, esto es, dos datos distintos no pueden codificarse por la misma cadena. Esto asegura que se recupera correctamente la información cuando se pasa del código a los datos. En particular, para que esta propiedad se cumpla se requiere que ninguna codificación produzca una cadena que sea prefijo de otra; para más cuestiones técnicas de este tipo recomendamos al lector que consulte el apéndice del artículo de Mavromatis [Mav08]. En general, las mejores codificaciones asignan los códigos más cortos a los símbolos más probables o frecuentes. Esto introduce la idea de probabilidad en el modelo, ya que se hace el recuento de las cadenas más frecuentes en la codificación. Se sabe que siempre hay una codificación óptima que minimiza la esperanza de la longitud de la descripción dada por la distribución de probabilidad P(D∣M). Se llama código de Shannon-Fao. Su función de longitud es En este punto interviene el teorema de Shannon, que establece que la esperanza mínima de la longitud de la codificación para la salida de un modelo probabilístico M con distribución P(x∣M) está dado por donde X es el conjunto de símbolos de la codificación. La cantidad HM recibe el nombre de entropía. La idea de Mavromatis es encontrar una función de codificación que se aproxime lo más posible a la cota impuesta por el teorema de Shannon. La función de codificación de Mavromatis se define como sigue. Sea una distribución de probabilidad pi sobre el conjunto de k símbolos y d un parámetro de truncamiento. donde L*(d) está definida por La L*(d) solo se suma sobre los términos positivos y por tanto la suma anterior es finita. 3. Modelos de Markov A continuación hacemos una revisión breve de las cadenas de Markov, que es un tipo de modelos probabilísticos. Este tipo de modelos son muy comunes en música, como ya hemos glosado en otras entregas de esta columna. Mavromatis los usa en conjunción con su modelo LDM. Una cadena de Markov es un modelo de un fenómeno que tiene los siguientes componentes: Un conjunto finito de estados ; Un conjunto de probabilidades constantes pij del estado si al estado sj; estas probabilidades reciben el nombre de probabilidades de transición. Falta de memoria: Se cumple la condición de que la probabilidad de ir del estado si al estado sj solo depende del estado actual. La matriz de transiciones es s1 s2 s3 T = s1 s2 s3 Por ser los números pij probabilidades, las filas de esta matriz siempre suman 1. En la figura de abajo se ve un esquema que refleja la estructura de una cadena de Markov. Este tipo de diagramas, llamados diagramas de estado, son comunes para describir cadenas de Markov. Figura 4: Una cadena de Markov de tres estados La condición de falta de memoria aparece de manera más general en modelos más abstractos. Se puede pedir que la probabilidad de ir a un estado a otro dependa de un cierto número de estados previos. Por ejemplo, en la figura de abajo a la izquierda se tienen las probabilidades de un conjunto de tres notas entre sí (la, do# y mi♭). En este caso, hablamos de matrices de primer orden. A la derecha de la figura aparecen las probabilidades de continuación de las secuencias de dos notas para otro conjunto de notas diferente (la, do , sol). Ahora la matriz es de orden dos (depende de dos estados previos). Figura 5: Cadenas de Markov aplicadas al análisis musical 4. Modelos de Markov de longitud de descripción mínima Mavromatis aplica los modelos de Markov de longitud de descripción mínima al canto litúrgico griego. Se trata de una música en que letra y melodía se asocian por medio de reglas estilística tanto musicales como prosódicas. En un trabajo anterior [Mav05] Mavromatis demostró la importancia estructural de ciertas fórmulas arquetípicas melódicas o arquetipos melódicos en este tipo de canto litúrgico. Dichas fórmulas son patrones melódicos de entre 6 a 9 notas y que se pueden acomodar a diferentes patrones prosódicos, incluyendo la longitud y los patrones de acentuación de las palabras. En la siguiente figura se muestran esos arquetipos melódicos; en este caso son todas fórmulas cadenciales. Figura 6: Fórmulas arquetípicas de la melodía en el canto litúrgico griego (figura tomada de  [Mav08]) En la figura se ha usado la siguiente convención: dos x significa sílaba acentuada y una x sílaba no acentuada. Asociado a este estilo musical tenemos unas cuantas reglas que rigen la formación y la sintaxis de los arquetipos melódicos (las reglas sintácticas de las que hablábamos arriba): R1 El sol final del arquetipo cae en sílaba acentuada. R2 Si la sílaba final está acentuada, entonces se asigna al sol final. Si, por otro lado, la última sílaba acentuada está seguida de sílabas no acentuadas, entonces en general se le asigna al penúltimo fa. En dicho caso, la sílaba no acentuada siguiente se asigna al sol. R3 Como máximo un sílaba acentuada puede intercalarse entre el sol inicial y la última sílaba acentuada del arquetipo. Si existe tal sílaba, el acento se asigna o bien al fa o al mi. R4 Una vez que las sílabas acentuadas se han fijado según las reglas R1-R3, el número de sílabas no acentuadas en el medio se puede acomodar mediante inserciones o borradas de las notas necesarias. El siguiente paso que da Mavromatis es construir la cadena de Markov. Empieza con un único estado s0 y calcula el total de LDM según las fórmulas que vimos antes. A partir de aquí empieza un proceso en que va añadiendo más estados; llega a hacer hasta 14 estados. En cada paso, calcula las probabilidades a partir de las frecuencias que encuentra en el corpus. En la figura siguiente se ve la cadena de Markov para 6 nodos; en la figura xx significa sílaba acentuada y x_ sílaba no acentuada. Figura 7: El modelo MDL En la tabla de abajo se ven los valores de LDM para los datos y el modelo así como el total de la LDM; nS se refiere al número de nodos de la cadena de Markov. El mínimo de la LDM total se alcanza con 10 nodos (marcado con un asterisco en la tabla). Figura 8: El modelo MDL De la ejecución del modelo sobre el corpus de canto litúrgico griego, Mavromatis obtiene las siguientes conclusiones: El modelo de un estado identifica las frecuencias de cada nota. El modelo de dos estados detecta el papel privilegiado de la nota sol como nota de referencia. El modelo de tres estado capta el papel de las notas fa y la como vecinas de sol El modelo de cuatro estados discierne entre el sol final e inicial. El modelo de cinco estados identifica el papel de la nota mi. En este punto cada estado de la cadena de Markov tiene una definición en términos de altura bien definida. El modelo de seis estados implementa la regla R1. El modelo de 7 estados aprende el contorno sol-fa-mi-fa-sol. El resto de los estados hasta el estado de 10 nodos incrementa progresivamente el aprendizaje de las reglas sobre las alturas. Dado que la LDM mínima se alcanza en 10 nodos, se elige este modelo como el óptimo. Usar más nodos daría lugar a sobreajuste y usar menos nodos a subajuste.   Bibliografía [Góm20] P. Gómez. Música y Entropía - I, julio de 2020. [Mav05] Panayotis Mavromatis. A hidden Markov model of melody production in Greek church cant. Computing in Musicology, 14:93–112, 2005. [Mav08] Panayotis Mavromatis. Minimum Description Length Modeling of Musical Structure. Journal of Mathematics and Music, 0:1–21, enero 2008. [Mey56] Leonard Meyer. Emotion and Meaning in Music. University of Chicago Press, Chicago, 1956. [Wik20] Wikipedia. Conceptual model, consultada en 2020.

Sábado, 01 de Agosto de 2020 | Imprimir | PDF |  Correo electrónico

104. 12. (Julio 2020) Geometría y arte: El cubo SOMA en las esculturas de David Umemoto

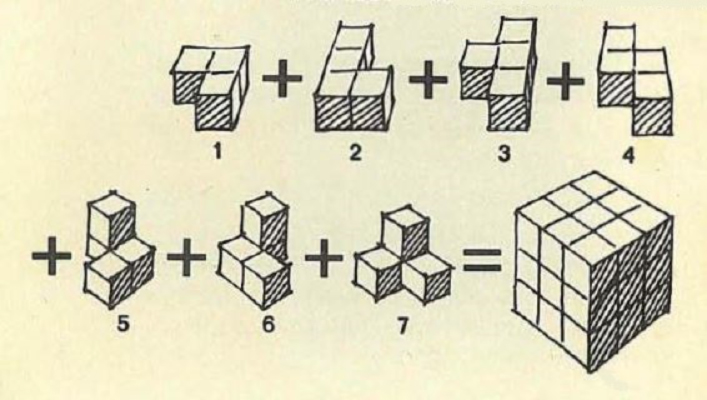
El rompecabezas geométrico SOMA, del que ya hemos hablado en otra ocasión[i], se compone de siete piezas (a las que de ahora en adelante llamaremos somaedros) como las de la figura siguiente. Ilustración de Piet Hein[ii] en el Manual del SOMA[iii] (p. 4) Con ellas, entre otros muchos objetos 3D, se puede construir un cubo 3x3x3 («problema fundamental»). Desde una óptica matemática, la resolución de este problema geométrico y de otros similares, es un reto intelectual que puede mantener ocupada durante un largo tiempo a cualquier persona con la mente despierta. Desde una perspectiva artística, el creador, al margen del «problema fundamental», se dedica a transformar los siete somaedros en estructuras estéticamente atractivas con las cuales (ensamblándolas de forma conveniente) puede generar auténticas obras de arte. En las líneas que siguen, ofrecemos un ejemplo de este enfoque presentando las esculturas SOMÁticas del arquitecto David Umemoto, residente en Montreal (Canadá). Las SOMAesculturas de Diego Umemoto En la página personal de Umemoto (https://davidumemoto.com/info) hemos localizado seis proyectos inspirados en el SOMA. En cada uno de ellos se presentan los siete elementos básicos con algunos resultados obtenidos después de su acoplamiento[iv]. A partir de aquí, dejamos que el lector disfrute de las originales y bellas esculturas del artista canadiense. [1] Soma Cube i (2015) [2] Soma cube ii [3] Soma cube iii [4] Soma cube vi [5] Soma Cube ix [6] Soma Cube xs   Notas: [i] SOMA: antepasados y descendientes (Divulgamat). [ii] Piet Hein (1905 – 1996), poeta, filósofo, matemático y científico danés, creador del SOMA. [iii] Parker Brothers distribuyó el SOMA en Estados Unidos. El manual editado por dicha empresa fue escrito e ilustrado por Piet Hein (Introducing SOMA, 1969). [iv] En algunas esculturas intervienen todos los somaedros y en otras no.

Miércoles, 29 de Julio de 2020 | Imprimir | PDF |  Correo electrónico

105. 11. (Julio 2020) SOMA: antepasados y descendientes

Las disecciones del cubo proporcionan una rica fuente de inspiración a los diseñadores de rompecabezas tridimensionales. En este artículo ofrecemos una selección de puzles 3D obtenidos a partir del poliedro regular que, en la cosmología platónica, representaba la tierra. 1. El cubo diabólico Profesor Hoffmann En 1893, el profesor Hoffmann[1] publicó en Londres sus Puzzles Old and New en los que introdujo un rompecabezas, el «cubo diabólico», formado por seis piezas con las que se puede construir un cubo 3x3x3. Puzzles Old and New, p. 108 Dichas piezas están formadas por 2, 3, 4, 5, 6 y 7 cubos unitarios, tal como puede verse en la figura adjunta. Las seis piezas del «cubo diabólico» En la páginas 142 y 143 del mismo libro, Angelo John Lewis propuso la siguiente construcción del cubo. Se colocan las piezas c [= 6], a [= 7] y e [= 4] una al lado de otra tal como se indica en la figura anterior. Acto seguido, la pieza f [= 2] se acopla delante de la e. Después, la pieza d [= 3] se sitúa entre a y f, completando una cara del cubo. Por último, en los espacios vacíos que quedan, se coloca la pieza b [= 5]. Para describir la construcción anterior de forma más precisa, utilizaremos tres cuadrados 3x3 que, escritos de izquierda a derecha, representan el primer, segundo, y tercer piso del hexaedro. Además, en cada cuadrícula escribiremos el número de la pieza que se apoya en él. Hay trece formas diferentes de construir un cubo 3  3  3 con las seis piezas del «cubo diabólico». Las presentamos con la ayuda del código que acabamos de describir. Notemos que la segunda de ellas es la propuesta por Hoffmann.     2. El cubo SOMA 2.1. El puzle El rompecabezas tridimensional SOMA fue ideado por el poeta, filósofo, matemático y científico danés Piet Hein. Piet Hein (1905 – 1996) Al parecer, la idea le surgió durante una conferencia sobre Física Cuántica. En la patente inglesa del SOMA, fechada el 19 de marzo de 1934, leemos: Mi invento se ilustra en los dibujos adjuntos, en los que: Las figuras 1-7 son dibujos en perspectiva de las siete piezas. Las figuras 8-13 son ejemplos de cuerpos o figuras geométricas sólidas que se pueden construir con las siete piezas. Cada una de las piezas de las figuras 1-7 se componen de tres o cuatro cubos yuxtapuestos. La pieza 1 está formada por tres cubos, mientras que cada una de las restantes está compuesta por cuatro cubos dispuestos de diferentes formas. El conjunto de todas las piezas equivale a veintisiete cubos. 2.2. El problema fundamental Con las siete piezas del SOMA, se puede generar un sinfín de objetos 3D. Objetos 3D que se pueden construir con el SOMA. Dibujos de Piet Hein (Manual del SOMA, pp. 20-21)[2] Además, se puede construir un cubo 3x3x3 («problema fundamental»). Ilustración del manual del SOMA (p. 4) En 1961, los matemáticos de la Universidad de Cambridge John Horton Conway y Michael J. T. Guy (1942) obtuvieron manualmente las 240 formas distintas de hacerlo. John Horton Conway (1937) En la figura adjunta reproducimos una posible solución del «problema fundamental» Construcción del cubo con las siete piezas del SOMA[3] Utilizando el código descrito en el parágrafo 1, la construcción anterior se convierte en: 2.3. Jugando con el SOMA Con dos juegos SOMA, dos jugadores pueden poner a prueba su habilidad tridimensional en un torneo intelectual que se ajusta a las siguientes reglas: Se determina por sorteo el jugador que inicia el juego. El jugador que inicia el juego elige una de las siete piezas y la posición que debe ocupar. Los dos jugadores, usando la misma pieza y posición de partida, deben construir un cubo 3x3x3 utilizando las restantes piezas del SOMA. Gana el jugador que alcanza el objetivo en menos tiempo. El jugador que pierde, elige la siguiente pieza y posición de partida. Los siguientes dibujos de Piet Hein muestran algunas posiciones teóricas de partida para la pieza 1. Proponemos algunas construcciones del cubo a partir de dichas posiciones. POSICIÓN A POSICIÓN B POSICIÓN C POSICIÓN D POSICIÓN E 3. El cubo de Mikusinski Jan Geniusz Mikusinski (1913 – 1987) El matemático polaco J. G. Mikusinski  obtuvo la siguiente disección del cubo en seis policubos. Las seis piezas del «cubo de Mikusinski» El «cubo de Mikusinski» también se conoce como «cubo de Steinhaus» dado que apareció por primera vez, que sepamos, en el libro Mathematical Snapshots (1950) del matemático y pedagogo polaco Hugo Steinhaus. Hugo Steinhaus (1887 – 1972) La reconstrucción del cubo con dichas piezas sólo admite las dos soluciones que se muestran en la figura siguiente. 4. Disecciones del cubo en piezas idénticas 4.1. El cubo de O’Berine Atendiendo al testimonio de Martin Gardner (Rosquillas anudadas, p. 33), se debe al escocés Thomas H. O’Berine la disección de un cubo en nueve «tricubos» como el de la figura adjunta. Según el divulgador norteamericano: Los intentos de atinar por tanteo a construir un cubo con los nueve tricubos pueden resultar verdaderamente exasperantes, salvo que, por fortuna se haya acertado en un procedimiento sistemático. ¿Cómo descubrir dicho procedimiento sistemático? En primera instancia, notemos que con dos tricubos se puede construir una estructura [= 2TC] como la del diagrama siguiente. Por consiguiente, con seis tricubos se pueden construir tres. Acto seguido, dispongamos los tres tricubos restantes tal como se detalla a continuación. A partir de aquí, añadiendo sucesivamente las tres estructuras 2TC a la «escalera» anterior, se puede completar un cubo 3x3x3 siguiendo las indicaciones de la figura adjunta. 4.2. Un cubo grande: el Gridlock Puzzle El Gridlock Puzzle es un rompecocos 3D compuesto por cincuenta y cuatro piezas como las de la figura adjunta. El objetivo que se persigue es el de construir un cubo 6x6x6 con todos los tetracubos del rompecabezas. Para conseguirlo, basta con construir (utilizando dieciocho piezas) dos capas del cubo superpuestas [= paralelepípedo 6x6x2], tal como se detalla en los diagramas adjuntos. Repitiendo este proceso dos veces más se consigue materializar el cubo con todas las piezas del puzle. 5. El puzle de Slothouber-Graatsma William Graatsma (1925) y Jan Slothouber (1918 – 2007) Se debe a los arquitectos holandeses Jan Slothouber y William Graatsma un puzle formado por seis bloques 1x2x2 y tres bloques 1x1x1 con los que se puede formar un cubo 3x3x3. La solución es única, salvo simetrías y rotaciones, y se comprende fácilmente a partir del esquema siguiente. 6. El cubo de Conway John Horton Conway, del que ya hemos hablado en el parágrafo 2.2., diseñó un puzle compuesto por las dieciocho piezas siguientes: Trece bloques 1x2x4. Tres bloques 1x1x3. Un bloque 2x2x2. Un bloque 1x2x2. Con ellas se debe formar un cubo 5x5x5. Los cuatro tipos de bloques Designando los trece bloques 1x2x4 por A, B, C, D, E, F, G, H, K, L, M, N  y P, los tres bloques 1x1x3 por a, b y c, el bloque 2x2x2 por α, y el bloque 1x2x2 por β, una posible construcción del cubo requerido es: 7. El cubo de Bedlam Acabamos este catálogo de rompecabezas hexaédricos con un puzle compuesto por trece piezas (doce pentacubos y un tetracubo), cuyos bocetos adjuntamos. Su creador es el británico Bruce Bedlam. Bruce Bedlam Con las trece piezas se puede montar un cubo 4x4x4 de 19186 formas diferentes. El reto de conseguir una no es fácil y se necesita una gran dosis de paciencia, organización y constancia. Una solución al cubo de Bedlam 8. Fábrica de rompecabezas cúbicos En las secciones precedentes hemos presentado varios puzles cúbicos sin prestar atención al procedimiento que pudieron seguir sus inventores a la hora de diseñarlos. Desde una óptica formativa, esta fase de creación resulta particularmente interesante. Por este motivo, en este último parágrafo (a modo de anexo), ofrecemos el alumbramiento de un «nuevo» rompecabezas hexaédrico. Un puzle 3x3x3 con seis piezas [1] Empezamos con un pentacubo A, cuatro de cuyos cubos ocupan el primer piso y uno ocupa el segundo. La apariencia tridimensional de A se ajusta al boceto siguiente. [2] Proseguimos con el tetracubo B, dos de cuyos cubos ocupan el primer piso y los dos restantes ocupan el segundo. En la figura siguiente se ofrece una representación en perspectiva de B. [3] En tercer lugar, concebimos el pentacubo C, tres de cuyos cubos ocupan el primer piso y los dos restantes el segundo. En el boceto adjunto se muestra una representación de C. [4] Acto seguido «creamos» el pentacubo D, tres de cuyos cubos están en el segundo piso y los dos restantes en el tercero. En la figura siguiente ofrecemos una representación de D. [5] Incluimos ahora el tetracubo E que tiene un cubo en el segundo piso y tres en el tercero. La representación 3D de dicho policubo se ofrece en el boceto siguiente. [6] Habiendo llegado a este punto, los huecos que quedan por cubrir sólo se pueden llenar con el tetracubo F. La figura adjunta es una representación plana del policubo F. Con esto, acabamos de «inventar» o «reinventar» un rompecabezas cúbico de seis piezas (tres tetracubos y tres pentacubos).   Referencias bibliográficas GARDNER, M. (1987). Rosquillas anudadas y otras amenidades matemáticas. Barcelona: Editorial Labor, S. A. HOFFMANN, P. (1893). Puzzles Old and New. London: Frederick Warne and Co. MEAVILLA SEGUÍ, V. (2011). El lobo, la cabra y la col. Córdoba: Editorial Almuzara, S. L.   Referencias online Cubic Block Puzzles. The 3x3x3 Cube Cubo de Bedlam Gridlock puzzle Cubo de Conway El puzzle de Slothouber-Graatsma Introducing SOMA (Manual del SOMA)   Notas: [1] Pseudónimo del inglés Angelo John Lewis (1839 – 1919). [2] Parker Brothers distribuyó el SOMA en Estados Unidos. El manual editado por dicha empresa fue escrito e ilustrado por Piet Hein (Introducing SOMA, 1969). [3] Manual del SOMA (Parker Brothers), p. 12.

Miércoles, 15 de Julio de 2020 | Imprimir | PDF |  Correo electrónico

106. 107. (Julio 2020) Música y entropía - I

Inauguramos una serie en la que vamos a examinar el concepto de entropía y su aplicación en el análisis musical. A primera vista, no parece que ambos conceptos tengan mucha relación entre sí o si la tienen que sea una relación directa. Además, hay varios conceptos de entropía. En Mecánica Estadística, entropía se refiere al número de configuraciones microscópicas que son consistentes con las cantidades macroscópicas que caracterizan un sistema, tales como el volumen, la presión o la temperatura (véase [Wik]). Esta entropía, llamada entropía termodinámica, está definida de manera que se puede interpretar como una medida del desorden interno del sistema y cuanto mayor es el valor de la entropía, mayor es el desorden del sistema. La segunda ley de la termodinámica establece que en un sistema aislado la entropía nunca decrece y que esta tiende a su máximo valor posible (máximo desorden del sistema). Más tarde, Shannon, en un artículo pionero [Sha10] A Mathematical Theory of Communication, tomó las ideas principales encerradas en el concepto físico de la entropía y las aplicó a la Teoría de la Información. Definió la entropía como la cantidad de información asociada a un mensaje en base a la sorpresa o novedad contenida en los símbolos de ese mensaje. Tal y como pasaba con la entropía termodinámica, la entropía de la teoría de la información está descrita en términos de distribución de probabilidades. Formalmente, la entropía de Shannon se define a partir de un conjunto de símbolos, xi, cada uno con probabilidad de aparición igual a P(xi), donde i = 1,…,n. Las parejas (xi,P(xi)) forman la distribución X de probabilidad de ese conjunto de símbolos. La fórmula matemática de la entropía de Shannon es En la práctica las probabilidades de los símbolos se obtienen observando la transmisión de los mismos. Cuando se aplican estas ideas al análisis musical, en primer lugar se interpreta la propia música como un conjunto de símbolos. Si queremos hallar la entropía de las alturas de sonido, entonces el conjunto de símbolos son las 12 alturas (si se consideran clases de alturas; en otro caso, cada altura es un símbolo distinto). Las probabilidades de dichas alturas (símbolos) se calculan a partir de las frecuencias de aparición en una pieza concreta o en general en un corpus musical. Esta famosa fórmula establece que la máxima cantidad de información contenida en mensajes escritos con los símbolos xi ocurre cuando cada símbolo tiene probabilidad 1∕n. Esta fórmula se puede interpretar como la esperanza de -log 2(X). La variable aleatoria -log 2(X) recibe el nombre de cantidad de información de X. Además, la entropía representa un límite absoluto de la capacidad de codificar un mensaje sin pérdidas en un canal sin ruido, resultado que es importante en teoría de la información. Tras esta breve definición de entropía, surge la pregunta de cómo se relaciona la entropía con la música y su análisis. La música es un fenómeno complejo y altamente estructurado. Desde el principio, músicos y musicólogos buscaron afanosamente conceptualizar, detectar, medir e interpretar esa complejidad. Asociada a la cuestión del estudio de la complejidad musical está una cuestión muy cercana: cómo se genera el significado en la música. De hecho, una cuestión aun más básica, y que todavía está bajo intenso estudio, es la de definir qué es el significado musical (véanse [Mey56, Bro00, Coo01, AaQ17, Chu19] y sus referencias). Muchos investigadores pensaron que la complejidad de la música estaba entroncada con su capacidad para generar significado. Meyer, en su famoso libro del año 56, Emotion and Meaning in Music [Mey56], afirma que el significado musical proviene de la capacidad de que un suceso musical implique otro suceso musical. He aquí sus palabras textuales: Musical meaning arises when an antecedent situation, requiring an estimate as to the probable modes of pattern continuation, produces uncertainty as to the temporal- tonal nature of the expected consequent. (Meyer, 1957, p. 416) Esta teoría supone que los sucesos musicales transcurren en base a un argumento musical cuya lógica encadena dichos sucesos uno tras otro. La mayor o menor sorpresa del argumento musical es proporcional al interés musical que despierta la pieza. Meyer ofrece, pues, una teoría en que explica la emoción musical en base a la creación y satisfacción de expectativas musicales. Obsérvese que Meyer asume una definición de significado musical en que lo extra-musical tiene poca importancia, esto es, el significado se genera a partir de los hechos meramente musicales. Otras teorías acuden, en cambio, a paralelismos con el lenguaje para explicar el significado musical. En un artículo publicado un año después que su libro, Meaning in music and information theory, [Mey57], Meyer ya formula su teoría del significado musical en términos de teoría de la información. En particular, afirma que “dado un antecedente musical, este induce una estimación de la probabilidad de las formas de continuación en el oyente” (página 416). Esta idea pronto atrajo la atención de muchos investigadores, quienes propusieron modelos de todo tipo para explicar la generación de significado musical. Por citar los principales modelos, tenemos Jackendoff y Lerdahl [LJ83] y su teoría generativa de la música tonal, el modelo de implicación-realization de Narmour [Nar90], el modelo de sistema y contraste de Bimbo y sus colaboradores [BDSV12], el modelo de tensión musical de Margulis [Mar05], la teoría de la expectativa de Huron [Hur06] o los modelos probabilísticos de Temperley [Tem10]. La teoría de Meyer contenía varios elementos que apuntaban hacia el uso de la entropía. Por un lado, al hablar de la estimación de la probabilidad de la continuación del discurso musical ya estaba sentando las bases para los modelos probabilísticos. Por otro lado, ¿cómo se estiman esas probabilidades? El oyente de una pieza musical va registrando los eventos musicales que oye y en función de ello y otros factores (familiaridad con el estilo, formación musical, conocimiento de la pieza en concreto) va construyendo un conjunto de probabilidades con que estima el próximo evento musical. Si el siguiente evento musical efectivamente confirma la estimación del oyente, la música producirá significado que si dicho evento rompe drásticamente su estimación. Dicho de otro modo, si la música es muy predecible, no tendrá interés musical para el oyente, mientras que si la música está llena de sorpresas, entonces sí generará mucho interés. A partir del trabajo de Meyer, muchos investigadores examinaron la cuestión de definir formalmente el significado musical a través de la entropía. Por orden cronológico, los esfuerzos más representativos se encuentran en los trabajos de Youngblood [You58], Cohen [Coh62], Knopoff y Hutchinson [KH83], Snyder [Sny90], Margulis [Mar05], Cox [Cox10], Laney y sus colaboradores [LSC15] y Febres y Jaffe [FJ17]. En efecto, la entropía es una medida de la cantidad de información contenida en la distribución de una variable aleatoria (véase [Góm16] para un repaso de estos conceptos). Cuanto más incertidumbre hay sobre los valores que toma la variable aleatoria, mayor es su entropía. Por otro lado, se puede interpretar que una pieza musical es más compleja cuanto más impredecible sea. Y entonces surge la deseada relación entre complejidad musical/significado musical y entropía. Sin embargo, Margulis [MB08], en un trabajo de 2008, llevó a cabo un análisis sistemático de la entropía como herramienta analítica y apunto a tres grandes problemas. El primero es de tipo epistemológico y es cómo hacer preguntas que sean relevantes musicalmente dentro del marco de la teoría de la información. La segunda es cómo recoger datos musicales que necesitan los modelos computacionales de la teoría de la información. La tercera es cómo determinar la unidad básica de análisis (la altura de sonido, el ritmo, las frases, los motivos o una combinación de ellos) que proporcione resultados válidos. Una de las principales virtudes de la entropía es que se puede concebir como una medida de la complejidad con que los elementos de una pieza están integrados entre sí. Sin embargo, no está tan claro cómo relacionar la entropía con la percepción del oyente de los elementos musicales. Varios autores [SJAN99, Mar14] han probado que los humanos pueden tomar propiedades estadísticas complejas cuando están escuchando música. Como Margulis ha escrito con elocuencia, “escuchar música es al mismo tiempo aprender a escuchar música”. Esto puede justificar el uso de la entropía, pero sigue quedando la cuestión de si la entropía se calcula sobre las mismas estadísticas que las que extrae un oyente humano. Otra cuestión fundamental es que la entropía no tiene en cuenta el significado intrínseco de los símbolos musicales, sino únicamente su frecuencia. Tampoco tiene en cuenta el orden en que estos aparecen y es razonable pensar que dicho orden tiene cierta importancia. Como veremos en las siguientes entregas de esta serie, los investigadores han hecho un gran esfuerzo por aplicar la entropía al análisis musical de manera que se superen estos obstáculos y se obtengan resultados que tengan relevancia en la explicación del fenómeno musical. Bibliografía [AaQ17] Pedro Atã and João Queiroz. Semiotic niche construction in musical meaning. Recherches sémiotiques / Semiotic Inquiry, 37(1-2):75–87, 2017. [BDSV12] Frédéric Bimbot, Emmanuel Deruty, Gabriel Sargent, and Emmanuel Vincent. Semiotic structure labeling of music pieces: concepts, methods and annotation conventions. In ISMIR (International Symposium on Music Information Retrieval), Curitiba, Brazil, October 2012. [Bro00] Candace Brower. A cognitive theory of musical meaning. Journal of Music Theory, 44(2):323–379, 2000. [Chu19] Andrew J. Chung. What is musical meaning? theorizing music as performative utterance. Music Theory Online, 25(1), 05 2019. [Coh62] J. E. Cohen. Information theory and music. Behavioral Science, 7(2):137–163, 1962. [Coo01] Nicholas. Cook. Theorizing musical meaning. Music Theory Spectrum, 23(2):170–195, 2001. [Cox10] G. Cox. On the relationship between entropy and meaning in music: An exploration with recurrent neural networks. In Proceeding Annual Meeting of the Cognitive Science Society, Portland, USA, August 2010. [FJ17] G. Febres and K. Jaffe. Music viewed by its entropy content: A novel window for comparative analysis. PLoS ONE, 12(10):1–30, 2017. [Góm16] P. Gómez. Música y Probabilidad (I), noviembre de 2016. [Hur06] David Huron. Sweet Anticipation. MIT Press Books, Massachusetts, 2006. [KH83] L. Knopoff and W. Hutchinson. Entropy as a measure of style: The influence of sample length. Journal of Music Theory, 27(1):75–97, 1983. [LJ83] F. Lerdahl and R. Jackendoff. A Generative Theory of Tonal Music. MIT Press, Cambridge, Massachussetts, 1983. [LSC15] Robin Laney, Robert Samuels, and Emilie Capulet. Cross entropy as a measure of musical contrast. In Tom Collins, David Meredith, and Anja Volk, editors, Mathematics and Computation in Music, volume 9110 of Lecture Notes in Computer Science, pages 193–198. Springer, Cham, Switzerland, 2015. [Mar05] Elizabeth H. Margulis. A model of melodic expectation. Music Perception: An Interdisciplinary Journal, 22(4):663–714, 2005. [Mar14] Elizabeth H. Margulis. On repeat: how the music plays the mind. Oxford University Press, New York, 2014. [MB08] Elizabeth H. Margulis and Andrew P. Beatty. Musical style psychoaesthetics and prospects for entropy as an analytic tool. Computer Music Journal, 32(4):64–78, 2008. [Mey56] Leonard Meyer. Emotion and Meaning in Music. University of Chicago Press, Chicago, 1956. [Mey57] Leonard Meyer. Meaning in music and information theory. Journal of Aesthetics & Art Criticism, 15:412–424, 1957. [Nar90] E. Narmour. The Analysis and Cognition of Basic Melodic Structures: The Implication-Realization Model. University of Chicago Press, Chicago, 1990. [Sha10] C. E. Shannon. A Mathematical Theory of Communication. Bell System Technical Journal, 27:379–423, 623–656, julio, octubre 2010. [SJAN99] J. R. Saffran, E. K. Johnson, R. N. Aslin, and E. L. Newport. Statistical learning of tone sequences by human infants and adults. Cognition, 70:27–52, 1999. [Sny90] J. L. Snyder. Entropy as a measure of musical style: The influence of a priori assumptions. Music Theory Spectrum, 12(1):121–160, 1990. [Tem10] D. Temperley. Music and Probability. MIT Press Ltd, 2010. [Wik] Wikipedia. Entropy. [You58] J. E Youngblood. Style as Information. Journal of Music Theory, 2(1):24–35, 1958.

Martes, 14 de Julio de 2020 | Imprimir | PDF |  Correo electrónico

107. 132. (Julio 2020) La Leyenda de Sissa (o el viaje a la luna doblando un papel) de Roberto Muñoz

La Leyenda de Sissa es una reflexión matemática y artística de nuestro compañero y amigo Roberto Muñoz (Universidad Rey Juan Carlos). La ha escrito durante los pasados días de confinamiento debidos a la pandemia provocada por el coronavirus SARS-CoV-2. El título alude a la famosa leyenda de Sissa, la del sirviente del brahmán Rai Bhalit que creó la chaturanga -el ajedrez- para entretener a su caprichoso y aburrido señor. El brahmán dejó elegir a Sissa su recompensa por tan entretenido juego. El inteligente sirviente solicitó como pago algo estrechamente relacionado con el tablero en el que se jugaba la chaturanga: pidió un grano de trigo por el primer cuadrado, dos por el segundo, cuatro en el tercero, dieciséis en el cuarto, etc. El brahmán aceptó lo que pensaba que era una modesta recompensa, hasta que fue consciente de que no había trigo suficiente en el país para pagar semejante petición… Sissa según un dibujo de Thiago Cruz (2007). Imagen: Wikimedia Commons. NOTA: Este texto fue publicado previamente en la revista de educación InkSpace, en su número de junio de 2020 dedicado a la educación y el arte. -OoO- Aplanar una curva, una maldita curva. Una curva que nace exponencial, dos elevado al tiempo que pasa, o quizás tres elevado al número de días, o cuatro. Cada uno contagiando a tantos, dando una mano o un beso, compartiendo un vaso, la saliva, la barandilla del autobús, cama. Diseminando un virus lejano, de pangolines y murciélagos. Un caso en La Rioja, o en Madrid, o en Igualada, qué importa, quién se acuerda, que contagia a dos, estos dos a otros dos y estos a otros: en comidas, en fiestas, en el metro, en el médico. Y sólo así, en veinte unidades de tiempo, dos elevado a la veinte, más de un millón (1.048.576 es el valor exacto de 2^20). En diez unidades de tiempo más, 2^30, esto es 1.073.741.824, imposible, increíble. 2^40= 1.099.511.627.776 2^50= 1.125.899.906.842.624 2^60= 1.152.921.504.606.846.976 Nos habían contado eso de llegar a la luna doblando un papel. Nos habían contado aquella leyenda del premio al creador del juego del ajedrez: granos de arroz que se duplican en cada casilla del tablero y que convertían aquel regalo en impagable pero no, no acabábamos de entender, no, no lo comprendíamos. Y sí. Aunque nosotros no éramos como los chinos -aquí seguro que no, aquí no existe la exponencial, aquí no-, lo somos. Aplanar la curva. Hacer que la segunda derivada sea negativa, que se decelere la función, que crezca más despacio, asfixian los datos, que deje de crecer, cuánto dolor, que deje de crecer, que deje, que empiece a decrecer, sentir alivio. Aplanar la curva para salir a la calle, para respirar árboles y dejar de oler enchufes, para quitarnos el chándal y comprar chisteras. Para producir vitamina D y deseo, para no beber solos, para gritar larga vida al rock and roll. La derivada ya no es un ejercicio académico de rutina, la del cuadrado de x es dos x, la del logaritmo de x es 1/x, ya no es sólo la velocidad, la pendiente de la recta tangente, la tasa de variación instantánea. Es ahora la derivada un deseo y es una expectativa, que la curva deje de ser exponencial y que se convierta en otra cosa, todavía no, todavía no lo ha hecho, unos plazos, no sé qué índice de contagio. Por favor que cambie de signo, que deje de ser positiva y cada vez más grande y empiece por aumentar cada vez más despacio para terminar siendo negativa. Pendiente positiva, crece, pendiente negativa, decrece. Que decrezca. Que decrezca. Un punto de inflexión y luego un máximo y luego para abajo. Si crece a esta velocidad, si la curva tiene esta forma, no podremos atender a todos, no seremos suficientes, no tendremos energía y será peor, nos contagiaremos más; los que cuidan todavía más. Ha de crecer más despacio, todos a casa, todos separados, profilácticos todos, aplausos a las ocho, series y bizcochos. Números en pantallas, números pronunciados, números que no son clases de equivalencia de conjuntos finitos módulo biyección, no. Son cincuentas que duelen, setecientos cincuenta y sietes que te dejan exhausto, o cientos de miles. Millones. Porcentajes. Novecientos cincuenta, dos de abril, 2020. Cero era un punto de equilibrio, las cosas no variaban, cuando no había contagiados nadie se podía contagiar. Se alteró ligeramente el equilibrio -una temperatura media ligeramente superior, unas emisiones que subieron un poco, un mar apenas unas décimas más caliente-, no mucho, epsilon, dos o tres infectados, quizás quince, unos que venían de aquí y de allá, que se movían, y el sistema se activó, se puso a buscar otro punto de equilibrio, ojalá el mismo punto de contagiados cero, en el que detenerse, estabilizarse. Aquella movida del comportamiento asintótico de una función (de un sistema dinámico), aquello de que la exponencial tiende a infinito, pero más rápido que cualquier polinomio, y que 1/x tiende a 0, y que si calcule usted las asíntotas horizontales de la siguiente función, es ahora un horizonte sin metáforas. El de los contagiados que habrá, el de los repuntes, el de las caídas a cero, el de la comparación entre los que podemos y los que debemos cuidar, el de la vida cotidiana que será igual, o no. Una curva que se aplanará, la gráfica de una función: en un eje el tiempo, en el otro los contagiados (o los fallecidos, o los ingresados en unidades especiales, o lo que vayan poniendo). Que se aplanará, al fin y al cabo el conjunto de personas es finito, pero que ni idea, los epidemiólogos algo esperan, pero con prudencia: mesetas, caídas, subidas, periodos. Ciencia. La que destruirá este texto cuando todo se entienda. Y mientras tanto, una cacofonía de enterados, de iluminados, de iracundos, de tontilanes, de toreros de salón. Y muchas dificultades para contar: uno, dos, tres, cuatro, para homogeneizar datos, para comparar, y pocas ganas de hacerlo. O mala intención. Una curva, en unos meses, una curva. -OoO-

Lunes, 06 de Julio de 2020 | Imprimir | PDF |  Correo electrónico

108. 44. CONCURSO DE VERANO 2020

Arthur Stone propuso esta disección del cuadrado en 1940. Un cuadrado se puede diseccionar en siete piezas triángulos rectángulos isósceles de distinto tamaño cumpliéndose que: cateto de G=1; cateto de E=2 y cateto de C=4. (http://www.squaring.net/tritri/twt.html) Existen varias maneras de obtener piezas triángulos rectángulos isósceles doblando un papel cuadrado o doblando un papel rectangular. Dos ejemplos se pueden ver en estos diagramas: RETO: Conseguir las 7 piezas de esta disección doblando los correspondientes papeles cuadrados o rectangulares sin utilizar regla para calcular el tamaño de los papeles utilizados. Para obtener las piezas triangulares se puede usar alguno de los dos métodos propuestos u otro. Podéis enviarnos vuestras soluciones (diagramas y foto del modelo terminado) a la dirección papiroflexiamates@gmail.com hasta el 31 de agosto. Los participantes aceptan que DivulgaMAT pueda publicar las soluciones, independientemente del fallo del concurso. El premio del concurso consiste en un libro de divulgación relacionado con las matemáticas. ¡Feliz verano!

Miércoles, 01 de Julio de 2020 | Imprimir | PDF |  Correo electrónico

109. 9. (Junio 2020) Paseo melancólico, matemático y artístico por un grabado alemán del siglo XVI

1. Introducción Alberto Durero. Melencolia I (1514, 28 x 18,8 cm) Galería Nacional de Arte de Karlsruhe El famoso y popular (entre el público matemático) grabado Melancolía I es obra del artista alemán Alberto Durero. Alberto Durero (1471 – 1528) Firma de A. Durero Junto con los grabados El caballero, la muerte y el diablo y San Jerónimo en su gabinete integra la trilogía Estampas maestras. Contemplada con ojos matemáticos, Melancolía I propone dos ambientes bien diferenciados: el aritmético y el geométrico. En el primero (parte superior derecha del grabado), se representa un cuadrado mágico 4 x 4 con los dieciséis primeros números naturales. En el segundo (parte izquierda) puede verse un poliedro peculiar (el sólido de Durero) y una esfera. Aritmética Geometría Boceto de Durero para el poliedro Melancolía 2. El ambiente aritmético En la parte superior derecha de su Melancolía, debajo de la campana, Durero nos  presenta una distribución numérica, en forma de cuadrado, en la que intervienen los dieciséis primeros números naturales (1, 2, 3, . . ., 14, 15, 16). 16 3 2 13 5 10 11 8 9 6 7 12 4 15 14 1 Notemos que la suma de los cuatro números de cada fila es igual a 34. Lo mismo sucede con la suma de los cuatro números de cada columna y con la suma de los cuatro números de cada diagonal. Además, los números 15 y 14 de la cuarta fila indican el año en que se estampó el grabado. Entre los matemáticos, cualquier distribución numérica similar a la de Durero se llama cuadrado mágico normal de orden 4. En general, se llama cuadrado mágico de orden n a un cuadrado formado por números naturales diferentes tales que los n números de cada fila, columna o diagonal, tienen la misma suma a la que se llama constante mágica [= M] del cuadrado. El cuadrado mágico de orden n se llama normal si los números que lo forman son los primeros números naturales. En el cuadrado mágico de Melancolía I, la suma de los números de las casillas grises en los diagramas siguientes también es igual a 34 [= M]. 16 3 2 13 5 10 11 8 9 6 7 12 4 15 14 1 16 3 2 13 5 10 11 8 9 6 7 12 4 15 14 1 16 3 2 13 5 10 11 8 9 6 7 12 4 15 14 1 16 3 2 13 5 10 11 8 9 6 7 12 4 15 14 1 Estas propiedades se pueden generalizar para cuadrados mágicos 4 x 4 en los siguientes términos: En todo cuadrado mágico de orden 4 la suma de los elementos que ocupan las esquinas es igual a la constante mágica. En todo cuadrado mágico de orden 4 la suma de los elementos que ocupan el cuadrado central de orden 2 es igual a la constante mágica. En todo cuadrado mágico de orden 4 la suma de los elementos que ocupan las esquinas de cualquier rectángulo medio es igual a la constante mágica. 3. El ambiente geométrico Antes de entrar de lleno en el estudio del sólido de Durero vamos a considerar otro poliedro llamado romboedro. El motivo de esta decisión es que, como se verá, aquél se genera a partir de éste. El romboedro es un hexaedro cuyas seis caras son rombos idénticos. Adviértase que el cubo es un caso especial de romboedro en el que las caras son cuadradas. Si se corta el romboedro del diagrama anterior por dos planos π y π´ perpendiculares a una de sus diagonales (por ejemplo, la CE) y tales que sus distancias respectivas a C y E sean iguales, entonces el romboedro se descompone en dos pirámides triangulares idénticas y en un poliedro dos de cuyas caras son triángulos equiláteros iguales y las seis restantes son pentágonos idénticos. Este último cuerpo geométrico es, precisamente, el poliedro Melancolía. Poliedro Melancolía Si el romboedro generador es un cubo, entonces el desarrollo del sólido de Durero toma la apariencia siguiente. 4. El ambiente artístico El poliedro Melancolía y el cuadrado mágico contenido en el grabado Melancolía I están presentes en diversas expresiones artísticas. Sirvan de ejemplo las siguientes. Hans Erni. Panta rhei (1979, detalle)[1]. Auditorio del Museo Hans Erni (Lucerna) Cortesía de la Hans Erni Foundation Giuseppe Modica. Mediterraneo-melanconia (2011). Óleo sobre tela,  20 x 25 cm. Cortesía del autor Giuseppe Modica. Melanconia-frammenti (2011). Óleo sobre tabla, tríptico, 150 x 225 cm. Cortesía del autor John Cornu. Melencolia (2011). 25 x 20 x 16 cm cada escultura. Cortesía del autor John Cornu. Melencolia (2011). 163 x 120 x 120 cm Cortesía del autor Román Jiménez Iranzo y Pedro Soler García. Melancolía (1992)[2] Sello de correos (Angola) Vicente Meavilla. Barcelona[3] (2004) George Widener. Magic Square (2009). 15,5 x 13 x 4 pulgadas Cortesía de la Andrew Edlin Gallery (New York) 5. A modo de epílogo Acabamos de dar un breve paseo por un grabado (Melencolia I) creado por el artista alemán Alberto Durero y estampado en 1514. A lo largo de esta corta excursión hemos pasado revista a los aspectos aritméticos (cuadrado mágico normal de orden cuatro y constante mágica 34), geométricos (poliedro Melancolía)  y artísticos de una obra maestra del arte universal. Con ello, hablando desde una óptica didáctica, hemos pretendido lanzar el siguiente mensaje a los docentes: cuando diseñéis actividades de enseñanza y aprendizaje procurad poner de manifiesto la relación de las Matemáticas con otras facetas de la cultura humana. Que así sea.   Referencias bibliográficas MEAVILLA SEGUÍ, V. (2004). Figuras imposibles. Geometría para heterodoxos. Granada: Proyecto Sur de Ediciones, S. L MEAVILLA SEGUÍ, V. (2016). El arte de las matemáticas. Córdoba: Editorial Guadalmazán. Referencias online Andrew Edlin Gallery (New York) Giuseppe Modica Hans Erni Foundation John Cornu Vicente Meavilla [1] A la izquierda de la imagen aparece Erasmo y a la derecha Lutero [2] La escultura de los arquitectos Jiménez Iranzo y Soler García estaba integrada en una fuente que se ubicó en la Plaza de la Ciudad de Brujas (Valencia). Dicha plaza estuvo en obras y, en la actualidad, desconocemos el paradero del sólido de Durero. [3] La distribución numérica encerrada en la B de Barcelona no es propiamente un cuadrado mágico de orden 4, dado que los números 10 y 14 se repiten dos veces. Este cuadrado cuasi-mágico está presente en la fachada de la Pasión de la Sagrada Familia (Barcelona). Notemos que la constante mágica es igual a 33 (edad de Cristo).

Martes, 23 de Junio de 2020 | Imprimir | PDF |  Correo electrónico

110. 10. (Julio 2020) El cuboctaedro, un poliedro arquimediano con catorce caras

1. Unas palabras introductorias Se llama poliedro semirregular o arquimediano1 a todo poliedro convexo en el que las caras son regulares, pero no iguales, y los ángulos poliedros son iguales y no regulares. Notemos que en un poliedro arquimediano todas las aristas son iguales. El primer documento en el que se alude a los poliedros semirrregulares se debe a Pappus de Alejandría (s. IV d. C.) que, en su Colección matemática, se expresa en los siguientes términos: (…) Es posible, en efecto, imaginar muchas figuras sólidas con superficies de cualquier clase; pero vamos a considerar especialmente aquellas que parecen regulares, las cuales no son solamente las cinco de que habla el divino Platón, a saber: el tetraedro, el hexaedro, el octaedro, el dodecaedro y el icosaedro, sino también las trece2 descubiertas por Arquímedes formadas por polígonos equiláteros y equiángulos, pero no semejantes. A lo largo de este artículo prestaremos nuestra atención al cuboctaedro, formado por ocho caras triangulares y seis cuadradas, dado que se genera fácilmente a partir de un cubo y está presente en múltiples manifestaciones artísticas y cotidianas. Cuboctaedro3 Estas razones justifican la introducción del antedicho poliedro arquimediano en las aulas no universitarias para poner de manifiesto la relación entre las Matemáticas, el Arte y el mundo en que vivimos. 2. Algunos textos y dibujos clásicos [1] Luca Pacioli describe el cuboctaedro en los siguientes términos. El hexaedro despuntado o absciso plano, igualmente sólido o hueco, tiene veinticuatro líneas que originan en él cuarenta y ocho ángulos superficiales, veinticuatro de los cuales son rectos y los demás agudos; tiene doce ángulos sólidos y está contenido por catorce superficies o bases, seis de las cuales son cuadradas y ocho triangulares (…). Y este cuerpo se origina del cubo mediante el corte uniforme en la mitad de sus lados, como demuestra de modo evidente su propia forma material. [De Divina Proportione (1509), cap. XLIX] Luca Pacioli (ca. 1445 – 1517) Leonardo da Vinci (1452 – 1519) Esta descripción se ilustra con dos dibujos de Leonardo da Vinci. Cuboctaedro Esqueleto4 del cuboctaedro [2] Por su parte, el alemán Alberto Durero, en su Underweysung der Messung, mit dem Zirckel und Richtscheyt (1525), ofrece un dibujo en el que se detalla el desarrollo del exacedron abscisus. Alberto Durero (1471 – 1528) Desarrollo del cuboctaedro [3] El holandés Simon Stevin también muestra el desarrollo del poliedro 5 en sus Problematum geometricorum (1583). Simon Stevin (1548 – 1620) Desarrollo del cuboctaedro [4] Juan de Arfe y Villafañe, natural de León, orfebre y autor de la Custodia de la Catedral de Sevilla, en De varia commensuracion para la Esculptura, y Architectura (1585) dibuja el arquimediano y su desarrollo. Juan de Arfe y Villafañe. Dibujos y desarrollo del cuboctaedro 3. El cuboctaedro: ficha técnica El cuboctaedro se obtiene truncando los vértices de un cubo a una distancia igual a  la mitad de la longitud de su arista. Tiene catorce caras (C = 14), doce vértices (V = 12), y veinticuatro aristas (A = 24). Como cualquier poliedro convexo cumple la fórmula de Euler C + V = A + 2. Si 2a es la longitud de la arista del cubo generador, entonces a√2 es la longitud de la arista del hexaedro despuntado. Su volumen V viene dado por la expresión: V = Vc - 8Vp siendo Vc el volumen del cubo generador y Vp el volumen de cada una de las pirámides cortadas. Entonces: Su área A viene dada por: 4. El exacedron abscisus en el dibujo y la pintura 4.1. Un grabado germano El grabador alemán Wenzel Jamnitzer en su Perspectiva Corporum Regularium (1568), nos ofrece una bellísima reproducción del poliedro . Wenzel Jamnitzer (1508 – 1585) Cuboctaedro 4.2. Los dibujos coloreados de Lorenz Stoer (1537 – 1621) A finales del siglo XX se descubrió una carpeta con dibujos coloreados del  alemán Lorenz Stoer (Geometria et Perspectiva: Corpora regulata et irregulata) que se conserva en la Biblioteca de la Universidad de Múnich. Ofrecemos dos de ellos en los que el arquimediano convive con otros cuerpos geométricos (sólidos platónicos, poliedros arquimedianos, poliedros estrellados   y cuerpos redondos). 4.3. Sueño arquimediano En el siguiente dibujo, hace ya unos años, diseñados una composición imposible en la que intervienen diversos poliedros arquimedianos. Vicente Meavilla. Sueño arquimediano (2005) Dejamos que el lector descubra la presencia del cuboctaedro. 4.4. Un cuadro de David Woodcock El artista y profesor británico David Woodcock (1952) dedica una de sus pinturas al hexaedro despuntado. David Woodcock. Cuboctahedron 11,5'' x 11,5'' 4.5. Pasión por el cuboctaedro El norteamericano John Arden Hiigli (1943 – 2017) consagró buena parte de su producción artística al exacedron abscisus. Hemos seleccionado el siguiente grupo de poliedros . 5. El arquimediano  y la marquetería Fray Giovanni de Verona (1433 – 1515), monje y artista italiano, fue el autor de diversas taraceas repartidas por la península italiana. En la Iglesia de Santa María in Organo (Verona) se encuentra una en la que, mirando desde arriba hacia abajo aparecen el exacedron elevatus vacuus6, el cuboctaedroy el duodecedron abscisus elevatus vacuus7. 6. Esculturas hexaédricas despuntadas El artesano carpintero Miguel Ángel Martín es autor de unas bellas esculturas en madera consagradas a los poliedros. En la figura adjunta reproducimos una dedicada al exacedron abscisus. Miguel Ángel Martín. Cuboctaedro Por otro lado, el escultor norteamericano (nacido en Seúl) Laird Hovland también rinde homenaje al poliedro en algunas de sus obras. Laird Hovland 7. Dados arquimedianos El cuboctaedro también forma parte de la nómina de dados poliédricos. Sirvan como ejemplo los dos siguientes cuyas aristas son curvilíneas. 8. Rompecabezas cuboctaédricos Entre los parientes del cubo de Rubik encontramos un puzle en forma de hexaedro despuntado. 9. Cristales La Madre Tierra también es capaz de producir bellísimos reproducciones cristalinas del exacedron abscisus. Cristal cuboctaédrico de galena. Cortesía de Fabre Minerals 10. Consideraciones didácticas En los parágrafos precedentes hemos contemplado un poliedro arquimediano, el cuboctaedro, desde distintos puntos de vista: el geométrico, el artístico, el cotidiano y el geológico. Así, hemos presentado algunos documentos históricos concernientes al exacedron abscisus; hemos efectuado algunos cálculos matemáticos; hemos ofrecido ejemplos concretos de la presencia del poliedro en grabados, pinturas, taraceas y esculturas; hemos mostrado objetos cotidianos (dados y rompecabezas) con formas cuboctaédricas y, por último, hemos admirado un bello cristal con la apariencia de hexaedro despuntado. Por consiguiente, hablando desde una óptica didáctica, podemos decir que en este artículo hemos propuesto un material que, estructurado de forma conveniente, puede ser útil al profesorado de los niveles no universitarios a la hora de diseñar actividades de enseñanza y aprendizaje que pueden involucrar a los departamentos de Matemáticas, Geografía e Historia y Ciencias Naturales.   Referencias bibliográficas ARFE y VILLAFAÑE, J. (1585). De varia commensuracion para la Esculptura, y Architectura. Sevilla: Andrea Pescioni y Iuan de Leon. DURERO, A. (1538)  Underweysung der Messung, mit dem Zirckel und Richtscheyt. Nürnberg. JAMNITZER, W. (1568). Perspectiva Corporum Regularium. Nuremberg: Gotlicher Hulff. KEPLER, J. (1619). Harmonices Mundi Libri V. Lincii Austriae: Sumptibus Godofredi Tampachii. MEAVILLA SEGUÍ, V. (2007). Las matemáticas del arte. Inspiración ma(r)temática. Córdoba: Editorial Almuzara, S. L. PACIOLI, L. (1991). La divina proporción (Introducción de Antonio M. González. Traducción de Juan Calatrava). Madrid: Ediciones Akal, S. A. STEVIN, S. (1583). Problematum geometricorum. Antwerpen: Johannes Bellerus. VERA, F. (1970). Científicos griegos (dos volúmenes). Madrid: Aguilar, S. A. de Ediciones. Referencias online David Woodcock Fabre Minerals John Arden Hiigli Laird Hovland Miguel Ángel Martín Vicente Meavilla Seguí 1 En honor al científico griego Arquímedes (s. III a. C.). 2 Pappus describe los trece poliedros siguientes: tetraedro truncado, cuboctaedro, octaedro truncado, cubo truncado, rombicuboctaedro, cuboctaedro truncado, icosidodecaedro, icosaedro truncado, dodecaedro truncado, cubo achatado, rombicosidodecaedro, icosidodecaedro truncado, y dodecaedro achatado. En esta lista no aparecen los prismas de Arquímedes, poliedros semirregulares cuyas bases son dos polígonos regulares del mismo tipo y cuyas caras laterales son cuadrados, y los antiprismas de Arquímedes o prismatoides regulares, poliedros arquimedianos cuyas bases son dos polígonos regulares del mismo tipo y cuyas caras laterales son triángulos equiláteros. 3 Ilustración contenida en el libro Harmonices mundi (1619. Lib.II, p. 62) de Johannes Kepler (1571 – 1630). 4 Estructura formada por las aristas de un poliedro. 5 El símbolo significa que de las catorce caras del poliedro, ocho son triángulos equiláteros y seis son cuadrados. 6 Poliedro estrellado formado por seis pirámides de base cuadrada, cuyas caras laterales son triángulos equiláteros, que se acoplan exactamente a las seis caras de un cubo. 7 El duodecedron abscisus elevatus vacuus [= icosidodecaedro estrellado] es un poliedro estrellado obtenido a partir de un icosidodecaedro acoplando a sus veinte caras triangulares y a sus doce caras pentagonales las correspondientes pirámides triangulares (cuyas caras laterales son triángulos equiláteros) y pentagonales (cuyas caras laterales son triángulos equiláteros).

Jueves, 02 de Julio de 2020 | Imprimir | PDF |  Correo electrónico