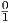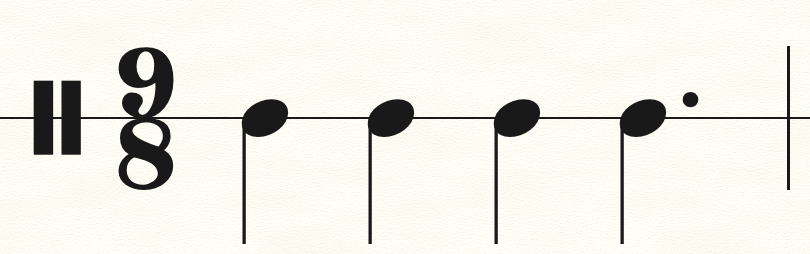Home » Cultura y matemáticas » Música y matemáticas
Música y matemáticas
El objetivo de esta sección es comprender la interesante y profunda relación de las Matemáticas con la Música.
Nuestro sincero agradecimiento a Francisco Gómez Martín (Universidad Politécnica de Madrid) por organizar y desarrollar esta sección, a sus anteriores responsables Rafael Losada y Vicente Liern, así como a todas las personas que colaboran con la misma.
Resultados 1 - 10 de 130
|
Cultura y matemáticas/Música y matemáticas
Autor:Luis Nuño (Universidad Politécnica de Valencia)
1. Introducción
El presente artículo fue presentado en junio de este año 2022 en la Conferencia Internacional de Matemáticas y Computación en Música, celebrada en Atlanta (GA, USA). Para facilitar su difusión entre un conjunto de lectores lo más amplio posible se ha simplificado en cierta medida su parte más teórica, pero se han mantenido en su totalidad los resultados obtenidos. En todo caso, el artículo completo puede consultarse en la referencia indicada al final de este artículo (Nuño 2022a).
La primera parte de este trabajo se ha dedicado a la selección de ocho tipos de escalas heptatónicas, al análisis de sus características armónicas y a la obtención de un grafo parsimónico, denominado 7-Cíclope, que relaciona dichas escalas mediante transformaciones monosemitonales. A continuación, se llevará a cabo un proceso análogo para las escalas pentatónicas y se estudiará la relación acústica existente entre las escalas heptatónicas y pentatónicas consideradas aquí. Finalmente, se incluye un ejemplo de análisis musical con escalas heptatónicas. En caso de duda sobre alguno de los conceptos utilizados aquí, se recomienda consultar los artículos de Nuño (2020, 2021a y 2021d), anteriormente publicados en esta misma página Web. Al igual que se hizo en la primera parte de este estudio, emplearemos la notación inglesa para las notas musicales (C=Do, D=Re, E=Mi, F=Fa, G=Sol, A=La y B=Si).
2. Escalas Pentatónicas
En esta sección se va a realizar la selección, análisis armónico y desarrollo de un grafo parsimónico para escalas pentatónicas, mediante un proceso totalmente análogo al seguido para las heptatónicas.
2.1. Selección de las Escalas Pentatónicas
Para mantener un completo paralelismo con las escalas heptatónicas previamente seleccionadas, tomaremos ahora como escalas pentatónicas las complementarias de aquellas. La Tabla 5 muestra estos tipos de escalas con sus nombres de Forte extendidos, los símbolos para representarlas, sus estructuras interválicas y sus vectores de clases de intervalos. Los símbolos de la forma “m…P” y “7…P” representan, respectivamente, variantes de las escalas pentatónica menor (mP) y pentatónica “dominante” (7P), cuyas estructuras interválicas son 32232 y 22332. Nótese que la escala “mP” es un modo de la escala pentatónica mayor (MP).
Tabla 5. Tipos de Escalas Pentatónicas considerados aquí.
Escala Pentatónica
Símbolo
Estructura Interválica
Vector de Clases de Intervalos
5-22 5-30a 5-30b 5-32a 5-32b 5-33 5-34 5-35
mΔ♯4P mΔP Δ♯5P m♯4P 7♯9P 7♯5P 7P MP
33141 32241 42231 33132 31332 22422 22332 22323
202321 121321 121321 113221 113221 040402 032221 032140
Estos ocho tipos de escalas también pueden obtenerse de forma análoga a como se obtuvieron las escalas heptatónicas combinando las cuatro notas alteradas más cercanas a la tonalidad de partida. Sin embargo, dado que las escalas pentatónicas no definen tonalidades, hablaremos ahora de notas modificadas en lugar de alteradas. Así, si partimos de la escala de C pentatónica mayor, debemos determinar, en primer lugar, cuáles de sus notas, modificadas en un semitono, dan lugar a otras escalas pentatónicas mayores. Un sencillo análisis nos revela que hay únicamente dos posibilidades: elevar E a F, obteniendo FMP, o bien rebajar C a B, obteniendo GMP. Y, a continuación, repetimos este proceso para hallar las siguientes escalas pentatónicas más cercanas a ellas, obteniendo así la Tabla 6, que es análoga a la Tabla 3 de la primera parte de este estudio, pero para las escalas pentatónicas. Podemos comprobar que, efectivamente, obtenemos los mismos ocho tipos de escalas de la Tabla 5.
Tabla 6. Escalas Pentatónicas obtenidas a partir de CMP combinando dos notas modificadas.
Notas Modificadas
-
E → F
A → B♭
E → F, A → B♭
- C → B G → F♯ C → B, G → F♯
CMP GMP D7P DMP
FMP G7P D7♯9P Bm♯4P
C7P Em♯4P D7♯5P BmΔP
B♭MP G7♯9P F♯Δ♯5P BmΔ♯4P
Las características armónicas de estas escalas se muestran en la Tabla 7, utilizando para ello los vectores de tipos de tricordos y de tetracordos. Esta tabla es análoga a la Tabla 4 de la primera parte de este estudio, pero para las escalas pentatónicas, y en ambas se han aplicado los mismos criterios.
Tabla 7. Vectores de Tipos de Tricordos y de Tetracordos para las Escalas Pentatónicas.
Escala
Vector de Tipos de Tricordos
Vector de Tipos de Tetracordos
5-22
000111111-0000001111
000000000010-000000000000000011110-0000000000
5-30a
000100110-1011110101
000000000000-000000000001001000100-0010100000
5-30b
000011001-1101110011
000000000000-000000000000110000010-0100100000
5-32a
000110010-0110101210
000000000000-000000000001000101000-0000001100
5-32b
000110001-0111001120
000000000000-000000000000100110000-0000001010
5-33
000000000-3003300001
000000000000-000000000000000000000-2000210000
5-34
000000000-2111111110
000000000000-000000000000000000000-1110000110
5-35
000000000-1220030110
000000000000-000000000000000000000-0112001000
2.2. Grafo Parsimónico para las Escalas Pentatónicas Seleccionadas
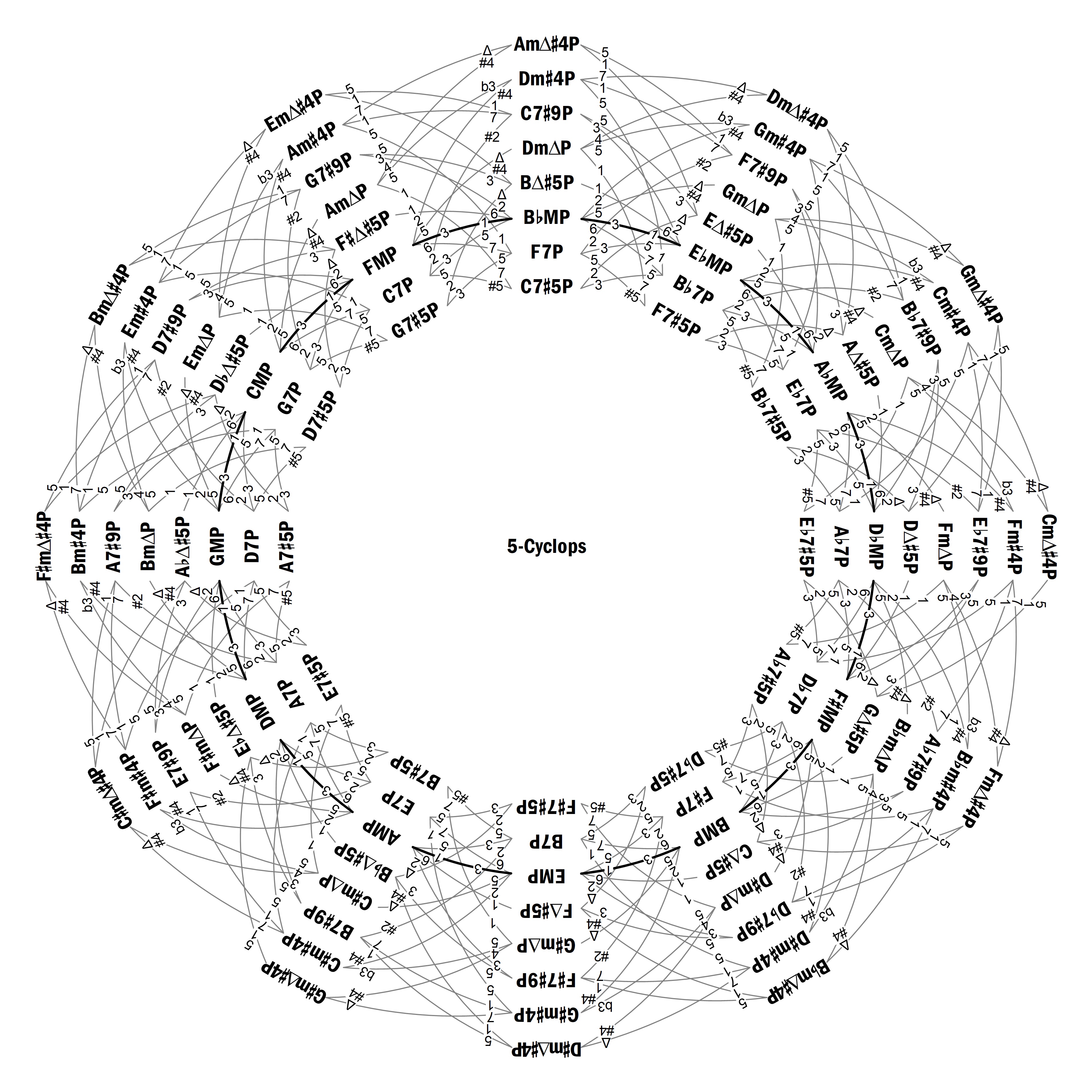
La Figura 2 es un grafo cíclico circular que he denominado 5-Cíclope, que muestra todas las escalas pentatónicas de los tipos incluidos en la Tabla 5, conectadas mediante transformaciones monosemitonales. Dado que, si dos escalas están relacionadas mediante una transformación monosemitonal, también lo estarán sus complementarias, resulta que esta figura es completamente análoga a la Figura 1, y en ambas se han aplicado los mismos criterios.
Puesto que los números 5 y 12 también son coprimos, en cada zona tenemos justamente una escala de cada tipo. Nótese que las escalas pentatónicas mayores son las únicas que pueden transformarse en otras de su mismo tipo, a la vez que los enlaces entre ellas forman ahora el ciclo de cuartas, que es la única circunferencia posible en este grafo (la línea gruesa).
Fig. 2. El 5-Cíclope, con los tipos de escalas pentatónicas considerados en la Tabla 5.
2.3. Relación entre las Escalas Heptatónicas y Pentatónicas Seleccionadas
Aparte de la relación de complementariedad que tenemos entre las escalas heptatónicas y pentatónicas consideradas aquí, existen entre ellas unas relaciones acústicas muy interesantes que pueden observarse mediante el vector de tipos de pentacordos, que es otra generalización del vector de tipos de intervalos. Este nuevo vector indica cuántos pentacordos (o escalas pentatónicas) de cada tipo contiene una escala dada. La Tabla 8 muestra este vector para las escalas heptatónicas incluidas en la Tabla 2 de la primera parte de este estudio, más el par 7-31a/7-31b considerado por Žabka (2014). En dicho vector, cada dígito corresponde a un tipo de escala pentatónica en el orden establecido por Nuño (2021c o, en español, 2020 y 2021a). Se han representado en negrita los dígitos correspondientes a las escalas pentatónicas consideradas aquí. Así, de izquierda a derecha, el primer dígito en negrita corresponde a la escala 5-22 y los últimos nueve dígitos (que están después de un espacio en blanco) corresponden a las escalas 5-30a, 5-30b, 5-31a, 5-31b, 5-32a, 5-32b, 5-33, 5-34 y 5-35.
Tabla 8. Vector de Tipos de Pentacordos para diversas Escalas Heptatónicas.
Escala
Vector de Tipos de Pentacordos
7-22
0000000001100-000000000000001111111110011112-00000000001100 000011000
7-30a
0000000000100-010001000010001000001010011100-00110001110100 200010110
7-30b
0000000001000-001000100001001000010100011010-00110010111000 020001110
7-31a
0000000000000-000210000000000120000002100000-00002100002100 003021000
7-31b
0000000000000-000120000000000210000001200000-00001200001200 000312000
7-32a
0000000000000-000100000100000010100110001101-10001011010011 102110000
7-32b
0000000000000-000010000100000100100110010011-01000111100011 011201000
7-33
0000000000000-111000000011001000000000000000-00110011001100 110000610
7-34
0000000000000-000110000000000000100000000000-11111111001111 110000121
7-35
0000000000000-000000000100000000000000011000-22111100220011 000000013
Como podemos ver en la tabla, la escala 7-35 contiene tres escalas del tipo 5-35. Este es, además, el máximo número de escalas 5-35 contenidas en cualquiera de las diferentes escalas heptatónicas (no solo las incluidas en la tabla), ya que en el resto de los casos este número no es superior a dos. Así mismo, las escalas 7-34, 7-33 y 7-22 contienen, respectivamente, el máximo número de escalas 5-34, 5-33 y 5-22, que son 2, 6 y 2 (el resto de las escalas heptatónicas no contienen más de una en cada caso). En cuanto a los pares de escalas formados por un tipo a y un tipo b, debemos tener en cuenta que la complementaria de un tipo a es un tipo b y viceversa (Nuño 2021c o, en español, 2020 y 2021a). Entonces, las escalas 7-30a y 7-30b contienen, respectivamente, el máximo número de escalas 5-30a y 5-30b (es decir, las inversas de sus complementarias), que es dos (el resto de las escalas heptatónicas no contienen más de una), mientras que no contienen ninguna de sus correspondientes escalas complementarias. Así mismo, las escalas 7-31a y 7-31b contienen, respectivamente, el máximo número de escalas 5-31a y 5-31b, que es tres (el resto de las escalas heptatónicas no contienen más de dos) y tampoco contienen a sus correspondientes escalas complementarias. Pero, en cuanto al contenido en escalas 5-32a y 5-32b, resulta que son las escalas heptatónicas 7-31a y 7-31b las que contienen, respectivamente, el máximo número de ellas, que es dos (el resto de las escalas heptatónicas no contienen más de una). Por su parte, las escalas 7-32a y 7-32b contienen, respectivamente, una escala 5-32a y una 5-32b (de nuevo, las inversas de sus complementarias) y no contienen a sus correspondientes escalas complementarias. Por tanto, en todos estos casos existe, en mayor o menor medida, una clara relación acústica entre cada tipo de escala heptatónica y la inversa de su complementaria (que es pentatónica).
3. Ejemplo de Análisis Musical
Žabka (2014) incluye en su artículo el análisis de un pasaje cromático muy interesante: la Fantasía en C menor, K. 475, de Mozart, compases 1–25. Para ello, determina cuáles son las escalas heptatónicas utilizadas en cada caso, aunque algunas de ellas aparecen de forma incompleta. Con la nomenclatura usada en el presente artículo, estas escalas son:
Ghh % FhM % D♭M E♭mm FNpm B♭hm B♭Npm BM % G♯Npm
D♭hL F♯Npm C♭hL BhM Bhm GM % % F♯Npm–F♯hh F♯hM % % %
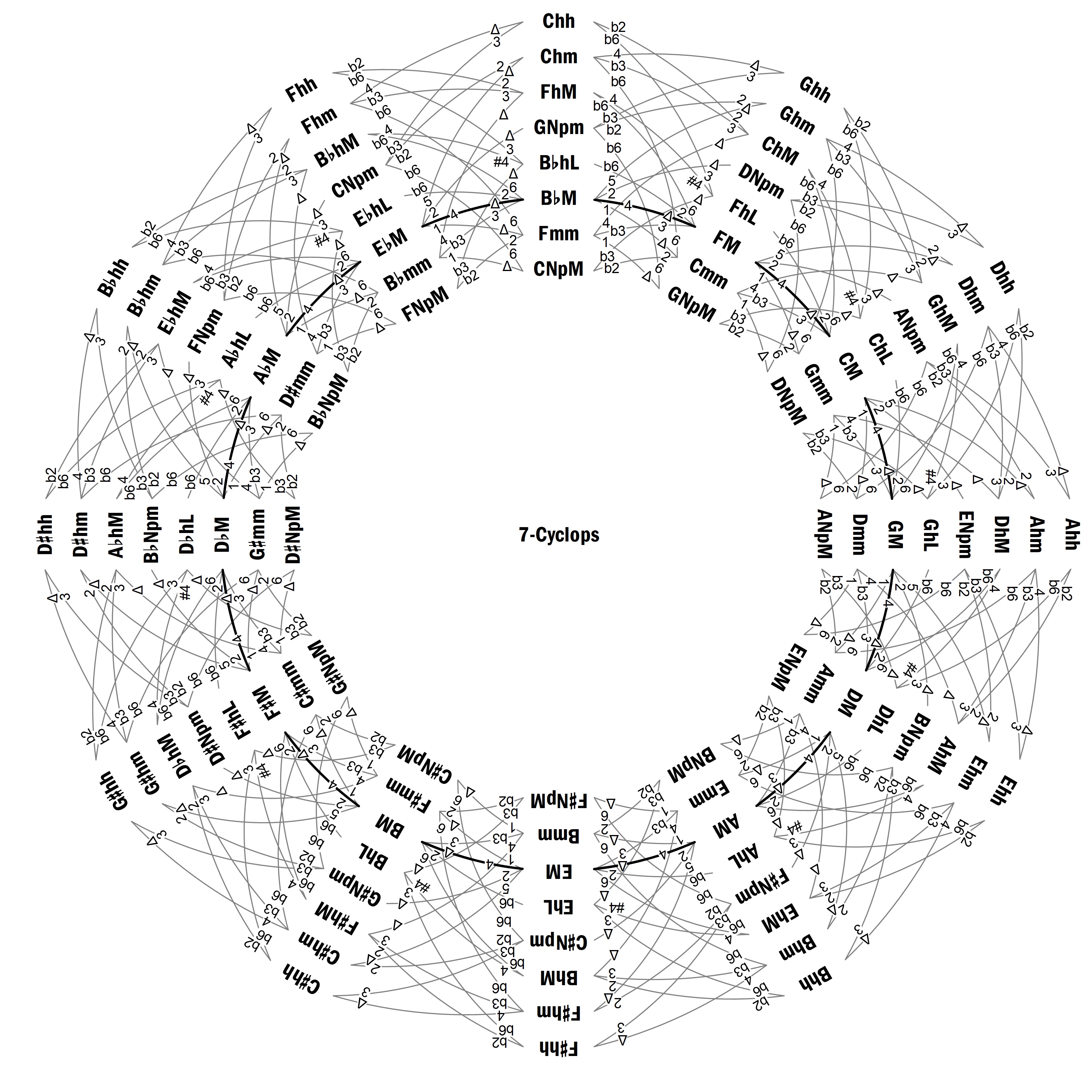
donde cada escala o cada pareja de escalas unidas por un guión dura un compás y el símbolo “%” significa repetir el compás anterior. Las representaciones de este pasaje realizadas por Žabka (2014) presentan algunas complicaciones y pueden compararse con la que se muestra en la Figura 3 en el 7-Cíclope, el cual contiene todas las escalas requeridas, y donde la primera de ellas se ha indicado con una línea doble.
Aunque la composición está en C menor, Mozart no incluye ninguna alteración en la armadura; y, como se aprecia en la Figura 3, no se utiliza ninguna de las escalas Chm, Cmm o C menor natural (E♭M). No obstante, la escala inicial, Ghh, contiene el acorde de C menor, cuyo arpegio se ejecuta empezando justamente por la nota C (cuarto modo de Ghh). A partir de ahí, las escalas se mueven en el diagrama en sentido antihorario, es decir, en la dirección de los bemoles (con algunos movimientos hacia delante y hacia atrás), hasta llegar a GM, cuya tónica (en el bajo) es la dominante de C. Sin embargo, la resolución no se hace sobre una escala de C menor, sino sobre varias escalas de tónica F♯, que está a un intervalo de tritono de C, y los últimos cuatro compases están basados, de hecho, en el acorde de F♯ mayor.
Fig. 3. Mozart, Fantasía en C menor, K. 475, compases 1–25. Análisis con el 7-Cíclope.
4. Conclusiones e Información Adicional
Como conclusiones del artículo completo, podemos decir que, siguiendo unos criterios puramente musicales, se han seleccionado ocho tipos de escalas heptatónicas y sus complementarias pentatónicas. Sus características armónicas se han analizado mediante los vectores de clases de intervalos, de tipos de tricordos y de tipos de tetracordos. Además, se han desarrollado dos nuevos grafos parsimónicos, denominados 7-Cíclope y 5-Cíclope, que relacionan cada uno de estos tipos de escalas mediante transformaciones monosemitonales. En estos grafos destacan, respectivamente, los ciclos de quintas y de cuartas, que son las únicas circunferencias posibles que conectan escalas del mismo tipo en esta clase de grafos (aparte de los casos triviales de escalas de una u once notas). Por otra parte, se ha encontrado una relación acústica entre cada escala heptatónica y la inversa de su complementaria, utilizando para ello el vector de tipos de pentacordos. Finalmente, se ha incluido un ejemplo de aplicación al análisis musical de una obra bastante compleja, por lo que toda esta información se estima que puede ser de interés tanto para teóricos como para compositores.
Los lectores interesados en los tipos de vectores utilizados aquí, tanto para el caso del sistema de afinación temperado de doce notas como para otros sistemas más generales, pueden encontrar información adicional en Nuño (2022b). En ese artículo se presenta un riguroso estudio considerando la división de la octava en un número arbitrario de notas n y se incluyen diferentes teoremas que proporcionan una visión global y un conocimiento detallado de estos tipos de vectores.
Referencias
Balzano, G. 1980. “The Group-Theoretic Description of 12-Fold and Microtonal Pitch Systems”. Computer Music Journal 4 (4), 66–84.
Cohn, R. 1996. “Maximally Smooth Cycles, Hexatonic Systems, and the Analysis of Late-Romantic Triadic Progressions”. Music Analysis 15 (1), 9–40.
Cohn, R. 2012. Audacious Euphony: Chromatic Harmony and the Triad’s Second Nature. New York: Oxford University Press.
Douthett, J., Steinbach, P. 1998. “Parsimonious Graphs: A Study in Parsimony, Contextual Transformations, and Modes of Limited Transposition”. Journal of Music Theory 42 (2), 241–263.
Forte, A. 1973. The Structure of Atonal Music. New Haven: Yale University Press.
Hook, J. 2011. “Spelled Heptachords”. En: Agon, C., et al. (eds.) Mathematics and Computation in Music 2011, pp. 84–97. Heidelberg: Springer.
Nuño, L. 2020. “La Tabla Periódica Musical (1/2).” DIVULGAMAT, Centro virtual de divulgación de las matemáticas, RSME: Real Sociedad Matemática Española, No. 111. Diciembre 2020. https://www.divulgamat.net/index.php?option=com_content&view=article&id=18500&directory=67
Nuño, L. 2021a. “La Tabla Periódica Musical (2/2).” DIVULGAMAT, Centro virtual de divulgación de las matemáticas, RSME: Real Sociedad Matemática Española, No. 112. Enero 2021. https://www.divulgamat.net/index.php?option=com_content&view=article&id=18516&directory=67
Nuño, L. 2021b. Parsimonious Graphs for the Most Common Trichords and Tetrachords. Journal of Mathematics and Music 15(2), 125–139 (2021).
Nuño, L. 2021c. A Detailed List and a Periodic Table of Set Classes. Journal of Mathematics and Music 15(3), 267–287.
Nuño, L. 2021d. “Grafos Parsimónicos para los Tricordos y Tetracordos más Comunes.” DIVULGAMAT, Centro virtual de divulgación de las matemáticas, RSME: Real Sociedad Matemática Española, No. 119. Octubre 2021. https://divulgamat.net/index.php?option=com_content&view=article&id=18666&directory=67
Nuño, L. 2022a. “Parsimonious Graphs for Selected Heptatonic and Pentatonic Scales”. En: Montiel, M., Agustín-Aquino, O.A., Gómez, F., Kastine, J., Lluis-Puebla, E., Milam, B. (eds) Mathematics and Computation in Music. MCM 2022. Lecture Notes in Computer Science, vol 13267. Springer, Cham. https://doi.org/10.1007/978-3-031-07015-0_3
Nuño, L. 2022b. “Type and Class Vectors and Matrices in ℤn. Application to ℤ6, ℤ7 and ℤ12.” Journal of Mathematics and Music. https://www.tandfonline.com/doi/full/10.1080/17459737.2022.2120214
Piston, W. 1988. Harmony. 5th edn. New York: W. W. Norton and Co.
Popley, H. A. 1921. The Music of India. London: Oxford University Press.
Ring, I. 2022 (15 marzo). The Exciting Universe of Music Theory, https://ianring.com/musictheory/scales/
Schönberg, A. 1983: Theory of Harmony. 3rd edn. Berkeley, Calif.: University of California Press.
Tymoczko, D. 2011. A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice. New York: Oxford University Press.
Žabka, M. 2014. “Dancing with the Scales: Subchromatic Generated Tone Systems”. Journal of Music Theory 58 (2), 179–233.
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Luis Nuño (Universidad Politécnica de Valencia)
Tenemos otra vez más el placer de contar como autor invitado a Luis Nuño, que ya ha escrito en esta columna anteriormente. Luis Nuño es catedrático de universidad en la Universidad Politécnica de Valencia y autor de la Rueda Armónica. Es un gran investigador de la teoría matemática y computacional de la música así como un divulgador de la misma. Ha publicado varios artículos de investigación en la prestigiosa revista Journal of Mathematics and Music. Siguiendo con su trabajo de grafos parsimónicos, esta vez estudia dichos grafos sobre escalas heptatónicas y pentatónicas. Este trabajo que trae a Divulgamat consta de dos partes; la segunda la veremos en enero. De nuevo, estamos ante un artículo iluminador y profundo. Espero que los lectores de esta columna lo disfruten tanto como lo he hecho al leerlo.
Paco Gómez Martín
1. Introducción
El presente artículo fue presentado en junio de este año 2022 en la Conferencia Internacional de Matemáticas y Computación en Música, celebrada en Atlanta (GA, USA). Para facilitar su difusión entre un conjunto de lectores lo más amplio posible se ha simplificado en cierta medida su parte más teórica, pero se han mantenido en su totalidad los resultados obtenidos. En todo caso, el artículo completo puede consultarse en la referencia indicada al final de este artículo (Nuño 2022a).
La escala mayor es la base de la música occidental. Por ello, aunque pueda parecer superfluo, conviene revisar algunas de sus principales características. Se trata de un conjunto de siete notas que guardan entre sí una gran afinidad acústica, de manera que es muy “completo y versátil”. Así, muchas canciones populares – y no tan populares – están compuestas en una tonalidad mayor. Nuestra notación musical, basada en el pentagrama y las armaduras, es idónea para escribir música en las tonalidades mayores. El piano, considerado el “instrumento rey”, está perfectamente adaptado para tocar en la tonalidad de Do mayor. Los nombres de las notas son siete – en lugar de doce –, precisamente las de la escala de Do mayor. El término octava (derivado de “ocho”) indica su extensión (repitiendo la tónica al final), mientras que los términos tono y semitono describen los intervalos entre dos de sus notas sucesivas. Así mismo, la calificación de los intervalos (justo, mayor, menor, etc.) se establece tomando como referencia una escala mayor. En resumen, la escala mayor es fundamental en teoría de la música y composición.
Además, a partir de la escala mayor pueden obtenerse directamente otros tipos de escalas. Por ejemplo, tomando cualquiera de sus notas como como tónica, obtenemos siete modos, de los cuales el eólico constituye la escala menor, que es también característica de la música occidental. En este caso, sus grados sexto y séptimo pueden ser naturales o alterados (elevados un semitono), lo que da lugar a las escalas menores natural, melódica y armónica.
Por otra parte, la escala complementaria de una escala mayor (es decir, la formada por el resto de las doce notas) es una escala pentatónica mayor. En general, las escalas pentatónicas – y no solo la pentatónica mayor – han sido utilizadas por diferentes culturas desde la antigüedad. Aunque son predominantes en los países del este (China, Japón, India, Java, etc.), también se han empleado en diferentes estilos occidentales, tanto en la música clásica como en la escocesa, andina, jazz, etc.
Este estudio está basado en el sistema de afinación temperado de doce notas, utilizándose como nomenclatura los nombres de Forte y las clases de conjuntos (Forte 1973), que aquí llamaremos clases de escalas. De entre ellas, las no inversionalmente simétricas se dividen en dos tipos de escalas relacionados entre sí por inversión, llamados a y b, de acuerdo con Nuño (2021c o, en español, 2020 y 2021a). Con respecto a las escalas mayor y pentatónica mayor podemos decir que son las escalas de siete y cinco notas, respectivamente, que tienen sus notas más uniformemente espaciadas. Y, además, poseen una propiedad exclusiva: aparte de los casos triviales de las escalas de una u once notas, son las únicas que pueden transformarse en otras de su mismo tipo mediante una transformación monosemitonal (es decir, cambiando una sola nota y solo un semitono, que puede ser ascendente o descendente). Por ejemplo, subiendo en la escala de Do mayor la nota Fa un semitono obtenemos la escala de Sol mayor. Esta propiedad, para el caso de las escalas mayores, da lugar al orden de los sostenidos y los bemoles, así como al ciclo de quintas (Balzano 1980, Cohn 1996), que es fundamental en la teoría de la modulación, es decir, el cambio de una tonalidad a otra. En este sentido, dada una tonalidad, las más “cercanas” a ella son las que tienen un sostenido o un bemol de más o de menos en su armadura (Schönberg 1983, Piston 1988). Esto también es aplicable a las tonalidades menores, ya que sus armaduras son las mismas que las de sus relativas mayores.
El concepto de transformación parsimónica es algo más general, ya que, en este caso, son una o más notas las que cambian en uno o dos semitonos (en la práctica, no más de dos semitonos en total), mientras el resto permanecen fijas (Douthett y Steinbach 1998). A este respecto, el Tonnetz es una primera representación de este tipo de transformaciones para las tríadas mayores y menores, mientras que Douthett y Steinbach (1998) presentan otros grafos más complejos e interesantes. En el s. XIX, diversos compositores hacen un uso extensivo de este tipo de transformaciones, varias de cuyas obras son analizadas por Cohn (2012). Por su parte, Tymoczko (2011) sigue un planteamiento distinto, representando los conjuntos de notas en unos espacios particulares denominados orbifolds. En cambio, Nuño (2021b o, en español, 2021d) desarrolla unos grafos cíclicos circulares, llamados Cíclopes, que relacionan los tricordos y tetracordos “más comunes”, mediante los cuales se puede analizar de forma práctica un buen número de dichos tipos de obras. En este artículo se presentan dos nuevos grafos similares a ellos para relacionar diferentes escalas heptatónicas y pentatónicas. En cada caso, se han seleccionado ocho tipos de escalas siguiendo unos criterios puramente musicales. Además, muestran de forma gráfica un resultado anteriormente mencionado: el ciclo de quintas para las escalas mayores, que es complementado con el ciclo de cuartas para las escalas pentatónicas mayores, los cuales corresponden a las únicas circunferencias posibles que conectan escalas del mismo tipo en estas clases de grafos (Balzano 1980, Cohn 1996).
Este trabajo consta de dos partes, la primera de las cuales se dedica a las escalas heptatónicas y la segunda a las pentatónicas, en la cual se estudiará también la relación acústica existente entre ambas y se incluye, además, un ejemplo de análisis musical con escalas heptatónicas. En caso de duda sobre alguno de los conceptos utilizados aquí, se recomienda consultar los artículos de Nuño (2020, 2021a y 2021d), anteriormente publicados en esta misma página Web.
2. Selección de las Escalas Heptatónicas
La música tonal está basada en las escalas mayor, menor melódica y menor armónica (Schönberg 1983, Piston 1988), cuyos nombres de Forte “extendidos” son 7-35, 7-34 y 7-32a, respectivamente. Para completar esta serie numérica podemos considerar también las escalas 7-32b (mayor armónica) y 7-33 (napolitana mayor, según la nomenclatura de Ring 2022). Estas son, además, las escalas heptatónicas cuyas notas están más uniformemente espaciadas, sobre todo la escala mayor (7-35).
Para obtener otras escalas heptatónicas a partir de ellas podemos, simplemente, descomponerlas en tetracordos (entendidos ahora como grupos de cuatro notas consecutivas) y combinar dos de ellos. Este es el procedimiento utilizado, por ejemplo, en la música tradicional de India para obtener las escalas heptatónicas denominadas “Melakarta ragas” (Popley 1921). Otra opción es partir de una escala mayor y elevar o rebajar una o más notas un semitono, tal como se hace con la escala menor natural para obtener las escalas menores armónica y melódica. En este caso, lo lógico es tomar las notas alteradas de las tonalidades más cercanas a la considerada.
A continuación, usaremos ambos procedimientos para obtener un número “razonable” de escalas heptatónicas que nos permitan obtener unos grafos de complejidad aceptable y que pueden ser de interés para teóricos y compositores. Por otra parte, en adelante emplearemos la notación inglesa para las notas musicales (C=Do, D=Re, E=Mi, F=Fa, G=Sol, A=La y B=Si).
2.1. Combinaciones de dos Tetracordos
Consideremos la escala de C mayor. Podemos ver que está compuesta por los tetracordos C – D – E – F y G – A – B – C, donde el primero de ellos comienza por la nota C y el segundo por G. En ambos casos, sus “estructuras interválicas”, en semitonos, son iguales: 221, siendo el intervalo entre los dos tetracordos de 2 semitonos. Por tanto, podemos escribir la estructura interválica de la escala completa como 221 2 221 y al tetracordo 221 lo llamaremos “mayor”. Si empezamos esa misma escala por las notas D o A, las primeras cuatro notas formarán un tetracordo de la forma 212, que llamaremos “menor”. Si, en cambio, empezamos por las notas E o B, resulta un tetracordo del tipo 122, que llamaremos “frigio”. Y, por último, si empezamos por la nota F, obtenemos un tetracordo del tipo 222, que llamaremos “lidio”.
Así, podemos obtener diferentes escalas heptatónicas combinando dos cualesquiera de estos cuatro tetracordos. Pero, para obtener las escalas armónicas, tanto mayores como menores, necesitamos otro tipo de tetracordo: el 131, que llamaremos “armónico”. La Tabla 1 muestra las 25 posibles combinaciones de dos de estos cinco tipos de tetracordos. Se indican también las estructuras interválicas de las escalas resultantes, así como los nombres y símbolos usados para representarlas. Los nombres menos comunes se han tomado de Ring (2022) y se ha utilizado el mismo nombre para todos los modos de una misma escala. Además, en todos los casos, el intervalo entre los dos tetracordos se ha elegido de manera que la primera y la última nota de cada escala sea la misma. Es decir, que la suma de todos los semitonos en cada escala sea igual a 12.
Tabla 1. Tipos de escalas heptatónicas obtenidas combinando dos de los cinco tetracordos considerados aquí, junto con sus correspondientes estructuras interválicas. Los símbolos utilizados para representar las escalas son: M: mayor, mm: menor melódica, hm: menor armónica, hM: mayor armónica, NpM: napolitana mayor, Npm: napolitana menor, hL: lidia armónica, hh: doble armónica o húngara y WT: escala de tonos.
1º ↓ \ 2º →
mayor
menor
frigio
lidio
armónico
mayor
221 2 221 M
221 2 212 M
221 2 122 mm
221 1 222 NpM
221 2 131 hM
menor
212 2 221 mm
212 2 212 M
212 2 122 M
212 1 222 mm
212 2 131 hm
frigio
122 2 221 NpM
122 2 212 mm
122 2 122 M
122 1 222 M
122 2 131 Npm
lidio
222 1 221 M
222 1 212 mm
222 1 122 NpM
222 222 WT
222 1 131 hL
armónico
131 2 221 hL
131 2 212 hM
131 2 122 hm
131 1 222 Npm
131 2 131 hh
Como podemos ver, la combinación de dos tetracordos lidios da lugar a la escala de tonos (WT), que solo tiene seis notas, por lo que no la incluiremos en este estudio. El resto de las combinaciones dan lugar a ocho tipos diferentes de escalas, entre las que se encuentran las cinco mencionadas al principio de la Sección 2, siendo, además, un número adecuado (ni muy grande ni muy pequeño) para desarrollar los grafos parsimónicos deseados. La Tabla 2 muestra estos tipos de escalas con sus nombres de Forte extendidos, los símbolos para representarlas y sus estructuras interválicas. La última columna es el vector de clases de intervalos, que consta de seis dígitos que indican correlativamente cuántos intervalos de cada clase (de 1 a 6 semitonos) contiene la escala considerada. Así, por ejemplo, este vector indica que la escala mayor (7-35) contiene “2” intervalos de 1 semitono, “5” intervalos de 2 semitonos, “4” intervalos de 3 semitonos, “3” intervalos de 4 semitonos, “6” intervalos de 5 semitonos y “1” intervalo de 6 semitonos.
Tabla 2. Tipos de Escalas Heptatónicas considerados aquí.
Escala Heptatónica
Símbolo
Estructura Interválica
Vector de Clases de Intervalos
7-22
hh
1312131
424542
7-30a
Npm
1222131
343542
7-30b
hL
2221131
343542
7-32a
hm
2122131
335442
7-32b
hM
2212131
335442
7-33
NpM
1222221
262623
7-34
mm
2122221
254442
7-35
M
2212221
254361
2.2. Combinaciones de las Notas Alteradas pertenecientes a las Tonalidades más Cercanas
Consideremos de nuevo la escala de C mayor. Sus dos tonalidades más cercanas, siguiendo tanto el orden de los sostenidos como el de los bemoles, dan lugar a las notas alteradas F♯, C♯, B♭ y E♭. Así, partiendo de la escala de C mayor y utilizando estas cuatro notas, bien naturales o alteradas, resultan 16 combinaciones, las cuales se muestran en la Tabla 3, junto con las escalas resultantes. Como puede verse, obtenemos los mismos ocho tipos de escalas heptatónicas que con el procedimiento anterior. Además, de acuerdo con el studio de Hook (2011), estas son justamente las escalas que tienen un “span” menor o igual que 10. Por todo ello, estos serán los tipos de escalas heptatónicas que consideraremos en este estudio y cuyas principales características están recogidas en la Tabla 2.
Tabla 3. Escalas Heptatónicas obtenidas a partir de CM combinando dos notas alteradas.
Notas Alteradas
-
F → F♯
C → C♯
F → F♯, C → C♯
-
CM
GM
Dmm
DM
B → B♭
FM
Gmm
Dhm
DhM
E → E♭
Cmm
GhM
DNpM
GhL
B → B♭, E → E♭
B♭ M
Ghm
DNpm
Dhh
2.3. Características Armónicas de las Escalas Heptatónicas Seleccionadas
Para analizar las características armónicas de las escalas heptatónicas seleccionadas podemos utilizar dos generalizaciones del vector de clases de intervalos: el vector de tipos de tricordos y el vector de tipos de tetracordos, los cuales indican, respectivamente, cuántos tricordos y tetracordos de cada tipo contiene la escala considerada. La Tabla 4 muestra estos vectores para las escalas seleccionadas, donde cada uno de sus dígitos corresponde a un tipo de acorde en el orden establecido por Nuño (2021c o, en español, 2020 y 2021a). Así, por ejemplo, los primeros dígitos del vector de tipos de tricordos, de derecha a izquierda, corresponden a las tríadas aumentada, mayor, menor y disminuida. Y los primeros dígitos del vector de tipos de tetracordos, también de derecha a izquierda, corresponden al acorde de séptima disminuida, acorde de séptima de dominante, acorde semidisminuido (o de séptima de sensible) y acorde menor con séptima menor. Los dígitos en negrita corresponden a los tricordos y tetracordos “más comunes”, según el artículo de Nuño (2021b o, en español, 2021d).
Tabla 4. Vectores de Tipos de Tricordos y de Tetracordos para las Escalas Heptatónicas.
Escala
Vector de Tipos de Tricordos
Vector de Tipos de Tetracordos
7-22
111333322-0112212331
000111110220-000110011111111222222-0000011110
7-30a
111212321-3123321321
010001110110-011010011112012101202-2120211110
7-30b
111123212-3213321231
001010110110-011100011110221110022-2210211110
7-32a
022222221-1221224321
000100000110-111212112011011112211-0011101211
7-32b
022222212-1222124231
000100000110-111121221100111121121-0101101121
7-33
111111111-6116611112
011000110000-011110000111111000110-6110630110
7-34
022111111-3333332221
000100000000-211111111111111000110-2222211220
7-35
022002211-3441151330
000000000010-222001122110011000002-1334003110
3. Grafo Parsimónico para las Escalas Heptatónicas Seleccionadas
La Figura 1 es un grafo cíclico circular que he denominado 7-Cíclope, que muestra todas las escalas heptatónicas de los tipos considerados en la Tabla 2, conectadas mediante transformaciones monosemitonales. Así, se pasa de una escala a otra adyacente cambiando una nota un semitono, el cual puede ser ascendente, si giramos en sentido horario, o descendente, si lo hacemos en sentido antihorario. Los números que hay en los extremos de las líneas que conectan las escalas indican las notas inicial y final referidas a las tónicas de estas escalas, donde 1 a 6 representan intervalos justos o mayores, que pueden alterarse mediante ♯ o ♭, mientras que las séptimas mayores y menores se representan mediante Δ y 7, respectivamente. Haciendo una analogía con la carátula de un reloj, cada acorde se ha colocado en una “zona”, que viene definida por “la suma de sus notas”, módulo 12 (Cohn 2012, p. 102). Así, por ejemplo, la escala CM = (C, D, E, F, G, A, B) está en la zona 0 + 2 + 4 + 5 + 7 + 9 + 11 = 2 (mod 12) y, análogamente, la escala B♭ M = (B♭ , C, D, E♭, F, G, A) está en la zona 0. De esta manera, si se sube o baja un semitono una nota de una escala, pasamos a la siguiente zona girando en sentido horario o antihorario, respectivamente. Y las escalas relacionadas por movimiento puramente contrario, como CM y Dhm = (D, E, F, G, A, B♭ , C♯) están en la misma zona (en este caso, 2).
Puesto que los números 7 y 12 son coprimos, en cada zona tenemos justamente una escala de cada tipo. Nótese que las escalas mayores son las únicas que pueden transformarse en otras de su mismo tipo, a la vez que los enlaces entre ellas forman el ciclo de quintas, que es la única circunferencia posible en este grafo (la línea gruesa).
Fig. 1. El 7-Cíclope, con los tipos de escalas heptatónicas considerados en la Tabla 2.
En cuanto a otros diagramas similares, tenemos el desarrollado por Tymoczko (2011, p. 136), el cual incluye las escalas mayores (que llama diatónicas), las menores melódicas (que llama acústicas y cuya tónica es la cuarta justa de la correspondiente escala menor melódica), las menores y mayores armónicas, más otras tres escalas no heptatónicas y con simetría transposicional: la escala de tonos (6-35), la hexatónica (6-20, también llamada aumentada) y la octatónica (8-28, también llamada disminuida semitono/tono), cuyas estructuras interválicas son, respectivamente, 222222, 131313 y 12121212. En este caso, para colocar adecuadamente todas estas escalas se utilizan 36 posiciones angulares que, lógicamente, no pueden coincidir con las zonas consideradas aquí, a la vez que no se indican las notas que cambian de una escala a otra. Así mismo, algunas de estas escalas están repetidas varias veces dentro del diagrama.
Otro trabajo relevante es el publicado por Žabka (2014), que está basado en lo que denomina “series de transición comática”, y que incluye, además de las escalas de la Tabla 2, el par 7-31a/7-31b y las escalas de tonos con una nota enarmónica adicional. Estas escalas las distribuye en tres diagramas diferentes, por lo que no se muestran las conexiones existentes entre algunas de ellas, a la vez que tampoco se indican las notas que cambian de una escala a otra. Por otra parte, la nomenclatura utilizada para algunas de estas escalas es distinta de la empleada aquí.
4. Conclusiones
Siguiendo unos criterios puramente musicales se han seleccionado ocho tipos de escalas heptatónicas. Sus características armónicas se han analizado mediante los vectores de clases de intervalos, de tipos de tricordos y de tipos de tetracordos. Además, se ha desarrollado un nuevo grafo parsimónico, denominado 7-Cíclope, que relaciona todas esas escalas mediante transformaciones monosemitonales. En este grafo destaca claramente el ciclo de quintas, que es la única circunferencia posible que conecta escalas del mismo tipo en este grafo.
En la segunda parte de este trabajo se llevará a cabo un proceso análogo para las escalas pentatónicas y se estudiará la relación acústica existente entre las escalas heptatónicas y pentatónicas consideradas aquí. Además, se incluirá un ejemplo de análisis musical con escalas heptatónicas. Finalmente, para los lectores interesados en un estudio más general de los vectores empleados en este estudio, se recomienda el artículo de Nuño (2022b), recientemente publicado.
Referencias
Balzano, G. 1980. “The Group-Theoretic Description of 12-Fold and Microtonal Pitch Systems”. Computer Music Journal 4 (4), 66–84.
Cohn, R. 1996. “Maximally Smooth Cycles, Hexatonic Systems, and the Analysis of Late-Romantic Triadic Progressions”. Music Analysis 15 (1), 9–40.
Cohn, R. 2012. Audacious Euphony: Chromatic Harmony and the Triad’s Second Nature. New York: Oxford University Press.
Douthett, J., Steinbach, P. 1998. “Parsimonious Graphs: A Study in Parsimony, Contextual Transformations, and Modes of Limited Transposition”. Journal of Music Theory 42 (2), 241–263.
Forte, A. 1973. The Structure of Atonal Music. New Haven: Yale University Press.
Hook, J. 2011. “Spelled Heptachords”. En: Agon, C., et al. (eds.) Mathematics and Computation in Music 2011, pp. 84–97. Heidelberg: Springer.
Nuño, L. 2020. “La Tabla Periódica Musical (1/2).” DIVULGAMAT, Centro virtual de divulgación de las matemáticas, RSME: Real Sociedad Matemática Española, No. 111. Diciembre 2020. https://www.divulgamat.net/index.php?option=com_content&view=article&id=18500&directory=67
Nuño, L. 2021a. “La Tabla Periódica Musical (2/2).” DIVULGAMAT, Centro virtual de divulgación de las matemáticas, RSME: Real Sociedad Matemática Española, No. 112. Enero 2021. https://www.divulgamat.net/index.php?option=com_content&view=article&id=18516&directory=67
Nuño, L. 2021b. Parsimonious Graphs for the Most Common Trichords and Tetrachords. Journal of Mathematics and Music 15(2), 125–139 (2021).
Nuño, L. 2021c. A Detailed List and a Periodic Table of Set Classes. Journal of Mathematics and Music 15(3), 267–287.
Nuño, L. 2021d. “Grafos Parsimónicos para los Tricordos y Tetracordos más Comunes.” DIVULGAMAT, Centro virtual de divulgación de las matemáticas, RSME: Real Sociedad Matemática Española, No. 119. Octubre 2021. https://divulgamat.net/index.php?option=com_content&view=article&id=18666&directory=67
Nuño, L. 2022a. “Parsimonious Graphs for Selected Heptatonic and Pentatonic Scales”. En: Montiel, M., Agustín-Aquino, O.A., Gómez, F., Kastine, J., Lluis-Puebla, E., Milam, B. (eds) Mathematics and Computation in Music. MCM 2022. Lecture Notes in Computer Science, vol 13267. Springer, Cham. https://doi.org/10.1007/978-3-031-07015-0_3
Nuño, L. 2022b. “Type and Class Vectors and Matrices in ℤn. Application to ℤ6, ℤ7 and ℤ12.” Journal of Mathematics and Music. https://www.tandfonline.com/doi/full/10.1080/17459737.2022.2120214
Piston, W. 1988. Harmony. 5th edn. New York: W. W. Norton and Co.
Popley, H. A. 1921. The Music of India. London: Oxford University Press.
Ring, I. 2022 (15 marzo). The Exciting Universe of Music Theory, https://ianring.com/musictheory/scales/
Schönberg, A. 1983: Theory of Harmony. 3rd edn. Berkeley, Calif.: University of California Press.
Tymoczko, D. 2011. A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice. New York: Oxford University Press.
Žabka, M. 2014. “Dancing with the Scales: Subchromatic Generated Tone Systems”. Journal of Music Theory 58 (2), 179–233.
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
1. Introducción
En el artículo de este otoñal octubre vamos a proponer al lector una serie de retos matemático-musicales, que están dirigidos principalmente a alumnos de los últimos cursos de primaria y a los de secundaria. Los encontré por pura casualidad en la excelente página web Get the math [DL22] producida por la organización sin ánimo de lucro Next Generation Learning Challenges [Aut22]. Los retos están diseñados por Manny Domínguez and Luis López, que forman el duo DobleFlo (véase su trabajo en Spotify en https://soundcloud.com/dobleflo). En el vídeo que aparece en la página de presentación, Luis López habla de cómo las matemáticas lo empujaron a seguir una carrera musical en hip-hop y achaca tal hecho a la figura del profesor durante sus años de instituto. En su caso, el profesor de matemáticas y el de música era la misma persona (¡hecho bastante inusual!). No cabe duda de que López estuvo en contacto con una persona que supo aunar ambas disciplinas y transmitirlas con la suficiente pasión como para que alguien quisiese seguir el camino de la música (pero con matemáticas). Ese es el verdadero papel de la divulgación.
Figura 1: Get the math in the music
En ese mismo vídeo, a partir del minuto 3:55 se presenta el primer reto matemático-musical. El reto se le presenta a un grupo de alumnos de instituto y consiste en sincronizar el tempo de dos pistas musicales. Hay varias ideas interesantes que aparecen en el reto. Primero, ha de haber una medida común del tempo para ambas pistas. Una vez fijada, hay que hacer los ajustes necesarios para sincronizar las pistas. El reto se puede encontrar aquí (está en inglés): https://www.thirteen.org/get-the-math/interactives/get-the-math-in-music-take-the-challenge/21/. En esta página se puede meter las soluciones a través de varias pantallas. En la página https://www.thirteen.org/get-the-math/video/get-the-math-in-music-see-how-the-teams-solved-the-challenge/22/ aparece la solución dada por los alumnos, solución que luego es probada en el estudio con DobleFlo. Tras el vídeo de la solución, DobleFlo propone al lector otros retos similares donde hay que mezclar correctamente tres extractos musicales (cada extracto comprende una muestra instrumental y una base rítmica). Esos retos se encuentran en https://www.thirteen.org/get-the-math/interactives/get-the-math-in-music-try-other-music-challenges/23/; véase la figura siguiente.
Figura 2: Retos matemático-musicales
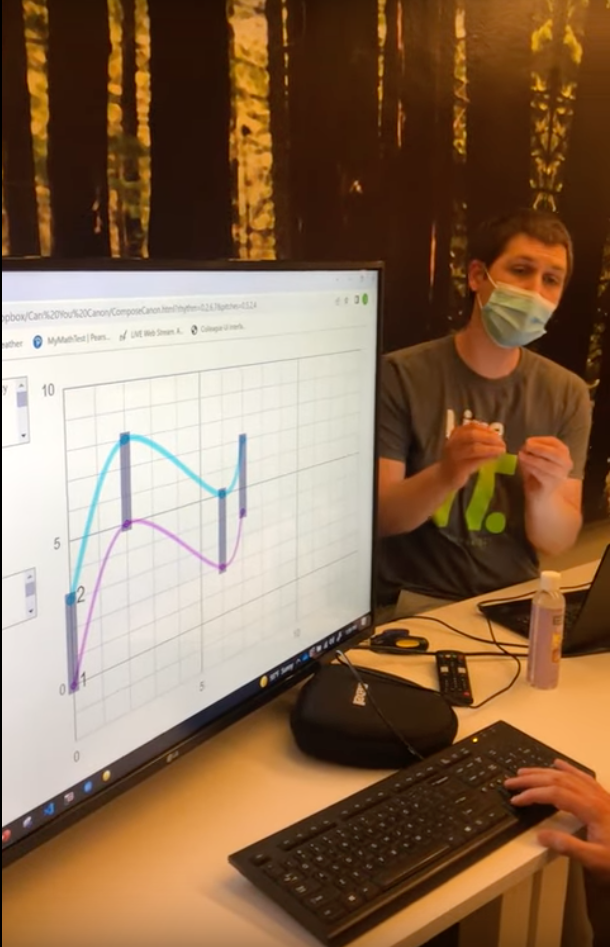
En otra sección de la página Get the math, encontramos una sección interesante, Math in Special Effects, presentada y escrita por Jeremy Chernick, quien trabaja para la compañía J&M Special Effects. Chernick aparece en un vídeo hablando de su trabajo y su experiencia con las matemáticas durante su vida; el vídeo está en https://www.thirteen.org/get-the-math/video/math-in-special-effects-introduction/243/. Durante el primer minuto, Chernick se queja de lo mal que se le daba aprender matemáticas en la escuela y el instituto. Menciona de hecho un defecto de aprendizaje que le dificulta memorizar hechos, en particular, hechos que presentan nexos lógicos entre sí. También menciona que la enseñanza de las matemáticas que tuvo fue altamente memorística y con poco razonamiento. ¿Cómo es tal cosa posible? ¿Cómo puede algo tan creativo y conceptual enseñarse de una manera memorística e irracional (siento que no hay otra palabra más adecuada aquí)? Más adelante en el vídeo, Chernick afirma que ya no tiene miedo a las matemáticas porque ahora las ve como una herramienta para solucionar los problemas que le surgen en el diseño de efectos especiales.
En este vídeo, este diseñador de efectos especiales plantea un reto matemático (ahora ya no musical) que está relacionado con la iluminación de una toma de vídeo. En el reto se investiga la relación entre distancia e iluminación de un sujeto en una toma. El reto está aquí: https://www.thirteen.org/get-the-math/interactives/math-in-special-effects-take-the-challenge/242/.
Figura 3: Retos matemático-musicales
Bibliografía
[Aut22] Varios Autores. Next Generation Learning. https://www.nextgenlearning.org/, consultado en septiembre de 2022.
[DL22] Manny Domínguez and Luis López. Math in music. https://www.thirteen.org/get-the-math/video/get-the-math-in-music-introduction/20/, consultado en septiembre de 2022.
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
La columna de este agosto caluroso está dividida en tres partes. En la primera, haremos unas cuantas reflexiones sobre la divulgación científica en general; en la segunda parte, aplicaremos esas reflexiones a la divulgación científica en el campo de la Teoría Matemática y Computacional de la Música (TMCM en adelante); y, por último, pondremos ejemplos de acciones de divulgación científica que tuvieron lugar en el reciente congreso Mathematics and Computation in Music 22 (MCM22) celebrado en Atlanta bajo la excelente organización de Mariana Montiel de la Universidad Estatal de Georgia (GSU en sus siglas inglesas).
1. Ciencia y divulgación
La ciencia es una aventura intelectual en la que las ideas de progreso y creatividad son esenciales. Además, la ciencia es una parte fundamental de la cultura moderna. El objetivo de la ciencia es construir conocimiento sólido, verificable, y a través de ese conocimiento llegar a la comprensión del mundo. De esa comprensión, surgen aplicaciones asombrosas y ubicuas que transforman nuestra sociedad constantemente. La ciencia, además y como parte de su genésis y praxis, nos plantea dilemas morales y éticos.
Los científicos tienen un compromiso con la sociedad en la que trabajan. La sociedad les ha proporcionado formación y medios para desarrollar su tarea. A cambio, deberían explicar los resultados que obtienen, pero no en forma de publicación en una revista de prestigio o en un congreso especializado, sino en un contexto y en unos términos adecuados para que el gran público entienda su relevancia y aplicaciones. Los científicos tenemos la obligación de divulgar y popularizar la ciencia que producimos. Igual que la universidad nos exige ser buenos profesores, buenos investigadores, buenos gestores, debemos ser también buenos divulgadores (de los sistemas de calidad universitaria hay mucho que hablar y nada bien desde luego). Sin embargo, en general, los científicos no hacen tal esfuerzo en divulgar sus resultados y este esfuerzo debe hacerse a todos los niveles de la educación, desde la educación infantil cuando sea posible hasta los adultos y especialmente en la primaria y secundaria.
Por su parte, la sociedad debería apreciar la naturaleza y los objetivos de la ciencia. Con frecuencia, la sociedad reacciona con resistencia o incredulidad ante los objetivos y resultados de la ciencia. Los científicos, a nuestra vez, no deberíamos reaccionar a tal resistencia con rechazo e indiferencia, como lamentablemente es el caso con harta frecuencia. Antes al contrario, deberíamos crear una diálogo abierto y libre de condescendencia con el gran público.
Mi teoría personal es que parte de esta resistencia reside en lo que el escritor C. P. Snow (1905–1980) llamó la gran división de las dos culturas; aquí por las dos culturas se refiere a las humanidades y a las ciencias, respectivamente. En una famosa conferencia que pronunció en 1959 en el Senate House en Cambridge, hizo una crítica en términos intelectuales y económicos de esa división y sus consecuencias. Desde que tengo uso de razón he presenciado una división inmediata de las personas entre persona de ciencias y persona de letras, división que, por cierto, el propio sistema educativo propicia (aquí en España y en otros muchos países occidentales). La “gente de letras” no conocen los más elementales hechos científicios ni está familiarizada con la más mínima lógica científica. La “gente de ciencia” ignora las grandes obras de la literatura y su capacidad de experiencia emocional y explicación del mundo. En su libro Las dos culturas [Sno77], Snow lo expone con bastante elocuencia. El extracto que reproduzco a continuación se refiere a la actitud de los no científicos ante la ignorancia de los científicos ante la cultura tradicional. En otras partes del libro, se queja amargamente de la situación contraria. Leamos a Snow:
Pero ¿qué ocurre del otro lado? También se han empobrecido —quizás más seriamente porque se enorgullecen de ello. Todavía les agrada fingir que la cultura tradicional es toda la “cultura”, como si no existiese el orden natural. Como si la exploración del orden natural no tuviese interés alguno de suyo ni por sus consecuencias. Como si el edificio científico del mundo físico no fuera, en su hondura intelectual, su complejidad y su coherencia, la obra colectiva más bella y maravillosa de la mente humana. Pero los no científicos no tienen ningún conocimiento del edificio. Aunque quieran tenerlo, no pueden. Es como si todo el grupo fuera incapaz de percibir el sonido de la cuerda inmensa de la experiencia intelectual. Solo que esa sordera no se tiene por naturaleza, sino por educación, o más bien por falta de educación.
Y como no perciben todos los tonos, no saben lo que se pierden. Hacen una mueca de risa piadosa al saber que hay científicos que no han leído jamás una obra importante de la literatura inglesa. Los descartan como especialistas ignorantes. Y sin embargo su propia ignorancia y su propia especialización son igualmente pasmosas. Muchas veces he estado en reuniones de gentes consideradas muy cultas según las normas de la cultura tradicional, y que con sumo placer expresaban su incredulidad ante la ignorancia de los hombres de ciencia. Una o dos veces me he incomodado y he preguntado a los presentes cuál era la segunda ley de la termodinámica. La respuesta fue fría, y también negativa. Sin embargo, yo estaba preguntando algo que es el equivalente científico de “¿Ha leído usted alguna obra de Shakespeare?”
Ahora pienso que si hubiese preguntado algo más simple —como que era la masa, o la aceleración, científicamente equivalente a preguntar ¿Sabe leer?—no más de una entre diez de las personas muy cultas habría sentido que yo hablaba el mismo idioma que ella. Así el gran edificio de la física moderna se va levantando, y la mayoría de la gente más inteligente del mundo occidental tiene de ello más o menos la misma consciencia que habrían tenido sus antepasados neolíticos.
Una manera de romper esta división, este muro invisible pero impermeable, es a través de la divulgación científica. La divulgación es narración, es contar historias, es dotar a los resultados científicos de valor emocional y moral.
2. Divulgación científica en la TMCM
La Teoría Matemática y Computacional de la música (TMCM) es una disciplina científica de pleno derecho. Analiza un fenómeno muy complejo: la música; con herramientas muy potentes: las matemáticas y la computación. La música está llena de patrones, reglas; está altamente estructurada, es compleja, rica en matices, desafiante desde un punto de vista cognitivo, altamente gratificante desde un punto de vista emocional y con importantes funciones sociales (véase [RB03] para mayor desarrollo de estas cuestiones). Las matemáticas es la ciencia que estudia los patrones en abstracto, desde el rigor, la ciencia que describe la estructura a altos niveles de complejidad; es también una disciplina altamente desafiante desde un punto de vista cognitivo. En la evidente convergencia de estas dos disciplinas nace la TMCM.
Y como disciplina, los practicantes de la TMCM tenemos la obligación de hacer divulgación científica. Hay muchas ventajas y facilidades para hacer tal cosa. La música siempre es atractiva para el gran público. Y con frecuencia, conceptos matemáticos simples pueden dar explicación novedosas a fenómenos musicales. Las matemáticas junto con la computación pueden proporcionar maneras muy efectivas y potentes de visualizar la música. Cierto es que el material de divulgación tiene que ser diseñado con creatividad y meticulosidad, además de adaptarlo con precisión al público final.
3. Divulgación científica en el MCM22
En los congresos de nuestro campo, especialmente en los dos últimos, se ha hecho hincapié en la divulgación. En el congreso MCM 22 (https://mcm2022.org/) en particular se realizaron una serie de actividades divulgativas que nos gustaría glosar aquí como muestra del interés y el compromiso de nuestra comunidad con la divulgación científica. En la tarde del 23 de junio de 2022 se llevó a cabo en el Museum of Design Atlanta (MODA; see https://www.museumofdesign.org/) una jornada de divulgación científica y que describimos a continuación.
3.1. Jeremy Kastine y su actividad Can you canon?
Jeremy Kastine, que fue el organizador del evento, presentó una actividad en que los participantes tenían que componer canones monofónicos con ciertas restricciones. Los participantes aprendieron que este problema se puede formular en términos de encontrar los cliques maximales de un grafo. El software con que se construían los cánones fue programado por el propio Kastine.
Figura 1: Jeremy Kastine y su actividad Can you canon?
3.2. Thomas Noll y The Collective Public Fourier Performance
En esta actividad hay tres participantes que controlan los coeficientes de Fourier de una onda sonora variando la altura de ciertas banderas. Estas alturas son captadas por dispositivos móviles, los cuales las transfieren a un ordenador que sintetiza una onda sonora. Se trata de una representación física de la transformada de Fourier. Desde un punto de vista musical, se hace una performance con los participantes.
Figura 2: Thomas Noll and The Collective Public Fourier Performance
3.3. Paco Gómez y los ritmos euclídeos
En esta actividad, presenté algunos resultados sencillos de divisibilidad y los conecté con la teoría del ritmo. De ahí pasamos a tocar con los famosos tubos afinados boomwhacker. Es esta una actividad que permite varios niveles de complejidad que se adaptan fácilmente al nivel del público.
Figura 3: Paco Gómez y Matherhythm or rhythm is a killer
3.4. Luis Nuño y su rueda armónica
Luis Nuño presentó una actividad basada en su rueda armónica, un dispositivo físico que consiste en el tonnetz pasado a coordenadas polares y donde se pueden ver las transformaciones entre distintas escalas.
Figura 4: Luis Nuño y su rueda armónica
3.5. Maria Manonne y su CubeHarmonic
Maria Mannone presentó su CubeHarmonic, un intrumento musical novedoso que emplea el concepto de triada en el tonnetz representado en el cubo de Rubik.
Figura 5: Maria Mannone y su CubeHarmonic
Bibliografía
[RB03] R. E. Radocy and D. J. Boyle. Psychological Foundations of Musical Behaviors. Charles C. Thomas, Springfield, Ill., 2003.
[Sno77] C. P. Snow. Las dos culturas. Editorial: Alianza, 1977.
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
1. Introducción
Esta es la cuarta entrega de la serie Modelos computacionales de ritmo y métrica. En la columna anterior [Góm22b] estudiamos las palabras de Christoffel y su relación con la teoría del ritmo; en particular, vimos cómo convertir palabras de Christoffel en ritmos y las operaciones que se podían hacer sobre estos ritmos. En la segunda entrega [Góm22a] examinamos los métodos de generación y recuento de ritmos, sobre todo los ritmos aksak. Y, finalmente, en esta columna vamos a estudiar las sucesiones de Farey y su relación con la teoría del ritmo.
2. Sucesiones de Farey
Las sucesiones de Farey son representaciones elegantes y útiles de las duraciones relativas en subdivisiones métricas. Una sucesión de Farey de orden n, Fn, es la sucesión de fracciones reducidas que se encuentran en el intervalo [0,1]. En la figura de abajo se ven las sucesiones de Farey desde orden 1 hasta orden 8. Las fracciones se suelen presentar en orden creciente. La primera fracción es siempre y la última . Existen calculadores en línea de las sucesiones de Farey; véase, por ejemplo, Think Calculator [Cal22].
Figura 1: La sucesión de Farey de orden 8
Las sucesiones de Farey presentan una estructura recursiva. En efecto, la sucesión Fn es igual a la sucesión Fn más los dos términos y (este hecho es relativamente fácil de probar). Podemos escribir, pues:
Otras propiedades que cumplen las sucesiones de Farey son:
Si y son dos términos consecutivos de una sucesión de Farey, entonces se cumple que bc - ad = 1;
Si ,, son tres términos consecutivos de una sucesión de Farey, entonces se tiene que = ; la fracción c∕d se dice que es la mediante de las fracciones a∕b y e∕f;
Si n > 1, entonces no hay dos términos consecutivos con el mismo denominador.
Sea |Fn| el cardinal de la sucesión de Farey de orden n y φ(n) la función de Euler, la cual da el número de primos relativos con n. Entonces, se cumple la bonita relación:
En la tabla siguiente se muestras los primeros valores para |Fn|:
Figura 2: Primeros valores de |Fn| (tabla tomada de [Ovs17])
Las sucesiones de Farey son simétricas en el sentido en que la subsucesión que de hasta es la imagen especular de la subsucesión que va desde hasta . En la figura siguiente se ilustra este hecho con la sucesión F5 (la sucesión se presenta en orden decreciente esta vez).
Figura 3: Simetría de las sucesiones de Farey (figura tomada de [Ovs17])
3. Ritmo y sucesiones de Farey
Dado que las sucesiones de Farey de orden n representan todas las fracciones irreducibles en el intervalo [0,1], basta con identificar dicho intervalo con el pulso y entonces tendremos representadas todas las divisiones del pulso. Por ejemplo, F2 = genera la subdivisión en corcheas de una negra. Por otro lado, los tresillos corresponden al conjunto . F3 es la unión de las corcheas y los tresillos: F3 = . La figura de abajo ilustra estos hechos.
Figura 4: Subdivisiones rítmicas asociadas a las sucesiones de Farey (figura tomada de [Boe18])
Se sigue de este razonamiento que las sucesiones de Farey de orden n contiene todos los ataques de los polirritmos en orden creciente para un pulso dado.
Sin embargo, es posible librarse de la restricción de tener que considerar un solo pulso. Una sucesión de Farey puede representar las duraciones de una frase rítmica o de una pieza entera de hecho. Para hacer esto es necesario aumentar el orden de la sucesión (en un modo relacionado con la duración mínima de la pieza en cuestión) y quitar aquellas fracciones que no se correspondan con un ataque en la pieza. Boenn [Boe18] llama a estas sucesiones sucesiones de Farey filtradas.
Otra restricción que se puede eliminar es la del rango de Fn, que hasta ahora es el intervalo [0,1]. La manera de hacerlo es escalar la sucesión original Fn al nuevo rango. Sea [x,y] un intervalo con x < y. Se designa por Fn[x,y] a la sucesión de Farey en [x,y] obtenida escalando Fn en dicho intervalo. Como ejemplo, consideremos F4, que es:
Las sucesiones F4[0,1∕2] y F4[1∕2,1] son entonces:
F4[0,1∕2] =
F4[1∕2,1] =
Es posible ahora considerar la unión de estas dos sucesiones de Farey (el término 1∕2 aparece solo una vez):
F4[0,1∕2] ∪ F4[1∕2,1]
= ∪
=
Nótese que F4[0,1∕2] ∪ F4[1∕2,1 ⊂ F8. Por completitud, F8 es:
Este método de generar nuevas sucesiones a partir de sucesiones de Farey se llama concatenación.
Las sucesiones de Farey son particularmente adecuadas para estudiar los polirritmos. Boenn [Boe18] en su libro estudia la música de varios compositores a través de estas sucesiones, compositores como de Stravinsky (analiza La consagración de la primavera), Messian o Ockeghem (analiza su famosa misa Missa prolationem). En la tabla de abajo se muestran patrones polirrítmicos (dados en notación SNMR) y sus correspondientes sucesiones de Farey filtradas.
Figura 5: Polirritmos y sucesiones de Farey filtradas (figura tomada de [Boe18])
4. Notación SNMR
Cuadro con la notación SNMR:
Figura 6: La codificación SNMR (figura tomada de [Boe18])
Bibliografía
[Boe18] Georg Boenn. Computational Models of Rhythm and Meter. Springer, New York, Berlín, 2018.
[Cal22] Think Calculator. Farey sequences, junio de 2022.
[Góm22a] P. Gómez. Modelos computacionales de ritmo y métrica (II), abril de 2022.
[Góm22b] P. Gómez. Modelos computacionales de ritmo y métrica (III), junio de 2022.
[Ovs17] Valentin Ovsienko. Partitions of unity in SL(2, г), negative continued fractions, and dissections of polygons. Research in the Mathematical Sciences, 5, 10 2017.
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
1. Introducción
Seguimos con la serie Modelos computacionales de ritmo y métrica y en la columna de este mes vamos a examinar la combinatoria de palabras aplicada a la música, en particular a la teoría del ritmo. En el primer artículo [Góm22a] de esta serie tratamos la definición de ritmo desde un punto de vista conceptual así como la presentación de diversos métodos de notación rítmica. En el segundo artículo [Góm22b] se estudiaron métodos de generación y recuento de ritmos, sobre todo los ritmos aksak.
La combinatoria de palabras —combinatorics on words en inglés —es una rama de la matemática discreta que pertenece a su vez al campo de la combinatoria. El campo de la combinatoria de palabras es relativamente nuevo y su objeto de estudio son las palabras y los lenguajes formales, con especial atención a los patrones. La combinatoria de palabras como tal se formaliza modernamente en el libro Combinatorics on words [Lot83], libro escrito por un grupo de matemáticos que tomó el nombre de Lothaire. Sin embargo, hay precedentes tan tempranos como Bernouilli en 1771 con su estudio de las fracciones continuas o los trabajos de Christoffel (1829–1900), de donde toman el nombre las palabras de Christoffel que estudiaremos en la columna de este mes. Para un buen examen histórico de la combinatoria de palabras, véase el artículo de Berstel y Perrin The origins of combinatorics on words [BP07].
La teoría de las palabras de Christoffel empieza a finales del siglo XIX, pero el término no se acuña oficialmente hasta 1990, y es Berstel [Ber90] quien lo hace por primera vez. Desde entonces, las palabras de Christoffel se han estudiado a fondo y hay muchas caracterizaciones y resultados, algunos de los cuales veremos aquí.
2. Palabras de Christoffel
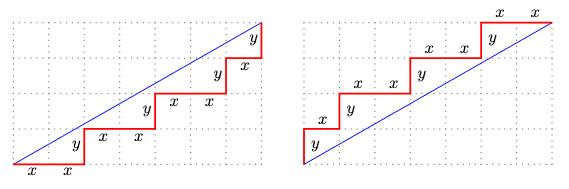
Empezaremos con la definición geométrica de las palabras de Christoffel. Sean a,b dos números naturales tales que su máximo común divisor es 1, esto es, que, salvo el 1, no tienen divisores comunes. Cuando esto ocurre decimos que a y b son primos relativos entre sí o coprimos y es costumbre en el campo de la combinatoria de palabras escribir a ⊥ b. Consideremos a continuación la recta que une (0,0) y (a,b) en el retículo ℤ × ℤ (en lugar de en ℝ2). Llamemos (0,0) → (a,b) al segmento dirigido que une (0,0) y (a,b). El camino inferior de Christoffel, o simplemente el camino inferior, es el camino que se ve en rojo en la parte izquierda de la figura 1. Está definido como sigue:
Es una poligonal de lados paralelos a los ejes que empieza en (0,0) y acaba en (a,b).
La región interior comprendida entre el segmento (0,0) → (a,b) y la poligonal no contiene ningún punto del retículo ℤ × ℤ.
Figura 1: Definición geométrica de las palabras de Christoffel (figura tomada de [BLRS08])
De manera análoga, se define camino superior de Christoffel. En todo lo que sigue, solo consideraremos el camino inferior, por lo que por camino siempre entenderemos el camino inferior de Christoffel. Si ahora asociamos a cada segmento horizontal unidad la letra x y a cada segmento vertical unidad la letra y, obtendremos una sucesión. Esta sucesión es una palabra de Christoffel sobre el alfabeto A = . El conjunto de las palabras formadas con elementos del alfabeto se designa por * y en dicho conjunto está la sucesión vacía, designada por ε. El número de elementos de una sucesión se llama la longitud de la palabra; la longitud de ε es cero y la de una palabra arbitraria la suma del número de símbolos x e y.
Si miramos la figura 1 de nuevo, vemos que (a,b) = (7,4) y que la palabra de Christoffel asociada es C(a,b) = xxyxxyxxyxy; donde C(a,b) es el símbolo para dicha palabra. Obsérvese que la pendiente de la recta que pasa por el segmento (0,0) → (a,b) es 4∕7. C(0,1) = y es la palabra de Christoffel de pendiente +∞; C(1,1) = xy; y la palabra vacía ε no es una palabra de Christoffel porque 0 no es relativamente primo consigo mismo.
Las palabras de Christoffel tienen la bonita propiedad de que toda palabra de longitud 2 o más es la concatenación de dos únicas palabras de Christoffel; véase [BLRS08] para una prueba de este resultado.
Para los lectores amantes de la computación, a continuación presentamos un algoritmo para generar palabras de Christoffel; aparece en el capítulo 6 del libro de Boenn [Boe18].
Figura 2: Algoritmo de generación de palabras de Christoffel (tomado de [Boe18])
3. Generación de ritmos a partir de palabras de Christoffel
3.1. Conversión de palabras en ritmos
La manera de generar ritmos a partir de palabras de Christoffel es bastante directa. Escojamos como alfabeto el conjunto A = , donde haremos que 1 represente una nota y 0 un silencio. Las palabras de Christoffel son ahora sucesiones formadas de por ceros y unos (por bits), que no son otra cosa que representación de ritmos, como vimos en la primera columna de esta serie. Por ejemplo, la palabra C(5,7) es la sucesión xyxyxyyxyxyy, pero cuando se la transforma en un ritmo es [1 0 1 0 1 0 0 1 0 1 0 0] (por claridad de lectura, pondremos los ritmos entre corchetes). Este ritmo no es sino la conocida clave son 6/8 de la tradición musical afrocubana. Un ritmo que proviene de una palabra de Christoffel se llamará ritmo de Christoffel.
3.2. Operaciones sobre ritmos de Christoffel
Matemática y musicalmente, vienen a la mente varias operaciones. La primera es el complementario, esto es, intercambiar los ceros por los unos y viceversa. Si C(a,b) es un ritmo de Christoffel, su complementario se designará por ¬C(a,b). Por ejemplo, si C(3,5) = [1 1 0 1 1 0 1 0], entonces el complementario será ¬C(3,5) = [0 0 1 0 0 1 0 1].
Otra operación, menos obvia de concebir, es la operación ν, que lleva un recuento de las repeticiones en dos elementos consecutivos. ν(C(a,b)) se define como sigue:
El primer bit del ritmo se queda como está en ν(C(a,b));
Si en C(a,b) el k-ésimo bit es igual al anterior, con k = 2,…,a + b, entonces el k-ésimo bit de ν(C(a,b)) es 0; en otro caso, es 1.
Abajo tenemos ejemplos de las operaciones anteriores:
C(3,5) = [1 1 0 1 1 0 1 0];
¬C(3,5) = [0 0 1 0 0 1 0 1];
ν(C(3,5) = [1 0 1 1 0 1 1 1]
¬ν(C(3,5) = [0 1 0 0 1 0 0 0]
Otras operaciones son posibles tales como las operaciones lógicas de o lógico ∨ o de y lógico ∧ (siempre que los ritmos tengan la misma longitud).
La rotación de ritmos de Christoffel es otra operación muy común. La rotación a la izquierda de k posiciones de un ritmo C(a,b), donde 0 ≤ k ≤ a + b, consiste en leer el ritmo desde la posición k hacia la izquierda volviendo al principio cuando se llega a la última posición del ritmo. La rotación a la izquierda de 3 posiciones de C(3,5) es el ritmo [1 1 0 1 0 1 1 0]. Análogamente, se pueden definir las rotaciones a la derecha. Las rotaciones a la izquierda de k posiciones se designan por ϱk(C(a,b)), donde k puede ser positivo o negativo.
Por último, una operación muy natural es la inversión del ritmo, que no consiste en otra cosa que en leer el ritmo de derecha a izquierda empezando por el último bit. Se usa la notación R(C(a,b)) para designar la inversión de C(a,b). La inversión de C(3,5) es R(C(3,5)) = [0 1 0 1 1 0 1 1]. No es muy difícil probar la igualdad:
C(b,a) = R(¬C (a,b))
4. Ritmos de Christoffel en música
Los ritmos de Christoffel se encuentran en la música y en la poesía griega. La poesía griega se basaba en un sistema de pies métricos. Un pie es la unidad de medida métrica y está compuesto por combinaciones de sílabas largas y cortas. Esto se traslada a la música combinando notas largas y cortas. Este sistema de pies métricos se ha usado con frecuencia para analizar la música occidental. La siguiente tabla muestra algunos ejemplos. En la primera columna se encuentra el nombre de los pies rítmicos, después su notación moderna, seguido por la notación SNMR y, por último la correspondiente palabra de Christoffel.
Ritmo
Notación
Notación SNMR
Palabra de Christoffel
Yambo
X
C(1,2) = 110
Troqueo
>
ϱ(C(1,2)) = ν(C(1,2)) = 101
Tribaco
i
C(0,3) = 111
Espondeo
II
C(2,2) = 1010
Anapesto
:I
C(1,3) = 1110
Tabla 1: Ritmos de Christoffel en los pies métricos de la poesía griega
También encontramos ritmos de Christoffel en las claves de las tradiciones musicales africanas y afro-americanas. Una clave es un ritmo que se toca a lo largo de una pieza y que tienes varias funciones, entre ellas la de estabilizador rítmico, marcar el fraseo o establecer referencia temporal. Para más información sobre las claves, véanse [Lon04] o [DGMM+09] y las referencias allí contenidas. La tabla siguiente muestra varias claves de diversas culturales musicales que son ritmos de Christoffel. Los ritmos están escritos en compás de 4/2. El punto en la segunda fila significa concatenación de ritmos.
Ritmo
Notación
Notación SNMR
Palabra de Christoffel
Clave son 2-3
- H - - -
ϱ4(C(11,5) = 0010100010010010
Clave rumba 3-2
- H - I H
ϱ(C(7,3)) ⋅ C(1,1) ⋅ C(3,1) = 1001000100101000
Bossa Nova
- - H - -
ϱ2(C(11,5) = 1001000100100100
Soukous
- -H XI
C(7,3) ⋅ ν(C(5,1)) = 1001001000110000
Tabla 2: Ritmos de Christoffel en los pies métricos de la poesía griega
En la música turca, los ritmos de Christoffel aparecen con mucha frecuencia. La tabla siguiente muestra unos cuantos de esos ritmos.
Figura 3: Ritmos de Christoffel que se encuentran en la música turca (lista tomada de [Boe18])
Para acabar esta columna, vamos a explorar la relación entre los ritmos de Christoffel y los ritmos euclídeos. La siguiente sección es una breve exposición de los ritmos euclídeos y sus propiedades.
5. Ritmos euclídeos
En lo que sigue vamos a seguir la exposición del trabajo Si Euclides lo supiese... se sentiría orgulloso [Góm09] del propio autor de estas líneas.
Los ritmos euclídeos reciben este nombre porque provienen de la aplicación del algoritmo de Euclides. Este algoritmo lo inventó Euclides para calcular el máximo común divisor de dos números y consiste en hacer divisiones sucesivas para hallar el máximo común divisor de dos números positivos (m.c.d. de aquí en adelante). Si queremos hallar el m.c.d. de dos números a y b, suponiendo que a > b, primero dividimos a entre b, y obtenemos el resto r de la división. Euclides se dio cuenta de que el m.c.d. de a y b era el mismo que el de b y r. Para verlo, observemos que al dividir a entre b, hallamos un cociente c y un resto r de tal manera que se cumple que:
a = c⋅b+ r, 0 ≤ r ≤ b- 1
Esta ecuación nos dice que todo divisor común de a y b tiene que serlo también de r. En particular, el m.c.d. de a y b es el m.c.d. de b y r. En efecto, si d es un divisor común de a y b, entonces
y, por tanto, r divide a d. Esto implica que m.c.d(a,b) = m.c.d.(b,r). Pero ¿por qué parar aquí? Aplicamos el mismo argumento a b y r y obtenemos una sucesión de restos estrictamente decreciente. En algún momento esa sucesión alcanza el 0. Se puede probar que el último resto no nulo es precisamente el máximo común divisor de a y b.
Por ejemplo, calculemos el máximo común de 17 y 7. Como 17 = 7 ⋅ 2 + 3, entonces el m.c.d.(17, 7) es igual al m.c.d.(7, 3). De nuevo, como 7 = 3 ⋅ 2 + 1, entonces el m.c.d.(7, 3) es igual al m.c.d.(3, 1). Aquí es claro que el m.c.d. entre 3 y 1 es simplemente 1. Por tanto, el m.c.d entre 17 y 7 es 1 también.
¿Cómo se transforma el cálculo del máximo común divisor en un método para generar patrones distribuidos con regularidad máxima? Ilustraremos el proceso con un ejemplo de ritmos. Supongamos que tenemos 17 pulsos y queremos distribuir de forma regular 7 notas entre los 17 pulsos. Sigamos los pasos dados en la figura 4. Primero, alineamos el número de notas y el número de silencios (siete unos y diez ceros); véase la figura 4-paso (1). A continuación, formamos grupos de 7, los cuales corresponden a efectuar la división de 17 entre 7; obtenemos, pues, 7 grupos formados por [1 0] (en columnas en el paso (2) de la figura 4). Sobran tres ceros, lo cual indica que en el paso siguiente formaremos grupos de 3. Tras formar el primer grupo —véase el paso (3) de la figura 4— nos quedamos sin ceros. Continuamos agrupando de 3 en 3 tomando los grupos de la otra caja, en la que quedan 4 columnas (figura 4-paso (4)). Procedemos así que queden uno o cero grupos; de nuevo, esto es equivalente a efectuar la división de 7 entre 3. En nuestro caso, queda un solo grupo y hemos terminado (paso (5)). Finalmente, el ritmo se obtiene leyendo por columnas y de izquierda a derecha la agrupación obtenida (paso (6)).
Figura 4: El algoritmo de Euclides para generar ritmos regulares.
Aquí cada 1 representa una nota [x] y cada 0, un silencio [.]. El ritmo que hemos generado con nuestra notación se escribe entonces como [x . . x . x . . x . x . . x . x .].
Los ritmos generados por este método se llaman ritmos euclídeos. El ritmo euclídeo de k notas y n pulsos se designa por E(k,n). Otra manera útil de designar un ritmo es mediante las duraciones de las notas en términos de pulsos. El ritmo euclídeo que acabamos de obtener con esta notación se escribe E(7,17) = [x . . x . x . . x . x . . x . x .]= (3232322). Para más información sobre ritmos euclídeos, véase el artículo Si Euclides lo supiese... se sentiría orgulloso [Góm09] del propio autor de estas líneas.
Demain y sus coautores [DGMM+09] probaron formalmente que este algoritmo proporciona, salvo rotaciones, la única manera de distribuir k objetos entre n del modo más regular posible. Aún más, había varios algoritmos propuestos de manera independiente y ellos probaron que, en realidad, eran todos equivalentes al viejo algoritmo de Euclides.
Damos a continuación una pequeñísima muestra de ritmos euclídeos que se encuentran en las músicas tradicionales del mundo.
E(5,8) =[x . x x . x x .]= (21212) es el cinquillo cubano, así como el malfuf de Egipto, o el ritmo coreano para tambor mong P’yon. Si el ritmo se empieza a tocar desde la segunda nota aparece un popular ritmo típico de Oriente Próximo, así como el timini de Senegal. Si se empieza en la tercera nota tenemos el ritmo del tango.
E(5,12) =[x . . x . x . . x . x .]= (32322) es un ritmo muy común en África central que tocan los pigmeos aka. Cuando se toca desde la segunda nota es, entre otros, la clave columbia de la música cubana y el ritmo de la danza chakacha de Kenya.
E(5,16) =[x . . x . . x . . x . . x . . . ]= (33334) es el ritmo de la bosa-nova de Brasil. Este ritmo se toca a partir de la tercera nota.
Existen cerca de dos centenares de ritmos de músicas del mundo documentados que son generados por el algoritmo de Euclides. De nuevo, véase el artículo The distance geometry of music de Demain y sus coautores [DGMM+09].
He aquí una lista de las principales propiedades de los ritmos regulares o ritmos euclídeos:
Los ritmos euclídeos tienen solo una o dos duraciones. En el caso de dos duraciones, estas difieren exactamente en una unidad. Por ejemplo, en este ritmo euclídeo (21212) hay dos duraciones de valor 2 y 1.
Cuando el número de notas no es primo relativo del número de pulsos, los ritmos euclídeos están formados por la repetición de un patrón. En caso contrario, el ritmo está compuesto por un patrón repetido un número máximo de veces más un único patrón más pequeño, que además es subpatrón del patrón que se repite.
Los patrones que forman los ritmos euclídeos son a su vez euclídeos. Esto crea una jerarquía de ritmos euclídeos anidados.
La rotación de un ritmo euclídeo es también euclídeo. Esto es consecuencia de que los ritmos euclídeos maximizan las distancias intercordales entre las notas y dichas distancias no cambian con las rotaciones.
Tomar el complementario de un ritmo euclídeo (esto es, intercambiar ceros por unos) devuelve un ritmo euclídeo.
6. Ritmos de Christoffel y ritmos euclídeos
Boenn prueba en su libro [Boe18] que si, dados a,b con a ⊥ b, existe un k ∈ ℕ tal que a-kb = 1, entonces el ritmo de Christoffel C(a,b) es igual al ritmo euclídeo E(b,a + b). Aquí por E(b,a + b) nos referimos al ritmo obtenido directamente del algoritmo de Bjorklund expuesto más arriba en la figura 4. En el caso en que no se cumpla la condición anterior, el ritmo de Christoffel C(a,b) es igual a una rotación del ritmo euclídeo E(b,a + b). Boenn presenta la siguiente tabla de ritmos euclídeos y sus correspondientes ritmos de Christoffel para ilustrar los resultados mencionados.
Figura 5: Ritmos euclídeos que son ritmos de Christoffel (figura tomada de [Boe18])
7. Notación SNMR
Cuadro con la notación SNMR:
Figura 6: La codificación SNMR (figura tomada de [Boe18])
Bibliografía
[Ber90] Jean Berstel. Tracé de droites, fractions continues et morphismes itérés. Mots, pages 298–309, 1990.
[BLRS08] Jean Berstel, Aaron Lauve, Christophe Reutenauer, and Franco Saliola. Combinatorics on Words: Christoffel Words and Repetition in Words. American Mathematical Society, Rhode Island, USA, 2008.
[Boe18] Georg Boenn. Computational Models of Rhythm and Meter. Springer, New York, Berlín, 2018.
[BP07] Jean Berstel and Dominique Perrin. The origins of combinatorics on words. European Journal of Combinatorics, pages 996–1022, 2007.
[DGMM+09] Erik D. Demaine, Francisco Gomez-Martin, Henk Meijer, David Rappaport, Perouz Taslakian, Godfried T. Toussaint, Terry Winograd, and David R. Wood. The distance geometry of music. Computational Geometry: Theory and Application, 42(5):429–454, 2009.
[Góm09] Paco Gómez. Si Euclides lo supiese... se sentiría orgulloso. http://www.upm.es/sfs/Rectorado/Vicerrectorado\%20de\%20Investigacion/Oficina\%20de\%20Transferencia\%20de\%20Resultados\%20de\%20Investigacion\%20(OTRI)/Divulgacion/documentos/Si_Euclides.pdf, Noviembre, 2009.
[Góm22a] P. Gómez. Modelos computacionales de ritmo y métrica (I). https://www.divulgamat.net/index.php?option=com_content&view=article&id=18789&directory=67, abril de 2022.
[Góm22b] P. Gómez. Modelos computacionales de ritmo y métrica (II). https://www.divulgamat.net/index.php?option=com_content&view=article&id=18810&directory=67, abril de 2022.
[Lon04] Justin London. Hearing in Time. Oxford University Press, Oxford, England, 2004.
[Lot83] M. Lothaire. Combinatorics on words. Addison-Wesley Publishing Co., Reading, Massachusetts., 1983. Encyclopedia of Mathematics and its Applications, vol. 17.
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
1. Introducción
En esta segunda columna de la serie Modelos computacionales de ritmo y métrica, vamos a tratar el recuento y la generación de ritmos con técnicas combinatorias.. En la primera columna [Góm], hicimos una breve recensión de los dos primeros capítulos del libro Computational Models of Rhythm and Meter de Boenn [Boe18]. En el primer capítulo se examinaba la definición de ritmo desde un punto de vista abstracto y filosófico; en el segundo, se definió la notación SNMR.
2. Recuento de listas
Esta sección tendrá un carácter indagatorio y orgánico. Empezamos considerando un entero positivo n > 1. Este entero representará el número total de pulsos de nuestro ritmo. Asociado a todo ritmo, tenemos k, otro entero positivo con 1 ≤ k ≤ n, que representa las notas del ritmo o ataques. Así, el ritmo
lo representamos por la lista R1 = (2,2,2,3). Marcamos en negrita la palabra lista como definición, la cual quiere decir que el orden de los elementos es importante y distingue entre listas (ritmos). Así, el ritmo R2 = (3,2,2,2) tiene un orden distinto de los elementos y es, por tanto, una lista y un ritmo distintos.
2.1. Permutaciones sin y con repetición
Investiguemos las listas un poco más en abstracto (el lector se lo merece). Tomemos un conjunto A = de n elementos donde los elementos son distintos entre sí (esto es, ai≠aj si i≠j). ¿Cuántas listas distintas se pueden formar con los elementos de A? Este es un argumento clásico. Para el primer elemento de la lista, tenemos n posibilidades, los n elementos de A. Para el segundo elemento, dado que no podemos usar el elemento de la primera posición, hay n - 1 posibilidades. Razonando así hasta completar la lista entera, llegamos a que hay n ⋅ (n - 1) ⋅… ⋅ 2 ⋅ 1. El número anterior se llama factorial de n y se escribe
Este argumento se puede ilustrar con el siguiente árbol, donde hemos hecho que A = :
El número de listas formadas por un conjunto de n elementos no repetidos se llama permutaciones sin repetición y se designa por Pn. Por lo visto antes, Pn = n!.
¿Qué ocurre si a continuación eliminamos la restricción de la repetición? Supongamos que tenemos un conjunto A de n elementos formado como sigue:
donde n = k1 + k2 + … + km. ¿Cuántas listas distintas se pueden formar con los elementos de A? Si hay repetidos, esto quiere decir que las permutaciones entre los elementos repetidos del mismo tipo dará lugar a la misma selección. Las repeticiones se quitan dividiendo por las permutaciones de la repetición. Por tanto, el número de listas ordenadas formadas con elementos de A, donde hay m grupos de elementos repetidos es:
Este número se designa por PRnk1,…,km, donde k1,…,km son los elementos repetidos
En el caso del ritmo de arriba R1 = (2,2,2,3), está claro que el conjunto de listas distintas es:
de las cuales hay 4. Si calculamos ese número, obtenemos PR43 = = = 4, como era de esperar.
3. Los ritmos aksak
Los ritmos aksak son ritmos que tienen solo dos duraciones posibles en términos de distancias, 2 o 3, y han de contener al menos un 2 y al menos un 3. Este tipo de ritmos aparecen en varias tradiciones musicales, entre ellas la música turca o la música búlgara. Autores como Simha Arom [Aro04], Brăiloiu [Bra51], Cler [Cle94], y en conexión con los ritmos euclídeos Demain y coautores [DGMM+09]. Arom clasificó los ritmos aksak para valores del número de pulsos n entre 5 y 29 y proporcionó una clasificación teórica. En su clasificación de ritmos aksak delinea tres categorías:
Un ritmo aksak se dice que es auténtico si n es primo.
Cuando n es impar pero no es primo, el ritmo aksak es llamado quasi-aksak.
En caso de que n sea par, el ritmo aksak se denomina pseudo-aksak.
A continuación listamos algunos ritmos aksak junto con sus categorizaciones (los representamos con la notación de notas y silencios, la notación de distancias y la notación SNMR):
Ritmos aksak auténticos:
[×⋅×⋅ ⋅ ]= (23))=I-, ritmo que se encuentra en la música clásica y en la música de entre otros Grecia, Macedonia, Namibia o Ruanda.
[×⋅×⋅×⋅ ] = (223)=II-, ritmo que se encuentra en la música de Bulgaria, Grecia, Sudán y Turquía.
[×⋅ ⋅×⋅ ⋅×⋅ ⋅×⋅ ]=(3332)=—I, ritmo que puede oír en la música del sur de la India.
[×⋅×⋅×⋅×⋅×⋅ ⋅ ]= (22223), ritmo que se encuentra en Bulgaria, el norte de la India y en Serbia, por nombrar unos pocos ejemplos.
Los ritmos [×⋅ ⋅×⋅×⋅ ⋅×⋅×⋅ ⋅ ]=(32323)=-I-I- y [×⋅×⋅×⋅×⋅×⋅×⋅ ⋅ ]=(222223)= =IIIII- se encuentran en la música de Macedonia.
Otros ritmos aksak auténticos de la tradición búlgara son: (3232322), (22222223), (32232232), o (323232323).
Como ejemplos de ritmos quasi-aksak tenemos:
[×⋅×⋅×⋅×⋅ ⋅ ]=(2223)=III-, que se pueden escuchar en la música de Grecia, Macedonia, Turquía o Zaire.
El ritmo búlgaro [×⋅×⋅×⋅×⋅×⋅×⋅×⋅ ⋅ ]=(2222223)=IIIIII-.
Por último, los siguientes son ritmos pseudo-aksak:
[×⋅ ⋅×⋅ ⋅×⋅ ]=(332)=–I, ritmo que se encuentra con frecuencia, por ejemplo, en la música de África central, Grecia, India, Latinoamérica, África del oeste o Sudán.
[×⋅ ⋅×⋅×⋅ ⋅×⋅×⋅ ]=(32322)=-I-II, que se encuentra en música de Macedonia o Sudáfrica.
Sea R un ritmo aksak de n pulsos con r doses y s tres. El número de ritmos aksak que hay con esos r doses y s treses es:
Además, se cumple la siguiente relación entre n,r y s:
Esta última relación es una ecuación diofántica y se puede usar para generar y contar ritmos aksak. Una ecuación diofántica es una ecuación de la forma c = ax + by, donde a,b,c son números enteros. El siguiente teorema determina cuándo hay solución y cuando existen cómo se calculan las soluciones. Cuando hay solución, existen infinitas soluciones como vemos en el enunciado del teorema.
Teorema. Resolución de ecuaciones diofánticas. Sean a,b,c tres números enteros, y sea d = mcd(a,b). Se considera la ecuación diofántica c = ax + by. Entonces:
(1) Si d no divide a c, entonces la ecuación diofántica no tiene solución. (2) Si d divide a c, entonces la ecuación diofántica tiene infinitas soluciones de la forma
x = x0 + m,
y = y0 -m
donde m ∈ ℤ y x0,y0 son soluciones particulares de la ecuación diofántica.
Aplicando el teorema a la relación (1) de arriba, vemos que el máximo común de 2 y 3 es 1 (son primos ambos números) y, por tanto, la ecuación (1) siempre tiene solución por el apartado (2) del teorema. La solución particular es, por ejemplo, x0 = -n,y0 = n, ya que 2x0 + 3y0 = -2n + 3n = n. Se sigue que la solución general es:
Fijado n, basta encontrar los valores de m que dan valores positivos de x,y (recuérdese que un ritmo aksak exige que haya al menos un 2 y un 3). Pongamos el ejemplo de los ritmos aksak de n = 17 pulsos. Según el teorema, las soluciones de x e y son, respectivamente, x = -17 + 3m,y = 17 - 2m. El valor m = 6 es el primer valor para el que x e y son positivos. La taba siguiente muestra los resultados:
m
x = -17 + 3m
y = 17 - 2m
Ritmo
SNMR
4
1
5
(233333)
I- - - - -
5
4
3
(2222333)
I I I I - - -
7
1
2
(22222223)
I I I I I I I -
Tabla 1: Ritmos aksak de 17 pulsos
4. Combinaciones sin y con repetición
La diferencia entre una lista y un conjunto es que en la primera el orden importa y en el segundo no. En los conjuntos el orden no importa; de hecho, la definición de conjunto habla de una colección no ordenada de elementos. Sea A = un conjunto de n elementos distintos. El número de listas de tamaño n es, como sabemos, Pn = n!. Si ahora queremos contar el número de subconjuntos tenemos que usar argumentos adicionales para contarlos.
En primer lugar, vamos a estudiar cómo contar el número de listas de tamaño k, donde 1 ≤ k ≤ n. Usando el argumento de más arriba, tenemos n posibilidades para la primera posición de la lista, n - 1 para la segunda y, siguiendo este proceso, tendremos n - k + 1 para la posición número k. Por tanto, el número final será n ⋅ (n - 1) ⋅… ⋅ (n - k + 1). Este número se llama variaciones sin repetición de n tomados de k en k o más corto V n,k. Este número se puede escribir como:
Continuemos. Sea L = (ai1,…,aik) una de esas listas. Cuando esta lista se transforma en un subconjunto, cualquier permutación de L da lugar al mismo subconjunto. Hay k! permutaciones de L y, por tanto, el número de subconjuntos de tamaño de k de A, al que llamaremos Cn,k, es:
Se llaman combinaciones sin repetición de conjuntos a los subconjuntos de tamaño k formados con los elementos de un conjunto dado, donde se supone que en el conjunto no hay elementos repetidos. Se designarán por Cn,k o por (n k) .
Por último, pedimos al lector que trate de resolver la ecuación
donde n,k son números enteros no negativos.
¿Alguna idea? He aquí una ingeniosa idea para resolverla. Consideremos el conjunto formado por un palote ∣ y un signo +. Queremos formar todas las listas distintas con n palotes y k - 1 signos más. Como los palotes y los signos más son indistinguibles entre sí, las listas difieren en la posición de los palotes y signos más. Cada lista da lugar a la solución de la ecuación x1 + x2 + … + xk = n sin más que contar los palotes entre dos signos más consecutivos. Y viceversa, una solución de x1 + x2 + … + xk = n da lugar a una lista de palotes y signos más. Vamos a contar esas listas pues. En vista de lo aprendido arriba, hay Pn+k-1 = (n + k - 1)! listas. Como se repiten los palotes, de los que hay nk, y las signos más, de los que hay k - 1, tendremos que dividir por n! y (k - 1)!. Así que el número de las listas es:
que son las combinaciones de n + k - 1 tomadas de k - 1 en k - 1.
5. Particiones de enteros y ritmos
Dado un ritmo de n pulsos, las soluciones positivas de la ecuación x1 + x2 + … + xk = n nos da todos los ritmos de k notas. La sucesión de distancias de ese ritmo sería sencillamente R = (x1,x2,…,xk). La siguiente tabla muestra cómo se generan ritmos a partir de esta ecuación:
x1
x2
x3
x4
x5
Ritmo
SNMR
5
(5)
H˜-
4
1
(41)
H-
3
2
(32)
- I
3
1
1
(311)
- . .
2
2
1
(221)
I I .
2
1
1
1
(2111)
I . . .
1
1
1
1
1
(11111)
. . . . .
Tabla 2: Las particiones de 5 y los ritmos asociados
Dado un ritmo R = (x1,x2,…,xk), donde los xi son positivos todos, hay
ritmos posibles con esa configuración de distancias. Por ejemplo, del cuarto ritmo de la tabla de arriba (3,1,1) hay 3!∕2! = 3 ritmos distintos, que son (3,1,1),(1,3,1),(1,1,3). Obsérvese que aquí k = 3 porque x4 = x5 = 0. Cuando todas las xi son diferentes, el número de ritmos es simplemente k!.
6. Notación SNMR
Cuadro con la notación SNMR:
Figura 1: La codificación SNMR (figura tomada de [Boe18]
Bibliografía
[Aro04] Simha Arom. L?aksak: Principes et typologie polyphony and polyrhythm. Cahiers de Musiques Traditionnelles, pages 12–48, 2004.
[Boe18] Georg Boenn. Computational Models of Rhythm and Meter. Springer, New York, Berlín, 2018.
[Bra51] C. Brailoiu. Le rythme aksak. Revue de Musicologie, pages 71–108, 1951.
[Cle94] J. Cler. Pour une théorie de l?aksak. Revue de Musicologie, pages 181–210, 1994.
[DGMM+09] Erik D. Demaine, Francisco Gomez-Martin, Henk Meijer, David Rappaport, Perouz Taslakian, Godfried T. Toussaint, Terry Winograd, and David R. Wood. The distance geometry of music. Computational Geometry: Theory and Application, 42(5):429–454, 2009.
[Góm] P. Gómez. Modelos computacionales de ritmo y métrica (I)
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
1. Introducción
En las siguientes columnas de matemáticas y músicas vamos a tratar de un tema apasionante: los modelos computacionales del ritmo y la métrica. Este tema ya ha sido tratado en otros artículos de esta columna. Por ejemplo, las medidas matemáticas de la síncopa ([Góm11] y siguientes y también [Góm18b]); medidas de complejidad rítmica ([Góm17] y siguientes); y ritmos euclídeos [Góm18a]. Haremos un examen de esta área a la luz de un libro de 2018, escrito por Georg Boenn, profesor del Departamento de Música de la Universidad de Lethbridge (Alberta, Canadá). Ese libro se llama nada más y nada menos que Computational Models of Rhythm and Meter [Boe18] y la portada se puede ver en la imagen de abajo.
Figura 1: Portada del libro Computational Models of Rhythm and Meter [Boe18]
Esta serie de artículos sobre el tema en cuestión es a la vez una revisión crítica del libro de Boenn y una exploración en sí misma de los modelos computacionales del ritmo y la métrica.
El libro está dividido en varios capítulos que cubren varias áreas de este tema:
El capítulo 1 es una introducción en que explica la estructura del libro.
El capítulo 2 se titula Phenomenology of rhythm and meter y constituye una reflexión filosófica sobre el fenómeno del ritmo y de la métrica.
En el tercer capítulo, el autor sienta las bases de notación para el resto del ritmo. Describe las principales notaciones del ritmo. En este capítulo, ya trata algunas consecuencias cognitivas del ritmo y analiza el fenómeno de la agrupación rítmica. Al final del capítulo, presenta ejemplos musicales reales (cosa que hace a lo largo de todo el libro).
Los capítulos 4 a 7 versan sobre los modelos computacionales y matemáticos del ritmo y la métrica. El capítulo 4 trata de la agrupación rítmica; el 5, del uso de la rueda de Burrows-Wheeler como herramienta de análisis rítmico así como de composición; el 6, es un estudio de los ritmos de Cristoffel; el 7, trata las sucesiones de Farey.
Los dos últimos capítulos, el 8 y el 9, es un profundo estudio de la métrica, la percepción del tiempo y la cuantización rítmica.
Boenn acompaña su libro de un proyecto de código abierto llamado Chunking (https://github.com/gboenn/chunking), donde se pueden encontrar los algoritmos más relevantes presentados en el libro.
En esta primera columna glosaremos los capítulos 2 y 3 del libro de Boenn.
2. ¿Qué es el ritmo?
“Hay una continuidad causal en la música”. Con esta poderosa afirmación comienza el capítulo 2 del libro de Boenn. En efecto, con una prosa concisa y abstracta, el autor describe cómo el sonido es causa y efecto. Argumenta que un sonido produce un efecto que es a su vez causa del siguiente, cómo el fluir de los sonidos teje una red de relaciones causa-efecto. Todo esto tiene un efecto en nuestra mente en forma de una compleja red de expectativas musicales. Estas expectativas crean entre otras cosas, fuerzas musicales, la tensión y el reposo musicales, en cuya dialéctica se basa mucha de la música existente. Boenn afirma, en referencia a que “si en tiempo de ejecución, esas fuerzas se equilibran por los sonidos durante el paso del tiempo, el fin último de la unidad se habrá alcanzado y la experiencia de la belleza surgirá” (página 7).
A continuación, Boenn argumenta que el ritmo está en el centro de esta causalidad y lo hace en su calidad de agente organizador de los eventos musicales. En particular, apela al hecho de que la organización rítmica está relacionada directamente con los modos perceptuales y cognitivos del oyente. Dicha organización temporal de los eventos musicales acaba en última instancia creando significado musical en el oyente. Este autor hace una comparación que me parece particularmente acertada: “el ritmo es a la música lo que la articulación es al lenguaje”.
En este capítulo también se aborda el papel del ritmo desde el punto de vista del compositor —como creador de la organización del material musical a través del ritmo—y del intérprete —como transmisor y a la vez oyente también del material musical—.
Tras esta introducción de tipo filosófica, el autor se enfrenta a la definición de ritmo. Como muchos otros autores, arranca de la idea de una sucesión ordenada de sonidos en el tiempo. En concreto, Boenn se refiere a pulsaciones quasi-isócronas, haciendo referencia aquí a que lo que se percibe como isócrono, cuando se mide con precisión, resulta no serlo. Se admite el evento isócrono dentro de unos límites temporales y perceptuales. También examina el papel del tempo como elemento que configura la percepción del ritmo, hecho bien conocido. El tempo tiene un papel importante en la percepción del significado musical del ritmo. Si el tempo es demasiado lento, entonces los eventos no se conectan bien entre sí; si es demasiado rápido, los eventos no se perciben como una unidad. Véase el libro de Justin London [Lon04] para un excelente análisis de esta cuestión.
Para Boenn, el metro es “la reiteración cíclica de un ritmo simple” (página 8). Como se puede ver, este autor ha optado por una definición abstracta, más bien buscando que sea operativa y aplicable a una gran variedad de situaciones. Imagino que algunos autores se quejarían de una cierta falta de matiz en la definición. Sin duda, para los propósitos de este libro, que son ambiciosos, no obstante, tiene la potencia conceptual suficiente. El autor advierte que los pulsos que constituyen una métrica pueden ser (quasi-)isócronos o no isócronos.
Un polirritmo es la superposición de ritmos (página 8). De esta superposición salen patrones musicales que se pueden describir en términos de duración, acento, agrupación, fraseo, timbre, alturas o cambios de armonía. El alineamiento con el metro, que determina las partes fuertes, refuerza la sensación de métrica.
En la sección 2.3 de su libro, Boenn se pregunta en qué sentido tiene una pieza forma orgánica. Aquí, tomando una cita de Schoenberg, el autor construye una comparación entre una pieza musical y un organismo vivo (lo apoya incluso etimológicamente). Un organismo vivo nace, vive y muere; una pieza musical tiene una introducción, un desarrollo y una conclusión o cierre. Como ocurre en la biología, donde hay órganos pequeños que contribuyen a crear órganos mayores, una pieza musical está formada por partes pequeñas que contribuyen a un todo musical.
3. La notación del ritmo
En el capítulo 3, Boenn estudia la notación del ritmo, tanto desde un punto de vista teórico como práctico, aplicándolo a diversas tradiciones musicales. Presenta el llamado SNMR o notación abreviada de ritmos musicales (shorthand notation for musical rhythms en sus siglas inglesas). Es una forma simple y operativa de anotar ritmos y métricas; el autor presenta una extensión del sistema estándar de SNMR (que está basado en el trabajo del percusionista suizo Giger). El SNMR está basado en la presencia de un pulso y no en las convenciones habituales de la notación musical occidental. Otra ventaja de esta notación es que se puede escribir en texto y en ASCII con suma facilidad.
En la sección 3.2, el autor hace una revisión bibliográfica de las principales notaciones que se encuentran en la práctica musical. Lo hace desde un punto de vista histórico, comenzando con la notación de la música árabe y acabando con las notaciones modernas (notación de caja, círculo, etc.).
Para describir su sistema SNMR, Boenn empieza por la siguiente codificación de ritmos (tomada del trabajo de Giger), llamada ritmoglifos:
Figura 2: Los ritmoglifos de Giger
donde los unos representan ataques de notas y los ceros silencios. Estos elementos básicos o primitivas del ritmo son llamados grupos (Boenn usa la palabra inglesa chunk).
A continuación, vemos patrones más complejos como consecuencia de la combinación de diferentes ritmoglifos.
Figura 3: Combinación de ritmoglifos
Originalmente, los ritmoglifos contienen los símbolos de un triángulo y un cuadrado, que no son imprimibles por el código ASCII. Con el fin de hacer el sistema de notación accessible en modo texto, Boenn sustituye estos dos símbolos por otros y amplía el catálogo de símbolos para recoger combinaciones complejas de ritmos. La tabla final es:
Figura 4: La codificación SNMR
Obsérvese que se supone que la unidad mínima del pulso es la corchea. Posteriormente, incluye divisiones rítmicas de la corchea. En otra tabla, se muestran tales subdivisiones rítmicas. El sistema consiste en poner el número que marca la subdivisión delante de la codificación SNMR.
Figura 5: La codificación SNMR de subdivisiones rítmicas
En el resto del capítulo, el autor ilustra la potencia del sistema de notación SNMR en varias músicas y compositores, que van desde la música Ewe, la música latinoamericana, los ritmos de la poesía griega, Messian, Beethoven, Mussorgsky, o Debussy. En la figura de abajo, vemos la notación SNMR aplicada a claves de la tradición africana y latinoamericana. La segunda columna marca las distancias entre ataques de notas en un compás de 16 semicorcheas (o equivalentes).
Figura 6: La codificación SNMR
Como se puede ver, el sistema SNMR es muy práctico para la transcripción, para el procesamiento computacional, para la visualización de los grupos dentro del ritmo, pero no tanto para la interpretación.
Bibliografía
[Boe18] Georg Boenn. Computational Models of Rhythm and Meter. Springer, New York, Berlín, 2018.
[Góm11] P. Gómez. Medidas matemáticas de la síncopa - I, octubre de 2011.
[Góm17] P. Gómez. Medidas de complejidad rítmica - I, octubre de 2017.
[Góm18a] P. Gómez. Ritmos euclídeos y ritmos equilibrados, marzo de 2018.
[Góm18b] P. Gómez. Más sobre medidas de síncopas, mayo de 2018.
[Lon04] Justin London. Hearing in Time. Oxford University Press, Oxford, England, 2004.
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
1. El infinito
Con frecuencia reflexiono sobre las similitudes y las diferencias entre las matemáticas y la música. Creo que una de las diferencias más notables es la presencia del infinito. El infinito está omnipresente en las matemáticas. Todo se puede llevar a extremos infinitos. El infinito lo encontramos en los números naturales, en los enteros, en los racionales; por supuesto, en los reales y en los complejos. Cualquier espacio de funciones va a ser infinito así como muchas estructuras discretas. Por ejemplo, en computación se estudia la complejidad de los algoritmos en función del tamaño n de la entrada (el número de datos de entrada). Esto podría parecer que es finito y, aunque lo es, es necesario estudiar la complejidad cuando n tiende a infinito, la llamada complejidad asintótica. Más ejemplos de la presencia del infinito en las matemáticas se pueden encontrar fácilmente.
Así, pues, el infinito es ubicuo en las matemáticas. ¿Y en la música? Parece que no, que la música tiene una naturaleza esencialmente finita. Para empezar, el universo de frecuencias es finito. El oído humano puede captar frecuencias entre 20 Hz y 20.000 Hz. Fuera de este rango la música, sencillamente, no ocurre. En cuanto al ritmo, algo similar ocurre. Las duraciones que podemos percibir son finitas, aunque es asombroso que el oído humano, especialmente el de un músico experto, pueda detectar diferencias en ritmos del orden de milisegundos. La memoria melódica es corta también así como la armónica. Véanse [Deu07, Deu12, Ben06] para más información sobre los mecanismos perceptuales de la música en humanos.
El ser humano parece ser en su vertiente perceptual un ser finito, de capacidad perceptual finita, pero en cambio es capaz de trabajar y concebir el infinito cuando contempla este desde un punto de vista matemático, como abstracción o como concepto. Creo que esta es una diferencia fundamental entre las matemáticas y la música.
2. Belleza
Hay algo que une a las matemáticas y a la música: su capacidad para generar belleza. Ambas disciplinas producen bellezas de diversas formas, que algunas veces son coincidentes y otras claramente no. Una de las principales formas en las matemáticas viene dada por la belleza que produce el entendimiento. Cuando un problema matemático se resuelve con claridad y profundidad, genera belleza. La prueba de Euclides de que hay infinitos números primos es bella sin lugar a discusión. Hay una estética, un sentido de la belleza, en la producción de resultados matemáticos. Con frecuencia los matemáticos hablamos de la belleza y la elegancia de una prueba, que es a la vez una combinación de la originalidad de las ideas y la elocuencia de la forma. En la música, la belleza viene dada por la propia estructura de la música y por su efecto cognitivo, perceptual, emocional y cultural.
3. La belleza de las matemáticas y la música - Charla TED de Marcus Miller
En la columna de hoy queremos glosar la charla de Marcus Miller titulada The beauty of mathematics and music (La belleza de las matemáticas y la música) y que está disponible más abajo. La razón de nuestro interés es que habla de los temas de esta columna: las matemáticas, la música, el infinito y la belleza. Marcus Miller es músico talentoso, virtuoso del saxofón, que empezó a tocar a los nueve años de edad y a los trece ya estaba en el circuito profesional del jazz. Además, de eso fue a la Universidad de Harvard donde obtuvo un grado en matemáticas. Véase su página web [Mil22] para más información sobre su fascinante biografía.
Figura 1: The beauty of mathematics and music - Marcus Miller
En los primeros minutos, Miller dice lo siguiente (en inglés original y luego mi traducción):
Hello I’m here today to talk to you about beauty in music and in mathematics. However, in order to get to the big takeaway, we are going to have to take two cold showers together, that is to say, we are going to have to address two sticking points that typically arise in this discussion. First cold shower is that most people are terrified of mathematics. For many of you at some point someone pointed a finger at you and told you that you weren’t smart enough to understand it or perhaps that you didn’t really need math in the real world so you were fine not knowing it. Often, that person was you.
(Hola, estoy aquí hoy para hablaros sobre la belleza en la música y las matemáticas. Sin embargo, antes de llegar a esa gran cuestión, vamos a tener que darnos dos duchas de agua fría juntos; es decir, vamos a tener que superar dos escollos que típicamente aparecen en esta discusión. La primera ducha de agua fría es que la mayor parte de la gente se horroriza ante las matemáticas. Para muchos de vosotros en algún momento alguien os señaló con el dedo y os dijo que no erais los suficientemente listos para entenderlas o quizás que en realidad no necesitabais matemáticas en el mundo real de modo que estaba bien si no las sabíais. Con frecuencia, esa persona eras tú.)
Con esta pequeña introducción, Marcus Miller trata el problema de la autoestima matemática y de la enseñanza de las matemáticas. Sin embargo, esta vez no señala como culpables a los profesores (que con frecuencia lo son) o al sistema (que siempre lo es); no, esta vez señala al propio aprendiente. Es este un tema importante y fascinante a la vez, pero la charla no va por ahí. Menciona esto como impedimento para apreciar la belleza en las matemáticas.
En la parte central de la charla, Marcus Miller cuenta de una manera divulgativa e instructiva algunos hechos paradójicos sobre el infinito. Cuando estamos tratando con conjuntos finitos, las cosas son lo que esperamos. Por ejemplo, si A es un subconjunto de un conjunto finito B y A es distinto a B, entonces claramente el número de elementos (el cardinal) de A es menor que el de B. ¡Esto no pasa con los conjuntos infinitos! Miller en su charla prueba que:
El conjunto de los números pares tiene el mismo cardinal que el conjunto de los números naturales;
El conjunto de los números naturales tiene el mismo cardinal que el conjunto de los números enteros;
El conjunto de los números naturales tiene el mismo cardinal que el conjunto de los números racionales;
El conjunto de los números reales tiene mayor cardinal que el conjunto de los números naturales.
Entre medias de estas pruebas toca música llena de belleza con su saxofón (minuto 10:33, por ejemplo).
En el minuto 12 y siguientes Miller hace un elogio de la imaginación y su fuerza como motor de la belleza. De hecho, tras explicar los hechos sobre el infinito pregunta al público cómo se sienten al conocer esos hechos.
Más tarde, enumera unos cuantos campos científicos que tienen relación fuerte y directa con las matemáticas (desde teoría de la señal a matemática discreta). De hecho, llega a mencionar ideas matemáticas que han servido para el análisis musical e ideas musicales que han servido de germen a la investigación matemática. Sin embargo, rechaza el lugar común de que las matemáticas son iguales a la música (en el minuto 13:22; yo lo rechazo igualmente). Continúa desmitificando varias de estas relaciones exageradas entre ambos campos, en particular, el llamado efecto Mozart. Miller afirma que “parece que la relación entre el conocimiento matemático y musical es interesante, pero no particularmente fundacional”.
Es realmente interesante la posición que mantiene en los minutos15:30 y siguientes sobre la conexión entre matemáticas y música. Mantiene que uno de los puntos de conexión entre ambas disciplinas es el placer que supone su aprendizaje. No puedo estar mas de acuerdo con Marcus Miller.
Bibliografía
[Ben06] D. Benson. Music: A Mathematical Offering. Cambridge University Press, 2006.
[Deu07] Diana Deutsch. Music perception. Frontiers In Bioscience, 12:4473–4482, 2007.
[Deu12] Diana Deutsch. In Diana Deutsch, editor, The Psychology of Music (Cognition and Perception), pages 183–248. Academy Press, San Diego, 2012.
[Mil22] Marcus Miller. Image with Marcus Miller. https://imaginewithmarcus.com/, accedido en marzo de 2022.
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
1. La función tonal y el tonnetz
En esta última entrega de la serie sobre modelos matemáticos de la función tonal vamos a estudiar un modelo de naturaleza geométrica: el tonnetz. Es un modelo que se basa en la clasificación clásica de los acordes en tónica, dominante y subdominante y que proporciona una visualización bella y elegante de la función tonal y de las relaciones entre los acordes. Una de sus visualizaciones es en forma de toro, como muestra la figura 1 (esta visualización es su interpretación moderna en términos de teoría neoriemanniana, que veremos más adelante en este artículo).
Figura 1: El tonnetz como un toro geométrico
El tonnetz fue definido por primera vez por Euler en 1739 en su obra Tentamen novae theoriae musicae ex certissismis harmoniae principiis dilucide expositae [Eul22]. Dado un acorde, Euler se fijó en tres relaciones respecto a ese acorde: el movimiento por quintas, el movimiento por terceras mayores y el movimiento por terceras menores. Fijado un acorde, la organización geométrica del tonnetz es entonces como sigue:
Los saltos por quintas a partir de ese acorde se representan en línea horizontales;
Los acordes a una tercera menor por arriba está en la diagonal superior derecha y los de tercera menor por abajo en la diagonal superior izquierda;
Análogamente, los acordes a distancia de tercera mayor están por debajo; los de tercera mayor ascendente se sitúan en la diagonal derecha y los de tercera mayor descendente en la diagonal izquierda.
Si fijamos el acorde de do, en la figura de abajo vemos los acordes relacionados con este por el modelo tonnetz. En la línea horizontal vemos un trozo del círculo de quintas, do–sol; en la línea inmediatamente superior están las notas que forman el acorde menor con do, la–do–mi, las cuales a su vez forman otro círculo de quintas; y en la línea inferior a do, vemos los notas a distancia de tercera mayor, también ordenadas por quintas ascendentes hacia la derecha. Las triadas en este modelo forman triángulos.
Figura 2: Acordes relacionados entre sí por el modelo tonnetz
Las triadas mayores son los triángulos formados por la nota de la diagonal superior derecha y la inmediatamente a la derecha; en la figura do–mi–sol sería el triángulo con la m mayúscula. Las triadas menores son el reflejo respecto al eje x de dicho triángulo; en la figura el triángulo do–mi♭–sol marcado con una m minúscula.
El modelo inicial de Euler estaba basado en la entonación justa (véanse las columnas de esta sección sobre afinación, [Góm21a], [Góm21b], [Lie04]). Por tanto, las quintas eran justas y el modelo se extendía hasta el infinito. De hecho, todos los intervalos del tonnetz en el modelo de Euler eran puros (las terceras y los demás intervalos también).
Más de un siglo después, el modelo de Euler llama la atención del físico y teórico de la música Arthur von Oettingen. El trabajo de este teórico a su vez llama la atención de Hugo Riemann, quien lo sistematiza y usa en sus análisis de las conducciones de voces y las progresiones armónicas. El cambio que se produce en el uso moderno del tonnetz es que se hace finito al establecer el sistema temperado como sistema de afinación. Esto es, al dividir la octava en 12 partes iguales, el tonnetz pierde su carácter infinito (de ahí la representación finita en forma de toro que vimos más arriba).
A la luz de la teoría neoriemanniana, el tonnetz se usa como modelo matemático de los acordes y las funciones tonales, donde las notas del tonnetz son ahora clases de alturas. En dicha teoría se definen tres tipos de operaciones o transformaciones:
La operación P, de paralelo, donde un acorde mayor se transforma en su versión menor y viceversa. Esto ocurre por el movimiento de la tercera bien ascendente o descendente.
La transformación R, donde un acorde mayor se transforma en su relativo menor y viceversa. En el acorde mayor la quinta sube un tono y en el acorde menor la fundamental baja medio tono.
La operación L (de leading-tone exchange en sus siglas inglesas) transforma un acorde mayor en el acorde menor a distancia de una tercera mayor bajando la fundamental medio tono. Así, por ejemplo, do mayor se transforma en mi menor bajando do a si. A la inversa, un acorde menor, como do menor, se transforma en mi♭ mayor bajando do a si♭.
En el tonnetz, estas operaciones se identifican con cuadrados como se muestra en la figura de abajo.
Figura 3: Versión moderna del modelo del tonnetz (figura tomada de [Wik22])
El tonnetz ha servido para modelizar música de la práctica común extendida y el jazz. Para una ilustración muy clara del uso del tonnetz en la música de jazz, véase [Wel20].
En los vídeos que se muestran a continuación, se muestran explicaciones más detalladas y visuales sobre el tonnetz. En el primero, se explica el tonnetz con ejemplos musicales en el piano.
Figura 4: Tonnetz explicado por Daniel Lewis
En el siguiente vídeo se oye un preludio de Chopin y se visualiza cómo evolucionan los acordes en el tonnetz.
Figura 5: Tonnetz explicado por Daniel Lewis
En el último vídeo se visualiza la Gimnopédie número 1 de Satie en el tonnetz.
Figura 6: Tonnetz explicado por Daniel Lewis
Por ultimo, recomendamos al lector la visita a la página de Imaginary [Ima22], donde puede encontrar una versión interactiva del tonnetz.
Bibliografía
[Eul22] Leonard Euler. Tentamen novae theoriae musicae ex certissismis harmoniae principiis dilucide expositae. http://eulerarchive.maa.org/backup/E033.html, Accedido en enero de 2022. Published on Euler archive.
[Góm21a] Paco Gómez. Afinamiento y temperamento (I). http://www.divulgamat.net/index.php?option=com_content&view=article&id=18644&directory=67, accedido el 20 de julio de 2021.
[Góm21b] Paco Gómez. Afinamiento y temperamento (II). http://www.divulgamat.net/index.php?option=com_content&view=article&id=18645&directory=67, accedido en agosto de 2021.
[Ima22] Imaginary.org. Tonnetz. https://www.imaginary.org/es/node/1523, accedido en enero de 2022.
[Lie04] Vicente Liern. Afinación. http://www.divulgamat.net/index.php?option=com_content&view=article&id=8747&directory=67, enero de 2004.
[Wel20] John Welsh. Using Tonnetz Tone Mesh To Understand Jazz Harmony. https://jazz-library.com/articles/tonnetz/, Abril de 2020.
[Wik22] Wikipedia. Tonnetz. https://en.wikipedia.org/wiki/Tonnetz, accedido en enero de 2022.
|
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |