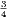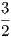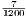11. 120. (Noviembre 2021) Modelos matemáticos de la función tonal (I)

1. La función tonal La nueva serie de artículos de esta columna versan sobre los modelos matemáticos de la función tonal. Este primer artículo se dedica a examinar las diferentes definiciones de función tonal en la música clásica y en el jazz. Walter Piston en su libro Armonía4 define función tonal como siguiente (página 50, sus cursivas): La tonalidad no es simplemente una manera de utilizar las notas de una escala particular. Es más bien un proceso de establecimiento de relaciones de estas notas con la nota que representa el centro tonal. Cada grado de la escala tiene su parte en el esquema de la tonalidad, su función tonal. Esta definición resulta demasiado general o incluso vaga. La expresión “una manera de utilizar las notas” necesita más concreción. De hecho, nos resulta sorprendente que muchos manuales de armonía no definan la función tonal con más formalidad (el libro de Piston ha sido una clásica referencia durante largo tiempo). A continuación vamos a revisar las definiciones más comunes; para el lector interesado daremos referencias a los trabajos que profundizan más en el concepto de función tonal. La definición más operativa y a la vez menos ambigua la hemos encontrado en el libro en línea Open Music Theory1, que es la base de un proyecto pedagógico basado fuertemente en el aprendizaje por indagación implementado con clase invertida y discusiones en clase. Este proyecto fue iniciado por un grupo de profesores de música formado por Kris Shaffer, Bryn Hughes y Brian Moseley. Esta definición tiene en cuenta la historia del acorde, esto es, su pasado —los acordes que lo precedieron —, el presente —las notas que forman el acorde y el orden en que se presentan —, y el futuro —las notas que suelen suceder a este acorde—. Las notas que siguen a un acorde dependen fuertemente del estilo y un cierto conjunto de notas son más probables que sucedan a un acorde dado en un estilo que en otro. En vista de lo anterior, el concepto de función tonal se basa en tres principios: (1) Los acordes son conjuntos de grados de escala. (2) Cada grado de la escala tiene sus propias tendencias. (3) La combinación de tendencias de los grados de la escala de las notas de un acorde constituye la función del acorde. Vamos a examinar los conceptos incluidos en esta definición de función tonal para su mejor entendimiento. Fijada una escala (do mayor, mi frigio, etc.), el grado de la escala es la posición de una nota en la escala. Como es sabido, los grados de la escala en orden ascendente son: tónica (I), supertónica (II), mediante (III), subdominante (IV), dominante (V), superdominante (VI) (también submediante), y sensible (VII). Los grados de la escala se suelen designar con números romanos, como aparece en la figura de abajo. Figura 1: Los grados de la escala La ausencia de los conceptos raíz del acorde y calidad del acorde no es casualidad; estos conceptos se discutirán más adelante. Dado que la tendencia de un acorde es función del estilo, empezaremos estudiando la función tonal en la llamada práctica común (el periodo de la música clásica comprendido aproximadamente desde 1600 hasta el principio del siglo XX) y luego seguiremos con otros estilos (pop, rock, la práctica común extendida). Un estudio del estilo y sus leyes se puede acometer a partir del trabajo de Meyer, empezando por sus libro Emoción y significado de la música2 y Style and Music3. Meyer usa tres conceptos para explicar el estilo musical: ley, regla y estrategia. Las leyes son características de orden biológico y cognitivo y tienen una naturaleza universal (muchas de esas leyes se explican a través de la psicología de la forma); la ley de la continuación, por ejemplo, es un ejemplo de leyes. Las reglas son características de tipo cultural y están asociadas a una cultura y a un tiempo histórico particulares; por ejemplo, las reglas de conducción de voces es una regla. Por último, las estrategias son las características propias de la obra de un compositor dado; considérese el lenguaje armónico de Chopin en particular. La función tonal se puede considerar como una clasificación de los acordes en términos de su relación a un centro tonal o tónica. Estos dos últimos términos son equivalentes, pero hay alguna pequeña diferencia de matiz. Fijada una escala, la tónica es la primera nota de la escala. Nótese que la escala es una sucesión ordenada de notas y, por tanto, la tónica siempre está bien definida. La tónica implica estabilidad y resolución de las tensiones armónicas. Cuando hablamos de centro tonal esto comprende la noción de tónica, pero también se puede referir a una nota que se ha convertido en una referencia tonal (bien por medio de dominantes secundarias, cambios de modo, u otros mecanismos) y que no necesariamente tiene que ser la primera nota de la escala. Nosotros usaremos ambos términos de manera equivalente. La teoría de la función tonal surgió de la combinación de dos teorías previas sobre la armonía, la teoría de Hugo Riemann (la llamada teoría alemana) y la teoría de Schenker y otros (la llamada teoría vienesa). Hugo Riemann presentó su teoría en su libro Vereinfachte Harmonielehre en 1893. En él, define los conceptos de tónica, subdominante y dominante y comienza la clasificación de acordes según dicha función. En la teoría vienesa, fueron teóricos como Schenker, Sechter, o el propio Schoenberg quienes la construyeron. Esta teoría se basa en los grados de la escala y se centra en el contexto de las progresiones armónicas. La teoría moderna es una síntesis de ambas escuelas de pensamiento. 2. Las tres funciones tonales de la práctica común En la práctica común se han usado tradicionalmente tres funciones tonales: función de tónica, función de subdominante y función de dominante. Se les designa por T, SD y D, respectivamente. La función de subdominante también recibe el nombre de predominante. Los grados de la escala asociados a estas funciones son: Función de tónica: grados I, III y VI; las triadas formadas sobre estos grados contienen todas al grado I. Función de subdominante: grados II y IV; todas las triadas de esta función contienen el grado IV Función de dominante: grados V y VII. Fijando la escala de do mayor, por ejemplo, si ponemos los grados de la escala por terceras, veremos la relación entre dichos grados y las funciones tonales, como ilustra la figura siguiente: Figura 2: Las tres funciones tonales Una característica de la música clásica del periodo de la práctica común es que las notas del acorde determinan por sí solas la función del acorde, circunstancia que no es cierta en otros estilos musicales, como veremos más adelante en esta serie. En la música pop o rock, por ejemplo, el acorde sobre IV puede tener distintas funciones de acuerdo al contexto en que se encuentre. Otros autores, como Ian Quinn5, dan definiciones más profundas y operativas, que permiten clasificar la función tonal de una variedad más amplia de acordes en un número mayor de contextos. La definición de Quinn se basa en clasificar las notas de un acorde según tres categorías, que aquí llamaremos primarias, secundarias y disonancias (en el inglés original, son llamadas triggers, associates y dissonnace). La tabla siguiente muestra las notas asociadas a cada función tonal: FUNCIÓN NOTAS NOTAS NOTAS PRIMARIAS SECUNDARIAS DISONANTES Tónica Notas I y III Notas V y VI V si VI está presente y 7 Subdominante Notas IV y VI Notas I y II I si II está presente y 3 Dominante Notas V y VII Nota II IV y VI Tabla 1: Funciones tonales según Quinn5 Quinn introduce una excepción en el esquema anterior. Un acorde con los grados VI, I, III lo considera un tipo especial de acorde de tónica, al que llama tónica inestable (destabilized tonic). Para este acorde usa el símbolo especial Tx en lugar de simplemente T. Volveremos a esta cuestión más adelante en esta serie. There is one exception to this (for now): a chord with scale degrees 6, 1, and 3 is a special kind of tonic chord, called a destabilized tonic. Quinn uses the special functional label is Tx, rather than simply T, for this chord. En la siguiente figura vemos un esquema del propio Quinn en que se ilustra la clasificación de las notas por sus funciones tonales. Figura 3: Las funciones tonales definidas por Quinn5 En el próximo artículo veremos modelos de función tonal más avanzados y empezaremos a examinar sus primeros modelos matemáticos. Bibliografía [1] Bry Hughes et al. Harmonic function. http://openmusictheory.com/harmonicFunctions.html. web page. accedido el 1 de noviembre de 2021. url: https://viva.pressbooks.pub/openmusictheory. [2] Leonard Meyer. Emoción y significado de la música. Madrid: Alianza Música, 1956/2000. [3] Leonard Meyer. Style and Music. Nueva York: University of Chicago Press, 1997. [4] Walter Piston. Harmony. London: Gollancz, 1950. [5] Ian Quinn. Harmonic Function without Primary Triads. web page. Artículo presentado en la reunión anual de la Society for Music Theory en Boston. 2005.

Martes, 16 de Noviembre de 2021 | Imprimir | PDF |  Correo electrónico

12. 119. (Octubre 2021) Grafos Parsimónicos para los Tricordos y Tetracordos más Comunes

Una vez más tengo el placer de contar como autor invitado a Luis Nuño, catedrático de universidad en la Universidad Politécnica de Valencia y autor de la Rueda Armónica, página web que presenta herramientas para el aprendizaje de la teoría de la música con una base matemática. Esta vez nos trae un fascinante artículo sobre grafos parsimónicos en triadas y tetracordos. Estamos ante un artículo profundo y bello a la vez. Espero que los lectores de esta columna lo disfruten tanto como lo he hecho al leerlo. Paco Gómez Martín 1. Introducción La prestigiosa revista internacional Journal of Mathematics and Music ha publicado este año 2021 un número especial titulado “Pattern in Music” (Patrones en Música), que incluye ocho artículos. A continuación se va a explicar resumidamente uno de ellos, titulado “Parsimonious graphs of the most common trichords and tetrachords” (Nuño, 2021b). La referencia completa de este artículo se encuentra en la Sección 6. Con el objetivo de que esta exposición sea de la máxima utilidad y para una variedad de lectores lo más amplia posible, se ha simplificado sustancialmente la parte teórica, pero se ha mantenido íntegramente la parte práctica. Así mismo, los acordes se han representado mediante la notación inglesa y con los símbolos más comúnmente utilizados. Entre las estructuras que se repiten de manera recurrente en las composiciones musicales tenemos las denominadas “transformaciones parsimónicas”, las cuales han sido ampliamente utilizadas en épocas y estilos musicales tan diferentes como el período Clásico, el Romanticismo, la música Latina o el Jazz, siendo por tanto unos patrones musicales perfectamente establecidos. Su análisis puede llevarse a cabo mediante la “teoría neo-riemanniana”, que surgió en la década de los años 1980 para analizar ciertos pasajes cromáticos de determinados compositores del s. XIX y está todavía en proceso de evolución gracias a las aportaciones del álgebra y la geometría. Según Gollin (2005), esta teoría se caracteriza por tres elementos: grupos matemáticos de transformaciones, conducción parsimónica de las voces y sus representaciones gráficas. El ejemplo por excelencia lo constituyen el grupo “PLR” y el Tonnetz, aunque se limitan únicamente a las tríadas mayores y menores. P, L y R son las operaciones básicas “Paralelo”, “Cambio de Sensible” (en inglés, Leading-tone exchange) y “Relativo”, las cuales transforman, respectivamente, por ejemplo, C mayor en C menor, C mayor en E menor y C mayor en A menor; y viceversa. Como punto de partida podemos tomar una regla básica en Armonía para conectar unos acordes con otros, que es la “ley del camino más corto” (Schönberg 1983, p. 39, citando a Bruckner). Esto significa mantener las notas comunes y mover las demás según los mínimos intervalos posibles. A este respecto, Douthett y Steinbach (1998) establecen que dos acordes de la misma “cardinalidad” (es decir, con el mismo número de notas) guardan entre sí una relación “Pm,n” si uno de ellos puede transformarse en el otro manteniendo las notas comunes y, en cuanto a las demás, moviendo m notas un semitono y n notas un tono. Entonces, diremos que dicha relación es “parsimónica” si los valores de m y n son bajos, generalmente m + 2n ≤ 2. El caso más simple es, lógicamente, P1,0, que denominaremos “monosemitonal” (en inglés, single-semitonal). Además, Douthett y Steinbach (1998) aportan también varios grafos parsimónicos de especial relevancia, como el “Chicken-Wire Torus” (grafo dual del Tonnetz) y el “Cube Dance” para los tricordos “más uniformes” (es decir, en los que los intervalos entre cada dos notas consecutivas son similares) o el “Towers Torus” y el “Power Towers” para los tetracordos más uniformes. Veinte años antes, sin embargo, Waller (1978) ya publicó un toroide equivalente al Chicken-Wire, pero que, además, mostraba claramente su división en hexágonos, así como los ciclos PL, PR y – aunque algo más difíciles de visualizar – los LR. Estas y otras relaciones PLR compuestas han sido estudiadas exhaustivamente por Cohn (2012). Por su parte, Tymoczko (2006) hace un planteamiento diferente, desarrollando una teoría para representar los acordes de n notas en una especie de banda de Möbius generalizada, que llamaremos “n-orbifold”. Además, proporciona las figuras del 2-orbifold y parte del 3-orbifold, antes de “torcerlos y doblarlos” para obtener los verdaderos orbifolds. Callender, Quinn y Tymoczko (2008) aportan nuevas representaciones de este tipo, aunque, en la práctica, dada su especial complejidad, solo se suelen representar las regiones centrales de los orbifolds. En este trabajo se presentan unos nuevos grafos circulares cíclicos, que he denominado “Cíclopes”, que incluyen un mayor número de tricordos y tetracordos que las representaciones anteriores, donde estos están conectados entre sí mediante transformaciones monosemitonales. Así mismo, proporcionan una visión más amplia de las regiones centrales de los correspondientes orbifolds. Por consiguiente, permiten representar un mayor número de obras musicales de una forma práctica y pueden utilizarse tanto para el análisis musical como para la composición. Se asume que el lector está familiarizado con los “nombres de Forte” (Forte 1973) y las “clases de conjuntos”, también llamadas “clases de acordes”. En este trabajo, las clases de acordes “no inversionalmente simétricas” se dividen en dos “tipos de acordes” relacionados entre sí por “inversión”, llamados “a” y “b”, de acuerdo con las definiciones dadas por Nuño (2020a). Todos estos conceptos pueden, de forma alternativa, consultarse en español en Nuño (2020b) y Nuño (2021a). Por otra parte, este estudio trata también, en gran medida, sobre la “geometría de los acordes” (Tymoczko 2011) y las “transformaciones de los acordes más uniformes” (Cohn 2012), aunque los principales conceptos se explican también aquí. 2. Selección de los Tricordos y Tetracordos Tal como se explica en las anteriores referencias, hay 12 clases diferentes de acordes de 3 notas, los tricordos, 5 de los cuales son inversionalmente simétricos, mientras que cada uno de los restantes 7 se puede dividir en dos tipos de acordes relacionados por inversión, lo que hace un total de 19 tipos de acordes. Y hay 29 clases diferentes de acordes de 4 notas, los tetracordos, 15 de los cuales son inversionalmente simétricos; y, dividiendo en dos los restantes 14, obtenemos un total de 43 tipos de acordes. En ambos casos, el número de tipos de acordes es demasiado elevado como para poder relacionarlos en unos grafos que sean visualmente sencillos y de utilidad práctica. Por tanto, nos centraremos únicamente en los tricordos y tetracordos “más comunes”. Veamos cómo podemos seleccionarlos. En el período de la práctica común (aproximadamente, 1650-1900), las armonías se forman mediante superposición de terceras sobre los siete grados de las escalas mayor, menor armónica y menor melódica (veáse, por ejemplo, Schönberg 1983 o Piston 1988). De aquí resultan las 4 tríadas y los 7 acordes de séptima básicos, cuyos nombres de Forte son 3-10, 3-11a, 3-11b, 3-12 y 4-19a, 4-19b, 4-20, 4-26, 4-27a, 4-27b, 4-28, respectivamente. A estos hay que añadir los acordes de sexta aumentada 3-8a (italiana) y 4-25 (francesa). Todos estos tipos de acordes son, por tanto, predominantes en la música occidental. Para una cardinalidad dada (3 o 4 notas en nuestro caso), las clases de acordes están ordenadas desde la que tiene las notas lo más juntas posible, es decir, en secuencia cromática hasta la que las tiene separadas lo más uniformemente posible (tríadas aumentadas y acordes de séptima disminuida, según se trate de acordes de 3 o de 4 notas). Así, el criterio seguido aquí ha sido seleccionar “series completas de tipos de acordes”, desde los “más cromáticos” de los grupos anteriores (3-8 y 4-19) hasta los más uniformes (3-12 y 4-28). Tabla 1. Tipos de tricordos y tetracordos considerados aquí. Un superíndice en los nombres de Forte indica el grado de simetría transposicional, en caso de ser mayor que 1. Un asterisco (*) significa “omit 5” y un doble asterisco (**) “omit b3”. Los acordes mayores (M) se representan, normalmente, mediante su fundamental, sin ningún símbolo adicional. El símbolo “(9)” significa “add 9”, mientras que el símbolo “9” significa añadir tanto la séptima menor como la novena mayor. Las formas interválicas empiezan desde la fundamental. Tricordo Símbolo Forma Int. Tetracordo Símbolo Forma Int. 3-8a 7* 462 4-19a mΔ 3441 3-8b Ø** 642 4-19b Δ#5 4431 3-9 sus4 525 4-20 Δ 4341 3-10 dim 336 4-21 9* 2262 3-11a m 345 4-22a (9) 2235 3-11b M 435 4-22b m4 3225 3-123 + 444 4-23 7sus 5232 4-24 7#5 4422 4-252 7b5 4242 4-26 m7 3432 4-27a Ø 3342 4-27b 7 4332 4-284 O 3333 La Tabla 1 muestra esos tricordos y tetracordos con los símbolos empleados aquí para representarlos y sus “formas interválicas” (Nuño 2020a) empezando desde la fundamental. La forma interválica de un tipo de acorde es la secuencia de intervalos, en semitonos, entre cada dos notas adyacentes, incluyendo el intervalo entre la última nota y la primera; o cualquiera de sus permutaciones circulares. Los acordes añadidos a los grupos anteriores son los siguientes: 3-8b, 3-9, 4-21, 4-22a, 4-22b, 4-23 y 4-24, los cuales se interpretan, en ocasiones, como acordes cromáticos, incompletos o de paso. En otros estilos musicales, como el Pop, la música latina o el Jazz se utilizan con frecuencia todos los tipos de acordes de la tabla (véase, por ejemplo, el listado de acordes proporcionado por Sher 1991, p. iv). Por tanto, la selección realizada de esta manera contiene un número razonable de tipos de acordes, a la vez que incluye, en todo caso, los más relevantes. 3. Grafos Parsimónicos Las Figuras 1 y 2 son unos grafos circulares que he denominado 3-Cíclope y 4-Cíclope, que muestran, respectivamente, los tricordos y tetracordos de la Tabla 1 conectados mediante transformaciones monosemitonales. Así, en cada grafo se pasa de un acorde a otro cambiando una nota un semitono, el cual puede ser ascendente, si giramos en sentido horario, o descendente, si lo hacemos en sentido antihorario. Los números que hay en los extremos de las líneas que conectan los acordes indican las notas inicial y final referidas a las fundamentales de dichos acordes, donde 1, 3, 4 y 5 representan intervalos justos o mayores, que pueden alterarse mediante # y b, mientras que las séptimas mayores, menores y disminuidas se representan mediante Δ, 7 y d7, respectivamente. Haciendo la analogía con la carátula de un reloj, cada acorde se ha colocado en una “zona”, que viene definida por “la suma de sus notas”, módulo 12 (Cohn 2012, p. 102). Así, por ejemplo, el acorde de C mayor está en la zona 0 + 4 + 7 = 11 del 3-Cíclope y el acorde BØ en la zona 11 + 2 + 5 + 9 = 27 = 3 (módulo 12) del 4-Cíclope. De esta manera, si se sube un semitono una nota de un acorde, pasamos a la siguiente zona girando en sentido horario. Además, esto hace que, en el 3-Cíclope, los tricordos del mismo tipo cuyas fundamentales están a distancia de 4 semitonos estén situados en la misma zona. Y lo mismo ocurre en el 4-Cíclope con los tetracordos del mismo tipo cuyas fundamentales están a distancia de 3 semitonos. Por otra parte, los acordes que tienen un grado de simetría transposicional “s” mayor que uno tienen, lógicamente, conexiones múltiples a acordes del mismo tipo. Este es el caso de las tríadas aumentadas (s = 3), los acordes de sexta aumentada francesa (s = 2) y los acordes de séptima disminuida (s = 4). Entre los grafos parsimónicos desarrollados hasta la fecha cabe destacar, para el caso de los tricordos, el “Cube Dance” de Douthett y Steinbach (1998), que muestra las transformaciones monosemitonales entre las tríadas aumentada (3-12), menor (3-11a) y mayor (3-11b), el cual contiene solo un tipo de acorde por zona. Tymoczko (2011, p. 105) representa estos mismos acordes en un cubo. Pero con anterioridad a ambos tenemos el Tonnetz, que es una representación de los acordes mayores y menores conectados mediante transformaciones PLR. Por su parte, el 3-Cíclope puede considerarse como un Cube Dance o un Tonnetz “de orden superior”, ya que incluye también los tipos de acordes 3-8 a 3-10. En total, contiene 7 tipos de acordes frente a los 3 del Cube Dance o los 2 del Tonnetz. Además, en él se visualizan claramente las transformaciones básicas PLR: P y L son líneas “oblicuas” con respecto a las circunferencias centradas en el grafo, y R son líneas que “atraviesan” las tríadas aumentadas, entrando y saliendo por la misma letra (“a”, “b” o “c”). Simbólicamente, P = /, L = \ y R = ^. Figura 1. El 3-Cíclope, con los tricordos considerados en la Tabla 1. Con respecto a los grafos parsimónicos para los tetracordos tenemos el “Power Towers” de Douthett y Steinbach (1998), que muestra las transformaciones monosemitonales entre los acordes disminuido (4-28), semidisminuido (4-27a), de séptima de dominante (4-27b) y menor con séptima (4-26), el cual contiene también solo un tipo de acorde por zona. Cannas (2018) añade a ellos los acordes mayores con séptima mayor (4-20), obteniendo el “Clover graph”. En cambio, tanto el “4-Cube Trio” de Douthett (Cohn 2012, p. 158), como la representación de Tymoczko en el 4-orbifold (2011, p. 106), lo que añaden son los acordes de sexta aumentada francesa (4-25), completando de esta manera un hipercubo en cuatro dimensiones o “teseracto” (tipos de acordes 4-25 a 4-28). Por su parte, el 4-Cíclope puede considerarse como un 4-Cube Trio “de orden superior”, ya que incluye también los tipos de acordes 4-19 a 4-24. En total, contiene 13 tipos de acordes frente a los 5 del 4-Cube Trio o el Clover graph, un número bastante alto que hace que este grafo sea más complejo que el 3-Cíclope. Figura 2. El 4-Cíclope, con los tetracordos considerados en la Tabla 1. 4. Patrones de Acordes Tanto el 3-Cíclope como el 4-Cíclope son especialmente adecuados para representar ciertos patrones de acordes que aparecen en determinadas composiciones musicales, los cuales se indican en la Tabla 2. Estos patrones también pueden representarse en el Tonnetz, pero solo hasta cierto punto, ya que este solo contiene las tríadas menores (3-11a) y mayores (3-11b); y, cuando se utilizan acordes de séptima de la clase 4-27, lo normal es reducirlos eliminando la séptima en los acordes “7” y la tónica en los acordes “Ø”. Cohn (2012) y Tymoczko (2011) analizan muchos ejemplos de este tipo, pero incluyen también las tríadas aumentadas (3-12); y, con respecto a los tetracordos, ambos consideran los cinco tipos más uniformes (4-25 a 4-28). Sin embargo, el 3- y el 4-Cíclope incluyen más del doble de tipos de acordes (3-8 a 3-12 y 4-19 a 4-28, respectivamente), por lo que permiten analizar un mayor número de piezas musicales, así como obtener unas representaciones más simples y compactas. Tabla 2. Patrones de acordes idóneos para ser representados en el 3- y el 4-Cíclope.   3-Cíclope   4-Cíclope     Progresiones Parsimónicas de Tricordos   Progresiones Parsimónicas de Tetracordos     Mismos Tipos de Tricordos a distancia de tercera mayor   Mismos Tipos de Tricordos a distancia de tercera menor   Consideremos, en primer lugar, varios ejemplos basados en tricordos a distancia de tercera mayor, los cuales están situados en la misma zona del 3-Cíclope, y que incluyen también progresiones parsimónicas. En cuanto a los acordes “7” y “Ø”, consideraremos sus formas incompletas, “7*” y “Ø**”, que son mejores aproximaciones a los acordes reales que las utilizadas en el Tonnetz y, lo que es muy ventajoso, conducen a representaciones mucho más compactas. Comencemos por la Sonata para Violín y Piano en Fa mayor, Op. 24 de Beethoven. Las armonías en el segundo movimiento, compases 38-54, son las siguientes:         donde cada acorde o cada pareja de acordes unidos por un guión dura un compás y el símbolo “%” significa repetir el compás anterior. Los acordes relacionados con una misma tríada consonante se han agrupado mediante llaves. Esta progresión de acordes se ha representado en la Figura 3 en el 3-Cíclope, donde el acorde inicial se ha marcado de manera especial. Los tres acordes menores (Bbm, F#m, Dm) están a distancia de tercera mayor descendente, al igual que los tres acordes mayores relacionados con ellos mediante operaciones L y P (Gb, D, Bb). Estos últimos se afirman mediante cadencias con acordes de séptima de dominante y de subdominante, estando cada uno de estos tipos de acordes situados en una misma zona. Debido a la utilización de los acordes “7” en su forma incompleta, es decir, “7*”, el resultado es muy compacto y solo ocupa tres zonas cercanas entre sí: 4, 5 y 8. Si hubiéramos usado los acordes “7” sin la séptima, como se hace en el Tonnetz, entonces estarían localizados en la zona 2 de la Figura 1. En cuanto a sus formas completas con 4 notas, estarían situadas en zonas diferentes (1, 5, 9) de la Figura 2, dejando de estar agrupados. Analicemos ahora la Consolación en Re bemol mayor, Op. 102, No. 3 de Liszt, compases 23-43, cuyas armonías son         donde algunos acordes se tocan sobre una nota pedal, lo cual se representa mediante una barra seguida de la nota pedal. Esta progresión de acordes se ha representado en la Figura 4 en el 3-Cíclope (sin los pedales) y se puede comparar con Cohn (2012, p. 187), quien aporta, además, una animación Web. Ahora los tres acordes mayores (Db, F, A) están a distancia de tercera mayor, pero ascendente, y solo hay dos acordes menores (Fm, Am) relacionados con ellos mediante operaciones L y P, los cuales se afirman mediante cadencias más largas. Hay, además, un acorde “Ø”, cuya forma incompleta (es decir, Ø**), junto con las de los acordes “7” (es decir, 7*), dan lugar a una representación muy compacta, que se extiende únicamente sobre dos zonas consecutivas (1 y 2). De hecho, el 3-Cíclope es también especialmente adecuado para representar las cadencias V7–I(m) y IIØ–V7–I(m), con acordes tónicos mayores o menores. En particular, el tema de Jazz “Giant Steps” de Coltrane (Sher 1991) está estrechamente relacionado con esto, ya que consta únicamente de cadencias V7–IΔ y IIm7–V7–IΔ a distancia de tercera mayor.   Figura 3. Beethoven, Sonata para Violín y Piano en Fa mayor, Op. 24, segundo movimiento, compases 38-54.   Figura 4. Liszt, Consolación en Re bemol mayor, Op. 102, No. 3, compases 23-43. En cuanto a ejemplos con el 4-Cíclope, consideremos el Concierto para Piano No. 2 en Do menor, Op. 18 de Rachmaninoff. En el primer movimiento, compases 1-8, hay una progresión puramente monosemitonal, representada en la Figura 4 en el 4-Cíclope mediante una simple línea: [Fm(5)]  DbΔ  DØ Fm7  F7  Fm7  DØ DbΔ Aquí, una nota entre paréntesis significa añadir dicha nota al acorde. Así, Fm(5) es Fm con la quinta duplicada (C). Este acorde se ha escrito entre corchetes porque no aparece en el 4-Cíclope, pero se ha incluido en la figura para ilustrar mejor el ejemplo. Son precisamente esos dos C los que suben y bajan por semitonos a lo largo de la progresión, excepto al pasar por F7. Hay un pedal F–C (en triple octava), que pertenece a todas las armonías y que da robustez a toda la progresión. También hay otro pedal Ab (en doble octava), excepto en F7. El primer acorde, Fm(5), pasa a DØ a través de DbΔ en lugar de DO, posiblemente porque este último no incluye el pedal C y además contiene dos tritonos, mientras que DbΔ no contiene ninguno. El siguiente ejemplo es Indudable (Bossa Nova) de Nuño (2012), cuyos compases 19-27 constan de los siguientes acordes (algunos de los cuales, en realidad, contienen más tensiones) G#m7  C#Δ  Fm7  BbΔ  Dm7  G6  Bm7  E7sus  G#m7 Esta progresión de acordes se ha representado en la Figura 6 en el 4-Cíclope. Los cuatro acordes menores con séptima (G#m7, Fm7, Dm7, Bm7) están a distancia de tercera menor, por lo que están situados en la misma zona. En cuanto a los demás acordes, sus tónicas están también a distancia de tercera menor, pero en lugar de tener la secuencia homogénea C#Δ, BbΔ, GΔ, EΔ, los dos últimos acordes (marcados con línea discontinua en la Figura 6) se han sustituido por G6 (enarmónico de Em7) y E7sus, respectivamente. En todo caso, la representación es nuevamente simple y compacta.   Figura 5. Rachmaninoff, Concierto para Piano No. 2 en Do menor, Op. 18, primer movimiento, compases 1-8.   Figura 6. Nuño, Indudable (Bossa Nova), compases 19-27. Como último ejemplo tomaremos el Preludio en Mi menor, Op. 28, No. 4 de Chopin, una de las piezas más interesantes analizadas por Tymoczko (2011, pp. 287-293) y Cohn (2012, pp. 160-166), los cuales aportan, además, animaciones Web. La figura 7 es una partitura simplificada con los compases 1-12. Figura 7. Chopin, Preludio en Mi menor, Op. 28, No. 4, compases 1-8. Melodía y estructura armónica. Figura 8. Chopin, Preludio en Mi menor, Op. 28, No. 4, compases 1-8. Armonías de las tres voces inferiores. Como se verá, esta composición se entiende mejor analizando primero las armonías de las tres voces inferiores, representadas en la Figura 8 en el 3-Cíclope, las cuales pasan por todos los tipos de tricordos considerados en este grafo, excepto las tríadas aumentadas (¿quizás son demasiado disonantes?). Chopin incluye, además, los tipos de acordes “m7*” (3-7a) y “Δ*” (3-4a), definidos por las formas interválicas y , que son los acordes tónicos de séptima incompletos de las tonalidades menor natural y mayor, respectivamente. Desde el segundo acorde (F#m7*), las tres voces inferiores realizan estrictamente una progresión monosemitonal (P1,0) descendente, que cubre algo más de una vuelta completa en el grafo. Después, se utilizan otras transformaciones parsimónicas para terminar la frase, las cuales se indican en la partitura. Figura 9. Chopin, Preludio en Mi menor, Op. 28, No. 4, compases 1-8. Armonías completas. Por su parte, la austera melodía describe también una línea descendente, B–A–G#–F#, que completa las armonías y conduce a una representación más compleja en el 4-Cíclope (Figura 9). Aparte de los acordes considerados en este grafo, Chopin también incluye el “(b9)” (4-18a) y el “Δb5” (4-16a), definidos por y , respectivamente. 5. Conclusiones Se han presentado dos nuevos grafos, denominados Cíclopes, que relacionan los tricordos y tetracordos más comunes mediante transformaciones monosemitonales. Ambos incluyen más del doble de tipos de acordes que los grafos publicados hasta la actualidad, por lo que permiten analizar un repertorio más extenso de forma práctica. Estos grafos son especialmente adecuados para representar progresiones de acordes parsimónicas, tricordos a distancia de tercera mayor y tetracordos a distancia de tercera menor, así como las cadencias V7–I(m) y IIØ–V7–I(m), con acordes tónicos mayores o menores. En todos estos casos, los resultados que se obtienen son simples y compactos, lo que nos permite visualizar claramente las relaciones entre los acordes involucrados y entender mejor los patrones de composición utilizados, a la vez que constituyen un excelente recurso mnemotécnico. Por todo ello, podemos concluir que estos grafos son unas herramientas de gran utilidad tanto para el análisis musical como para la composición. 6. Referencias Callender, Clifton, Ian Quinn, and Dmitri Tymoczko. 2008. “Generalized Voice-Leading Spaces.” Science 320 (5874): 346–348. Cannas, Sonia. 2018. “Geometric Representation and Algebraic Formalization of Musical Structures.” Ph.D. dissertation, Université de Strasbourg and Università degli Studi di Pavia e di Milano-Bicocca. Cohn, Richard. 2012. Audacious Euphony: Chromatic Harmony and the Triad’s Second Nature. New York: Oxford University Press. Douthett, Jack, and Peter Steinbach. 1998. “Parsimonious Graphs: A Study in Parsimony, Contextual Transformations, and Modes of Limited Transposition.” Journal of Music Theory 42 (2): 241–263. Forte, Allen. 1973. The Structure of Atonal Music. New Haven: Yale University Press. Gollin, Edward. 2005. “Neo-Riemannian Theory.” Zeitschrift der Gesellschaft für Musiktheorie (ZGMTH) 2 (2–3): 153–155. Nuño, Luis. 2012. Puesta de Sol. Vol. 1. Madrid: Acordes Concert, S.L. Nuño, Luis. 2020a. “A Detailed List and a Periodic Table of Set Classes.” Journal of Mathematics and Music 1–21. https://doi.org/10.1080/17459737.2020.1775902 Nuño, Luis. 2020b. “La Tabla Periódica Musical (1/2).” DIVULGAMAT, Centro virtual de divulgación de las matemáticas, RSME: Real Sociedad Matemática Española, No. 111. Diciembre 2020. http://www.divulgamat.net/divulgamat15/index.php?option=com_alphacontent&section=11&category=67&Itemid=67 Nuño, Luis. 2021a. “La Tabla Periódica Musical (2/2).” DIVULGAMAT, Centro virtual de divulgación de las matemáticas, RSME: Real Sociedad Matemática Española, No. 112. Enero 2021. http://www.divulgamat.net/divulgamat15/index.php?option=com_alphacontent&section=11&category=67&Itemid=67 Nuño, Luis. 2021b. “Parsimonious Graphs for the Most Common Trichords and Tetrachords.” Journal of Mathematics and Music 15 (2): 125–139. https://doi.org/10.1080/17459737.2021.1923844 Piston, Walter. 1988. Harmony. 5th ed. New York: W. W. Norton and Co. Schönberg, Arnold. 1983. Theory of Harmony. 3rd ed. Berkeley, Calif.: University of California Press. Sher, Chuck. 1991. The New Real Book. Vol. 2. Petaluma, Calif.: Sher Music Co. Tymoczko, Dmitri. 2006. “The Geometry of Musical Chords.” Science 313 (5783): 72–74. Tymoczko, Dmitri. 2011. A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice. New York: Oxford University Press. Waller, Derek A. 1978. “Some Combinatorial Aspects of the Musical Chords.” The Mathematical Gazette 62 (419): 12–15.

Lunes, 11 de Octubre de 2021 | Imprimir | PDF |  Correo electrónico

13. 118. (Septiembre 2021) Afinación y temperamento (III)

1. Introducción En los dos artículos anteriores [4, 5] hicimos un recorrido por los principales sistemas de afinación y por algunos temperamentos. En el primero, cubrimos los fundamentos físicos de la afinación y la afinación pitagórica; en el segundo, la afinación justa y los sistemas mesotónicos. En este tercer artículo, estudiaremos los temperamentos irregulares y el temperamento igual. 2. Temperamentos irregulares Un temperamento irregular —que también recibe el nombre de temperamentos circulares o buenos temperamentos—son temperamentos que partiendo de los sistemas mesotónicos modifican algunas notas para la quinta del lobo desaparezca o al menos se atenúe. Otra manera de expresarlo es que se modifican notas para que la “espiral” de quintas se convierta en un verdadero círculo de quintas donde sea posible la modulación. De hecho, la aparición de los temperamentos irregulares están fuertemente ligados a la necesidad de modulación que de modo creciente se estableció a partir del siglo XVI. Los temperamentos irregulares coexistieron con los sistemas mesotónicos y al menos estuvieron en uso dos siglos antes de que el temperamento igual se generalizara como sistema de afinación estándar. Hay estudios sobre el Clave bien temperado que defienden la idea de que Bach lo escribió para temperamentos irregulares, ya que musicalmente es más rico que si se toca en el sistema mesotónico. Para una buena revisión histórica breve y concisa, véanse el libro de Benson [2] (páginas 206 y siguientes) y el capítulo 7 del libro de Barbour [1]. La quinta del lobo del sistema mesotónico es 35 cents más aguda de lo que debería ser. En general, los temperamentos irregulares se pueden clasificar en función de cómo tal diferencia se distribuye por el resto de las notas. Uno de los temperamentos irregulares más usados fue el llamado Werckmeister III. Siguiendo la notación de Eitz introducida en el artículo anterior y designando por p la coma pitagórica, su diagrama está en la figura de abajo. mi-p si-p fa#-p do#-p sol#-p do0 sol-p re-p la-p mi-p mi♭0 si♭0 fa♭0 do0 Figura 1: Temperamento irregular de Werckmeister III Si miramos a la segunda fila, observaremos que la coma pitagórica está distribuida a partes iguales entre las quintas do-sol-re-la y si-fa♯. A partir del la, la sucesión de notas sigue por quintas puras (pero partiendo desde la-p hasta el si-p, donde ahora salta a fa#-p. Y desde aquí sigue de nuevo por quintas puras. Estos temperamentos permitían obtener resultados más o menos satisfactorios cuando se modulaba a tonalidades relativamente lejanas de la principal. También dieron lugar a “personalidades” en las tonalidades, con frecuencia asignadas de manera subjetiva. Por ejemplo, Daniel Schubart en su obra Ideen zu einer Aesthetik der Tonkunst asigna las personalidades que se ven en la tabla de abajo (la tabla está tomada de la entrada de Wikipedia Tonalidad [6]). En algunos casos las descripciones de estas personalidades resultan algo excesivas. No es el único autor que confeccionó este tipo de tablas de personalidades o características afectivas (piénsese en la teoría de los afectos del periodo barroco). Tonalidad Personalidad Do mayor Alegre, guerrero, completamente puro. Su carácter es de inocencia y de simplicidad. Do menor Oscuro y triste. Declaración de amor y a la vez lamento de un amor no correspondido. Anhelos y suspiros. Do ♯ mayor Miradas lascivas. Pena y éxtasis. No puede reír, pero puede sonreír. No puede aullar, solo puede hacer una mueca de su llanto, bello. Caracteres y sentimientos inusuales. Do ♯ menor Sentimientos de ansiedad, angustia y dolor profundo en el alma, desesperación, depresión, sentimientos sombríos, miedos, indecisiones, escalofríos. Si los fantasmas hablaran se aproximarían a esta tonalidad. Re mayor Feliz y muy guerrero. El triunfo, aleluyas, júbilo, victoria. Re menor Grave y devoto. Melancolía femenina. El rencor. Mi ♭ mayor Crueldad, dureza, amor, devoción, conversación íntima con Dios. Mi ♭ menor Horrible, espantoso. Mi mayor Querellante, chillón, gritos ruidosos de alegría, placer al reírse. Mi menor Afeminado, amoroso, melancólico. Fa mayor Furioso, arrebatado, nostalgia solemne, maravilloso, dulce. Fa menor Oscuro, doliente, depresivo, lamento funerario, gemidos de miseria. Fa ♯ mayor Triunfo sobre la dificultad, libertad, alivio, superación de obstáculos, el eco de un alma que ferozmente ha lidiado y finalmente conquistó. Fa ♯ menor Pesimista, triste, sombrío, oscuro, terco a la pasión, resentimientos, descontentos. Sol mayor Dulcemente jovial, idílico, lírico, calmado, pasión satisfecha, gratitud por la amistad verdadera y el amor esperanzado, emociones gentiles y pacíficas. Sol menor Serio, magnífico, descontento, preocupado por el rompimiento de los esquemas, mal templado, rechinamiento de dientes, disgusto. La ♭ mayor Gravedad, muerte y putrefacción. La ♭ menor Quejándose todo el tiempo, poco complaciente, insatisfecho, corazón sofocado, lamentos, dificultades. La mayor Alegre, campestre, declaración de amor inocente, satisfacción, la esperanza de volver lo que le pertenece a uno de nuevo al regresar de una partida, juventud, aplausos y creencia en Dios. La menor Tierno, lloroso, piedad femenina. Si ♭ mayor Magnífico, alegría, amor alegre, conciencia limpia, metas y deseos por un mundo mejor. Si ♭ menor Oscuro, terrible, criatura pintoresca y curiosa, ropa de noche, tosco, maleducado, burlesco, descortés, descontento con sí mismo, sonidos del suicidio. Si mayor Duro, doliente, deslumbrante, fuertemente coloreado, anunciando pasiones salvajes, enfado, odios y resentimientos. Si menor Solitario, melancólico, ermitaño, paciencia, fe y sumisión esperando el perdón divino. La idea de concentrar la distribución de la coma en ciertas notas y no en otras es la de hacer ciertas tonalidades más aceptables que otras. Con esta estrategia, las terceras de las tonalidades “buenas” suenan casi como las terceras justas, como es el caso de la triada de do mayor do0-mi0-sol-p∕4 del sistema de Werckmeister III (la diferencia es de 4 cents). Si embargo, las terceras construidas sobre do♯ o fa♯ suenan más agudas (ahora la diferencia es de 22 cents, que es una diferencia notable). Para una lista completa y exhaustiva junto con el contexto histórico, consúltense los libros de Goldáraz [3] y Barbour [1]. 3. Temperamento igual Los temperamentos descritos hasta ahora tienen el problema de que la elección de las notas esencialmente favorecía una tonalidad en particular junto a sus vecinas y dejaba el resto con afinaciones deficientes. Los esfuerzos por distribuir la coma pitagórica o sintónica de algunos temperamentos entre las quintas, como en el caso de los temperamentos irregulares, llega a su punto natural con el temperamento igual, cuyo principio consiste en dividir la octava en 12 partes iguales. O dicho de otro modo, hacer que todas las quintas tengan el mismo tamaño. Históricamente y matemáticamente, esto fue difícil. Históricamente, fueron los constructores e intérpretes de instrumentos de afinación fija (órganos, clavecines, laudes, guitarras, etc.) los que empezaron a explorar el temperamento igual. Según Barbour [1] (página 56), Giovanni Maria Lanfranco en 1533 fue el primero en abogar y sistematizar el temperamento igual. Lanfranco recomienda que “las quintas se achiquen de manera que no sean agradables del todo al oído y que las terceras se puedan soportar”. Matemáticamente, la dificultad era construir de manera geométrica (con regla y compás) el número irracional , que es la proporción con que se construye el temperamento igual. En el temperamento igual, una octava se divide en 12 partes iguales; esto equivale a decir que la proporción entre dos notas consecutivas es 2 : 1 o, si se miden en cents, simplemente 100 cents. La tabla siguiente resume la construcción del temperamento igual. Notas Do Do♯ Re Re♯ Mi Fa Fa♯ Proporción 1/1 2 : 1 2 : 1 2 : 1 2 : 1 2 : 1 2 : 1 Cents 0 100 200 300 400 500 600 Notas Sol Sol♯ La La♯ Si Do Proporción 2 : 1 2 : 1 2 : 1 2 : 1 2 : 1 2 Cents 700 800 900 1000 1100 1200 Tabla 1: Temperamento igual Las terceras del temperamento igual son 14 cents más agudas que las terceras justas. Y como dice Benson en su libro [2] (página 204), “suenan nerviosas y agitadas” (estoy de acuerdo con esta afirmación). En la siguiente tabla se ven de nuevo las proporciones de la afinación pitagórica y su comparación con el temperamento igual (medido en cents). Notas Do Sol Re La Mi Si Fa# Do# Sol# Proporción 1/1 3/2 9/8 27/16 81/64 243/128 729/512 Cents 0 701.96 203.91 905.87 407.82 1109.78 611.73 113.68 815.64 Notas Do Fa Si♭ Mi♭ La♭ ~Sol# Proporción 1/1 4/3 9/16 32/27 128/81 Cents 0 498.04 996.09 294.13 792.18 Tabla 2: Afinación pitagórica para la escala cromática En general, la afinación justa y el sistema mesotónico producen terceras con más sensación de calma. Los temperamentos irregulares tienen la ventaja de dotar a cada tonalidad de una personalidad y un color distintos, como consecuencia de la distribución irregular de la coma. En el temperamento igual todas las tonalidades tienen esencialmente la misma personalidad. 4. Para saber más A continuación ponemos algunos vídeos con música en el temperamento Werckmeister III. Empezamos con una sonata de Domenico Scarlatti, la sonata en la menor K. 54. Figura 2: Sonata en la menor K. 54 en el temperamento Werckmeister III Figura 3: Preludio en do mayor del Clave bien temperado de Bach en 7 temperamentos (incluido Werckmeister III)   Bibliografía [1] J. Murray Barbour. Tuning and temperament: a historical survey. New York: Dover Publications, Inc., 1951. [2] D. Benson. Music: A Mathematical Offering. Cambridge University Press, 2006. [3] J. Javier Goldáraz. Afinación y temperamentos históricos. Madrid: Alianza Editorial, 2004. [4] Paco Gómez. Afinación y temperamento (I). http://www.divulgamat.net/index.php?option=com_content&view=article&id=18644&directory=67. web page. accedido el 20 de julio de 2021. [5] Paco Gómez. Afinación y temperamento (II). http://www.divulgamat.net/index.php?option=com_content&view=article&id=18645&directory=67. web page. accedido en agosto de 2021. [6] Wikipedia. Tonalidad_(música). https://es.wikipedia.org/wiki/Tonalidad\_(msica). web page. accedido el 10 de julio de 2021.

Jueves, 09 de Septiembre de 2021 | Imprimir | PDF |  Correo electrónico

14. 117. (Agosto 2021) Afinación y temperamento (II)

1. Introducción En el artículo anterior [Góm21], presentamos los conceptos básicos de afinación y temperamento (manejo de frecuencias, división de la octava, cents, la serie armónica) y la afinación pitagórica, cuyos generadores son la octava y la quinta. En este artículo vamos a estudiar los siguientes temas: la afinación justa, en su versión diatónica y cromática junto con algunas afinaciones históricas; hablaremos de los problemas armónicos que se derivan del uso de la afinación justa; continuaremos con los sistemas mesotónicos, de los cuales proporcionaremos los ejemplos más sobresalientes; y, por último, sugeriremos al lector vídeos y referencias para seguir ahondando en ambos; y eso sin olvidar sugerencias de música, por supuesto. 2. Afinación justa 2.1. Escala diatónica justa Si consideramos las proporciones de la afinación pitagórica, las cuales reproducimos por completitud en la tabla 1, observaremos que ciertas notas tienen proporciones complicadas, como pueden ser las notas mi, la y si. En la afinación justa se persigue simplificar estas proporciones. Después de la octava y la quinta, la siguiente proporción más simple es la cuarta 4:3. Sin embargo, concatenar cuartas y quintas, o viceversa, no produce nuevos intervalos. En efecto, si añadimos una cuarta justa a una quinta justa, entonces tenemos que ⋅ = 2 y se genera una octava. Tampoco la concatenación de cuartas a partir de la nota do produce proporciones sencillas para las notas mi, la y si. Notas Do Re Mi Fa Sol La Si Do Proporción 1/1 9/8 81/64 4/3 3/2 27/16 243/128 2/1 Cents 0 203.91 407.82 498.04 701.96 905.87 1109.78 1200 Tabla 1: Afinación pitagórica para la escala diatónica Una opción es usar la proporción 5:4, que es la proporción asociada al quinto armónico, como muestra la serie armónica de la figura 1 (encima de cada armónico aparece la diferencia en cents con respecto a la división igual de la octava redondeado al entero más cercano). Figura 1: Serie armónica (figura adaptada de [Wik21a]) La proporción 5:4 genera una tercera mayor más consonante que la tercera pitagórica, que está dada por la proporción 81:64. Para comprobar esta afirmación, pínchese en el vídeo de más abajo, en que se pueden escuchar dos terceras mayores, la primera pitagórica y la segunda justa. Figura 2: Diferencia entre las terceras pitagórica y justa Si tomamos esta nueva proporción como base de la triada mayor, su proporción es 4:5:6, que significa que 5:4 es la proporción para do–mi y 6:4 = 3:2, la del intervalo do–sol. Saltando por quintas hacia arriba a partir de mi, obtenemos la nota si con una proporción de ⋅ = ; y si en cambio saltamos hacia abajo, entonces llegamos a la nota la mediante el siguiente cálculo: Este sistema de generar las notas de la escala diatónica se llama afinación justa o entonación justa. La tabla 2 muestra las proporciones y los valores en cents de la afinación justa, así como las diferencias entre esta y el temperamento igual y la afinación pitagórica. Obsérvese que la diferencia con las notas mi, la y si son grandes. Notas Do Re Mi Fa Sol La Si Do Proporción 1/1 9/8 5/4 4/3 3/2 5/3 15/8 2/1 Cents 0 203.91 386.31 498.04 701.96 884.35 1088.26 1200 Diferencia con el temperamento igual 0 3.91 -13.68 -1.96 1.96 -15.64 -11.73 1200 Diferencia con la afinación pitagórica 0 0 -21.51 0 0 -21.51 -21.51 0 Tabla 2: Afinación justa para la escala diatónica La diferencia entre las quintas justas (que son iguales que las pitagóricas) y las de temperamento igual no es tan pronunciada. Escúchese el vídeo de más abajo para apreciar las diferencias. Figura 3: Diferencia entre las quintas pitagórica y justa La triada mayor es un acorde que aparece en muchas culturas musicales; en particular, en la música occidental es un acorde fundamental de su armonía. Las afinaciones justas ya eran conocidas por los griegos. Dídimo primero alrededor del siglo I a.C. y más tarde Ptolomeo en el siglo II d.C. estudiaron y desarrollaron estas afinaciones en que la proporción 5:4 aparecen como generador de la afinación o de la escala. La tercer pitagórica tiene una proporción de 81:64 y la justa de 5:4. Su diferencia es = = 1.0125 y esta recibe varios nombres: coma sintónica, coma de Dídimo, coma ptolemaica o coma ordinaria. Si la palabra coma en esta serie aparece sin ningún adjetivo, nos estaremos refiriendo a la coma sintónica. En el audio de abajo aparecen la diferencia entre un do (frecuencia de 261.63 hercios) y un do más una coma sintónica (frecuencia de 264.900375 hercios). Figura 4: Diferencia de una coma sintónica entre dos notas 2.2. Escala cromática justa La afinación justa es en esencia un sistema de afinación en que las triadas mayores siguen la proporción 4:5:6. Las variaciones en las afinaciones justas provienen de cómo generan el resto de las notas hasta conseguir la escala cromática. Con el fin de describir mejor las afinaciones justas cromáticas, vamos a presentar la notación de Eitz; para una buena exposición de su origen y manejo, véanse [Bar51] y [Ben06]. La notación Eitz fue desarrollada por el músico y matemático del mismo nombre en 1891. Se basa en la idea de poner superíndices y subíndices a las notas que indiquen la desviación por comas sintónicas de la quintas puras. Así, la afinación pitagórica se escribe como: do0 - re0 - mi0 - fa0 - sol0 - la0 - si0 - do0 El superíndice 0 significa que todas las quintas son puras. Una nota que diga, por ejemplo, do-1 es un do obtenido por quintas menos una coma sintónica; análogamente, ocurre si nos encontramos do+1. Las notas que están a una coma por debajo se colocan en la fila de arriba y las que están una coma por encima se abajo. Entonces, la afinación justa de la escala diatónica aparece como sigue: la-1 mi-1 si-1 fa0 do0 sol0 re0 Figura 5: Afinación justa en la notación de Eitz La idea de colocar las notas con desviaciones de las quintas puras encima y debajo se debe al teórico de la música y compositor Hugo Riemann (no confundir con el matemático Bernhard Riemann de la hipótesis de Riemann). La notación de Eitz se generalizado en varias direcciones, por ejemplo, poniendo notas con diferentes comas (coma pitagórica, coma septimal, etc.). Siguiendo el libro de Barbour [Bar51] por su excelente exposición, vamos a describir algunas de las afinaciones justas más importantes descritas por su notación de Eitz. Empezamos con la afinación de Ramis de Pareja presentada en su libro Musica Practica de 1482. En sentido descendente de Pareja afina por quintas justas las sucesión sol-la♭ y luego partiendo de re-1 sube por quintas hasta el do#-1. Los acordes que quedan “bien afinados” son los correspondientes a las tonalidades do mayor, fa mayor y si♭ mayor. re-1 la-1 mi-1 si-1 fa#-1 do#-1 la♭0 mi♭0 si♭0 fa0 do0 sol0 Figura 6: Afinación justa de Ramis de Pareja Otra afinación justa interesante es la de Mersenne, publicada en 1637 (figura 7), donde se ven tres sucesiones de notas afinadas por quintas justas donde cada sucesión empieza a distancia respectiva de +1 coma, 0 comas y -1 coma contado desde la línea inferior. En realidad, Mersenne divide el círculo de quintas en tres sectores que afina por quintas justas. Ahora se aprecia que hay más triadas con afinación justa. re-1 la-1 mi-1 si-1 si♭0 fa♭0 do0 sol0 sol♭+1 re♭+1 la♭+1 mi♭+1 Figura 7: Afinación justa de Ramis de Pareja Hay muchas otras afinaciones justas, con frecuencia adaptadas al tipo concreto de instrumento (laúd, vihuela, órgano, etc.). De nuevo, recomendamos el libro de Barbour [Bar51] para un tratamiento riguroso e histórico de estas afinaciones. A modo de resumen, presentamos las principales características de las afinaciones justas: Los semitonos cromáticos son más pequeños que los semitonos diatónicos. Así, por ejemplo, sol# es más grave que la♭. Esto obligaba en los instrumentos de tecla a tener dos teclas diferentes, como se puede ver en la figura 8. Figura 8: Teclados con teclas para los semitonos cromáticos (figura adaptada de [Wik21b]) Como hemos visto más arriba, las terceras mayores justas son más pequeñas que las terceras pitagóricas y que las terceras del temperamento igual. Sin embargo, la situación es la contraria cuando se observan las terceras menores justas, que son más pequeñas que las correspondientes pitagóricas y de igual temperamento. La nota sensible es más grave en la afinación justa que en el caso pitagórico y de temperamento igual. Todos los tonos no tienen el mismo tamaño. Hay tonos grandes, como do–re, fa–sol, la–si, y tonos pequeños, como re–mi y sol–la. Los tonos grandes son mayores que los temperados, pero los tonos pequeños son menores. 3. Problemas armónicos de la afinación justa Volvamos a la afinación justa presentada más arriba: la-1 mi-1 si-1 fa0 do0 sol0 re0 Fijemos como tonalidad de referencia do mayor. Las triadas más importantes son las de los grados I, IV y V. En esta afinación esas triadas son do0-mi-1-sol0, sol0-si-1-re0 y fa0-la-1-do0. Las triadas menores vi y iii y vi, en cambio, tienen otra estructura en términos de afinación, a saber la-1-do0-mi-1 y mi-1-sol0-si-1. El problema aparece con la otra triada menor, la de ii, que es re0-fa0-la-1. En realidad, debería ser re-1-fa0-la-1. Si hiciésemos tal cosa, entonces el acorde del quinto grado se convertiría en sol0-si-1-re-1, y no funcionaría como un auténtico acorde de dominante. Para mayor comprensión de los problemas armónicos de la afinación justa, tomemos una progresión armónica muy común en la música occidental: I – vi – ii – V – I Parece razonablemente musicalmente hablando que cuando dos acordes adyacentes compartan una nota, esta no cambie de altura dentro de la afinación. Suponiendo de nuevo que la tonalidad es do mayor, el grado I es do0-mi-1-sol0. Por la regla que acabamos de establecer, el grado vi es la-1-do0-mi-1. Entonces, el grado ii es ahora re-1-fa0-la-1 porque la-1 es una nota en común y para mantener la distancia de quinta entre la primera nota del acorde y la tercera tenemos que establecer el re como re-1. A continuación, estaría el acorde de sol mayor. Como la nota re-1 es común, obtendremos el acorde sol-1- si-2-re-1. Por último, al caer en el primer grado, llegamos al acorde do-1- mi-2-sol-1. Hemos acabado una coma sintónica más bajo que cuando empezó la progresión. Esto en términos musicales no es aceptable. Escúchese de nuevo el audio de la figura 4. Esta situación se repite en secuencias de acordes tan usuales como I–IV–ii–V–I y I–iii–vi–ii–V–I, entre otras. Por último, recomendamos la lectura el libro de Benson [Ben06], páginas 173–176, para una discusión más profunda sobre los problemas armónicas de la afinación justa. 4. Escalas mesotónicas En esta sección entramos ya en las escalas mesotónicas. Este tipo de escalas pueden deducirse bien por una afinación, esto es, usando siempre proporciones enteras, o por temperamento, introduciendo números irracionales. Mostraremos ambos casos y empezaremos por los temperamentos. La idea esencial del temperamento mesotónico es la de afinar por terceras mayores puras a partir de la proporción 5:4. La escala mesotónica más común es la llamada escala mesotónica clásica o escala mesotónica de cuarto de tono. Las notas que se encuentran entre las notas afinadas por terceras justas se toman equidistantes con el siguiente procedimiento. Empezamos por la primera tercera mayor do–mi, de proporción 5∕4. La nota equidistante, la nota re, se afina con la proporción = ∕2. Esto nos deja la secuencia do–re–mi con las proporciones 1:∕2:5∕4. Con estas proporciones se afinan las secuencias fa–sol–la y sol–la–si. Sin embargo, antes de hacer afinar esas dos secuencias hay que decidir donde empiezan el fa. Hay dos semitonos que fijar, mi–fa y si–do. Las secuencias do–re–mi, fa–sol–la y sol–la–si suman 5 tonos de proporción ∕2 cada uno y, por tanto, quedan dos semitonos. Como hay que hacerlos equidistantes, se dividen por la mitad exacta. Eso en términos de proporciones equivale a extraer la raíz cuadrada. El semitono tiene, pues, el valor de: En esta cuenta estamos restando de la octava (el 2) los 5 semitonos (el 5) y la raíz cuadrada exterior aparece por la división en dos partes iguales. Entonces, para calcular la proporción de la nota fa, tenemos ⋅ = . Las proporciones finales del temperamento mesotónico clásico son: Notas Do Re Mi Fa Sol La Si Do Proporción 1/1 ∕2 5/4 2/1 Cents 0 193.15 386.31 503.42 696.57 884.73 1082.89 1200 Tabla 3: Temperamento mesotónico clásico para la escala diatónica Como se aprecia fácilmente en la tabla, las quintas ya no son puras (500 cents) y las terceras mayores son más pequeñas que en el temperamento igual. La nota sensible es más grave que en el temperamento igual. En cambio el semitono diatónico mi–fa es más grande. En la página web teoria.com [JRA21] el lector puede escuchar el Preludio en la bemol mayor BWV 862 de J. S. Bach en temperamento mesotónico. Una afinación mesotónica se puede conseguir a partir de la afinación pitagórica tomando la serie de quintas sucesivas y bajándolas un cuarto de coma sintónica en cada paso. Si empezamos en do, el diagrama de Eitz de una afinación mesotónica es este: mi-1 si-5∕4 do0 sol-1∕4 re-1∕2 la-3∕4 mi-1 fa+1∕4 do0 En general, una escala cromática se puede completar aplicando los principios anteriores, bien del temperamento o de la afinación. A modo de ejemplo, aquí tenemos la afinación mesotónica de Pietro Aaron del siglo XVI. mi-1 si-5∕4 fai#-3∕2 do#-7∕4 do0 sol-1∕4 re-1∕2 la-3∕4 mi-1 la♭+1 mi♭+3∕4 si♭+1∕2 fa♭+1∕4 do0 Figura 9: Afinación mesotónica de Pietro Aaron Se supone que las notas comunes de ambos extremos del diagrama de Eitz son las mismas (el do0 y el mi-1). La quinta del lobo se produce entre do# y la♭. Haciendo un ejercicio de abstracción, se pueden tomar diferentes divisiones de la coma sintónica. En el ejemplo anterior fue 1∕4, pero en general puede ser un número α ∈ (0,1). Cuando se piensa así, el esquema general de las afinaciones mesotónicas queda como sigue: mi-4α si-5α fa#-6α do#-7α sol#-8α doo sol-α re-2α la-3α mi-4α mi♭+3α si♭+2α fa♭α do0 Figura 10: Afinación mesotónica general 5. Para saber más El catedrático Luis Nuño, de la Universidad Politécnica de Valencia, y autor invitado de pasadas columnas, ha sacado varios vídeos ilustrando las afinaciones justas y pitagóricas. Dejamos dos de ellos a continuación. Figura 11: Entonación Justa: Batidos Figura 12: Entonación Justa: Implementación Práctica Desde la perspectiva histórica, dejamos otro vídeo de Elam Rotem, este sobre la afinación justa en el Renacimiento: Figura 13: Afinación justa en el Renacimiento En este vídeo se puede escuchar las suites y transcripciones para clave de Jean-Henry d'Anglebert, interpretadas por Byron Schenkman en un clave afinado con temperamento mesotónico de cuarto de tono. Figura 14: Suites y transcripciones para clave de Jean-Henry d'Anglebert, interpretadas por Byron Schenkman Una opción más sencilla que el programa de Audacity se puede encontrar en esta web: https://onlinetonegenerator.com/binauralbeats.html   Bibliografía [Bar51] J. Murray Barbour. Tuning and temperament: a historical survey. Dover Publications, Inc., New York, 1951. [Ben06] D. Benson. Music: A Mathematical Offering. Cambridge University Press, 2006. [Góm21] Paco Gómez. Afinamiento y temperamento (I), accedido el 20 de julio de 2021. [JRA21] José José Rodríguez Alvira. 2,500 años de temperamentos musicales, accedido el 20 de julio de 2021. [Wik21a] Wikipedia. Harmonic serie, accedido el 10 de julio de 2021. [Wik21b] Wikipedia. Split sharp, accedido el 20 de julio de 2021.

Domingo, 01 de Agosto de 2021 | Imprimir | PDF |  Correo electrónico

15. 116. (Julio 2021) Afinación y temperamento (I)

1. Introducción Este artículo inaugura una serie sobre la afinación y el temperamento. Tras más de diez años de columna nunca habíamos tratado este fascinante e importante tema, cuyas implicaciones matemáticas, como veremos, son notables. Curiosamente, el primer artículo de esta columna, publicado nada menos que en enero de 2004 por Vicente Liern [Lie04], versaba sobre afinaciones y temperamentos. Ha llegado el momento de reparar semejante postergación y zambullirnos con entusiasmo en el fantástico reino de la afinación y el temperamento. Comenzamos aclarando la diferencia entre afinación y temperamento. Un sistema de afinación es la elección de notas en base a proporciones de números enteros entre frecuencias, esto es, en base a números racionales. Por ejemplo, una quinta en el sistema de afinación pitagórico tiene proporción 3:2. Un temperamento es un sistema de afinación en que algunos de los intervalos no se pueden expresar como números racionales. En el temperamento igual una quinta tiene proporción 2, que es claramente un número irracional. Intentar un examen de los sistemas de afinación y temperamento antes de la época de los griegos implica per se una alta cuota de especulación, ya que no han quedado restos escritos, únicamente restos arqueológicos fragmentarios y escasos. Como excepción, un grupo de arqueólogos descubrió en 2008 fragmentos de una flauta hecha perforando huesos de buitre y de mamut la cueva de Hohle Fels, al sur de Alemania [Jon15]. Estas flautas han recibido el nombre de flautas neardentales y su construcción se remontan a una horquilla de 42.000-43.000 años a.C. En el siguiente vídeo se muestra una reconstrucción de la flauta y se ve a un flautista profesional tocarla (véase del minuto 0:50 al 1:32). La flauta tiene 4 agujeros y las notas que emite corresponden aproximadamente a una escala diatónica (como se aprecia en el vídeo). Figura 1: Flauta neardental En este primer artículo vamos a cubrir los conceptos básicos de afinación y temperamento, que requieren solo matemáticas básicas, y a continuación a estudiar la afinación pitagórica. 2. Elementos básicos de la afinación y el temperamento 2.1. Frecuencias Empezaremos a la manera clásica, a partir del monocordio. El monocordio consiste en una cuerda montada sobre una caja de resonancia E como la de una guitarra o un violín. La cuerda está atada en el extremo A. Hay dos puentes movibles, B y C, que se usan para cambiar las frecuencias. D es una rueda movible y W es un peso, el cual se usa para estudiar la relación entre la tensión y la frecuencia; véase la figura 2. Para esta exposición, consideraremos que C está fijo y únicamente moveremos el puente B. El monocordio fue un instrumento con el que se enseñaba teoría de la música, especialmente intervalos y afinación, desde la antigüedad hasta la Edad Media. Figura 2: El monocordo (figura adaptada de [Wik21b]) Si ahora pulsamos la cuerda en algún punto del segmento BC, se producirá un sonido de frecuencia f. Si ahora movemos el puente B hasta la mitad del segmento AC, que es el punto F en la figura 3, y volvemos a pulsar la cuerda, ahora en algún punto intermedio de CF, el sonido producido tendrá frecuencia 2f.   Figura 3: Producción de un sonido una octava más agudo (figura adaptada de [Wik21b]) El sonido de frecuencia 2f lo oiremos como una octava más alto que el sonido de frecuencia f. Este hecho era ya conocido por los griegos y en especial por Pitágoras. Si tomamos la proporción entre la frecuencia del segundo sonido con respecto a la del primero, esta será de 2:1 y se corresponderá también con el cociente . Se pueden explorar otras proporciones, como por ejemplo, 3:2 o 4:3. Si movemos el puente B a un punto F de modo que , el sonido obtenido será el de una quinta perfecta. En general, dados dos sonidos de frecuencias f1,f2 con f1 < f2, el cociente da la diferencia de altura entre ellos. Así, si el cociente es 2, la diferencia es una octava; si el cociente es 3/2, es una quinta perfecta, y así sucesivamente. 2.2. División igual de la octava y cents Para precisar las diferencias entre los intervalos que aparecerán en los distintos sistemas de afinación y temperamento, necesitaremos un método para comparar intervalos. Hay muchos métodos, pero uno que permite una comparación cómoda y precisa es el de los cents. Formalmente, el cent es una unidad de comparación de frecuencias y se basa en la división de una octava en 1.200 partes. Un cent equivale a c = ≈ 1.00057778950655. Nótese que está definición se basa en el hecho de que las diferencias interválicas son factores multiplicativos de las frecuencias, como vimos en la sección anterior. En la escala cromática habitual, un semitono son 100 cents; una quinta, 700; y una octava, 1200. La ventaja de medir las diferencias de frecuencias con cents es que las octavas aparecen igualmente espaciadas y ello es porque los cents es una escala logarítmica. Si esas diferencias de frecuencias se miden en el espacio de las frecuencias, no aparecen igualmente espaciadas y la comparación es mucho más difícil. Dadas dos notas de frecuencias f1,f2, la diferencia en cents entre las dos (suponiendo f1 < f2) es Y, recíprocamente, si la frecuencia de la primera nota f1 es conocida así como el número de cents n hasta la segunda nota es En el temperamento igual, una tercera mayor son 400 cents, mientras que en la afinación pitagórica es de 407.82 cents; esta última cantidad se ha obtenido de introducir en la fórmula anterior la proporción entre las frecuencias, que es de , como veremos más adelante. 2.3. La serie armónica Para terminar esta sección, vamos a tratar la serie armónica, pues tiene importancia notable en los sistema de afinación y temperamentos. Muchos instrumentos musicales están basados en la emisión de frecuencias de una caja de resonancia, como por ejemplo en el caso de las cuerdas o de los instrumentos de viento. El sonido que se oye en esos instrumentos es una combinación de varias frecuencias que suenan a la vez. La frecuencia más grave se llama frecuencia fundamental y el resto de las frecuencias son los armónicos. Los armónicos tienen frecuencias que son múltiplos enteros de la frecuencia fundamental. Este conjuntos de armónicos asociados a una frecuencia fundamental se llama serie armónica. En la figura 4 se puede ver los primeros 20 términos de la serie armónica de un sonido de frecuencia 32.70, el do1 en notación científica. Encima de cada armónico aparece la diferencia en cents con respecto a la división igual de la octava redondeado al entero más cercano. Las notas marcadas en azul son resultan demasiado bajas y las notas en rojo, demasiado altas. En el caso del la♭, la diferencia es de +41 cents, que es casi un cuarto de tono, diferencia que es claramente perceptible por un oído normal. Figura 4: Serie armónica (figura adaptada de [Wik21a]) El segundo armónico es la octava, como se ve en la serie; el tercero es la quinta; el cuarto vuelve a ser la octava; el quinto es la tercera mayor (algo más baja que la tercera mayor de la división igual de la octava, unos 14 cents menos); y el sexto es la quinta. 3. Afinación pitagórica Los griegos tenían múltiples sistemas de afinación, que glosamos brevemente en la siguiente sección, pero la afinación que permaneció en la práctica común fue la afinación pitagórica. La afinación pitagórica establece las notas en base a los dos primeros intervalos de la serie armónica, esto es, la octava y la quinta, que tienen proporciones 2:1 y 3:2, respectivamente. Veamos cómo funciona tal construcción. Empecemos por tomar una nota cualquiera, digamos do. Usar la octava no da ningún intervalo nuevo distinto de la octava, de modo que aplicamos la proporción 3:2 para obtener nuevos intervalos. Como 3:2 es una quinta, llegamos a sol. Si multiplicamos la frecuencia de sol por 3:2, obtenemos re en la segunda octava, de proporción 9:4. Como queremos mantener las notas en una sola octava, pasamos este re a la primera octava dividiendo por 2. Esto da como resultado 9:8 como proporción del intervalo do–re; véase la tabla 1. Continuamos con este procedimiento y saltamos otra quinta desde re, multiplicando por 3∕2, y aterrizamos en la nota la, de proporción 27:16, que se mantiene en la octava de referencia. Damos otro salto, ahora a mi, pero salimos de la octava. Dividimos por dos la proporción y obtenemos 81:64. Por último, llegamos a la nota con otro salto de quinta y llegamos a la nota si, que nos da la proporción 243:128. En la tabla 1 se muestran todas las proporciones de la afinación pitagórica así como sus valores en cents. Se puede apreciar que todos los intervalos no son iguales con respecto al temperamento igual. Nótese además que la nota fa ha sido obtenida dan un salto hacia el registro grave en lugar de hacia el registro agudo. Su proporción se ha conseguido multiplicando por 2∕3 para bajar una quinta y por 2 para subir a la octava, lo que da una proporción de 4:3. Notas Do Re Mi Fa Sol La Si Do Proporción 1/1 9/8 81/64 4/3 3/2 27/16 243/128 2/1 Cents 0 203.91 407.82 498.04 701.96 905.87 1109.78 1200 Tabla 1: Afinación pitagórica para la escala diatónica La afinación pitagórica presenta varios problemas. El primero de ellos es el del tamaño de los semitonos. Un tono tiene proporción 9∕8, por ejemplo, do–re. Si tomamos el semitono si–do, que tiene proporción y formamos un tono con estos dos semitonos, obtenemos  ⋅ = ≈ 1.10985715, que claramente no es igual a 9∕8 = 1.125. El segundo problema viene dado por el círculo de quintas (más bien la espiral de quintas, como veremos). La tabla de arriba se puede completar de modo que incluya las 12 notas de la escala cromática. Se puede partir de un do y subir por quintas hasta el sol# y luego completar las notas que faltan, que son de do hasta la♭, descendiendo por quintas. La tabla de proporciones que resulta siguiendo este procedimiento se muestra a continuación: Notas Do Sol Re La Mi Si Fa# Do# Sol# Proporción 1/1 3/2 9/8 27/16 81/64 243/128 729/512 Cents 0 701.96 203.91 905.87 407.82 1109.78 611.73 113.68 815.64 Notas Do Fa Si♭ Mi♭ La♭ ~Sol# Proporción 1/1 4/3 9/16 32/27 128/81 Cents 0 498.04 996.09 294.13 792.18 Tabla 2: Afinación pitagórica para la escala cromática Si la tabla anterior la ponemos en forma de círculo de quintas, se entenderá el problema más claramente. En efecto, cuando se recorre el círculo de quintas en ambos sentidos las notas la♭ y sol# no coinciden, es decir, el círculo de quintas no se cierra. ¡En realidad, es una espiral de quintas! Y una espiral potencialmente infinita. Figura 5: Círculo de quintas con la afinación pitagórica (figura tomada de [Ben06]) La diferencia entre las notas la♭ y sol# se llama coma pitagórica o coma ditónica (el círculo en la figura) y corresponde a Esto significa que la afinación pitagórica funciona sobre el principio de que subir 12 quintas y bajar 7 octavas nos deja casi en el mismo sitio de que partimos. La diferencia es precisamente la coma pitagórica. Entre todas las quintas que produce el sistema pitagórico, la más desafinada es la quinta sol#-mi♭ (notada como una sexta disminuida). Recibe el elocuente nombre de quinta del lobo (se consideraba que se asemejaba al aullido de un lobo). Dado que los saltos de quinta nunca cierran el círculo, aparecen nuevas notas, como se muestra en la figura 6, donde se aprecia las dos primeras vueltas de la espiral. Figura 6: Espiral de quintas con la afinación pitagórica (figura tomada de [Ben06]) 4. Para saber más En música que no requiere cambios de tonalidad, como puede ser la música modal o la monodia, la afinación pitagórica es factible en la práctica musical; de hecho, ha sido así durante siglos y en muchas tradiciones musicales. A continuación, se mencionan varios ejemplos entre muchos posibles. El primero es del grupo Gothic voices, especializado en música antigua. Figura 7: Gothic voices - Il nome del bel fior El siguiente vídeo es un ejemplo en música instrumental, en este caso con un órgano portátil. Figura 8: Catalina Vicens - Audi Pontus, Audi Tellus, del Códice de Las Huelgas Para el lector ávido de profundizar en los sistemas de afinación y temperamento recomendamos el libro de Goldáraz Afinación y temperamentos históricos [Gol04] y con un sabor más matemático, el libro de Benson A mathematical offering [Ben06]. Un libro que brilla por su erudición es el de Barber [Bar51], de título Tuning and temperament: a historical survey. Recomendamos al lector la exposición de los sistemas de afinación griegos, que no han sido incluidos aquí por su excesiva longitud. Por último, no podemos dejar de recomendar los vídeos de Elam Rotem del proyecto Early Music Sources; el vídeo relevante en la columna de este mes es Temperaments - What you need to know [Rot20].   Bibliografía [Bar51] J. Murray Barbour. Tuning and temperament: a historical survey. Dover Publications, Inc., New York, 1951. [Ben06] D. Benson. Music: A Mathematical Offering. Cambridge University Press, 2006. [Gol04] J. Javier Goldáraz. Afinación y temperamentos históricos. Alianza Editorial, Madrid, 2004. [Jon15] Josh Jones. Hear the World's Oldest Instrument, the "Neanderthal Flute", Dating Back Over 43,000 Years, 10 de febrero de 2015. [Lie04] Vicente Liern. Afinación, enero de 2004. [Rot20] Elam Rotem. Temperaments - What you need to know, 9 de mayo de 2020. [Wik21a] Wikipedia. Harmonic series, accedido el 10 de julio de 2021. [Wik21b] Wikipedia. Monochord, accedido el 10 de julio de 2021.

Viernes, 16 de Julio de 2021 | Imprimir | PDF |  Correo electrónico

16. 115. (Abril 2021) Herramientas de MIR en MatLab

1. Tecnología Musical y Musicología Computacional Hoy en día la música se investiga desde muchos puntos de vista, tal es su complejidad por un lado y tal es la variedad y potencia de los métodos de investigación modernos por otro lado. Las siglas de MIR, Music Information Retrieval, vienen del inglés y es el nombre que se le da actualmente al campo de la Computación Musical en un sentido muy amplio. Originalmente, el campo del MIR empezó en los años 60 con un pequeño grupo de ingenieros y músicos intentando resolver problemas prácticos de tratamiento musical, entre los cuales se contaba el de la recuperación de la información. Poco a poco se fueron juntando investigadores y profesionales de este incipiente campo y tras no mucho tiempo explotó como disciplina científica. Aunque los objetivos y métodos pronto engulleron a los problemas de tratamiento de la información musical de los primeros tiempos, por razones que aun hoy en día no alcanzo a comprender, se mantuvo el nombre de MIR. Creo que un nombre más adecuado sería el de Computación Musical (que uso en mis columnas aquí y en otros trabajos). Sea como fuere, el nombre se ha quedado por razones históricas y es el más usado para referirse a esta disciplina. Actualmente, la Computación Musical (MIR) es un campo multidisciplinar que se nutre de la propia Música, la Musicología, Computación —en particular, de la Inteligencia Artificial y la Ciencia de Datos —, Cognición y Psicología, diversas disciplinas de humanidades tales como la Lingüística, la Sociología. Entre los problemas que aborda la Computación Musical están el análisis musical (problemas tales como la similitud melódica, la detección del pulso, el reconocimiento de la estructura musical, las medidas de complejidad rítmica, melódica, armónica, solo por nombrar unos pocos); y a estos se añade, la clasificación de la música, los sistemas de recomendación, la generación automática de música, el estudio de la conexión entre música y emoción por métodos computacionales, la transcripción automática de la música, la separación de fuentes en una señal de audio musical, entre otros. En esta columna se han tratado de manera divulgativa muchos de estos problemas; véanse las siguientes columnas y las referencias que tienen: [Góm12a, Góm11a, Góm12b, Góm13, Góm11b, Góm14, Góm16, Góm18, Góm20b]. Dentro del MIR hay una rama evidentemente tecnológica e industrial y, de hecho, empresas importantes tales como Yamaha, Pandora, Sony, Spotify, por ejemplo, trabajan en las aplicaciones de los conceptos y métodos del MIR (quizás sea el problema de la recomendación musical el más arquetípico). Otra disciplina distinta de la Computación Musical es la Musicología Computacional. Este último campo consiste en el estudio musicológico a través de métodos computacionales. Esta rama de la musicología, de origen moderno cuando se compara con la musicología histórica, por ejemplo, se suele considerar como una parte de la Musicología Sistemática. La Musicología Computacional no llegó sin rechazo e incomprensión en un principio; y, por otra parte, algunos de sus practicantes cometieron excesos que alimentaron tal rechazo. Para un resumen de este debate, véase el artículo de esta columna Alcance y extralimitaciones de las matemáticas y la computación en la música [Góm20a]. Por otra parte, la Computacional Musical ha prestado apoyo metodológico e inspirado varios problemas a la Musicología Computacional. 2. La herramienta MIRtoolbox En la columna de este mes nos vamos a centrar en algo más práctico. Es algo que me han pedido algunos lectores, músicos principalmente, y es que describa y comente herramientas de computación musical. En particular, voy a describir la herramienta MIRtoolbox, diseñada y construida por los investigadores Lartillot y Toiviainen (con la intervención de Tuomas en la primera parte) [LT07a, LTE07]. MIRtoolbox es una herramienta escrita en MATLAB y está concebida para la extracción de características musicales de bajo y medio nivel de música dada en formato de audio (y no en formato simbólico como pueda ser el MIDI). Una de sus ventajas es que MIRtoolbox ha sido diseñado con un usuario no experto en programación en mente y, como consecuencia de ello, la sintaxis y la interfaz son muy fáciles de usar. MATLAB es el acrónimo de MATrix LABoratory. Inicialmente, este paquete de cálculo se especializó en el cálculo de matrices. Posteriormente, se convirtió en un paquete de cálculo multi-propósito y hoy en día es el estándar en ingeniería y en buena parte de las matemáticas. MATLAB es multi-plataforma y existen versiones para Windows, macOS, Unix y GNU/Linux. Tiene tanto cálculo simbólico como cálculo numérico y a través de sus toolboxes, módulos especializados, se pueden ampliar sus capacidades de cómputo a campos concretos tales como el procesamiento de la señal, la simulación, la biología computacional, la estadística avanzada, entre otros. La web de este paquete se puede encontrar en [Mat21]. En la figura de abajo se puede ver el interfaz gráfico de MATLAB. Figura 1: Interfaz gráfica de MATLAB MIRtoolbox es una herramienta gratuita y se puede descargar en [LT07b]. Sirve tanto para la investigación como para la docencia. A continuación vamos a describir las principales características de interés para el musicólogo computacional y/o sistemático. 3. Extracción de caracerísticas musicales en MIRtoolbox En la figura 1, tomada del propio artículo [LT07a] de presentación de la herramienta, muestra los distintos niveles de extracción. Todos los procesos empiezan por considerar la señal (a la izquierda) y se van aplicando diversas operaciones según se va hacia la izquierda. Leída de izquierda a derecha, las características musicales van de bajo nivel a medio nivel. Leída en de arriba abajo la figura 1 nos devuelve las principales operaciones del MIRtoolbox en orden creciente de complejidad computacional. Figura 2: Características musicales extraíbles con el MIRtoolbox (figura tomada de [LT07a] He aquí una lista con sucintas explicaciones de las principales características extraíbles desde MIRtoolbox: La tasa de cambios de signo (zero-crossing rate), que se usa en procesamiento musical y del habla y que sirve para identificar sonidos percusivos (por ejemplo, en problemas de separación de fuentes). La energía de la señal, medida como el valor cuadrático medio (RMS). El contorno de una señal, que da importante información sobre su comportamiento desde un punto de vista musical, por ejemplo, sobre el timbre o la finalidad melódica. El espectro de la señal, obtenido a través de la transformada de Fourier, del cual se obtienen medidas relevantes para la identificación de la señal así como la detección de patrones dentro de la misma. Entre esas medidas, encontramos las básicas tales como el centroide, la curtosis o el coeficiente de asimetría; y luego más complejas, el flujo espectral, la disonancia textural (roughness), la escala Mel. A partir de estas medidas se pueden obtener los descriptores de medio nivel tales como tempo, claridad del pulso, altura o fluctuación. Como muestra de la sencillez de uso de MIRtoolbox, en la figura 2 se pueden ver los comandos para obtener algunas de las medidas anteriores. Empezamos por cargar un fichero de audio (1); lo descomponemos en secuencias (2); extraemos el espectro (3); convertimos el espectro del dominio de la frecuencia al dominio de la escala de Mel (4); por último, obtenemos los coeficientes MFCC. Figura 3: Sintaxis de MIRtoolbox (figura tomada de [LT07a] El proceso anterior se puede resumir más gráficamente como se muestra en la figura 4: Figura 4: Cálculo de los coeficientes MCC en MIRtoolbox (figura tomada de [LT07a] Por último, ilustramos el proceso de estimación de la fuerza tonal; véase la figura 4. Esta medida cuantifica cuán predominante es una tonalidad en una pieza de música. El método sigue las ideas de Krumhansl y Kessler; véanse [KK82, Kru90]. En primer lugar, se pasa del dominio de la frecuencia al de las alturas mediante una transformación logarítmica de aquellas. Esta representación es el cromagrama. Este cromagrama se consolida y se ponen en las mismas clases las alturas que están a distancia de un múltiplo de una octava entre sí. Esto da una representación en forma de histograma de las clases de alturas. Se aplica entonces correlación cruzada entre el histograma obtenido y los histogramas de las 12 tonalidades posibles dados en [KK82], los cuales provienen de experimentos hechos con oyentes. Figura 5: Cálculo de los coeficientes MCC en MIRtoolbox (figura tomada de [LT07a] 4. Conclusiones El MIRtoolbox permite muchos más análisis y procesos de computación musical que los brevemente glosados aquí. Por ejemplo, el análisis rítmico, la segmentación a varios niveles, el análisis de grandes volúmenes de datos, el análisis de secuencias. Remitimos al lector al manual de la herramienta, que se puede encontrar en [LT07a]. En este artículo se encontrarán también detalles técnicos de la arquitectura y la representación de datos de la herramienta.   Bibliografía [Góm11a] Paco Gómez. Distancia y similitud musical, mayo de 2011. [Góm11b] Paco Gómez. Distancia y similitud musical (I), mayo de 2011. [Góm12a] Paco Gómez. El teorema del hexacordo (I), Octubre de 2012. [Góm12b] Paco Gómez. Medidas matemática de síncopa (I), Octubre de 2012. [Góm13] Paco Gómez. COFLA: la música flamenca y su estudio computacional, agosto de 2013. [Góm14] Paco Gómez. Teoría generativa de la música (I), junio de 2014. [Góm16] Paco Gómez. Composición algorítmica (I), junio de 2016. [Góm18] Paco Gómez. Ritmos euclídeos y ritmos equilibrados, marzo de 2018. [Góm20a] Paco Gómez. Alcance y extralimitaciones de las matemáticas y la computación en la música, julio de 2020. [Góm20b] Paco Gómez. Música y entropía - I, julio de 2020. [KK82] C. L. Krumhansl and E. J. Kessler. Tracing the dynamic changes in perceived tonal organization in a spatial representation of musical keys. Psychological Review, 89:334–368, 1982. [Kru90] C. L. Krumhansl. Cognitive Foundations of Musical Pitch. Oxford University Press, New York, 1990. [LT07a] Olivier Lartillot and Petri Toiviainen. Mir in matlab (ii): A toolbox for musical feature extraction from audio. pages 127–130, 01 2007. [LT07b] Olivier Lartillot and Petri Toiviainen. MIRtoolbox, 2007. [LTE07] Olivier Lartillot, Petri Toiviainen, and Tuomas Eerola. A matlab toolbox for music information retrieval. volume 4, pages 261–268, 01 2007. [Mat21] Mathworks. MATLAB, 1994–2021.

Lunes, 12 de Abril de 2021 | Imprimir | PDF |  Correo electrónico

17. 114. (Marzo 2021) Escalas multioctavas

Las escalas multi-octavas La música es un fenómeno altamente estructurado que depende de una serie de principios organizativos. Con estos principios, que posibilitan su existencia, están familiarizados tanto músico como oyentes, si bien a menudo de forma inconsciente. Entre esos principios se cuenta la organización rítmica y melódica, y dentro de esta última destacan las escalas. El concepto de escala está presente en la mayoría de tradiciones musicales. La escala, en su papel estructural, constituye una forma de determinar el contenido tonal de una pieza. Aunque existe una gran variedad de escalas en el mundo, diferentes en muchos sentidos, la mayoría tiene ciertos elementos en común. Como señala Patel [Pa08] en Music, Language and the Brain, las escalas generalmente contienen de 5 a 7 notas por octava, progresan por grados continuos de entre 1 y 3 semitonos y normalmente no son simétricas. Una característica muy extendida, y que suele ser parte de la propia definición de escala en la mayoría de los casos, es que la escala consta de una serie de notas que se repite en cada octava. Esto no es sorprendente teniendo en cuenta que está demostrado que los seres humanos percibimos las notas a distancia de octava como equivalentes, seguramente uno de los pocos universales de la música; véase [BJ11] para más información sobre los universales musicales. Lo anterior nos lleva a preguntarnos: ¿es la repetición en la octava un requisito indispensable de toda escala? ¿Es posible una escala en que no repitiese en la octava? ¿Tendría sentido musical? Aunque para la mayoría sea un fenómeno seguramente desconocido, la realidad es que sí existen escalas que no se repiten en la octava. De hecho, hay culturas musicales centenarias en las que el contenido tonal es determinado por escalas que no se repiten en la octava o escalas multi-octava. La escala del Znamenny Rospev –el canto litúrgico de la iglesia ortodoxa rusa, probablemente de origen bizantino [Sw40]– es un claro ejemplo. Como se puede observar en la figura 1, consta de una serie de tetracordios mayores consecutivos, repitiendo así en la cuarta, en vez de en la octava. Mientras que la primera octava contiene la nota si natural, la segunda contiene un si bemol y si se prolongara la estructura a lo largo de más octavas, irían apareciendo cada vez más notas diferentes en cada octava. Este tipo de escala es común en la música folclórica rusa, así como de países de la región tales como Albania, Georgia, Azerbaiyán o Bulgaria [N16]. Figura 1: Construcción de escalas – La escala Znamenny Las escalas multi-octavas, aunque poco comunes, fueron utilizadas y estudiadas a mediados de la primera mitad del siglo XX por músicos y musicólogos como Nicolás Slonimsky, Joseph Shillinger, Elliot Carter, Alfred Schnittke; también por músicos de jazz como David Liebman, David Baker o Dennis Sandole; así como por compositores actuales como Joel Hoffman, Gao Weijie o Ramón Paús. Estas escalas suelen estar construidas de una de las siguientes maneras: Escalas simétricas a partir de un intervalo que divide un determinado número de octavas de manera equidistante; véanse [Sl47], [Sh46] y [Ym13]. Por una sucesión de tetracordios diferentes; véanse [P61], [Ba90] y [Li91]. Por una sucesión de tetracordios similares; véase [P61]. Por la combinación de dos escalas de una octava con una misma tónica; véanse [P61] y  [Ym13]. La gran variedad de música que ha brindado este concepto justifica la validez del mismo, pero, por ahora, pocos investigadores se han dedicado a estudiar las características y propiedades estructurales de estas escalas. Por razones evidentes, la escala que más ha sido estudiada en este sentido ha sido probablemente la escala mayor. Estudios de investigadores como Carlton Gamer [Ga67], Clough y Douthett [CD91], Clough y Myerson [CM85], o Carey y Clampitt [CM89], han conseguido desvelar propiedades auténticamente sorprendentes y fascinantes de esta colección tan determinante en la historia de la música. A continuación, vamos a describir brevemente algunas de estas características con la siguiente pregunta en mente: ¿Es posible construir una escala multi-octava que comparta algunas de estas características? Propiedades de la escala mayor La escala diatónica, así como la escala pentatónica, son sin duda de las escalas más relevantes en la historia de la música. Han definido y estructurado el contenido tonal en múltiples culturas musicales y épocas. Lo cierto es que están íntimamente relacionadas y sus propiedades han sido estudiadas por numerosos investigadores de lo que se denomina la teoría diatónica. Para un excelente resumen de la teoría diatónica, véase el primer capítulo de la tesis de Carey [Ca98]. Tomemos un momento para pensar en el teclado del piano, que consta de 7 teclas blancas y 5 teclas negras por octava. Las teclas blancas corresponden a la escala mayor (en concreto a la escala de Do mayor) y las teclas negras corresponden a la escala pentatónica (en concreto a la escala pentatónica de Sol bemol mayor). Por lo que, si tomamos las doce notas de la colección cromática y omitimos las siete notas de la escala mayor, quedan las cinco notas de la escala pentatónica. Muchos investigadores se refieren a este hecho como el complemento de la escala mayor. Es llamativo que la cardinalidad de estas escalas –esto es, el número de notas de la escala–, cinco y siete, sean primos relativos con 12, el número de semitonos en que se divide la octava (primos relativos significa que no tienen divisores comunes). Con estas cardinalidades es imposible la formación de escalas simétricas1. Además, ambas escalas comparten el mismo intervalo generador, la quinta, ya que sus notas pueden ser obtenidas recorriendo el ciclo de quintas siete y cinco pasos, respectivamente. Como muestra la figura 2, si recorremos siete pasos desde la nota fa, obtenemos las notas de la escala de do mayor, mientras que, si recorremos solo cinco, obtenemos las notas de la pentatónica de fa mayor. Si repitiéramos esto desde cada una de las 12 notas en el ciclo de quintas, obtendríamos los 12 tonos de la escala mayor y pentatónica, respectivamente. Figura 2: Intervalo generador En las siguientes secciones estudiaremos algunas propiedades estructurales de la escala diatónica. Escalas de regularidad máxima o escalas euclídeas Para definir este tipo de escalas, supondremos que tenemos una colección de notas, llamada el universo cromático o la colección cromática, de la cual elegiremos un subconjunto de notas que formará la escala. En las escalas occidentales, el universo cromático suele estar formado por 12 semitonos y el número de notas de las escalas más comunes suele ser 5 o 7. La propiedad de regularidad máxima fue definida por Clough y Douthett [CD91] y consiste en exigir que las notas de la escala estén distribuidas de la manera más regular posible entre las notas del universo cromático. Una analogía común para explicar este fenómeno es el de una mesa redonda en la que hay 12 sillas distribuidas de manera uniforme, fijadas de manera que no se pueden cambiar, y hay que distribuir a los invitados de la manera más regular posible. En el caso de seis invitados, solo hay una solución correcta, como muestra la figura 3. En el caso de, por ejemplo, siete invitados, como en la escala mayor, la solución no es tan evidente. No es posible distribuir siete en doce de una manera totalmente uniforme, por lo que hay que buscar la manera más uniforme posible o de máxima regularidad (maximally even). Las escalas con regularidad máxima se llamarán ME (por sus siglas en inglés). Figura 3: Distribución uniforme de 6 en 12 En lo que sigue, vamos a referirnos al artículo de esta misma columna de marzo del 18 Ritmos euclídeos y ritmos equilibrados [Go18]. Ilustraremos el proceso con un ejemplo de escalas. Supongamos que tenemos 17 semitonos y queremos distribuir de forma regular 7 notas entre los 17 semitonos. Estas 7 notas formarán la escala heptatónica en un universo cromático de 17 semitonos. Sigamos los pasos dados en la figura 4. Primero, alineamos las notas de la escala y añadimos notas que no son de la escala hasta completar las 17 notas totales. Esto se representa por siete unos (la escala) y diez ceros (el resto); véase la figura 4-paso (1). A continuación, formamos grupos de 7, los cuales corresponden a efectuar la división de 17 entre 7; obtenemos, pues, 7 grupos formados por [1 0] (en columnas en el paso (2) de la figura 4). Sobran tres ceros, lo cual indica que en el paso siguiente formaremos grupos de 3. Tras formar el primer grupo —véase el paso (3) de la figura 4— nos quedamos sin ceros. Continuamos agrupando de 3 en 3 tomando los grupos de la otra caja, en la que quedan 4 columnas (figura 4-paso (4)). Procedemos así que queden uno o cero grupos; de nuevo, esto es equivalente a efectuar la división de 7 entre 3. En nuestro caso, queda un solo grupo y hemos terminado (paso (5)). Finalmente, la escala se obtiene leyendo por columnas y de izquierda a derecha la agrupación obtenida (paso (6)). Figura 4: Escalas regulares Tras este proceso hemos obtenido una escala microtonal de 7 notas en un universo cromático de 17 notas. Para más información sobre distribuciones regulares en ritmos y escalas, véanse [DGMM+09], [GTT09a] y [GTT09b]. Por último, querríamos incluir la observación de que, si una escala es de regularidad máxima (ME), entonces su complementario también lo es. El complementario de una escala se construye intercambiando notas de la escala por notas que no lo son y viceversa. En términos de la notación de ceros y unos de arriba, el complementario consiste en intercambiar ceros y unos. La idea que hay detrás de este hecho es que toda distribución regular de notas en un universo cromático implica también una distribución regular de las notas que no están en la escala. Las escalas profundas o de multiplicidad única Esta propiedad fue definida por Carlton Gamer [Ga67] en 1967. Las escalas con la propiedad de profundidad (deep scale property) muestran una propiedad denominada multiplicidad única de distancias (unique multiplicity property). Esta propiedad significa que cada intervalo se repite un número único de veces, donde se cuentan todos los intervalos posibles entre las notas de la escala. La escala mayor contiene, por ejemplo, dos intervalos de segunda menor (o séptima mayor), cinco intervalos de segunda mayor (o séptima menor), cuatro intervalos de tercera menor (o sexta mayor), tres intervalos de tercera mayor (o sexta menor), seis intervalos de cuarta justa (o quinta justa) y un intervalo de cuarta aumentada (o quinta disminuida). Esta relación se refleja en las notas en común en las diferentes transposiciones de la escala; dos escalas mayores a distancia de semitono tendrán dos notas en común, dos escalas a distancia de tono tendrán cinco notas en común, etc. Para que una escala tenga la propiedad de la profundidad tiene que generarse mediante un intervalo primo relativo con el número de semitonos de la colección cromática completa. Además, el número de notas de la escala corresponderá a la mitad o la mitad más uno de la colección cromática. Si el número de notas es d y la colección cromática completa es n, el número de notas de una escala profunda será d = [n/2] o d = [n/2] + 1. En el caso de la escala mayor, su intervalo generador es la quinta– que abarca siete semitonos, siendo así relativamente primo a la colección cromática de 12– y su número de notas sería 7= 12/2 + 1. Las escalas bien formadas Esta propiedad la definieron Carey y Clampitt [CC89] en un conocido artículo de 1989. En esencia, implica que la simetría de su intervalo generador se mantiene al reordenar las notas dentro de una octava por grados conjuntos para formar la escala. Esto se entiende mejor de una manera gráfica. La figura 5 muestra las notas de la escala de do mayor en un ciclo de quintas. A la izquierda, las notas han sido unidas siguiendo el ciclo de quintas; a la derecha por grados conjuntos (do-re-mi-fa-sol-la-si-do). Como se puede observar, ambas opciones resultan en polígonos con simetría rotacional. Figura 5: Simetría en la escala mayor (figura tomada de [CC89]) También es el caso de la escala pentatónica, como podemos observar en la figura 6: Figura 6: Simetría en la escala pentatónica (figura tomada de [CC89]) Pero no es así si recorremos, por ejemplo, seis pasos en el ciclo de quintas para formar una escala hexátona, como en la figura 7: Figura 7: Ejemplo de escala en la que simetría del intervalo generador no se mantiene en la escala (figura tomada de [CC89]) En busca de escalas multi-octava con buenas propiedades estructurales Posiblemente, en parte, gracias a las sorprendentes propiedades estructurales descritas en la sección anterior, la colección diatónica es sin lugar a duda la más utilizada de las 462 posibilidades teóricas de escalas heptatónicas de una octava. La pregunta que nos hacemos en este artículo es bastante natural: ¿es posible encontrar las mismas propiedades en una escala multi-octava? Las propiedades de escala profunda y de ser bien formada parecen, a priori, imposibles de aplicar en un contexto de escala multi-octava. En primer lugar, si las notas de la escala deben poder obtenerse por un intervalo generador ¿cómo se ordenan luego para formar una escala? En el caso de una escala de una octava la solución es evidente (se ordenan por grado conjunto de grave a agudo dentro de una octava), pero, al abarcar la escala más octavas, ¿cómo se disponen las notas a lo largo del registro completo sino es de manera arbitraria? Este problema se amplifica cuando consideramos que una escala multi-octava puede contener potencialmente los 12 tonos a lo largo de su registro total. ¿De qué nos sirve el concepto de intervalo generador para obtener las notas de la escala si finalmente las vamos a incluir todas? No obstante, en esta sección nos vamos a armar de valor y embarcar en la búsqueda de una escala multi-octava que muestre las tres propiedades descritas anteriormente en relación a la escala mayor. Escalas de regularidad máxima La cantidad de escalas multi-octava posibles es prácticamente infinita, por lo que es importante delimitar nuestra búsqueda. Nos restringiremos a las escalas de dos octavas. Vamos a empezar por la propiedad de regularidad máxima, que es relativamente sencilla de aplicar a este tipo de escalas. Cualquier número de notas d pueden ser distribuidas de la manera más uniforme a lo largo de un rango total de c semitonos, en el caso de dos octavas, 24. Evidentemente, no todas las opciones tienen sentido como escala. Si elegimos un número demasiado grande para d, tendremos que agrupar las notas demasiado para lo que solemos entender como escala; por ejemplo, si d = 23, la escala será prácticamente cromática. Por lo contrario, si d es un número demasiado pequeño, los espacios entre las notas serán demasiado grandes para funcionar como escala; imaginemos, por ejemplo, las posibles agrupaciones de d = 2. Por esta razón, vamos a imponer tres restricciones en cuanto a la sucesión de intervalos dentro de las escalas, comunes a la mayoría de escalas utilizadas en la música occidental2 (véanse [Ty04] y [Pr78]): No consideraremos escalas en las que existan intervalos de dos semitonos consecutivos. No consideraremos escalas en las que existan intervalos mayores a tres semitonos. No consideraremos escalas en las que existen dos intervalos de tres semitonos consecutivos. Con estas tres restricciones garantizaremos que nuestras escalas tengan una construcción interválica equivalente a la mayoría de las escalas que utilizamos. En dos octavas, consideraremos, por lo tanto, escalas en las que d sea un número entre 10 y 15. En d ≤ 9 e inferior no podremos cumplir con las condiciones b) y/o c). Si d ≥ 17, no podremos cumplir con la condición a). Considerando d =16 solo hay dos opciones que cumplen las tres condiciones, siendo la secuencia interválica de estas, respectivamente: 1-2-1-2-1-2-1-2-1-2-1-2-1-2-1-2 2-1-2-1-2-1-2-1-2-1-2-1-2-1-2-1 Estas dos secuencias son rotaciones de la misma escala y corresponden al segundo modo de transposición limitada de Messiaen [Me44], también conocido como escala disminuida u octotónica. Esta escala repite en la octava, por lo que no nos interesa para nuestros propósitos. Con lo cual, nos quedan seis opciones para formar escalas de dos octavas bien formadas, que detallaremos a continuación: ME d = 10 Secuencia interválica: 3-2-2-3-2-3-2-2-3-2 ME d = 11 Secuencia interválica: 3-2-2-2-2-2-3-2-2-2-2 ME d = 12 Secuencia interválica: 2-2-2-2-2-2-2-2-2-2-2-2 ME d =13 Secuencia interválica: 2-1-2-2-2-2-2-2-1-2-2-2-2 ME d = 14 Secuencia interválica: 2-2-1-2-2-2-1-2-2-1-2-2-2-1 ME d = 15 Secuencia interválica: 2-1-2-2-1-2-1-2-2-1-2-1-2-2-1 De estas descartaremos, naturalmente, d = 10 (escala pentatónica en dos octavas), d = 12 (escala simétrica de tonos enteros en dos octavas) y d =14 (escala mayor en dos octavas) al ser en realidad escalas que repiten a la octava. De las escalas bien formadas que quedan, d = 15 tiene máximo común divisor (mcd a partir de ahora) mcd(24, 15)=3. Esto hace que la escala presente simetrías (para más información sobre por qué ocurre esto, véase [GTT09a]). Al ser el mcd(24, 15)=3, la escala divide el rango de dos octavas en tres partes iguales, siendo cada uno de los tres tramos de escala interválicamente idénticos. Nicolas Slonimsky recoge una gran cantidad de escalas de este tipo en su Thesaurus of scales and melodic patterns [Sl47]. La escala regular con d = 15 corresponde a la escala nº 707 del Thesaurus. Las escalas regulares con d = 11 y d =13 cumplen que mcd(24, d)=1 y parecen estar relacionadas, ya que d =13 contiene la totalidad de d =9, donde la diferencia entre ambas escalas es únicamente dos notas. Escalas profundas y bien formadas Para poder empezar a hablar de las siguientes dos propiedades, es necesario solucionar el problema del intervalo generador. ¿Cómo se disponen las notas generadas por un intervalo generador i a lo largo del registro completo c si no se hace de manera arbitraria? Si mi escala puede incluir potencialmente las 12 notas ¿qué sentido tiene un intervalo generador? La solución puede ser más sencilla de lo que parece. El pensar un rango modular de 12 notas es lógico, ya que, como indicábamos antes, los seres humanos percibimos notas a distancia de octava como equivalentes (dos notas se piensan equivalentes si están a una distancia de una octava). Pensar en las clases de equivalencias de las alturas (pitch-class equivalence) de esta manera tiene sentido incluso en escalas multi-octava, puesto que aporta información valiosa sobre la sonoridad de las mismas; cuantas más notas de la colección cromática contenga, más densa será su sonoridad, por ejemplo. Pero, por otro lado, las escalas que estamos estudiando transcurren en un rango modular de 24 semitonos, no de 12. Entonces, para poder entender mejor sus propiedades estructurales ¿no sería más revelador pensar en una equivalencia dentro de módulo 24 en vez de módulo 12? De esta manera do1 sería equivalente a do3, do2 equivalente a do4, etc.  La figura 8 muestra un ciclo de 24 semitonos que abarca 2 octavas. Figura 8: Ciclo de 24 semitonos Ahora vamos a comenzar nuestra búsqueda de una escala de dos octavas con la propiedad de la profundidad. Trasladando el caso de la escala mayor, una escala profunda cumple , a dos octavas, estaríamos buscando una escala de 13 notas. Ahora nos falta un intervalo generador i, relativamente primo con el rango cromático n, del que obtener las notas de nuestra escala. Como podemos observar en la escala mayor, el número de semitonos que abarca el intervalo generador i corresponde al número de notas d de la escala, es decir i = d. Por ejemplo, la escala mayor contiene siete notas y el intervalo generador de la escala mayor, la 5ª, abarca siete semitonos. El que d = i sea una propiedad de la colección diatónica fue demostrado definitivamente por Clough y Dhoutett [CD91]. Siguiendo esta lógica, nuestro intervalo generador en dos octavas debería abarcar 13 semitonos. La figura 9 muestra un ciclo de 13 semitonos dentro de un rango modular de 24 semitonos; al ser ambos números i y n relativamente primos, esto es, mcd(i,n)=1, el ciclo abarca los 24 tonos. Figura 9: Ciclo de 13 semitonos dentro de un rango modular de 24 semitonos Ahora podemos reparar en un hecho asombroso. Si recorremos 13 pasos en el sentido de las agujas del reloj desde la nota Eb1, obtenemos la colección de la escala regular con d =13; si recorremos 11 pasos, obtenemos la colección de la escala regular d =11. Tenemos dos escalas regulares con mcd(d,n)=1, que se diferencian en tan solo dos notas y tienen un mismo intervalo generador. ¿Nos resulta familiar? Efectivamente, guardan la misma relación entre sí que la pentatónica y la escala mayor. De hecho, la escala regular d =11 es el complementario de la escala regular d =13. Si omitimos las 13 notas de la escala d =13 de la colección completa n, nos quedamos con las 11 notas de la escala d =11. Es más, si nos fijamos en el número total de intervalos de la escala regular d =13, veremos que la escala es profunda, puesto que contiene cada tipo de intervalo un número limitado de veces. Para observar esto es necesario considerar los intervalos en un rango modular de 24 semitonos como en el cuadro 1. Si recorremos un paso en un sentido, es necesario recorrer 23 en el sentido contrario para llegar al mismo punto, no 11 como en un rango modular de 12. Por lo que las equivalencias interválicas, en vez de ser 1-11, 2-10, 3-9, 4-8, 5-7, 6-6, como de costumbre en un rango modular de 12, serán 1-23, 2-22, 3-21, etc. La siguiente tabla muestra el vector interválico (las ocurrencias de las distancias interválicas) de la escala regular de 13 notas, evidenciando que se trata de una escala profunda. Vector interválico módulo 24 de la escala regular con d = 13 Clase de intervalo 1 2 3 4 5 6 7 8 9 10 11 12 Número de ocurrencias 2 11 4 9 6 7 8 5 10 3 12 1 Cuadro 1: Vector interválico módulo 24 Considerar el vector interválico en un rango modular de 24 semitonos es esencial para poder apreciar esta propiedad, ya que en el vector interválico en un rango modular de 12 semitonos no se aprecia la propiedad de multiplicidad única. En cambio, el vector interválico en un rango modular de 12 semitonos sí es útil para evidenciar el alto contenido cromático de esta escala (cuadro 2). Vector interválico módulo 12 de la escala regular con d = 13 Clase de intervalo 1 2 3 4 5 6 Número de ocurrencias 14 14 14 14 14 7 Cuadro 2: Vector interválico módulo 12 Ahora únicamente queda por comprobar que esta escala está bien formada. Para ello, comprobamos si la simetría del intervalo generador (como en la figura 7) se mantiene al agrupar las notas por grados conjuntos para formar la escala. Como muestra la Figura10, definitivamente es el caso: Figura 10: Simetría en las escalas regulares con d =13 y d =11 Conclusión Aunque no es un hecho conocido y pueda parecer sorprendente, gracias a una idea tan sencilla como considerar las propiedades estructurales de una escala de dos octavas dentro de un rango modular de 24 semitonos, es posible encontrar escalas que comparten propiedades importantes con la escala diatónica y su complementario, la escala pentatónica. En el caso de escalas de dos octavas, estas son la escala regular d = 13 y su complementario, la escala regular con d = 11. Un dato a considerar es que la escala regular con d = 13 contiene las 12 notas de la colección cromática, lo cual permitiría a un compositor crear música en un contexto cromático que a la vez muestra propiedades importantes en común con la escala diatónica. Será interesante descubrir cómo este dato tan contundente a nivel teórico se traduce en la práctica musical.   Bibliografía [Ba90] Baker, D. (1990). Modern concepts in jazz improvisation. Alfred Music Publishing Co., Inc. [BJ11] S. Brown and J. Jordania. Music evokes vicarious emotions in listeners. Psychology of Music, 41(2):229–248, 2011. [Ca98] Carey, N. (1998) Distribution Modulo 1 and Musical Scales. PhD. Dissertation, University of Rochester [CC89] N. Carey y D. Clampitt (1989). Aspects of well-formed scales. Music Theory Spectrum, páginas 187–206. [CD91] J. Clough y J. Douthett (1991). Maximally even sets. Journal of Music Theory, páginas 93–173, 1991. [CM85] J. Clough y G. Myerson (1985). Variety and multiplicity in diatonic systems. Journal of Music Theory, 29(2):249–270, 1985. [DGMM+09] Erik D. Demaine, Francisco Gomez-Martin, Henk Meijer, David Rappaport, Perouz Taslakian, Godfried T. Toussaint, Terry Winograd, and David R. Wood. The distance geometry of music. Computational Geometry: Theory and Application, 42(5):429–454, 2009. [Ga67] C. Gamer (1967). Deep scales and difference sets in equal-tempered systems. In Proceedings of the 2nd Annual Conference of the American Society of University Composers, páginas 113–122. [GTT09a] F. Gomez-Martin, P. Taslakian, and G. T. Toussaint. Interlocking and euclidean rhythms. Journal of Mathematics and Music, 3(1), 2009. [GTT09b] F. Gomez-Martin, P. Taslakian, and G. T. Toussaint. Structural properties of euclidean rhythms. Journal of Mathematics and Music, 3(1), 2009. [Li91] Liebman, D. (1991). A chromatic approach to jazz harmony and melody. Advance Music. [Me44] Messiaen, O. (1944). Technique de mon langage musical (No. v. 1). Alphonse Leduc. [N16] Nikolsky, A. (2016). Evolution of tonal organization in music optimized neural mechanisms in symbolic encoding of perceptual reality. Part-2: Ancient to seventeenth century. Frontiers in Psychology, 7, 211. [Pa08] Patel, A., Patel, P., & Press, O. U. (2008). Music, language, and the brain. Oxford University Press, USA. Retrieved from https://books.google.es/books?id=EkItxyZqNecC [P61] Persichetti, V. (1961). Twentieth century harmony: Creative aspects and practice. W. W. Norton & Company, Inc. [Pr78] Pressing, Jeff. 1978. “Towards an Understanding of Scales in Jazz.” Jazz Research 9:25-35. [Sl47] Slonimsky, N. (1947). Thesaurus of scales and melodic patterns. Shirmer Books. [Sh46] Shillinger, J. (1946). The Schillinger System of Musical Composition. C. Fischer, Incorporated. [SW40] Swan, A. J. (1940). The Znamenny chant of the Russian church: part I. The Musical Quarterly, 26 (2). [Ty04] Tymoczko, D. (2004). Scale Networks and Debussy. Journal of Music Theory, vol. 48, nº2. Duke University Press. [Ym13] Ymaguchi, M. (2013). Synthetic Scales for Jazz Improvisation: Two-Octave and Multi-Octave Scales. Masaya Music Services. Notas: [1] Es cierto que el número once también muestra esta característica, pero en vista de que contiene prácticamente la colección cromática completa, no es una opción muy viable para una escala de una octava. [2] Este hecho ha sido observado por investigadores como Tymoczco o Pressing.

Lunes, 15 de Marzo de 2021 | Imprimir | PDF |  Correo electrónico

18. 113. (Febrero 2021) Métodos cuantitativos de investigación en Musicología

1. ¿Qué es la musicología? La musicología es, simple y llanamente, el estudio de la música. Y modernamente ese estudio se efectúa desde muchas ramas del conocimiento como corresponde al espíritu de los tiempos. Tradicionalmente, la musicología se ha dividido en tres grandes ramas: la musicología histórica, la musicología sistemática, y la etnomusicología. Durante un cierto tiempo la rama dominante fue la musicología histórica, al menos en España (pero también en otras partes de Europa). Sin embargo, desde hace unas décadas la musicología sistemática y la etnomusicología han cobrado fuerza e influencia. En el caso de la musicología sistemática, su éxito se ha basado en su carácter interdisciplinar. De las tres ramas, esta es la que ha sabido incorporar más acertadamente metodologías y conocimientos de otras disciplinas. El musicólogo Richard Parncutt [Par07] da una definición de musicología que a su vez se inspira en la entrada correspondiente del prestigioso diccionario The New Grove Dictionary of Music and Musicians [SSE01] (nuestra traducción, sus cursivas): “Sugiere (el diccionario) que la musicología hoy comprende todas las disciplinas que estudian toda la música en todas sus manifestaciones y en todos sus contextos, sean estos, físicos, acústicos, digitales, multimedia, sociales, sociológicos, culturales, históricos, geográficos, etnológicos, psicológicos, médicos, pedagógicos, terapéuticos, o en relación a cualquier otra disciplina o contexto musicalmente relevante”. En ese mismo artículo, en el resumen inicial, Parncutt da una definición de musicología sistemática que refleja el carácter interdisciplinar de que hablamos (nuestra traducción): La musicología sistemática es un término general, usado principalmente en Centroeuropa, para las subdisciplinas de la musicología que principalmente estudian la música en general más bien que las manifestaciones específicas de la música. (…) La musicología sistemática científica (o musicología científica) es principalmente empírica y orientada a los datos; en ella están implicadas disciplinas tales como la psicología empírica, la sociología, la fisiología, la neurociencia, las ciencias cognitivas, la computación y la tecnología. Como hemos dicho antes, esta combinación fértil de disciplinas aplicadas al estudio de la música se formó hace apenas unas cuatro o cinco décadas. Anterior a eso, la musicología se ocupa del estudio de la música occidental, principalmente usando métodos históricos. La mayor parte de los departamentos de musicología estaban formados por musicólogos históricos. Junto a la musicología histórica se encontraba se encontraba la etnomusicología (que al principio se denominaba musicología comparada, término que se abandono por eurocéntrico). Según la investigación musical se fue abordando desde dimensiones más amplias, otras disciplinas fueron uniéndose a su estudio. Al principio, lo hicieron disciplinas humanísticas, que aportaron perspectivas históricas, literarias o filosóficas. Posteriormente, se incorporaron otras disciplinas provenientes de las ciencias. Entre estas, destacan dos en particular, las cuales dieron un gran impulso a la investigación musicológica: la psicología y las ciencias de la computación. En este punto, es innegable la importancia de la componente cognitiva en la investigación musical. Diana Deutsch fue una pionera en la investigación de la música desde el prisma de la percepción y la cognición. Véase el excelente libro de Radocy y Boyle [RB03] para un amplio y profundo tratamiento de la cognición musical, sus logros, su investigación y sus retos actuales. Respecto a las ciencias de la computación, los modelos computacionales se hicieron totalmente necesarios para la comprensión de la música así como para su procesamiento. Por ejemplo, Jackendoff y Lerdahl [LJ83], inspirándose en las teorías de la gramática generativa de Chomsky, desarrollan una teoría generativa de la música que identifica estructuras y propone reglas de transformación de varios fenómenos musicales a varios niveles. Temperley [Tem10] construye modelos probabilísticos de los fenómenos musicales; Mavromatis [Mav05] usa modelos de Markov para estudiar la estructura interna de la música, por citar unos cuantos ejemplos. Según el tipo de metodología, la musicología se puede clasificar como musicología cualitativa, cuantitativa y etnográfica1 . Véase el libro Research methods in education [CMM13], que aunque se centra en la educación, se trata de una concisa y a la vez profunda exposición de estos métodos y su aplicación totalmente transferible al campo de la musicología. Como es lógico, la musicología cualitativa usa métodos cualitativos (entrevistas, observaciones, análisis de documentos, archivística, interpretación de textos, estudio de casos, etc.). Estos métodos provienen principalmente de las humanidades. Los métodos etnográficos consisten en la investigación vía la integración del investigador en el contexto de la investigación; si el investigador mismo es el protagonista se habla entonces de métodos autoetnográficos (por ejemplo, el musicólogo que entra en una formación musical de una cultura dada para investigarla desde dentro y no como observador externo). Dentro de los métodos (auto-)etnográficos se encuentra la redacción de diarios, los cuadernos de campo, las grabaciones en audio y vídeo, así como técnicas específicas de análisis. En último lugar está la musicología cuantitativa, de más reciente aplicación y que en gran medida es computacional debido a la pujanza del pensamiento computacional y la tecnología de los ordenadores. Esta musicología se basa en la idea de que la música tiene aspectos cuantificables y modelizables computacionalmente y, por tanto, se busca construir modelos, reconocer estructuras y producir algoritmos que permitan procesar la música para su mejor comprensión, análisis y procesamiento. Ejemplos de esta musicología sistemática se pueden encontrar en varios artículos de esta columna: el problema de la similitud musical y su cuantificación [Góm11], modelos de binarizaciones y ternarizaciones de ritmos en el contexto de la música afro-cubana [Góm13b], modelos computacionales de la música flamenca [Góm13a], modelos probabilísticos en música [Góm15], el problema del consenso entre experto en música [Góm16a], o teoría geométrica de la música [Góm16b], entre otros. 2. Musicología Sistemática: su investigación En el artículo de este mes queremos analizar la situación de la investigación en musicología sistemática en este país, al menos desde nuestra modesta perspectiva. Dado que estamos considerando la investigación, pensemos en un estudiante de doctorado que quiera investigar en musicología sistemática. ¿Qué conocimientos y destrezas debería adquirir para abordar la realización de una tesis doctoral con éxito? Su mundo se va a componer del estudio de artículos sobre el problema de su tesis, en hacer efectiva su investigación y por último de la escritura de los resultados en forma de artículos publicables en revistas de prestigio (más sobre esto más adelante). Ese estudiante debe contar con las siguientes capacidades: Un alto nivel de inglés, tanto leído como hablado y escrito. Leído, porque tendrá que enfrentarse a textos escritos en inglés académico, que es abstracto, complejo, rico en matices y de un vocabulario elevado. Hablado, porque lo lógico es que el estudiante presente sus resultados a la comunidad internacional y ello se hace en la lingua franca que hoy en día es, en efecto, el inglés. Por último, escrito, porque la mayor parte de las revistas de prestigio están en inglés. Unas altas capacidades de comunicación orales y escritas. Aparte del problema del inglés, cuya enseñanza en nuestro país es nefasta, está el problema de que un estudiante de doctorado debe ser capaz de escribir un documento científico en condiciones. Esto equivale a tener un sentido del estilo, un vocabulario rico, una lógica impecable, mostrar una adecuada erudición, y presentar un texto conciso y lúcido. Unas altas capacidades de investigación. Esto supone ser capaz de: (1) Entender un campo y los problemas abiertos en el mismo; (2) Estudiar el trabajo previo en el campo de interés; (3) Formular preguntas de investigación relevantes; (4) Evaluar y seleccionar las metodologías adecuadas para resolver el problema que se plantea en la tesis doctoral; (5) Llevar a cabo de manera eficiente y fiable las acciones marcadas por la metodología; (6) Razonar con lógica (musical y de otros tipos) y con creatividad sobre los datos; (7) Interpretar y evaluar con sentido crítico los resultados obtenidos; (8) Poner en contexto y señalar las limitaciones del trabajo de investigación; (9) A la luz de la investigación realizada, proponer líneas futuras de investigación; (10) Tener habilidades sociales y emocionales como para ejercer la colaboración científica con éxito e integridad moral; (11) Ser una persona resiliente, trabajadora, creativa y entusiasta. Capacidad de comunicar sus resultados en forma de indicios de calidad, que frecuentemente consistirán en artículos publicables en revistas de prestigio. Típicamente, las agencias de calidad universitaria exigen a los programas de doctorado que los doctorandos publiquen en el tercer cuartil o superior de revistas en rankings de prestigio. Una revista de prestigio se suele definir como una revista que usa un sistema de revisión por pares (que puede ser ciego simple o doble ciego) y que tiene un alto índice de impacto, medido este por métricas de citas. En musicología, por ejemplo, uno de los rankings habituales es el de Scopus [Ran21]. En la figura de abajo se muestra la primera página de tal ranking. Figura 1: La primera página del ranking de Scimago) En cada fila se puede leer el factor de impacto, que es el número encima del cuartil y yendo hacia la derecha los distintos datos bibliométricos. En la última columna aparece el país de origen de la revista; muchas de ellas, aunque no sean de países de habla inglesa, publican solo en inglés o en ambos idiomas obligatoriamente. En el primer cuartil no hay ninguna revista de habla española. En el segundo cuartil está la Revista de Musicología [SED21], el Anuario Musical [CSI21], la Revista Electronica Complutense de Investigación Musical [Uni21]. En el tercer cuartil hay solo dos revistas en español. Menciono esto a raíz del problema del inglés entre los estudiantes de doctorado. 3. Musicología Sistemática y métodos cuantitativos de investigación Dentro del apartado de metodología que mencionábamos antes, el estudiante de doctorado tiene que usar todos los métodos a su disposición para resolver el problema planteado en su tesis. Dada la interdisciplinariedad de la musicología sistemática, con frecuencia ese estudiante se enfrentará a artículos en que expongan resultados cuantitativos y él/ella tendrá a su vez que llevar a cabos estudios cuantitativos también. Tendrá que interpretar contrastes de hipótesis, tests de correlación, análisis ANOVA, entender el formulamiento de las preguntas de investigación, analizar críticamente un diseño experimental, entre otros. Es aquí donde hago una reflexión —y hasta una crítica —de la situación en que se encuentran estos estudiantes. En los Conservatorios, me pesa decir, no se proporciona tal formación en las especialidades de Musicología. En algunos másteres de investigación musical tocan esos métodos pero desde una perspectiva bastante limitada. Por ejemplo, no he oído de ningún máster de ese tipo donde lleguen a cubrir algo tan esencial como es un análisis ANOVA y en muy pocas ocasiones lo que es un contraste de hipótesis. Sin embargo, la bibliografía de investigación de la musicología sistemática está llena de resultados cuantitativos en forma de estadística descriptiva, de contrastes de hipótesis, de correlaciones, de regresiones múltiples, de análisis ANOVA, entre otros. Urge que a los estudiantes de maestría y doctorado de esta rama de la musicología se les dote de la debida formación matemática y computacional para desarrollar una carrera competitiva en el mundo actual. A continuación propones una plausible asignatura de Métodos de Investigación en Musicología Sistemática (incluimos métodos cuantitativos y cualitativos). Esta asignatura podría impartirse o bien como una asignatura completa en un máster o como actividades formativas en un programa de doctorado. Primero van los resultados de aprendizaje y luego el temario. Resultados de aprendizaje Tras la superación de las pruebas de evaluación del curso, el alumno deberá haber adquirido los siguientes resultados de aprendizaje. RA01: Comprender las fases de una investigación en el ámbito musical. Ser capaz de evaluar críticamente los resultados de investigación de otros autores así como los suyos propios. RA02: Ser capaz de hacer una búsqueda bibliográfica sistemática e identificar el estado del arte para un problema de investigación dado. RA03: Ser capaz de formular un problema de investigación original y relevante así como evaluar el alcance de su resolución. RA04: Adquirir destreza suficiente en materia de tratamiento estadístico de datos como para llevar una investigación rigurosa en el campo de la música. En particular, se espera que el alumno sepa interpretar probabilidades, identificar distribuciones relevantes, construir intervalos de confianza y contrastes de hipótesis, y hacer análisis factoriales. RA05: Manejarse con destreza con los métodos cualitativos más importantes, en particular la teoría fundamentada aplicada al análisis de textos así como las metodologías Delfi. RA06: Ser capaz de ejecutar una investigación propia desde la definición de la pregunta de investigación hasta la escritura del artículo. Descripción de la asignatura Tema 1. La investigación. ¿Qué es la investigación? ¿Qué es la investigación en música? La pregunta de investigación. El método científico. Tema 2. La bibliografía. Principales fuentes bibliográficas en música. Cómo hacer una búsqueda sistemática de la bibliográfica. Evaluación crítica de la bibliografía. Tema 3. Planteamiento de una investigación en música. Identificación del objeto de investigación. Descripción del problema. Aspectos cuantitativos, cualitativos y performativos. Interdisciplinariedad de los problemas de investigación en música. Diseño experimental. Tema 4. Métodos cuantitativos. 1. Estadística descriptiva aplicada a la investigación musical. Variables estadísticas y sus tipos. Medidas de centralización, dispersión y asimetría. Visualización de la información. 2. Estudios de correlación. Regresión. Regresión lineal. Coeficiente de correlación y de determinación. Correlación y causalidad. 3. Estudios de correlación. Regresión. Regresión lineal. Coeficiente de correlación y de determinación. Correlación y causalidad. 4. Introducción a la probabilidad. Espacio muestral, suceso y probabilidad. Probabilidad condicionada. Independencia de sucesos. El teorema de Bayes. 5. Distribución de probabilidades. Variables aleatorias. Media y varianza de una variable aleatoria. Distribuciones importantes (binomial, uniforme, normal). 6. Inferencia estadística. Muestra y población. La distribución en el muestreo. El teorema del límite central. 7. Intervalos de confianza. Intervalos de confianza para la media y la varianza de poblaciones normales. Intervalo de confianza para la proporción. 8. Contraste de hipótesis. Definición de un contraste: el razonamiento probabilístico. Construcción de un contraste. El p-valor. El tamaño muestral de un contraste. Contraste en poblaciones no normales. Contrastes de hipótesis entre dos poblaciones. 9. Análisis factorial. Análisis de modelo de efectos fijos. Análisis de modelo de efectos aleatorios. Métodos ANOVA. Diseños factoriales. 10. Escalas e instrumentos para medir variables en música. Diseño y uso. Medida de la consistencia interna de las respuestas. Tratamiento estadístico e interpretación de las respuestas. Tema 5. Métodos cualitativos. 1. Definición y filosofía de los métodos cualitativos. Necesidad y alcance. Ontología, epistemología y fenomenología. Subjetividad y rigor en la metodología cualitativa. 2. Recolección de datos, análisis de datos y diseño experimental. Estudios de casos, teoría fundamentada y otras formas de investigación cualitativa. Codificación de datos y abstracción recursiva. Rondas Delphi. Análisis estadístico de la información cualitativa. Uso de programas informáticos para dicho análisis (MAXQDA y otros). 3. Ejemplos de investigación cualitativa. Revisión de casos paradigmáticos en música. Tema 6. Ejecución de una investigación. Planteamiento de un problema de investigación. Evaluación de la pregunta de investigación. Recogida de datos. Procesamiento de los datos. Análisis de los resultados. Conclusiones de la investigación. Escritura de un artículo científico. Como recursos, sugeriríamos los siguientes: Paquete estadístico SPPS y MAXQDA. Editor científico de textos Latex. Como libros de referencia, se usarían los siguientes (véase la bibliografía): [Ber04], [Par07], [RB03], [POD11], [Fie17], [Cor11] y [CMM13]. 4. Conclusiones En este punto es posible que el estudiante de doctorado en musicología sistemática se sienta intimidado por el anterior programa. Probablemente, se trate de un alumno que tuve malas experiencias con las matemáticas (la docencia de las mismas es mala en este país, siento reconocer). Sin embargo, es posible enseñar el material de más arriba si se usan los métodos adecuados. Entre ellos, mencionaríamos los métodos de aprendizaje activo y el aprendizaje basado en destrezas. Un investigador de verdad debe conocer los métodos cuantitativos tanto como los cualitativos y ello es especialmente cierto en el caso de los musicólogos.   Nota: 1 También se encuentra la expresión de estudios performativos de la música, que tiene difícil traducción en castellano. Hemos preferido llamarlos estudios etnográficos. Bibliografía [Ber04] J. Beran. Statistics in Musicology. Chapman & Hall/CRC, 2004. [CMM13] Louis Cohen, Lawrence Manion, and Keith Morrison. Research methods in education. Routledge, 2013. [Cor11] IBM Corporation. Guía breve de IBM SPSS Statistics 20. IBM Corporation, 2011. ftp://public.dhe.ibm.com/software/analytics/spss/documentation/statistics/20.0/es/client/Manuals/IBM_SPSS_Statistics_Brief_Guide.pdf. [CSI21] CSIC. Anuario Musical. http://anuariomusical.revistas.csic.es/index.php/anuariomusical/about/submissions#authorGuidelines, consultada en febrero de 2021. [Fie17] Andy Field. Discovering Statistics Using IBM SPSS Statistics. SAGE Publications Ltd, 2017. [Góm11] Paco Gómez. Distancia y similitud musical. http://www.divulgamat.net/index.php?option=com_content&view=article&id=12763&directory=67, mayo de 2011. [Góm13a] Paco Gómez. COFLA: la música flamenca y su estudio computacional. http://www.divulgamat.net/index.php?option=com_content&view=article&id=15959&directory=67, agosto de 2013. [Góm13b] Paco Gómez. Transformaciones rítmicas: de binarizaciones y ternarizaciones. http://www.divulgamat.net/index.php?option=com_content&view=article&id=15246&directory=67, agosto de 2013. [Góm15] Paco Gómez. Música y probabilidad. http://www.divulgamat.net/index.php?option=com_content&view=article&id=16871&directory=67, noviembre de 2015. [Góm16a] Paco Gómez. Consenso entre expertos en música: un enfoque matemático. http://www.divulgamat.net/index.php?option=com_content&view=article&id=17164&directory=67, abril de 2016. [Góm16b] Paco Gómez. La geometría de la música. http://www.divulgamat.net/index.php?option=com_content&view=article&id=18000&directory=67, abril de 2016. [LJ83] F. Lerdahl and R. Jackendoff. A Generative Theory of Tonal Music. MIT Press, Cambridge, Massachussetts, 1983. [Mav05] P. Mavromatis. A hidden markov model of melody production in greek church chant. Computing in Musicology, 14:93–12, 2005. [Par07] Richard Parncutt. Systematic musicology and the history and future of western musical scholarship. Journal of Interdisciplinary Music Studies, 1:1–32, 2007. [POD11] R. Peck, C. Olsen, and J.L. Devore. Introduction to Statistics and Data Analysis. Brooks/Cole, 2011. [Ran21] Scimago Journal & Country Ranks. Music Journals. https://www.scimagojr.com/journalrank.php?category=1210, consultado en febrero de 2021. [RB03] R. E. Radocy and D. J. Boyle. Psychological Foundations of Musical Behaviors. Charles C. Thomas, Springfield, Ill., 2003. [SED21] SEDEM. Revista de Musicología. https://www.sedem.es/es/revista-de-musicologia/tematica-y-alcance.asp, consultada en febrero de 2021. [SSE01] John Tyrrell (Editor) Stanley Sadie (Editor). The New Grove Dictionary of Music and Musicians. Akal, 2001. [Tem10] D. Temperley. Music and Probability. MIT Press Ltd, 2010. [Uni21] Universidad Complutense de Madrid. Revista Electronica Complutense de Investigación Musical. https://revistas.ucm.es/index.php/RECI/about/submissions, consultada en febrero de 2021.

Martes, 09 de Febrero de 2021 | Imprimir | PDF |  Correo electrónico

19. 112. (Enero 2021) La Tabla Periódica Musical (2/2)

1. Introducción En la primera parte de este trabajo hemos visto la forma interválica y el vector de clases de intervalos o ICV, que indica el contenido de un conjunto de notas en cuanto a intervalos, es decir, clases de cardinalidad c = 2. En esta segunda parte introduciremos unas versiones avanzadas del mismo, que son el “Vector de Tipos de Tricordos” y el “Vector de Clases de Tricordos”, los cuales indican el contenido de un conjunto de notas en cuanto a tricordos, es decir, tipos y clases de cardinalidad c = 3. Estos tres vectores han sido claves para elaborar la Tabla Periódica vista anteriormente, cuyo estudio completaremos ahora con la información relativa a los tipos de conjuntos y a los pares de clases Z-relacionadas. Por último, veremos también las formas primas de Forte y de Rahn, ampliamente utilizadas para representar las clases de conjuntos y que pueden obtenerse muy fácilmente a partir de la forma interválica introducida aquí, lo que constituye otra de sus interesantes propiedades. 2. Vector de Tipos de Tricordos: TTV Para c = 3, hay 12 clases de conjuntos, los tricordos, cuyas formas interválicas primas, ordenadas por ICV decreciente, pueden verse en la Tabla Periódica (Tabla 1). Todas ellas tienen s = 1 salvo la 3-12, la tríada aumentada, que tiene s = 3. Cinco de ellas son inversionalmente simétricas, concretamente 3-1, 3-6, 3-9, 3-10 y 3-12. Y cada una de las otras 7 está formada por dos tipos de conjuntos, relacionados entre sí por inversión. Los dos tipos que forman una clase tienen el mismo ICV, pero una sonoridad diferente, así como una forma interválica también diferente. Un claro ejemplo es la clase 3-11, formada por las tríadas mayor y menor, cuyas formas interválicas normales son, respectivamente, y . En estos casos, al tipo de conjunto que tenga la menor de ellas le llamaremos “tipo a” y al otro “tipo b”. Por tanto, la tríada menor será de tipo a y la tríada mayor de tipo b (ya que 345 es menor que 354). En total, para c = 3 tenemos 5 + 2x7 = 19 tipos de tricordos. Tabla 1. Tabla Periódica de las Clases de Conjuntos. Para los conjuntos de más de 3 notas, podemos determinar cuántos tricordos de cada tipo se pueden formar con sus notas. El resultado son 19 números que forman el “Vector de Tipos de Tricordos” o TTV. Por claridad, este vector lo escribiremos como dos grupos de 9 y 10 números separados por un guion, el primero de los cuales corresponde a los tricordos 3-1, 3-2a, 3-2b, 3-3a, 3-3b, 3-4a, 3-4b, 3-5a y 3-5b (los cuales contienen al menos un semitono) y el segundo a 3-6, 3-7a, 3-7b, 3-8a, 3-8b, 3-9, 3-10, 3-11a, 3-11b y 3-12 (los cuales no contienen ningún semitono). Por ejemplo, el TTV de la clase 4-28 (acorde de séptima disminuida) es (000000000-0000004000), ya que solo contiene 4 tricordos del tipo 3-10, que es la tríada disminuida. El TTV de la clase 5-35 (escala pentatónica) es (000000000-1220030110), donde el primer grupo de números son todos ceros porque esta clase no contiene semitonos, y el TTV de la clase 7-35 (escala mayor) es (022002211-3441151330), donde los últimos cuatro elementos indican que hay 1 tríada disminuida, 3 menores, 3 mayores y ninguna aumentada. Se ha comprobado que solo hay dos tipos de conjuntos con el mismo TTV, que son los pertenecientes a la clase 6-14, el cual es (111222200-1110010221). Todos los demás tipos tienen TTV diferentes, por lo que este vector caracteriza completamente su sonoridad. En las clases de conjuntos de más de 3 notas que tienen dos tipos, la asignación de los tipos a y b ya no se hace según su forma interválica normal, sino que se asigna el tipo a al que tenga mayor TTV, siendo el otro de tipo b. De esta forma, se demuestra que el complementario de un tipo a es siempre un tipo b y viceversa [1]. La única excepción son los dos tipos de la clase 6-14, ya que tienen el mismo TTV, lo cual se indica en la Tabla Periódica mediante un superíndice con el símbolo “=”. Además, ambos son autocomplementarios, es decir, cada uno es el complementario de sí mismo. Entonces, en este caso, sí asignamos el tipo a al de menor forma interválica normal, es decir, al que tiene la forma interválica prima. Con estos criterios, la mayoría de las formas interválicas primas resultan ser de tipo a. Hay, sin embargo, excepciones, en donde la forma interválica prima es de tipo b, que son 6-10, 6-18, 7-11, 7-26, 7-28, 8-12, 8-14, todas las cuales ocurren para c ≥ 6 y se indican en la Tabla Periódica mediante un asterisco (*). Por otra parte, los TTV de los tipos a y b de una misma clase de conjunto están relacionados entre sí de una forma muy sencilla, de manera que podemos obtener el TTV de uno de ellos a partir del del otro. Para ello solo hay que intercambiar los elementos que corresponden a dos tipos de la misma clase de tricordo, tal como se muestra en la Figura 2. Por ejemplo, para la clase , considerada en la Sección 2 del artículo anterior, si conocemos el TTV de su tipo a, que es (010001211-0001010110), podemos obtener el del tipo b, que es (001002111-0000110110). Figura 2. Relación ente los TTV de los tipos a y b de una misma clase de conjunto. 3. Vector de Clases de Tricordos: TCV De forma alternativa al TTV, podemos definir también un “Vector de Clases de Tricordos” o TCV, que indique cuántos tricordos de cada clase contiene un conjunto dado de más de 3 notas. Este vector constará de 12 elementos, los cuales se pueden obtener fácilmente del TTV, simplemente sumando los elementos que corresponden a dos tipos de la misma clase de tricordo. Esta operación se muestra en la Figura 3, donde t1 … t19 son los elementos del TTV (cualquiera de los dos tipos, a o b) y f1 … f12 los elementos del TCV. Así, por ejemplo, el TCV de la clase 4-28 (acorde de séptima disminuida) es (00000-0000400), el de la clase 5-35 (escala pentatónica) es (00000-1403020), el de la clase 7-35 (escala mayor) es (04042-3825160) y el de la clase es (01032-0011020). Figura 3. Relación entre la TTV y la TCV de una misma clase de conjunto. Se puede comprobar que cada clase de conjunto tiene un TCV diferente, por lo que este vector caracteriza completamente su sonoridad. Esto no ocurre con el ICV ya que, como hemos visto, hay pares de clases con el mismo ICV o Z-relacionadas. En estos casos, la que tiene mayor TCV diremos que es “dura”, ya que siempre tiene los intervalos menores más juntos, y la otra “blanda”. Además, se demuestra que la complementaria de una clase dura siempre es blanda y viceversa [1]. En el caso particular de los hexacordos (c = 6) esto implica que, si dos clases están Z-relacionadas, cada una es la complementaria de la otra. En la Tabla Periódica, los pares de clases Z-relacionadas, como ya se ha indicado, están en la misma celda, ya que tienen el mismo ICV. Entonces, para identificarlas, la dura se ha colocado en la parte superior. Como ejemplo, consideremos las clases 5-Z12 y 5-Z36, cuyo ICV común es (222121). Sus TCV son, respectivamente, (02022-1200100) y (11102-1101110), por lo que la primera es blanda (parte inferior de la celda) y la segunda dura (parte superior de la celda). Sus formas interválicas primas son, respectivamente, y , donde podemos comprobar que la segunda tiene, efectivamente, los intervalos menores más juntos (dos “1” seguidos frente a dos “1” separados cuatro semitonos). Sus clases complementarias son, respectivamente, 7-Z12 (dura) y 7-Z36 (blanda), pudiéndose comprobar que la primera tiene los intervalos menores más juntos. Además, la clase 5-Z36 está formada por dos tipos, 5-Z36a y 5-Z36b, por los que sus complementarios son, respectivamente, 7-Z36b y 7-Z36a. Una última característica de la Tabla Periódica es que, en cada período, las clases que tienen el mismo número de semitonos (número de “1” en la forma interválica o el primer elemento del ICV) se han representado con un mismo color de fondo. Y este color se ha asignado también a sus clases complementarias. De esta manera, dada una forma interválica prima, es más fácil localizarla en la tabla. Por ejemplo, la forma interválica prima , considerada en la Sección 2 del artículo anterior, tiene 5 notas y 2 semitonos, por lo que está en el período 5, en las celdas de color azul, y es la clase 5-20. Conviene señalar que este grupo de celdas es uno de los más numerosos, por lo que en otros casos esta búsqueda resulta mucho más sencilla. En la Tabla 2 se muestra, para cada período, el número de clases de conjuntos que tienen el mismo número de semitonos, es decir, el mismo color de fondo en la Tabla 1 (se ha seguido una disposición similar en ambas tablas). Así mismo, para cada período se muestra el número total de clases, tipos y conjuntos de notas. Dado que también se ha incluido la clase 0-1 (silencio), el número total de conjuntos de notas es, lógicamente, 212 = 4096, que pueden agruparse en 352 tipos o 224 clases. Nótense las simetrías que hay entre los períodos complementarios. Tabla 2. Número de Clases, Tipos y Conjuntos de Notas. Período Clases de conjuntos con el mismo número de Semitonos Clases Tipos Conj. Notas 12 11 10 9 8 7 6 5 4 3 2 1 0 0- 1 1 1 1 1- 1 1 1 12 2- 1 5 6 6 66 3- 1 4 7 12 19 220 4- 1 8 12 8 29 43 495 5- 1 6 18 10 3 38 66 792 6- 1 9 19 17 3 1 50 80 924 7- 1 6 18 10 3 38 66 792 8- 1 8 12 8 29 43 495 9- 1 4 7 12 19 220 10- 1 5 6 6 66 11- 1 1 1 12 12- 1 1 1 1 Total 1 0 1 1 6 5 16 19 36 36 47 30 26 224 352 4096 4. Formas Primas de Forte y de Rahn Como hemos visto en la primera parte de este trabajo, la forma interválica que hemos introducido aquí es realmente útil para representar los tipos de conjuntos, dadas sus importantes propiedades. Sin embargo, en los listados proporcionados por Forte [2] y Rahn [3] solo se incluyen las clases de conjuntos y se representan mediante sus propias “formas primas”, que en la mayoría de los casos son iguales, pero no siempre. Lo mismo ocurre en los listados de Straus [4], quien utiliza las formas primas de Rahn. Por otra parte, estas formas primas no están basadas en intervalos, sino en notas y empiezan siempre por el Do. Por ejemplo, la forma prima, tanto de Forte como de Rahn, de la clase 3-11 (tríadas mayores y menores) es [037], es decir, las notas Do, Mib, Sol, que corresponden al acorde de Do menor. Y la forma prima de la clase 3-12 (tríada aumentada) es [048] (Do, Mi, Sol#). En otros casos, sin embargo, la forma prima no es tan fácil de reconocer. Por ejemplo, la forma prima, tanto de Forte como de Rahn, de la clase 7-35 (escala mayor) es [013568A], que corresponde a la escala de Reb mayor. Esto es consecuencia de los procedimientos utilizados por Forte y Rahn para obtener sus formas primas, que por cierto son bastante laboriosos. Sin embargo, ambas pueden obtenerse fácilmente a partir de la forma interválica vista aquí. A continuación, veremos cómo y lo ilustraremos con el conjunto de notas [59A24], visto en la Sección 2 del artículo anterior, cuya forma interválica es . Forma Normal de Rahn: tomamos la permutación circular que corresponda al número mayor, pero visto de derecha a izquierda (es decir, en “orden colexicográfico”), que es . Y ahora, empezando por “0”, escribimos las demás notas separadas por los intervalos indicados en esa forma interválica (salvo el último), es decir, [02378]. Forma Normal de Forte: tomamos la permutación circular que tenga el mayor intervalo a la derecha y, si hay varias opciones (como ocurre aquí, ya que hay dos “4”), la que corresponda al número menor (visto de izquierda a derecha), que es . Y ahora, empezando por “0”, escribimos las demás notas separadas por los intervalos indicados en esa forma interválica (salvo el último), es decir, [01578]. Aunque en este caso las formas normales de Forte y de Rahn son distintas, en la mayoría de los casos son iguales. Forma Prima de Rahn: hay que hallar las formas normales del conjunto dado y de su inverso, y tomar la menor de ellas. La forma interválica del conjunto inverso es , que es también su forma interválica prima. Su permutación circular que corresponde al número mayor visto de derecha a izquierda es , que da lugar al conjunto de notas empezando por “0”: [01568]. Esta es también la forma prima de Rahn, ya que es menor que [02378]. Forma Prima de Forte: también hay que hallar las formas normales del conjunto dado y de su inverso, y tomar la menor de ellas. Para el conjunto inverso, la forma interválica que tiene el mayor intervalo a la derecha y corresponde al número menor es precisamente , que da lugar al conjunto de notas empezando por “0”: [01378]. Esta es también la forma prima de Forte, ya que es menor que [01578]. De nuevo, en este caso las formas normales de Forte y de Rahn para el conjunto inverso son distintas, aunque en la mayoría de los casos son iguales. No obstante, siempre coinciden en si la forma prima corresponde al conjunto dado o a su inverso. En este sentido, la forma interválica prima también suele coincidir con ellas, como ocurre en este ejemplo, pero no siempre es así. La mayoría de las formas primas de Forte y de Rahn son de tipo a, pero algunas son de tipo b, las cuales se indican en la Tabla Periódica mediante el superíndice “+”. Sorprendentemente, son justo las complementarias de las marcadas con “*” más la 6-14, por lo que todas ellas ocurren para c ≤ 6. Como se puede observar, dada la forma normal de Forte o de Rahn de un conjunto de notas, no es nada obvio obtener, a partir de ella y sin usar la forma interválica, la correspondiente forma normal de su inverso o su complementario. Y tampoco permite determinar fácilmente sus simetrías, ni inversional ni transposicional. Por tanto, lo más práctico y sencillo es usar siempre la forma interválica introducida aquí y, a partir de ella, obtener las formas de Forte y de Rahn que sean necesarias. 5. Conclusiones e Información Adicional En la segunda parte de este trabajo se han realizado dos generalizaciones del vector de clases de intervalos o ICV: el vector de clases de tricordos o TCV y el vector de tipos de tricordos o TTV. El TCV permite distinguir entre dos clases Z-relacionadas, por lo que caracteriza la sonoridad de las clases de conjuntos. Y el TTV permite distinguir entre los dos tipos de una misma clase, por lo que caracteriza la sonoridad de los tipos de conjuntos, salvo el 6-14a y el 6-14b, que son los únicos que tienen un mismo TTV. Además, hemos visto una nueva utilidad de la forma interválica, que es la obtención de las formas normales y primas de Forte y de Rahn. Como resumen final diremos que, en la Tabla Periódica que se ha desarrollado, aparecen ordenadas todas las clases de conjuntos y permite ver, de un simple vistazo, sus principales características y las relaciones entre ellas. En particular, proporciona la siguiente información: los nombres de Forte, los tipos de simetría inversional y transposicional, las relaciones Z y las clases complementarias, las formas interválicas primas y la indicación de su tipo (a o b), lo cual permite obtener las formas normales de todos los tipos de conjuntos y, a partir de ellas, las correspondientes formas de Forte y de Rahn. Además, dada una forma interválica prima, es fácil localizarla en la tabla. Los tres vectores ICV, TCV y TTV han sido claves para elaborar esta tabla. En la publicación [1], además de la Tabla Periódica, se incluye un apéndice matemático donde se obtienen las fórmulas que relacionan los ICV y los TTV de un conjunto y su complementario, mediante las cuales se demuestran las afirmaciones que se han dado aquí sin demostración. Además, se incluye un segundo apéndice que es un listado pormenorizado de las clases y tipos de conjuntos, donde se da, para cada uno de ellos, la forma interválica normal, la forma normal de Rahn (y la de Forte cuando es diferente de ella), el nombre de Forte “extendido” (incluyendo el tipo, a o b, y su Z-relacionado si lo tiene), el ICV y el TTV. La inclusión de este último vector representa una diferencia significativa con respecto a los listados publicados con anterioridad en la bibliografía. Puede encontrarse más información sobre esta y otras materias similares en la página Web www.ruedaarmonica.com o www.harmonicwheel.com. 6. Referencias [1] Nuño, Luis. (2020). A Detailed List and a Periodic Table of Set Classes. Journal of Mathematics and Music, DOI: 10.1080/17459737.2020.1775902. [2] Forte, A. (1973). The Structure of Atonal Music. New Haven: Yale University Press. [3] Rahn, J. (1980). Basic Atonal Theory. New York: Schirmer Books. [4] Straus, J. N. (2016). Introduction to Post-Tonal Theory, 4th Edition. New York: W. W. Norton.

Martes, 12 de Enero de 2021 | Imprimir | PDF |  Correo electrónico

20. 111. (Diciembre 2020) La Tabla Periódica Musical (1/2)

1. Introducción Recientemente se ha publicado la Tabla Periódica Musical en la prestigiosa revista internacional Journal of Mathematics and Music [1] y ha recibido una calurosa acogida por parte de varios medios de comunicación. En el presente trabajo se desarrollan las principales ideas contenidas en dicha publicación y, con el objetivo de darle una mayor difusión, se ha hecho de manera que solo sean necesarios por parte del lector unos conocimientos musicales básicos. Para ello se ha simplificado la parte matemática y se han dado más detalles de la parte musical, realizando todas las explicaciones en lenguaje corriente y por medio de ejemplos, pero sin perder por ello rigurosidad. La denominada “Teoría de Conjuntos” o, modernamente, la “Teoría Post-Tonal”, se ha consolidado durante la segunda mitad del s. XX y ha demostrado ser una potente herramienta para el análisis y composición de la música atonal, siendo también aplicable a la música tonal. En esta teoría, los conjuntos de notas relacionados entre sí por “transposición” o “inversión” se agrupan en una “clase de conjunto”, cada una de las cuales tiene asignado un “nombre de Forte” y una “forma prima” [2, 3]. Así mismo, cada una de ellas contiene un cierto número de las distintas clases de intervalos, y estos números forman el correspondiente “Vector de Clases de Intervalos”, el cual caracteriza en gran medida la sonoridad de una clase, aunque no completamente. Los listados de las diferentes clases y sus vectores de clases de intervalos son parte esencial de esta teoría y pueden encontrarse en muchos textos, así como en [1]. Aparte de las referencias mencionadas [2, 3], cabe destacar en esta materia el artículo introductorio [4] y el libro de texto [5]. A diferencia de las referencias anteriores, para analizar los conjuntos de notas usaremos aquí la denominada “forma interválica”, y las clases no “inversionalmente simétricas” las desdoblaremos en dos “tipos de conjuntos” relacionados entre sí por inversión, lo que permite distinguir, por ejemplo, entre los acordes mayor y menor, los cuales forman una misma clase. Además, se han desarrollado unas versiones avanzadas del “Vector de Clases de Intervalos”, que son el “Vector de Tipos de Tricordos” y el “Vector de Clases de Tricordos”. Utilizando estos tres vectores se ha elaborado la mencionada Tabla Periódica, que muestra ordenadamente todas las clases de conjuntos y permite ver sus principales características y las relaciones entre ellas de un vistazo. Este trabajo consta de dos partes, en la primera de las cuales se ha incluido la explicación de los conceptos fundamentales propios de esta teoría (muchos de los cuales ya se han utilizado en esta introducción), de manera que el trabajo global sea autocontenido. 2. Conjuntos de Notas Utilizaremos el habitual sistema temperado de afinación de 12 notas, que representaremos mediante los números 0 al 11, donde el 0 corresponde al Do y el 11 al Si. Podemos imaginarnos estas notas en la carátula de un reloj donde el Do está en la posición de las 12, el Do# en la 1 y así sucesivamente hasta el Si, que está en las 11. Dado que a veces escribiremos varios números seguidos, para evitar confusiones representaremos los números 10 y 11 por las letras A y B, respectivamente. Los conjuntos de notas los escribiremos entre corchetes. Así, por ejemplo, las notas del acorde de Do mayor (Do, Mi, Sol) formarán el conjunto [047], las del acorde de La menor (La, Do, Mi) el conjunto [904] y las de la escala de Do mayor (Do, Re, Mi, Fa, Sol, La, Si) el conjunto [024579B]. Nótese que las notas de un conjunto pueden referirse a sonidos que se tocan simultánea o sucesivamente, y además en cualquier orden, por lo que también pueden, en principio, escribirse en cualquier orden. Sin embargo, lo normal será escribir las notas de un conjunto ordenadas en sentido ascendente dentro de una octava (teniendo en cuenta que después de la B viene de nuevo el 0). Por ejemplo, el conjunto [95A24], formado por las notas La, Fa, Sib, Re, Mi, lo escribiremos normalmente como [59A24], [2459A] o análogamente empezando por cualquier otra nota de ese conjunto. Diremos que dos conjuntos de notas son del mismo “tipo” si están relacionados por “transposición”, es decir, si un conjunto se obtiene a partir del otro transportando todas sus notas un mismo número de semitonos. Esto significa que, por ejemplo, los 12 acordes mayores forman un solo tipo de conjunto, al igual que ocurre con los 12 acordes menores o con las 12 escalas mayores. En el caso del conjunto [59A24], si elevamos todas sus notas 3 semitonos resulta [80157], siendo ambos conjuntos del mismo tipo. Para representar de una forma sencilla todos los conjuntos de un mismo tipo, tomamos uno cualquiera de ellos, ordenamos sus notas en sentido ascendente dentro de una octava y escribimos la secuencia de intervalos, en semitonos, entre cada dos notas consecutivas, incluyendo el intervalo entre la última nota y la primera. Al resultado obtenido, o cualquiera de sus “permutaciones circulares”, le llamaremos “forma interválica” y la escribiremos entre llaves. Por ejemplo, todos los acordes mayores, como es el caso de Do mayor, tienen la forma interválica , ya que los intervalos entre dos notas consecutivas (Do, Mi, Sol) son 4, 3 y 5 semitonos (donde el 5 corresponde al intervalo entre Sol y Do). Sus permutaciones circulares son y , que también corresponden al acorde mayor, pero empezando por diferentes notas. Análogamente, todos los acordes menores tienen la forma interválica y todas las escalas mayores , o cualquiera de sus permutaciones circulares. Para el conjunto [59A24] (u [80157]), su forma interválica es . Y, si hubiéramos escrito ese conjunto como [2459A], habríamos obtenido , que es una permutación circular de la forma interválica anterior y, por tanto, equivalente a ella. Lógicamente, la suma de todos los elementos de una forma interválica es siempre igual a 12, que es el número de semitonos que hay en una octava. Cuando comparemos formas interválicas entre sí (o “vectores”, que veremos más adelante), la “mayor” y la “menor” de ellas se determinarán a partir del número formado por sus elementos (es decir, según el “orden lexicográfico”). Así, diremos que la forma interválica es menor que (ya que el número 21414 es menor que 41421). A la menor de todas las posibles permutaciones circulares de una forma interválica le llamaremos “forma interválica normal”. En este último ejemplo, será . 3. Conjuntos Inverso y Complementario Se entiende por “inversión” de un conjunto de notas el resultado de invertir el sentido de sus intervalos. Por ejemplo, dado el conjunto [59A24], su inversión es [51086], ya que, en el primer conjunto, se pasa de 5 a 9 subiendo 4 semitonos, mientras que en el segundo conjunto se pasa de 5 a 1 bajando 4 semitonos; y análogamente para el resto de las notas. Nótese que las notas de este último conjunto están ordenadas en sentido descendente dentro de una octava. Si las escribimos en sentido ascendente, por ejemplo, [56801], podemos obtener su forma interválica, que es , la cual representa a todos los conjuntos de este tipo. Esta es, además, su forma interválica normal. Como podemos ver, las formas interválicas de un conjunto y su inversión son las mismas pero escribiendo los números en sentido inverso. En el caso del acorde mayor, cuya forma interválica es , su inversión es , que es equivalente a (por permutación circular), es decir, el acorde menor. Diremos que dos conjuntos de notas son de la misma “clase” si están relacionados por transposición, inversión o una combinación de ambas. Es decir, si sus formas interválicas son las mismas o inversas entre sí (o permutaciones cíclicas equivalentes a ellas). Por tanto, los 12 acordes mayores más los 12 acordes menores forman una sola clase de conjunto. Dadas las formas interválicas normales de un conjunto y su inversión, a la menor de ellas le llamaremos “forma interválica prima” y será la que se utilice para representar a todos los conjuntos de la misma clase. Así, la clase formada por todos los acordes mayores y menores tendrá como forma interválica prima . Y, para el conjunto de notas [59A24], la forma interválica prima será la menor de y , es decir, esta última. En general, una clase de conjunto está formada por dos tipos de conjuntos relacionados entre sí por inversión. Sin embargo, algunas formas interválicas son iguales a sus inversiones, como ocurre por ejemplo con la escala mayor, , por lo que esta clase está formada por un solo tipo y se dice entonces que es “inversionalmente simétrica”. Por su parte, un tipo de conjunto está formado, en general, por 12 conjuntos de notas, que son sus 12 posibles transposiciones, pero esto no siempre es así. Por ejemplo, un acorde como Do aumentado (cuyas notas son Do, Mi, Sol#) tiene la forma interválica ; y, debido a su estructura “periódica” (el número “4” está escrito 3 veces), solo existen cuatro acordes aumentados diferentes (es decir, 12/3). Este tipo de conjuntos se dice que son “transposicionalmente simétricos” y al número de períodos que hay en su forma interválica se le llama “grado de simetría transposicional”, el cual representaremos por la letra “s”. Así, en los acordes aumentados, s = 3. Si un tipo de conjunto no presenta simetría transposicional, diremos que s = 1 (toda la forma interválica es un único período), por lo que el número de conjuntos de notas correspondientes a un tipo de conjunto dado es siempre 12/s. Otro ejemplo es la escala disminuida, formada por 8 notas en sucesión de tono-semitono o semitono-tono. Su forma interválica es , que consta de 4 períodos (“12” o “21” escrito 4 veces), es decir, s = 4, por lo que solo hay 12/4 = 3 conjuntos de notas de ese tipo. Lógicamente, el valor de s para un conjunto y su inverso es el mismo. Por tanto, una clase que sea inversionalmente simétrica tendrá 12/s conjuntos de notas y una que no lo sea tendrá 24/s. Dado un conjunto de notas, su “complementario” es el conjunto formado por las demás notas. Por ejemplo, el complementario del conjunto [59A24] es [013678B]. Si conocemos la forma interválica de un conjunto dado, es fácil obtener mentalmente la del complementario. Para ello, nos imaginamos la forma interválica inicial, en este caso , como en la Figura 1.a), es decir, sobre una línea con 13 marcas, donde la última es equivalente a la primera y los círculos representan las notas de ese conjunto. Puesto que su complementario tiene los círculos en las demás marcas, como se observa en la Figura 1.b), su forma interválica será , o cualquiera de sus permutaciones circulares. Como otro ejemplo, la escala mayor tiene la forma interválica , por lo que la de su complementario será , que corresponde a la escala pentatónica (mayor o menor). Es fácil comprobar que un conjunto y su complementario tienen el mismo tipo de simetría, tanto inversional como transposicional. Por ejemplo, la forma interválica del acorde aumentado es , por lo que la de su complementario es , siendo ambas inversionalmente simétricas y transposicionalmente simétricas de grado s = 3. Y la forma interválica de la escala disminuida es , por lo que la de su complementario es , el acorde de séptima disminuida, siendo ambas inversionalmente simétricas y transposicionalmente simétricas de grado s = 4. Figura 1. Formas interválicas de un conjunto de notas y su complementario. 4. Vector de Clases de Intervalos: ICV El número de notas de un conjunto es su “cardinalidad”, que la representaremos por la letra “c” y podrá tomar los valores desde 0 hasta 12. Para c = 2, hay 6 clases de conjuntos, llamadas díadas, que son simplemente los intervalos de 1 a 6 semitonos. Sus formas interválicas primas, ordenadas de menor a mayor, son: , , , , y . Todas ellas son inversionalmente simétricas y tienen s = 1, salvo la clase , el tritono, que tiene s = 2. Los intervalos de más de 6 semitonos se reducen por inversión a una de las clases anteriores. Para los conjuntos de más de 2 notas, podemos determinar cuántos intervalos de cada clase se pueden formar con sus notas. El resultado son 6 números que forman el “Vector de Clases de Intervalos” o ICV (por sus siglas en inglés) y los escribiremos entre paréntesis. Por ejemplo, en un acorde aumentado sus notas forman 3 intervalos de cuatro semitonos, por lo que su ICV es (000300). Y, en un acorde mayor (como Do mayor), sus notas forman un intervalo de tres semitonos (Mi – Sol), uno de cuatro (Do – Mi) y uno de cinco (Sol – Do), por lo que su ICV es (001110). Un acorde menor tiene ese mismo ICV, ya que un conjunto y su inversión siempre tienen el mismo ICV. Así mismo, se puede comprobar que el ICV de la escala mayor es (254361), ya que tiene 2 intervalos de semitono, 5 de tono, 4 de tercera menor, 3 de tercera mayor, 6 de cuarta justa y 1 de tritono. De este modo, cada clase de conjunto tiene un ICV, el cual determina en buena parte su sonoridad, pero no completamente, ya que hay algunas clases que, siendo diferentes, tienen el mismo ICV. En ese caso se dice que esas clases guardan una “relación Z” o que están “Z-relacionadas” y se ha comprobado que el número de clases con el mismo ICV nunca es superior a dos. Una propiedad importante es que, si tomamos todas las clases de una cierta cardinalidad y las ordenamos según sus ICV, bien por valores crecientes o decrecientes, se puede demostrar que sus complementarios quedan ordenados del mismo modo [1]. De hecho, a cada clase se le asigna un “nombre de Forte” [2], que consta de dos números separados por un guion, el primero de los cuales es su cardinalidad y el segundo un ordinal. Y los ordinales se asignan según su ICV en sentido decreciente. Por ejemplo, la clase formada por los acordes mayores y menores es la 3-11, cuyo ICV es (001110); y la clase siguiente, 3-12, son los acordes aumentados, cuyo ICV es (000300), que es menor que el anterior (el número 000300 es menor que 001110). De esta manera, cada clase y su complementaria tienen el mismo ordinal. Por ejemplo, la escala mayor es la clase 7-35, y su clase complementaria, que es la escala pentatónica, es la 5-35. En el caso de dos clases Z-relacionadas, a una de ellas se le asigna el último ordinal del correspondiente grupo y en ambas se incluye una “Z” delante del ordinal. Por ejemplo, 4-Z15 y 4-Z29. La Tabla 1 es la Tabla Periódica aquí desarrollada, donde cada “periodo” corresponde a un valor de c y se representa mediante ese valor seguido de un guion, como en la parte inicial del nombre de Forte (columna izquierda de la tabla). Para hacer la tabla más compacta, los períodos 0, 1 y 2 se han colocado en la misma fila, al igual que se ha hecho con los períodos 12, 11 y 10. Dentro de cada período se han colocado las correspondientes clases ordenadas por ICV decreciente (el ICV no aparece en la tabla) y se les ha asignado el mismo ordinal que en su nombre de Forte (número grande en cada celda de la tabla). Así, cada celda tiene asignado un ICV diferente y, en el caso de dos clases Z-relacionadas, ambas están en la misma celda. Este es el caso de las clases 4-Z15 y 4-Z29, cuyo ICV común es (111111). A pesar de que 29 es el último ordinal del período 4, la clase que está en la última celda del mismo es la 4-28, el acorde de séptima disminuida, ya que su ICV, (004002), es el menor de este período. Por otra parte, cada clase y su complementaria, al tener el mismo ordinal, están en la misma columna. Por ejemplo, 5-35 y 7-35, o 3-11 y 9-11. Las clases que son inversionalmente simétricas tienen el ordinal subrayado y las que son transposicionalmente simétricas llevan en el ordinal un superíndice, que es su grado s. Por ejemplo, 3-123 o 6-302. Debajo de cada ordinal está la forma interválica prima, escrita sin llaves por simplicidad. Además, cuando en ella aparecen varios “1” seguidos se escriben “en forma de potencia”. Por ejemplo, 1119 se escribe 13 9 (clase 4-1). Como puede observarse, cada período comienza con la clase que tiene sus notas lo más juntas posible (es decir, en secuencia cromática) y termina con la clase que tiene sus notas separadas lo más uniformemente posible. Así, el período 4 empieza con la clase o (las 4 notas en secuencia cromática) y termina con la clase , que es el acorde de séptima disminuida (en el que dos notas consecutivas siempre están separadas la misma distancia, 3 semitonos). Tabla 1. Tabla Periódica de las Clases de Conjuntos. 5. Conclusiones Los conjuntos de notas relacionados entre sí por transposición forman un tipo de conjunto, que representamos por su forma interválica o su forma interválica normal. Si a estos conjuntos les añadimos sus inversos obtenemos una clase de conjunto, que representamos por su forma interválica prima. La forma interválica que hemos introducido aquí ha resultado ser tremendamente útil y versátil, ya que permite obtener de manera sencilla las formas interválicas de los conjuntos inverso y complementario; y, obviamente, también la del inverso del complementario (que es igual a la del complementario del inverso). Y, además, permite determinar fácilmente sus simetrías, tanto inversional como transposicional. Como hemos visto, un conjunto y su complementario (y, obviamente, su inverso) tienen siempre el mismo tipo de simetría, tanto inversional como transposicional. En la Tabla Periódica que se ha desarrollado aparecen todas las clases de conjuntos ordenadas por ICV decreciente y se incluye la siguiente información: nombres de Forte, tipos de simetría inversional y transposicional, relaciones Z y clases complementarias, así como las formas interválicas primas. No obstante, esta tabla contiene aún más información relevante, que se explicará en la segunda parte de este trabajo. 6. Referencias [1] Nuño, Luis. (2020). A Detailed List and a Periodic Table of Set Classes. Journal of Mathematics and Music, DOI: 10.1080/17459737.2020.1775902. [2] Forte, A. (1973). The Structure of Atonal Music. New Haven: Yale University Press. [3] Rahn, J. (1980). Basic Atonal Theory. New York: Schirmer Books. [4] Straus, J. N. (1991). A Primer for Atonal Set Theory. College Music Symposium, 31, 1-26. [5] Straus, J. N. (2016). Introduction to Post-Tonal Theory, 4th Edition. New York: W. W. Norton.

Martes, 15 de Diciembre de 2020 | Imprimir | PDF |  Correo electrónico