121. 2. (Julio 2007) Prehistoria musical

Vibraciones y propagación Desde mucho antes de la aparición de la vida, en nuestro planeta se generan vibraciones provocadas por los objetos al chocar o rozarse entre ellos. Como ejemplos -muy usados en las bandas sonoras de algunas películas- tenemos las provocadas por la lluvia y el granizo, el viento, fuentes y ríos, olas, volcanes y terremotos, truenos, meteoritos, desprendimientos y aludes, agrietamientos... Estas vibraciones pueden propagarse si encuentran un medio, sea gaseoso, líquido o sólido, por el que hacerlo. Los medios más abundantes en nuestro planeta, que sirven de transmisores de las vibraciones, son la tierra, el agua y el aire. Para nuestros propósitos, nos centraremos en este último. La presión atmosférica o la danza invisible Las moléculas del aire nunca se encuentran quietas. Al contrario, cada molécula se desplaza continuamente de lugar con una velocidad media de unos 500 m/s (1.800 km/h). Dado que las moléculas se encuentran muy cercanas unas de las otras, a sólo 6.10-8 m, el número medio de colisiones elásticas por segundo es muy elevado (dividiendo las anteriores cantidades lo obtenemos: casi 1010 colisiones en cada segundo). Esta es la razón por la que las moléculas del aire desafían en parte la fuerza gravitatoria y  “no caen” sobre la superficie terrestre. Tanta danza frenética no les deja tiempo. En su frenesí, las moléculas del aire también bombardean constantemente la superficie de cualquier objeto presente. Este cúmulo de muchísimos aunque ligerísimos impactos crean una fuerza constante en cada unidad de superficie. Es lo que llamamos presión atmosférica. La unidad de presión es el pascal (la presión atmosférica a nivel del mar, 1 atmósfera, equivale a unos 100.000 Pa). La presión atmosférica puede variar de un sitio a otro, o con el tiempo, pero tales variaciones son muy lentas, como puede comprobar cualquiera que se quede contemplando un barómetro. La onda sonora Los objetos vibrantes provocan sucesivas tandas de compresiones y depresiones del aire que les rodea, rapidísimos y ligerísimos cambios de presión que obligan a las moléculas a desplazarse en un “vaivén” –oscilación- que se propaga por el aire. Esta propagación, en un efecto dominó de alteraciones de presión, se conoce como onda sonora. Se debe tener presente que lo que se propaga es la oscilación de las moléculas, el tren de compresiones y depresiones, no las moléculas en sí. La oscilación de las moléculas se realiza en la misma dirección que la propagación de la onda. La onda sonora es, pues, una onda longitudinal (por contraste con las olas marinas, que son ondas transversales, es decir, perpendiculares a la dirección de propagación). En todo caso, la energía primaria causante de la vibración se consume –se transforma en calor–, debido al rozamiento en el movimiento de todas esas moléculas hasta su vuelta al estado de relativo reposo (si se puede llamar así a su frenética e invisible danza). Los seres vivos Pero antes de desaparecer, tal vez algún testigo haya registrado esas ligeras alteraciones de presión. Los animales, nosotros entre ellos, hemos desarrollado órganos específicos para que actúen de receptores de esas alteraciones. En nuestro caso, el oído. A la vez, los animales producimos vibraciones. Captar las ondas que generan ha sido y es importante para nuestra supervivencia, ya sea como aviso ante un peligro, como reclamo ante una posible presa o como parte del sistema de comunicación. Primera variable independiente: la frecuencia de oscilación Los rápidos cambios de presión en las moléculas del aire se realizan a una determinada velocidad, distinta para cada sonido. Esta velocidad se conoce como frecuencia y representa el número de oscilaciones que la molécula realiza en un segundo. Su unidad es el hercio (400 Hz = 400 oscilaciones en un segundo). Segunda variable independiente: la intensidad. La amplitud y el volumen Independientemente del número de oscilaciones que realicen por segundo las moléculas, es decir, independientemente de su frecuencia, el recorrido de ida y vuelta de la oscilación puede ser más o menos amplio. Cuanta más presión ejerzan (proporcional a la energía de la fuente vibrante), mayor será la distancia recorrida –amplitud– en cada vibración. Esta intensidad de presión en el aire la percibimos como volumen del sonido y nos permite distinguir entre sonidos fuertes y débiles. Para hacernos una idea de lo pequeños que son estos cambios de presión, comparados con la presión atmosférica habitual, baste decir que un sonido que provoque un cambio de presión de 1 Pa, en un rango de frecuencias que podamos captar sin esfuerzo, lo percibimos como un sonido fuerte. Recordemos que la presión atmosférica equivalía a unos 100.000 Pa. Pero, ¿por qué nuestro oído no “oye” la presión atmosférica y en cambio si oye el sonido? La respuesta la encontramos en la velocidad a la que se producen ambos fenómenos. El sonido produce un cambio de presión leve pero brusco (la onda se mueve a 340 m/s), de forma que el aire presente en el interior de la trompa de Eustaquio no puede compensarlo instantáneamente, produciéndose una diferencia de presión que mueve el tímpano. La resonancia Puede suceder que la frecuencia de la onda coincida con la frecuencia con la que puede vibrar un objeto al ser golpeado. Si la energía de la onda es suficiente, al alcanzar uno de estos objetos, la oscilación en la superficie del objeto se transmite a todo su interior, haciéndolo entrar en vibración a su vez, y, por lo tanto, comportándose como nueva fuente sonora. Este fenómeno se conoce como “resonancia”. La famosa escena de la copa de cristal que se rompe ante la nota intensa y precisa de una soprano o un tenor es un ejemplo extremo de resonancia. Si golpeásemos –ligeramente– la copa de cristal, produciría un sonido de la misma frecuencia que la emitida por la cantante. Al recibir la onda sonora, el cristal entra en resonancia y se pone a vibrar en “su frecuencia natural”. Si la vibración supera la capacidad de elasticidad del cristal –que no es mucha– se acaba produciendo su rotura. El oído Dada la enorme cantidad de vibraciones que simultáneamente pueden incidir en nuestro tímpano, haciéndolo vibrar a su vez, hemos desarrollado un complejo sistema discriminatorio, capaz de “separar” la combinación recibida en “partes más simples”. Este sistema se basa en la disposición, en el oído interno, de células especializadas en activarse sólo ante determinadas frecuencias, al estar situadas en medios que sólo entrarán en resonancia en esas frecuencias. Simplifiquemos un poco en aras de mayor claridad. Nuestro oído puede percibir vibraciones con frecuencias comprendidas entre unos 18 Hz y unos 18.000 Hz. Si percibimos un sonido resultado de la combinación de cuatro vibraciones: sonido=, las células especializadas en la recepción de cada tipo de vibración cribarán las componentes del sonido: sólo se activarán las células situadas en zonas que entren en resonancia con las frecuencias 200, 708, 1.524 y 3.967. Al sonido percibido lo podemos llamar “200-708-1.524-3.967”, pero es muy importante para la comprensión de la relación entre música y matemáticas tener en cuenta desde un principio que registramos cada frecuencia por separado. Cuantas menos vibraciones compongan un sonido, menos actividad se registrará en nuestro oído. Nuestra percepción mental es de un sonido “puro”, “claro”, “nítido”. El sonido producido por un diapasón es un buen ejemplo. Su equivalente visual podría ser un cielo despejado. Por el contrario, si son muchas y de diverso tipo las vibraciones que conforman el sonido, percibiremos éste como “oscuro”, “confuso”, “impreciso”. Su equivalente visual podría ser un tupido bosque. Además, aunque en principio la intensidad del sonido es independiente de la frecuencia, no lo es en nuestra recepción del sonido. Nuestro oído es más sensible a las altas frecuencias, de forma que con la misma intensidad de sonido percibimos un volumen mayor en frecuencias altas respecto a las bajas. El ritmo Muchos sonidos naturales se repiten con cierta fidelidad en períodos cortos de tiempo. Goteos diversos después de la lluvia, las olas, los pasos al caminar o correr, el canto de algunos pájaros, los latidos del corazón, los ladridos del perro del vecino... El oído forma parte de nuestro sistema de vigilancia. Si el ritmo es suficientemente pausado y suave la esperada repetición de los sonidos relaja nuestros receptores auditivos, provocando una disminución en nuestro estado de alerta y la consecuente sensación de relajamiento –que en ocasiones llega a dormirnos–. En contraste, si deseamos provocar el estado opuesto en los que están alrededor nuestra, nada mejor que estimular sus células receptoras con sonidos intensos, rápidos y cambiantes, dando fuertes palmadas y gritos, a la vez que brincamos, gesticulamos y cambiamos frecuentemente de lugar para alertar también al sistema visual (¿el nacimiento de la danza?). El poderoso cerebro Hace un millón de años el cerebro humano ya se había desarrollado mucho más que el de sus vecinos primates. El descenso desde el árbol a la planicie y el enfrentamiento a un medio hostil, creó en el Homo necesidades sociales especiales (¿el nacimiento de la diplomacia?) que provocaron el desarrollo de un cerebro más poderoso. Éste debía ser capaz de supeditar su primera reacción instintiva a una cierta contención que evitase enfrentamientos internos y mantuviese la cohesión del grupo, fundamental para sobrevivir sin otras defensas. (Una consecuencia indeseada del aumento del cráneo para albergar al crecido cerebro, unido al estrechamiento de la cadera que exigía la movilidad bípeda, fue la transformación del parto en un suceso doloroso y arriesgado.) El habla Este poderoso cerebro era capaz de experimentar y aprender más deprisa, pero no lo suficiente. Hace unos 200.000 años, la necesidad de una comunicación más precisa que capacitase la transmisión rápida y eficaz de una gran variedad de conocimientos (¿el nacimiento del sistema educativo?), provocó el paulatino descenso de nuestro principal órgano fonador: la laringe. A pesar del peligro, en ocasiones mortal, que esto supone –y que seguimos padeciendo cada vez que nos atragantamos al ingerir algún alimento–, el premio obtenido con esta evolución es de valor incalculable: podemos hablar. El placer mental Cuando el receptor del mensaje (sea hablado o no) lo interpreta adecuadamente experimenta placer. Lo que denominamos placer –mental- es una recompensa química producida en el cerebro como agradecimiento a cierta actividad neuronal, cierto tipo de reconocimiento, en este caso del significado de la idea transmitida. A su vez, la manifestación física de este placer (signos de complicidad, asombro o sorpresa, risas, caricias) acentúan el interés del emisor por intentar reproducirlo, al tiempo que acelera en el receptor un deseo de convertirse también en emisor. La voz Ahora bien, hablar no es tan sencillo como gruñir (aunque, a veces, sea difícil encontrar la diferencia en algunos individuos). Por una parte, se necesita una cierta cadencia al emitir los sonidos. Por otra, los sonidos emitidos deben disponer de un mínimo de claridad. Para potenciar al máximo el sistema de recompensas cerebrales periódicas (¿el nacimiento de la “motivación”?), tan importante en la transmisión de conocimientos, las voces se aclaran, se dulcifican, se suavizan, se afinan, se templan. El resultado de todo este proceso es una voz muy alejada del primitivo gruñido. Una voz más armoniosa. Los instrumentos Podemos considerar nuestro sistema fonador como un sofisticado instrumento musical (muchos defienden que el más perfecto de todos). Pero la naturaleza dispone de un amplio repertorio de sonidos que no pueden dejar de ser percibidos. Por un lado, los generados por los elementos sin vida, que para el Homo no lo estaban tanto, pues se movían, “hablaban” y hasta aterraban en ocasiones: mar, lluvia, relámpagos... Por otro, los de la naturaleza viva: aves, insectos, mamíferos (los temidos felinos entre ellos), incluso las hojas de los árboles parecen tener “su habla propia” al mecerse con el aire. El ser humano fue descubriendo que con algunos objetos, como huesos y piedras, debidamente dispuestos y manejados, también podía generar sonidos “curiosos” y rítmicos, sobre todo si los objetos dejaban algo de aire entre ellos o dentro de ellos. El aire contenido en una caja o un tubo, o el que separa dos objetos cercanos, puede comportarse como un objeto cuya masa entra en resonancia con la fuente sonora, aumentando la intensidad del sonido. Algunos de estos sonidos resultaban particularmente agradables. A partir de caracolas, huesos, cuernos, juncos y troncos, el hombre aprendió a construir diversos tubos que “hablaban como el viento” al soplar en ellos, o que “hablaban como el trueno” al golpearlos. Incluso logró que algunos tubos “hablasen como los pájaros”. El placer era doble, pues el intérprete podía hacer que el viento, el trueno o los pájaros sonasen a su conveniencia, más o menos fuerte, más o menos prolongado, más o menos “alegre”. La cuerda del arco empleado en la caza también emitía, tensándola al máximo, cierto sonido característico y “tembloroso” que tampoco pasó desapercibido. La invención de la metalurgia (cobre, bronce, hierro) aumentó las posibilidades sonoras de los instrumentos de percusión y viento. El tono o altura Muchos de los sonidos producidos por los nuevos instrumentos tenían una característica común con la voz humana: se percibía en ellos una agudeza o gravedad bien definidas, lo que se conoce como altura o tono. Este concepto corresponde a nuestra percepción de la frecuencia de la vibración. Cuanto mayor es la frecuencia, es decir, cuanto más rápido vibran las moléculas de aire que alcanzan nuestro tímpano, más alto es el tono percibido. Así, distinguimos entre sonidos graves (frecuencia baja, hasta 300 Hz), medios (frecuencia media, entre 300 y 2.000 Hz) y agudos (frecuencia alta, más de 2.000 Hz). Para que la altura sea percibida de forma nítida es necesario que en el sonido, frecuentemente complejo, predomine una determinada frecuencia o tono fundamental. Así, una trompeta emite un sonido con pocas frecuencias, lo que percibimos como “sonido claro o brillante”, mientras que un tambor produce muchas distintas por lo que no le otorgamos una altura definida. La melodía La melodía es una sucesión, en el tiempo, de sonidos que forman “palabras” y “frases”. Los “espacios” entre ellas son los silencios. Estos términos son más que una analogía. Las frases melódicas tienen su origen en la repetición más o menos igual de frases entonadas, es decir, en la voz y en el canto. La armonía Cuando varias voces se superponen en el mismo instante, cada una con su particular frecuencia o tono fundamental, el resultado será, casi siempre, caótico. La armonía consiste en buscar, para cada instante, aquellos sonidos que guarden cierta relación de orden entre sí. Matemáticas Este rápido resumen nos aporta las claves para la presencia de las Matemáticas en la Música. Las Matemáticas estudian las cantidades, las formas, sus relaciones y sus variaciones. La Música es la combinación y variación de ciertas cantidades (frecuencia, intensidad) en un mismo instante (armonía) y a lo largo del tiempo (ritmo, melodía). Comprender estas claves es el objeto de esta sección de Divulgamat.

Domingo, 01 de Julio de 2007 | Imprimir | PDF |  Correo electrónico

122. 3. (Septiembre 2007) Funciones musicales

La insoportable levedad del ser La constancia de lo pasajero de la existencia humana provoca en el poderoso cerebro del Homo la necesidad de dejar constancia, de algún modo, de su propia y fugaz existencia. Como reacción a la dolorosa conciencia del paso del tiempo hemos creado sistemas para mitigarla: aprecio familiar y social, celebraciones, valores morales, fama y poder, religiones, investigación, ciencia y... artes. La línea del tiempo El arte surge de la necesidad de cada individuo de comunicar su propia sensibilidad, por lo que no precisa una finalidad material. La artesanía, la arquitectura, la escultura, la pintura o la fotografía se convierten en arte cuando logran esa comunicación con alguien que no sea algún admirador incondicional, lo que les dota de cierta intemporalidad. Pero, además, otras artes incluyen un tiempo narrativo específico como elemento artístico, como es el caso de la literatura, el teatro, la cinematografía, la danza y, sobre todo, la música. Funciones Función. 3. Acto organizado, que constituye un espectáculo de cualquier clase, al que concurre gente. 5. Mat. Con respecto a una cantidad, otra cuyo valor depende del de aquella. (Diccionario de uso del español de María Moliner.) La música comparte estas dos acepciones. Por una parte, necesita de una ejecución interpretativa, ya sea propia o ajena, que le confiere carácter de espectáculo. Por otra, su dependencia de la variable tiempo es total. Huellas musicales Basta una piedra o algo de barro para dejar una huella que nos sobreviva pero, hasta hace muy poco, nuestra voz moría con nosotros. De la misma forma que podemos enseñar palabras y frases, también podemos enseñar canciones. Durante siglos, las canciones populares (y los bailes asociados) no necesitaron de ningún registro material para su transmisión y enriquecimiento de generación en generación. Cuando las canciones se fueron acumulando se hizo patente la necesidad de registrarlas como ya se registraba la palabra: por escrito. Ahora bien, ¿cómo? Frecuencias fundamentales: hacia la abstracción Cuando cantamos bajo la ducha Cantando bajo la lluvia, gloriosos reyes de nuestro privado espectáculo musical, cualquier parecido con E. J. Curran (Gene Kelly) será, normalmente, una calumnia. Sin embargo, casi milagrosamente, los sufridos familiares o vecinos seguramente habrán reconocido la canción subyacente a nuestra infame interpretación. Independientemente de nuestra voz, nos hemos acercado (valga el eufemismo) lo suficiente a “la secuencia de distancias –intervalos- entre sucesivas frecuencias fundamentales” que rigen la canción para hacerla reconocible. Así que si disponemos de alguna forma de anotar estos intervalos tendríamos una especie de “esqueleto” de la canción. En eso consiste una partitura. “Las sinfonías de Beethoven no existen” (Daniel Baremboim) Esta frase del conocido pianista resume contundentemente su propia labor como intérprete y director. Las partituras registran la duración y frecuencia de cada sonido en cada instante, pero carecen de “carne palpitante”. Necesitan de una segunda inteligencia creadora, un “recreador” (el intérprete o el director, según el caso) que intente reconstruir la idea original del compositor. Con otras palabras, la partitura muestra un código abstracto que deberá concretarse en la interpretación. Volviendo a la ducha, supongamos que nos escucha alguien que oye por vez primera nuestra personalísima versión de Singin’ in the rain. Al margen de su más que probable estupefacción, sólo una recreación completa a partir de nuestras vagas indicaciones sonoras, basada en el conocimiento y estudio de otras composiciones análogas, le haría posible reconstruir algo similar al original. El periódico ABC Como las letras ya estaban inventadas, los primeros intentos para escribir música se basaron en ellas, asignando una frecuencia concreta a cada una de las primeras letras del alfabeto. Así, las siete notas básicas se representan en la notación inglesa y alemana como A, B, C, D, E, F y G, que corresponden, respectivamente, a la notación latina Mi, Fa, Sol, La, Si, Do y Re. La famosa canción Do-Re-Mi de The Sound of Music (Sonrisas y lágrimas) nos recuerda el carácter cíclico de las notas (en inglés, Do Re Mi Fa So La Ti). El doblaje no tiene desperdicio. En realidad, se trata de una versión moderna, y muy buena, al estilo del poema elegido por el monje Guido d'Arezzo (992-1050) para enseñar a solfear, y de donde provienen los nombres de las notas (la nota Si se añadió posteriormente). En este tipo de notación –nomenclatura– se observan graves deficiencias. Primero, se limita a siete frecuencias fundamentales. Esto es fácilmente superable añadiendo más letras. Segundo, no indica la duración de cada sonido. También superable, añadiendo las indicaciones correspondientes. Tercero, y lo más grave, no ofrece una visión global rápida de la evolución de las notas y sus duraciones, algo fundamental para una correcta reconstrucción de la composición. Podemos ver cada nota por separado, pero resulta difícil ver su evolución al variar el tiempo. Subamos el volumen Mientras tanto, los matemáticos se enfrentaban a un problema similar. Es sencillo reconocer visualmente una forma, como un cubo (el cuerpo regular, no el recipiente de la fregona), y calcular su volumen. En principio, este cálculo se hacía para cada cubo particular. Así, para cubos con aristas de longitudes 1, 2, 3, 4,... se obtuvieron los correspondientes volúmenes 1, 8, 27, 60 (perdón, 64),... Posteriormente, se generalizó a cualquier lado x, obteniendo el volumen x3. Esta potencia heredó el nombre de su origen geométrico: “número cúbico”, “elevar al cubo”, “x al cubo” o “el cubo de x”. Tenemos entonces que podemos ver cada volumen por separado, pero resulta difícil ver su evolución al variar el lado. ¡El mismo problema de notación que en música! Los músicos se adelantan Dado que gran parte de las antiguas composiciones musicales se dirigían hacia el canto, no parecía conveniente añadir más letras a las propias de la canción. Tampoco se pretendía “leer música” tal como ahora lo conocemos. Simplemente, había que crear una notación que ayudase a recordar si la sílaba a cantar tenía una altura o frecuencia mayor o menor que la precedente. Surgieron así en la Edad Media los neumas, unos signos que se colocaban sobre el texto ayudando a refrescar la memoria. Al principio, la posición de estos signos no dependía de su indicación sobre la altura de la nota –notación adiastemática–, sólo acompañaba al texto. Posteriormente, se añadió una línea base llamada pauta (¡el eje de abscisas!) sobre la que distanciar los neumas en función de su altura (¡el eje de ordenadas!). Para mayor precisión, se añadieron más líneas horizontales –más pautas–, primero hasta cuatro (tetragrama), y por fin hasta cinco (pentagrama). Si es necesario, se pueden añadir tantas líneas auxiliares como se desee. Sistema ortogonal La representación basada en pautas es, básicamente, bidimensional. El eje horizontal, la pauta, no sigue exactamente la línea del tiempo, pues la duración de los sonidos (o silencios) viene dada por ciertas modificaciones en la forma de anotar la nota. Sin embargo, simplificando, si todas las notas tuvieran la misma duración el eje horizontal coincidiría con la línea del tiempo. El eje vertical, la altura, tampoco sigue exactamente la frecuencia del sonido. Para empezar, entre una frecuencia y su doble (es decir, entre dos notas consecutivas del mismo nombre) siempre hay exactamente la misma distancia (3 ½ pautas). Así que la escala del eje vertical parece ser logarítmica (base 2). Pero la proporción (que es el equivalente a distancia en escalas logarítmicas) entre dos notas consecutivas tampoco es siempre la misma, pues, por ejemplo, del Mi al Fa hay la mitad de distancia que del Re al Mi. Tenemos que hablar, por lo tanto, de una escala pseudologarítmica. Incluso así, tenemos dos ejes perpendiculares, con la variable vertical evolucionando sobre la horizontal. Nicole d’Oresme René Descartes (1596-1650) publica en 1637 su Discours de la méthode (Discurso del método). El apéndice La géométrie (La geometría) se considera la base de la Geometría Analítica y del Cálculo.  Sin embargo, las ideas contenidas en este apéndice no hacen mención en absoluto de ningún sistema de referencia coordenado. Su éxito se debe a la bidireccionalidad que establece entre los métodos geométricos y algebraicos para el cálculo de soluciones. Si no fue Descartes, ¿a quién debemos la idea de un sistema gráfico que permita cuantificar las formas variables?  El sistema “cartesiano” debería llamarse, en realidad, “oresmiano”, pues, tal como señala Boyer (1968) fue Nicole d’Oresme (1323-1382), quien casi tres siglos antes que Descartes tiene la gran idea de intentar dibujar cómo varía una cierta cantidad. Para ello recurre a los términos de longitud y latitud, equivalentes a las abscisas y ordenadas actuales. Gráficas y funciones Dado que las pautas aparecen con Guido otros tres siglos antes, parecería que Nicole imita su notación musical. Sin embargo, existe una gran diferencia. La notación de Guido permite, ciertamente, una visión rápida de la evolución de las notas con el tiempo, pero no establece un sistema de referencia auténtico. A los cantantes no les preocupaba a qué distancia está determinada nota del origen del canto, sólo a qué altura está en un instante determinado. Por lo tanto, no se establece una relación funcional entre el tiempo transcurrido y la nota a emitir. Considerar las dos variables a la vez dotó al sistema de Oresme de una verdadera notación dinámica. Referencias: Boyer (1968) “Historia de la Matemática”, Alianza Universidad 1986.

Sábado, 01 de Septiembre de 2007 | Imprimir | PDF |  Correo electrónico

123. 4. (Noviembre 2007) Análisis Armónico

Una vibración misteriosa El curioso comportamiento de los instrumentos musicales generó dos de los problemas matemáticos que a lo largo de la historia despertaron un interés excepcional dando lugar a una de las controversias más encendidas y fructíferas en la historia de las matemáticas. Veamos un resumen de la fascinante investigación que consiguió desentrañar el misterio. Pitágoras Desde los tiempos de Pitágoras se conoce, empíricamente, que la altura del sonido fundamental percibido al pulsar una cuerda con extremos fijos depende de la longitud de la cuerda, resultando la frecuencia inversamente proporcional a la longitud. (Una dependencia similar se observa respecto a la longitud de los tubos en los instrumentos de viento, problema que analizaremos en otra ocasión.) Mersenne (sin sus primos) Marin Mersenne en su obra “Armonía Universal” (1636) describe con precisión, pero sin demostrarla, la relación entre la frecuencia del sonido fundamental de una cuerda y su longitud, tensión y densidad, algo que también consigue, independientemente, Galileo. La obra de Mersenne se convirtió en fuente teórica de la música del siglo XVII, sobre todo en Francia. Dos problemas peliagudos Hasta el siglo XVIII, la matemática no se encuentra lo suficientemente avanzada como para abordar dos problemas intrigantes: El problema de la cuerda vibrante: Determinar el movimiento de una cuerda tensa al pulsarla. Demostrar o rebatir la relación de Mersenne: Dada la longitud y el peso de una cuerda, así como la fuerza que la tensa, encontrar el tiempo de vibración. Brook Taylor En 1715, Taylor encuentra que el movimiento de un punto arbitrario de la cuerda es el de un péndulo simple y determina su tiempo de vibración (periodo). Obtiene en su lenguaje propio, un tanto distinto del nuestro, la ecuación diferencial de la cuerda vibrante, es decir la ecuación unidimensional de ondas, y a partir de ella halla una solución: la forma de la curva que toma la cuerda en un instante dado es sinusoidal. Parciales armónicos Para entender el problema de la cuerda vibrante es necesaria la observación de su comportamiento. El sonido fundamental no es el único que emite la cuerda al vibrar. Simultáneamente, se producen otros sonidos (parciales) de menor intensidad. La distribución e intensidad de estos parciales (timbre) diferencian instrumentos o voces que ejecuten la misma nota. En el caso de los instrumentos de cuerda y viento, las frecuencias de estos parciales son múltiplos de la frecuencia fundamental F. De estos múltiplos (armónicos), el primero es la propia frecuencia fundamental, el segundo el doble (2F), el tercer armónico el triple (3F), etc. ¿Por qué múltiplos exactos? Al pulsar la cuerda se produce una onda transversal viajera, como una ola, que recorre la cuerda hasta los extremos, con una cierta amplitud (separación máxima respecto del punto de reposo). Allí, incapaz de continuar su propagación, se refleja. Esto ocasiona que dos ondas reflejadas en los extremos viajen una contra otra hasta superponerse en la cuerda. La suma de estas dos ondas reflejadas es una onda longitudinal llamada onda estacionaria. Este nombre se debe a que, al superponerse, las ondas reflejadas parecen dejar de propagarse, convirtiéndose en una oscilación de la cuerda. Esta oscilación es la que se propagará al aire. Cada onda reflejada habrá recorrido dos veces la longitud de la cuerda hasta encontrarse de nuevo en el extremo de partida. Así que la longitud de la onda estacionaria es el doble de la longitud de la cuerda. Ahora bien, al superponerse las dos ondas transversales para formar la onda estacionaria, podrán aparecer puntos (vientres) en donde las dos ondas coincidan en fase, así que la amplitud será el doble. También pueden aparecer puntos (nodos) en donde las ondas se encuentren desfasadas 180º, así que en ellos la amplitud será nula (no se mueven). Estos nodos actúan como extremos fijos de partes de la cuerda, por lo que la vibración de estas partes emitirá un sonido más agudo (con mayor frecuencia). Para que los nodos aparezcan, tienen que estar distribuidos por igual a lo largo de la cuerda. Por lo tanto, las longitudes de esos trozos de cuerda tienen que ser divisores de la longitud total de la cuerda. Como la frecuencia es inversamente proporcional a la longitud, se deduce que los nuevos sonidos tienen que tener como frecuencia un múltiplo de la frecuencia fundamental, es decir, tienen que ser armónicos. El problema de la cuerda vibrante Ahora bien, lo curioso es que la cuerda no varía alternativamente entre un armónico y otro, sino que emite todos los sonidos armónicos al mismo tiempo. He aquí el quid de la cuestión, causa de intriga y discusión entre los matemáticos: ¿cómo se las arregla la cuerda para vibrar de varias formas distintas a la vez? D’Alembert, Daniel Bernoulli y Euler El problema de la cuerda vibrante promueve la intensa búsqueda de una explicación. En esta búsqueda, d'Alembert muestra la solución general de la ecuación de onda como suma de dos funciones generales y periódicas. Inmediatamente, surge una fuerte controversia entre la solución establecida por Taylor y la nueva de d’Alembert: ¿la solución es general o sólo admite soluciones sinusoidales? Para echar más leña al fuego se meten por medio otros dos genios: Euler y Daniel Bernoulli, que no hacen sino aumentar la consciencia de la tremenda confusión que todos sentían. En medio de esta polémica, Bernoulli encuentra la ecuación de cada armónico y, en consecuencia, demuestra la relación que ya había encontrado empíricamente Mersenne entre frecuencia, longitud de la cuerda, tensión y densidad. El segundo de los problemas había sido resuelto. Otra consecuencia de la ecuación de Bernoulli es que la envolvente de las posiciones de la cuerda son dos parábolas. El problema de la cuerda vibrante se resiste La causa de la confusión entre estos genios estriba en que los matemáticos de esta época concebían una función a modo de polinomio, es decir, lo que hoy llamamos función analítica.  ¡Pero un polinomio queda perfectamente determinado para todos los valores una vez que se conocen sus valores en un intervalo por pequeño que sea! Para ellos, el estado de vibración de una parte de la cuerda debería determinar la vibración de la cuerda entera. Fourier Fourier fue discípulo de Lagrange, Monge y Laplace. En su Teoría analítica del calor recurre a series trigonométricas para modelizar ciertos comportamientos evolutivos. Estas series permiten resolver, por fin, el problema de la cuerda vibrante, al servir de puente entre las sinusoidales de Taylor y las funciones generales de d’Alembert. La gran diferencia entre la serie trigonométrica de Fourier y otras series, como la serie de potencias de Taylor, reside en que estas últimas representan una función analítica: toda ella está determinada por su comportamiento en cualquier pequeño intervalo. La serie de Fourier puede representar a una función mucho más general (aquí un ejemplo) y tiene un carácter local: el valor de la serie en un entorno no contiene ninguna información sobre el valor de la serie en otro entorno disjunto del anterior. Solución al problema de la cuerda vibrante Resulta, pues, que la cuerda no vibra de ninguno de los modos que vimos, sino de una suma ponderada de ellos. Los coeficientes de la serie de Fourier varían según los distintos armónicos (y por lo tanto, según el timbre del instrumento). En el caso de la cuerda, también varían según la posición del punto de pulsación. Ante un movimiento tan complejo, no es de extrañar la perplejidad causada en los matemáticos. Algo va mal Aunque el problema de la cuerda vibrante parecía resuelto, el modo (digamos “alegre”) en que Fourier empleaba sus series trigonométricas provocó la crítica, más que razonable, de otros tres genios matemáticos: Lagrange, Laplace y Abel. El problema residía en que Fourier manejaba las series infinitas sin establecer previamente su convergencia. Este proceder puede conducir a resultados absolutamente erróneos. Así las cosas, el problema de la cuerda vibrante parecía resuelto en la práctica, pero sin un fundamento teórico consistente. Un año histórico Por fin, en 1829, Dirichlet, discípulo de Fourier, establece las condiciones de convergencia de las series de Fourier. Esto marcó un hito en la historia de las matemáticas. El análisis armónico El desarrollo del análisis matemático del siglo XIX tiene como hilo conductor el deseo de proporcionar respuestas satisfactorias a las muchas preguntas originadas en el estudio de la cuerda vibrante. Durante todo ese siglo, y hasta hoy, el análisis armónico empieza a aplicarse a una amplia variedad de fenómenos, desde la naturaleza de la luz o la estructura del átomo hasta los ordenadores, a la vez que impulsa la investigación sobre los fundamentos de las matemáticas. Por último, la “Teoría de las cuerdas”, actualmente la mejor candidata para unificar las fuerzas fundamentales, se sirve de la analogía con las cuerdas vibrantes para definir su modelo físico del comportamiento de la materia.

Jueves, 01 de Noviembre de 2007 | Imprimir | PDF |  Correo electrónico

124. 6. (Marzo 2008) Melodías Moduladas

Un día especial El 12 de mayo, Día Escolar de las Matemáticas y víspera de martes 13, se dedica este año a la relación entre Música y Matemáticas, eje central de esta sección de Divulgamat. Uno de los pilares de esa relación lo representa el sistema de escalas musicales y su conexión con la afinación, tema que se puede ver desarrollado en el artículo de Vicente Liem con el que se inauguró esta sección. Como dedicatoria al Día Escolar de las Matemáticas, comenzaremos hablando de días especiales y, siguiendo el hilo, retomaremos las escalas musicales desde un punto de vista ligeramente distinto. Querida Alicia Me la dieron -continuó diciendo Humpty Dumpty con mucha prosopopeya, cruzando una pierna sobre la otra y luego ambas manos por encima de la rodilla- me la dieron... como regalo de no-cumpleaños. (Lewis Carroll, A través del espejo y lo que Alicia encontró al otro lado.) El más básico sistema de clasificación es el que atiende a opuestos o complementarios: positivo o negativo, cara o cruz, par o impar, sonido o silencio, ser o no ser. Estas dicotomías toman frecuentemente la forma de criterios con los que dilucidar rápidamente algunas cuestiones. Criterios basados en la paridad son utilizados tanto en matemáticas como en la transmisión codificada de información digital para comprobar la existencia de soluciones o la coherencia de datos. La propia aritmética interna del ordenador es del tipo encendido-apagado. Estamos ante un caso sencillo de lo que se conoce como clases de equivalencia. Alicia cumple años el mismo día del año, independientemente del año de su vida. Todos estos días tienen, pues, una relación común, llamada relación de equivalencia, que los diferencia de los días de no-cumpleaños. Para Alicia, los días de cualquier año se separan, bajo esta relación, en dos clases de equivalencia: [cumpleaños] y [no-cumpleaños] (los corchetes denotan que nos referimos a clases). Sin embargo, estas dos clases no constan de igual número de elementos. Hay muchos más días de no-cumpleaños que días de cumpleaños, así que, como advierte Humpty Dumpty a Alicia, más vale celebrar los primeros que los segundos. Seven Up Más interesantes, en un sentido práctico, resultan las clases que reparten por igual los elementos. Un caso cotidiano -nunca mejor dicho- lo encontramos en las clases llamadas “días de semana”. Arbitrariamente, se elige un día y se le hace corresponder el número 1. Lo denominamos “lunes“, según la norma actual, si bien en sus orígenes hebreos el primer día no fue lunes sino domingo y correspondería al primer día de la creación, fijado en fecha tan reciente, históricamente hablando, como es el 7 de octubre del año 3761 a.C. Los días siguientes reciben nuevos nombres, hasta el séptimo, “domingo“. A partir de ahí, la secuencia se repite, de forma que el octavo día vuelve a ser “lunes“, el noveno “martes”, etc. Llamamos semana al tiempo que separa (distancia temporal) un día del siguiente del mismo nombre, es decir, de la misma clase. También usamos aquel mismo nombre, semana, para el intervalo de días correspondiente a esa distancia temporal. Por ejemplo, si hoy es miércoles decimos que para el próximo miércoles falta una semana. Pero también llamamos semana al intervalo que abarca el miércoles, jueves, viernes, sábado, domingo, lunes y martes, es decir, a la serie de días comprendidos entre dos miércoles consecutivos. ¿Por qué se convino en repetir la secuencia precisamente cada siete días? Seguramente porque cada siete días la luna cambia de fase (llena, menguante, nueva y creciente), por lo que desde tiempos prehistóricos basta su observación para determinar el tiempo transcurrido entre dos acontecimientos alejados algunos días, lo que resulta mucho más práctico que llevar cuenta de los amaneceres. Si deseamos distinguir un lunes de otro hace falta señalar la semana correspondiente. La forma más sencilla de conseguirlo es numerándolas. A la primera semana, ya sea la supuesta de la creación o cualquier otra semana que convengamos como inicial, le asignaremos el número 0, y a las sucesivas semanas 1, 2, 3, etc. Estos números se mostrarán como subíndices del día de la semana. Por ejemplo, M5 indica el martes de la quinta semana a partir de la inicial (que hemos denotado como semana 0). En suma, tenemos que las semanas, consideradas como intervalos, abarcan los días de lunes a domingo: semana 0 (inicial) = = semana 1 = = … que los días de la semana son las clases: [lunes] = = [martes] = = ... y también que usamos la palabra semana para la diferencia de siete unidades-día entre dos días consecutivos del mismo nombre: semana = Ln – Ln-1 = Mn – Mn-1 =... = 7 De oca a oca Una progresión aritmética es una sucesión -de números- en donde, a partir de un número inicial, la diferencia entre cada término y el anterior siempre es constante (esta constante se denomina, precisamente, diferencia). Por ejemplo, los números impares forman una progresión  aritmética de primer término 1 y diferencia 2. Observamos entonces que cada elemento de la clase [martes] forma parte de una progresión aritmética cuyo primer término, el martes de la semana inicial (M0), corresponde al día 2 y cuya diferencia es 7. El término general, es decir, el número correspondiente al martes de la enésima semana (sin contar la inicial), será: Mn = M0 + 7n donde n es cualquier número natural. La expresión anterior sintetiza cada uno de los elementos de la clase [martes]. Por supuesto, esta expresión se puede aplicar a cualquier otro día. Al viernes, por ejemplo: Vn = V0 + 7n Congruencias modulares Analicemos ahora cómo efectuamos los cálculos para averiguar qué día de la semana caerá un día determinado a partir de hoy. Para ello no emplearemos la notación introducida por Gauss en su obra cumbre, Disquisiciones aritméticas (1801), referencia obligatoria en la Teoría de Números, sino una muy similar –derivada de aquella- que actualmente se utiliza en los programas informáticos. Carl Friedrich Gauss (1777 – 1855). Caricatura de la exposición El rostro humano de las Matemáticas. Como los días de la semana vuelven a repetirse cada 7 días, es decir, vuelven a ser de la misma clase, sumar 7 y no sumar nada viene a ser lo mismo a efectos de cálculo: 7 (mod7) = 0 La expresión anterior se lee “7 módulo 7 es igual a 0”, y significa que el resto del número 7 al ser dividido por 7 es 0. Una consecuencia de ese resultado es la siguiente igualdad: L + 7 (mod7) = L (mod7) = 1 Es decir, el resultado de sumar 7 días a un lunes cualquiera vuelve a dar lunes. A este tipo de operaciones se le conoce como aritmética modular. Como los restos posibles de dividir cualquier número entre 7 son 0, 1, 2, 3, 4, 5 y 6, el resultado de aplicar a una expresión cualquiera el módulo 7 arrojará como resultado uno de estos números. Resumiendo, decir que “L+7 es igual que L módulo 7” simplemente significa que ambos días, L+7 y L, pertenecen a la misma clase de equivalencia [lunes] (llamada clase de congruencia en la aritmética modular), y por lo tanto los números correspondientes a esos lunes arrojan el mismo resto 1 al ser ambos divididos por 7. Sigamos con los cálculos. Observamos que: L + 14 (mod7) = 1 pues añadir 14 días equivale a sumar dos semanas enteras. De igual forma, para cualquier número natural n: L + 7n (mod7) = 1 pues hemos sumado n semanas enteras, por lo que todos ellos son elementos de la misma clase [lunes]. Por otra parte, tenemos que: L + 8 (mod7) ≡ L+ 1 (mod7) = M (mod7) = 2 pues 8 = 1 + 7, por lo que al sumar 8 y al sumar 1 se obtienen elementos de la misma clase (en este caso, [martes]). En general, como cada siete días la cuenta vuelve a cero, sumar N días a un día de semana particular equivale a sumar el resto de dividir N entre 7, es decir, sumar N (mod 7), tal como indica la siguiente tabla: Días añadidos L M X J V S D 7n L M X J V S D 7n + 1 M X J V S D L 7n + 2 X J V S D L M 7n + 3 J V S D L M X 7n + 4 V S D L M X J 7n + 5 S D L M X J V 7n + 6 D L M X J V S Es importante señalar aquí, para nuestros propósitos, que la aritmética modular se puede aplicar con éxito tanto a los días de la misma clase como de diferentes clases porque todos ellos guardan la misma distancia entre sí: entre el lunes y el miércoles de una semana determinada hay la misma distancia que entre el miércoles y el viernes. El año sin martes 13 Veamos cómo el empleo de la aritmética modular nos permite resolver rápidamente esta cuestión: ¿es posible un año de nuestro calendario actual en donde no coincida ningún agresivo martes con un nefasto 13? Ya sabemos que no es el caso de este año 2008, pues el día siguiente al Día Escolar de las Matemáticas es el 13 de mayo, martes. Pero, ¿habrá algún año que se libre de esta coincidencia? Para averiguarlo, tomemos la semana del 13 de enero de ese supuesto año como semana inicial y llamemos C al cardinal o número correspondiente al día de la semana de ese 13 de enero. Así, el número C puede variar entre 1 y 7, es decir, entre lunes y domingo. Como enero tiene 31 días, lo que ofrece resto 3 al dividirlo por 7, el día de semana correspondiente al 13 de febrero será igual C+3, módulo 7: C + 31 (mod7) = C + 3 (mod7) Hagamos lo mismo con los distintos meses. Ya que su número de días, de enero a noviembre, sigue la secuencia , añadidos al número C y quedándonos con el resto de dividir entre 7, obtenemos: Tipo de año Ene. Feb. Mar. Abr. May. Jun. Jul. Ago. Sep. Oct. Nov. Dic. 365 días C C+3 C+3 C+6 C+1 C+4 C+6 C+2 C+5 C C+3 C+5 Bisiesto C C+3 C+4 C C+2 C+5 C C+3 C+6 C+1 C+4 C+6 Por ejemplo, en este año bisiesto 2008 los días de la semana correspondientes al 13 son: Año Ene. Feb. Mar. Abr. May. Jun. Jul. Ago. Sep. Oct. Nov. Dic. 2008 D X J D M V D X S L J S Ordenando los días de la semana entre C y C+6, como muestra la siguiente tabla, observamos que cada uno aparece al menos una vez. Esto significa que independientemente del valor de C, el día 13 cae al menos una vez en cada uno de los días de la semana. Luego es imposible que exista un año en el que ningún 13 caiga en martes. Lo sentimos por los supersticiosos. Día de semana del 13 Frecuencia (año de 365 días) Frecuencia (año bisiesto) C 2 3 C + 1 1 1 C + 2 1 1 C + 3 3 2 C + 4 1 2 C + 5 2 1 C + 6 2 2 Es más, gracias a esta tabla de frecuencias también podemos predecir cuáles son los fatídicos años en donde hasta tres veces el día 13 coincide en martes: son los años no bisiestos en donde el 13 de enero (C) corresponde a sábado (y por lo tanto C+3 a martes) y los años bisiestos en donde el 13 de enero cae en martes. Eso fue lo que sucedió en el 2007 y, afortunadamente, no volverá a suceder hasta el año 2018. Mientras tanto, vamos a ver qué tiene que ver todo esto con la música. La Octava Si emitimos un sonido -Sonido 1- a cierta frecuencia (es decir, con cierta agudeza o gravedad) y lo volvemos a emitir a doble frecuencia -Sonido 2- obtenemos un sonido más agudo que el primero. Sin embargo, percibimos cierta similitud entre ambos sonidos. Más aún, escuchados simultáneamente, comprobamos que se “acoplan” bien, de forma agradable, con consonancia. Existe una causa física para este “perfecto acople”. Generalmente, al vibrar, un objeto no emite una única frecuencia fundamental F, sino que además emite otros sonidos parciales, de menor intensidad, que en muchos casos son armónicos, es decir, sonidos cuya frecuencia es un múltiplo de la fundamental. Este fenómeno ya se ha analizado en el artículo Análisis Armónico. Lo que percibimos como “similitud” no es más que la coincidencia de frecuencias entre todos los armónicos, incluido el primero o fundamental, del Sonido 2 con los armónicos pares del Sonido 1, como podemos ver en la siguiente tabla (en color naranja, las frecuencias fundamentales de cada uno): Sonido 1 F 2 F 3 F 4 F 5 F 6 F 7 F 8 F 9 F 10 F 11 F 12 F Sonido 2 2 F 4 F 6 F 8 F 10 F 12 F A la distancia (entendiendo como tal la razón o proporción entre frecuencias, en este caso 2:1) de ambos sonidos le llamamos octava. El motivo de este nombre se verá más adelante. Por otra parte, también se conoce como octava al intervalo de frecuencias entre dos sonidos separados por esa distancia. Lá, la-la lá Veamos un ejemplo. La frecuencia que se toma como referencia para afinar un piano es la de 440 Hz, correspondiente a una nota La. Tomando esta frecuencia como Sonido 1, decimos que el Sonido 2 de 880 Hz está una octava por encima porque la razón de sus frecuencias es 2:1. ¿Cómo llamaremos al nuevo sonido de 880 Hz? Pues exactamente igual que al que está una octava por debajo: La. Pero, ¿por qué? ¿No es liar las cosas llamarle igual a dos sonidos diferentes? 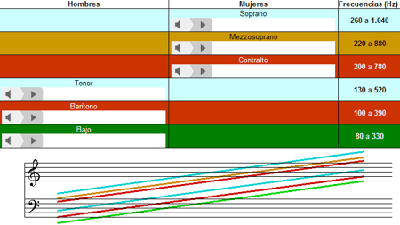El origen de conservar el mismo nombre reside en la diferencia de altura (percepción de la frecuencia) entre las voces humanas (y muchos instrumentos). Las hay más agudas y las hay más graves. Las de los hombres suelen ser más graves que las de las mujeres. Si varias personas cantan la misma melodía “Do-Sol-Fa” cada una lo hará con distinta frecuencia, pero aún así reconocemos en cada una de esas voces los mismos intervalos (de Do a Sol y de Sol a Fa), independientemente de la octava, por lo que nos parece que cantan “lo mismo”. Es decir, el oído atiende más a las distancias entre frecuencias que a las propias frecuencias, siempre que exista consonancia entre los armónicos (siempre que armonicen). Como vemos, la situación es muy similar a la de los días de la semana. El domingo 20 no es el mismo día que el domingo 27, pero su distancia al resto de los días de la semana permanece invariable. A cada domingo le sucede, desgraciadamente, un lunes. En música, se llama [La] a la clase de equivalencia formada por la frecuencia 440 Hz y todos sus múltiplos y submúltiplos, no necesariamente enteros, obtenidos al multiplicar o dividir esa frecuencia por una potencia de 2. Así, si deseamos determinar la frecuencia de una nota musical no basta con saber su nombre (Do, La, Mi...) sino que además debemos señalar la octava correspondiente. Ya habíamos visto que para determinar un día del año no basta decir si es lunes o jueves, se debe especificar la semana. Igualmente, necesitamos numerar las octavas para poder concretar el sonido de una nota. Por un convenio establecido en función de la capacidad de percepción sonora del oído humano, la octava 4 corresponde al intervalo que incluye a la nota La de 440 Hz, La4, mientras que la nota La de 880 Hz, denotada como La5, corresponde a la octava 5. En la siguiente imagen las teclas del piano correspondientes a La4 y La5, normalmente blancas, aparecen ahora en rojo: En la siguiente tabla se puede ver la correspondencia entre cada octava de un piano y la frecuencia de la nota La dentro de ella (al menos teóricamente, pues en la práctica se reajustan las frecuencias a medida que se alejan del La4 buscando un sonido más acorde con la percepción esperada por el oído): Número de octava 0 1 2 3 4 5 6 7 Frecuencia de La (Hz) 27,5 55 110 220 440 880 1.760 3.520 El oído humano puede percibir un rango mayor de frecuencias, desde los 16 ó 20 Hz hasta los 16.000 ó 20.000 Hz, es decir, casi diez octavas. No obstante, a partir de unos 4.000 Hz los sonidos se perciben demasiado agudos tanto para resultar agradables como para diferenciar con precisión su altura. Doble o nada Una progresión geométrica es una sucesión de números en donde, a partir de un número inicial,  la razón entre cada término y el anterior siempre es constante (esta constante se denomina, precisamente, razón). En la tabla anterior se observa que cada frecuencia se duplica entre una octava y la siguiente, lo cual es evidente por la propia definición de octava. Esta secuencia abarca los primeros términos de una progresión geométrica cuyo primer término, La0, corresponde 27,5 Hz y cuya razón es 2. El término general, es decir, la frecuencia correspondiente a la nota La de una octava cualquiera a partir de la inicial, se puede expresar entonces como: Lan = La0 · 2n La expresión anterior sintetiza cada uno de los elementos de la clase [La]. Por supuesto, esta relación se puede generalizar a cualquier otra nota. Por ejemplo: Don = Do0 · 2n Teclas blancas: incongruencias módulo 7 Volvamos al piano, con sus 52 teclas blancas (del total de 88 teclas): Observamos que cada octava, entre la 1 y la 7, comprende siete teclas blancas que, de izquierda a derecha, corresponden a las notas Do, Re, Mi, Fa, Sol, La y Si. Podemos comprobar la gran similitud entre las definiciones de octava y nota con las ya mencionadas de semana y día de semana: semana 1 = octava 1 = [viernes] = = [La] = = ¿Estamos entonces ante la misma situación que los siete días de la semana, correspondiendo Do al lunes y Si al domingo? No exactamente, por desgracia. La diferencia fundamental reside en que la distancia de un lunes al día siguiente, martes (más precisamente, la distancia entre el comienzo de ambos días), es de un día, la misma que hay entre un miércoles y su consecutivo jueves. Sin embargo, la “distancia sonora” (razón entre frecuencias) entre el Do y el Re es mayor que entre el Mi y el Fa. Pero, ¡esto es un gran problema! Si las distancias no son iguales, los cálculos con aritmética modular se vienen abajo, pues sólo son practicables con notas del mismo nombre (separadas un número entero de octavas). Así que... ¡es preciso modular la escala! El ciclo de quintas El origen de este problema se remonta al nacimiento de esas notas, cuyos intervalos o distancias fueron establecidas por los pitagóricos. En esencia, los pitagóricos aplicaron sistemáticamente dos intervalos fijos, la octava y la quinta, para obtener los demás, aparte de la cuarta (ver el artículo de Vicente Liem ya mencionado). Los intervalos resultantes resultaron simples, pero desiguales, dando lugar a la popular escala diatónica: Do, Re, Mi... La quinta es el intervalo que separa la altura de sonidos cuyas frecuencias están en proporción 3:2. Así, partiendo del La4, y subiendo cada vez una quinta, se obtienen las siguientes frecuencias: Número de quintas aplicadas 0 1 2 3 4 Frecuencia (Hz) 440 660 990 1.485 2.227,5 Ejemplificaremos ahora el método seguido por los pitagóricos para construir la escala diatónica. Los pitagóricos se dieron cuenta que había cierta relación entre la longitud de una cuerda y el sonido que producía. Hoy sabemos que esa relación se basa en que la frecuencia es inversamente proporcional a la longitud. Empezamos con una frecuencia determinada (correspondiente a la frecuencia fundamental de vibración de una cuerda de longitud dada). Supondremos, para mayor claridad, que esa frecuencia F es justamente la del Do central del piano: Do4. Sigamos los siguientes pasos: Do4 = F (unísono). Dividiendo la cuerda en dos partes iguales (no hace falta cortarla, basta sujetarla), se obtiene una cuerda la mitad de larga que, al ser pulsada, emite una frecuencia fundamental exactamente el doble que la anterior: Do5 = 2 F. Ya tenemos el intervalo de octava (en griego, diapasón), que es el intervalo que queremos dividir en intervalos menores. Dividiendo la cuerda original en tres partes iguales, la cuerda de longitud 2/3 emite una frecuencia fundamental exactamente 3/2 de veces la original: Sol4 = 3/2 F. Este es el intervalo de quinta (en griego, diapente). Dividiendo la cuerda original en cuatro partes iguales, la cuerda de longitud 3/4 emite una frecuencia fundamental exactamente 4/3 de veces la original: Fa4 = 4/3 F. Este es el intervalo de cuarta (en griego, diatesaron). Observemos que las notas creadas guardan gran consonancia entre sí (entre paréntesis se señala el número del armónico correspondiente): Unísono: Do4 F (1) 2 F (2) 3 F (3) 4 F (4) 5 F (5) 6 F (6) 7 F (7) 8 F (8) 9 F (9) 10 F (10) 11 F (11) 12 F (12) Octava: Do5 2 F (1) 4 F (2) 6 F (3) 8 F (4) 10 F (5) 12 F (6) Quinta: Sol4 3/2F (1) 3 F (2) 6 F (4) 9 F (6) 12 F (8) Cuarta: Fa4 4/3F (1) 4 F (3) 8 F (6) 12 F (9) Ahora proseguimos con el método conocido como ciclo de quintas: Subiendo una quinta a partir de la quinta, es decir, tomando 4/9 de la longitud de la cuerda obtenemos la nota Re5 = 9/4 F. Como hemos sobrepasado la octava, nos quedamos con el doble de esa longitud, y por tanto la mitad de frecuencia: Re4 = 9/8 F. Este es el intervalo de segunda. Subiendo de nuevo una quinta, es decir, tomando 2/3 de 8/9 de la longitud original, obtenemos una nueva longitud de cuerda cuya frecuencia corresponde a La4 = 27/16 F. Este es el intervalo de sexta. Subiendo otra quinta a partir de la anterior obtenemos Mi5 = 81/32 F. Como nos volvemos a pasar de octava, duplicamos la cuerda para obtener la mitad de frecuencia: Mi4 = 81/64 F. Este es el intervalo de tercera. Por último, subiendo otra quinta más a partir de la anterior obtenemos Si4 = 243/128 F. Este es el intervalo de séptima. Veamos como quedaron las frecuencias, tomando F como unidad: Nota Do Re Mi Fa Sol La Si Do Frecuencia 1 9 8 81 64 4 3 2 3 27 16 243 128 2 Factor de incremento 9 8 9 8 256 243 9 8 9 8 9 8 256 243 Pulsa en el siguiente enlace para ver el proceso seguido, paso a paso: construcción de la escala. El nombre de la Octava Ahora ya podemos conocer la procedencia de este nombre. Corresponde al número de notas que marcan la escala diatónica. Como hay 7 intervalos (5 de tono y 2 de hemitono), el número total de notas necesarias para definirlos es ocho. Por ejemplo: Do-Re-Mi-Fa-Sol-La-Si-Do. Así, si la primera nota es un Do, la “octava” nota también lo es. Por ejemplo, si tocamos un Re, decimos que para el próximo Re falta una octava. Pero también llamamos octava al intervalo que abarca el Re, Mi, Fa, Sol, La, Si y Do, es decir, a la serie de notas comprendidas entre dos Re consecutivos. Escala, modo y tonalidad Podemos imaginar una escala musical como la distribución de peldaños, no necesariamente de la misma altura, en una escalera. Esta distribución es periódica, cualquier tramo con un número predeterminado de peldaños se repite a lo largo de la escalera. Los protagonistas de Sonrisas y Lágrimas juegan con esta analogía al final de la famosa escena de la canción Do-Re-Mi. En la escala diatónica, este número predeterminado es de 7 peldaños. Si empezamos en la nota Do, estos 7 peldaños son: el que va de Do a Re, de Re a Mi, etc., hasta el último que une Si con el Do correspondiente al siguiente tramo. El problema es que, como hemos visto, la altura de estos peldaños en la escala diatónica no es siempre igual. Hay peldaños “altos” como el que va de Do a Re, y peldaños “bajos”, como el que va de Mi a Si. A la altura del peldaño alto se le llama tono (T = 9/8) y a la del peldaño bajo hemitono (h = 256/243). Por ejemplo, a partir de un Do, resulta que las sucesivas distancias o “subidas” son las que muestra la siguiente tabla: Nota Do Re Mi Fa Sol La Si Do Subida T T h T T T h Toda la escalera seguirá entonces el patrón: ...T h T T h T T T h T T h T T T h T T h T T T h T T h T T ... ¿Y por qué partir de Do? Podemos elegir otro peldaño de partida para establecer otro tramo periódico. Por ejemplo, partiendo de La obtenemos la misma escala (escalera): Nota La Si Do Re Mi Fa Sol La Subida T h T T h T T Como se ve, la distribución de los peldaños en el tramo ha cambiado, pero la distribución de toda la escalera permanece invariable. Podemos obtener distintos tramos, pero en esencia la escala no varía. A cada uno de estos tramos-patrón se le conoce como modo, y a su primera nota tónica. Los dos modos anteriormente representados son los modos principales usados en la música occidental. La información conjunta de la tónica y el modo se denomina tonalidad. Así, a la secuencia T T h T T T h se le conoce como modo Mayor, y a la tonalidad que sigue esa secuencia comenzando en Do se le llama “Do mayor”. Análogamente, la serie T h T T h T T se denomina modo Menor, y la tonalidad que sigue esa pauta empezando en  La se llama “La menor”. Pulsa en los siguientes enlaces para oír ambos modos y sendas composiciones basadas en ellos: Modo Ejemplos Mayor: T T h T T T h Tramo de la escala Composición de Do mayor Menor: T h T T h T T Tramo de la escala Composición en La menor El siguiente gráfico muestra la distribución periódica de la escala diatónica. Para establecer una tonalidad basta elegir una nota inicial (tónica) y seguir el sentido señalado. La escala cromática Pero, ¿qué sucede si elegimos la tonalidad Do menor? Es decir, empezar en Do pero siguiendo la pauta: T h T T h T T marcada por el modo menor. La respuesta fácil sería: “no se puede” y ya está. Pero esta respuesta no es satisfactoria, pues el motivo de la pregunta no es caprichoso. Podemos imaginar una melodía como una serie de instrucciones para subir o bajar los peldaños de la escala-escalera, al estilo “sube 1, después baja 3 y vuelve a subir 4”. Tal como están las cosas, si dos personas quieren cantar a la vez la misma melodía, sólo se ajustarán sus voces si la diferencia de altura entre ambas es exactamente un número entero de octavas. Lo mismo pasará con los diferentes instrumentos. Por ejemplo, si una persona comienza a cantar en Do y sube un peldaño se encuentra en Re, mientras que otra que suba la misma altura comenzando en Mi se encontrará en... ¿en dónde? Según el gráfico, en un punto intermedio entre Fa y Sol, que no corresponde con ninguna nota de la escala diatónica. Hace falta añadir nuevas notas intermedias o, como se dice en Música, añadir color. Según el gráfico necesitamos notas entre cada dos separadas por un tono. Estas nuevas notas, cinco en total, reciben el nombre de alteraciones. Por ejemplo, podemos considerar la nueva nota entre Re y Mi como una alteración del Re (Re sostenido, Re#), aumentando un hemitono la frecuencia del Re, o una alteración del Mi (Mi bemol, Mi♭), disminuyendo un hemitono su frecuencia: Tónica Modo Tonalidad Do Mayor Do Menor La escala así obtenida, con más color, se denomina escala cromática. Como ahora hay doce notas posibles que puedan elegirse como iniciales (tónicas), existirán 12 tonalidades diferentes en modo mayor y otras 12 tonalidades diferentes en modo menor. Pero observamos que el problema está resuelto a medias. Hemos creado las cinco nuevas notas, en un proceso conocido como transposición, disminuyendo un hemitono las notas Re, Mi, Sol, La y Si, por lo que los intervalos rojos y azules coinciden en medida. Sin embargo, no son exactamente iguales a los intervalos verdes. El factor de incremento del hemitono es de 28/35, mientras que el de cada intervalo verde es de 37/211. Ambas fracciones no son equivalentes. Dicho de otra forma, Re sostenido (Re aumentado un hemitono) no coincide con Mi bemol (Mi disminuido un hemitono). Para que ambas notas alteradas coincidiesen, es decir, para que las anteriores fracciones fuesen equivalentes, la fracción 312/219 =1,0136... debería ser exactamente la unidad. O, si se prefiere, 12 quintas (312/212) deberían coincidir con 7 octavas (27). Este pequeño desajuste, conocido como “coma pitagórica”, ha sido motivo de preocupación e investigación durante siglos. El problema es que este desajuste, aunque ligero, es acumulativo, es decir, a medida que nos alejamos de la tónica, desplazándonos entre distintas octavas, el desajuste entre los intervalos se hace más evidente al oído. Melodías moduladas Decíamos que podemos imaginar una melodía como una serie de instrucciones para subir o bajar los peldaños de la escala-escalera, tipo “sube 2, baja 5 y sube 6”. Para que la altura alcanzada en cada paso al seguir estas instrucciones, medida desde el peldaño de partida (tónica), no dependa del peldaño inicial (no dependa de la tonalidad), todos los peldaños deberían tener la misma altura. Pero ya hemos visto que en la escala cromática esto no se cumple. La distancia entre Mi bemol y Fa, por ejemplo, no alcanza el tono entero. El tono corresponde a una razón de 9:8, mientras que el hemitono equivalía a la razón 256:243. Aplicar dos hemitonos consecutivos equivale a multiplicar por (256/243)2 que no llega a alcanzar el valor 9/8. Esto significa que no podemos cambiar de modo, y por tanto de tonalidad, a lo largo de la melodía. Los compositores e intérpretes rechazan esta limitación. Un cambio de tonalidad se denomina modulación y abre las puertas a toda la riqueza de expresión musical, al poder desplazarse sin problemas entre distintas octavas. Además, los instrumentos afinados con una escala modulada podrían interpretar cualquier tonalidad sin reajustar continuamente su afinación (lo que no siempre es posible). Una posible idea para atajar este problema consiste en considerar otro hemitono auxiliar, la raíz cuadrada de 9/8, para dividir en dos partes semejantes el tono diatónico. De esta forma, el tono de la escala diatónica se mantiene y dos hemitonos auxiliares equivalen exactamente a un tono. Desgraciadamente, esta idea no iguala los peldaños, pues los hemitonos originales no coinciden con estos auxiliares. Exponencial base 2 Por supuesto, esto no podía quedar así. Para distribuir por igual las notas, se necesita que formen el mismo tipo de progresión que se guardaba entre las octavas: una progresión geométrica. Para ello, los hemitonos deben ser siempre iguales, aunque esto conlleve variar ligeramente las frecuencias de las notas diatónicas (con la consiguiente pérdida de consonancia perfecta que ello supone). Estos nuevos intervalos básicos que buscamos los llamaremos semitonos, de forma que subir dos semitonos debe equivaler a subir un tono. Observemos la tabla de frecuencias: Nota Do Re♭ Re Mi♭ Mi Fa Sol♭ Sol La♭ La Si♭ Si Do Frecuencia f0 f1 f2 f3 f4 f5 f6 f7 f8 f9 f10 f11 f12 Por una parte, entre el primer Do y el segundo Do, separados por una octava, la razón tiene que ser 2:1. Por otra, entre una nota y la anterior tiene que haber la misma razón de frecuencias, el semitono (s) que queremos hallar: f12 = 2 f0 fn = s fn-1 Iterando sucesivamente la segunda igualdad, para n igual a 12, obtenemos: f12 = s f11 = s2 f10 = s3 f9 = ... = s12 f0 Lo que, al reunirlo con la primera igualdad, nos permite hallar el valor buscado para el semitono: s12 f0 = 2 f0 ⇒ s12 = 2 ⇒ s = 12√2 Hemos encontrado que, para permitir la modulación sin problemas, cada semitono debe establecerse en la raíz duodécima de 2. Juntándolo todo, vemos que las frecuencias siguen la función exponencial: f(x) = f0 2x/12 donde f0 es la frecuencia inicial y las notas corresponden a valores enteros de x. Logaritmo base 2 La relación anterior entre la frecuencia de las notas, de tipo funcional, se vuelve más manejable si atendemos sólo al exponente. La forma matemática de conseguirlo es mediante aplicación del logaritmo de la base utilizada, en este caso 2: log2(f(x)) = log2(f0 2x/12) = log2(f0) + x/12 12 log2(f(x)/f0) = x Esta nueva relación entre los logaritmos de frecuencias, de tipo lineal, se ajusta además mucho mejor a lo que normalmente percibimos como “distancia de altura sonora” entre dos frecuencias distintas. El oído se comporta realmente como si siguiera esta relación lineal entre la diferencia de logaritmos, pues nuestra percepción de las frecuencias es también de tipo logarítmico. Es decir, percibimos la misma diferencia de altura entre la frecuencia F y la frecuencia 2F que entre esta última y la frecuencia 4F. Teclas blancas y negras: congruencias módulo 12 La nueva escala obtenida, basada en el semitono “igual”, se denomina escala cromática de temperamento igual, y es la que se utiliza en el piano moderno. Las nuevas notas intermedias obtenidas corresponden a las teclas negras del piano. La tabla de logaritmos de frecuencias, a partir de la primera tecla La0, con frecuencia f0 = 22,5 Hz, muestra la proporcionalidad ya señalada: Nota La0 Si0 12 log2(f(x)/f0) 0 1 2 Nota Do1 Re1 Mi1 Fa1 Sol1 La1 Si1 12 log2(f(x)/f0) 3 4 5 6 7 8 9 10 11 12 13 14 Nota Do2 Re2 Mi2 Fa2 Sol2 La2 Si2 12 log2(f(x)/f0) 15 16 17 18 19 20 21 22 23 24 25 26 Nota Do3 Re3 Mi3 Fa3 Sol3 La3 Si3 12 log2(f(x)/f0) 27 28 29 30 31 32 33 34 35 36 37 38 Nota Do4 Re4 Mi4 Fa4 Sol4 La4 Si4 12 log2(f(x)/f0) 39 40 41 42 43 44 45 46 47 48 49 50 Nota Do5 Re5 Mi5 Fa5 Sol5 La5 Si5 12 log2(f(x)/f0) 51 52 53 54 55 56 57 58 59 60 61 62 Nota Do6 Re6 Mi6 Fa6 Sol6 La6 Si6 12 log2(f(x)/f0) 63 64 65 66 67 68 69 70 71 72 73 74 Nota Do7 Re7 Mi7 Fa7 Sol7 La7 Si7 12 log2(f(x)/f0) 75 76 77 78 79 80 81 82 83 84 85 86 Nota Do8 12 log2(f(x)/f0) 87 Observamos que ahora sí sucede lo mismo que con los días de la semana. Claro que esta semana tiene 12 días en vez de siete: Lan = La0 + 12n La tabla de la “suma módulo 12” queda ahora así: Semitonos añadidos La La# Si Do Do# Re Re# Mi Fa Fa# Sol Sol# 12n La La# Si Do Do# Re Re# Mi Fa Fa# Sol Sol# 12n + 1 La# Si Do Do# Re Re# Mi Fa Fa# Sol Sol# La 12n + 2 Si Do Do# Re Re# Mi Fa Fa# Sol Sol# La La# 12n + 3 Do Do# Re Re# Mi Fa Fa# Sol Sol# La La# Si 12n + 4 Do# Re Re# Mi Fa Fa# Sol Sol# La La# Si Do 12n + 5 Re Re# Mi Fa Fa# Sol Sol# La La# Si Do Do# 12n + 6 Re# Mi Fa Fa# Sol Sol# La La# Si Do Do# Re 12n + 7 Mi Fa Fa# Sol Sol# La La# Si Do Do# Re Re# 12n + 8 Fa Fa# Sol Sol# La La# Si Do Do# Re Re# Mi 12n + 9 Fa# Sol Sol# La La# Si Do Do# Re Re# Mi Fa 12n + 10 Sol Sol# La La# Si Do Do# Re Re# Mi Fa Fa# 12n + 11 Sol# La La# Si Do Do# Re Re# Mi Fa Fa# Sol El reloj musical Las congruencias módulo 12 que recoge la tabla anterior tal vez resulten familiares. Es el mismo tipo de congruencia que aplicamos al declarar que las 19 horas son las 7 de la tarde. Cada semitono reemplaza a cada hora: 19 (mod12) = 7 El compositor polaco Chopin describió la fuga como lógica pura. Era un gran admirador de la obra de Bach. Siguiendo sus pasos, aplicó el principio del contraste, alternando los modos mayor y menor, en su obra 24 preludios (op. 28). Las tonalidades de estos preludios de Chopin siguen el orden: Do mayor, La menor, Sol mayor, Mi menor, Re mayor... ¿Qué orden es éste? Podemos disponer estas 24 tonalidades en un reloj. La parte externa indica el modo mayor y la interna el modo menor. Así expuesto, se ve claramente que Chopin sigue el ciclo de quintas. Es decir, cada nueva tonalidad está 7 semitonos más arriba que la tonalidad anterior del mismo modo. Matemáticamente, esto equivale a sumar 7 (módulo 12) en sentido horario:

Sábado, 01 de Marzo de 2008 | Imprimir | PDF |  Correo electrónico

125. 8. (Julio 2008) Geometría Musical (1)

Emoción y reconocimiento ¿Por qué la música emociona tanto a tantas personas? Una primera clave para responder a esta difícil pregunta la encontramos en los orígenes orales de la música. Podemos considerar en parte la música como un lenguaje subliminal. En la comunicación con nuestros semejantes a través de la palabra no sólo transmitimos la información textual, sino que la intensidad, inflexiones y cadencia de la voz aportan otro tipo de información tan valiosa o más, para una acertada comunicación emocional, que el propio texto. Son esas características del habla (intensidad, cadencia, inflexión) las que se exportan a la música, primero en la canción y posteriormente en la interpretación de algún instrumento. Hablar con absoluta monotonía, además de exponernos a aburrir considerablemente al interlocutor, priva a la comunicación de la información emotiva, a no ser que ésta se aporte mediante otros signos (como el lenguaje corporal). Ahora bien, la experiencia es fundamental para una correcta interpretación en el proceso de comunicación. Aquí es donde aparece la segunda clave, a la que dedicaremos algunos artículos: el reconocimiento de una experiencia anterior. Reconocer es un proceso básico en cualquier tipo de emoción. Un simple chiste del tipo “¿cuál es el animal que tiene entre 3 y 4 ojos?” (el piojo) puede que haga gracia o no, pero en ningún caso la hará si nuestro interlocutor desconoce o no reconoce el valor del número Pi. Igualmente, para emocionarse con una composición musical se necesita cierto tipo de reconocimiento. La repetición Tal vez la forma más eficaz de provocar el reconocimiento sea la repetición, conocida como una de las estrategias básicas, junto con la relación, en los procesos de aprendizaje. En el irónico e inquietamente divertido libro de Mark Twain Cartas desde la Tierra (Letter from the Recording Angel), se puede leer: >> ¡En el cielo del hombre todo el mundo canta! El que no cantaba sobre la tierra canta allí; el que no sabía cantar sobre la tierra sabe hacerlo allí. Este canto universal no es casual, ni ocasional, ni interrumpido por intervalos de silencio; es continuo, perdura todo el día y todos los días, durante un periodo de doce horas. Y todo el mundo permanece allí; a pesar de que en cualquier otra parte de la tierra el lugar estaría vacío en dos horas. Los cantos son solo himnos. Más aún, es un único himno. Las palabras son siempre las mismas, alrededor de una docena, no hay rima, no hay poesía; “Hosanna, hosanna, hosanna, Señor Dios del Sabbat, ¡ra! ¡ra! ¡ra! ¡siss!... ¡boom!... ¡ah!”. >> Mientras tanto, todas las personas tocan un arpa -¡millones y millones!- en tanto que sólo veinte de cada mil sabían tocar ese instrumento en la tierra, o siquiera deseaban hacerlo. >> Considerad ese sordo huracán de sonido: ¡millones y millones de voces chillando al unísono y millones de arpas haciendo rechinar los dientes al mismo tiempo! Les pregunto: ¿no es abominable, es odioso, es horroroso? La repetición forma parte tanto de la música como del propio medio sonoro. Las ondas sonoras no son más que perturbaciones periódicas de la presión del aire. El reconocimiento de estos “patrones sonoros”, más o menos complejos, se realiza normalmente gracias a ciertos tipos de repeticiones. Sin embargo, la repetición constante (aparte de ser abominable, odiosa, horrorosa) puede provocar efectos no deseados, el más leve de los cuales es simplemente la insensibilización. Esto es lo que sucede cuando dejamos de percibir el sonido de una lámpara después de un rato. Excepcionalmente, existen casos en donde la repetición machacona es justo lo deseado. Por ejemplo, en la danza indonesa Kecak (pronúnciese “kachak”) un coro masculino no para de repetir kachakachakachak... precisamente para crear un clima hipnótico. Algo similar ocurre en algunos rituales vuduistas. El preciso equilibrio entre reconocimiento y repetición obliga, por tanto, a que ésta se realice de forma moderada y con ligeros cambios. En geometría aparecen cierto tipo de transformaciones que “cambian” una figura geométrica “conservando” características fundamentales que permiten su reconocimiento. Nos referimos a las transformaciones que conservan la forma de la figura: los movimientos (isometrías) y las homotecias. Figuras semejantes Cualquier movimiento (traslación, giro, reflexión) y cualquier homotecia (ampliación/reducción) de una figura conserva su forma. Esto permite su rápido reconocimiento visual, incluso aunque la orientación haya variado, a la vez que evita la repetición exacta del motivo. Todas esas transformaciones son experimentadas, visualmente, todos los días. Nuestro propio cuerpo (al menos externamente), y el de muchos seres o partes de seres vivos, está dotado de una fuerte simetría. La parte izquierda parece reflejarse en la derecha, o viceversa. Las traslaciones y los giros los observamos cada vez que vemos un objeto desplazarse o girar respecto a nosotros. Nadie duda que se trata realmente del mismo objeto, a pesar de ocupar una nueva posición visual. Pulsa sobre la imagen para interactuar con ella Las homotecias aparecen de forma natural cada vez que nos aproximamos o alejamos de un objeto. De nuevo, su cambio de tamaño aparente no nos impide continuar identificando el objeto como el mismo. Pulsa sobre la imagen para interactuar con ella Tenemos, por tanto, gran experiencia en la observación de todo tipo de variaciones ópticas con una misma característica común: la semejanza entre figuras. Pulsa sobre la imagen para interactuar con ella Orden y belleza La característica fundamental de la simetría musical es la repetición. Todos los tipos de simetría son formas de repetición. Sin embargo, también estamos acostumbrados a observar y apreciar pequeñas desviaciones de la semejanza perfecta. Estas desviaciones dotan a la transformación de “personalidad”, la individualizan frente a otras similares, le otorgan “carácter”. Si el lector o la lectora todavía no ha realizado el siguiente experimento digital, le recomendamos encarecidamente que lo haga. Es sencillo y... cómo expresarlo... “íntimamente fascinante”. Se trata simplemente de realizar un montaje con una foto frontal del rostro. Con ayuda de un editor de imágenes, cortamos la imagen de la cara por la mitad, separando nuestro lado derecho del izquierdo. Finalmente, reflejamos cada uno de esos lados, obteniendo dos nuevas caras. La siguiente imagen no corresponde a ninguna persona que haya existido. Simplemente, es el resultado de efectuar el proceso descrito con la parte derecha (su parte derecha) de la cara mostrada en una fotografía de Cameron Diaz. La simetría es perfecta. Veamos el resultado de reflejar su parte izquierda. La simetría vuelve a ser perfecta, pero las dos imágenes muestran claras diferencias. Por último, observemos la fotografía original: Podemos apreciar cómo pequeñas alteraciones de la simetría humanizan nuestra percepción de la misma, le añaden estilo, personalidad y expresión. De la misma forma, la combinación de simetría y asimetría es el principio básico de la música, pues sólo así se puede conjugar unidad y libertad. Recubrimientos Las simetrías permiten trasladar un motivo o patrón a lo largo del tiempo, como sucede en música, o del espacio, como sucede en los teselados. La repetición no continúa indefinidamente en su manifestación física, pero nos ofrece una imagen del infinito que en potencia contiene. En la siguiente escena podemos mover los vértices del cuadrilátero central y comprobar que, gracias a las simetrías, un cuadrilátero cualquiera tesela el plano. Pulsa sobre la imagen para interactuar con ella Al superponer diversos teselados o patrones simples, se enriquece el diseño. Esta es la idea de varias manifestaciones musicales (armonía, contrapunto...) y de los diseños propios del arte musulmán. El trabajo gráfico de Escher estuvo muy influenciado por estos diseños que descubrió visitando Granada. Escher “animó” estas construcciones reemplazando los abstractos diseños geométricos por figuras reconocibles: peces, aves, lagartos, hombres... como se puede apreciar en la siguiente imagen de uno de sus famosos grabados en madera: No obstante, trabajos de esta naturaleza no constituyen buenas analogías respecto al mundo musical, pues carecen de “dirección”. Una composición musical precisa de un tiempo para su ejecución. Inevitablemente, este tiempo establece un orden en la misma, un “antes” y “después” en cada nota. En cambio, su serie Metamorfosis es un ejempo visual perfecto de las diversas transformaciones melódicas y armónicas que caracterizan una composición musical. En esta obra la mirada del espectador debe recorrer el cuadro de izquierda a derecha, en un proceso de transformación en el tiempo (como una película). El teselado se transforma gradualmente, adquiriendo dirección, como en música. Pulsa sobre la imagen para interactuar con ella Algunos ejemplos musicales Las transformaciones geométricas que conservan la forma se corresponden en el mundo musical con transformaciones que conservan los intervalos (distancia de altura entre dos notas consecutivas) en el caso de los movimientos, o que conservan la proporción entre ellos en el caso de las homotecias. En los siguientes ejemplos se muestran algunas posibilidades sencillas que ofrecen este tipo de transformaciones. No son ejemplos extraordinarios. En prácticamente cualquier composición se pueden encontrar ejemplos semejantes. Esto no significa, por supuesto, que el compositor sea consciente de estar realizando “transformaciones geométricas”. Simplemente, su oído y experiencia le indican que conservar los intervalos o sus proporciones es una excelente forma de “repetir sin repetir”, es decir, de hacer “en cierto modo” familiar al oyente el motivo musical sin repetirlo exactamente. Empezamos con cuatro tipos de reflexión: de la altura en la melodía (reflexión horizontal), de la altura en el acorde (reflexión vertical), del ritmo y de la intensidad (piano, forte, piano). Pulsa sobre la imagen para interactuar con ella Veamos ahora una rotación y otro tipo de reflexión (inversión). Pulsa sobre la imagen para interactuar con ella Continuemos con una reflexión desplazada y dos tipos de reflexión con homotecia: Pulsa sobre la imagen para interactuar con ella Ahora, una veloz doble traslación. Pulsa sobre la imagen para interactuar con ella Pasemos a una exquisita homotecia en la duración. Pulsa sobre la imagen para interactuar con ella Para finalizar, en el siguiente ejemplo podemos ver parte de un pasaje de la sonata Hammerklavier de Beethoven (sonata cuya buena ejecución continúa siendo un reto incluso para un virtuoso), concretamente los compases comprendidos entre el 16 y el 22. No habría nada especialmente extraordinario en ellos, si no fuera porque todos, excepto uno (en rojo) se vuelven a repetir exactamente al revés (reflexión desplazada), nota por nota, nada menos que ¡132 compases más adelante! Es evidente que, en este caso, Beethoven era muy consciente de la aplicación de esta transformación geométrica. Pulsa sobre la imagen para interactuar con ella En el próximo artículo podremos ver y oír más ejemplos de transformaciones geométricas en la música en las que se evidenciará, como en el ejemplo anterior, el uso consciente de las simetrías.

Martes, 01 de Julio de 2008 | Imprimir | PDF |  Correo electrónico

126. 9. (Septiembre 2008) Geometría Musical (2)

Dábale arroz a la zorra el abad En el artículo anterior podíamos ver y oír un ejemplo de transformación geométrica en la música, realizada de forma claramente consciente por Ludwig van Beethoven en su sonata Hammerklavier. Ahora podremos ver y oír algunos ejemplos extremos de este uso consciente de la simetría en la composición musical. Comenzaremos por una pieza exquisita en su sencillez. Se trata del Minueto al Rovescio, uno de los movimientos de la Sonata en La mayor (Hob XVI-26) que Haydn, padre de la sinfonía y el cuarteto, compuso en 1773. La composición se divide en dos partes, donde la segunda es una reflexión exacta de la primera. Dicho de otro modo, ambas juntas forman un palíndromo musical, una partitura “capicúa”. El propio Haydn también es el autor de la sinfonía El palíndromo (Sinfonía nº 47) que contiene otro minueto y un trío palindrómicos. Pulsa sobre la imagen para interactuar con ella Observemos que a pesar de la perfecta simetría, la composición no suena “artificial”. Justamente ahí reside la dificultad en la realización de este tipo de composiciones, algo similar a lo que ocurre cuando intentamos construir un palíndromo en castellano (como el que da título a este apartado). A medida que se añaden nuevas notas resulta más difícil mantener la simetría sin perder la “naturalidad”. En el minueto anterior, Haydn construye una frase musical cuya reflexión no sólo combina bien con la original sino que “la completa”, “la resuelve”, es una consecuencia “natural” de ella. La simetría de las notas también se puede apreciar recurriendo al espectrograma de los sonidos correspondientes. Pulsa sobre la imagen para ampliarla Sin embargo, si nos fijamos con detalle, podemos apreciar que la gráfica no muestra una simetría exactamente perfecta. Ello se debe a que, aunque sean las mismas notas, la ejecución de cada una no suena exactamente igual al reflejarse. Cuando se comienza a ejecutar (“atacar”) una nota se tarda un tiempo en alcanzar el sonido de la nota con la intensidad deseada. Algo similar ocurre al dejar de ejecutarla. Aunque estos periodos de tiempo suelen ser muy breves, son suficientes para provocar ligeras asimetrías. De nuevo, podemos comparar este fenómeno con las palabras: si respetamos el acento y tiempo dedicado a cada fonema, no suena exactamente igual “dábale arroz a la zorra el abad” que “daba le arroz al a zorra elabad”. De todas formas, los espectrogramas resultan muy descriptivos de algunas transformaciones simples. Por ejemplo, un vistazo a la siguiente imagen nos permite deducir en pocos segundos, sin siquiera oír los sonidos correspondientes, que la onda sonora correspondiente a la imagen derecha es una reflexión en el tiempo, con homotecia en la amplitud (intensidad), del sonido de la izquierda. Espejo, espejito La siguiente composición, “El dueto del espejo”, se trata de un divertimento en Sol mayor para dos violines,  atribuido a Mozart. La partitura está diseñada para que ambos violinistas puedan ejecutarla a la vez, ¡pero cada uno leyéndola en sentido contrario! Por ejemplo, colocando la partitura en una mesa, los dos violinistas se deben colocar enfrentados, en lados opuestos de la mesa, con la partitura situada entre ambos. De esta forma, comenzando a la vez, mientras uno interpreta el primer compás, el otro se encuentra ejecutando el último (que para él es el primero, naturalmente), y cuando el primer violinista avanza hasta el segundo compás, el otro violinista avanza hasta el penúltimo. Pulsa sobre la imagen para interactuar con ella ¿Cómo se ha creado esta curiosa composición y, sobre todo, cuál es “el truco” que permite a ambos violinistas intercambiarse sus voces (principal y acompañamiento) sin dejar de armonizar en ningún momento? Para ello, observemos la siguiente partitura. Se trata de la primera mitad de la partitura anterior (para el primer violinista), a la que se le ha añadido la segunda mitad de la partitura anterior “girada 180 grados” (que es la primera mitad que interpreta el segundo violinista). Se han coloreado las figuras en función del intervalo -diferencia de altura- que separa cada dos notas ejecutadas al mismo tiempo. Azul significa la misma nota (aunque sea en distinta octava), en verde los intervalos de tercera, en dorado los de sexta y en rojo el resto. Pulsa sobre la imagen para ampliarla De esta forma, podemos comprobar que a lo largo de la mitad de la ejecución, los intérpretes están ejecutando o bien las mismas notas o bien notas separadas por intervalos de tercera o sexta, pues las veces que se desvían de esta norma (figuras rojas) son meros adornos. Así que la segunda voz no sólo armoniza con la primera, sino que sigue un camino “casi paralelo” a ella. Con ello se consigue que cuando reconstruimos la partitura completa, volviendo a girar la segunda voz 180 grados, cada una de las dos voces, al encontrarse con “el camino” seguido por la otra, no lo encuentre extraño (y nuestro oído tampoco, por supuesto). En la siguiente imagen se recoge de nuevo la partitura completa atendiendo sólo al tipo de intervalo. Ahora resulta mucho más evidente la rotación producida en esos intervalos. Ejercicio de audición: transporte Intentaremos ahora que el oído reconozca las simetrías. Para estos pequeños ejercicios hemos elegido como base una melodía infantil universalmente conocida: el canon Frère Jacques. Veremos -y oiremos- cómo afectan a esta sencilla melodía distintas simetrías. Algunos movimientos son mucho más fáciles de reconocer que otros, debido a nuestra abundante experiencia sobre ellos. El caso más evidente lo tenemos en la traslación en la altura, tan familiar que incluso decimos que el sonido es “el mismo” aunque suena más grave o más agudo. Esto se conoce como “transporte”. Cualquier frase dicha (o cantada) por voces con distinta altura es un ejemplo cotidiano de transporte. Al transportar se conservan los intervalos entre dos notas consecutivas mientras permanece inalterada la secuencia de los mismos. No nos cuesta ningún esfuerzo, dada nuestra experiencia cotidiana, en reconocer la similitud entre una melodía cualquiera y su transporte a cualquier otra altura. Nosotros mismos, a voluntad, podemos muy fácilmente bajar o subir la altura de nuestra voz sin dejar de entonar la misma canción. Veamos un ejemplo. A partir del canon Frère Jacques (en la tonalidad de Do mayor), realicemos un transporte (en este caso, descenso de la altura) hasta la tonalidad de Re menor. Observemos que no nos cuesta ningún esfuerzo identificar el nuevo sonido como el mismo canon Frère Jacques. A continuación, variamos ligeramente cuatro notas, dividiéndolas en dos más breves. Ahora sí apreciamos una diferencia melódica, pero lo suficientemente aislada y breve como para que no tengamos dificultad en seguir reconociendo la canción. ¿A qué viene, nos preguntaremos, realizar esa pequeña alteración de la melodía? La respuesta es simple. Precisamente esta leve modificación es la misma que realizó Mahler para servirse de esta canción infantil en el 3º movimiento de su Sinfonía nº 1, Titán. La presencia de la canción en medio de la marcha fúnebre es el recurso empleado por Mahler para mostrar el macabro cortejo como una bufonada. Mahler sabía que ni el cambio de tonalidad ni la ligera modificación melódica ni el descenso en el tempo (ejecución más lenta) impediría reconocer la canción infantil. Pulsa sobre la imagen para interactuar con ella Experiencia y reconocimiento No todos los movimientos resultan tan sencillos de reconocer. Las simetrías en donde intervienen reflexiones y rotaciones son mucho menos frecuentes en la vida cotidiana, así que su reconocimiento exige normalmente un entrenamiento previo. La relación entre experiencia y reconocimiento es una relación mental, y no depende del sentido (el oído en este caso) que transmite al cerebro la información. Para demostrarlo, busquemos ejemplos visuales a los que estemos poco acostumbrados. La siguiente imagen representa uno de ellos. Estamos muy acostumbrados a reconocer una sonrisa y unos ojos vivos, pero sólo en el contexto de una cara “derecha”. En cuanto invertimos la cara, nuestra poca experiencia sobre la forma de los rasgos en tales condiciones de inversión provocan que la percepción se base más en el brillo de los dientes y los ojos que en la forma real.  Incluso sabiendo cómo es el rostro puesto del “derecho”, en cuanto volvemos a invertir la imagen, cambia instantáneamente nuestra percepción y nuestro impulso de “rechazo” se transforma nuevamente en “agrado”. Pulsa sobre la imagen para interactuar con ella En el ejemplo anterior se podría argüir que la falsa percepción se debe a nuestro “extraño” posicionamiento respecto a la imagen, de forma que nos basta ladear la cabeza para salir del engaño. Sin embargo, el siguiente ejemplo muestra que nuestra percepción visual puede equivocarse “coloquemos como coloquemos” nuestra cabeza. Las dos superficies (amarilla y verde) de ambas mesas son idénticas en forma y tamaño. Es evidente, ¿verdad? Pulsa sobre la imagen para interactuar con ella De nuevo, es el contexto inusual (colocación y orientación de las patas de las mesas, en este caso) el que provoca que nuestra experiencia con objetos similares en el pasado no nos sirva como referencia fiable. Ejercicio de audición: movimiento retrógrado Lo que sucede con lo que nos entra por un ojo también ocurre con lo que nos entra por un oído (incluso aunque no nos salga por el otro), pero en grado mayor debido a que habitualmente se nos exige más observación visual que auditiva. Por eso no resulta extraño que movimientos muy simples y nítidos no los distingamos o lo hagamos de forma confusa. Veamos algunos ejemplos. En el siguiente ejercicio simplemente reflejamos la melodía de la canción, como había hecho Beethoven en su Hammerklavier. Esto se conoce como movimiento retrógrado. Si no nos previenen, ¿realmente reconoceríamos la canción original “al otro lado del espejo”? Pulsa sobre la imagen para interactuar con ella Ejercicio de audición: inversión En el siguiente ejercicio realizamos una reflexión de los intervalos (si antes subíamos una cierta altura al pasar de una nota a la siguiente, ahora descendemos esa misma altura, y viceversa). En la partitura, equivale a reflejar las figuras sobre un eje horizontal. Esto se conoce como inversión melódica. Debemos observar que, debido a la inversión de intervalos, cualquier inversión melódica conlleva a menudo un cambio en la tonalidad. En este caso, el canon pasa de Do mayor a Re menor. Pulsa sobre la imagen para interactuar con ella Ejercicio de audición: inversión retrógrada Antes de abandonar esta canción infantil, veamos qué sucede si combinamos las dos reflexiones anteriores: una reflexión vertical (movimiento retrógrado) y una horizontal (inversión). Geométricamente, el resultado es una rotación de 180 grados. En música, a esta rotación se le denomina inversión retrógrada o movimiento cangrejo. Pulsa sobre la imagen para interactuar con ella Ejercicio de audición: variación Por último, veamos lo que puede hacer un auténtico “profesional” cuando combina estos simples movimientos y los “arropa” adecuadamente. Se trata de la famosa variación 18 de la obra "Rapsodia sobre un tema de Paganini", de Rachmaninov, utilizada en varias bandas sonoras de películas. El tema de Paganini se invierte. Esta inversión ya es suficiente, como hemos visto (o más bien oído), para que la melodía resultante parezca completamente nueva, o casi. Pero si además, como hace Rachmaninov, realizamos cambios en la tonalidad, en el tempo, en el compás y en la orquestación, el resultado puede ser espectacular. Pulsa sobre la imagen para interactuar con ella Un buen ejemplo de cómo un simple movimiento geométrico puede convertir el tema “incisivo” de Paganini en la última gran pieza romántica de Rachmaninov.

Lunes, 01 de Septiembre de 2008 | Imprimir | PDF |  Correo electrónico

127. 10. (Noviembre 2008) Pequeños Terremotos

Pop art En la siguiente figura aparecen 30 patrones dispuestos en cinco columnas. ¿Se trata de una obra de arte abstracto? ¿Quizás dibujos ornamentales hallados en tallas, cerámicas o telas de algún pueblo africano? ¿Serán diseños para la moda de la próxima temporada? ¿Qué decir de estos otros enmarcados en cuadrados, como si fueran baldosas? ¿Tienen el mismo origen que los anteriores? ¿Qué representan, de dónde surgen? Estos motivos son tan conocidos entre muchos científicos que incluso existen versiones comerciales con llamativos colores, como esta del físico Eric Heller: Olas superpuestas En el artículo Análisis Armónico comentábamos  el problema de la cuerda vibrante: Al pulsar la cuerda se produce una onda transversal viajera, como una ola, que recorre la cuerda hasta los extremos, con una cierta amplitud (separación máxima respecto del punto de reposo). Allí, incapaz de continuar su propagación, se refleja. Esto ocasiona que dos ondas reflejadas en los extremos viajen una contra otra hasta superponerse en la cuerda. La suma de estas dos ondas reflejadas es una onda longitudinal llamada onda estacionaria. Este nombre se debe a que, al superponerse, las ondas reflejadas parecen dejar de propagarse, convirtiéndose en una oscilación de la cuerda. Esta oscilación es la que se propagará al aire. Cada onda reflejada habrá recorrido dos veces la longitud de la cuerda hasta encontrarse de nuevo en el extremo de partida. Así que la longitud de la onda estacionaria es el doble de la longitud de la cuerda. Ahora bien, al superponerse las dos ondas transversales para formar la onda estacionaria, podrán aparecer puntos (vientres) en donde las dos ondas coincidan en fase, así que la amplitud será el doble. También pueden aparecer puntos (nodos) en donde las ondas se encuentren desfasadas 180º, así que en ellos la amplitud será nula (no se mueven). Estos nodos actúan como extremos fijos de partes de la cuerda, por lo que la vibración de estas partes emitirá un sonido más agudo (con mayor frecuencia). Si ahora añadimos una dimensión más, pasando de la linealidad de una cuerda a las dos dimensiones de la superficie de una placa, un platillo o una membrana tirante, obtenemos el mismo fenómeno de superposición de ondas transversales. Ahora, sin embargo, los nodos (puntos donde una onda y su reflejo se superponen anulándose) no son puntos aislados sino que forman líneas nodales en donde la placa o membrana no vibra. El sonido puede verse Hacia 1787, el alemán Chladni, considerado uno de los pioneros de la física acústica, estudia por primera vez estas líneas nodales. Ernst Chladni (1756 - 1827) Con estudios de Derecho, músico aficionado y un entusiasta de la ciencia, Chladni encuentra la ley que lleva su nombre, una relación sencilla entre los modos propios de vibración de una placa. Para ello, se valió de placas sujetas por el centro sobre las que espolvoreaba arena fina. Al hacerlas vibrar con un arco de violín, los patrones de las líneas nodales se hacen visibles, pues sobre esas líneas se acumula la arena rebotada de las otras zonas vibrantes. De esta forma, cada frecuencia natural de vibración de la placa corresponde con un patrón determinado. Chladni trasladó cuidadosamente al papel cada uno de los patrones que iba encontrando, lo que permitió popularizarlos, mientras se dedicaba a realizar demostraciones ante el fascinado público europeo. Pulsa sobre la imagen para ver el resto Cuando Chladni repitió este experimento en la Academia de Ciencias de París, en 1808, se oyó una exclamación de asombro: “¡el sonido puede verse!”. Era la voz de Napoleón Bonaparte. La ley de Chladni relaciona la frecuencia aproximada de la vibración de un platillo circular, de centro fijo, con el número de líneas nodales radiales (m) y no radiales (n): f = C (m + 2n)2 donde el valor de la constante C sólo depende, en principio, de las propiedades del platillo. Sin embargo, el exponente puede sufrir variaciones en distintos rangos de frecuencias incluso para el mismo platillo, aunque siempre ronda el valor 2. Una expresión más general, del tipo: f = C (m + bn)c amplía la relación anterior, para distintos valores de b y c, a platillos circulares no planos como los címbalos, las campanas y las campanillas. En el caso de placas y membranas circulares sujetas por su borde (tambores y timbales, por ejemplo), los patrones obtenidos se componen de diámetros y circunferencias concéntricas. En la siguiente imagen vemos algunos. Debajo de cada dibujo aparece la frecuencia relativa con respecto a la frecuencia fundamental. Observemos que, al contrario de lo que pasaba con la cuerda vibrante, las sucesivas frecuencias naturales (los sucesivos parciales) no son múltiplos enteros de la fundamental (no son armónicos). Curiosamente, patrones similares aparecen al representar gráficamente la función de probabilidad de los distintos orbitales de los electrones: La protagonista Pero la ley de Chladni, además de ser una aproximación, sólo recoge la observación del fenómeno, clasificando las figuras obtenidas, pero no las explica. Napoleón había quedado tan profundamente impresionado por las figuras que mostraban las placas que ofreció una fuerte recompensa por una explicación. Naturalmente, para encontrar esta explicación será necesario modelizar matemáticamente el fenómeno físico. En 1809, la matemática francesa Sophie Germain comienza a trabajar en el problema, pero no es hasta 1816 cuando, en su tercer intento, consigue ganar el premio otorgado por la Academia Francesa de las Ciencias. El éxito de Germain se considera mucho más que un premio. Ella había luchado toda su vida por poner su talento por encima de los prejuicios contra su sexo. También es sabido que mantuvo correspondencia y amistad con el príncipe de las matemáticas, Gauss, a quien le protegió, gracias a su influencia con Napoleón, al invadir las fuerzas napoleónicas la ciudad natal de Gauss, Brunswick (cerca de Hannover), por temor a que le ocurriese algo similar a lo que le sucedió a Arquímedes. En la siguiente imagen podemos ver la caricatura de esta valiente matemática, reproducción de la que aparece en la exposición El rostro humano de las Matemáticas. Sophie Germain (1776 - 1831) La aceptación de la Academia de los argumentos de Germain, pese a “su condición de mujer”, es un hito más en la lucha de la mujer a lo largo de la historia por ser aceptada como igual en los diferentes sectores intelectuales “reservados para hombres”. La ecuación anterior pertenece al trabajo de Germain sobre platillos. En la siguiente imagen, siguiendo el estilo pop, hemos coloreado a nuestro antojo la ilustración que aparece en la página dedicada a ella en “El rostro humano de las matemáticas”. Resonancia La placa se puede hacer vibrar por excitación directa, frotándola con un arco o agitándola con algún tipo de sistema mecánico o electromecánico. Pero también podemos conseguir que vibre por resonancia, mediante un emisor de sonidos con suficiente intensidad. Esto suele hacerse colocando un altavoz justo encima o debajo de la placa, como sucede en la siguiente película, en donde la arena ha sido reemplazada por sal. Pulsa sobre la imagen para ver el video Vibraciones líquidas Si, en vez de provocar la vibración de una superficie sólida, usamos una fina película líquida colocada sobre una membrana tirante y la exponemos a una intensa iluminación lateral, el resultado puede ser realmente espectacular, como muestran las siguientes fotografías de Alexander Lauterwasser (cuyo apellido resulta ser de lo más apropiado). Pulsa sobre la imagen para ampliarla Los instrumentos de cuerda Los patrones que hemos visto resultan de gran utilidad para mejorar la calidad en la construcción de violines y otros instrumentos de cuerda al poder comprobar el luthier si se reproducen o no las figuras de Chladni sobre la tapa y la base, corrigiendo cualquier asimetría que pudiera presentarse. En esta fotografía podemos ver el resultado de un experimento sobre el fondo de la caja de un violín. Los siguiente dibujos corresponden a distintos modos naturales de vibración de una guitarra. Laboratorio virtual Con ayuda de los siguientes applets de Paul Fasltad podemos recrearnos en la visualización (en dos o en tres dimensiones) de los distintos modos de vibración de membranas rectangulares y circulares. Aunque las etiquetas y las instrucciones se encuentran en inglés, basta jugar un poco con el ratón y los deslizadores (lo que recomendamos vivamente) para apreciar el funcionamiento. ¡Incluso podemos oír el sonido correspondiente, activando la casilla Sound! Resulta particularmente atractiva la opción “Mouse = Poke membrane” (Display 3D), pues con ella basta hacer un clic en la ventana de la membrana para visualizar tanto la onda transversal inicial como sus sucesivos reflejos. Laboratorio de membranas rectangulares: Pulsa sobre la imagen para interactuar con ella Laboratorio de membranas circulares: Pulsa sobre la imagen para interactuar con ella Figuras de Lissajous Estas curvas fueron descubiertas y estudiadas por el matemático francés J.A. Lissajous al intentar hacer visible el movimiento vibratorio provocado por el sonido. En el experimento original, Lissajous tomó dos diapasones de distintas frecuencias de vibración y colocó un espejo pequeño sobre cada diapasón. Después colocó el conjunto de forma que un rayo de luz se reflejase, sucesivamente, en ambos espejos antes de proyectarse sobre una pantalla. La imagen que aparece en la pantalla (con apariencia de continuidad, dada la su persistencia en la retina del espectador) es la figura. Estas figuras también se pueden trazar con un armonógrafo simple. Pulsa sobre la imagen para interactuar con ella Armonógrafo simple Un armonógrafo simple es un aparato que traza figuras, compuesto de dos péndulos. Un péndulo mueve la punta que dibuja a lo largo de una dirección, adelante y atrás. El otro péndulo empuja, al mismo tiempo, la punta a lo largo de una dirección perpendicular a la anterior. Variando la relación de las frecuencias entre ambos péndulos (y la fase en que se encuentra cada uno), se pueden crear multitud de patrones diferentes: circunferencias, elipses, “ochos” y otras figuras de Lissajous. Pulsa sobre la imagen para interactuar con ella El fonoautógrafo El armonógrafo, las curvas de Lissajous y las figuras de Chladni son los precursores de un instrumento actualmente básico en el análisis de ondas: el osciloscopio. Sin embargo, también pueden considerarse como precursores de uno de los grandes inventos de la humanidad: el grabador-reproductor de sonidos. En 1857, el francés Édouard-Léon Scott de Martinville inventa el primer grabador de sonido: el fonoautógrafo, pretendiendo conseguir una figura gráfica de la voz humana. Para ello, se inspiró en el oído medio: conectó una membrana elástica (un tímpano) a un estilete de forma que la vibración del tímpano se trasladase hasta extremo suelto del estilete que descansaba sobre un cilindro recubierto de papel ahumado. Al girar el cilindro, el estilete iba dejando la huella de las sucesivas vibraciones. El fonoautógrafo Evidentemente el  Fonoautógrafo se  limitó a trazar una gráfica y nunca llegaría a grabar ningún sonido, en el sentido de poder reproducir la grabación, pero quedaban formulados unos principios teóricos que más tarde se retomarían.  Posteriormente, en 1877, Edison inventaría el fonógrafo, el primer grabador-reproductor. El sonido de otro tiempo Sin embargo, la tecnología actual nos permite reinterpretar aquellas señales dejadas en el papel ahumado y  oír algunas de aquellas grabaciones en papel realizadas años antes del invento del fonógrafo. Entre ellas destaca la que se considera la primera huella sonora reconocible -aunque francamente, con bastante imaginación- de una voz humana. La grabación, del año 1860, corresponde a una voz de mujer que canta una canción tradicional francesa, Au Clair de la Lune. Este papel con la gráfica de apenas diez segundos de voz humana (aunque no lo parezca y cause más bien escalofríos) fue descubierta en marzo de este año 2008 por un grupo de historiadores en París y convertido nuevamente en sonidos por un laboratorio especializado de California.

Sábado, 01 de Noviembre de 2008 | Imprimir | PDF |  Correo electrónico

128. 11. (Enero 2009) Como lo oyes

La tesitura La altura de un sonido es la percepción que tenemos de la frecuencia. Esto nos permite clasificar algunos sonidos como agudos y otros como graves. Cuanto más alta sea la frecuencia de un sonido, más agudo lo percibiremos. Generalmente, las mujeres tienen la voz más aguda que los hombres (esto es, sus cuerdas vocales vibran más rápido). En lenguaje musical se dice que un sonido agudo tiene un tono alto y que uno grave tiene un tono bajo. Las notas musicales se caracterizan por su altura o frecuencia. En un piano, por ejemplo, a cada tecla le corresponde un sonido diferente de frecuencia. Las teclas que se hallan a la izquierda del pianista corresponden a las notas de frecuencia baja (sonidos graves, tonos bajos), y las de la derecha son las notas de frecuencia elevada (sonidos agudos, tonos altos). Los instrumentos y los cantantes de música clásica se clasifican de acuerdo con la frecuencia de las notas que son capaces de reproducir. Al conjunto de frecuencias que un instrumento o una voz puede emitir se le llama tesitura. Pulsando sobre la siguiente imagen podremos oír el rango de frecuencias correspondiente a cada una de las voces. Hay que advertir que sólo son valores medios, pues en cada una de esas voces existen fluctuaciones. Por ejemplo, hay sopranos que pueden cantar con mayor rango de frecuencias o en frecuencias más altas. Además, como veremos, el timbre también es otra cualidad a tener en cuenta. Así, se distinguen entre voces de soprano líricas, ligeras y dramáticas, entre otras. Pulsa sobre la imagen para interactuar con ella El timbre Pero incluso ante dos voces que cantan con la misma frecuencia fundamental, normalmente observamos sin dificultad diferencias, a menudo lo suficientemente grandes para poder identificar cada una sin temor a equivocarnos. En anteriores artículos habíamos visto que cuando introducimos energía en una cuerda al pulsarla, la energía se reparte entre varios modos naturales de oscilación de la cuerda. La cuerda vibrará en una superposición de todos ellos, sin vibrar en una frecuencia pura. Esta combinación de frecuencias (múltiplos de la fundamental) caracteriza el sonido, de forma que dependiendo del instrumento (violín, guitarra, voz humana, etc.) se obtendrán distintos sonidos con la misma frecuencia fundamental. Esta característica se denomina timbre. En el artículo Análisis Armónico, podíamos leer: El sonido fundamental no es el único que emite la cuerda al vibrar. Simultáneamente, se producen otros sonidos (parciales) de menor intensidad. La distribución e intensidad de estos parciales (timbre) diferencian instrumentos o voces que ejecuten la misma nota. En el caso de los instrumentos de cuerda y viento, las frecuencias de estos parciales son múltiplos de la frecuencia fundamental. Y en el artículo Geometría Musical (2): Algunos movimientos son mucho más fáciles de reconocer que otros, debido a nuestra abundante experiencia sobre ellos. El caso más evidente lo tenemos en la traslación en la altura, tan familiar que incluso decimos que el sonido es “el mismo” aunque suena más grave o más agudo. Esto se conoce como “transporte”. Cualquier frase dicha (o cantada) por voces con distinta altura es un ejemplo cotidiano de transporte. Al transportar se conservan los intervalos entre dos notas consecutivas mientras permanece inalterada la secuencia de los mismos. No nos cuesta ningún esfuerzo, dada nuestra experiencia cotidiana, reconocer la similitud entre una melodía cualquiera y su transporte a cualquier otra altura. Nosotros mismos, a voluntad, podemos muy fácilmente bajar o subir la altura de nuestra voz sin dejar de entonar la misma canción. De todo ello, concluimos que por timbre entendemos la distribución de diversos sonidos que, por razones inherentes a la naturaleza de la vibración, forman un conjunto. Este conjunto de sonidos elementales caracteriza a una voz humana o a un instrumento, independientemente de la altura del registro sonoro. En cierta forma, podemos “fotografiar” el timbre de un sonido. Para ello, basta obtener el espectrograma que nos muestra el conjunto de intensidades de todas las frecuencias producidas por el objeto vibrante según pasa el tiempo. Ese espectrograma viene a ser como una “radiografía” del timbre. De esta forma, el espectrograma de un instrumento tocando “re” es la traslación, en la altura, del mismo espectrograma tocando en “do”, puesto que la distribución de parciales permanece invariable. Observemos que este es un caso especial de traslación de la altura, así que una línea muy fina separa el timbre de la armonía. Espectrogramas Pulsando sobre la siguiente imagen podremos oír la misma secuencia de cuatro notas producidas por ocho instrumentos diferentes. Al oído no le cuesta trabajo ni identificar la secuencia como “la misma” en todos los casos ni decidir que se trata de distintos instrumentos. Pulsa sobre la imagen para interactuar con ella Veamos ahora los espectrogramas de siete de ellos (prueba de observación: ¿cuál falta?) y del diapasón, en la nota do. Pulsa sobre la imagen para interactuar con ella Podemos realizar una serie de observaciones. El espectrograma del diapasón muestra el tono fundamental con toda intensidad, y apenas nada más. Bajo él, el espetrograma del órgano añade algunos armónicos, también muy marcados. A la izquierda del órgano, los tres instrumentos de viento muestran líneas de armónicos bastante definidas, al contrario de lo que sucede con los tres instrumentos de cuerda sobre ellos. La onda Otra forma de recoger la información del timbre es mediante la gráfica de la onda sonora, es decir, de la serie de Fourier (ver el artículo Análisis Armónico) correspondiente a la suma baremada, según su intensidad, de todos esos sonidos parciales. Veamos la onda del diapasón: Su sencilla forma senoidal refleja la sencillez de su composición. Se trata de prácticamente un único sonido fundamental, sin parciales apreciables. Comparemos la gráfica anterior con la correspondiente a una trompeta: La presencia de varios armónicos complica la gráfica, provocando crestas e irregularidades. Veamos ahora la gráfica de un clarinete: Podemos apreciar que ahora la distribución de armónicos es todavía más compleja. Esa riqueza de matices muestra al clarinete como más próximo a la voz humana, más “cálido” o “íntimo”, bajo nuestra percepción. Luthiers En el artículo Prehistoria musical, aparece: Dada la enorme cantidad de vibraciones que simultáneamente pueden incidir en nuestro tímpano, haciéndolo vibrar a su vez, hemos desarrollado un complejo sistema discriminatorio, capaz de “separar” la combinación recibida en “partes más simples”. Este sistema se basa en la disposición, en el oído interno, de células especializadas en activarse sólo ante determinadas frecuencias, al estar situadas en medios que sólo entrarán en resonancia en esas frecuencias. Simplifiquemos un poco en aras de mayor claridad. Nuestro oído puede percibir vibraciones con frecuencias comprendidas entre unos 18 Hz y unos 18.000 Hz. Si percibimos un sonido resultado de la combinación de cuatro vibraciones: sonido=, las células especializadas en la recepción de cada tipo de vibración cribarán las componentes del sonido: sólo se activarán las células situadas en zonas que entren en resonancia con las frecuencias 200, 708, 1.524 y 3.967. Al sonido percibido lo podemos llamar “200-708-1.524-3.967”, pero es muy importante para la comprensión de la relación entre música y matemáticas tener en cuenta desde un principio que registramos cada frecuencia por separado. Cuantas menos vibraciones compongan un sonido, menos actividad se registrará en nuestro oído. Nuestra percepción mental es de un sonido “puro”, “claro”, “nítido”. El sonido producido por un diapasón es un buen ejemplo. Su equivalente visual podría ser un cielo despejado. Por el contrario, si son muchas y de diverso tipo las vibraciones que conforman el sonido, percibiremos éste como “oscuro”, “confuso”, “impreciso”. Su equivalente visual podría ser un tupido bosque. Además, aunque en principio la intensidad del sonido es independiente de la frecuencia, no lo es en nuestra recepción del sonido. Nuestro oído es más sensible a las altas frecuencias, de forma que con la misma intensidad de sonido percibimos un volumen mayor en frecuencias altas respecto a las bajas. Las combinaciones de vibraciones componen el timbre de cada instrumento. En la creación de los instrumentos se resaltan aquellos armónicos naturales que le confieren timbre propio. La misión principal de un luthier es justamente dotar al instrumento del timbre que se espera de él. Sirva la mención al luthier como excusa para mencionar a aquellos que “unen canto con humor”, el grupo argentino autor de una de las escasísimas canciones dedicadas expresamente a las matemáticas: el divertimento matemático opus 48, Teorema de Thales, plagio milimétrico de la obra del mismo nombre del casi siempre impresentable compositor Johann Sebastian Mastropiero. Pulsando sobre la siguiente imagen podemos oír una frase musical de esta obra y el sonido de uno de los originales instrumentos creados por Les Luthiers. Pulsa sobre la imagen para interactuar con ella Intensidad y frecuencia La presión es una medida objetiva de la intensidad del sonido, pero está lejos de representar con precisión lo que realmente se percibe. Esto se debe a que la sensibilidad del oído depende fuertemente de la frecuencia. En general, hace falta menos intensidad para oír un sonido agudo que uno grave. Mientras que un sonido de 1.000 Hz y 3 dB ya es audible, es necesario llegar a los 50 dB para poder escuchar un tono de 50 Hz, aunque sólo un uno por ciento de las personas pueden oír esta frecuencia tan baja a ese volumen. En la siguiente imagen podemos comprobar gráficamente que el oído no se muestra igual de sensible en el rango de frecuencias. Este tipo de gráficas se conocen como curvas de audibilidad. Recogen el resultado de experimentar con un conjunto de personas su percepción de la intensidad de un sonido a medida que variamos su frecuencia. Observemos que la escala de frecuencias (en hercios) sitúa a igual distancia las sucesivas potencias de diez. A este tipo de escalas se les llama escalas logarítmicas y se utilizan cuando la diferencia entre el valor máximo y el valor mínimo es muy grande, como en este caso. Cada curva de la gráfica parte de la percepción de volumen que tenemos de una intensidad (por ejemplo de 40 dB) cuando la frecuencia es de 1.000 Hz. Después, variamos la frecuencia y registramos en la gráfica las variaciones necesarias de intensidad para mantener constante nuestra percepción de volumen. La línea inferior marca el umbral de audición (por debajo de ella no se oye nada), mientras que la curva superior señala la cota a partir de la cual sentimos dolor. La línea que marca el umbral de audición recoge los datos de los que tienen un oído muy fino. El umbral de audición de la mayoría de las personas sigue la línea azul. La línea que marca el umbral de dolor varía poco, manteniéndose alrededor de los 110 dB, salvo en las proximidades de los 4 kHz, que es la zona en donde el oído humano se muestra más sensible. Originalmente (curvas correspondientes al diagrama anterior, calculadas por Fletcher y Munson) el umbral de audibilidad había sido definido como la mínima presión necesaria para percibir un diapasón de 1 kHz, es decir, el umbral de audibilidad era de 0 dB para 1 kHz. Sin embargo, cálculos posteriores y más precisos de las curvas mostraron que el umbral de audibilidad es de 3 dB para 1 kHz. Esa maravillosa espiral llamada caracol Dentro del oído interno, un tubo espiral llamado caracol (o cóclea) mantiene en su interior tres estanques llenos de líquido, separados por dos membranas (basilar y tectorial). En el que se encuentra entre estas dos membranas reside nuestro receptor de sonidos: el órgano de Corti, una formación de cuatro largas hileras con unas seis mil células ciliadas (o pilosas) cada una conectadas al nervio auditivo. En la siguiente imagen se muestra una fotografía de una de esas 24.000 células ciliadas, nuestros fonorreceptores. Ahora bien, ¿cómo se las arreglan estas células para discriminar las distintas frecuencias que componen el sonido de una única onda sonora compleja? ¿Cómo podemos distinguir varios instrumentos tocando a la vez, así como los distintos armónicos de cada uno? La clave está en la membrana basilar. Esta membrana no tiene un grosor ni rigidez uniforme, de manera que vibran sólo aquellas partes de la membrana correspondientes a la frecuencia capaz de hacerlas resonar. En la figura podemos ver un esquema de la membrana basilar, desenrrollada. Las células ciliadas recogen esta información mecánica y convierten ese movimiento en impulsos eléctricos. De esta forma, las células ciliadas crean series distintas de impulsos, cuya combinación se comporta como un auténtico “espectrograma” de la onda sonora, diferenciando cada frecuencia. Desgraciadamente, las células ciliadas no pueden regenerarse, así que una lesión en esa zona puede provocar la sordera total e irreparable. Por otra parte, la membrana basilar pierde elasticidad con la edad, por ello la sensibilidad o agudeza auditiva también merma al envejecer. Afortunadamente (no todo en el paso del tiempo van a ser inconvenientes) la experiencia de un oído entrenado permite al sujeto captar matices que para un oído inexperto resultan inexistentes. Para hacernos una idea de la alta especialización y eficacia de nuestro sistema fonorreceptor, hagamos una comparación con otra joya de la evolución, sin duda uno de los milímetros cuadrados más valiosos del cuerpo: la fóvea, nuestra área fotorreceptora dentro de la retina. En la fóvea se distribuyen casi cien millones de células fotorreceptoras, entre bastones y conos. Es decir, hay cuatro mil células “encargadas de ver” por cada una “encargada de oír”. Sin embargo, somos capaces de percibir frecuencias sonoras de 16.000 Hz (ciclos/segundo), mientras que un avance a una velocidad de tan solo 24 cuadros por segundo nos hace percibir movimiento donde sólo hay imágenes estáticas (de ahí el éxito del cine). Ilusiones En el artículo Geometría Musical (2), nos divertimos con algunas ilusiones ópticas. Pulsa sobre la imagen para interactuar con ella   Pulsa sobre la imagen para interactuar con ella Veamos ahora alguna ilusión acústica. A pesar de la eficacia y fidelidad de nuestro sistema auditivo, existen algunos fenómenos que consiguen que percibamos de forma indebida algunos sonidos. El efecto muaré y el sonido diferencial Cuando dos patrones visuales similares se superponen se produce una interferencia. Nuestro cerebro tiende a encontrar nuevos patrones en estas interferencias. Esto se conoce como el efecto muaré. A veces podemos observar cómo algunos diseños o líneas supuestamente inmóviles comienzan a "bailar" ante la vista, produciendo "figuras fantasmas" que percibimos aunque realmente no existan. Aparecen frecuentemente en fotografía y en las imágenes televisivas, cuando reproducen una serie de líneas paralelas, o casi paralelas, demasiado juntas (por ejemplo, en una camisa de rayas finas). También aparecen al imprimir o escanear algunas imágenes, debido al tramado usado en la impresión. Las líneas pueden ser rectas o curvas, en cada caso podrán formarse patrones muy diversos. Los que vemos como "arcos o círculos fantasmas" no son más que la forma que tiene nuestra mente de percibir un alto número de intersecciones demasiado próximas. Cada intersección es "un punto notable", es decir, un punto que capta más la atención que los que le rodean (hay mayor longitud de borde o frontera de contraste claro-oscuro en sus proximidades). Si observamos varios "puntos notables" próximos, inmediatamente intentamos captar la configuración de su distribución, en este caso circular. En la siguiente construcción, cuanto más cercanos se encuentren los círculos azules, menor será el ángulo de corte en cada intersección, por lo que parecerá que las rectas, en vez de cortarse en un solo punto, se cortan a lo largo de un segmento. Al marcar los puntos de intersección, el efecto de "círculos, lunas o lúnulas fantasmas" desaparece. Pulsa sobre la imagen para interactuar con ella Pues bien, en música existe un fenómeno similar, denominado “sonido diferencial” o “tono de Tartini”. Es muy frecuente que percibamos un sonido que no ha sido emitido sino que es una percepción nuestra causada por la interferencia de dos notas. El sonido que percibimos se produce en nuestro propio oído y corresponde a la diferencia de frecuencias entre las dos notas. Curiosamente, ambos fenómenos tienen aplicaciones prácticas. El efecto muaré sirve para la detección de la fatiga en los materiales, pues al superponer dos patrones que deberían ser iguales cualquier mínima desviación en una de ellas provocará el efecto y alertará de su deterioro. La aparición del sonido diferencial es útil para determinar que dos cuerdas se encuentran perfectamente afinadas una respecto a la otra (generalmente con una octava exacta de diferencia), pues es entonces cuando surge el “tono de Tartini” y nos parece percibir un sonido inexistente de frecuencia más baja. El efecto Shepard Al igual que se puede utilizar la perspectiva óptica para engañar a los ojos (como en la famosa Escalinata de Penrose, que da más y más vueltas sin perder altura, lo que se puede apreciar en el famoso cuadro de Escher, Ascendiendo y Descendiendo), la perspectiva acústica puede engañar a nuestros oídos. Pulsa en la siguiente imagen para escuchar una ilusión sonora denominada efecto Shepard. Nos parece estar oyendo una subida continua en la altura sonora, mientras que la realidad es que al final no nos hemos elevado en absoluto: el último sonido es equivalente al primero. El engaño se produce porque cada nota es en realidad un acorde compuesto por la misma nota en distintas octavas. A pesar de lo maravillosamente que funciona nuestro oído, esto consigue engañarlo. Pulsa sobre la imagen para interactuar con ella La siguiente imagen corresponde al espectrograma del efecto Shepard. Observemos que aunque efectivamente se produce un movimiento creciente en las frecuencias, las más altas van desapareciendo paulatinamente, mientras que surgen nuevos sonidos de baja frecuencia que paulatinamente ganan en intensidad. Al final, obtenemos una combinación de frecuencias similar a la de partida. Si repetimos sucesivamente el efecto, tenemos la impresión de ir siempre “hacia arriba”. Este efecto se ha usado en canciones y videojuegos para provocar en el oyente esa sensación de “caída libre hacia arriba”, de ascenso perpetuo. Bibliografía Introducción a la psicoacústica. Federico Miyara

Jueves, 01 de Enero de 2009 | Imprimir | PDF |  Correo electrónico

129. 13. (Septiembre 2009) Topología Musical (2)

Mazzola En 1989 el matemático suizo Guerino Mazzola publica "Geometría del Tono" que aplica los grupos de isometría, la teoría de Galois sobre conceptos -en vez de sobre polinomios algebraicos- y el álgebra categórica al análisis musical.     Topos   En 2002, Mazzola publica una profunda y mejorada ampliación de ese trabajo, bajo el título “The Topos of Music”. Este título tiene doble sentido. Por una parte, se puede traducir de forma general como “El lugar de la música”. Pero admite otro sentido mucho más concreto. Los “Topos” son objetos matemáticos (un tipo particular de Categoría) que vienen a reflejar las posibles visiones o perspectivas de un lugar abstracto a partir de las propiedades o relaciones matemáticas necesarias para su coherencia lógica.   Intuitivamente, en la Teoría de Categorías se usan flechas en vez de puntos, es decir, los objetos no son entes estáticos, sino el cúmulo de todas las posibles visiones o perspectivas en un lugar (topos) dado. Dicho de otra forma, se priman “las relaciones entre los objetos individuales” que conserven la estructura, más que los propios objetos en sí.   The Topos of Music   En esta obra de Mazzola se puede observar el gran progreso de las Matemáticas, la Teoría de la Música y el desarrollo de las Nuevas Tecnologías en la última década del siglo XX.     Mazzola crea una base, basada en los fundamentos teóricos de los Topos, que permite establecer relaciones lógicas y geométricas entre los objetos básicos de la Teoría Musical. Esta base incluye el análisis del ritmo, la melodía y la armonía.   A partir de esa base teórica, Mazzola puede establecer topologías y clasificaciones de los objetos musicales, analizando sus relaciones dentro de ese Topos. Un punto clave en esas relaciones, como no podía ser de otro modo, reside en la presencia de la periodicidad como uno de los fundamentos musicales. La aritmética modular tiene un importante papel en muchas de las relaciones rítmicas, melódicas y armónicas.   Dado el amplio abanico de recursos matemáticos necesarios para establecer el Topos que permita el estudio de los objetos musicales, en la propia obra se incorporan anexos sobre las teorías de Conjuntos, Correspondencias, Monoides, Grupos, Anillos, Álgebras, Módulos, Transformaciones lineales y afines, Cálculo, Geometría y Topología algebraica, Categorías, Topos y Lógica.     Igualmente, otro anexo recoge los fundamentos de la naturaleza y análisis del Sonido y nuestra Percepción del mismo, mostrando especial interés por los modelos de consonancia y la disonancia.     Intentar sintetizar aquí esta extensa obra de Mazzola es inviable. La publicación cuenta con más de 1300 páginas cuajadas de densa información, además de un CD con ejemplos del uso de programas informáticos creados específicamente para el análisis musical. Nos limitaremos a describir brevemente algunas de las imágenes que ilustran The Topos of Music, con la esperanza de que tal vez, casi por sí mismas, comuniquen algunas de las líneas de investigación que allí aparecen.   Conjuntos y representaciones   Así, la siguiente imagen representa el primer paso hacia la digitalización, la asignación de coordenadas a los distintos aspectos de una nota musical.     Junto con los conjuntos numéricos, para una correcta trascripción se necesita incorporar uno o más tipos de orden, como el que muestra la siguiente imagen, que representa un orden de tipo lineal.     Además de las notaciones formales, podemos ayudarnos de notaciones más intuitivas, como por ejemplo flechas para indicar transformaciones. Por ejemplo, el aumento o disminución de un semitono (sostenido y bemol) puede ser representado mediante la flecha correspondiente.     Distancias   En la siguiente imagen vemos una proyección de un compás de un Preludio de Chopin sobre el plano y sus dos proyecciones unidimensionales asociadas. El análisis de estas dos proyecciones revela los aspectos métrico-rítmicos de la notación plana.     Las diferencias relativas entre notas son claves en la armonía (notas simultáneas) y la melodía (notas consecutivas). La siguiente imagen muestra las cuatro soluciones para las cuales, a partir de una nota de referencia, la segunda se sitúa a cuatro semitonos de distancia y la tercera a tres de la segunda.     Escalas   La periodicidad de los 12 semitonos permite establecer la relación con Z12.  De esta forma, se pueden parametrizar las distintas transformaciones de Z12 en sí mismo.     Por ejemplo, podemos establecer las diferentes escalas basadas en secuencias de tonos y semitonos. La siguiente imagen recoge algunas de las escalas más comunes, donde la nota base está representada por el punto más alto del ciclo y las demás notas siguen el sentido horario.     Motivos   Las notas, individualmente, son como los puntos en una figura geométrica: no se perciben como tales sino que generan figuras, formas, agrupaciones, que son los objetos reales de estudio y composición. Las agrupaciones más pequeñas forman los motivos. En la siguiente imagen se señalan tres motivos (M1, M2 y M3) y una agrupación que no lo es, M0 (sólo son cuatro notas formando un armónico). La reducción de los parámetros implicados en cada motivo -algo así como quedarse con el baricentro de un triángulo en vez de con todo el triángulo- es una vía para poder comparar diferentes distribuciones de motivos a lo largo de una misma obra o entre obras distintas.     Simetrías   En la parte izquierda de la siguiente imagen vemos la representación de dos inversiones. La primera, sin centro fijo, es decir, entre notas. La segunda, con centro fijo. En la parte derecha vemos la representación de una inversión en el plano como un giro de 180º (una simetría central).     La siguiente representación plana corresponde a tres series dodecafónicas de Webern. Recordemos que en el serialismo la presencia de la simetría es parte de su propio fundamento teórico. Observemos como las diagonales hacen de ejes de simetría.     El lema de Yoneda   Uno de los puntos cruciales en The Topos of Music es el lema de Yoneda. Este importante resultado viene a mostrar cómo podemos ampliar el conocimiento de una Categoría estableciendo una correspondencia entre sus objetos y las relaciones entre ellos.   Tras el lema de Yoneda hay un cambio de filosofía en el entendimiento de los núcleos de información. Ya no son los objetos los centros de atención, sino las diferentes perspectivas que podemos obtener de ellos. La comparación entre las distintas perspectivas de dos objetos nos ofrece, precisamente, la información deseada acerca del parecido o diferencia entre ambos objetos.   Los dos siguientes diagramas muestran un ejemplo intuitivo de este procedimiento. Aunque los motivos M1 y M2 son diferentes, podemos establecer una biyección entre las relaciones que mantienen ambos motivos (flechas) con otras notas fundamentales de la composición. La existencia de esta biyección nos indica que tales motivos pueden cumplir un papel similar en la composición, pero si hacemos solamente esto (sustituir cada motivo por sus relaciones) podemos llegar a la errónea conclusión de que ambos motivos son similares.     Sin embargo, si seguimos estudiando todas las perspectivas, es decir, todos los tipos de relación de ambos motivos entre sí y con los otros objetos, la diferente naturaleza de cada uno queda revelada.     La composición de las proyecciones de M1 sobre la altura de la primera nota (q) y sobre la diagonal (s) da por resultado precisamente M2. Así que, intuitivamente, podemos ver a M2 como una transformación de M1. Pero esta transformación es irreversible. M1 “puede ver” a M2 pero M2 no “puede ver” a M1.   Un buen ejemplo de cómo el cambio de perspectiva ayuda al conocimiento lo tenemos en la pintura. La siguiente imagen muestra el famoso cuadro La escuela de Atenas, de Rafael.     Tomemos los elementos arquitectónicos esenciales, además de 58 figuras humanas, y simulemos en el espacio virtual del ordenador la estructura básica del cuadro:     Ahora rotamos el espacio virtual obteniendo una nueva perspectiva. Su análisis muestra simetrías que no podían encontrarse bajo la perspectiva del cuadro original.     Programación orientada a objetos   Los modernos lenguajes de programación orientada a objetos, como Java, son en esencia un acceso a la programación desde un punto de vista de Categorías. Sus características, como el encapsulado, las herencias, los métodos, clases e instancias, realizan precisamente lo que sugiere el lema de Yoneda: reemplazar las entidades por la respuesta ante determinadas condiciones, es decir, la identificación mediante el comportamiento.     Probablemente el más excitante campo actual de investigación en la música se refiere a su análisis mediante las más avanzadas aplicaciones de software orientado a objetos, como Rubato, OpenMusic o Symbolic Composer (imagen anterior).   Gracias a Mazzola y otros matemáticos hoy podemos disfrutar de estas poderosas herramientas de composición y análisis musical, modernos frutos de importantes teoremas algebraicos.

Martes, 15 de Septiembre de 2009 | Imprimir | PDF |  Correo electrónico

130. 12. (Marzo 2009) Topología Musical (1)

Buscando El Modelo Nadie duda hoy en día de la extraordinaria eficacia de las Matemáticas para resolver los más variados, complejos y difíciles problemas. Pero para poder aplicar las sofisticadas y potentes herramientas matemáticas se precisa un modelo de la realidad que se desea analizar, un modelo que conserve las características que determinan la naturaleza del fenómeno o estructura a estudiar. En el caso de la Música, desde Pitágoras, los matemáticos de todas las épocas han buscado la forma de aproximarse a ese modelo. La tecnología necesaria para grabar y reproducir el sonido ha contribuido, indudablemente, al conocimiento profundo de las características sonoras fundamentales. Sin embargo, el análisis de una estructura musical suele ser bastante diferente del análisis de los sonidos que la componen. Nos interesa más la relación entre los distintos sonidos que la naturaleza de los mismos. Actualmente, la búsqueda de modelos matemáticos que reflejen las estructuras musicales sigue siendo una aventura que enciende pasiones y controversias. En la siguiente imagen podemos ver el anuncio del programa de un seminario permanente, MaMuX, cuyo objetivo es precisamente reunir y discutir las nuevas aportaciones que vayan surgiendo en la milenaria relación entre música y matemáticas. Teoría matemática del ritmo En 2002, el matemático Godfried Toussaint desarrolla una investigación de los ritmos con herramientas matemáticas, introduciendo nuevas técnicas geométricas, gráficas, matriciales y combinatorias. Esto permite el análisis, visualización y reconocimiento de ritmos. Toussaint continúa trabajando, en la actualidad, en el Centro de Investigación Interdisciplinaria de Medios de Música y Tecnología (Centre for Interdisciplinary Research in Music Media and Technology) de la universidad McGill en Canadá. En el año 2005, en su sección “La Columna de Matemática Computacional” de La Gaceta de la RSME (Vol. 8.2), Tomás Recio recoge un artículo firmado por José-Miguel Díaz-Báñez, Giovanna Farigu, Francisco Gómez, David Rappaporty y Godfried T. Toussaint, con el título Similaridad y evolución en la rítmica del flamenco: una incursión de la matemática computacional. Los resultados de ese artículo fueron obtenidos durante el First Interna­tional Workshop on Computational Music Theory celebrado bajo el auspicio del Departamento de Matemática Aplicada de la Escuela Universitaria de Informática (U.P.M.) en junio de 2003. El artículo es enormemente esclarecedor sobre la metodología seguida para la creación de un modelo matemático de una parte del mundo musical. A continuación reproducimos un resumen del mismo. Introducción Usaremos la palabra ritmo en su sentido general (contrapuesto a los conceptos de altura y timbre), patrón rítmico para su sentido específico (sucesión de tiempos en que se atacan las notas) y compás como sinónimo de metro musical. Muchos estilos musicales se caracterizan por la presencia de ciertos patrones rítmicos que se repiten a lo largo de la pieza y que tienen muchas funciones tales como ser estabilizadores rítmicos, marcar el fraseo, definir el carácter, definir el género, etc. Ejemplos de tales patrones rítmicos, llamados claves en la tradición africana y otras, abundan en estilos musicales tan dispares como el son cubano, el gahu de Ghana o el fandango del flamenco. Muchas preguntas surgen en torno a estos patrones rítmicos que funcionan como elementos estructurantes: ¿qué características tienen esos patrones rítmicos para determinar ciertos estilos musicales?, ¿qué similaridad podemos encontrar entre esos patrones rítmicos? Entonces una pregunta previa: ¿qué medida de similaridad podemos definir entre patrones rítmicos? ¿Puede ser una medida en el sentido matemático? Muchas de estas preguntas han encontrado respuestas en los trabajos de diversos autores, tanto para las claves binarias y ternarias de géneros musicales pertenecientes a las tradiciones africanas, afrocubanas y brasileñas, como para la música flamenca o como para la preferencia rítmica y otros problemas. Nosotros vamos a ocuparnos aquí del caso del flamenco. La idea de este estudio consiste en construir un análisis que refleje ciertas relaciones entre los estilos flamencos. Indudablemente, hay muchos aspectos en que dichas relaciones podían basarse, dada la riqueza estilística del flamenco. Nosotros nos hemos centrado en el ritmo porque, entre los muchos factores musicales que constituyen el flamenco, sin duda, es de los más sobresalientes. Una manera sencilla de llevar a cabo este análisis sería la de desnudar la música flamenca de letra, armonía y melodía y dejar sólo el ritmo (en su sentido general) como único elemento. Esta simplificación no se basa sólo en la sencillez de análisis, sino que también es consecuencia de las dificultades para formalizar la armonía y sobre todo la melodía. Además, es lógico pensar en el ritmo a la hora de simplificar el estilo por el papel de estabilizadores rítmicos que desempeñan los patrones rítmicos en los distintos cantes flamencos. Apoyándonos en esta idea, hemos realizado un estudio de los patrones rítmicos ternarios de palmas del flamenco. Este estudio está inspirado en el análisis filogenético que se usa habitualmente en Biología. Ese análisis requiere la existencia de una distancia, que está definida sobre el material genético. Normalmente, la distancia consiste en medir cuán diferentes son dos materiales genéticos dados. La distancia da lugar a su vez a una matriz de distancias. A partir de ésta, y gracias a técnicas de Bioinformática, se reconstruye un árbol que refleja las relaciones evolutivas entre especies. Nosotros sustituiremos el código genético por ritmos y, en primer lugar, definiremos una distancia entre patrones rítmicos. Existen varias distancias que se pueden usar para medir cuán lejos se encuentran dos patrones rítmicos. Nosotros hemos usado dos distancias, la cronotónica y la de permutación dirigida, que captan adecuadamente la idea de lejanía entre patrones rítmicos. Por último, aplicando las herramientas adecuadas obtenemos el árbol filogenético para los patrones rítmicos del flamenco. Algunas nociones sobre los ritmos flamencos Si existe una clara seña de identidad del flamenco con respecto a otras músicas, ésta es la ejecución de los ritmos con palmas, donde el patrón rítmico subyacente se manifiesta a través de palmas acentuadas. El flamenco usa predominantemente compases ternarios de 12/8, esto es, compases de 12 pulsos agrupados en grupos de tres. En principio, se tocan las 12 palmas que marca el compás de 12/8 y el patrón rítmico emerge acentuando unas cuantas. En el fandango, por ejemplo, se da un acento (palmada fuerte) seguido de dos silencios (palmada débil) cuatro veces seguidas. Puede verse aquí, a la luz de las definiciones dadas en la introducción, la íntima relación que hay en la música flamenca entre patrón rítmico (ritmo en su sentido restringido) y compás. De hecho, es habitual en el mundo flamenco hablar de “compás” en lugar de patrón rítmico. Además de este patrón, que podemos llamar periódico, existen otros aperiódicos, llamados de amalgama. Estos patrones rítmicos se pueden pensar como una combinación de un compás de 3/4 (compuesto por dos acentos fuertes con dos acentos débiles intercalados) y un compás de 6/8 (compuesto por tres acentos fuertes con un acento débil intercalado). Claro es entonces que el juego rítmico reside en la distribución de los acentos y buena parte del atractivo del flamenco descansa en esa distribución. Patrones rítmicos de amalgama son los utilizados en las soleares, las bulerías, las alegrías, las seguiriyas o las guajiras. A continuación detallamos los patrones rítmicos ternarios del flamenco y alguna de sus posibles notaciones o representaciones. La notación que habitualmente se usa en la didáctica del flamenco es numérica, resaltando los lugares donde se produce un acento. Fandango: [1 2 3 4 5 6 7 8 9 10 11 12] Soleá: [1 2 3 4 5 6 7 8 9 10 11 12] Bulería: [1 2 3 4 5 6 7 8 9 10 11 12] Seguiriya: [1 2 3 4 5 6 7 8 9 10 11 12] Guajira: [1 2 3 4 5 6 7 8 9 10 11 12] Cada patrón rítmico ha sido etiquetado por un estilo de cante que lo usa. Esto no significa ni mucho menos que cada patrón rítmico sea exclusivo de ese cante. Por ejemplo, el patrón del fandango es el de las sevillanas; el de la soleá se usa también para las bulerías o alegrías; el de la bulería para las bulerías por soleá; el de la seguiriya para las serranas o saetas; y, finalmente, el de la guajira para las peteneras. La representación numérica anterior no resulta útil para contabilizar diferencias ni visualizar ciertas propiedades geométricas en las que estamos interesados. Proponemos aquí dos notaciones más ilustrativas como aparecen en las siguientes figuras. La primera presenta la notación binaria donde los espacios negros-blancos se identifican con unos-ceros. En la representación como polígonos convexos de la siguiente figura, el “0” marca la posición en el tiempo en la cual comienza el patrón rítmico y los vértices indican dónde están los acentos. Medidas de similaridad rítmica Como advertimos en la introducción, para construir árboles filogenéticos es necesario contar con una distancia que mida la similaridad rítmica. La distancia debería comportarse de modo que cuanto mayor sea la distancia entre los patrones rítmicos, menor sea la similaridad rítmica. De hecho, este problema está relacionado con problemas de aproximación de patrones en la teoría de reconocimiento de formas. Nosotros usaremos dos distancias que han demostrado funcionar bien en otros estudios sobre el ritmo: la distancia de cronotónica y la distancia de permutación dirigida. La idoneidad de una distancia u otra para el estudio de ritmos es un tema actual de investigación. La distancia cronotónica Consideremos el ritmo de la seguiriya, dado por [1 2 3 4 5 6 7 8 9 10 11 12]. En esta representación, las duraciones relativas de los intervalos de tiempo no se pueden observar fácilmente. En una visualización de ritmos vía histogramas los sucesos importantes, tales como el comienzo, el final y el ataque de las notas, se dibujan a lo largo del eje Y, lo que da como resultado el espectro de intervalos adyacentes del ritmo. En dicha representación la longitud relativa de los intervalos es claramente visible, pero se pierde la información temporal a lo largo del eje X. Para obtener una representación gráfica que posea las ventajas de ambos métodos, se puede usar el tiempo en ambas dimensiones. El resultado de esa unión se ilustra en la figura siguiente, que muestra los cinco patrones rítmicos del flamenco en notación cronotónica. Cada elemento temporal entre sucesos (intervalos) es ahora una caja y ambos ejes X e Y representan la longitud temporal del intervalo. Las uniones de los cuadrados representadas en la figura anterior se pueden ver como funciones rectilíneas monótonas del tiempo. Dada la representación cronotónica de dos ritmos, hay un gran número de formas de medir la disimilaridad. Aquí lo haremos por el área que queda entre ambas funciones. La matriz de distancias obtenida con esa distancia se muestra en la siguiente tabla. La distancia de permutación Aquí llamaremos permutación al intercambio de dos elementos adyacentes, es decir, al intercambio de un ‘uno’ y un ‘cero’ que son adyacentes en una cadena binaria. La distancia de permutación entre dos patrones rítmicos se define como el mínimo número de permutaciones que se necesitan para convertir un patrón rítmico en otro. Por ejemplo, el patrón X = [101011010101] puede convertirse en el patrón Y = [101101101010] con un mínimo de cuatro permutaciones, a saber, intercambiando la tercera, la quinta, la sexta y la séptima posición con los correspondientes silencios que van detrás de ellos. Desde el punto de vista musical es razonable usar esta distancia. El oído humano considera como próximos dos patrones rítmicos si el número de cambios entre acentos es pequeño y si tales cambios ocurren entre acentos adyacentes. Además, es interesante observar que el compás bulería resulta precisamente de la permutación de un uno y un cero en el compás soleá. Un ejemplo de esta distancia aplicada a patrones rítmicos del flamenco se ilustra en la siguiente figura, que muestra una distancia de permutación entre la seguiriya y el fandango igual a 4. Ciertos autores sugieren que ésa es la evolución natural entre ambos patrones rítmicos. Computación eficiente de la distancia de permutación Claramente, la distancia de permutación puede obtenerse calculándose todas las permutaciones posibles. Sin embargo, este método básico sería muy costoso para vectores n-dimensionales si n es un valor grande. Un algoritmo mucho más eficiente puede obtenerse si comparamos las distancias de las notas al origen. Lo describimos aquí brevemente. Primero hacemos un barrido de la sucesión binaria y almacenamos un vector con la información del lugar que ocupa cada acento. Por ejemplo, si consideramos: X = [ 1 0 1 0 1 1 0 1 0 1 0 1 ] Y = [ 1 0 1 1 0 1 1 0 1 0 1 0 ] entonces almacenamos: U = (u1, u2,..., u7) = (1, 3, 5, 6, 8, 10, 12) para X y V = (v1, v2,..., v7) = (1, 3, 4, 6, 7, 9, 11) para Y, respectivamente. De esta forma, la diferencia entre ui y vi es el número mínimo de permutaciones que tienen que realizarse para alinear ambos acentos. Por tanto, en general, la distancia de permutación entre dos conjuntos de U y V con k notas está dado por: Calcular U y V a partir de X e Y se puede hacer en tiempo lineal con un simple barrido. Por tanto, en tiempo O(n) podemos calcular dP(U, V), lo cual da como consecuencia una gran ganancia sobre el uso del algoritmo básico que considera todas las posibles permutaciones. El lector se debe estar preguntando a qué viene toda esta discusión sobre la reducción de la complejidad de O(n2) a O(n) cuando en el caso de los ritmos flamencos tenemos n = 12 y la cota cuadrática es computacionalmente aceptable. La razón es que la diferencia de la complejidad resulta crucial cuando estas distancias se pretenden usar en aplicaciones de recuperación de la información musical, donde hay que extraer piezas enteras de una base de datos en la que n puede ser muy grande. La distancia de permutación dirigida La distancia de permutación dirigida es una generalización de la distancia de permutación, pensada para tratar la comparación de patrones que no tienen el mismo número de acentos (unos). Por ejemplo, el fandango tiene cuatro acentos en lugar de cinco y, por tanto, esta generalización se hace necesaria. A continuación definimos formalmente esta distancia. Sean X e Y dos sucesiones binarias de longitud n que representan dos patrones. Se puede suponer, sin pérdida de generalidad, que X tiene más unos que Y . La distancia de permutación dirigida es el mínimo número de permutaciones necesarias para convertir X en Y bajo las siguientes condiciones: Cada “1” de X tiene que moverse a una posición “1” de Y. Todas las posiciones “1” de Y tienen que recibir al menos un “1” de X. Ningún “1” puede viajar a través de la frontera entre la posición cero y la n-ésima. Un ejemplo de esta distancia se ilustra en la siguiente figura, que muestra una distancia de permutación dirigida entre la seguiriya y el fandango igual a 4. La búsqueda de algoritmos eficientes de computación para la distancia de permutación dirigida se encuentra actualmente bajo investigación. En el caso que nos ocupa, se pueden realizar los cálculos a mano obteniendo la siguiente matriz de distancias. Árboles filogenéticos Con objeto de estudiar las posibles relaciones genealógicas entre los distintos patrones rítmicos, utilizaremos una técnica común en análisis filogenético que nos ayudará a analizar y visualizar el conjunto de datos obtenidos en la matriz de distancias. Esta técnica de análisis de datos se basa en la generación de los llamados árboles filogenéticos. Concretamente aquí hablaremos de la técnica llamada SplitsTree. La técnica está basada en un proceso iterativo de división y que da como resultado una inmersión de un grafo plano con la propiedad de que la distancia en el dibujo entre dos nodos refleja, tanto como es posible, la verdadera distancia entre los dos patrones rítmicos correspondientes en la matriz de distancias. Este método tiene además la buena propiedad de que produce un grafo y no un árbol cuando la estructura de proximidad subyacente no es intrínsecamente de tipo árbol. De hecho, si la estructura de árbol no coincide con los datos perfectamente, se introducen nuevos nodos con objeto de obtener un mejor ajuste. Pueden visualizarse estos nodos sin etiquetas en las dos siguientes figuras, que han sido calculados para la matriz de distancias de permutación dirigida y distancia cronotónica respectivamente. La interpretación del grafo obtenido es la siguiente. La suma de las longitudes de las aristas del camino más corto entre un patrón y otro es proporcional a la distancia real entre ellos. Los nuevos nodos incorporados (aparecen sin etiqueta) sugieren la existencia de patrones rítmicos “ancestrales” de donde los actuales podrían haber evolucionado. Las aristas se pueden dividir para formar paralelogramos, como se ve en el centro de la figura anterior. Los tamaños relativos de estos paralelogramos son proporcionales a su índice de aislamiento, que indica cuán significativas son las relaciones de agrupamiento en la matriz de distancias. La herramienta SplitsTree también calcula el índice de descomposición, una medida de la bondad del ajuste del grafo entero. El ajuste se obtiene dividiendo la suma de todas las distancias aproximadas en el grafo por la suma de todas las distancias originales en la matriz de distancias. En este caso obtenemos un sorprendente ajuste del 100%. A continuación, se describen los resultados obtenidos en el grafo SplitsTree para las dos distancias. El SplitsTree con la distancia cronotónica El grafo de la distancia cronotónica sugiere un agrupamiento en tres grupos. Uno está formado por el fandango y la seguiriya; el segundo, por la soleá y bulería; y el tercero, en solitario, la guajira. El compás bulería es el más “alejado” de todos con una suma de distancias igual a 40. En cambio, la guajira es el más similar a los demás con una suma igual a 26. Aparecen cuatro nodos sin etiquetas, esto es, de los que no corresponden a ninguno de los patrones rítmicos dados. El SplitsTree con la distancia de permutación dirigida El agrupamiento en el grafo de la distancia de permutación dirigida es ligeramente distinto al de la cronotónica. Un primer grupo lo componen soleá y bulería, otro central, guajira y fandango, mientras que seguiriya permanece en un tercer y solitario grupo. Los patrones rítmicos más similares a los otros son la guajira y el fandango, que empatan a 21. Es por esto que aparecen en el ‘centro’ del grafo. Aparecen dos nodos sin etiqueta, cerca de la guajira y el fandango. También es de destacar que seguiriya y bulería se encuentran en los extremos del grafo y son los patrones mas ‘alejados’ de los demás, con un total igual a 31 y 29, respectivamente. Propiedades geométricas de preferencia Una cuestión que suscita gran curiosidad entre los músicos es la de saber por qué ciertos tipos de ritmos se prefieren a otros en ciertas tradiciones musicales. Por ejemplo, en la tradición musical africana aparecen con mucha frecuencia patrones rítmicos asimétricos y sincopados (con acentos fuera de los pulsos). En un intento de caracterizar esas propiedades de preferencia desde un punto de vista geométrico se han introducido dos conceptos nuevos: la asimetría rítmica y el índice de contratiempo. En la siguiente tabla aparecen los datos de estas medidas para los patrones rítmicos del flamenco. Patrón rítmico Asimetría rítmica Contratiempo Fandango No 0 Soleá No 3 Bulería Sí 2 Seguiriya No 1 Guajira No 0 Se dice que un patrón rítmico tiene la propiedad de la asimetría rítmica si no contiene dos conjuntos de notas que dividan al patrón (dibujado en un círculo) en dos semicírculos. En la siguiente figura aparecen las diagonales divisorias que existen para los patrones rítmicos flamencos. (No aparece el fandango porque es totalmente simétrico.) Es interesante observar que de los cinco patrones, la bulería es el único que tiene la propiedad de la asimetría rítmica. Un detalle interesante es que, a diferencia del resto de los patrones, la bulería es el único que contiene intervalos de longitud 1, 2, 3 y 4. Los otros patrones sólo tienen intervalos de longitud 2 y 3. El índice de contratiempo de un patrón rítmico se define como el número de notas que posee en las posiciones 1, 5, 7, y 11. Estas posiciones resultan ser las no ocupadas si se consideran las posibles divisiones en espacios iguales del compás de 12/8 usando los divisores de 12 (distintos de 1 y 12). Aparte de la tabla de más arriba, en la figura anterior el índice de contratiempo de cada patrón rítmico se indica en la parte superior derecha de cada círculo. En nuestro caso, se observa que la guajira es el único patrón de 5 acentos con un índice de contratiempo igual a cero. La soleá es, por otra parte, el estilo flamenco con mayor índice de contratiempo. Conclusiones En primer lugar, observamos el hecho de que la guajira aparezca prácticamente en el centro de los patrones rítmicos ternarios indica su cercanía o similitud a los demás estilos. ¿Podría esto interpretarse como la huella de la influencia que han ejercido los otros estilos en dicho patrón rítmico? La guajira, como es sabido, es un estilo flamenco de los llamados de ida y vuelta, esto es, que fueron llevados a Sudamérica y, tras una remodelación según los gustos de los músicos sudamericanos, fueron posteriormente incorporados a la música flamenca. ¿Está probada musicalmente dicha influencia en los aspectos rítmicos que aquí tratamos? ¿Hasta qué punto? Teniendo en cuenta la ‘reciente’ incorporación de la guajira, y fijándonos en el árbol filogenético generado por la distancia de permutación dirigida, cabe pensar que el fandango es el más primitivo, dado que es el otro patrón rítmico que se encuentra en el centro. ¿Hay hechos musicológicos que confirman esta teoría, por otra parte, cada vez más extendida dentro del mundo del flamenco? Por ejemplo, en todas las provincias andaluzas se encuentra una modalidad evolucionada del fandango. Nos estamos refiriendo a los estilos de malagueñas, granaínas o tarantas etc. Un nuevo aspecto que volvería a indicar la importancia genealógica del fandango es la reconstrucción de los patrones rítmicos ancestrales citados en la construcción de los grafos con la herramienta SplitsTree y que allí aparecen sin etiqueta. Haciendo uso de la distancia de permutación dirigida, se puede obtener un hipotético patrón ancestral que se encuentra justo en el centro del árbol. Actualmente, es un problema abierto el diseño de algoritmos eficientes que reconstruyan los nodos ancestrales. En ocasiones, puede hacerse el cálculo a mano. Para el caso de patrones rítmicos flamencos con la distancia de permutación dirigida, la representación rítmica obtenida es [1 0 0 1 0 0 1 0 0 1 1 0], que de hecho, se usa en el flamenco como terminación o coletilla para los fandangos de Huelva. Por otra parte, si eliminamos la guajira de nuestro estudio, estilo que hemos dicho parece ser posterior a los demás en el flamenco, el fandango y la soleá son los nodos que juegan un papel central en el análisis filogenético (con respecto a la distancia de permutación dirigida). ¿Sugeriría esto que además del fandango aparece la soleá como patrón rítmico primitivo? ¿Se entendería entonces que, de estos patrones primitivos y, tras un proceso evolutivo, fueron apareciendo los demás? Un hecho que respaldaría esta hipótesis puede encontrarse en el reciente uso del patrón rítmico aquí llamado bulería, y que proviene de la soleá sin más que permutar un acento con un silencio. Por su parte, ya existen teorías que indican que la seguiriya es un estilo incorporado al flamenco a finales del siglo XIX y principios del XX. Finalmente, aventuraremos algunas hipótesis sobre las medidas de preferencia en el flamenco. Es conocida la inclinación de los flamencos llamados “puristas” por los estilos que usan el patrón de la soleá. ¿Podría residir la explicación de este hecho en su alto índice de contratiempo? Por otro lado, también es conocida la popularidad que goza la bulería entre el público flamenco en general. ¿Constituye la propiedad de la asimetría rítmica una posible explicación de ese hecho?

Domingo, 01 de Marzo de 2009 | Imprimir | PDF |  Correo electrónico