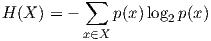Home » Cultura y matemáticas » Música y matemáticas
Música y matemáticas
El objetivo de esta sección es comprender la interesante y profunda relación de las Matemáticas con la Música.
Nuestro sincero agradecimiento a Francisco Gómez Martín (Universidad Politécnica de Madrid) por organizar y desarrollar esta sección, a sus anteriores responsables Rafael Losada y Vicente Liern, así como a todas las personas que colaboran con la misma.
Resultados 41 - 50 de 130
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
1. Ritmos equilibrados y euclídeos
La columna de este mes de mayo estará dedicada a la síncopa. Este es un fenómeno siempre fascinante y al que le hemos dedicado en esta columna varios artículos; véase, por ejemplo, la serie Medidas matemáticas de síncopa [Góm11c, Góm11b, Góm11a] en el año 2011, o recientemente la serie Medidas de complejidad rítmica [Góm17a, Góm17b, Góm18]. En este artículo vamos a examinar un trabajo de Chunyang Song y sus coautores, Syncopation and the Score (la síncopa y la partitura) [SAJRCA+13]. En este interesante trabajo sus autores investigan la relación entre el ritmo escrito (la partitura) y la síncopa percibida. Dado que este trabajo versa sobre la síncopa percibida, esto es, la sensación de síncopa comunicada por sujetos, claramente se trata de un estudio de cognición musical.
2. Síncopa y partitura
Rememorando lo dicho en nuestra serie sobre la síncopa de 2011 [Góm11c], volvemos al fidedigno Harvard Dictionary of Music [Ran86] para una definición conceptual sólida: “Síncopa: una contradicción momentánea de la métrica o pulso predominante”. El autor de la definición la amplía y enseguida añade que “la síncopa se puede crear por los los valores de las notas mismos o por la acentuación, la articulación, el contorno melódico o el cambio armónico en el contexto por otro lado de una sucesión de notas no sincopadas”. Los autores del artículo, sin duda conscientes de esta definición, la desarrollan en el dominio de la cognición musical. Así, definen pulso como el percepto periódico subyacente que los oyentes humanos extraen de los patrones temporales de la música. Por percepto, aquí se entiende el objeto tal y como lo percibe el sujeto. La definición de pulso está tomada de Trainor [Tra07]. Cuando los oyentes humanos infieren una estructura a partir de las periodicidades destacables en los grupos de pulsos, se produce un constructo abstracto de duraciones temporales que se conoce como métrica. Esas agrupaciones de duraciones temporales se pueden a varios niveles y por tanto la métrica posee una estructura jerárquica.
La partitura se puede concebir como una codificación simbólica que describe los eventos que ocurren en una pieza musical. Estos eventos han de ser interpretados por un músico para que el oyente pueda percibir el resultado de la partitura. Si nos restringimos a la música occidental (que en el artículo de Song y sus coautores es una hipótesis implicita), la partitura estará escrita en un compás dado. El compás indica en qué tipo de métrica va a estar la pieza. Hay dos tipos de compases principales: los de subdivisión binaria y los de subdivisión ternaria. Los primeros nos dicen que la agrupación de las duraciones se hará en grupos de dos, mientras que en el caso ternario dicha agrupación será en grupos de tres.
Como decíamos arriba, cuando la estructura métrica predominante es contradicha momentáneamente, hablamos de síncopa. Para que dicha contradicción tenga lugar hace falta que la estructura métrica se haya establecido durante un tiempo suficientemente largo como para que el oyente la integre en la escucha de la pieza. Los autores del artículo, y con bastante razón, argumentan que muchas de las medidas de síncopas definidas hasta la fecha no tienen en cuenta este hecho.
Una vez establecido el contexto métrico, ¿cómo se produce la síncopa? Se sabe que hay varios mecanismos para ello y Song y sus coautores los identifican con exhaustividad. En la partitura, hay síncopas que se indican poniendo acentos en las partes débiles de la métrica. Son las llamadas síncopas por acentuación (Stravinsky es un experto en este tipo de síncopas). Otro tipo de síncopa es la llamada síncopa de ataque; consiste en que una nota que empieza en parte débil es prolongada hasta otra parte débil. Típicamente, esto se consigue poniendo silencios en partes fuertes o ligando notas entre partes débiles consecutivas. Otra forma de síncopa es la polirritmia. Una polirritmia es la presentación de dos o más ritmos que no comparten las mismas agrupaciones temporales, lo que con frecuencia da una sensación de métricas que compiten entre sí. Hay unas cuantas tradiciones musicales en que es normal las polirritmicas, especialmente las africanas y las afro-cubanas. En la serie Transformaciones rítmicas: de binarizaciones y ternarizaciones [Góm13] del año 2013 analizamos las polirritmias en las tradicionales musicales de la franja atlántica del continente americano; se remite al lector a esa serie para más información sobre este asombroso fenómeno musical y también al libro de Simha Aaron African Polyphony and Polyrhythm [Aro91].
Los autores son conscientes de las medidas de síncopa que hay en la bibliografía y mencionan, entre otras, las siguientes: la medida de complejidad cognitiva de Pressing [Pre99], la medida de síncopa de Longuet-Higgins [LHC84], la medida de complejidad rítmica de Lempel y Ziv [LZ76], la medida de síncopa de Keith [Kei91], o la medida WBND [GMRT05] (WBND significa distancia ponderada de pulso a nota en sus siglas inglesas). Véase [Góm11c, Góm17a, Góm17b, Góm18] para un exposición divulgativa de esos trabajos. Para la definición operativa de polirritmia, Song y sus coautores se basan en el trabajo de Handel y Oshinsky[SJ81].
3. Síncopa percibida
3.1. Las preguntas de investigación
Los autores del trabajo midieron la síncopa percibida a través de experimentos con sujetos. Se reclutaron a 10 músicos, voluntarios, sin pago alguno por la participación en el experimento, con una media de 15 años de formación y práctica (desviación típica 5). Seis de los participantes eran multi-instrumentistas. Las hipótesis que los investigadores querían estudiar eran las siguientes:
El papel de la métrica en la percepción de la síncopa;
El papel que desempeña la presencia o ausencia de la parte fuerte en la percepción de la síncopa;
Si la síncopa se percibe más fuertemente en presencia de polirritmos o bien en presencia de ritmos simples;
El papel de la posición de la síncopa dentro del compás.
3.2. Los experimentos
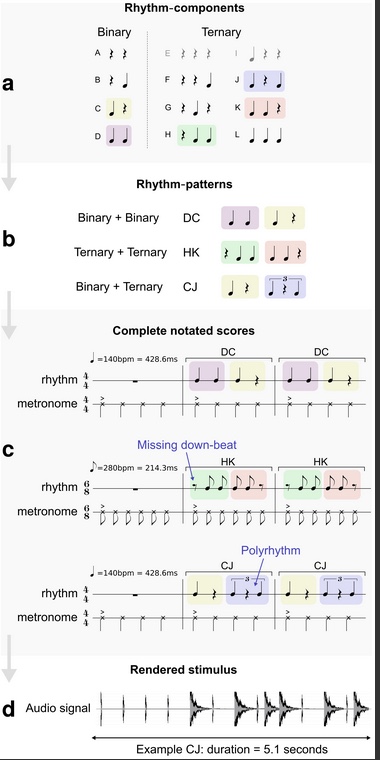
La música que escucharon los sujetos estaba compuesta por tres compases, bien en 4/4 o bien en 6/8. El primer compás era siempre el pulso dado por un metrónomo. El segundo y el tercer compás era una repetición de un ritmo que a su vez estaba compuesto por dos medios ritmos básicos. Estos ritmos básicos se combinaban de varias maneras para generar todos los estímulos a que se exponían a los sujetos. La figura 1 muestra un esquema de cómo funciona la generación de los ritmos. Los ritmos básicos tienen o bien dos o bien tres notas. Cada uno de los ritmos básicos se combina con otro para dar un ritmo principal. Las letras mayúsculas en la figura de abajo designan los ritmos básicos, que van desde la A hasta la L. Así, DC quiere decir la combinación del ritmo D con el C en ese preciso orden. El metrónomo se toca al mismo tiempo que los ritmos como referencia.
Figura 1: Generación de los ritmos para los experimentos (figura tomada de [SAJRCA+13])
Los ritmos básicos contienen todas las categorías de síncopas (síncopas de acentuación, síncopas de ataque y polirritmias) descritas más arriba. Se generaron en total 99 patrones rítmicos y se aleatorizó la presentación dentro de las categorías de síncopas. El estímulo final fue el de una caja clara para el patrón principal y de un cencerro para el metrónomo. El metrónomo fue acentuado ligeramente en dinámica cuando caía en la primera nota del compás. El tempo del metrónomo fue de 140 pulsos por minuto para el compás de 4/4 y de 280 para el de 6/8. Los sujetos escuchaban los ritmos y tenían que puntuarlos entre 0 y 4, donde 0 es no hay síncopa y 4 tiene máximo nivel de síncopa. Los sujetos podían escuchar tantas veces como quisieran los patrones rítmicos. Además, tuvieron sesiones de práctica para entender bien el procedimiento experimental. Los investigadores sugerían a los sujetos que tomasen descansos para evitar el cansancio auditivo.
3.3. Los resultados
La figura 2 muestra un resumen de los resultados. La matriz mostrada en (a) contiene una representación de la media de las puntuaciones para cada patrón rítmico. El eje horizontal muestra el primer ritmo básico y el eje vertical el segundo. La parte (b) muestra la matriz de (a) ahora descompuesta en regiones que corresponden a los patrones rítmicos de los experimentos. La parte (c) muestra intervalos de confianza al 95% para las puntuaciones dadas por los sujetos. Por último, (d) muestra intervalos de confianza para la media de las puntuaciones por ritmo básico.
Figura 2: Generación de los ritmos para los experimentos (figura tomada de [SAJRCA+13])
Los resultados que se desprenden de los experimentos de Song y sus coautores son los siguientes:
El compás de 6/8 es más sincopado que el de 4/4.
Los polirritmos son más sincopados que los ritmos simples.
La ausencia de notas en las partes fuertes dan más sensación de síncopa.
El cambio de orden en los ritmos básicos afecta a la sensación de síncopa.
Dónde se produce la síncopa dentro del compás afecta a su percepción.
4. Conclusiones
El trabajo de Song y sus coautores es profundo y metodológicamente impecable. En la parte final del artículo discuten varias medidas de síncopa y señalan fallos de diseño en dichas medidas. Todas las medidas mencionadas en la sección 2, por ejemplo, no tienen en cuenta la posición de la síncopa dentro del compás y dan el mismo peso a la síncopa ocurra donde ocurra. Es el caso de la medida WBND (uno de cuyos coautores es el humilde redactor de este artículo). Esta medida cuantifica la síncopa en base a las notas en parte débil tomando la distancia de la parte débil a la siguiente parte fuerte, pero no modifica la distancia en función de dónde ocurre la nota en parte débil. Lo mismo ocurre con la distancia de Longuet-Higins.
La razón por la que hemos analizado este artículo en esta columna es que muestra cómo el rigor que proporcionan las matemáticas es necesario para cualquier investigación mínimamente seria sobre cualquier tema, en este caso el maravilloso mundo de las síncopas.
En resumen, un buen artículo, bien escrito, bien investigado, que trata un tema fascinante: la síncopa.
Bibliografía
[Aro91] Simha Arom. African Polyphony and Polyrhythm. Cambridge University Press, Cambridge, England, 1991.
[GMRT05] Francisco Gómez, Andrew Melvin, David Rapapport, and Godfried Toussaint. Mathematical measures of syncopation. In Proceedings of BRIDGES: Mathematical Connections in Art, Music and Science, pages 73–84, Banff, Alberta, July 31 - August 3 2005.
[Góm11a] Paco Gómez. Medidas matemáticas de síncopa (III). Diciembre, 2011.
[Góm11b] Paco Gómez. Medidas matemáticas de síncopa (II). Noviembre, 2011.
[Góm11c] Paco Gómez. Medidas matemáticas de síncopa (I). Octubre, 2011.
[Góm13] Paco Gómez. Transformaciones rítmicas: de binarizaciones y ternarizaciones (I). Agosto, 2013.
[Góm17a] Paco Gómez. Medidas de complejidad rítmica (I). Octubre, 2017.
[Góm17b] Paco Gómez. Medidas de complejidad rítmica (II). Octubre, 2017.
[Góm18] Paco Gómez. Medidas de complejidad rítmica (III). Enero, 2018.
[Kei91] Michael Keith. From Polychords to Pólya: Adventures in Musical Combinatorics. Vinculum Press, Princeton, 1991.
[LHC84] H.C. Longuet-Higgins and C.S. The rhythmic interpretation of monophonic music. Music Perception, 1:424–441, 1984.
[LZ76] A. Lempel and J. Ziv. On the complexity of finite sequences. IEEE Transactions on Information Theory, 22(1):75–81, 1976.
[Pre99] J. Pressing. Cognitive complexity and the structure of musical patterns, 1999.
[Ran86] Donald Randel(editor). The New Grove Dictionary of Music and Musicians. Akal, London, 1986.
[SAJRCA+13] Chunyang Song, Simpson Andrew J. R., Harte Christopher A., Pearce Marcus T., and Sandler Mark B. Septiembre de 2013.
[SJ81] Handel S. and Oshinsky JS. The meter of syncopated auditory polyrhythms. Percept Psychophys, 30:1–9, 1981.
[Tra07] L. J. Trainor. Do preferred beat rate and entrainment to the beat have a common origin in movement? Empirical Musicology Review, 2:17–21, 2007.
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
1. Ritmos equilibrados y euclídeos
La representación geométrica de ritmos y escalas ha sido con frecuencia una herramienta útil para su análisis y para el descubrimiento de nuevos objetos musicales. En esta columna vamos a tratar los patrones rítmicos y de escalas llamados equilibrados y también examinaremos una herramienta, XronoMorph, diseñada por Andrew Milne y Roger Dean [MD16], que permite experimentar con esos ritmos. Para las definiciones que vamos a presentar, necesitamos previamente fijar una circunferencia en la que pondremos los objetos musicales —alturas de sonido o duraciones —. En el vídeo siguiente, A different way to visualize rhythm, John Varney habla de las ventajas de la representación geométrica del ritmo, sobre todo cuando los ritmos son cíclicos y estos se visualizan en una circunferencia.
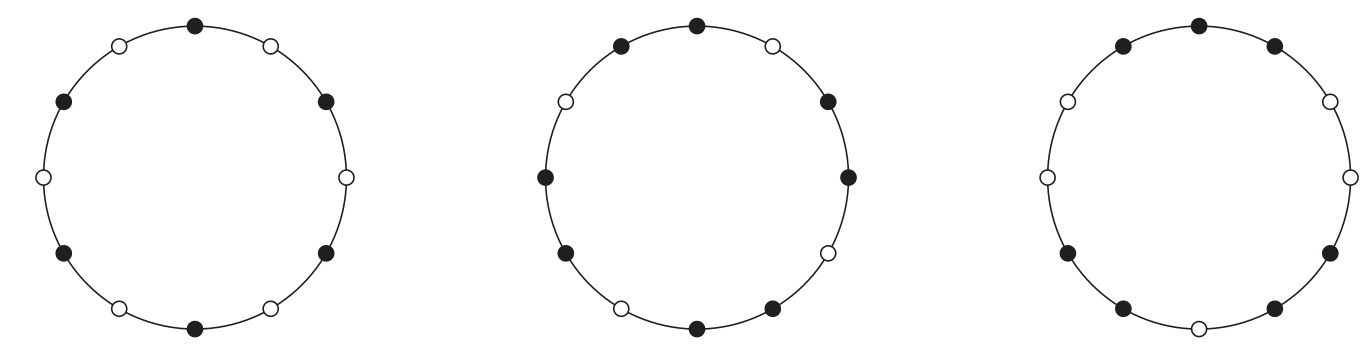
Por sencillez de la exposición, supondremos que los objetos musicales ritmos y, por tanto, los puntos en la circunferencia marcan duraciones consecutivas. El análisis es el mismo si tratamos las escalas. Un ritmo es equilibrado si el centro de gravedad es el propio centro de la circunferencia. Para hablar con propiedad del centro de gravedad, supondremos que cada nota sobre la circunferencia tiene masa unidad y entonces dicho centro es el punto de aplicación de la resultante de todas las fuerzas de gravedad dada por las notas. Por ejemplo, en la figura de abajo, los tres ritmos, dados por los círculos negros, son ritmos equilibrados; aquí se ha tomado doce como número de pulsos para los ritmos.
Figura 1: Ejemplos de ritmos equilibrados.
El concepto de ritmo equilibrado está relacionado con el de ritmo regular. Un ritmo regular es aquel que tiene las notas distribuidas tan regularmente como sea posible a lo largo del círculo. Se sabe que los ritmos regulares solo pueden tener una o dos duraciones posibles y que estas tienen que estar colocadas en un orden especial. Se conocen varios algoritmos para generar ritmos regulares; entre ellos los más importantes son el de Bjorklund [GMTT09b], el de Clough y Douthett [CD91], o el mismísimo algoritmo de Euclides, que cuando se adapta a la formación de grupos, produce ritmos regulares. Los dos primeros ritmos de la figura 1 son regulares. En una columna anterior [Góm12], Amalgamas, aksaks y métricas euclídeas, se trataron a fondo los ritmos regulares, también llamados ritmos euclídeos. Para información más sobre los algoritmos, propiedades de los ritmos regulares y sus aplicciones en música, véanse [DGMM+09, GMTT09b, GMTT09a, CD91].
En lo que sigue usaremos tres notaciones para designar los ritmos: la notación de ceros y unos, adecuada para el tratamiento algorítmico; la notación de x y ., que es cómoda para la lectura musical; y la notación de distancia. Si no se dice nada en contra, cuando un ritmo se represente sobre el círculo, empezaremos a describirlo desde las doce del mediodía. Así, los ritmos de la figura 1, de izquierda a derecha, se designan por
R1 = [101010101010 ] = [x . x .x .x .x .x ] = (222222)
R2 = [101101101101] = [x .x x . x x . x x . x] = (21212121)
R3 = [110011011001] = [x x ..x x . x x . .x] = (1312131)
2. Ritmos equilibrados y euclídeos
2.1. Ritmos euclídeos
En lo que sigue vamos a seguir la exposición del trabajo Si Euclides lo supiese... se sentiría orgulloso [Góm09] del propio autor de estas líneas. El algoritmo de Euclides consiste en hacer divisiones sucesivas para hallar el máximo común divisor de dos números positivos (m.c.d. de aquí en adelante). Si queremos hallar el m.c.d. de dos números a y b, suponiendo que a > b, primero dividimos a entre b, y obtenemos el resto r de la división. Euclides se dio cuenta de que el m.c.d. de a y b era el mismo que el de b y r. En efecto, cuando dividimos a entre b, hallamos un cociente c y un resto r de tal manera que se cumple que:
a = c⋅b + r
Esta ecuación nos dice que todo divisor común de a y b tiene que serlo también de r. En particular, el m.c.d. de a y b es el m.c.d. de b y r. Por ejemplo, calculemos el máximo común de 17 y 7. Como 17 = 7 ⋅ 2 + 3, entonces el m.c.d.(17, 7) es igual al m.c.d.(7, 3). De nuevo, como 7 = 3 ⋅ 2 + 1, entonces el m.c.d.(7, 3) es igual al m.c.d.(3, 1). Aquí es claro que el m.c.d. entre 3 y 1 es simplemente 1. Por tanto, el m.c.d entre 17 y 7 es 1 también.
¿Cómo se transforma el cálculo del máximo común divisor en un método para generar patrones distribuidos con regularidad máxima?
Ilustraremos el proceso con un ejemplo de ritmos. Supongamos que tenemos 17 pulsos y queremos distribuir de forma regular 7 notas entre los 17 pulsos. Sigamos los pasos dados en la figura 2. Primero, alineamos el número de notas y el número de silencios (siete unos y diez ceros); véase la figura 2-paso (1). A continuación, formamos grupos de 7, los cuales corresponden a efectuar la división de 17 entre 7; obtenemos, pues, 7 grupos formados por [1 0] (en columnas en el paso (2) de la figura 2). Sobran tres ceros, lo cual indica que en el paso siguiente formaremos grupos de 3. Tras formar el primer grupo —véase el paso (3) de la figura 2— nos quedamos sin ceros. Continuamos agrupando de 3 en 3 tomando los grupos de la otra caja, en la que quedan 4 columnas (figura 2-paso (4)). Procedemos así que queden uno o cero grupos; de nuevo, esto es equivalente a efectuar la división de 7 entre 3. En nuestro caso, queda un solo grupo y hemos terminado (paso (5)). Finalmente, el ritmo se obtiene leyendo por columnas y de izquierda a derecha la agrupación obtenida (paso (6)).
Figura 2: El algoritmo de Euclides para generar ritmos regulares.
Aquí cada 1 representa una nota [x] y cada 0, un silencio [.]. El ritmo que hemos generado con nuestra notación se escribe entonces como [x . . x . x . . x . x . . x . x .].
Los ritmos generados por este método se llaman ritmos euclídeos. El ritmo euclídeo de k notas y n pulsos se designa por E(k,n). Otra manera útil de designar un ritmo es mediante las duraciones de las notas en términos de pulsos. El ritmo euclídeo que acabamos de obtener con esta notación se escribe E(7,17) = [x . . x . x . . x . x . . x . x .]= (3232322).
Demain y sus coautores [DGMM+09] probaron formalmente que este algoritmo proporciona, salvo rotaciones, la única manera de distribuir k objetos entre n del modo más regular posible. Aún más, había varios algoritmos propuestos de manera independiente y ellos probaron que, en realidad, eran todos equivalentes al viejo algoritmo de Euclides.
Damos a continuación una pequeñísima muestra de ritmos euclídeos que se encuentran en las músicas tradicionales del mundo.
E(5,8) =[x . x x . x x .]= (21212) es el cinquillo cubano, así como el malfuf de Egipto, o el ritmo coreano para tambor mong P’yon. Si el ritmo se empieza a tocar desde la segunda nota aparece un popular ritmo típico de Oriente Próximo, así como el timini de Senegal. Si se empieza en la tercera nota tenemos el ritmo del tango.
E(5,12) =[x . . x . x . . x . x .]= (32322) es un ritmo muy común en África central que tocan los pigmeos aka. Cuando se toca desde la segunda nota es, entre otros, la clave columbia de la música cubana y el ritmo de la danza chakacha de Kenya.
E(5,16) =[x . . x . . x . . x . . x . . . ]= (33334) es el ritmo de la bosa-nova de Brasil. Este ritmo se toca a partir de la tercera nota.
Existen cerca de dos centenares de ritmos de músicas del mundo documentados que son generados por el algoritmo de Euclides. De nuevo, véase el artículo The distance geometry of music de Demain y sus coautores [DGMM+09].
He aquí una lista de las principales propiedades de los ritmos regulares o ritmos euclídeos:
Los ritmos euclídeos tienen solo una o dos duraciones. En el caso de dos duraciones, estas difieren exactamente en una unidad. Por ejemplo, en este ritmo euclídeo (21212) hay dos duraciones de valor 2 y 1.
Cuando el número de notas no es primo relativo del número de pulsos, los ritmos euclídeos están formados por la repetición de un patrón. En caso contrario, el ritmo está compuesto por un patrón repetido un número máximo de veces más un único patrón más pequeño, que además es subpatrón del patrón que se repite.
Los patrones que forman los ritmos euclídeos son a su vez euclídeos. Esto crea una jerarquía de ritmos euclídeos anidados.
La rotación de un ritmo euclídeo es también euclídeo. Esto es consecuencia de que los ritmos euclídeos maximizan las distancias intercordales entre las notas y dichas distancias no cambian con las rotaciones.
Tomar el complementario de un ritmo euclídeo (esto es, intercambiar ceros por unos) devuelve un ritmo euclídeo.
Los ritmos regulares son ritmos equilibrados, pero el recíproco no es cierto.
2.2. Ritmos equilibrados
Cuando se considera el círculo donde se inscriben los ritmos, si el polígono resultante al unir las notas consecutivas del ritmo es regular, entonces el ritmo es equilibrado. De nuevo, el recíproco no es cierto, como atestiguan los polígonos de la figura de arriba. En el artículo Perfect balance: A novel principle for the construction of musical scales and meters, de Milne y coautores [MBHW15], se estudian a fondo las propiedades de los ritmos equilibrados. En dicho artículo los autores asocian a cada ritmo una serie de Fourier discreta uno de cuyos coeficientes es una medida del equilibrio del ritmo. La condición de ser equilibrado se puede pensar como la varianza circular. Si el ritmo tiene varianza cero, entonces se reduce a un único punto. En cambio, si la varianza es máxima entonces el ritmo será equilibrado; véase el artículo mencionado para los detalles técnicos.
3. XronoMorph: una aplicación para la experimentación rítmica
Para terminar, querríamos comentar el programa XronoMorph. Se trata de una aplicación que permite experimentar con ritmos equilibrados y ritmos euclídeos. Es una aplicación gratis y funciona en los sistemas operativos Mac OS X y Windows. Usa como objeto centrar para la representación una circunferencia y permite describir polirritmos en términos de polígonos inscritos. Abajo tenemos un vídeo donde se ve la interfaz.
En el vídeo de abajo podemos ver un ejemplo en que varios polígonos regulares se superponen. Estos polígonos representan ritmos euclídeos y aparecen organizados en una polirritmia.
En el siguiente vídeo tenemos ritmos equilibrados que también forman una polirritmia, en este caso la superposición de un ritmo binario con uno ternario.
En este otro vídeo vemos un 3 contra 5.
Por último, XronoMorph permite varias operaciones con polígonos, como por ejemplo, la rotación. Se pueden componer polirritmias muy complicadas asignando un instrumento a cada rotación de un polígono. Véase una muestra en el siguiente vídeo.
Bibliografía
[CD91] J. Clough and J. Douthett. Maximally even sets. Journal of Music Theory, 35:93–173, 1991.
[DGMM+09] Erik D. Demaine, Francisco Gomez-Martin, Henk Meijer, David Rappaport, Perouz Taslakian, Godfried T. Toussaint, Terry Winograd, and David R. Wood. The distance geometry of music. Computational Geometry: Theory and Application, 42(5):429–454, 2009.
[GMTT09a] F. Gomez-Martin, P. Taslakian, and G. T. Toussaint. Interlocking and euclidean rhythms. Journal of Mathematics and Music, 3(1), 2009.
[GMTT09b] F. Gomez-Martin, P. Taslakian, and G. T. Toussaint. Structural properties of euclidean rhythms. Journal of Mathematics and Music, 3(1), 2009.
[Góm09] Paco Gómez. Si Euclides lo supiese... se sentiría orgulloso, Noviembre, 2009.
[Góm12] Paco Gómez. Amalgamas, aksaks y métricas euclídeas, Noviembre, 2012.
[MBHW15] A. Milne, D. Bulger, S. Herff, and Sethares W. Perfect balance: A novel principle for the construction of musical scales and meters. In T. Collins, D. Meredith, and A. editor Volk, editors, Proceedings of the 5th International Conference on Mathematics and Computation in Music, pages 97–108. Springer, Berlin, 2015.
[MD16] Andrew J. Milne and Roger T. Dean. Computational creation and morphing of multilevel rhythms by control of evenness. Computer Music Journal, 40(1):35–53, 2016.
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
1. Introducción
Este artículo es la continuación de la serie sobre medidas de complejidad rítmica. Los dos primeros artículos fueron las columnas de octubre [Góm17a] y noviembre [Góm17b], respectivamente. En estas dos columnas se presentaron las principales medidas de complejidad rítmica, que se dividieron en dos grandes categorías: la primera, las medidas métricas, las medidas basadas en patrones y las medidas basadas en distancias; la segunda, las medidas formales de complejidad, tales como las medidas basadas en la entropía de la información, las basadas en los histogramas de intervalos entre notas consecutivas y las llamadas de irregularidad matemática, que incluyeron el índice de asimetría rítmica y la medida de contratiempo. En esta tercera columna, la última de la serie, tratamos la evaluación perceptual de esas medidas. Sabemos que cada medida ha sido diseñada poniendo atención a ciertos aspectos del fenómeno rítmico. El objetivo final es que las medidas reflejen lo más fielmente posible la medida humana de la complejidad rítmica. Tal medida humana es, por sí misma, un objetivo muy difícil de definir y aun más de medir. Varias preguntas de manera natural e inmediata surgen. ¿Es la percepción humana de la complejidad rítmica un universal? Si no lo es, ¿depende de la cultura?, ¿de la exposición a determinado estilo?; ¿varía con la predisposición genética? Para un individuo fijo, ¿es dicha percepción consistente en el tiempo?; ¿o depende del estado emocional, de su cansancio o de otros factores?; y si es así, ¿de qué factores? En general, ¿cómo se debería medir la complejidad rítmica? ¿Como ritmos puros o bien inmersa en la melodía o en un contexto armónico? En este último caso, ¿cómo se aísla la complejidad melódica de la complejidad rítmica? ¿Qué factores generales afectan la percepción de la complejidad rítmica? Por ejemplo, Vinke [Vin10], en su tesis de maestría, identifica varios factores tales como tempo, formación musical, timbre, acciones motrices asociadas o producidas durante la percepción de los ritmos, pero sabemos que hay otros factores, como el agrupamiento.
En su tesis de maestría Thule [Thu08] contesta en parte a estas preguntas, apoyándose en experimentos que psicólogos de la música habían llevado a cabo para tratar de medir la complejidad rítmica. El mérito de Thul y Toussaint, su director de tesis, fue usar esas medidas cognitivas para evaluar la bondad de las múltiples medidas que se habían propuesto, pero que inexplicablemente no se habían evaluado. Puede parecer extraño que un investigador presente una medida de complejidad rítmica y no la evalúe con datos reales para determinar su efectividad. Sin embargo, esta ha sido la situación para la gran parte de las medidas examinadas por Thul.
2. Las medidas humanas de complejidad rítmica
En esta sección examinaremos los datos experimentales de tres trabajos diferentes, el de Povel y Essens [PE85], el de Shmulevich y Povel [SP00], y el de Fitch y Rosenfield [FR07], y que sirvieron de base para obtener las medidas humanas de complejidad rítmica. Los dos primeros estudios usan los mismos ritmos como estímulo de entrada, los cuales se pueden ver en la figura 1 más abajo. El primer estudio, el de Povel y Essens, data de 1985 y en él estos autores investigaron la medida de la complejidad rítmica de la ejecución. Estrictamente hablando, no es una medida de la complejidad rítmica, pero la hipótesis subyacente era que la complejidad rítmica y de reproducción están estrechamente relacionadas. Al fin y al cabo, un ritmo complejo debería ser más difícil de reproducir que uno que no lo es. Quince años más tarde, en 2000, Shmulevich and Povel usaron los mismos ritmos para su propio estudio, pero esta vez el objetivo sí era la complejidad rítmica. En 2007 Fitch y Rosenfeld estudiaron la complejidad de la ejecución así como la complejidad métrica; estos autores usaron otros ritmos diferentes a los de los dos primeros estudios.
2.1. Los datos de Povel y Essens
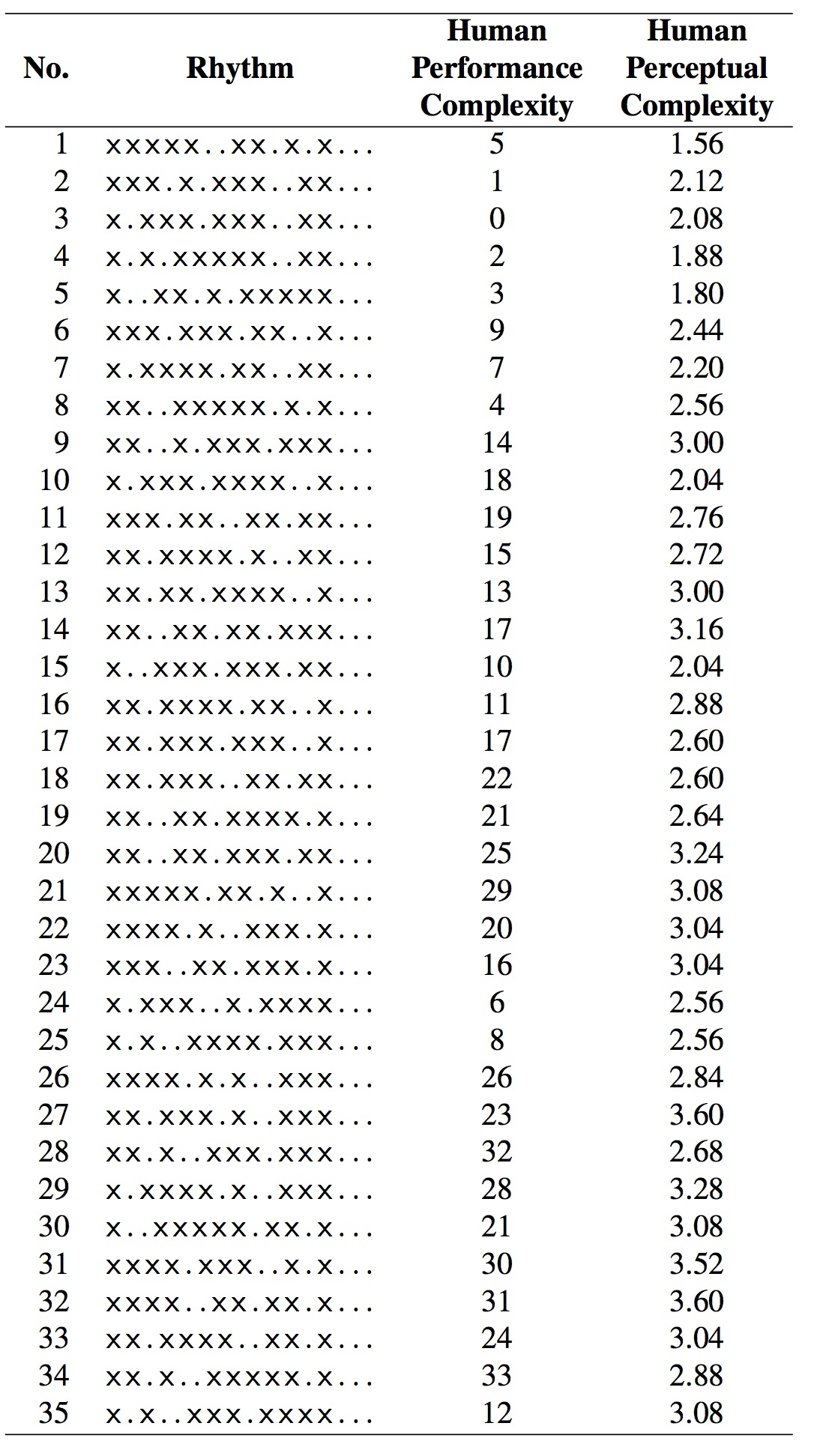
Povel y Essens decidieron en su estudio usar ritmos sintetizados por un ordenador con el fin de aislar variables tales como el timbre o la altura del sonido. Los ritmos se pueden ver en la figura 1.
Figura 1: Ritmos usados en los experimentos (figura tomada de [Thu08])
La pregunta de investigación que se plantearon estos autores tenía un carácter muy cognitivo. Querían comprobar si los ritmos que inducen un carácter métrico fuerte generan mejores representaciones internas que los ritmos que tienen un carácter métrico débil. En el lenguaje de Povel y Essens, el carácter métrico es descrito como un reloj interno. Los ritmos que usaron en sus experimentos tienen una estructura muy fija. Son todas las permutaciones del patrón de los intervalos de duraciones entre notas consecutivas (IDNC) del conjunto . Según estos autores, este conjunto solo admite variaciones estructurales. Nos queda la duda, sin embargo, de qué resultados se habrían obtenido con un conjunto de ritmos más variado. Por ejemplo, los ritmos en este estudio tienen el mismo número de notas, pero sabemos que la medida de complejidad variaría notablemente con el número de notas.
El estudio usa 24 sujetos, los cuales tenían que reproducir un ritmo que acababan de oír. El ritmo se podía oír tantas veces como el sujeto quisiera y además podían tocarlo a la vez si así lo querían (de hecho, en el experimento se les animaba a que así lo hiciesen). Pero cuando daban al botón de parar la reproducción del ritmo, entonces tenían que tocarlo y no tenían la oportunidad de volverlo a tocar. Se exigía al sujeto una reproducción de al menos cuatro veces seguidas. Si un sujeto no estaba satisfecho con la reproducción de un ritmo, podía empezar el proceso desde el principio para ese ritmo concreto. La manera en que Povel y Essens midieron la complejidad rítmica de la reproducción fue a través de un porcentaje que medía la discrepancia de las reproducciones de los sujetos con respecto al ritmo presentado. Los resultados de los experimentos se puede ver en la columna que reza human performance complexity en la figura 1.
2.2. Los datos de Povel y Shmulevich
En el experimento de Shmulevich y Povel, como hemos dicho, se usaron los mismos ritmos que antes. Los sujetos fueron reclutados de la Universidad de Nijmegen y todos eran músicos con una media de 9,2 años de experiencia musical. Los ritmos se presentaron a los sujetos sintetizados por MIDI con un sonido de marimba y de manera aleatoria. Los participantes tenían que puntuar los ritmos según la complejidad rítmica en una escala de números enteros que iba de 1 (más sencillo) a 5 (más complejo). En la última columna de la tabla de la figura 1, la que reza human perceptual complexity.
2.3. Los datos de Fitch y Rosenfeld
En 2007, Fitch y Rosenfeld llevaron a cabo dos experimentos, uno de reproducción rítmica y otro de complejidad métrica. Los estímulos de sus experimentos se pueden consultar en la figura 2. Los ritmos fueron generados de tal manera que la cantidad de síncopa variara sustancialmente, y donde la síncopa se midió usando la medida de Longuet-Higgins y Lee (véase [LHC84] y [Góm17a]). Los 16 participantes tenían entre 0 y 15 años de experiencia musical y realizaron las dos tareas propuestas en el experimento.
Figura 2: Ritmos usados en los experimentos de Fitch y Rosenfeld (figura tomada de [Thu08])
En estos experimentos el ordenador toca un pulso sobre el cual se oye el ritmo y sobre el cual los sujetos tienen también que reproducir dicho ritmo. En el segundo experimento, después de cierto tiempo se supreme el pulso de referencia y el sujeto tiene que seguir reproduciendo el ritmo y además el pulso. Antes de que se suprima el pulso, el ordenador cambia un poco el tempo. Se producen así errores de ritmo que sirven a Fitch y Rosenfeld para evaluar la complejidad rítmica. En la figura 2 las columnas human performance complexity y human metrical complexity corresponden a las medidas obtenidas. La tercera columna se refiere a otro experimento que no hemos descrito aquí.
3. La comparación de las medidas de complejidad
Una vez que tenemos las medidas formales de complejidad rítmica y las medidas humanas (los datos experimentales), ¿cómo se lleva a cabo la comparación entre ellas? Cada medida formal debe ser validada con los datos experimentales. Una posible técnica es la correlación. La correlación es una técnica estadística para detectar relaciones entre dos variables, sean aquellas causales o no. Tal detección puede ser muy útil cuando el objetivo es predecir el comportamiento de una variable en función de otra. Cuando una variable es la causa de la otra, entonces hablamos de causalidad. Cuando hay causalidad, se produce correlación entre las variables, pero al revés no es cierto. Es el famoso cántico que entona todo investigador constantemente: correlación no implica causalidad. Para ver ejemplos muy llamativos y también simpáticos de correlaciones que no implican causalidad, véase la página web de Tyler Virgen, Spurious correlations [Vir17], donde uno se entera de que hay una alta correlación el porcentaje de matrimonios en Kentucky y el número de personas que se ahogaron tras caerse de un bote al mar. Para más información sobre la correlación, véanse [CC83] para los detalles técnicos y [Wik17] para un tratamiento más general.
¿Cómo se cuantifica el grado de correlación entre dos variables? La técnica habitual es a través del llamado coeficiente de correlación de Pearson. Supongamos que X e Y son dos variables (en nuestro caso las medidas), que toman valores n valores xi, yi, respectivamente; ademas, sean X e Y sus medias. El coeficiente de correlación lineal r se define por
El coeficiente r toma valores entre -1 y 1. Valores cercanos a bien -1 o 1 indican una alta correlación lineal, esto es, que las variables dependen la una de la otra en la forma de una ecuación lineal del tipo Y = aX + b, donde a,b son ciertas constantes. Si r está próximo a cero, entonces se entiende que no hay dependencia lineal. Esto, por supuesto, no implica que no haya otro tipo de dependencia (cuadrática, exponencial, etc.). De hecho, hay otros coeficientes para medir otros tipos de dependencia aparte de las lineales. Para un tratamiento riguroso y ameno de los problemas de interpretación de la correlación, recomendamos vehementemente al lector el libro de Ellenberg How Not To Be Wrong. The Power Of Mathematical Thinking [Ell15].
Sin embargo, los coeficientes de correlación como el de arriba no son aplicables en nuestro caso porque las variables son ordinales, esto es, reflejan un orden entre objetos. Para el caso concreto de variables ordinales se usa otro coeficiente, el llamado coeficiente de correlación de rangos de Spearman. Aquí la palabra rango significa el orden del objeto (en nuestro caso medidas de complejidad rítmica) en la clasificación general. Si designamos por di la diferencia entre los rangos xi e yi, y n el número de datos, entonces el nuevo coeficiente, rs, se define por:
Esta fórmula solo es válida si los rangos no contienen repetidos; ese fue el caso de las medidas de complejidad rítmica.
Otro problema matemático que surge ahora es cómo visualizar adecuadamente todos esos coeficientes de correlación. Nótese que el coeficiente de arriba, rs, se tiene que calcular n2 veces, una vez por cada par de medidas. Una vez hecho esto, es posible aplicar una técnica de visualización de análisis de grupos llamada árboles filogenéticos [HB06]. Esta técnica está tomada de la Bioinformática, donde se usa para visualizar la evolución de especies. En este campo, la distancia entre dos especies se toma como la distancia de edición entre el ADN. Para obtener un árbol filogenético hace falta una distancia. En nuestro caso no tenemos una distancia propiamente dicha, pero se pueden transformar los coeficientes de correlación en una distancia con la fórmula ds = 1 - rs.
Las etiquetas que aparecen en la figura 3 son las distintas medidas con sus variantes que Thul calculó. No todas las medidas de su tesis han sido descritas aquí. La potencia de los árboles filogenéticos es que la distancia entre dos nodos en el árbol se corresponde con la distancia real en la matriz. Así, por ejemplo, observando la figura de arriba, a la derecha en la parte superior, vemos que están las medidas humanas de complejidad (las etiquetas human perceptual complexity y human performance complexity), y que las medidas más cercanas a ellas son la medida DPNP (WNBD2 en el gráfico), el índice de contratiempo (offbeatness) y la medida de Keith (keith).
Figura 3: Árboles filogenéticos para el análisis de grupos (figura tomada de [Thu08])
4. Conclusiones
A lo largo de estas tres columnas hemos estudiado un buen grupo de medidas formales de complejidad rítmica, cómo se obtienen medidas humanas de complejidad rítmica y cómo se correlacionan las unas con las otras para ver cuáles son las más adecuadas. Varias observaciones críticas se pueden hacer al proceso. Por una parte, nos damos cuenta de que algunas medidas formales se definieron de una manera abstracta, sin atender a principios musicales y cognitivos. Un ejemplo de esta categoría podría ser la medida de Lempel-Ziv o la medida de Keith. Esta última se basa en combinatoria y asigna los pesos de las plantillas de manera bastante arbitraria. Por otro lado, las medidas humanas fueron generadas a partir de experimentos no siempre directamente relacionados con la complejidad rítmica y en algunos casos usando conjuntos de ritmos ciertamente limitados. En este sentido, es claro que hacen falta nuevos experimentos para mejorar las medidas humanas. Por último, hace falta un marco teórico más claro con respecto a lo que queremos decir cuando hablamos de complejidad rítmica. En la propia tesis de Thul se listan unos cuantos problemas abiertos.
Bibliografía
[CC83] J. Cohen and P. Cohen. Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences. Lawrence Erlbaum Associates, 1983.
[Ell15] Jordan Ellenberg. How Not To Be Wrong. The Power Of Mathematical Thinking. Penguin, 2015.
[FR07] W.T. Fitch and A. J. Rosenfeld. Perception and production of syncopated rhythms. Music Perception, 25(1):43–58, 2007.
[Góm17a] Paco Gómez. Medidas de complejidad rítmica (I), 2017.
[Góm17b] Paco Gómez. Medidas de complejidad rítmica (II), 2017.
[HB06] Daniel H Huson and David Bryant. Application of phylogenetic networks in evolutionary studies. Mol Biol Evol, 23(2):254–267, 2006.
[LHC84] H.C. Longuet-Higgins and C.S. The rhythmic interpretation of monophonic music. Music Perception, 1:424–441, 1984.
[PE85] D. Povel and P. Essens. Perception of temporal patterns. Music Perception, 2:411–440, 1985.
[SP00] I. Shmulevich and D.-J. Povel. Measures of temporal pattern complexity. Journal of New Music Research, 29(1):61–69, 2000.
[Thu08] Eric Thul. Measuring the complexity of musical rhythm. Master’s thesis, McGill University, Canada, 2008.
[Vin10] Louis Nicholas Vinke. Factors affecting the perceived rhythmic complexity of auditory rhythms. Master’s thesis, Bowling Green State University, United States of America, 2010.
[Vir17] Tyler Virgen. Spurious Correlations. http://www.tylervigen.com/spurious-correlations, consultado en diciembre de 2017.
[Wik17] Wikipedia. Correlation and dependence. https://en.wikipedia.org/wiki/Correlation_and_dependence, consultado en diciembre de 2017.
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
1. Introducción
Este es el segundo artículo de la serie sobre medidas de complejidad rítmica. En el primer artículo [Góm17] se presentaron las principales preguntas alrededor de la cuestión de cómo medir la complejidad rítmica y se pasó a revista a unas cuantas medidas (las medidas métricas, las medidas basadas en patrones y las medidas basadas en distancias). En la columna de hoy continuaremos con el examen de las medidas formales de complejidad; en particular, estudiaremos las basadas en la entropía de la información, las basadas en los histogramas de intervalos entre notas consecutivas y las llamadas de irregularidad matemática, que incluirán el índice de asimetría rítmica y la medida de contratiempo. En la siguiente columna estudiaremos cómo medir la bondad de todas esas medidas desde distintos puntos de vista, pero pondremos especial énfasis en la evaluación perceptual de las medidas.
2. Entropía de la información
2.1. La medida H de complejidad
Las medidas de complejidad rítmica de esta sección se basan en la idea de la entropía definida por Shannon [Sha48]; la entropía también se llama incertidumbre de la información. Este es un concepto que aparece en varias disciplinas científicas tales como la termodinámica, la mecánica estadística y por supuesto la teoría de la información. La idea que subyace debajo de la definición es que las palabras más inesperadas son las que más información aportan. La idea de lo inesperado es formalizado a través de las distribuciones de probabilidad de modo que lo más inesperado tiene menos probabilidad. Supongamos que X e Y son dos variables aleatorias discretas con distribuciones de probabilidad p(x) y p(y), respectivamente. Se define la entropía H(X) por la expresión
Se supone que 0 ⋅ log 2(0) = 0. Si p(x,y) es la probabilidad del vector aleatorio (X,Y) su entropía conjunta es
La medida H de la complejidad rítmica se basa en modelos de percepción de estímulos binarios [VT69]. Los ritmos se pueden ver como un estímulo binario, una nota o un silencio. La medida construye un espacio de probabilidad sobre el conjunto de ritmos de manera recursiva y luego aplica las fórmulas de arriba para obtener la entropía. Los detalles son un tanto técnicos y nos conformaremos con esta breve descripción. Para más información, véase las páginas 29 a 36 de la tesis de Thul [Thu08].
2.2. Codificación de Lempel-Ziv
La complejidad rítmica se puede medir en términos de la capacidad de compresión del ritmo en particular. En efecto, la idea que subyace debajo es que si un ritmo es muy complejo se podrá comprimir poco y si es poco complejo admitirá un alto grado de compresión. Este enfoque, como es claro, pertenece a la teoría de la información. Pero ¿cómo se comprime la información? Uno de los algoritmos más populares es el de Lempel-Ziv [LZ76]. Este algoritmo toma una secuencia (que puede ser un texto o en nuestro caso un ritmo) y lo analiza de izquierda a derecha. A partir de ese análisis construye un diccionario que contiene el vocabulario necesario para describir la secuencia entera. Por ejemplo, si la secuencia es (aa), el diccionario estará formado por la expresión an, donde aquí la potencia significa la concatenación de la letra a n veces. Como se puede ver, dado que la secuencia es muy simple, su diccionario es muy corto. Sin embargo, la cadena r = 0001101001000101 tiene como diccionario D = , que tiene tamaño 6, y que es más largo que el de la secuencia an. La complejidad de ese ritmo sería 6. Los detalles de la construcción también en este caso revisten cierto carácter técnicos y hemos optado por remitir al lector interesado a la sección 3.4.4 de la tesis de Thule [Thu08] o también al artículo de Lempel-Ziv [LZ76].
3. Histogramas de las duraciones de las notas
Los histogramas se han usado en Estadística largamente como forma de resumir y visualizar información, especial una gran cantidad de datos, de manera que su interpretación fuera más fácil y efectiva. Un histograma está formada por una serie de rectángulos o barras cuya superficie es proporcional a la frecuencia de los valores asociados a cada barra.
En teoría de la música, los intervalos de duraciones entre notas consecutivas (IDNC) es el número de pulso que hay entre ambas. Aquí se está suponiendo implícitamente que el pulso es una unidad mínima en el ritmo y que aquel no admite subdivisiones. En la mayoría de los casos es posible suponer la existencia de tal pulso mínimo. Los histogramas se pueden calcular con IDNCs locales o IDNCs globales. Los IDNCs locales no son más que los intervalos obtenidos entre dos notas consecutivas del ritmo. Por ejemplo, para la clave son, de ritmo [x . . x . . x . . . x . x . . .], su histograma es el que muestra la figura 1; a la izquierda de la figura se ve la representación de este ritmo sobre el círculo. Las duraciones de este ritmo son (3, 3, 4, 2, 4).
Figura 1: Histogramas locales de los intervalos de duraciones entre notas consecutivas (figura tomada de [Thu08])
Los histogramas globales de los IDNCs, en cambio, consideran todos los intervalos que se generan entre todos los pares de notas posibles. Si el ritmo tiene k notas, entonces ese número es (k 2) = . La figura 2 muestra el histograma global para la clave son. Este ritmo tiene 5 notas y 10 posibles intervalos entre pares de notas, que son (3,3,4,2,4,7,6,7,6,6).
Figura 2: Histogramas globales de los intervalos de duraciones entre notas consecutivas (figura tomada de [Thu08])
3.1. Desviación estándar de los INCDs
La desviación estándar de un conjuntos de datos es una medida de dispersión respecto a la media. La media, a su vez, es una medida de centralización. Si los datos son , entonces la media x se define como
y la desviación estándar dv como
La desviación estándar hace un promedio de los errores cuadráticos cometidos al sustituir cada dato por la media. Cuando la desviación es cero, implica que todos los datos son iguales entre sí y los datos alcanzan la máxima homogeneidad. Según la desviación típica se hace más grande, los datos se vuelven más homogéneos. La desviación típica se puede ver cómo una medida de cuán representativa es la media respecto al conjunto de datos. Cuando se usa en este sentido se suele complementar con el coeficiente de variación, que se define como . Este coeficiente, normalmente expresado como un porcentaje, nos da la cantidad de dispersión por unidad de media.
Para la medida de la complejidad rítmica, se considera que un ritmo que tiene baja desviación estándar tiene poca complejidad. Tendrá pocos valores diferentes para los INDCs. En cambio, si su desviación estándar es alta, esto significará que hay mucha diversidad de valores de los INDCs. No se le escapa al lector que está medida tendrá sus limitaciones, como mostrarán los experimentos, pues no siempre la variedad de duraciones implicará una complejidad intrínseca de los mismos. La desviación estándar se puede calcular tanto para los histogramas locales como los histogramas globales.
3.2. Entropía de la información sobre los histogramas
El histograma de un conjunto de datos siempre da lugar a una distribución de probabilidad. Si hay n datos, cada dato tiene probabilidad 1∕n de aparecer. Si un dato aparece k veces, su probabilidad será k∕n. Siendo esto así, se puede aplicar todas las ideas desarrolladas más arriba sobre la teoría de la información, esto es, usando la fórmula H(X) = -∑x∈X p(x)log2 p(x), donde X es la distribución dada por los histogramas.
4. Irregularidad matemática
Las medidas que estudiaremos en esta sección tienen su base en ideas matemáticas. Constituyen las ideas más formales de todas las presentadas hasta ahora. En otro contexto similar, la medida de síncopa, estudiamos las dos medidas siguientes, el índice de asimetría rítmica y la medida de contratiempo; véanse las columnas de octubre a diciembre de 2011 [Góm11a, Góm11b, Góm11c].
4.1. Índice de asimetría rítmica
Simha Arom [Aro91] descubrió que los pigmeos aka usan ritmos que tienen lo que él llama la propiedad de asimetría rítmica [CT03, Che02]. Un ritmo con un tramo temporal consistente en un número par de unidades de tiempo tiene la propiedad de asimetría rítmica si no hay dos notas que partan el ciclo (el tramo temporal entero) en dos subintervalos de igual longitud. Tal partición se llama un bipartición igual. Nótese que la propiedad de asimetría rítmica se define solo para tramos temporales de longitud par. Para tramos de longitud impar todos los ritmos tiene esa propiedad, lo que desprovee a la medida de todo interés. Aunque limitada, esta propiedad es un primer paso hacia una definición matemática de la complejidad rítmica.
Toussaint [Tou03] propuso una generalización de esta propiedad que tenía más capacidad de discriminación. Originalmente, Simha Arom [Aro91] definió la propiedad de asimetría rítmica de una manera estrictamente dicotómica, blanco o negro, todo o nada, esto es, el ritmo o tiene la propiedad o no la tiene. Este concepto se puede generalizar a una variable que tome más valores y que mida la cantidad de asimetría rítmica que un ritmo posee. Esta variable de asimetría rítmica se define como el número de biparticiones iguales que admite un ritmo. Cuantas menos biparticiones un ritmo admita, más asimetría rítmica tendrá. La medida de asimetría se concibe entonces como una medida de complejidad rítmica.
4.2. La medida de contratiempo
Consideremos en primer lugar los ritmos definidos sobre un tramo temporal de 12 unidades de tiempo. Un intervalo de 12 unidades se puede dividir de manera exacta, sin resto, por cuatro números mayores estrictamente que 1 y menores que 12. Estos números son 6, 4, 3 y 2. Dividir el círculo de 12 unidades por estos números da lugar a un segmento, un triángulo, un cuadrado y un hexágono, respectivamente. Normalmente, la música africana incorpora un tambor u otro instrumento de percusión que toca al menos una porción de estos patrones. A veces la música se acompaña con ritmos de palmas que usan alguno de estos patrones. Por ejemplo, la musica funeral neporo del noroeste de Ghana emplea el triángulo, el cuadrado y el hexágono en sus ritmos de palmas [Wig98]. En cualquier caso, el ritmo tiene un pulso que podemos asociar con la posición “cero” en el ciclo. En la música polirrítmica estos cuatro subpatrones forman los posibles patrones métricos. Dos de estos patrones, el segmento y el cuadrado, son binarios y dos, el triángulo y el hexágono, ternarios. En la figura 3 se muestra las subdivisiones dadas por los divisores de 12 para los ritmos bembé y la clave son. El primero es ternario y es [x . . x . x x . x . x . x] y el segundo es binario y se describe como [x . . x . . x . . . x . x . . .].
Figura 3: La medida de contratiempo (figura tomada de [Thu08])
Por tanto, las notas que se tocan en otras posiciones están en posiciones de contratiempo en un sentido fuertemente polirrítmico. Hay cuatro posiciones que no aparecen en ninguno de estos cuatro patrones. Esas posiciones son 1, 5, 7 y 11. Las notas en esas posiciones se llamarán notas a contratiempo. Un ritmo que contenga al menos una nota en una de esas posiciones se dirá que tiene la propiedad del contratiempo. La medida de contratiempo es el número de notas a contratiempo que contiene. Estas notas a contratiempo (1, 5, 7, y 11) tienen una interpretación en términos de teoría de grupos. Las 12 posiciones para las 12 posibles notas forman un grupo cíclico de orden 12 designado por C12. Los valores de las posiciones de las notas a contratiempo corresponden a los tamaños de los intervalos que tienen la propiedad de que, si se recorre el ciclo empezando en “cero” en sentido horario en saltos de tamaño igual al tamaño de uno de estos intervalos, entonces en algún momento se vuelve al punto de inicio tras haber visitado todas las 12 posiciones. Recíprocamente, si las longitudes de los saltos se toman del conjunto complementario , entonces el punto de inicio se alcanzará sin haber visitado las 12 posiciones del ciclo. Por esta razón, los elementos 1, 5, 7 y 11 se llaman generadores del grupo C12
Los números que indican la posición de las notas a contratiempo en el ciclo también tienen una interpretación desde el punto de vista de la teoría de números. Consideremos un tramo temporal de n unidades. Las posiciones de las notas a contratiempo se conocen como coprimos de n (véase[CG96]) . Los coprimos de n son los enteros positivos menores que n que son primos relativos con n. Dos números son primos relativos si el único divisor que tienen en común es 1. La función indicatriz de Euler, designada por ϕ(n), es el número de coprimos de n, y es por tanto el valor máximo que la medida de contratiempo puede tomar para un ritmo con un tramo temporal de n unidades.
Ya que cada grupo cíclico Cn tiene un conjunto de generadores, la medida de contratiempo descrita se puede generalizar a ritmos definidos sobre tramos temporales de n unidades, donde n puede tomar otros valores distintos a 12. Aunque la medida funciona mejor con valores pares de n, tiene alguna aplicabilidad para valores impares de n. Por otra parte, si n es un número primo p, entonces todos los números entre 1 y p - 1 son coprimos con p. En tal caso la medida es infructuosa, ya que todas las posiciones entre 1 y p - 1 serían notas a contratiempo bajo la presente definición de contratiempo.
5. Conclusiones
En este artículo hemos presentado medidas métricas y medidas basadas en patrones y medidas basadas en distancias para la complejidad rítmica. Como ha podido comprobar el lector, los enfoques son muy distintos y producen a su vez resultados también distintos. Queda para los siguientes artículos estudiar su validación perceptual.
Bibliografía
[Aro91] Simha Arom. African Polyphony and Polyrhythm. Cambridge University Press, Cambridge, England, 1991.
[CG96] J. H. Conway and R. K. Guy. Euler’s Totient Numbers. The Book of Numbers, pages 154–156, 1996.
[Che02] Marc Chemillier. Ethnomusicology, ethnomathematics. The logic underlying orally transmitted artistic practices. In G. Assayag, H. G. Feichtinger, and J. F. Rodrigues, editors, Mathematics and Music, pages 161–183. Springer-Verlag, 2002.
[CT03] Marc Chemillier and Charlotte Truchet. Computation of words satisfying the “rhythmic oddity property” (after Simha Arom’s works). Information Processing Letters, 86:255–261, 2003.
[Góm11a] Paco Gómez. Medidas matemática de síncopa (I), 2011.
[Góm11b] Paco Gómez. Medidas matemática de síncopa (II), 2011.
[Góm11c] Paco Gómez. Medidas matemática de síncopa (III), 2011.
[Góm17] Paco Gómez. Medidas de complejidad rítmica (I), 2017.
[LZ76] A. Lempel and J. Ziv. On the complexity of finite sequences. IEEE Transactions on Information Theory, 22(1):75–81, 1976.
[Sha48] C.E. Shannon. A mathematical theory of communication. The Bell System Technical Journal, 27:623–656, 1948.
[Thu08] Eric Thul. Measuring the complexity of musical rhythm. Master’s thesis, McGill University, Canada, 2008.
[Tou03] Godfried T. Toussaint. Classification and phylogenetic analysis of African ternary rhythm timelines. In Proceedings of BRIDGES: Mathematical Connections in Art, Music and Science, pages 25–36, Granada, Spain, July 23-27 2003.
[VT69] P. C. Vitz and T. C. Todd. A coded element model of the perceptual processing of sequential stimuli. Psycological Review, 75(6):443–449, 1969.
[Wig98] Trevor Wiggins. Techniques of variation and concepts of musical understanding in Northern Ghana. British Journal of Ethnomusicology, 7:117–142, 1998.
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
1. Medidas de complejidad rítmica
El artículo de este mes inaugura una serie sobre el apasionante tema de las medidas de complejidad rítmica. El material que se presenta en esta serie recoge, de forma divulgativa, el trabajo de autores que han investigado preguntas tales como: dados dos ritmos, ¿cuál de ellos es más complejo?; si el lector es capaz de designar un cierto ritmo como más complejo que otro, ¿puede describir los criterios que rigieron su elección?; ¿depende la complejidad rítmica de la métrica o del agrupamiento?; ¿qué determina la complejidad rítmica?; ¿es una medida asociada intrínsecamente a la estructura del ritmo o depende de la percepción del oyente?; ¿depende la complejidad rítmica de la enculturación del oyente?; ¿lo que es sencillo rítmicamente en una cultura es complejo en otra?; ¿existen universales de complejidad rítmica? Hay más preguntas que se han hecho en la investigación sobre la complejidad rítmica, pero creemos que esta muestra es suficientemente ilustrativa. En esta serie vamos a pasar revista a las medidas de complejidad rítmica más importantes. Seguiremos en buena parte la excelente tesis de maestría de Eric Thul [Thu08]. Primero, empezaremos con las medidas basadas en síncopas, las basadas en patrones y las basadas en distancias. Parte del material que se presenta en este artículo ya fue tratado en 2011 en esta misma revista en la serie Medidas matemáticas de la síncopa; véase [Góm11a, Góm11b, Góm11c]. Dada la distancia en el tiempo y que en esta serie se aborda un problema mayor que en la serie de 2011, consideramos que el lector no se aburrirá.
Por medidas de complejidad rítmica queremos decir medidas formales, esto es, medidas definidas desde un punto de vista teórico. Dependiendo del enfoque conceptual, la medida presentará unas u otras características. Si se mira desde un punto de vista computacional, por ejemplo, se puede pensar en la complejidad de Kolmogorov [LV97]; esta medida se define como el programa más corto que, dada una cadena, hay que escribir para producir como salida dicha cadena. Un experto en teoría de la información diría que la entropía de Shannon, que describe la complejidad como la longitud de la representación más pequeña posible de un mensaje (ritmo, en nuestro caso). Quizás el lector no haya pensado que la complejidad rítmica se pueda medir desde estas perspectivas tan inusuales. Falta de perspectiva es lo único que no está ausente en este tema: Lloyd compiló 42 medidas de complejidad y su artículo se llama Medidas de complejidad: una lista no exhaustiva [Llo01]. No cabe duda de que la complejidad rítmica tiene muchos ángulos desde que atacar su definición.
Aunque algunos psicólogos a principio de siglo se habían interesado por el problema de la complejidad rítmica (Stetson en 1905 y Weaver en 1939), no fue hasta los años 60 en que los psicólogos empezaron a aplicar la entropía de Shannon en sus estudios que el tema empezó a despertar verdadero interés en la investigación. La entropía de Shannon se puede considerar como la cantidad de información promedio que contienen los símbolos usados; véase, por ejemplo, el trabajo de Vitz y Todd de 1969 [VT69]. A partir de los años ochenta, con los trabajos de Essens, Povel y Schumulevich, se empezó a considerar la necesidad de la validación perceptual , esto es, de que seres humanos validaran perceptualmente la complejidad de las medidas y no solo por su estructura interna; véanse [PE85, Ess95, SP00]. Para un discusión de la variedad de medidas de complejidad y las disciplinas que se han interesado por esta cuestión, véase la introducción de la tesis de maestría de Thul [Thu08], páginas 3 y 4.
La intención de esta serie es mostrar cómo funcionan las medidas de complejidad más importantes, cómo se han evaluado y compararlas entre sí. Respecto a la bondad de las medidas, haremos hincapié en la evaluación perceptual así como en su comparación en diversas tradiciones musicales.
2. Medidas métricas
2.1. La medida de complejidad métrica de Toussaint
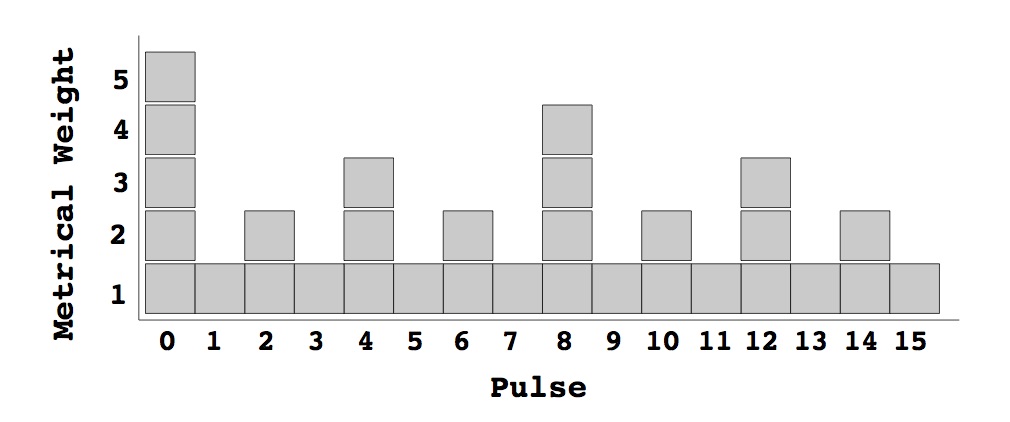
Las medidas que se presentan en esta sección se inspiran en las gramática generativa de la música de Lerdahl y Jackendoff [LJ83]; en su momento dedicamos a su libro Una teoría generativa de la música una serie de título homónimo [Góm14]. En particular, se basan en la jerarquía métrica de pesos, que consiste en asignar un peso a cada subdivisión o pulso del compás en función de su importancia métrica. La importancia métrica se define en función de los divisores del número total de pulsos del ritmo. Para ilustrar esto, consideremos un compás con 16 partes numeradas de 0 a 15, como en la figura de abajo. La posición 0 recibe peso 1 cuando se considera que el compás contiene una redonda. En ninguna otra posición puede empezar una redonda sin salirse del compás. Las posiciones 0 y 8 reciben peso 1 cada una porque en ellas se puede poner una blanca. Las posiciones 0, 4, 8, 12 reciben peso 1 cada una porque pueden albergar las negras. Las posiciones pares reciben 1 cada una porque pueden contener corcheas. Por último, todas las posiciones reciben peso 1 porque en cualquiera se puede poner una semicorchea. El peso final de una posición es la suma de los pesos que ha recibido.
Figura 1: Jerarquía métrica de pesos (figura tomada de [Thu08])
Ahora dado un ritmo la complejidad métrica de Toussaint o simplemente la complejidad métrica es la suma de los pesos de las posiciones en que se encuentran las notas de ese ritmo. Por ejemplo, el ritmo [x . . x . . . x . . x . x . . . ], donde x denota una nota y el punto un silencio, tiene notas en las posiciones 0, 3, 7, 10 y 12. Entonces, su complejidad rítmica es 5+1+1+2+3=12. La idea de esta medida es que la complejidad del ritmo está asociada a la complejidad métrica.
Al lector no se le habrá escapado que el ejemplo que hemos puesto con un número de pulsos igual a 16 es un caso muy fácil. En realidad, los pesos de la jerarquía métrica dependen de los divisores del número de pulsos. Con 16 = 2 ⋅ 2 ⋅ 2 ⋅ 2 la jerarquía es única porque la factorización de 16 es única. Por ejemplo, con 12 no es así. El número 12 se puede escribir como 2 ⋅ 2 ⋅ 3, 2 ⋅ 3 ⋅ 2 y 3 ⋅ 2 ⋅ 2 y ello da lugar a tres jerarquías métricas, como muestra la figura de abajo.
Figura 2: Jerarquía métrica de pesos para 12 pulsos (figura tomada de [Thu08])
En este caso la medida de un ritmo es la media de las medidas en cada jerarquía métrica.
Esta medida tal cual fue presentada inicialmente sufría carencias. Dado que es una medida aditiva, ritmos con más notas serán más complejos que ritmos con menos notas. Varias normalizaciones respecto al número de notas del ritmo y el número de pulsos del compás se han propuesto para corregir esta situación. Por otro lado, la medida premia las notas en las posiciones métricas fuertes, pero no está claro que la complejidad dependa intrínsecamente de pulsos en esas posiciones.
Palmer y Krumhansl [PK90] estudiaron empíricamente la cuestión de los pesos de la jerarquía métrica. Llevaron a cabo experimentos con músicos y no músicos para determinar el peso de cada pulso para varios compases. Estos pesos se han usado para modificar la medida de Toussaint y hacer que su diseñe se base en datos perceptuales.
2.2. La medida de Longuet-Higgins y Lee
La medida de Longuet-Higgins y Lee (LHL a partir de ahora, por brevedad) es una medida también inspirada en los niveles métricos, como la medida de Toussaint. Los niveles métricos se representan mediante una estructura de árbol que se construye recursivamente. Sea n el número de pulsos que tiene el ritmo. Se factoriza n y se consideran los factores primos de n. Sea p un factor primo de n y ℓ el nivel del árbol que estamos construyendo actualmente. A continuación se genera un árbol con las siguientes reglas:
Para todos los nodos m a nivel ℓ, créense p hijos con padre común m.
Increméntese ℓ en 1.
Elimínese p de la lista de primos y procésese el siguiente factor primo en la lista.
Si n = 16, como en el ejemplo anterior, el árbol resultante es el que aparece en la parte de arriba de la figura 4 (el árbol sin pesos). El siguiente paso es agregar los pesos a esta jerarquía métrica. La manera de hacerlo es como sigue. El índice ℓ indica el nivel de la jerarquía métrica y empieza con ℓ = 1. Consideremos las hojas o nodos finales del árbol, y numerémoslos de 0 a 15. Inicializamos todas las hojas a cero. Siempre restamos uno a las hojas, excepto cuando i es cero o i es múltiplo de n/ℓ. Después de procesar el árbol con ℓ = 1, asignamos a ℓ el valor del producto del valor actual de ℓ por el primer factor primo de la factorización de n. Se vuelven a asignar los pesos a este nivel. Se multiplica por el siguiente factor primo y continuamos hasta que todos los factores primos son procesados. El valor final del peso de cada hoja es la suma de los pesos en cada uno de los pasos anteriores. En la figura de abajo aparecen los pesos para el ejemplo con n = 16.
Índice
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
ℓ = 1
0
-1
-1
-1
-1
-1
-1
-1
-1
-1
-1
-1
-1
-1
-1
-1
ℓ = 2
0
-1
-1
-1
-1
-1
-1
-1
0
-1
-1
-1
-1
-1
-1
-1
ℓ = 3
0
-1
-1
-1
0
-1
-1
-1
0
-1
-1
-1
0
-1
-1
-1
ℓ = 4
0
-1
0
-1
0
-1
0
-1
0
-1
0
-1
0
-1
0
-1
ℓ = 5
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
Suma
0
-4
-3
-4
-2
-4
-3
-4
-1
-4
-3
-4
-2
-4
-3
-4
Figura 3: Construcción de los pesos en el árbol de jerarquía métrica de la medida LHL
El segundo árbol de la figura 4 muestra los pesos finales en las hojas. Obsérvese que los pesos todavía son mayores en las posiciones métricamente fuertes, aunque tomen valores negativos.
Figura 4: Jerarquía métrica de la medida LHL (figura tomada de [Thu08])
De nuevo, cuando n no tiene una factorización única se producen varios árboles con diversas jerarquías métricas. La distancia LHL final será una distancia ponderada entre las distintas jerarquías métricas. La figura 5 muestra las jerarquías métricas asociadas a n = 12.
Figura 5: Jerarquía métrica de la medida LHL (figura tomada de [Thu08])
Una vez que la jerarquía métrica y los pesos se han generado, dado un ritmo, la complejidad métrica LHL se calcula examinando los pulsos que tienen silencio y que tienen un peso mayor que la nota inmediatamente anterior. Si estamos procesando el pulso i de un ritmo y este resulta ser un silencio, buscamos la nota inmediatamente anterior a él. Sea j el índice donde tal nota se halla. Si wi,wj son los pesos de los pulsos i y j, respectivamente, entonces el peso del pulso i es la cantidad wi -wj. En el resto de los pulsos los pesos valen cero. La medida LHL es la suma de todos los pesos de los pulsos del ritmo.
En la figura 6 se el cálculo de la medida LHL para el ritmo soukous [x . . x . . x . . . x x . . . . ]. Los pulsos en que se producen pesos positivos son en 4, 8 y 12. Como se puede apreciar, la nota que precede a esos pulsos tiene un peso métrico menor que el del silencio.
Figura 6: Cálculo de la medida LHL para el ritmo del soukous (figura tomada de [Thu08])
3. Medidas basadas en patrones
3.1. La complejidad cognitiva de Pressing
La idea de Pressing [Pre99] descansa en las jerarquías métricas, pero en la fase final adopta un enfoque de búsqueda de patrones. A partir de los resultados de los patrones determina la medida de la complejidad del ritmo.
Pressing primero crea una jerarquía métrica al estilo de Longuet-Higgins y Lee, dividiendo sucesivamente el número de pulsos. Si n = 16, como la factorización es única, da lugar a una sola estructura métrica, como se muestra en la figura 7; se ha dividido el ritmo acorde a los divisores de n.
Figura 7: Complejidad cognitiva de Pressing para la clave son (figura tomada de [Thu08])
Para medir la complejidad del ritmo, Pressing define unos pesos asociados a cinco tipos de patrones específicos. Usando la terminología de Pressing, llamaremos sub-ritmos a los patrones que se encuentran en un determinado nivel métrico. Por ejemplo, en la figura anterior el segundo nivel tiene dos sub-ritmos; el tercero, cuatro, y así sucesivamente.
En la figura 8 se ven los patrones básicos que definió Pressing para su medida para el tercer nivel (nivel (c) en la figura). Estos patrones reciben los nombres de: a) patrón de relleno; b) patrón continuo; c) patrón de parte fuerte; d) patrón de subparte fuerte; e) patrón de síncopa; f) patrón nulo. Los pesos para cada patrón son, respectivamente, 1, 2, 3, 4, 5, y 6. Pressing da una definición de estos patrones para todos los niveles posibles, pero aquí solo hemos mostrado la del tercer nivel.
Figura 8: Patrones básicos en la complejidad cognitiva de Pressing
La medida es una media ponderada de los patrones que se suman a todos los niveles de la descomposición del ritmo.
Pressing no justificó la asignación de los pesos a estos patrones, lo cual le restó aceptación. Otro inconveniente es que Pressing solo definió la medida para ritmo binarios. No obstante, es posible definirla para ritmos ternarios y para un número de pulsos que no tenga factorización única (por vía de una media ponderada de las distintas medidas de cada descomposición del ritmo).
3.2. La complejidad de Keith
En [Kei91] Keith examina varios fenómenos de naturaleza rítmica y lleva a cabo un análisis matemático de ellos. Como ejemplo ilustrativo, Keith aborda el problema de medir el grado de síncopa de un ritmo dado. Su definición se apoya en la distinción de tres eventos: retardo, cuando una nota empieza en parte fuerte1 y termina fuera de ella; anticipación, cuando la nota empieza fuera de parte y termina sobre parte fuerte; y síncopa, que se concibe como una combinación de los dos eventos previos (véase la figura 9; de izquierda a derecha: retardo, anticipación y síncopa).
Figura 9: Retardo, anticipación y síncopa.
De manera algo arbitraria, Keith asigna valores de 1 al retardo, de 2 a la anticipación y de 3 a la síncopa. Esta asignación parece, por lo menos, subjetiva y el propio Keith reconoce que “el problema de decidir la “fuerza” rítmica relativa del retardo, la anticipación y la síncopa es un interesante problema filosófico”.
La medida de Keith se limita a métricas compuesta de n pulsos, donde n es una potencia de 2. Vamos a dar su definición detallada con el fin de entender esta limitación. Su idea principal es que, dadoa un evento musical (una nota), para saber si está en parte fuerte o no hay que compararla con una plantilla métrica, que indica las partes fuertes y débiles según el tamaño (duraciones) del evento. Por ejemplo, si la potencia de 2 es 3, entonces habrá 23 = 8 corcheas y las plantillas de partes fuertes y débiles se ilustra en la tabla abajo (F es para la parte fuerte y D para la débil).
F
D
D
D
D
D
D
D
F
D
D
D
F
D
D
D
F
D
F
D
F
D
F
D
F
F
F
F
F
F
F
F
Figura 10: Diferentes niveles métricos en la definición de síncopa de Keith.
Un evento de tamaño 8 se compara con la primera plantilla (léase de arriba abajo). Los eventos de tamaño entre 4 y 7 se comparan con la segunda plantilla; los que van de 2 a 3, con la tercera plantilla; y finalmente, las corcheas, de tamaño 1, con la última plantilla, que solo está formada por partes fuertes. Esta plantilla de partes fuertes y débiles recuerda mucho a las jerarquías métricas de la medida de Toussaint y de Longuet-Higgins y Lee.
Podemos representar un ritmo de n notas por una sucesión circular (s0,s1,…,sn-1). Usaremos también la sucesión de intervalos entre notas (δ0,δ1,…,δn-1), donde δi = si+1 - si, para 0 ≤ i < n. El número δn es igual a L - sn-1, siendo L la longitud del ritmo completo. La localización de las partes fuertes es una función de la longitud del intervalo entre notas consecutivas. Una hipótesis implícita es que la métrica es siempre binaria y que las partes fuertes ocurren en algún múltiplo de una potencia de dos. Para cualquier nota dada si, la partes fuertes adyacentes se pueden describir como j2k y (j + 1)2k, donde k es el entero tal que 2k ≤ δi < 2k+1, y j es el entero tal que j2k ≤ si < (j + 1)2k.
Hagamos un ejemplo que ilustre cómo se calcula la medida de síncopa de Keith para el ritmo de la bossa-nova; véase la figura 11. La bossa-nova tiene la sucesión de notas (0,3,6,10,13,16) y la sucesión de intervalos entre notas (3,3,4,3,3) (hemos incluido el 16 para enfatizar que la última distancia se obtiene entre la última nota del ritmo y la primera). Nótese que la sucesión que damos para la bossa-nova tiene una nota de más para enfatizar el carácter circular de la sucesión. La siguiente tabla muestra los cálculos para obtener 9, el valor de la medida de síncopa, que está dado por la suma de los pesos wi.
0
1
2
3
4
5
si
0
3
6
10
13
16
δi
3
3
4
3
3
wi
1
2
3
1
2
Figura 11: Anotación de los cálculos de la medida de síncopa de Keith para el ritmo de la bossa-nova.
4. Medidas basadas en distancias
4.1. La distancia de permutación
La distancia de permutación dirigida se basa en contar el número mínimo de operaciones para transformar un ritmo dado en otro. Es una generalización de la distancia de Hamming. Esas operaciones se limitan a intercambios de notas o silencios entre posiciones adyacentes y tienen las siguientes restricciones:
Ambos ritmos han de tener el mismo número de pulsos.
Se convierte el ritmo de más notas, R1, al de menos notas, R2.
Cada nota de R1 tiene que moverse a una nota de R2.
Cada nota de R2 ha de recibir al menos una nota de R1.
Las notas no pueden cruzar el final del ritmo y aparecer por el principio.
En la figura 12 se muestra la distancia de permutación dirigida entre dos ritmos flamencos, el fandango y la seguiriya; se pueden apreciar los movimientos de las notas de la seguiriya para transformarse en el fandango. El número de movimientos es mínimo.
Figura 12: La distancia de permutación dirigida entre el fandango y la seguiriya).
La distancia de permutación dirigida es entonces 4.
4.2. La medida ponderada de nota a parte
En la definición de la medida ponderada de nota a parte (DPNP a partir de ahora) medida centramos nuestra atención en los ataques de las notas entre partes fuertes en lugar de la estructura métrica, como hace Keith. Esta medida se basa en el concepto de distancia y es más flexible en cuanto que nos permite cuantificar el nivel de síncopa (de complejidad rítmica) de un amplio abanico de ritmos. Por ejemplo, consideremos los ritmos que se muestran en la figura 13; la medida de Keith no es adecuada para medir ritmos de esta complejidad.
Figura 13: Ritmos que no pueden medirse con la medida de Keith.
Sin embargo, con la medida ponderada de nota a parte sí es posible medirlo; de hecho, tiene valor igual a 41∕8.
La distancia ponderada de nota a parte se define como sigue. En primer lugar, supondremos que cada nota termina donde empieza la siguiente. Sean pi,pi+1 dos partes fuertes de la métrica. Sea sj una nota que empieza después o sobre la parte fuerte pi pero antes de la parte fuerte pi+1; primero definimos T(sj) = mín, donde d es la distancia entre notas en términos de duraciones. Aquí la distancia entre dos partes fuertes se toma como la unidad, y, por tanto, la distancia d es siempre una fracción. Por ejemplo, las negras en un compás de 4/4 son partes fuertes, y, si las notas de la figura 14 se refieren a la parte fuerte más cercana:
Figura 14: Síncopa medida con la medida DPNP.
entonces, las distancias respectivas T(sj) son 1/2, 1/4, 1/4, 1/3, 1/3, 1/5.
En la medida de síncopa de Keith la parte fuerte más cercana a una nota estaba implícita. Para permitir una mayor variedad de ritmo la medida DPNP exige especificar cuales son las partes fuertes. En el ejemplo anterior las partes fuertes están dadas por el compás. Así, en el ejemplo de la figura 13 las partes fuertes se encuentran a intervalos de negra. La medida DPNP está especialmente diseñada para entradas en notación estándar, ya que las partes fuertes se deducen del compás.
La medida DPNP D(sj) de una nota sj se define entonces como sigue: 0, si sj = pi; , si la nota sj ≠ pi termina antes o en pi+1; , si la nota sj ≠ pi termina después de pi+1 pero antes de o en pi+2; y , si la nota sj ≠ pi termina después de pi+2. Sea n el número de notas de un ritmo. Entonces la medida DPNP de un ritmo es la suma D(sj), para todas las notas sj, dividida por n. La tabla de la figura 16 proporciona una lista de los valores DPNP para varios ritmos.
Usaremos la notación que introdujimos antes para representar un ritmo como una sucesión circular, junto con una sucesión de intervalos entre notas y las partes fuertes dadas por el compás para escribir el algoritmo de la medida DPNP. Consideremos una nota si. Esta nota puede empezar en una parte fuerte pj o puede caer entre dos partes fuertes consecutivas. Definimos di como
Ahora asignamos un peso wi a una nota si como sigue:
si si = pj entonces wi ← 0 si pj < si < si+1 ≤ pj+1 entonces wi ← 1∕di si pj < si < pj+1 < si+1 < pj+2 entonces wi ← 2∕di si pj < si < pj+1 < pj+2 ≤ si+1 entonces wi ← 1∕di
Nótese que asignamos el mayor valor de síncopa a una nota si en el caso en que si y si+1 caigan entre dos partes fuertes consecutivas.
En la figura 15 hemos registrado los cálculos para determinar la medida DPNP para el ritmo de la bossa-nova. Nótese que el compás implica que las partes fuertes son las blancas. Esto se traduce en un vector de partes fuertes igual a (0,4,8,12,16). La suma de las D(x) para este ritmo es 20 y da una distancia final de 20∕5 = 4.
0
1
2
3
4
5
si
0
3
6
10
13
16
di
0
1/4
1/2
1/2
1/4
wi
0
2×4
2×2
2×2
1×4
Figura 15: Anotación de los cálculos de la medida DPNP para el ritmo de bossa-nova.
Nótese que si n no se introduce en la definición de DPNP, entonces la medida crece según lo hace el número de notas del ritmo. Eso daría como resultado una medida incorrecta. En la tabla 16 hay una columna que muestra la suma de las distancias D(x). Se puede apreciar cómo se comporta tal suma en términos de n y la influencia del número de notas en la medida.
Ritmo
Notación partitura
∑ xD(x)
DPNP
Retardo
2
1/2
Anticipación
2
1/2
Síncopa
6
6∕5 = 1.2
Tresillo
6
6/6=1
Quintillo
15
15/8=1.875
Bembé
21
21/7=3
Son
14
14/5=2.8
Bossa-Nova
20
20/5=4
Ritmo irregular
35
35/7=5
Figura 16: Ejemplos de la medida DPNP.
Los pesos que aparecen en la definición de la medida merecen una explicación. Es razonable dar un peso a una nota que se toca fuera de una parte fuerte. Nuestra medida da menos peso cuando la nota aparece entre dos partes fuertes consecutivas y, según se aproxima la nota a la siguiente parte fuerte, gana más peso. Sin embargo, hay una gran diferencia si la nota cruza una parte fuerte o sencillamente termina antes o en la siguiente parte fuerte. En el primer caso hay una sensación de síncopa más fuerte que en el segundo. Por tanto, recibe más peso con el fin de reflejar este hecho musical.
5. Conclusiones
En este artículo hemos presentado medidas métricas y medidas basadas en patrones y medidas basadas en distancias para la complejidad rítmica. Como ha podido comprobar el lector, los enfoques son muy distintos y producen a su vez resultados también distintos. Queda para los siguientes artículos estudiar su validación perceptual.
Nota:
1 La terminología española es parte fuerte para lo que en inglés llaman strong beat o sencillamente beat; a veces el término pulse se usa como equivalente a parte fuerte.
Bibliografía
[Ess95] P. Essens. Structuring temporal sequences: Comparison of models and factors of complexity. Perception and Psychophysics, 57(4):519–532, 1995.
[Góm11a] Paco Gómez. Medidas matemática de síncopa (I), 2011.
[Góm11b] Paco Gómez. Medidas matemática de síncopa (II), 2011.
[Góm11c] Paco Gómez. Medidas matemática de síncopa (III), 2011.
[Góm14] F. Gómez. Teoría generativa de la música - I, junio de 2014.
[Kei91] Michael Keith. From Polychords to Pólya: Adventures in Musical Combinatorics. Vinculum Press, Princeton, 1991.
[LJ83] F. Lerdahl and R. Jackendoff. A Generative Theory of Tonal Music. MIT Press, Cambridge, Massachussetts, 1983.
[Llo01] S. Lloyd. Measures of complexity: a nonexhaustive list. IEEE Control Systems Magazine, 21(4):7–8, 2001.
[LV97] M. Li and P. Vitányi. An introduction to Kolmogorov complexity and its applications. Springer, 1997.
[PE85] D. Povel and P. Essens. Perception of temporal patterns. Music Perception, 2:411–440, 1985.
[PK90] C. Palmer and C. L. Krumhansl. Mental representations for musical meter. Journal of Experimental Psychology, 16(4):708–741, 1990.
[Pre99] J. Pressing. Cognitive complexity and the structure of musical patterns, 1999.
[SP00] I. Shmulevich and D.-J. Povel. Measures of temporal pattern complexity. Journal of New Music Research, 29(1):61–69, 2000.
[Thu08] Eric Thul. Measuring the complexity of musical rhythm. Master’s thesis, McGill University, Canada, 2008.
[VT69] P. C. Vitz and T. C. Todd. A coded element model of the perceptual processing of sequential stimuli. Psycological Review, 75(6):443–449, 1969.
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
1. Objetivo del libro y autores
En este artículo del mes de septiembre queremos hacer una recensión del libro All about music (Todo sobre la música) [MMP+16b], escrito por Guerino Mazzola y sus alumnos de doctorado y grado Maria Mannone, Yan Pang, Margaret O’Brien y Nathan Torunsky, todos ellos en la Escuela de Música de la Universidad de Minnesota, en Estados Unidos. Mazzola es un provocador irredento e inexorable y el título es una buena muestra de ello. El libro está escrito con la intención de que sirva de libro de texto a alumnos de primer y segundo año de universidad para un curso en que se enseñe varios aspectos musicales, desde los físicos hasta los psicológicos, pero pasando también por los semióticos o incluso los ontológicos. Es habitual en las universidades anglosajonas que los alumnos de ciencias tomen cursos de humanidades y a su vez los de humanidades los tomen de ciencias. Dentro de esa tradición, este texto está pensado para alumnos de ambos mundos sin mucha experiencia ni en las matemáticas ni en la música. Ambos tipos de alumnos podrán aprender y apreciar las conexiones que existen entre la música y otras muchas áreas de conocimiento (incluidas las matemáticas).
Figura 1
All about music es un libro que proporciona interesantes conexiones culturales entre la música y otras disciplinas. Sin embargo, el tipo de conexiones que hace Mazzola y sus coautores no revisten un aparato matemático fuerte; el lector habitual de esta columna debería estar tranquilo si planea leer el libro. Dichas conexiones son abstractas en el sentido en que se reinterpreta la música y los fenómenos asociados a ella de modo que se pueden conectar conceptos y relaciones con otros campos. Empero, una vez hechas esas conexiones y construidos los conceptos correspondientes, los autores no profundizan mucho en las relaciones entre esos conceptos. En particular, renuncian a formalismos fuertes —apenas hay notación matemática y no hay resultados en forma de teoremas—en favor de un tono divulgativo, que por otro lado está francamente conseguido en la mayor parte del libro. En otros libros de Mazzola, como por ejemplo Cool Math for Hot Music [MMP16a], ese formalismo sí está presente, pero la intención y el público final son distintos del libro que nos ocupa en la columna de este mes. El libro está dividido en cuatro capítulos: la realidad física, donde los autores pasan revistas a las dimensiones físicas de la música; la realidad psicológica, donde se ocupan de cuestiones de cognición musical; la semiótica y comunicación; y, finalmente, el capítulo titulado materialización, que es donde introduce su teoría de gestos.
Guerino Mazzola nació en Suiza en 1947 y se graduó en matemáticas, física teórica y cristalografía en la Universidad de Zúrich en 1971; también tiene una sólida formación en computación, pues pasó el examen de habilitación universitario para ese campo. Paralelamente a sus estudios en matemáticas llevó también estudios en piano, aunque de una manera no formal. En el aspecto musical se puede decir que Mazzola en gran medida es autodidacta. Esto no le ha impedido desarrollar una carrera profesional en el mundo de la música, en particular en el del free jazz o jazz libre. Mazzola ha grabado varios álbumes de jazz libre con músicos de la talla de Mat Maneri, Heinz Geisser, Sirone, Jeff Kaiser, Scott Fields, Matt Turner o Rob Brown. En el vídeo de abajo podemos ver una actuación de Mazzola
En la dirección http://www.encyclospace.org/CV/mazzola.html#Music se puede encontrar la discografía completa de Mazzola. Para conocer las ideas de Mazzola acerca del jazz libre, recomendamos al lector su libro Flow, Gesture, and Spaces in Free Jazz [MC09]. En la actualidad Mazzola es profesor de la Escuela de Música de la Universidad de Minnesota. También es el presidente de la Sociedad para las Matemáticas y Computación en la Música [SMC07].
Mazzola es conocido por la formalización de fenómenos y objetos musicales a través de herramientas matemáticas de alta abstracción, como es la teoría de categoría, la geometría algebraica [Maz02], con Stefan Göller y Stefan Müller como colaboradores del libro. Esta obra de Mazzola no está exenta de polémica. Hay autores que celebran la escritura de la obra como un hito en la teoría matemática de la música mientras que otros autores sostienen que las formalizaciones de Mazzola pecan de una abstracción excesiva y no guardan una relación profunda con la música. El lector interesado puede consultar las recensiones críticas [Vet03], [Roe93] o [Tym17], entre otras.
Los otros autores del libro son María Mannone que tiene grados de máster en física teórica y también composición, interpretación y piano; ha estudiado en el IRCAM. Yan Pang es una alumna de doctorado en la Escuela de Música de la Universidad de Minnesota. Maggie O’Brien y Nathan Torunsky son alumnos de grado de dicha universidad.
2. Recensión de All about music
El libro empieza por examinar las dimensiones que van a constituir el libro en el capítulo llamado Ontology and oniontology (un juego de palabras en inglés, ya que onto es próximo fonéticamente a onion). Según Mazzola y sus coautores, la música ontológicamente está formada por tres dimensiones principales, la física, la psicológica y la semiótica-comunicativa, a la cual añade la cuarta, que es la materialización (embodiment lo llaman en el libro); véase la figura de abajo, tomada del libro (las ilustraciones del libro, hechas por María Mannone, son originales e instructivas).
Figura 2: Las dimensiones de la música; figura tomada de [MMP+16b]
2.1. Realidad física
En esta sección los autores exponen material clásico, fundamentalmente de la física del sonido y de la fisiología del oído. Sin embargo, el mérito de la obra no reside tanto en la originalidad del contenido —recordemos que está dirigido a alumnos de primer y segundo año— como en la originalidad de la exposición. Y es aquí donde el texto cobra vida propia. Es un ejemplo de concisión y claridad cómo está escrito el material teniendo en cuenta que trata principios de acústica, series de Fourier, frecuencia modulada, ondículas (wavelets) y síntesis del sonido. Esto en cuanto a la parte física; en la parte fisiológica del oído, los autores proporcionan al lector excelentes descripciones del funcionamiento del oído, desde la llegada del sonido al pabellón auditivo hasta su decodificación por el cerebro.
2.2. Realidad psicológica
El tratamiento de la realidad psicológica, en la terminología de Mazzola y sus coautores, aparece en los capítulos 4 y 5 del libro. En el capítulo 4 examina el papel de las emociones en la música y en el 5 las representaciones mentales que se derivan de la música escrita.
Mazzola y sus coautores pasan revista al papel que las emociones desempeñan en la música. Usan para ello la declaración de principios dada por John Sloboda y Patrick Juslin en su famoso Handbook of Music and Emotion [JS10], esto es, que la enfoque psicológico de la música debe buscar explicar cómo y por qué experimentamos reacciones emocionales ante la música. En otras palabras, los autores de All about music reconocen la importancia del estudio de las emociones como parte esencial del estudio de la música.
A continuación examinan varias cuestiones relacionadas con las emociones en la música. La primera cuestión es cómo medir la emociones. Clásicamente, hay tres maneras de hacerlo: por medio de la autoevaluación (descripciones verbales o escritas, escalas, señalar la emoción en concreto, etc.); por medio del comportamiento expresivo (observando expresiones faciales, gestos, vocalizaciones, tensión muscular, etc.); y, por último, a través de medidas fisiológicas (presión arterial, conductividad de la piel, EEG, ECG, etc.). La discusión que aparece en el libro es concisa y altamente instructiva.
La segunda cuestión que trata es cómo modelizar las emociones. Se sabe que las emociones son multidimensionales y que un modelo preciso es muy difícil de obtener; es, de hecho, un problema abierto obtener tal modelo. Un modelo muy usado por su simplicidad y versatilidad es el de Russell y Barret. Es un modelo bidimensional, en que las emociones se caracterizan por dos variables, la valencia y la activación. La valencia es el tipo de emoción y va sobre el eje Ox; si la emoción es positiva, como la alegría, va en la parte positiva del eje Ox y en caso contrario en la parte negativa. La activación es la intensidad de la emoción y va en el eje Oy. En la figura de abajo se ven algunas de las emociones del modelo de Russell y Barret. La emoción adormilado, por ejemplo, tiene poca valencia y mucha activación negativa. La emoción emocionado tiene alta valencia y activación positiva. Frustado, en cambio, tiene valencia negativa y no mucha activación.
Figura 3: El modelo de las emociones de Russell y Barret
Por último, Mazzola y sus coautores presentan un modelo de las emociones que se basan en los neurotransmisores. Tras esta presentación, discuten la teoría de Langer y Gabrielsson [Gab95] de que hay una correspondencia uno a uno entre la música, las emociones y el movimiento. En realidad, la palabra que usan Langer y Gabrielsson es isomorfismo y ello parece un peligroso préstamo de la terminología matemática. Cuando dos objetos matemáticos tienen la misma estructura, un isomorfismo es una aplicación que determina esa identidad entre ambos objetos. Como demuestran Mazzola y sus coautores, la idea del isomorfismo entre emoción y música no es válido (ellos aportan un sencillo argumento combinatorio). El resto del capítulo 4 es un estudio de las maneras en que se mide las emociones por medios fisiológicos, en especial los EEG (electroencefalogramas).
El capítulo 5, titulado la realidad mental, es en esencia un estudio de la realidad musical generada en la mente a partir de la partitura. Los autores analizan el espacio de las alturas de sonido y algunas de las ideas que se han dado a lo largo de la historia para modelizar dicho espacio (se describen en el libro el espacio de Euler y las ideas de Zarlino, entre otros).
2.3. Semiótica y comunicación
2.3.1. Semiótica
Los capítulos 6 a 10 de All about music tratan de la semiótica y la comunicación en la música. La semiótica es la ciencia que estudia los signos y su significado en el contexto de la comunicación humana. En primer lugar, Mazzola y sus coautores estudian la brevemente la semiótica de la música, esto es, aplican los conceptos de la semiótica a la música e identifican qué constituye signo y significado (la discusión es breve y está en las páginas 59 a 61). A continuación pasan revista a la teoría propiamente lingüística de la semiótica. Revisan en el capítulo 7 las teorías estructurales de la semiótica a través de la obra de cuatro lingüistas de importancia, a saber, Charles Pierce, fundador del pragmatismo y considerado el padre de la semiótica moderna; Ferdinand de Saussure, considerado el padre de la linguística estructural; Louis Hjelmslev, creador de la teoría glosemática y continuador de la obra de Saussure; y, por último, Roland Barthes, quien extendió la obra de los dos autores anteriores. En el capítulo 8 los autores del libro trasladan los conceptos lingüísticos desarrollados antes a la música a través de un estudio de la función armónica tal cual está descrita por la teoría de Riemann. En este punto en el libro aparecen ejemplos detallados de dicha traslación.
El capítulo 9 trata sobre las seis dicotomías de De Saussure. Estas dicotomías son significante/significado, arbitrario/motivado, sintagma/paradigma, habla/lenguaje, sincronía/diacronía y mutabilidad/inmutabilidad. La manera en que los autores desarrollan estos conceptos es algo superficial. Los explican con unos pocos ejemplos, pero sin duda habrían merecido más desarrollo, dada su complejidad. La parte final del capítulo es una aplicación de estas dicotomía a la música. Se analiza en el libro la dicotomía habla/lenguaje aplicada a la música de Bach y Schönberg. La última sección de este capítulo está dedicada a la aplicación de esta teoría semiótica a la interpretación musical. Mazzola y sus coautores ilustran tal aplicación con un examen de las ideas sobre la interpretación del director de orquesta Sergiu Celibidache.
En el capítulo 10, el último de la sección sobre semiótica, los autores de All about music analizan el llamado principio de babushka, que no es más que un principio que establece la estructura recursiva de los sistemas de signos. La expresión (el símbolo), la relación (la relación entre el símbolo y el objeto representado) y el contenido (el significado expresado por el símbolo) admiten, a su vez, una descripción en términos de ellos mismos, que reciben el nombre de expansiones. Cuando se expande la expresión se obtiene la connotación; cuando se expande la relación se deriva la motivación; y cuando se expande el contenido se llega al metasistema. Mazzola y sus coautores aplican estos conceptos a la música. Como primer sistema de signos toman la partitura, la lectura de esta y la intención del compositor al escribir la música (respectivamente, expresión, relación y contenido). Si se expande este sistema de signos, entonces se puede explicar otra actividad musical, que es el análisis de la partitura. En un segundo sistema de signos tenemos la intención del compositor, el análisis musical por parte de un músico y la forma que toma la música en la mente del compositor tras el análisis de la partitura.
2.3.2. Comunicación
Esta sección del libro es una mescolanza que tiene un carácter más cultural que nada. Mazzola y sus coautores pasan revista a temas muy diversos con ilustraciones tomadas de la obra de varios autores de muy distinta procedencia.
El capítulo 11 se llama What is art?, pero el lector no debería esperar una sesuda disquisición sobre la definición de arte; véase, por ejemplo, la entrada de Wikipedia [Wik17] para una definición más elaborada. La de los autores de All about music se limita a decir que “el arte es una manera de comunicarse con la gente”, lo cual no es demasiado iluminador. Cierto es que la definición se va complementando con los análisis de las obras de ciertos artistas cuidadosamente seleccionados. Entre otros, se examinan aspectos artísticos de John Cage (y su obra 4’ 33”), los klaverstücke de Stockhausen, la música de Alanis Morisssete, Angel Haze, Jackson Pollock, François Villon, Schubert, Rafael, Garden State, las películas El satiricón y 8 y medio así como Onibaba, y también el album Bitches Brew de Miles Davis y, por último, música del propio Mazzola, en concreto su Tetrade Group. Este capítulo resulta algo abigarrado y deja la impresión al lector de una combinación heterogénea de materiales, que, si bien resultan interesantes como recorrido cultural, carecen de unidad de discurso.
El capítulo 12 está dedicado por entero a describir el estándar MIDI de comunicación de información musical codificada digitalemente. De nuevo, el capítulo es una buena síntesis de dicho estándar, pero realmente no se entiende por qué está este capítulo en el libro y, en particular, por qué está en ese lugar concreto.
El capítulo 13 es también irregular. Comienza con una definición de música global, que Mazzola y sus coautores ven como la superposición de las músicas de diferentes tradiciones (es decir, música global concebida como la convivencia estrecha de distintas tradiciones musicales). A continuación vienen discusiones de distintos proyectos y obras musicales. Empieza con el proyecto The synthesis project, en el que participa el propio Mazzola, y sigue un breve análisis de las jerarquías temporales del impromptu opus 29 de Chopin, una descripción de la arquitectura del programa Rubato, las composiciones cósmicas de Braxton, la ópera Brain Opera, de Machover, entre otras. El nexo de unión de todas estas descripciones de obras musicales parece ser (porque no siempre es claro que sea así) que hay una componente gestual importante en ellas. Sin embargo, el material resulta demasiado escueto con frecuencia y o bien los análisis estáb poco desarrollados o bien algunas obras parecen estar fuera de contexto.
2.4. Materialización
En la última sección del libro, que comprende de los capítulos 15 al 20, Mazzola y sus coautores presentan una teoría matemática de los gestos musicales. En el capítulo 15 se desarrollan justificaciones de por qué es necesaria una teoría del gesto en la música (no necesariamente una teoría matemática). Empieza con una análisis de los neumas del canto gregoriano y su relación con el gesto. Brevemente, revisan las ideas de David Lewin, Theodor Adorno y Robert Hatten. sobre la música como acción. En estas discusiones se nota el nivel intencionadamente pedagógico que usan los autores, dado que el libro está dirigido a alumnos de los dos primeros años de carrera. Sin embargo, a veces las explicaciones resultan algo simplistas. Por último, Mazzola y sus coautores glosan las contribuciones del propio Mazzola, a veces en un tono claramente falto de modestia. Narran los autores la colaboración del grupo de jazz de Mazzola con un grupo de músicos indonesios con quienes no tenían una lengua común de comunicación. A través del gesto pudieron entenderse y comunicarse musicalmente.
El capítulo 16 se titula Frege’s Prison of Functions. En él, los autores del libro relacionan varios conceptos matemáticos (rotación, números complejos) con los gestos. Sin embargo, la manera en que lo hace resulta en ocasiones superficial, o al menos incompleta. Los autores están discutiendo una trayectoria en el plano entre dos puntos; por razones de su argumento, solo están interesados en los puntos inicial y final. Para justificar tal interés mencionan el formalismo funcional de Frege sucintamente. El lector se queda o bien esperando más o bien con la sensación de que esa mención no era necesaria.
En el capítulo 17 se profundiza en la teoría de gestos y los autores de All about music presentan una interesante discusión sobre qué papel desempeña la partitura en la actividad musical. A partir de esta discusión, continúan con su análisis del gesto en la música. Para ilustrarlo estudian la obra del músico de jazz Cecil Taylor, en concreto a través del vídeo Burning Poles; se puede ver el vídeo más abajo. Cecil Taylor tiene un estilo de tocar el piano muy característico, altamente percusivo y basado en la improvisación.
El resto del capítulo está dedicado al gesto en la robótica.
El capítulo 18 es una exposición bastante didáctica de las bases neuronales de los gestos en general y de los gestos musicales en particular. Esta exposición lleva a los autores a afirmar enfáticamente que “¡Sin gestos, la música sería un error!” (la cursiva es suya), en una paráfrasis de la famosa frase de Nietzsche. El resto del capítulo describe un proyecto llevado a cabo por Mazzola junto con Rachmi Diyah Larasati, profesor de danza en la Universidad de Minnesota. En este proyecto bailarines de danza tradicional del este de Java, que se caracteriza por sus giros, tenían acoplados unos sensores de movimiento, los cuales mandaban la información a un ordenador que producía música. Los bailarines producían la música con sus movimientos. Según Mazzola y sus coautores, este proyecto es una matematización de la teoría de Fourier y “contribuye a crear puentes entre las matemáticas y el arte” (página 159).
El capítulo 19 está dedicado a la teoría matemática del gesto. Tras unas cuantas secciones en que analiza los precedentes históricos de los gestos (en las obras de Tommaso Campanella, Hugues de Saint Victor y Paul Valéry, entre otros), los autores dan por fin la definición matemática (páginas 166 a 168). Esta resulta ser la de una aplicación (en el sentido matemático) que describe el gesto con tres coordenadas, la altura del sonido, el ataque de la nota y la posición de la mano. El gesto se ve como una trayectoria en este espacio. Cuando se abstrae el gesto y se considera este inmerso en un espacio de gestos, entonces hablamos del hipergesto. Y esto y unas cuantas referencias al trabajo de Mazzola y Mannone (que han investigado la cuestión) es todo lo que contiene el capítulo sobre teoría matemática del gesto. Un poco decepcionante, dado toda la expectación que creó en los capítulos anteriores.
3. Conclusiones
El libro de Mazzola y sus coautores tiene un mérito irregular, con aspectos muy destacables que conviven sorprendentemente con deficiencias de contenido y estilo. En lo destacable, descuella la amplísima y rica muestra de referencias culturales que contiene el libro. El análisis de las secciones anteriores da fe de ello. Se encuentran referencias desde Cecil Taylor hasta Chopin, pasando por De Saussure, Adorno, la inteligencia artificial, la semiótica, las matemáticas, la teoría musical. Hay capítulos donde la exposición es brillante por sucinta y clara, especialmente en los primeros capítulos; en otros, nos vemos obligados a decir que peca de un exceso de concisión que llega a dar la sensación de superficialidad (por ejemplo, el capítulo sobre creatividad). Entre las deficiencias, encontramos que las relaciones que se establecen entre los conceptos de un cierto campo y la música son débiles o la identificación entre dichos conceptos no está suficientemente matizada. También creemos que el libro está en ocasiones demasiado centrado en la figura de Mazzola, hecho que genera una sensación de cierta ampulosidad. Todo esto crea un efecto de irregularidad en el libro. Donde en algunos capítulos vemos un pulso firme en la exposición, con definiciones certeras y significativas, con ejemplos relevantes y explicaciones claras, en otros vemos definiciones vagas, frases efectistas, falta de puentes sólidos entre conceptos de distintas disciplinas, o argumentos más basados en la enumeración de grandes nombres de la cultura. Esperemos que en futuras ediciones de este libro estas deficiencias se corrijan.
Bibliografía
[Gab95] A. Gabrielsson. Expressive intention and performance.tellectual property rights. In R. Steinberg, editor, Music and the mind machine. Springer, Berlín, 1995.
[JS10] P. Juslin and J. Slovoda. Handbook of Music and Emotion. Oxford University Press, 2010.
[Maz02] G. Mazzola. The Topos of Music: Geometric Logic of Concepts, Theory, and Performance. Springer, 2002.
[MC09] G. Mazzola and Paul B. Cherlin. Flow, Gesture, and Spaces in Free Jazz. Springer, 2009.
[MMP16a] G. Mazzola, M. Mannone, and Y. Pang. Cool Math for Hot Music. Springer, 2016.
[MMP+16b] G. Mazzola, M. Mannone, Y. Pang, M. O’Brien, and N. Torunsky. All about music. Springer, 2016.
[Roe93] J. Roeder. Review: A mamuth achievement: Geometrie der töne: Elemente der mathematischen musiktheorie by guerino mazzola. Perspectives of New Music, 31(2):294–312, 1993.
[SMC07] SMCM. Society for Mathematics and Computation in Music. http://www.smcm-net.info/, 2007.
[Tym17] D. Tymoczko. Mazzola?s Counterpoint Theory . http://dmitri.mycpanel.princeton.edu/files/publications/mazzola.pdf, consultado en agosto de 2017.
[Vet03] H. Vetter. Book review: The topos of music. geometric logic of concepts, theory, and performance. Musicae Scientiae, 7(2):315–321, 2003.
[Wik17] Wikipedia. Arte. https://es.wikipedia.org/wiki/Arte, consultado en agosto de 2017.
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
1. Introducción
Con el artículo de este mes queremos debatir una cuestión que aparece con frecuencia cuando un observador escéptico oye hablar de las relaciones entre las matemáticas y la música, y esa cuestión es sencillamente la de si esas relaciones son reales. En otras palabras,¿hay de verdad matemáticas en la música? ¿O no será que estamos forzando la existencia de esa relación? ¿En qué sentido hay matemáticas en la música? La respuesta a esto vendrá dada por la definición de matemáticas que estemos usando. Vamos a explorar un poco más en su definición para poder dilucidar esta cuestión.
En su famoso libro Las matemáticas: contenidos, métodos y significado Aleksandrov et al. [AKL12] dan tres rasgos característicos de las matemáticas, a saber: abstracción, demostraciones y aplicaciones. Cualquier persona que haya tenido un mínimo contacto con las matemáticas convendrá en que esos tres rasgos forman parte de la esencia de las matemáticas. Un matemático profesional o en general un científico podrá añadir más.
No hay duda de que la abstracción está en cada pliegue de las matemáticas. Las matemáticas operan con objetos (números, funciones, objetos geométricos) sin preocupación alguna sobre su significado real. Las aplicaciones pondrán nombre a esos objetos abstractos cuando sea menester. Los matemáticos examinan propiedades de objetos en apariencia dispares e identifican propiedades comunes a ellos, a partir de las cuales crean otros objetos más abstractos. Así, por ejemplo, es fácil imaginar como surgieron los números naturales ℕ. Sería probablemente a partir de la abstracción del cardinal de colecciones de objetos cotidianos, fuesen un rebaño de ovejas o los dedos de la mano. Tras el descubrimiento de los números naturales vendría las operaciones de suma y resta, y con ellas, inevitablemente, el descubrimiento de los números enteros ℤ, como extensión natural para contener los resultados de ciertas operaciones de resta, las que dan números negativos. La división de números enteros debió conducir a los números racionales ℚ, como conjunto que contendría a todos los resultados posibles de las divisiones en ℤ. Hasta aquí tendríamos todos los conjuntos de números que nos permitirían operar con cantidades discretas. Si surgiese la necesidad de operar con cantidades continuas, entonces habría que construir un conjunto adecuado y ese el de los números reales ℝ (y aquí ya estamos hablando de conjuntos cuya construcción es compleja). Si aún deseásemos abstraer aun más, podríamos ampliar los números reales de modo que contuviese a todas las raíces de los polinomios de coeficientes reales; habríamos topado con los números complejos ℂ. Estos pueden incluirse en conjuntos más abstractos tales como cuaterniones. Este es un típico proceso de abstracción de las matemáticas.
La abstracción existe en otras ciencias, desde la física a la biología. Por ejemplo, piénsese en los esfuerzos de la física por dar una teoría unificada de las fuerzas en el universo. Sin embargo, en las matemáticas la abstracción tiene características distintivas. Las matemáticas normalmente prescinden de todas las propiedades de un objeto salvo sus relaciones cuantitativas y sus formas espaciales. Dicha abstracción ocurre en un proceso gradual de lo más concreto hacia lo más general, como hemos mostrado en el ejemplo anterior con los distintos conjuntos de números. Además, las matemáticas no se mueven de ese mundo de abstracción. Mientras que un físico u otro científico comprueba sus teorías mediante experimentos, esto es, volviendo al mundo sensible, el matemático comprueba la veracidad de las teorías únicamente a través de la argumentación lógica y la computación. Ciertamente, muchos problemas de gran abstracción matemática se han originado en problemas prácticos. Estos han servido de inspiración, pero una vez que han sido formulados matemáticamente en términos abstractos, su origen se ha olvidado.
La siguiente característica son las demostraciones, el rigor lógico, en suma. Las demostraciones matemáticas son cadenas de razonamientos lógicamente válidos que enlazan las hipótesis con la tesis o conclusión. Esos razonamientos tienen que ser impoluto, escrupulosamente rigurosos, y como dice Aleksandrov y sus coautores, tiene que ser incontestable y completamente convincente por cualquiera que lo entienda (página 3 de [AKL12]). Ese rigor tiene sus límites y ha evolucionado mucho a lo largo de la historia. El rigor tal y como lo entendemos modernamente se empezó a establecer a finales del siglo XIX, como ya hemos mencionado, con los esfuerzos de matemáticos como Cauchy, Riemann, Cantor, Dedekind y otros. Hasta entonces el concepto de “prueba” era relativo. A veces una prueba se reducía a una explicación convincente pero no rigurosa, incluso podía ser una explicación literaria. La notación también era un problema; no era tan concisa y potente como lo es hoy en día y con frecuencia había problemas de ambigüedad. En otras ocasiones se encontraban en las pruebas misticismo o razonamientos religiosos o filosóficos. Incluso hoy en día el concepto de demostración es relativo según el lector a quien esté dirigida. Una demostración de un teorema destinada a ser publicada en una revista de investigación no es lo mismo que una demostración que se explica a un estudiante de bachillerato. El nivel de rigor varía así como la retórica con que se transmite. La escritura de una demostración es un tema importante en la enseñanza de las matemáticas.
La última característica de las matemáticas es su inmenso y asombroso abanico de aplicaciones. Las matemáticas las usamos constantemente en nuestra vida cotidiana. Medimos el tiempo, hacemos estimaciones de cantidades, calculamos valores medios para tomar decisiones, comprobamos la cuenta de la compra, evaluamos probabilidades, interpretamos estadísticas, entre otras. Y todo esto es sin apenas darnos cuenta; diríamos que son las matemáticas inconscientes. Las matemáticas son el fundamento de la tecnología en su sentido más amplio. El reinado de las matemáticas se ha extendido aun más con el advenimiento del ordenador. Se ha añadido una capa más de significado a las matemáticas y esta es la de computacional. Ya no solo se quiere resolver un problema, sino que se quiere dar una solución que sea computable y en muchos casos programable. Las matemáticas tienen una formidable capacidad para modelizar fenómenos de la naturaleza, desde modelos climáticos a modelos atómicos, las matemáticas aparecen como herramienta fundamental. En las últimas décadas las matemáticas han empezado a modelizar fenómenos típicos de disciplinas de letras y artes. Así, se habla de lingüística computacional, de teoría computacional de la música, por poner dos ejemplos sobresalientes.
A las tres características de la matemática añadiría una más: su capacidad de belleza. Sabemos que esto puedo sonar extraño, incluso algo frívolo, pero nada más lejos de la realidad. Y en unas notas sobre didáctica de la matemática es obligado hablar de ello, pues esa belleza que poseen las matemáticas puede transmitirse y, lo que es mejor, puede ser un eficaz medio de enseñanza. Es inevitable en este punto no citar a Bertrand Russell [Rus19] (nuestra traducción):
Mathematics, rightly viewed, possesses not only truth, but supreme beauty, a beauty cold and austere, like that of sculpture, without appeal to any part of our weaker nature, without the gorgeous trappings of painting or music, yet sublimely pure, and capable of a stern perfection such as only the greatest art can show. The true spirit of delight, the exaltation, the sense of being more than Man, which is the touchstone of the highest excellence, is to be found in mathematics as surely as poetry.
[Las matemáticas, cuando se ven correctamente, no solo poseen verdad, sino belleza suprema, una belleza fría y austera, como la de una escultura, sin los ropajes preciosos de la música, y aun sublimemente pura, y capaz de una severa perfección solo como un arte grande puede mostrar. El verdadero espíritu del deleite, la exaltación, el sentido de ser más que el Hombre, que es la piedra de toque de la más alta excelencia, se encuentra en las matemáticas tanto como en la poesía.]
Nosotros no concebimos la comprensión no ya artística, sino científica sin la mediación de la belleza. La experiencia estética interior descubre caminos a la comprensión que de otra manera pasarían completamente inadvertidos o a los cuales arribaría dando un largo y penoso rodeo. La experiencia estética es como un fogonazo súbito que nos alumbra senderos ocultos conducentes a tierras ignotas. En realidad, no sabemos que hay al final del camino, pero hace tiempo que comprendimos que es el tránsito por el camino lo importante. Hay belleza en toda construcción que muestre unidad orgánica, coherencia formal, afán de indagación, visión profunda y original y, sobre todo, autenticidad. Y esto se puede encontrar en la novena sinfonía de Beethoven o en teoremas de la teoría de números. En matemáticas esa belleza se encuentra en sus resultados y en sus métodos. La fórmula de Euler, eπi + 1 = 0 es un resultado de gran belleza por su concisión y profundidad. Otra fuente de belleza son las demostraciones. Cuando una demostración usa un número mínimo de hipótesis, es sorprendentemente sucinta, obtiene un resultado a partir de resultados aparentemente no relacionados, entonces seguramente nos hallamos ante una prueba bella.
Volvamos a la pregunta inicial: ¿son reales las matemáticas que vemos en la música? La respuesta es, a la luz de la definición anterior, que sí lo son. La música proporciona objetos que comparten varias propiedades y que permiten a las matemáticas realizar su ejercicio de abstracción. De hecho, en muchas ocasiones es posible aplicar teorías matemáticas ya consolidadas a la música. Por ejemplo, como vamos a ver en el artículo de este mes, se puede analizar una pieza musical usando aritmética modular y operaciones geométricas (transposiciones e inversiones). El rigor se emplea de una manera más limitada en la teoría matemática de la música, principalmente para probar teoremas. Las aplicaciones, sin embargo, son numerosas, sobre todo para modelizar la música y para su tratamiento computacional.
2. Aritmética modular y transposiciones e inversiones
2.1. Aritmética modular
El uso de la aritmética modular tiene que ver con el principio de equivalencia de la octava. Este principio establece que dos notas que están separadas por una octava perfecta se perciben como más cercanas que cuando están separadas por cualquier otro intervalo (distinto del unísono). Dos notas a una octava de distancia tienen una proporción de sus frecuencias de 2:1, tomando el cociente entre la nota más aguda y la más grave. Cuando se tocan dos notas en octava la cantidad de armónicos comunes entre ambas notas es muy alto; esto podría ser una de las razones por las que este fenómeno ocurre. Sin embargo, se sabe que es un fenómeno cultural, aprendido. Los sumerios, por ejemplo, no tenían ni siquiera una palabra para el concepto de octava ni del estudio de sus escritos sobre teoría musical para deducirse su existencia o uso. En otras culturas se encuentra la palabra octava, pero no con el sentido que se le da en la música occidental, en el sentido de equivalencia de notas; en esas culturas está más asociado al concepto de tesitura. Hay estudios que han examinado la cuestión en primates y bebés y parece que hay una cierta base biológica, pero está lejos de entenderse el fenómeno por el momento; véase [DL84, Deu99] para más información. En ciertos sistemas musicales, como el occidental, el principio de equivalencia de la octava hace que las notas separadas por una octava se consideran como la misma.
La aritmética modular es un tipo de aritmética que es adecuada para describir una aritmética circular. El ejemplo clásico que se suele dar es el de la hora en el reloj. Las horas están definidas desde las cero horas, la media noche, hasta las 11 horas, una hora antes del mediodía. A partir de ahí se repite el mismo ciclo. Como el día está compuesto de dos periodos de horas, añadimos la etiqueta de “por la mañana” si es el primer periodo o “por la tarde” si es el segundo periodo. Pero la idea es la misma: volvemos al punto de partida una vez que hemos recorrido un tramo de 12 horas.
¿Cómo formalizamos esto en matemáticas? ¿Cómo introducimos abstracción aquí? ¿Cómo aplicamos estas ideas a la música? Empezamos considerando ℤ, el conjunto de los números enteros, como conjunto de partida. ¿Por qué ℤ y no, por ejemplo, ℕ, los números naturales? La razón es que no siempre recorreremos en sentido positivo el conjunto; a veces, lo recorreremos en sentido negativo y necesitaremos contemplar valores negativos. Siguiendo con la abstracción, en el caso del reloj el periodo era 12, pero en general será cualquier número natural no negativo, pongamos n. Entonces diremos que dos números a,b son equivalentes si puedo pasar de uno a otro dando saltos del tamaño del periodo n. El número n se llama módulo. En términos matemáticos diríamos que a y b son congruentes y lo definiríamos diciendo que a es congruente con b si existe un entero k tal que
a - b = k ⋅ n
Si a y b son congruentes módulo n, se escribe a ≡ b mod n.
Por ejemplo, si tomamos n = 2, entonces todos los números enteros pares son congruentes entre sí. En efecto, si a,b son dos números pares, entonces se pueden escribir como a = 2k1 y b = 2k2, para ciertos k1,k2. Su diferencia será a - b = 2(k1 - k2), que muestra que son congruentes. De modo similar, se puede ver que todos los números impares son congruentes entre sí. Si n = 3, entonces todos los números de la forma 3k + 1, con k un número entero, son congruentes entre sí. Y de modo similar, lo serán los de la forma 3k entre sí, y los de la forma 3k + 2 entre sí. Si n es un módulo arbitrario y a un número entero cualquiera, para saber cuál es el número congruente más pequeño con a basta hacer la división entera de a entre n. De esta división tendremos la relación a = c ⋅ n + r, donde c es el cociente de la división y r el resto. De esa expresión se sigue que a y r son congruentes módulo n. Como el resto r siempre cumple que mayor o igual que 0 y menor o igual que n - 1, r es el menor entero positivo congruente con a. Hemos probado que el resto de la división entera de a por el módulo es congruente con a.
En música la aritmética modular que interesa es la de módulo 12, es decir, cuando n = 12. ¿Por qué es esto así? Sencillamente, porque la octava en la música occidental se divide en 12 semitonos iguales.
La aritmética modular además redefine ligeramente las operaciones aritméticas habituales. Si estamos en aritmética módulo 12, entonces 7 + 6 no son 13, sino 1, porque 13 ≡ 1 mod 12. Así todos los resultados de operaciones aritméticas se reducen a su correspondiente valor módulo entre 0 y 12. Por ejemplo, 7 ⋅ 5 mod 12 es 11 porque 35 - 11 = 2 ⋅ 12.
La aritmética módulo 12 en música nos permite centrarnos en los tonos en particular sin tener que considerar en que octava aparecen. Esto es muy útil para el análisis armónico y orquestal. Por ejemplo, en el análisis de obras orquestales nos fijamos en las notas que aparecen en un cierto compás, pero no dónde aparecen ni en qué instrumentos están distribuidas. Un acorde de do mayor tendrá las notas do, mi y sol, aunque estas puedan asignarse a una gran cantidad de combinación de instrumentos. Para el análisis de la textura o de la orquestación es relevante qué instrumentos tocan esas notas, pero no en cambio para el análisis armónico o melódico. Usar la aritmética modular para el análisis armónico facilita el mismo porque implícitamente usa el principio de la equivalencia de la octava.
3. Transposiciones e inversiones
Fijemos en todo lo que sigue el módulo en 12, según justificamos antes. Dada una nota x, una transposición Tm(x), donde m es un entero fijo, es la nota
Tm(x) = x + m mod12
Esto, como se ve inmediatamente, no es más que añadir una nota fija de valor m y aplicar la equivalencia de la octava. La idea de la transposición en la aritmética refleja exactamente la idea de la transposición en música. Si a cada nota de una melodía se le añade 12, se ha transpuesto una octava; si se le añade 7, entonces la transposición es una quinta justa (7 semitonos es una quinta), y así de modo similar con cualquier otro valor que se añada.
La otra operación que nos interesa es la inversión. En música invertir un intervalo da otro, que es su complementario respecto a la octava. La inversión de una quinta es una cuarta; la de una tercera, una sexta; la de una segunda, una séptima; y así con el resto de los intervalos. No obstante, también es interesante invertir respecto a una nota fija, como cuando se invierte un acorde. La primera inversión de un acorde de do mayor en posición fundamental es una inversión respecto a la tercera nota, el sol. La función que capta la esencia de la inversión musical es la función inversión, definida por
Im(x) = - x+ m mod12
Si m = 12, la inversión es respecto a la octava y entonces estamos ante las inversiones interválicas normales (unísono va a octava, segunda a séptima y así sucesivamente). Cuando m toma otros valores, la inversión es respecto a la nota que representa m.
Para fijar ideas, supongamos las siguientes asignaciones de notas y números:
do = 0, re♭ = 1, re = 2, mi♭ = 3, mi = 4, fa = 5, fa# = 6
sol = 7, sol# = 8, la = 9, la# = 10, si = 11
El acorde de do mayor corresponde al conjunto . Una transposición por una quinta es
T7() = = =
donde se ha aplicado el módulo 12. Esto nos ha llevado el acorde de do mayor al de sol mayor; véase la figura 1.
Figura 1: Transposición del acorde de do mayor
Calculemos la inversión I7 de este mismo acorde:
I7() = = =
Las notas obtenidas corresponden al acorde de do menor. En efecto, el acorde de do mayor está compuesto por una tercera mayor seguida de una tercera menor. La función inversión I7 intercambia estos dos intervalos en el acorde y entonces se produce un acorde menor; véase la figura 2.
Figura 2: Inversión del acorde de do mayor respecto a sol
En general, la inversión Im produce la reflexión de las notas con respecto al eje que pasa por la nota m. Por ejemplo, si la nota x está a k semitonos de distancia por debajo de m, Im(x) estará a k semitonos por encima de x. Si la nota x está a k semitonos por encima de m, la situación es análoga.
4. La fuga número 6 en re menor de El clave bien temperado, libro I, de Johann Sebastian Bach
Para ilustrar el uso de las transposiciones e inversiones en la música, y cómo estas son presencias vivas de las matemáticas en la música, vamos a analizar la fuga número 6 en re menor de El clave bien temperado, libro I, de Johann Sebastian Bach. La partitura de la fuga se encuentra al final del artículo (ha sido tomada de la página Musecore: https://musescore.com/classicman/scores/298826). Para este análisis nos hemos apoyado en los excelentes trabajos de José Rodríguez Alvira [Alv17] y Tim Smith [Smi17] así como las notas del curso sobre matemáticas y música de Thomas Fiore [Fio17].
La fuga es a tres voces y comienza con la exposición del sujeto; véase la figura 3 (S significa sujeto). El sujeto está dividido en tres partes, a, b1 y b2. La parte a o cabeza es una subida por grados conjuntos hasta una cuarta seguida de un tercera menor descendente; la figuración es toda en corcheas. El motivo b, divido en dos partes, primero tiene una caída de una tercera menor seguida por dos grados conjuntos, todos dados en semicorcheas. El motivo b2 viene dado en negras, con un salto y un grado conjunto.
Figura 3: Sujeto de la fuga
En el tercer compás aparece de nuevo el sujeto, ahora empezando en la dominante, en la. El contrasujeto CS está divido en dos partes, CSa y CSb. Mientras, la primera voz expone el contrasujeto.
Figura 4: Contrasujeto de la fuga
La primera parte del contrasujeto, CSa, es una inversión de a del sujeto, con una figuración de semicorcheas, que se puede interpretar como una disminución rítmica. La segunda parte, CSb, es una secuencia de b1 del sujeto, transpuesta en distintas notas. Obsérvese que con estas repeticiones de los motivos Bach crea una obra que tiene una gran unidad formal. Para ver cómo se distribuyen los motivos, recomendamos al lector que vea la excelente animación de la fuga hecha por Tim Smith [Smi17].
Figura 5: Descomposición del contrasujeto en submotivos
En el compás 6 de la fuga entra la tercera voz, que expone de nuevo el sujeto sin transposición alguna, tal y como lo hizo la voz uno en el compás 1.
Figura 6: Entrada de la tercera voz
En el compás 8 empieza el primer episodio, que es donde se desarrolla el material melódico presentado hasta en forma de sujetos y contrasujetos. Ahora Bach cogerá distintas partes de los motivos melódicos y jugará con ellos por medio de transposiciones, inversiones y otros mecanismos. El sujeto se expone en el soprano sobre la nota mi, pero ahora el intervalo final es de una tercera disminuida. El motivo b1 se repite con distintas transposiciones. En la segunda voz, el motivo b se repite entero, creando así una especie de eco entre b y b1. Por su parte el contrasujeto sigue en el bajo, donde se oye el contrasujeto CSb repetirse en forma de secuencia (que no es más que nuevas transposiciones). En el compás 12 la voz alto expone el sujeto con una inversión.
Figura 7: El primer episodio de la fuga
Tras el episodio, viene el stretto. Es un recurso imitativo en que los diferentes sujetos y contrasujetos, con sus respectivos motivos, se solapan entre ellos. Esto da más densidad rítmica y textural a la fuga. El stretto suele ser un pasaje de clímax en la fuga. En esta fuga oímos el tema en la voz de soprano, que es respondida en el compás siguiente por el bajo. Tras la respuesta el bajo sigue exponiendo el sujeto en forma invertida. La voz interior también usa el motivo a como respuesta a la voz del soprano, pero luego se pasa bruscamente al motivo b1, que aparece también invertido. Esta sección acaba con una cadencia a la menor.
Figura 8: El stretto de la fuga
Tras el stretto viene un segundo episodio, que comienza en el compás 36 y llega hasta el final de la fuga. El contrasujeto CSa se expone con múltiples transposiciones mientras que en las voces alto y bajo se toca el motivo a del sujeto a una distancia de tercera entre cada voz.
Figura 9: El segundo episodio de la fuga
Como podemos ver tras este sucinto análisis, la presencia de transposiciones e inversiones en esta fuga es constante. Interpretar la estructura de la fuga en términos matemáticos da otra visión a la escucha de la fuga. Sin duda, enriquece su escucha porque refuerza el entendimiento de la estructura de la fuga. A la pregunta, hecha con frecuencia, de si Bach tenía en mente estas estructuras matemáticas cuando componía la fuga, la respuesta más probable es que no. El uso de esas operaciones matemáticas sobre los motivos musicales tienen fines estrictamente musicales, relacionados con dotar a la obra de estructura y expresividad, pero no la de satisfacer ninguna pretensión matemática o formalista. Podemos percibir todas esas transposiciones e inversiones, pero mucho antes que eso está la expresividad y la musicalidad de la fuga.
Figura 10: La fuga número 6 en re menor de El clave bien temperado, libro I, de Johann Sebastian Bach
Bibliografía
[AKL12] A.D. Aleksandrov, A.N. Kolmogorov, and M.A. Lavrentiev. Mathematics: Its Content, Methods and Meaning. Dover Publications, 2012. Primera edición en 1956.
[Alv17] José Rodríguez Alvira. Analysis of bach’s fugue bwv 851 in d minor (wtc i). https://www.teoria.com/en/articles/2017/BWV851/index.php, accedido en mayo de 2017.
[Deu99] Diana Deutsch. The psychology of music. San Diego: Academic Press, 1999. Intervals, Scales, and Tuning, capítulo escrito por Burns, Edward M.
[DL84] Armand F. Demany L. The perceptual reality of tone chroma in early infancy. Journal of Acoustical Society of America, 76:57–66, 1984.
[Fio17] Thomas Fiore. Mathematics and music. http://www-personal.umd.umich.edu/~tmfiore/1/musictotal.pdf, accedido en mayo de 2017.
[Rus19] Bertrand Russell. ”The Study of Mathematics”. Mysticism and Logic: And Other Essays. Longman, 1919.
[Smi17] Tim Smith. The canons and fugues of j. s. bach. http://bach.nau.edu/clavier/nature/fugues/Fugue06.html, accedido en mayo de 2017.
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
1. Introducción
En la anterior columna [Góm17] empezamos por el estudio de los fractales desde un punto de vista matemático. Esbozamos una breve historia, que, como vimos, no empezaba en Mandelbrot, sino mucho antes, y proporcionamos al lector los ejemplos más notables de conjuntos fractales, el triángulo de Serpienski, el conjunto de Cantor, la curva de Koch y el conjunto de Julia. Ofrecimos, asimismo, una clasificación general de los fractales (por reglas recursivas, iteraciones de funciones, atractores, sistemas L y fractales aleatorios). Por último, definimos formalmente los fractales y calculamos la dimensión de Haussdorf para los ejemplos tratados anteriormente. En esta columna vamos a ver las aplicaciones a la música de los fractales. Nos centraremos primero en ejemplos musicales en que la autosemejanza, la característica más sobresaliente de los fractales, se usa como mecanismo compositivo. A continuación, examinaremos un programa para transformar las estructuras fractales en material musical. También discutiremos el papel que juegan los fractales en la composición musical y cuál es el papel del compositor.
2. Autosemejanza musical
Como vimos en la anterior columna, los fractales se caracterizan por la autosemejanza a cualquier escala. Se ha denominado música fractal a aquella que exhibe un cierto grado de autosemejanza. La autosemejanza infinita, tal cual ocurre en los objetos matemáticos, no es posible en el dominio de la música. Nuestros sistema perceptual tiene unos límites para detectar altura de notas y duraciones. Sin embargo, si hay presencia de autosemejanza a varios niveles, el cerebro es capaz de percibirla. Déjenos el lector darle un ejemplo de este tipo de música fractal, ejemplos que se pueden encontrar no solo en compositores modernos o de vanguardia sino en compositores netamente clásicos. Harlan J. Brothers, en un artículo publicado en la revista Fractals [Bro09] analiza las seis suites para violonchelo solo y encuentra que hay estructuras fractales en ella (de nuevo a ciertos niveles, no en todos los niveles). Para ilustrar el ejemplo, vamos a seguir la presentación Ivars Peterson [Pet17], autor del blog de divulgación The mathematical tourist. Si examinamos los primeros compases de la bourrée de la suite número 3, se observa una fuerte autosemejanza. La figura 1 muestra la partitura de esos compases.
Figura 1: primeros compases de la bourrée de la suite número 3 para violonchelo solo, de Johan Sebastian Bach (figura tomada de [Pet17])
Se han anotado los motivos que componen las frases de la pieza (m1,m2,m3 y sus variaciones). El primer motivo m1 está formado por dos corcheas y una negra; el segundo, también, pero las dos primeras corcheas están en legato. El tercer motivo lo componen dos negras, dos corcheas y una negra. El motivo m3 es el doble de largo que los dos primeros. Los tres motivos forman una frase, s1. A su vez los siguientes motivos forman una frase s2, que es seguida por una frase más larga, s3, que dura el doble que las anteriores. El patrón que se revela es AAB, donde B tiene el doble de longitud que A. Si se analiza la bourrée entera (descartando las repeticiones), entonces la estructura que se percibe es igual a la de los cuatro primeros niveles del conjunto de Cantor; esos cuatro niveles se muestran en la figura 2.
Figura 2: Los cuatro primeros niveles del conjunto de Cantor (figura tomada de [Pet17])
Otras obras de Bach muestran esta autosemejanza, como por ejemplo la coral del final de El arte de la fuga BWV 1080. Véase el vídeo de youtube https://www.youtube.com/watch?v=XXQY2dS1Srk, a partir del minuto 1:23:05 para una versión con partitura, y en la que se puede observar cómo los motivos aparecen repetidos y transformados varias veces con cierta estructura fractal.
Aunque Bach es un compositor en cuya obra se pueden encontrar estructuras fractales, compositores anteriores a él ya habían usado la idea de la autosemejanza como técnica compositivo. Steynberg, en su tesis de maestría [Ste14], estudia y analiza críticamente varios ejemplos de compositores que usaron estructuras fractales. En la figura 3 tenemos los primeros compases del Kyrie de la Missa Prolationum, de Johannes Ockeghem, para cuatro voces, soprano, contratenor, tenor y bajo. La voz soprano y contratenor tienen la misma melodía, pero el tenor la canta con duraciones de notas más largas. El bajo y el tenor tienen líneas melódicas diferentes, donde el bajo tiene notas más largas que el tenor. Sin embargo, cuando el bajo canta la palabra eleison vuelve a la figuración rítmica del tenor. Todas estas relaciones entre las duraciones producen una autosimilitud rítmica que se puede calificar de fractal.
Figura 3: Kyrie de la Missa Prolationum, de Johannes Ockeghem (figura tomada de [Ste14])
Tom Johson, a quien dedicamos la serie Otras armonías son posibles [Góm15] por su libro Other harmonies are possible [Joh14], ha usa la autosemejanza en el dominio rítmico. En su serie Counting Duets tiene una pieza 1 2 3 en que los cantantes tienen que contar en voz alta. Las entradas de cada voz están pensadas de tal manera que se producen efectos de autosimilitud rítmica; véase la partitura en la figura 4 abajo.
Figura 4: 1 2 3, de la serie Counting duets, de Tom Johnson (figura tomada de [Ste14])
En la tesis de Steynberg se pueden encontrar más ejemplos de compositores que han usado estructuras fractales y análisis detallados de las mismas. Steynberg analiza entre otras la música de Beethoven, Ligeti, Josquin de Prez y Arvo Pärt.
3. Composiciones fractales más avanzadas
Quitando la idea de la autosemejanza, en general la música fractal está compuesta tomando como idea compositiva principal una o varias características de los fractales. Por ello, es difícil dar unas técnicas generales de composición fractal. La verdadera imaginación musical surge de encontrar la inspiración en los fractales. FracMus [DJ01] es un programa para generar material musical de tipo fractal escrito por el pianista Gustavo Díaz-Jérez. Decimos material musical de tipo fractal porque, acertada y lúcidamente, en la página web del programa, el propio Gustavo Díaz-Jérez, advierte que el programa es una herramienta y que nunca podrá sustituir al compositor y su inspiración musical. En sus palabras:
A word of caution: YOU are the composer, FractMus will create no masterpiece for you, nor was it designed for that. Think of it as a tool that gives you raw material that you can later use in your compositions.
Para ilustrar cómo se pueden aplicar las características de los fractales a la composición vamos a examinar unos cuantos algoritmos de FractMus. El primer algoritmo de FractMus es la sucesión de Morse-Thue. Es una sucesión binaria infinita con una fuerte autosemejanza. Para generarla, primero se toma el 0; a continuación, se duplica la longitud de la sucesión anterior y se rellena con su complementario (tomar el complementario es intercambiar ceros por unos y viceversa). Así pues, el siguiente término sería 01, el siguiente 0110. Los primeros términos de esta sucesión son:
0,01,0110,01101001,0110100110010110, 01101001100101101001011001101001, ...
Esta sucesión es claramente aperiódica y, sin embargo, es autosemejante. Si se eliminan los términos pares de cada término de la sucesión, se obtiene la sucesión original:
¿Cómo se pasa esta sucesión, que solo toma dos valores, 0 y 1, a una melodía que toma valores en la escala cromática de 12 notas? Y es aquí donde reside el ingenio del compositor para transformar el material dado, en bruto y sin pulir, en una idea musical. Díaz-Jérez propone un método que sigue los siguientes pasos (llamemos an a la sucesión de Morse-Thue):
Se elige un número c llamado el multiplicador. Cada término an se multiplica por c.
Se elige una base d y se calcula la expresión de c ⋅ an en dicha base.
A continuación se suman los dígitos de esa expresión en base 10. Este último número es el número de semitonos desde la nota anterior.
Típicamente se elige una nota inicial y se procede con el algoritmo anterior para generar el resto de las notas. Se puede aplicar un procedimiento similar para obtener los valores de otros parámetros musicales como las duraciones, las articulaciones o la textura. También es habitual introducir algún tipo de regla para que la melodía suba y baje; de lo contrario, si los términos se tomaran siempre positivos, tendríamos melodías siempre ascendentes. Díaz-Jérez compuso un canon usando la sucesión de Morse-Thue; se puede ver la partitura en la figura 5 más abajo. En el vídeo https://www.youtube.com/watch?v=6VZq7EurckI se puede escuchar otra sonificación de la sucesión de Morse-Thue compuesta por Steven Gilliland (a partir del minuto 1:37). La sonificación (la transformación de objetos en sonido) ya había sido empleada antes de la invención de los fractales, y en particular en matemáticas. Xenakis, en su libro Formalized Music: Thought and Mathematics in Composition [Xen01], desarrolla toda una teoría al respecto y da múltiples ejemplos a partir de sus propias obras; nosotros dedicamos una serie al análisis de ese libro [Góm10].
Como apunta Díaz-Jérez, algunas combinaciones de multiplicadores y bases dan melodías terriblemente aburridas, mientras que otras proporcionan melodías interesantes. El trabajo del compositor es entonces seleccionar esas melodías acorde a su criterio artístico. Las melodías fractales generadas por estos algoritmos, en general, carecerán de las características habituales de las melodías tonales. Habrá ausencia de propincuidad (alta frecuencia de tonos conjuntos), repetición y finalidad (intención melódica de ir a ciertos grados y en particular la finalización de la melodía); véase el libro de Radocy y Boyle [RB06] para profundizar en la definición de melodía. Sin embargo, en la partitura de abajo sí vemos algunas características formales de las melodías. Es obvio que Díaz-Jérez tomó el material proporcionado por su programa e inspirándose en él construyó su canon acorde a ciertas convenciones estilísticas, y en última instancia poniendo ese material al servicio de su concepto artístico.
Figura 5: Canon basado en la sucesión Morse-Thue compuesto por Gustavo Díaz-Jérez
Aquellos lectores interesados en profundizar en la música compuesta a través de fractales pueden consultar el libro Fractals in Music: Introductory Mathematics for Musical Analysis [Mad07]. Este libro requiere un cierto nivel técnico tanto matemático como musical.
Bibliografía
[Bro09] H. J. Brothers. Intervallic scaling in the bach cello suites. Fractals, 17(4):537–545, 2009.
[DJ01] Gustavo Díaz-Jérez. Fractmus, 2001.
[Góm10] P. Gómez. Las matemáticas en la música de Xenakis I, octubre de 2010.
[Góm15] P. Gómez. Otras armonías son posibles, febrero de 2015.
[Góm17] P. Gómez. Música fractal (I), marzo de 2017.
[Joh14] Tom Johnson. Other harmony. 75 Editions, 2014.
[Mad07] Charles Madden. Fractals in Music: Introductory Mathematics for Musical Analysis. High Art Press, 2007.
[Pet17] Ivars Peterson. A fractal in bach’s cello suite, abril de 2017.
[RB06] Rudolf E. Radocy and J. David Boyle. Psychological Foundations of Musical Behavior. Charles C Thomas, Illinois, 2006.
[Ste14] Ilse Steynberg. The applications of fractal geometry and self-similarity to art music. Master’s thesis, University of Praetoria, New Zealand, 2014.
[Xen01] Iannis Xenakis. Formalized Music: Thought and Mathematics in Composition. Number 6 in Harmonologia. Pendragon Press, Hillsdale, NY, 2001.
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
1. Introducción
Un tema que lleva tiempo pendiente en esta columna, quizás más del deseable, es el de la música fractal, tema fascinante donde los haya. Y ha llegado la hora de dedicarle una serie con la profundidad que se merece. Los artículos de los próximos meses estarán dedicados a la música fractal. Empezaremos con el del mes de marzo, que es una introducción a los fractales desde un punto de vista matemático. Esperamos dar el tono adecuado para no aburrir a nuestros lectores matemáticos y a la vez ser claros y amenos para nuestros lectores músicos. También esperamos que las conexiones entre los fractales y la composición musical despierten el interés de nuestros lectores a lo largo de esta serie de artículos. La música fractal se puede pensar como una forma de composición algorítmica. Recientemente, hicimos una serie sobre composición algorítmica (véase [Góm16]), pero no incluimos la música fractal porque, dada su entidad, consideramos que merecía una serie por sí misma. Empezaremos este artículo con una sucinta reseña histórica de los fractales; a continuación, entraremos a definir de modo intuitivo qué son y daremos varios ejemplos importantes; por último, daremos una definición más formal.
2. Historia de los fractales
El término fractal fue inventado por Benoît Mandelbrot para designar conjuntos con ciertas características de autosemejanza. Sus investigaciones sobre fractales empezaron en los años 60 (véase el artículo How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension [Man67]), pero no es hasta 1975 cuando Mandelbrot empieza a usar el término fractal. Ya en su libro Fractals: Form, Chance and Dimension [Man77] lo presenta formalmente y lo emplea con toda su potencia conceptual. El término está tomado del latín, de fractus, que significa fracturado. Más tarde escribe The fractal geometry of nature [Man83], libro que populariza los fractales definitivamente. Una primera definición, intuitiva y sencilla, es que un fractal es un conjunto de autosemejanza infinita, esto es, un conjunto que cuando se reduce o se agranda su escala el conjunto no cambia. Esta idea ya conlleva una cierta idea del infinito dentro de sí. En la figura 1 vemos un famoso fractal, el triángulo de Serpienski, que ilustra la idea de fractal. Con frecuencia los fractales se construyen mediante un proceso infinito que, sin embargo, se especifica con una serie de reglas finitas. En el caso del triángulo de Serpienski, el proceso empieza con un triángulo equilátero; se sigue dividiendo este triángulo en cuatro insertando un triángulo a escala un tercio en el centro. Esto genera cuatro triángulos y, de los nuevos triángulos, el del centro permanece tal cual está y en el resto se repite este proceso hasta el infinito. El fractal es el resultado de este proceso infinito. Los fractales definidos de esta manera están fuertemente relacionados con la recursión [Wik17c]; la recursión es la definición de un objeto en términos de sí mismo. En el caso de este fractal, la definición empieza por un objeto fijo, que es el triángulo equilátero inicial y continúa con una definición recursiva, que es que en cada paso se subdividan ciertos triángulos y se aplique el proceso de construcción otra vez.
Figura 1: El triángulo de Serpienski
La autosemejanza se puede manifestar de múltiples maneras:
Autosemejanza exacta, donde el mismo patrón o conjunto se repiten idénticamente a cualquier escala, como en el ejemplo anterior.
Autosemejanza aproximada, donde el mismo patrón o conjunto se repite aproximadamente a cualquier escala. Por aproximadamente quiere decir que el patrón puede aparecer con algún tipo de distorsión.
Autosemejanza estadística, donde los patrones se repite y lo que se preserva son ciertas medidas estadísticas.
Autosemejanza cualitativa, donde ciertas propiedades cualitativas se conservan; ejemplos de esto aparecen en los mercados y los modelos de volatilidad.
La definición técnica que dio Mandelbrot es la de que un fractal es un objeto cuya dimensión de Haussdorf no es un entero. En la siguiente sección explicaremos con detalle esta definición; es más sencillo de lo que parece y es el lenguaje matemático que aquí puede intimidar un poco al principio.
Sin embargo, aunque Mandelbrot bautizó a estos conjuntos tan peculiares, los fractales habían aparecido mucho antes en la historia de las matemáticas y más recientemente en la computación. Los fractales están fuertemente relacionados con la idea del infinito y está ya había aparecido con frecuencia en las matemáticas, por ejemplo, en las series infinitas. Las series infinitas son sumas infinitas de números. Uno pensaría a primera vista que la suma infinita de números tiene que dar infinito, pero sin embargo eso no es cierto. Por ejemplo, la suma de
que es una suma infinita da simplemente 1. Pickover [Pic09] (página 310) documenta los primeros rastros de los fractales en la obra del matemático y filósofo del siglo XVII Gottfried Leibniz, quien estudió las series infinitas. Esos rastros consisten en especulaciones sobre estructuras recursivas autosemejantes en los que se acerca mucho a la idea de dimensión fraccionaria. Crilly y sus coautores [CEJ91] localizan indicios de fractales en la obra de Durero (1471–1528), que es anterior a Leibniz. Durero tiene una construcción de pentágonos similar a la de Serpienski.
Dos siglos más tarde, a finales del siglo XIX, Cantor encontró una serie de conjuntos en la recta real, que se conocen hoy en día como conjuntos de Cantor, y que tenían propiedades muy peculiares. Con la terminología moderna, resultan ser ejemplos de estructuras fractales. Los conjuntos de Cantor se construían a partir de reglas recursivas como las del triángulo de Serpienski. Otros matemáticos, como Felix Klein y Henri Poincaré, trabajaron con conjuntos que son netamente fractales, en particular en los fractales autoinversos.
El artista Mauritus Escher tenía una fascinación por la recursividad y la autosemejanza. En la figura de abajo tenemos uno de sus grabados; en él se la idea de la autosemejanza así como la de la simetría y recubrimiento. Las figuras negras delimitan a las figuras blancas y entre las dos cubren el círculo; las figuras van reduciendo su escala según se acercan a la circunferencia.
Figura 2: Grabado de M. C. Escher con un motivo autosemejante
Otros matemáticos que trabajaron con los fractales fueron Peano, Hilbert y von Koch, quienes dieron conjuntos fractales cada vez más complejos; Haussdorf, quien generalizó el concepto de dimensión; y más modernamente Julia y Fatou, quienes extendieron las ideas fractales al plano complejo. Con la invención de los ordenadores ya era posible visualizarlos. Las visualizaciones de los fractales producen imágenes muy atractivas y sus aplicaciones han demostrado ser ubicuas (paisajes de videojuegos, compresión de imágenes, arte en sí mismo). En la feria de computación más importante, SIGGRAPH, Loren Carpenter en 1980 hizo una presentación del primer software para generar paisajes fractales. A partir de ahí se popularizaron enormemente. Véanse los libros The fractal geometry of nature [Man83] y Fractal and Chaos [CEJ91] para más información sobre la historia de los fractales. Otros libros interesantes sobre fractales son los siguientes: como un libro para profundizar más sobre fractales, véase [Fel12]; sobre la presencia de los fractales en diversos campos, véase [DeC15]; para la programación de fractales, véase el libro de Ben Trube [Tru13]; para modelos fractales del comportamiento de los mercados, véase [PP94].
3. ¿Qué son los fractales?
Los fractales aparecen en muchos contextos y se pueden generar de múltiples formas. Las más comunes caen en las siguientes categorías (que no son exhaustivas ni mucho menos; véanse [Man83, CEJ91, Wik17a] para más información):
Reglas recursivas de subdivisión. Estos fractales corresponden al tipo del triángulo de Serpienski. Se definen una serie de reglas recursivas a través de las cuales se construye el conjunto fractal.
Iteración de funciones. Una función se evalúa repetidamente en un punto inicial. La función puede ser de tipo determinista o estocástica.
Atractores. Se usan soluciones de un sistema de ecuaciones (diferencial o de otro tipo), sobre todo de ecuaciones que son muy sensibles a las condiciones iniciales.
Sistemas L. Se basan en cadenas y su generación a través de reglas de escritura. Suelen generar fractales asociados a procesos de ramificaciones.
Fractales aleatorios. Son los fractales que aparecen en procesos aleatorios tales como movimiento browniano, paisajes fractales y otros.
Vamos a empezar dando unos cuantos ejemplos de conjuntos fractales y, tras haber adquirido intuición, pasaremos a definiciones más formales.
3.1. Fractales construidos por reglas recursivas
El primer conjunto que presentamos es el conjunto de Cantor. Es un fractal que se construye recursivamente. Se toma el intervalo [0,1] de la recta real y se le quita el tercio central, (,). Nos quedan los intervalos [0,] y [,1]. A continuación, se repite el proceso en estos intervalos de manera recursiva y ad infinitum. En la figura 3 tenemos cómo resulta el conjunto de Cantor para las primeras iteraciones.
Figura 3: El conjunto de Cantor
En cada paso de la construcción del conjunto de Cantor se extrae un tercio del conjunto anterior. Por ejemplo, en el primer paso, se extrae el intervalo [,]; en el segundo, los intervalos [,] y [,]; y así sucesivamente. Si sumamos todas las longitudes de esos intervalos tenemos
Usando la fórmula clásica de la suma de progresiones geométricas, sale que la suma de estos intervalos es 1, que es un resultado que al menos a primera vista es sorprendente. Hemos quitado un conjunto infinito de puntos del intervalo [0,1] y lo que resta aun suma 1, la longitud de dicho intervalo.
El siguiente fractal que vamos a presentar es el copo de nieve de Koch. Se empieza con un triángulo equilátero, digamos de lado 1, y recursivamente se modifica cada lado como sigue:
Divídase los lados en tres segmentos de igual longitud.
Dibújese un triángulo equilátero sobre el segmento central obtenido en el paso 1 de manera que apunte hacia fuera.
Quítese el segmento central sobre el que se basa el triángulo equilátero del paso 2
En la figura 4 se puede ver a la izquierda el detalle de las reglas recursivas y a la derecha el copo de nieve de Koch.
Figura 4: El copo de nieve de Koch
El copo de nieve de Koch tiene la propiedad de que su perímetro es infinito, pero el área que encierra es finita. En efecto, llamemos Nn al número de lados del copo de nieve en el paso n. Se tiene que:
La anterior expresión es recursiva y con un poco de cálculo se puede ver que la forma explícita es Nn = 3 ⋅ 4n. Si Ln designa la longitud del lado que aparece en el copo de nieve en el paso n, entonces Ln es igual a porque la longitud se reduce a un tercio en cada paso. Por tanto, el perímetro Pn es igual a
Pn tiende a infinito cuando n tiende a infinito, pues 4∕3 es mayor que 1. De modo que la longitud del copo de nieve es infinito. Un cálculo con series infinitas prueba que, sin embargo, el área es finita e igual a ; véase [Wik17b] para los detalles de dicho cálculo (que solo requiere matemáticas de secundaria).
Esta curva también exhibe la sorprendente propiedad de que es continua en todos los puntos, pero no es diferenciable en ninguno. Probar que esto es así requiere matemáticas que van más allá del propósito de esta columna.
3.2. Fractales construidos por iteración de funciones
Hay otra gran familia de fractales, que son los que se basan en la iteración del valor de una función. Por ejemplo, si tenemos la función f(x) = + 1 y tomamos un valor inicial, digamos x0 = 1, entonces las iteraciones sucesivas de f(x) en x0 son:
f(x0) = + 1 = ;
f(2)(x0) = f(f(x0)) = f() = + 1 = ;
f(3)(x0) = f(f(2)(x0)) = f() = + 1 = ;
Para un n arbitrario la n-ésima iteración es f(n)(x0) = .
Los fractales de este tipo se desarrollan con los números complejos, de modo que las funciones son complejas y no reales. Los números complejos son números de forma x + yi, donde x,y son números reales habituales e i es la unidad imaginaria, que se define por la relación i2 = -1. El número x se llama la parte real e y la parte imaginaria. Los números complejos se pueden sumar y multiplicar. Solo hay que seguir las reglas habituales de cálculo. Si z1 = x1 + y1i y z2 = x2 + y2i son números complejos su suma y producto se calculan como sigue:
Consideremos ahora la función compleja f(z) = z2 + c, donde c = a + bi es una constante. Y consideremos también las iteraciones de f(z) en un punto inicial z0, esto es, f(z0),f(2)(z0),…,f(n)(z0). ¿A dónde tiene la iteración de f en z0 cuando n tiende a infinito? Hay varios posibles resultados, dependiendo del valor inicial:
La iteración de f se queda fija. Si z0 = 0, obviamente f(n)(z0) = c, para todo n.
La iteración de f converge a un punto al cual se acerca cada vez más; esto pasaría, por ejemplo, si hacemos que z0 = - i y c = ; de nuevo, se deja su comprobación al lector.
La iteración de f diverge, esto es, f(n)(z0) se aleja infinitamente de z0. Por ejemplo, esto ocurre si tomamos z0 = 2 + 2i y c = 1 (el lector puede comprobar esto).
También es posible que para algunos valores se produzca una serie cíclica de valores en las iteraciones.
Los casos 1 y 2 anteriores constituyen lo que llamamos el conjunto de puntos convergentes y los casos 3 y 4 el conjunto de puntos divergentes. El conjunto de Julia es el conjunto de puntos que son convergentes pero que están justo al lado de puntos divergentes; es, por así decir, la frontera entre los puntos convergentes y divergentes. El conjunto de Julia tiene naturaleza fractal como puede verse en la figura 5; este conjunto corresponde a la función z2 + c, con c = -0.8 + 0.156i.
Figura 5: El conjunto de Julia
La coloración de los píxeles (los puntos del plano) se establece en función del comportamiento de los puntos al converger o diverger. Se puede asignar un mismo color a todos los puntos del conjunto divergente o se puede asignar un color en función de la velocidad con que diverjan. Esto explica por qué en la figura 5 vemos más de un color y no dos como cabría esperar si solo asignásemos un color a cada conjunto de puntos convergentes y divergentes.
3.3. Definición matemática de fractal
Como dijimos más arriba, un fractal se puede definir como un objeto cuya dimensión de Haussdorff es fraccionaria. Analicemos esta definición con más detalle. Un punto tiene dimensión cero; una línea, dimensión uno, puesto que la podemos describir por un solo parámetro, que es la distancia desde un punto fijo. Un plano tiene dimensión dos y cualquier punto en él se puede localizar unívocamente con dos parámetros. En el espacio de tres dimensiones, alto, largo y ancho son las coordenadas que nos hacen falta para describir cualquier objeto en él. Los conjuntos de dimensiones superiores no se pueden visualizar, pero se pueden conocer y probar muchos resultados acerca de ellos.
Los conjuntos fractales que estamos considerando aquí no se acomodan de una manera tan clara en los espacios geométricos habituales. Tomemos, por ejemplo, el copo de nieve de Koch. Dado que es una curva parece que tiene dimensión uno. Sin embargo, la distancia entre dos puntos cualesquiera es infinito. Entonces, será un objeto bidimensional. Pero esta curva no rellena el espacio bidimensional en que se encuentra y, por tanto, difícilmente puede tener dimensión dos. Parece que su dimensión debe estar entre 1 y 2. Esta discusión prueba que necesitamos una definición de dimensión que dé cuenta de estos objetos que parecen estar en dimensiones no enteras. Esa definición es la llamada dimensión de Haussdorf o dimensión fractal. Para ilustrar cómo funciona nos centraremos en los fractales de construcción recursiva. Presentamos dos conceptos primero, el factor de escala f y el número de copias n. La dimensión de Haussdorf d se define como el número que cumple que
o tomando logaritmos
Calculemos unas cuantas dimensiones de los conjuntos vistos más arriba para ilustrar este concepto. En el conjunto de Cantor en cada paso tenemos un factor de escala de 1∕3 y aparecen dos copias nuevas. Entonces la dimensión es
En el número final de la dimensión se ha tomado los cuatro primeros decimales; el número exacto no es relevante.
En el caso del triángulo de Serpienski tenemos 3 copias a escala 1∕2 cada una y, por tanto, su dimensión es
un número mayor que 1 y menor que 2.
Para la curva de Koch, observamos que hay 4 copias y cada una está a escala 1∕3. Por tanto:
Como vemos, todos los números anteriores son números fraccionarios. El lector ya se habrá dado cuenta de que en el caso de los fractales construidos por reglas recursivas, con la definición dada es fácil calcular la dimensión de Haussdorf, pero que no lo es en otros tipos de fractales, como pueden ser los construidos por iteración de funciones. La definición que dio Haussdorf permite calcular esa dimensión, pero los detalles se vuelven demasiado técnicos para exponerlos aquí; de nuevo, remitimos el lector al libro de Crilly y sus coautores [CEJ91] para una exposición asequible y clara de esta cuestión.
Bibliografía
[CEJ91] A. J. Crilly, R.A. Earnshaw, and H. Jones. Fractals and Chaos. Springer-Verlag, 1991.
[DeC15] William DeCotiis. The Fractal. Editado por el autor, 2015.
[Fel12] David P. Feldman. Chaos and Fractals: An Elementary Introduction. OUP Oxford, 2012.
[Góm16] P. Gómez. Composición algorítmica, mayo de 2016.
[Man67] Benoît Mandelbrot. How long is the coast of britain? statistical self-similarity and fractional dimension. Science, 156(3775), 1967.
[Man77] Benoît Mandelbrot. Fractals: Form, Chance and Dimension. W H Freeman and Co, 1977.
[Man83] Benoît Mandelbrot. The fractal geometry of nature. Macmillan, 1983.
[Pic09] Clifford Pickover. The Math Book: From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics. Sterling, 2009.
[PP94] Edgar E. Peters and Donada Peters. Fractal Market Analysis: Applying Chaos Theory to Investment and Economics. John Wiley and Sons, 1994.
[Tru13] Ben Trube. Fractals: A Programmer’s Approach. Editado por el autor, 2013.
[Wik17a] Wikipedia. Fractals, consultada en febrero de 2017.
[Wik17b] Wikipedia. Koch snowflake, consultada en febrero de 2017.
[Wik17c] Wikipedia. Recursion algorítmica, consultada en febrero de 2017.
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
1. Introducción
Por circunstancias puramente casuales he recibido en las últimas semanas peticiones de varios lectores preguntando por referencias de libros y artículos sobre matemáticas y música. En vista de ello y para satisfacer su deseo, vamos a dedicar el artículo de este mes a hacer una recensión de algunos libros sobre matemáticas y música. Ya avisamos que, como toda recensión, tendrá un cierto grado de subjetividad y que algunos lectores encontrarán que faltan cierta referencia mientras que otros en cambio pensarán que sobran tal otra referencia. Intentaré cubrir el mayor número de aspectos del campo, lo que no es fácil, y con una profundidad razonable, lo cual sigue sin ser fácil. La lista que viene a continuación cubre desde textos de divulgación hasta textos que se pueden encontrar en cursos avanzados en la universidad.
Hemos dividido en tres secciones las referencias. Primero están los libros de divulgación, que pueden leer los lectores interesados en las relaciones entre las matemáticas y la música. Son textos que son esencialmente divulgativos y que con unos mínimos conocimientos en ambos campos son posibles de seguir y disfrutar. La segunda colección de referencias ya son libros más avanzados, tanto en extensión como en profundidad. Algunos son textos universitarios que requieren matemáticas avanzadas y teoría de la música también avanzada. Comentaremos las características más sobresalientes de cada uno. Por último, hay unas pocas referencias de libros avanzados, dirigidos a musicólogos sistemáticos y computacionales, o lectores que tengan un nivel muy alto en ambas disciplinas.
2. Libros de divulgación
2.1. La armonía es numérica
Un reciente número de la revista National Geographic consistía en un monográfico de título La armonía es numérica [AM16] redactado por Javier Arbonés y Pablo Milrud. Está deliciosamente escrito y maquetado y está compuesto de cinco capítulos. En el primero los autores explican la teoría de la afinación pitágorica con un sentido exquisito de la exposición. El segundo capítulo es una teoría del ritmo, que revisan desde una perspectiva histórica. Es muy adecuado para aquellos que quieran entender los fundamentos matemáticos del ritmo en la música occidental (que es de carácter esencialmente divisivo frente a otras músicas que son aditivas). El capítulo 3 es una revisión de la fructífera relación que hay entre geometría y composición. Los autores muestran de una manera atractiva cómo se pueden usar transformaciones geométricas para generar variación en el material musical. Se habla, pues, de traslaciones, rotaciones, inversiones y de sus equivalencias musicales. Todo ello está profusamente ilustrado con ejemplos musicales tomados de los grandes compositores, desde Bach a Messian. El cuarto capítulo está dedicado a estudiar la digitalización del sonido; es el capítulo más técnico, más informático si queréis, y es enormemente instructivo. El último capítulo se titula Matemática para componer y versa sobre las matemáticas para la composición y es básicamente una excelente exposición de la teoría dodecafónica.
2.2. The math behind the music
Harkleroad escribió un delicioso libro, no demasiado largo, de 130 páginas, titulado The math behind the music [Har06]. El autor toca varios temas, siempre con una prosa cristalina, con abundantes ejemplos musicales y con una férrea voluntad de claridad conceptual. El libro empieza con una defensa de la existencia de la relación entre las matemáticas y la música y termina con un capítulo cuyo título es Cómo no mezclar matemáticas y música, donde previene al lector sobre las relaciones forzadas o triviales entre ambos campos. En el resto de los capítulos Harkleroad estudia varios temas: la altura del sonido, en primer lugar; la teoría de la afinación; las transformaciones matemáticas del material musical (como hacían arriba Arbonés y Milrud); la teoría de grupos aplicada al tañido de campanas; la teoría de la probabilidad; y el estudio de los patrones melódicos.
2.3. La columna de Matemáticas y música de Divulgamat
Espero que el lector pueda perdonar a este humilde autor la necesidad de tener que citarse. He puesto todo mi esfuerzo y honestidad por hacer de esta columna una fuente de divulgación para las matemáticas y la música. Como puede ver el lector, en la columna de este mes casi todas las referencias están en inglés. En castellano no parece haber una tradición de estudio de estas dos disciplinas, matemáticas y música, como una unidad. Una de mis preocupaciones con esta columna ha sido la de proporcionar al lector en castellano de material de calidad para adentrarse en esa disciplina.
En las columnas de Divulgamat sobre matemáticas y música el lector puede encontrar artículos sobre los siguientes temas:
Música y geometría: la serie sobre el teorema del hexacordo [Góm10a], conjuntos de área máxima y armonía [Rap10], modelos geométricos del ritmo [Góm12a] [Góm12b].
Matemáticas y composición: la serie sobre Xenakis [Góm10b], primero compositores automáticos [Góm11a], Minimalismo y matemáticas: Clapping Music [Góm12f].
Modelización matemática de fenómenos musicales: estudio de la síncopa [Góm11d], estudio de la similitud melódica [Góm11c], amalgamas, aksaks y métricas euclídas [SG12], transformaciones rítmicas (binarizaciones y ternarizaciones) [Góm12d].
Estudio matemático de tradiciones musicales: la similitud melódica en el flamenco [Góm11b] y [GGMDB14].
Aplicaciones de las matemáticas en la música y su enseñanza: Estadística en la Musicología [Góm12e], enseñanza de las matemáticas por vía de la música [Góm12c].
Teorías matemáticas y computacionales de la música: teoría generativa de la música [Góm14b], teorías matemáticas de la armonía [Góm14a], fractales en la percusión [Góm15], música y probabilidad [Góm16a], cadenas de Markov e improvisación en el jazz [Góm16b], composición algorítmica [Góm16c].
Cognición musical: Paradojas matemáticas y musicales [Góm14c].
3. Libros para profundizar
3.1. Music and Mathematics: From Pythagoras to Fractals
Nuestro primer libro es Music and Mathematics: From Pythagoras to Fractals [FFW03], editado por John Fauvel, Raymond Flood y Robin Wilson y tienen entre sus autores a primeras plumas como Ian Stewart, por ejemplo, entre otros. El libro está dividido en cuatro partes. La primera se llama música y matemáticas a través de la historia y proporciona una visión sucinta pero suficientemente rica del asunto, todo ello con ilustraciones históricas de calidad. Se centra en dos aspectos principalmente, la afinación y el temperamento, explicados soberbiamente, y la cosmología musical, donde presenta la teoría de Kepler.
Figura 1: Music and Mathematics: From Pythagoras to Fractals
El segundo capítulo revisa la teoría matemática del sonido (el capítulo se llama las matemáticas del sonido musical). Los autores pasan revista a los principios fundamentales de la producción del sonido en tres excelentes artículos. Quizás el más llamativo es de Ian Stewart, con su estilo divertido e incisivo, heredero directo de Martin Gardner, quien explica por qué no se puede construir un fagot con trastes. El último artículo describe la teoría de la combinación de tonos y consonancia de Helmholtz y está redactado por David Fowler.
El tercer capítulo es el estudio de la estructura en música. Empieza con un capítulo sobre la geometría en la música, donde se describen las operaciones geométricas más importantes aplicadas a la música. Se analizan varios pasajes musicales en este contexto. El siguiente capítulo versa sobre el tañido de campanas con cuerdas. Como se sabe, este tipo de toque es altamente susceptible de un estudio combinatorio y la teoría de grupos tiene mucho que decir aquí. El análisis que hacen en el texto es bastante profundo y claro. El tercer capítulo es un recorrido por técnicas matemáticas de composición, donde se hace un especial énfasis en obras de Schoenberg, Boulez y Xenakis.
El último capítulo, The composer speaks, tiene más nivel conceptual. Se estudia la relación entre los microtonos y los planos proyectivos y sigue para terminar el libro la composición fractal.
3.2. Music: a Mathematical Offering
Music: a Mathematical Offering, escrito por David Benson, es uno de los mejores libros que hay disponibles ahora mismo para adentrarse a un nivel alto en esta disciplina. El libro está tan bien escrito que es posible adaptarlo desde el nivel de bachillerato hasta los últimos años de la carrera de matemáticas. Hay muchas cosas que me gustan de este libro. Como ya he dicho su escritura, en un inglés conciso pero no conceptista; con una clarísima voluntad pedagógica; con una notación matemática mínima y potente a la vez; con una visión del campo profunda y rica; y hasta diría que con un sentido del juego y del humor que hacen que su lectura sea una auténtico placer.
El libro está compuesto por nueve capítulos. En el primero Benson estudia las ondas y los armónicos. Me gusta de este capítulo que entra de lleno en los mecanismos de audición humana y esto va a ser muy útil para explicar la percepción musical más tarde. El segundo capítulo se llama teoría de Fourier y es una exposición soberbia en que alterna conceptos matemáticos fuertes (funciones de Bessel, el teorema de Fejer, las convoluciones, los coeficientes cepstrum, entre otras) con implicaciones musicales profundas. Mantiene al mínimo imprescindible las pruebas y los detalles técnicos y se centra con acierto en iluminar las relaciones entre esas matemáticas y la música.
Figura 2: Music: a Mathematical Offering
El tercer capítulo es una guía matemática de la orquesta. Benson explica con un estilo muy ágil e ilustrativo la física y las matemáticas de los instrumentos de cuerda, los instrumentos de viento y los de percusión. No se limita únicamente a los instrumentos de la tradición occidental y, por ejemplo, estudia la mbira, un tipo de arpa de pulgar de África.
En el cuarto capítulo el autor examina la teoría de la consonancia en base a fenómenos psico-acústicos. Incluye explicaciones históricas de la consonancia y, como siempre, puesto en contexto musical. Llega a adentrarse en temas tan apasionantes como los espectros artificiales.
El quinto capítulo es uno de nuestros favoritos: las escalas y el temperamento. Y lo es por el estilo con que está escrito y por la profundidad que alcanza. Benson empieza, como era de esperar, con la teoría pitagórica de la afinación y, haciendo un recorrido histórico, pasa por la entonación justa y después por todos los temperamentos posteriores. Justifica muy bien el nacimiento del temperamento igual. En el siguiente capítulo se va a los temperamentos modernos e investiga las escalas de Harry Partch y otras escalas similares, escalas con más de 12 notas o con afinaciones especiales, como las escalas de 31 tonos, las escalas de Wendy Carlos o de Bohlen-Pierce.
El capítulo ocho es un exhaustivo estudio de la síntesis del sonido. Incluye todo lo que se debe saber para estar a un básico en este campo, desde envolventes y LFO hasta polinomios de Chebychev.
El último capítulo es otro gozo intelectual y emocional. Trata sobre al simetría en música. Benson usa teoría de grupos y aritmética modular para analizar y estudiar todo tipo de ejemplos musicales, desde los patrones en el arpa de Nzara, el tañido de campanas, la modulación por quintas, el dodecafonismo, entre otros.
3.3. Teoría generativa de la música
Un libro imprescindible para los lectores con ansia de profundización es A Generative Theory of Tonal Music, de Lerdahl y Jackendoff [LJ83]. Este libro está inspirado a su vez en la teoría generativa de la lingüística de Noam Chomsky. Estos autores se preguntaron si era posible construir una gramática musical que explicase el fenómeno de la escucha musical tal y como había hecho Chomsky con el lenguaje.
Figura 3: A Generative Theory of Tonal Music
Lerdahl y Jackendoff estudiaron la música desde un punto de vista de la cognición musical (tienen en cuenta muchos principios de esta disciplina) y con un afán de encontrar elementos estructurales en la música (ellos solo estudiaron la música tonal occidental). En la columna de julio de 2014 y siguientes [Góm14b], estudiamos en profundidad este libro. Allí decíamos que estos autores propone una estructura jerárquica compuesta por cuatro partes y que forma la base sobre la cual proporcionarán una descripción estructural de una pieza musical. Esas cuatro jerarquías son:
Estructura de agrupación. Expresa la segmentación jerárquica de la pieza en términos de motivos, frases y períodos.
Estructura métrica. Expresa los fenómenos métricos, esto es, los relacionados con la alternancia de tiempos fuertes y débiles.
Reducción interválica-temporal. Asigna una jerarquía a los tonos de una pieza en función de la estructura de agrupación y métrica.
Reducción de prolongación. Más abstracta que las anteriores, asigna a los tonos una jerarquía que expresa la dialéctica tensión-relajación en los aspectos armónicos y melódicos.
La lectura de este libro requiere un buen conocimiento del repertorio de la música clásica occidental, pues el libro está trufado por doquier de ejemplos musicales muy detallados.
3.4. Musimathics
Este libro de dos volúmenes está escrito por el músico, compositor, ingeniero de sistemas y multimedia Gareth Loy. Su libro, Musimathics [Loy11], está en la estela del libro de Benson. El libro de Loy contiene 10 capítulos, escritos con intensidad y profundidad. Empieza con un primer capítulo en que presenta conceptos musicales básicos, desde tono hasta timbre pasando por ritmo o escala. Tras esto entra directamente en la teoría de la afinación y cubre desde la afinación pitagórica hasta el temperamento igual y algunas afinaciones no tradicionales. El tercer y cuarto capítulo son una revisión bastante completa de la física del sonido. En el quinto, Loy estudia los fundamentos psicoacústicos del sonido. Los capítulos siete y ocho son más técnicos y en ellos se estudia acústica avanzada. Como se puede apreciar, está describiendo el fenómeno musical desde distintos puntos de vista antes de entrar en los capítulos finales, donde hace uso de todo lo anterior. El capítulo nueve versa sobre composición y métodos matemáticos. Se pasan revista principalmente a métodos estocásticos de composición, sobre todo a cadenas de Markov, pero también se tocan otros temas interesantes, como la teoría de la información y la representación del conocimiento musical. El volumen dos está dedicado principalmente a teoría de la señal y tiene menos interés para nosotros.
3.5. From Polychords to Pólya: Adventures in Musical Combinatorics
Michael Keith es un experto en combinatoria, ingeniero de software y además un escritor especializado en la escritura con restricciones al estilo de Oulipo y otros. En el año 91 se autopublicó el libro From Polychords to Pólya: Adventures in Musical Combinatorics [Kei91], que es una delicia en que explora las relaciones entre la combinatoria y la música. En este libro aparecen conceptos como los coeficientes binomiales, el triángulo de Pascal, la sucesión de Fibonacci y el teorema de enumeración de Pólya, con las cuales Keith procede a la enumeración de acordes, escalas y ritmos así como a la clasificación de todas ellas. Este texto se podría usar para motivar el estudio de la combinatoria desde alumnos de bachillerato hasta músicos con ciertos conocimientos matemáticos. En todo el texto se siente la presencia de la idea de la relevancia de la enumeración exhaustiva de elementos musicales. Aparte de la clasificación y enumeración, Keith propone medidas matemáticas de fenómenos musicales. En el libro encontramos, por ejemplo, una definición de síncopa, que fue analizada en esta columna en octubre de 2011, en el artículo de título Medidas matemáticas de síncopa [Góm11d], así como también una medida que cuantifica la bondad de una escala.
3.6. The cognition of basic musical structures
La mejor manera de describir el propósito de este libro, The Cognition of Basic Musical Structures es citar las palabras de su prefacio (nuestra traducción):
This book addresses a fundamental question about music cognition: how do we extract basic kinds of musical information —meter, phrase structure, counterpoint, pitch spelling, harmony, and key—from music as we hear it? My approach to this question is computational.
[En este libro se trata una pregunta fundamental sobre la cognición musical: ¿cómo se extrae los tipos básicos de información musical information —métrica, estructura de la frase, contrapunto, notas, armonía y tonalidad—a partir de la música que oímos? Mi enfoque para contestar a esta cuestión es computacional.]
Figura 4: The Cognition of Basic Musical Structures
Escrito por David Temperley [Tem04], este libro es una continuación y una extensión de las ideas generativas de la música de Lerdahl y Jackendoff [LJ83]. Uno de los conceptos principales de la obra es la regla de preferencia. Temperley establece una serie de reglas de preferencia para varios parámetros musicales (métrica, melodía, armonía) y ante el análisis de una pieza escoge la interpretación que mejor satisface esas reglas de preferencia. Dichas reglas tienen un carácter computacional bastante marcado (entiéndase computacional como modelo computacional antes que como programación).
Otra virtud que tiene el libro de Temperley es que las reglas de preferencia están fuertemente basadas en la investigación en cognición musical. Así, por ejemplo, su algoritmo para determinar la tonalidad sigue los hallazgos de Krumhansl y Schmuckler sobre los perfiles de tonalidad. En el libro, en los capítulos 9 y 10, encontramos felizmente análisis de música no clásica, en particular, de rock y música africana.
El libro, aparte de la teoría que propone, plantea un buen número de preguntas que invitan a la reflexión y a la investigación. Por ejemplo, en la sección 11.3 se pregunta si existe música que no sea métrica. En resumen, es un libro que todo lector interesado en los modelos computacionales de la música debería leer, más aun si hablamos de musicólogos sistemáticos.
3.7. Other Harmony
En este excelente libro de Tom Johnson, Other Harmony [Joh14], se examina desde un punto divulgativo pero riguroso, varios sistemas de armonía musical, algunos de los cuales tienen principios matemáticos. El autor no se limita solo a la armonía tonal, sino que explora la armonía atonal y lo que provocativamente llama Otras Armonías (sí, con esta ortografía). El mayor mérito de este libro, aparte de su escritura transparente y sencilla, es la exploración de lo heterodoxo, una exploración que siempre es necesaria y que hay que practicar con cierta regularidad, siquiera sea para adquirir una perspectiva más amplia. En la serie de artículos que empezaron en febrero de 2014 analizamos profundamente este libro y entonces de este libro dijimos lo siguiente:
Una fuerza vigorosa dentro de la música occidental ha sido siempre la superación del sistema armónico en curso. Nuevas reglas permitieron que lo que antes eran disonancias o progresiones prohibidas ahora se usen con total naturalidad. Ese empuje llevó la armonía tonal a su límite a principios del siglo XX. En ese tiempo la superación de la armonía tonal clásica era en muchos casos una elección estética inevitable. Sin embargo, como ilustra Johnson en su libro, las formas en que los compositores superaron la armonía tonal fueron extraordinariamente variadas. Muchas de ellas son desconocidas, bien porque no tuvieron éxito entre los compositores, o bien porque otras sistemas compositivos les hicieron sombra y cayeron en el olvido. En el libro de Johnson se rescatan algunos de esos sistemas compositivos.
3.8. The geometry of musical rhythm
Godfried Toussaint, que fue mi director de tesis, fue profesor en McGill University durante tres décadas y ahora enseña en la Universidad de New York en Abu Dhabi. Es el autor del libro The geometry of musical rhythm, un libro donde se explora profundamente las relaciones entre ritmo y matemáticas, sobre todo geometría. A lo largo de 38 capítulos, Toussaint expone varias modelos del ritmo y estudia múltiples propiedades suyos. El núcleo principal del libro es el examen de las propiedades que caracterizan a los “buenos” ritmos (también hay una discusión de que es un “buen” ritmo) y su descripción matemática.
El libro presenta un primer bloque de seis capítulos donde Toussaint define la terminología que usará en el resto del texto: ritmo, métrica, claves, ostinatos, y otros. Después procede al estudio de seis claves binarias que son muy usadas en las músicas del mundo (en tradiciones no occidentales diversas). Los siguientes capítulos tratan los ritmos binarios y ternarios y las operaciones que transforman unos en otros (este tema se trato en una columna de esta sección [Góm12d]). Otro tema que toca el libro son las medidas de complejidad rítmica y en particular las medidas de síncopa. Toussaint pasa revista a las medidas más comunes y las compara entre sí.
Del capítulo 19 al 31 Toussaint investiga familias importantes de ritmos. Empieza por los famosos ritmos euclídeos, aquellos que tienen sus notas distribuidas entre los pulsos lo más regularmente posible, y sigue con los ritmos cuasi-regulares, los ritmos complementarios, los ritmos profundos, los ritmos en cáscara (diferentes de las cáscaras de la música afro-cubana), ritmos simétricos, entre otros. En los siguientes capítulos se estudia la combinatoria de los ritmos y la filogénesis de los ritmos (la reconstrucción de ritmos por vía de algoritmos filogenéticos tomados de la Bioinformática). Por último, Toussaint dedica el capítulo 37 a hacer una defensa del ritmo de la clave son como el mejor ritmo pues, según el autor, posee muchas de las cualidades buenas que se han ido estudiando a lo largo del libro.
3.9. Foundations of diatonic theory
Este libro es digno de mencionar porque es uno de los intentos más acertados y sinceros por enseñar música a través de la matemática sin que esto sea un ejercicio de voluntad sino una necesidad intelectual. En su Foundations of diatonic theory [Joh08], el autor, Timothy Johnson, explica la teoría de escalas diatónicas a través de principios básicos de divisibilidad y aritmética modular. En realidad, aunque no lo usa, está hablando todo el tiempo de ritmos euclídeos. También llama la atención cómo ha organizado el material, de una excelencia pedagógica poco común, y el exquisito equilibrio entre música y matemáticas, estas últimas siempre al servicio de las primeras. Hicimos en su momento una serie entera, Enseñanza de música por vía de las matemáticas, dedicada a este libro; véase [Góm12c].
4. Libros avanzados
4.1. Statistics for Musicologists
Consideramos que el libro de Jan Beran [Ber04], Statistics for Musicologists, es de obligada lectura y asimilación para cualquier músico profesional y en especial para los musicólogos. En su momento dedicamos dos columnas [Góm12e] a glosar el contenido del libro. En la primera columna, nos hacíamos eco de la definición de Richard Parncutt [Par07], que volvemos a recordar:
Sugiere (el diccionario New Grove Dictionary of Music and Musicians) que la musicología hoy comprende todas las disciplinas que estudian toda la música en todas sus manifestaciones y en todos sus contextos, sean estos, físicos, acústicos, digitales, multimedias, sociales, sociológicos, culturales, históricos, geográficos, etnológicos, psicológicos, médicos, pedagógicos, terapéuticos, o en relación a cualquier otra disciplina o contexto musicalmente relevante.
Figura 5: Statistics in Musicology
A estas alturas, negar que la música tiene fenómenos que son cuantificables y modelizables computacionalmente parece algo miope intelectualmente. Y dentro de los aspectos cuantificables de la música, la estadística es una herramienta muy potente. El libro de Beran tiene once capítulos y en cada uno estudia una técnica estadística distinta, la cual aplica al análisis musical. Una virtud de este libro es el gran número y calidad de los ejemplos musicales. Empieza con un capítulo general, de terminología, y continúa con un segundo que versa sobre minería de datos. Algo tan aparentemente simple como son las técnicas de estadística descriptiva se muestran en acción para extraer conclusiones sobre varios corpus bajo estudio. En el capítulo 3 se estudian las medidas globales de estructura. En el cuarto, se presentan las series temporales y sus aplicaciones en el análisis musical. El capítulo 5 trata de los métodos jerárquicos y su aplicación al estudio de la forma musical. En el capítulo 6 se estudian los modelos Markov y muchas de sus variadas aplicaciones al análisis musical. El resto de los capítulos tratan del análisis de componentes principales, el análisis de grupos y el escalado multidimensional. Hay que advertir que el nivel matemático del libro es bastante alto.
4.2. A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice
El libro A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice [Tym11] debería ser otro libro de obligada lectura a todo alumno de música que tenga aspiraciones profesionales y aun más en el caso particular de los compositores. La explicación de la música tonal expuesta por Tymoczko en su libro es de una gran versatilidad y exhaustividad. Además, la abstracción y potencia conceptual de su enfoque permite que se explique con igual facilidad la música pop y el romanticismo, por poner un ejemplo. Las herramientas analíticas que propone Tymoczko, basadas en principios geométricos, consisten en ver las progresiones armónicas y el contrapunto como puntos de un cierto espacio geométrico y caracterizar esos movimientos armónicos a través de ciertas propiedades matemáticas. Este modelo, como prueba su autor, tiene una gran potencia explicatoria de una gran cantidad de música de la práctica común y de la práctica común extendida. La escritura de Tymoczko es digna de mención. A pesar de la envergadura conceptual, es seria cuando es pertinente serlo y humana y divertida en el resto del tiempo.
4.3. The Topos of Music: Geometric Logic of Concepts, Theory, and Performance
Si hay una obra monumental sobre matemáticas y música esa esa es el The Topos of Music: Geometric Logic of Concepts, Theory, and Performance [MG02] de Guerino Mazzola, músico de jazz y matemático, disciplinas ambas en que ejerce profesionalmente. Su libro es una obra titánica de abstracción en que usa teoría de categorías y otras artillería pesada matemática para explicar la música. Aviso desde este instante al estimado lector que este libro solo puede ser entendido por personas con una fuerte formación en ambas disciplinas.
Glosaremos brevemente algunas partes del libro, casi el índice, diríamos, dado que dicho contenido está muy por encima del nivel divulgativo de esta columna. El libro empieza con un capítulo llamado Topography, donde Mazzola describe la terminología que usará a lo largo de su extensa obra. Los conceptos son extremadamente abstractos y las teorías que los alimentan, igual. Se habla de estética, psicología, semiótica, filosofía de la música, entre otras. Sigue otro capítulo que directamente se llama ontología musical y que versa exactamente sobre la ontología musical. En el capítulo cuarto Mazzola reflexiona sobre la Musicología y sus métodos. Tras este capítulo el libro contiene con varias grandes secciones, y en cada una se recoge unidades independientes de su teoría. En la primera sección, llamada navegación y espacios de conceptos, se presentan los espacios de conceptos y los denotadores, elementos básicos de la teoría musical de Mazzola. En la siguiente sección se desarrolla la teoría local, que se ocupa de los parámetros musicales de medio nivel (melodía, ritmo, armonía, etc.). En la siguiente sección, Mazzola aborda la teoría global, que analiza los elementos más abstractos y globales de la música. El resto de las secciones contienen una teoría matemática de la semántica, una teoría matemática de la interpretación y métodos estadísticos de análisis musical.
5. La divulgación en matemáticas y música
La divulgación en matemáticas y música es difícil en nuestro entorno y en los tiempos que vivimos.
Bibliografía
[AM16] Javier Arbonés and Pablo Milrud. La armonía es numérica. National Geographic, 2016.
[Ber04] Jan Beran. Statistics in Musicology. Chapman & Hall/CRC, 2004.
[FFW03] John Fauvel, Raymond Flood, and Robin Wilson. Music and Mathematics from Pythagoras to Fractals. Oxford University Press, Oxford, England, 2003.
[GGMDB14] P. Gómez, E. Gómez, J. Mora, and J.M. Díaz-Báñez. Cofla: la música flamenca y su estudio computacional, abril de 2014.
[Góm10a] P. Gómez. El teorema del hexacordo, mayo de 2010.
[Góm10b] P. Gómez. Las matemáticas en la música de Xenakis, octubre de 2010.
[Góm11a] P. Gómez. La liga de los compositores de música automática, septiembre de 2011.
[Góm11b] P. Gómez. Similitud rítmica en el flamenco, marzo de 2011.
[Góm11c] P. Gómez. Distancia y similitud musical, mayo de 2011.
[Góm11d] P. Gómez. Medidas matemáticas de síncopa, octubre de 2011.
[Góm12a] P. Gómez. Polígonos regulares y percusión, abril de 2012.
[Góm12b] P. Gómez. Rotaciones de ritmos, mayo de 2012.
[Góm12c] P. Gómez. Enseñanza de música por vía de las matemáticas, diciembre de 2012.
[Góm12d] P. Gómez. Transformaciones rítmicas: de binarizaciones y ternarizaciones, agosto de 2013.
[Góm12e] P. Gómez. Estadística en la musicología, julio de 2012.
[Góm12f] P. Gómez. Minimalismo y matemáticas: Clapping music, marzo de 2012.
[Góm14a] P. Gómez. Otras armonías son posibles, febrero de 2015.
[Góm14b] P. Gómez. Teoría generativa de la música, junio de 2014.
[Góm14c] P. Gómez. Paradojas matemáticas y musicales, noviembre de 2014.
[Góm15] P. Gómez. Fractales y percusión, septiembre de 2015.
[Góm16a] P. Gómez. Música y probabilidad, noviembre de 2015.
[Góm16b] P. Gómez. Cadenas de markov con restricciones aplicadas a modelos cognitivos en la improvisación del jazz, mayo de 2016.
[Góm16c] P. Gómez. Composición algorítmica, junio de 2016.
[Har06] Leon Harkleroad. The Math Behind the Music. Cambridge University Press, Cambridge, 2006.
[Joh08] T.A. Johnson. Foundations of Diatonic Theory: A Mathematically Based Approach to Music Fundamentals. Mathematics Across the Curriculum. Scarecrow Press, 2008.
[Joh14] Tom Johnson. Other harmony. 75 Editions, 2014.
[Kei91] Michael Keith. From Polychords to Pólya: Adventures in Musical Combinatorics. Vinculum Press, Princeton, 1991.
[LJ83] F. Lerdahl and R. Jackendoff. A Generative Theory of Tonal Music. MIT Press, Cambridge, Massachussetts, 1983.
[Loy11] Gareth Loy. Musimathicsrds. MIT Press, 2011.
[MG02] G. Mazzola and S. Göller. The Topos of Music: Geometric Logic of Concepts, Theory, and Performance. Number v. 1 in The Topos of Music: Geometric Logic of Concepts, Theory, and Performance. Birkhäuser Basel, 2002.
[Par07] Richard Parncutt. Systematic musicology and the history and future of western musical scholarship. Journal of Interdisciplinary Music Studies, 1:1–32, 2007.
[Rap10] David Rappaport. Conjuntos de área máxima y la armonía, septiembre de 2010.
[SG12] Ricardo Sanz and Paco Gómez. Amalgamas, aksaks y métricas euclídeas, noviembre de 2012.
[Tem04] D. Temperley. The Cognition of Basic Musical Structures. MIT Press, 2004.
[Tym11] Dmitri Tymoczko. A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice. OUP USA, 2011.
|
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |