Home » Cultura y matemáticas » Música y matemáticas
Música y matemáticas
El objetivo de esta sección es comprender la interesante y profunda relación de las Matemáticas con la Música.
Nuestro sincero agradecimiento a Francisco Gómez Martín (Universidad Politécnica de Madrid) por organizar y desarrollar esta sección, a sus anteriores responsables Rafael Losada y Vicente Liern, así como a todas las personas que colaboran con la misma.
Resultados 51 - 60 de 130
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
1. Introducción
Esta es la última entrega de la serie sobre composición algorítmica. Inicialmente, teníamos planeado que esta entrega versara principalmente sobre música fractal. Tras sopesarlo cuidadosamente y escuchar a unos cuantos amigos músicos, hemos pensado que la música fractal merece una serie por sí misma. En este artículo, en su lugar, describiremos de modo general algunas de las técnicas de composición algorítmica que más lejos han llegado. Es imposible tratarlas todas con detalle, pero daremos sus principales características y proporcionaremos al lector la bibliografía adecuada para que profundice llegado el caso. En la primera entrega [Góm16d] estudiamos qué es un algoritmo. En la segunda entrega [Góm16e] nos centramos en el fenómeno de la composición musical; nuestra aproximación conceptual incluía, como decíamos allí, un gran rango de prácticas. En la tercera entrega [Góm16a] examinamos los algoritmos genéticos con cierto detalle y desarrollamos unos cuantos ejemplos en que se aplicaban esas técnicas a diversos elementos musicales (seguimos en nuestra exposición de esta parte el trabajo de Bruce Jacob [Jac96]).
2. Técnicas matemáticas de composición
Aunque es muy difícil caracterizar las técnicas matemáticas de composición en general, por su variedad y riqueza, un rasgo común que se aprecia en todas ellas es la importancia que posee la obtención de modelos computacionales. No puede haber composición algorítmica sin modelos computacionales de la música. Estos modelos se generan observando qué características musicales son susceptibles de ser traducidas a términos computacionales. Hay muchas características musicales que tienen tal susceptibilidad, desde la altura del sonido, que se rige por principios físicos, hasta la duración, que en la misma tradición occidental es divisiva y, por tanto, se puede describir mediante teoría de números; pero también de otras características, en principio más alejadas de una descripción computacional, como puede ser la armonía, la conducción de voces o el timbre, se han descrito modelos computacionales bastante potentes. Véase, para mayor información sobre este tema, el excelente libro de Benson [Ben06] Music: A Mathematical Offering; para ver un ejemplo de cómo Xenakis modeliza los parámetros musicales, véase en esta columna el número de octubre de 2010 [Góm16c]. Los primeros modelos computacionales eran pobres, entre otras razones porque no tuvieron en cuenta la cognición musical, esto es, los fenómenos perceptuales y psicológicos de la escucha musical. Posteriormente, los modelos poco a poco empezaron a incorporar la información sobre los procesos cognitivos y entonces mejoraron sustancialmente; véase [PHG+08] para más información sobre modelos computacionales de la percepción y la cognición. Una vez que el problema del modelo computacional de la música estuvo resuelto, o al menos mínimamente encaminado, frente al compositor se abrieron muchas posibilidades para la composición algorítmica. ¿Qué se puede hacer con esos modelos? ¿Cómo manipularlos de modo que salga música con significado?
Dos grandes categorías de técnicas compositivas se pueden reconocer en la composición algorítmica: la composición basada en conocimiento y la composición estocástica. La primera categoría es muy amplia e incluye, por ejemplo, la composición basada en gramáticas o la composición basada en patrones. La segunda no es menos amplia y en ella encontramos la composición mediante algoritmos genéticos, la composición basada en modelos matemáticos (al estilo de Xenakis, por ejemplo) o la composición basada en modelos de Markov.
3. Composición basada en conocimiento
Tanto la composición basada en gramáticas como la basada en patrones buscan extraer cierta información esencial de la música para, una vez descrita en términos computacionales, diseñar algoritmos para producir nueva música. En el caso de las gramáticas, sus teóricos ven la música como un lenguaje y como tal tiene una gramática, con su sintaxis, su semántica, su pragmática y sus reglas de estilo. Chomsky, con su teoría generativa del lenguaje [Cho65], mostró cómo era posible formalizar las reglas del lenguaje. Veinte años después de Chomsky, en 1983, Lerdahl y R. Jackendoff [LJ83], formalizaron la música tonal occidental en el libro A Generative Theory of Tonal Music. Estos dos autores mostraron que la música occidental tiene una cierta estructura recursiva y que existen ciertas reglas que permiten una descripción satisfactoria de la música en términos computacionales.
Como ejemplo de composición algorítmica basada en gramática tenemos el algoritmo de William Shottstaedt [Sho89] que genera piezas contrapuntística basadas en las reglas de contrapunto del Gradus ad Parnassum establecidas por Johann Joseph Fux (1660–1741), un teórico del Barroco tardío. El algoritmo contiene más de 75 reglas para producir las melodías. Entre esas reglas están la prohibición de las quintas paralelas y de los tritonos en ciertas situaciones. Kemal Ebcioglu [Ebc90] desarrolló un algoritmo que generaba corales a cuatro voces en el estilo de Bach teniendo en cuenta más de 350 reglas. Estos son ejemplos de algoritmos usados para la composición y que están basados en reglas. Véase el artículo Algorithmic composition, a definition [Bur] para más información sobre estas técnicas.
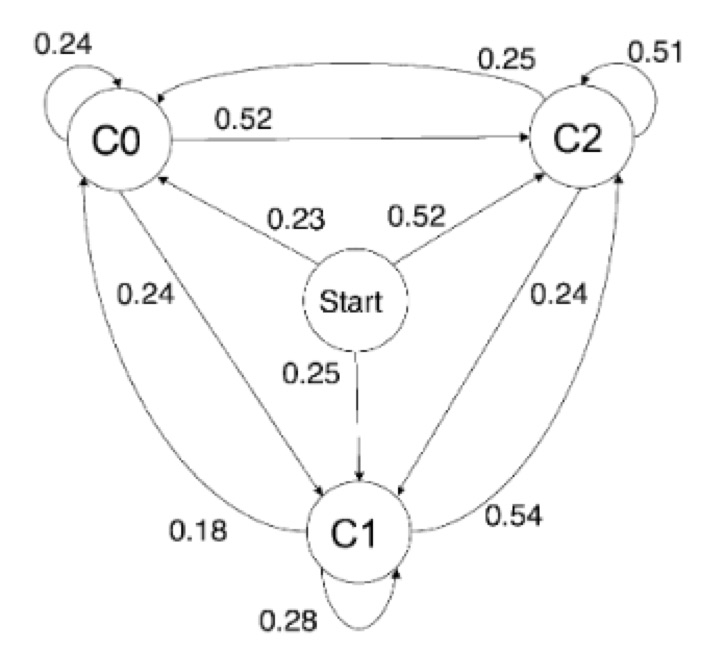
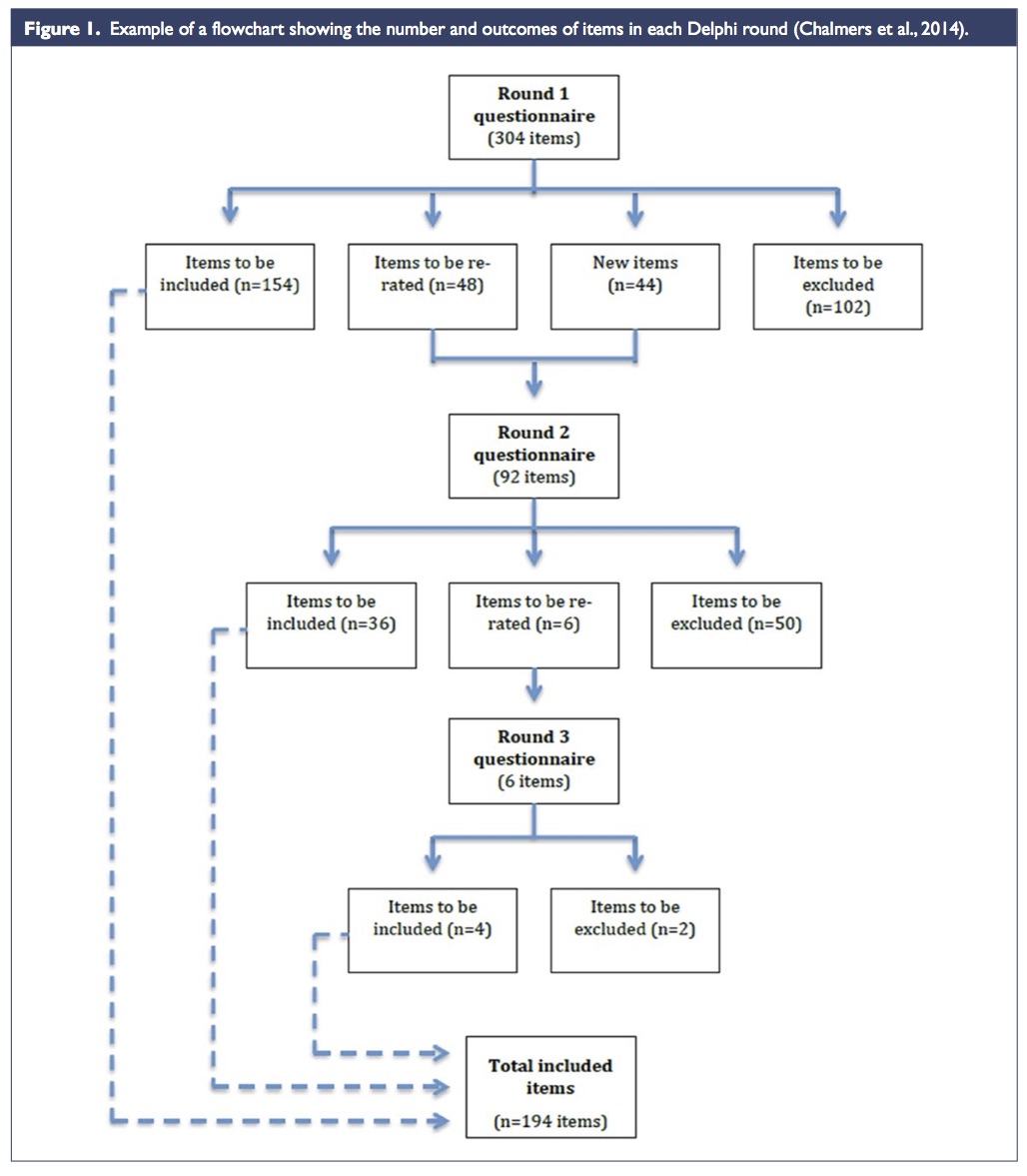
En los ejemplos anteriores las gramáticas musicales se extrajeron de modo manual, por mediación humana. Sin embargo, el gran reto es llegar a un modelo computacional en que la intervención humana no sea necesaria y que los resultados sean de calidad. Con el avance de las técnicas de aprendizaje automático, basadas a su vez en técnicas estadísticas de gran potencia, la caracterización automática de las gramáticas musicales fue posible. Gillick, Keller y Tang presentaron en 2010 [GKT10] un sistema de aprendizaje automático de gramáticas de jazz llamado Impro-Visor (es un programa de libre distribución). Empezaron escogiendo un autor concreto y un corpus de sus solos transcritos por expertos. A partir de él y usando cadenas de Markov y técnicas de aprendizaje automático generaban solos en el estilo del autor. La primera dificultad estriba en la representación de la gramática. El algoritmo busca patrones rítmicos y melódicos y a partir de ellos crea cadenas de Markov; para más información sobre este proceso en concreto, véase el artículo del mes de mayo de 2016 escrito por Kristy Yun y Mariana Montiel [JM16] en esta misma columna. En la figura 1 vemos el grafo asociado a una cadena de Markov para unos ciertos estados. Obsérvese que la suma de los pesos de las aristas de salida de cualquier nodo es 1, como corresponde a una distribución de probabilidad.
Figura 1: Cadenas de Markov para el aprendizaje automático de gramáticas musicales (figura tomada de [GKT10])
Los autores describen el proceso de generación de la gramática como sigue:
Descomponer el corpus en fragmentos melódicos, típicamente de un compás aproximadamente.
Traducir cada fragmento en una melodía abstracta. Esta melodía está compuesta por los contornos melódicos, categorías de notas, duraciones y otras características.
Ejecutar un algoritmo de agrupamiento en las melodías abstractas. La salida del algoritmo dará grupos, que normalmente tendrán unas diez melodías en media.
Comparar los grupos con el corpus para determinar el orden en que aparecen los grupos en el corpus.
Extraer los n-gramas de los grupos, donde n típicamente varía entre 2 y 4. Este parámetro lo ajusta el usuario. Véase la columna [Góm16b] para mayor información sobre el uso de los n-gramas en música.
Los autores dieron a un grupo de expertos los resultados para que evaluasen la calidad de los solos. Para solos de entre 4 y 8 compases, el algoritmo es capaz de generar solos la mayor parte de las veces que suenan razonablemente bien como el autor del corpus. Solos más largos de 8 compases ya no suenan bien, sobre todo por la falta de finalidad melódica. Los resultados mejores se obtienen para 4-gramas, que permiten sacar solos convincentes de mayor longitud. Los solos que se generan con n-gramas con n ≥ 5 no se parecen a los del autor del corpus. Los solos con 2-gramas o 3-gramas no dan resultados coherentes de modo regular.
El otro enfoque dentro de los métodos de composición basados en conocimiento es el de patrones. En el contexto de la improvisación, que sin duda es una forma de composición, hay dos teorías que tratan de explicar su funcionamiento. Una teoría se basa en la idea, de nuevo, de las gramáticas y sus defensores sostienen que los improvisadores aprenden la gramática del estilo musical dado y luego la ponen en juego en tiempo real; digamos, que sencillamente hablan en el lenguaje que han aprendido. Esa gramática consiste en una serie de reglas sintácticas y estilísticas; el trabajo de Gillick y sus colaboradores es un exponente de este enfoque. La otra teoría mantiene que el improvisador aprende en base a patrones. Tras estudiar el estilo aprende que ciertos patrones son musicalmente idiomáticos y otros no, y en tiempo de improvisación los combina dentro unos límites y bajo una sintaxis. Martin Norgaard y sus colaboradores [NSM13] diseñaron y programaron un algoritmo que obtenía los patrones más importantes de un corpus para un autor dado y creaba una base de datos con ellos. A partir de esa base de datos se construía una cadena de Markov que luego era capaz de generar una improvisación en el estilo del autor. Los resultados de este algoritmo fueron satisfactorios, pero solo incluían el ritmo y la altura del sonido. Defensores de ambas teorías reconocen que lo más probable es que en la práctica la improvisación sea una combinación de ambos enfoques, que se aprendan a la vez la gramática y los patrones característicos; sin embargo, nadie sabe cómo funciona esa combinación.
Los avances en inteligencia artificial han hecho también que algunos algoritmos sean capaces de crear sus propias gramáticas musicales a partir de gramáticas aprendidas de un cierto estilo. Algunos algoritmos han producido obras que imitan los estilos de los grandes maestros de la música clásica y cuyos resultados son bastante convincentes; véase el trabajo de Maurer [Mau] para más información.
4. Composición estocástica
El pionero indiscutible de composición estocástica en el sentido moderno del término es Xenakis. Antes que él ya había habido intentos de componer aleatoriamente: Mozart tirando los dados para componer melodías o John Cage con su indeterminismo. Xenakis rechaza el indeterminismo de Cage por su falta de un principio causal en la concepción musical. Escuchando Music for piano, de Cage, por ejemplo, donde las alturas del sonido están elegidas en base alas imperfecciones de un papel, Xenakis se preguntaba cuál es el sentido musical y estético de tal elección. El crítico Pousseur [Pou66] apoya esta objeción y añade que “donde se usan las más abstractas construcciones, uno tiene la impresión de encontrarse ante la presencia de las consecuencias de sonidos tocados libre y aleatoriamente”. En el caso de Xenakis, hay que insistir vehementemente en que no usaba el ordenador para producir la música en forma final, sino que se servía del ordenador como ayuda a causa de su rápida capacidad de procesamiento. En Xenakis, el concepto artístico es lo principal y todo lo demás está subordinado a él, incluso los mismos conceptos matemáticos y computacionales; véase su libro Formalized music [Xen01] para una exposición completa de sus ideas musicales y estéticas. En cambio, otros compositores, como Hiller e Isaacson [HI79], delegan en el ordenador la toma de las decisiones creativas.
En una columna de Divulgamat [Góm16c] analizamos la obra de Xenakis Pithokrapta, que se puede considerar una representación sonora (una sonificación [vaaat10]) del fenómeno físico de los gases ideales. En esta obra Xenakis aplicó dos principios musicales: primero, el sonido ha de tener total independencia; segundo, la música ha de poseer un significado global, derivado éste de la acumulación de los efectos individuales de las partes. La manera en que Xenakis fundió ambos principios es ingeniosa y original. Acudió a la ley de los grandes números, que enunciamos más abajo.
Teorema 4.1 (Ley débil de los grande números.) Sean X1, X2,... una sucesión infinita de variables aleatorias independientes con la misma media μ y varianza σ2, ambas finitas. Sea = la media muestral de las n primeras variables aleatorias y ϵ > 0 un número real positivo. Entonces se tiene:
Este importante y bellísimo teorema nos explica por qué observamos causas macroscópicas como resultado de la acción de múltiples causas pequeñas e independientes. Aquí el significado musical resultante está representado por la media μ común a todas las variables independientes. Xenakis asignó a grupos de cuerda pequeñas voces que actuaban de manera independiente respecto al total, pero que sin embargo generaban un resultado global claro. En la figura de abajo se ve el resultado final de Pithokrapta en forma de partitura gráfica.
Figura 2: Grafo de Pithoprakta
El problema de la composición estocástica en que el algoritmo toma decisiones estético-musicales es la evaluación final del resultado. En el caso de Xenakis no hay tal delegación de esas decisiones y el resultado es totalmente coherente con su visión estética. Cuando es el algoritmo el que dicta la estética resultante los resultados no son tan convincentes. Discutiremos estas cuestiones en la sección de conclusiones.
5. Conclusiones
Por mucho que ensanchemos hasta sus límites el concepto de composición musical, siempre tiene que haber una evaluación musical y estética de esas composiciones. Entonces, la pregunta es: ¿cómo decidimos si una composición que usa algoritmos tiene mérito estético? Algunos autores han considerado que el mérito estético de la composición algorítmica residía en la propia belleza del algoritmo, pero aquí la cuestión es juzgar el mérito estético y no la del algoritmo que la produce. Otros autores mantienen que se debe juzgar ambos aspectos, el algoritmo y su resultado musical. El argumento que se esgrime en contra de la evaluación estética de los algoritmos es que estos son meros medios para conseguir un resultado artístico y que, por tanto, no son susceptibles de juzgar su mérito estético en el contexto musical.
En su libro digital Algorithmic composition: a gentle introduction to music composition using common LISP and common music, Simoni [Sim03] (capítulo 2, sección final) hace las siguientes reflexiones sobre la cuestión estética (nuestra traducción):
All of these responses to the process and product of algorithmic composition are valid as each view is simply a manifestation of a personal aesthetic. Unfortunately, composers of algorithmic music have not been formally surveyed regarding their views on the aesthetics of algorithmic composition so we do not know how many composers fall into which category at any given time or if there are more categories to consider.
In the absence of a formal survey, we let the repertoire of algorithmic composition speak for itself. In reviewing algorithmic processes throughout the twentieth century, the number of compositions that are supported by documented algorithms are dwarfed by those that are not. In fact, when asking composers to provide algorithms accompanied by software implementation for this book, many composers confided that their code is not up to Knuth’s standards of simplicity, elegance, parsimony, and tractability.
[Todas las anteriores respuestas (las dadas al principio de estas conclusiones) al proceso y resultado de la composición algorítmica son válidas en cuanto que cada juicio es simplemente la manifestación de una estética personal. Desafortunadamente, los compositores de música algorítmica no han evaluado formalmente sus juicios sobre la estética de la composición algorítmica, de modo que no sabemos cuántos compositores caen en cada categoría en un momento dado o si ni siquiera hay más categorías que considerar.
En ausencia de una evaluación formal, dejemos que sea el repertorio de la composición algorítmica el que hable por sí mismo. Revisando las composiciones algorítmicas a lo largo del siglo XX, el número de composiciones que tienen sus algoritmos documentados es nimia comparado con los que no lo tienen. De hecho, cuando se pidió a los compositores que proporcionaran algoritmos acompañados por programas implementados para este libro, muchos revelaron que el código no estaba a la altura de los estándares de Knuth en cuanto simplicidad, elegancia, parsimonia y tratabilidad. ]
Otros artistas, incidiendo en el aspecto conceptual del arte, defienden que el criterio estético para juzgar esta música debería ser la calidad poética de la visión del artista. Aquí incluyen elementos como la idea artística y su materialización, la eficacia con que dicha idea se transmite, la superación de los medios tradicionales para comunicar la idea y la originalidad asociada a la idea y/o su materialización. Estos criterios presuponen un gran conocimiento del artista y de su ideal estético, lo cual, desgraciadamente, no ocurre con mucha frecuencia.
Como puede apreciar el lector, la cuestión de la evaluación estética de la música algorítmica está más que abierta a discusión.
Bibliografía
[Ben06] D. Benson. Music: A Mathematical Offering. Cambridge University Press, 2006.
[Bur] Kristine Burns. Algorithmic composition, a definition. http://music.dartmouth.edu/~wowem/hardware/algorithmdefinition.html.
[Cho65] N. Chomsky. Aspects of the theory of syntax. MIT Press, Cambridge, Massachussetts, 1965.
[Ebc90] Kemal Ebcioglu. An expert system for harmonizing chorales in the style of Bach. Journal of Logical Programming, 8:145–185, 1990.
[GKT10] J. Gillick, R. M. Keller, y M. Tang, K. Machine learning of jazz grammars. Computer Music Journal, 34:56–66, 2010.
[Góm16a] P. Gómez. Composición algorítmica (iii). Consultado en diciembre de 2016.
[Góm16b] P. Gómez. Distancia y similitud musical - ii. Consultado en diciembre de 2016.
[Góm16c] P. Gómez. Las matemáticas en la música de xenakis - i. Consultado en diciembre de 2016.
[Góm16d] P. Gómez. Composición algorítmica (i). Consultado en julio de 2016.
[Góm16e] P. Gómez. Composición algorítmica (ii). Consultado en octubre de 2016.
[HI79] L. A. Hiller y L. M. E. Knuth Isaacson. Experimental music: Composition with an electronic computer. Greeenwood Publishing Group Inc., 1979.
[Jac96] B.L. Jacob. Algorithmic Composition as a Model of Creativity. Organized Sound, 1(3):157–165, 1996.
[JM16] Kristy Jun y Mariana Montiel. Cadenas de markov con restricciones aplicadas a modelos cognitivos en la improvisación del jazz. Consultado en diciembre de 2016.
[LJ83] F. Lerdahl y R. Jackendoff. A Generative Theory of Tonal Music. MIT Press, Cambridge, Massachussetts, 1983.
[Mau] John Maurer. A Brief History of Algorithmic Composition. https://ccrma.stanford.edu/~blackrse/algorithm.html.
[NSM13] M. Norgaard, J. Spencer, y M. Montiel. Testing cognitive theories by creating a pattern-based probabilistic algorithm for melody and rhythm in jazz improvisation. Psychomusicology, 23:243–254, 2013.
[PHG+08] Hendrik Purwins, Perfecto Herrera, Maarten Grachten, Amaury Hazan, Ricard Marxer, y Xavier Serra. Computational models of music perception and cognition i: The perceptual and cognitive processing chain. Physics of Life Reviews, 5(3):151 – 168, 2008.
[Pou66] Henry Pousseur. The question of order in the new music. Perspectives in New Music, 1:93–111, 1966.
[Sho89] William Shottstaedt. Current directions in computer music research. chapter Automatic Counterpoint, pages 199–214. MIT Press, Cambridge, MA, USA, 1989.
[Sim03] Mari Simoni. Algorithmic composition: a gentle introduction to music composition using common LISP and common music. SPO Scholarly Monograph Series. The Scholarly Publishing Office, The University of Michigan, University Library, Ann Arbor, Michigan, 2003. https://quod.lib.umich.edu/s/spobooks/bbv9810.0001.001/1:1/--algorithmic-composition-a-gentle-introduction-to-music?rgn=div1;view=fulltext.
[vaaat10] Varios autores asociados a International Community for Auditory Display. Sonification report: Status of the field and research agenda. http://www.icad.org/websiteV2.0/References/nsf.html, accedido en septiembre de 2010.
[Xen01] Iannis Xenakis. Formalized Music: Thought and Mathematics in Composition. Number 6 in Harmonologia. Pendragon Press, Hillsdale, NY, 2001.
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
1.Técnicas matemáticas de composición
Esta entrega es la tercera de la serie composición algorítmica. En la primera [Góm16a] dimos una visión general de algoritmo (con ejemplos tomados de [CLRS01, Knu73]) e ilustramos ese concepto con algoritmos de ordenación. Allí insistimos en la importancia de distinguir entre algoritmo y código. En la segunda entrega [Góm16b] reflexionamos sobre la definición de composición musical. Como decíamos en la introducción de esa entrega, por composición musical se puede entender un gran rango de prácticas y merecía la pena reflexionar sobre ellas antes de entrar en la descripción de las técnicas de composición algorítmica propiamente dichas. En este artículo estudiaremos algoritmos genéticos y los procesos estocásticos.
La idea de componer mediante algoritmos ya apareció antes de la propia invención del ordenador. Si se interpreta el concepto de algoritmo como una solución constructiva a un problema, entonces se encuentran precedentes de la composición algorítmica moderna ya en el Renacimiento. Durante este periodo eran relativamente populares los juegos de dados para componer música. Componían a partir de un conjunto de fragmentos que juntaban según el orden dado por las tiradas de un dado. La primer pieza de que tenemos noticia que se compuso con un ordenador fue escrita por Hiller e Isaacson [HI79] en 1957. Era un cuarteto de cuerda y usaron un ordenador de la Universidad de Illinois. La composición algorítmica cobró un gran impulso cuando en 1991 Horner y Goldberg en la IV Conferencia Internacional sobre Algoritmos Genéticos presentan un artículo [HG91] donde muestran como aplicar los algoritmos genéticos a la composición musical. Los algoritmos genéticos como tales fueron presentados por John Holland a principios de los años 70 [Hol92].
2. Algoritmos genéticos y composición musical
2.1. Descripción de los algoritmos genéticos
La expresión algoritmo genético viene de que están inspirados (y descritos) en la biología, en particular, en la teoría de la evolución genético-molecular. Vamos a describir los elementos formales de un algoritmo genético y luego ver cómo se aplican a la composición musical.
Un algoritmo genético está diseñado para resolver algún tipo de problema (para nosotros será obtener una composición musical). La solución se obtiene a través de un proceso iterativo que converge hacia dicha solución. Un algoritmo genético tiene los siguientes elementos:
Una población inicial de candidatos a solución del problema. La población inicial recibe otros nombres como soluciones potenciales, individuos, criaturas. Los individuos tienen una serie de características que los definen y que son los fenotipos.
La información del fenotipo es codificada de una manera específica (binaria, con frecuencia). Esta codificación constituye el genotipo. Cada conjunto de valores del genotipo recibe el nombre de cromosomas.
Se empieza un proceso iterativo, llamado evolución, en el cual el fenotipo de la población cambia a través de una serie de operaciones, llamadas operadores genéticos, entre los que se incluyen selección, recombinación o cruzamiento, mutación y reemplazo.
Para evaluar la idoneidad de un candidato a solución se define una función de aptitud, o simplemente función de evaluación, sobre los candidatos y que toma valores numéricos. La función se aplica en cada paso de la evolución y se espera que las soluciones sucesivas mejoren las propiedades de las generaciones anteriores. Este proceso se llama también evaluación de la descendencia.
Un aspecto importante a tener en cuenta en el diseño de los algoritmos genéticos es cómo codificar la información. Los operadores genéticos actuarán sobre la codificación de las propiedades de los candidatos a solución. La codificación tiene que ser lo suficientemente potente y flexible como para que recoja las propiedades y sea fácil aplicar los operadores genéticos. Véase el libro de Melanie Mitchell [Mit96] para más detalles técnicos sobre el diseño de algoritmos genéticos.
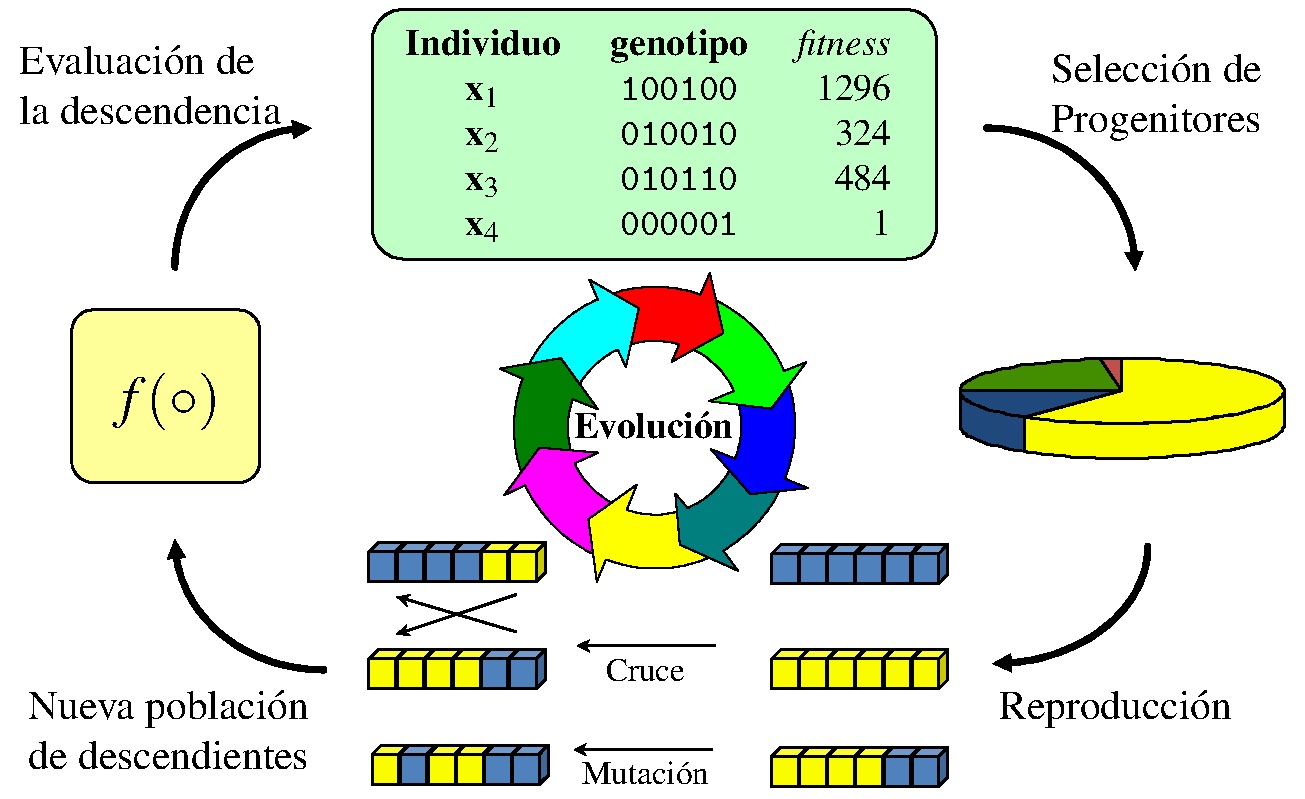
En la figura 1 se muestra un esquema del funcionamiento de un algoritmo genético.
Figura 1: Esquema del funcionamiento de un algoritmo genético (figura tomada de [Lat16])
Vamos a poner un ejemplo tomado de unas notas de clase bastante claras e instructivas publicadas por el Intelligent System Group de la Euskal Herriko Unibertsitatea [Int16]. La descripción del algoritmo se basará en la figura 2, que proporciona un pseudocódigo del algoritmo genético estándar.
Figura 2: Pseudocódigo de un algoritmo genético (figura tomada de [Int16])
Los algoritmos genéticos tratan de resolver problemas de optimización, con frecuencia la obtención de un máximo o mínimo global de una función. Como dijimos arriba, la población inicial representa las soluciones potenciales del problema. La codificación típica suele ser binaria, en parte porque es muy flexible y en parte por tradición histórica (Holland lo presentó así en su trabajo inicial [Hol92]). En nuestro ejemplo, usaremos también la codificación binaria. En realidad, la elección de la codificación depende en buena medida del problema. La analogía entre genotipo —la composición genética de un organismo—y el fenotipo —y la forma en que esa composición se expresa—se traslada aquí asignando a los valores de las variables independientes el papel del fenotipo y al de su codificación final el papel del genotipo. Los valores de las variables independientes, vistas como vectores numéricos, son los cromosomas. La función de adaptación sirve para evaluar la adaptación al problema de un cierto individuo (solución potencial al problema). La figura 3 ilustra estos conceptos para la función de una variable f(x) = x2. La primera columna es el número de individuo; la segunda contiene los fenotipos o valores de la variable independiente así como su codificación binaria o genotipo; la tercera columna, el valor decimal del genotipo; la cuarta columna muestra el valor de la función de adaptación.
Figura 3: Genotipo, fenotipo y función de adaptación (figura tomada de [Int16])
Durante la fase reproductiva (las iteraciones sucesivas del algoritmo), se seleccionan individuos de la población para cruzarse (véase la quinta columna de la figura 3). Dicho cruce ocurre por medio de los operadores genéticos. Una vez seleccionados dos individuos para cruzarse, sus cromosomas se combinan. El cruce y la mutación son dos de los operadores más frecuentes. En el operador de cruce se elige un punto al azar del cromosoma y se intercambian los códigos genéticos entre dos individuos; véase la figura 4.
Figura 4: Operador de cruce (figura tomada de [Int16])
El operador de cruce no se aplica a todos los individuos sistemáticamente, sino que se establece una función de probabilidad para determinar las parejas de individuos que sufrirán el cruce genético.
El otro operador, el de mutación, no consiste más que en cambiar un valor del cromosoma de un individuo. También lleva asociado una distribución de probabilidad. Se aplica a cada hijo, pero la probabilidad de mutación suele ser pequeña; véase la figura 5.
Figura 5: Mutación de un cromosoma (figura tomada de [Int16])
Si el algoritmo genético está implementado correctamente, entonces se supone que la adaptación media y la adaptación del mejor individuo se acercarán al máximo o mínimo global buscados. Normalmente, se toma como solución final la adaptación del mejor individuo.
2.2. Algoritmos genéticos aplicados a la composición musical
La composición a través de algoritmos genéticos despertó un gran interés desde principios de los años 90 y existe una gran variedad de caminos para usarla. Algunos de esos caminos son:
Composición de variaciones de un motivo o composición existentes [Ral95, Jac96].
Composición de música similar a otra composición dada [Hoc06].
Composición de solos o improvisación de melodías a partir de plantillas existentes (por ejemplo, se dan las duraciones o las secuencias de acordes) [Jac96, OE08].
Composición de las alturas y de las duraciones a la vez a través del algoritmo genético [Jac96, Bil94].
Veamos a continuación cómo pasar los elementos del algoritmo genético al contexto musical. En nuestro ejemplo tomaremos dos parámetros musicales: altura y ritmo. Para el caso de la altura, fijaremos el do central como nota de referencia y a partir de ella, contando en semitonos, codificamos las alturas; véase la figura 6.
Figura 6: Codificación de altura de sonidos
La duración se puede codificar de muchas maneras. A veces se codifica dando el tiempo en milisegundos; otras veces se define una duración mínima y todas las demás duraciones son múltiplos de esta; o también se puede usar el sistema del midi, donde se define el número de pulsos por negra en relación al tempo expresado en partes por minuto. En nuestro caso, supondremos que la duración mínima es la semicorchea y pondremos todas las duraciones en función de ella. Hay que añadir una variable que indique si estamos en presencia de un silencio o de una nota; será 0 si es silencio y 1 si es nota. Entonces, la codificación para el primer compás de la figura 6 es:
(0,0,2),(3,1,2),(6,1,2),(7,1,2),(8,1,6),(7,1,2)
donde el primer campo es la altura, el segundo el indicador de nota o silencio y el último la duración.
Elegir una función de adaptación que tenga significado musical es todavía un problema abierto. La música es demasiado compleja para que haya una función de expresión sencilla que produzca resultados aceptables. La forma general de la función de adaptación que se ha empleado en diversos sistemas es:
f = a1 ⋅ f1 + a2 ⋅ f2 + ...+ an ⋅ fn
donde cada fi es un factor musical del sistema y ai un peso que se da a dicho factor. Ejemplos de dichos factores podrían ser el número de intervalos disonantes, el número de apariciones de ciertos patrones interválicos, la frecuencia de ciertos intervalos, el rango de la melodía, entre muchos otros. La determinación de los pesos ai es también una cuestión muy delicada; no se sabe cómo elegirlos y normalmente se hace de una manera subjetiva o al menos aproximada. Esta fórmula implica que los factores fi tienen la misma preponderancia en todos los compases o en todas las partes de la composición. Se puede generalizar la función para que los pesos de los factores cambien de compás a compás. Si suponemos que la pieza tiene m compases la función es ahora
f = a11 ⋅ f1 + a21 ⋅ f2 + ...+ an1 ⋅ fn + ......+ a1m ⋅ f1 + a2m ⋅ f2 + ...+ anm ⋅ fn
donde el peso aij representa el peso del factor i en el compás j.
Los operadores genéticos se pueden definir de muchas maneras en la codificación musical. He aquí una breve descripción de las más frecuentes:
Cruzamiento de la melodía. Se toman dos melodías, se cortan en cierto puntos y se intercambian los fragmentos entre sí. La tonalidad se tiene en cuenta y se trasponen acorde a ella.
Mutaciones. En el ámbito de las alturas se tienen: cambios de octava en un tono (para evitar, por ejemplo, los intervalos grandes); cambio de un tono; cambio de una nota cromática. En el ámbito de las duraciones: cambios de las duraciones (con los correspondientes ajustes en el compás); cambio de figuración.
En la figura siguiente tenemos el resultado musical obtenido por Bruce Jacob [Jac96]. En este ejemplo se ha partido de unos motivos básicos que han constituido la población inicial. La función de evaluación incluye parte de evaluación humana.
Figura 7: Composición musical usando algoritmos genéticos (figura tomada de [Jac96]
En el siguiente vídeo tenemos una charla en la que se explica detalladamente una implementación de los algoritmos genéticos en Phyton:
En este otro vídeo se ve la evolución de una melodía. Los factores usados son autosimilitud, linealidad, tonalidad y rango.
Bibliografía
[Bil94] J.A. Biles. Genjam: A genetic algorithm for generating jazz solos. In Seventh International Conference on Genetic Algorithms, 1994.
[CLRS01] Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms. McGraw-Hill Book Company, Cambridge, London, 2. edition, 2001. 1. editon 1993.
[Góm16a] P. Gómez. Composición algorítmica (i). Consultado en julio de 2016.
[Góm16b] P. Gómez. Composición algorítmica (ii). Consultado en octubre de 2016.
[HG91] A. Horner and D. Goldberg. Genetic algorithms and computer-assisted music composition. In Fourth International Conference on Genetic Algorithms, San Mateo, CA, 1991.
[HI79] L. A. Hiller and L. M. E. Knuth Isaacson. Experimental music: Composition with an electronic computer. Greeenwood Publishing Group Inc., 1979.
[Hoc06] R. Hochreiter. Audible Convergence for Optimal Base Melody Extension with Statistical Genre-Specific Interval Distance Evaluation. Lecture Notes in Computer Science, 3907, 2006.
[Hol92] John Holland. Adaptation in Natural and Artificial Systems. MIT, Cambridge, MA, 1992. Edición revisada de la de 1975.
[Int16] Intelligent System Group (EHU). Algoritmos genéticos. Consultado en octubre de 2016.
[Jac96] B.L. Jacob. Algorithmic Composition as a Model of Creativity. Organized Sound, 1(3):157–165, 1996.
[Knu73] Donald E. Knuth. The Art of Computer Programming, Volume I: Fundamental Algorithms, 2nd Edition. Addison-Wesley, 1973.
[Lat16] Proyecto Latin. Algoritmos genéticos clásicos. Consultado en octubre de 2016.
[Mit96] Melanie Mitchell. An Introduction to Genetic Algorithms. MIT Press, Cambridge, MA, 1996.
[OE08] E. Özcan and T. Erçal. A Genetic Algorithm for Generating Improvised Music. Lecture Notes in Computer Science, 4927, 2008.
[Ral95] D. Ralley. Genetic algorithm as a tool for melodic development. In Proceedings of the 1995 International Computer Music Conference, San Francisco, CA, 1995.
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
1. Introducción
Este es el segundo artículo de la serie composición algorítmica. En el primero [Góm16] exploramos la definición formal de algoritmo ([CLRS01, Knu73]) y proporcionamos algunos ejemplos (algoritmos de ordenación). Hicimos hincapié en la importante distinción entre algoritmo y código, distinción que de no hacerse en tiempo y forma convierte al estudiante de computación en un profesional superficial. En esta segunda entrega nos centraremos en la composición musical propiamente dicha. Merece la pena una reflexión y una formalización sobre el concepto de composición musical antes de entrar en las siguientes entregas, donde estudiaremos las principales corrientes dentro de la composición algorítmica.
2. La creación musical
La pregunta del título de la sección es, como era de esperar, complicada, llena de matices, y sin una respuesta cerrada. Se puede elaborar una respuesta desde una perspectiva histórica y ver cómo en una cultura determinada el concepto de composición ha evolucionado. También es posible estudiar la composición musical en varias culturas y resaltar sus diferencias y analogías. Por último, es posible especular sobre el concepto de composición de una manera abstracta. En este artículo combinaremos estos tres puntos de vista.
En su forma más simple, la composición musical es el proceso de crear música, lo cual deja la dificultad conceptual en el término música. En su definición más general, se puede decir que la música es una actividad artística y cultural cuyo medio es el sonido y el silencio. Si atendemos a las implicaciones artísticas y culturales de esta definición, entonces hemos de admitir que la música no existe en sí misma sino en cuanto significado construido por seres humanos, en cuanto constructo cultural. La experiencia musical consiste en un diálogo entre el oyente y la composición musical en que aquel ha de estar dispuesto a dejar que la música le hable, le muestre su sentido interno, su significado último. En esa escucha el oyente verá cuestionadas sus expectativas musicales y ello producirá progreso en el discurso musical percibido. Y es en este diálogo entre oyente y música que se produce el significado musical. Véase [Cli83] para una discusión más en profundidad de estas cuestiones.
La definición de música implica a su vez que el sonido tiene algún tipo de organización para poder ser clasificado como música. Y aquí aparece la fascinante cuestión de si la música es un fenómeno universal o un constructo cultural. Algunos autores sostienen que existen ciertos universales musicales; he aquí algunos que aparecen en la bibliografía:
Ideales musicales que poseen una estructura profunda;
Estrategias para agrupar el sonido;
El uso de alturas de referencia para crear estabilidad;
La división de la octava para crear escalas;
El uso de pulsos de referencia;
La formación de patrones rítmicos a través de la división asimétrica de pulsos temporales.
Otras investigaciones apuntan a que la música tiene aspectos típicos de un constructo cultural. Ciertas obras han sonado como ruido al público de una determinada época pero más tarde fueron comprendidas y subidas al rango de música. Ejemplos de obras así son la La gran fuga opus 133 de Beethoven, La consagración de la primavera de Stravinsky, Ionisation de Varèse, entre otras muchísimas. Recomendamos vivamente al lector el libro de Slonimsky Lexicon of Musical Invective: Critical Assaults on Composers Since Beethoven’s Time [Slo00] para una recopilación de obras que sonaron “ruidosas” en su estreno —y cuyos críticos masacraron inmisericordemente en las recensiones— per que más tarde fueron reconocidas en su justa valía. Para más información sobre los aspectos culturales de la música y en particular sobre la función social de la música, véase el libro de Radocy y Boyle [RB06] y las citas contenidas en él.
Si atendemos a otras culturas que no sean la occidental, veremos que muchas no tienen el concepto de música como género artístico. La música tiene una componente funcional muy fuerte y es sencillamente parte de la vida cotidiana. No poseen un grupo de miembros de su cultura que se dedica en exclusiva a la música, sino que todos los miembros de esa sociedad participa en distinto grado en el fenómeno musical. Además, la mayor parte de las culturas son de transmisión oral y no se pueden describir con la notación musical occidental.
Si la música implica la organización del sonido, tendremos qué señalar qué parámetros del sonido son susceptibles de dicha organización. En las próximas secciones daremos aquellos parámetros más comunes y aportaremos ejemplos para ilustrarlos.
2.1. Altura del sonido y melodía
La altura del sonido se refiere a la cualidad que nos hace distinguir un sonido grave de uno agudo; dicha cualidad está relacionada con la frecuencia. Un sonido complejo puede estar formado por la superposición de varias frecuencias simultáneas. Cuando un sonido tiene una frecuencia clara y estable hablamos más bien de notas, como por ejemplo las notas de la mayor parte de los instrumentos musicales (la caja clara, por ejemplo, no tiene una frecuencia definida). En muchas culturas la organización del sonido en notas es la base de su estructura musical. La elección de las notas se obtiene dividiendo la octava en partes fijas. Es muy frecuente encontrar escalas pentatónicas (de cinco sonidos) y heptatónicas (de siete sonidos). La octava se divide en doce semitonos en la música occidental; en otras tradiciones musicales, como la árabe se divide en más partes que doce, lo hace en diecisiete.
Asociada a la altura del sonido está la melodía, que en su definición más amplia es la presentación de una sucesión de tonos. Hay dos aspectos a considerar aquí: las relaciones entre las notas, sobre todo entre las notas consecutivas, y su duración en el tiempo. Obviamente, no toda sucesión de notas constituye una melodía. Autores como Lundin [Lun67] ya propusieron atributos como propincuidad, repetición y finalidad para definir con más precisión el concepto de melodía. Propincuidad alude a la propiedad de que la melodía principalmente se mueva por grados conjuntos dentro de la escala; repetición se refiere a que la melodía repita partes de ella a fin de consolidar su percepción; y finalidad significa que la melodía tenga ciertas intenciones musicales que le den coherencia. Ilustremos con un ejemplo lo anterior; en la figura 1 tenemos la melodía del capricho número 24 de Paganini.
Figura 1: Melodía del capricho número 24 de Paganini
Se trata de un tema con variaciones y lo que está en esta figura es la melodía principal el tema. El tema, que está en la menor, tiene dos partes claras, que hemos llamado antecedente y consecuente. El antecedente está armonizado con una alternancia de tónica-dominante (grado I y grado V de la escala, respectivamente). La función del antecedente es presentar el material melódico principal, que en este caso es un pequeño motivo que se repite constantemente; ese motivo tiene el rango de una tercera y se mueve principalmente por grados conjuntos (propincuidad y repetición). El consecuente presenta variación melódica del antecedente, creando tensión. La armonización del consecuente es (repetida dos veces):
I–IV–VII–III–VI-II-V–I
El consecuente termina con una cadencia implicada por la melodía (II–V–I) que sirven para reforzar el sentido conclusivo de la melodía (finalidad). Como vemos en el breve análisis de esta melodía, las tres características mencionadas arriba están presentes. En el vídeo de la figura 2 tenemos la interpretación del capricho entero con la partitura.
Figura 2: Capricho número 24 de Paganini (vídeo con partitura)
El ejemplo anterior está tomado de la música occidental. En otras culturas el concepto de melodía puede variar bastante y de nuevo aparece el debate de los universales musicales versus los constructos culturales. En el siguiente ejemplo tenemos el placer de escuchar una pieza de shakuhachi, una flauta de bambú que se usa en la música tradicional japonesa (en el vídeo hasta el minuto 6:05).
Figura 3: Música tradicional japonesa para shakuhachi (flauta de bambú)
En este caso la melodía se desvía de algunas de las características señaladas más arriba. Ya no hay tanto movimiento por grados conjuntos; de hecho, abundan los saltos. El timbre desempeña un papel muy importante y hay transiciones continuas entre notas (portamenti). La repetición motívica no está presente como en el caso de Paganini. Sin embargo, el sentido de finalidad es claro en la pieza.
Varios autores, tras el análisis de melodías de numerosas culturales, llegan al consenso de que una melodía tiene los siguientes atributos estructurales: (1) primera y última nota; (2) nota más grave y más aguda; (3) notas repetidas; (4) tamaño de los intervalos melódicos; (5) dirección melódica (contorno melódico); (6) proximidad entre notas; (7) énfasis en grupos de notas; (8) las relaciones interválicas; (9) grado de énfasis en las notas. Véase [RB06], página 209 y siguientes para una discusión sobre las características estructurales de la melodía.
2.2. Armonía
La melodía representa la dimensión horizontal de las notas y la armonía, en cambio, la dimensión vertical; esto es, cómo suenan varias notas al mismo tiempo. La armonía es particularmente importante en la música occidental, pero no lo es en otras tradiciones musicales. Muchas tradiciones no occidentales no tienen armonía alguna o está basada en escalas distintas a las occidentales con funciones distintas también. Es muy común la música monofónica (una sola voz) y la música heterofónica (con más de una voz, con variaciones de una sola línea melódica).
Varios autores (Lundin [Lun67] y otros) mantienen que la respuesta a la armonía es un fenómeno cultural. Se sabe que la respuesta a la armonía se produce a la totalidad y no a cada acorde individual. Solo a través de un entrenamiento especial el oyente puede reconocer y analizar los acordes individualmente. Hay tres atributos que son importantes en la armonía: la tonalidad, el movimiento armónico y la finalidad. Tonalidad se refiere aquí a la organización armónica alrededor de un tono especial, que tiene mayor relevancia y que representa el centro tonal de la pieza. Típicamente, cuando se dice que una obra está en do mayor, por ejemplo, estamos especificando el centro tonal, la nota do, y la escala, la escala mayor.
En la música occidental el movimiento armónico es un fenómeno relativo que ocurre en función de la tonalidad de referencia. Existen ciertas convenciones, que han cambiado a lo largo de la historia, sobre cómo enlazar los acordes entre sí. En el ejemplo del vídeo de la figura 4 podemos apreciar el movimiento de los acordes en el rondo a la turca de Mozart de su sonata KV 331. Los acordes en ese vídeo se han representado por números romanos, donde cada número representa un grado de la escala; los números en mayúsculas son los acordes mayores y los que van en minúsculas, los acordes menores. El lector se percatará de que en muchos compases solo hay un acorde y de que cuando Mozart quiere crear tensión aumenta el ritmo al que los acordes cambian.
Figura 4: Movimiento armónico en el movimiento final del rondo a la turca de Mozart, KV 331
Asimismo, el lector apreciará que hay un gran sentido de la finalidad en la elección de los acordes, el cual acompaña igualmente a la melodía. El uso de ciertas cadencias al final de las frases es un ejemplo de ello (los acordes con sextas aumentadas, la progresión ii-V-I). Las cadencias son secuencias de acordes que se usan para el fin de una frase, sección o pieza musical.
2.3. Ritmo
El ritmo es todo aquello que se refiere a la cualidad temporal de la música. En sí el ritmo es un elemento unificador de los otros aspectos musicales. Hay muchas teorías del ritmo, más de las que podemos glosar con solvencia en el breve espacio de este artículo. En general, los investigadores coinciden en que las propiedades del ritmo incluyen: (1) tempo o velocidad a que va la pieza; (2) las duraciones de las notas; (3) las relaciones de agrupamiento; y (4) la métrica. Por relaciones de agrupamiento nos referimos a conjuntos de duraciones que en función de mecanismos perceptuales (leyes de continuación y otras leyes de psicología de la forma) son percibidas como un todo. La métrica es más difícil de explicar y hay que tener en cuenta que es un constructo típico de la música occidental; la mayor parte de las tradiciones musicales carecen de la métrica tal cual la conocemos en la cultura occidental. La manera de marcar el compás en la música occidental es por medio de una fracción. El denominador indica la figura rítmica básica (corchea, negra, blanca, etcétera). El numerador indica el número de esas unidades rítmicas por compás. Así un compás de 3/4 indica que cada compás tiene tres negras (el 4 es el número de la negra). Pero el numerador aporta más información que el número de partes. Nos dice que hay un patrón de partes en que la primera es acentuada y las dos siguientes no, esto es, un patrón fuerte-débil-débil. Observe el lector que en la música occidental se supone que hay un pulso regular, en nuestro ejemplo, de negras, y que la métrica impone un patrón de acentos sobre dichos pulsos. Cuando un patrón rítmico contradice la métrica durante un periodo corto de tiempo se dice que es una síncopa.
Cambiando las duraciones de los patrones rítmicos se consigue generar relaciones de tensión y relajación en la música. Como ejemplo, veamos en el canon en re de Pachelbel cómo los cambios en las duraciones dan cohesión y dinamismo a la pieza. El vídeo es autoexplicativo.
Figura 5: Las transformaciones rítmicas en el canon en re de Pachelbel
Consideremos ahora un ejemplo tomado de una tradición musical donde el ritmo tiene otra concepción muy distinta a la occidental. En la música occidental la armonía ha restringido el desarrollo rítmico porque los cambios de acordes suelen producirse en las partes fuertes, sobre todo a principio de compás. En otras culturales el ritmo ha alcanzado cotas altísimas de desarrollo. En el gahu, que es música de la cultura Ewe de Ghana, el ritmo posee un papel primordial. Este género está asociado a la danza y al canto y su instrumentación consiste en tambores de distintos tamaños, campanas (gankoguis) y voz (coros). En la tradición musical de los Ewe existe el concepto de pulso, pero no el de métrica; además los ritmos no se piensan de modo divisivo sino más bien aditivo. La campana gankogui toca un ritmo que actúa de elemento unificador. Cada tambor (sogo, kidi y kaganu) toca un ritmo y debido a las texturas de los tambores y a los acentos de los ritmos surgen melodías rítmicas, si así podemos llamarlas; en la figura 6 aparece una transcripción de los ritmos básicos del gahu con círculos en esas melodías rítmicas. Para un estudio serio y profundo del gahu recomendamos el libro Drum Gahu: An Introduction to African Rhythm [Loc98] del etnomusicólogo David Locke.
Figura 6: Transcripción a notación occidental del gahu
En el vídeo de la figura 7 el lector puede disfrutar de una interpretación de gahu.
Figura 7: Danza gahu en el Teatro Nacional de Ghana
Otra tradición que se basa fuertemente en el ritmo es la japonesa, con sus famosos tambores taiko. Los tambores taiko varían desde aquellos con 30 centímetros de diámetro hasta los de un metro y medio de diámetro. Los patrones rítmicos, los acentos, la textura y la velocidad son los parámetros con que juega este género; la melodía y la armonía están ausentes en este género. En la figura 8 podemos ver una actuación con tambores taiko.
Figura 8: Actuación de percusionistas de taiko
2.4. Textura
La textura musical es el resultado final en términos de sonido que percibimos al escuchar una pieza musical. Es la suma de los sonidos individuales. Una pieza para un instrumento solo tiene una textura simple comparada a una pieza de orquesta. Se habla, pues, de textura más densa o menos densa en función de las voces que intervienen en la pieza en concreto. La textura, empero, no depende solo del número de voces, sino que es función también de la melodía, la armonía, el ritmo y de cómo se combinan entre sí. Por ejemplo, voces que no se contradicen entre sí musicalmente o que no crean tensión entre sí dan la sensación de una textura más ligera.
Atendiendo al número de voces, clasificamos las texturas en monofónicas, heterofónicas, polifónicas y homofónicas. Las texturas monofónicas están compuestas de una única voz. En el ejemplo de más abajo tenemos al extraordinario Agujetas cantando un martinete a capella.
Figura 9: Monofonía ilustrada con unos martinetes cantados por Agujetas
En la heterofonía dos instrumentos o voces tocan la misma melodía, pero uno de los intérpretes hace variaciones de dicha melodía. Este tipo de textura es común en tradiciones no occidentales tales como el bluegrass o el gamelán (música tradicional de Indonesia). En el siguiente vídeo podemos ver un ejemplo de heterofonía con el gamelán.
Figura 10: Heterofonía en la música de gamelán
Las texturas polifónicas se dan cuando varias voces independientes se combinan entre sí. La música coral del Renacimiento y de buena parte del Barroco tenían esta escritura. En las texturas polifónicas la armonía toma un papel especialmente importante pues ha de regir cómo combinar las voces de manera acorde al estilo dado. En el vídeo siguiente tenemos un ejemplo de una gran tradición polifónica, los cantos de Georgia (el país de Europa Oriental; no confundir con el estado del mismo nombre en EEUU).
Figura 11: Polifonía en la tradición vocal de Georgia
Por último, la textura homofónica, que es similar a la polifónica pero ahora una de las voces toma el protagonismo melódico y el resto proporciona soporte armónico. Otra manera de describirlo es decir que la textura homofónica es melodía con acompañamiento. El ejemplo dado en la figura 4, con el rondo a la turca de la sonata KV 331 de Mozart, es textura homofónica.
2.5. Timbre
El timbre es la cualidad característica de cada instrumento en términos de su sonido. Una misma nota tocada en un violín suena distinta a la de una flauta porque cada instrumento produce distintos armónicos (las frecuencias secundarias asociadas a una nota). Los compositores siempre tienen una gran preocupación por el timbre de su música. En una orquesta sinfónica hay muchos grupos de instrumentos y la combinación sonidos es importante en el discurso musical. Como ejemplo llamativo de textura musical, sugerimos al lector la escucha del concierto para violín, percusión y mesa de ping-pong de Andy Akiho, obra de 2015. Sí, ha leído bien el lector, mesa de ping-pong.
Figura 12: Concierto para violín, percusión y mesa de ping-pong
2.6. Forma
En general, la música no occidental tiene una forma más libre que la música occidental. Ello es comprensible dado que muchas tradiciones musicales no occidentales se basan en la improvisación de un material previo. Por forma entendemos la estructura de una pieza y por estructura, la organización del material a nivel local, digamos al nivel de frase, hasta al nivel de la misma pieza, como cuando describimos esta por sus secciones. Ejemplos de formas que han surgido a lo largo de la historia de la música occidental son las formas de danza (allemande, bourrée, chaconne, gavotte, menuet, entre otras), la fuga, la invención, la sonata, el tema y las variaciones, el concierto, la sinfonía concertante y la sinfonía. Además, varios de estas formas evolucionaron a los largo de la historia; no es lo mismo la forma sonata en el clasicismo temprano que en el post-romanticismo.
En una forma dada se especifican las secciones y el material que hay en ellas. En una forma sonata típica hay una sección de exposición en la que se presentan dos temas. Después de exponer el primer tema en la tonalidad de la pieza, es frecuente que el segundo tema aparezca en la dominante. La exposición de estos dos temas constituye la llamada sección A de la sonata o sección de exposición; se suele repetir dos veces. Tras la sección A viene la sección del desarrollo, que es una sección mucho más libre, donde se modula a otras tonalidades y se desarrolla motívicamente los temas de la sección A. La sección del desarrollo desemboca en la reexposición de la sección A. En esta segunda exposición es normal que el segundo tema se presente en la tonalidad de la pieza para dirigirnos a su conclusión. A veces la sonata termina con una coda o pasaje de carácter conclusivo donde se resume el material presentado en la pieza. La estructura de la sonata es, pues, A+A+B+A+C. En el vídeo siguiente tenemos los conceptos anteriores explicados sobre la sinfonía número 29 de Mozart.
Figura 13: La forma sonata con la sinfonía número 29 de Mozart
Otro ejemplo menos ortodoxo es el que se puede ver en el vídeo de más abajo, que es la forma musical en el tema Overworld del videojuego Mario Bros. En este caso la estructura es
Introducción+A+B+B+C+Introducción+A+D+D+C+D
Figura 14: Forma musical en el tema Overworld del videojuego Mario Bros.
3. ¿Qué es composición musical?
Tras todo lo visto hasta ahora comprendemos que el concepto de composición musical es muy amplio. Implica la elección de unos cuantos parámetros musicales y su manipulación para conseguir una organización del sonido que sea significativa. El término significativo aquí estará muy en función del contexto cultural. Composición se puede entender como improvisación, como por ejemplo en el caso de muchas tradiciones orales, o bien como una obra escrita en notación hasta sus últimos detalles. Los ejemplos que nos aguardan en las siguientes entregas de esta serie, donde examinaremos la composición algorítmica, requerirán de un concepto muy flexible de composición.
Bibliografía
[Cli83] Thomas Clifton. Music as Heard: A Study in Applied Phenomenology. Yale University Press, 1983.
[CLRS01] Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms. McGraw-Hill Book Company, Cambridge, London, 2. edition, 2001. 1. editon 1993.
[Góm16] P.. Gómez. Composición algorítmica (i). http://vps280516.ovh.net/divulgamat15/index.php?option=com_content&view=article&id=17290&directory=67, consultado en julio de 2016.
[Knu73] Donald E. Knuth. The Art of Computer Programming, Volume I: Fundamental Algorithms, 2nd Edition. Addison-Wesley, 1973.
[Loc98] David Locke. Drum Gahu: An Introduction to African Rhythm. White Cliffs Media, Gilsum, New Hampshire, 1998.
[Lun67] R.W. Lundin. An objective psychology of music. Ronald Press, 1967.
[RB06] Rudolf E. Radocy and J. David Boyle. Psychological Foundations of Musical Behavior. Charles C Thomas, Illinois, 2006.
[Slo00] Nicolas Slonimsky. Lexicon of Musical Invective: Critical Assaults on Composers Since Beethoven’s Time. W W Norton & Co Inc., 2000.
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
1. Introducción
Este artículo inaugura una serie sobre un tema apasionante: la composición algorítmica. Si queremos una definición concisa y breve, diríamos que la composición algorítmica se refiere al uso de algoritmos para la composición musical. En este viaje pretendemos que nuestros lectores, tanto músicos como matemáticos y en general cualquier lector curioso, comprendan los fundamentos de la teoría de algoritmos, de la composición musical y en última instancia cómo se han usado los algoritmos para componer música. En esta primera entrega trataremos los algoritmos y su definición formal y daremos ejemplos. En la segunda entrega examinaremos la definición de composición musical y sus características. En las siguientes entregas estudiaremos las principales corrientes dentro de la composición algorítmica.
2. ¿Qué es un algoritmo?
El concepto de algoritmo está asociado a la resolución de problemas. Desde este punto de vista, los algoritmos son una manera de pensar. En general, esos problemas han de ser susceptibles de ser cuantificables numéricamente y resolubles por medios matemáticos. Por ejemplo, cuando nos referimos al algoritmo de Euclides [Wik] estamos hablando de un procedimiento para resolver el problema de hallar el máximo común divisor de dos números. Sin embargo, no toda solución de un problema es un algoritmo. La solución necesita tener unas características especiales, como vamos a ver enseguida. La definición de algoritmo ha ido evolucionando según el nivel científico de la época, desde los tiempos del matemático al-Khwarizmi (siglo IX d.C.) en que algoritmo se refería a reglas aritméticas de cálculo, pasando por la formalización de Touring, hasta llegar a la definición de Donald Knuth [Knu73], una de las más aceptadas modernamente y que seguiremos aquí. Dado un problema a resolver, un algoritmo es un procedimiento que toma una entrada o valores iniciales del problema y, después realizar una serie de operaciones bien definidas, produce una salida o solución del problema. La definición de Knuth identifica cinco propiedades que un algoritmo ha de tener:
Entrada: Los valores iniciales del problema.
Precisión: Todo algoritmo tiene que estar definido de manera precisa de modo que no haya ambigüedad. En particular, los algoritmos están basados en un conjunto normalmente pequeño de operaciones básicas, que se suelen llamar operaciones primitivas. Estas suelen ser las operaciones matemáticas y reglas lógicas.
Finitud: Todo algoritmo tiene que terminar después de un número finito de pasos (y cuanto menor sea ese número, mejor).
Salida: Todo algoritmo ha de devolver un resultado.
Efectividad: Las operaciones que intervienen en el algoritmo han de ser suficientemente básicas.
Por supuesto, todo algoritmo que (aparentemente) resuelva un problema tiene que ir acompañado de una prueba matemática de que, en efecto, resuelve tal problema. Puesto que un algoritmo tiene que terminar en un número finito de pasos, los problemas que pueden resolverse de manera algorítmica deben tener una cierta naturaleza discreta (los problemas debe ser o bien finitos o bien si son infinitos tener una caracterización finita). Por ejemplo, el problema de enumerar todos los números primos implica dar una salida que es infinita y, en la definición dada aquí, no hay algoritmo que realice tal tarea. Sin embargo, para calcular el máximo común divisor de dos números sí es posible diseñar un algoritmo para resolver tal problema. El máximo divisor de dos números siempre existe y es un número finito comprendido entre los divisores de ambos números.
Un problema inherente a los algoritmos es su descripción. Los algoritmos pueden expresarse de muchas maneras: en primer lugar, en lenguaje natural, pero también como pseudocódigo y en última instancia en términos de un lenguaje de programación. Un algoritmo se puede ver como una serie de reglas formales para resolver un problema y su descripción es la enumeración de dichas reglas en el lenguaje apropiado. El inconveniente que surge al describir un algoritmo con lenguaje natural es que el grado de ambigüedad en su descripción puede ser demasiado alto porque el lenguaje natural es ambiguo. Consideremos el problema siguiente:
Problema: Dado un conjunto M de n números reales y otro número x, determinar si x está en el conjunto M.
Este problema es conocido como el problema de la búsqueda. Supongamos que los elementos de M son M[1],M[2],…,M[n]; note el lector que nos referimos a los elementos de M a través de un índice en notación matricial. Una manera de describir un algoritmo en lenguaje natural sería la siguiente:
Algoritmo en lenguaje natural: Para cada elemento M[i] de M, con i = 1 hasta i = n, comprobar si dicho elemento es x.
Se puede apreciar que en esta descripción aparecen las características de la definición de algoritmo dadas anteriormente. Empero, esta descripción es más abstracta e ignora ciertos detalles técnicos. La idea que transmite es de que la solución se encuentra comparando cada elemento de M con x. Con frecuencia la descripción en lenguaje natural no es suficiente para detallar las ideas detrás de un algoritmo y a veces tampoco para probar su corrección. El siguiente paso es definir una serie de operaciones básicas y estructuras de datos con que describir el algoritmo. Esa descripción se llama pseudocódigo. Por ejemplo, el siguiente pseudocódigo corresponde al algoritmo de búsqueda.
BÚSQUEDA-LINEAL(M, x)
1
i ← 1
2
while i ≤ length(M)
Bucle que recorre la matriz
3
if M[i] = x then
Comprueba si x es el elemento i
4
r ← i
5
i ← length(M) + 2
Fuerza la salida del bucle
6
if i = length(M) + 1 then r = -1
7
return r
Figura 1: El algoritmo de búsqueda lineal
La entrada está especificada en la línea BÚSQUEDA-LINEAL(M, x) y es el conjunto M y el número x. El cuerpo del pseudocódigo contiene instrucciones de control, tal como el bucle while o la sentencia condicional if. En el pseudocódigo ya aparecen objetos matemáticos, tales como variables (la variable i), y operaciones entre ellos, tales como la asignación de valores, con el operador ← (líneas 4 y 5), o la comparación de valores, con el operador = (línea 6). La salida se produce en la línea 7 con la instrucción return. Este pseudocódigo facilita la prueba de la corrección del algoritmo. En este artículo no entraremos en la delicada cuestión de la prueba de algoritmos. Recomendamos al lector interesado acudir al magnífico libro de Cormen, Leiserson y Rivest [CLRS01] Introduction to Algorithms para profundizar en este importante tema.
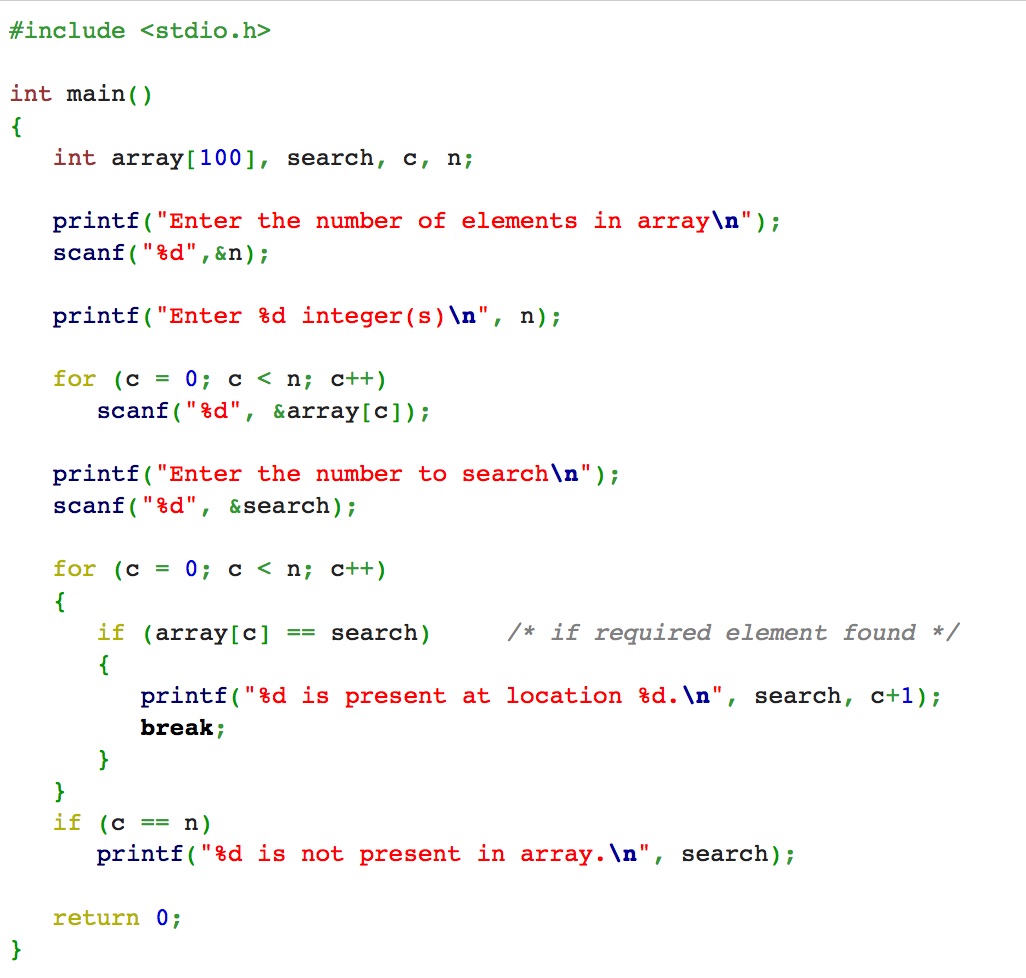
En la figura 2, por último, tenemos el algoritmo codificado en lenguaje C. Como se puede observar ya no hay lenguaje natural y los detalles del algoritmo están entreverados con los detalles propios del lenguaje. Para más información sobre programación de algoritmos en lenguajes de programación, véanse [GBY91, Sed90].
Figura 2: Búsqueda lineal codificada en lenguaje C.
El orden natural de abstracción es el presentado aquí. Primero se describe el algoritmo en lenguaje natural; se comprueba que las ideas contenidas en esa solución algorítmica descrita en lenguaje natural son correctas y que poseen esa naturaleza algorítmica, que cumplen con la definición de Knuth. Después se escribe en pseudocódigo y se prueba formalmente el algoritmo; la prueba ha de ser una prueba matemática, que con frecuencia es por inducción. Por último, se codifica en el lenguaje de programación elegido.
Un aspecto que no tratamos aquí es el de la complejidad de los algoritmos. La complejidad de un algoritmo es una medida del tiempo que tarda en resolver el problema en función del tamaño de la entrada. Para los propósitos de esta serie de artículos, la complejidad no desempeña un papel importante. El lector interesado puede consultar el libro de libro de Cormen, Leiserson y Rivest [CLRS01].
3. Algoritmos y música
La música, como ya hemos dicho muchas veces, es un fenómeno muy complejo, compuesto por una multitud de otros fenómenos provenientes a su vez de otros campos. La música tiene una dimensión física, pues es sonido. Ese sonido es oído por el ser humano que lo procesa según leyes básicas de la percepción pero también a través del crisol cultural, el cual puede incluir desde la exposición a un estilo determinado hasta la asociación emocional con la música. Para un estudio profundo y exhaustivo de todas estas cuestiones, recomendamos al lector la lectura del libro de Radocy y Boyle [RB06].
Pero la música posee una riqueza interminable en términos de patrones y estructuras y, por tanto, puede ser objeto de estudio de las matemáticas. Muchos de los fenómenos que constituyen la música son matematizables (por ejemplo, la armonía a través de la teoría de grupos) y en buena medida susceptibles de tratamiento algorítmico. En la mayoría de las culturas, la altura de sonido está discretizada. En el caso de la música occidental, al menos en la práctica común, se tiene una división de la octava en 12 notas. Esta discretización del continuo de la altura de sonido permite ya tratamiento algorítmico. En las duraciones de las notas, la situación es similar. El conjunto de duraciones posibles es finito y relativamente pequeño. Todo esto permite que se pueda modelizar la música (algunos aspectos de la música) matemática y algorítmicamente.
Los algoritmos de ordenador suelen tratar la música usando un formato llamado MIDI. Existe una asociación [Ass], The Midi Association, en cuya página web el lector encontrará abundante información sobre este importante estándar. El estándar MIDI no es solo una manera de codificar la música sino que también se ocupa de la comunicación entre instrumentos que funcionan con este estándar.
Un fichero MIDI contiene al menos la siguiente información: ataques de las notas, duración de las notas, altura de sonido como nota en una escala de igual temperamento, la voz en que suena la nota, la intensidad de volumen de la nota, la letra asociada (si la hay) y la información de los acordes.
Una vez que la música está codificada en formato numérico las posibilidades son infinitas. Todas las técnicas matemáticas están al servicio del tratamiento de la información musical, en particular al servicio de la composición musical a través de algoritmos. En el próximo artículo examinaremos los fundamentos básicos de la composición musical de modo similar a como hicimos en este artículo con los algoritmos.
Bibliografía
[Ass] The Midi Association. The Midi Associaton.
[CLRS01] Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms. McGraw-Hill Book Company, Cambridge, London, 2. edition, 2001. 1. editon 1993.
[GBY91] G.H. Gonnet and R. Baeza-Yates. Handbook of Algorithms and Data Structures. Addison-Wesley, 1991.
[Knu73] Donald E. Knuth. The Art of Computer Programming, Volume I: Fundamental Algorithms, 2nd Edition. Addison-Wesley, 1973.
[RB06] Rudolf E. Radocy and J. David Boyle. Psychological Foundations of Musical Behavior. Charles C Thomas, Illinois, 2006.
[Sed90] R. Sedgewick. Algorithms in C. Addison-Wesley, Reading, MA, 1990.
[Wik] Wikipedia. Euclidean algorithm.
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Kristy Yun y Mariana Montiel (Georgia State University)
Este mes vamos a presentar un trabajo hecho por Kristy Yun y Mariana Montiel, de Georgia State University, en Atlanta (donde estoy pasando mi sabático). Kristy es una estudiante de licenciatura que está a punto de obtener su título. En las universidades americanas los estudiantes de licenciatura acuden a unas conferencias llamadas conferencias de investigación para alumnos de grado. En esas conferencias los alumnos de licenciatura presentan pequeños proyectos de investigación supervisados por un profesor. Ni en el campo de las matemáticas ni en el de la música existen en España estas conferencias. Y es una pena. Primero, habla del nivel de nuestras universidades. ¿Es que no pueden nuestros alumnos de los últimos años de grado adentrarse en el mundo de la investigación y presentar pequeños resultados en una conferencia de estas características? Constituyen una experiencia previa para ellos que es muy valiosa en tantos aspectos: se enfrentan a problemas de investigación; se prueban a sí mismos; conviven con su profesor; supone una gran emoción presentar su trabajo antes sus compañeros (normalmente, en forma de póster o de comunicación corta); ponen en práctica sus habilidades de escritura y orales, entre otras.
Me llamó la atención el trabajo de Kristy Yun y Mariana Montiel en la conferencia de este año y les propuse publicarlo en formato divulgativo en esta columna. Les agradezco profundamente que hayan aceptado la invitación. Espero que este ejemplo cunda y empecemos a celebrar este tipo de conferencias para alumnos de licenciatura en España también de modo generalizado. Los investigadores más productivos que he conocido siempre han tenido una amplia red de alumnos a su alrededor con quienes han desarrollado relaciones personales excelentes y en quienes han podido depositar sus ideas para llevarlas a cabo, todo ello en el contexto de una cálida simbiosis humana y científica.
Paco Gómez Martín (Universidad Politécnica de Madrid)
Resumen del estudio
Las improvisaciones en el jazz consisten en ciertos patrones rítmicos y melódicos que oímos en cierto orden. Por medio del estudio de la genésis de estos patrones podemos entender el proceso de la toma de decisiones en tiempo real en el contexto de una estructura dada en que consiste la improvisación. No hay teorías que describan a fondo y con precisión la improvisación, pero entre las existentes destacan dos escuelas de pensamiento: una es la teoría basada en patrones; la otra se basa en gramáticas o reglas. La primera teoría propone que los improvisadores se nutren de un corpus de patrones rítmicos y melódicos memorizados y que dichos patrones se insertan en el proceso de una improvisación en curso dentro de unas ciertas reglas de estilo. Otra teoría, encontrada con la primera, asevera que los improvisadores generan notas por medio de los algoritmos y las reglas del jazz tonal, sin la ayuda de patrones memorizados. Para comprobar la validez de estas teorías, en un estudio previo [7] llevado a cabo por Martin Norgaard y sus coloaboradores se analizó un corpus de 48 solos improvisados por el gran saxofonista de jazz Charlie Parker. Los resultados del estudio mostraron que la incidencia de patrones en el corpus de Charlie Parker coincide con el algoritmo basado en patrones implementado en ese estudio. En cambio, las improvisaciones generadas por Impro-Visor, un software desarrollado en base a gramáticas y reglas tomadas de los acordes musicales introducidos por el usuario, no generó una presencia de patrones similar a la del corpus real de Parker. En vista de los resultados positivos del algoritmo, el siguiente paso era la incorporación de acordes; sin embargo, se quería evitar que dichos acordes dictasen la melodía y el contorno de la salida musical de manera excesivamente estricta, ya que la coincidencia de patrones era muy apegada a las improvisaciones de Parker. Se vio que una posible solución era el empleo de modelos de Markov no homogéneos, en que los acordes se entendiesen como restricciones. Cabe mencionar que podría haber aplicaciones de ese algoritmo que transcendiesen el género de jazz y aún la música, ya que se basa en patrones. La creatividad en áreas tales como los video juegos se puede modelar, dado que los jugadores deben responder de forma creativa en tanto adquieren ciertos patrones de respuesta con restricciones inherentes al contexto.
Introducción
Normalmente, cuando los músicos profesionales de jazz tocan en pequeños grupos no leen partituras, sino que improvisan. Los ejecutantes escogen frases que al público podría parecerles prescritas, pero que realmente se crean en el acto. Estos músicos profesionales desarrollan una forma muy intrincada de tema y variación; cada uno es consciente de su tonada y su papel; esto explica la razón por la que la improvisación de jazz sirve como un paradigma excelente para el estudios de la creatividad en tiempo real. La improvisación en el jazz es también un prototipo de la actividad mental común al reconocimiento del habla y otras áreas de interés en la inteligencia artificial.
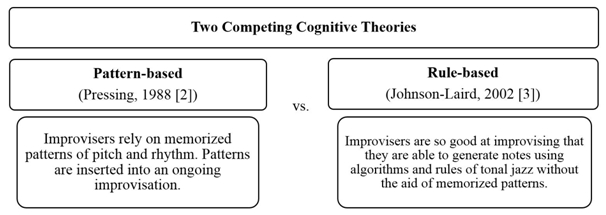
Actualmente hay dos teorías encontradas en el estudio de la improvisación en el jazz: (1) el enfoque basado en los patrones y (2) el enfoque basado en reglas; la figura 1 ilustra esta situación esquemáticamente (se ha dejado el texto en el inglés original).
Figura 1. Teorías cognitivas encontradas
Hay varios softwares para la improvisación en el jazz que se basan en una de las teorías descritas más arriba, patrones o reglas. Un ejemplo de un software basado en reglas es Impro-Visor, un software para la notación musical diseñada para ayudar a los estudiantes de jazz componer y escuchar solos similares a los que podrían improvisarse sobre los acordes dados. Martin y sus colaboradores [7], en un artículo de 2013, analizaron las dos teorías cognitivas prevalecientes por medio del análsis de un corpus de solos de Charlie Parker. Los resultados del estudio (mostrados en la figura 2, primera parte) demostró que el porcentaje de notas que inician un patrón de 4 intervalos como una función del número de veces el patrón ocurre en las improvisaciones no es coherente con el corpus de Charlie Parker cuando se emplea el software Impro-Visor (mostrados en la figura 2, segunda parte).
Figura 2 (primera parte). Comparación del porcentaje de notas que inician un patrón de 4 intervalos como una función del número de veces que el patrón ocurre en el corpus. [2]
Figura 2 (segunda parte). Comparación de los porcentajes de notas que inician en un patrón de 4 intervalos como una función del número de veces que el patrón ocurre en 1) una melodía generada según la gramática de Parker en el software Impro-Visor y 2) utilizando nuestro algoritmo. [2]
No obstante, un algoritmo basado en patrones melódicos parece reflejar el corpus de Parker con mucha más fidelidad. Tras los buenos resultados conseguidos por este último algoritmo, los autores pensaron en incorporar los acordes a la generación de los solos. Los acordes son fundamentales en la improvisación en el jazz y existe una íntima relación entre melodía y acordes que no es posible deslindar en modo alguno en este estilo. Existía, empero, el peligro de que la incorporación de los acordes restringiese excesivamente las posibilidades de elección de los patrones si dicha incorporación no se hacía de modo cuidadoso. Entonces, para incorporar los acordes y, a la vez, modificar lo menos posible las improvisaciones que resultan de nuestro algoritmo, decidimos explorar las cadenas de Markov no homogéneos.
Modelos de Markov
Los procesos de Markov son una herramienta popular de modelaje que se emplean en la generación de contenido, tales como la generación de textos, la composición musical y la interacción. El principio básico de la suposición de Markov es que los estados futuros dependen sólo del pasado inmediato y de la sucesión de eventos que ocurrió anteriormente. Matemáticamente, para una sucesión :
p(qi|q1,...,qi-1) = p(qi|qi-1)(1)
Ejemplo de un proceso de Markov[4] El pronóstico del tiempo consiste en adivinar el estado del clima mañana basado en una historia de observaciones en torno al tiempo. En base a la tabla 1 de números escogidos aleatoriamente, mas el autómata generado de esta tabla en la figura 3, intentaremos pronosticar el tiempo.
Tabla 1. Probabilidades escogidas aleatoriamente para el tiempo.
Figura 3. Autómatas generadas de la Tabla 1.
Por ejemplo, en vista de que hoy es un día soleado, ¿cuál es la probabilidad que mañana sea soleado y que el día siguiente sea lluvioso? Esto se traduce en los siguientes cálculos:
P(q2 = soleado, q3 = lluvioso | q1 = soleado)
= P(q3 = lluvioso | q2 = soleado, q1 = soleado) x
P(q2 = soleado | q1 = soleado)
= P(q3 = lluvioso | q2 = soleado) x
P(q2 = soleado | q1 = soleado)
= (0.05)(0.8)
= 0.04
Esta probabilidad también se puede obtener a través del autómata de la figura 3, multiplicando las probabilidades correspondientes en el proceso.
Resultados
En el artículo de Pachet, Finite-length Markov processes with constraints [5], se muestra que las restricciones pueden compilarse en un nuevo modelo de Markov cuyas probabilidades sean equivalentes al modelo inicial. Según el propio Pachet, al hablar su método, “esto nos deja con la ventaja de retener la sencillez de los trayectos aleatorios, en tanto asegura que las restricciones de control se satisfagan"[5].
Estos resultados se pueden aplicar a nuestro algoritmo melódico y rítmico actual para mantener las probabilidades de la salida musical original (la “improvisación”), en tanto los acordes son incorporados como restricciones. Una vez más se enfatiza que la meta es no dejar que los acordes “dicten” el contenido melódico, cosa que sí sucede en el software Impro-Visor, donde la incidencia de patrones presentes en el corpus de solos de Parker se pierde en las improvisaciones generadas (aunque somos los primeros en reconocer lo ingenioso y la utilidad didáctica de Impro-Visor).
Nuestra meta es generar un modelo no homogéneo de Markov, representado por una serie de matrices de transición. Para mostrar cómo las restricciones se pueden compilar en un modelo no homogéneo de Markov, tomaremos un ejemplo de generación de melodía con una restricción simple. La restricción se reduce a que toda melodía de 4 notas tiene que terminar en C (do); de nuevo se usarán el ejemplo original en inglés. Considérese un modelo de Markov estimado a partir de las sucesiones de la figura 4. El vector a priori es:
C D E
donde las entradas se originan en las melodías de la figura 4. Por ejemplo, para encontrar la probabilidad de C, primeramente se toman el número total de notas en cada melodía, que en este caso son 6 para cada una. Por lo tanto, de las doce notas C aparece 4 veces y esto arroja la probabilidad 4/12 = 1/3.
Figura 4. Dos melodías sencillas de entrada usadas para estimar M.
Las probabilidades de transición de M también se pueden generar de las dos melodías de entrada.
Por ejemplo, cuando C va a D (re), podemos ver de nuestras melodías que la totalidad de posibles transiciones que comienzan con C son:
C va a D (primera melodía)
C va a E (segunda melodía)
C va a D (segunda melodía).
De las tres transiciones posibles, 2 de las 3 terminan de D. Por lo tanto, la probabilidad de ir de C a D es 2/3.
Por medio de un programa sencillo creado para generar todas las posibles combinaciones de melodías de 4 notas (véase la figura 5), obtenemos 12 posibilidades de probabilidades diferentes de cero, como se ve en la tabla 2.
Figura 5. Todas las posibles combinaciones de melodías de 4 notas que satisfacen la restricción.
Tabla 2. Las 12 melodías de 4 notas que satisfacen la restricción del control y sus probabilidades en M, donde la suma de las probabilidades para estas sucesiones es s.
Las probabilidades de obtener melodías de 4 notas que terminan en C pueden detectarse por medio de nuestro vector a priori M, junto con las probabilidades de transición. Por ejemplo:
Después de la generación de estas matrices primarias, el primer paso en nuestro proceso es hacer que nuestro problema inducido de satisfación de restricciones (CSP) cumpla con la consistencia de arcos. La consistencia de arcos consiste en la propagación de las restricciones en todo el problema de la satisfacción de restricciones através de un algoritmo de punto fijo que considera la restricciones de manera individual [6]. Para nuestro ejemplo, la consistencia de arcos elimina C y E del dominio de V3 y arroja los siguientes dominios:
donde Ki es el estado de transición entre Z(i-1) a Zi y Vi es el estado. Esto asegura que durante cualquier trayecto aleatorio no habrá una situación en la cual se escoja una alternativa que no tenga continuación. El siguiente paso es extraer las matrices de los dominios.
Por medio del algoritmo de Pachet[5]:
mantenemos las siguientes matrices:
Finalmente, construimos las matrices de transición definitivas M̃(i) a M̃ através de un proceso sencillo de derecha-a-izquierda para poder propagar las perturbaciones en las matrices inducidas por la normalización individual al revés, comenzando con la que está más a la derecha.[5]
Para lograr lo anterior, primeramente normalizamos la última matriz Z(L-1)individualmente. En seguida se propaga la normalización de la derecha a la izquierda hasta llegar al vector a priori Z(0). Los elementos de las matrices M̃(i) y el vector a priori M̃(0) se definen através de las siguientes relaciones de recurrencia:
Por medio de la relación arriba expuesta, logramos las siguientes matrices de transición para nuestro ejemplo.
Por medio de calculos similares para i = 1 y i = 0, como resultado contamos con las siguientes matrices de transición:
Discusión
Este es un enfoque eficiente para controlar la generación de Markov con restricciones que pueden:
garantizar que las sucesiones generadas satisfagan las restricciones.
seguir la distribución de probabilidad del modelo de Markov inicial.
Podemos ver que la matriz final de transición M̃ mantuvo la misma distribución de probabilidad que el vector a priori M.
La tabla 3 muestra las probabilidades M̃ de todas las posibles sucesiones de soluciones, donde estas probabilidades son iguales a las probabilidades iniciales hasta un factor constante de multiplicación α(0).
Tabla 3. La probabilidad del conjunto de sucesiones de soluciones en M̃. La razón de probabilidades es constante.
Este algoritmo no tienen que ser específico al género de jazz, ya que se basa en los patrones reales de un corpus. Ha habido implementaciones con música clásica, música blue grass y otras músicas. Se piensa que este algoritmo puede trascender la música y utilizarse para estudiar la creatividad en áreas tales como los video juegos, donde la improvisación juega un papel significativo dado que los participantes deben responder de manera creativa en tanto adquieren ciertos patrones de respuesta como resultado de las restricciones.
Actualmente estamos trabajando en la incorporación de los acordes en el algoritmo y este método parece prometedor. Mi contribución en este proyecto de investigación consistió en encontrar esta técnica y mostrar su relevancia para el siguiente paso importante en el desarrollo de este software para la improvisación.
Reconocimientos
Primeramente quiero agradecer a mi asesora de investigación, Dr. Mariana Montiel. Sin su ayuda e involucramiento dedicado en cada paso de este proceso, este trabajo jamás se habría realizado. Me gustaría darle las gracias por su apoyo, orientación, paciencia y, sobre todo, su tutoría. También me gustaría mostrar mi gratitud a mi grupo de investigación de la neurofísica, incluyendo al Dr. Mukesh Dhamala, el Dr. Martin Norgaard, y a Kiran Dhakal por compartir mi interés y emoción durante el transcurso de esta investigación. Sin la oportunidad que me aportó el Dr. Dhamala de trabajar junto con Kiran en el registro de los datos fMRI de los músicos de jazz, no habría podido trabajar tan cercanamente con la Dra. Montiel y con el Dr. Norgaard en este proyecto. Asimismo, gracias al Dr. Paco Gómez por su ayuda con las últimas partes de los cálculos.
Referencias
[1] "Jazz Improvisation." A Passion for Jazz! Music History & Education. http://www.apassion4jazz.net
[2] Pressing, J. (1988). Improvisation: Methods and model. In J. A. Sloboda (Ed.), Generative processes in music (pp.129-178). Oxford, UK: Oxford University Press.
[3] Johson-Laird,P.N.(2002).How jazz musicians improvise. Music Perception., 19, 415-442.
[4] Resch, Barbara, Hidden Markov Models: A Tutorial for the Course Computational Intelligence. http://www.igi.tugraz.at/lehre/CI
[5] Pachet , Pierre Roy , Gabriele Barbieri, Finite-length Markov processes with constraints, Proceedings of the Twenty-Second International joint conference on Artificial Intelligence, July 16-22, 2011
[6] C. Bessiere, E. C. Freuder, and J.-C. Regin. Using inference to reduce arc consistency computation. In Proc. of the IJCAI95, pages 592-598. Morgan Kaufmann, 1995.
[7] Norgaard, Martin; Spencer, Jonathan; Montiel, Mariana. Testing Cognitive Theories by Creating a Pattern-Based Probabilistic Algorithm for Melody and Rhythm in Jazz Improvisation. Psychomusicology, vol. 23, No. 4. 2013
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
1. Sobre el consenso entre expertos en música
El artículo de este mes versa sobre un problema que me he encontrado con cierta frecuencia en el campo de la teoría musical y de la musicología. Ese problema es el del consenso entre expertos en música. A la hora de evaluar un fenómeno musical, ¿cómo se ponen de acuerdo los expertos? ¿Son capaces de formalizar los criterios por los cuales toman su decisión? Si hay desacuerdo entre ellos, ¿cómo se formula tal desacuerdo? ¿Qué metodología usan para evaluar el fenómeno y poner en común una evaluación final? ¿Cómo se matiza tal evaluación? ¿Cuántos expertos es recomendable tener para una evaluación mínimamente fiable? Estas preguntas aparecen en el transcurso de la investigación en música. Por asombroso que parezca, en numerosas ocasiones he visto evaluaciones hechas por un único experto y que el resto de la comunidad ha dado por buena o al menos con muy pocas voces discordantes. De que ese único experto tenía un conocimiento y experiencia formidables no cabía ninguna duda; pero incluso los expertos cometen errores de juicio; pero además no es riguroso aceptar la opinión de un solo experto, por muy prestigioso que este sea. He visto también, por ejemplo, que un experto prestigioso ha basado su evaluación en pequeñísimo número de piezas musicales, a veces tres, pero en otros casos no más de una decena. También aquí parece que falta rigor. Lo observable en un número tan pequeño de piezas puede no ser generalizable al resto y si así lo es habría que justificarlo adecuadamente (normalmente tal justificación está ausente).
En el transcurso de mis investigaciones me he encontrado con ejemplos de esta situación, tanto al estudiar artículos como en los proyectos de investigación en que he participado. Por ejemplo, en el caso del flamenco no hay consenso en cuanto a cómo se tiene que transcribir, si bien creando una nueva notación, posiblemente partiendo de la notación occidental, o bien tomando la notación occidental como método único de transcripción. La notación occidental se creó para escribir una música cuyas características no coinciden totalmente con las del flamenco. Además, hay diferencias entre proponer un sistema de transcripción para la guitarra y otro para la voz. La guitarra es un instrumento de afinación fija, pero la voz y menos en el flamenco, no lo es. Donnier para la voz propone un sistema que parte del cante gregoriano [Don11, Don96], pero otros autores como los hermanos Hurtado abogan rotundamente por la notación occidental para todo el flamenco; véase [HH02]. El guitarrista y musicólogo Rafael Hoces, en su tesis doctoral La transcripción para guitarra flamenca [Hoc13], apoya la idea del uso de la notación occidental solo para la transcripción de la guitarra. Entre los flamencólogos, cuando se presenta este debate, algunos llegan a decir es mejor seguir con la notación occidental pues no se alcanzaría acuerdo en diseñar una nueva notación que se adecuase a las peculiaridades del flamenco. De nuevo, aquí estamos en presencia del problema del consenso entre expertos.
En los últimos años se está investigando con fuerza los mecanismos que subyacen en la improvisación. Hay dos escuelas de pensamiento al respecto, una que propone que la improvisación se configura a partir de reglas, al estilo de las gramáticas generativas de Chomsky, o trasladado al ámbito músical, al estilo de la teoría generativa de la música de Fred Lerdahl y Ray Jackendoff [LJ03] (véase la serie correspondiente en esta columna [Góm14]). Cada estilo (jazz, flamenco, etc.) tiene sus reglas precisas que hacen que una improvisación se vea dentro del estilo o fuera de él. La otra escuela mantiene que la improvisación se hace a base de patrones, que pueden ser de todo tipo: melódicos, armónicos, rítmicos, formales; y que entonces la calidad de la improvisación está en función de la combinación acertada de esos patrones. Probablemente, la improvisación venga dada por una combinación de ambas. No se sabe, empero, para qué parámetros musicales y en qué grado se produce tal combinación. Investigadores de ambas escuelas de pensamiento han escrito programas que toman, por ejemplo, un corpus de solos de un trompetista de jazz (Parker, Coltrane u otros) y a partir de ese corpus, bien por reglas [GKT10] o por patrones [NSM13], componen solos en su estilo. A la hora de evaluar los resultados del programa, esto es, cuán fielmente se reflejan las características del músico en cuestión, con frecuencia nos encontramos que es la opinión de los autores del artículo el único criterio de evaluación. Los autores afirman que los solos son buenos porque “suenan al trompetista”, o porque “reflejan su pensamiento musical”, pero no aportan razones que sostengan estas afirmaciones. Y no dudo de la honestidad intelectual de estos investigadores, pero desde el punto de vista del rigor metodológico, en ciencia (y la musicología lo es) es difícil aceptar esas afirmaciones.
2. ¿Qué pueden hacer las matemáticas?
En otros campos ya ha surgido el problema de alcanzar consenso entre expertos. En medicina, por ejemplo, es un problema que aparece con frecuencia. ¿Cómo lo resuelven en medicina? Hay varios métodos, pero uno de ellos, que goza de cierta popularidad, es el llamado método Delphi. La técnica Delphi es un método para recoger información de expertos y construir consenso a partir de dicha información. Vamos a describir ese método y ver cómo se podría aplicar a la teoría de la música.
Jorm [Jor15], en un artículo titulado Using the Delphi expert consensus method in mental health research, investiga la aplicación del método Delphi al acuerdo entre expertos en el campo de la salud mental. El primer paso en la implementación del método es la selección de los expertos. Basándose en el trabajo de Surowiecki [Sur04], el famoso libro The wisdom of crowds: why the many are smarter than the few, propone las siguientes condiciones para elegirlos:
Diversidad de expertos. Un grupo heterogéneo de expertos previsiblemente producirá resultados de mayor calidad que un grupo fuertemente homogéneo.
Independencia. Los expertos han de tomar sus decisiones de modo independiente y sin influencia externa.
Descentralización. Los expertos trabajan de manera autónoma en la producción de sus resultados.
Coordinación. Para los resultados finales existe un mecanismo de coordinación entre los expertos.
Aunque no en todas las circunstancias el trabajo de un grupo de expertos da buenos resultados, se han estudiado las condiciones bajo las cuales esto ocurre. Hay una gran variedad de contextos en que dicho trabajo es útil y valioso; para más detalles, véanse las referencias del artículo de Jorm [Jor15] (página 888).
Hay muchas variantes del método Delphi, sobre todo en función de la aplicación particular, pero se puede describir de forma general como una serie de rondas en que el coordinador del método manda a los expertos unos cuestionarios. Los expertos han de responder a estos cuestionarios y devolverlos al coordinador, quien a su ve estructura la información y los vuelve a mandar a los expertos, quienes, a su vez, han de revisar y criticar sus respuestas anteriores. Este proceso se repite hasta que se alcanza el máximo número de rondas establecido o se alcanza consenso. Asociado al método suele haber tratamiento estadístico de los datos, tanto cuantitativo como cualitativo.
Veamos más en concreto cómo se implementa el método Delphi; seguimos aquí el trabajo de Jorm. Los pasos que este establece son los siguientes:
Establecimiento de la pregunta de investigación. Como en toda investigación, hay una serie de pregunta o preguntas que se esperan responder en este caso a partir del consenso entre los expertos.
Selección del panel de expertos. Más arriba se describió cómo elegirlos.
Determinación del tamaño del panel de expertos. Esta cuestión es delicada y depende en gran medida de la disponibilidad de los expertos y del problema en concreto. Obviamente, un número excesivamente pequeño de expertos no proporciona buenos resultados, pues la opinión de cada experto tendría mucha influencia. Lo ideal es encontrar el número mínimo de expertos que garanticen la estabilidad en los resultados. Algunos autores recomiendan un número alrededor de 23 expertos. En ciertos contextos, esto no es posible porque no hay un número tan alto de expertos o porque los expertos no siguen la metodología Delphi fielmente (y entonces hay que descartar su aportación).
Diseño del cuestionario. El cuestionario se basa en una fase previa de documentación, la cual se hace mediante una revisión de la bibliografía existente. Es importante hacer preguntas que sean de máxima relevancia (estamos usando el precioso tiempo de los expertos). Cuanto mejor esté formulada la pregunta de investigación, más relevantes serán las preguntas en el cuestionario. Existen metodologías específicas para redactar los cuestionarios; véanse las referencias citadas en [Jor15].
Información previa proporcionada al panel de expertos. En algunos casos, los expertos reciben información sobre cómo puntuar las preguntas (si estas así lo exigen, típicamente en una escala de Likert), el formato de las preguntas o la justificación de las respuestas. Es importante que las instrucciones de cómo contestar a los cuestionarios sean muy claras de modo que los expertos contesten correctamente.
Distribución del cuestionario. Los expertos no tienen que reunirse para contestar a los cuestionarios. Los medios para distribuir son variados, desde una encuesta por vía de un formulario web hasta el clásico correo electrónico.
Análisis y crítica de las información recogida en las rondas. El método Delphi requiere una definición de consenso. Una definición general y aplicable a cada no existe. Cada equipo de investigadores tiene que construir su propia definición y ponerla a prueba durante el proceso. Tras la primera ronda, el equipo de investigadores analiza los resultados y en función de ellos vuelve a mandar una segunda ronda de cuestionarios. Los expertos reciben críticas y comentarios a las respuestas de su primera ronda y se les pide que contesten a esta segunda ronda. Este proceso se repite cierto número de veces. Algunos autores recomiendan que sea tres o cuatro veces. De nuevo, depende de la investigación, pero no puede ser muy alto ya que se produce cansancio intelectual y psicológico en los expertos. El tiempo entre ronda y ronda no debería ser muy alto, pues de lo contrario se pierde interés en el proceso. Si la naturaleza del problema lo permite, se pueden tomar medidas cuantitativas y cualitativas y llevar a cabo análisis estadísticos.
Informe de los resultados. El informe de resultados puede adoptar muchas formas. Puede consistir simplemente en un recuento de los puntos en los que hubo acuerdo o puede llegar a ser algo muy complejo que se puede describir en términos de grafos, mapas conceptuales, análisis de agrupamientos, entre otros. En la figura 1 se ve un ejemplo tomado del artículo de Jorm donde se esquematiza el proceso de las rondas y se informa del número de ítems incluidos en una investigación médica.
Figura 1: Diagrama de flujo asociado a un proceso Delphi (figura tomada de [Jor15])
En un reciente artículo (junio de 2015), Albert Fornells y sus coautores [FRR+15] aplican la metodología Delphi a problemas de consenso entre expertos en el campo de la hostelería. Los resultados de su método aparecen en forma de mapa conceptual. La formalización matemática de su método es muy alta. Formalizan el razonamiento cualitativo de los expertos usando teoría de conjuntos y tras pasar revista varios índices de consenso, proponen el suyo propio. Los mapas conceptuales los construyen usando técnicas clásicas de agrupamiento tales como los grafos filogenéticos. Este trabajo da una idea del nivel de formalización que se puede introducir en el problema del consenso entre expertos.
3. Conclusiones
El método que hemos examinado es totalmente aplicable al problema de alcanzar consenso entre expertos en música. Su uso contribuiría, sin duda, a dar más rigor a las conclusiones en las investigaciones musicales. ¿Cuál es, pues, la contribución de las matemáticas aquí? El rigor; el rigor metodológico. La aplicación de las matemáticas a la música que proponemos en la columna de este mes no está relacionada con la formalización de una propiedad musical en términos matemáticos o en la aplicación de una idea matemática a la composición musical, por poner dos ejemplos clásicos; no, está relacionada con el espíritu de las matemáticas, con la voluntad de rigor que poseen.
Bibliografía
[Don96] Ph. Donnier. Flamenco, structures temporelles et processus d’improvisation. PhD thesis, Université Paris X. Nanterre, 1996.
[Don11] P. Donnier. Flamenco: elementos para la transcripción. Del cante y de la guitarra. http://divulgamat2.ehu.es/divulgamat15/index.php?option=com_content&view=article&id=12354&directory=67, abril de 2011.
[FRR+15] Albert Fornells, Zaida Rodrigo, Xari Rovira, Mónica Sánchez, Ricard Santomà, Francesc Teixidó-Navarro, and Elisabet Golobardes. Promoting consensus in the concept mapping methodology: An application in the hospitality sector. Pattern Recognition Letters, 67:39–48, 2015.
[GKT10] J. Gillick, R. M. Keller, and M. Tang, K. Machine learning of jazz grammars. Computer Music Journal, 34:56–66, 2010.
[Góm14] P. Gómez. Teoría generativa de la música - I. http://divulgamat2.ehu.es/divulgamat15/index.php?option=com_content&view=article&id=16037&directory=67, junio de 2014.
[HH02] A. Hurtado and D. Hurtado. La voz de la tierra: estudio y transcripción de los cantes campesinos en las provincias de Jaén y Córdoba. Junta de Andalucía, Centro Andaluz de Flamenco, Sevilla, 2002.
[Hoc13] R. Hoces. La transcripción para guitarra flamenca. PhD thesis, Universidad de Sevilla, 2013.
[Jor15] A. F. Jorm. Using the Delphi expert consensus method in mental health research. Australian and New Zealand Journal of Psychiatry, 49(10):887–897, 2015.
[LJ03] Fred Lerdahl and Ray Jachendoff. Teoría generativa de la música tonal. Akal, Madrid, 2003.
[NSM13] M. Norgaard, J. Spencer, and M. Montiel. Testing cognitive theories by creating a pattern-based probabilistic algorithm for melody and rhythm in jazz improvisation. Psychomusicology, 23:243–254, 2013.
[Sur04] J.. Surowiecki. The wisdom of crowds: why the many are smarter than the few. Abacus, Londres, 2004.
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
Esta es la última entrega de la serie Música y probabilidad en la que estamos estudiando modelos probabilísticos siguiendo el libro de Temperley Music and Probability [Tem10]. Estudiaremos en esta cuarta entrega los modelos de expectativa musical, tanto de ritmo como de altura del sonido así como los de detección de errores. La primera entrega [Góm16c] consistió en un argumentario a favor del estudio de la probabilidad por parte de los músicos y una introducción al libro de Temperley. En la segunda entrega [Góm16a], estudiamos los modelos computacionales y probabilísticos para el ritmo, y en la tercera entrega [Góm16b], los modelos probabilísticos de la altura del sonido. Esperamos que con estos cuatro artículos hayamos convencido, o al menos ablandado, al lector escéptico acerca de las bondades del conocimiento de la probabilidad para el estudiante de música, en especial para el futuro musicólogo.
1. Probabilidad de una melodía
En las dos entregas anteriores se trató el ritmo y la altura del sonido por separado. En esta entrega vamos a combinar ambos para dar un modelo conjunto de la melodía. La hipótesis principal que Temperley hace sobre el modelo conjunto es que ritmo y altura se pueden elegir independiente de modo que la probabilidad de una melodía es el producto de la probabilidad de los patrones rítmicos (duraciones) por la probabilidad de la sucesión de alturas. El estudio que lleva a cabo sobre la probabilidad de la melodía (capítulo 5) se centra en dos fenómenos, a saber, las expectativas musicales y la detección de errores. Las expectativas se refiere a las notas que el oyente espera tras haber oído una melodía previa. La detección de errores se refiere a cómo el oyente detecta errores en la melodía. Las expectativas en la melodía se dividen en las expectativas sobre la altura del sonido y sobre el ritmo, las cuales tratamos por separado.
2. Expectativas en la altura de la melodía
En la percepción de la melodía, las expectativas desempeñan un papel importante. La investigación en cognición musical ha estudiado esta cuestión desde hace mucho tiempo. Los oyentes se forman expectativas en cuanto a las notas que siguen una sucesión de notas previas —tanto en términos de ritmo como de altura del sonido— y ello crea y disuelve la tensión musical, que es entre otros factores la manera en que el discurso musical progresa. Se sabe que la creación, la confirmación y la negación de las expectativas musicales es una parte fundamental del proceso de creación del significado musical. Ya Meyer [Mey56] en su libro de 1956 Emotion and Meaning in Music analiza exhaustivamente esta cuestión en base a la teoría de la percepción de la forma (Gestalt). Posteriormente, Narmour [Nar90], en 1990, con su libro The Analysis and Cognition of Basic Melodic Structures: The Implication- Realization Model extiende y profundiza notablemente el estudio de las expectativas musicales.
Desde un punto de vista experimental, hay dos enfoques o paradigmas: el paradigma de la percepción y el de la producción. En los estudios pertenecientes al primer paradigma se pide a los sujetos que, tras oír un fragmento de una melodía, juzguen si una cierta nota es la mejor continuación; véanse los trabajos de Schmuckler [Sch89] y Cuddy y Lunney [CL95]. En el paradigma de la producción, en cambio, se pide a los sujetos que produzcan la nota que consideran más adecuada para continuar la melodía; véanse los artículos de [Pov96], [TCP97], and [Lar04] así como las referencias del propio libro de Temperley.
El modelo de Temperley se basa en el trabajo de Cuddy y Lunney [CL95]. En los experimentos llevados a cabo por estos autores, los sujetos tenían que juzgar una melodía de dos notas que era continuada por una tercera nota en una escala de 1 a 7, donde 1 corresponde a una “extremadamente mala continuación” y 7 a una “extremadamente buena continuación”. Las melodías (o contextos musicales, como los llama Temperley) fueron los siguientes: (A) segunda mayor ascendente; (B) segunda mayor descendente; (C) tercera menor ascendente; (D) tercera menor descendente; (E) sexta mayor ascendente; (F) sexta mayor descendente; (G) séptima mayor ascendente; (H) séptima mayor descendente; véase la figura 1.
Figura 1: Melodías de dos notas usadas en los experimentos de Cuddy y Lunney [CL95] (figura tomada de [Tem10])
Los autores presentaron 25 continuaciones diferentes para cada par de notas; esas continuaciones se generaron tomando todos los tonos posibles dentro de una octava hacia arriba y hacia abajo. A partir de estos datos, Cuddy y Lunney dieron la clasificación media para cada continuación tomada entre todos los sujetos.
Entre los numerosos modelos de expectativa de las alturas de sonido, Temperley se fijó en los modelos perceptuales y descartó los teóricos, es decir, se quedó con aquellos modelos que tenían su base en experimentos perceptuales con sujetos reales. Estos modelos suelen usar regresión múltiple como método para obtener las mejores continuaciones. Uno de esos ejemplos se encuentra en el trabajo de Schmuckler [Sch89], en el que el autor asigna una puntuación a cada posible continuación que es una combinación lineal de varios factores. La regresión múltiple se usa para ajustar estas variables a los resultados de los sujetos de manera óptima (minimizando el error de la predicción). Otro grupo de trabajos se centró en la teoría de la implicación-realización de Narmour [Nar90]. En particular, Krumhansl [Kru95] y Schellenger [Sch96] dieron cobertura experimental a la teoría de Narmour. Schellenger consiguió un coeficiente de correlación de 0.8 al aplicar regresión múltiple usando como variables independientes las dadas por el modelo de Narmour y como variables dependientes las medidas experimentales de Cuddy y Lunney.
En su libro Temperley toma los datos de Cuddy y Lunney y los reinterpreta en términos probabilísticos. Tras comparar varios métodos, decide interpretar las puntuaciones de las continuaciones dadas por los sujetos como los logaritmos de las probabilidades. En concreto, se interpretan como los logaritmos de las probabilidades condicionadas, es decir, los logaritmos de la probabilidad de que un tono sea una continuación dada un contexto previo de dos notas. Usando los parámetros obtenidos a partir del corpus Essen Folksong Collection [Sch95], Temperley es capaz de obtener un coeficiente de correlación de 0.729. Tras algunos ajustes en el modelo, llega a obtener un coeficiente de 0.87. En la figura 2 se comparan el modelo de Cuddy y Lunney y el de Temperley para dos intervalos dados, la segunda mayor ascendente y la sexta mayor descendente. El eje horizontal muestra las posibles continuaciones descritas en términos de semitonos (de ahí el rango de +12 a -12); el eje vertical proporciona la puntuación media de los sujetos.
Figura 2: Comparación de los datos de los experimentos de Cuddy y Lunney [CL95] y del modelo de Temperley (figura tomada de [Tem10])
En su modelo probabilístico, Temperley tiene en cuenta el fenómeno de las inversiones post-salto. Es un hecho comprobado que grandes saltos en la melodía suelen estar seguidos por cambios en la dirección melódica. Tanto los modelos de Narmour como el de Schellenger tienen en cuenta este fenómeno. Otros autores, como von Hippel y Huron [vHH00], lo niegan y argumentan que se trata de un efecto debido a la regresión a la media, que no expresa sino la tendencia a estar en el centro de la tesitura. La manera en que se trata la inversiones post-salto se refleja en las probabilidades que se obtienen en el modelo. No entraremos a describir la implementación de este fenómeno; el lector interesado puede consultar el libro de Temperley en las páginas 69 a 70.
3. Expectativas en el ritmo
El modelo probabilístico de Temperley también considera la componente rítmica. Las expectativas son similares a las del caso de la altura de sonido. Tras escuchar unas secuencias de duraciones, el oyente espera con más probabilidad ciertas continuaciones que otras. Este hecho se puede justificar en base a la ley de continuación de la percepción de la forma (véase el libro de Meyer [Mey56]). Por ejemplo, tras oír una sucesión de notas de igual duración, el oyente espera encontrar otra nota de igual duración; véase la figura 3.
Figura 3: Comparación de los datos de los experimentos de Cuddy y Lunney [CL95] y del modelo de Temperley (figura tomada de [Tem10])
Esta expectativa del oyente influye en la percepción de la altura. En efecto, cuando una nota ocurre en la posición de mayor expectativa, la altura es evaluada con más precisión por el oyente que si ocurre un poco o bien un poco después. Large y Jones, dos autores que han estudiado este fenómeno en profundidad, lo llaman el modelo del oscilador [LJ99]
Para su modelo de expectativa del ritmo, Temperley acude al modelo de ritmo que presentó previamente (capítulo 3 de su libro [Tem10]; tercera entrega de nuestra serie [Góm16b]). La expectativa de una continuación será la probabilidad condicionada de la continuación dado el contexto. En el caso del ritmo, la adaptación del modelo de ritmo a un modelo de expectativa del ritmo no es directa, como sí ocurrió en el caso de la altura del sonido. Hay una discusión técnica de cómo se puede llevar a cabo tal adaptación, discusión que no reproduciremos aquí, pero que el lector con suficiente entrenamiento en probabilidad puede seguir en las páginas 72 y 73 del libro de Temperley. Las probabilidades que aparecen en la figura 3 están calculadas con el modelo de ritmo y esa adaptación de la que hablamos.
4. Detección de errores
Temperley aprovecha su modelo para estudiar otro fenómeno musical: la detección de errores. Se sabe por los experimentos llevados a cabo en la investigación que los oyentes pueden detectar errores en la música, incluso aunque se trate de música de tradiciones que les son desconocidas. Esto se debe a que en la escucha el cerebro detecta patrones con mucha eficiencia y, aunque el oyente no conozca el estilo, detecta dichos errores. Los errores en las notas se pueden clasificar en varias categorías: errores en la nota, donde el intérprete toca una nota por otra; errores en la afinación (cuartos de tono en las cuerdas o las notas en la octava aguda dadas por la sobrepresión en los vientos); errores que el oyente no percibe (porque su cerebro corrige la nota); errores detectados, entre otros.
De nuevo, Temperley recurre al corpus de Essen [Sch95], que ya empleara para probar el modelo de alturas. Modifica aleatoriamente el ritmo y la altura de las notas y obtiene un nuevo corpus de 650 piezas, sumadas las piezas originales y las modificadas (esto es, las versiones con errores). A continuación obtiene las probabilidades de continuación para las melodías y compara las versiones originales con las versiones modificadas. Para la altura de sonido, en 573 de las 650 melodías el modelo asignó mayor probabilidad a la versión original que a la versión modificada. En el caso del ritmo, en 49 de 650 casos, el modelo no detectó como diferente la versión modificada. De los restantes casos, 601, el modelo asignó correctamente la probabilidad en 493 de los casos, que es un 82%.
5. Conclusiones
Esperamos haber ilustrado fehacientemente las conexiones entre la probabilidad y la música. Esas conexiones son mucho más extensas y profundas que las mostradas en las cuatro entregas de esta serie, como se puede ver en los restantes capítulos del libro de Temperley (nosotros hemos glosado aquí solo los cinco primeros) y en sus referencias. Asimismo, esperamos haber convencido al lector escéptico, especialmente el músico, de las bondades de incluir la formación matemática en la música, en particular la de la probabilidad.
Durante estos primeros seis meses de 2016 estoy pasando una estancia de investigación en la Universidad del Estado de Georgia, Atlanta. Estoy un curso cuyo título es Introducción a los modelos matemáticos y que está dirigido a alumnos que no son de matemáticas. En mi clase tengo a estudiantes de cine, enfermería, ciencias políticas, criminología, trabajo social... y música. Sí, música. Aquí hacen estudiar a los alumnos de ciencias humanidades y artes; y a los de humanidades y artes, ciencias. Y he decir que los alumnos de música están entre los mejores a la hora de razonar matemáticamente. No me imagino en ningún conservatorio de España poniendo en el plan de estudios asignaturas de matemáticas. Fuera de nuestras fronteras, lleva años haciéndose. Quizás sea esa la razón por la que apenas nadie destaca en este país en Musicología Sistemática y menos aún en Musicología Computacional.
Bibliografía
[CL95] L. L. Cuddy and C. A. Lunney. Expectancies generated by melodic intervals: Perceptual judgments of melodic continuity. Perception and Psychophysics, 57:451–462, 1995.
[Góm16a] P. Gómez. Música y Probabilidad (II). http://divulgamat2.ehu.es/divulgamat15/index.php?option=com_content&view=article&id=16921&directory=67, diciembre de 2016.
[Góm16b] P. Gómez. Música y Probabilidad (III). http://divulgamat2.ehu.es/divulgamat15/index.php?option=com_content&view=article&id=16940&directory=67, diciembre de 2016.
[Góm16c] P. Gómez. Música y Probabilidad (I). http://divulgamat2.ehu.es/divulgamat15/index.php?option=com_content&view=article&id=16871&directory=67, noviembre de 2016.
[Kru95] C. L. Krumhansl. Music psychology and music theory: Problems and prospects. Music Theory Spectrum, 17:53–80, 1995.
[Lar04] S. Larson. Musical forces and melodic expectations: Comparing computer models and experimental results. Music Perception, 21:457–498, 2004.
[LJ99] E. W. Large and M. R. Jones. The dynamics of attending: How people track time varying events. Psychological Review, 106:119–159, 1999.
[Mey56] Leonard Meyer. Emotion and Meaning in Music. University of Chicago Press, Chicago, 1956.
[Nar90] E. Narmour. The Analysis and Cognition of Basic Melodic Structures: The Implication-Realization Model. University of Chicago Press, Chicago, 1990.
[Pov96] D.-J. Povel. Exploring the fundamental harmonic forces in the tonal system. Psychological Research, 58:274–283, 1996.
[Sch89] M. Schmuckler. Expectation and music: Investigation of melodic and harmonic processes. Music Perception, 7:109–150, 1989.
[Sch95] H. Schaffrath. The Essen Folksong Collection. Center for Computer-Assisted Research in the Humanities, Stanford, Calif., 1995. Editado por D. Huron.
[Sch96] E. G. Schellenberg. Expectancy in melody: Tests of the implication–realization model. Cognition, 58:75–125, 1996.
[TCP97] W. F. Thompson, L. L. Cuddy, and C. Plaus. Expectancies generated by melodic intervals: Evaluation of principles of melodic implication in a melody-completion task. Perception & Psychophysics, 59:1069–1076, 1997.
[Tem10] D. Temperley. Music and Probability. MIT Press Ltd, 2010.
[vHH00] P. von Hippel and D. Huron. Why do skips precede reversals? The effect of tessitura on melodic structure. Music Perception, 18:59–85, 2000.
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
En la anterior entrega [Góm16] de la serie Música y probabilidad estudiamos los modelos computacionales del ritmo, en particular, los modelos probabilísticos. La presenta entrega de la serie versa sobre los modelos probabilísticos de la altura del sonido. De nuevo, seguiremos para nuestra exposición el excelente libro de Temperley Music and Probability.
1. El modelo de alturas
Por modelo de alturas se puede entender muchos conceptos. La altura es la cualidad que permite distinguir un sonido grave de uno agudo y está directamente relacionada con la frecuencia del sonido en cuestión, pero hay otros muchos factores que influyen en su percepción final (los sonidos vecinos, el contexto tonal, el timbre, el volumen, entre otros). En nuestro caso, nos vamos a centrar en los modelos de percepción de la tonalidad. La música que vamos a analizar, la música occidental de la práctica común, está en el marco de la música tonal y los modelos de alturas están estrechamente relacionados con la percepción de la tonalidad. En cuanto a las voces, nos vamos a concentrar en una sola voz, esto es, en entradas monofónicas.
El libro de Temperley empieza su estudio de los modelos de alturas con una revisión bastante exhaustiva de la bibliografía sobre percepción de alturas en el campo de la cognición musical. La mayor parte de los estudios que glosa Temperley usa un contexto tonal. Por ejemplo, una grupo de estudios se podrían clasificar bajo el epígrafe de estudios de notas de contraste (probe-tone studies, en inglés). En estos estudios se proporciona a los sujetos una melodía con una tonalidad bien establecida y luego se presenta una nota aparte y se pide a los sujetos que digan si esa nota pertenece a la tonalidad de la melodía; véase los estudios de Krumhansl [Kru90] o Brown y colaboradores [BBJ94]. Otros estudios investigaron el papel de la tonalidad en la percepción de la altura y de la melodía en contextos más generales. Se concluyó que la tonalidad establece jerarquía en las alturas (véase [PK87]), afecta a la memoria, influye en el reconocimiento de melodías (véase [CCM81]) y condiciona las expectativas musicales (véase [CL95]).
Otros autores han investigado la cuestión de cómo los oyentes deducen la tonalidad, problema que se llama determinación de la tonalidad. Esta cuestión fue estudiada por Longuet-Higgins y Steedman [LHS71] en un artículo de 1971. Su modelo estaba diseñado únicamente para música monofónica y se basaba en la relación que hay entre tonalidad y escala. Esos autores explotan la idea de que la escala refleja la tonalidad y a partir de ello construyeron un algoritmo para determinar la tonalidad. Por ejemplo, la escala asociada a la tonalidad de sol mayor son y en una melodía en esa tonalidad deberíamos esperar que la mayor parte de las notas perteneciesen a ese conjunto. El algoritmo procesa una a una las notas de la melodía de principio a fin y para cada nota elimina las tonalidades que no tienen a esa nota en su escala. Si al final del proceso, solo queda una tonalidad, esa será la tonalidad elegida. Si por el contrario, no quedan tonalidades candidatas, entonces el algoritmo toma la primera nota y establece la tonalidad en que esa nota es la fundamental. Si esa decisión no es coherente, entonces el algoritmo elige como tonalidad aquella en que la primera nota es la dominante. Por ejemplo, si la primera nota fuese sol, hay siete posibles tonalidades que tienen la nota sol; se elige en primera opción la tonalidad de sol y si esta no funciona se toma do (para la que sol es la dominante).
Longuett-Higgins y Steedman comprobaron la validez de su modelo con los temas de las fugas de El clave bien temperado de Bach. En todos los casos su algoritmo dio con la tonalidad correcta. Sin embargo, es fácil darse cuenta de que el modelo de estos autores no funciona en todos los casos. Cuando los centros tonales de la melodía se refuerzan mediante cromatismo, entonces el modelo puede asignar una tonalidad errónea. Por ejemplo, en la figura 1 tenemos dos melodías. La primera, la A, está claramente en la tonalidad de si♭ mayor; empero, el modelo, por falta de más información, tendría que decidir entre varias tonalidades, a saber, fa mayor, si♭ mayor, mi♭ y otras. Aplicando la regla de la primera nota, establecería que la tonalidad es fa mayor, lo que es incorrecto. En la segunda melodía, la B, se ve inmediatamente que está en do mayor, especialmente gracias a los compases dos y cuatro. No obstante, a causa de las notas cromáticas fa# y do#, las tonalidades que incluyen estas notas se considerarían candidatas, lo que no es lógico por la forma de esta melodía.
Figura 1: El algoritmo de Longuett-Higgins y Steedman (figura tomada de [Tem10])
El trabajo de Krumhansl-Schmuckler (K-S de ahora en adelante), y el cual se resume magníficamente en el libro de Krumhansl Cognitive Foundations of Musical Pitch [Kru90], presenta un algoritmo más robusto y con base empírica. El algoritmo K-S se basa en los denominados perfiles de tonalidad, que miden la compatibilidad de cada altura con su tonalidad. Estos perfiles de tonalidad se obtuvieron a partir de cuidadosos experimentos con sujetos que llevaron a cabo los autores. Para cada tonalidad concreta se construyeron dos perfiles, uno para el modo mayor y otro para el modo menor (en total hay 24 perfiles de tonalidad). La figura 2 muestra dos ejemplos de perfiles; el primer perfil corresponde al modo mayor y el segundo, al modo menor. En el modo mayor se puede que en orden decreciente de compatibilidad tenemos la tónica, la dominante, la tercera, la subdominante y luego el resto de los grados. La situación es diferente para el modo menor, donde el tercer grado menor tiene más compatibilidad que la dominante.
Figura 2: Perfiles de tonalidades (figura tomada de [Tem10])
La manera en que el algoritmo K-S funciona es por correlación. Dada una pieza cuya tonalidad se quiere determinar, se toman las duraciones de las doce notas de la escala cromática en la pieza (algunas, claro es, podrían ser cero). Llamémos x a ese vector de duraciones. Si y es el vector dado por los perfiles tonales, entonces el algoritmo K-S calcula el coeficiente de correlación r como sigue:
donde y son las medias de los vectores x e y, respectivamente. Se calculan todos los coeficientes de correlación para todas las tonalidades en ambos modos y se elige como tonalidad definitiva aquella que maximice el coeficiente de correlación.
El lector avispado —es decir, cualquier lector de esta columna—ya se habrá dado cuenta de un inconveniente que tiene el modelo K-S. Si una nota se repite mucho, aunque no pertenezca a la tonalidad, proporcionará mucho peso en el coeficiente de correlación, pero no reflejará la verdadera tonalidad. Extensiones y críticas al modelo K-S han aparecido en la bibliografía. En general, es un modelo válido y está basado en principios musicales y apoyado por experimentos con sujetos.
2. El modelo de Temperley
El modelo de Temperley es un modelo probabilístico que se basa en inferencia bayesiana. Sigue unos principios similares a su modelo rítmico, aunque es más complejo que en el caso del ritmo y lo describiremos sin entrar en el aparato matemático. Se especifica un modelo que depende de unos parámetros iniciales, los cuales se deducen a partir de un corpus musical. El corpus elegido es de nuevo la Essen Folksong Collection [Sch95]. La idea de Temperley para construir su modelo es refinar la idea de Krumhansl-Schmuckler de los perfiles de tonalidad. Temperley escoge tres perfiles para los cuales estudia su distribución en el corpus. Esos tres perfiles son: el perfil de alturas, el perfil de rango y el perfil de proximidad.
El perfil de alturas de la colección Essen es el que aparece en la figura siguiente, donde las alturas se han representado por números enteros con C4=60.
Figura 3: Distribución de las alturas en el corpus Essen (figura tomada de [Tem10])
Temperley estudia la media y la varianza del corpus entero así como de las melodías individuales. A pesar de los valles y picos que tiene la gráfica anterior, Temperley impone como modelo probabilístico una normal cuyos parámetros extrae del corpus (usa el método de los momentos, donde identifica los momentos muestrales con los momentos poblacionales). A continuación crea una segunda distribución que modeliza el rango de la melodía y para la que también usa una distribución normal. Por último, modeliza la distribución de los intervalos melódicos con una distribución normal, pero esta vez con una peculiaridad: la media de una nota particular depende de la nota anterior. Esto refleja el hecho conocido de que la probabilidad de que una nota siga a otra no es uniforme, sino que depende del contexto armónico-melódico. Con estos tres perfiles se crea un perfil global, llamado perfil RPK, que es el producto de los tres perfiles, el de alturas, el de rango y el de proximidad. En la figura siguente se muestran los parámetros del modelo de Temperley.
Figura 4: Distribución de las alturas en el corpus Essen (figura tomada de [Tem10])
Tras configurar los valores iniciales del modelo, a continuación se calcula la probabilidad de una melodía en una tonalidad dada. Esto se hace para todas las tonalidades posibles. La tonalidad que maximiza la probabilidad es la que el algoritmo de Temperley devuelve como tonalidad de la melodía.
Temperley probó su sistema con un subconjunto de melodías del corpus Essen que no usó para configurar su algoritmo. Acertó en el 87,7% de los casos. Analizando en particular los casos en que falló, Temperley vio que se trataba de casos claros de melodías modales (que estaban en otros modos que no eran el mayor y el menor). Para las melodías en modos mayor y menor no falló nunca.
3. Conclusiones
Los fallos del modelo de Temperley no son excesivamente graves. Su modelo está diseñado para la detección de tonalidad en los modos mayor y menor y no en otros. Sin embargo, eso se puede enmendar sin más que crear perfiles de tonalidad para todos los demás modos. Esto, por supuesto, implica inicializar el modelo con corpus que contengan el resto de los modos.
Bibliografía
[BBJ94] H. Brown, D. Butler, and M. R. Jones. Musical and temporal influences on key discovery. Music Perception, 11:371–407, 1994.
[CCM81] L. L. Cuddy, A. J. Cohen, and D. J. K. Mewhort. Perception of structure in short melodic sequences. Journal of Experimental Psychology: Human Perception and Performance, 7:869–883, 1981.
[CL95] L. L. Cuddy and C. A. Lunney. Expectancies generated by melodic intervals: Perceptual judgments of melodic continuity. Perception and Psychophysics, 57:451–462, 1995.
[Góm16] P. Gómez. Música y Probabilidad (II). http://divulgamat2.ehu.es/divulgamat15/index.php?option=com_content&view=article&id=16921&directory=67, diciembre de 2016.
[Kru90] C. L.. Krumhansl. Cognitive Foundations of Musical Pitch. Oxford University Press, New York, 1990. Capítulo del libro Representing Musical Structure, P. Howell, R. West, and I. Cross (eds.).
[LHS71] H. C. Longuet-Higgins and M. J. Steedman. On interpreting Bach. Machine Intelligence, 6:221–241, 1971.
[PK87] C. Palmer and C. Krumhansl. Pitch and temporal contributions to musical phrase perception: Effects of harmony, performance timing, and familiarity. Perception and Psychophysics, 41:505–518, 1987.
[Sch95] H. Schaffrath. The Essen Folksong Collection. Center for Computer-Assisted Research in the Humanities, Stanford, Calif., 1995. Editado por D. Huron.
[Tem10] D. Temperley. Music and Probability. MIT Press Ltd, 2010.
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
1. El modelo rítmico
En esta segunda entrega de la serie Música y probabilidad vamos a examinar los modelos computacionales del ritmo y, en particular, el de Temperley [Tem10], que es un modelo probabilístico y computacional. Seguiremos la exposición que hace Temperley en su libro. En el artículo pasado [Góm16] discutimos la pertinencia del estudio de las matemáticas en la formación de los músicos y en concreto la probabilidad así como los problemas que hay en su enseñanza. Los artículos que siguen en esta serie tienen un cierto nivel matemático y es posible que a algunos lectores les cueste seguirlo, sobre todo a los de menos formación matemática. He intentado mantener el nivel de formalización lo más bajo posible sin comprometer la precisión con el fin de hacer el texto lo más divulgativo posible. Es un poco sorprendente, pero hasta lo que nuestro conocimiento alcanza no existen textos de probabilidad dirigidos exclusivamente a músicos. Es una laguna que habría que cubrir con cierta urgencia. La mejor opción para un músico que quisiese aprender probabilidad (y estadística) sería la de encontrar un buen profesor, con un método de aprendizaje activo, con sensibilidad hacia el perfil de estos alumnos, y con pasión por la materia. A falta de tan favorables circunstancias, una posibilidad alternativa es la de los cursos en línea como Statistics One [Con16] o Statistics: Making Sense Out of Data [GJ16]; estos cursos requieren esfuerzo continuado en el tiempo así como una voluntad de aprendizaje sólida.
2. Ritmo y métrica
La escucha de una melodía no consiste en la mera detección de los patrones de duración. El cerebro interpreta el ritmo de la melodía extrayendo una gran cantidad de información previa y combinándola con la información recibida durante la propia escucha de la pieza. Así, impone a la interpretación del patrón rítmico de la melodía una estructura perceptual y cognitiva rica y compleja. Esta estructura incluye la familiaridad con el estilo, la enculturación del oyente, su estado de ánimo, su formación musical, entre otros factores.
Como ejemplo de dicha complejidad, consideremos la figura 1, donde podemos ver en la parte de arriba un patrón rítmico, dado por sus ataques medidos en milisegundos. Debajo del patrón vemos hasta cinco interpretaciones diferentes en términos de métrica. La interpretación A asocia el patrón a un compás de 2/4, dando una negra con puntillo, una corchea y dos negras. Aquí los tiempos fuertes son el primero y el tercero. En la interpretación B tenemos un compás de 3/4. El patrón queda ahora incompleto, pues el último compás solo tiene una negra. Los tiempos fuertes ahora son el primero y el cuarto. Para la interpretación C tenemos un compás de 6/8, de subdivisión ternaria, donde de nuevo los tiempos fuertes son el primero y el cuarto. En la interpretación D la segunda nota es una nota de adorno de nuevo dentro de un compás de 2/4. Por último, en la interpretación E nos topamos con una visión del patrón que empieza con un silencio. Ahora solo hay un tiempo fuerte en la segunda nota (esta última interpretación está más bien forzada). De entre todas las interpretaciones ofrecidas aquí, parece que la más probable es la primera, aunque sin duda habrá lectores que discrepen de esta afirmación. Este ejemplo ilustra el problema de encontrar el contexto métrico más adecuado para enmarcar un patrón rítmico. Aquí el sentido la expresión “más adecuado” significa más musical, lo cual, una vez más, es relativo al estilo musical concreto (supondremos aquí que hablamos de la música tonal occidental).
Figura 1: Un patrón rítmico con diversas interpretaciones (figura tomada de [Tem10])
La métrica se define como un patrón de acentos que se producen de manera regular y sobre los cuales se construyen los patrones rítmicos. Los tiempos acentuados se llaman fuertes y los no acentuados, débiles. En esta definición se supone que hay pulso asíncrono encima del cual se define la métrica. La figura 2 muestra la estructura métrica de algunos de los compases más frecuentes en la música tonal occidental. El patrón de acentos se reproduce a distintos niveles, donde el más bajo suele ser el del pulso. Los tiempos que tienen más puntos encima son los tiempos que tienen más prominencia métrica. En la figura se ve que esos tiempos coinciden con el primer tiempo de cada compás.
Figura 2: Métricas para compases frecuentes (figura tomada de [Tem10])
En su libro, Temperley argumenta la importancia de la estructura métrica. Para ello, cita varios artículos de autores ilustres, como el artículo clásico de Gabrielsson [Gab73], donde que melodías con estructuras métricas similares se tienden a juzgar como más similares; o los trabajos más recientes de Sloboda [Slo85] y Povel y Essens [PE85] donde prueban que la ambigüedad métrica influye en la complejidad rítmica. Temperley alude a trabajos que han tratado otros aspectos de la métrica, como el papel de esta en la percepción de otras variables musicales (como la armonía y la estructura de la frase), su función en la interpretación o cómo configura la expectativa musical (véanse las referencias de la página 26 de citetemper-10).
Hay, sin embargo, un autor que humildemente consideramos que Temperley ha pasado por alto y es Stephen Handel. En su artículo The interplay between metric and figural rhythmic organization [Han98] de 1998 prueba que la agrupación (en inglés, figural organization) es mucho más preponderante que la estructura rítmica. Lo hace a partir de una serie de experimentos muy exhaustivos y bien diseñados donde confronta patrones de agrupación contra patrones métricos. No obstante, el trabajo de Temperley consiste en diseñar modelos computaciones para la métrica y no para la agrupación. Pero dado el trabajo de Handel, parece una buena idea construir modelos computacionales para la agrupación.
3. Modelos de percepción rítmica
La modelización de la percepción rítmica ha sido un problema de investigación que ha atraído a muchos investigadores de diversas áreas desde hace varias décadas. El propio Temperley, en una obra anterior, The cognition of basic musical structures [Tem01], hace una revisión bastante exhaustiva de esos modelos.
Hay varios criterios para clasificar los modelos de percepción rítmica. Uno muy general es el tipo de entrada, que puede ser simbólica, cuando la entrada es una partitura o un fichero tipo midi, o de audio, cuando la entrada es un fichero de audio. Atendiendo a la estrategia de modelización, tenemos los siguientes modelos:
Métodos basados en reglas: El patrón rítmico se analiza en orden cronológico y se construye los niveles métricos basados en reglas explícitas de carácter deductivo; véase [Lee91].
Métodos conexionistas: El patron rítmico es representado en una red neuronal de la cual se infiere la estructura métrica; véase [DH99].
Métodos basados en reglas de preferencia: En base al análisis de muchos patrones rítmicos se construyen reglas que determinan la estructura métrica preferida por el oyente en un patrón rítmico dado; véase [Tem01].
Métodos probabilísticos: Son métodos basados principalmente en la inferencia bayesiana; para más información, véase [CKH00]
Como el libro de Temperley se centra en esta última categoría, vamos a profundizar un poco más en ellos. Típicamente, en un método probabilístico, se consideran una interpretación de un patrón rítmico Int y una representación de ese patrón o partitura Par (normalmente dada duraciones en milisegundos). El objetivo es determinar la partitura Par que maximiza la probabilidad
P(Par|Int)
Esta probabilidad representa la fidelidad de la partitura respecto a la interpretación. En la figura 3 tenemos un ritmo (en la primera línea) y dos posibles interpretaciones, dadas por los histogramas debajo del ritmo. Es claro que la primera interpretación es mucho más probable que la segunda.
Figura 3: Un patrón rítmico y dos posibles interpretaciones (figura tomada de [Tem10])
Se puede probar usando argumentos de probabilidad bayesiana que maximizar P(Par|Int) es equivalente a maximizar P(Int|Par) ⋅ P(Par).
4. El modelo probabilístico de Temperley
4.1. El proceso generativo
Temperley, tras examinar un par de modelos probabilísticos y mostrar sus limitaciones, propone el suyo, que también está basado en el teorema de Bayes. El objetivo de su modelo es inferir la estructura métrica a partir de un patrón rítmico. Si PR designa un patrón rítmico y M una estructura métrica, la ecuación que relaciona a ambas es
P (M|PR) = P(PR|M)⋅P(M)
La estructura métrica M que maximiza la expresión anterior será la más probable para el patrón rítmico dado. El autor usa un modelo generativo de ritmo para calcular las probabilidades de la ecuación anterior. El modelo generativo no es un modelo del proceso creativo sino que intenta capturar el proceso de escucha y decodificación de la información rítmica por parte del oyente. Véase [Góm14] para más información sobre modelos generativos en música.
El modelo generativo está basado en una estructura métrica de tres niveles. El primer nivel es una malla de pulsos regulares. El segundo nivel es el tactus, también llamado pulso percibido y el tercero es un nivel más abstracto, que cabalga sobre los otros dos, y que representa el compás. Las notas tienen que ocurrir sobre la malla de puntos regulares del primer nivel.
El modelo se concibe como un grafo cuyos nodos contienen información y flechas que muestran las relaciones entre los nodos. La información de los nodos se puede concebir como variables aleatorias con ciertas distribuciones de probabilidad. Las variables implicadas en el modelo son las siguientes (dejamos los nombres originales de las variables del libro):
UT: Define si el compás es de subdivisión binaria o ternaria.
UPh: Controla la fase del nivel 3 con relación al nivel 2, esto es, qué posición ocupa la primera nota del nivel 3 en el nivel 2.
L: Detecta si el nivel 2 es de subdivisión binaria o ternaria con respecto al nivel 1.
A partir de estas variables el nivel del tactus se puede generar ya. La generación del nivel de tactus es independiente de la determinación del compás. Se empieza con una primera nota del tactus en el tiempo cero y la variable T1 marca la duración de esta primera nota. En general, Tn será la n-ésima duración del tactus y es una variable distribución de probabilidad que se apoya en la duración de la variable Tn-1. Acompañando a están las variables An, que dictan si en cada paso hay que generar otra nota de tactus o el proceso se finaliza.
La combinación de los pasos anteriores de la generación del tactus da automáticamente las notas del tactus, la fase y el periodo en el siguiente nivel. Pero aun falta la generación de las notas de nivel 2. Toda nota de nivel 2 lo es de nivel 1, pero hay otras notas entre medias que están en el primero y no en el segundo nivel. En función de si el compás es de subdivisión binaria o ternaria así se rellenarán. La variable DBn representan la posición de estas notas intermedias cuando la subdivisión es binaria y TB1n y TB2n cuando la subdivisión es ternaria. Poniendo en combinación todo lo anterior se generan las notas del patrón rítmico; la variable Np indica si hay una nota en la posición p. La figura 4 muestra un esquema de todo el proceso.
Figura 4: El proceso generativo del modelo probabilístico de Temperley (figura tomada de [Tem10])
El modelo funciona a partir de unos parámetros probabilísticos. ¿Cómo se eligen los valores de esos parámetros? La manera en que Temperley lo soluciona es recurriendo a un corpus musical suficientemente extenso, el cual analiza y extrae las probabilidades para inicializar su modelo. Lo ideal sería que esos parámetros reflejasen las decisiones de los oyentes en la decodificación de los patrones rítmicos. A falta de tales parámetros, Temperley escogió el corpus Essen Folksong Collection [Sch95]. Con este corpus, por ejemplo, se puede asignar una probabilidad al suceso de que una canción tenga un compás de subdivisión binaria o ternaria. No habría más que calcular su frecuencia relativa en el corpus.
Otros parámetros no tienen tan obvia y directa traslación en el corpus. Por ejemplo, la distribución de Tn tiene la siguiente definición:
donde Tn se mide en unidades enteras de 50 milisegundos. Esta definición refleja el hecho conocido en psicología de la música que el tactus suele rondar los 700 milisegundos y que suele ser regular a lo largo de la pieza.
No vamos a entrar en una explicación detallada de todos los parámetros del modelo y su inicialización porque sería excesivamente prolijo. Las tablas siguientes muestran los valores ya inicializados:
Figura 5: Los parámetros del modelo de Temperley (I) (figura tomada de [Tem10])
Figura 6: Los parámetros del modelo de Temperley (II) (figura tomada de [Tem10])
4.2. El proceso de búsqueda de la métrica
Como dijimos más arriba, el objetivo es maximizar P(M|PR), que es a su vez equivalente a maximizar P(PR|M) ⋅P(M). Aplicando el modelo construido tenemos que la forma final de la ecuación a maximizar es
P(M|PR) =
P(PR|M) ⋅ P(M)
=
P(UT) ⋅ P(LT) ⋅ P(UPh) ⋅ P(T1) ⋅∏n=2tP(An)⋅
∏n=2t-1P(Tn|Tn-1) ⋅∏n=1tP(DBn) ⋅∏p=1qP(Np)
donde t es el número de tactus en la pieza y q es su número de notas. Para alcanzar el máximo es necesario considerar todas las posibles estructuras métricas. Ello no es ni computacionalmente tratable ni psicológicamente razonable. Muchas de las estructuras métricas no tendrían sentido musical ni cognitivo y añadirían coste computacional de modo innecesario. Gracias a ciertas suposiciones que se pueden realizar sobre las distribuciones de probabilidad del modelo, se puede bajar la complejidad a cotas razonables. Cómo se hace esto se escapa del propósito de este artículo de divulgación. El lector interesado puede consultar las páginas 36 a 40 del libro de Temperley.
4.3. Prueba del modelo
Tras la construcción del modelo, Temperley hace pruebas para determinar la bondad del mismo. Introduce las piezas en el sistema y examina el porcentaje de análisis correctos, es decir, de estructuras métricas correctas asociadas a cada pieza del corpus de Essens. Como comparación adicional usa otro sistema, Melisma, que persigue los mismos objetivos que su modelo. El porcentaje de análisis correctos para el sistema de Temperley es del 79.3% y del del 86.5% para Melisma. En la figura 7 vemos dos análisis; el primero corresponde al correcto y el segundo al proporcionado por el sistema. Vemos que el sistema ha asignado incorrectamente el compás confundiendo un 6/8 con un 3/4.
Figura 7: Determinación de la estructura métrica con el sistema de Temperley (figura tomada de [Tem10])
5. Conclusiones
Al final del capítulo 3, Temperley analiza las limitaciones de su sistema y las posibilidades de mejora. Su sistema no tiene en cuenta otros parámetros que contribuyen a la percepción rítmica, tales como la armonía, el acento o la estructura melódica. El modelo de Temperley es generalizable a música polifónica, aunque es claro que la complejidad conceptual y computacional aumentará. También argumenta Temperley que su modelo es extrapolable a otras tradiciones musicales porque en la construcción del mismo no se ha basado fuertemente en los principios musicales de la tradición occidental. Esto necesita más argumentación porque la estructura métrica que se estudia aquí es la de la tradición occidental y nosotros en particular cómo se podría aplicar a tradiciones donde el ritmo es aditivo o carecen de métrica, por poner dos ejemplos extremos.
Bibliografía
[CKH00] A. T. B. Cemgil, P. Desain Kappen, and H. Honing. On tempo tracking: Tempogram representation and Kalman filtering. Journal of New Music Research, 29:259–273, 2000.
[Con16] Andrew Conway. Statistics 101. https://es.coursera.org/course/stats1, consultado en noviembre de 2016. Universidad de Princeton.
[DH99] P. Desain and H. Honing. Computational models of beat induction: The rule-based approach. Journal of New Music Research, 28:29–42, 1999.
[Gab73] A. Gabrielsson. Studies in rhythm. Acta Universitatis Upsaliensis, 7:3–19, 1973.
[GJ16] Alison Gibbs and Rosenthal Jeffrey. Statistics: Making Sense Out of Data. https://es.coursera.org/course/introstats, consultado en noviembre de 2016. Universidad de Toronto.
[Góm14] P. Gómez. Teoría generativa de la música - I. http://divulgamat2.ehu.es/divulgamat15/index.php?option=com_content&view=article&id=16037&directory=67, junio de 2014.
[Góm16] P. Gómez. Música y Probabilidad (I). http://divulgamat2.ehu.es/divulgamat15/index.php?option=com_content&view=article&id=16871&directory=67, noviembre de 2016.
[Han98] Stephen Handel. The interplay between metric and figural rhythmic organization. Journal of Experimental Psychology: Human Perception and Performance, 24(5):1546–1561, 1998. Documento accesible en http://dx.doi.org/10.1037/0096-1523.24.5.1546.
[Lee91] C. Lee. The perception of metrical structure: Experimental evidence and a model. Academic Press., Londres, 1991. Capítulo del libro Representing Musical Structure, P. Howell, R. West, and I. Cross (eds.).
[PE85] D.-J. Povel and P. Essens. Perception of temporal patterns. Music Perception, 2:411–440, 1985.
[Sch95] H. Schaffrath. The Essen Folksong Collection. Center for Computer-Assisted Research in the Humanities, Stanford, Calif., 1995. Editado por D. Huron.
[Slo85] J. A. Sloboda. The Musical Mind. Oxford: Clarendon Press, 1985.
[Tem01] D. Temperley. The Cognition of Basic Musical Structures. MIT Press, Cambridge, Mass., 2001.
[Tem10] D. Temperley. Music and Probability. MIT Press Ltd, 2010.
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
1. ¿Por qué estudiar Probabilidad en Música?
El ser humano ha convivido desde siempre con la incertidumbre. Estamos tan acostumbrados a aceptar hechos que conocemos de manera fragmentaria, a razonar a partir de premisas incompletas, a tomar decisiones basadas en creencias subjetivas, que la presencia de la incertidumbre nos resulta natural. Si salimos a la calle, lo más probable es que, antes de decidir qué ropa ponernos, consideremos las posibilidades de lluvia, quizás sólo observando el trozo de cielo que nos deja ver la ventana, quizás recordando la estación del año y el tiempo que hizo en los últimos días. En todo caso, lo único que hemos hecho es decidir en base a un razonamiento aproximado y cargado de incertidumbre. La causa de esa presencia ubicua de la incertidumbre es la extraordinaria complejidad de la realidad, la multitud de causas que se esconden detrás de hechos simples y que nos resulta difícil de comprender. Sin embargo, sobrevivimos en medio de esa sopa de incertidumbre que nos rodea: tomamos decisiones, creamos modelos para explicar la realidad, nos esforzamos por comprender esa aleatoriedad, por tratarla y sacar provecho de ella, razonamos en su presencia e incluso acumulamos conocimiento a su pesar.
Hay muchos fenómenos físicos gobernados por la incertidumbre, como por ejemplo los fenómenos microscópicos. Pensemos en el comportamiento de los gases, formados por muchísimas partículas cuyo comportamiento se describe teniendo en cuenta las interacciones aleatorias entre ellas. A pesar de esto, hay una teoría de los gases que predice con bastante exactitud el comportamiento macroscópico, lo cual no deja de sorprendernos. Sin duda, donde reina la incertidumbre por sus fueros es en la Mecánica Cuántica, entronizada por el principio de Heisenberg enunciado en el año 1927. Este principio afirma que cuanto más precisa es la medida de la posición de un electrón, más imprecisa es la medida de su velocidad, de modo que no es posible conocer ambos con precisión absoluta. ¿Hay una afirmación más rotunda de la incertidumbre? Las consecuencias de este principio son profundísimas y alcanzan a la ciencia y la técnica de nuestros días, pues termina con una manera determinista de concebir el conocimiento.
No sólo en los fenómenos cuánticos aparece la incertidumbre; quizás en este campo es más patente a causa del principio de incertidumbre, pero a medida que el progreso científico exigió un conocimiento en profundidad de los fenómenos, con más capacidad de predicción, la incertidumbre empieza a aparecer de modo natural. Antes del desarrollo de la probabilidad y la estadística los análisis de los problemas eran deterministas, y sus conclusiones, limitadas. La incertidumbre, entre otros muchos campos, aparece en:
Economía y Ciencias Sociales: comportamiento de mercados, índices bursátiles, tendencias sociales, resultados de elecciones, etc.
Ingeniería: procesos de fabricación, control de calidad, planificación de tareas, mediciones de características, etc.
Informática y Computación: tráfico en redes de comunicaciones, tiempo de ejecución de programas, accesos a páginas web, comportamiento de estructuras de datos, gestión de recursos, etc.
Esa incertidumbre es consecuencia de que los fenómenos que estudiamos vienen dados por un alto número de causas, muchas de ellas de pequeño efecto, interdependientes de un modo desconocido, y de comportamiento difícil de explicar o modelizar. De esto se sigue la necesidad de incorporar la incertidumbre al razonamiento, a la deducción, en suma, al método científico. Si pretendemos tener modelos que expliquen la realidad, entonces no podemos ignorar ese aspecto. La Teoría de la Probabilidad es la rama de las Matemáticas que materializa tal incorporación. Podríamos decir que la probabilidad es la lógica de la incertidumbre.
Feller (1906 - 1970), uno de los grandes probabilistas del siglo XX, resaltaba de la probabilidad tres características, que a su juicio, le proporcionan su utilidad y belleza [Fel63]:
Intuición. La probabilidad es intuitiva porque la usamos en el razonamiento cotidiano. Nos sirve para cuantificar el conocimiento subjetivo que tenemos de un hecho y tomar decisiones.
Formalismo lógico. La probabilidad es de suma importancia para el método científico. A partir de Kolmogorov, que introduce la definición axiomática de probabilidad, esta se une con la lógica, esto es, con las leyes del pensamiento. Esto permitió que la probabilidad, ahora con el soporte de la lógica, se desarrollase como una rama del conocimiento plenamente independiente. Esta unión de la lógica y la intuición parece que es lo que desconcierta al estudiante en un primer momento.
Aplicaciones. Son muchas y en los ámbitos más diversos. Nombrar todas sus aplicaciones sería largo, pero, dado que este material está dirigido a alumnos de estudios musicales, merece la pena nombrar algunas de las más relevantes. Sin embargo, dejamos al alumno que las busque él por su cuenta.
Esta introducción que está en cursiva corresponde a la introducción de mis notas de estadística que doy a mis alumnos de informática. Sin embargo, cambié el título y algo tramposamente en su lugar puse ¿Por qué estudiar Probabilidad en Música? ¿No es esta introducción igualmente válida si se tratase de alumnos del conservatorio? Pensamos que sí, que lo sería, que las diferencias serían pocas. Esta introducción es general y sirve para cualquier disciplina. Sin embargo, como no nos hemos cansado de señalar, los estudios científicos —ya ni siquiera las matemáticas— están casi ausentes por completo en los planes de estudio de los conservatorios españoles (la excepción es la asignatura de acústica, por supuesto).
Pero ¿por qué debería estudiar un músico una materia como probabilidad? Daría dos razones rápidas en este momento, a falta de más desarrollo. La primera es porque le enseña a pensar de un modo que es fundamental en cualquier persona que tenga una educación superior (de secundaria en adelante, digamos). La segunda razón es que en especialidades como musicología y composición estos conocimientos son importantes, sobre todo a la luz del desarrollo moderno de ambos campos (musicología sistemática y computacional y música de los siglos XX y XXI).
Mis notas siguen con una definición de la disciplina de Informática dada por la ACM, la prestigiosa asociación de informática estadounidense; dicha definición está contenida en un informe periódico sobre el estado de la informática, el informe The Joint Task Force for Computing Curricula; véase [Cur05]. Reproduzco aquí, por completitud, la definición que establecen los autores de dicho informe (nuestra traducción):
De modo general, podemos dar el significado de computación a toda actividad que específicamente requiera ordenadores, se beneficie de ellos o los cree. Así pues, la computación incluye: el diseño de sistemas hardware y software para un amplio rango de objetivos; procesamiento, estructuración y gestión de varios tipos de información; la realización de estudios científicos; hacer que los ordenadores se comporten inteligentemente; crear y usar comunicaciones y entretenimiento multimedia; buscar y recopilar información relevante para cualquier objetivo particular, entre otros. La lista es virtualmente interminable y las posibilidades son infinitas. Computación tiene otros significados que son más específicos, basados en el contexto en que se usa el término. Por ejemplo, un especialista en sistemas de información verá el término computación de modo diferente al de un ingeniero de software. Con independencia del contexto, hacer computación de calidad puede ser complicada difícil y complicado. Porque la sociedad necesita gente que haga computación de calidad, concebimos la computación no solamente como una profesión sino como una disciplina científica.
Trasladando lo anterior a nuestro objeto de interés, la música, nos preguntamos ¿qué es la música? ¿De qué definición de música disponemos? Quizás estamos profundamente equivocados y la definición de música no deja resquicio alguno para la necesidad del estudio de las matemáticas en la música y aun menos de la probabilidad. Una definición de la música es una empresa mucho más arriesgada que la definición de la actividad informática. En torno a la definición de la música no hay consenso en absoluto, tal es su complejidad fenomenológica, cultural, social, semiótica, funcional, cognitiva y perceptual. Como ejemplo de la disparidad de definiciones de música que podemos encontrar, aquí está la de Xenakis, tomada de su libro Formalized music [Xen01] (la dejamos en inglés por ser lo suficientemente clara y por respeto al original):
It[Music] is a sort of comportment necessary for whoever thinks it and makes it.
It is an individual pleroma, a realization.
It is a fixing in sound of imagined virtualities (cosmological, philosophical,…, arguments)
It is normative, that is, unconsciously it is a model for being or for doing by sympathetic drive.
It is catalytic: its mere presence permits internal psychic or mental transformations in the same way as the crystal ball of the hypnotist.
It is the gratuitous play of a child.
It is a mystical (but atheistic) asceticism. Consequently, expressions of sadness, joy, love and dramatic situations are only very limited particular instances.
Es una definición que combina elementos poéticos (gratuitous play of a child) con elementos cognitivos (mental transformations) y con elementos espirituales (asceticism). En una aparente paradoja, parece que esta definición deja poca oportunidad al estudio de la probabilidad en la música. Sin embargo, ¡Xenakis compuso música con métodos probabilísticos! (véanse los artículos de esta columna de finales de 2010 [Góm10c, Góm10b, Góm10a] para análisis de la música de Xenakis, en particular de la música que usa probabilidad).
Otra definición de música muy citada por su versatilidad es la que dio Edgard Varèse: música es sonido organizado. Varèse hacía referencia a su propia estética musical como compositor modernista que era, pero a la vez resume elegantemente múltiples aspectos de la definición de música. ¿Quién organiza la música o decide qué organizaciones del sonido son válidas? La cultura y la sociedad. Pero eso, aunque no está en su definición, aparece sutilmente implícito.
Otras escuelas de pensamiento hablan de la música como constructo social y afirman que la música es un acto totalmente social. Su definición y tratamiento dependen esencialmente de su consideración como fenómeno social. Otros autores consideran la música como un lenguaje enmarcado dentro de un contexto cultural y llegan a estudiar la música como un fenómeno semiótico. Aun otros autores ligan la definición de música a la capacidad del sonido de producir emociones en el oyente (la visión psicológica).
En el libro Psychological Foundations of Musical Behavior [RB06], Radocy y Boyle llevan a cabo un análisis exhaustivo de varios aspectos fundamentales de la música. Empiezan con la biomusicología, en particular, con la musicología evolutiva, que intenta explicar los orígenes evolutivos de la música, y con la neuromusicología, que se ocupa del estudio de los procesos neuronales y cognitivos que subyacen en la actividad musical. La música es un universal humano, pues todas las sociedades humanas conocidas tienen música vocal y prácticamente todas tienen alguna forma instrumental. Continúan con la perspectiva antropológica de la música. Porque la música es creada por el ser humano, aquella ha de servir a un fin y entonces hablamos de las funciones de la música (hay muchas: desde el entretenimiento hasta el ritual religioso). Estos autores prosiguen examinando la interesante perspectiva de la música como canalizador de la actividad motora, en especial su relación con el baile, y de ahí a la música como refuerzo de la conformidad con las normas sociales o como elemento integrador en el contexto social.
Sin embargo, sea cual sea la definición de música que intentemos establecer, hay un aspecto innegable en la música: se trata de un fenómeno. Nos puede interesar sus efectos emocionales en nosotros, o su raíces sociales y culturales, o sus aspectos organizativos, pero siempre permanecerá el hecho de que se puede estudiar como fenómeno. En este sentido, es lícito y necesario usar métodos científicos para su estudio. Obviamente, no abogamos aquí porque el estudio de la música se haga exclusivamente con esos métodos. Si la música es tal fenómeno multidimensional y complejo, los métodos de su estudio tendrán que tener esos atributos, y entre ellos se contará el método científico. Cualquier fenómeno lo suficientemente complejo—y la música ciertamente lo es — necesitará el razonamiento y el análisis en presencia de la incertidumbre del que hablaba en la introducción más arriba.
En los siguientes cuatro artículos de esta columna estudiaremos varios ejemplos de análisis musical por vía de la probabilidad. En 2010 David Temperley publicó un excelente libro [Tem10], Music and Probability, cuyo título no puede ser más elocuente; véase la portada del libro en la figura abajo. Aprovecharemos este recorrido por la música de la mano de la probabilidad para analizar el libro.
Figura 1: Music and probability, de David Temperley
Ciertamente, el libro de Temperley no se podría considerar como un texto posible para un curso de probabilidad para músicos (o al menos para musicólogos), especialmente el capítulo 2. Cubre demasiado rápido y de una manera algo superficial el material básico de probabilidad (apenas siete páginas). Por el contrario, tiene el mérito de que sus ejemplos y explicaciones intuitivas son muy efectivos y originales. En verdad, la verdadera valía del libro reside en las aplicaciones que presenta. Para que el lector se haga una idea precisa de su contenido, en la figura 2 de abajo se encuentra el índice de contenidos.
Figura 2: Índice de contenidos de Music and probability
¿Cuál sería, pues, una buena introducción a la probabilidad para músicos? Eso, claro es, depende del nivel previo de conocimiento que traigan esos músicos. Para fijar ideas, pensaremos en un alumno medio que estudia música con intención de llegar a ser profesional y que hizo el bachillerato, uno de letras (como mucho el de ciencias sociales). Con frecuencia, la última vez que estudió matemáticas fue en 4o de la ESO. El programa de este curso, de 4o de la ESO, tomado de [BOC15] (páginas 104–105), consiste en lo siguiente:
Contenidos de matemáticas de 4o de la ESO:
Aritmética: números reales y radicales.
Álgebra: polinomios, fracciones algebraicas, ecuaciones y sistemas no lineales.
Geometría y trigonometría: razones trigonométricas, triángulos rectángulos, distancias, vectores en el plano, ecuaciones de la recta en el plano.
Funciones: conceptos básicos, representación gráfica de parábolas e hipérbolas, representación de raíces, exponenciales y funciones definidas a trozos.
Estadística, combinatoria y probabilidad: estudio de una variable estadística, distribuciones bidimensionales, recta de regresión, combinatoria y técnicas de recuento, conceptos básicos de probabilidad.
Como se puede apreciar, los contenidos son los habituales, nada fuera de lo esperado. Este es, sin embargo, el problema. Son los contenidos habituales. Esto significa, en el contexto de España, enseñanza tradicional, donde el alumno es un sujeto pasivo, donde hay más énfasis en la enseñanza del profesor que en el aprendizaje del alumno, donde el profesor ejerce una autoridad que no favorece el aprendizaje, donde el conocimiento se le da al alumno construido externamente y donde los contenidos se centran en los aspectos calculísticos y operativos en lugar de en las ideas y los conceptos, que es la verdadera riqueza y goce de las matemáticas. Para una crítica certera y feroz de la enseñanza actual de las matemáticas, urgimos encarecidamente al lector que lea el legendario artículo El lamento de un matemático de Paul Lockhart [Loc08]. Y por más paradójico que pueda sonar, el propio BOCM propone, a continuación de los contenidos, objetivos de aprendizaje de tipo conceptual e incluso emocional (“Confianza en las propias capacidades”). He aquí esa paradójica lista de objetivos de aprendizaje:
Procesos, métodos y actitudes en matemáticas:
1. Resolución de problemas.
Planificación del proceso de resolución de problemas.
Estrategias y procedimientos puestos en práctica: uso del lenguaje apropiado: (gráfico, numérico, algebraico, etc.), reformulación del problema, resolver subproblemas, recuento exhaustivo, empezar por casos particulares sencillos, buscar regularidades y leyes, etc.
Reflexión sobre los resultados: revisión de las operaciones utilizadas, asignación de unidades a los resultados, comprobación e interpretación de las soluciones en el contexto de la situación, búsqueda de otras formas de resolución, etc.
2. Investigaciones matemáticas.
Planteamiento de investigaciones matemáticas escolares en contextos numéricos, geométricos, funcionales, estadísticos y probabilísticos.
Práctica de los procesos de matematización y modelización, en contextos de la realidad y en contextos matemáticos.
Confianza en las propias capacidades para desarrollar actitudes adecuadas y afrontar las dificultades propias del trabajo científico.
3. Utilización de medios tecnológicos en el proceso de aprendizaje para: (a) la recogida ordenada y la organización de datos. (b) la elaboración y creación de representaciones gráficas de datos numéricos, funcionales o estadísticos. (c) facilitar la comprensión de propiedades geométricas o funcionales y la realización de cálculos de tipo numérico, algebraico o estadístico. (d) el diseño de simulaciones y la elaboración de predicciones sobre situaciones matemáticas diversas. (e) la elaboración de informes y documentos sobre los procesos llevados a cabo y los resultados y conclusiones obtenidos. (f) comunicar y compartir, en entornos apropiados, la información y las ideas matemáticas.
Las razones por las que calificamos esta lista de paradójica son que, en la realidad —en la triste realidad diríamos— esto no se enseña o se mal enseña. Por un lado, los profesores persisten en la enseñanza tradicional de las matemáticas, a pesar de su fracaso evidente. Por otro lado, los alumnos adoptan una actitud de vómito (memorizar la materia, sin comprenderla, con frecuencia el día anterior, y vomitarla el día del examen para después olvidarlo todo y así fomentar la ignorancia). A esto se añade el mal funcionamiento del sistema educativo (¿existe la inspección educativa en este país?), que permite lo anterior, junto una confusión pedagógica notable (¿quién enseña pedagogía a los profesores de instituto y universidad?, ¿cómo es posible que no conozcan nada sobre la psicología de los alumnos, su primordial material de trabajo?, ¿cómo es posible que algunos presuman de esta ignorancia y otros muchos nunca se decidan a cubrir esa laguna?).
Si de verdad queremos enseñar probabilidad a los músicos, debe ser desde el aprendizaje auténtico y significativo y no desde la enseñanza tradicional. En realidad, el capítulo 2 del libro de Temperley abunda en esa enseñanza tradicional. Se apresura por cubrir los rudimentos porque quiere llegar a las fascinantes y emocionantes aplicaciones. Pero este enfoque es un error porque los lectores se rendirán mucho antes si no entienden el capítulos de los fundamentos de la probabilidad.
2. Aprendizaje de la Probabilidad para músicos
En esta sección vamos a explicar brevemente cómo enfocaríamos la enseñanza de la probabilidad a músicos. La probabilidad, como dijimos antes, es razonamiento en presencia de la incertidumbre y se rinda a la evidencia de que los modos deterministas de razonamiento no funcionan en muchos contextos. Por tanto, la única manera de que alguien, músico o no, aprenda probabilidad es que se enfrente a problemas de probabilidad. De modo que empezaríamos proponiendo algunos problemas, por ejemplo, el clásico problema de Monty Hall. Helo aquí.
Problema 2.1 El nombre de la paradoja viene por el nombre del presentador del concurso Let’s make a deal. En el concurso se presenta al concursante tres puertas; detrás de una ellas hay un coche y detrás de cada una de las otras dos una cabra. El concursante elige una puerta y entonces Monty Hall, el presentador, abre otra puerta que siempre corresponde a la de una cabra. En este momento el presentador ofrece al concursante la posibilidad de cambiar su elección. ¿Debe el concursante mantener su elección original o escoger la otra puerta? ¿Supone alguna diferencia?
Este problema lo resolverían los alumnos en clase, no importa cuánto tarden, no importa cuántos errores cometan, no importan cuánto se resistan a razonar (muchos traerán baja autoestima matemática). Con este problema evaluaría su capacidad de argumentación, su rigor intelectual, su lenguaje, la precisión de su vocabulario, su autoestima matemática, su empatía, entre otras variables de importancia para el aprendizaje individual y colectivo.
Tras unas pocas sesiones de problemas de probabilidad, entraríamos en un mínimo de formalización y de terminología. En las discusiones habría aparecido la necesidad de dicha terminología y formalización. Habríamos de dar los conceptos de experimento aleatorio, espacio muestral, espacio de sucesos, sucesos elementales y compuestos, sucesos incompatibles. Dado que nuestros alumnos tendrían muy lejos los conjuntos, se haría necesario un repaso de este material, siempre en forma de problemas y discusiones, y dejando que ellos mismos se expliquen la materia entre sí.
De ahí entraríamos a la definición de espacio de probabilidad, que sería la definición axiomática de Kolmogorov. Esta definición, si se presenta adecuadamente, la puede comprender un alumno de primero de grado superior, por ejemplo. Tras esta definición vendrían la prueba de propiedades y, de nuevo, la resolución de problemas. Como ejemplo de propiedades, podríamos poner las siguientes:
Teorema 2.2 Sea (E,℘,P) un espacio de probabilidad.
(a) Si A,B son dos sucesos cualesquiera y A ⊆ B, entonces P(A) ≤ P(B). (b) La probabilidad es un número entre 0 y 1. (c) Para todo A ∈ ℘, se tiene que P(A) = 1 - P(A). (d) Si A,B son dos sucesos cualesquiera, entonces P(A ∪ B ) = P (A) + P(B )- P (A ∩ B )
Tras este primer bloque de contacto con la probabilidad, entraríamos en la probabilidad condicionada. Con mis alumnos de informática, suelo emplear cerca de una hora en discutir cuál es el concepto que está detrás de la probabilidad condicionada y por qué llegamos a la fórmula
Profundizando en este contexto, aprenderían el teorema de la probabilidad total y el concepto de independencia. Este aprendizaje tiene que venir reforzado por problemas y discusiones. No aprenderán todo este aparato conceptual sin el crecimiento intelectual que supone resolver problemas y explicarle la solución a sus compañeros.
Y, por fin, iríamos al grandioso teorema de Bayes. Aquí es muy importante que entiendan este teorema en el contexto epistemológico, esto es, como mejora de los modelos de conocimiento. Los problemas deben elegirse cuidadosamente. En particular, y esto vale para todo lo anterior, los problemas que se propongan a los alumnos deben suponerles dificultades de lectura comprensiva y deben ser problemas que contengan una fuerte carga de interpretación (no deben ser problemas de respuesta cerrada).
En [Góm15b, Góm15c] se pueden encontrar las notas de probabilidad en la asignatura que damos para ingenieros informáticos. Sobre mis métodos de aprendizaje, que son una combinación del método Moore (aprendizaje por indagación) y del aprendizaje colaborativo, se puede consultar [Góm15a]. Sobre la aplicación de dichos métodos al aprendizaje de la música, véase [TG15] (escrito en colaboración con Manuel Tizón).
Bibliografía
[BOC15] BOCM. Decreto 48/2015. http://www.bocm.es/boletin/CM_Orden_BOCM/2015/05/20/BOCM-20150520-1.PDF, mayo de 2015.
[Cur05] ACM Computing Curricula. The joint task force for computing curricula 2005. http://www.acm.org/education/curricvols/CC2005-March06Final.pdf, 2005.
[Fel63] W. Feller. An Introduction to Probability Theory and Its Applications. Wiley, 1963.
[Góm10a] P. Gómez. Las matemáticas en la música de Xenakis III. http://divulgamat2.ehu.es/divulgamat15/index.php?option=com_content&view=article&id=11648&directory=67, diciembre de 2010.
[Góm10b] P. Gómez. Las matemáticas en la música de Xenakis II. http://divulgamat2.ehu.es/divulgamat15/index.php?option=com_content&view=article&id=11510&directory=67, noviembre de 2010.
[Góm10c] P. Gómez. Las matemáticas en la música de Xenakis I. http://divulgamat2.ehu.es/divulgamat15/index.php?option=com_content&view=article&id=11360&directory=67, octubre de 2010.
[Góm15a] P. Gómez. El método Moore o el aprendizaje por indagación. http://webpgomez.com/social/educacion/408-metodo-moore, consultado en septiembre de 2015.
[Góm15b] P. Gómez. Probabilidad (I) (notas de la asignatura de estadística). http://www.ma.eui.upm.es/usuarios/Fmartin/Docencia/Estadistica-15/Guion-Estad-15-16-tema-2-(I).pdf, septiembre de 2015.
[Góm15c] P. Gómez. Probabilidad (II) (notas de la asignatura de estadística). http://www.ma.eui.upm.es/usuarios/Fmartin/Docencia/Estadistica-15/Guion-Estad-15-16-tema-2-%28II%29.pdf, septiembre de 2015.
[Loc08] Paul Lockhart. El lamento de un matemático. La gaceta de la Real Sociedad Matemática Española, 11(4):737–766, 2008. Documento accesible en http://www.rsme.es/gacetadigital/abrir.php?id=824.
[RB06] Rudolf E. Radocy and J. David Boyle. Psychological Foundations of Musical Behavior. Charles C Thomas, Illinois, 2006.
[Tem10] D. Temperley. Music and Probability. MIT Press Ltd, 2010.
[TG15] M. Tizón and P. Gómez. El aprendizaje por indagación II. http://divulgamat2.ehu.es/divulgamat15/index.php?option=com_content&view=article&id=14957&directory=67, consultado en septiembre de 2015.
[Xen01] Iannis Xenakis. Formalized Music: Thought and Mathematics in Composition. Number 6 in Harmonologia. Pendragon Press, Hillsdale, NY, 2001.
|
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |