Home » Cultura y matemáticas » Música y matemáticas
Música y matemáticas
El objetivo de esta sección es comprender la interesante y profunda relación de las Matemáticas con la Música.
Nuestro sincero agradecimiento a Francisco Gómez Martín (Universidad Politécnica de Madrid) por organizar y desarrollar esta sección, a sus anteriores responsables Rafael Losada y Vicente Liern, así como a todas las personas que colaboran con la misma.
Resultados 71 - 80 de 130
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
1. Introducción
¿Qué es una paradoja? Si algo caracteriza una paradoja es la capacidad de sumirnos en un estado de perplejidad, el cual suele ir seguido de una disposición a resolver la aparente contradicción. El diccionario de la Real Academia de la Lengua [Rea14] trae varias acepciones de la palabra paradoja. En primer lugar habla de “idea extraña u opuesta a la común opinión y al sentir de las personas”. En efecto, una paradoja siempre causa extrañeza porque desafía la lógica en su sentido más habitual, porque nos muestra una situación bajo una luz diferente y cuyos resultados nos son inesperados. Enfrentados a una paradoja siempre tenemos la sospecha de que estamos en presencia de una trampa. La paradoja es más potente cuanta más perplejidad causa en nosotros. En la siguiente acepción, la RAE habla de “una aserción inverosímil o absurda, que se presenta con apariencias de verdadera”. Y he aquí una segunda característica de las paradojas: han de ser aparentemente contradictorias. El diccionario de la RAE quizás se excede en esta definición cuando dice que la aserción es absurda o inverosímil. Hay paradojas —sobre todo en matemáticas—que no fueron absurdas en su momento y que mostraron serias grietas en los fundamentos de las matemáticas; piénsese en las paradojas de Russell, de las que hablaremos más abajo. Las paradojas, empero, no se limitan a las matemáticas. Las hay lógicas, psicológicas, filosóficas, físicas, biológicas, lingüísticas y musicales, entre otras; véase [Wik14] para una lista más larga de ellas. En la columna de este mes vamos a examinar las paradojas matemáticas y las paradojas musicales.
2. Paradojas matemáticas
2.1. Las paradojas de Zenón de Elea
Las paradojas de Zenón de Elea (490-430 a.C.) se cuentan entre las más conocidas en matemáticas. Estas paradojas tienen consecuencias matemáticas y filosóficas; véanse [Sai09] y [Pal08] para más información sobre este filósofo y sus paradojas. Como ejemplo, vamos a presentar en la columna de este mes la paradoja de Aquiles y la tortuga.
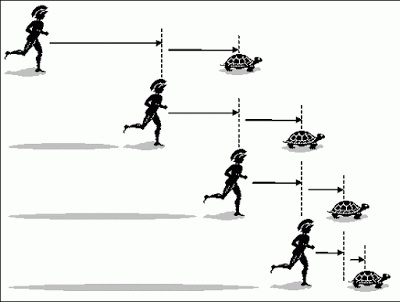
Aquiles es un famoso guerrero aqueo por la velocidad de su carrera hasta tal punto que es conocido como “el de los pies ligeros”. Entre sus hazañas se cuenta haber matado al príncipe troyano Héctor durante la guerra de Troya. La paradoja propone una carrera entre el rápido Aquiles y una tortuga. Para equilibrar la carrera, la tortuga cuenta con una ventaja inicial. La carrera empieza y Aquiles corre raudo y veloz y en poco tiempo alcanza el punto en que estaba la tortuga al inicio de la carrera. Sin embargo, la tortuga ya no está allí. En el tiempo que ha empleado Aquiles en recorrer esa distancia, la tortuga ha avanzado un cierto trecho. Aquiles corre, otra vez raudo y veloz, hasta ese nuevo punto solo para encontrarse con que la tortuga ya no está, ha seguido avanzando. Cada vez que Aquiles llega a un nuevo punto, la tortuga ya no se encuentra allí. Este proceso se repite todo el tiempo. Llegamos a la conclusión de que Aquiles, por muy raudo que sea, nunca alcanzará a la tortuga. En la figura 1 se ilustra la paradoja.
Figura 1: La paradoja de Aquiles y la tortuga (figura tomada de [Rub14]).
Como vemos, la paradoja provoca perplejidad, pues nuestra experiencia cotidiana nos dice que no ocurre lo que describe la paradoja. Sabemos que hay algo que no funciona, pero ¿qué es? Hay varias maneras de explicar la paradoja y señalar dónde está el error en la paradoja. Hay una explicación filosófica y es la de advertir que la paradoja de Zenon confunde el espacio real con su modelo matemático. Para fijar ideas, supongamos que Aquiles es diez veces más rápido que la tortuga y que la distancia inicial entre Aquiles y la tortuga era de 10 metros. Después de n pasos Aquiles se encontrará a una distancia de . Cuando n sea muy grande, esa cantidad en el mundo matemático es todavía positiva, pero en el mundo real eso significa que Aquiles ya ha alcanzado a la tortuga.
Desde el punto de vista estrictamente matemático la paradoja se puede explicar también usando series numéricas. Teniendo en cuenta la distancia inicial y la velocidad de Aquiles, la distancia que recorre Aquiles viene dada por la siguiente suma:
La serie infinita que aparece es la suma de una progresión geométrica de razón menor que uno, la cual es convergente. Tenemos entonces que:
que es una cantidad finita. Por tanto, la suma infinita de números puede dar un resultado finito. La paradoja nos estaba haciendo creer que eso era imposible y que, por tanto, Aquiles nunca alcanzaría a la tortuga. Sin embargo, los cálculos anteriores desenmascaran la paradoja.
2.2. Las paradojas autorreferenciales
Las paradojas autorreferenciales son aquellas que se derivan de enunciados que se refieren a sí mismos. La historia de estas paradojas es instructiva e interesante. A finales del siglo XIX hubo una escuela de pensamiento matemático, el formalismo, que concebía las matemáticas únicamente como un sistema formal basado en axiomas y demostraciones. Hoy en día se acepta mayoritariamente que las matemáticas tienen como características la abstracción, las demostraciones y las aplicaciones (véanse [AKL12, Sna79] para más detalles sobre las posibles definiciones de matemáticas). Obviamente, el formalismo enfatizó la segunda característica, las demostraciones. Durante un cierto tiempo los formalistas creyeron que la lógica y la teoría de conjuntos, tal cual estaban definidas entonces, constituirían los fundamentos de las matemáticas. Entonces aparecieron una serie de paradojas que les hicieron replantearse esa idea. Una de ellas fue la paradoja del barbero de Bertrand Russell.
La paradoja va como sigue. Hay una ciudad donde hay un único barbero, que resulta ser un hombre. En esa ciudad misteriosa no hay hombres que se dejen barba. Para afeitarse hacen una de las dos cosas siguientes: o bien se afeitan a sí mismos o bien acuden a la barbería para afeitarse. Además el barbero solo afeita a aquellos que no se afeitan a sí mismos. La pregunta es quién afeita al barbero. Si el barbero se afeita a sí mismo, caemos en una contradicción, ya que el barbero no afeita a quien se afeita a sí mismo. Si declaramos al barbero como miembro del conjunto de los que no se afeitan a sí mismo, por las condiciones del problema, tendría que ir a la barbería a que le afeitaran. Pero entonces se afeitaría a sí mismo y ya hemos visto que eso es contradictorio. La paradoja del barbero pone de manifiesto que no es posible definir un conjunto cuya definición se refiera a sí mismo.
Relacionadas con esta paradoja están las paradojas lógicas consistentes en enunciados cuyo valor de verdad no se puede establecer. Por ejemplo, ”esta frase es falsa”, es un ejemplo clásico (la paradoja del mentiroso). Estos enunciados no son objeto de la lógica de proposiciones, la cual requiere que todo enunciado que participe en un razonamiento sea susceptible de determinarse su valor de verdad.
La autorreferencia o circularidad ha aparecido en otros campos como la literatura o las artes plásticas. Escher la usó mucho; abajo tenemos una famosa litografía suya tratando este tema.
Figura 2: Drawing hands, de M. Escher.
2.3. Las paradojas relativas a conjuntos infinitos
A veces la paradoja no es tal, sino el producto de un sesgo cognitivo. La idea de que el todo es mayor que sus partes nos parece natural e incontestable. En realidad, eso solo ocurre para conjuntos finitos. Con los conjuntos infinitos las cosas siempre son más divertidas. Consideremos el siempre inocente y familiar conjunto de los números naturales ℕ. Ilustraremos sus curiosas propiedades a través de la paradoja del Gran Hotel debida a Hilbert (véase, por ejemplo, [Gar89, Dek14]).
El Gran Hotel es un hotel especial; tiene infinitas habitaciones, infinitas del tipo de los números naturales (el lector ya me entiende). Estamos en el fin de semana en que se celebra el aniversario del nacimiento de Martin Gardner, el ya conocido Celebration of Mind, y el hotel se encuentra totalmente lleno. No queda ni una sola habitación libre. Su recepcionista, Adolfo Diligente, es el ser más servicial que quepa imaginar, amén de un amante de las matemáticas. Cerca del mediodía llega Maryam Mirzakhani, la medalla Fields de 2014. Entre tanta entrega y homenaje, olvidó hacer la reserva y ahora no tiene habitación. Preguna, compungida, a Adolfo qué puede hacer él. Este, que la admira profundamente, responde resueltamente a su petición.
— No se preocupe, señora Mirzakhani, estamos en el Grand Hotel, un hotel infinito donde los haya, y aquí hay solución para todos los problemas. Mire lo que haré. Pediré a cada huésped que se vaya a la habitación siguiente a la suya. Esto nos dejará la habitación número uno libre para usted. Esta es, señora Mirzakhani, una de las mejores del hotel —y Adolfo sonrió cálidamente al tiempo que dejaba ver sus blancos dientes—.
— Gracias, Adolfo. Nunca olvidaré esto —dijo la señora Mirzakhani con una expresión sincera—.
Adolfo se sumió en sus quehaceres y aunque fijaba su atención en ellos se sentía secretamente feliz por haber tenido la oportunidad de hablar con una matemática de la talla de la señora Mirzakhani.
Al poco entró un grupo de viajeros. Se identificaron como matemáticos que iban a asistir a la Celebration of Mind, pero, igual que la señora Mirzakhani, habían olvidado reservar habitación. El resto de los hoteles de la ciudad eran finitos y todos, que también estaban llenos, les habían mandado al Grand Hotel, el único hotel infinito en la zona. Amablemente preguntaron a Adolfo si algo se podía hacer. Adolfo, mientras hablaba con el portavoz del grupo, los contó disimuladamente. Es un número finito, pensó, y eso se puede arreglar.
— Estimados señores, veo que su grupo consta de 25 personas. Dado que este hotel es infinito, les puedo acomodar. Pediré a cada huésped que amablemente se cambia a la habitación que marca su número más 25, salvo la primera habitación. En ella se aloja la señora Mirzakhani y no se la puede molestar, ya me comprenden ustedes —el grupo de viajero asintió con seriedad—. Tienen ustedes las habitaciones de la 2 a la 26. Permítanme su documentación, por favor.
Y así fue como Adolfo acomodó a este grupo. Dos horas más tarde, cerca de la hora del aperitivo, cuando los infinitos huéspedes departían relajadamente en el infinito salón del Grand Hotel (hotel infinito para huéspedes infinitos, claro), un nuevo grupo de viajeros llegó. Pero esta vez el grupo era diferente: era un grupo infinito de personas. Este grupo de matemáticos absortos habían tratado de probar un teorema y tal fue la concentración que pensaron que habían reservado el hotel, pero, de hecho, solo fue una intención que nunca se materializó.
Adolfo escuchó educadamente la historia de los infinitos matemáticos. Luego hizo la siguiente pregunta:
— Señor, el infinito de ustedes, ¿es numerable?, esto es, ¿es el infinito de los números naturales? En otro caso, me temo que nada podría hacer.
— Venimos en número infinito numerable, señor; nos podemos poner en biyección con los números naturales, sí, en efecto.
Adolfo sonrió e informó que sus habitaciones estarían listas después de comer. De momento, los condujo a la consigna para que dejasen sus maletas allí. Durante la comida pediría a los huéspedes que se mudasen a la habitación cuyo número es el doble de la que ahora tienen. De este modo se quedarían libres un número infinito de habitaciones. Ese infinito es numerable y, por tanto, los nuevos huéspedes cabrían. Sentía tener que mover a la señora Mirzakhani, pero estaba seguro de que era comprensiva.
Y hasta aquí nuestra versión de la paradoja del infinito. Como vemos, la paradoja apela a la intuición bastante común de que las partes son más pequeñas que el todo, pero se resuelve en cuanto estudiamos mínimamente las propiedades de los conjuntos infinitos. Se sabe que los números pares tiene el mismo cardinal que el propio conjunto ℕ; en realidad, el conjunto de los múltiplos de cualquier número k ∈ ℕ fijo tiene el mismo cardinal que ℕ.
3. Paradojas musicales
Hay varias paradojas en el mundo de la música. Vamos a describir una de las más conocidas, la paradoja del tritono, que fue descubierta por la psicóloga de la música Diana Deutsch [Deu86]. En su página web tiene un artículo excelente, donde explica con mucho detalle la paradoja y sus consecuencias; consúltese [Deu14]. Para un buen artículo de divulgación sobre las paradojas, véase Paradoxes of musical pitch [Deu92] de la la misma autora.
La paradoja del tritono presenta dos sonidos producidos uno después del otro y separados por un tritono, esto es, exactamente por la mitad de una octava. Cuando estos sonidos se tocan en sucesión ascendente ocurre que a veces se oyen como descendentes (el primer sonido es más agudo que el segundo) cuando en realidad se han tocado ascendentes (el primer sonido es más grave que el segundo). Esto no pasa en todas las ocasiones ni con todos los sujetos, pero a Deutsch le pareció que merecía la pena investigarlo.
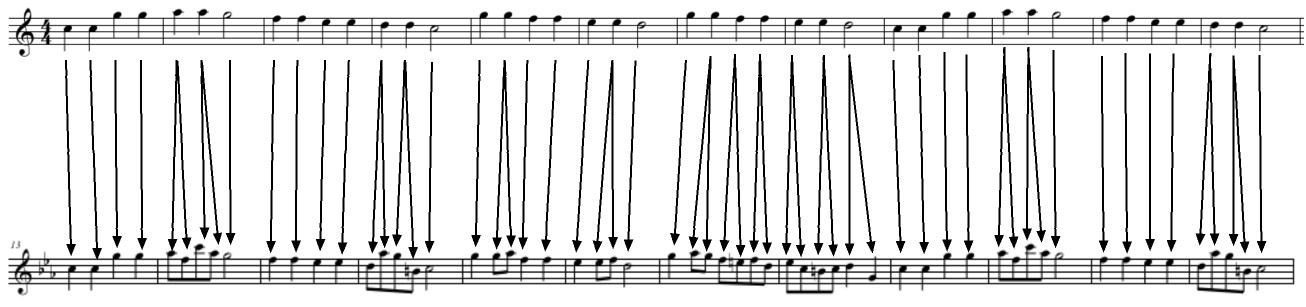
Para ello diseñó un experimento en que presentó a los sujetos una sucesión de intervalos de tritono que primero subían y luego bajaban. Cuando un sujeto percibía que el intervalo subía, dibujaba una flecha hacia arriba; en caso contrario, dibujaba una flecha hacia abajo. El experimento se repitió varias veces con los mismos sujetos y los mismos patrones melódicos. En la figura 3 tenemos los resultados de un sujeto en particular. La gráfica muestra el porcentaje de veces que el sujeto oyó el patrón melódico como descendente. Uno esperaría que la gráfica tomase dos valores solo, 0 y 100, pero en lugar de eso vemos que hay una curva que indica que ciertos intervalos ascendentes se oyen como descendentes. Deutsch conjeturó que este fenómeno no se da uniformemente y que depende de los tonos en particular.
Figura 3: Experimento asociado a la paradoja del tritono.
También conjeturó que esa circunstancia varía de un sujeto a otro y que está relacionada incluso con la procedencia geográfica, la posesión de oído absoluto, la lengua madre o los patrones del habla a que estamos acostumbrados o expuestos. En la figura 4 vemos los resultados de otro sujeto. Son muy diferentes a los del sujeto de más arriba. Ahora la confusión en la dirección melódica ocurre cerca de de otros tonos, en este caso do# y re. Las gráficas de las dos figuras parecen casi complementarias.
Figura 4: Experimento asociado a la paradoja del tritono.
4. Conclusiones
En este artículo hemos examinado las paradojas en las matemáticas y en la música. La naturaleza de las paradojas en música es de tipo cognitivo. La sorpresa viene de que nuestro sistema cognitivo percibe un estímulo de modo incorrecto, pero nada podemos hacer al respecto (Deutsch incluyó músicos en sus experimentos y eso no cambió los resultados). En el caso de las matemáticas, las paradojas se pueden resolver bien ofreciendo explicaciones más finas (como en el caso de las paradojas de Zenón de Elea o del infinito) o bien fortaleciendo los matemáticas en sí (como en el caso de las paradojas autorreferenciales).
Bibliografía
[AKL12] A.D. Aleksandrov, A.N. Kolmogorov, and M.A. Lavrentiev. Mathematics: Its Content, Methods and Meaning. Dover Publications, 2012. Primera edición en 1956.
[Dek14] Jeff Dekofsky. The Infinite Hotel Paradox. http://ed.ted.com/lessons/the-infinite-hotel-paradox-jeff-dekofsky/, consultado en octubre de 2014.
[Deu86] D. Deutsch. A musical paradox. Music Perception, 3:275–280, 1986.
[Deu92] D. Deutsch. Paradoxes of musical pitch. Scientific American, 267:88–95, 1992.
[Deu14] D. Deutsch. Tritone paradox. http://deutsch.ucsd.edu/psychology/pages.php?i=206, consultado en octubre de 2014.
[Gar89] Martin Gardner. ¡Ajá! inspiración. Editorial Labor, 1989.
[Pal08] John Palmer. Zeno of Elea. Stanford Encyclopedia of Philosophy. Springer, 2008.
[Rea14] Real Academia de la Lengua. Diccionario de la RAE. http://lema.rae.es/drae/?val=paradoja, consultado en octubre de 2014.
[Rub14] Rosa Rubicondior. Xeno’s Religious Paradox. http://rosarubicondior.blogspot.com.es/2011/11/xenos-religious-paradox.html, consultado en octubre de 2014.
[Sai09] R. M. Sainsbury. Paradoxes. Cambridge University Press, 2009.
[Sna79] Ernst Snapper. The Three Crises in Mathematics: Logicism, Intuitionism and Formalism. Mathematics Magazine, 52(4):207–216, 1979.
[Wik14] Wikipedia. List of paradoxes. http://en.wikipedia.org/wiki/List_of_paradoxes, consultado en octubre de 2014.
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
En la columna de octubre cerramos el ciclo sobre la teoría generativa de la música tonal de Fred Lerdahl y Ray Jackendoff. La expusieron en su libro A Generative Theory of Tonal Music [LJ83], publicado en 1983 (en castellano se publicó en 2003 por Akal [LJ03] con traducción de Juan González-Castelao). En los tres primeros artículos ([Góm14a], [Góm14b] y [Góm14c]) hemos glosado la teoría de estos autores en cuanto a sus aspectos descriptivos y formales. Examinamos cómo Lerdahl y Jackendoff describen el agrupamiento y la métrica y presentan las reglas de formación correcta y de preferencia. En este último artículo vamos a entrar en los aspectos analíticos de su libro. En un solo artículo de la extensión habitual de esta columna no podríamos tratarlo en suma profundidad. Daremos una visión de conjunto y remitiremos al lector interesado a los capítulos cinco a diez del libro.
1. Las reducciones en música
La música que escuchamos es el resultado de la compleja interacción entre sus elementos, que son múltiples: ritmo, melodía, armonía, conducción de voces, timbre, textura, forman, etc. Una manera muy frecuente de analizar la música es la reducción. Por reducción se entendemos una eliminación de los elementos no esenciales de manera que nos permitan comprender la música en cuestión. Son típicas las reducciones de una partitura orquestal a piano solo o piano a cuatro manos. En esas reducciones se eliminan los instrumentos que doblan una voz y se recoge únicamente aquel material que nos permite reconocer la pieza como tal, con la mayor parte de su personalidad (hay que alcanzar un equilibrio, pues toda reducción implica cercenar en parte el original). Hay una gran tradición de reducciones en la música tonal como instrumento de análisis. Quizás uno de los más conocidos es el análisis schenkeriano; véase [FG82] para más información. En la figura siguiente se ve una reducción de un conocido coral de Bach.
Figura 1: Reducción de un coral de Bach (figura tomada de [LJ83]).
Como el lector ya se habrá dado cuenta, no hay criterios absolutos a la hora de hacer una reducción; un problema similar aparece en la transcripción musical. Diferentes músicos pueden presentar diferentes reducciones de una misma pieza. En su libro Lerdahl y Jackendoff presentan una serie de criterios para llevar a cabo las reducciones y, por ende, el análisis musical. Esos criterios están en buena parte basados en factores psicológicos.
Como primer paso, los autores formula su hipótesis de reducción. Esa hipótesis establece que el oyente siempre intenta organizar los eventos tonales en un todo coherente de manera que estos se oigan de manera jerárquica. Una vez aceptada esta hipótesis, la reducción consistiría en detectar esa estructura y proceder a una simplificación paso a paso de la música. Lerdahl y Jackendoff, no contentos con esta primera hipótesis de reducción, la enriquecen con dos nuevas condiciones:
Los eventos tonales se oyen en estricta jerarquía según se describe en la teoría de los autores (véase [Góm14b]).
Los eventos que son estructuralmente menos importantes no se oyen como simples elementos aislados, sino en relación específica a eventos de más importancia.
Volviendo a la figura 1, esta debería leerse de arriba abajo y “cada paso debería sonar como una simplificación natural del anterior” (página 108, [LJ83]). En este punto los autores advierten de una posible confusión conceptual entre importancia estructural y prominencia musical. Con frecuencia ambas coinciden, pero no siempre. Solo la primera, la importancia estructural, es la base de las reducciones que se proponen en la teoría generativa. Por ejemplo, en la partitura de arriba, de la figura 1, el acorde de sol es prominente por la distribución de las voces, pero no tiene una importancia estructural grande y, de hecho, en la segunda reducción ya no aparece. Lerdahl y Jackendoff no desprecian la importancia musical o analítica de los eventos prominentes; sencillamente, las reducciones están pensadas para extraer la estructura generativa —gramatical, diremos—de la música.
2. Las reducciones de la teoría generativa
Lerdahl y Jackendoff rechazan el análisis schenkeriano, basado también en reducciones, por no ser un análisis como tal sino una interpretación hasta cierto punto subjetiva de la música; no obstante, reconocen la importancia del análisis schenkeriano en su momento y los caminos que abrió. Los autores se fijan como objetivo dar un conjunto de criterios para hacer las reducciones y que estos reflejen en la medida de lo posible la experiencia del oyente. Para ello, toman prestado de la lingüística la notación de árbol (si bien avisan que solo es la notación que toman prestada y que hay sustanciales diferencias en significado de estos árboles en ambas disciplinas).
Veamos cómo se construyen estos árboles y su uso como herramienta de análisis musical. Dados dos eventos tonales x e y, si y es una elaboración de x, entonces y es una rama derecha en el árbol tal y como se muestra en la figura 2 (a). Aquí se entiende que el evento y es subordinado al evento x. Si la situación contraria se produce, esto es, que x es una elaboración de y, entonces nos encontramos con una rama izquierda, como muestra la figura 2 (b). Por último, cuando no hay relaciones de dominancia clara entre los dos eventos se produce una ramificación central, como la mostrada en la figura 2 (c).
Figura 2: Ramificaciones en los árboles de reducciones (figura tomada de [LJ83]).
Huelga decir que, de acuerdo a la hipótesis de reducción formulada más arriba, estas ramificaciones tienen que cumplir con las reglas de formación correcta expuestas hasta ahora. Los árboles tienen que cumplir con las restricciones de no solapamiento, adyacencia y recursión que vimos en los tres primeros artículos de esta serie. En la figura 3 (a) a (d), vemos una serie de árboles que violan algunas de las reglas de formación correcta. Por ejemplo, en los árboles de (a) y (b) se ve que el principio de no solapamiento no se respeta puesto que hay cruces entre las ramas de los árboles. En el árbol (c) tenemos que un mismo evento tiene más de una rama, situación que está prohibida también. Finalmente, en (d) vemos un evento aislado que no recibe rama, y eso está prohibido igualmente. Los árboles (e) a (h) son árboles correctos.
Figura 3: Ejemplos de árboles de reducción (figura tomada de [LJ83]).
En la figura 4 podemos apreciar la reducción del coral de Bach más arriba junto con su correspondiente árbol de reducción. Los niveles de abstracción crecen según se va desde las hojas o nodos finales del árbol hasta su raíz.
Figura 4: Un coral de Bach junto con su árbol de reducción (figura tomada de [LJ83]).
Lerdahl y Jackendoff pronto se dan cuenta que su método de análisis se quedaría corto si sus métodos de reducción se basasen únicamente en criterios tonales. Indudablemente, hay muchos aspectos musicales de importancia subordinados al ritmo o al menos cuya interacción con el ritmo desempeña un papel esencial. En consecuencia, agrupamiento y métrica se incorporan al modelo de reducciones. En la figura 5 tenemos la primera frase de la sonata número 11 en la mayor KV. 331 de Mozart con el árbol de reducción y la estructura métrica y de agrupamiento en la parte de abajo.
Figura 5: Análisis de una frase (figura tomada de [LJ83]).
Por último, Lerdahl y Jackendoff sentían que el modelo tal cual estaba especificado hasta aquí tenía todavía serias limitaciones. En particular, notaban que no explicaba la música en un sentido más horizontal. Ciertamente, explicaba con detalle los eventos tonales pero a cierto nivel local, digamos, a nivel de segmento. No explicaba, sin embargo, cómo fluía la música de un segmento a otro. Los autores ampliaron su sistema de reducción introduciendo un nuevo tipo de reducciones, las llamadas reducciones de prolongación. Por falta de espacio, en este artículo no entraremos en la descripción de las reducciones de prolongación (véanse los capítulos 8 y 9 de su libro).
3. Conclusiones
En estos cuatro artículos hemos hecho un recorrido sucinto por la A Generative Theory of Tonal Music de Lerdahl y Jackendoff, obra en la que se presenta una formalización de la música tonal y su análisis. En esa formalización hemos encontrado elementos típicamente matemáticos. Ha habido voluntad de abstracción, la cual se ha construido desde un procedimiento inductivo; ha habido afán de rigor; y hemos evidenciado una voluntad de autocrítica constante (en ese sentido el texto muestra muy claramente el camino mental que ha llevado a los autores a la construcción de su teoría). Asimismo, hemos visto en la teoría objetos tan matemáticos como recursión (en la descripción del agrupamiento y la métrica), la especificación de una sintaxis y, en general, de una gramática. Esto es muy similar a, por ejemplo, definir un lenguaje formal en computación o describir la lógica proposicional o de predicados.
Incluso aunque la formalización detrás de la teoría generativa no haya sido muy alta, es indudable que hay pensamiento matemático en su construcción. Es un ejemplo más de dónde podemos encontrar matemáticas en la música.
Bibliografía
[FG82] A. Forte and S.E. Gilbert. Introduction to Schenkerian Analysis. W. W. Norton and Co., 1982.
[Góm14a] F. Gómez. Teoría generativa de la música - I, consultado en julio de 2014.
[Góm14b] F. Gómez. Teoría generativa de la música - II, consultado en junio de 2014.
[Góm14c] F. Gómez. Teoría generativa de la música - III, consultado en septiembre de 2014.
[LJ83] F. Lerdahl and R. Jackendoff. A Generative Theory of Tonal Music. MIT Press, Cambridge, Massachussetts, 1983.
[LJ03] F. Lerdahl and R. Jackendoff. Teoría generativa de la música tonal. Akal, 2003. Traducción de Juan González-Castelao Martínez.
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
Tras el descanso de verano, continuamos con la tercera entrega de la serie sobre la obra de Fred Lerdahl y Ray Jackendoff A Generative Theory of Tonal Music [LJ83], publicada en 1983 (en castellano se publicó en 2003 por Akal [LJ03] con traducción de Juan González-Castelao). En el primer artículo de la serie [Góm14b] examinamos la génesis de esta obra y sus fundamentos teóricos generales junto con su base matemática. En el segundo artículo [Góm14a], estudiamos el agrupamiento y la métrica así como las reglas de formación del agrupamiento y las reglas de preferencia del agrupamiento. En este tercer artículo estudiaremos aquellos fenómenos que, según los autores, permiten al oyente reconocer una estructura métrica en el flujo musical (considerado este como el resultado final de todas los parámetros musicales juntos: melodía, conducción de voces, ritmo, armonía, textura, etc.). Tal y como ocurrió en el artículo anterior, las reglas se dividirán en dos tipos, las reglas de formación correcta de la métrica (RFCM de aquí en adelante) y las reglas de preferencia de la métrica (RPM por abreviar). Las RFCM describen las estructuras métricas que son posibles y las RPM especifican los criterios bajo los cuales un oyente considera más estables las estructuras métricas.
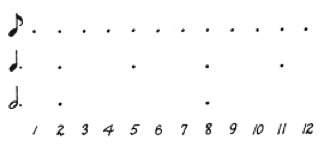
Antes de continuar, recordamos al lector que una parte en un cierto nivel que lo es también a un nivel superior se dice que es parte fuerte; en otro caso, se dice que la parte es débil. En la figura siguiente, por ejemplo, las partes 2, 5, 8 y 11 son partes fuertes al nivel de la corchea y las partes 2 y 8 son fuertes al nivel de la negra con puntillo y la blanca con puntillo. En cambio, las partes 3, 4, 6, 7, 9, 10 son partes débiles. No todas las partes fuertes tienen que serlo a todos los niveles.
Figura 1: Partes fuertes y débiles (figura tomada de [LJ83]).
1. Reglas de formación de la estructura métrica
Las reglas formuladas por Lerdahl y Jackendoff en el capítulo 4 de su libro son fundamentalmente reglas extraídas de la observación empírica, como podremos comprobar enseguida.
RFCM 1: Cada punto de ataque debe estar asociado con un tiempo en el nivel más bajo de la estructura métrica. RFCM 2: Cada parte en un nivel métrico dado tiene que ser una parte en los niveles inferiores a él. RFCM 3: En cada nivel métrico, las partes fuertes están a distancia entre sí de o bien dos partes o bien tres partes. RFCM 4: La distancia entre las partes de cada nivel métrico debe ser constante.
La primera regla establece que no hay puntos de ataque fuera de la malla proporcionada por la estructura métrica. Como es natural, el problema de los adornos o los valores irregulares no está contemplado en esta regla. Más adelante los autores tratan este problema.
La regla RFCM 2 refleja la estructura jerárquica de la métrica de la música tonal. En el ejemplo de la figura 2, parte (b) , se puede apreciar una violación de esta regla en la cuarta nota, que tiene ausencia de un tiempo en un nivel inferior de la métrica. La asignación de los tiempos en la métrica de la figura, parte (a), es correcta según la regla RFCM 2.
Figura 2: Ilustración de la regla RFCM 2 (figura tomada de [LJ83]).
La regla RFCM 3 establece nada más y nada menos que las subdivisiones de los tiempos solo pueden ser binarias y ternarias. En una gran parte de la música occidental esto es así, al menos en la música clásica del periodo de la práctica común (en la música tonal) y en la música popular moderna.
La regla RFCM 4 observa un hecho fundamental de la música tonal aquí analizada: descansa sobre una malla isócrona de pulsos regulares. La métrica se organiza alrededor de estos pulsos con un sistema de acentos recurrentes.
Cualquier lector con un mínimo de experiencia musical (bien como oyente atento o como intérprete) caerá en la cuenta de que estas reglas pecan venialmente de estrictas. Por ejemplo, en rigor sabemos que los pulsos no son regulares en todas las ocasiones. Pensemos en el rubato expresivo tan frecuente e importante en la música clásica. Incluso sin ir a algo tan patente como el rubato, basta considerar las microvariaciones rítmicas que se producen en toda interpretación y que caracterizan las interpretaciones musicales (opuesto, por ejemplo, a las interpretaciones de música hechas por ordenador).
Los mismos autores son conscientes del exceso de rigor descriptivo de las reglas y ponen el siguiente ejemplo (véase la figura 3) para ilustrar la necesidad de relajar esas reglas y hacerlas más fieles a la realidad musical. La presencia de las semicorcheas, que son meras notas de paso aquí, fuerzan una estructura métrica demasiado extensa, cuando en realidad no es necesario; la figuración rítmica gravita en torno a las corcheas con puntillo, las negras y las corcheas.
Figura 3: Niveles métricos del comienzo de la sonata KV 331 de Mozart (figura tomada de [LJ83]).
En pasajes como el de la figura 4, comunes en la música tonal, encontramos subdivisiones métricas dentro de la misma frase. La aplicación de las reglas anteriores, tal cual están formuladas, produciría una estructura métrica ciertamente farragosa, que por encima de todo no se correspondería con la escucha del oyente. El oyente no percibiría el pasaje de la figura con una métrica cuyas partes son el mínimo común múltiplo de sus partes binarias y de sus partes ternarias. Antes al contrario, interpretará, de manera natural, como que tiene una alternancia de estructuras métricas.
Figura 4: Música con diferentes subdivisiones (sonata para clarinete de Brahms) (figura tomada de [LJ83]).
Lerdahl y Jackendoff resuelven este problema introduciendo el concepto de tactus. El tactus es el nivel métrico más prominente y al cual típicamente se asocia el tempo con que el director conduce o con el que de modo natural seguimos el ritmo (con el cuerpo, dando palmas, etc.). El tactus suele ser situarse en un tempo medio. Si el tempo de la obra es rápido, el tactus tiene una figuración de notas largas; si, en cambio, es lento, la figuración es de notas cortas.
Con ayuda del tactus los autores refinan las reglas dadas más arriba. La nueva premisa es que el tactus debe ser constante, pero en función del contexto musical ciertos niveles métricos se pueden descartar, aquellos que están muy lejos del tactus, normalmente más allá de tres niveles métricos por arriba y por abajo. Las nuevas reglas RFCM 1 y RFCM 2, ahora refinadas, son las siguientes:
RFCM 1 (refinada): Cada punto de ataque tiene que estar asociado a una tiempo en el nivel métrico más pequeño que haya en ese momento preciso en la pieza. RFCM 2 (refinada): Cada parte de un nivel determinado debe ser parte en todos los niveles inferiores que haya en ese momento preciso de la pieza.
Empero, el refinamiento de estas dos reglas no soluciona el problema planteado por la pieza de Brahms más arriba (figura 4). Con el siguiente refinamiento de la regla RFCM 4 Lerdahl y Jackendoff solucionan ese caso.
RFCM 4 (refinada): El tactus y los niveles métricos inmediatamente superiores deben estar formados por partes cuya distancia sea constante en una pieza dada. En los niveles inferiores al del tactus, las partes débiles deben tener una distancia constante entre las partes fuertes.
2. Reglas de preferencia de la estructura métrica
Asociadas a una misma pieza musical varias estructuras métricas son posibles. Los autores ilustran este punto con un fragmento de la sinfonía número 40 de Mozart (figura 5). Cada una de las posibilidades métricas cumple las reglas de formación correctas de la métrica enunciadas más arriba. Entonces ¿cuál elegir como la más adecuada para describir la escucha de esta pieza por un oyente ideal? He aquí cuando entran en juego las reglas de preferencia de la métrica (RPM). Con estas reglas los autores quieren modelizar cómo escucha la música su oyente ideal. Es interesante hacer notar que Lerdahl y Jackendoff hablan constantemente del oyente ideal. Ese oyente lo tienen ellos en mente y es producto de su experiencia musical, pero tal oyente no ha sido caracterizado de modo empírico, esto es, ellos no llevaron a cabo experimentos para contrastar hasta qué punto su oyente ideal compartía características con el oyente real.
Figura 5: Varias posibles estructuras métricas asociadas a una misma pieza (figura tomada de [LJ83]).
De las tres posibles estructuras métricas presentadas abajo, Lerdahl y Jackendoff concluyen que es la primera la que mejor se ajusta a la intuición de su oyente ideal. Para formalizar tal decisión enuncian las reglas de preferencia de la métrica, que son las siguientes:
RPM 1 (paralelismo): Allá donde dos o más grupos o partes de grupo se puedan construir con paralelismo, recibirán preferiblemente una estructura métrica que refleje ese paralelismo. RPM 2 (parte fuerte pronto): Prefiérase relativamente una estructura métrica en que la parte fuerte de un grupo aparezca pronto en el grupo. RPM 3 (eventos): Prefiérase una estructura métrica en la cual un parte en el nivel Ni que da lugar a un evento tonal sea parte fuerte en Ni. RPM 4 (acento): Prefiérase una estructura métrica en la cual las partes en el nivel Ni que tienen acento son también partes fuertes en el nivel Ni. RPA 5 (duración): Prefiérase la estructura métrica en la que los tiempos relativamente fuertes tengan lugar al comienzo de: (a) o bien un evento tonal relativamente largo, (b) o bien de una duración relativamente larga de una dinámica, (c) o bien de una ligadura relativamente larga, (d) o bien de un patrón de articulación relativamente largo, (e) o bien de una duración relativamente larga de una nota en varios niveles métricos, (f) o bien de una duración relativamente larga de una armonía en varios niveles métricos.
La primera regla es bastante intuitiva. Nuestro oído tiende a percibir como similares aquellos grupos que poseen paralelismo entre sí y esto se extiende de manera natural a la estructura métrica.
Para la segunda regla los autores dan el siguiente ejemplo (la coda de la obertura Leonora de Beethoven). En él, observamos una secuencia formada por una escala descendente. La escala tiene longitud seis, pero en la realización de la séptima escala —marcada con un asterisco en la figura —encontramos que tiene longitud siete. A pesar de ello, se percibe la primera nota de cada escala como el tiempo fuerte a causa del salto interválico ascendente.
Figura 6: Segunda regla de preferencia de la métrica (figura tomada de [LJ83]).
Con respecto a la tercera regla, el ejemplo anterior sirve para su análisis. La regla RFCM 3 exige que las partes fuertes estén igualmente espaciadas. Eso no ocurre en muchas ocasiones, en el ejemplo anterior sin ir más lejos. La regla RPM 3 establece que se debe preferir una estructura métrica de modo que se minimice la quiebra de RFCM 3.
La regla RFCM 4 establece se debe preferir una métrica en que los acentos fenoménicos (véase [Góm14b]) caigan sobre las partes fuertes y que, si ello no es posible, también se minimicen las excepciones.
La regla RFCM 5 propone que la estructura métrica sea tal que los tiempos fuertes caigan sobre aquellos fenómenos musicales de longitud relativamente larga. Lerdahl y Jackendoff hacen un análisis detallado de dichos fenómenos, que van desde los eventos tonales hasta el ritmo armónico (de ahí lo prolijo de esta regla).
3. Conclusiones
Las reglas que hemos analizado en este capítulo siguen la misma filosofía que encontramos en su momento en reglas del agrupamiento. Lerdahl y Jackendoff describen primero unas reglas de formación correcta, que intentan formalizar los fenómenos observados en la práctica musical, y más tarde dan reglas de preferencia, que tratan de definir qué estructuras métricas son más naturales en la percepción de la música tonal. De nuevo, la descripción de estas reglas está hecha de manera no matemática, aunque de hecho admitirían una descripción matemática.
En el siguiente artículo de la serie, el último, estudiaremos el sistema analítico de Lerdahl y Jackendoff, el cual se basa en las reglas examinadas en estos tres primeros artículos.
Bibliografía
[Góm14a] F. Gómez. Teoría generativa de la música - I, consultado en julio de 2014.
[Góm14b] F. Gómez. Teoría generativa de la música - II, consultado en junio de 2014.
[LJ83] F. Lerdahl and R. Jackendoff. A Generative Theory of Tonal Music. MIT Press, Cambridge, Massachussetts, 1983.
[LJ03] F. Lerdahl and R. Jackendoff. Teoría generativa de la música tonal. Akal, 2003. Traducción de Juan González-Castelao Martínez.
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
Esta es la segunda entrega de la serie sobre la obra de Fred Lerdahl y Ray Jackendoff A Generative Theory of Tonal Music [LJ83], publicada en 1983 (en castellano se publicó en 2003 por Akal [LJ03] con traducción de Juan González-Castelao). En el primer artículo de la serie [Góm14] examinamos la génesis de esta obra y sus fundamentos teóricos. En este artículo estudiaremos el agrupamiento y la métrica en primer lugar; a continuación, veremos cómo es la interacción entre ambos; seguiremos con la definición de las reglas de formación del agrupamiento y acabaremos con las reglas de preferencia del agrupamiento. Cerraremos con una breve conclusión en que discutiremos las matemáticas que se encuentran en la teoría generativa de Lerdahl y Jackendoff.
1. La estructura rítmica: agrupamiento y métrica
En los primeros capítulos Lerdahl y Jackendoff estudian el ritmo en profundidad. Se fijan en dos fenómenos rítmicos en particular: el grupo y la métrica. Según estos autores, el grupo aparece de manera natural cuando un oyente escucha una pieza de música; su oído detecta los motivos, los temas, las frases, los periodos, los grupos temáticos, las secciones y finalmente integra todo en la pieza entera. A la vez, como es el caso de la música tonal analizada en el libro, se encuentra la métrica, que está relacionada con los patrones regulares de acentos fuertes y débiles. Ambos fenómenos son distintos en esencia, pero su interacción constituye una importante fuerza musical. En esta sección examinaremos cada uno por separado y en la siguiente sección la interacción entre ellos.
1.1. La estructura de la agrupación
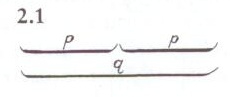
Lerdahl y Jackendoff apelan para la definición de agrupación a la tendencia del ser humano a percibir los objetos en grupos (ambos son perfectos conocedores de la teorías gestaltistas de la percepción, como se demuestra a lo largo de todo el libro). Ellos ven el grupo como un componente básico del entendimiento musical (página 13). La primera hipótesis que formulan acerca de la agrupación en la percepción musical es que esta ocurre de manera jerárquica. Por ejemplo, un motivo es parte de un tema, el cual a su vez es parte de un grupo temático formado por dos o más temas, el cual es parte de una sección, y así sucesivamente. Esta jerarquía clasifica los grupos por su tamaño (un motivo es menor que una sección) e incluye un grupo en otro mayor en base a las relaciones musicales entre ellos. En su lenguaje, si un grupo está incluido en otro se dice que el primero está subordinado al segundo; si un grupo contiene a otro, del primero se dice que domina o está superordinado al segundo. Los autores representan los grupos mediante conjuntos de ligaduras, como en el ejemplo de la figura 1. En dicha figura vemos que dos instancias del grupo p están incluidas en el grupo q.
Figura 1:
Representación de grupos (figura tomada de [LJ83]).
La segunda hipótesis sobre el agrupamiento es el solapamiento. Dada la estructura estrictamente jerárquica de los grupos, el solapamiento no está permitido entre grupos que pertenecen a un mismo grupo dominante. Así, el agrupamiento de la izquierda de la figura 2 constituye un agrupamiento aceptable, mientras que el de la derecha no lo es a causa de los solapamientos.
Figura 2:
Representación de grupos (figura tomada de [LJ83]).
A partir de estas dos hipótesis, Lerdahl y Jackendoff añaden otras dos, que ya no son tan generales y que perfilan y definen el sentido de su teoría generativa. La primera hipótesis es la estructura recursiva de los agrupamientos. Si un grupo dominante contiene un determinado número de subgrupos, esta relación, sin cambios sustanciales, se da en cualquier nivel. El ejemplo que ponen para ilustrar esto es el comienzo del scherzo de la sonata opus 2, número 2, en la mayor, de Beethoven, que vemos reproducido en la figura 3.
Figura 3:
Estructura recursiva de los grupos (figura tomada de [LJ83]).
La segunda hipótesis se refiere a la formación de los grupos y se sigue del principio de no solapamiento enunciado más arriba. Establece que el agrupamiento de grupos no contiguos no está permitido. Los grupos que pueden agruparse en otro más grande han de ser grupos contiguos. De otro modo, se producirían solapamientos prohibidos entre grupos. Así, si tenemos estos dos grupos (a,a,b) y (a,a,b) a un cierto nivel, el agrupamiento permitido es (a,a,b,a,a,b), pero no, por ejemplo, los grupos (a,a) y (b,a,a,b). Este principio aparece reflejado también en el ejemplo de la figura 3, donde todos los agrupamientos se producen entre grupos contiguos.
1.2. La estructura métrica
Siendo conscientes de los problemas terminológicos que el concepto de acento posee, Lerdahl y Jackendoff empiezan esta sección (página 17) definiendo este término de manera precisa. Distinguen tres tipos de acentos: el acento fenoménico, el acento estructural y el acento métrico. El acento fenoménico, el más general en su definición, es cualquier evento en la superficie musical que haga énfasis sobre algún elemento musical en un momento dado de la música. En el ejemplo de la figura 4, una reducción para piano de La danza de las jóvenes de La consagración de la primavera, tenemos ejemplos de acentos fenoménicos, que son los acentos que Stravinsky marcó en tiempos inesperados (marcados con el signo > en la partitura).
Figura 4:
Ejemplo de los distintos tipos de acentos.
El acento estructural es el producido por los puntos de gravedad armónicos y melódicos en una frase o sección; está fuertemente relacionado con el ritmo armónico o con el sentido final de la melodía. Por último, el acento métrico es cualquier tiempo que es relativamente fuerte en su contexto métrico. Para hablar de métrica es necesario suponer que existe una red de tiempos y que existe un patrón regular de tiempos fuertes y débiles. En el ejemplo anterior, el compás 2/4 marca que la primera negra es fuerte y la segunda débil; al nivel de la semicorchea ese patrón se hereda y tenemos cuatro corcheas en que las corcheas impares son fuertes y las corcheas pares débiles.
Obviamente, los tres tipos de acentos tienen estrechas relaciones en muchas ocasiones. A veces el acento fenoménico coincide con el métrico como pasa en el ejemplo de Stravinsky, donde algunas partes fuertes del compás de 2/4 coinciden con los acentos (pero otras, en cambio, no).
El acento fenoménico suele tener bastante relevancia perceptual y puede contradecir o no el acento métrico. Si el acento fenoménico es regular y se alinea con el métrico, se apoyan mútuamente, podríamos decir, entonces la sensación de regularidad es muy alta. Si por el contrario, el acento fenoménico, aun siendo regular, entra en claro conflicto con el métrico, entonces se produce una gran tensión rítmica.
Muy interesantes son los comentarios de la página 18 sobre la naturaleza de la métrica que hacen Lerdahl y Jackendoff (nuestra traducción).
Before proceeding, we should note that the principles of grouping structure are more universal than those of metrical structure. In fact, though all music groups into units of various kinds, some music does not have metric structure at all, in the specific sense that the listener is unable to extrapolate from the musical signal a hierarchy of beats.
(Antes de proseguir, deberíamos hacer notar que los principios de agrupamiento son más universales que los de la estructura métrica. De hecho, aunque todas las músicas agrupan en unidades de diversos tipos, algunas músicas no tienen estructura métrica en absoluto, en el sentido específico de que el oyente es incapaz de extrapolar una jerarquía de tiempos a partir de la señal musical.)
Aquí los autores reconocen que la estructura métrica es un constructo mental; en cambio, el agrupamiento es producto de un proceso perceptual.
Como dijimos arriba, los elementos básicos de la métrica son los tiempos. Estos tiempos son puntos temporales y como tales no tienen duración. La duración entre los tiempos se llama intervalo temporal y estos sí tienen duración. Una hipótesis que hacen Lerdahl y Jackendoff es que los tiempos están igualmente espaciados.
A partir de aquí, y a imagen y semejanza de lo que pasó con el agrupamiento, se dota a la métrica de una estructura jerárquica. Esto es típico de la música tonal objeto del análisis del libro, la música tonal de la práctica común. Un tiempo fuerte a cierto nivel métrico es descompuesto en dos o tres tiempos, dependiendo la división del compás, donde el primer tiempo fuerte sigue siéndolo en el nuevo nivel métrico. Los autores ilustran este punto con la siguiente figura:
Figura 5:
Jerarquía de la estructura métrica (figura tomada de[LJ83]).
Los principios que se establecieron para el agrupamiento —recursión, no solapamiento y adyacencia—se aplican con igual vigencia a la estructura métrica. En la figura 5 (a) tenemos un primer nivel en que todos los tiempos son fuertes (indicado por los puntos); en el siguiente nivel son los impares y, por último, en el siguiente nivel los tiempos fuertes son los múltiplos de cuatro. La figura 5 (b) muestra un esquema similar pero con un compás de 3/4.
En una pieza suele haber alrededor de cinco o seis niveles métricos. La métrica indicada por el compás suele ser la del nivel medio. No todos los niveles métricos se oyen con la misma prominencia. De hecho, un oyente puede centrar su atención en diversos niveles métricos a voluntad, pero los más prominentes son aquellos en que los tiempos van a una velocidad moderada.
Ledahl y Jackendoff son conscientes de los peligros que implica llevar un análisis métrico a gran escala. Ilustran estos peligros con el análisis del comienzo de la sinfonía número 40 de Mozart. Mientras que el análisis de la estructura métrica a pequeña escala es claro y unívoco, al análisis a gran escala (analizaron solo 9 compases) presenta muchas dificultades formales, hasta el punto que ellos mismos hablan ya de interpretación y no de análisis en sí mismo. Esta es una de las virtudes metodológicas de este libro: en general, delimita muy bien el alcance de sus hipótesis tanto por la discusión desarrollada como por los ejemplos que poner.
2. La interacción entre el agrupamiento y la estructura métrica
Para los autores es importante que las propiedades del agrupamiento y la estructura métrica, aunque sean semejantes, se mantengan separadas para el análisis. Ello no obsta para que investiguen sus interacciones, si bien desde definiciones formales diferentes. El siguiente pasaje del minueto de la sinfonía de Haydn número 104, en el que se ven ambos análisis, el de agrupamiento y el métrico, esclarece el porqué de ese empeño.
Figura 6:
Interacción entre agrupamiento y estructura métrica (figura tomada de [LJ83]).
Vemos que el agrupamiento no está alineado con la estructura métrica, que lleva su propia regularidad independiente de esta. Hay tiempos fuertes que caen en diversas partes de los grupos. Sin embargo, lo que oímos es el resultado de ambas interacciones.
3. Reglas de formación del agrupamiento
Esta sección es una síntesis del capítulo 3 del libro, capítulo que dedica a estudiar la organización de la superficie musical en grupos (página 36). Desde el primer momento, los autores mantienen que las reglas de formación del agrupamiento son independientes del lenguaje musical concreto. Esto significa que un oyente poco familiarizado con un lenguaje musical puede inferir el agrupamiento de una pieza en ese lenguaje. Aunque el libro fue publicado en el año 83, cuando la cognición musical ya había empezado a desarrollarse con fuerza, se echa de menos en esta parte referencias a la investigación empírica. Esta afirmación de que la formación de grupos es un principio general y que no depende del lenguaje musical requiere referencias a estudios con sujetos procedentes de diversas culturas. Hoy en día sabemos que, aunque es cierto que hay principios perceptuales que operan de modo general, hay muchos mecanismos de agrupación que provienen de la enculturación, sea esta consciente o no.
Tras los dos primeros capítulos, donde Lerdahl y Jackendoff describieron el agrupamiento y la métrica e hicieron las pertinentes hipótesis, ahora se centran en detallar la gramática generativa. Para ello dan una serie de reglas de formación correcta del agrupamiento (abreviadamente de aquí en adelante como RFCA). Antes de empezar a enumerar, los autores ponen encima de la mesa una limitación en el alcance de la teoría. Su teoría solo explica la música que es esencialmente homofónica y no la polifónica. Dejan como problema abierto esta cuestión, es decir, generalizar esta teoría de modo que pueda explicar la música contrapuntística y heterofónica.
Las reglas de formación especifican en qué condiciones se pueden formar los grupos. Estas reglas rezan como sigue:
RFCA 1: Cualquier sucesión contigua de eventos tonales, golpes de tambor o similares pueden constituir un grupo, y solo sucesiones contiguas pueden constituir grupos. RFCA 2: Una pieza constituye un grupo. RFCA 3: Un grupo puede estar constituido por otros grupos. RFCA 4: Si un grupo G1 contiene parte de otro grupo G2, entonces tiene que contener a todo G2 entero. RFCA 5: Si un grupo G1 contiene un grupo más pequeño G2, entonces G1 tiene que descomponerse en grupos más pequeños.
Para ilustrar estas reglas, los autores toman los primeros compases de la sinfonía de Mozart número 40, en sol menor. En la figura 7 vemos la formación de grupos a tres niveles, las cuales se han realizado acorde a las RFCA.
Figura 7:
Reglas de formación correcta del agrupamiento (figura tomada de [LJ83]).
La regla RFCA 1 no es más que la consecuencia inmediata de las definiciones de agrupamiento dadas más arriba, en la sección 1.1. Esta regla, por ejemplo, impide que las notas re del pasaje anterior se puedan considerar un grupo, ya que no son contiguas. Aquí se percibe que detrás de esta regla está el principio de contigüidad de la psicología gestaltista.
Las reglas RFCA 2 y RFCA 3 son una especie de condición de frontera; la pieza entera ha de percibirse como un todo y no como sucesión aislada de eventos.
Las reglas RFCA 4 y RFCA 5 tienen más calado musical. Determinan cómo ha de realizarse la inclusión de unos grupos dentro de otros. La regla RFCA 4 está pensada para que agrupaciones como las de abajo no ocurran:
Figura 8:
Agrupamientos incorrectos (figura tomada de [LJ83]).
Estos agrupamientos tienen solapamiento (el de la izquierda) y también vemos que G1 contiene parcialmente una instancia de G2 (ejemplo de la derecha).
La regla RFCA 5 por su parte prohibe estructuras de agrupamiento como la de la figura 9.
Figura 9:
Otros agrupamientos incorrectos (figura tomada de [LJ83]).
En estos agrupamientos vemos descomposiciones en grupos incompletas; la unión de G2 y G3 no da el grupo G1. Esta regla no prohibe, sin embargo, la descomposición de un grupo mientras que otra instancia de ese mismo grupo pueda no estar descompuesta. Véase el agrupamiento en el ejemplo de Mozart de la figura 7, en los tres primeros compases.
Lerdahl y Jackendoff son perfectamente conscientes que estas reglas no cubren todos los casos que se pueden encontrar en la práctica musical. En particular, no cubren las solapamientos de grupos y elisiones. La manera de tratar estos dos fenómenos musicales en su teoría no fue la de ampliar las reglas anteriores, sino crear una nueva categoría de reglas, llamadas reglas de transformación, que presentarán más tarde. Estas reglas de transformación tratarán el problema del solapamiento de grupos y las elisiones.
4. Reglas de preferencia del agrupamiento
De nuevo, con su habitual honestidad intelectual, Lerdahl y Jackendoff reconocen que las reglas que han enumerado hasta ahora pueden dar lugar a agrupamientos que van en contra de la intuición musical más básica. De hecho, ellos mismos ponen los siguientes ejemplos (página 39).
Figura 10:
Agrupamientos poco intuitivos permitidos por las RFCA (figura tomada de [LJ83]).
En efecto, parece que ninguna de estas agrupaciones podría corresponder al agrupamiento “natural” (bien van contra armonía, o contra la agrupación melódica). Los autores no se enfrentan a esta situación aumentando las reglas de formación. En su lugar, proporcionan un nuevo tipo de reglas, las reglas de preferencia de la agrupación (RPA a partir de ahora) . Estas reglas de preferencia se basan fuertemente en los principios gestaltistas de proximidad y similitud (y en el libro emplean un buen número de páginas a explicarlas a partir de ejemplos tomados del campo visual).
Las reglas de preferencia están divididas, a su vez, en dos categorías: las reglas de detalle local y las reglas de alto nivel. Dentro de la jerarquía ascendente de agrupamiento, las reglas de detalle local formalizan los grupos a bajo nivel y las reglas de alto nivel, los grupos que comprenden los grupos más grandes. Empezaremos por las reglas de detalle local, que son las siguientes:
RPA 1: Evítense los grupos que contengan un único evento. RPA 2 (proximidad): Considérense cuatro notas (n1,n2,n3,n4). Si el resto permanece igual, la transición n2 - n3 se puede oír como la frontera de un grupo si:
(Ligadura/silencio) el intervalo de tiempo desde el final de n2 hasta el principio de n3 es mayor que el del final de n1 al principio de n2 y que el del final de n3 al principio de n4, o bien si
(Punto de ataque) el intervalo de tiempo entre el ataque de n2 y n3 es mayor que el que va de n1 a n2 y el que va de n3 a n4.
RPA 3 (cambio): Considérense cuatro notas (n1,n2,n3,n4). Si el resto permanece igual, la transición n2 - n3 se puede oír como la frontera de un grupo si:
(registro) la transición n2 -n3 implica una distancia interválica mayor que la de n1 -n2 y la de n3 - n4, o si
(dinámica) la transición n2-n3 implica un cambio en dinámica y las transiciones n1-n2 y la de n3 - n4 no tienen ese cambio, o si
(articulación) la transición n2 - n3 implica un cambio de articulación y las transiciones n1 - n2 y la de n3 - n4 no tienen ese cambio, o si
(longitud) n2 y n3 son de diferente longitud y los dos pares n1,n2 y n3,n4 no difieren en longitud.
La primera regla RPA 1 tiene la intención de recoger la idea de que no se tiende a oír notas aisladas como eventos musicales significativos, sino que se tiende a integrarlos en grupos mayores. Solo en casos muy justificados (por otros elementos musicales apoyando fuertemente) podría identificarse una sola nota como un evento musical.
La segunda regla de preferencia RPA 2 establece las condiciones en que se forman las fronteras entre grupos consecutivos. La regla trata el caso de cuatro notas, donde la frontera se crea entre las notas segunda y tercera. Esta creación ocurre cuando hay un elemento musical más prominente (distancia interválica, dinámica o articulación) exactamente antes y después. En el ejemplo de abajo vemos la aplicación de esta regla de preferencia. Gracias a ella se puede explicar como las tres primeras notas en (a), (b) y (c) de la figura 11 se oyen como un grupo y el resto de las notas como perteneciente a otro grupo distinto.
Figura 11:
Reglas de preferencia de proximidad (figura tomada de [LJ83]).
La regla RPA 3 tiene bastantes paralelismos con la RPA 2. Los propios autores afirman en su libro que otros elementos musicales se pueden incorporar a esta regla, tales como la textura o el timbre. En la figura 12 tenemos un ejemplo en que se dan los cuatros casos de la regla de preferencia de cambio.
Figura 12:
Reglas de preferencia de cambio (figura tomada de[LJ83]).
Por último, tenemos en la figura 13 el mismo pasaje de la sinfonía número 40 de Mozart donde se pueden apreciar distintas aplicaciones de las reglas de preferencia anteriores.
Figura 13:
Reglas de preferencia de cambio (figura tomada de [LJ83]).
A continuación detallamos las reglas de organización de alto nivel. Son reglas que tratan de explicar y formalizar periodos más grandes de música que el motivo o simplemente que unos pocos compases. Para la regla RPA 7 necesitamos presentar dos nuevos conceptos, la reducción del tramo temporal y reducción de prolongación. La primera se refiere a cómo asignar a las alturas una jerarquía de importancia estructural con respecto a su posición en el agrupamiento y la métrica. La reducción de prolongación asigna a las alturas una jerarquía que expresa la tensión y relajación así como continuidad y progresión en los elementos armónicos y melódicos. En el artículo de septiembre se desarrollarán más a fondo estos dos conceptos.
RPA 4 (intensificación): Fórmese una frontera que dé lugar a un grupo mayor allí donde los efectos dados por las reglas RPA 2 y RPA 3 sean más pronunciados. RPA 5 (simetría): Prefiéranse los análisis de agrupamientos que se acerquen más al ideal de subdivisión de un grupo en dos subgrupos de igual longitud. RPA 6 (paralelismo): Allí donde dos o más segmentos de la música se puedan concebir como paralelos, preferiblemente deberán formar partes paralelas de un mismo grupo. RPA 7 (estabilidad del intervalo temporal y de prolongación): Prefiérase una estructura de agrupamiento que dé como resultado un intervalo temporal o una reducción de prolongación más estable.
En el ejemplo de la figura 14, la mera aplicación de las reglas RPA 2 (a) y (b) detectaría correctamente las fronteras entre los grupos de tresillos. Sin embargo, no marcaría la agrupación al siguiente nivel, el segundo, ya que esas reglas construyen las fronteras sobre las ligaduras y los ataques. La regla RPA 4 sí permite obtener las agrupaciones posteriores.
Figura 14:
Agrupaciones asociadas a tresillos (figura tomada de [LJ83]).
Las reglas RPA 5 y RPA 6 construyen las fronteras de los grupos a base de maximizar la simetría y el paralelismo. En el caso de la simetría, la regla de preferencia aconseja que en lo posible los subgrupos tengan la misma duración. En la figura 15vemos dos conjuntos de tresillos. En la figura 15 (a), dado que son cuatro tresillos, es inmediato que la agrupación natural es la que está desarrollada ahí. En figura 15 (b) tenemos seis grupos de tresillos y ahora estamos en presencia de dos interpretaciones posibles, la (i) y la (ii). Ninguna de las dos satisface a todos los niveles la regla RPA 5. En este caso, hay que acudir a otras consideraciones (ritmo armónico, textura u otros).
Figura 15:
Diversas agrupaciones posibles asociadas a tresillos (figura tomada de [LJ83]).
Para el caso del paralelismo, la regla RPA 6, tenemos el siguiente ejemplo.
Figura 16:
Agrupación basada en el paralelismo (figura tomada de [LJ83]).
El grupo de notas de la figura 16 (a) puede agruparse de varias maneras, pero según la regla RPA 6 esto ha de hacerse en grupos de tres notas porque de este modo el paralelismo entre los grupos se hace patente. Lo mismo puede decirse de la figura 16 (b), en este caso siendo la agrupación de cuatro notas.
En el próximo artículo se desarrollará y pondrán ejemplos de aplicación de la regla RPA 7.
5. Conclusiones
Del estudio de las reglas anteriores se extraen interesantes conclusiones. Lerdahl y Jackendoff optan por una descripción no matemática de su teoría, incluso aunque esta sea claramente matematizable. La formalización del agrupamiento, como hemos visto arriba, lleva implícita el concepto de recursión, concepto matemático donde los haya. Además la formación de los grupos es muy similar a una relación binaria tal como puede ser la inclusión; dicha relación de formación de grupos posee unas reglas para evitar los solapamientos y las elisiones. La formalización para la métrica es muy similar a la del agrupamiento, incluyendo también el concepto de recursión. Los casos que faltan por cubrir en el primer estadio de la formalización se suplen con la definición de las reglas de preferencia, que recogen fenómenos musicales más complejos (creación de grupos en base a articulación, diferencia interválica o de longitud, paralelismo, simetría, etc.). Como vemos, la teoría generativa tiene un sustrato matemático nítido.
La razón por la que Lerdahl y Jackendoff no exponen su teoría con un lenguaje abiertamente matemático (con símbolos y una formalización más dura) es porque no tienen interés en probar teoremas a partir de esta formalización (página 53, último párrafo). En su caso, se conforman con la exposición de su teoría en lenguaje natural (lo cual no quita que lo hagan con rigor) y confían en crear un sistema formal que constituya una buena descripción de la música tonal, que cubra cuanta más música posible y, por último, que sea lo más predictivo posible. También rechazan los aspectos cuantitativos de la teoría. No se esfuerzan en ningún momento en asignar funciones que puedan devolver números que expresen, por ejemplo, el grado de reducción de prolongación o la intensidad de la creación de la frontera de un grupo. Reconocen con total honestidad que no están interesados en esa cuantificación. Ellos quieren identificar las variables que son relevantes a la hora de establecer la intuición musical así como esas variables interactúan entre sí (página 54), pero no desde un punto de vista numérico.
Bibliografía
[Góm14] F. Gómez. Teoría generativa de la música - I, consultado en junio de 2014.
[LJ83] F. Lerdahl and R. Jackendoff. A Generative Theory of Tonal Music. MIT Press, Cambridge, Massachussetts, 1983.
[LJ03] F. Lerdahl and R. Jackendoff. Teoría generativa de la música tonal. Akal, 2003. Traducción de Juan González-Castelao Martínez.
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
Inauguramos una serie de artículos en la que estudiaremos la obra de Fred Lerdahl y Ray Jackendoff A Generative Theory of Tonal Music [LJ83], publicada en 1983. En castellano se publicó en 2003 por Akal [LJ03] con traducción de Juan González-Castelao. En este primer artículo estudiaremos la génesis de esta obra y sus fundamentos teóricos. En los siguientes artículos describiremos con cierto detalle las ideas de estos autores. Estos autores proponen una teoría generativa de la música tonal, es decir, una teoría que a partir de la definición de una serie de conceptos y reglas jerárquicas describan la estructura de una pieza de música tonal.
Figura 1:
Portada del libro original en inglés.
1. La génesis de la obra
El director de orquesta Leonard Bernstein, hombre por otro lado profundamente interesado en la teoría, fue un impulsor de la obra de Lerdahl y Jackendoff. En el otoño de 1973, Bernstein se encontraba impartiendo un seminario en la universidad de Harvard. Los trabajos de Noam Chomsky [Cho65] en pos de la construcción de una teoría generativa en el campo de la lingüística habían impresionado a Bernstein y este se preguntaba si esa teoría no se podía transferir al campo musical. ¿Era posible construir una gramática musical que explicase el fenómeno de la escucha musical?, tal era la pregunta que planteaba Bernstein a sus alumnos en aquel seminario. Entre los asistentes se encontraba el músico, compositor y teórico Fred Lerdahl y el lingüista y clarinetista Ray Jackendoff. Bernstein pedía a sus alumnos que expusiesen los resultados de su trabajo ante la clase cada semana y era frecuente que los alumnos se ayudasen entre sí. Jackendoff y Lerdahl se leían mutuamente sus trabajos en busca de la crítica constructiva del otro. Como fruto de esto, se percataron de que tenían preocupaciones intelectuales similares y empezaron a colaborar más seriamente. Con el tiempo fueron dando forma a sus ideas y estas cuales acabaron por cristalizar en A Generative Theory of Tonal Music. En el prefacio del libro (página x), hablan de la división del trabajo en el libro entre los dos autores. Lerdahl, el músico, planteaba problemas en términos musicales y proporcionaba ejemplos, y Jackendoff, el lingüista, construía los sistemas formales que trataban de explicar los fenómenos musicales. Sin embargo, Lerdahl conocía muy bien los sistemas formales en lingüística y Jackendoff era clarinetista con una sólida formación musical. Ambos estaban perfectamente capacitados para contribuir con ideas y críticas en ambos aspectos de la obra y así lo reconocen explícitamente en su obra (Our individual contributions are hopelessly intertwined.)
Tras el seminario impartido por Bernstein, Lerdahl y Jackendoff continuaron trabajando asiduamente hasta el año 1979. Se reunían semanalmente para desarrollar su teoría, la cual fueron presentando en diversos seminarios y publicando por partes en varias revistas (Journal of Music Theory, The Music Quaterly y en el libro Music, Mind and the Brain). Con el tiempo se dieron cuenta de que el material que habían producido daba de de sí como para escribir un libro en lugar de presentarlo en artículos sueltos o en conferencias. Después del año 79, la colaboración siguió, aunque no tan intensa, pues Lerdahl se fue a la Universidad de Columbia. En el año 83 publicaron su obra. Para una visión de uno de los autores (Lerdahl) sobre la génesis de este libro, véase [Ler09].
2. Teoría de la música como objeto de estudio psicológico
El capítulo uno de su libro abre con la siguiente declaración de intenciones (las cursivas son suyas; nuestra traducción):
We take the goal of a theory of music to be a formal description of the musical intuitions of a listener who is experienced in a musical idiom.
(Nos hemos fijado el objetivo de una teoría de la música que sea una descripción formal de las intuiciones musicales de un oyente que tenga experiencia en una tradición musical.)
Esta frase marca el tono de la obra y su metodología. Lerdahl y Jackendoff buscan una nueva manera de analizar la música. Para ello, recurren a la psicología para construir esa nueva metodología. Ambos autores tenían un gran conocimiento de la bibliografía relevante y en particular estaban familiarizados con las obras de Meyer y Cooper (especialmente [Mey56] y [CM63]), Narmour, Sloboda, Bregaman y Krumhansl, entre otros. Para justificar este nuevo análisis formulan una crítica de las viejas metodologías de análisis. Está, por un lado, el análisis de piezas individuales, un análisis clásico que se vale del estudio melódico, armónico, rítmico, entre otros, y que persigue resaltar facetas interesantes de la pieza. Para ellos, sin embargo, este tipo de análisis, aunque revela hechos interesantes sobre una pieza, no es riguroso ni sistemático en muchas ocasiones, y no permite generalizaciones o una sistematización útil. Con frecuencia depende de la habilidad y la brillantez del crítico a la hora de analizar la pieza. La opción contraria es crear un sistema altamente riguroso y formalista dentro del cual estudiar todas las piezas de una tradición musical. Los ejemplos históricos que ponen los autores tampoco les convencen: la teoría musical de la Edad Media, basada en la teología; los sistemas de Rameau y Hindemith, basados en los principios físicos de la serie de armónicos; o las teorías matemáticas de la música del siglo XX.
Merece la pena detenerse en este último punto, sobre todo por el tema de una columna como esta. Lerdahl y Jackendoff objetan al hecho de que las matemáticas den fundamento a los constructos y relaciones en la teoría de la música porque “las matemáticas son capaces de describir cualquier tipo de organización concebible”. Una teoría satisfactoria no solo debe ser capaz de describir ciertos constructos, sino además determinar porque se usan unos ciertos constructos y no otros. La crítica hacia el uso de las matemáticas que hacen los autores refleja excesos formalistas del pasado. A la vista de la cantidad de investigación que ha habido en música desde un punto de vista matemático desde la publicación de A Generative Theory of Tonal Music, y teniendo en cuenta la calidad y la metodología de dicha investigación, su crítica aparece teñida de cierta ingenuidad. Si la formalización matemática ignora la realidad que analiza y se convierte en un mero juego axiomático-deductivo, ¿qué significado asignará a esa formalización? Ninguno, claro; pero ese es un uso incorrecto de las matemáticas. La formalización correcta parte de los hechos musicales y trata de explicarlos y predecir otros, y en última instancia está siempre sometida al contraste con la propia música.
Por último, los autores rechazan el análisis basado puramente en la intuición artística. No desprecian este análisis; simplemente no creen que la música se deba analizar únicamente con dicho método.
¿Qué método, pues, proponen Lerdahl y Jackendoff? Uno basado en la psicología. Por un lado, sostienen que una pieza de música es una entidad construida mentalmente (página 2). Su objetivo es explicar la música como el sonido organizado en nuestra mente. Desde este punto de vista, la música es objeto de estudio psicológico. La teoría de estos autores necesita la introducción de un concepto nuevo: las intuiciones musicales de un oyente experimentado (página 3). Por intuiciones musicales se refieren a procesos inconscientes de escucha musical que vienen determinados por la enculturación del oyente en cierto lenguaje musical. Además, el concepto de oyente experimentado es una idealización del oyente y del grado de conocimiento de un lenguaje musical. Esa asimilación dentro de un lenguaje musical dado viene gobernada por ciertas reglas y con su teoría Lerdahl y Jackendoff persiguen describir esas reglas en términos de una gramática formal de la música. Hay una segunda idealización de este oyente y su escucha y es que en la teoría generativa se explica el estado final del entendimiento musical y no explica la percepción durante la la escucha musical.
3. Teoría de la música y lingüística
A pesar de su inspiración en la teoría generativa de Chomsky, Lerdahl y Jackendoff ponen mucho énfasis en distinguir lenguaje y música y en que ambas teorías -si bien se encuentran paralelismos importantes entre ambas- son esencialmente diferentes. En particular, los autores rechazan los peligros de sobreformalización que puede llevar una aplicación excesivamente literal de la teoría generativa de Chomsky a la música. Entre esos peligros los autores apuntan a un afán de validación de la teoría en meros términos computacionales, perder de vista el papel que juega el significado en la música y en el lenguaje -papel que difiere en una y otra-, o pasar inadvertidas las diferencias estructurales entre música y lenguaje.
4. La forma general de la teoría generativa
Lerdahl y Jackendoff proponen una estructura jerárquica compuesta por cuatro partes y que forma la base sobre la cual proporcionarán una descripción estructural de una pieza musical. Esas cuatro jerarquías son:
Estructura de agrupación. Expresa la segmentación jerárquica de la pieza en términos de motivos, frases y períodos.
Estructura métrica. Expresa los fenómenos métricos, esto es, los relacionados con la alternancia de tiempos fuertes y débiles.
Reducción interválica-temporal. Asigna una jerarquía a los tonos de una pieza en función de la estructura de agrupación y métrica.
Reducción de prolongación. Más abstracta que las anteriores, asigna a los tonos una jerarquía que expresa la dialéctica tensión-relajación en los aspectos armónicos y melódicos.
La teoría generativa además proporciona dos tipos de reglas, las de formación correcta y las de preferencia. Su función es determinar qué descripciones estructurales son correctas y sobre estas cuáles tienen más preferencia. Como dicen los mismos autores, el criterio empírico de éxito de la teoría es cuán adecuadamente describe las intuiciones musicales. Estas reglas están concebidas con este objetivo. Cuando empezaron a probar su teoría con ejemplos musicales concretos, vieron que las reglas de formación correcta no eran suficientes e introdujeron las reglas de transformación. La figura de abajo, tomada de su libro, representa un esquema de la teoría generativa de la música.
Figura 2:
Esquema de la teoría de Jackendoff y Lerdahl.
Bibliografía
[Cho65] N. Chomsky. Aspects of the theory of syntax. MIT Press, Cambridge, Massachussetts, 1965.
[CM63] G. Cooper and L.B. Meyer. The Rhythmic Structure of Music. University of Chicago Press, Chicago, 1963.
[Ler09] F. Lerdahl. Genesis and architecture of the gttm project. Music Perception, 26:187–194, 2009.
[LJ83] F. Lerdahl and R. Jackendoff. A Generative Theory of Tonal Music. MIT Press, Cambridge, Massachussetts, 1983.
[LJ03] F. Lerdahl and R. Jackendoff. Teoría generativa de la música tonal. Akal, 2003. Traducción de Juan González-Castelao Martínez.
[Mey56] Leonard Meyer. Emotion and Meaning in Music. University of Chicago Press, Chicago, 1956.
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
En la columna de este mes de febrero vamos a glosar un artículo del famoso teórico de la computación Donald Knuth [Wik14] cuyo título reza Randomness in Music (La aleatoriedad en la música) y que aparece en el excelente volumen recopilatorio The best writing on mathematics 2013 [Knu13]. Este volumen comprende los mejores escritos de matemáticas publicados en el año 2013 (según, al menos, sus editores), pero recomendamos su lectura (toca temas que van desde la definición de las matemáticas, la importancia de estas, la ansiedad matemática, y otros temas apasionantes).
Respecto al autor, es sobradamente conocido. Se le considera el padre del análisis de los algoritmos pues ha contribuido decisivamente a su fundamentación teórica. Escribió The Art of Computer Programming (El arte de programar ordenadores) [Knu97], donde describió algoritmos fundamentales así como estructuras de datos y proporcionó el análisis de su complejidad. Knuth es también el creador del programa TeX, el editor de textos científicos universal por antonomasia, así como del diseño de tipos Metafont. Aquí en España fue galardonado en 2010 con el Premio Fundación BBVA Fronteras del Conocimiento en la categoría de Tecnologías de la Información y la Comunicación.
1. Armonizaciones matemáticas
En su artículo Knuth propone un método para armonizar melodías a partir de un algoritmo matemático, el cual introduce aleatoriedad en dichas armonizaciones. Knuth elabora el concepto de imperfección planeada, la idea de que los sistemas perfectos no producen belleza y que la presencia de microvariaciones en los patrones musicales o visuales hacen a estos más atractivos. La idea que presenta se le ocurrió a partir de las clases de armonía que tomó (Knuth es también músico) con David Kraehenbuehl en el Westminter Choir College. El texto de Knuth nos dará una buena oportunidad de analizar críticamente las relaciones entre las matemáticas y la música —una vez más—.
1.1. Conceptos previos de música
Revisaremos rápidamente algunos conceptos de armonía. El lector con experiencia musical puede saltarse esta sección sin ningún remordimiento de conciencia. Las siguientes definiciones están tomadas del excelente libro de Walter Piston [Pis91]. Un acorde es la combinación de dos o más intervalos armónicos. El acorde más habitual en el periodo de la práctica común es la triada, que es un acorde formado por tres notas a distancia de tercera entre sí. La primera nota se llama fundamental; la segunda, la tercera; y la última, la quinta; véase la figura 1.
Figura 1:
Acordes y triadas.
Esta definición de acorde se aplica a cualquier clave. Las anteriores triadas estaban en do mayor, pero se podrían reescribir en cualquier otra tonalidad.
Los acordes admiten inversiones. Estas consisten en cambiar una nota a su octava superior más inmediata. Una triada con la fundamental como nota más grave se dice que está en estado fundamental; si es la tercera la nota más grave se dice que la triada está en la primera inversión; y si es la quinta la nota más grave hablamos de triada en segunda inversión. La figura 2 ilustra estas definiciones (de izquierda a derecha: estado fundamental, primera inversión y segunda inversión).
Figura 2:
Inversiones de las triadas.
Como la armonía se percibe desde la nota fundamental hacia arriba, hacia los armónicos, la nota fundamental tiene bastante importancia en la armonía tonal. En su artículo Knuth describe la idea de su profesor de armonía, Kraehenbuehl, que consiste en fijarse en la nota superior, que es la nota de la melodía o nota soprano (se llama así porque es la nota más aguda) en lugar de la nota fundamental para las armonizaciones. Kraehenbuehl constata que, dada una nota en particular, esta forma parte de tres triadas, una en posición fundamental, una en primera inversión y otra en segunda inversión. Knuth las denota por 0, 1 y 2, respectivamente. La figura 3 está tomada de su artículo [Knu13].
Figura 3:
Triadas asociadas a una misma nota soprano (tomado de [Knu13]).
Si duplicamos la nota más grave en la secuencia de acordes anterior, tendremos lo siguiente:
Figura 4:
Triadas con bajo (tomado de [Knu13]).
1.2. Y ahora el algoritmo de armonización
Según Knuth, su profesor de armonía propuso armonizar una melodía dada eligiendo acordes de modo que no haya dos seguidos con el mismo tipo de inversión. Si una melodía tiene n notas, entonces hay 3⋅2n-1 maneras de armonizarla. Para ilustrar este algoritmo o procedimiento tomemos la melodía de la conocida marcha no 1 en re mayor de Pompa y circunstancia, de Edward Elgar (figura 5). En su artículo usa otra melodía, la también conocida London Bridge is falling down, my fair lady.
Figura 5:
Marcha no 1 en re mayor de Pompa y circunstancia, de Edward Elgar.
Y es aquí donde Knuth propone una estrategia un tanto insólita para elegir las inversiones de los acordes, aquí es donde viene la aleatoriedad. Propone obtener la sucesión de las inversiones a partir de constantes matemáticas, en particular, de e, pi y φ (dice que es una elección mejor que “tirar un dado”). La parte entera de la constante módulo 3 servirá para elegir la primera inversión. La parte decimal se escribe entonces en notación binaria y se establece que un 0 suma +1 a la inversión anterior y un 1 resta +1. Todos los cálculos, por supuesto, son módulo 3.
Ilustremos este algoritmo con la melodía de Elgar. Las constantes mencionadas, escritas en notación binaria, son:
π = 3 + (0,0010010000111111011 ...)2 e = 2 + (0,10110111111000010101 ...)2 φ = 1 + (0,10011110001101110111 ...)2
donde el subíndice significa que esa parte está escrita en notación binaria. Usando la idea de Knuth, obtendríamos las siguientes sucesiones de inversiones:
pi
0,
0
0
1
0
0
1
0
0
0
0
1
1
1
1
1
1
0
1
Secuencia:
0
1
2
1
2
0
2
0
1
2
0
2
1
0
2
1
0
1
0
e
2,
1
0
1
1
0
1
1
1
1
1
1
0
0
0
0
1
0
1
Secuencia:
2
1
2
1
0
1
0
2
1
0
2
1
2
0
1
2
1
2
1
φ
1,
1
0
0
1
1
1
1
0
0
0
1
1
0
1
1
1
0
1
Secuencia:
1
0
1
2
1
0
2
1
2
0
1
0
2
0
2
1
0
1
0
Tabla 1:
Obtención de las sucesiones de inversiones.
Si aplicamos la sucesión de inversiones a nuestra melodía, obtenemos la armonización de la partitura de abajo. Como había algunas síncopas, me he tomado ciertas libertades en el ritmo armónico.
Figura 6:
Armonización según la constante pi.
En el caso anterior, y solo por pura casualidad, el estado del último acorde fue en estado fundamental. En la música tonal de la práctica común es una regla que la última nota corresponda a la tonalidad y que esta se presente con una acorde en estado fundamental. Esta regla dejó de observarse al final del periodo de la práctica común. Knuth es consciente de ello y propone un sencillo truco, el cual consiste en repetir la última nota de la melodía y poner a esa nota el acorde en estado fundamental. Por ejemplo, en la siguiente armonización, que corresponde a la de la constante e, vemos que no acaba según exige la armonía clásica.
Figura 7:
Armonización según la constante e.
En la figura 8 tenemos —siguiendo las ideas de Knuth y su profesor de armonía— una solución para acabar con el acorde adecuado en la marcha de Elgar. Obsérvese que hubo que romper la ligadura entre las dos últimas notas.
Figura 8:
Ajuste del acorde final.
2. Conclusiones
Este artículo de Knuth, en nuestra humilde opinión, es un ejemplo de mala relación entre las matemáticas y la música. Si pretende ser un divertimento musico-matemático, entonces no tenemos ninguna objeción. Cualquier excusa es buena para divertirse con las matemáticas, incluida las musicales. Si, por el contrario, pretende proporcionar una manera de armonizar musicalmente válida basada en una idea matemática como esta, hemos de decir con toda sinceridad que carece de seriedad y enjundia. Las secuencias de acordes siguen normas estilísticas bastante concretas, que, por cierto, varían de una época a otra, y, en general, no admiten el grado de aleatoriedad que Knuth propone. Hay ciertos acordes que con más frecuencia siguen a otros (véase [Pis91]). Los compositores persiguen ciertas tensiones musicales al diseñar la sucesión de acordes, tensiones que se perderían de poner en práctica la idea de Knuth. Aun más, la idea de usar las constantes pi,e y φ como generadores de la sucesión de inversión no tiene fundamento. Ni siquiera como una sonificación de dichas constantes se podría justificar estas armonizaciones. De hecho, nos preguntamos cómo es posible que este artículo este en un volumen que se llama The best writing on mathematics. Por último, dejamos aquí un vídeo en que se puede escuchar la armonización de Elgar.
Figura 9: Marcha no 1 en re mayor de Pompa y circunstancia de Edward Elgar (versión para piano con partitura de órgano).
Bibliografía
[Knu97] D. Knuth. The Art of Computer Programming. Addison-Wesley Professional, 1997.
[Knu13] D. Knuth. Randomness in music. Princeton University Press, 2013. Capítulo del libro The best writing on mathematics 2013, editado por Mircea Pitici.
[Pis91] Walter Piston. Armonía. Editorial Labor (versión española), 1991.
[Wik14] Wikipedia. Donal Knuth. http://en.wikipedia.org/wiki/Donald˙Knuth, consultado en febrero de 2014.
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
Con este artículo se acaba la serie sobre la similitud melódica como transformación de cadenas. Estamos tratando este tema principalmente a partir del artículo de Mongeau y Sankoff [MS90] Comparison of musical sequences. En los primeros artículos [Góm13a, Góm13b] vimos cómo adaptar la distancia de edición, en principio pensada para computar la distancia entre cadenas de caracteres, a la distancia melódica. Esta adaptación incluyó ampliar la distancia con operaciones más complejas que la inserción, borrado y sustitución. En este artículo veremos cómo evaluaron la calidad de su distancia.
1. Evaluación de la distancia
En el artículo anterior vimos que el modelo de similitud melódica de Mongeau y Sankoff incluía una serie de parámetros que había que determinar de modo heurístico. Los autores lo hacen tomando pares de pieza cuya similitud melódica es fácilmente calculable. Esa pieza que eligen son las variaciones KV. 265 Ah, vous dirai-je maman, de Mozart. Se trata de un tema y 12 variaciones para piano; el tema es una canción infantil muy conocida. En el vídeo de abajo tenemos una interpretación en pianoforte, el instrumento original para el que se escribieron; el pianista es Steven Lubin.
Figura 1: Las variaciones KV. 265 de Mozart.
Sin embargo, Mongeau y Sankoff no usaron finalmente las variaciones originales de Mozart. Encontraron que tenían mucha variación entre sí como para afinar los parámetros de su modelo. Tomaron un arreglo del flautista de pico Duchesnes [Duc62] (páginas 69-72) de la misma obra de Mozart. La ventaja que tenía el arreglo de Duchesnes es que casi todas las variaciones tenían el mismo número, aproximadamente, de compases. Este arreglo contiene solo 9 variaciones en lugar de las 12 de Mozart. En la figura de abajo tenemos el tema principal y la variación número 5. Vemos que la variación consiste en figuraciones relativamente simples de la melodía. Las flechas muestran cómo se transforma cada nota del tema principal en la variación.
Figura 2: Relación entre la variación 5 y el tema principal.
El parámetro que necesitaban determinar Mongeau y Sankoff era k1 (véase [Góm13b]). Estudiaron varios pares de secuencias musicales para este fin y estos fueron: el tema principal y la variación 5, las variaciones 2 y 3, y las variaciones 3 y 7. Cada variación tiene un gran distinto de similitud. Sus pruebas dieron un valor final de k1 = 0,348.
Una vez tuvieron el algoritmo con todos los parámetros completos pudieron ejecutarlo y obtener las distancias entre el tema y las variaciones. La tabla de abajo muestra esas distancias. Observando la tabla se sigue que la variación 5 es la más similar al tema, con una distancia de 17,2, y la más diferente la variación 9, con distancia 45,1.
Tema
Var. 1
Var. 2
Var. 3
Var. 4
Var. 5
Var. 6
Var. 7
Var. 8
Var. 9
Tema
0
Var. 1
19,1
0
Var. 2
29,1
29,1
0
Var. 3
17,2
22,7
26,6
0
Var. 4
33,1
33,3
33,2
33,5
0
Var. 5
17,6
20,0
30,3
21,0
34,0
0
Var. 6
33,1
41,8
44,1
39,1
46,7
34,8
0
Var. 7
40,5
41,7
49,5
45,1
44,5
45,0
40,3
0
Var. 8
41,5
43,9
44,4
39,7
42,1
40,1
47,4
54,4
0
Var. 9
45,1
48,3
49,2
38,1
45,9
46,8
44,7
49,3
38,0
0
Tabla 1: Tabla de con las disimilitudes.
A falta de métodos más modernos de agrupación, los autores llevaron a cabo un análisis de componentes principales tomando como datos de entrada la matriz de distancias. Los resultados están en la figura de abajo (es el análisis original que se encuentra en [MS90]). Se ven las variaciones 6 y 7 en un grupo, relativamente cercanas entre sí; las variaciones 8 y 9 en otro, aunque más alejadas entre sí; y por fin un gran grupo con el tema y el resto de las variaciones.
Figura 3: Análisis de componentes principales [MS90].
Las dos siguientes figuras muestran las variaciones 6 y 7. La variación 7 está construida sobre tresillos, salvo un par de negras con puntillo de final de frase, mientras que la variación 6 tiene más variación en la figuración rítmica (contiene corchea seguida de tresillo de semicorcheas, corchea seguida de cuatro fusas, corcheas con puntillo, negra ligada con semicorcheas). El lector puede apreciar la estructura de ambas variaciones y cómo se podría transformar una en otra en términos de la distancia de edición que hemos construido.
Figura 4: Variación 6 del arreglo de Duchesnes.
Figura 5: Variación 7 del arreglo de Duchesnes.
El análisis de componentes principales es una técnica estadística cuyo objetivo es reducir la dimensionalidad de los datos y así favorecer su visualización. La idea que hay detrás de esta técnica es hacer un cambio de base, por vía de una transformación lineal, de modo que en el primer elemento de la nueva base tenga la mayor varianza posible; el segundo, la segunda mayor varianza, y así sucesivamente. Después se proyectan los datos sobre la nueva base, que ha de tener menos elementos que el número original de variables. Cuando Mongeau y Sankoff escribieron el artículo corría el año 90 y no se conocían técnicas de visualización de datos provenientes de distancias; por ello, usaron el análisis de componentes principales. A mediados de los años 90 se empiezan a inventar técnicas específicas de visualización en Biología, en particular para visualizar las relaciones entre datos genéticos. Pronto esas técnicas se generalizan a otros campos, incluyendo la computación. En 1998 Huson [Hus98] lanza un paquete informático Splitstree que contiene los principales algoritmos para construir grafos filogenéticos; este es el nombre que reciben estas estructuras de visualización de datos. La última versión de su paquete se puede encontrar en [HB06]. Para construir un grafo filogenético se toma una matriz de entrada que contiene las distancias entre un conjunto de objetos (en nuestro caso piezas musicales, pero pueden especies animales, cadenas de caracteres, etc.). Un algoritmo típico filogenético devuelve un grafo plano en que la distancia entre dos nodos se corresponde tan fielmente como es posible con la distancia en la matriz. En principio, el algoritmo intenta ajustar la matriz a un árbol; si ello no es posible, introduce un número mínimo de nodos para realizar el ajuste y produce grafos con ciclos (que ya no son árboles). El algoritmo proporciona un índice de ajuste, el LS-fit, que indica el nivel de correspondencia entre las distancias en la matriz y las distancias en el grafo; se expresa como un porcentaje. Cuanto más alto, mayor es esa correspondencia. Para el caso que nos ocupa, el índice es LS-fit=99,85%, que indica que la correspondencia es muy alta.
La ventaja de los grafos filogenéticos sobre el análisis de componentes principales es que se basan en las distancias reales entre los objetos. El agrupamiento que se observa en el grafo es el que revela la propia distancia. Abajo tenemos el árbol filogenético asociado a la matriz de distancias.
Figura 6: Árbol de distancias.
Vemos que hay tres variaciones, la uno, la tres y la cinco, que están muy cercanas al tema. A mayor distancia de estas se encuentran las variaciones dos y cuatro; las más lejanas son las seis, siete, ocho y nueve. Las variaciones seis y siete son similares entre sí; lo mismo le ocurre a las variaciones ocho y nueve.
En la figura de abajo tenemos un filograma, que es un árbol filogenético donde la longitud de las ramas es proporcional a la distancia entre los objetos. Este tipo de grafo refleja mejor las relaciones de transformación entre las piezas musicales.
Figura 7: Filograma de distancias.
2. Conclusiones
Esta serie de artículos ha mostrado cómo usar la distancia de edición para medir la similitud melódica. Este fue uno de los artículos pioneros en el tema. Posteriormente, la investigación en este campo se desarrolló extraordinariamente y hoy en día se pueden encontrar decenas de artículos que proponen generalizaciones de la distancia de edición. Entre las más interesantes se encuentran las que han introducido resultados de cognición musical en el diseño de la distancia. En otra futura serie de artículos expondremos la filosofía y el funcionamiento de esas distancias.
Bibliografía
[Duc62] Mario Duchesnes. Méthodes de flûte à bec. BMI Canada Ltd., Toronto, 1962.
[Góm13a] F. Gómez. Similitud melódica como transformación de cadenas - I. http://divulgamat2.ehu.es/divulgamat15/index.php?option=com˙content&view=article&id=15541&directory=67, consultado en noviembre de 2013.
[Góm13b] F. Gómez. Similitud melódica como transformación de cadenas - II. http://divulgamat2.ehu.es/divulgamat15/index.php?option=com˙content&view=article&id=15633&directory=67, consultado en noviembre de 2013.
[HB06] D. H. Huson and D. Bryant. Application of phylogenetic networks in evolutionary studies. Molecular Biology and Evolution, 23(2):254–267, 2006.
[Hus98] Daniel H. Huson. SplitsTree: Analyzing and visualizing evolutionary data. Bioinformatics, 14:68–73, 1998.
[MS90] M. Mongeau and D. Sankoff. Comparison of musical sequences. Computers and the Humanities, 24:161–175, 1990.
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
En el artículo de este mes, el de frío diciembre, explicaremos la primera parte del artículo de Mongeau y Sankoff [MS90] Comparison of musical sequences, en la que se detalla cómo se aplica la distancia de edición a la similitud melódica desde un punto de vista algorítmico (véase la columna del mes pasado [Góm13] para un repaso de los conceptos básicos). En concreto, veremos como estos autores aumentan el arsenal de operaciones sobre las cadenas para acomodar la distancia de edición al contexto musical. Para el mes siguiente dejaremos la descripción de los experimentos que realizaron para probar la bondad de la medida.
1. La distancia de edición para cadenas musicales
El método que proponen Mongeau y Sankoff es particularmente apropiado para la música que está representada simbólicamente, es decir, dada por la codificación de la notación tradicional musical. La codificación más habitual es la midi (programas de edición musical como Finale o Sibelius exportan a midi, por ejemplo). El método de estos autores no se adecua en cambio a música codificada en formato de audio, tales como wav o mp3, que son codificaciones orientadas a describir la música desde un punto de vista físico. De la notación tradicional el algoritmo de Mongeau y Sankoff emplea la sucesión de alturas y duraciones y la tonalidad de la pieza.
Recordamos de la columna del mes pasado que la ecuación básica de la distancia de edición es, dadas dos cadenas A,B de longitudes respectivas n,m, la siguiente:
donde los índices cumplen que i = 1,…,n y j = 1,…,m.
El algoritmo de Mongeau y Sankoff examina las diferencias en altura y en duración de las notas. Esto implica que el modelo anterior, tan simple, donde los pesos cI,cB y cS son constantes, ya no es válido. Reescribimos la ecuación como sigue para reflejar que ahora los pesos dependen de la posición del elemento de la cadena (usamos la notación de [MS90]; d(ai,bj) se designará indistintamente por di,j ).
(1)
con las condiciones iniciales
(2)
En todas estas fórmulas se cumple que w(x,y) = w(y,x) para cualesquiera caracteres x,y.
Mongeau y Sankoff se fijaron en dos parámetros a la hora de diseñar su distancia para medir la disimilitud (la distancia de edición mide precisamente eso, la disimilitud entre dos cadenas; algunos autores empero hablan de similitud). Esos parámetros son la altura y la duración de las notas. La forma general de los pesos se descompone en dos términos como sigue:
donde wint(ai,bj) es el peso asociado al intervalo entre la nota ai y bj, y, análogamente, wdur(ai,bj) es el peso asociado a las duraciones de ai y bj. El parámetro k1, cuya determinación se hará más adelante, sirve para afinar el modelo. k1 representa la importancia de la contribución de la duración frente a la altura del sonido. El peso wint(ai,bj) es la diferencia entre la posición relativa de las notas ai y bj multiplicada por la menor de las duraciones de las dos notas. wdur(ai,bj) es sencillamente la diferencia en duración entre ai y bj. Los pesos de los intervalos se toman módulo la octava; esto es, el peso asociado a un par de notas a,b es el mismo que el asociado a a y a b más un múltiplo de una octava.
El lector se habrá dado cuenta inmediata de que esta elección de los pesos refleja un confinamiento a la música tonal. Para medir la distancia entre dos notas los autores exigen que la pieza tenga una tonalidad establecida; de este modo, la altura de cada nota es la distancia a la tónica, y la distancia entre dos notas, la diferencia de alturas. Además, los pesos de las alturas reflejan las relaciones de consonancia entre las notas. Así, una octava y un quinta, intervalos muy consonantes, reciben poco peso; en cambio, una segunda o una séptima reciben mucho mayor peso. En cuanto a las duraciones, están codificadas en términos de una unidad mínima, que Mongeau y Sankoff toman como la semicorchea.
Con el fin de asegurarse que el peso del intervalo no depende de la tonalidad o del modo de la pieza, las alturas se convierten a grados de la escala. Esto implica que ahora la distancia entre una tercera mayor y una tercera menor puede ser cero. Esto corrige el peligro de una misma pieza escrita en modo mayor no aparezca como excesivamente diferente de su correlato en modo menor. En la tabla siguiente tenemos los grados de la escala mayor y menor junto con las diferencias correspondientes en semitonos.
Grados de la
1
2
3
4
5
6
7
escala mayor
Grados de la
1
2
3
4
5
6
7
escala menor
Semitonos
0
1
2
3
4
5
6
7
8
9
10
11
de diferencia
Tabla 1:
Grados de las escala mayor y menor dentro de la escala cromática.
Sin embargo, este esquema es insuficiente porque en una pieza pueden aparecer notas que no pertenecen a la escala en que se encuentra escrita. Las razones son múltiples: dominantes secundarias, cambios temporales de modo, color aplicado a través del cromatismo, alteraciones armónicas, etc. Mongeau y Sankoff implementan un esquema más fino para este caso. Llaman gr(n) al peso asociado a dos notas cuya diferencia es n grados en la escala. Cuando una de las dos notas no pertenece a la escala emplean entonces ton(m), que está dada por la relación:
donde μ y δ son parámetros a determinar y donde n(m) es el grado de la escala más cercano dado por m semitonos. Por ejemplo, n(7) es 4, ya que la quinta el intervalo dado por cuatro grados de la escala consiste en 7 semitonos; n(4) = 2 para una escala mayor y n(3) = 2 para una escala menor.
Otro caso que hubieron de contemplar Mongeau y Sankoff fue el de una nota que se transforma en un silencio –caso distinto de una nota que se suprime o inserta–. Los autores introducen un nuevo peso, wsil, para tratar esta situación. Cuando se da el caso de dos silencios de la misma duración, wsil toma el valor que tendría si hubiese dos notas de la misma altura.
2. Nuevas operaciones
Mongeau y Sankoff, inspirándose en los estudios de reconocimiento de habla (véase [KL83]), añadieron dos operaciones más: la fragmentación y la consolidación. La primera consiste en la sustitución de varios elementos por un solo y la segunda es la operación inversa, la sustitución un único elemento por varios; en la figura 1 se ilustran estas operaciones. Con el modelo usado hasta ahora, la descomposición de una nota redonda en cuatro negras, algo muy habitual en música, sería irrazonablemente costoso.
Figura 1:
Las nuevas operaciones de fragmentación y consolidación.
Los pesos asociados a estas dos nuevas operaciones siguen la misma lógica usada hasta ahora y, en consecuencia, se escribirán como combinaciones lineales de los pesos wint y wdur de las notas que se consolidan o fragmentan. Para la fragmentación el peso total de wint será una combinación lineal de los pesos de cada nota por la nota sustituida final. De manera análoga, se definen los pesos para consolidación.
3. El algoritmo completo
Con las ampliaciones definidas en las secciones anteriores, podemos presentar la relación final para la distancia de edición:
(3)
donde 1 ≤ i ≤ n,1 ≤ j ≤ m, y donde w(ai,bj-k+1,…,bj) y w(ai-k+1,…,ai,bj) son los pesos asociados con la fragmentación y la consolidación, respectivamente. Las condiciones iniciales son las que aparecen en la ecuación (2equation) más arriba.
No entraremos en este artículo divulgativo en cuestiones de complejidad, pero los autores del artículo probaron que la recursión dada por la fórmula anterior se puede calcular en tiempo proporcional al producto n⋅m. En particular, se dieron cuenta que, dada la condición de minimalidad de la definición de distancia de edición, no hacía falta calcular la recursión completa para las operaciones de fragmentación y la consolidación.
En este punto el lector debe estar extrañado de que no hayamos entrado todavía en la cuestión de los numerosos parámetros que quedan pendiente para que la recursión (3) se pueda calcular. Mongeau y Sankoff los calculan de modo heurístico comparando pares de piezas musicales para las que conocen aproximadamente sus valores de similitud; esto se profundizará en el último artículo de esta serie. De todos modos, los autores mismos reconocen que “los valores precisos que han calculado son muy debatibles o que podían optimizarse con respecto a un conjunto dado de datos”. Los valores que dieron para los parámetros son los siguientes:
Peso y valor
Intervalo
gr(1) = 0
unísono
gr(2) = 0,9
segunda
gr(3) = 0,2
tercera
gr(4) = 0,5
cuarta
gr(5) = 0,1
quinta
gr(6) = 0,35
sexta
gr(7) = 0,8
séptima
Peso y valor
wsil = 0,1
μ = 2
δ = 0,6
k1 = 0,348
Peso y valor
Intervalo
ton(0) = 0
unísono
ton(1) = 2,6
segunda menor
ton(2) = 2,3
segunda mayor
ton(3) = 1
tercera menor
ton(4) = 1
tercera mayor
ton(5) = 1,6
cuarta justa
ton(6) = 1,8
cuarta aumentada
ton(7) = 0,8
quinta justa
ton(8) = 1,3
sexta menor
ton(9) = 1,3
sexta mayor
ton(10) = 2,2
séptima menor
ton(11) = 2,5
séptima mayor
Tabla 2:
Pesos del algoritmo.
4. Conclusiones
Es posible que el lector que se asome por primera vez a este tipo de aplicaciones de las matemáticas se sorprenda de cómo se eligen los parámetros del algoritmo. En muchos casos, parece que es una elección demasiado dependiente del contexto o que no hay principios suficientemente generales que guíe tal elección. En parte, este lector tendría razón. Mirado con perspectiva histórica, ese juicio severo se suavizaría. El artículo de Mongeau y Sankoff es del año 1990 y fue pionero en el estudio de la similitud musical por vía de la distancia de edición. Muchos algoritmos vinieron después que mejoraron sus ideas y que se basaron en posteriores estudios de cognición musical. Hemos escogido este artículo para presentar al lector una introducción a la similitud musical desde la computación precisamente por su carácter de artículo pionero. Normalmente, así es cómo ocurren las cosas en ciencia y tecnología. La primera solución suele ser imperfecta, ardua, poco elegante, pero siempre necesaria. Primero se lucha por resolver el problema; más tarde viene la satisfacción estética de la solución limpia y elegante.
Bibliografía
[Góm13] F. Gómez. Similitud melódica como transformación de cadenas - I, consultado en noviembre de 2013.
[KL83] J.B. Kruskal and M. Liberman. Time warps, string edits, and macromolecules: the theory and practice of sequence comparison, chapter The symmetric time-warping problem: from continuous to discrete, pages 125–159. Addison-Wesley, 1983.
[MS90] M. Mongeau and D. Sankoff. Comparison of musical sequences. Computers and the Humanities, 24:161–175, 1990.
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
He aquí una nueva serie de tres artículos que investigan desde un punto de vista divulgativo la relación entre la similitud melódica y la teoría de cadenas (una rama de la computación). La similitud melódica, bajo ciertas hipótesis que simplifican el complejo fenómeno que es, se puede concebir como un problema de comparación de cadenas, donde las cadenas aquí representan sucesiones de notas. En un artículo titulado Comparison of musical sequences Mongeau y Sankoff [MS90] explotaron esta idea. En esta serie glosaremos su trabajo con detalle. En el artículo de este mes discutimos el concepto de similitud melódica, por la parte musical, el concepto de comparación de cadenas, con especial énfasis en la distancia de edición, y finalmente analizamos los aspectos computacionales de dicha distancia. En el siguiente artículo veremos cómo Mongeau y Sankoff adaptaron la distancia de edición para computar la disimilitud entre dos melodías dadas. En el último artículo de la serie examinaremos los experimentos llevados a cabo por estos autores para comprobar la bondad de su medida. Esos experimentos consisten en medir la similitud melódica de las nueve variaciones sobre el tema Ah, vous dirai-je, Maman, K. 265, de Mozart y analizar los resultados obtenidos.
1. Similitud melódica
Los fenómenos musicales son básicamente perceptuales y cognitivos en su naturaleza ([Deu98], página 158). Esta aseveración puede sonar a los oídos de hoy como evidente, pero la tradición racionalista del análisis musical la relegó al olvido durante mucho tiempo. De hecho, la psicología misma empezó a reconocer la música como objeto de estudio serio hace solo unas pocas décadas. Hasta entonces el análisis musical se había basado en las matemáticas (desde la tradición pitagórica al sistema de doce tonos de Schoenberg), la física (empezando con el trabajo de Helmhotz [Hel85]), y la música (análisis schenkeriano, análisis armónico, etc.), y los aspectos cognitivos de la música se habían desatendido por completo.
La melodía se encuentra entre los fenómenos musicales más investigados. Los teóricos de la música han examinado miles de melodías con el fin de describir sus características estructurales, mientras que los psicólogos han ceñido su atención a la manera en que el ser humano percibe y responde a la melodía. Un teórico de la música bien puede preguntarse cuáles son los elementos constituyentes de la melodía, y su respuesta, probablemente, vendrá dada en términos de altura y relaciones de duración, tales como dirección melódica, relación interválica, altura más grave y más aguda, entre otras [Ort37]; o incluso en términos de atributos más abstractos, tales como propincuidad, repetición de tonos y finalidad [?]. En contraste con esto, un psicólogo de la música se podría preguntar, por ejemplo, cuáles son los factores psicológicos que transforman una sucesión de notas en una melodía, y esta vez, probablemente, la respuesta se presentaría en términos de leyes de percepción (Bower y Hilgard [BH81]), esquemas melódicos (Dowling and Hardwood [DH86]), o modelos de estructuración jerárquica perceptual (West et al. [WHC85], Sloboda [Slo85], Lerdahl [LJ83]). Hoy en día es inconcebible estudiar el fenómeno melódico sin examinar ambas facetas.
Pero cuando se trata de procesar música o de establecer algún esquema cuantitativo o en última instancia computacional, ¿es posible incorporar el conocimiento proveniente de ambos campos? Cuando empezó el estudio computacional de la música, los modelos de entonces no permitían tener esos aspectos en consideración. Aunque hoy los pasos son más seguros en esa dirección, todavía son lentos. En este artículo vamos a estudiar un modelo computacional de similitud melódica. El modelo simplifica en buena medida la complejidad de ese fascinante fenómeno que es la melodía. A cambio obtiene una medida que permite comparar melodías bajo ciertas condiciones. Sigue, qué duda cabe, una evaluación del método para ver cuánto afectó la mencionada simplificación.
La similitud melódica es un concepto fundamental, tanto desde el punto de vista teórico como desde el práctico. Es esencial en el proceso musical porque sirve como evaluación de la variación del material, del reconocimiento del estilo y del compositor, de la interpretación, del aprendizaje musical, o en la clasificación musical; véase McAdams and Matzkin [MM01]. Acicateados por el creciente número de aplicaciones de la similitud melódica (sistemas de recomendación, leyes de propiedad intelectual, búsqueda en bases de datos musicales, clasificación de estilos, atribución de obras dudosas), muchos matemáticos e informáticos han diseñado algoritmos para computar la similitud melódica basados en muy diversas técnicas: medidas geométricas, distancias de transporte, medidas de probabilidad, similitud estadística, proximidad geográfica, entre otros; para una lista exhaustiva, véase [HSF98] y las referencias allí listadas.
Mongeau y Sankoff, en su artículo del año 90 [MS90], arguyen que los aspectos puramente musicales son bastante difíciles de evaluar y que están sujetos a un alto grado de subjetividad (en realidad, van más lejos y dicen arbitrariedad, que es una palabra con implicaciones más serias). Deciden centrarse en dos variables fundamentales: la altura del sonido y las duraciones (el ritmo). En su trabajo adaptan las distancias de edición clásicas (la distancia de Levenshtein) y la amplía con más operaciones. Ello les permite definir una distancia con más poder de discriminación y aplicar a la comparación de piezas musicales.
2. Distancias entre cadenas de símbolos
En Informática el problema de la distancia entre cadenas es un problema que aparece en muchos contextos y que tiene muchas aplicaciones. En su versión más básica se formula como sigue: dadas dos cadenas A,B de símbolos (tomados de un alfabeto común), hallar el mínimo número de operaciones que hay que realizar para transforma A en B. Las operaciones se definen previamente y las tres más elementales son borrado, inserción y sustitución. Ese número mínimo de operaciones se toma como la distancia entre A y B. Como veremos en las aplicaciones prácticas se añaden operaciones más complejas tales como fragmentación y consolidación.
Esta distancia fue descubierta por Levenshtein en el año 1965 y publicada en una revista rusa de informática. Se la conoce como distancia de Levenshtein y también como distancia de edición. A partir de ella se han definido otras muchas: distancias de Levenshtein ponderadas, distancia de Damerau-Levenshtein (que permite trasposiciones), distancias de Hamming, entre otras.
Antes de definir formalmente la distancia de edición, vamos a poner un ejemplo. Las operaciones usadas serán las que mencionamos arriba: borrado, inserción y sustitución. Asignaremos un coste de 1 a cada operación. Consideremos la cadena A = TENER y B = PERDER. Una posible secuencia de operaciones para transformar A en B es la siguiente:
Borrado de T: TENER => ENER.
Inserción de P: ENER => PENER.
Sustitución de N por R: PENER => PERER.
Inserción de D: PERER => PERDER.
La transformación se ha hecho en 4 operaciones. No es la mínima ya que las operaciones 1) y 2) se pueden reemplazar por una sustitución directa a coste 1 solo. En ese caso, el número de operaciones sería mínimo y la distancia valdría 3.
Para definir formalmente la edición hace falta especificar un conjunto de operaciones y a cada una de ellas asignarles un coste. Una vez hecho eso, la distancia de edición es, como dijimos, el número mínimo de operaciones necesario para transformar una cadena en otra.
2.1. Algoritmo para calcular la distancia de edición
En esta sección vamos a estudiar los aspectos computacionales de la distancia de edición. Su definición nos parece clara, pero ¿cómo es posible calcularla? Sean A,B dos cadenas de longitudes n y m, respectivamente, con caracteres pertenecientes a un alfabeto común. Un algoritmo clásico para resolver el problema de la distancia de edición es la programación dinámica. Esta técnica algorítmica se aplica a problemas en que la solución local es parte de la solución global, como ocurre en el caso que nos ocupa.
Por comodidad en la descripción del algoritmo, designamos por A[1..i] la subcadena (a1,…,ai) de A, donde 1 ≤ i ≤ n; y análogamente con la subcadena B[1..j] de B, con 1 ≤ j ≤ m. El algoritmo calcula la distancia de A a B usando una matriz como estructura de datos, matriz que tiene dimensiones (n + 1) × (m + 1). Dicha matriz sirve para almacenar las distancias entre todas las subcadenas A[1..i] y B[1..j]. En un paso genérico el algoritmo calcula la distancia d(A[1..i],B[1..j]) y para ello se apoya en las distancias de subcadenas más pequeñas, en particular, en las distancias entres subcadenas. Si cI,cB,cS son, respectivamente, los coste de la inserción, borrado y sustitución, la distancia d(A[1..i],B[1..j]) se calcula con la fórmula siguiente:
Es, como se puede apreciar, una fórmula que usa los valores previos para calcular el valor actual. La solución se construye de manera local, en cada paso, y la solución global es el resultado del procesamiento de todos las subcadenas de A y B. No obstante, dado que en cada paso se usan valores de subcadenas más pequeñas, solo se procesan dos caracteres, ai y bj, en cada paso del algoritmo. Para que la sucesión de operaciones no se reduzca a las sustituciones, en las aplicaciones suele aparecer la condición cS < cI + cB.
Como paso de inicialización el algoritmo necesita tener calculados las distancias de d(A[1..i],∅) y d(∅,B[1..j]), donde i = 1,…,n, j = 1,…,m y ∅ es la cadena vacía. El valor de d(A[1..i],∅) es j ⋅cB y el de d(∅,B[1..j]) es i ⋅ cI.
A continuación se muestra un pseudocódigo (adaptado de [Wik13]).
int LevenshteinDistance(char cad1[1..longCad1], char cad2[1..longCad2]) // d es una matriz con longCad1+1 filas y longCad2+1 columnas declare int d[0..longCad1, 0..longCad2] // i y j se usan como variables para el bucle iterativo declare int i, j, costeBorrado, costeInsercion, costeSustitucion
(1) for i from 0 to longCad1 d[i, 0] := i*costeInsercion (2) for j from 0 to longCad2 d[0, j] := j*costeBorrado
(3) for i from 1 to longCad1 (4) for j from 1 to longCad2 (5) if cad1[i] = cad2[j] then d[i, j]:=d[i-1, j-1] else d[i, j] := minimo( d[i-1, j] + costeBorrado, // Borrado d[i, j-1] + costeInsercion, // Inserción d[i-1, j-1] + costeSustitucion // Sustitución )
return d[longCad1, longCad2]
La prueba de corrección del algoritmo se basa en un invariante que se mantiene a lo largo de todo el algoritmo: el hecho de que el elemento d(i,j) de la matriz contiene la distancia de edición de las subcadenas A[1..i] y B[1..j]. No es inmediatamente evidente que d(i,j) proporciona de hecho el número mínimo de transformaciones entre dichas subcadenas; require una prueba por inducción que no damos aquí. En ciertos contextos, no solo es necesario la distancia entre las cadenas, sino también la sucesión de operaciones que transforma una en la otra. En un ejemplo desarrollado más abajo se muestra cómo conseguir esa sucesión.
2.2. Un ejemplo de la distancia de Levenshtein
Tomemos para nuestro ejemplo dos inocentes cadenas, dicho en el sentido estricto de la palabra, A = y B = . En un mundo ideal, volterianamente cándido, la distancia entre ambas cadenas debería ser infinita. En el mundo que nos ocupa, y más en el de las secas cadenas de caracteres, sabemos que esa distancia es finita, dolorosamente finita. Computemos cuán finita. Nos ayudaremos del applet que ha escrito Scott Fescher [Fes13] para ilustrar el funcionamiento de la distancia de edición; las figuras de más abajo han sido generadas con ayuda de ese applet. Como pesos para las operaciones tomaremos cI = cB = cS = 1, esto es, la distancia original de Levenshtein. Obsérvese que se cumple la condición cS < cI + cB.
El primer paso, como sabemos, es la inicialización. Esta consiste en calcular las distancias de la cadena vacía a las cadenas A = y B = ; véanse los bucles (1) y (2) del pseudocódigo presentado más arriba. Todas las operaciones se reducen a inserciones (en la fila) y a borrados (en la columna), como se puede apreciar en la matriz de la figura 1.
Figura 1: Inicialización del algoritmo de la distancia de edición.
A continuación empiezan a procesarse el primer carácter de A y todas las subcadenas B[1..j] de B para j = 1,…,10 (10 es la longitud de la ). En la figura 2 nos hemos parado en el cálculo de la distancia de las subcadenas subcadenas y . En ese momento el algoritmo tiene que rellenar el elemento (2,7) de la matriz. Primero se comprueba que la los caracteres a procesar son distintos. No es el caso aquí, pues ambos se reducen al carácter . La distancia se iguala a la del elemento (1,6), cuyo valor es 5.
Figura 2: Detalle del cálculo de la distancia de las subcadenas y .
En la figura 3 vemos unos cuantos casos más donde se dan la igualdad entre caracteres de las dos cadenas (aparecen rodeados con un círculo rojo). Véase el if, línea (5), en el pseudocódigo arriba.
Figura 3: Casos en que los caracteres a procesar son iguales.
En un paso genérico, cuando los caracteres a procesar no son iguales, el algoritmo calcula las distancias a partir de tres distancias inmediatamente anteriores. En el caso de la figura 4 se va a calcular la distancia d(6,5). Las distancias de los anteriores elementos son d(6,4) = 4,d(5,4) = 3 y d(5,5) = 3. El algoritmo especifica que la nueva distancia ha de ser el mínimo entre los números , que es 4.
Figura 4: Paso genérico del algoritmo.
Si continuamos todo el proceso hasta el final, la matriz que obtenemos es la de la figura 5. La distancia de edición viene dada por el elemento (9,11), el más abajo a la izquierda, rodeado por un círculo rojo. Su valor es 7.
Figura 5: Matriz completa de la distancia de edición.
El algoritmo se puede ampliar con un sistema de punteros de tal manera que se puede reconstruir la sucesión de operaciones que transforma una cadena en la otra. Dada una distancia d(i,j) a calcular en un paso genérico del algoritmo, si el mínimo se alcanza con la distancia d(i,j - 1) estamos ante una inserción, si se alcanza con d(i - 1,j) estamos ante un borrado y si se alcanza con d(i - 1,j - 1), ante una sustitución. A partir de la distancia final, y disponiendo de esta información, se puede recorrer la matriz desde el elemento (n + 1,m + 1) hasta el (1,1) y listar la sucesión de operaciones. En general, el camino que va del elemento que da la distancia de edición hasta el (1,1) no es único. En la figura 6 se muestra un posible camino. Los números rodeados por un círculo rojo corresponden a los momento en que los caracteres a procesar eran idénticos.
Figura 6: Obtención de la sucesión de operaciones.
Si I y S representan inserción y borrado, la sucesión de operaciones de la figura anterior es (S,S,S,S,S,I,I) y la sucesión de transformaciones es:
3. Conclusiones
Como vemos la distancia entre político y corrupción no es mucha, siete pasos, aunque, como dijimos antes, debería ser infinita o al menos ser finita solo en el mundo de la computación. El mes que viene veremos cómo se puede aplicar la distancia de edición a la comparación de cadenas con significado musical.
Bibliografía
[BH81] G. H. Bower and E. R. Hilgard. Theories of learning. Prentice-Hall, Englewwod Cliffs, NJ, 1981.
[Deu98] D. Deutsch. The Psychology of Music. Academic Press, 1998.
[DH86] W. J. Dowling and D. L. Hardwood. Music cognition. Academic Press, Orlando, FL, 1986.
[Fes13] S. Fescher. Edit Distance ILM. http://csilm.usu.edu/lms/nav/activity.jsp?sid=˙˙shared&cid=emready@cs5070˙projects&lid=10, consultado en octubre de 2013.
[Hel85] H. Von Helmholtz. On the sensations of tone as a physiological basis for the theory of music. Dover, New York, 1954 (publicado originalmente en 1885).
[HSF98] W. B. Hewlett and E. Selfridge-Field. Melodic Similarity: Concepts, Procedures, and Applications. MIT Press, Cambridge, Massachussetts, 1998.
[LJ83] F. Lerdahl and R. Jackendoff. A Generative Theory of Tonal Music. MIT Press, Cambridge, Massachussetts, 1983.
[Lun67] R. W. Lundin. An objective psychology of music. Ronald Press (segunda edición), New York, 1967.
[MM01] S. McAdams and D. Matzkin. Similarity, invariance and musical variation. Annals of the New York Academy of Sciences, 90:62–76, 2001.
[MS90] M. Mongeau and D. Sankoff. Comparison of musical sequences. Computers and the Humanities, 24:161–175, 1990.
[Ort37] O. Ortmann. Interval frequency as a determinant of melodic style. Peabody Bulletin, pages 3–10, 1937.
[Slo85] J. A. Sloboda. The musical mind. Clarendon Press, Oxford, 1985.
[WHC85] R. West, P. Howell, and I. Cross. Modelling perceived musical structures. In Howell, Cross, and West (Eds.), Musical structure and cognition. Academic Press, Londres, 1985.
[Wik13] Wikipedia. The Levenshtein distance. http://en.wikipedia.org/wiki/Levenshtein˙distance, consultado en octubre de 2013.
|
|
Cultura y matemáticas/Música y matemáticas
Autor:Paco Gómez Martín (Universidad Politécnica de Madrid)
8. Introducción
En este último artículo vamos a estudiar las propiedades matemáticas de las binarizaciones y ternarizaciones. Avisamos al lector de que el contenido matemático es un poco más alto que el de las dos entregas anteriores. A partir de los fenómenos musicales descritos anteriormente desarrollaremos el estudio de estas transformaciones. El principal resultado que se ve en este artículo es que la aplicación de las reglas de aproximación produce idénticos resultados si se aplican al pie métrico y luego se concatenan los resultados parciales que si se aplican las reglas al patrón rítmico desde el principio.
9. Binarizaciones y ternarizaciones desde un punto de vista matemático
9.1. Preliminares
En este artículo asumiremos que los ritmos son isócronos; Pérez Fernández supone lo mismo en sus libros [Pér86] [Pér79]. Esto implica que ambos ritmos tienen tramos temporales de igual duración. Ya que los patrones ternarios tienen menos pulsos (12 frente a 16), se sigue que sus pulsos durarán más que en el caso de los patrones binarios.
Primero, probaremos un lema que se usará en los resultados que siguen. Sea K un patrón rítmico compuesto por p grupos de k pulsos cada uno y M otro patrón compuesto por p grupos de m pulsos cada uno. Supongamos que k,m > 1. Consideremos la transformación de K a M.
Lema 1 Hay dos pulsos consecutivos en M que son equidistantes a un pulso en K si y solo si k es par y m es impar.
Prueba:
Para la implicación del si: Ya que 2 divide a k, el punto (k/2)/k = 1/2 es un pulso de K. Como m es impar, se sigue que . Consideremos los pulsos consecutivos y de M. Entonces (k/2)/k es equidistante de y . En efecto:
Para la implicación del y solo si: Sean i,j dos índices tales que i/m y (i+1)/m son equidistantes de j/k. Se tienen las siguientes igualdades:
La última igualdad implica que k tiene que ser par y m, impar.
9.2. Reglas de aproximación aplicadas a la concatenación de pies métricos - binarización
Sea T un patrón ternario compuesto de p grupos 3 pulsos cada uno. Sea B el patrón binario formado por p grupos de 4 pulsos cada uno. En el análisis que hemos hecho, p toma bien el valor 2 o bien 4. Consideremos la transformación de T en B bajo las reglas de aproximación (véanse los números de agosto y septiembre de 2013 de esta columna). Los pulsos de T y B (para p ≥ 1) están dados por las siguientes sucesiones:
Por la definición de las reglas de aproximación, los pulsos en T de la forma , para i = 0,…,p- 1, se asignan a en B. Consideremos los pulsos restantes, a saber, aquellos d ela forma y , para i = 0,…,p- 1. Dado un pulso fijo ti de T, cuando T y B se ponen uno encima del otro, se sigue del lema de más arriba que la función distancia de ti a los pulsos de B posee solo un valor mínimo, el cual se alcanza solo por un pulso de B. Nótese que esta afirmación no es cierta si se intercambia T por B.
A continuación probamos un par de pequeños resultados concernientes a los vecinos más cercanos:
Resultado 1: Los dos vecinos más cercanos de los pulsos en B son y , y el mínimo se alcanza en .
Resultado 2: Los dos vecinos más cercanos de los pulsos en B son y , y el mínimo se alcanza en .
Para (1), de los tres siguientes cálculos se sigue el resultado:
Distancia de a :
- = =
Distancia de a :
- = =
Distancia de a :
- = =
A partir de estos cálculos se deduce que el vecino más cercano en sentido antihorario de es , y su vecino más lejano en sentido horario es .
Para (2), cálculos análogos establecen el resultado:
Distancia de a :
- = =
Distancia de a :
- = =
Distancia de a :
- = =
El vecino más cercano en sentido horario de es , y su vecino más lejano en sentido antihorario es .
9.3. Concatenación the los pies métricos tras aplicar las reglas de aproximación - binarización
Ahora transformaremos patrones ternarios en patrones binarios (de 4 pulsos) por vía de las reglas de aproximación. Esta vez se concatenarán p grupos. Queremos probar que la concatenación de los patrones transformados al nivel del pie métrico producen los mismos resultados que aplicar las reglas de aproximación al patrón entero. Un patrón ternario de 3 pulsos se describe con la sucesión . Un patrón binario de 4 pulsos, con la sucesión . Reproducimos de nuevo la figura que ilustra las reglas de aproximación (la figura está en el segundo artículo de esta serie, en el mes de septiembre)
Figura 1:
Reglas de aproximación para la binarización de los pies métricos.
Resumiendo la información de la figura 1, tenemos:
Los vecinos más cercano, más lejano, horario y antihorario de 0 es 0.
Los vecinos más cercano y antihorario de son a distancia , y los vecinos más lejano y horario son a distancia .
Los vecinos más cercano y horario de son a distancia , y los vecinos más lejano y horario son a distancia .
Cuando los patrones ternarios se concatenan, estos tienen que meterse en un tramo temporal común. Para ello, los patrones ternarios tienen que cambiar de escala en un factor de 1/p. Este cambio de escala no afecta a las distancias relativas entre los pulsos y, por tanto, tampoco afecta a los vecinos de un pulso. Por ejemplo, si p = 4, la sucesión se transforma en la sucesión , la cual a su vez se transforma en cuando los cuatro patrones ternarios son concatenados. El vecino más cercano de 1∕12 es ⋅ = .
Cuando se efectúa la división por p y los ritmos se concatenan, se obtiene lo siguiente:
Los pulsos de la forma , i = 0,…,p - 1 se transforman en bajo todas las reglas de aproximación.
Para los pulsos de la forma , para i = 0,…,p - 1, tenemos: < < , donde es el vecino más cercano de .
Para los pulsos de la forma , para i = 0,…,p - 1, tenemos: < < , donde es el vecino más cercano de .
En consecuencia, encontramos que las reglas de aproximación son las mismas que las dedujimos más arriba.
9.4. Reglas de aproximación aplicadas a la concatenación de pies métricos - ternarización
Consideremos la ternarización, esto es, la transformación de B a T. Cálculos similares a los hechos para el caso de la binarización conducen a la siguiente tabla:
Elemento de B
Primer vecino más cercano
Distancia
Segundo vecino más cercano
Distancia
Tercer vecino más cercano
Distancia
0
NA
NA
NA
NA
,
Tabla 1:
Tabla de distancias para la ternarización.
Leyenda: El primer vecino más cercano se refiere al vecino más cercano del elemento de B con respecto a los elementos de T; la siguiente columna muestra la distancia entre el pulso de B y su vecino más cercano. A continuación está el segundo vecino más cercano seguido de su distancia. Similar definición se aplica para el tercer vecino más cercano y la distancia. NA significa no aplicable, ya que siempre se proyecta en según todas las reglas de aproximación.
Nótese que para el pulso de B hay dos pulsos, y , a igual distancia. La función todavía alcanza un mínimo, pero lo hace en dos valores. Esta situación ocurre porque B es un ritmo binario y tiene un pulso en el medio de cada intervalo [0,],…,[,]. Por tanto, en este caso el vecino más cercano no es único, así como tampoco el vecino más lejano.
9.5. Concatenación los pies métricos tras aplicar las reglas de aproximación - ternarización
La figura 2 muestra las reglas de aproximación para la ternarización de los pies métricos. La presencia de notas comunes es evidente. Los vecinos más cercano y más lejano no son únicos.
Figura 2:
Reglas de aproximación para la ternarización de los pies métricos.
De nuevo, razonando de manera similar al caso de la binarización se puede probar que la concatenación de los pies métricos dan reglas equivalentes a las de aproximación definidas para el tramo temporal entero.
Bibliografía
[Pér79] Rolando A. Pérez. Ritmos de cencerro, palmadas y clave en la música cubana. Manuscrito no publicado y presentado al Concurso Premio Musicología, Casa de las Américas, 1979.
[Pér86] Rolando A. Pérez. La binarización de los ritmos ternarios africanos en América Latina. Casa de las Américas, Havana, 1986.
|
| © Real Sociedad Matemática Española. Aviso legal. Desarrollo web |