91. 40. (Octubre 2012) Alcance y extralimitaciones de las matemáticas y la computación en la música

1. Introducción Con frecuencia, cuando un recién conocido se interesa por mi trabajo y le informo de que trabajo con matemáticas y música, la reacción suele ser una divertida mezcla de sorpresa e incredulidad. Tras esos momentos iniciales de desconcierto, las posturas se vuelven tan variadas como los colores. Hay algunos que afirman con aplomo: “Sí, ya se sabe que las matemáticas y la música están muy relacionadas” (pero en ocasiones no estoy seguro de que a se refieren exactamente). Otros, más despistados, mencionan varios físicos conocidos por su gran amor a la música, principalmente Einstein. Otros, más sinceros, confiesan no entender cómo algo tan abstracto como las matemáticas puede tener algo que ver con la música, algo tan artístico y emocional (como si las matemáticas no compartiesen esas características con la música). Actualmente, el estudio de la música por parte de las matemáticas y la computación en el mundo de la investigación está consolidado en buena medida y ya se ve, en general, como algo normal. Sin embargo, esa relación no ha estado, ni probablemente en el futuro lo estará, libre de tensiones respecto a los alcances y extralimitaciones de las matemáticas y la computación en la música. El artículo de este mes trata de acercar al gran público la naturaleza de esa relación y esbozar las tensiones epistemológicas que hay entre ellas. En el tercer congreso International Conference on Mathematics and Computation in Music (MCM) celebrado en el IRCAM en 2011 se abordó el problema del alcance y extralimitaciones de los métodos matemáticos y computaciones en la investigación en música. Para tal fin, la organización del congreso invitó a tres panelistas, figuras reconocidas en su campo: Alan Marsden, profesor de música en la Universidad de Lancaster; Guerino Mazzola, matemático, músico, musicólogo y profesor en la Universidad de Minnesota; y Geraint Wiggins, profesor de creatividad computacional en la Universidad de Londres (Queen Mary) y musicólogo computacional. El tema de la sesión fue bridging the gap: computational and mathematical approaches in music research (acortando distancias: métodos matemáticos y computacionales en la investigación de la música). La sesión resultó ser fructífera, con gran participación del público, y por ello los editores de la revista Journal of Mathematics and Music decidieron dedicar un número especial a esta cuestión bajo el título Mathematical and computational approaches to music: challenges in an interdisciplinary enterprise; véase [VH12]. Los panelistas recibieron cuatro preguntas sobre las que elaborar sus intervenciones. Estas fueron: Beneficios: ¿cuáles han sido las contribuciones claves de las matemáticas y la computación a la investigación de la música? Errores: ¿Cuáles son los ejemplos de errores en la aplicación de los métodos matemáticos y computacionales a la investigación de la música en el pasado? ¿Cómo podemos aprender de esos errores? Retos: ¿A qué retos se enfrentan los métodos matemáticos y computacionales en la investigación de la música? ¿Cuáles son las cuestiones por explorar que tienen el potencial de ampliar nuestro entendimiento de la música con la ayuda de las matemáticas y la computación? ¿Qué pasos han de darse para que las matemáticas y la computación desarrollen todo su potencial en la investigación de la música? Discurso interdisciplinar: ¿Cómo se pueden fortalecer las conexiones entre los tres campos? ¿Hay maneras diferentes de entender la música en las tres disciplinas? ¿En qué contextos son las diferencias entre los tres campos útiles para fomentar investigaciones originales y novedosas? ¿Cuándo dichas diferencias suponen un escollo para una verdadera investigación interdisciplinar y qué se necesita hacer para superarlo? El mencionado artículo [VH12] contiene un resumen de las discusiones entre los panelistas. En este artículo expondré las principales aportaciones de los panelistas (en la sección siguiente, en cursiva) y las comentaré para el lector (en tipo de letra normal). 2. Beneficios, errores, retos y discurso interdisciplinar Beneficios: Contribuciones importantes a la tecnología (formato mp3, sistema de recomendación, análisis automático, etc.). Los panelistas nombran estas pocas, pero en realidad hay muchísima computación y matemáticas detrás de ellas. Por ejemplo, los sistemas de recomendación llevan implícitos sistemas de similitud musical –que incluyen similitud melódica, rítmica y tímbrica–, así como complejos procesos de etiquetación, reconocimiento de patrones, búsqueda en bases de datos y otros. Clarificación conceptual de términos musicales. Ciertamente, la formalización matemática de ciertos conceptos musicales ha llevado a una clarificación de estos. Por ejemplo, la teoría de la afinación ha sufrido una gran formalización por parte de matemáticos e informáticos; véase, por ejemplo, el capítulo 5 del libro de Benson [Ben06]. Visión más general de la música. Sin duda, el estudio de la música desde otros puntos de vista, como puede ser el de encontrar sus estructuras básicas o sus reglas de formación, ha contribuido a una comprensión más profunda de ese fenómeno multidimensional y complejo que es la música. Estudio de la evolución musical. Este es un problema fascinante en que varios autores han trabajado: ¿Cómo cambia el fenómeno musical? Para un ejemplo en el campo del ritmo véanse [Tou02] y [Tou03]. Creación de herramientas para la enseñanza musical. En varios conservatorios ya se usa un enfoque mixto en la enseñanza de la música. Por ejemplo, la teoría de escalas o el círculo de quintas se puede enseñar en un contexto músico-matemático. Véase el excelente libro de Scott Beall [Bea00]. Fracasos: Estudio de la música en sí misma sin tener en cuenta sus procesos. Este error es más común de lo deseable entre matemáticos e informáticos que estudian la música. Sin lugar a dudas, la música es un fenómeno y como tal puede estudiarse, pero también es el resultado de un complejo proceso que va desde la onda de sonido a la emoción. A veces ignorar la importante dimensión de proceso de la música invalida una investigación. Estudiar la teoría de la música sin tener en cuenta su dimensión cognitiva. Este es, a mi juicio, uno de los errores más graves que se pueden cometer en el estudio de la música. En última instancia, la música cobra sentido porque hay un oyente que la escucha y procesa. Ignorar la dimensión cognitiva vacía de sentido a la investigación musical. Lamentablemente, muchos investigadores rechazan ponerse al día de la bibliografía de cognición musical. Para una primera toma de contacto, recomendamos el libro de Radocy y Boyle [RB03]. Ignorar los aspectos físico-acústicos a favor de los aspectos puramente formales. No es posible estudiar la música con profundidad y de manera pertinente si no se estudian varios de sus aspectos más importantes. Formalización excesiva de algunos objetos musicales (escalas, modos, etc.). En ocasiones, el aparato matemático-computacional que se usa para formalizar los objetos y procesos musicales no está justificado. Parece más una querencia del investigador que una necesidad real de tal formalización. Uso excesivo de la abstracción. Alcanzar un punto razonable de abstracción en la investigación matemática de la música no es fácil, y a veces se han cometido excesos al respecto. Desafíos: Los musicólogos desconocen las herramientas que ofrecen las matemáticas y la computación. Este es un hecho triste. Creo que por una parte tiene que ver con el rechazo de una parte de los musicólogos hacia la musicología cuantitativa y, en particular, a la computacional. Y por otro lado, sospecho que tiene que ver con la falta de formación computacional. También culparía a los propios matemáticos e informáticos, cuyo lenguaje e interfaces no son desde luego un ejemplo atrayente para los musicólogos menos expertos en computación. El desafío, pues, consiste en que los musicólogos -sobre todos los históricos y culturales- empiecen a usar estas formidables herramientas. Modelizar el carácter impreciso y multidimensional de la música. Indudablemente, hacen falta modelos flexibles y potentes que sean capaces de reflejar toda la complejidad de la música. Comprobación empírica de los modelos computacionales. Este es otro de los problemas más graves en este tipo de investigación. Con frecuencia, se presenta un modelo que trata de explicar un proceso musical. En el peor caso, se pone encima de la mesa sin ninguna comprobación de ningún tipo; en otros casos, las comprobaciones son sobre búsquedas en base de datos o con experimentos más o menos artificiales. Como dije antes, hace falta la comprobación empírica sobre sujetos, esto es, con seres humanos. En la columna de marzo de 2011 de esta sección se puede leer un ejemplo explicado; es el de la similitud rítmica en el flamenco. Se describen tanto el modelo matemático como su validación perceptual. Aumentar el uso de las técnicas estadísticas. El uso de los métodos estadísticos permite procesar mucha información musical, especialmente en los estudios de grandes corpus de música. Construir una mejor conexión entre racionalismo y empirismo. Este es un desafío que casi podríamos calificar de eterno. La música es susceptible de estudiarse desde ambos puntos de vista y el verdadero carácter interdisciplinar consiste en la sabia combinación de ambos. Construir una metateoría de la música que integre varias disciplinas. De nuevo, esta es una aspiración interdisciplinar que de materializarse haría avanzar sustancialmente la musicología en su conjunto. Modelizar el comportamiento musical y no solo la música en sí. Este desafío reivindica el aspecto conductual de la música; de nuevo, véase el libro de Radocy y Boyle [RB03]. Discurso interdisciplinar: La humildad es esencial para el trabajo interdisciplinar. Si se lleva a cabo un estudio interdisciplinar, esta es la actitud mínima que uno puede pedir al respecto. Sin embargo, hay mucha arrogancia tanto por parte de los estudiosos desde el punto de vista científico como del de las humanidades. Con mucho acierto y buena dosis de valentía, Parncutt denuncia esta situación en un artículo de 2007 [Par07]; recomendamos vivamente su lectura. Hay que ser honesto respecto al alcance de la investigación. No porque se investigue la música desde un campo este ha de ser el más importante. Es fundamental reconocer el papel del resto de las disciplinas que estudian la música. Hay que ser honesto respecto a lo que es importante. Sin honestidad no hay investigación verdadera. Reconocer sinceramente las múltiples facetas de la música. El estudio de la música requiere una verdadera actitud humanista. Contrastar las teorías computacionales con experimentos requiere mucha colaboración interdisciplinar. Este punto recoge la necesidad antes expresada de la validación perceptual de las teorías matemáticas y computacionales. 3. Conclusión Como puede comprobar el lector los retos en estos campos interdisciplinares de la musicología computacional y la tecnología musical son formidables. Una vez más insistimos en que el avance de las disciplinas esta condicionado a la verdadera colaboración interdisciplinar, algo que a mucha gente le encanta nombrar como sello de modernidad, pero que pocos practican con fe. Uno de los grandes escollos para esa colaboración es la formación de los investigadores. La mayoría o bien son científicos o musicólogos, y muy pocos son ambos. Mi opinión es que hace falta ser las dos cosas, siquiera sea por un problema de lenguaje. Lamentablemente, el tipo de carrera mixta que exigiría esa nueva formación no existe en casi ninguna facultad. Bibliografía [Bea00] S. Beall. Functional melodies: Finding mathematical relationships in music. Key Curriculum Press, 2000. [Ben06] D. Benson. Music: A Mathematical Offering. Cambridge University Press, 2006. [Par07] R. Parncutt. Systematic musicology and the history and future of western musical scholarship. Journal of Interdisciplinary Music Studies, 1:1–32, 2007. [RB03] R. E. Radocy and D. J. Boyle. Psychological Foundations of Musical Behaviors. Charles C. Thomas, Springfield, Ill., 2003. [Tou02] Godfried T. Toussaint. A mathematical analysis of African, Brazilian, and Cuban clave rhythms. In Proceedings of BRIDGES: Mathematical Connections in Art, Music and Science, pages 157–168, Towson University, Towson, Maryland, U.S.A., July 27-29 2002. [Tou03] Godfried T. Toussaint. Classification and phylogenetic analysis of African ternary rhythm timelines. In Proceedings of BRIDGES: Mathematical Connections in Art, Music and Science, pages 25–36, Granada, Spain, July 23-27 2003. [VH12] A. Volk and A. Honingh. Mathematical and computational approaches to music: challenges in an interdisciplinary enterprise. Journal of Mathematics and Music, 6(2):73–81, 2012.

Miércoles, 24 de Octubre de 2012 | Imprimir | PDF |  Correo electrónico

92. 39. (Septiembre 2012) Estadística en la musicología II

1. Música tonal Las escalas son piezas primordiales en la música de todas las culturas. Hay géneros musicales que se caracterizan en buena medida por el tipo de escala que emplean. Una escala es un conjunto de notas normalmente dadas en orden ascendente y que sirven como material principal a una pieza musical. La mayor parte de las escalas sigue el principio de equivalencia de la octava. Dos notas están separadas por una octava si la frecuencia de la nota más aguda es exactamente el doble de la más grave. El principio de la equivalencia de la octava establece que dos notas que están a una distancia de una octava se consideran como la misma nota pero en registros distintos. Una misma escala puede empezar en diferentes notas; la primera nota de la escala suele ser la nota principal de la escala. Por ejemplo, afirmar que una pieza está escrita en la escala de do mayor significa que sus notas principales están tomadas del siguiente conjunto de notas (do-re-mi-fa-sol-la-si): Figura 1: Escala de do mayor. La nota principal de la escala anterior es do y el tipo de escala el mayor. El hecho de que aparezca la nota do en ese conjunto implica que se puede usar cualquier do en cualquier octava. En realidad, una escala especifica una clase de alturas que se usan en una pieza dada. Una pieza musical se puede escribir usando una sola escala, o con alternancia de escalas, o también con desviaciones temporales de la escala principal (normalmente por razones expresivas). Puesto que los ejemplos que vamos a analizar estadísticamente pertenecen a la música clásica occidental, nos centraremos en las escalas tal y como se definen en esa tradición musical. Para definir una escala primero se toma la octava y se divide en 12 semitonos iguales -el temperamento igual-. Después se escogen las notas de la escala entre las notas producidas por la subdivisión en partes iguales. Las escalas más comunes en la música clásica occidental, al menos en el periodo de la práctica común (aproximadamente, entre 1600 y 1900), son la escala mayor y la escala menor. La escala mayor empezando en la nota do está representada en la figura 1; en la figura 2 tenemos la escala menor natural basada en la nota do también. Figura 2: Escala de do menor natural. Si designamos por S la distancia de un semitono y por T la de un tono entero entre dos notas consecutivas, entonces la escala mayor tiene como sucesión de distancias entre notas T - T - S - T - T - T - S, mientras que la escala menor tiene la sucesión T - S - T - T - S - T - T. Las escalas mayor y menor son igualmente importantes y ubicuas en la música popular (pop, rock, música latina, mucha música folklórica, etc.). ¿Por qué son estas dos escalas tan comunes en la música occidental? A partir de 1600 los músicos fueron sintiendo una necesidad creciente de modular, esto es, de cambiar la tonalidad dentro de una misma pieza. Las escalas mayor y menor permitían la modulación más fácilmente que otras. Veamos brevemente por qué es así. Supongamos que estamos en la tonalidad de do mayor y, por tanto, la escala que rige es la dada en la figura 1. Si queremos modular a otra tonalidad, ¿cuál serían las tonalidades a las que podríamos cambiar de modo que el cambio no le resultase brusco al oído? Aquí hay que hacer un inciso y avisar de que el concepto de brusquedad depende de muchísimos factores: el periodo histórico, la teoría de la consonancia predominante, el estilo musical en particular, el contexto cultural, entre otros. Para el desarrollo que vamos a hacer aquí, el concepto de brusquedad equivale a buscar la tonalidad cuya escala mayor comparta el mayor número de notas. En el caso de do mayor esas tonalidades son sol mayor (sol-la-si-do-re-mi-fa♯) y fa mayor (fa-sol-la-si♭-do-re-mi). Con la primera tonalidad la única nota de diferencia es fa♯ y con la segunda, si♭, como se aprecia en la figura 3. Figura 3: Modulación desde do mayor. En la música tonal las notas se clasifican jerárquicamente en función de su relación con la nota principal de la escala (la primera). En este contexto, las notas de la escala reciben el nombre de grados y estos a su vez reciben nombres especiales: Primer grado I Tónica Segundo grado II Supertónica Tercer grado III Mediante Cuarto grado IV Subdominante Quinto grado V Dominante Sexto grado VI Superdominante Séptimo grado VII Sensible/Subtónica Tabla 1: Nombres de los grados de la escala Cuando el séptimo grado está a distancia de medio tono de la tónica se le llama sensible, como en ocurre en la escala mayor. Si está a distancia de un tono, como en la escala menor, se llama subtónica. Los grados que coinciden con las notas en cuyas escalas es más fácil modular son el cuarto y el quinto, la subdominante y la dominante. Pero no solo son estos grados de la escala importantes por su facilidad de modulación. También permiten una fuerte afirmación de la tonalidad de la escala vía la armonía. Veamos cómo. Los acordes se construyen como triadas, como grupos de tres notas que suenan simultáneamente. En la figura siguiente tenemos los acordes que se forman sobre la escala de do mayor; obsérvese que a cada grado de la escala se le ha añadido dos notas a distancias tres y cinco (en términos de grados y contando el grado de que partimos). Así, por ejemplo, el acorde sobre el grado I está formado por I-III-V, sobre el grado por II-IV-VI, y así sucesivamente. Figura 4: Triadas asociadas a la escala de do mayor. Otro hecho a considerar es que en la escala mayor el séptimo grado está a distancia de un semitono. Este grado tiene una gran tendencia a ir hacia la tónica, el primer grado. De entre los dos acordes más próximos al acorde de tónica, el de subdominante y dominante, es este último el que contiene la nota sensible. Por tanto, la secuencia V-I refuerza más a la tónica que la secuencia IV-I. Las secuencias de acordes que crean una sensación de resolución se llaman cadencias. De hecho, la secuencia IV-V-I es llamada cadencia perfecta y es la cadencia más usada para afirmar la tonalidad de una pieza. En el caso de la escala menor, que no tiene sensible, el séptimo grado se modifica, elevándolo medio tono, para que durante la cadencia perfecta aparezca la nota sensible. La siguiente en importancia es la cadencia IV-I, la cadencia plagal. Vemos, pues, que los grados IV, V y I son importantes en la música tonal. Otro grado importante es el III, la mediante. Si estamos en una escala mayor, el III grado está a dos tonos de distancia; si es una escala menor, a un tono y medio. Esta diferencia es importante musicalmente. Obsérvese que entre las escalas mayor y menor (figuras 1 y 2) los grados IV y V no varían (la construcción de sus correspondientes acordes, sí). El resto de los grados tienen ya menos importancia dentro de la música tonal. Se usan, por ejemplo, como parte de secuencia de acordes, como la famosa secuencia de caída de quintas VI-II-V-I. A finales del siglo XIX y principios del XX surgieron otros sistemas musicales en los que no se seguían estas relaciones de jerarquía. Se ampliaron los límites de la disonancia, se inventaron nuevos acordes y nuevas formas de resolver las disonancias, poco a poco se fue borrando la dependencia de un centro tonal, hasta que llegamos a la música dodecafónica en que no existe el concepto de tónica, pues todos los grados aparecen por igual en la pieza. 2. Detección de música tonal Es fácil para un oído mínimamente entrenado saber si una pieza es tonal o no. Aquí planteamos cómo lo haría un ordenador de modo automático. Con un poco de estadística, ello es posible. Si la música es tonal, los grados más importantes, el I, el V y el IV, aparecerán más frecuentemente. Para ilustrar este hecho hemos escogido las siguientes piezas (de nuevo, estos ejemplos están tomados del del libro de Beran [Ber04]): La fuga no 1 de El clave bien temperado, libro I, de Bach (1685- 1750). Sonata KV 545, primer movimiento, de Mozart(1756-1791). Escenas de niños, números 2 y 3, de Schumann(1810-1856). Preludios números 2 y 4 de la opus 51, de Scriabin (1872-1915). Preludios números 6 y 7, de F. Martin (1890-1971). En las figuras 5 y 6 se muestran los primeros compases de la fuga de Bach y del segundo preludio de Scriabin respectivamente. De la observación de las partituras se sigue que Bach es plenamente tonal, mientras que Scriabin y aun más se apartan ya significativamente. Figura 5: Comienzo de la fuga no. 1, de El clave bien temperado, libro I, de Bach (1685-1750). Figura 6: Comienzo del preludio no. 2, opus 51, de Scriabin (1872-1915). Para cada pieza elegida vamos a representar por las notas que aparecen en los tiempos t1,t2,…,tn. Los posibles valores que encontramos en ese conjunto pertenecerán a , por las 12 notas posibles del temperamento igual. Por supuesto, se aplicará el principio de equivalencia de la octava, ya que una nota está asociada a un grado de la escala no importa en qué octava aparezca. Los tiempos ti están tomados en orden creciente, t1 ≤ t2 ≤… ≤ tn. Con el fin de comparar adecuadamente las piezas, se han normalizado las piezas de modo que todas tenga la misma tonalidad. Una vez hecho esto, calculamos las frecuencias relativas de cada nota del siguiente modo. Se fija un número entero k, en nuestro caso de k = 16, y se cuenta el número de veces que aparece cada nota en intervalo de tiempo 2k + 1. Esas frecuencias, para una nota x, están dadas por la fórmula: donde la función I devuelve 1 si x(ti) = x y 0 en otro caso (la función característica). En las figuras 7 y 8 se muestran las correspondientes curvas de frecuencias. Cada curva se ha obtenido uniendo las frecuencias pj(0),pj(1),…,pj(11) consecutivamente para un valor j = 4,…,64. Las curvas se han superpuesto en la misma gráfica. Recordamos que, dado que estamos midiendo en semitonos, en el eje de ordenadas el 0 corresponde a la tónica, el 3 al grado III en la escala menor, el 4 al grado III en la escala mayor, el 5 a la cuarta justa, el 7 a la quinta justa, el 8 a la sexta menor, y el 9 a la sexta mayor. Figura 7: Frecuencias de las notas 0,1,…,11 en intervalos de longitud 16 notas [Ber04]. Figura 8: Frecuencias de las notas 0,1,…,11 en intervalos de longitud 16 notas [Ber04]. En Bach se aprecia claramente que los máximos se encuentran en los grados IV, V y III, seguidos del séptimo grado (a causa de los acordes de séptima de dominante) y de la propia tónica. En Mozart, los máximos están en la tónica y la subdominante; también vemos que los grados II, V y VI son frecuentes. En la escena 2 de Schumann la tónica es la nota más frecuente, seguida de lejos por el III y IV grado. La dominante, en cambio, aparece mucho menos y el sexto grado es más frecuente que el quinto. En la escena 3 de Schumann la música es mucho más tonal, con una predominio claro de los grados tonales I, IV y V. La situación cambia con Scriabin y Martin. En el preludio número 2 el quinto grado apenas se encuentra y son los grados III, IV y VI los que predominan. El preludio número 4 es menos tonal aún. Los grados más frecuentes son el I, el IV y V♭. Este último grado es cromático en la escala y forma una quinta disminuida con la tónica. El sistema tonal se deslíe y las funciones tonales clásicas quedan desdibujadas. No obstante, todavía vemos que ciertos grados son prominentes, aunque no los que esperábamos. En el caso de Martin, las funciones tonales se disuelven aún más, especialmente en el preludio número 6. Los máximos se alcanzan en la tónica, la mediante, pero también en V♯, el quinto grado aumentado (en el octavo semitono), y en el grado VI menor (en el noveno semitono). Sin embargo, por el número de veces que pasan las curvas por esos grados, nos damos cuenta de que hay una influencia del dodecafonismo, corriente que trata todos los grados por igual en términos de funciones tonales. En efecto, la gráfica del preludio número 6 parece una malla más o menos uniforme en contraste con, por ejemplo, la gráfica de la sonata de Mozart. Bibliografía [Ber04] J. Beran. Statistics in Musicology. Chapman & Hall/CRC, 2004.

Martes, 11 de Septiembre de 2012 | Imprimir | PDF |  Correo electrónico

93. 38. (Julio 2012) Estadística en la musicología I

1. Introducción Este artículo inaugura una serie que se titula Estadística en la musicología. El título de la serie puede parecer una provocación, pero no es así, y ello merece una explicación. La musicología -en su definición más amplia- es el estudio de la música. El musicólogo Richard Parncutt [Par07] da una definición de musicología que se inspira en la entrada correspondiente del prestigioso diccionario The New Grove Dictionary of Music and Musicians [SSE01] (nuestra traducción, sus cursivas): “Sugiere (el diccionario) que la musicología hoy comprende todas las disciplinas que estudian toda la música en todas sus manifestaciones y en todos sus contextos, sean estos, físicos, acústicos, digitales, multimedias, sociales, sociológicos, culturales, históricos, geográficos, etnológicos, psicológicos, médicos, pedagógicos, terapéuticos, o en relación a cualquier otra disciplina o contexto musicalmente relevante”. A pesar de que la edición del diccionario es de 2001 y el artículo de Parncutt de 2004 todavía echo de menos disciplinas que se han ocupado muy activamente de la música como objeto de estudio, como por ejemplo: las neurociencias, los estudios (auto-)etnográficos, los estudios de género, la estética, la semiótica, la antropología, pero también las ciencias de la computación1 y, lo que es pertinente a esta columna, las matemáticas. Por su longitud y amplitud, la lista anterior puede intimidar un poco, pero hay que advertir que ni todos los enfoques ni todos los métodos son válidos en musicología. De hecho, se pueden encontrar casos en que la aplicación de ciertos métodos ha producido extralimitaciones conceptuales. Sin embargo, esta rica mezcla de disciplinas aplicadas al estudio de la música no se formó sino hace relativamente poco tiempo, unas cuatro o cinco décadas aproximadamente. Al principio, la musicología era simplemente el estudio de la música occidental, principalmente con métodos históricos. Como disciplina más o menos independiente se encontraba la musicología comparada, que más tarde devino en la etnomusicología. Poco a poco el fenómeno musical se fue investigando en un sentido más amplio y otras disciplinas se incorporaron a su estudio, si bien esas disciplinas pertenecían fundamentalmente al campo de las humanidades. Se estudiaba la música desde la perspectiva histórica, literaria, filosófica o del análisis musical occidental. Poco a poco se empezó a aceptar que había otras músicas, con sus propias estructuras, estilos e instrumentos. Más tarde se unieron otras disciplinas, pero destacan dos que han dado un fuerte impulso a la investigación y señalado ángulos de estudio necesarios para la consolidación de una musicología moderna: la psicología y las ciencias de la computación. La música tiene una componente cognitiva muy importante que hasta finales de los años sesenta había sido casi ignorada por completa. Con trabajos pioneros como los de Diana Deutch se inauguró una intensa era de investigación de los mecanismos perceptuales y cognitivos de la música; véase [RB03] para una excelente visión del campo. Respecto a las ciencias de la computación, los modelos computacionales se hicieron totalmente necesarios para la comprensión de la música así como para su procesamiento. Por ejemplo, Jackendoff y Lerdahl [LJ83], inspirándose en las teorías de la gramática generativa de Chomsky, desarrollan una teoría generativa de la música que identifica estructuras y propone reglas de transformación. Según su metodología, la musicología se ha clasificado en cualitativa, cuantitativa y etnográfica2. La musicología cualitativa usa métodos cualitativos (entrevistas, observaciones, análisis de documentos, archivística, interpretación de textos, estudio de casos, etc.). Estos métodos provienen principalmente de las humanidades. Los métodos etnográficos consisten en la investigación vía la integración del investigador en el contexto de la investigación; si el investigador mismo es el protagonista se habla entonces de métodos autoetnográficos (por ejemplo, el musicólogo que entra en una formación musical de una cultura dada para investigarla desde dentro y no como observador externo). Dentro de los métodos (auto-)etnográficos se encuentra la redacción de diarios, los cuadernos de campo, las grabaciones en audio y vídeo, así como técnicas específicas de análisis. Por último, está la musicología más reciente, la cuantitativa, que en buena medida es computacional. Esta musicología reconoce que la música tiene aspectos cuantificables y modelizables computacionalmente y busca construir modelos, reconocer estructuras y producir algoritmos que permitan procesar la música para su mejor comprensión y análisis. Un ejemplo sencillo de este tipo de musicología lo tenemos en el procesamiento automático de música. Con los nuevos medios de representación y almacenamiento, podemos disponer de corpus de música de varios cientos de horas. Buscar una característica común -digamos un cierto patrón melódico-, a mano (a oído, más bien), puede llevar al menos tantas horas como el corpus mismo. Un procesamiento adecuado del corpus puede localizar ese patrón en cuestión de minutos, y darnos datos de los que sacar información valiosa. Incluso hoy en día, la musicología cuantitativa no goza de la aceptación incondicional de toda la comunidad de estudiosos de la música. En este artículo, como decía más arriba, vamos a ver unas cuantas aplicaciones de la estadística a la musicología. La serie está pensada más para músicos que para matemáticos y en la entrega de hoy exploraremos las posibilidades de la estadística descriptiva. El resto de este artículo sigue la presentación del excelente libro Statistics in Musicology [Ber04], de Jan Beran, capítulo uno. Recomiendo vivamente la lectura de este libro. 2. Estadística descriptiva El objetivo de la estadística descriptiva es encontrar una serie de medidas que sean representativas de un conjunto de datos numéricos. Normalmente, el conjunto de datos es muy grande y la serie de medidas es pequeña. El conjunto de datos recibe el nombre de muestra. Las medidas se clasifican en tres grandes grupos: Las medidas de centralización, que tratan de encontrar un valor representativo de la muestra de tal manera que, bajo ciertas condiciones, podamos caracterizar la muestra a través de esas medidas. Las medidas de dispersión, que miden cuán dispersos se encuentran los datos respecto a las medidas de centralización. Las medidas de asimetría, que miden cómo se agrupan los datos alrededor de las medidas de centralización. Para dar un ejemplo claro de esta clasificación, proponemos al lector, al músico en especial, la siguiente cuestión: dado un conjunto de n números reales S = , la muestra, ¿cómo elegir un número μ que lo represente en algún sentido? Una primera idea sería tomar las distancias de μ a todos los puntos de S, esto es, la suma de los errores cometidos al sustituir los puntos de S por el valor μ, y dividirlo por el número de puntos. Dividimos por el número de puntos para que este no influya en el error final. Entonces, el error cometido en la sustitución es una función E(μ), que se escribe como: (El símbolo ∑ significa hacer la suma desde i=1 hasta n de la expresión que sigue a continuación; se llama sumatorio). El valor que buscamos y que resume el conjunto S en uno solo es aquel que minimice esta función E(μ), que haga el error lo más pequeño posible. Encontrar el mínimo de esta función vía las derivadas no es factible, ya que el valor absoluto no es derivable (esta es una razón técnica que los músicos pueden saltarse sin ningún complejo de culpabilidad). En su lugar se usa la siguiente función E(μ): Calculemos el valor mínimo de E(μ) con las derivadas: E(μ)′ = 0 => - (x1 - μ) - (x2 - μ) -… - (xn - μ) = 0 => - 2(x1 + x2 + … + xn) + 2n ⋅ μ = 0 => - 2 ∑ni=1x i + 2n ⋅ μ = 0 => 2n ⋅ μ = 2 ∑ni=1x i => μ = ∑ni=1x i Como E′′(μ) = 2n para todo μ, el valor que hemos obtenido es, en efecto, un mínimo para E(μ). Obsérvese que esta función da la suma de los cuadrados de los errores al sustituir los puntos de S por el único valor μ. Este valor recibe el nombre de media muestral y se escribe . El valor del error en μ = = ∑ni=1xi es: y recibe el nombre de varianza; volveremos a ella enseguida. Como medida de centralización, la media muestral tiene el inconveniente de que es muy sensible a datos anómalos. Pensemos en el conjunto ; claramente, su media será μ = 5. Sin embargo, si por error uno de los cincos se transforma en un cero, entonces la nueva media es μ = 25∕6 ≈ 4′1666. Las dos siguientes medidas sirven para representar el conjunto y son más robustas ante datos anómalos: Mediana M. Para calcularla se ordena la muestra de menor a mayor y se divide en dos partes iguales. El valor central será la mediana. Si hay un número par de datos, se toma, por convenio, la semisuma de los dos valores centrales. Nótese que esta medida se basa en el orden relativo de los datos y no en el valor de los mismos. Por ejemplo, si S = , la mediana M es 5; si S = , entonces es M = = 4. Moda es el valor o valores más frecuentes que aparecen en la muestra. Una vez establecidas las medidas de centralización, la pregunta más natural es cuándo son representativas esas medidas. Ciertamente, no siempre son representativas, y de ahí la posibilidad de manipulación de los datos. Las medidas de dispersión proporcionan criterios para determinar cuándo las medidas de centralización son representativas. La primera medida que presentamos es la varianza, vista ya anteriormente. Por razones técnicas (que se pueden encontrar en el capítulo 8 de [RES00]), la varianza que se usa en estadística descriptiva se llama varianza muestral s2 y su definición es: La varianza muestral tiene el inconveniente de que está no está expresada en las unidades de los números x1,x2,…,xn. Por ello, se define la desviación típica s, que es sencillamente +. Si la desviación típica es pequeña, quiere decir que los datos tienen poca dispersión y la media es, entonces, representativa. Veamos con un ejemplo sencillo por qué. Tomemos estos dos conjuntos de datos, S1 = , S2 = . La media en ambos casos es 5 y sus desviaciones típicas respectivas son s1 = 0 y s2 = ≈ 5′7735. Estos números nos dicen que en el caso de S1 la media es representativa, mientras que en el caso de S2 no lo es. Esta es una de las razones por las cuales no nos podemos creer ninguna media que nos den en las noticias. Otras medidas de dispersión son: El rango R, que se define como la diferencia entre el máximo y el mínimo de los datos, o dicho más formalmente, R = xmax-xmin, donde xmax = max y xmin = min. El rango intercuartílico RI, que es una medida asociada al orden de los datos. Primero necesitamos definir los cuartiles Q1,Q2 y Q3. El cuartil Q1 es el punto que, una vez ordenados los datos de menor a mayor, deja el 25% a la izquierda y el 75% a la derecha. Q2 es la mediana. Q3 deja, en cambio, el 75% a la izquierda y el 25% a la izquierda. El rango intercuartílico se define como la diferencia RI = Q3 - Q1. Los valor anómalos se definen como aquellos que están fuera del intervalo Una manera gráfica de ver los valores anómalos es construir el diagrama de caja. Se construye una caja cuyo límite inferior es Q1 y cuyo límite superior es Q3; en el medio de la caja se marca la mediana M. Después se dibujan sendas patas, que van desde la caja hasta el valor no anómalos más alejados, como se indica en la figura 1. Los datos anómalos son los círculos negros fuera de la patas de la caja. Figura 1: Diagrama de caja de un conjunto de datos. Por último, vamos a ver el coeficiente de asimetría, que está definido por la fórmula: y que indica la simetría de los datos respecto a la media. Si m3 > 0, entonces los datos están más concentrados a la derecha de la media muestral; si m3 < 0, lo están a la derecha; y si m3 = 0, son perfectamente simétricos respecto a la medida muestral. Dejamos aquí este breve repaso de estadística descriptiva, repaso que nos servirá para ilustrar unas cuantas aplicaciones en musicología cuantitativa. Para profundizar más en la estadística descriptiva, véase [POD11]. 3. Aplicación a espacios musicales Para ilustrar el uso de la estadística descriptiva, tomaremos la obra Träumerei, de Robert Schumann, una exquisita pieza. Abajo tenemos un vídeo con la interpretación de esta pieza por la pianista Valentina Lisitsa. La partitura de la pieza se puede ver en la figura 2. Figura 2: Träumerei, de Robert Schumann. Vamos a analizar las curvas de tempo de varias interpretaciones de esta pieza. En general, los cambios de tempo suelen locales más que globales y se usan como medio para dotar de expresividad a la interpretación. En la figura 3 se muestran tres interpretaciones del pianista Vladimir Horowitz. Las curvas se parecen bastante entre sí cuando se consideran en su totalidad, pero se aprecian cambios a nivel local, cambios que se pueden estudiar mediante técnicas estadísticas. Las curvas de tempo se han tomado en escala logarítmica. Típicamente el tempo se mide en pulsos por minuto y puede variar desde 20 pulsos por minuto, Larghissimo, hasta 240 pulsos por minuto, Prestissimo con fuoco. Tal rango de valores se representa mejor bajo una escala logarítmica, esto es, tomando el logaritmo del tempo. Las curvas de tempo se han obtenido muestreando las grabaciones a intervalos muy pequeños e interpolando los puntos obtenidos. Figura 3: Curvas de tempo de tres interpretaciones de Horowitch [Ber04]. Podría esperarse que el tempo fuera más o menos constante dentro de una pieza, pero estas curvas muestran que no es así. Todas estas microvariaciones dan expresividad a la interpretación. Vamos a llevar un análisis un poco más complejo. Consideremos las 28 curvas de tempo de la figura 4; corresponden a 28 interpretaciones de Träumerei de los siguientes pianistas: Martha Argerich (antes de 1983), Claudio Arrau (1974), Vladimir Ashkenazy (1987), Alfred Brendel (antes de 1980), Stanislav Bunin (1988), Sylvia Capova (antes de 1987), Alfred Cortot (1935, 1947 y 1953), Cli?ord Curzon (alrededor de 1955), Fanny Davies (1929), Jörg Demus (alrededor de 1960), Christoph Eschenbach (antes de 1966), Reine Gianoli (1974), Vladimir Horowitz (1947, antes de 1963 y 1965), Cyprien Katsaris (1980), Walter Klien (fecha desconocida), André Krust (sobre 1960), Antonin Kubalek (1988), Benno Moisewitsch (sobre 1950), Elly Ney (sobre 1935), Guiomar Novaes (antes de 1954), Cristina Ortiz (antes de 1988), Artur Schnabel (1947), Howard Shelley (antes de 1990), Yakov Zak (sobre 1960). Figura 4: 28 curvas de tempo para 24 interpretaciones de Träumerei [Ber04]. Desde un punto de vista de la forma, Träumerei se puede dividir en cuatro secciones, que, siguiendo la notación de [Ber04], llamaremos A, A′, B y A′′. La sección A expone el material temático, en la sección A′ ese material temático se desarrolla, a continuación viene una sección, la B, que contrasta, y finalmente la pieza acaba con una sección que recapitula con el material de la sección A. Para las 28 interpretaciones, en la figura 5 se ha calculado la media muestral , la media M, las desviaciones típicas y el coeficiente de asimetría m3 para cada sección de la pieza. Además, se ha dibujado un diagrama de caja verticalmente para cada medida. Examinando las medidas se sacan varias conclusiones. El tempo es siempre más lento en la sección A′′ que en el resto; además, la sección A′ se toca ligeramente más lenta que A. Esto se aprecia examinando las dos primeras gráficas de la figura 5, las correspondientes a la media y mediana muestrales. El tempo cambia hacia el final de la pieza en la mayor parte de los casos y mucho menos en la primera mitad de la pieza, como nos informa la tercera gráfica, la de la desviación típica. En la gráfica de más a la izquierda, la que corresponde al coeficiente de asimetría m3, observamos que en general es negativa, sobre todo en la sección B. En esa misma gráfica se observan valores anómalos, los cuales corresponden a ritardandi extremos pero ocasionales por parte de algunos pianistas (Fanny Davies y Jörg Demus). Figura 5: Medidas estadísticas para Träumerei [Ber04]. Se puede realizar un análisis más profundo añadiendo más medidas estadísticas. De nuevo, consúltese el capítulo 2 de [Ber04] para información más detallada.   Notas: 1 Evito aquí el término informática. Se podría interpretar como la programación de aplicaciones cuando, en realidad, me estoy refiriendo a la creación de modelos computacionales de la música. 2 También se encuentra la expresión de estudios performativos de la música, que tiene difícil traducción en castellano. Hemos preferido llamarlos estudios etnográficos.   Bibliografía: [Ber04] J. Beran. Statistics in Musicology. Chapman & Hall/CRC, 2004. [LJ83] F. Lerdahl and R. Jackendoff. A Generative Theory of Tonal Music. MIT Press, Cambridge, Massachussetts, 1983. [Par07] Richard Parncutt. Systematic musicology and the history and future of western musical scholarship. Journal of Interdisciplinary Music Studies, 1:1–32, 2007. [POD11] R. Peck, C. Olsen, and J.L. Devore. Introduction to Statistics and Data Analysis. Brooks/Cole, 2011. [RB03] R. E. Radocy and D. J. Boyle. Psychological Foundations of Musical Behaviors. Charles C. Thomas, Springfield, Ill., 2003. [RES00] V. Rohatgi and A. K. Ehsanes Saleh. An Introduction to Probability and Statistics. Wiley-Interscience, 2000. [SSE01] John Tyrrell (Editor) Stanley Sadie (Editor). The New Grove Dictionary of Music and Musicians. Akal, 2001.

Miércoles, 25 de Julio de 2012 | Imprimir | PDF |  Correo electrónico

94. 37. (Junio 2012) Matemáticas y música en niños pequeños

1. La educación entre los 0 y 3 años En el artículo de este mes querría tratar un tema que es totalmente pertinente a esta columna: Las matemáticas y la música en los niños de 0 a 3 años. El lector desprevenido quizás se sonría escéptico y ello no me extrañaría. Hay muchos errores de concepto y prejuicios alrededor de la educación en la etapa de infantil, en especial, en la que va de 0 a 3 años. Llevo muchos años oyendo a padres decir que tienen que buscar "guardería", ante lo cual les pregunto con suavidad: "¿Quieres decir guardería o escuela infantil?". La respuesta en la mayor parte de los casos es: "¡Ah!, ¿pero hay alguna diferencia?" Sí, sí la hay. En la guardería, salvo excepciones, te cuidan a los niños, te los vigilan más bien, te los entretienen, intentan que den el menor número posible de problemas, pero eso es todo. En cambio, en una escuela infantil el personal tiene una cierta cualificación, hay una programación hecha en base a unos objetivos, se realizan actividades durante el curso para cubrir esos objetivos, se acuerda una metodología, se evalúan los resultados, entre otras muchas diferencias. Algunos padres que han tenido la paciencia de escucharme, se quedan boquiabiertos. No se les había ocurrido pensar que hubiese tal diferencia. Por supuesto, la diferencia radica en el concepto mismo del niño y su educación. Cada vez más estudios demuestran cuán crucial es la estimulación y el aprendizaje en los tres primeros años de vida. Por ejemplo, se sabe que el oído absoluto se forma en esa etapa, por no hablar del lenguaje, las habilidades psicomotrices y otras. Sin embargo, la educación infantil, al menos en España, tiene una bajísima consideración social, tanto fuera como dentro del sistema educativo. He oído a profesores de primaria calificar el trabajo de sus compañeros de educación infantil de "fácil, ya que solo tienen que pintar fichas". Durante varios años actué con un grupo de teatro para niños de esas edades, La farándula musical. Hacíamos teatro en el aula y tras las actuaciones las profesoras departían relajadamente con nosotros en el comedor. Siempre les hacía la misma pregunta que me torturaba: ¿Cómo creían ellas que la sociedad y en particular el mundo de la educación veía su trabajo? La mayoría de las veces recibía una mirada descreída, con un punto de amargor, seguida de una media sonrisa compasiva (por mi ingenua pregunta). Recuerdo una profesora muy joven, con seguridad no tenía 30 años, quien sin molestarse en levantar la cabeza del plato de fruta que estaba comiendo me dijo que "la educación infantil es el culo de la educación". Elocuente. En este artículo vamos a examinar qué matemáticas y qué música pueden absorber, aprender, percibir niños de entre 0 y 3 años de edad. Veremos que incluso hay puntos comunes entre esas dos disciplinas también en este contexto tan especial.   2. Las matemáticas Las investigaciones llevadas a cabo en las dos últimas décadas del siglo XX sobre las matemáticas y su aprendizaje a edades tempranas llevó a muchos países a replantearse los contenidos del primer ciclo de educación infantil (0 a 3 años). En particular, la prestigiosa National Council of Teachers of Matematics (NCTM) americana decidió en 2000 reformar la programación de la etapa de infantil. Tal decisión se tomó en vista de los resultados de los investigadores, los cuales demostraban que había efectivamente aprendizaje de las matemáticas en esas edades, si bien a través de mecanismos distintos a los que usan adultos o niños mayores. El NCTM no solo reformó la programación, sino que hizo una serie de reflexiones y recomendaciones acerca de la metodología para enseñar esas matemáticas. Según la investigadora Rosalind Charlesworth [Ch05], los niños de esta etapa construyen las matemáticas a través de actividades cotidianas de carácter exploratorio, siguiendo su natural curiosidad, en respuesta a las preguntas de otros niños, a través del juego y a partir de experiencas de narración oral. Algunos autores enfatizan el papel del juego [S03] como forma vivencial de las matemáticas. Otros autores, como Diane Tiessen [Tie04], han estudiado el papel de la narración oral en la asimilación de conceptos matemáticos. Dado que el lenguaje se está formando en esta etapa y que es uno de los principales medios por los que el niño recibe información, está asociación matemática-lenguaje necesita poca justificación. Los niños de estas edades no han desarrollado aún una fuerte capacidad de abstracción y, en consecuencia, las matemáticas que practican son fundamentalmente sensoriales; las absorben a través de sus sentidos. Tampoco su memoria y su sentido del tiempo son fuertes; requieren repetición y una fuerte implicación por parte del niño en el descubrimiento matemático. De ahí el carácter exploratorio de su aprendizaje del que habla Charlesworth en su artículo. Los niños adquieren conceptos a través de tres formas de aprendizaje [Ch04]: por aprendizaje espontáneo, en las que el niño toma la iniciativa de aprender algo bajo su control; por aprendizaje informal, como consecuencia de la interacción con sus iguales; y por aprendizaje estructurado, que es el que ocurre cuando el niño está en el aula haciendo una actividad planificada. Cualquiera que sea la forma de aprendizaje, el niño ha de estar inmerso en un ambiente que le dé seguridad emocional. En [SKW04] se estudia la relación entre status social y aprendizaje de las matemáticas a estas edades, relación que se revela estrecha y fundamental. Este estudio sorprende porque llega a predecir con bastante fiabilidad el fracaso en los últimos cursos de primaria y primeros de la educación secundaria en base a la calidad del aprendizaje de las matemáticas en edades tempranas. El libro Engaging Young Children in Mathematics: Standards for Early Childhood Mathematics Education[CSDD03] contiene un resumen bastante completo de las investigaciones de los últimos años sobre las matemáticas y su aprendizaje en estas edades. Se trata de un libro que recoge artículos de expertos que van desde diseñar la programación (capítulos 2 y 3), pasando por los aspectos cognitivos (capítulos 5 y 6) hasta las técnicas particulares para enseñar las matemáticas. Nos llama la atención, y mucho, el constante énfasis que hacen todo tipo de autores en el uso de las artes para enseñar matemáticas. Es curioso que tal integración curricular se vaya erosionando en etapas superiores de la educación hasta llegar a una total separación en la educación universitaria. Más información sobre el diseño de la programación se puede encontrar en [NCTM], con su definición de puntos clave de la programación. Como libro que desarrolla muchos conceptos matemáticos y da formas efectivas de ponerlas en práctica en el aula, recomendamos el de Richardson, O'Neill y Starr [ROS08]. En la página web de recursos educativos IXL aparecen recogidos contenidos matemáticos que se pueden trabajar entre 0 y 3 años. Un extracto de dicha página web está abajo. Formas: Identificar círculos, cuadrados y triángulos. Identificar rectángulos y cuadrados. Identificar cubos y pirámides. Posiciones: Dentro y fuera. Izquierda y derecha. Izquierda, medio y derecha. Encima y debajo. Abajo y arriba. Contar hasta 3: Contar hasta 3 puntos. Contar hasta 3 formas. Contar hasta 3 objetos. Clasificación: Mismo. Distinto. Mismo y diferente. Clasificación por color. Comparaciones: Comparar grupos en términos de menos y más. Comparar cuántos objetos hay en un gráfico. Comparar en un grupo de objetos mixto. Tamaño: Largo y corto. Alto y bajo. Pesado y ligero. Ancho y estrecho. Contiene más o menos. Tabla 1: Conceptos matemáticos que pueden experimentar niños entre 0 y 3 años. Un matemático profesional probablemente no calificaría alguno de estos contenidos como "matemáticos"; y, sin embargo, lo son. Estas son matemáticas de raigambre sensorial, si se quiere, pero siguen siendo matemáticas tan dignas como el teorema de Bolzano. Y han de enseñarse igualmente.   3. La música Una de las investigadoras que más activas se ha mostrado en el estudio de la percepción y cognición musical en niños entre 0 y 3 años es Beatriz Ilari, de la Universidad de McGill (Canadá). En su artículo de 2002 Music and Babies: A Review of Research with Implications for Music Educators [Ila02], estudia los factores más importantes en la percepción musical en niños durante su primer año de vida. El artículo es bastante exhaustivo, no solo por el número de variables musicales que tiene en cuenta, sino porque sus hallazgos científicos están basados en estudios psicológicos llevados a cabo de unos 15 años (entre 1984 y 2000 aproximadamente). Vamos, de la mano de Ilari, a revisar qué pueden percibir musicalmente los niños de edad temprana. 3.1. Percepción de la altura Los niños empiezan a reaccionar a los estímulos sonoros a partir del tercer mes de gestación y, de hecho, hay estudios que prueban que niños a los que se les ha sometido a estimulación musical en el útero muestran mejores aptitudes para la música. Centrándonos en los niños una vez fuera de la placenta, la percepción de la altura presenta un curioso comportamiento. Los niños de entre 3 meses de gestación hasta 3 meses después de nacer son capaces de discriminar sonidos graves mejor que los agudos; aún más, muestran preferencia por los sonidos graves. Alrededor de los 6 meses, ese comportamiento se invierte y discriminan mejor los sonidos agudos y además los prefieren a los graves. 3.2 Percepción de melodía y contorno melódico Niños de entre 6 y 8 meses de edad ya son capaces de detectar un cambio de una sola nota en una corta melodía de 6 notas, incluso aunque el cambio sea sutil. Además, el contorno melódico parece ser incluso más importante que la propia melodía. El contorno melódico se refiere a los cambios de dirección, ascendente y descendente, en la melodía. Trehub y sus coautores [Tie04] presentaron a niños de entre 8 y 11 meses de edad 5 versiones de una misma melodía de 6 notas. Esas 5 versiones incluían la original, una transposición, una donde se conservaba el contorno melódico con unos pocos cambios en las notas, una con cambios de octava con el mismo contorno y una con cambio de contorno. Los niños no distinguieron entre las versiones original y las que tenían el mismo contorno, pero discriminaron enseguida aquellas en que el contorno se había cambiado. Estos hallazgos son realmente importantes porque la melodía y el contorno melódico son variables que intervienen en la adquisición del lenguaje. 3.3 Enculturación musical La enculturación es el proceso por el cual se transmite la cultura a la nueva generación. Una pregunta a la que los investigadores llevan tiempo intentando dar respuesta es la de qué aptitudes musicales son innatas y cuáles son producto de la enculturación musical. En un interesante estudio [LEOU90] Lynch y sus coautores compararon la habilidad de niños de 6 meses y adultos (músicos y no músicos) para detectar notas ligeramente desafinadas en melodías basadas en la escala mayor, la escala menor y la escala pelog de Java. Una versión temperada de esta última escala sería: do-reb-mib-fa#-sol-lab-sib. Los niños detectaron las notas desafinadas en todas las escalas, mientras que los adultos solo en las occidentales. Este estudio y otros posteriores de los mismo autores prueban que la enculturación musical desempeña un importante papel en la percepción musical. 3.4 Percepción de la armonía La armonía es un fenómeno más complejo pues implica la clasificación de intervalos así como la percepción simultánea de sonidos. Las investigaciones mostraron que los niños tienen preferencia por las consonancias que por las disonancias. Aquí consonancia se refiere a los intervalos unísono, terceras, cuarta, quinta, sextas y octavas. También se constató que los niños perciben con mayor dificultad los intervalos y acordes complejos que los simples. Las melodías simples con acompañamientos repetitivos y claros son, en general, mejor procesadas por los niños de estas edades. 3.5 Percepción del timbre Hay algunos estudios sobre la percepción del timbre musical, pero este es un campo que todavía ha de investigarse con mayor profundidad. Se sabe que los niños de estas edades tienen memoria para el timbres de ciertos instrumentos. El timbre de la voz humana, especialmente el de la madre, sí ha sido estudiado exhaustivamente. 3.6 Forma musical Niños de un año de edad ya pueden reconocer frases musicales. Ello no es de extrañar ya que la habilidad de segmentar el sonido es importante en el habla también. Los estudios han demostrado que los niños detectan los finales de frase, incluyendo las pausas, las desviaciones expresivas de tiempo o las líneas descendentes en la melodía. Aún más, son capaces de reconocer motivos, memorizarlos y, cuando ciertas características rítmicas y melódicas se dejaban intactas, pueden detectar variaciones. 3.7 Percepción de eventos temporales El reconocimiento de eventos temporales (patrones rítmicos, tempo y métrica) ocurre casi desde el principio. Por ejemplo, Winkler y sus coautores [WHLSH09] han demostrado que recién nacidos pueden reconocer un pulso. La capacidad de reconocer patrones rítmicos basados en similitud de las figuras rítmicas y en la proximidad temporal de las figuras. Esta estrategia, por cierto, es la que usan adultos sin formación musical. También se ha comprobado, hablando de métrica, que hay una preferencia por las métricas binarias ante las métricas ternarias. Respecto a la parte acentual de la métrica, todavía faltan por llevarse a cabo estudios. 3.8 Memoria musical a largo plazo Hay estudios que han investigado la memoria musical a largo plazo (se toca una melodía y se comprueba si se recuerda dos semanas después, por ejemplo). Los niños de menos de un año de edad son capaces de recordar melodías después de dos semanas de haberla oído por primera vez. No obstante, esa memoria está muy relacionada al estímulo. Los niños no la podían recordar si la melodía se tocaba con otros instrumentos o con otro tempo.   4. Conclusiones ¿Qué decir ante todo lo anterior? No cabe duda de que la sociedad no es consciente de todos hechos y de que los redactores de la programación para la etapa de infantil, tampoco. ¿Qué podemos decir de una educación que ignora una etapa tan fundamental en la formación de una persona y que tanto la condicionará en el futuro?   Referencias [CSDD03] Editores: Clements, D.H.; Sarama, J.; DiBiase E.; DiBiase, A.-M. Engaging Young Children in Mathematics: Standards for Early Childhood Mathematics Education.Studies in Mathematical Thinking and Learning Series.Routledge. 2003. [Ch04] Charlesworth, Rosalind. Experiences in math for young children. Clifton Park. Delmar Learning. 2004. [Ch05] Charlesworth, Rosalind. Prekindergarten Mathematics: Connecting with National Standards. Early Childhood Education Journal, v. 32, nº 4, 229-236, 2005. [Ila02] Ilari, B. Music and Babies: A Review of Research with Implications for Music Educators. Applications of Research in Music Education. 21: 17-26. 2002. [IXL] Página web IXL Pre-k. Consultada entre los meses de noviembre de 2011 y mayo de 2012. [Korn] Barry Kornhauser. Baby Maybe. Artículo que se encuentra en la bitácora HowlRound. Consultado en marzo de 2012. [LEOU90] Lynch, M. P.; Eilers, R. E.; Oller, D. K.; Urbano, R. C. Innateness, experience and music perception. Psychological Science, 1, 272–276. 1990. [NCTM] Página web del National Council of Teachers of Mathematics. Curriculum Focal Points for Prekindergarten through Grade eight. Consultado en diciembre de 2011. [ROS08] Kathy Richardson (autora), Lucinda O'Neill (editora), Linda Starr (ilustradora). Developing Math Concepts in Pre-Kindergarten. Maths Perspectives. 2008. [S03] SEO, K. What children's play tells us about teaching mathematics. Young Children, 58(1), 28-33. 2003. [SKW04] Starkey, P.; Klein, A. y Wakeley, A. Enhancing young children’s mathematical knowledge through a pre-kindergarten mathematics intervention. Early Childhood Research Quarterly. Volumen 19, nº 1, primer trimestre, páginas 99-120. 2004. [Tie04] Thiessen, Diane. Exploring Mathematics Through Literature: Articles and Lessons for Prekindergarten Through Grade 8. National Council of Teachers of Mathematics. 2004. [TBT84] Trehub, S. E;, Bull, D.; Thorpe, L. A. Infants’ perception of melodies: The role of melodic contour. Child Development, 55, 821–830. 1984. [WHLSH09] Winkler, I.; Hádena, G.; Ladinig, O.; Sziller, I.; Honing, H. Newborn infants detect the beat in music. Proceeding of the National Academy of Sciences of USA. 106/(7) 2468-2471. 2009.

Martes, 26 de Junio de 2012 | Imprimir | PDF |  Correo electrónico

95. 36. (Mayo 2012) Rotaciones de ritmos

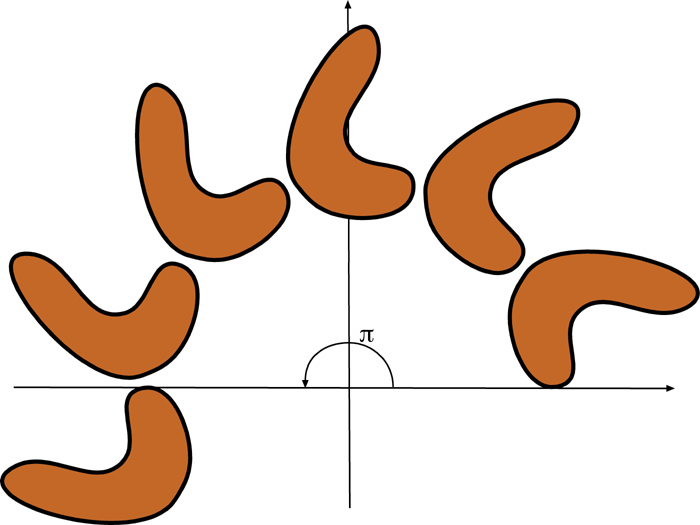
1. Rotaciones matemáticas Las rotaciones son transformaciones que desde siempre han suscitado mucho interés y, por ello, se han estudiado con profundidad y de modo exhaustivo. Una rotación se define como un movimiento rígido alrededor de un punto fijo. Ese movimiento tiene lugar en algún espacio, que puede ser todo lo abstracto que queramos, pero las rotaciones en el plano están entre las más estudiadas. En la figura de abajo tenemos la rotación de un objeto plano alrededor del punto O = (0,0). La rotación es de 180 grados y se muestran varios pasos intermedios. Figura 1: Rotaciones en el plano. Las ecuaciones que transforman el punto (x1,y1) del plano mediante una rotación de ángulo θ [0,2π) alrededor del origen O = (0,0) son las siguientes: (He escrito las ecuaciones porque viene al caso, pero también por su belleza.) Las rotaciones pertenecen a la clase de las isometrías, que son las transformaciones que no cambian la distancias entre los puntos. Esto viene a decir que si la distancia entre dos puntos antes y después de aplicar la rotación es la misma. Una pregunta inmediata es por qué las rotaciones en el plano se han investigado tanto. Ciertamente, nos resultan familiares. Nuestras extremidades pueden rotarse en cierto grado, la cabeza, los ojos; manipulamos muchos objetos con las manos y les aplicamos rotaciones; también las usamos para cambiar el sentido de la marcha. La psicología de la forma o psicología Gestalt puede explicar esa familiaridad. Esta teoría psicológica surgió para explicar los mecanismos de la percepción. La teoría se articula en torno a una serie de leyes o principios que explican los procesos organizativos de la percepción. Entre esos principios se cuentan el de invariancia, que establece que elementos geométricos simples se perciben como iguales o semejantes si son el producto de rotaciones, traslaciones o simetrías. También está el principio de semejanza, que agrupa objetos semejantes si son similares. Estos principios explican la importancia perceptual de las rotaciones. Las matemáticas se encargaron más tarde de formalizar el concepto de rotación. Dado que la percepción es fundamental, la teoría de la forma ha ejercido una gran influencia en el arte. Véanse [WBS92], [DMM10] y [Lem97] para saber más sobre las relaciones de la psicología de la forma y las artes en general. 2. Rotaciones musicales Lo que nos interesa en este artículo es profundizar en el significado de las rotaciones aplicadas a la música, en particular, a los ritmos. De entre los ritmos nos quedaremos con los llamados ritmos de clave. Los ritmos de clave son ritmos que se repiten a lo largo de toda una pieza y cuyas funciones musicales incluyen la estabilización rítmica, la organización del fraseo o la referencia temporal [Uri96], [Ort95]. Esa repetición en el tiempo los hace muy adecuados para estudiar sus rotaciones. Además muchas de esas claves son características de ciertos géneros. Por ejemplo, el son cubano se toca con la clave son, que escrita en notación de caja es [x . . x . . x . . . x . x . . .]. Se puede tocar esta versión, la llamada 3-2 o la versión [. . x . x . . . x . . x . . x . ], llamada 2-3, pero es esencialmente la misma versión (una es la rotación de la otra en ocho posiciones). Y es raro encontrar el son cubano tocado con otro tipo de clave, sobre todo en el son tradicional. Los ritmos de clave, o sencillamente claves, aparecen en muchísimas tradiciones musicales tales como la afro-cubana, brasileña, africana, asiática, el flamenco, etc. Véanse para más información [Tou02], [DBFG+04]. En el vídeo siguiente tenemos un bembé tocado por el grupo Isla Percusión. Un músico, el de la camiseta amarilla, toca una clave ternaria, conocida como clave bembé o patrón estándar. Su partitura es [x . x . x x . x . x . x]. Obsérvese como el fraseo y las entradas se estructuran alrededor de la clave. Figura 2: Bembé tocado por Isla Percusión. Vamos a estudiar las rotaciones en las claves ternarias, esto es, las que están formadas por 12 o 6 pulsos normalmente agrupados en 4 o 2 partes de tres pulsos cada una. En el siguiente vídeo aparece un percusionista tocando varias claves ternarias. Veámoslo y luego analizamos las más relevantes (en el vídeo se toca un pulso de referencia con una caja china que no se ve). Figura 3: Claves ternarias. En la tabla de abajo están las claves más importantes de las que han aparecido en el vídeo. Algunos patrones rítmicos no se considerarían musicalmente claves, a pesar de que cumplen algunas de sus características. Por ejemplo, el ritmo del Kenkeni [. x x . x x . x x . x x] no es característico ni mucho menos de África. Aparece en muchísimos géneros musicales; algunos musicólogos incluso lo llamarían referente de densidad en lugar de clave (un referente de densidad es un ritmo que marca la velocidad de las figuras más rápidas de una pieza). Normalmente, una clave suele tener un factor de tensión rítmica, bien sea en forma de síncopa, de estructura de pregunta y respuesta, de ambigüedad métrica o acentual, o similares. Se han elegido las claves más importantes, como digo, pero además con el mismo número de notas, siete, hecho que nos permitirá un análisis más ágil en términos de las rotaciones. Figura 4: Partituras de algunas claves africanas para campanas. 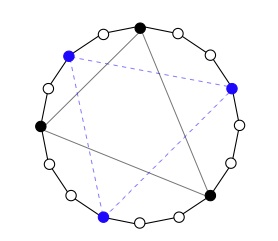El lector atento -es decir, cualquier lector de Divulgamat- habrá visto que la tabla anterior está divida en tres partes. Cada parte corresponde a aquellos ritmos que se obtienen unos de otros a partir de una rotación. Si los representamos sobre un círculo, para reforzar más la idea de ciclo y de rotación, se visualiza mejor la situación. En primer lugar, vamos a estudiar los ritmos generados por la clave bembé. En la figura 5 tenemos el círculo dividido en 12 partes y en el centro la clave bembé. Alrededor y en sentido antihorario las rotaciones del bembé que dan lugar a otros ritmos. Las rotaciones de los ritmos se han tomado en sentido horario. Así, tenemos que la bemba es una rotación del bembé de 60 grados; el tambú, de 150; el yoruba, de 210; el ashanti, de 270; y el bembé-2, de 330. Figura 5: Rotaciones de las claves asociadas al bembé. La clave de bembé es un ritmo importantísimo en la música africana, tanto que recibe el nombre de patrón estándar. Se encuentra en muchísimas culturas africanas bajo distintos nombres y tocado de muy diversas maneras. En el análisis musical ha despertado mucho interés y se ha estudiado desde muchos puntos de vista. Toussaint [Tou02] ha aplicado técnicas geométricas y de matemática discreta para analizarlo. Por ejemplo, la clave del bembé es un ritmo euclídeo [DGMM+08]. Un ritmo euclídeo es un ritmo de máxima regularidad en el sentido en que la elección de las notas sobre los pulsos están distribuidos de la manera más regular posible; véase también [GPT09] para más información. Pressing [Pre83] llega a hablar -más como metáfora que como correspondencia estricta- de un isomorfismo cognitivo entre la escala diatónica y la clave estándar. Si consideramos la octava dividida en 12 semitonos, entonces la sucesión de distancias entre las notas de la escala diatónica se escribe como (2212221). Si ahora interpretamos esta sucesión en el dominio temporal, rítmico, obtenemos exactamente la clave del bembé. El autor que ha prestado una atención especial a la clave estándar es el musicólogo Agawu [Aga06]. En su artículo Structural Analysis or Cultural Analysis? Competing Perspectives on the“Standard Pattern” of West African Rhythm analiza aspectos culturales y estructurales de este singular patrón rítmico. Por ejemplo, observa que el patrón admite varias lecturas y todas ellas son rítmicamente interesantes. Se puede pensar con estructura aditivamente, como una sucesión de negras y corcheas, de eventos de duración 2 y 1. Argumenta, no obstante, que la música africana no es, en general, aditiva. También investiga este autor la relación de este patrón con la danza así como una interpretación métrica -sobreponiendo el patrón en una malla de pulsos con ciertos acentos recurrentes-. Por último, Agawu se acerca también al análisis generativo [LJ83] de este patrón. La clave del soli genera a su vez las del asaadua, con una rotación de 60 grados, y la tonada, con una de 180 grados, como vemos en al figura 6. Figura 6: Rotaciones de las claves asociadas al soli. Para hacernos una idea de cómo suena el soli en una grabación en directo, aquí tenemos el siguiente vídeo: Figura 7: Toque de soli. En principio, el soli tiene menos posibilidades rotacionales que el bembé. Su sucesión de distancias es (2222121). Las tres primeras notas, las tres negras, crean una sensación de regularidad que se rompe en la segunda mitad con las corcheas quinta y séptima. En este último vídeo presentamos claves binarias sobre 16 pulsos. No obstante, no las analizaremos en este artículo. Figura 8: Claves binarias. 3. ¿Hasta qué punto son semejantes? Hemos visto que las leyes de la psicología de la forma consideran objetos rotados como similares o equivalentes. ¿Es eso cierto en la música? ¿Dos ritmos que difieren en una rotación se los puede considerar como similares? No, no ocurre como en el mundo visual; el oído funciona de manera diferente. El propio Agawu[Aga06], página 29, dice: La “permutación de elementos” (un procedimiento por el cual los mismos elementos se someten a reordenamientos) tiene tales consecuencias musicales radicales -incluyendo desafíos básicos de percepción- que parece poco probable que sea un auténtico modo de estructuración temporal. En efecto, el mismo Pressing reconoce que la permutación de los elementos produce un “trastorno estructural” más drástico que el que se produce con otras técnicas de transformación. Agawu proporciona una lista de recursos de transformación musical que son propios de la música africana, entre los que se cuenta la estructura de llamada y respuesta, la complementación y la competición y los cambios de alineación de segmentos musicales, pero no incluye las rotaciones. Para poner un ejemplo de esto, tomemos el bembé y el bembé-2. Este último es una rotación de una nota hacia adelante del bembé, una mera rotación de 30 grados en sentido horario (véase la figura 5). Pero perceptual y musicalmente son muy diferentes. Pinchando en las partituras de más abajo se puede escuchar cada uno y apreciar las diferencias entre ambos. [x . x . x x . x . x . x] BEMBÉ [x x . x . x x . x . x .] BEMBÉ-2   Bibliografía [Aga06] K. Agawu. Structural analysis or cultural analysis? competing perspectives on the “standard pattern” of west african rhythm. Journal of the American Musicological Society, 59(1):1–46, 2006. [DBFG+04] Miguel Díaz-Bañez, Giovanna Farigu, Francisco Gómez, David Rappaport, and Godfried T. Toussaint. El compás flamenco: a phylogenetic analysis. In Proceedings of BRIDGES: Mathematical Connections in Art, Music and Science, pages 61–70, Southwestern College, Winfield, Kansas, July 30 - August 1 2004. [DGMM+08] Erik D. Demaine, Francisco Gomez-Martin, Henk Meijer, David Rappaport, Perouz Taslakian, Godfried T. Toussaint, Terry Winograd, and David R. Wood. The distance geometry of music. Computational Geometry: Theory and Application, 2008. [DMM10] A. Desolneux, L. Moisan, and J.-M. Morel. From Gestalt Theory to Image Analysis: A Probabilistic Approach. Springer, 2010. Reprint of the first 2008 edition. [GPT09] F. Gómez, Talaskian P., and G.T. Toussaint. Structural properties of euclidean rhythms. Journal of Mathematics and Music, 3:1–14, 2009. [Lem97] M. Leman. Music, Gestalt, and Computing: Studies in Cognitive and Systematic Musicology. Springer, 1997. [LJ83] F. Lerdahl and R. Jackendoff. A Generative Theory of Tonal Music. MIT Press, Cambridge, Massachussetts, 1983. [Ort95] Fernando Ortiz. La Clave. Editorial Letras Cubanas, La Habana, Cuba, 1995. [Pre83] Jeff Pressing. Cognitive isomorphisms between pitch and rhythm in world musics: West Africa, the Balkans and Western tonality. Studies in Music, 17:38–61, 1983. [Tou02] Godfried T. Toussaint. A mathematical analysis of African, Brazilian, and Cuban clave rhythms. In Proceedings of BRIDGES: Mathematical Connections in Art, Music and Science, pages 157–168, Towson University, Towson, Maryland, U.S.A., July 27-29 2002. [Uri96] Ed Uribe. The Essence of Afro-Cuban Persussion and Drum Set. Warner Brothers Publications, Miami, Florida, 1996. [WBS92] C. Wallschlaeger and C. Busic-Snyder. Basic Visual Concepts And Principles For Artists, Architects And Designers Time Exposures. McGraw-Hill Humanities/Social Sciences/Languages, 1992.

Miércoles, 30 de Mayo de 2012 | Imprimir | PDF |  Correo electrónico

96. 35. (Abril 2012) Polígonos regulares y percusión

1. Los ritmos de sombra En la columna de este mes voy a ilustrar lo que he descrito como muchas veces como hacer matemáticas a partir de una excusa musical. Esto es perfectamente lícito siempre y cuando no se engañe al lector -y el autor mismo- respecto a su significado musical. No hay nada malo en tomar un fenómeno musical y extraer de él una estructura matematizable y, a partir de ella, hacer matemáticas. El problema es cuando se recorre el camino contrario y se afirma que las matemáticas que se han obtenido explican o rigen la música. En muchos instrumentos de percusión, la dinámica (el volumen al que tocas) se controla con la altura de la baqueta o de la mano. Lo hemos visto muchas veces en las orquestas clásicas, cuando un redoble del timbalero empieza muy bajito y luego sube el volumen. Al principio, las mazas suben un poquito, pero más tarde el recorrido es mucho mayor. Esta técnica, que aparece igualmente en la percusión africana, en el flamenco o en el jazz, aprovecha la caída de la maza para controlar la dinámica. En el vídeo de más abajo, podemos apreciar esa técnica. Esto produce una asociación entre la actividad motriz de golpear la piel del timbal y el propio ritmo. Para autores como el musicólogo Jay Rahn [Rah96] el punto álgido al que llega la maza antes de volver a la piel forma otro ritmo, silencioso, pero igualmente importante, que ayuda a mantener la precisión rítmica del ritmo que se oye. Rahn lo llama la la sombra del ritmo. En ritmos de clave, esto es, ritmos que se repiten a lo largo de toda una obra (la clave son, por ejemplo, en la música cubana), es especialmente frecuente encontrar este modo de tocar. Pensemos en el ritmo del tresillo cubano, que escrito en notación de caja es[x . . . . . x . . . . . x . . .], tiene como sombra al ritmo [. . . x . . . . . x . . . . x .], ritmo que a su vez tiene como sombra a [x . . . . . x . . . . x . . . .]. En la figura 1 se ve el tresillo con los puntos negros y su primera sombra con puntos azules. Figura 1: El tresillo cubano y sus sombras. En lo que sigue trabajaremos con ritmos que representaremos sobre el círculo unidad. Además, supondremos que una nota puede estar en cualquier punto del círculo y no en una serie de pulsos como en el ejemplo del tresillo cubano. 2. ¿Hacia dónde van las sombras de un ritmo? La operación de tomar la sombra de un ritmo aumenta su regularidad. ¿En qué sentido hablamos aquí de regularidad? Si se permite que las notas estén en cualquier punto del círculo, entonces el ritmo más regular está formado por duraciones iguales. Esa duración común es 1/n, donde n es el número de notas del ritmo. Interpretando el ritmo como un polígono, el ritmo más regular corresponde con el polígono regular inscrito en la circunferencia unidad. Si ante este objeto matemático, producido a partir de la excusa musical de las sombras de un ritmo, nos ponemos en actitud matemática, la pregunta que viene enseguida a la cabeza es qué pasa si aplicamos infinitas veces (¡el infinito!) la operación de la sombra. ¿A qué convergerá el ritmo final, eso suponiendo que converja a algo (no sea que oscile entre un conjunto de polígonos)? El estudio de las propiedades de sucesiones de polígonos generadas a través de procesos iterativos a partir de un polígono inicial P0 ha despertado mucho interés en la bibliografía matemática. El ritmo de una sombra es solo una de las muchas operaciones que se han investigado. Schoenberg [Sch82] ha estudiado las sucesiones de sombras de polígonos tomando puntos entre dos vértices consecutivos que no son los puntos medios. Hitt y Zhang [HZ01] probaron que la sucesión de sombras de un ritmo converge a un polígono regular. En  [GTT08] aparece una demostración muy elegante que es la que vamos a reproducir a continuación. La prueba es algo probabilística. Sea P0 el polígono inicial y la sucesión de sombras. Detengámonos en el paso del polígono Pk al Pk+1 y sea las duraciones consecutivas del polígono Pi. Consideraremos esas duraciones aj,j = 1,,n como variables aleatorias que toman valores en [0,1]. La media μk de las duraciones es la misma para cualquier polígono: En cuanto a la varianza Vk en el paso k, esta es: Las duraciones del polígono Pk+1 son ai' = y la media sigue de ai' sigue inmutable en 1∕n. Entonces, tenemos lo siguiente: Fijemos nuestra atención en el término ∑ni=1 aiai+1. Se puede considerar como una función de n variables a1,,an. Para poder acotar la última expresión obtenida nos interesa encontrar su máximo valor sujeta a la restricción ∑ni=1 ai = 1. Si usamos multiplicadores de Lagrange, encontraremos que ese máximo se alcanza en cuando todas las ai son iguales, esto es, cuando ai = 1∕n. Aún más, el máximo se alcanza si y solo si ai = 1∕n para todo i = 1,,n. Por tanto, el valor del máximo es ∑ni=1 (1∕n)⋅(1∕n) = 1∕n. Siguiendo con las cuentas anteriores: Esta igualdad significa que la varianza tiende a cero. El polígono regular es el único polígono que tiene esa propiedad, que su varianza es precisamente cero. 3. Conclusiones Y hemos hecho matemáticas divertidas a partir de una excusa musical, el recorrido de la baqueta o la mano que hacen los percusionistas para controlar la dinámica. A partir de ahí, hemos probado de una manera elegante que la sucesión de sombras converge al polígono regular. Y esto es todo. Es incorrecto extraer conclusiones como que los ritmos dados por el polígono regular son importantes o bellos musicalmente. Eso no se sigue de las matemáticas que hemos hecho. De hecho, la división en partes iguales de un compás, como ritmo, es bastante aburrido. Este tipo de excesos se ven con más frecuencia de la deseada en textos sobre matemáticas y música.   Bibliografía [GTT08] F. Gómez, T. Taslakian, and G.T. Toussaint. Convergence of the shadow sequence of inscribed polygons. In Proceedings of the 18th Fall Workshop on Computational Geometry, pages 10–11, Rensselaer Polytechnic Institute, Troy, New York, October 31st 2008. [HZ01] Richard Hitt and Xin-Min Zhang. Dynamic geometry of polygons. Elemente der Mathematik, 56:21–37, 2001. [Rah96] J. Rahn. Turning the analysis around: African-derived rhythms and europe-derived music theory. Black Music Research Journal, 16(1):71–89, 1996. [Sch82] I. J. Schoenberg. Mathematical Time Exposures. Mathematical Association of America, Washington, DC, 1982.

Miércoles, 11 de Abril de 2012 | Imprimir | PDF |  Correo electrónico

97. 34. (Marzo 2012) Minimalismo y matemáticas: Clapping Music

1. Introducción La historia de la música es con frecuencia la historia de las reacciones humanas a la música misma1. Un buen ejemplo de ello se puede observar en el minimalismo. Desde la Segunda Guerra Mundial, el panorama en la música clásica estuvo dominado principalmente por compositores como Boulez, Berio, Cage, Ligete y Stockhausen, entre otros. Estos compositores representan el modernismo de posguerra. Tal modernismo se puede entender bien como postserialismo, siendo Boulez una de sus figuras más prominentes, o bien como el indeterminismo, donde Cage se convierte en una de sus figuras más notables. Aunque el término minimalismo se usó en principio en las artes visuales, más tarde se aplicó a un estilo de música caracterizado por un vocabulario rítmico, melódico y armónico simplificado (véase [15]). En efecto, Timothy Johnson sostiene que el término minimalismo se puede definir de modo más fructífero si se concibe como una técnica en lugar de una estética o un estilo [7]. Los principales representantes del minimalismo son LaMonte Young, Philip Glass, Terry Riley y Steve Reich. Su música e ideas se convirtieron en la mayor reacción al modernismo personificado por los compositores antes mencionados. En efecto, allí donde el modernismo es resueltamente atonal, el minimalismo es claramente modal o tonal; allí donde el modernismo se muestra aperiódico, fragmentario, el minimalismo se caracteriza por una gran regularidad rítmica; y allí donde el modernismo se presenta con una gran complejidad de estructura y de textura, el minimalismo es simplemente transparente. El minimalismo tiene diferentes materializaciones dependiendo del compositor, pero las obras minimalistas comparten una preocupación por la tonalidad no funcional y repetición de frases musicales, frecuentemente pequeños motivos o células que evolucionan gradualmente. Por ejemplo, Young usa notas bordón, al estilo de las isocrátimas, sostenidas durante largos periodos de tiempo, Glass selecciona arpegios de un acorde que se repiten recurrentemente, y Riley y Reich incorporan melodías que se repiten con armonías de pulso rápido. No menos significante es el hecho de que la música minimalista no posea casi ninguna de las características de la música occidental (al menos desde el periodo romántico), esto es, movimiento armónico, modulación tonal, desarrollo temático, texturas complejas o formas musicales con estructuras diseñadas cuidadosamente. Por el contrario, esta música evita cualquier sentido o consciencia de clímax o desarrollo, y parece ignorar la dialéctica de tensión y reposo, al menos tal cual se manifiesta en la música clásica occidental. En palabras de Roger Sutherland [19]2 : “(...) al oyente se le invita, no a seguir un argumento musical complejo, sino a concentrarse en el sonido que cambia lentamente y a centrarse con consciencia microscópica en diferentes aspectos del mismo”. Es probablemente Reich el compositor minimalista que más abiertamente repudio la tradición clásica occidental. Reich se opone a la vez al serialismo europeo y al indeterminismo americano porque en estos dos estilos los procesos por los cuales se construye la música no se pueden oír y discernir claramente por el oyente. Antes que él, el crítico musical Pousseur [13], así como Xenakis [24], había señalado ya que “donde las más abstractas construcciones se emplean... uno tiene la impresión de encontrarse en presencia de las consecuencias de un libre juego aleatorio”. Este rechazo, formulado no solo por Reich, sino por otros compositores minimalistas, bien puede ser la razón por la que la música minimalista ha sido tan incomprensiblemente ignorada por críticos y estudiosos. Algunos estudios hay, más bien recientes; véase [13, 8, 19, 12] y, evidentemente, los ensayos de Reich [16, 17]. En su ensayo Music as a Gradual Process, incluido en [16], Reich establece sus principios como sigue: “Estoy interesado en los procesos perceptibles. Quiero ser capaz de oír el proceso en desarrollo según suena la música”. Para que tales procesos sean accesibles al oyente, estos tienen que fluir de manera extremadamente gradual. El proceso mismo tiene que estar relacionado con la idea de cambio de fase. Primero, dos o tres intérpretes tocan una melodía y después de un tiempo uno de ellos cambia de fase. Al principio del cambio de fase se produce una especie de ondulación en forma de acorde arpegiado; más tarde, según el proceso de cambio de fase continúa, la segunda melodía se encuentra a una distancia de corchea y una nueva melodía entrelazada surge. El proceso continúa hasta que las dos melodías están en fase, en unísono, otra vez. Estas ideas se realizan en muchas de las obras de Reich compuestas entre 1965 y 1973  [11]. Toda esta experimentación empieza con It’s Gonna Rain y Come out (ambas compuestas en 1966), donde usa el cambio de fase con música en cinta; continúa con Piano Phase (1967) y Violin Phase (1967), donde experimenta dentro de un contexto acústico, sin instrumentos eléctricos; y finalmente Reich alcanza el punto de máximo desarrollo con Drumming (1970-71), Clapping Music (1972) y Music for Mallet Instruments, Voices and Organ (1973), donde incorpora cambios graduales de timbre y aumentación rítmica, entre otros recursos musicales. A finales de 1972, abandona los cambios graduales de fase, porque “ya era la hora de algo nuevo” [16]. En la columna de este mes vamos a analizar una pieza emblemática de esta época de Steve Reich: Clapping Music. En [2], Colaninno y sus coautores contemplan la hipótesis de que esta pieza le fuese inspirada a Reich en África. En efecto, en el verano de 1970 Reich viajó a Ghana, donde estudió percusión africana [9]. Aprendió gahu, agdabza y otros estilos musicales, los cuales sin duda influyeron en su música (más tarde llegó a estudiar gamelán). La influencia de la música africana se puede percibir en obras tales como Drumming y Clapping Music, donde el cambio de fase es discreto, pero esa influencia es incluso perceptible en piezas de cambio de fase continuo, como en Phase Patterns, Violin Phase y New York Counterpoint. Sin embargo, en un vídeo reciente, de 2011, Reich explica que la inspiración para la pieza le vino de la música flamenca; en particular, de un espectáculo que vio en un tablao flamenco en Bruselas. El vídeo se puede ver en la siguiente sección. 2. Clapping Music Clapping Music es una pieza de cambio de fase para dos intérpretes que tocan únicamente las palmas. Cada uno de ellos toca el mismo patrón a lo largo de toda la pieza. El cambio de fase es discreto, con un intérprete que empieza el patrón desde un punto distinto, el cual va avanzando después de unas cuantas repeticiones del patrón. El otro intérprete permanece imperturbable tocando el patrón sin cambio alguno. En la figura 7 se ha reproducido la partitura de Clapping Music. Las variaciones que se producen en cada cambio de fase se han numerado en orden ascendente , donde V0 = V12 indica que los dos intérpretes tocan al unísono. Figura 1: La partitura de Clapping Music. Para mejor apreciar y comprender Clapping Music, vamos a comentar unos cuantos vídeos de la obra. En primer lugar, tenemos un vídeo de Steve Reich en la época en que compuso Clapping Music; él mismo es uno de los intérpretes. A continuación, tenemos un vídeo de Reich, más moderno, en que explica los principios compositivos de la obra. Aquí revela el origen de la inspiración, como mencionamos más arriba. El siguiente vídeo muestra una animación gráfica de Clapping Music, que por su excelente visualización hemos querido incluir aquí. Seguimos con otra versión de Clapping Music, esta vez con un solo intérprete sobre dos cajas. Toca cada patrón en una mano y supone un delicado ejercicio de coordinación. Y por último, traemos una original coreografía de Anne Teresa De Keersmaeker sobre la música de Clapping Music bailada por la coreógrafa misma y Michèle Anne De Mey. Es muy interesante ver los movimientos elegidos para recrear el patrón de Clapping Music y cómo el patrón corporal sufre también los cambios de fase. Esta pieza, a pesar de su aparente simplicidad, no esta desposeída de interés musical. En primer lugar, Clapping Music consiste en una síntesis y estilización de las ideas de Reich a través de una pieza con unos pocos elementos muy bien combinados. En segundo lugar, Clapping Music muestra una profunda ambigüedad métrica -algo muy común en las piezas de Reich- así como una gran cantidad de ritmos entrelazados. En el análisis siguiente profundizaremos en estas ideas. 3. Análisis de Clapping Music Cuando uno oye Clapping Music, la pregunta que surge de manera natural es cómo llegó Reich a elegir este patrón. Según el patrón rota, cambia de fase, una serie de ritmos entrelazados emergen, creando una gran variedad rítmica. Aún más, en la pieza hay un gran sentido del equilibrio entre las variaciones resultantes. Una vez que el patrón se define, sin embargo, las reglas aplicadas a esta composición no permiten cambiarlo. Por tanto, el patrón tiene que elegirse con extremo cuidado. A continuación, vamos a analizar unos cuantos aspectos musicales de Clapping Music para entender cómo funciona esta música proceso (música en que el proceso se oye claramente, música en que la elección de un patrón y unas reglas de juego ya determinan la composición entera). 3.1 Análisis musical de Clapping Music Usaremos las etiquetas dadas en la figura 7 para referirnos a las variaciones V0,V1,...,V11,V12 = V0. Clapping Music tiene una estructura global muy definida. En cierto sentido que vamos a explicar enseguida, se tiene que la variación Vi es igual a la variación V12-i, para cualquier i = 0,1,...,12. Véamos por qué. V0 = V12. Esto es trivial por cómo está construida la pieza. V1 = V11. En principio, mirando la partitura al menos, vemos que la variación V1 no es igual a la V11. Sin embargo, cuando se tocan unas cuantas veces seguidas, las percibimos como iguales. Estas dos variaciones no tienen ningún silencio común; están constituidas, por tanto, por un patrón continuo, sin roturas por silencios. Esa falta de reposo, esa ausencia de silencios, confiere una extraordinaria energía y agitación a la variación. Además, la variación V1 es igual a la variación V11, salvo que los intérpretes están intercambiados. Si los dos intérpretes pudieran sacar exactamente el mismo sonido de las palmas, ambas variaciones serían virtualmente indistinguibles. Reich juega de modo fundamental con el timbre en esta pieza como elemento que genera variedad ante otros elementos ausentes (armonía o melodía) u otros que son muy estables (el patrón de la primera voz). Figura 2: Las variaciones V1 y V11. V2 = V10. En la variación V2 encontramos una posición con un silencio común, en la séptima posición. Cuando se oyen las primeras repeticiones de la variación, el oído no comprende la estructura de la variación. Después, percibe el silencio como el final de la variación y en realidad concibe la variación empezando en la posición 8; véase la figura más abajo. Esta variación está formada por una única célula que acaba en un silencio. Las variaciones V2 y V10 son iguales, salvo que las partes de los intérpretes están intercambiadas; de nuevo, el juego del timbre. Además, si miramos la variación desde la posición 8, que es el principio perceptual de la variación, encontramos que la sucesión de notas para la primera voz es 1 - 2 - 3 - 2 y para la segunda 2 - 3 - 2 - 1, esto es, una es la otra leída en sentido contrario. De nuevo, la variación V10 es simétrica de la V2. Figura 3: Las variaciones V2 y V10. V3 = V9. En la variación V3 encontramos dos posiciones con silencios en común, lo que da lugar a dos frases. La variación tiene, pues, una estructura de pregunta-respuesta. La pregunta estaría formada desde la posición 10 hasta la 3 y la respuesta, de la 5 a la 8. La simetría es muy fuerte en esta variación. La primera voz de la pregunta tiene como sucesión de notas a 2 - 3 y la voz de abajo, 3 - 2. La respuesta tiene sucesión 1-2 y 2-1. La variación es V9 es simétrica de V3. Figura 4: Las variaciones V3 y V9. V4 = V8. La variación V4 está constituida por una única frase con un solo silencio en la última posición, en la 12. De nuevo, se produce la simetría en la sucesión de notas: 3 - 2 - 1 - 2 en la voz primera y 2 - 1 - 2 - 3 en la segunda. La variación V8 es la correspondiente simétrica. Figura 5: Las variaciones V4 y V8. V5 = V7. La variación V5 tiene otra vez estructura de pregunta-respuesta. La pregunta empieza en la posición 8 y se extiende hasta la posición 3; la respuesta está compuesta por dos corcheas seguidas que empiezan en la posición 5. Una vez más, tenemos la simetría en la sucesión de notas en la pregunta, 1 - 2 - 3 para la primera voz y 3 - 2 - 1 para la segunda. La respuesta es un unísono de dos corcheas en ambas voces. La variación V7 es la simétrica de V5. Figura 6: Las variaciones V5 y V7. La variación central V6. La variación V6 es muy interesante. Estamos en la mitad exacta de la pieza. Han pasado 6 rotaciones del patrón en la segunda voz. El patrón global resultante es continuo, es decir, no hay ningún silencio que corte este tren rítmico. Existe una simetría en las voces. La primera mitad de la variación es igual a la segunda pero con las voces intercambiadas; véase la figura de abajo. Figura 7: La variación V6. 3.2 Análisis con grafos filogenéticos Los grafos filogenéticos, originalmente una herramienta de la Bioinformática, se han usado para analizar ritmos. En [20] se usaron para estudiar las claves binarias de Brasil, Cuba y África. Una clave es un patrón rítmico que se repite a lo largo de una pieza y que sirve como referencia temporal [10, 23]. También se han empleado para el análisis de los ritmos flamencos [3]. Estos grafos se usan en biología para determinar la proximidad y evolución entre especies. Los biólogos miden el grado de proximidad entre dos especies comparando sus genes. En nuestro contexto, los ritmos desempeñarán el papel de los genes, y emplearemos medidas especialmente diseñadas para ritmos. La cuestión de cómo definir esas medidas ha sido estudiada en varios trabajos [20, 21, 22, 3]. Entre las distancias existentes la más satisfactoria resulta ser la distancia de permutación dirigida [3]. La distancia de permutación dirigida se basa en contar el número mínimo de operaciones para transformar un ritmo dado en otro. Esas operaciones se limitan a intercambios de notas o silencios entre posiciones adyacentes y tienen las siguientes restricciones: Ambos ritmos han de tener el mismo número de pulsos. En nuestro caso todos tienen 12 pulsos. Se convierte el ritmo de más notas, R1, al de menos notas, R2. Cada nota de R1 tiene que moverse a una nota de R2. Cada nota de R2 ha de recibir al menos una nota de R1. Las notas no pueden cruzar el final del ritmo y aparecer por el principio. Por ejemplo, la distancia de permutación dirigida (DPD) entre la primera voz y la segunda en la variación V1 es 4 puesto que hay que realizar cuatro permutaciones en la primera voz en las posiciones 3,6,8 y 11 para convertirla en la voz segunda; véase la figura 8. Así, tendríamos d(V0,V1) = 4. Observando el ejemplo de la figura, tendríamos que d(V0,V2) = 8 y d(V0,V3) = 12 Figura 8: La distancia de permutación dirigida. La matriz de distancias correspondiente a todas las variaciones de Clapping Music se puede ver en la figura 9. Se ha usado notación de caja para las variaciones. Variations V0 V1 V2 V3 V4 V5 V6 V7 V8 V9 V10 V11 V0=xxx.xx.x.xx. 0 V1=xx.xx.x.xx.x 4 0 V2=x.xx.x.xx.xx 8 4 0 V3=.xx.x.xx.xxx 12 8 4 0 V4=xx.x.xx.xxx. 4 2 4 8 0 V5=x.x.xx.xxx.x 8 4 2 4 4 0 V6=.x.xx.xxx.xx 12 8 4 2 8 4 0 V7=x.xx.xxx.xx. 4 4 4 8 2 4 8 0 V8=.xx.xxx.xx.x 8 4 4 4 4 2 4 4 0 V9=xx.xxx.xx.x. 2 4 8 12 4 8 12 4 8 0 V10=x.xxx.xx.x.x 4 2 4 8 4 4 8 2 4 4 0 V11=.xxx.xx.x.xx 8 4 2 4 4 4 4 4 2 8 4 0 ∑ 74 48 48 74 48 48 74 48 48 74 48 48 Figura 9: La matriz de distancias para las variaciones de Clapping Music. En la figura 10 se muestra el grafo filogenético asociado a la matriz de arriba. En este grafo la distancia entre nodos se corresponde exactamente con la distancia en la matriz. Esto permite visualizar más fácilmente propiedades de la distancia -en particular, agrupamientos- que de otro modo en la matriz de distancias no se perciben; véase [6] para obtener más información sobre grafos filogenéticos. En la figura los puntos negros pertenecen a las variaciones.   Figura 10: El grafo filogenético de Clapping Music pattern. El grafo filogenético tiene cuatro grupos distinguibles a simple vista en la figura 10, a saber, C1, C2, C3 y C4. Si los disponemos en orden de aparición en la pieza, resulta la tabla 11: Clusters C1 C2 C3 C4 V0 V1 V2 V3 V4 V5 V6 V7 V8 V9 V10 V11 V12 Figura 11: Agrupación en Clapping Music. A partir de esta sucesión de grupos podemos observar la evolución de las variaciones a través del tiempo según la DPD. Hay una primera sección formada por las variaciones V0 a V3; aquí las variaciones se alejan lo más posible de V0. En la segunda sección, que va de V4 a V6, las variaciones están todavía alejadas de V0. En la tercera sección, las variaciones V7 y V8 se quedan alrededor del centro del grafo, lo que representa un punto de retorno a partir del cual las siguientes variaciones volverán a V0. Las variaciones de la sección cuatro, consistentes en V9, V10 y V11, tienden a V0. Por último, Clapping Music se cierra volviendo al patrón del principio (V0 = V12). 4. Para saber más Richard Cohn [1] fue pionero en el análisis de la música de Reich desde el punto de vista rítmico; véase también [14] para otros enfoques formalistas. Colaninno y sus coautores [2] estudiaron Clapping Music desde el punto de vista de la tensión rítmica y también en comparación con claves africanas. En los trabajos [4, 1, 5, 20] se pueden encontrar análisis de la música de Reich desde un punto de vista maemático.   Notas 1 Esta introducción está inspirada en el artículo [2], del que es coautor este mismo columnista. 2 Todas las traducciones de citas de este artículo son del autor.   Referencias [1] Cohn, R. Transpositional Combination of Beat-Class Sets in Steve Reich’s Phase-Shifting Music. Perspectives of New Music, 30:2:146-176, 1992. [2] Colannino, J., Gómez, F., and Toussaint, G.T. Analysis of Emergent Beat-Class Sets in Steve Reich’s Clapping Music and the Yoruba Bell Timeline. Perspectives of New Music, 47:1:111–134, 2009. [3] Díaz-Báñez, J. M.; Farigu, G.; Gómez, F.; Rappaport, D.; Toussaint, G. T. El Compás Flamenco: A Phylogenetic Analysis. In Proceedings of BRIDGES: Mathematical Connections in Art, Music, and Science, Winfield, Kansas, 61-70, July, 2004. [4] Haack, J. K. Clapping Music – a Combinatorial Problem. The College Mathematical Journal, 22:224-227, May, 1991. [5] Haack, J. K.; ”Mathematics of Steve Reich’s Clapping Music. In Proceedings of BRIDGES: Mathematical Connections in Art, Music and Science, pp. 87-92, Winfield, Kansas, 1998. [6] Huson, D. H. SplitsTree: Analyzing and visualizing evolutionary data. Bioinformatics, 14:68-73, 1998. [7] Johnson, T.A. Minimalism: Aesthetic, Style or Technique? The Music Quarterly, 78:4:742-773, Winter 1994. [8] Mertens, W. American Minimal Music. Kahn and Averill, London, 1983. [9] Nyman, M. Steve Reich. The Musical Times, 112:1537:229–231, March, 1971. [10] Ortiz, F. La Clave. Editorial Letras Cubanas. La Habana, Cuba, 1995. [11] Potter, K. Steve Reich: Thoughts for his 50th-Birthday Year. The Musical Times, 127:1715:13–17, January, 1986. [12] Potter, K. Four Musical Minimalists: LaMonte Young, Terry Riley, Steve Reich and Philip Glass. Cambridge University Press, 2000. [13] Pousseur, H. The Question of Order in the New Music. Perspectives in New Music, volumen 1, 1966. [14] Quinn, I. Minimal Challenges: Process Music and the Uses of Formalist Analysis. Contemporary Music Review, 9:2:283–294, June, 2006. [15] Randel, D. (editor). The New Grove Dictionary of Music and Musicians. Akal, 1986. [16] Reich, S. Writings about Music. The Press of the Nova Scotia College of Art and Design, New York, 1974. [17] Reich, S.; Writings about Music 1965-2000, Oxford University Press, 2002. [18] Roeder, J. Beat-Class Modulation in Steve Reich’s Music. Music Theory Spectrum, 25:2:275–304, Autumn 2003. [19] Sutherland, R. New Perspectives in Music. Sun Tavern Fields, 1994. The quotation cited in the paper also can be found on an on-line paper at http://media.hyperreal.org/zines/est/articles/reich.html [20] Toussaint, G. T. A Mathematical Analysis of African, Brazilian, and Cuban Clave Rhythms. In Proceedings of BRIDGES: Mathematical Connections in Art, Music and Science, pp. 157-168, Towson University, Towson, MD, 2002. [21] Toussaint, G. T. Classification and Phylogenetic Analysis of African Ternary Rhythm Timelines. In Proceedings of BRIDGES: Mathematical Connections in Art, Music and Science, pp. 25-36, Universidad de Granada, Granada, 2003. [22] Toussaint, G.T. A Comparison of Rhythmic Similarity Measures. In Proceedings of the Fifth International Conference on Music Information Retrieval, pages 10-14, Barcelona, Spain, October, 2004. [23] Uribe, E. The Essence of Afro-Cuban Percussion and Drum Set. Warner Bros., Miami, 1996. [24] Xenakis, I. The Crisis in Serial Music. Gravesaner Blatter, No. 1, 1965.

Viernes, 09 de Marzo de 2012 | Imprimir | PDF |  Correo electrónico

98. 33. (Febrero 2012) La belleza en las matemáticas y la música

Leticia, colaboradora de la bitácora ConCIENCIA musical, escribió una breve entrada titulada Música, poesía, danza... ¿matemáticas?, que reza así: “Haberlas... las habrá, no digo yo que no, pero después de ver este vídeo no me habléis de matemáticas, por favor”. El vídeo al que se refiere es este: Al leer la entrada de Leticia me di cuenta de que tenía que tratar -casi diría con cierta urgencia- el asunto de la belleza en la música y en las matemáticas. Debajo del comentario breve, casual, de Leticia subyace una concepción muy común de qué es la belleza, su tipología y en qué campos se encuentra. En estas por fuerza breves notas quiero ahondar en el concepto de belleza y cómo esta se percibe desde las dos ricas áreas que nos ocupan aquí: la música y las matemáticas. Leticia, si no te importa, te trataré de tú. Podemos discutir el tipo de belleza que hay en la música o en las matemáticas, pero no podemos discutir la necesidad de la belleza. ¿Y por qué necesitamos la belleza? Para mí, desde luego, para comprender; no concibo la comprensión no ya artística, sino científica sin la mediación de la belleza. La experiencia estética interior descubre caminos a la comprensión que de otra manera pasarían completamente inadvertidos o a los cuales arribaría dando un largo y penoso rodeo. La experiencia estética es como un fogonazo súbito que nos alumbra senderos ocultos conducentes a tierras ignotas. En realidad, no sabemos que hay al final del camino, pero hace tiempo que comprendimos que es el tránsito por el camino lo importante. -Bien -me dirás, Leticia-, pero ¿qué es la belleza? La belleza se encuentra en multitud de campos del saber y en multitud de estados. Hay belleza en toda construcción que muestre unidad orgánica, coherencia formal, afán de indagación, visión profunda y original y, sobre todo, autenticidad. Y esto lo puedes encontrar en la novena sinfonía de Beethoven o en teoremas de la teoría de números. -Hum... -hace un gesto de incredulidad Leticia. -Veo que no te convenzo. -Hum..., no mucho -Leticia se sincera. Déjame que te hable más a fondo de la belleza en las matemáticas y en la música y, después de ello, examinemos sus puntos comunes (si crees que los tienen, claro). Leticia, escucha, el hombre es poca cosa, muy poquita cosa. Pero mientras vivimos nos es dado ser inmortales. Sí, porque comprender lo que te trasciende te hace, siquiera momentáneamente, inmortal. Aprehender el infinito, lo infinito, es un buen ejemplo de ello. Cuando un niño aprende a contar asocia cada número a un dedo, tú lo sabes mejor que yo. Cuando más tarde alcanza a contar números grandes, se da cuenta de que ni siquiera en el lenguaje existen palabras para cada número. De hecho, más tarde en su formación descubrirá algo perturbado que en realidad no se nombran todos los números porque algunos se usen poco, no, ¡es porque hay infinitos! No podemos tener infinitas palabras. Sí, el infinito: el niño descubre que hay infinitos números porque dado cualquier número, al sumarle 1, nos da un nuevo número, tan legítimo y elegante como el anterior. Y así podemos repetir esto hasta el infinito, que es como decir hasta la eternidad. Comprendemos entonces lo aparentemente inasible. Y aquí hay belleza. ¿He dicho comprendemos? Comprender es otro placer, coincidirás conmigo Leticia, ¿no? Las leyes del pensamiento, el ejercicio del razonamiento, la ordenación lógica en un sistema autocontenido, la confrontación de ese sistema lógico con el mundo real, en todo esto hay también belleza. A través del razonamiento percibimos belleza. Vuelvo a los números, esta vez a los números primos; sí, aquellos que solo son divisibles por sí mismos y la unidad. ¿Cuántos hay? ¿Pocos, muchos o infinitos? Si hay infinitos, ¿cómo contarlos! Los griegos, mediante una bella (← fíjate en este adjetivo) técnica de demostración llamada reducción al absurdo, probaron que los primos eran infinitos en número. El argumento funciona como sigue (atenta, Leticia). Si hubiese solo un número finito de números primos, podría probar el siguiente truco: los multiplico todos y al resultado le añado 1. Este nuevo número, ¿es primo o no es primo? Supongamos que el nuevo número no es primo. Alguno de los números primos originales tendría que dividirlo. Por su construcción, eso es imposible. Por tanto, ha de ser primo. Esto quiere decir que hay infinitos primos, pues este proceso lo puedo repetir siempre ad infinitum. Leticia, escucha, este razonamiento es bello. A veces los matemáticos nos emocionamos ante fórmulas porque encierran tanta verdad, tanta inteligencia, tanto afán de comprensión, tanta abstracción (de algún modo tanta humanidad), porque son capaces de unir mundos de tan dispares universos. Una de mis fórmulas favoritas es la fórmula de Euler: eπi + 1 = 0 Te juro que encierra belleza; no, mal dicho, irradia belleza. Esta fórmula, una vez que la has comprendido, te embriaga. Volviendo a las leyes del pensamiento, las pruebas o demostraciones nos llenan de gozo con frecuencia. Las hay de muchas clases: pruebas directas, por casos, por reducción al absurdo, por contraposición, por construcción, por inducción, etc. A mí me gustan mucho las pruebas por inducción. Se aplican a propiedades que dependen de números naturales. Por ejemplo, la fórmula es cierta, donde n = 1,2,... (Leticia, una fórmula enunciada para infinitos números: ¡de nuevo, el infinito!). Constan de dos pasos: en el primero buscan un número n0 para el cual la propiedad sea cierta; en el segundo pruebas que si la propiedad es cierta para un número natural n, entonces es cierta también para n + 1. Una vez hecho esto, habrás probado la propiedad para cualquier número mayor o igual que n0. ¿No hay algo de inmortalidad en todo esto y, por tanto, de belleza? Vamos a hacer la prueba por inducción de esta última fórmula. ¿Es cierta la fórmula para n = 1? Sí, porque Supongamos que es cierta para n y probemos que es cierta para n + 1 y probemos entonces que es cierta para n + 1: La expresión que ha salido en último lugar, , es la correspondiente fórmula de sustituyendo n por n + 1. Y esto completa la prueba. Leticia, esto es bello. Hay otro tipo de belleza que está íntimamente ligada a la actividad matemática. Me refiero a la belleza que se encuentra al resolver problemas de matemáticas, sobre todo si es un problema abierto. En primer lugar, no sabes muy por qué te prendaste del problema. ¿No es un poco loco todo esto, Leticia? Quizás fue que presentías que la solución de ese problema completaría tu conocimiento del asunto; sí, a veces nos enamoramos de los problemas por afán de completitud. Acaso fuese porque querías probar tus fuerzas intelectuales; eso también ocurre, las ganas de sentirnos vivos por el ejercicio del pensamiento. Sea cual sea la razón el problema está delante de ti, quietecito, modoso, esperando algo indolentemente no sabemos muy bien qué. Al principio, le haces poco caso; le dedicas algún pensamiento suelto aquí y acá. Lo miras con ojos benévolos e indulgentes. Sin embargo, un día te levantas con un extraño nivel de conciencia, a veces acompañado de un aguzamiento de los sentidos, y entonces abordas el problema. En los primeros acercamientos, todo es vano y ridículo. Todas tus hipótesis iniciales son falsas o se aplican a casos muy particulares exentos de interés. Sabes que esto no es comprender todavía. Pero sigues. En esto consiste la mentalidad del matemático: tesón. Miras al problema desde otro punto de vista, imaginas que fuera parte de un objeto mayor, de una estructura superior, y si así fuese, ¿cómo lo entenderías entonces? Avanzas en el mejor de los casos, pero el avance es minúsculo. En el peor caso, das vueltas sobre ti mismo. Y ahora viene lo que llamo la travesía del desierto. Si no te pierdes, la solución está al final del desierto. Pero, Leticia, ¡cuidado!, el desierto está lleno de espejismos. Recuerda que el Sol de tu orgullo te calentará hasta la extenuación. Ahora la convivencia con el problema es constante. Sueñas con él, te acompaña en el pensamiento por doquier, la realidad la ves teñida del color del problema, todo se interpreta en función de él. En ocasiones, desesperas. A veces desearías que ya estuviese resuelto y acabar con esto. Quizás construyas una bonita teoría solo para descubrir al cabo de unos días que era incorrecta. O aún peor, quizás hayas dado con la solución correcta del problema, pero no sabes cómo probarlo. ¿Recuerdas, Leticia, que en matemáticas todo ha de ser probado según las leyes de la lógica y con demostraciones? A lo peor es la prueba lo que se escapa entre los resquicios de la inteligencia. Sí, porque las matemáticas, si se practican con honestidad, te dan la medida de ti mismo. Y eso es una profunda y constante lección de humildad. En cuanto estás una temporada resolviendo problemas sabes inmediatamente cuáles son tus límites. Lo extraordinario de las matemáticas es que te muestran cómo romperlos. Poco a poco vas progresando. Descompones el problema en otro más pequeños, y con tesón y creatividad los vas resolviendo. Empero, notas que falta una idea que unifique todo lo que has descubierto hasta ahora. Un día, probablemente de una manera casual, te llegará la idea. Pero escucha, Leticia, solo te llegará si tu espíritu está abierto. Probablemente, la idea pasó antes delante de ti, pero no la viste, es decir, no la comprendiste, no estabas preparado. La travesía del desierto te prepara para esa comprensión. En efecto, habrás pasado la fase de obsesión por el problema y estarás en la de comprensión lúcida. Y viste la idea feliz. En los primeros momentos te mostrarás incluso incrédula, tanto has fracasado en el pasado. Luego, sonreirás, y también te maldecirás por lo ciega que estuviste. Finalmente, llorarás de alegría. Los matemáticos apreciamos la belleza en las matemáticas según varios criterios. Antes que nada, en los resultados. Resultados bellos en matemáticas hay muchos. Recuerda la fórmula de Euler eπi + 1 = 0, o también el teorema de Pitágoras, o el teorema de Abel-Ruffini, o el teorema fundamental del cálculo, o el algoritmo de Euclides, o el teorema de Fermat... Leticia, podría seguir así a riesgo de emborracharme. En las pruebas se encuentra otra fuente de belleza. Nos gustan las pruebas que usen el menor número de hipótesis; es una especie de austeridad intelectual. Asimismo, nos gustan que sean cortas y concisas, que estén libres de notación farragosa (que es una forma de pedantería); es una preferencia de estilo, digamos. En el vídeo que hay abajo un matemático contemporáneo muy famoso, Michael Atiyah, habla de la belleza de las matemáticas como de la densidad de significado, lo cual es una hermosa forma de resumir lo que acabo de decir. Figura 1: Vídeo de Atiyah hablando sobre la belleza de las matemáticas. Quizás las pruebas que más nos gustan son las inesperadas. Recuerdo una prueba de un resultado geométrico que un colega probó con una ingeniosa demostración probabilística. Al leerla, los ojos se me quedaron en blanco, empecé a tartamudear y finalmente rompí a reír a carcajada limpia. Las pruebas inesperadas lo son por la conexión que establecen entre áreas aparentemente alejadas o por la profunda comprensión del problema. También se aprecian mucho las pruebas que demuestran el resultado en situaciones muy generales (¡ah!, el famoso afán de generalidad de los matemáticos). Y hasta aquí, querida Leticia, la belleza en las matemáticas. Vamos a ver qué pasa en esa actividad misteriosa y vivífica que es la música. La música puede cumplir muchas funciones, entre ellas, entretenimiento, validación social, refuerzo de la sensación de pertenencia al grupo, comunicación, venta de productos, etc. Sin embargo, yo te voy a hablar primero de la música como instrumento de comprensión. Sí, Leticia, otra vez la comprensión asociada a la belleza. Ahora es una comprensión algo distinta a la dada por las matemáticas. Creo que me explicaré mejor si te pongo ejemplos. Te voy a hablar de una obra que a mí me hizo comprender algo tan importante como la necesidad de consuelo del ser humano. Yo era un joven atolondrado e ignorante del mundo, que rondaba los veintipocos años. Un viernes por la noche quedé con unos amigos. Muy probablemente, acabaríamos emborrachándonos en algún garito de la zona de copas donde habíamos acordado encontrarnos; nada fuera de lo normal en la sociedad alienante en que vivimos. Un amigo me pidió que lo acompañase a su piso a coger algo que se le había olvidado. Al entrar, su compañero de piso estaba escuchando El cuarteto para el final de los tiempos, de Olivier Messian. Me quedé petrificado. Era música de una expresividad desbordante, de una verdad musical absoluta. Pero esa música no hablaba de lo placentero, no era música que solo halagase los sentidos. En absoluto. Hablaba del horror de la condición humana, sin ninguna justificación ni ambigüedad, con absoluta desnudez; y al mismo tiempo esa música hablaba aún más elocuentemente de esperanza. Estaba llena de esperanza y consuelo para el ser humano. Despedí a mi compañero de juerga de modo un poco cortante y rogué a su compañero de piso que pusiese el cuarteto desde el principio. Lo escuché con fruición, con vehemencia, absorbiendo cada detalle del argumento musical y emocional. ¿De dónde había salido esa música? Busqué información sobre la obra y me enteré de que había sido compuesta en unas circunstancias terribles, en un campo de concentración durante la Segunda Guerra Mundial. Ese cuarteto me había cambiado la vida al hacerme comprender que existe el horror de lo humano -más de lo que yo habría podido suponer-, que necesitamos consuelo ante ese horror, y que hay esperanza para nuestra condición. Musicalmente, aprendí muchas otras cosas: la teoría rítmica de Messian, su lenguaje armónico, su sistema de modos de transposición limitada, sus procedimientos formales, el tratamiento de la dinámica (llegué a estudiarme al piano algunos movimientos del cuarteto). Sin embargo, lo más importante radicaba en la parte emocional y estética. La música de Messian me había explicado emociones que antes solo comprendía de modo artificial, como resultado de un frío análisis intelectual o como mucho de una lectura histórica. Con este cuarteto había vivido el horror, había vivido la posibilidad del consuelo y había vivido en mi propia piel la esperanza. Fíjate en el último movimiento del cuarteto; lo puedes escuchar en el siguiente vídeo. Figura 2: Último movimiento del Cuarteto para el final de los tiempos, de Messian. Es un movimiento lento, de un gran estatismo, escrito solo para piano y violín. El piano toca la misma figuración rítmica, dos notas, una muy corta y otra larga, y durante gran parte del movimiento se queda en el registro medio. El violín sigue una línea melódica que en esencia está compuesta por una subida hasta un si agudo, seguida de una bajada, todo ello repetidos dos veces, para en último lugar emprender la poderosa subida a un mi sobreagudo tocado con armónicos artificiales. Tomo prestado de la excelente página web [LU] del Conservatorio de Lawrence University un gráfico (figura 3) que muestra la evolución de la línea melódica. Figura 3: Último movimiento del Cuarteto para el final de los tiempos, de Messian. La subida final del violín es acompañada por el piano en el registro sobreagudo, con acordes de séptima en tercera inversión. Tanto el violín como el piano tocan notas muy agudas, con apenas armónicos. Oímos, pues, tonos de gran pureza, limpios, que nos transmiten esa sensación de esperanza, de recogimiento, de ascetismo. Eso es todo lo que vemos en este movimiento. Sobriedad extrema de medios para conseguir máxima expresividad. Sin vivirlo en persona, me pregunto de qué otra forma podría haber comprendido con esa profundidad el horror de la condición humana y la posibilidad de esperanza. Otro aspecto muy importante para mí es el análisis de la obra, análisis que presta atención a aspectos como la perfección formal, la originalidad, la técnica compositiva, el contexto musical e histórico y otros factores. De nuevo, otro ejemplo, Leticia. Seguro que conoces la Rapsodia sobre un tema de Paganini, de Rachmaninov, una obra para piano y orquesta. Hace un tiempo escribí un análisis sobre esa obra. Formalmente, es un tema con variaciones. Para que me comprendas mejor, te transcribo el análisis del tema y las dos primeras variaciones. (...) Como dijimos antes, la Rapsodia consiste en un tema y 24 variaciones. Muy juguetonamente, Rachmaninov no expone el tema en primer lugar, sino que presenta la primera variación antes que el tema. Esta variación la llama precedente. He aquí una descripción de las variaciones. Introducción: Allegro vivace. La introducción tiene como misión crear una gran expectación en el oyente, expectación que se resolverá más adelante cuando aparezca el tema principal. La introducción presenta el tema de Paganini, la-do-si-la-mi, escrito en semicorcheas; lo llamaremos motivo X. Dicho motivo no es más que el acorde de la menor (la-do-mi) en una forma arpegiada. Figura 4: Motivo de la introducción. Aparecen también acordes de séptima sin resolver así como quintas paralelas; todo esto contribuye a la tensión musical. ¿Qué es esto de los acordes sin resolver? Los acordes de séptima tienen intervalos que se consideran disonantes, al menos en el periodo de la práctica común, y es norma que esas disonancias se resuelvan. Rachmaninov hace lo siguiente en su introducción (pínchese en la figura para oír una versión midi): Figura 5: Introducción de la Rapsodia. Es claro que la introducción acumula mucha tensión a causa de esos acordes. Compárese con la siguiente versión en que no aparecen esas séptimas (pínchese en la figura para oír una versión midi). Figura 6: Versión de la introducción sin séptimas. Es, sin duda, una versión mucho más débil, que no crea tanta expectación; no es desde luego la llamada a las armas que produce la versión de Rachamaninov. En cuanto a las quintas paralelas, son voces que están a una distancia de quinta (5 notas) una de otra. Tienen una sonoridad muy peculiar, que era considerada como desagradable desde el Barroco al Romanticismo. Aquí Rachmaninov la usa sin preocupaciones. La introducción termina en el compás 9 con el acorde de séptima de dominante de la, de nuevo con disonancias sin resolver, que nos deja expectantes. Variación I (Precedente): Allegro vivace. Rachmaninov continúa con su duende juguetón y una vez más rompe las expectativas que nos había creado. Tras la tensión, esperábamos la exposición del tema, pero no es así. La variación I no es más que una presentación del esqueleto armónico del tema de Paganini, con entradas más o menos inesperadas de los instrumentos y con muy poco material melódico. Armónicamente, es una alternancia entre la tónica y la dominante, hasta el compás 8, seguida de una caída de quintas que se repite dos veces. Aquí están los acordes de esta variación (pínchese en la figura para oír una versión midi). Figura 7: Acordes del tema de Paganini. De nuevo hay que descubrirse ante el sentido de la tensión musical de Rachmaninov. En la variación 1 no aparecen los acordes anteriores tocados con todas las notas. He mostrado la armonía completa en la figura 7 más bien para referencias futuras, pero Rachmaninov hace tocar a la orquesta solo las notas fundamentales de cada acorde, esto es, la primera, la más grave, de cada acorde. Así, los acordes quedan indefinidos al faltar el resto de las notas. Aparece la nota la, por ejemplo, pero ¿es la del acorde de la mayor, de la menor, de la séptima u otro? Esta variación fue añadida en el último momento a tenor de lo que se deduce del cuaderno de bocetos de Rachmaninov. El compositor la añadió, se cree, para crear una atmósfera más sugerente antes de la introducción del tema. Tema: L’istesso tempo (sin variar el tempo), en la menor. La orquesta toca el tema original de Paganini y el piano la acompaña con un patrón similar al de la variación anterior. El tema consiste en un antecedente de 8 compases, seguido de un consecuente de 16 compases. ¿Qué significan estas dos palabrejas? En música, una frase es una unidad que posee sentido musical completo. En nuestro caso, el tema de Paganini está formado por dos frases, la primera que actúa de antecedente, o de pregunta si queréis, y la segunda, el consecuente, que tiene carácter concluyente; también se le conoce como la respuesta. En la figura 8 tenéis la división en antecedente y consecuente del tema de Paganini. Figura 8: Antecedente y consecuente en el tema de Paganini. El antecedente está armonizado con una alternancia de tónica-dominante (grado I y grado V de la escala). El consecuente sigue la armonización de arriba, compases 9 a 24 de la figura 4, aunque cambia algunos acordes en la cadencia final. ¿Más palabrejas? Tranquilidad, son solo términos técnicos, palabras como otras cualquiera. Una cadencia en una serie de acordes que marcan el final de una frase; sirven para reforzar el sentido conclusivo de la frase. Muy sutilmente el piano enuncia un motivo que, sometido a diversas transformaciones melódicas y rítmicas, aparecerá con mucha frecuencia. Es uno de los motivos melódicos principales de la Rapsodia. Lo llamaremos Y; está formado por una cuarta descendente. Figura 9: Antecedente y consecuente en el tema de Paganini. (...) Leticia, conocer todo estos detalles aumenta el nivel de consciencia de la obra y, en consecuencia, se percibe la belleza derivada de la perfección formal de la obra. Aclaro que la complejidad compositiva no equivale a perfección formal. Eso es rematadamente falso. Recordemos el motivo de la quinta sinfonía de Beethoven: sol-mi♭-mi♭-mi♭; más simple, imposible. Llegados a este punto nos preguntamos, Leticia, que si ambas son bellas, ¿qué diferencia a la música y a las matemáticas? Para mí, tienen mucho en común, pero una gran diferencia es el tratamiento del tiempo. La potencia emocional de la música está fuertemente asociada a una periodo fijo de tiempo. En el corto tiempo que dura la escucha musical, todo se transforma. Nuestros sentidos se ponen a prueba, se crean conexiones emocionales antes desconocidas, la sensibilidad se aventura por tierras ignotas y de resultas la comprensión vital se ensancha. Hay una gran densidad de significado comprimido en un corto espacio de tiempo. En cuanto a la densidad, matemáticas y música son muy parejas. Los objetos matemáticos son también densos en significados, pero no tienen las ataduras temporales de la música. Un problema de matemáticas nos puede acompañar a todas partes durante las veinticuatro horas del día: La música tiene su clímax durante la escucha; fuera de ella, su intensidad mengua, pues falta la estimulación sensorial. Leticia, ha sido un placer charlar contigo sobre la belleza, sea matemática o musical. Gracias. PARA SABER MÁS Para informarse sobre aspectos cognitivos de la música de una manera divulgativa recomiendo el libro Musicofilia, de Oliver Sack [Sac09]. Para aquellos que quieran profundizar de verdad está el libro Psychological Foundations of Musical Behaviors [RB03]. Para ahondar en los aspectos sociales y antropológicos de la música, recomiendo el libro clásico de Merriam [Me64]. En la sección Mis conciertos de mi página web se encuentran análisis de obras clásicas. La demostración de un resultado siempre viene después de su concepción siquiera sea intuitiva. A veces hay demostraciones visuales que muestran, a veces de modo inesperado, resultados que normalmente se prueban con árida manipulación algebraica. En la página Proofs without words [Wik-a] hay unas cuantas. Este tipo de pruebas se encuentran también en el campo de la matemagia. El famoso libro de Imre Lakatos Proofs and refutations [Lak76] es una buena referencia para entender qué es el arte de las prueba matemática. Para estudiar la estética de la música el libro de Scruton [Scr-97] es muy riguroso y completo. Una divertidísima historia de la crítica musical es el Lexicon of musical invective, de Slonimsky [Slo-00]. En ese libro relata las críticas feroces y se aprecia lo subjetivo que es el concepto de belleza, tan sujeto a modas, a tirrias personales, a prejuicios. Bibliografía [Gom11] Página web de Paco Gómez. Rapsodia sobre un tema de Paganini,, de Rachmaninov. Sección Mis conciertos. Mayo de 2010. [Lak76] Lakatos, I. Proofs and refutations. Cambridge University Press. 1976. [LU] Lawrence University, Conservatory of Music. Quatour por la find de temps, de Olivier Messian. Consultado en enero de 2012. [Me64] Merriam, A.P. The anthropology of music. Northwestern University Press. 1964. [Sac09] Sack, O. Musicofilia. Anagrama. 2009. [RB03] R. E. Radocy and D. J. Boyle. Psychological Foundations of Musical Behaviors. Charles C. Thomas. 2003. [Scr-97] Scruton, R. The Aesthetics of Music. Oxford University Press. 1997. [Slo-00] Slonimsky, N. Lexicon of musical invective. Norton and Company. 2000. [Wik-a] Wikipedia. Proof without words. Consultado en enero de 2012.

Viernes, 17 de Febrero de 2012 | Imprimir | PDF |  Correo electrónico

99. 32. (Enero 2012) Curiosidades y misceláneas

En este primer artículo del año vamos a recopilar material que puede ser interesante para el aficionado a las matemáticas y a la música (tenía que poner esa y en cursiva). Parte de ese material tiene un evidente sentido humorístico y otra parte es más serio. Con frecuencia, cuando le preguntas a alguien cuál es la relación entre matemáticas y música te encuentras con que te canta una canción cuya letra es un enunciado matemático. Bueno, es cierto, hay una tradición de entender la relación entre las matemáticas y la música de esta manera. Aquí van unos cuantos vídeos al respecto (la mayor parte sacados de la divertida e instructiva página Division by Zero): Este primer vídeo es una canción muy graciosa sobre los grupos finitos simples de orden 2: Grupos finitos simples de orden 2. En el siguiente vídeo tenemos una parodia de I will survive, de Gloria Gaynor, ahora transformada en I will derive: I will derive Ahora nos encontramos con el típico cantante de voz vaga, sin mucha proyección, un poco en plan canción protesta, narrando las dificultades que se encontraron los matemáticos con la irracionalidad del número pi. ¿Adivina el lector de quién tomó la música? Basta esperar al estribillo: Mathematical Pi Miramos a continuación al género del rap, donde también se encuentran canciones que glosan las bondades de las matemáticas: Rhythm of Structure: The Math Graffiti Wall En español y con mucha conciencia, Tote-King, un grupo de rap, enumera reflexiones, una tras otra: Tote-King: Matemáticas. Para acabar esta sección, no podíamos dejar sin mencionar el famoso teorema de Tales de Les Luthier: Les Luthier: El teorema de Tales. Pero aún más sorpresas para el audaz lector: rock matemático. Sí, ha leído bien el amable lector. Se trata de una tendencia rock que usa compases irregulares -como 7/8, 11/8 y similares-, disonancias más atrevidas y preocupación por el uso de las texturas. Ciertamente, llamarlo rock matemático por el uso de esos compases es un poco exagerado, pero nada se puede hacer ya al respecto. El caso es que las percusiones de estos grupos son más interesantes que la de los grupos de rock clásicos, donde el uso de los compases binarios llega a resultar cansino. Para más información, véase la entrada de la Wikipedia Math Rock. Del rock matemático se pasó al metal matemático. Sí, ello es posible. Si el lector está interesado en adquirir una visión de conjunto de los géneros del metal, recomiendo que vaya a Map of Metal, página que los contiene todos, con información muy completa, tanto histórica como musical, y que permite escucharlos según se pasea uno por el mapa de los géneros. En la figura de abajo, hemos sacado un pantallazo de la parte del mathcore. Detalle del mathcore del mapa del metal. En el vídeo de abajo, tenemos un ejemplo de este metal matemático, del grupo The Dillinger Escape Plan, el tema 43% Burnt sacado en el album con el elocuente título Calculating Infinity (pincha en la imagen para ver el vídeo): The Dillinger Escape Plan - 43% Burnt Otro enfoque interesante, en la misma línea de cantar las matemáticas pero con propósitos didáctics, es la de Educational Rap, un sitio web que ofrece canciones rap para enseñar una gran variedad de materias, las duras matemáticas entre ellos. En el apartado de música, tienen un album con pistas que versan sobre gráficas de funciones, números negativos, fracciones, superficies, el sistema métrico decimal y otros temas. Siguiendo este enfoque, la página Songs for Teaching tiene un amplio repertorio de canciones, muy bien compuestas y grabadas, para enseñar numerosos conceptos matemáticos, principalmente para educación primaria. Los conceptos van desde los números en educación infantil hasta media, moda y mediana que se ven en sexto de primaria. Las canciones forman parte del material pedagógico que ofrecen y por el cual hay que pagar. En español, quitando las canciones populares que incluyen números (la famosa Un elefante se balanceaba...), no he encontrado referencias que ofrezcan canciones en la línea de Songs for Teaching. A veces, cuando un conocido se entera de que mi labor investigadora versa sobre las matemáticas y la música, me dicen cosas peregrinas, que me llevan a preguntarme qué idea tienen de ambas disciplinas. He oído cosas como:"están muy relacionadas, ¿no? Al principio de cada pieza hay una fracción", o también "en ambas materias se cuenta", o "¿qué es la música sino duración?, ¿y las matemáticas?: pues lo mismo. ¿no?". Huelga decir que las cejas se me fruncen de sorpresa. La relación entre las matemáticas y la música no se reduce al símil entre la disciplina métrica de la música y el rigor lógico de las matemáticas, o a que ambas inspiran belleza. Hay otros muchos aspectos, que pasan desapercibidos al observador ocasional, que unen a las matemáticas y a la música, como pueden ser las estructuras matemáticas que se encuentran en la música o el nivel de abstracción que comparten. Para ahondar en esa relación y hacerlo de manera gozosa y relevante, vamos a recomendar al lector un libro. La mayor parte de los libros sobre matemáticas y música se quedan en la descripción física del sonido, en la afinación pitagórica y como mucho mencionan la sucesión de Fibonacci. Como digo, hay mucha más matemática detrás de la música. Una referencia inmejorable es el libro de David Benson Music: a Mathematical Offering. Music: a Mathematical Offering, de David Benson. Este libro creció a partir de unos apuntes de un curso que Benson empezó a impartir hace algunos años y se ha convertido ya en un clásico, por la exposición, clara y concisa, y por el material que cubre. Para que el lector aprecie el libro en su justa medida mostramos más abajo el índice (en inglés). Puede verse que aborda, sí, los clásicos fundamentos físicos, pero también cuestiones de forma (capítulo 9), de afinación incluyendo temperamentos modernos (capítulos 5 y 6), organología (capítulo 3), etc. No menos meritoria es la cantidad y la calidad de las referencias que se encuentra en el libro. Y hasta aquí ha sido el artículo de este mes. Se pueden cantar las matemáticas y eso las relaciona con la música -al menos, en su práctica-, pero si lees el libro de Benson, entonces esa relación se hace más profunda y patente. REFERENCIAS David Benson. Music: A mathematical offering. Existe una versión impresa publicada por Cambridge University Press en 2006. ISBN: 0521853877 Division by Zero. Página web con puzzles, recursos académicos y tecnología aplicada a la enseñanza. Educational Rap. Página web con canciones rap para aprender diversos conceptos matemáticos. Música y matemáticas. Web creada bajo la dirección de Rafael Losada. Map of metal. Página web donde se muestran los géneros del metal. Wikipedia. Artículo Math Rock. Artículo consultado en diciembre de 2011. Songs for Teaching. Página con material para enseñar conceptos matemáticos a través de canciones.     Índice (versión en línea): 1. Waves and harmonics 1.1 What is sound? 1.2 The human ear 1.3 Limitations of the ear 1.4 Why sine waves? 1.5 Harmonic motion 1.6 Vibrating strings 1.7 Sine waves and frequency spectrum 1.8 Trigonometric identities and beats 1.9 Superposition 1.10 Damped harmonic motion 1.11 Resonance 2. Fourier theory 2.1 Introduction 2.2 Fourier coefficients 2.3 Even and odd functions 2.4 Conditions for convergence 2.5 The Gibbs phenomenon 2.6 Complex coefficients 2.7 Proof of Fejér's theorem 2.8 Bessel functions 2.9 Properties of Bessel functions 2.10 Bessel's equation and power series 2.11 Fourier series for FM synthesis and planetary motion 2.12 Pulse streams 2.13 The Fourier transform 2.14 Proof of the inversion formula 2.15 Spectrum 2.16 The Poisson summation formula 2.17 The Dirac delta function 2.18 Convolution 2.19 Cepstrum 2.20 The Hilbert transform and instantaneous frequency 2.21 Wavelets 3. A mathematician's guide to the orchestra 3.1 Introduction 3.2 The wave equation for strings 3.3 Initial conditions 3.4 The bowed string 3.5 Wind instruments 3.6 The drum 3.7 Eigenvalues of the Laplace operator 3.8 The horn 3.9 Xylophones and tubular bells 3.10 The mbira 3.11 The gong 3.12 The bell 3.13 Acoustics 4. Consonance and dissonance 4.1 Harmonics 4.2 Simple integer ratios 4.3 Historical explanations of consonance 4.4 Critical bandwidth 4.5 Complex tones 4.6 Artificial spectra 4.7 Combination tones 4.8 Musical paradoxes 5. Scales and temperaments: the fivefold way 5.1 Introduction 5.2 Pythagorean scale 5.3 The cycle of fifths 5.4 Cents 5.5 Just intonation 5.6 Major and minor 5.7 The dominant seventh 5.8 Commas and schismas 5.9 Eitz's notation 5.10 Examples of just scales 5.11 Classical harmony 5.12 Meantone scale 5.13 Irregular temparaments 5.14 Equal temperament 5.15 Historical remarks 6. More scales and temperaments 6.1 Harry Partch's 43 tone and other super just scales 6.2 Continued fractions 6.3 Fifty-three tone scale 6.4 Other equal tempered scales 6.5 Thirty-one tone scale 6.6 The scales of Wendy Carlos 6.7 The Bohlen-Pierce scale 6.8 Unison vectors and periodicity blocks 6.9 Septimal harmony 7. Digital music 7.1 Digital signals 7.2 Dithering 7.3 WAV and MP3 files 7.4 MIDI 7.5 Delta functions and sampling 7.6 Nyquist's theorem 7.7 The z-transform 7.8 Digital filters 7.9 The discrete Fourier transform 7.10 The fast Fourier transform 8. Synthesis 8.1 Introduction 8.2 Envelopes and LFOs 8.3 Additive synthesis 8.4 Physical modeling 8.5 The Karplus-Strong algorithm 8.6 Filter analysis for the Karplus-Strong algorithm 8.7 Amplitude and frequency modulation 8.8 The Yamaha DX7 and FM synthesis 8.9 Feedback, or self-modulation 8.10 CSound 8.11 FM synthesis using CSound 8.12 Simple FM instruments 8.13 Further techniques in CSound 8.14 Other methods of synthesis 8.15 The phase vocoder 8.16 Chebychev polynomials 9. Symmetry in music 9.1 Symmetries 9.2 The harp of the Nzakara 9.3 Sets and groups 9.4 Change ringing 9.5 Cayley's theorem 9.6 Clock arithmetic and octave equivalence 9.7 Generators 9.8 Tone rows 9.9 Cartesian products 9.10 Dihedral groups 9.11 Normal subgroups and quotients 9.12 Orbits and cosets 9.13 Burnside's lemma 9.14 Pitch class sets 9.15 Pólya's enumeration theorem 9.16 The Mathieu group M12 Appendices Appendix A: Answers to Almost All Exercices Appendix B: Bessel functions Appendix C: Complex numbers Appendix D: Dictionary Appendix E: Equal tempered scales Appendix F: Frequency and MIDI chart Appendix G: Getting stuff from the internet Appendix I: Intervals Appendix J: Just, equal and meantone scales compared Appendix L: Logarithms Appendix M: Music theory Appendix O: Online papers Appendix P: Partial derivatives Appendix R: Recordings Appendix W: The wave equation Green's identities Gauss' formula Green's functions Hilbert space The Fredholm alternative Solving Laplace's equation Conservation of energy Uniqueness of solutions Eigenvalues are nonnegative and real Orthogonality Inverting the Laplace operator Compact operators The inverse of the Laplace operator is compact Eigenvalue stripping Solving the wave equation Polyhedra and finite groups An example Bibliography Index

Lunes, 02 de Enero de 2012 | Imprimir | PDF |  Correo electrónico

100. 31. (Diciembre 2011) Medidas matemáticas de síncopa (III)

Esta es la última entrega de la serie de tres artículos sobre la medida matemática de síncopa. En el primer artículo estudiamos el fenómeno de la síncopa desde el punto de vista puramente musical; en el segundo, revisamos las principales medidas matemáticas de síncopa y propusimos la nuestra propia; y en este artículo comparamos la efectividad de varias medidas sobre ritmos de clave tomados de tradiciones de música étnica. 1. Medición de la síncopas en ritmos En esta sección examinamos y comparamos las medidas de síncopa introducidas en los dos artículos anteriores probándolas con varios ritmos. Ciertamente, parece difícil seleccionar una familia de ritmos que uno pudiese calificar como representativa para semejante tarea. Una primera idea sería seleccionar ritmos que formen parte esencial de un género musical. En la llamada música étnica o música del mundo se pueden encontrar abundantes ejemplos de esto. En [3, 4], Toussaint recoge los principales ritmos de clave (o simplemente claves) de las tradiciones africana, cubana y brasileña, y lleva a cabo un estudio rítmico de dichas claves. En estas tradiciones hay un ritmo, que con frecuencia se toca en una campana de metal o en un par de claves de madera o en una caja china, y que se mantiene a lo largo de toda la pieza y cuyas funciones incluyen la estabilización rítmica y la organización del fraseo [2, 5]; este ritmo se llama de clave. En música clásica, el concepto más cercano al de clave es el de ostinato, como podemos apreciar, por ejemplo, en Purcell (Dido y Aeneas), Marin Marais (Sonnerie de Sainte Geneviève du Mont de Paris), Beethoven (la sonata para piano La tempestad opus 31, no 2), Ravel (Bolero), Holst (Marte en los Los planetas) y otros muchos casos. Las claves se pueden dividir en dos grupos atendiendo a su estructura métrica: claves binarias y ternarias, que se estudiarán separadamente. Ya que las claves se tocan en campanas o en claves de madera, que dan lugar a ataques más bien que a notas sostenidas, la medida de Keith se ha calculado teniendo en cuenta simplemente si D divide a S para determinar si una nota está a contratiempo o no; véase el anterior artículo de esta serie. 1.1. Ritmos binarios Las seis claves binarias fundamentales son: shiko, son, rumba, soukous, bossa-nova y gahu. Refiérase el lector a [3] y a la bibliografía contenida en ese artículo para una completa información sobre ritmos de clave. En la figura 1 podemos ver que la partitura musical y las correspondientes medidas de síncopa calculadas con la medida de Keith, el índice de contratiempo y la medida DPNP. Ritmos Partitura Medida de Keith Índice contratiempo ∑ xD(x) DPNP Clásico-1 0 3 18 18/10 = 1’8 Clásico-2 3 3 12 12/7 = 1’71 Shiko 1 0 6 6/5 = 1’2 Son 2 1 14 14/5 = 2’8 Rumba 2 2 18 18/5 = 3’6 Soukous 3 2 18 18/5 = 3’6 Gahu 3 1 18 18/5 = 3’6 Bossa-Nova 3 2 20 20/5 = 4 Figura 1: Ritmos binarios. Claramente, shiko es la menos sincopada; la clave son es más sincopada que la shiko, y la rumba más sincopada que la son. Sin embargo, no está claro qué ritmo entre la rumba, el soukous y el gahu es el más sincopado. Bossa-nova es ciertamente la más sincopada. En general, las tres medidas apoyan estas conclusiones, aunque hay algunas divergencias que nos permiten extraer conclusiones interesantes acerca de su utilidad. La medida de Keith en la mayoría de los casos devuelve valores razonables para la medida de la síncopa, aunque no entra en detalles sutiles. Por ejemplo, la bossa-nova se siente más sincopada que cualquier otro ritmo, pero la medida de Keith le asigna los mismos valores que al soukous y el gahu. Sorprendentemente también, asigna la misma cantidad de síncopa a la rumba y el son. Es algo extraño que esta medida devuelva un valor de 3 para el motivo rítmico clásico-2, poniéndolo al mismo nivel que la bossa-nova o el gahu. El índice de contratiempo parece estar más cerca de la percepción humana de la síncopa que la medida de Keith, aunque también da lugar a conclusiones dignas de debate. Por ejemplo, gahu recibe valor 1, pero se siente más sincopado que el son, que también tiene valor 1. Es desconcertante que los dos motivos clásicos obtengan una puntuación mayor que cualquiera de las restantes claves, incluida la bossa-nova. La medida DPNP sugiere conclusiones razonables y en general muestra una mayor coincidencia con la percepción humana de la síncopa. La bossa-nova alcanza la mayor puntuación en el grupo. La medida pone a la rumba, el soukous y el gahu en la misma categoría. En un nivel inferior, encontramos al son, y debajo de este, el shiko, el ritmo menos sincopado; véase la figura 3. Nótese que sin la corrección del número de notas un ritmo con tan poco nivel de síncopa como el motivo rítmico clásico-1 obtendría una puntuación tan alta como la clave gahu, que es mucho más sincopada. Véase la columna que contiene la suma ∑ xD(x) en la figura 1. Volvamos al delicado asunto de elegir los pesos para la medida DPNP. En la definición de of D(x), cuando una nota x cruza una parte fuerte y termina antes de la siguiente parte fuerte, entonces la distancia es  . ¿Por qué ? Podría ser o , por ejemplo. De manera general, supongamos que la distancia D(x) en el caso descrito está dada por , donde a es un peso arbitrario con a > 1. Entonces, la tabla de la figura 2 contiene la clasificación de las claves binarias en función de a. Rhythms Weights Shiko 2a + 2 Son 6a + 2 Soukous 6a + 6 Gahu 8a + 2 Rumba 8a + 2 Boss-Nova 8a + 4 Figura 2: Pesos para las claves binarias Figura 3: Ordenación de las claves binarias según a. Considérese el grafo que se muestra en la figura 3. Ahí cada nivel designa una medida de síncopa. No importa qué valores de a,a > 1, se elijan, el orden se preservará, excepto por soukous. Unas pocas operaciones algebraicas con desigualdades muestran enseguida que esta afirmación es cierta. Con respecto al soukous, si 1 < a < 2, entonces soukous sería más sincopado que el gahu y la rumba (esta situación se muestra en la figura 3 con la línea a puntos); si a = 2, entonces los tres serían igualmente sincopados; finalmente, si a > 2, entonces soukous sale como el menos sincopado (véase la otra línea de puntos en la figura  3). 1.2. Ritmos ternarios En el artículo anterior introdujimos las diez claves fundamentales son: soli, tambú, bembé, bembé-2, yoruba, tonada, asaadua, sorsonet, bemba y ashanti. Véase [4] y sus referencias para una descripción completa de estos ritmos. Las partituras y los correspondientes valores del índice de contratiempo y de la medida DPNP se muestran en la figura 4. Ritmos Partitura Índice de ∑ xD(x) DPNP contratiempo Clasico-1 2 12 12/8=1’5 Clasico-2 2 12 12/8=1’5 Soli 1 15 15/7=2’142 Tambú 2 15 15/7=2’142 Bembé 3 21 21/7=3 Bembé-2 2 15 15/7=2’142 Yoruba 2 21 21/7=3 Tonada 1 15 15/7=2’142 Asaadua 1 15 15/7=2’142 Sorsonet 1 21 21/7=3 Bemba 2 15 15/7=2’142 Ashanti 2 21 21/7=3 Figura 4: Ritmos ternarios. De nuevo, ambas medidas parecen tener sentido de manera global para estos ritmos. En el caso del índice de contratiempo solo el bembé obtiene la máxima puntuación, mientras que la medida DPNP tiene al bembé, al yoruba, al sorsonet y al ashanti como los ritmos más sincopados. Los diez ritmos de clave pertenecen a tres collares (patrones) canónicos distintos [1, 4]. El patrón canónico I corresponde al sorsonet solo; el patrón canónico II genera soli, tonada y asaadua; el patrón canónico III incluye el bembé, el bembé-2, el tambú, la tonada, el yoruba, la bemba y el ashanti. El índice de contratiempo clasifica los ritmos originados por los patrones canónicos I y II como los menos sincopados. Todos los ritmos de clave generados por el patrón canónico III, excepto el bembé, cuyo índice de contratiempo es el más alto, irían en segundo lugar. La medida DPNP agrupa los ritmos de diferente manera. El grupo con el mayor valor está constituido por el bembé, el yoruba, el ashanti y el sorsonet; en el siguiente grupo encontramos el tambú, el bembé-2, la bemba, el soli, la tonada y la asaadua. Esto último grupo comprende todos los ritmos del patrón canónico II más el tambú, el bembé-2 y la bemba. La pregunta que surge de modo natural es cómo construye la medida DPNP esta clasificación. Observemos que todos los ritmos en el grupo menos sincopados tienen tres notas en parte fuerte y solo una nota que cruza la parte fuerte restante. Por el contrario, los ritmos más sincopados tienen dos notas en parte fuerte y otras dos notas que cruzan una parte fuerte. Sin embargo, el índice de contratiempo no detecta esta situación y lleva al tambú, al bembé-2 y a la bemba del grupo menos sincopado al más sincopado. Por el contrario, el índice de contratiempo lleva el sorsonet, que es considerado por la medida DPNP como sincopado, al grupo menos sincopado. La comparación entre los ritmos de clave y mótivos rítmicos de la música clásica produce resultados más consistentes que en el caso de las claves binarias (véase la columna que contiene la suma ∑ xD(x) en la figura 4). El índice de contratiempo considera los dos motivos tan sincopados como el yoruba o el ashanti, pero esto parece erróneo. La medida DPNP detecta correctamente que son menos sincopados que los ritmos de clave. Los pesos en la medida DPNP no tiene influencia en el orden relativo de los ritmos ternarios, porque todas las medidas son de la forma 3a + ci, donde ci es una constante aditiva para el ritmo i. 2. Conclusiones finales Vamos a extraer conclusiones de los resultados empíricos obtenidos en la sección anterior; empezaremos por los puntos débiles de cada medida. Los mayores inconvenientes de la medida de Keith son: (1) No se puede medir ritmos cuyas métricas no tengan un número de notas que no sea una potencia de 2; (2) No se puede usar para medir ritmos irregulares; (3) La elección de los pesos es subjetiva; (4) Muestra una coincidencia limitada con la percepción humana de la síncopa. Con respecto al índice de contratiempo, encontramos los siguientes inconvenientes: (1) Es limitada en su aplicación, ya que para métricas con un número primo de notas todas las notas están a contratiempo; (2) No se puede usar para medir ritmos irregulares; (3) No mide la síncopa en toda su generalidad. Por ejemplo, en un compás de 12/8, las posiciones a contratiempo son 1,5,7,11. Sin embargo, un ritmo puede ser muy sincopado sin tener notas en esas posiciones; (4) Es independiente del número de notas. Por ejemplo, el bembé y [x x . . . x . x . . . x] tienen contratiempo 3, pero un número diferente de notas; (5) Aunque muestra más coincidencia con la percepción humana de la síncopa que la medida de Keith, esa coincidencia es todavía limitada. El único inconveniente que la medida DPNP parece tener es la ambigüedad en la elección de los pesos. Sin embargo, la elección de los pesos no parece tener un efecto en los resultados finales tan dramático como en el caso de la medida de Keith. Un algoritmo mejor para elegir los pesos sería altamente deseable. Finalmente, concluimos que la medida DPNP tiene mayor coincidencia con la percepción humana de la síncopas que el resto de las medidas y también un mayor grado de aplicación. Cerramos este artículo con unos cuantos problemas abiertos. Sería interesante generalizar la medida de Keith de manera que admitiese métricas más generales. Otra dirección de investigación sería la generalización del índice de contratiempo para que contemplase satisfactoriamente el caso de los números primos. Con respecto a la medida DPNP, nos gustaría obtener resultados empíricos adicionales -quizás en forma de experimentos con sujetos- de manera que los pesos se obtuviesen de manera más precisa. Agradecimientos Los resultados de este artículo se obtuvieron en el Second International Workshop on Computational Music Theory organizado por el Departamento de Matemática Aplicada en la Escuela Universitaria de Informática de la Universidad Politécnica de Madrid en junio de 2004. Nos gustaría dar las gracias a Giovanna Farigu y Shima Kobayashi por sus clarividentes discusiones sobre el problema de la síncopa. Bibliografía [1] Keith, M.; From Polychords to Pólya: Adventures in Music Combinatorics, Vinculum Press, Princeton, 1991. [2] Ortiz, F.; La Clave, Editorial Letras Cubanas, La Habana, Cuba, 1995. [3] Toussaint, G. T.; A Mathematical Analysis of African, Brazilian, and Cuban Clave Rhythms, Proceedings of BRIDGES: Mathematical Connections in Art, Music and Science, pp. 157-168, Towson University, Towson, MD, 2002. [4] Toussaint, G. T.; Classification and Phylogenetic Analysis of African Ternary Rhythm Timelines, Proceedings of BRIDGES: Mathematical Connections in Art, Music and Science, pp. 25-36, Universidad de Granada, Granada, 2003. [5] Uribe, E.; The Essence of Afro-Cuban Percussion and Drum Set, Warner Bros., Miami, 1996.

Viernes, 02 de Diciembre de 2011 | Imprimir | PDF |  Correo electrónico